Bayesian variable selection using Knockoffs with applications to genomics

Abstract

Given the costliness of HIV drug therapy research, it is important not only to maximize true positive rate (TPR) by identifying which genetic markers are related to drug resistance, but also to minimize false discovery rate (FDR) by reducing the number of incorrect markers unrelated to drug resistance. In this study, we propose a multiple testing procedure that unifies key concepts in computational statistics, namely Model-free Knockoffs, Bayesian variable selection, and the local false discovery rate. We develop an algorithm that utilizes the augmented data-Knockoff matrix and implement Bayesian Lasso. We then identify signals using test statistics based on Markov Chain Monte Carlo outputs and local false discovery rate. We test our proposed methods against non-bayesian methods such as Benjamini–Hochberg (BHq) and Lasso regression in terms TPR and FDR. Using numerical studies, we show the proposed method yields lower FDR compared to BHq and Lasso for certain cases, such as for low and equi-dimensional cases. We also discuss an application to an HIV-1 data set, which aims to be applied analyzing genetic markers linked to drug resistant HIV in the Philippines in future work.

Introduction

Through the continued development of modern computing technology, it has become easier to store, synthesize, and extract insights from large-scale data. A major focus of these developments is on variable selection, which deals with identifying a subset of characteristics, features, or covariates that are important in describing a certain observed phenomenon. For instance, regression has been a go-to technique in many fields to determine significant features from a diverse set of variables. Several methods have been developed over the years for specialized purposes such as high dimensional and sparse data, among which are Bayesian statistical methods (Guan and Stephens 2011; Sindhu et al. 2017, 2019). The main objective of these techniques is to increase the accuracy of variable selection using a novel Bayesian technique, eventually gaining more insights about the outcome of interest.

This development is particularly evident in genomics, which is the field of study concerned with the structure, function, evolution, and mapping of genomes—the genetic material that describes an organism (McKusick and Ruddle 1987). Advancements in the discovery of genetic markers for various applications such as studying genetic variabilities, species identification, and medical applications have flourished over the past decade. Moreover, the detection of significant single-nuceotide polymorphisms (SNPs), which are genetic variations in DNA, have paved the way for specialized drug delivery through detecting genetic markers that point to drug resistance (Metzner 2016). Recently, it is typical to observe thousands or millions of covariates in genome-wide association studies (GWAS). In the typical GWAS, a large number of genetic markers such as SNPs are measured from thousands of individuals where the primary goal is to identify which parts of the genome harbor markers that affect some physical characteristics, such as drug resistance (Guan and Stephens 2011).

One particular important application of genomics is the study of the global Human Immunodeficiency Virus (HIV) pandemic. Researchers agree that understanding the virus’ genetic sequence is key in developing both vaccines and treatments for those affected. Yet, one problem that arises in developing treatments is HIV drug resistance, which happens when false positive genetic markers are incorrectly detected as significant contributors to drug resistance. This is especially risky due to possible complications and side effects from taking the wrong HIV drug. For example, if identified genomic traits in individuals falsely lead to determining resistance to a certain drug, then a wrong drug may be administered, leading to various side effects. Also, given the wrong drug, patients may have to take larger doses to compensate for the resistance (Jaymalin 2018). Meanwhile, undetected drug resistance may lead to an increase in viral load in the hosts body, severely weakening the immune system, potentially leading to full blown Acquired Immunodeficiency Syndrome (AIDS) (Nasir et al. 2017; Kuritzkes 2011; National Institutes of Health 2020).

The study is motivated by the growing HIV problem in the Philippines. It is one of the few countries in the world where the HIV infection rate is accelerating (World Health Organization 2018), while also experiencing rising Drug resistant HIV. Unfortunately, testing for drug resistance is not part of the routine due to unavailability of testing kits or expenses involved (Jaymalin 2018). With the understanding that the country has limited access to both testing and a wide range of anti-retroviral drugs, the University of the Philippines National Institutes of Health (UP NIH) is working on developing a cheap and accessible diagnostic kit for HIV drug resistance testing (Macan 2019). The authors aim to develop a methodology for the analysis of genetic markers linked to drug resistant HIV in the Philippines, once the diagnostic kit is made publicly available and mass testing allows for the collection of data.

All-in-all, this study aims to propose a method to detect true signals from nulls while ensuring false discovery control. We bridge the concepts in computational statistics, namely false discovery control (Efron et al. 2001) and Bayesian Lasso Regression (Park and Casella 2008) with the new concept called “Knockoffs” introduced by Barber and Candès (2015). We use both numerically simulated data and a real-world HIV-1 dataset in demonstrating the proposed method’s potential for detecting genetic markers with false discovery control as compared to existing methodologies.

Review of related literature

False discovery rate and Knockoffs

Multiple testing procedures have been increasingly important in the era of big data. In order to weave through large datasets and find tiny nuggets of gold that are significant variables, innovations in multiple testing procedures have been introduced since the 1990s (Westfall and Young 1993; Efron et al. 2001; Dudoit et al. 2003; Efron 2008). This is especially important in fields like genomics where minimizing false discoveries in gene and mutation detection allows for more accurate drug delivery, specialized treatments, among other important discoveries. The primary objective is to test p pairs of null and alternative hypotheses (Efron et al. 2001), $H_{0_1},H_{0_2},\dots ,H_{0_p}$, in which we generally have a decision rule based on a pre-defined test statistic that will decide whether each p is null or non-null. Our goal is to minimize the false discovery proportion Q, where $Q=\frac{V}{V+S}=\frac{V}{1\vee R}$ and V and S are the number of false and true discoveries, respectively, among the rejected null hypotheses.

Benjamini and Hochberg (1995) proposed the concept of False Discovery Rate (FDR), which is defined as the expected value of the proportion of false rejections among rejected hypotheses $\text{FDR}:=E\left(\frac{V}{1\vee R}\right)$ where R is the number of discoveries or the number of variables tagged as significant. Furthermore, they also proposed a distribution-free, linear step-up method that controls the FDR.

While Benjamini and Hochberg (1995)’s method has since been the standard for false discovery control, the landmark framework by Barber and Candès implemented a key innovation in false discovery control by introducing the idea of constructing a “fake” or knockoff design matrix $\tilde{\mathbf{X}}$ that mimics the correlation structure of $\mathbf{X}$, it becomes possible to create test statistics, say $Z_j$, for the corresponding ${\mathbf{X}}_j$ such that the differences between the original $Z_j$ and its knockoff $\widetilde{Z_j}$ are large for non-null cases, and small for null cases (Barber and Candès 2015). They were able to prove theoretically that the procedure controls FDR using a data-dependent threshold. By ensuring FDR is not too high, discoveries are reliably true and replicable. Implementing the knockoffs framework can generally be summarized in three steps:

1. Construct knockoffs $\tilde{\mathbf{X}}$ from the original design matrix $\mathbf{X}$

2. Compute knockoff statistics

3. Find the knockoff threshold

Our proposed method primarily focuses on creating new test statistics for controlled variable selection. To compute test statistics, 2p $Z_j$’s are computed based on the augmented data matrix $[\mathbf{X},\tilde{\mathbf{X}}]$: ($Z_1,Z_2,\dots ,Z_p,{\tilde{Z}}_1,{\tilde{Z}}_2,\dots ,{\tilde{Z}}_p$), and then compute each $W_j$ based on each pair of $Z_j$ and ${\tilde{Z}}_j$. A large positive value of $W_j$ means the original parameter j enters the model before its knockoff (index $j+p$). The crux to the knockoff method’s guaranteed FDR control is through the choosing of a data-dependent threshold. We select $W_j$ such that it is larger than t and positive ($W_j\ge t$), where t is the threshold Barber and Candès (2015).

While the Benjamini-Hochberg procedure is phrased in terms of the classical p-value, for the case of large-scale testing where thousands of these p-values are measured at once, it is important that outcomes are judged on their own terms and not with respect to the hypothetical possibility of more extreme results (Efron 2012). Thus, Efron et al. (2001) introduced local false discovery rates (lfdr), prompted by a Bayesian idea and implemented using empirical Bayes methods for large-scale testing. Local false discovery rate measures confidence in each effect being non-zero among a large number of imprecise measurements in large scale multiple testing Korthauer et al. (2019). Efron et al. (2001) defined local false discovery rate as:

$$\begin{array}{c}\hfill \ell =P(\text{null}|z)=\frac{{\pi }_0{f}_0(z)}{{\pi }_0{f}_0(z)+{\pi }_1{f}_1(z)}\end{array}$$ 1

where ${\pi }_0$ is the proportion of nulls, ${\pi }_1$ is the proportion of non-nulls, $f_0$ is the null density, and $f_1$ is the non-null density. The null distribution $f_0$ is assumed known while ${\pi }_0$ can be estimated. Consequently, we can either estimate the mixture distribution f or estimate $f_1$ and then plug in to ${\pi }_0{f}_0+{\pi }_1{f}_1$ in order to determine f (Efron 2012). The interpretation of the local FDR value is analogous to the frequentist’s p-value wherein local FDR values less than a specified level of significance provide stronger evidence against the null hypothesis.

Bayesian Lasso

Regression methods are ubiquitous in statistics for its ability to relate a dependent variable $\mathbf{y}$ to a design matrix of independent variables $\mathbf{X}$. While there are many types of regression methods available from simple linear, to non-linear regression, and even nonparametric methods, Bayesian methods have gained ground in recent years due to increased access to computational facilities (O’Hara and Sillanpää 2009; Bijak and Bryant 2016; Robert and Casella 2011). In conjunction with the knockoffs framework, to be discussed in the next sect. 2.1, it is fitting to implement more straightforward Bayesian regression methods. It is advantageous to use these methods because they are easy to understand and utilize for most end-users rather than sophisticated adaptive approaches.

Park and Casella (2008) suggested that based from the form of Tibshirani (1996), Lasso may be interpreted as a Bayesian posterior mode estimate when the parameters ${\beta }_j$ have independent and identical double exponential (Laplace) priors. They formulated a hierarchical specification of the prior distribution for $\mathit{\theta }=(\mathit{\beta },{\sigma }^2,{\mathit{\tau }}^2,{\lambda }^2,\mu )$ as follows:

$$\begin{array}{cc}\hfill \mathit{\beta }\mid {\sigma }^2,{\mathit{\tau }}^2& \sim N_p(\mathbf{0},{\sigma }^2{\mathbf{D}}_{\tau })\hfill \end{array}$$ 2

$$\begin{array}{cc}\hfill {\mathbf{D}}_{\tau }& =\text{diag}({\tau }_1^2,{\tau }_2^2,\dots ,{\tau }_p^2)\hfill \end{array}$$ 3

$$\begin{array}{cc}\hfill {\sigma }^2& \sim \text{Inverse Gamma}(A,B)A,B>0\hfill \end{array}$$ 4

$$\begin{array}{cc}\hfill {\tau }_j^2\mid {\lambda }^2& {\displaystyle \sim \prod _{j=1}^p\frac{{\lambda }^2}{2}exp\left\{-,\frac{{\lambda }^2{\tau }_j^2}{2}\right\},j=1,2,\dots ,p}\hfill \end{array}$$ 5

$$\begin{array}{cc}\hfill {\lambda }^2& \sim \text{Gamma}(C,D)C,D>0\hfill \end{array}$$ 6

Since $\mu$ may be integrated out, the joint density (marginal only over $\mu$) is proportional to

$$\begin{array}{cc}\hfill \mathrm{p}(\mathit{\beta },{\sigma }^2,{\mathit{\tau }}^2,\lambda \mid \tilde{\mathbf{y}},\mathbf{X})& \propto {\left({\sigma }^2\right)}^{-\frac{n-1}{2}}\hfill \\ \hfill \&exp\left\{-,\frac{1}{2{\sigma }^2},{\left(\tilde{\mathbf{y}},-,\mathbf{X},\mathit{\beta }\right)}^{\top },\left(\tilde{\mathbf{y}},-,\mathbf{X},\mathit{\beta }\right)\right\}\\ \hfill & \times {\left({\sigma }^2\right)}^{-\frac{p}{2}}\prod _{j=1}^p{\left({\tau }_j^2\right)}^{-\frac{1}{2}}\hfill \\ \hfill & exp\left\{-,\frac{1}{2{\sigma }^2},\sum _{j=1}^p,\frac{{\beta }_j^2}{{\tau }_j^2}\right\}\hfill \\ \hfill & \times {\left({\sigma }^2\right)}^{-A-1}exp\left\{-,\frac{B}{{\sigma }^2}\right\}\hfill \\ \hfill & \times {\lambda }^{2p}exp\left\{-,\frac{{\lambda }^2}{2},\sum _{j=1}^p,{\tau }_j^2\right\}\hfill \\ \hfill & \times {({\lambda }^2)}^{C-1}exp\left\{-,D,{\lambda }^2\right\}\hfill \end{array}$$ 7

where (7) depends on $\mathbf{y}$ only through $\tilde{\mathbf{y}}$. It is then more simple to form a Gibbs sampler for $\mathit{\beta }$, ${\sigma }^2$, ${\mathit{\tau }}^2$, and ${\lambda }^2$ based on this density because the conjugacy of the other parameters remains unaffected (Park and Casella 2008).

Methodology

As mentioned previously, the primary objective of GWAS is to identify the relevant genetic markers. Statistically, this translates to identifying the nonzero regression coefficients of ${\beta }_j,j=1,2,\dots ,p$. In order to test our p pairs of null and alternative hypotheses,

$$\begin{array}{c}\hfill H_{0j}:{\beta }_j=0\text{and}{H}_{1j}:{\beta }_j\ne 0,\text{for}1\le j\le p,\end{array}$$

we propose a multiple testing procedure based on the Bayesian Lasso and the Knockoffs framework. In conjunction with Bayesian regression methods, local false discovery rate is used in order to detect signals from noise and control FDR appropriately.

Existing literature on the knockoffs framework implementing Bayesian methods is currently scarce (Gimenez et al. 2018; Candès et al. 2018). This paper aims to show it is feasible to apply computationally-intensive Bayesian methods in creating knockoff statistics for accurate inference. By carefully applying techniques previously done by Barber and Candès (2015) and Efron et al. (2001), in conjunction with Bayesian techniques also allows for incorporating appropriate prior information on the data through the choice of prior distribution. Our application of local false discovery (Efron et al. 2001) also allows for easily interpretable measures of importance, previously not possible with penalized regression approaches like Lasso. Most importantly, benchmarking from Barber and Candès (2015)’s challenge to understand and choose statistics that yield high power with FDR control, we aim to show that the proposed feature importance statistics obtain the desired FDR control and display comparable performance in statistical power more commonly used frequentist methods.

In order to detect which hypotheses are non-nulls from nulls, we calculate the posterior probability that ${\beta }_j=0$ given the observed data $\mathbf{y}$, $\mathbf{X}$ and the knockoffs $\tilde{\mathbf{X}}$, $j=1,2,\dots ,p$. We utilize Efron et al. (2001)’s local false discovery rate ${\ell }_j$ to compute this probability.

However, the local FDR formulation consists of unknown quantities ${\pi }_0,f_0$ and $f_1$, which must be estimated accordingly. We assume that ${\pi }_1$ follows a Beta distribution. Using the draws of ${\pi }_1$ generated from the Gibbs sampler, we can arrive at an estimate $min\left(1,,,{\widehat{\pi }}_1\right)$, where ${\widehat{\pi }}_0+{\widehat{\pi }}_1=1$. Secondly, we assume that $f_0$ and $f_1$ follow the normal distribution. Using the draws of ${\beta }_j$ and ${\sigma }^2$ generated from the Gibbs sampler, we can estimate the unknown parameters of the null and the non-null distribution, respectively.

We specify that the null distribution is centered at zero while there is a location-shift in the non-null distribution from zero. This follows from Efron (2007)’s “zero assumption” where observations around the central peak of the distribution consists mainly of null cases. Also, both null and non-null distribution have the same variance ${\sigma }^2$.

Algorithm for Bayesian Lasso with Knockoffs

Following the discussion of Bayesian Lasso in Sect. 2.2, we draw ${\sigma }^2$ from the Inverse Gamma distribution. We use the conditional posterior of $\beta$ where we use the augmented data vector $\stackrel{\circ }{\mathbf{X}}$, the augmented parameter vector $\stackrel{\circ }{\mathit{\beta }}$, and hyperparameters A and B to get

$$\begin{array}{cc}\hfill A_{\mathit{Blasso}}& =\frac{n+2p-1}{2}+A\hfill \end{array}$$ 8

$$\begin{array}{cc}\hfill B_{t,Blasso}& =\frac{\Vert \tilde{\mathbf{y}}-\stackrel{\circ }{\mathbf{X}}{\stackrel{\circ }{\mathit{\beta }}}^{(t-1)}{\Vert }^2+{\stackrel{\circ }{\mathit{\beta }}}^{\top (t-1)}{\left[{\mathbf{D}}_{\stackrel{\circ }{\mathit{\tau }}}^{-1}\right]}^{(t-1)}{\stackrel{\circ }{\mathit{\beta }}}^{(t-1)}}{2}+B\hfill \end{array}$$ 9

Meanwhile, we draw the augmented parameter ${\stackrel{\circ }{\mathit{\beta }}}^{(t)}$ from the Multivariate Normal distribution as mentioned. The augmented data vector $\stackrel{\circ }{\mathbf{X}}$, augmented tuning parameter vector $\stackrel{\circ }{\mathit{\tau }}$, and the current iterate of ${\sigma }^2$ are used to specify the parameters of MVN as shown below:

$$\begin{array}{c}\hfill {\mathit{\mu }}_{\mathit{Blasso}}={\mathit{\Psi }}^{-1}{\stackrel{\circ }{\mathbf{X}}}^{\top }\tilde{\mathbf{y}}\end{array}$$ 10

$$\begin{array}{c}\hfill {\mathit{\Sigma }}_{\mathit{Blasso}}={\sigma }^{2(t)}{\mathit{\Psi }}^{-1}\end{array}$$ 11

$$\begin{array}{c}\hfill \mathit{\Psi }={\stackrel{\circ }{\mathbf{X}}}^{\top }\stackrel{\circ }{\mathbf{X}}+{\left[{\mathbf{D}}_{\stackrel{\circ }{\mathit{\tau }}}^{-1}\right]}^{(t-1)}\end{array}$$ 12

To update ${\tau }_j^{2(t)}$ in step 6, we use the previous iterate of $\lambda$ and the current iterates of ${\beta }_j$, and $\sigma$ to get

$$\begin{array}{c}\hfill {\Phi }_{\mathit{Blasso}}=\sqrt{\frac{{\lambda }^{2(t-1)}{\sigma }^{2(t)}}{{\beta }_j^{2(t)}}},{\lambda }_{\mathit{Blasso}}={\lambda }^{2(t-1)}\end{array}$$ 13

Finally, to update ${\lambda }^{2(t)}$ in step 7, we use the current iterates of $\tau$, as well as the hyperparameters C and D to get

$$\begin{array}{c}\hfill C_{\mathit{Blasso}}=2p+C,D_{\mathit{Blasso}}=\sum _{j=1}^{2p}\frac{{\tau }_j^{2(t)}}{2}+D\end{array}$$ 14

To detect non-null covariates using the Gibbs sampler iterates from Bayesian regression models, we use the concept of local false discovery rate introduced in Sect. 2.1. For each iteration t, we compute ${\ell }_j^{(t)}$:

$$\begin{array}{cc}\hfill {\ell }_j^{(t)}=& \frac{{\pi }_0^{(t)}{f}_{0_j}({\beta }_j^{(t)})}{{\pi }_0^{(t)}{f}_{0_j}({\beta }_j^{(t)})+{\pi }_1^{(t)}{f}_{1_j}({\beta }_j^{(t)})}\hfill \end{array}$$ 15

where

$$\begin{array}{cc}\hfill f_{0_j}({\beta }_j^{(t)})=& \frac{1}{\sqrt{2\pi {\sigma }^{2(t)}}}exp\left\{-,\frac{{({\beta }_j^{(t)})}^2}{2{\sigma }^{2(t)}}\right\}\hfill \end{array}$$ 16

$$\begin{array}{cc}\hfill f_{1_j}({\beta }_j^{(t)})=& \frac{1}{\sqrt{2\pi {\sigma }^{2(t)}}}exp\left\{-,\frac{{({\beta }_j^{(t)}-\overline{{\beta }_j})}^2}{2{\sigma }^{2(t)}}\right\}\hfill \end{array}$$ 17

$$\begin{array}{cc}\hfill \overline{{\beta }_j}=& {\displaystyle \frac{1}{T}\sum _{t=1}^T{\beta }_j^{(t)}}\hfill \end{array}$$ 18

After computing the local false discovery rate ${\ell }_j$, we use it to compute for $\delta$, defined below. We will use for computing the test statistics, and it also provides a connection between ${\pi }_1$ and $\ell$.

$$\begin{array}{c}\hfill {\delta }_j=\left\{\begin{array}{cc}1,\hfill & {\ell }_j\le \alpha \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right)\end{array}$$ 19

Moreover, in the general case when we truly do not know the number of non-null covariates, then a computational procedure based on local false discovery rate is used to estimate it. Suppose

$$\begin{array}{cc}\hfill {\pi }_1& \sim \text{Beta}(a,b),a,b>0\hfill \end{array}$$ 20

The full conditional posterior of ${\pi }_1^{(t)}$ given $\sum _{j=1}^p{\delta }_j^{(t-1)}$ is

$$\begin{array}{c}\hfill \text{Beta}\left(a,+,\sum _{j=1}^p,{\delta }_j^{(t-1)},,,,b,+,p,-,\sum _{j=1}^p,{\delta }_j^{(t-1)}\right)\end{array}$$ 21

The steps of the algorithm are outlined below:

Proposed test statistics

In this section, we present two distinct test statistics and two thresholds for the decision rule. These statistics-threshold combinations yield 4 different decision rules for choosing whether to reject the null hypothesis or not, which for simplicity we refer to as test statistics. We denote these decision rules as $T_{{\rm Y}}$, where ${\rm Y}\in \{1a,1b,2a,2b\}$. The summary is provided in Table 1 in the Annex.

Table 1.

Test statistics using iterates of Gibbs samples

$T_{{\rm Y}}$	Test statistic	Reject $H_{0j}$ if .
$T_{1_a}$	${\overline{\delta }}_j-{\overline{\tilde{\delta }}}_j={\displaystyle \frac{1}{V}}\left[\sum _{t=U+1}^T,{\delta }_j^{(t)},-,\sum _{t=U+1}^T,{\tilde{\delta }}_j^{(t)}\right]$	${\overline{\delta }}_j-{\overline{\tilde{\delta }}}_j\ge t_k$.
$T_{1_b}$		${\overline{\delta }}_j-{\overline{\tilde{\delta }}}_j\ge t_{k+}$.
$T_{2_a}$	${\overline{\ell }}_j-{\overline{\tilde{\ell }}}_j={\displaystyle \frac{1}{V}}\left[\sum _{t=U+1}^T,{\ell }_j^{(t)},-,\sum _{t=U+1}^T,{\tilde{\ell }}_j^{(t)}\right]$	${\overline{\ell }}_j-{\overline{\tilde{\ell }}}_j\ge t_k$.
$T_{2_b}$		${\overline{\ell }}_j-{\overline{\tilde{\ell }}}_j\ge t_{k+}$.

After drawing T samples and burning-in U iterates, we are left with V draws. The proposed test statistics are based on the posterior means of the remaining V iterates. The decision rule utilizes $t_k$ which is the knockoff threshold defined by Barber and Candès (2015). Similarly, we will also use $t_{k+}$ which is the knockoff threshold that guarantees the modified FDR control.

In the results section, the posterior means used for the proposed decision rules presented in Table 1 are computed from a Gibbs sampler with 5000 iterations and a burn-in of 1000 iterations.

Numerical simulation study

To gather insights on the performance of our proposed models, numerical simulation studies are performed. We investigate the settings required among the data generation procedure first and then proceed to the proposed methods. As an overview, the following settings are used:

1. Number of observations n: 50, 100, 200

2. Number of parameters p: 50, 100, 200

3. Signal noise $\xi$: 1, 2.5, 3.5

4. Decision rules: $T_{1a},T_{1b},T_{2a},T_{2b}$

5. Prior specifications for ${\sigma }^2$: Exponential Distribution Shaped Prior (EXP), Right-Skewed Prior (RSK), Normal-Distribution Shaped Prior (NOR)

To ensure that we cover the settings on number of observations n and number of parameters p, we consider nine $n\times p$ combinations. The choice of the number of observations and parameters intentionally reflects the original knockoffs literature. Barber and Candès (2015) discussed two cases ($n\ge 2p$ and $p\le n<2p$). In this paper, we simulate on $n\ge 2p$ and a subset of $p\le n<2p$, which is $n=p$. We also explore a high-dimensional case not explored in the original 2015 study: $p\ge 2n$.

The choice for amplitude reflects the maximal noise level where it is possible, but not trivial, to distinguish signal from noise (Barber and Candès 2015). They chose the maximal signal amplitude $\xi =3.5$ as it is approximately the expected value of $\underset{1\le j\le p}{max}|{\mathbf{X}}_j^{\top }z|$, where $z\sim N(0,1)$.

Results and discussions

Numerical simulations

As discussed in Sect. 3.3, we consider several combinations of settings of (1) number of observations ‘n’, (2) number of parameters ‘p’, (3) signal noise ‘$\xi$’, (4) decision rules ‘$T_{{\rm Y}}$’, and (5) 3 proposed prior specifications. Thus, there is a total of 324 scenarios for the proposed methods as a result of 9 $n\times p$ combinations, 3 priors, 4 decision rules, and 3 values for the signal noise $\xi$.

The False Discovery Rate (FDR) and True Positive Rate (TPR) using the above proposed methods will then be compared to FDR and TPR obtained using existing non-Bayesian methods (Frequentist), namely the (1) Benjamini Hochberg procedure (BHq in Figure 1), and (2) Lasso regression. Lasso regression was applied to the Knockoffs framework using both the original Knockoff and modified threshold. The resulting statistics using Lasso regression with Knockoffs are referred to as LCDK and LCDK+, respectively. We average FDR and TPR over 1000 trials.

In this study, we compare BHq, LCDK, and LCDK+ methods to each of the method-prior combinations given a nominal FDR target level of $q=10\%$.

The summary tables in the Annex (Tables 2, 3, 4) displays the FDR and TPR of the ‘best’ decision rule T for each of prior setting, number of observations n, number of parameters p, and signal noise $\xi$. The ‘best’ decision rule for each row (method-prior combination) in each table is chosen such that it has the highest TPR, while maintaining FDR under target level 10%.

Table 2.

Comparison of results for proposed methods when $n\ge p$

$\xi$	Prior	Best $T_{{\rm Y}}$	FDR	TPR	$D_{\mathit{TPR}}$	$D_{\mathit{FDR}}$
n=100, p=50
1	EXP	$T_{2b}$	0.01 (0.073)	0.019 (0.137)	− 0.981, BHq	− 0.077
	RSK	$T_{2b}$	0.009 (0.069)	0.017 (0.129)	− 0.983, BHq	− 0.079
	NOR	$T_{2b}$	0.008 (0.065)	0.014 (0.116)	− 0.986, BHq	− 0.08
2.5	EXP	$T_{1a}$	0 (0)	0.939 (0.116)	− 0.061, BHq	− 0.088
	RSK	$T_{1a}$	0 (0)	0.939 (0.115)	− 0.061, BHq	− 0.088
	NOR	$T_{1a}$	0 (0)	0.939 (0.116)	− 0.061, BHq	− 0.088
3.5	EXP	$T_{1a}$	0 (0)	0.939 (0.12)	− 0.061, BHq	− 0.088
	RSK	$T_{1a}$	0 (0)	0.938 (0.12)	− 0.062, BHq	− 0.088
	NOR	$T_{1a}$	0 (0)	0.938 (0.121)	− 0.062, BHq	− 0.088
n=200, p=50
1	EXP	$T_{2b}$	0.013 (0.083)	0.024 (0.153)	− 0.976, BHq	− 0.075
	RSK	$T_{2b}$	0.013 (0.084)	0.024 (0.152)	− 0.976, BHq	− 0.074
	NOR	$T_{2b}$	0.013 (0.083)	0.024 (0.153)	− 0.976, BHq	− 0.074
2.5	EXP	$T_{1a}$	0 (0)	0.996 (0.029)	− 0.004, BHq	− 0.087
	RSK	$T_{1a}$	0 (0)	0.996 (0.029)	− 0.004, BHq	− 0.087
	NOR	$T_{1a}$	0 (0)	0.995 (0.031)	− 0.005, BHq	− 0.087
3.5	EXP	$T_{1a}$	0 (0)	0.997 (0.027)	− 0.003, BHq	− 0.087
	RSK	$T_{1a}$	0 (0)	0.997 (0.026)	− 0.003, BHq	− 0.087
	NOR	$T_{1a}$	0 (0)	0.997 (0.026)	− 0.003, BHq	− 0.087
n=200, p=100
1	EXP	$T_{2b}$	0.045 (0.083)	0.588 (0.489)	− 0.412, BHq	− 0.048
	RSK	$T_{2b}$	0.046 (0.084)	0.593 (0.487)	− 0.407, BHq	− 0.047
	NOR	$T_{2b}$	0.045 (0.084)	0.585 (0.49)	− 0.415, BHq	− 0.048
2.5	EXP	$T_{1a}$	0 (0)	0.946 (0.081)	− 0.054, BHq	− 0.092
	RSK	$T_{1a}$	0 (0)	0.946 (0.081)	− 0.054, BHq	− 0.092
	NOR	$T_{1a}$	0 (0)	0.946 (0.081)	− 0.054, BHq	− 0.092
3.5	EXP	$T_{1a}$	0 (0)	0.947 (0.081)	− 0.053, BHq	− 0.092
	RSK	$T_{1a}$	0 (0)	0.947 (0.081)	− 0.053, BHq	− 0.092
	NOR	$T_{1a}$	0 (0)	0.946 (0.082)	− 0.054, BHq	− 0.092

Table 3.

Comparison of results for proposed methods when $n=p$

$\xi$	Prior	Best $T_{{\rm Y}}$	FDR	TPR	$D_{\mathit{TPR}}$	$D_{\mathit{FDR}}$
n=50, p=50
1	EXP	$T_{2b}$	0.014 (0.089)	0.025 (0.156)	0.005, LCDK+	0.003
	RSK	$T_{2b}$	0.016 (0.093)	0.028 (0.165)	0.008, LCDK+	0.005
	NOR	$T_{2b}$	0.014 (0.087)	0.024 (0.152)	0.004, LCDK+	0.003
2.5	EXP	$T_{1a}$	0 (0)	0.999 (0.015)	0.977, LCDK+	− 0.012
	RSK	$T_{1a}$	0 (0)	0.999 (0.015)	0.977, LCDK+	− 0.012
	NOR	$T_{1a}$	0 (0)	0.99 (0.05)	0.968, LCDK+	− 0.012
3.5	EXP	$T_{1a}$	0 (0.009)	1 (0)	0.979, LCDK+	− 0.011
	RSK	$T_{1a}$	0 (0.009)	1 (0)	0.979, LCDK+	− 0.011
	NOR	$T_{1a}$	0 (0.005)	1 (0)	0.979, LCDK+	− 0.011
n=100, p=100
1	EXP	$T_{2b}$	0.081 (0.103)	0.959 (0.196)	− 0.035, LCDK+	0.005
	RSK	$T_{2b}$	0.08 (0.103)	0.96 (0.194)	− 0.034, LCDK+	0.005
	NOR	$T_{2b}$	0.081 (0.104)	0.958 (0.199)	− 0.036, LCDK+	0.005
2.5	EXP	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	−  0.076
	RSK	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.076
	NOR	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.076
3.5	EXP	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.076
	RSK	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.076
	NOR	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.076
n=200, p=200
1	EXP	$T_{2b}$	0.084 (0.076)	1 (0)	0, LCDK+	0.001
	RSK	$T_{2b}$	0.084 (0.076)	1 (0)	0, LCDK+	0.001
	NOR	$T_{2b}$	0.085 (0.078)	1 (0)	0, LCDK+	0.002
2.5	EXP	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082
	RSK	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082
	NOR	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082
3.5	EXP	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082
	RSK	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082
	NOR	$T_{1a}$	0 (0)	1 (0)	0, LCDK+	− 0.082

Table 4.

Comparison of Results for Proposed Methods when $p\ge 2n$

$\xi$	Prior	Best $T_{{\rm Y}}$	FDR	TPR	$D_{\mathit{TPR}}$	$D_{\mathit{FDR}}$
n=50, p=100
1	EXP	$T_{2b}$	0.035 (0.105)	0.1 (0.268)	−0.179, LCDK+	−0.015
	RSK	$T_{2b}$	0.035 (0.105)	0.1 (0.269)	− 0.179, LCDK+	− 0.015
	NOR	$T_{2b}$	0.034 (0.104)	0.096 (0.264)	− 0.183, LCDK+	− 0.016
2.5	EXP	$T_{1a}$	0.03 (0.077)	0.817 (0.228)	−  0.037, LCDK+	− 0.05
	RSK	$T_{1a}$	0.029 (0.072)	0.816 (0.228)	− 0.037, LCDK+	− 0.051
	NOR	$T_{1a}$	0.021 (0.067)	0.761 (0.245)	− 0.093, LCDK+	− 0.059
3.5	EXP	$T_{1a}$	0.064 (0.094)	0.936 (0.166)	0.042, LCDK+	− 0.016
	RSK	$T_{1a}$	0.063 (0.094)	0.936 (0.167)	0.042, LCDK+	− 0.018
	NOR	$T_{1a}$	0.049 (0.086)	0.928 (0.175)	0.035, LCDK+	− 0.031
n=50, p=200
1	EXP	$T_{2b}$	0.015 (0.084)	0.013 (0.068)	0.008, LCDK+	0.009
	RSK	$T_{2b}$	0.015 (0.082)	0.012 (0.067)	0.008, LCDK+	0.008
	NOR	$T_{2b}$	0.016 (0.086)	0.013 (0.068)	0.009, LCDK+	0.01
2.5	EXP	$T_{1b}$	0.017 (0.084)	0.016 (0.075)	0.006, LCDK+	0.009
	RSK	$T_{1b}$	0.017 (0.081)	0.016 (0.075)	0.006, LCDK+	0.008
	NOR	$T_{2b}$	0.016 (0.082)	0.016 (0.076)	0.006, LCDK+	0.008
3.5	EXP	$T_{1b}$	0.018 (0.087)	0.017 (0.079)	0.006, LCDK+	0.008
	RSK	$T_{1b}$	0.018 (0.087)	0.017 (0.08)	0.006, LCDK+	0.008
	NOR	$T_{1b}$	0.017 (0.085)	0.017 (0.081)	0.007, LCDK+	0.007
n=100, p=200
1	EXP	$T_{2b}$	0.077 (0.101)	0.455 (0.343)	− 0.338, LCDK+	− 0.005
	RSK	$T_{2b}$	0.077 (0.1)	0.456 (0.344)	− 0.337, LCDK+	− 0.005
	NOR	$T_{2b}$	0.077 (0.1)	0.447 (0.343)	− 0.345, LCDK+	− 0.005
2.5	EXP	$T_{1a}$	0.019 (0.043)	0.953 (0.116)	− 0.026, LCDK+	− 0.068
	RSK	$T_{1a}$	0.018 (0.043)	0.952 (0.116)	− 0.026, LCDK+	− 0.068
	NOR	$T_{1a}$	0.014 (0.037)	0.942 (0.125)	− 0.036, LCDK+	− 0.072
3.5	EXP	$T_2$	0.037 (0.060)	0.982 (0.094)	0, LCDK+	− 0.039
	RSK	$T_{1a}$	0.036 (0.059)	0.982 (0.093)	0, LCDK+	− 0.040
	NOR	$T_{1a}$	0.031 (0.058)	0.982 (0.095)	0, LCDK+	− 0.054

To illustrate, Table 2 summarizes the results for $n\ge 2p$, in which the first row shows the results when $n=100$, $p=50$, $\xi =1$, using an exponential-distribution shaped (EXP) prior. The ‘best’ decision rule, or the decision rule that has the highest TPR while maintaining FDR control, is $T_{2b}$, with FDR 0.01 and TPR 0.019.

$D_{\mathit{FDR}}$ and $D_{\mathit{TPR}}$ represents the difference between the FDR and TPR, respectively, of the ‘best’ decision rule of that proposed Bayesian setting, and the FDR and TPR for the ‘best’ non-Bayesian method among BHq, LCDK, and LCDK+. For example, for the first setting (first row) in Table 2, the best frequentist method is BHq with TPR 1 and FDR 0.087. Since the ‘best’ proposed decision rule is $T_{2b}$ with TPR 0.019 and FDR 0.01, then our proposed decision rule $T_{2b}$ bests BHq’s FDR by 0.77 (eg. $D_{\mathit{FDR}}=-0.077=0.10-0.087$), and lags behind TPR by 0.981 (eg. $D_{\mathit{TPR}}=-0.981=0.019-1$).

For these results, a negative $D_{\mathit{FDR}}$ means our proposed method for that setting is superior to the ‘best’ frequentist method in terms of minimizing FDR. Conversely, a positive $D_{\mathit{TPR}}$ means our proposed method is better than the ‘best’ frequentist method in selecting signals. Thus, for optimality, we want $D_{\mathit{FDR}}$ to be negative and $D_{\mathit{TPR}}$ to be positive.

For brevity, only the tables for $\xi =1,2.5,$ and 3.5 is featured in this section. Each of $\xi =1,2.5,$ and 3.5 represent the settings when nulls and signals are heavily-mixed, moderately-mixed, and well-separated respectively.

Table 2 summarizes the simulation study results for the first case when $n\ge 2p$. We are able to detect signals consistently for cases where $\xi =$ 2.5 or 3.5. TPR is only less than 5% worse than BHq, but improves on FDR by more than 7%. For the case where signals are heavily-mixed ($\xi =1$), the method had difficulties in detecting signals for the low parameter case $p=50$, while for $n=200$, $p=100$, we were able to detect a respectable 59% of signals. For this case, results for all 3 prior specification were quite similar.

Table 3 summarizes the simulation study results for the second case when $n=p$. We are able to detect signals consistently for cases where $\xi =$ 2.5 or 3.5. TPR is similarly effective as Lasso with the modified knockoffs threshold, but with 1 to 8% improvement in FDR. Similar to the previous case where $n\ge 2p$, for the case where signals are heavily-mixed ($\xi =1$), the method had difficulties in detecting signals for the low parameter case $p=50$. When $p\ge 100$, we were able to detect a respectable 96 to 100% of signals. For this case, results for all 3 prior specification were quite consistent.

Table 4 summarizes the simulation study results for the final case when $p\ge 2n$. For this highest dimensional case ($n=50$, $p=200$), we were not able to successfully detect signals using both Lasso and the proposed method. For the other two subcases ($n=50$, $p=100$ and $n=100$, $p=200$), we were able to detect at 76 to 98% of signals using our proposed method. The EXP and RSK prior specifications were superior in both subcases to the NOR prior. When $\xi =2.5$, our proposed methods were 4 to 9% inferior to Lasso in terms of TPR, but reduced FDR by 5 to 6%. For the well-separated signal case ($\xi =3.5$), our proposed method was either tied with Lasso or 1 to 4% superior in terms of TPR, while redicung FDR by 2 to 7%.

Results on HIV-1 data

In order to apply the proposed procedures and test whether FDR control and sufficient TPR is achieved, we will use a publicly available data set: the Human Immunodeficiency Virus Type 1 (HIV-1) drug resistance database (Rhee et al. 2005). We limit the analysis the analysis of drug resistance measurements on genotype information related to non-nucleoside reverse transcriptase inhibitor (NNRTI) drug class, which has three generic drugs classified under it, namely Delavirdine (DLV), Efavirenz (EFV), and Nevirapine (NVP).

To validate the results, we compare the selected markers p with existing treatment-selected mutation panels (TSM) from Rhee et al. (2005). While this is a previously conducted and vetted study, ground truth or an oracle to which determines the true nulls and non-nulls are not available. Nevertheless, using this previous study is a good approximation to determine the effectiveness of our method. We aim to see replicability, which means we wish to see how many of the markers identified by our methods also appear in the TSM panel.

For each prior specification, we will be comparing each of the proposed test statistics to BHq and Lasso Coefficient Difference (using both the original and modified thresholds), similar to the numerical study in the previous section. Instead of using FDR and TPR, we assess these results based on the number of selections that appear in the TSM lists, representing True Positives, and the number of selections hose that don’t appear in TSM lists, representing False Discoveries. The figures and tables show the number of selections averaged over 1000 trials.1

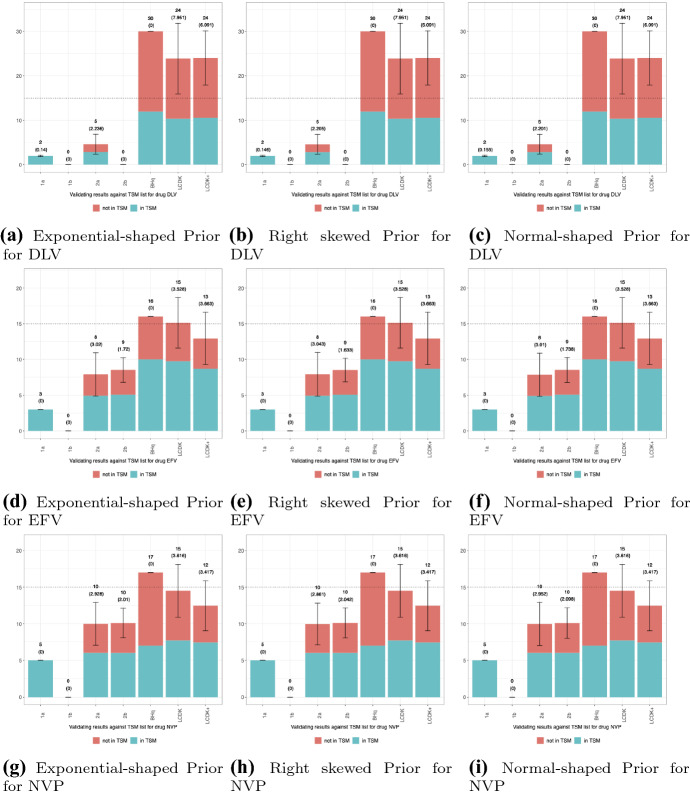
Figure 1 shows the agreement between the TSM lists and our proposed method for the 3 priors $\times$ 3 generic drug combinations. In each chart, we see the decision rules (Table 1) in the X-axis, and the # of selected markers in the Y-axis. The blue bars represent the markers that are confirmed TSM lists (True Positives), while the red bars represent those that are not in the TSM lists (False Discoveries).

Fig. 1.

Results for HIV Data

We see in Figure 1 the non-Bayesian methods, BHq and Lasso, select a lot more markers that do no agree with the TSM list (in red). Our proposed methods are able to more conservatively select the markers previously confirmed by the TSM lists (True Positives in blue), while reducing potential false discoveries (in red). The results are especially outstanding for the drug Nevirapine (NVP) since a similar number of markers were selected compared to the frequentist methods, while choosing less markers not in the TSM lists. Thus, for Nevirapine, our proposed method and test statistics were able to more accurately replicate the selections of Rhee et al. (2005)’s study while minimizing the selection of possible false discoveries. In practice, our method is more viable for researchers who aim ensure the selected genetic markers for drug resistance have minimal false discoveries. This is important since out of the 3 drugs, Nevirapine is typically the cheapest and most accessible.

While the number of TSM-validated selections vary per drug and test statistic, overall, the proposed methods show promise in selecting positions that correspond to real effects, as verified by the TSM list. Researchers are always looking for ways to minimize false discoveries given the costs related to proceeding experiments for each genetic marker. We have demonstrated our proposed methods can help researchers achieve this, while maintaining competitive TPR.

Conclusions and recommendations

Motivated by the growing HIV epidemic in the Philippines, our proposed methods show potential in being used by genomic researchers to find significant genetic marker, while minimizing the number of false discoveries in HIV data. Our numerical studies show that the proposed methods not only had competitive TPR compared to BHq and Lasso, but had less FDR in most of the cases discussed. This contributes to computational statistics by demonstrating that unifying Bayesian Lasso with Model-free Knockoff unlocks the potential for achieving high TPR, while reducing FDR for low and equi-dimensional cases.

We are also able to demonstrate this through the HIV-1 data set, where we were able to select many of Rhee et al. (2005)’s identified genetic markers, while minimizing selecting those outside their study. While this work only focused on a small genomic dataset due to the number of replicates needed and the large computational power needed by the Bayesian methods, we believe this was able to demonstrate its potential for application to larger datasets that are similar in design and structure. A small reduction in FDR may seem insignificant in a scale of this study, but in future, larger scale studies, a 1–2% FDR reduction means hundreds of hours and millions of dollars saved on manpower. For example, in a 20,000 SNP dataset with 2000 selections, a 1% reduction in FDR means 20 less positions that need time and resources for further experimentation and research.

These findings not only aim to contribute to more accurate and cost-effective HIV drug resistance research in the Philippines, but more so lives saved as it aims to help patients receive proper treatment and prevent unnecessary costs, risks, and burdens associated with taking the wrong drug. Given that we were able to show this method’s potential in identifying significant genetic markers towards detecting drug resistance, perhaps one day it can be used to detect drug resistance towards other fast-mutating viruses, such as COVID-19.

Annex

See Tables 1, 2, 3, 4 and Figure 1

Declaration

Conflict of interest

The authors declare that they have no conflict of interest.