EdgeSHAPer: Bond-centric Shapley value-based explanation method for graph neural networks

Summary

Graph neural networks (GNNs) recursively propagate signals along the edges of an input graph, integrate node feature information with graph structure, and learn object representations. Like other deep neural network models, GNNs have notorious black box character. For GNNs, only few approaches are available to rationalize model decisions. We introduce EdgeSHAPer, a generally applicable method for explaining GNN-based models. The approach is devised to assess edge importance for predictions. Therefore, EdgeSHAPer makes use of the Shapley value concept from game theory. For proof-of-concept, EdgeSHAPer is applied to compound activity prediction, a central task in drug discovery. EdgeSHAPer’s edge centricity is relevant for molecular graphs where edges represent chemical bonds. Combined with feature mapping, EdgeSHAPer produces intuitive explanations for compound activity predictions. Compared to a popular node-centric and another edge-centric GNN explanation method, EdgeSHAPer reveals higher resolution in differentiating features determining predictions and identifies minimal pertinent positive feature sets.

Graphical abstract

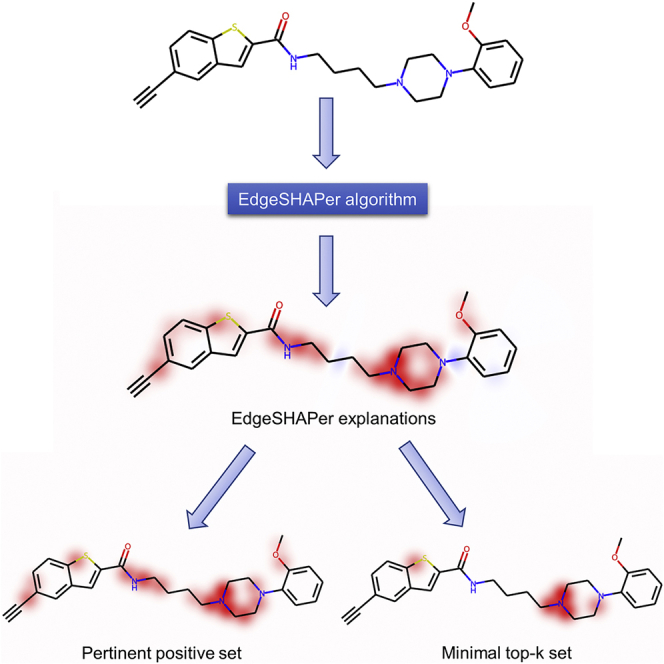
Highlights

• •EdgeSHAPer is new methodology for explaining graph neural network models
• •Edge centricity represents a characteristic feature of the approach
• •EdgeSHAPer is generally applicable including molecular predictions
• •EdgeSHAPer produces explanations of compound predictions at a high resolution

Drugs; Bioinformatics; Artificial intelligence

Introduction

The increasing popularity of deep neural network (DNN) architectures for machine learning (ML) across many areas of science and business has pros and cons. On the one hand, deep learning (DL) has led to unprecedented progress in areas such as computer vision, natural language processing, or network analysis (LeCun et al., 2015) and opened the door to new scientific applications going beyond the capacity of standard ML; on the other hand, it has partly mystified ML, among both non-experts and ML experts, and—at least in the authors’ opinion—frequently triggered unrealistic expectations concerning the problem-solving ability of machines and their putative ability to arrive at decisions beyond human reasoning. Such trends have been corroborated by the frequent synonymous use of the terms artificial intelligence (AI) and ML, implying that intrinsically statistical approaches would be equipped with some special form of new “machine intelligence”, which is not the case. In computer science, AI is well defined and ML is classified as a part of the AI spectrum, together with other approaches such as expert systems or robotics (Rapaport, 2020). DNNs have definitely not added new forms of “intelligence” to this spectrum. However, a characteristic feature of most ML methods—by no means confined to DNNs—is their often quoted “black box” character (Castelvecchi, 2016), meaning that decisions of ML models remain machine-internal and are hard, if not impossible to comprehend for humans. The black box issue has been on the ML agenda for decades, working against the acceptance of ML results to guide experimental design in many areas. With increasingly complex DNN architectures being employed for many scientific applications, the problem has further increased in magnitude. In interdisciplinary research settings in the life sciences including drug discovery, the natural reluctance of experimentalists to rely on ML results that they cannot rationalize in biological or chemical terms often limits the impact of ML (Rodríguez-Pérez and Bajorath, 2021a, 2021b). Such limitations are being recognized. As a consequence, with the advent of DL, there are increasing discussions in the field about the relationship between ML model complexity and interpretability and the tendency to use models that are too complicated for prediction tasks at hand (Rudin, 2019). Furthermore, increasing attention is paid to explainable ML (Belle and Papantonis, 2021; Rodríguez-Pérez and Bajorath, 2021a) and the overarching area of explainable AI (XAI) (Gunning et al., 2019, 2021; Jiménez-Luna et al., 2020; Xu et al., 2019). XAI refers to different categories of computational approaches for rationalizing ML models and their decisions in different areas of basic and applied research (Gunning et al., 2019; Jiménez-Luna et al., 2020; Xu et al., 2019) as well as in scientific teaching (Clancey and Hoffman, 2021). Explanation methods are equally relevant for classification and regression models (Letzgus et al., 2021; Rodríguez-Pérez and Bajorath, 2020a). Conceptually different XAI approaches include methods for feature weighting or attribution, causal methods, counterfactuals and contrastive explanations, transparent probabilistic models, or graph convolution analysis methods (Gunning et al., 2021; Jiménez-Luna et al., 2020). In addition, local approximation models have been introduced for instance-based explanations of decisions by complex black box models (Ribeiro et al., 2016; Lundberg and Lee, 2017). Furthermore, methods for uncertainty estimation (Feng et al., 2020) and feature visualization at different levels of abstraction from test objects (Bertolini et al., 2022; Rodríguez-Pérez and Bajorath, 2020b) fall into the XAI spectrum. Hence, there is considerable methodological diversity among XAI approaches, which can be further classified into model/algorithm-dependent and -independent (-agnostic) methods. Given their general applicability to algorithms and models of varying complexity, model-agnostic approaches are particularly sought after.

In ML, explanation methods typically attempt to identify representation features that determine predictions. These include, for example, algorithm-dependent approaches such as feature weighting and visualization techniques as well as model-agnostic methods (Belle and Papantonis, 2021; Rodríguez-Pérez and Bajorath, 2021a, 2021b). Graph neural networks (GNNs) represent an increasingly popular class of DNNs for deep learning in the life sciences and chemistry, with message passing neural networks (MPNNs) being a prominent example (Scarselli et al., 2008; Gilmer et al., 2017). This is at least in part due to their ability to learn directly from graph representations, which alleviates the need for the use of pre-defined features and descriptor engineering. These GNNs are particularly attractive for representation learning in chemistry (Gilmer et al., 2017), given that molecular graphs are the primary data structure for conveying molecular structure, implicit structure-based properties, or molecular interactions. In a typical molecular graph, nodes represent atoms and edges represent bonds connecting atoms. Like other DNNs, GNNs have black box character, which also confines their acceptance in chemistry (and other fields). In this work, we report the development and assessment of a new explanation method for GNNs.

Results

Scientific context of EdgeSHAPer

The EdgeSHAPer approach introduced herein was devised to assess edge importance for GNN predictions. The GNNExplainer approach is also edge-centric, but applied to identify the subgraph for an object determining its prediction (Ying et al., 2019). In addition to GNNExplainer, a method termed GNN Explanation Supervision has been reported that combines node- and edge-based model explanation through graph regularization techniques, aiming to achieve consistency between node- and edge-based explanations through supervised adaptive learning (Gao et al., 2021). For graph convolutional networks (GCNs), edges important for model decisions have also been identified using previously introduced agnostic local explanation models (Kasanishi et al., 2021). In addition, MPNN variants with self-attention mechanisms have been reported to enable the extraction of learned attention weights (Tang et al., 2020; Xiong et al., 2020). Furthermore, self-explainable GNNs are investigated that aim to identify K-nearest labeled nodes for each unlabeled node based on node and graph structural similarity to generate an explainable node classification (Dai and Wang, 2021). There are only a few more approaches currently available to aid in the rationalization of GNN learning, as further discussed below, which employ the Shapley value concept introduced in the next section.

EdgeSHAPer was originally conceptualized for assessing the importance of bond information for graph-based compound activity prediction, representing a novel approach, and was specifically evaluated in this context. Compound activity prediction is a central task for ML in chemoinformatics and medicinal chemistry. However, our new methodology is generalizable and applicable to many tasks in GNNs learning where edge distributions play a role, including any node degree-sensitive MPNNs.

Shapley values in explainable machine learning

EdgeSHAPer makes use of Shapley values that were first introduced in cooperative game theory (Shapley, 1953) to quantify the contributions of individual players to the performance of a team. The Shapley value concept has recently gained popularity in XAI as a model-agnostic framework for rationalizing ML decisions. In this context, Shapley values are calculated to quantitatively assess feature importance for individual predictions. Since the calculation of Shapley values depends on the order of players (features) and is thus combinatorial in nature, it becomes computationally demanding in high-dimensional feature spaces (which are typically used for compound activity predictions). Therefore, the Shapley additive explanations (SHAP) approach has been introduced, which approximates a complex ML model in the feature space vicinity of a test instance with a simpler local model based upon a kernel function (Lundberg and Lee, 2017). SHAP can be perceived as an extension of the locally interpretable model-agnostic explanations (LIME) approach (Ribeiro et al., 2016). SHAP-based methodologies have also been introduced and evaluated for compound activity, multi-target activity, and potency predictions (Rodríguez-Pérez and Bajorath, 2020a, 2020b). While SHAP-based explanations have been proposed for rationalizing different types of activity predictions in chemoinformatics, they have exclusively been applied to ML and DNN models trained using pre-computed descriptors (Rodríguez-Pérez and Bajorath, 2021a).

The Shapley value concept has recently also been applied to graphs in other fields. For example, GraphSVX (Duval and Malliaros, 2021) was introduced as a decomposition method for GNNs that relies on a linear approximation of Shapley values to determine node and node feature contributions. The method offers post-hoc local explanations by using a surrogate model on a perturbed dataset, similar to LIME. In addition, SubgraphX (Yuan et al., 2021) is a subgraph-centric method that approximates Shapley values to determine the most relevant fully connected subgraph for predictions. Finally, GRAPHSHAP (Perotti et al., 2022) was specifically developed as a motif-focused explanatory approach for generic graph classification with node awareness (Gutiérrez-Gómez and Delvenne, 2019). This methodology is based on motif masking and uses an approximation kernel for Shapley values to assess the most influential motifs in the graph.

While these SHAP-based methodologies produce explanations focused on nodes, subgraphs, or motifs, none of them quantifies edge importance, although graph information is primarily distributed through edges. The missing SHAP-dependent quantification of edge importance for GNN predictions has partly motivated the development of our new approach in the context of molecular graphs. The principal methodological differences between EdgeSHAPer, as introduced herein, and the other SHAP-based explanatory approaches for graph learning preclude a meaningful direct comparison. However, in light of edge centricity, results of EdgeSHAPer applications can be compared to those of GNNExplainer, although the approaches are also conceptually distinct.

EdgeSHAPer algorithm

The Shapley value concept has been adapted for EdgeSHAPer using the following analogies: we consider a setting in which “players” corresponding to edges in a graph work collaboratively toward a team (graph) reward, which represents the probability of a prediction for a test instance obtained with an ML model. Each player makes an individual contribution to the reward (payout), which is represented by its Shapley value and computed as the average marginal contribution over all possible feature coalitions (orderings). Since enumerating all possible coalitions becomes computationally hard for larger feature sets, Shapley values are approximated for ML applications.

In our approach, each edge of a graph has its own payout contribution to the predicted output probability (value $v$). The Shapley value for edge $j$ is computed as:

$${\phi }_j\left(v\right)=\frac{1}{\left|E\right|}\sum _{S\subseteq E\backslash \left\{j\right\}}\frac{v\left(S\cup j\right)-v\left(S\right)}{\left(\begin{array}{l}\left|E\right|-1\\ \left|S\right|\end{array}\right)}$$

where $E$ is the set of all edges and $\left|E\right|$ its cardinality, $S$ indicates all the possible subsets of edges excluding $j$ and $\left|S\right|$ its cardinality, $v\left(S\right)$ is the value achieved by subset $S$, and $v(s\cup j)$ is the value obtained when edge $j$ joins the subset $S$ (considering the edge’s marginal contribution).

Monte Carlo sampling of edges

In ML, the practical inability to compute Shapley values directly in many cases requires the use of approximation methods. We developed a Monte Carlo sampling strategy for graph edges, which is central to the EdgeSHAPer algorithm. Instead of randomly sampling a data point from a dataset (Štrumbelj and Kononenko, 2014), which is not applicable in this context, we generate a random graph $Z$ that contains the same number of nodes as the explained graph $G$ according to a binomial probability distribution. If an edge $e$ exists in $G$, it exists in $Z$ with a probability equal to P. The density of graph $G$, which is analogous to the probability for an edge to exist in this graph, proved to be a meaningful choice for P, as further described below. At any Monte Carlo step, a new graph $Z$ is generated. The complete EdgeSHAPer algorithm with Monte Carlo sampling is provided in Algorithm 1.

Algorithm 1. Description of the EdgeSHAPer methodology.

Here, $G$ is the graph to explain, $E$ the list of edges of this graph, and $N$ are the nodes; $j$ is the edge for which the current Shapley value is computed, $P$ the probability of an edge to exist in graph $Z$ (density of $G$ in our implementation), $M$ the number of Monte Carlo steps (corresponding to the number of randomly generated graphs $Z$), and $\hat{f}$ is the function learned by the GNN. Hence, EdgeSHAPer creates a random permutation $\pi$ and sorts the edges in $E$ and in $E_z$ according to this permutation. Then, two edge lists are created by appending edges from the two permuted lists, considering the permuted position of $j$, $j^{\pi },$ as a split point: in $E_{+j}$ edge $j$ originates from the original graph $G$ while in $E_{-j}$, its counterpart originates from $Z$. Thereby, the contribution of an edge to the output is calculated. The algorithm is repeated for each edge in the graph. In practice, new edge lists are created by sorting and appending edge indices and binary masks defining the presence or absence of edges.

Notably, the random graph used for Monte Carlo sampling is not an Erdős–Rényi (E-R) random graph (Erdős and Rényi, 1960). Here, an edge with probability P exists in the generated random graph only if it also exists in the original molecular graph. This enables the quantification of specific edge contributions in coalitions with other edges and thus the determination of the importance of a particular bond in a given compound. The underlying idea is the use of random graphs starting from a test molecule to define information baselines relative to which the contribution of each edge/bond can be quantified. Moreover, the use of this specifically generated random graph enables the generalization of EdgeSHAPer for applications in different domains.

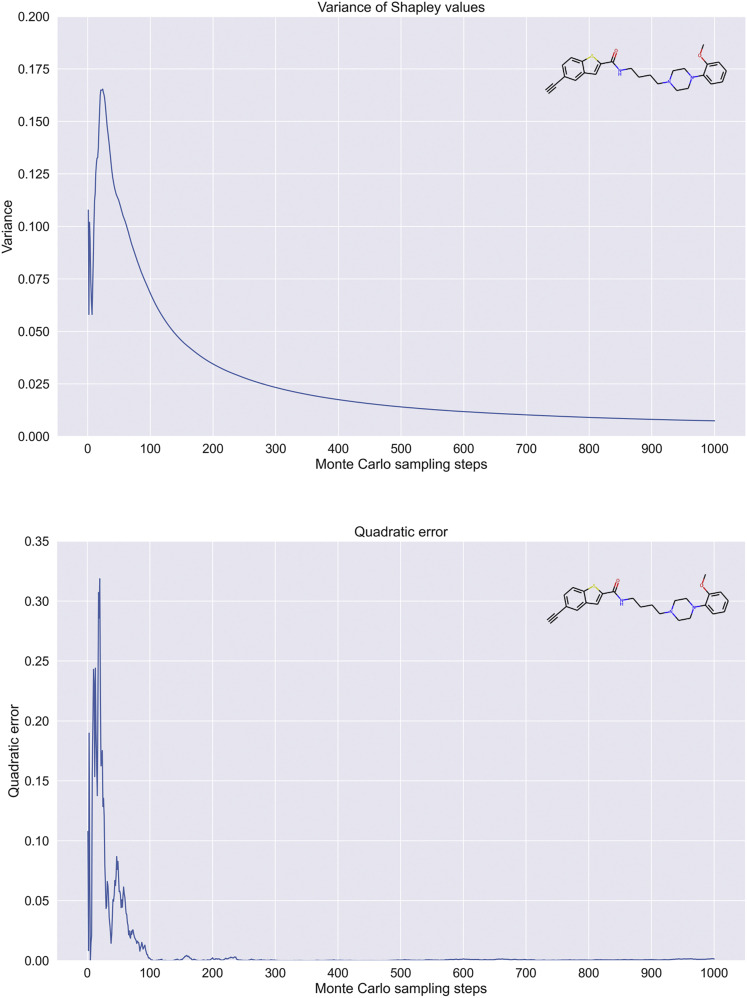
To study the evolution of the approximation over sampling steps and determine the number of steps required for a reliable approximation value, we analyzed the variance and convergence for EdgeSHAPer. The random variable was given by the sum of Shapley values ${\phi }_j\left(G\right)$, for any edge $j$ of the graph, and the expected value by output probability for the prediction. Figure 1A shows the evolution of variance and Figure 1B of the quadratic error for a test compound. The quadratic error represents the deviation between the predicted probability and the sum of Shapley values.

Figure 1.

EdgeSHAPer variance and error convergence

Shown are variance (top graph) and error convergence (bottom) for an exemplary test compound over increasing numbers of Monte Carlo sampling steps.

Increasing numbers of Monte Carlo sampling steps yielded an accurate and stable approximation of the prediction probability as the sum of the Shapley values. During sampling, the variance decreased asymptotically against 0 (Figure 1A) and the quadratic error was already very close to 0 after only 100 steps (Figure 1A). Therefore, given the need to evaluate EdgeSHAPer on a large set of samples, $M=100$ was considered a proper choice, providing a favorable compromise between approximation accuracy and computational time requirements. In addition, a termination criterion was implemented for the sampling procedure defining a permitted deviation between the sum of the Shapley values and the predicted probability.

Consistent with GNN learning, EdgeSHAPer considers both directions for edges; each direction has its own contribution. Given the additivity property of Shapley values, the total contribution of an edge can be calculated by summing the Shapley values for the two directions. The final output of the algorithm is a ranking of edges on the basis of approximated Shapley values.

Specific evaluation metrics

To quantitatively evaluate the performance of GNN explanation methods, two metrics were introduced including FID+ (Fidelity) and FID- (Infidelity) (Yuan et al., 2022). These metrics evaluate the quality of unimportant and important features, respectively, and are defined as:

$$FID+=\frac{1}{N}\sum _{i=0}^{N}f\left(G_i\right)–f\left(U_i\right)$$

and

$$FID-=\frac{1}{N}\sum _{i=0}^{N}f\left(G_i\right)–f\left(I_i\right)$$

where $G_i$ is the original graph, $U_i$ is the graph obtained from $G_i$ exclusively containing unimportant features (nodes, edges, or node/edge features), $I_i$ is the graph obtained by $G_i$ exclusively containing important features, and $N$ is the number of samples (graphs) for which the metric is computed. Herein, the probability version of FID+ and FID- was used, as introduced previously (Yuan et al., 2021). An ML model with meaningful feature representation should tend to produce high FID+ and low FID- scores.

In our work, we used an adapted version of these metrics relying on minimal sets of relevant features. The pertinent positive set ($P_{POS}$) (Herman, 2016) represents the minimal set of features required for a given class label prediction of an instance. Moreover, we defined the minimal top-k set ($T_K$) as the minimal set of features that need to be removed to invert the class label (here from active to inactive). Those sets are composed of the features with the highest Shapley value estimates from EdgeSHAPer. $P_{POS}$ is created in an inductive manner by adding edges with the highest Shapley values one by one to the graph until a test compound is correctly predicted to be active. By contrast, $T_K$ is obtained following a deductive approach; starting from a compound correctly predicted to be active, the most important edges are removed until the molecule is classified as inactive. The consideration of such minimal feature sets determining class label predictions is related to the concept of contrastive explanations (Lipton, 1990; Molnar, 2020). This feature selection scheme ensured that most influential features for predictions were identified on the basis of (molecular) graphs with varying numbers of edges (bonds). FID+ and FID- are computed on the basis of $T_K$ and $P_{POS}$, respectively.

Compound classification

We applied GCN and random forest (RF) (Breiman, 2001) models to a compound classification task aiming to systematically distinguish between dopamine D2 receptor ligands and other randomly selected active compounds.

For the RF model, a balanced accuracy (BA) of 0.99 was obtained for the test set. Furthermore, 99% of the active compounds were successfully identified, while maintaining a high precision of 0.99. The GCN model also achieved a high BA of 0.97 for the test set. In addition, to evaluate the stability of the predictive performance and model explanations, the training set was divided into three disjoint subsets and the GCN was re-trained on each of these size-reduced partitions. Despite the smaller number of training samples, only slightly lower mean classification BA of 0.95 was obtained. Hence, these results confirmed the stability of the GCN predictions. The high level of classification accuracy achieved by RF and alternative GCN models provided a sound basis for explaining compound activity predictions and comparing different methods. Predictions of these models were first used to evaluate the consistency of EdgeSHAPer explanations, followed by orthogonal feature mapping analysis in comparison to TreeExplainer for RF as well as quantitative and qualitative comparisons to GNNExplainer.

Explaining GCN predictions

EdgeSHAPer explanations and their consistency

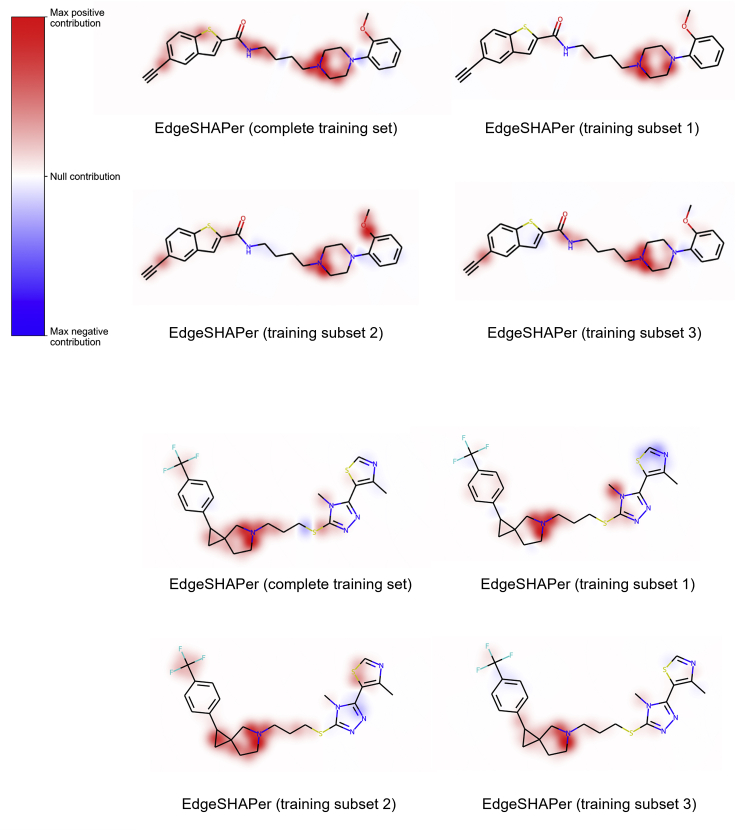
Initially, we evaluated EdgeSHAPer explanations and their consistency for training sets of different size and composition. EdgeSHAPer was applied to multiple GCN models derived on the basis of a complete training set or random training data subsets. These explanation results were quantitatively and qualitatively compared. Quantitative comparisons were carried out on the basis of the FID+ and FID- metric variants to assess minimal features sets determining correct predictions of active compounds. Qualitative comparison with feature visualizations was also obtained by mapping minimal feature sets on correctly predicted test compounds.

Edges prioritized by EdgeSHAPer were mapped on test compounds (Figure 2). In this and the following figures, coloring identifies most important edges representing covalent bonds. Red coloring indicates positive (supporting the prediction) and blue negative contributions (opposing the prediction). The intensity of the color scales with increasing edge importance. For test compounds belonging to different chemical series, depicted in Figures 2A and 2B, respectively, feature mapping revealed that edges prioritized by EdgeSHAPer consistently formed the same coherent substructures in test compounds predicted with GCN models derived on full and partial training sets. Minor differences between features prioritized using non-overlapping subsets with distinct compounds are expected. Importantly, for each chemical series, the same coherent substructures responsible for correct predictions were identified in different test compounds using distinct subsets of only one-third of the size of the original training set, indicating the stability of the EdgeSHAPer results. For GCN models generated with different training subsets of reduced size, the identified substructures were slightly smaller than for the model trained on complete training set, due to the lower number of training instances and features in subsets. It is emphasized that the formation of coherent substructures of limited size by prioritized features in both compound series revealed that these features delineated chemically meaningful substructures determining the predictions. Furthermore, as also shown in Figure 2, positive contributions clearly dominated correct compound activity predictions, with only very little balancing influence of negative contributions.

Figure 2.

EdgeSHAPer explanations for differently trained models

In (A, top)) and (B, bottom), explanations are provided for exemplary test compounds. The color bar in (A) applies to Figure 2, Figure 3, Figure 4.

Visual analysis was complemented and confirmed by the quantitative assessment in Table 1, reporting differences on the basis of FID+ and FID- values and the cardinalities of the minimally informative sets. Hence, EdgeSHAPer explanations were non-ambiguous, consistent, and stable.

Table 1.

Mean test set FID+ and FID- scores for EdgeSHAPer and the complete training set as well as non-overlapping subsets of the training set and the mean number of edges comprising the minimal sets

	FID+	FID-	# edges in ${\mathit{P}}_{\mathit{POS}}$	# edges in ${\mathit{T}}_{\mathit{k}}$
Training set	0.934	0.137	12.85	3.75
Training subset 1	0.886	0.108	5.50	4.80
Training subset 2	0.851	0.245	7.20	3.75
Training subset 3	0.926	0.120	7.45	4.10

EdgeSHAPer vs. TreeExplainer

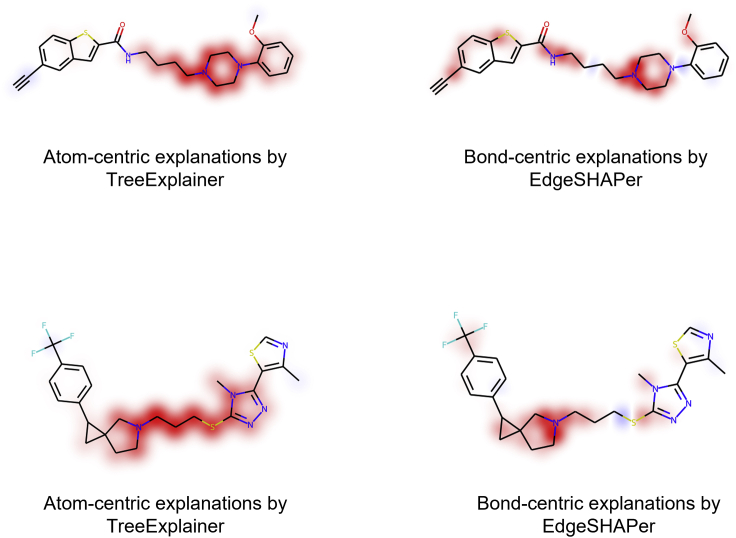
An orthogonal qualitative comparison of features determining GCN and RF predictions was also carried out. Therefore, the EdgeSHAPer and TreeExplainer methods were applied to rationalize GCN and RF predictions, respectively. In this case, substructures delineated by principally distinct molecular features, that is, pre-defined structural features for RF and the representation learned by GCN, were compared. For this analysis, RF models were implemented in combination with TreeExplainer since it enables exact (rather than locally approximated) calculation of SHAP values for decision tree methods and is node (atom)-centric, in contrast to EdgeSHAPer. Figure 3 shows representative results.

Figure 3.

Mapping of features determining RF and GCN predictions

In (A, top) and (B, bottom), mappings are shown for exemplary test compounds.

EdgeSHAPer’s bond-centric and TreeExplainer’s atom-centric explanations delineated overlapping yet distinct substructures responsible for correct predictions, despite the use of different ML algorithms with pre-defined vs. learned representation features, respectively. While these results were not necessarily expected, they supported the relevance and robustness of the SHAP-based explanatory framework. Notably, substructures identified by EdgeSHAPer explanations were smaller than those identified by TreeExplainer, which either resulted from the different features used or corresponded to higher resolution of EdgeSHAPer explanations, focusing on substructures decisive for predictions.

EdgeSHAPer vs. GNNExplainer

EdgeSHAPer was then compared to GNNExplainer, which is also exclusively considering edges for model explanation and does not employ other local approximation methods. The same quantitative/qualitative analysis scheme as above was applied. Table 2 reports the quantitative comparison. EdgeSHAPer identified smaller pertinent positive sets of chemical bonds required for accurate predictions, similar to the observations discussed above. Furthermore, EdgeSHAPer yielded higher FID+ scores than GNNExplainer and identified smaller minimal top-k sets. GNNExplainer produced low FID- scores since it identified minimal sets with larger numbers of edges. Indeed, pertinent positive sets with increasing numbers of features rendered predicted probabilities closer to the original probability of a prediction, which led to decreasing FID- values. However, EdgeSHAPer scores were of comparable magnitude showing that its smaller pertinent positive sets conveyed important information. Table 3 shows the comparison of the explanations for the training subsets, again confirming the stability of the results and higher resolution of EdgeSHAPer’s explanations.

Table 2.

Mean test set FID+ and FID- scores for EdgeSHAPer and GNNExplainer for the complete training set and mean number of edges comprising the minimal sets

	FID+	FID-	# edges in ${\mathit{P}}_{\mathit{POS}}$	# edges in ${\mathit{T}}_{\mathit{k}}$
EdgeSHAPer	0.934	0.137	12.85	3.75
GNNExplainer	0.813	0.154	31.10	15.55

Table 3.

Mean test set FID+ and FID- scores for EdgeSHAPer and GNNExplainer for the training subsets and mean number of edges comprising the minimal sets of the subsets

	FID+	FID-	# edges in ${\mathit{P}}_{\mathit{POS}}$	# edges in ${\mathit{T}}_{\mathit{k}}$
EdgeSHAPer	0.888	0.158	6.72	4.22
GNNExplainer	0.782	0.176	22.40	21.83

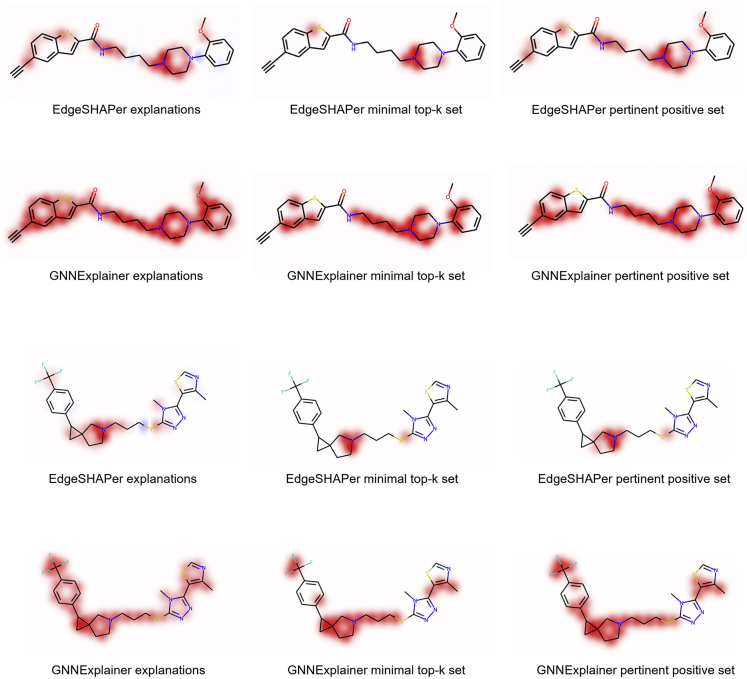
Feature mapping gave consistent results (Figure 4). As observed in the comparisons discussed above, EdgeSHAPer identified small coherent substructures in test compounds driving correct predictions, whereas features prioritized by GNNExplainer frequently covered entire compounds, making it difficult to rationalize and differentiate between predictions. As discussed above, the formation of coherent substructures by features prioritized by EdgeSHAPer that were much smaller than the ones delineated by GNNExplainer clearly indicated that chemically meaningful structural motifs were driving the predictions, as identified by EdgeSHAPer.

Figure 4.

Mapping of minimal feature sets identified by EdgeSHAPer or GNNExplainer

In (A, top) and (B, bottom), mappings are shown for exemplary test compounds.

Taken together, the results indicated that EdgeSHAPer distinguished between bonds of different relevance for correct predictions at a higher resolution than GNNExplainer. Moreover, $T_K$ edges found by EdgeSHAPer were critically important for the predictions. Removal of these bonds eliminated substructural coherency while determining $P_{POS}$ edges using EdgeSHAPer revealed how salient substructures evolved, representing a high level of consistency between feature importance assessment and mapping.

We also determined the correlation between edge/bond importance derived using the different explanation methods. Since the absolute values from the different methods could not be directly compared, we computed different rank correlation coefficients for importance-based edge rankings including Spearman’s, Pearson’s, and Kendall $\text{τ}$ coefficients (Forthofer and Lehnen, 1981), as reported in Table 4. For both the complete ranking and the top 25% of ranked edges, correlation coefficients were generally close to 0, indicating the presence of largely distinct rankings produced with the different methods. These findings also reinforced the need for feature mapping and identification of coherent substructures determining the predictions, which are indicative of meaningful bond ensembles prioritize for model explanation, as shown for EdgeSHAPer above.

Table 4.

Rank correlation coefficients for EdgeSHAPer compared to TreeExplainer and GNNExplainer for the complete ranking and the most important edges (top 25%), reported as the mean over the test set

	Spearman	Pearson	Kendall $\mathbf{\tau }$
Complete ranking
TreeExplainer	0.097	0.097	0.070
GNNExplainer	−0.010	−0.010	0.022
Top 25%
TreeExplainer	0.013	0.055	0.022
GNNExplainer	0.012	0.012	0.016

Discussion

With EdgeSHAPer, we have introduced a novel methodology devised to assess the importance of edge information for GNN-based predictions. Even though GNNs are increasingly popular in many fields, including chemoinformatics and medicinal chemistry, they are among the most challenging ML models to explain (Jimenez-Luna et al., 2022). EdgeSHAPer combines the Shapley value concept from cooperative game theory and a novel Monte Carlo sampling strategy. Shapley values determining predictions are estimated for each edge of a graph. By analyzing Shapley value contributions, informative graph pathways can be identified. Given its edge-centric nature, EdgeSHAPer is particularly attractive for chemical applications where edges correspond to bonds connecting atoms in a molecular graph. However, EdgeSHAPer is by no means confined to rationalizing compound predictions, but generally applicable to any GNN.

In our proof-of-concept investigation, ML-based compound activity predictions were carried out and explained. Feature attributions from EdgeSHAPer were compared to a popular SHAP method for explaining decision tree models (TreeExplainer) and the only other edge-centric explanation method that is currently available, representing the state-of-the-art in the field (GNNExplainer). For correct predictions, EdgeSHAPer yielded high fidelity scores and smallest pertinent positive feature sets. Although GNNExplainer is designed to identify the subgraph determining an individual prediction, EdgeSHAPer produced smaller edge sets driving correct model decisions, leading to simpler interpretations.

Feature mapping on compound structure representations provides intuitive access to predictions for chemists. Substructures delineated by edges determining correct predictions can be interpreted in molecular terms. Such visualizations revealed the formation of coherent substructural motifs by bonds prioritized by EdgeSHAPer. The reference methods identified larger feature sets responsible for activity predictions, which often encompassed nearly complete compound structures. These findings indicated higher resolution of EdgeSHAPer explanations.

Our analysis clearly showed that GNN-based molecular predictions can be rationalized on the basis of edge/bond information, rather than node/atom information, which has mostly been attempted thus far. This might be especially interesting for MPNNs centered on bonds instead of atoms, which avoid unnecessary loops during the message passing phase, as proposed for molecular property prediction (Yang et al., 2019). Taken together, our findings indicate that EdgeSHAPer further extends the spectrum of current XAI approaches for chemical applications and beyond and should merit further consideration. To these ends, EdgeSHAPer code is made freely available to the scientific community to support methodological extensions and refinements as well as further applications in different areas.

Limitations of the study

EdgeSHAPer depends on a Monte-Carlo sampling procedure that is heuristic in nature and requires application-specific monitoring.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Compound activity data	ChEMBL 30	https://doi.org/10.6019/CHEMBL.database.30
Confirmed aggregators	Aggregator advisor	http://advisor.docking.org/faq/#Data
Datasets	This paper	https://github.com/AndMastro/EdgeSHAPer/tree/main/experiments/data https://doi.org/10.17632/bs6myg75tr.1
Software and algorithms
RDKit	Zenodo	https://doi.org/10.5281/zenodo.6605135
Lilly-Medchem-Rules	GitHub	https://github.com/IanAWatson/Lilly-Medchem-Rules
Scikit-learn	GitHub	https://github.com/scikit-learn/scikit-learn
PyTorch	GitHub	https://github.com/pytorch/pytorch
EdgeSHAPer	This paper	https://github.com/AndMastro/EdgeSHAPer

Resource availability

Lead contact

Further information and requests for code and resources should be directed to and will be fulfilled by the lead contact, Jürgen Bajorath (bajorath@bit.uni-bonn.de).

Materials availability

This study did not generate new unique reagents.

Method details

Graph convolutional network model

Any GNN model can be explained using EdgeSHAPer. For our proof-of-concept study, we used a graph convolutional network (GCN) (Kipf and Welling, 2016), due to its increasing popularity in chemistry. The model was constituted by four convolutional layers with 256 hidden units and rectified linear unit (ReLU) as activation function. Global mean pooling and dropout with probability of 0.5 were considered. The GCN was trained for 100 epochs with a batch size of 32, Adam optimizer (Kingma and Ba, 2014) and a learning rate of 0.001. The model was implemented in PyTorch (Paszke et al., 2019).

Application to compound activity prediction

To provide a meaningful basis for the assessment and comparison of explanation methods, we selected a test case that was expected to yield high ML classification accuracy based on prior experience. Therefore, compounds with activity against the dopamine D2 receptor were selected. Compounds and corresponding exact (“ = ”) standard potency measurements (K_i, K_d or IC₅₀) of at least 10 μM were obtained from ChEMBL (version 29) (Bento et al., 2014) and recorded as the negative decadic logarithm. Only direct interactions (target relationship type: “D”) against human wild-type proteins at the highest target confidence level (target confidence score: 9) were retained, while discarding measurements flagged as “potential author error'” or “potential transcription error”. Using publicly available filters (Landrum, 2013; Irwin et al., 2015; Bruns and Watson, 2012) molecules exceeding a mass of 1000 Da were removed along with potential assay interference compounds. Based on this protocol, 4174 active compounds were obtained and complemented with an equal number of randomly selected active compounds (omitting ligands with activity against functionally related G protein-coupled receptors). The compound dataset was divided into training (80%), validation (10%) and test (10%) sets.

Random forest classifier

The random forest (RF) algorithm consists of an ensemble of decision trees built with bootstrapping and feature bagging. The scikit-learn RF implementation was utilized (Pedregosa et al., 2011). For RF classification, structural features of compounds were generated and hashed using the RDKit implementation of the Morgan fingerprint with a bond radius of 2 (Landrum, 2013; Rogers and Hahn, 2010). The presence or absence of generated features was recorded in a binary feature vector in which features were mapped to unique positions.

RF classifiers with different hyperparameter settings were derived for 50% of the training set and evaluated on the remaining training set compounds (representing a validation set). Hyperparameters’ grid search included number of decision trees (25, 50, 100, 200, 400), minimum number of samples per node split (2, 3, 5, 10), and minimum number of samples per leaf node (1, 2, 5, 10) and hyperparameter value combinations with the highest balanced accuracy (BA) over 10 independent training-validation partitions were used to derive the final classifier on the complete training set. BA is defined below, where TP, TN, FP, FN are true positive, true negative, false positive, and false negative predictions, respectively.

$$BA=\frac{1}{2}·\left(\frac{TP}{TP+FN}+\frac{TN}{TN+FP}\right)$$

Exact Shapley values for predicted class probabilities of RF classifiers (fraction of positive predictions in the tree ensemble) were calculated using the TreeExplainer algorithm with the interventional feature perturbation approach, for which the training data served as a background sample (Rodríguez-Pérez and Bajorath, 2020b; Lundberg et al., 2020).

Computational complexity of EdgeSHAPer

The computational complexity of EdgeSHAPer with Monte Carlo sampling for a single graph is $O\left({\left|E\right|}^2\right)·O\left(M\right)$, as derived below.

In Algorithm 1, the loop starting at line 2 contains operations with cost $O\left(\left|N\right|\right)$ (line 3) and $O\left(\left|E\right|\right)$ (lines 4, 6, 8, 9, 10 and 11). The cost of the remaining operations is constant. We note that the complexity of the GNN forward pass at line 13 is omitted from the analysis, given that it is highly dependent on the architecture used. Thus, operations in the loop have an asymptotic cost of $O\left(\left|N\right|\right)+O\left(\left|E\right|\right)$. Given that the loop is iterated M times, the overall cost for a single edge becomes $O\left(M\right)·\left(O\left(\left|N\right|\right)+O\left(\left|E\right|\right)\right)$. Furthermore, given that the number of nodes and edges in a molecular graph typically is of comparable magnitude, we can approximate $\left|N\right|\sim \left|E\right|$, obtaining an asymptotic cost of $O\left(M\right)·2\left(O\left(\left|E\right|\right)\right)=O\left(M\right)·\text{O}\left(\left|\text{E}\right|\right)$. Since the operation must be repeated for all the edges in a molecular graph, the overall asymptotic cost is $O\left({\left|E\right|}^2\right)·O\left(M\right)$.

Published: October 21, 2022

Data and code availability

• Compound data and model results have been deposited at GitHub and are publicly available as of the date of publication. Accession numbers are listed in the Key resources table.

• The source code and compound data used in this study can be accessed at https://github.com/AndMastro/EdgeSHAPer. The compound data, training, validation and test sets are also available as a Mendeley Data.

• All original code has been deposited at GitHub and is publicly available as of the date of publication.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.