Abstract
Embolic stroke (ES) is characterized by high morbidity and mortality. Its mortality predictors remain unclear. The present study aimed to use machine learning (ML) to identify the key predictors of mortality for ES patients in the intensive care unit (ICU). Data were extracted from two large ICU databases: Medical Information Mart for Intensive Care (MIMIC)-IV for training and internal validation, and eICU Collaborative Research Database (eICU-CRD) for external validation. We developed predictive models of ES mortality based on 15 ML algorithms. We relied on the synthetic minority oversampling technique (SMOTE) to address class imbalance. Our main performance metric was area under the receiver operating characteristic (AUROC). We adopted recursive feature elimination (RFE) for feature selection. We assessed model performance using three disease-severity scoring systems as benchmarks. Of the 1566 and 207 ES patients enrolled in the two databases, there were 173 (15.70%), 73 (15.57%), and 36 (17.39%) hospital mortality in the training, internal validation, and external validation cohort, respectively. The random forest (RF) model had the largest AUROC (0.806) in the internal validation phase and was chosen as the best model. The AUROC of the RF compact (RF-COM) model containing the top six features identified by RFE was 0.795. In the external validation phase, the AUROC of the RF model was 0.838, and the RF-COM model was 0.830, outperforming other models. Our findings suggest that the RF model was the best model and the top six predictors of ES hospital mortality were Glasgow Coma Scale, white blood cell, blood urea nitrogen, bicarbonate, age, and mechanical ventilation.
Keywords: feature selection, machine learning, MIMIC-IV, prediction model, random forest
Introduction
According to the systematic analysis for the Global Burden of Disease Study 2019, stroke was the second-leading cause of death and the third-leading cause of disability and death [1]. Ischemic stroke (IS) accounts for ∼62.4% of all new-onset strokes [1]. Embolic stroke (ES), also called cerebral embolism, is the most common subtype of IS and the most rapidly developing type of all strokes [2,3]. Furthermore, compared with other stroke subtypes, ES has a higher disease severity, a poorer prognosis, and a higher recurrence rate [4]. Therefore, ES is a huge burden on society due to reduced quality of life, lost productivity, premature mortality, and intangible costs, particularly for the critically ill patients in the intensive care unit (ICU) [5,6].
Prediction and prognosis are central to medicine. All diagnostic and therapeutic measures aim at improving prognosis outcomes [7]. Clinicians need to make predictions on the disease prognosis to support their decision-making. However, it is challenging for clinicians to accurately assess the disease severity and predict the outcome in patients with various clinical data based on initial intuition. Consequently, several disease-severity scoring systems have been developed over the last few decades, such as the Acute Physiology and Chronic Health Evaluation III (APACHE III) [8], Sequential Organ Failure Assessment (SOFA) score [9], and Oxford Acute Severity of Illness Score (OASIS) [10]. The scoring systems are intrinsically prediction models. They combine a variety of variables that represent predictors of disease severity to predict the prognostic outcome. Due to their predictive validity, they gradually became essential tools for clinical decision-making.
A notable fact is that almost all scoring systems depend on linear models to identify relevant predictors. With the increase in clinical data on potential predictors of outcome, nonlinearity may exist. Scoring systems may fail to capture nonlinear relationships and complex interactions among predictors. Moreover, scoring systems artificially discretize continuous variables, which may cause the loss of predictive information [11]. Additionally, they are generalistic severity of illness scoring systems that are not targeted to specific diseases; therefore, they have shown mixed prediction accuracy in different diseases [12], high for some diseases, such as sepsis, but low for most diseases, such as craniocerebral diseases [13–15].
In recent years, machine learning (ML) applications have grown in popularity across a wide range of domains [16]. ML makes fewer assumptions in prediction modeling than traditional statistical approaches. It is a demonstrably powerful technique because it can handle a high number of features (i.e., predictors), consider all possible permutations, and learn nonlinear relationships and interactions without requiring a predetermined linear relationship input by the researcher [17,18]. Feature selection is an important aspect in practical applications of ML. It reduces the dimensionality by choosing relevant features and eliminating irrelevant features to improve the prediction performance of the predictors and provide cost-effective predictors [19].
ML has been successfully used to aid clinical diagnosis and improve the ability to predict patient outcomes [20], while the feature selection strategies have often been used to identify key prognosis risk factors, genes, and proteins for diseases [21,22]. However, as far as we know at present, there has been no ML-based study to explore the mortality predictors for ES patients to date. Therefore, the present study attempts to apply multiple ML algorithms to the data derived from the ES patient cohorts of two large ICU databases. Through rigorous ML modeling and feature selection techniques, we hope to build an ML model that has a better prediction performance for critically ill ES patients than the commonly used scoring systems and identify the key mortality predictors.
Materials and methods
Data sources
This is a retrospective cohort study with the data of ES patients derived from two public ICU databases: Medical Information Mart for Intensive Care (MIMIC)-IV [23] and eICU Collaborative Research Database (eICU-CRD) [24]. MIMIC-IV is an updated version of the MIMIC-III database and contains comprehensive clinical data of patients admitted to the ICU at Beth Israel Deaconess Medical Center between 2008 and 2019. eICU-CRD is a multicenter database with de-identified health data for >200,000 admissions to ICU in the United States between 2014 and 2015. An author (Wei Liu) of the present study was granted access to the databases (Record ID: 36180968). The present study is reported according to the guidelines of the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement [25]. Informed consent is not required because all the health information data are anonymous.
Selection of participants
To describe and analyze the two databases, we used PostgreSQL (version 13) and Navicat Premium (version 15). An author (Wei Liu) extracted the data, which was then double-checked by another author (Wei Ma) of the present study. The search terms are presented in Supplementary Material Table S1. Patients’ exclusion criteria were as follows: (i) age <18 years, (ii) not first ICU admission, (iii) inability to obtain Acute Physiology Score III (APSIII), OASIS, SOFA, and Glasgow Coma Scale (GCS) scores and (iv) missing outcome (death or survival).
Predictors and outcome
Most disease-severity scoring systems, such as APSIII, SOFA, and OASIS, collect data from the first 24 h after admission. We thus extracted predictors during the patient’s first 24 h in the ICU. We initially included 90 readily available candidate predictors based on literature reviews [26,27], expert clinical opinion, and clinical availability in practice. After removing predictors with a missing proportion of >20%, we included a total of 58 predictors in both databases (see Supplementary Material Table S2). In our analysis, we used the mean values for some predictors that were measured multiple times to determine the central tendency of the patients’ condition. The outcome was hospital mortality, defined as the vital status for survival or death at hospital discharge.
Model building and tuning
ML methods were performed using R software (version 4.1.3). The ‘caret’ package (version 6.0-92) was used for model building, tuning, and validation [28]. We build 15 ML models to improve the probability of identifying the best ML model, including linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), partial least squares discriminant analysis (PLSDA), logistic regression (LR), least absolute shrinkage and selection operator (LASSO), naive Bayes (NB), and support vector machine (SVM) with three types of kernel: a radial basis function kernel (SVM-R), a linear kernel (SVM-L), a polynomial kernel (SVM-P), k-nearest neighbor (KNN), C5.0 decision tree, repeated incremental pruning to produce error reduction (RIPPER), random forest (RF), extreme gradient boosting machine (XGBoost), and neural network (NNET). For models with tuning parameters that needed optimization, we adjusted parameters via random search with tune length of 15 whenever applicable.
Data preprocessing
As most ML models cannot handle missing data [29], we performed a multiple imputation model using multiple imputation by chained equation (MICE) in the R software [30]. Dummy variables were created for categorical predictors. Some models benefit from the predictors that are on a common scale and with reduced skewness (LDA, QDA, PLSDA, KNN, LR, LASSO, NB, SVM, and NNET); therefore, data were scaled, centered, and BoxCox transformed [29]. No data transformation was performed for the tree-based models (C5.0, RF, and XGBoost) and rule-based models (RIPPER).
Model improvement and evaluation
Data distribution from MIMIC-IV and eICU-CRD is unbalanced: the survival and death groups ratio are about 1:5. The imbalance may result in a classification bias toward the majority class [31]. Therefore, we used the synthetic minority oversampling technique (SMOTE) to tackle the imbalance [32]. All models were subjected to three repetitions of 10-fold cross-validation to evaluate their performance. Receiver operating characteristic (ROC) curves were plotted, and the area under the ROC (AUROC) was used as the performance metric because of the data imbalance [33]. The best threshold of the AUROC (BTOA), area under the precision-recall curve (AUPRC), accuracy, positive predictive value (PPV), negative predictive value (NPV), F1-score, and Cohen’s kappa value were also reported. LR was used to construct models of the scoring systems as benchmarks for evaluating ML models.
Feature selection
Feature selection was performed using recursive feature elimination (RFE) algorithm with the function ‘rfe’ in R package ‘caret’ (version 6.0-92) for the 14 ML models (LASSO was excluded because of its inherent feature selection function) [34]. RFE begins by building a model on the entire set of features, and the importance of each feature is calculated either using the provided ML model (e.g., some algorithms like RF offer importance scores) or by using a statistical method (e.g., the AUROC). Then, the least important features are removed, the model is re-built, and importance scores are computed again. This procedure is recursively repeated until the desired number of feature subsets is eventually reached. However, considering the highly time-consuming calculation of RFE, the feature subset sizes we ran contained ten items: 2, 3, 4, 5, 6, 10, 20, 35, 45, and 58.
Model interpretation
The feature selection models can be regarded as the global interpretability method and can help understand the predictors and their overall relationship with the outcome; however, they cannot realize individual predictions. Therefore, we used the local interpretable model-agnostic explanation (LIME) to explain the impact of key features at the individual level [35]. LIME explains the classifier using a local linear model to approximate key features. Its output is an explanation list, indicating the contribution of key features to the outcome in an individual patient.
Statistical analysis
Baseline characteristics were compared between the survival and death groups to determine their baseline comparability. The Kolmogorov–Smirnov test was used to determine normality. Continuous variables were expressed as the mean [standard deviation (SD)] (normal) or the median [interquartile range (IQR)] (non-normal). Categorical variables were expressed as the total number (percentages). The Student’s t-test (normal) or rank-sum test for continuous variables (non-normal) and chi-square test for categorical variables were used. All statistical analyses were performed in R (version 4.1.3). A two-tailed P-value < 0.05 was considered statistically significant.
Results
Baseline characteristics
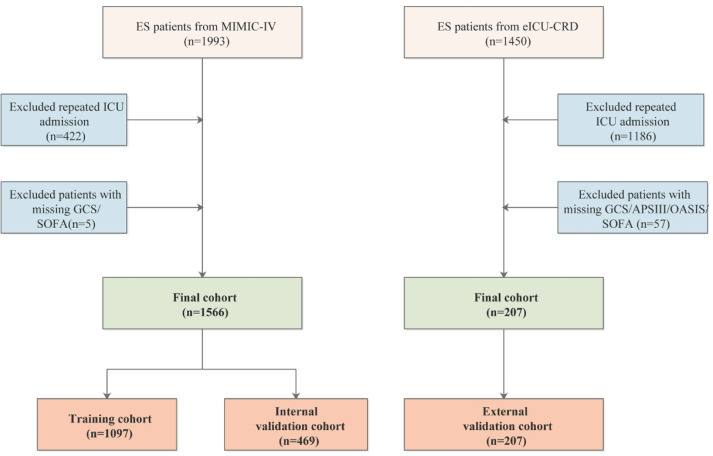
Figure 1 showed the flow chart of participants’ selection in the present study. A total of 1566 and 207 ES patients were enrolled in the MIMIC-IV and eICU-CRD cohorts, respectively. The MIMIC-IV cohort was randomly split into a training cohort (70%, n=1097) and an internal validation cohort (30%, n=469). The eICU-CRD cohort was used as an external validation cohort. Demographics and baseline characteristics between the survival and death groups are summarized in Table 1. In the present study, there were 173 (15.70%), 73(15.57%), and 36 (17.39%) hospital mortality in the training cohort, internal validation cohort, and external validation cohort, respectively. There were 37 variables with statistically significant differences between the survival and death groups at the MIMIC-IV baseline, 15 variables at the eICU-CRD baseline, only 13 variables in both the databases, including APSIII, SOFA, OASIS, GCS, heart rate, red cell volume distribution width (RDW), blood urea nitrogen (BUN), creatinine, potassium, endocarditis, thrombocytopenia, coagulopathy, and mechanical ventilation (MV).
Figure 1. Flow chart of participants selection.
Table 1. Baseline characteristics of the MIMIC-IV and eICU-CRD cohorts.
| Patient characteristics | MIMIC IV cohort (n=1566) | eICU-CRD cohort (n=207) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Training set (n=1097) | Internal validation set (n=469) | External validation set (n=207) | |||||||
| Death, n=173 | Survival, n=924 | P | Death, n=73 | Survival, n=396 | P | Death, n=36 | Survival, n=171 | P | |
| Demographic characteristics | |||||||||
| Age (years) | 80.00 | 71.00 | <0.001 | 77.00 | 72.00 | 0.016 | 69.50 | 72.00 | 0.972 |
| [67.00, 86.00] | [61.00, 82.00] | [67.00, 87.00] | [60.00, 83.25] | [56.25, 83.00] | [59.00, 80.00] | ||||
| Weight (kg) | 74.20 | 76.10 | 0.120 | 75.00 | 77.25 | 0.618 | 75.67 | 79.65 | 0.193 |
| [62.30, 88.30] | [63.58, 91.05] | [63.90, 88.25] | [64.97, 90.05] | [62.75, 85.12] | [69.40, 92.78] | ||||
| Gender (n, %) | 0.424 | ∼1 | |||||||
| Women | 96 (55.5) | 479 (51.8) | 36 (49.3) | 197 (49.7) | 20 (55.6) | 87 (51.2) | 0.769 | ||
| Man | 77 (44.5) | 445 (48.2) | 37 (50.7) | 199 (50.3) | 16 (44.4) | 83 (48.8) | |||
| Ethnicity (%) | 0.017 | 0.060 | |||||||
| Caucasian | 102 (59.0) | 584 (63.2) | 40 (54.8) | 257 (64.9) | 31 (86.1) | 139 (81.3) | 0.691 | ||
| African American | 10 (5.8) | 94 (10.2) | 6 (8.2) | 43 (10.9) | 1 (2.8) | 14 (8.2) | |||
| Asian | 6 (3.5) | 20 (2.2) | 2 (2.7) | 12 (3.0) | 0 (0.0) | 3 (1.8) | |||
| Hispanic/Latino | 3 (1.7) | 35 (3.8) | 2 (2.7) | 18 (4.5) | 2 (5.6) | 6 (3.5) | |||
| Others/Unknown | 52 (30.1) | 191 (20.7) | 23 (31.5) | 66 (16.7) | 2 (5.6) | 9 (5.3) | |||
| Vital signs | |||||||||
| SBP (mmHg) | 123.50 | 130.00 | 0.001 | 129.00 | 130.00 | 0.560 | 126.33 | 131.74 | 0.267 |
| [109.00, 142.00] | [117.00, 144.00] | [115.00, 146.00] | [118.00, 144.75] | [111.49, 141.40] | [118.51, 147.52] | ||||
| DBP (mmHg) | 64.00 | 70.00 | <0.001 | 64.00 | 68.00 | 0.004 | 69.58 | 69.96 | 0.868 |
| [56.75, 74.25] | [60.00, 78.00] | [57.00, 74.00] | [61.00, 80.00] | (11.24) | (12.22) | ||||
| Heart_Rate (beat/min) | 88.50 | 80.00 | <0.001 | 87.00 | 80.00 | 0.003 | 92.97 | 81.24 | 0.002 |
| [74.75, 100.00] | [70.00, 91.00] | [74.00, 97.00] | [70.00, 91.00] | [81.31, 102.44] | [72.94, 93.00] | ||||
| Respiratory_Rate (breaths/min) | 21.00 | 19.00 | <0.001 | 19.00 | 19.00 | 0.119 | 19.74 | 18.18 | 0.092 |
| [18.00, 23.00] | [17.00, 21.00] | [18.00, 22.00] | [17.00, 21.00] | [17.71, 21.71] | [16.39, 21.00] | ||||
| Temperature (°C) | 36.90 | 36.80 | 0.338 | 36.90 | 36.90 | 0.175 | 37.17 | 36.80 | 0.010 |
| [36.60, 37.30] | [36.70, 37.10] | [36.70, 37.40] | [36.70, 37.10] | [36.79, 37.40] | [36.63, 37.14] | ||||
| SpO2 (%) | 97.10 | 96.90 | 0.254 | 97.70 | 97.00 | 0.018 | 97.65 | 97.25 | 0.215 |
| [95.65, 98.70] | [95.80, 98.10] | [96.30, 99.30] | [96.00, 98.30] | [96.48, 99.18] | [95.59, 98.43] | ||||
| Laboratory tests | |||||||||
| WBC(109/L) | 12.25 | 9.90 | <0.001 | 12.25 | 9.80 | <0.001 | 3.94 | 4.10 | 0.227 |
| [9.03, 15.79] | [8.00, 12.90] | [9.61, 16.85] | [7.70, 12.75] | (0.64) | (0.69) | ||||
| RBC(1012/L) | 3.66 | 4.04 | <0.001 | 3.76 | 3.93 | 0.035 | 3.89 | 4.12 | 0.205 |
| [3.13, 4.30] | [3.47, 4.51] | [3.09, 4.27] | [3.44, 4.42] | [3.45, 4.33] | [3.64, 4.60] | ||||
| MCH (pg) | 30.18 | 30.00 | 0.402 | 30.12 | 30.05 | 0.726 | 30.08 | 30.02 | 0.713 |
| [28.55, 31.50] | [28.60, 31.40] | [28.70, 31.45] | [28.60, 31.35] | [28.81, 31.88] | [28.71, 31.50] | ||||
| MCHC (g/dL) | 32.64 | 33.00 | <0.001 | 32.76 | 32.97 | 0.157 | 32.87 | 33.07 | 0.376 |
| [31.51, 33.50] | [32.03, 34.00] | [31.55, 33.81] | [32.10, 33.80] | (1.25) | (1.20) | ||||
| RDW (%) | 14.72 | 13.97 | <0.001 | 14.42 | 14.07 | 0.046 | 15.00 | 14.15 | 0.023 |
| [13.66, 16.54] | [13.20, 15.00] | [13.65, 15.68] | [13.20, 15.37] | [13.95, 16.03] | [13.40, 15.43] | ||||
| Hematocrit (%) | 34.50 | 36.42 | 0.001 | 32.73 | 35.60 | 0.015 | 35.72 | 36.83 | 0.334 |
| [28.61, 38.51] | [31.20, 40.40] | [28.02, 38.01] | [30.75, 39.60] | (5.82) | (6.18) | ||||
| Hemoglobin (g/dL) | 11.20 | 11.95 | <0.001 | 10.59 | 11.70 | 0.009 | 11.78 | 12.18 | 0.319 |
| [9.20, 12.74] | [10.20, 13.52] | [9.07, 12.53] | [10.17, 13.25] | (2.11) | (2.16) | ||||
| Platelets (109/L) | 198.50 | 207.67 | 0.389 | 195.50 | 201.50 | 0.234 | 195.50 | 203.00 | 0.055 |
| [147.50, 268.00] | [160.00, 260.25] | [137.50, 252.50] | [162.00, 258.50] | [133.58, 237.33] | [168.12, 256.00] | ||||
| Aniongap (mEq/L) | 16.00 | 14.50 | <0.001 | 15.00 | 14.67 | 0.040 | 9.37 | 9.00 | 0.947 |
| [13.67, 19.00] | [12.62, 16.50] | [13.00, 18.00] | [13.00, 17.00] | [7.00, 11.50] | [7.25, 12.00] | ||||
| Bicarbonate (mEq/L) | 21.80 | 23.50 | <0.001 | 22.50 | 23.00 | 0.011 | 25.50 | 25.00 | 0.876 |
| [19.00, 24.50] | [21.33, 25.50] | [19.84, 23.88] | [21.00, 25.00] | [22.15, 27.25] | [23.00, 26.63] | ||||
| BUN (mg/dL) | 26.84 | 18.33 | <0.001 | 22.60 | 18.00 | 0.042 | 25.86 | 17.00 | <0.001 |
| [18.46, 41.00] | [13.00, 26.00] | [14.16, 33.66] | [13.50, 26.50] | [20.50, 38.50] | [12.00, 23.50] | ||||
| Creatinine (mg/dL) | 1.19 | 0.95 | <0.001 | 1.10 | 0.97 | 0.167 | 1.16 | 0.90 | 0.001 |
| [0.85, 1.75] | [0.75, 1.25] | [0.78, 1.51] | [0.78, 1.35] | [0.91, 1.51] | [0.70, 1.17] | ||||
| Glucose (mEq/L) | 148.00 | 119.00 | <0.001 | 138.33 | 122.75 | 0.012 | 145.00 | 124.43 | 0.090 |
| [119.00, 194.92] | [102.16, 149.83] | [116.25, 172.88] | [105.38, 155.12] | [106.92, 194.90] | [106.00, 152.31] | ||||
| Chloride (mEq/L) | 104.00 | 104.00 | 0.873 | 104.60 | 104.00 | 0.546 | 105.10 | 105.16 | 0.942 |
| [99.50, 108.00] | [101.00, 107.00] | [101.00, 107.50] | [100.50, 107.00] | (5.21) | (4.10) | ||||
| Sodium (mEq/L) | 139.50 | 139.33 | 0.922 | 138.67 | 139.00 | 0.482 | 139.20 | 138.86 | 0.712 |
| [136.10, 142.00] | [137.00, 141.50] | [135.88, 141.22] | [136.50, 142.00] | [136.25, 141.50] | [137.00, 141.00] | ||||
| Potassium (mEq/L) | 4.25 | 4.10 | 0.002 | 4.17 | 4.10 | 0.378 | 4.30 | 3.94 | 0.001 |
| [3.90, 4.72] | [3.80, 4.40] | [3.84, 4.48] | [3.80, 4.45] | [3.72, 4.61] | [3.67, 4.15] | ||||
| Calcium (mg/dL) | 8.40 | 8.70 | <0.001 | 8.43 | 8.70 | 0.001 | 8.41 | 8.59 | 0.145 |
| [7.98, 8.95] | [8.25, 9.10] | [8.05, 8.72] | [8.20, 9.05] | (0.69) | (0.66) | ||||
| Comorbidities (%) | |||||||||
| COPD | 0.045 | 0.929 | 0.195 | ||||||
| No (n, %) | 129 (74.6) | 753 (81.5) | 59 (80.8) | 325 (82.1) | 32 (88.9) | 164 (95.9) | |||
| Yes (n, %) | 44 (25.4) | 171 (18.5) | 14 (19.2) | 71 (17.9) | 4 (11.1) | 7 (4.1) | |||
| CHD | 0.010 | 0.444 | 0.448 | ||||||
| No (n, %) | 113 (65.3) | 694 (75.1) | 57 (78.1) | 289 (73.0) | 30 (83.3) | 153 (89.5) | |||
| Yes (n, %) | 60 (34.7) | 230 (24.9) | 16 (21.9) | 107 (27.0) | 6 (16.7) | 18 (10.5) | |||
| CHF | <0.001 | 0.146 | 0.673 | ||||||
| No (n, %) | 100 (57.8) | 668 (72.3) | 44 (60.3) | 276 (69.7) | 28 (77.8) | 141 (82.5) | |||
| Yes (n, %) | 73 (42.2) | 256 (27.7) | 29 (39.7) | 120 (30.3) | 8 (22.2) | 30 (17.5) | |||
| Hypertension | 0.653 | ∼1 | ∼1 | ||||||
| No (n, %) | 133 (54.1) | 637 (48.3) | 35 (47.9) | 192 (48.5) | 20 (55.6) | 93 (54.4) | |||
| Yes (n, %) | 113 (45.9) | 683 (51.7) | 38 (52.1) | 204 (51.5) | 16 (44.4) | 78 (45.6) | |||
| Hyperlipidemia | 0.049 | 0.003 | 0.809 | ||||||
| No (n, %) | 98 (56.6) | 445 (48.2) | 51 (69.9) | 198 (50.0) | 30 (83.3) | 148 (86.5) | |||
| Yes (n, %) | 75 (43.4) | 479 (51.8) | 22 (30.1) | 198 (50.0) | 6 (16.7) | 23 (13.5) | |||
| AF | 0.002 | 0.433 | 0.611 | ||||||
| No (n, %) | 67 (38.7) | 482 (52.2) | 33 (45.2) | 202 (51.0) | 19 (52.8) | 101 (59.1) | |||
| Yes (n, %) | 106 (61.3) | 442 (47.8) | 40 (54.8) | 194 (49.0) | 17 (47.2) | 70 (40.9) | |||
| Endocarditis | 0.017 | 0.391 | 0.029 | ||||||
| No (n, %) | 151 (87.3) | 859 (93.0) | 66 (90.4) | 372 (93.9) | 28 (77.8) | 157 (91.8) | |||
| Yes (n, %) | 22 (12.7) | 65 (7.0) | 7 (9.6) | 24 (6.1) | 8 (22.2) | 14 (8.2) | |||
| Cardiomyopathy | 0.408 | 0.962 | ∼1.000 | ||||||
| No (n, %) | 162 (93.6) | 882 (95.5) | 70 (95.9) | 376 (94.9) | 34 (94.4) | 164 (95.9) | |||
| Yes (n, %) | 11 (6.4) | 42 (4.5) | 3 (4.1) | 20 (5.1) | 2 (5.6) | 7 (4.1) | |||
| Valve | 0.504 | 0.111 | 0.631 | ||||||
| No (n, %) | 164 (94.8) | 860 (93.1) | 71 (97.3) | 360 (90.9) | 33 (91.7) | 163 (95.3) | |||
| Yes (n, %) | 9 (5.2) | 64 (6.9) | 2 (2.7) | 36 (9.1) | 3 (8.3) | 8 (4.7) | |||
| PVD | 0.638 | 0.820 | 0.401 | ||||||
| No (n, %) | 150 (86.7) | 816 (88.3) | 64 (87.7) | 340 (85.9) | 33 (91.7) | 165 (96.5) | |||
| Yes (n, %) | 23 (13.3) | 108 (11.7) | 9 (12.3) | 56 (14.1) | 3 (8.3) | 6 (3.5) | |||
| Liver | 0.001 | 0.094 | ∼1.000 | ||||||
| No (n, %) | 154 (89.0) | 885 (95.8) | 63 (86.3) | 368 (92.9) | 35 (97.2) | 169 (98.8) | |||
| Yes (n, %) | 19 (11.0) | 39 (4.2) | 10 (13.7) | 28 (7.1) | 1 (2.8) | 2 (1.2) | |||
| Renal | <0.001 | 0.939 | 0.061 | ||||||
| No (n, %) | 119 (68.8) | 755 (81.7) | 57 (78.1) | 314 (79.3) | 29 (80.6) | 158 (92.4) | |||
| Yes (n, %) | 54 (31.2) | 169 (18.3) | 16 (21.9) | 82 (20.7) | 7 (19.4) | 13 (7.6) | |||
| Diabetes | 0.007 | 0.966 | 0.921 | ||||||
| No (n, %) | 97 (56.1) | 620 (67.1) | 50 (68.5) | 267 (67.4) | 27 (75.0) | 124 (72.5) | |||
| Yes (n, %) | 76 (43.9) | 304 (32.9) | 23 (31.5) | 129 (32.6) | 9 (25.0) | 47 (27.5) | |||
| Malignancy | 0.004 | 0.062 | 0.268 | ||||||
| No (n, %) | 149 (86.1) | 859 (93.0) | 63 (86.3) | 370 (93.4) | 32 (88.9) | 163 (95.3) | |||
| Yes (n, %) | 24 (13.9) | 65 (7.0) | 10 (13.7) | 26 (6.6) | 4 (11.1) | 8 (4.7) | |||
| Anemia | 0.009 | 0.776 | 0.202 | ||||||
| No (n, %) | 109 (63.0) | 676 (73.2) | 50 (68.5) | 281 (71.0) | 25 (69.4) | 138 (80.7) | |||
| Yes (n, %) | 64 (37.0) | 248 (26.8) | 23 (31.5) | 115 (29.0) | 11 (30.6) | 33 (19.3) | |||
| Thrombocytopenia | 0.009 | 0.002 | <0.001 | ||||||
| No (n, %) | 142 (82.1) | 826 (89.4) | 56 (76.7) | 358 (90.4) | 30 (83.3) | 168 (98.2) | |||
| Yes (n, %) | 31 (17.9) | 98 (10.6) | 17 (23.3) | 38 (9.6) | 6 (16.7) | 3 (1.8) | |||
| Coagulopathy | <0.001 | 0.014 | 0.022 | ||||||
| No (n, %) | 144 (83.2) | 856 (92.6) | 59 (80.8) | 361 (91.2) | 36 (100.0) | 144 (84.2) | |||
| Yes (n, %) | 29 (16.8) | 68 (7.4) | 14 (19.2) | 35 (8.8) | 0 (0.0) | 27 (15.8) | |||
| Delirium | 0.535 | 0.892 | ∼1 | ||||||
| No (n, %) | 164 (94.8) | 861 (93.2) | 70 (95.9) | 375 (94.7) | 35 (97.2) | 168 (98.2) | |||
| Yes (n, %) | 9 (5.2) | 63 (6.8) | 3 (4.1) | 21 (5.3) | 1 (2.8) | 3 (1.8) | |||
| Dementia | 0.808 | 0.645 | 0.794 | ||||||
| No (n, %) | 162 (93.6) | 882 (95.5) | 70 (95.9) | 371 (93.7) | 36 (100.0) | 167 (97.7) | |||
| Yes (n, %) | 11 (6.4) | 42 (4.5) | 3 (4.1) | 25 (6.3) | 0 (0.0) | 4 (2.3) | |||
| Treatments and drugs (%) | |||||||||
| Aspirin | 0.178 | 0.867 | 0.562 | ||||||
| No (n, %) | 121 (69.9) | 594 (64.3) | 44 (60.3) | 246 (62.1) | 28 (77.8) | 122 (71.3) | |||
| Yes (n, %) | 52 (30.1) | 330 (35.7) | 29 (39.7) | 150 (37.9) | 8 (22.2) | 49 (28.7) | |||
| Alteplase | 0.749 | 0.767 | 0.775 | ||||||
| No (n, %) | 169 (97.7) | 909 (98.4) | 72 (98.6) | 385 (97.2) | 35 (97.2) | 170 (99.4) | |||
| Yes (n, %) | 4 (2.3) | 15 (1.6) | 1 (1.4) | 11 (2.8) | 1 (2.8) | 1 (0.6) | |||
| Warfarin | 0.195 | 0.487 | 0.289 | ||||||
| No (n, %) | 170 (98.3) | 886 (95.9) | 72 (98.6) | 381 (96.2) | 36 (100.0) | 161 (94.2) | |||
| Yes (n, %) | 3 (1.7) | 38 (4.1) | 1 (1.4) | 15 (3.8) | 0 (0.0) | 10 (5.8) | |||
| Albumin | ∼1 | 0.278 | 0.133 | ||||||
| No (n, %) | 162 (93.6) | 866 (93.7) | 65 (89.0) | 370 (93.4) | 34 (94.4) | 170 (99.4) | |||
| Yes (n, %) | 11 (6.4) | 58 (6.3) | 8 (11.0) | 26 (6.6) | 2 (5.6) | 1 (0.6) | |||
| Epinephrine | 0.965 | ∼1 | 0.001 | ||||||
| No (n, %) | 168 (97.1) | 901 (97.5) | 71 (97.3) | 383 (96.7) | 30 (83.3) | 167 (97.7) | |||
| Yes (n, %) | 5 (2.9) | 23 (2.5) | 2 (2.7) | 13 (3.3) | 6 (16.7) | 4 (2.3) | |||
| Vasopressin | <0.001 | 0.001 | 0.381 | ||||||
| No (n, %) | 161 (93.1) | 907 (98.2) | 65 (89.0) | 387 (97.7) | 30 (83.3) | 154 (90.1) | |||
| Yes (n, %) | 12 (6.9) | 17 (1.8) | 8 (11.0) | 9 (2.3) | 6 (16.7) | 17 (9.9) | |||
| RRT | 0.001 | 0.643 | 0.618 | ||||||
| No (n, %) | 160 (92.5) | 905 (97.9) | 69 (94.5) | 382 (96.5) | 34 (94.4) | 167 (97.7) | |||
| Yes (n, %) | 13 (7.5) | 19 (2.1) | 4 (5.5) | 14 (3.5) | 2 (5.6) | 4 (2.3) | |||
| MV | <0.001 | <0.001 | 0.004 | ||||||
| No (n, %) | 80 (46.2) | 656 (71.0) | 29 (39.7) | 274 (69.2) | 18 (50.0) | 129 (75.4) | |||
| Yes (n, %) | 93 (53.8) | 268 (29.0) | 44 (60.3) | 122 (30.8) | 18 (50.0) | 42 (24.6) | |||
| Scores (median [IQR]) | |||||||||
| APSIII | 65.00 | 39.00 | <0.001 | 62.00 | 42.50 | <0.001 | 66.50 | 36.00 | <0.001 |
| [48.00, 86.00] | [29.00, 54.00] | [46.00, 83.00] | [31.00, 57.00] | [44.00, 91.75] | [26.00, 49.00] | ||||
| OASIS | 40.00 | 31.00 | <0.001 | 40.00 | 32.00 | <0.001 | 33.00 | 23.00 | <0.001 |
| [34.00, 45.00] | [25.00, 37.00] | [33.00, 46.00] | [26.00, 38.00] | [26.00, 40.25] | [18.00, 30.00] | ||||
| SOFA | 6.00 | 3.00 | <0.001 | 6.00 | 4.00 | <0.001 | 6.00 | 2.00 | <0.001 |
| [4.00, 10.00] | [2.00, 6.00] | [4.00, 7.00] | [2.00, 6.00] | [4.00, 8.00] | [1.00, 4.00] | ||||
| GCS | 8.00 | 13.00 | <0.001 | 9.00 | 12.00 | 0.001 | 8.00 | 13.00 | <0.001 |
| [5.00, 13.00] | [9.00, 14.00] | [6.00, 13.00] | [8.00, 14.00] | [3.75, 12.00] | [10.00, 15.00] | ||||
Continuous variables were expressed as the mean (standard deviation) (normal) or the median [interquartile range] (non-normal). Categorical variables were expressed as the total number(percentages).
Abbreviations: AF, atrial fibrillation; APSIII, Acute Physiology and Chronic Health Evaluation III; BUN, blood urea nitrogen; CHD, coronary heart disease; CHF, congestive heart failure; COPD, chronic obstructive pulmonary disease; DBP, diastolic blood pressure; eICU-CRD, eICU Collaborative Research Database; GCS, Glasgow Coma Scale; HR, heart rate; MCH, mean corpuscular hemoglobin; MCHC, mean corpuscular hemoglobin contentration; MIMIC, Medical Information Mart for Intensive Care; MV, mechanical ventilation; OASIS, Oxford Acute Severity of Illness Score; PVD, peripheral vascular disease; RBC, red blood cell count; RDW, red cell volume distribution width; RR, respiratory rate; RRT, renal replacement therapy; SBP, systolic blood pressure; SOFA, Sequential Organ Failure Assessment; SpO2, peripheral oxygen saturation; WBC, white blood cell count.
Model development and internal validation
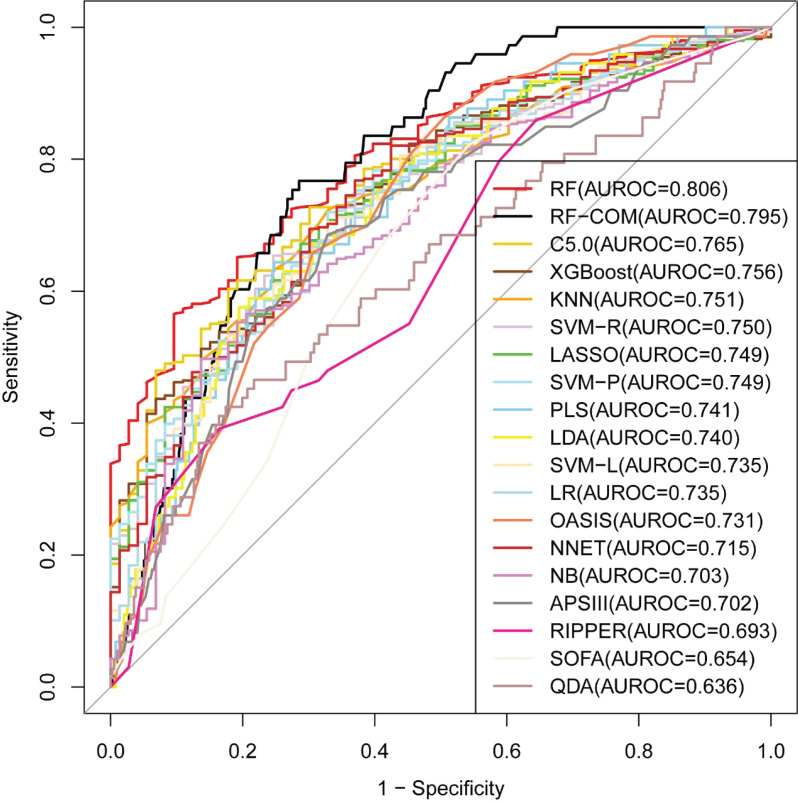
The training cohort was used for model development with a 3 × 10-fold cross-validation. The RF full model (i.e., all of the predictors) had the largest AUROC, AUPRC, accuracy, precision, and Cohen’s kappa value (see Supplementary Figure S1). In the internal validation phase, the RF full model still had the largest AUROC (0.806) (see Figure 2 and Table 2). Within the scoring systems, SOFA had the worst performance (AUROC = 0.654) and OASIS had an acceptable performance (AUROC = 0.731). We preferred to choose RF as the best model. The performance of RF is primarily dictated by two parameters: ntree (the number of trees) and mtry (the number of variables randomly sampled at each node). We performed extensive parameter tuning with a random combination of 30 mtry values, and manually set ntree to four values (500, 1000, 2000, 3000, and 5000). The configuration with the largest AUROC was mtry = 23 and ntree = 500.
Figure 2. Comparison of model performance in the internal validation cohort.
Table 2. Model performance in the internal and external validation cohorts.
| Internal validation | External validation | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUROC | BTOA | AUPRC | Accuracy | PPV | NPV | F1 | Kappa | AUROC | BTOA | AUPRC | Accuracy | PPV | NPV | F1 | Kappa | ||
| Full set | Size | ||||||||||||||||
| RF | 58 | 0.806 | 0.183 | 0.402 | 0.832 | 0.438 | 0.876 | 0.350 | 0.260 | 0.838 | 0.161 | 0.472 | 0.849 | 0.563 | 0.849 | 0.275 | 0.192 |
| C5.0 | 58 | 0.765 | 0.279 | 0.314 | 0.821 | 0.366 | 0.864 | 0.263 | 0.170 | 0.810 | 0.246 | 0.458 | 0.826 | 0.500 | 0.846 | 0.250 | 0.179 |
| XGBoost | 58 | 0.756 | 0.096 | 0.304 | 0.817 | 0.341 | 0.862 | 0.246 | 0.151 | 0.826 | 0.112 | 0.500 | 0.821 | 0.474 | 0.856 | 0.327 | 0.235 |
| KNN | 58 | 0.751 | 0.635 | 0.310 | 0.550 | 0.243 | 0.960 | 0.381 | 0.181 | 0.775 | 0.441 | 0.392 | 0.744 | 0.379 | 0.928 | 0.481 | 0.328 |
| LASSO | 28 | 0.749 | 0.454 | 0.318 | 0.706 | 0.290 | 0.911 | 0.395 | 0.232 | 0.821 | 0.268 | 0.485 | 0.821 | 0.487 | 0.899 | 0.507 | 0.398 |
| SVM-P | 58 | 0.749 | 0.460 | 0.327 | 0.721 | 0.307 | 0.915 | 0.413 | 0.257 | 0.817 | 0.199 | 0.443 | 0.807 | 0.447 | 0.888 | 0.459 | 0.342 |
| SVM-R | 58 | 0.742 | 0.275 | 0.377 | 0.800 | 0.360 | 0.883 | 0.365 | 0.246 | 0.801 | 0.123 | 0.356 | 0.792 | 0.267 | 0.833 | 0.157 | 0.061 |
| PLSDA | 58 | 0.741 | 0.512 | 0.320 | 0.706 | 0.293 | 0.913 | 0.400 | 0.238 | 0.814 | 0.389 | 0.456 | 0.816 | 0.475 | 0.898 | 0.500 | 0.388 |
| LDA | 58 | 0.737 | 0.623 | 0.319 | 0.706 | 0.293 | 0.913 | 0.400 | 0.238 | 0.817 | 0.395 | 0.483 | 0.811 | 0.465 | 0.902 | 0.506 | 0.391 |
| SVM-L | 58 | 0.735 | 0.426 | 0.323 | 0.719 | 0.294 | 0.905 | 0.389 | 0.230 | 0.808 | 0.204 | 0.463 | 0.840 | 0.541 | 0.906 | 0.548 | 0.451 |
| LR | 58 | 0.735 | 0.349 | 0.323 | 0.723 | 0.303 | 0.910 | 0.404 | 0.248 | 0.801 | 0.308 | 0.472 | 0.816 | 0.474 | 0.893 | 0.486 | 0.375 |
| OASIS | 10 | 0.731 | 0.393 | 0.301 | 0.653 | 0.263 | 0.918 | 0.380 | 0.200 | 0.754 | 0.202 | 0.369 | 0.783 | 0.395 | 0.884 | 0.430 | 0.297 |
| NNET | 58 | 0.715 | 0.522 | 0.293 | 0.761 | 0.303 | 0.884 | 0.348 | 0.207 | 0.731 | 0.246 | 0.357 | 0.802 | 0.414 | 0.865 | 0.369 | 0.253 |
| NB | 58 | 0.708 | 0.006 | 0.273 | 0.778 | 0.293 | 0.871 | 0.297 | 0.166 | 0.765 | 0.007 | 0.373 | 0.826 | 0.500 | 0.865 | 0.379 | 0.285 |
| APSIII | 16 | 0.702 | 0.456 | 0.303 | 0.702 | 0.287 | 0.910 | 0.391 | 0.227 | 0.805 | 0.328 | 0.493 | 0.763 | 0.373 | 0.891 | 0.437 | 0.293 |
| RIPPER | 58 | 0.693 | 0.021 | 0.241 | 0.725 | 0.245 | 0.872 | 0.295 | 0.133 | 0.699 | 0.021 | 0.339 | 0.797 | 0.417 | 0.877 | 0.417 | 0.294 |
| SOFA | 12 | 0.654 | 0.399 | 0.235 | 0.667 | 0.236 | 0.885 | 0.322 | 0.139 | 0.791 | 0.507 | 0.459 | 0.816 | 0.477 | 0.908 | 0.525 | 0.413 |
| QDA | 58 | 0.636 | 0.011 | 0.281 | 0.823 | 0.375 | 0.865 | 0.266 | 0.175 | 0.535 | 0.010 | 0.797 | 0.198 | 0.250 | 0.831 | 0.125 | 0.042 |
| RFE set | Size | ||||||||||||||||
| RF-COM | 6 | 0.795 | 0.315 | 0.352 | 0.793 | 0.364 | 0.892 | 0.397 | 0.274 | 0.830 | 0.169 | 0.417 | 0.816 | 0.450 | 0.856 | 0.321 | 0.225 |
| RF | 35 | 0.774 | 0.178 | 0.312 | 0.834 | 0.353 | 0.852 | 0.133 | 0.079 | 0.832 | 0.119 | 0.539 | 0.850 | 1.000 | 0.847 | 0.244 | 0.210 |
| SVM-R | 45 | 0.751 | 0.084 | 0.283 | 0.812 | 0.241 | 0.850 | 0.137 | 0.054 | 0.764 | 0.088 | 0.419 | 0.831 | 0.571 | 0.840 | 0.186 | 0.137 |
| LR | 45 | 0.743 | 0.235 | 0.321 | 0.825 | 0.395 | 0.869 | 0.293 | 0.201 | 0.757 | 0.064 | 0.456 | 0.831 | 0.538 | 0.851 | 0.286 | 0.213 |
| SVM-L | 35 | 0.736 | 0.316 | 0.337 | 0.710 | 0.291 | 0.908 | 0.393 | 0.232 | 0.811 | 0.186 | 0.481 | 0.845 | 0.559 | 0.902 | 0.543 | 0.450 |
| PLSDA | 45 | 0.731 | 0.520 | 0.310 | 0.710 | 0.294 | 0.911 | 0.398 | 0.238 | 0.817 | 0.465 | 0.501 | 0.816 | 0.477 | 0.908 | 0.525 | 0.413 |
| QDA | 10 | 0.720 | 0.023 | 0.256 | 0.785 | 0.281 | 0.864 | 0.263 | 0.137 | 0.796 | 0.201 | 0.449 | 0.836 | 0.545 | 0.870 | 0.414 | 0.325 |
| LDA | 20 | 0.718 | 0.093 | 0.276 | 0.819 | 0.350 | 0.862 | 0.248 | 0.155 | 0.785 | 0.107 | 0.465 | 0.826 | 0.500 | 0.843 | 0.217 | 0.153 |
| XGBoost | 35 | 0.709 | 0.083 | 0.269 | 0.817 | 0.324 | 0.859 | 0.218 | 0.817 | 0.815 | 0.088 | 0.472 | 0.831 | 0.533 | 0.854 | 0.314 | 0.236 |
| NB | 58 | 0.708 | 0.006 | 0.273 | 0.778 | 0.293 | 0.871 | 0.297 | 0.166 | 0.765 | 0.007 | 0.373 | 0.826 | 0.500 | 0.865 | 0.379 | 0.285 |
| SVM-P | 35 | 0.704 | 0.160 | 0.295 | 0.815 | 0.267 | 0.852 | 0.156 | 0.071 | 0.819 | 0.128 | 0.477 | 0.841 | 1.000 | 0.838 | 0.154 | 0.131 |
| C5.0 | 45 | 0.701 | 0.097 | 0.269 | 0.821 | 0.333 | 0.858 | 0.208 | 0.122 | 0.773 | 0.102 | 0.473 | 0.855 | 0.800 | 0.858 | 0.348 | 0.295 |
| RIPPER | 45 | 0.689 | 0.127 | 0.255 | 0.744 | 0.280 | 0.881 | 0.333 | 0.182 | 0.661 | 0.085 | 0.266 | 0.759 | 0.306 | 0.854 | 0.306 | 0.159 |
| KNN | 20 | 0.637 | 0.218 | 0.277 | 0.838 | 0.385 | 0.851 | 0.116 | 0.073 | 0.772 | 0.211 | 0.296 | 0.831 | 0.600 | 0.837 | 0.146 | 0.109 |
| NNET | 10 | 0.572 | 0.615 | 0.190 | 0.567 | 0.165 | 0.851 | 0.240 | 0.018 | 0.687 | 0.580 | 0.306 | 0.289 | 0.916 | 0.826 | 0.413 | 0.219 |
Models are ordered according to their area under the receiver operating characteristic curve (AUROC) in the internal validation set. The bold values indicate the largest value in the internal or external validation.
Abbreviations: APSIII, acute physiology and chronic health evaluation III; AUPRC, area under the precision-recall curve; AUROC, area under the receiver operating characteristic curve; BTOA, best threshold of AUROC; COM, compact; KNN, k-nearest neighbor; LASSO, least absolute shrinkage and selection operator; LDA, linear discriminant analysis; LR, logistic regression; NB, naive bayes; NNET, neural network; NPV, negative predictive value; OASIS, oxford acute severity of illness score; PLSDA, partial least squares discriminant analysis; PPV, positive predictive value; QDA, quadratic discriminant analysis; RF, random forest; RFE, recursive feature elimination; RIPPER, repeated incremental pruning to produce error reduction; SOFA, sequential organ failure assessment; SVM, support vector machine; SVM-L, SVM with linear kernel; SVM-P, SVM with a polynomial kernel; SVM-R, SVM with radial basis function kernel; XGBoost, extreme gradient boosting machine.
Feature selection and the subset model
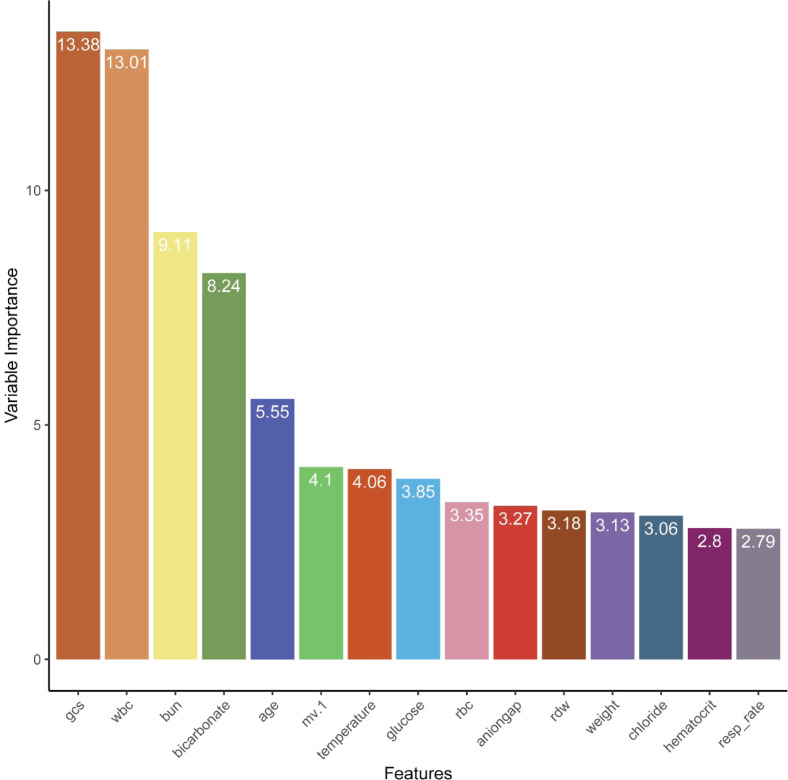
Supplementary Figure S2 showed results for each ML model generated by the RFE process in the training set. Of the evaluated models, the RF model (labeled as RF-RFE) performed best (AUROC = 0.859), and the screened feature subset counted 35 features. Figure 3 showed the top 15 key features. Despite some minor inconsistencies, the internal validation results showed trends that were comparable to those associated with the training results. The RF-RFE model retained largest AUROC (=0.774) among all RFE models (see Table 2). Generally, an AUROC of 0.9–1.0 is considered outstanding, 0.8–0.9 is considered good, 0.7–0.8 is considered fair, and 0.6–0.7 is considered poor [36]. Therefore, based on the clinical availability, we selected the minimum feature subset of AUROC > 0.840 to develop an RF compact model (labeled as RF-COM) with the top six features (GCS, WBC, BUN, bicarbonate, age, and MV). In the internal validation phase, the AUROC of the RF-COM model was 0.795, only second to the RF full model (AUROC = 0.806) (see Figure 2 and Table 2).
Figure 3. The top 15 key features identified by recursive feature elimination coupled with random forest.
External validation
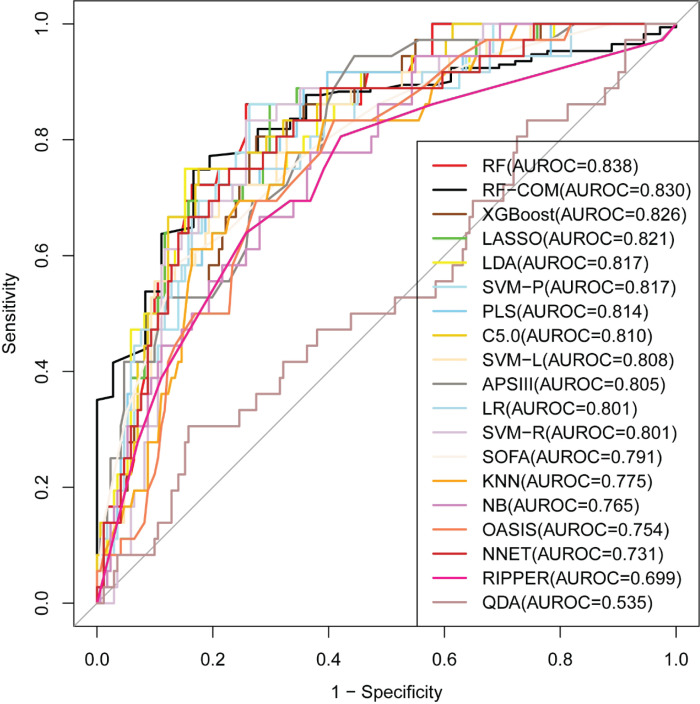
The external validation results of full models and RFE models are presented in Figure 4 and Table 2. Almost all models had larger AUROC than the internal validation. The RF full model still performed the best (AUROC = 0.838), followed by the RF-RFE model (AUROC = 0.832) and RF-COM model (AUROC = 0.830). Among the scoring systems, OASIS performed the worst (AUROC = 0.754), with smaller AUROC than APSIII (AUROC = 0.805) and SOFA (AUROC = 0.791).
Figure 4. Comparison of model performance in the external validation cohort.
Explanation of the model at the individual level
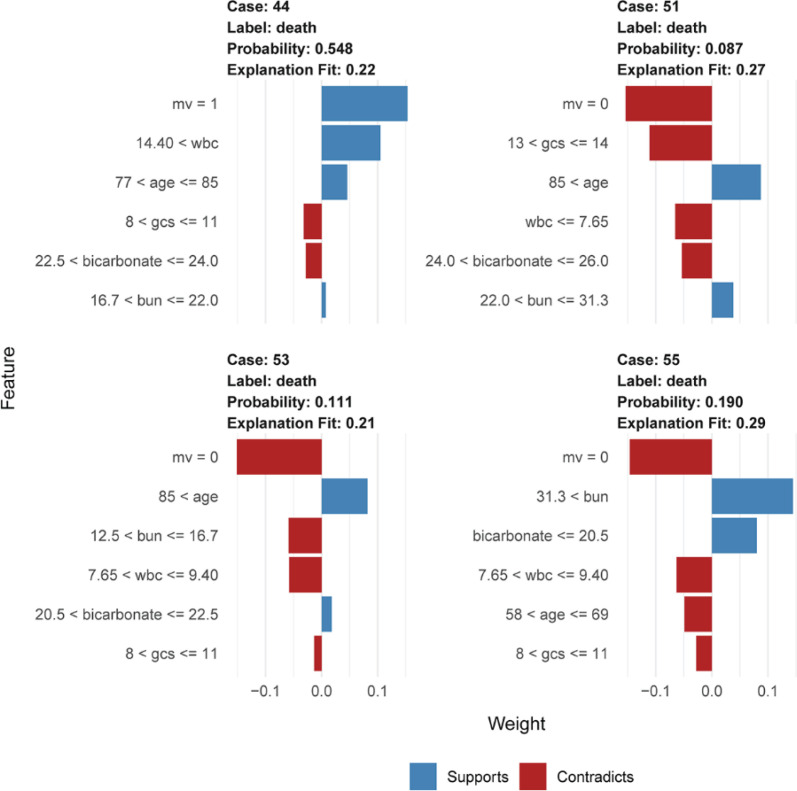
LIME plots were used to illustrate the impact of key features on individual patients. We presented four cases whose mortality had been correctly predicted using the RF-COM model in the internal validation cohort (see Figure 5). Case 44 from the ‘true positive’ group was correctly predicted for death, and the other three cases from the ‘true negative’ group were correctly predicted for survival. Taking case 44 as an example, the death probability was 0.548 owing to the influence of the support conditions, including the required MV, WBC > 14.4 × 109/L (= 19.24 × 109/L), and age > 77 years (= 83 years).
Figure 5. LIME plots of four representative instances.
Results of LIME with RF-COM model applied to one positive (case 44) and three negative instances (case 51, case53, and case 55). The blue indicates a condition that supports death, and the red indicates a condition that does not support death. mv = 1 represents the use of mechanical ventilation, mv = 0 represents no use of mechanical ventilation
Discussion
By developing ML models, the present study identified the mortality predictors for ES patients in ICU. We combined ML with feature selection methods to determine the best ML model and the key predictors for predicting mortality of the critically ill patients with ES. Our result showed that the RF model exhibited the best prediction accuracy, stability, and generalization. RF is a powerful ensemble learning algorithm. It has several advantages, including high accuracy, robustness to overfitting, estimation of important features, and handling unbalanced and missing data [37]. Compared with hundreds of other ML algorithms applied to many datasets, RF has emerged as the best performer overall [38]. RF has also shown a high degree of accuracy in mortality prediction for a plethora of diseases in ICU, such as acute kidney injury [39], acute respiratory distress syndrome [40], and cerebral hemorrhage [41].
The RF full model comprises 58 features and the RF-RFE model comprises 35 features. Evaluating more than 30 variables at once is time-consuming and may not be feasible in conventional clinical practice. As reported in a previous study, 37.3 min on average were required to perform a complete APACHE III assessment with several tens of variables [42]. There is no doubt that this is a heavy clinical workload for a clinician. A model with lesser features could be more clinically applicable and less expensive from a practical standpoint. Therefore, we constructed an RF-COM model with the top six features and discovered that the RF-COM model has approximately the same predictive power as the RF full model.
We then compared the features in the RF-COM model with those in the three scoring systems (see Supplementary Table S3). There are 16 features in APSIII, 12 in SOFA, and 10 in OASIS. GCS, mean arterial pressure (MAP), and urine output (24 h) are common recognition features among the scoring systems. Of the six features of RF-COM model, three features were included in APSIII (GCS, WBC, and BUN), three features in OASIS (GCS, age, and MV), and two features in SOFA (GCS and MV). GCS is not only the feature commonly identified by RF-COM model and scoring systems but also the most important feature identified by RF-COM model. GCS is used as a measure of consciousness and has the advantages of speed and ease of evaluation. A large number of studies have found that GCS is a strong predictor of hospital mortality and poor neurological outcome [26,27,43], which might be the reason that most of the scoring systems use GCS as the neurological assessment tool rather than other neurological scales, such as the National Institute of Health Stroke Scale (NIHSS).
When we tested the predictive performance of GCS as a univariate predictor, we discovered that GCS has comparable performance with the three scoring systems. The AUROC is 0.626 in the internal validation cohort, slightly lower than SOFA (= 0.654), and the AUROC is 0.757 in the external validation cohort, slightly higher than OASIS (= 0.754). Interestingly, similar findings have been found in some other studies. Bhagwanjee et al. evaluated APACHE II and GCS for mortality prediction in 105 cases of severe eclampsia and concluded that the prediction performance were very similar with both methods [14]. Cho et al. used APACHE II, APACHE III, and GCS to predict the mortality of 200 patients with acute craniocerebral injury and found that GCS had almost the same predictive ability as the other two scoring systems [13]. Raj et al. found that a simple model based on GCS and age was comparable to APACHE II, SAPS II, and SOFA in predicting 6-month mortality in patients with traumatic brain injury [15].
We then investigated the five other features and found that they had all been reported as the predictors of mortality for stroke and other diseases. For example, several studies have shown that acute stroke patients requiring MV have high in-hospital mortality and survival patients remain deeply disabled [44,45]. BUN is usually considered a less specific marker of renal function. It is independently associated with mortality in many diseases [46,47]. Bicarbonate has been reported to be associated with mortality from various diseases, which can be attributed to numerous factors in most cases [48–50]. An increasing number of studies have focused on discovering the association between high WBC and the poor outcome of IS [47,51]. Inflammation and stress responses caused by IS have been proposed as plausible explanations for the association [45]. Age was found to be a strong predictor of death after IS [52,53].
Subsequently, we compared the prediction power of the top six features by univariable analysis. Surprisingly, the AUROC of GCS was not the largest in either internal or external validation phrases (see Supplementary Figure S3). This result reminds us that (i) the predictive power of a feature is different in univariate and multivariate analyses, (ii) the predictive power of a feature is limited, and the combination of multiple features using an appropriate algorithm is better than that of any single feature. In the present study, although the AUROC of GCS is not dissimilar to that of the three scoring systems, it is significantly lower than the RF-COM model with six features. Therefore, the most critical step is finding the appropriate algorithm and combination of appropriate feature subsets. According to the ‘no free lunch’ theorem, no algorithm can always perform better than others [54]. Researchers need to put more effort into systematically exploring a wide variety of algorithms and testing their performance of different subsets of features. The present study attempted to realize such an approach. By combining multiple features, the RF model improved the predictive power of hospital mortality for ES patients significantly better than a single feature and the scoring systems.
Furthermore, there are several other advantages of the study. First, the MIMIC-IV and eICU-CRD databases are publicly available, high-quality, and large-scale. To the best of our knowledge, a total of 1763 (1556 + 207) ES samples is a considerable sample size in the population-based study of ES. Second, this is the first study on the prediction of ES mortality using ML models. We compared a representative set of 15 ML models and three scoring systems and optimized their performances using different preprocessing methods for different models, thus allowing a more objective selection of the best model. Third, the top six features identified by RFE are easily obtained and assessed in clinical practice. We modeled them and performed rigorous internal and external validation. The good predictive performance of the RF-COM model confirmed the six features’ reliability as key mortality predictors for ES patients. Fourth, to provide clinicians with reliable insight into the key predictors, we used LIME to show each feature’s contribution to individual predictions.
At the same time, we must acknowledge that our study has some limitations. First, although the two databases are of high quality, they still have a substantial amount of missing data. Thus we had to drop many variables, which may lead to losing some important predictors for predicting ES mortality. Second, the two databases are non-neurospecialty ICU databases; therefore, some variables that may be useful for assessing the condition of ES patients are not available, such as NIHSS, infarct volume, and infarct location. Third, internal validation typically outperforms external validation. However, in this study, the AUROC of external validation exceeded that of internal validation in almost all ML models. In our view, the main reason may be that the AUROC of top two features (BUN = 0.771, GCS = 0.757) in the external validation set was significantly larger than the top two features (WBC = 0.660, MV = 0.647)) in the internal validation set (P<0.05). And the larger AUROC of the top two features may result from the more significant statistical differences between the death and survival groups in the external validation set than in the internal validation set (see Table 1). Fourth, the results were based on a standard ML prediction modeling in the present study. We did not intensively investigate the detailed mechanism of the six features associated with ES mortality. Future studies are needed to explore the underlying mechanism. Finally, although AUROC is currently regarded as the best and most commonly used evaluation metrics for binary classification models, it is only an index of comprehensive evaluation of sensitivity and specificity, and cannot reflect the degree of clinical harm caused by missed diagnosis (false negative) or misdiagnosis (false positive). Future clinical confirmatory research may need to select appropriate cutoff points based on individual characteristics of specific patients, the clinical impact of predicted results, economic cost and other factors. For example, in order to reduce the waste and disarray of medical resources caused by misdiagnosis, a cutoff point associated with higher specificity may represent a more effective choice. In order to mitigate delayed diagnosis caused by initially missed diagnosis, a cutoff point associated with higher sensitivity may represent a more appropriate choice. Only in specific patients and under specific conditions can the applicability of the predictive model be engaged to its full extent.
Conclusion
The RF model outperformed other ML models and scoring systems in terms of accuracy, stability, and generalization. GCS, WBC, BUN, bicarbonate, age, and MV are the key mortality predictors for critically ill ES patients. The findings of this study provide clinicians with insights; however, further validation in prospective cohorts is required before they can be considered clinically acceptable.
Supplementary Material
Acknowledgements
We would like to thank Dr Yingchuan Zhu (West China Medical School, Sichuan University) for her kindly help with the paper.
Abbreviations
- APACHE III
Acute Physiology and Chronic Health Evaluation III
- APSIII
Acute Physiology Score III
- AUPRC
area under the precision-recall curve
- AUROC
area under the receiver operating characteristic curve
- eICU-CRD
eICU Collaborative Research Database
- ES
embolic stroke
- GCS
Glasgow Coma Scale
- ICU
intensive care units
- IQR
interquartile range
- IS
ischemic stroke
- KNN
k-nearest neighbor
- LASSO
least absolute shrinkage and selection operator
- LDA
linear discriminant analysis
- LIME
local interpretable model-agnostic explanations
- LR
logistic regression
- MIMIC
Medical Information Mart for Intensive Care
- ML
machine learning
- MV
mechanical ventilation
- NB
naive bayes
- NIHSS
National Institute of Health Stroke Scale
- NNET
neural network
- NPV
negative predictive value
- OASIS
Oxford Acute Severity of Illness Score
- PLSDA
partial least squares discriminant analysis
- PPV
positive predictive value
- QDA
(quadratic discriminant analysis)
- RF
random forest
- RFE
recursive feature elimination
- RIPPER
repeated incremental pruning to produce error reduction
- SD
standard deviation
- SMOTE
synthetic minority oversampling technology
- SOFA
Sequential Organ Failure Assessment
- SVM
support vector machine
- TRIPOD
Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis
- XGBoost
extreme gradient boosting machine
Contributor Information
Jianhui Guo, Email: guojianhuikm@163.com.
Liyan Li, Email: liliyan@kmmu.edu.cn.
Data Availability
Publicly available datasets were analyzed in this study. These data can be found here: https://mimic.mit.edu/iv/; https://eicu-crd.mit.edu/.
Competing Interests
The authors declare that there are no competing interests associated with the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China, China [grant number 82160263 (to Liyan Li)]; Research Innovation Team of Yunnan Province, China [grant number 2019HC022 (to Liyan Li)]; Ten Thousand Person Plan for Famous Doctors of Yunnan Province [grant number YNWR-MY-2018-015]; Yunnan Applied Basic Research Projects [grant number 202101AY070001-253 and 2019FE001(-175) (to Jinwei Yang)]; and the Foundation of Yunnan Provincial Education Department [grant number 2019J1257 (to Chunyan Li)].
CRediT Author Contribution
Wei Liu: Conceptualization, Resources, Formal analysis, Validation, Investigation, Writing—original draft. Wei Ma: Data curation, Formal analysis, Writing—original draft. Na Bai: Software. Chunyan Li: Software. Kuangpin Liu: Software, Methodology. Jinwei Yang: Data curation, Funding acquisition. Sijia Zhang: Methodology. Kewei Zhu: Validation. Qiang Zhou: Validation. Hua Liu: Supervision, Writing—review & editing. Jianhui Guo: Supervision, Project administration, Writing—review & editing. Liyan Li: Conceptualization, Funding acquisition, Writing—review & editing.
Ethics Approval and Consent to Participate
The study was an analysis of two third-party anonymized publicly available databases with pre-existing institutional review board (IRB) approval.
References
- 1. (2021) Global, Regional, and National Burden of Stroke and Its Risk Factors, 1990-2019: A Systematic Analysis for the Global Burden of Disease Study 2019. Lancet Neurol. 20, 795–820 10.1016/S1474-4422(21)00252-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hart R.G., Diener H.C., Coutts S.B., Easton J.D., Granger C.B., O'Donnell M.J.et al. (2014) Embolic strokes of undetermined source: the case for a new clinical construct. Lancet Neurol. 13, 429–438 10.1016/S1474-4422(13)70310-7 [DOI] [PubMed] [Google Scholar]
- 3.Ntaios G. and Hart R.G. (2017) Embolic stroke. Circulation 136, 2403–2405 10.1161/CIRCULATIONAHA.117.030509 [DOI] [PubMed] [Google Scholar]
- 4.Bjerkreim A.T., Khanevski A.N., Thomassen L., Selvik H.A., Waje-Andreassen U., Naess H.et al. (2019) Five-year readmission and mortality differ by ischemic stroke subtype. J. Neurol. Sci. 403, 31–37 10.1016/j.jns.2019.06.007 [DOI] [PubMed] [Google Scholar]
- 5.Yiin G.S., Howard D.P., Paul N.L., Li L., Luengo-Fernandez R., Bull L.M.et al. (2014) Age-specific incidence, outcome, cost, and projected future burden of atrial fibrillation-related embolic vascular events: a population-based study. Circulation 130, 1236–1244 10.1161/CIRCULATIONAHA.114.010942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bogiatzi C., Hackam D.G., McLeod A.I. and Spence J.D. (2014) Secular trends in ischemic stroke subtypes and stroke risk factors. Stroke 45, 3208–3213 10.1161/STROKEAHA.114.006536 [DOI] [PubMed] [Google Scholar]
- 7.Steyerberg E.W. (2019) Clinical Prediction Models, Springer [Google Scholar]
- 8.Knaus W.A., Wagner D.P., Draper E.A., Zimmerman J.E., Bergner M., Bastos P.G.et al. (1991) The Apache Iii Prognostic System. Risk Prediction of Hospital Mortality for Critically Ill Hospitalized Adults. Chest 100, 1619–1636 10.1378/chest.100.6.1619 [DOI] [PubMed] [Google Scholar]
- 9.Vincent J.L., Moreno R., Takala J., Willatts S., De Mendonça A., Bruining H.et al. (1996) The Sofa (Sepsis-Related Organ Failure Assessment) score to describe organ dysfunction/failure. On behalf of the working group on sepsis-related problems of the European Society of Intensive Care Medicine. Intensive Care Med. 22, 707–710 10.1007/BF01709751 [DOI] [PubMed] [Google Scholar]
- 10.Johnson A.E., Kramer A.A. and Clifford G.D. (2013) A new severity of illness scale using a subset of acute physiology and chronic health evaluation data elements shows comparable predictive accuracy. Crit. Care Med. 41, 1711–1718 10.1097/CCM.0b013e31828a24fe [DOI] [PubMed] [Google Scholar]
- 11.Austin P.C. and Brunner L.J. (2004) Inflation of the type I error rate when a continuous confounding variable is categorized in logistic regression analyses. Stat. Med. 23, 1159–1178 10.1002/sim.1687 [DOI] [PubMed] [Google Scholar]
- 12.Nistal-Nuño B. (2022) Developing machine learning models for prediction of mortality in the medical intensive care unit. Comput. Methods Programs Biomed. 216, 106663 10.1016/j.cmpb.2022.106663 [DOI] [PubMed] [Google Scholar]
- 13.Cho D.Y. and Wang Y.C. (1997) Comparison of the Apache Iii, Apache Ii and Glasgow Coma Scale in acute head injury for prediction of mortality and functional outcome. Intensive Care Med. 23, 77–84 10.1007/s001340050294 [DOI] [PubMed] [Google Scholar]
- 14.Bhagwanjee S., Paruk F., Moodley J. and Muckart D.J. (2000) Intensive Care Unit morbidity and mortality from eclampsia: an evaluation of the acute physiology and chronic health evaluation Ii Score and the Glasgow Coma Scale Score. Crit. Care Med. 28, 120–124 10.1097/00003246-200001000-00020 [DOI] [PubMed] [Google Scholar]
- 15.Raj R., Skrifvars M., Bendel S., Selander T., Kivisaari R., Siironen J.et al. (2014) Predicting six-month mortality of patients with traumatic brain injury: usefulness of common intensive care severity scores. Crit. Care 18, R60 10.1186/cc13814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Obermeyer Z. and Emanuel E.J. (2016) Predicting the future - big data, machine learning, and clinical medicine. N. Engl. J. Med. 375, 1216–1219 10.1056/NEJMp1606181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Deo R.C. (2015) Machine learning in medicine. Circulation 132, 1920–1930 10.1161/CIRCULATIONAHA.115.001593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kourou K., Exarchos T.P., Exarchos K.P., Karamouzis M.V. and Fotiadis D.I. (2015) Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 13, 8–17 10.1016/j.csbj.2014.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aksoy S. and Haralick R.M. (2001) Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 22, 563–582 10.1016/S0167-8655(00)00112-4 [DOI] [Google Scholar]
- 20.Motwani M., Dey D., Berman D.S., Germano G., Achenbach S., Al-Mallah M.H.et al. (2017) Machine learning for prediction of all-cause mortality in patients with suspected coronary artery disease: a 5-year multicentre prospective registry analysis. Eur. Heart J. 38, 500–507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fang G., Liu W. and Wang L. (2020) A machine learning approach to select features important to stroke prognosis. Comput. Biol. Chem. 88, 107316 10.1016/j.compbiolchem.2020.107316 [DOI] [PubMed] [Google Scholar]
- 22.Degenhardt F., Seifert S. and Szymczak S. (2019) Evaluation of variable selection methods for random forests and omics data sets. Brief. Bioinform. 20, 492–503 10.1093/bib/bbx124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goldberger A.L., Amaral L.A., Glass L., Hausdorff J.M., Ivanov P.C., Mark R.G.et al. (2000) Physiobank, physiotoolkit, and physionet: components of a new research resource for complex physiologic signals. Circulation 101, E215–E220 10.1161/01.CIR.101.23.e215 [DOI] [PubMed] [Google Scholar]
- 24.Pollard T.J., Johnson A.E.W., Raffa J.D., Celi L.A., Mark R.G. and Badawi O. (2018) The Eicu Collaborative Research Database, a freely available multi-center database for critical care research. Sci. Data 5, 180178 10.1038/sdata.2018.178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Collins G.S., Reitsma J.B., Altman D.G. and Moons K.G. (2015) Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (tripod): the tripod statement. BMJ 350, g7594 10.1136/bmj.g7594 [DOI] [PubMed] [Google Scholar]
- 26.Arboix A., García-Eroles L., Massons J. and Oliveres M. (1998) Predictive clinical factors of in-hospital mortality in 231 consecutive patients with cardioembolic cerebral infarction. Cerebrovasc. Dis. 8, 8–13 10.1159/000015809 [DOI] [PubMed] [Google Scholar]
- 27.Huang Z.X., Gu H.Q., Yang X., Wang C.J., Wang Y.J. and Li Z.X. (2021) Risk factors for in-hospital mortality among acute ischemic stroke patients in China: a nationwide prospective study. Neurol. Res. 43, 387–395 10.1080/01616412.2020.1866356 [DOI] [PubMed] [Google Scholar]
- 28.Kuhn M. (2008) Building predictive models in R using the Caret Package. J. Statistical Software 28, 1–26 10.18637/jss.v028.i05 [DOI] [Google Scholar]
- 29.Kuhn M. and Johnson K. (2013) Applied Predictive Modeling, Springer [Google Scholar]
- 30.van Buuren S. and Groothuis-Oudshoorn K. (2011) Mice: multivariate imputation by chained equations in R. J. Statistical Software 45, 1–67 10.18637/jss.v045.i03 [DOI] [Google Scholar]
- 31.Li D.C., Liu C.W. and Hu S.C. (2010) A learning method for the class imbalance problem with medical data sets. Comput. Biol. Med. 40, 509–518 10.1016/j.compbiomed.2010.03.005 [DOI] [PubMed] [Google Scholar]
- 32.Chawla N.V., Bowyer K.W. and Hall L.O. (2002) Kegelmeyer WPJJoair. Smote: Synthetic Minority over-Sampling Technique. 16, 321–357 [Google Scholar]
- 33.Liu C.L., Soong R.S., Lee W.C., Jiang G.W. and Lin Y.C. (2020) Predicting short-term survival after liver transplantation using machine learning. Sci. Rep. 10, 5654 10.1038/s41598-020-62387-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guyon I., Weston J., Barnhill S. and Vapnik V. (2002) Gene selection for cancer classification using support vector machines. Machine Learning 46, 389–422 10.1023/A:1012487302797 [DOI] [Google Scholar]
- 35.Ribeiro M.T., Singh S. and Guestrin C. (2016) “Why Should I Trust You?”: Explaining the Predictions of Any Classifier Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1135–1144, Association for Computing Machinery, San Francisco, California, USA: 10.18653/v1/N16-3020 [DOI] [Google Scholar]
- 36.Muller M.P., Tomlinson G., Marrie T.J., Tang P., McGeer A., Low D.E.et al. (2005) Can Routine Laboratory Tests Discriminate between Severe Acute Respiratory Syndrome and Other Causes of Community-Acquired Pneumonia? Clin. Infect. Dis. 40, 1079–1086 10.1086/428577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Franklin J. (2005) The elements of statistical learning: data mining, inference and prediction. Math. Intell. 27, 83–85 10.1007/BF02985802 [DOI] [Google Scholar]
- 38.Fernández-Delgado M., Cernadas E., Barro S. and Amorim D. (2014) Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 15, 3133–3181 [Google Scholar]
- 39.Lin K., Hu Y. and Kong G. (2019) Predicting in-hospital mortality of patients with acute kidney injury in the icu using random forest model. Int. J. Med. Inform. 125, 55–61 10.1016/j.ijmedinf.2019.02.002 [DOI] [PubMed] [Google Scholar]
- 40.Huang B., Liang D., Zou R., Yu X., Dan G., Huang H.et al. (2021) Mortality prediction for patients with acute respiratory distress syndrome based on machine learning: a population-based study. Ann. Transl. Med. 9, 794 10.21037/atm-20-6624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nie X., Cai Y., Liu J., Liu X., Zhao J., Yang Z.et al. (2020) Mortality prediction in cerebral hemorrhage patients using machine learning algorithms in intensive care units. Front. Neurol. 11, 610531 10.3389/fneur.2020.610531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Niewiński G., Starczewska M. and Kański A. (2014) Prognostic scoring systems for mortality in intensive care units–the apache model. Anaesthesiol. Intensive Therapy 46, 46–49 10.5603/AIT.2014.0010 [DOI] [PubMed] [Google Scholar]
- 43.Nyam T.E., Ao K.H., Hung S.Y., Shen M.L. and Yu T.C. (2017) Kuo JR. Four score predicts early outcome in patients after traumatic brain injury. Neurocritical Care 26, 225–231 10.1007/s12028-016-0326-y [DOI] [PubMed] [Google Scholar]
- 44.Mayer S.A., Copeland D., Bernardini G.L., Boden-Albala B., Lennihan L., Kossoff S.et al. (2000) Cost and outcome of mechanical ventilation for life-threatening stroke. Stroke 31, 2346–2353 10.1161/01.STR.31.10.2346 [DOI] [PubMed] [Google Scholar]
- 45.Popat C., Ruthirago D., Shehabeldin M., Yang S. and Nugent K. (2018) Outcomes in patients with acute stroke requiring mechanical ventilation: predictors of mortality and successful extubation. Am. J. Med. Sci. 356, 3–9 10.1016/j.amjms.2018.03.013 [DOI] [PubMed] [Google Scholar]
- 46.Arihan O., Wernly B., Lichtenauer M., Franz M., Kabisch B., Muessig J.et al. (2018) Blood urea nitrogen (Bun) is independently associated with mortality in critically Ill patients admitted to ICU. PloS ONE 13, e0191697 10.1371/journal.pone.0191697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.You S., Ou Z., Zhang W., Zheng D., Zhong C., Dong X.et al. (2019) Combined Utility of white blood cell count and blood glucose for predicting in-hospital outcomes in acute ischemic stroke. J. Neuroinflammation 16, 37 10.1186/s12974-019-1422-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Libório A.B., Noritomi D.T., Leite T.T., de Melo Bezerra C.T., de Faria E.R. and Kellum J.A. (2015) Increased serum bicarbonate in critically Ill patients: a retrospective analysis. Intensive Care Med. 41, 479–486 10.1007/s00134-015-3649-9 [DOI] [PubMed] [Google Scholar]
- 49.Wigger O., Bloechlinger S., Berger D., Häner J., Zanchin T., Windecker S.et al. (2018) Baseline serum bicarbonate levels independently predict short-term mortality in critically Ill patients with ischaemic cardiogenic shock. Eur. Heart J. Acute Cardiovasc. Care 7, 45–52 10.1177/2048872616683526 [DOI] [PubMed] [Google Scholar]
- 50.Schopis M., Kumar A., Parides M., Tepler A. and Sigal S. (2021) Admission serum bicarbonate predicts adverse clinical outcomes in hospitalized cirrhotic patients. Can J. Gastroenterol. Hepatol. 2021, 9915055 10.1155/2021/9915055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Furlan J.C., Vergouwen M.D., Fang J. and Silver F.L. (2014) White blood cell count is an independent predictor of outcomes after acute ischaemic stroke. Eur. J. Neurol. 21, 215–222 10.1111/ene.12233 [DOI] [PubMed] [Google Scholar]
- 52.Soriano-Tárraga C., Giralt-Steinhauer E., Mola-Caminal M., Ois A., Rodríguez-Campello A., Cuadrado-Godia E.et al. (2018) Biological age is a predictor of mortality in ischemic stroke. Sci. Rep. 8, 4148 10.1038/s41598-018-22579-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chongruksut W., Limpastan K., Jetjumnong C., Watcharasaksilp W., Vaniyapong T., Norasetthada T.et al. (2020) Age as a prognostic factor of 30-day mortality in hemorrhagic stroke patients: A Thai Large Tertiary Care Referral Center. Asian J. Surg. 43, 991–995 10.1016/j.asjsur.2019.11.010 [DOI] [PubMed] [Google Scholar]
- 54.Wolpert D.H. (1996) The lack of a priori distinctions between learning algorithms. Neural Comput. 8, 1341–1390 10.1162/neco.1996.8.7.1341 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: https://mimic.mit.edu/iv/; https://eicu-crd.mit.edu/.