Abstract
Hypothesis:
While the lack of efficient tools yielding controllable uniform supersaturations (S) has delayed basic experimental heterogeneous nucleation studies, common diffusive condensation particle counters (DCPCs) would fill this gap if their present substantial S-variation could be minimized.
Analysis:
For an initially saturated vapor in two-dimensional (2D) parabolic flow, with discontinuous wall temperature change from Ts to Tc, we calculate the spatial S(x,y) distribution, including the curve Smax(Ψ) of maximal supersaturations versus streamline Ψ. Activation probability curves P(Ts,Tc) are also calculated assuming that nucleation goes from zero to 100% at a critical supersaturation S*.
Findings:
Two new approaches to achieve a nearly constant Smax(Ψ) are discovered. (i) Sampling only the central 50% of the flow is most effective because the [dSmax(Ψ)/Dψ]Ψ=0 = 0. This advantage is lost in the more common axisymmetric configuration. (ii) When the ratio Le = α/D between gas–vapor heat and mass diffusivities is unity, we find the quite general property that Smax(Ψ) is exactly constant. This singular condition may be achieved in special vapor/gas mixtures (ethanol/CO2; methanol/CO2; H2O/air, all seeded with lighter or heavier gases). With greater generality, Le = 1 also in turbulent flows. Therefore, basic heterogeneous nucleation studies with newly available seed particles of fixed size and composition are viable in DCPCs.
Keywords: Heterogeneous nucleation, Condensation particle counter, Lewis number, Critical supersaturation, Nucleation kinetics
Graphical Abstract
1. Introduction on heterogeneous nucleation studies
For a long time the field of homogeneous nucleation received considerably more attention than heterogeneous nucleation. More recently, the advent of techniques to produce monodisperse particles of nanometer dimensions, and the ability to detect them in condensation particle counters (CPCs) with practically no lower size limit (at least for charged particles), has greatly stimulated the study of heterogeneous nucleation. The size of the nuclei that can be activated has become so small that one wonders if a clear distinction between homogeneous and heterogeneous nucleation can be made. For instance, it is possible to activate vapor condensation on neutral species of about 1 nm in diameter [1]. Yet, many large organic molecules of that size exist in the atmosphere as well as in most laboratory instruments not handled with the rigorous methods typical of high vacuum studies. Since the number density of ambient air is 2.5 1019 cm3, a vapor impurity present at parts per billion concentrations would still offer 2.5 1010 heterogeneous condensation nuclei. The currently very active field of atmospheric nucleation research offers many similar examples. When the nucleation process is initiated by the presence of a small nitrate or sulfate cluster, is the nucleation homogeneous or heterogeneous? In recent heterogeneous nucleation studies the seed particles were atomic ions [2], evidently much smaller than many small organic molecules present at considerable concentrations in the atmosphere. Perhaps, then, one difference between the more recent heterogeneous nucleation studies and their homogeneous predecessors is that a seed particle of precisely known composition and size can now be introduced in or removed from the vapor.
The new possibility to controllably introduce pure species as small as Na+ into a supersaturated vapor was primarily opened up by Fenn’s work on electrospray ionization (ESI) [3]. There were of course precedents going back to Wilson’s studies on the nucleation of water on small molecular ions of unknown composition [4]. In a few singular cases, the initial nature of the seed ion has been controlled by generating it via resonant laser excitation from seeded traces of neutral vapors [5,6]. Nonetheless, ESI increased dramatically the range of chemical compositions sizes and charges of the seed particles available for basic heterogeneous nucleation studies. The first time that a differential mobility analyzer (DMA) of high resolution was used to isolate small gas phase ions of known composition to study heterogeneous nucleation in dibutyl phthalate (DBP) vapors in a turbulent mixing CPC, it was found that cluster ions slightly larger than 1.5 nm were readily grown to visible sizes (activated) [7], in paradoxical contrast with the common view that the smallest particle size detectable in a CPC at that time was about 2.5 nm. Rather sharp activation probability versus supersaturation curves P(S) were also reported for various singly and doubly charged cations, and no activation at all for any of the anions investigated [7]. Shortly after, a modification of that turbulent mixing CPC demonstrated that arbitrarily small ions could also be activated [8]. This was, after all, not so surprising, given Wilson’s precedent of experimental activation of molecular ions of subnanometer dimensions [4]. Another interesting finding was the fast-rising activation curves determined for a series of singly charged salt aggregates [A+-B−]nA+ of tetraheptyl ammonium bromide, to the point that clusters differing by only one neutral ion pair AB had distinguishable activation curves [8]. Sizing nanoparticles with excellent resolution in a CPC was therefore seen to be viable. This possibility was nonetheless not further pursued for over a decade for sizing purposes, and was in fact puzzling. The dependence of the activation probability on supersaturation is theoretically expected based on Fletcher’s theory to be rather steep (Fig. SI-1 in the Supporting Information). However, the turbulent mixing CPC used in references [7,8] did not have a uniform supersaturation S, but spanned an S range from unity at the instrument’s walls to values of the order of 1000 at its center. Why was the activation probability curve not as broad as would have been expected from a convolution of the sharp response curve to S with the exceedingly broad range of S values existing within the CPCs? Some insight into this paradox was contributed in a study of the activation probability of DMA-purified cluster ions carried out at the SANC facility at the University of Vienna [9]. Unlike most other schemes to achieve controlled supersaturation, SANC uses an expansion in time to deliver a spatially uniform supersaturation profile in the full region containing seed particles. Activation curves measured in this instrument should accordingly be as steep as expected from heterogeneous nucleation theory. And indeed, an excellent match between the expected and the observed steepness of the activation curve was obtained, as may be seen in Fig. SI-1 [10]. This fact had been previously exploited to determine theoretically the otherwise unmeasurable size of the critical nucleus via the nucleation theorem [9]. In contrast, DMA-selected WOx particles from a heated tungsten wire had much duller activation curves (small gray symbols in Figure SI-1) than chemically pure cluster ions, precluding the use of the nucleation theorem. Evidently, mobility-selected particles from the tungsten wire source suffered from some heterogeneity, either in shape or in chemical composition (various oxides). Inspired by these notable Viennese findings, a comparison between Fletcher’s [11] heterogeneous nucleation model and the earlier cluster measurements [8] was made, and showed that the activation curves measured in the turbulent mixing CPC (black data points in Figure SI-1) matched the theory approximately [10], being accordingly as steep as those obtained in Vienna’s SANC. Therefore, for unclear reasons, a turbulent mixing CPC spanning supersaturations between 1 and 1000 appeared to operate as if the supersaturation was as uniform as that in an adiabatic expansion.
Accordingly, at least two experimental tools have been available for two decades, where particles of controlled size, charge and composition could be exposed to various vapors at an effectively uniform and controllable supersaturation. This flexibility would have permitted two most valuable developments: First, systematic studies of heterogeneous nucleation phenomena at nanometer dimensions as a function of size, charge and chemical composition. Second, a splendid tool to determine at high resolution the size of an aerosol of charged or neutral, particles by simply measuring the activation probability as a function of supersaturation. Surprisingly this development has taken place only to a very limited extent. The total sum of studies on heterogeneous nucleation with controlled clusters and controlled S goes little beyond the four articles previously cited [1,2,8,9,12]. Several reasons have contributed to this slow progress. First, Gamero’s [8] improved version of the CPC of Seto et al. [7] was difficult to operate, and produced no further results after his graduation. Also, the motivation to develop an easier to run variant of that instrument for basic nucleation studies was moderated by the difficulty to reconcile its steep response with the high level of heterogeneity in supersaturation present within the device. On the other hand, Vienna’s SANC achieves a uniform S and is relatively free from experimental ambiguities. However its exploitation in practice appears to be relatively slow, due in part to its batch operation. A chamber is first cleaned, then filled with a mixture of vapor and DMA-selected particles, then the chamber gas is expanded, and the activated particles are finally counted. Measuring a single point of the activation curve under just one thermodynamic condition for just one cluster is an arduous job, perhaps explaining how only three molecular clusters have been studied at Vienna in a period of many years, while Gamero’s steady flow CPC [8,12] did investigate 42 purified species in a few months. Particle losses in the SANC facility during these various steps are also important, and had in fact precluded measurements with atomic ions prior to the recent availability of a parallel plate DMA of exceptionally high transmission [2]. Evidently, basic progress in heterogeneous nucleation would be greatly accelerated if a more practical device became available, ideally capable of steady operation at variable but effectively uniform S.
Given the success of Gamero’s modification [8] of the turbulent mixing CPC of Seto et al. [7], a more detailed description of the various variants tested of this and related CPCs is appropriate here. The instrument was originally described by Kogan and Burnasheva [13], and further developed by Okuyama et al. [14]. Supersaturation calculations giving steep P(S) curves with purified cluster ions in the work of Seto et al. [7] were originally carried out on the assumption that the turbulent mixing process was adiabatic, with no solvent losses upstream of the mixing region. A later detailed investigation revealed vapor losses prior to the mixing and suggested that the mixing was closer to isothermal than adiabatic [8]. These problems had previously led to an incorrect determination of the supersaturation scale, and were responsible for the instrument’s inability to detect arbitrarily small ions [8]. The vapor losses were then removed by introducing a reheater in the vapor path, and the isothermal mixing hypothesis was confirmed and used for the determination of S [8]. Several subsequent variants of the turbulent mixing CPC have been described [15–20], none of which has reported activation curves as steep as those of references [7,8].
In view of this situation, and given that the great majority of currently existing CPCs are of the diffusive kind, here we pose the question of whether a diffusive CPC, perhaps with a suitable inversion, might be used to carry out basic heterogeneous nucleation studies, as well as to infer particle size distribution information with high resolution. As a first step we consider the widely used idealized two-dimensional or axisymmetric geometry where the velocity field is fully developed parabolic flow, the entering gas is uniformly saturated at an inlet temperature Ts, and the wall temperature varies in a step fashion to a condenser downstream temperature Tc. A local analysis near the condenser wall shows that all particle streamlines proceeding in the vicinity of the wall go through a common maximum in the supersaturation Smax,w, which is independent of the distance to the wall. Particle trajectories along the center of the channel also go (by symmetry) through a common maximum Smax,c in the supersaturation. However, Smax at the wall and the center are generally different from each other. As a result, there is a finite range of maximal supersaturations Smax ∈ [Smax,c, Smax,w] experienced by particles moving along different streamlines. Consequently, the activation curve P(S) must span at least the whole range between Smax,c and Smax,w, and can only be steep when the ratio Poly = Smax,c/Smax,w approaches unity. Although the range [Smax,c, Smax,w] may be wide, it is considerably narrower than the full range of supersaturations represented inside the CPC, 1 ≤ S ≤ max[Smax,c, Smax,w]. A second finding relates to the ratio Poly = Smax,c/Smax,w quantifying how wide is the range of different maximal supersaturations experienced by different seed particles within the CPC. In the special case Poly = 1, all particles in the CPC experience the same maximal supersaturation, resulting in an instrument ideal for particle sizing as well as for fundamental heterogeneous nucleation studies. For given equilibrium vapor pressure curve pv(T), flow and temperature conditions, Poly is a function of only the Lewis number Le = α/D, the ratio between the thermal diffusivity and the mass diffusivity of the gas/vapor mixture. A most interesting finding is that Poly(Le) tends to unity as Le → 1. In other words, a diffusive CPC could be an ideal tool for sizing and heterogeneous nucleation studies if the vapor/gas combination were suitably manipulated to achieve a unit Lewis number. In a final discussion we consider how the singular condition Le = 1 may be achieved in practice, by either manipulating the carrier gas, or by making the flow turbulent.
2. Theory
2.1. The near-wall problem
Understanding the near-wall region is important because equilibrium prevails right at the wall, forcing the wall boundary condition S = 1. The wall is hence typically where the supersaturation is lowest, apparently precluding the desired condition that all seed particles experience the same level of supersaturation. However, when the wall temperature changes abruptly, it is possible to show with complete generality that the maximum supersaturation achieved along near-wall streamlines is considerably larger than unity, and is the same for all near-wall streamlines. These facts are most relevant to CPC design, and it is important to be sure that they are generally true, especially when their proof offered below is rather simple. One could argue that the same conclusion could be arrived at by numerical analysis, making the present section unnecessary. However, numerical evidence is always tied to concrete calculations and it is hard to know how generally it applies. Furthermore, numerical analysis in the vicinity of a singularity (a temperature step at the wall) is always subject to numerical inaccuracies, therefore not offering the same level of certainty as the local analytical solution provided here. This point is illustrated in the numerical calculations of Section 2.2, which cannot be accurately extended to the close vicinity of the wall. Furthermore, our near-wall analysis for a temperature discontinuity at the wall can be readily extended to a more realistic situation when the temperature jump occurs over an insulating gap of finite width.
In the near-wall region the fluid velocity field u is parallel to the wall and grows linearly with the distance y to the wall. The planar and cylindrical geometries behave similarly:
| (1) |
where the function a(x) depends on the flow field. In fully developed Poiseuille flow a(x) is constant. Neglecting diffusion along streamlines, the conservation equations for the vapor number concentration n and the gas temperature T are
| (2a) |
| (2b) |
where D and α are the vapor and heat diffusivities. Introducing the time-like variable
| (3) |
turns (2) into
| (4) |
The boundary condition is idealized to a hot–cold junction on the wall of a tube or a plate, with
| (5) |
The initial condition is that
| (6) |
where Ts is the saturator temperature, and Tc is the condenser temperature. The corresponding conditions for n involve the saturated (equilibrium) vapor concentration
We focus on the solution to the equation for T, since the equation for n is analogous except for an interchange between α and D. The problem admits a similarity solution in terms of the variables
| (7) |
| (8) |
and analogously for the vapor concentration,
| (10) |
As an example, we take D = 66/760 cm2/s for 1-butanol vapor at 298 K, [21] and α = 0.211 cm2/s for air at the same temperature [22]. Therefore
| (11) |
A number of diffusive and mixing CPC designs have used low diffusivity vapors such as butanol, diethylene glycol and dibutyl phthalate. Even for volatile species substantially larger than butanol, Le1/3 would not depart sufficiently from unity to result in serious differences in the structure of the diffusive concentration change near the wall.
We now calculate the supersaturation:
| (12) |
For the particular case of butanol, we describe the equilibrium vapor pressure via: [23]
| (13) |
where T is in °K, and pv in Torr. We take the representative values Tc = 12 °C and Ts = 45 °C, which for Kanomax’s 3650 fast CPC is close to the onset for homogeneous nucleation in butanol. S is represented in Fig. 1 as a function of η for various values of D/α. In the low diffusivity limit S reaches very high values near the wall, and decays to unity only in a very thin boundary layer. But this limit is approached only at physically unattainably large values of α/D. For butanol with Tc = 9 °C, Ts = 41 °C, Le = 2.5, the maximal supersaturation is 2.13476 at η ~ 0.6074.
Fig. 1.
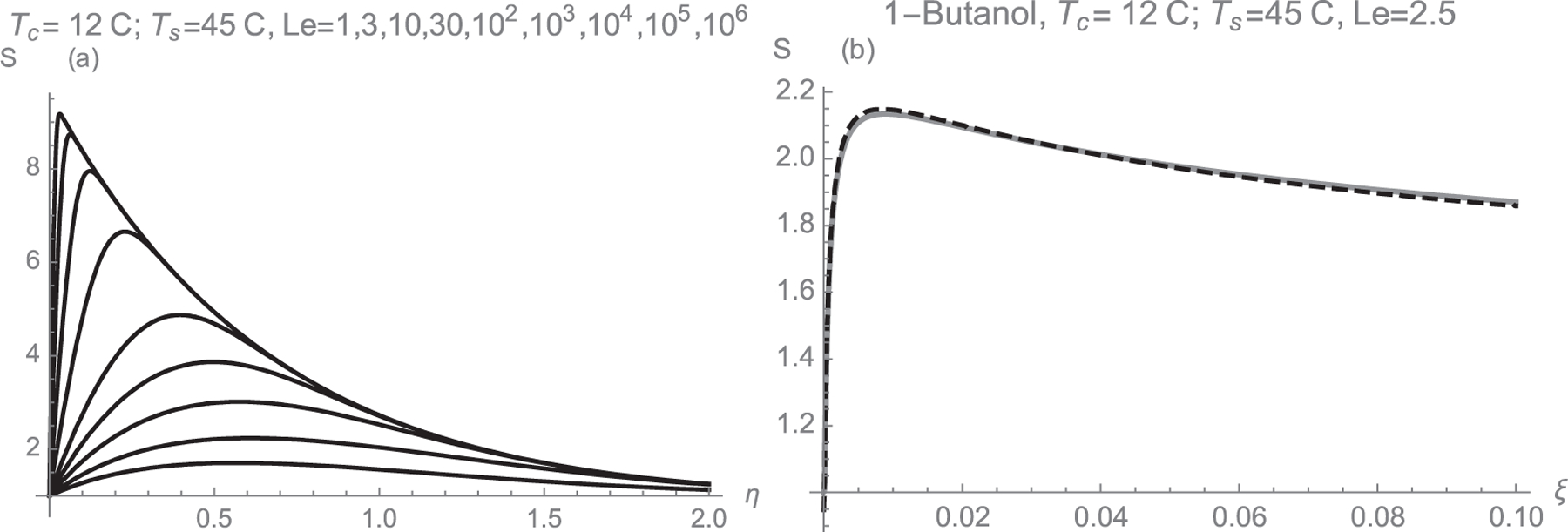
(a): Supersaturation versus η in the vicinity of the wall for butanol, with Tc = 12 °C, Ts = 45 °C, and Le ={1, 3, 10, 30, 102, 103, 104, 105, 106} (bottom to top). (b): Comparison of the near-wall approximation (Gray) to the exact solution to the 2-D Graetz problem (Black, Dashed) at y = 0.1 Le = 2.5.
One can see in Fig. 1 that S tends to unity both at η = 0 and η→∞, and is highly non-uniform. However, for a given system (given Le, pv(T), Tc, Ts), the S(η) curve is unique for all x and y positions close enough to the wall for the linear approximation (1) to apply. A particle moving axially with the flow (fixed y, varying x) will have a variable η value. It will start at x = 0 (t = 0, η=∞) with S = 1, and will return to S = 1 far downstream (x→∞, t→∞, η→0). In between it will go through a maximal S at a given critical η. Although this critical η corresponds to different x values at different y values (different particle streamlines), Smax is the same for all near-wall trajectories. Accordingly, the particles going closest to the wall, instead of being exposed just to the smallest supersaturations close to unity, will rather go through the same Smax as all other particles evolving sufficiently near the wall. For instance, in the case of an approximately developed parabolic flow a(x) = ao is constant, t = x/ao (x measured from the point where the wall temperature changes abruptly from Ts to Tc), and the maximal supersaturation achieved at η = 0.5 corresponds to y = 0.5 (Dx/ao)1/3. The particles closest to the wall are activated immediately at the temperature step (x = 0, the junction between the saturator and the condenser), and more interior particles with larger initial y are activated at larger x further downstream. A similar behavior would apply to a more general situation with variable a(x), as in a flow developing towards the parabolic asymptote, as long as the particles are close enough to the wall for the linear relation (1) to apply. Within this near-wall region, interestingly, all particles reach exactly the same maximal supersaturation, at exactly the same temperature and vapor concentration (both of which depend only on the single variable η).
Because nucleation takes place primarily near the region of maximal supersaturation encountered by a particle moving along a streamline, having just shown that this maximum is always well above S = 1, it follows that the near-wall region close to saturation conditions is effectively irrelevant. However, it is important to note that this favorable theoretical prediction is by no means general. It is rather a special consequence of the singular boundary condition imposed of a discontinuous temperature jump at the wall. Lewis and Hering [24] have shown that the situation changes radically when the transition from Ts to Tc occurs not discontinuously, but somewhat gradually over a finite wall length. In that case, there is a finite range of distances to the wall at which the maximal supersaturation is arbitrarily close to unity. This problem is probably more pronounced in the case of the water CPCs studied by Hering and colleagues, where the wall is not just a passive metal surface, but must inject hot vapor into the system. Nonetheless, the idealized notion that Smax near the wall takes a value well above 1, almost independently of the distance to the wall plays an important role in the present study, suggesting the need of a special effort to either minimize the length of the thermal transition region, or of removing particles from the near-wall region by means of sheath gas. Otherwise some of our most promising theoretical conclusions may not be approximated in practice.
Returning now to the ideal situation of a discontinuous temperature jump, we must also note that the independence of Smax on y applies only in the vicinity of the wall. Particles in the core of the CPC are governed by different laws and do not necessarily achieve that same maximal supersaturation. In fact, when D < α, the center of the channel is more prone than the wall region to produce a higher S because the diffusivity ratio enters into the equations raised to the first power, rather than to the 1/3 power. Therefore a substantial difference in Smax between the channel core and its walls will often be found.
2.2. The two-dimensional Graetz problem
To model the full channel we assume one-directional flow along the x direction in a two-dimensional (2D) channel bound by two parallel plates in the planes y=±R, with a parabolic velocity profile (Poiseuille flow). Here we consider only the 2D problem, where physical variables change only in the x, y plane. The interest of this geometry follows first from the fact that it enables rapid cooling and therefore a very fast instrument response [25]. The characteristic time for heat diffusion over a distance R is R2/α, where α is the thermal diffusivity and R is the half width of the channel. A sufficient channel width W in the z direction enables a narrow gap between the two walls, without reducing the flow rate Q needed to achieve a certain signal. The transfer of heat from the center to the walls may hence be very fast, greatly decreasing the time required to cool the gas and achieve the maximal supersaturation. A second advantage of the 2D configuration is that, unlike the axisymmetric geometry, the curve giving the activation probability versus the supersaturation has infinite slope at the onset of nucleation, increasing considerably the steepness of the P(S) curves.
The equation governing the 2D temperature profile is:
| (15) |
where x and y are the original coordinates made dimensionless with R, and the velocity U is the maximal (not the mean) velocity, related to the flow rate Q’=Q/W per unit length in the z direction as
| (16) |
Axial diffusion has been neglected, and α is the thermal diffusivity of the gas. R is the half width of the channel such that its center is located at y = 0, and the walls at y =±1. (15) then becomes
| (17a-c) |
with initial condition
| (18) |
and boundary conditions
| (19) |
Note that the variable y used here is dimensionless and vanishes at the center of the channel, while the quantity y used in the near-wall analysis of section 2.1 had dimensions of length and vanished at the channel wall.
Because power series solutions to the classical problem (17–19) are known both in planar (2D) and cylindrical geometries, the details of the calculation of θ are given in the Supporting Material, where use of the computer program Mathematica greatly improves the accuracy of the published expansion parameters. The numbering of the equations in both sections continue each other.
2.2.1. The supersaturation
The number density n of the vapor (particles/cm3) is governed by the same diffusion equation (15) as the temperature, except for the substitution of the mass diffusivity D in place of the thermal diffusivity α. We further assume that the gas stream is initially saturated with vapor at the inlet gas temperature, while at the wall its saturation is unity:
| (30) |
where neq(T) is the equilibrium concentration of the vapor at temperature T. Therefore,
| (31) |
| (32) |
| (33) |
Finally the supersaturation may be expressed as
| (34) |
Given Le, Tc, Ts, and the vapor pressure function nv(T), S may be calculated at any position ξ ≥ 0, 0 ≤ y ≤ 1.
The summation involved in the calculation of θ and S is carried out by a Mathematica program. θ is computed at 23 different values of y, the sum (15) is carried out through 37 terms. The process is accelerated by defining and computing only once the 23x37 matrix of Fi(yj) values.
Fig. 2 is an example of the dependence of S(x,y) for n-butanol (Le = 2.5) in the particular case Tc = 12 °C, Ts = 45 °C. Each of the curves shown for fixed y starts with S = 1 at x = 0, goes at larger x through an absolute maximum (two local maxima for some y values), and decays back slowly towards S = 1 far downstream. Accordingly, a particle streamline with fixed y goes always through a certain maximal value of S which depends on y, and which we will denote as Smax(y). Naturally, most of the particles that nucleate will be activated as they go through this maximal S region, so the functional dependence Smax(y) is a key quantity of interest for heterogeneous nucleation. Fig. 2 shows the considerable dependence of this maximal S on y: For Le > 1 it is easier to activate the particles that go through the center of the channel than those that go near the channel walls. Fig. 2 includes also the near-wall result for dimensionless wall distances of 0.05, 0.1 and 0.125, 0.15, 0.175 (colored curves), showing excellent agreement for the two smallest y values. The representation uses the fact that η=(1-y)/(ξ/2)1/3. The dashed lines in the figure represent S(ξ, y) computed with θ(ξ, y) given by Equation (29), which keeps only the first eigenmode.
Fig. 2.
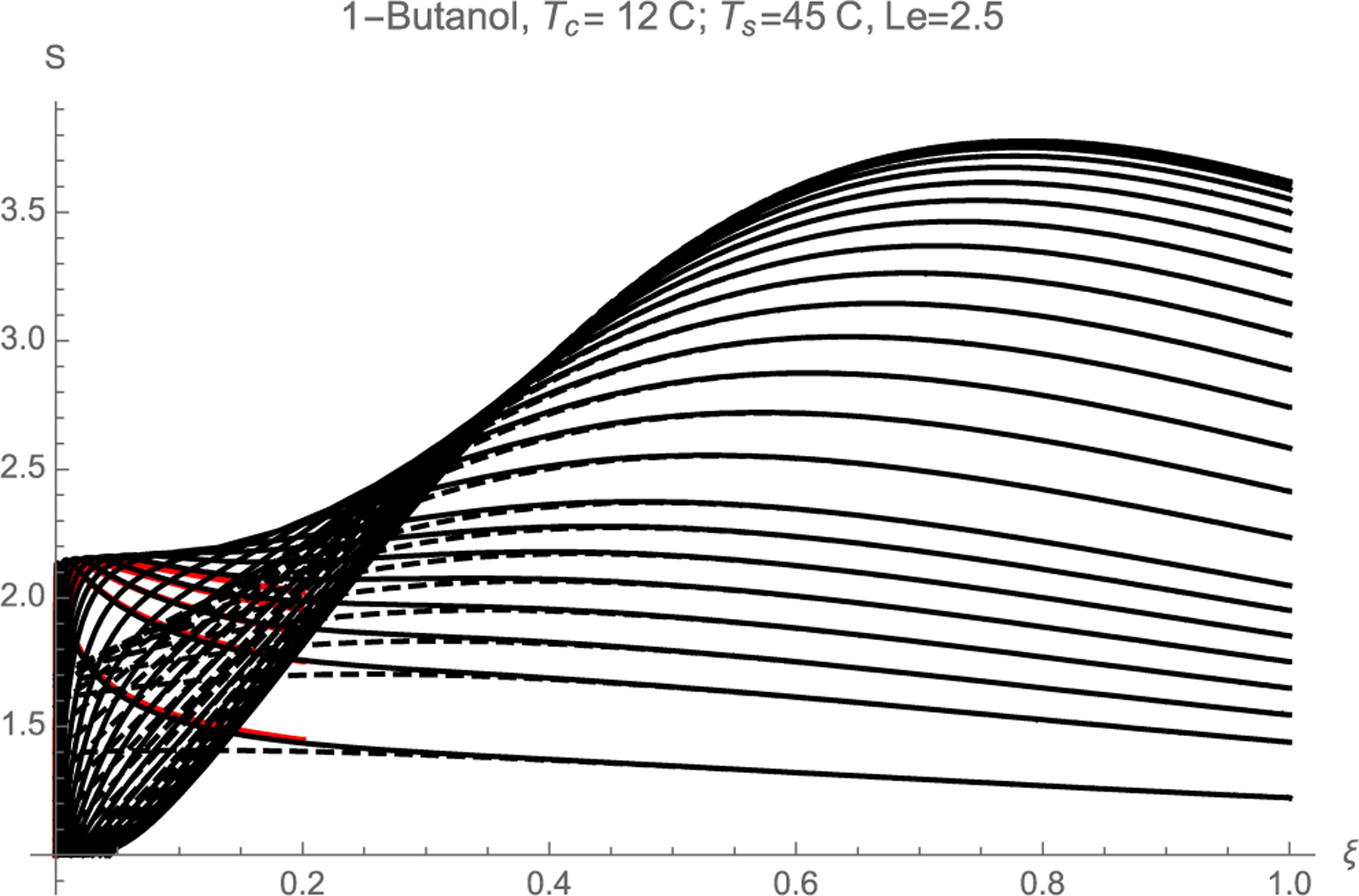
Supersaturation S versus dimensionless axial position ξ = xε downstream from the temperature discontinuity. The different curves correspond to different positions y within the chamber: y={0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.775, 0.8, 0.825, 0.85, 0.875, 0.9, 0.95}, from top to bottom. The colored curves are the near-wall approximation [Equation (12) with η= (1-y)/(ξ/2)1/3] for dimensionless distances to the wall y = {0.825, 0.85, 0.875, 0.9, 0.95}. The dashed curves keep only the first eigenmode (29) in the calculation of θ(ξ, y,Le).
In Fig. 2 one can see that Smax spans a finite range of values from 2.17 to 3.79. Fig. 3 represents Smax values obtained from graphs similar to those of Fig. 2, each curve corresponding to a fixed Tc = 12 °C, and different Ts (oC) of {20, 21, 22, . . ., 43, 44, 45}. The highest among these curves corresponds to the data of Fig. 2, with Ts = 45 °C. The curves below it, each correspond to successive 1 °C decreases in Ts. The structure of the curves is of some interest. As already noted Smax reaches its highest value Ssup at y = 0. This feature is general when Le > 1. Smax changes little in the vicinity of the axis, and decreases uniformly with increasing y, eventually reaching an almost y-independent value Sinf near the wall. It is numerically difficult to compute Smax near the wall because, when y→1, the maximum in S arises at very small x values, while the Graëtz series (20) converges rather slowly as x→0. For this reason we do not attempt the direct determination of Smax near the wall, relying instead on calculations farther from the wall (y = 0.9) and on the analytical knowledge that Smax is constant near the wall (as shown in section 2.1, and as can be seen in the small x region of Fig. 2). Note that Smax is represented in Fig. 3, not as a function of y, but as a function of a dimensionless streamfunction Ψ taking values 0 at the center of the channel and 1 at y = 1. The reason for this choice is that Ψ will be seen to be closely connected with the activation probability, so the representation of Smax versus Ψ enables the determination of the desired P(S) curves. For the plane Poiseuille flow considered in this study,
| (35) |
Fig. 3.
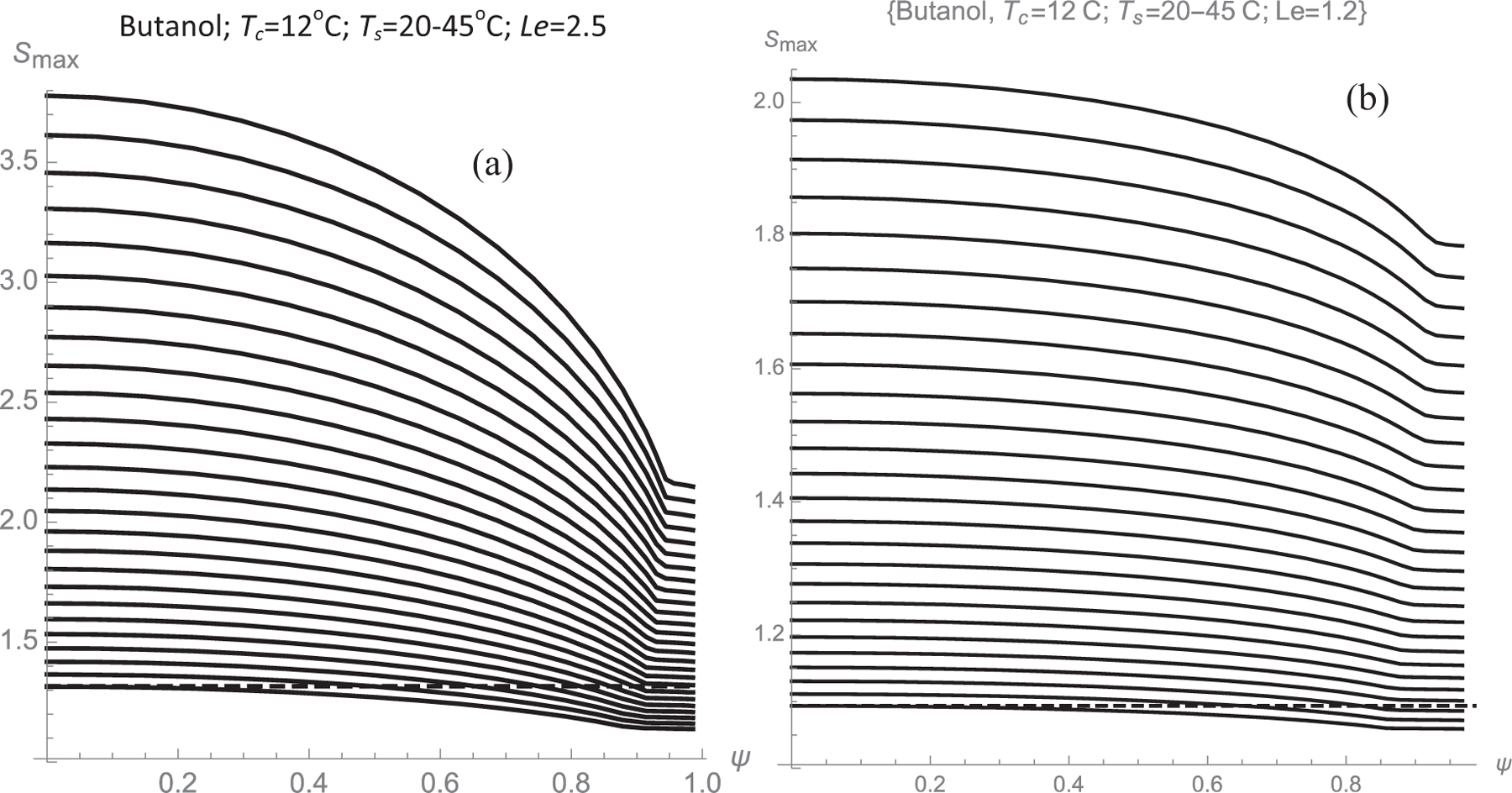
Maximal supersaturation versus streamfunction Ψ achieved in butanol for Tc = 12° and various saturator temperatures Ts (o C) ={20, 21, 22, . . ., 43, 44, 45}, from bottom to top. (a) Le = 2.5; (b) Le = 1.2.
The curves in Fig. 3 show what appears to be a discontinuity in the slope of the Smax(Ψ) curves near their Ψ = 1 boundary. This behavior is real and can be understood by examining the maxima in Fig. 2. The S(ξ) curves for small y have a maximum at values of order unity of the axial variable ξ. As y increases, this maximum decreases and shifts to smaller values of ξ. The region of small y has its own maximum analyzed in Section 2.1. Accordingly, there is a range of y values for which there are two different local maxima, S1,max(Ψ) and S2,max(Ψ), each with its own Ψ dependence. Smax is naturally defined as the largest of these two maxima. The slope discontinuity arises at the value of Ψ at which the curves S1,max(Ψ) and S2,max(Ψ) cross each other. For smaller Ψ the relevant maximum is the near-wall one, and for larger Ψ it is the one closer to the center of the channel.
For Le > 1 the largest and the smallest of the values of Smax(Ψ) encountered at a certain CPC setting are always at the center and at the wall of the channel: Ssup = Smax(0); Sinf = Smax(1). The roles of Ssup and Sinf tend to be inverted when Le < 1.
A measure of the maximum variation in Smax within the CPC is given by the polydispersity ratio
| (36) |
If a certain particle size is activated at a critical supersaturation S*, its activation probability P will be zero when Ssup ≤ S*, and 100% when Sinf ≥ S*. If one changes the CPC setting to go from zero to 100% activation for this particle size, one will have to cover the range of conditions from an initial one where Ssup = S* to a final one in which Sinf = S*. Since the ratio Ssup/Sinf is 1.75 for the conditions of Fig. 2, the resolution with which one could measure particle size by scanning over the CPC setting will necessarily be poor. Manipulating Ssup/Sinf such that it approaches unity would be very helpful in this respect.
Figure SI-3 shows that Poly cannot be seriously reduced by control of the CPC temperatures. Poly only approaches unity when the temperature difference between saturator and condenser tends to zero, in which case Ssup→1, and no nucleation may take place. Likewise, varying the expression for vapor pressure pv(T) by changing substances does not seem to diminish the polydispersity. The chief parameter available to control Poly is Le, to be discussed in section 2.3.
An important feature of the Smax(Ψ) curves in Fig. 3 is their zero slope at the plane of symmetry Ψ = 0. This offers a practical method to bring Poly much closer to unity by sampling only say 50% of the central flow region (0 < Ψ < 0.5) and rejecting the balance of low-S region flowing near the walls. As further discussed at the end of section 2.4, this is a special feature of Oberreit’s unconventional two-dimensional geometry considered here. It is absent from the commonly used cylindrical CPC geometry, though it could be recovered in an axisymmetric annular configuration.
In contrast to the behavior found at Ψ = 0, Fig. 3 shows that the slope of the Smax(Ψ) curves at the channel wall Ψ = 1 is small but finite. We have seen in section 2.1 that dSmax(y)/dy is null at the wall, but because dΨ/dy vanishes also at the wall, a finite slope dSmax(Ψ)/dΨ results. The situation is similar in planar and cylindrical geometries. As a result, the possibility of moderating Poly by sampling only the near wall regions appears as far less interesting than the center-sampling alternative. Near-wall sampling is undesirable for an additional reason already broached at the end of Section 2.1. If the wall temperature change from Ts to Tc does not take place discontinuously, there will be a finite region very near the wall over which Smax will depart from the constant value depicted in Fig. 2, dropping abruptly to unity. Similarly, the right boundary of all the curves in Fig. 3 will fall abruptly down to S = 1 in the close vicinity of Ψ = 1. The near-wall region should accordingly be singled out for exclusion rather than for preferential sampling, not only for the reasons just noted, but also because it is subject to the largest diffusive particle losses.
2.3. The role of the Lewis number
The drastic effect of the Lewis number on the S(ξ, y) curves can be seen by computing curves similar to those in Fig. 2 over a wider range of Le (Figs. 4 and SI-4). The vapor pressure used in these calculations is that of butanol. Taking Le to be variable for a fixed working liquid is somewhat artificial. However, it is in principle possible to decrease Le via the carrier gas, shifting from H2, He, N2, air to CO2, SF6, and even heavier fluorocarbons. The main results from Figs. 4 and SI-4 are more compactly summarized in the Smax(Ψ) curves of Fig. 5. The most striking finding in Figs. 4, SI-4 and 5 is that the condition Le = 1 is singular in yielding a uniform maximal supersaturation for all streamlines. The ideal diffusive CPC for basic heterogeneous nucleation studies would accordingly not be a fiction if one could match the thermal and mass diffusivities.
Fig. 4.
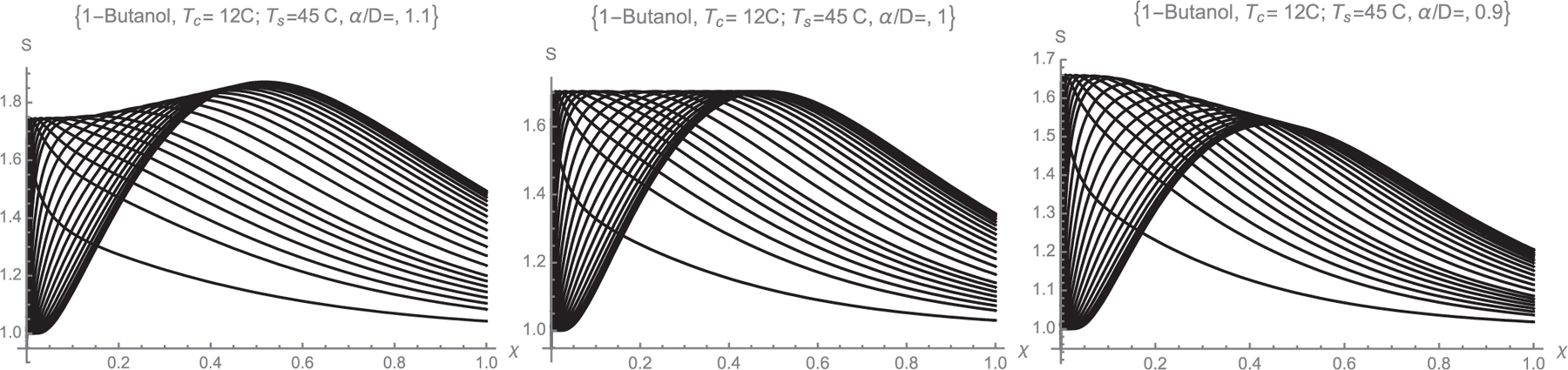
Dependence of the S(ξ, y) curves on Le for Butanol with Tc = 12 °C, Ts = 45 °C. Each curve corresponds to a different value of y = {0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.775, 0.8, 0.825, 0.85, 0.875, 0.9, 0.95}. Smax becomes spatially uniform at Le = 1. Additional information for other Le values is included in Figure SI-4.
Fig. 5.
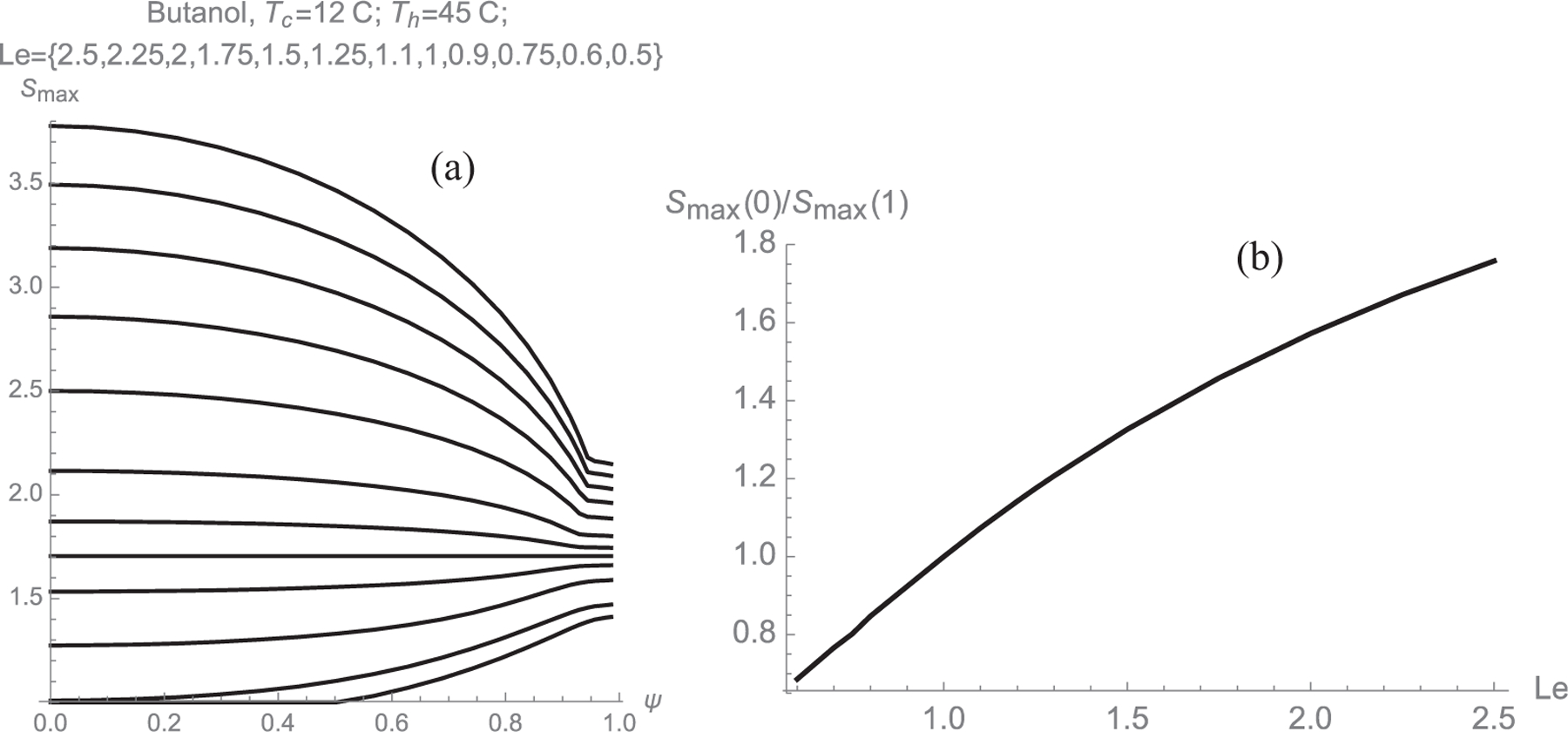
Spatial variation of Smax for butanol at different Lewis numbers, with Tc = 12 °C, Ts = 45 °C, showing that the special condition Le = 1 leads to a uniform Smax for all streamlines (a): Smax(Ψ), with Le= {2.5, 2.25, 2, 1.75, 1.5, 1.25, 1.1, 1, 0.9, 0.75, 0.6, 0.5} from top to bottom. (b) Poly(Le).
One can reason that the Le = 1 singularity found in Figs. 4, SI4 and 5 for a particular working fluid at a particular Tc should be completely general independently of the boundary temperatures or the details of the vapor pressure curve. For any given boundary temperatures and vapor pressure curve, if Le = 1, Equation (34) shows that S(ξ, y) is not a function of the two variables (ξ, y), but only of the single quantity θ: S=S(θ). Therefore, if there is a value of θ for which S is a maximum over one streamline, any other streamline along which the same θ is encountered will present exactly the same maximal supersaturation, temperature and vapor concentration. Furthermore, since θ spans its full range from 0 to 1 along all streamlines, if any streamline presents a maximum for S, all streamlines will present exactly the same maximum.
Other features of the calculations reported in Figs. 4, SI-4 and 5 deserve comment. One is that, for given wall temperatures {Ts, Tc}, the maximum value of Smax(Ψ) decreases considerably as Le decreases. This appears to imply that, at Le = 1, far more heating and cooling (hence instrument power) is required than at Le = 2.5 in order to reach the same Smax. However, heterogeneous nucleation on ions is not determined by a fixed value of S for all vapors. The required critical supersaturation increases exponentially with the physical properties of the liquid, especially the molecular volume. Scrit for ions is close to unity for small vapors (1.35 for toluene cations in methanol) [6], while exceeding 1000 for large vapor molecules such as DBP [8]. Kelvin Thomson capillary theory indicates that nucleation of small ions must always take place for [7,8]
| (37) |
The condition αN < 3/44/3 of this model is generally satisfied in practice [10]. The quantity αN is accordingly much preferable to S as a predictor of nucleation on charged particles. We have run calculations similar to those shown in Figs. 2 and 4 for the four lightest normal alcohols (with their appropriate temperature-dependent physical properties taken from 23), representing αN rather than S with Tc = 12 and Ts = 45 °C. As seen in Figures SI-5, αT takes a maximal value slightly above 0.4 almost independently of the alcohol. Therefore, for ions, the fact that Smax decreases with decreasing vapor size as Le approaches unity does in no way reduce the nucleation ability of smaller vapors compared with larger vapor molecules.
The preceding theoretical considerations on αN are based on classical capillary theory, which is not necessarily obeyed in practice. They also ignore the fact that the smallest particle that can be activated is generally not determined by the maximal S achievable in practice, but by homogeneous nucleation. Nevertheless, even for the smallest ions, prior studies have shown that heterogeneous nucleation typically takes place before homogeneous nucleation (though the same is apparently untrue for neutral particles). A final consideration suggests that approaching Le = 1 is favorable rather than unfavorable with respect to the limitations imposed by the onset of homogeneous nucleation. Indeed, when Poly = 1, the uniformity of Smax assures that full activation is achieved when S*= Ssup. In contrast, when Poly ≠ 1, full activation requires S*= Sinf, at which point some regions of the CPC reach supersaturation larger than S* by a factor Ssup/Sinf, with an increased risk of homogeneous nucleation.
Another interesting feature of Fig. 5 is the behavior when Le < 1, a special situation that arises in water CPCs in air. The trend noted of a reduction of Ssup with decreasing Le naturally continues below Le = 1. Sinf decreases even further, to the point that, at Le = 0.5, trajectories having Ψ < 0.5 do not experience any supersaturation at all. Nonetheless, Le for moist air is in the range 0.8–0.9, for which Fig. 5a shows that it is still possible to operate a conventional diffusive water CPC. However, for Le < 1, it is much preferable to invert the ordering of the temperatures, placing the hot wall downstream and the cold wall upstream, as done in the elegant developments of Hering and colleagues [26–28].
2.4. Achieving Le = 1 in real gas/vapor systems
The two basic elements of a condensation system are the permanent gas (the gas) and the condensible vapor (the vapor). In the common case when the vapor is in small quantities in the gas, the thermal diffusivity α is fundamentally a property of the gas only. The mass diffusivity D is a binary property of the gas and the vapor. Le may accordingly be controlled by changing the vapor, and/or the gas. Because air has a thermal diffusivity (0.216 cm2/s at 300 K) larger than the mass diffusivity of most vapors usable as working fluids, most vapors have Le = α/D > 1 in air. However, there are a few exceptionally small and sufficiently condensible fluids such as H2O (D = 0.24 cm2/s at 300 K), ammonia (D = 0.28 cm2/s at 300 K), etc., for which Le < 1 in air. In these cases Le can be tuned to approach unity by seeding the air with more thermally diffusive gases, such as Ne, He, H2, etc. Relatively small additions of He and H2 produce substantial changes in the thermal diffusivity of air because their thermal conductivity is about an order of magnitude larger than that of air. By analogy, the route to find vapor/gas combinations with Le close to unity is clear. Roughly speaking, the vapor needs to have a somewhat smaller size than the gas. This can be seen in Table SI-1 (Supporting Information) collecting diffusivities and Lewis numbers for normal alcohols in air [21]. When Le is plotted versus molecular weight for the first five alcohols in the Table, an approximately straight line is obtained that intersects the Le = 1 line at a molecular weight of about 22 g/mol, below that of N2. Unfortunately, due to the smallness of N2 molecules, most condensible vapors are considerably bulkier and heavier than air, and have Le well above unity. Even though methanol is comparable in size to air molecules, the air/methanol system has D = 0.14 cm2/s, [29] compared to air’s α = 0.216 [22] (both at 300 K), with Le = 1.54. Additional diffusivity data for alcohols and glycols in air are given in Table SI-1 with corresponding Le, which in all cases considerably exceed unity.
Greater flexibility in the selection of the vapor can be achieved by using a gas heavier and bulkier than air. An excellent example is CO2, which is about half way in size between methanol and ethanol. Its thermal diffusivity at 1 atmosphere may be correlated as α = 0.00000109 T2 + 0.00007913 T − 0.01183110, [30] with T in °C [α(298 K) = 0.109 cm2/s]. We are not aware of diffusivity data of alcohols in CO2, and have alternatively estimated D (probably with substantial errors) according to Eq. (6) and Table 3 of [31]:
| (38) |
In this formula D is in cm2/s, p in atmospheres, T in K, and the molecular weights Mi in g/mol. The molecular volumes Vi are obtained by summing those of the atomic constituents in the units given in [31] (VC = 14.8, VH = 3.7; VN between 10.5 and 15.6; VO between 7.4 and 12). In our calculations we have taken VN = 10.5 and VO = 8, which gives a fair agreement between predicted D in N2 and measured values for propanol and butanol in air [31]. The corresponding Le predictions are included in Fig. 6 for the first four normal alcohols in both air and CO2 as a function of the number n of carbons in the alcohol molecule. Interestingly methanol/CO2 and ethanol/CO2 approach the desired Le = 1 condition. Simple adjustments to slightly reduce or augment Le to bring it closer to unity with as much precision as desired can be made by mixing the CO2 with small amounts of a gas either lighter (such as N2 or air) or heavier (such as butane, with Tboil = 0 °C). With these and related strategies it is certainly possible to achieve Le = 1 with water, methanol and perhaps also ethanol vapors in safe and relatively inexpensive gas mixtures. The range of viable solvents may be further widened by using even larger and heavier species as the carrier gas. Among many other examples of substances with high enough vapor pressure and mass to act as non-condensing carrier gases are SF6, BF3, the wide range of commonly used halogenated hydrocarbons (Freons), etc.
Fig. 6.
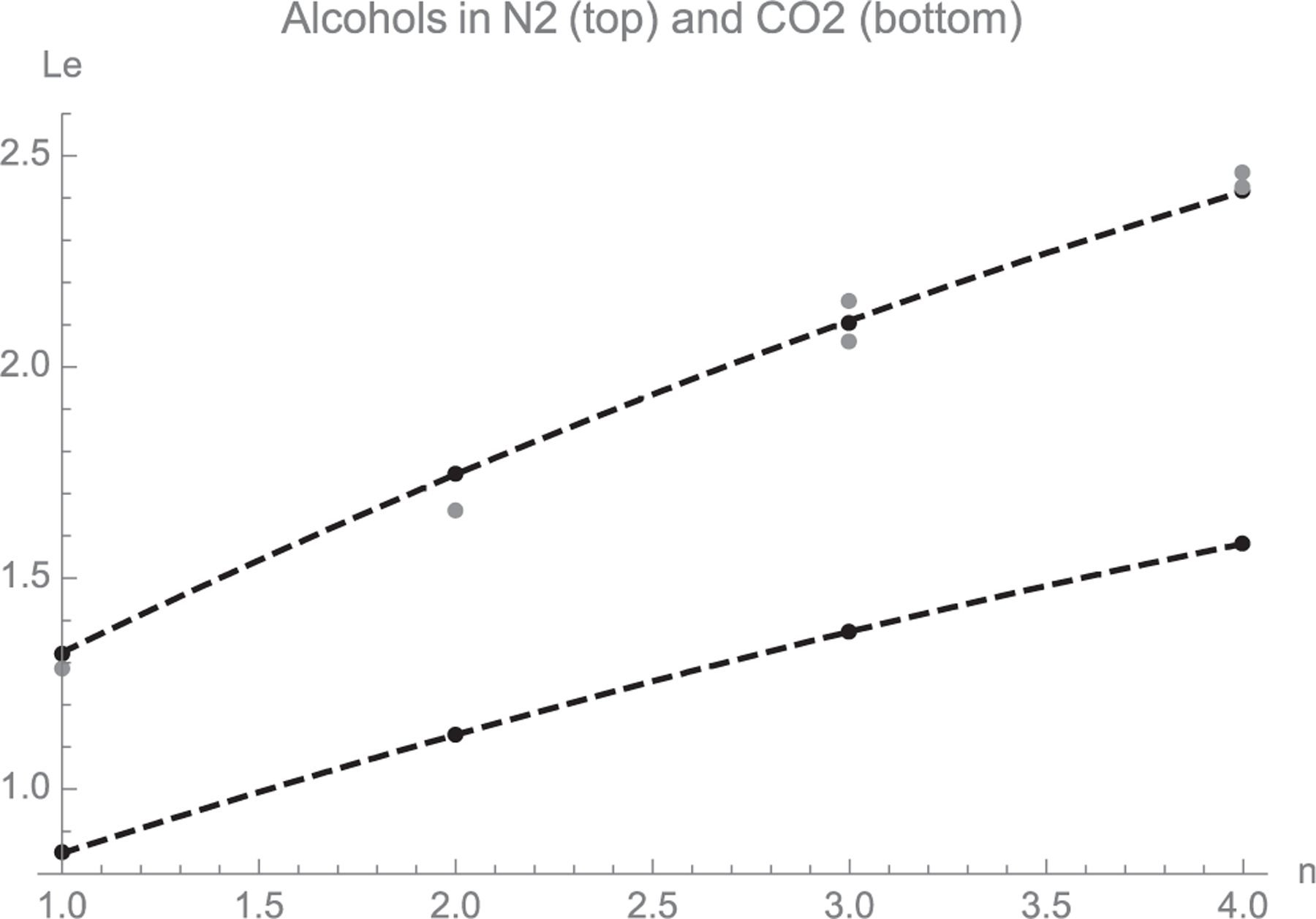
Calculated Le in N2 and CO2 versus the number of n of C atoms in the alcohol for the first four normal alcohols at 293 K [Equation (38)]. The singular condition Le = 1 is approached by methanol and ethanol in CO2. The gray symbols are the air/alcohol data from Table SI-1, with α = 0.214 cm2/V/s. For CO2 we use α = 0.109 cm2/s.
2.5. Approximate calculation of the activation curves based on a critical supersaturation
Here we use a simple routine to compute activation curves to be compared in forthcoming studies with those obtained experimentally. In an ideal CPC having a single Smax (Ssup/Sinf = 1) the activation curve obtained upon scanning over supersaturation would span a narrow S range ∆Sideal. This ideal width is determined by heterogeneous nucleation kinetics, and has been measured experimentally in a few instances (Figure SI-1). It is typically much narrower than the range of supersaturations ∆Sreal spanned by any of the curves of Fig. 3 corresponding to various CPC settings:
| (39) |
Accordingly, ∆Sideal will be taken to be zero for the purposes of this simplified calculation. In other words, the ideal activation curve is assumed to be a step function Pi(S) = H[S–S*(d)], where S*(d) is the critical supersaturation at which a particle of diameter d is activated. An important limitation of this critical supersaturation model is the fact that the activation probability is related to the product of the nucleation rate times the residence time τ in the region of maximal supersaturation. Even when Smax is uniform for all streamlines, τ is not. The Ψ dependence of τ generally has a modest effect, as τ enters in the preexponential factor rather than the exponent of the nucleation kinetics. However, because τ(Ψ) tends to zero as Ψ→1, the effect is not necessarily minor near the walls. This complicating circumstance would be avoided by use of a modest fraction of near wall sheathing.
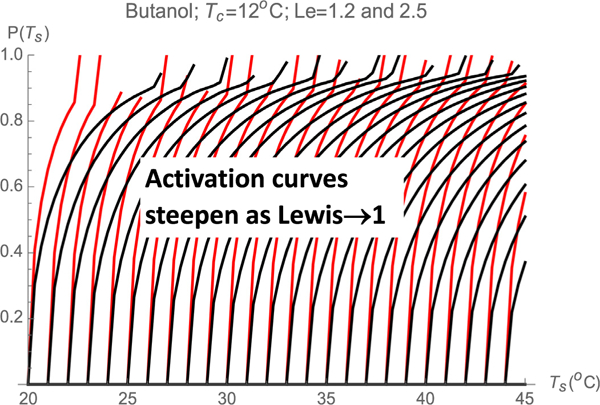
We now imagine an experiment in which identical particles of diameter d are steadily passed though the CPC, and the activation probability P(d) is determined by scanning over a certain spectral variable s defining a set of saturator and condenser temperatures Ts(s), Tc(s), all other parameters of the CPC remaining fixed. For the sake of simplicity we choose the family of CPC settings with Tc fixed at 12 °C and Ts(s) varying, in which case the spectral or scanning variable s is simply Ts. The distributions of supersaturations for this series of settings and the corresponding Smax(Ψ) curves have already been calculated and reported in Fig. 3 for Ts from 20 to 45 °C. Let us first consider the bottom curve in Fig. 3a, corresponding to Ts = 20 °C and Tc = 12 °C, with Ssup = 1.3147. For this CPC setting, a particle having a critical supersaturation S*=1.3147 will activate with zero probability. If we now increase Ts from 20 to 21 °C, the corresponding Ssup increases to 1.365, and all particles in streamlines with S > S* will be activated. The corresponding activation probability for this CPC setting is therefore the Ψ value at the intersection between the Smax vs. Ψ curve with Ssup = 1.365 in Fig. 3a with the horizontal line S=S* (dashed horizontal line in Fig. 3a). This intersection takes place at Ψ=0.495. We conclude that, when Ts = 21 °C, the activation probability is 0.495. The intersections of the critical horizontal line Smax = 1.3147 with the other Smax(Ψ) curves at different CPC settings (different Ssup) give additional (Ssup, Ψ) or, equivalently, (Ts, Ψ) pairs. Recall that this Ψ is the activation probability P, while Ssup or Ts are just convenient variables to characterize the CPC setting. From the experimental viewpoint it is preferable to use Ts as the variable characterizing the CPC setting. These various intersections then enable the construction of the activation curve (P,Ts) for particles with S*=1.3147, which is shown as the continuous black curve most to the left in Fig. 3. Similarly, launching other horizontal lines corresponding to different critical supersaturations, their intersections with the curves of Fig. 3a generate (Ts, Ψ) pairs defining their corresponding activation probabilities, also shown in Fig. 7. These intersections may be determined graphically, though we have obtained them by generating interpolating functions for the curves in Fig. 3 and computing their intersection with various horizontal lines. Of particular interest is the fact that, in the region near 100% activation, the activation curves rise with a high slope. This is a natural result of the fact that there is a finite region near the wall where Smax varies very little for a finite range of streamlines. The activation curve rises with infinite slope at the onset of activation, when P→0. This singular slope is not visually clear from the discrete set of calculated values in Fig. 7 due to the finite (1/3°C) step used for Ts. This singularity is a result of the symmetry condition at y = 0, whence Smax(y)= Ssup + βy2+…= Ssup+ γψ2 where β and γ are proportionality constants. In the two-dimensional geometry considered, y and Ψ are proportional to each other near the plane of symmetry, leading to Ψ~(S-Ssup)1/2~(Ts-Ts*)1/2 and therefore to the singular initial slope associated to P~(S-Ssup)1/2~(Ts-Ts*)1/2. The same is not true in a cylindrical geometry. In this case symmetry still implies that Smax(r) = Ssup + br2+. . ., but now Ψ~r2 near the axis, and the starting slope is finite. Besides it’s fast response time, Oberreit’s planar CPC has a second noteworthy advantage over cylindrical designs. By using 50–60% of sheath gas on the wall region (or by sampling only the 40–50% central region of the flow), the activation curve may be made quite steep. Not surprisingly, Kanomax’s fast CPC does in fact use 50% outer sheath gas. The considerable benefit of this level of sheathing is compromised when Le < 1 by the fact that the central region has the smallest rather than the largest Smax. Nevertheless, the advantages of using outer sheath gas in WCPCs run in Hering’s favorable inverted temperature step have been widely appreciated [24]. In perspective, the success of this approach owes much to the fact that Le is relatively close to unity for the water/air system. Although the approach is generally less effective in achieving a uniform S than in 2D devices, various forms of sheathing have been used also in cylindrical CPCs operating with Le > 1 [32,33].
Fig. 7.
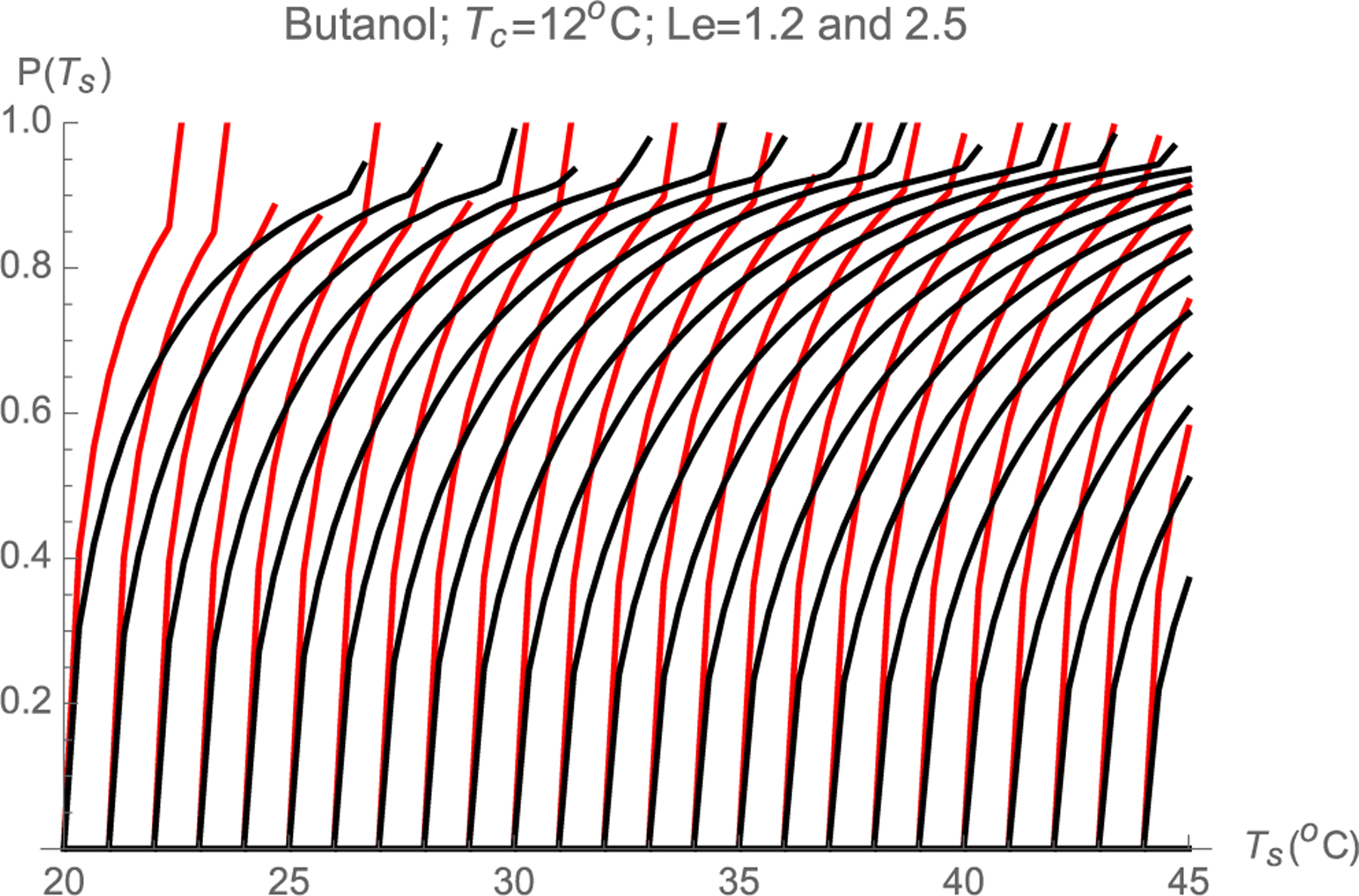
Calculated activation curves in a butanol CPC of variable Ts for particles having fixed critical supersaturations. The black lines are for Le = 2.5 (in air). The steeper colored lines are for Le = 1.2 (in a hypothetical heavy carrier gas).
2.6. The turbulent CPC
We have noted the previously paradoxical observations of rather sharp activation curves in earlier turbulent mixing CPC studies, [7,8] in spite of the vast range of supersaturations present in the CPC, from S = 1 up to S~1000. We have also remarked that the magnitude of this large S interval is reduced by the fact that the relevant S range is really defined by the maximal supersaturations encountered along particle trajectories, whose minimum value is generally well above unity (section 2.1). This feature is as true in diffusive as in turbulent mixing CPCs. Next we remark that in turbulent flow the mass and thermal diffusivities are much larger than their molecular values, with magnitudes determined by the turbulence, which results in a turbulent Lewis number effectively of unity:
| (39) |
While the sharp activation curves previously reported in turbulent mixing CPC studies [7,8] are now easier to understand, the attainment of high sizing resolution surely involves additional subtleties, as evident from the fact that not all turbulent mixing CPCs have shown comparable performance.
We finally note that the useful property Leturb = 1 applies not only to mixing CPCs (where a hot vapor is violently mixed with a cold gas), but would extend to (non-mixing) diffusive CPCs run under turbulent flow. Achieving Le = 1 in practice may be simpler to implement via turbulence (certainly in air) than by manipulating the gas/vapor mixture under laminar flow. A turbulent CPC has apparent advantages well beyond those possible in laminar flows at Le = 1. For example, a laminar CPC in which either the vapor/gas composition or the absolute temperature undergoes substantial changes with position, Le would be spatially varying and would not easily take a unit value everywhere. The condition Le = 1 would however be preserved under turbulent conditions, even under large changes in temperature and gas/vapor composition. Le would be particularly difficult to keep uniformly near unity in the case of the smallest vapor molecules for which it is possible in practice to approach this singular condition. The reason is that the high volatility of low molecular weight vapors often gives them vapor pressures hardly negligible compared to 1 atmosphere. For instance, some of the water CPCs approach and exceed 90 °C at the vapor injection wall. As a result, the composition changes from mostly water at this wall (where Le > 1), to dominantly air at the colder core (where Le < 1). A methanol CPC will probably suffer from the same problem, perhaps forcing operating conditions at relatively low temperatures at which freezing of ambient water brings additional complications. In light of these possible difficulties, a turbulent diffusive CPC seems very worth considering.
On the other hand, an anonymous referee has noted that it would be far simpler to increase substantially the fraction of wall sheathing in existing CPCs than developing entirely new turbulent devices. While the approach would be inefficient in conventional CPC detection, it would be most appropriate for basic nucleation studies.
3. Conclusions
Due to experimental limitations, only 5 articles have been published over the last two decades on basic heterogeneous nucleation with controlled clusters [1,2,8,9,12]. By model calculations of supersaturation fields S(x,y), we have lent substantial conceptual credibility to the hypothesis that commonly used diffusive CPCs have a high potential to revolutionize these studies. Exploitation of this theoretical possibility will allow the entry into this presently highly exclusive and slowly progressing field of many laboratories having commercial or other diffusive CPCs. Concrete approaches shown to be able to achieve this goal are:
Determine S* experimentally for a selected seed particle by comparing observed and predicted activation curves versus CPC temperatures.
Run existing CPCs with relatively light vapors (ethanol, methanol, water) with gases other than pure air, tuned such as to approach the singularly favorable condition Le = 1.
run existing CPCs with any gas or vapor under turbulent conditions, effectively producing Leturb = 1. Although the turbulent approach may require developing completely new instruments, knowing now why turbulent mixing CPCs do sometimes achieve such high size resolution should stimulate experimentation with novel turbulent configurations, both of the diffusive and the mixing types.
Develop planar (or annular) CPCs sampling only about 50% of the flow away from the walls, or exploit Kanomax’s existing fast CPC.
An anonymous referee has noted the interesting possibility to carry out basic nucleation studies on CPCs where a small flow of aerosol is introduced into a much larger flow of saturated air. An excellent example would be TSI’s widely used ultrafine CPC developed by Stolzenburg and McMurry [32].
Method (i) is compatible with many existing CPCs, in spite of the wide Smax range they tend to span under their ordinary operating conditions. Use of method (i), however, is limited to the determination of critical supersaturations, rather than the more fundamental measurement of nucleation rates. Methods (ii-v) are compatible with the direct and fast measurement of heterogeneous nucleation kinetics.
In addition to these concrete proposed solutions to the challenge of producing a device with effectively uniform Smax, this paper makes conceptual contributions that will help develop alternative methods to achieve that same experimental goal. One simplifying notion is that not all the S field is relevant. What is decisive is only the Smax(Ψ) field, which involves just one independent variable (Ψ) rather than two (x,y). Another theoretical concept advanced is the key influence of the Lewis number parameter Le. Most prior CPC work has focused on either water/air (Le < 1) or vapors with large molecular volumes (Le>>1). The discovery of the singular advantage of Le = 1 situations will help free this field from concentrating on either large or small vapor species, to focus rather on the more promising middle ground. The fruitfulness of these ideas is illustrated by their ability to rationalize the previously mysterious reasons why turbulent mixing CPCs had attained such high size-resolving powers.
This study has focused on 2D devices because of the greater efficiency of moderate amounts of sheathing that can be expected in this geometry. Nevertheless, our near-wall analysis and many other considerations made apply qualitatively also to axisymmetric geometries.
While this study has focused on systems with Le ≥ 1, with occasional reference to water CPCs, the development of WCPCs is conceptually strongly connected to many of our main conclusions. First, water/air is by far the system having previously best approached the ideal condition Le = 1. Second, it has been previously noted that the level of variability of Smax in WCPCs is considerably less than in butanol CPCs. For instance, Fig. 3 in [26] shows that the ratio of the maximal to the minimal values of Smax is<1.09 in a WCPC. The unusually sharp rise of activation curves in WCPCs compared to other CPCs has also been discussed in the literature [24].
Future work should evidently focus on implementing the proposed designs and concepts, turning them into actual instruments able to quickly advance the measurement of heterogeneous nucleation kinetics, either by approaches (i-v) or by other means.
Supplementary Material
Acknowledgments
I am grateful to Mario Amo and Pablo Hernandez of SEADM for the stimulus provided by our joint attempts to develop a CPC of high sizing resolution. Also to Dr. Derek Oberreit and his Kanomax colleagues for encouraging the present studies, especially through the loan of Kanomax’s fast CPC, and through discussions on its characteristics. My interest in laminar diffusive CPCs owes much to many discussions with Professor Michel Attoui. Partial support is gratefully acknowledge from NIH SBIR Phase I Grant Number 1 R43 GM131542–01A1 (National Institute of General Medical Sciences, under Dr. Dmitriy Krepki)
Abbreviations:
- 2D
Two Dimensional
- CPC
Condensation particle counter
- DBP
Dibutyl phthalate
- DCPC
Diffusive CPC
- WCPC
Water CPC
- Ψ
dimensionless streamfunction
- S
Supersaturation
- Smax(Ψ)
maximal supersaturation encountered along streamline Ψ
- α
thermal diffusivity
- D
mass diffusivity
- Le
α/D = Lewis number
Footnotes
Appendix A. Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jcis.2020.03.050.
References
- [1].Winkler PM, Steiner G, Vrtala A, Vehkamäki H, Noppel M, Lehtinen KEJ, Reischl GP, Wagner PE, Kulmala M, Heterogeneous nucleation experiments bridging the scale from molecular ion clusters to nanoparticles, Science 319 (2008) 1374–1377. [DOI] [PubMed] [Google Scholar]
- [2].Tauber C, Chen X, Wagner PE, Winkler PM, Hogan CJ Jr., A. Maißer, Heterogeneous nucleation onto monoatomic ions: support for the kelvinthomson theory, ChemPhysChem 19 (2018) 3144–3149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Fenn JB, Mann M, Meng CK, Wong SF, Whitehouse C, Electrospray ionization for mass-spectrometry of large biomolecules, Science 246 (1989) 64–71. [DOI] [PubMed] [Google Scholar]
- [4].Wilson CTR, On the cloud method of making visible ions and the tracks of ionizing particles. In Nobel Lectures: Physics Elsevier, New York, 1965, 1927. [Google Scholar]
- [5].Kane D, Daly GM, El-Shall S, Condensation of supersaturated vapors on benzene ions generated by resonant two-photonionization: a new technique for ion nucleation, J. Phys. Chem 99 (1995) 7867. [Google Scholar]
- [6].Kane D, El-Shall S, Ion nucleation as a detector: application of REMPI to generate selected ions in supersaturated vapors, Chem. Phys. Lett 259 (1996) 482. [Google Scholar]
- [7].Seto T, Okuyama K, de la Mora J. Fernandez, Condensation of supersaturated vapors on monovalent and divalent ions of varying size, J. Chem. Phys 107 (1997) 1576–1585. [Google Scholar]
- [8].Gamero-Castaño M, de la Mora J. Fernandez, A condensation nucleus counter (CNC) sensitive to singly charged subnanometer particles, J. Aerosol Sci 31 (2000) 757–772. [Google Scholar]
- [9].Winkler PM, Vrtala A, Steiner G, Wimmer D, Vehkamaki H, Lehtinen KEJ, Reischl GP, Kulmala M, Wagner PE, Quantitative characterization of critical nanoclusters nucleated on large single molecules, Phys. Rev. Lett 108 (2012) 085701. [DOI] [PubMed] [Google Scholar]
- [10].de la Mora J. Fernandez, Heterogeneous nucleation with finite activation energy and perfect wetting: Capillary theory versus experiments with nanometer particles, and extrapolations on the smallest detectable nucleus, Aerosol Sci. Technol 45 (4) (2011) 543–554. [Google Scholar]
- [11].Fletcher N (1962). The Physics of Rainclouds Cambridge University Press, chapter 3. (1962). [Google Scholar]
- [12].Gamero-Castaño M, de la Mora J. Fernandez, Ion-induced nucleation: measurement of the effect of embryo’s size and charge state on the critical supersaturation, J. Chem. Phys 117 (7) (2002) 3345–3353. [Google Scholar]
- [13].Kogan JI, Burnasheva AG, Growth and measurement of condensation nuclei in a continuous stream, Phys. Chem. Moscow 34 (1960) 2630. [Google Scholar]
- [14].Okuyama K, Kousaka Y, Motouchi T, Condensational growth of ultrafine aerosol-particles in a new particle-size magnifier, Aerosol Sci. Technol 3 (4) (1984) 353–366. [Google Scholar]
- [15].Sgro LA, de la Mora J. Fernandez, A simple turbulent mixing CNC for charged particle detection down to 1.2 nm, Aerosol Sci. Technol 38 (2004) 1–11. [Google Scholar]
- [16].Kim CS, Okuyama K, de la Mora J. Fernández, 2003. Performance Evaluation of Improved Particle Size Magnifier (PSM) for Single Nanoparticle Detection, Aerosol Sci. & Techn, 37, 791–803. See correction on Aerosol Sci. & Techn., 38, 4, 409 (2004). [Google Scholar]
- [17].Vanhanen J, Mikkila J, Lehtipalo K, Sipila M, Manninen HE, Siivola E, Petaja T, Kulmala M, Particle size magnifier for nano-CN detection, Aerosol Sci. Technol 45 (4) (2011) 533–542. [Google Scholar]
- [18].Kangasluoma J, Franchin A, Duplissy J, Ahonen L, Korhonen F, Attoui M, Mikkilä J, Lehtipalo K, Vanhanen J, Kulmala M, Petäjä T, Operation of the airmodus A11 nano condensation nucleus counter at various inlet pressures and various operation temperatures, and design of a new inlet system, Atmos. Meas. Tech 9 (7) (2016) 2977–2988. [Google Scholar]
- [19].Kim S, Iida K, Kuromiya Y, Seto T, Higashi H, Otani Y, Effect of nucleation temperature on detecting molecular ions and charged nanoparticles with a diethylene glycol-based particle size magnifier, Aerosol Sci. Technol 49 (2015) 35–44. [Google Scholar]
- [20].Mavliev R, Hopke PK, Wang HC, Lee DW, A transition from heterogeneous to homogeneous nucleation in the turbulent mixing CNC, Aerosol Sci. Tech 35 (2001) 586–595. [Google Scholar]
- [21].Tang MJ, Shiraiwa M, Pöschl U, Cox RA, Kalberer M, Compilation and evaluation of gas phase diffusion coefficients of reactive trace gases in the atmosphere: volume 2. Diffusivities of organic compounds, pressure-normalised mean free paths, and average Knudsen numbers for gas uptake calculations, Atmos. Chem. Phys 15 (2015) 5585–5598. [Google Scholar]
- [22].Batchelor GK, An introduction to Fluid Dynamics (Appendix 1), Cambridge University Press, 1967. [Google Scholar]
- [23].Magnusson LE, Koropchak JA, Anisimov MP, Poznjakovskiy VM, Fernandez J de la Mora, Correlations for vapor nucleating critical embryo parameters, J. Phys. Chem. Ref. Data, 32, 1387–1409 (2003). [Google Scholar]
- [24].Lewis GS, Hering SV, Minimizing concentration effects in water-based laminar-flow condensation particle counters, Aerosol Sci. Technol 47 (2013) 645–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Oberreit D (2017) Compact condensation particle counter technology, US Patent Application 20170276589
- [26].Hering SV, Stolzenburg MR, Quant FR, Oberreit DR, Keady PB, A laminarflow, water-based condensation particle counter (WCPC), Aerosol Sci. Technol 39 (7) (2005) 659–672. [Google Scholar]
- [27].Hering SV, Spielman SR, Lewis GS, Moderated, water-based, condensational particle growth in a laminar flow, Aerosol Sci. Technol 48 (4) (2014) 401–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Hering SV, Lewis GS, Spielman SR, Eiguren-Fernandez A, Kreisberg NM, Kuang C, Attoui M, Detection near 1-nm with a laminar-flow, water-based condensation particle counter, Aerosol Sci. Technol 51 (3) (2017) 354–362. [Google Scholar]
- [29]. http://webserver.dmt.upm.es/isidoro/dat1/Mass%20diffusivity%20data.pdf.
- [30].Incropera FP, Dewitt DP, Bergman TL, Lavine AS, Fundamentals of Heat and Mass Transfer, John Wiley and sons, 6th ed., 2007, p. 942. [Google Scholar]
- [31].Gilliland ER, Diffusion coefficients in gaseous systems, Ind. Eng. Chem 26 (6) (1934) 681–685. [Google Scholar]
- [32].Stolzenburg MR, McMurry PH, An ultrafine aerosol condensation nucleus counter, Aerosol Sci. Techn 14 (1991) 48–65. [Google Scholar]
- [33].Iida K, Stolzenburg MR, McMurry PH, Smith JN, Quant FR, Oberreit DR, Keady PB, Eiguren-Fernandez A, Lewis GS, Kreisberg NM, Hering SV, An ultrafine, water-based condensation particlecounter and its evaluation under field conditions, Aerosol Sci. Techn 42 (2008) 862–871. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


