Abstract
The optical properties of blood encode oxygen-dependent information. Noninvasive optical detection of these properties is increasingly desirable to extract biomarkers for tissue health. Recently, visible-light optical coherence tomography (vis-OCT) demonstrated retinal oxygen saturation (sO2) measurements by inversely measuring the oxygen-dependent absorption and scattering coefficients of whole blood. However, vis-OCT may be sensitive to optical scattering properties of whole blood, different from those reported in the literature. Incorrect assumptions of such properties can add additional uncertainties or biases to vis-OCT’s sO2 model. This work investigates whole blood’s scattering coefficient measured by vis-OCT. Using Monte Carlo simulation of a retinal vessel, we determined that vis-OCT almost exclusively detects multiple-scattered photons in whole blood. Meanwhile, photons mostly forward scatter in whole blood within the visible spectral range, allowing photons to maintain ballistic paths and penetrate deeply, leading to a reduction in the measured scattering coefficient. We defined a scattering scaling factor (SSF) to account for such a reduction and found that SSF varied with measurement conditions, such as numerical aperture, depth resolution, and depth selection. We further experimentally validated SSF in ex vivo blood phantoms with pre-set sO2 levels and in the human retina, both of which agreed well with our simulation.
1. Introduction
Optical coherence tomography (OCT) enabled noninvasive three-dimensional (3D) retinal imaging at micrometer-scale volumetric resolutions [1,2]. Since its first report 30 years ago, OCT has become the clinical gold standard for diagnosing and monitoring nearly all major ocular diseases [3,4].
OCT’s sensitivity to optical scattering and absorption provides imaging contrast between tissues and may be used to probe tissue health [5–8]. These capabilities extend to whole blood (further referred to as blood), where absorption and scattering are wavelength-dependent and oxygen-dependent [9–12]. Applying short-time Fourier transforms (STFTs), OCT can measure wavelength-dependent attenuations of blood with micrometer-scale depth resolution, enabling the measurement of oxygen saturation (sO2) in discrete blood vessels [13–17]. Studies suggested that alterations in retinal sO2 can be a sensitive biomarker for blindness-causing diseases, including glaucoma and diabetic retinopathy [18,19]. Hence, accurate and noninvasive retinal sO2 measurement can improve the clinical management of these diseases.
Blood’s optical absorption properties are 2-3 orders of magnitude higher in the visible spectral range than the near-infrared (NIR) spectral range [12], enabling recently developed visible-light OCT (vis-OCT) [14] to overcome the fundamental optical contrast limit in NIR OCTs [16,20]. In 2013, Yi et al. showed that vis-OCT is sensitive to retinal sO2 in rodents. Later on, vis-OCT retinal oximetry was demonstrated in rodents [21–24] and humans [25,26].
Vis-OCT relies on the reported optical properties of whole blood to estimate sO2. In the visible spectral range, Mie theory predicts an average absorption coefficient (µa) near 150 cm-1 and an average scattering coefficient (µs) near 3000 cm-1 [12,27]. However, a wide range of experimentally measured values have been reported, suggesting uncertainty in the measured optical properties of blood, and potentially reducing the reliability of vis-OCT oximetry [9–11,27–29]. For example, some measured µs values are ∼ 1/3 of the Mie theory prediction [9,28,30]. Researchers attributed such a reduction in µs to the blood’s ‘packing factor’, which describes correlated optical interactions between densely packed RBCs and their hematocrit-dependence [9,28]. Our group previously used the packing factor (denoted as W) to scale µs in the vis-OCT inverse fitting model for sO2 measurement [30]. Specifically, our group found that the model’s goodness of fit (R2) maximized when W was between 0.2 and 0.4. This W value was consistent with the definition of the packing factor, which scales µs by ∼ 1/3 at physiological hematocrit [9]. Several other vis-OCT retinal oximetry works also used this W range to scale µs [21,25,30,31].
However, reported vis-OCT oximetry methods accounted for blood’s µs differently, among which significant discrepancies exist [7,22,23,30,32–35]. Since vis-OCT oximetry fits the measured spectrum to the literature-reported µa and µs, deviations between the measured and reported µs can introduce sO2 measurement error. Therefore, accurate and consistent quantification of sO2 benefits from a systemic investigation on how vis-OCT measures µs. We systemically investigated measuring optical scattering properties of blood detected by vis-OCT. First, we performed Monte Carlo (MC) simulations of a retinal blood vessel and photon detection by vis-OCT.
MC simulation provides a statistical approximation of complex light-tissue interactions that are not trivial to be modeled mathematically. Furthermore, MC simulation is not susceptible to systemic biases present in practical OCT detection or image reconstruction [35–37] and, therefore, is useful for modeling OCT images of tissue. For each photon packet exiting the tissue, we monitored the number of scattering events and optical pathlength traveled in tissue to investigate the impact of multiple scattering on the vis-OCT signal. We reconstructed simulated vis-OCT A-lines to establish a direct relationship between multiple scattering and the measured µs. Then we established the scattering scaling factor (SSF), a generalized scaling coefficient for µs. Since multiple scattering influenced the measured µs, we further investigated photon detection by different numerical apertures (NAs), because NA acts as a geometric filter in detecting multiply scattered photons. Second, we compared our simulation results to experimental vis-OCT imaging of ex vivo blood phantoms. We found excellent agreement between the simulated and experimentally measured values across pre-set oxygenation levels. Finally, we validated our SSF analysis in human retina vis-OCT imaging and found a strong agreement with our simulated results. Validated by simulation, ex vivo blood phantom imaging, and in vivo human retinal imaging, we provide evidence that vis-OCT measured µs is smaller than the reported packing factor but higher than the reduced scattering coefficient ( ) [35,38]. This work sets the foundation for a unified theory of vis-OCT-measured optical properties of blood and more robust retinal oximetry.
1.1. Detecting scattered light with OCT
Most OCT’s use NIR (800 nm – 1300 nm) illumination, where biological tissues have lower optical scattering coefficients (µs < 100 cm-1), lower optical absorption coefficients (µa < 1 cm-1), and moderately high scattering anisotropy (0.7 < g < 0.9) [39]. Such optical properties yield mean-free-paths (MFPs) of several hundred micrometers in tissue, meaning photons can travel deep into tissues before being multiply scattered. Since OCT’s axial resolution is dominated by light’s coherence length and not geometrical optics, OCT can use a low NA to image deeply penetrating photons across several hundred micrometers with axial resolutions < 10 µm [40]. Another benefit of imaging weakly scattering tissues with a low NA is high sensitivity to single-scattered or ballistic photons [41]. In this work, we define ballistic photons as Class I photons [35], which satisfy
| (1) |
where [µm] is the maximum depth a photon travels in the tissue with respect to the OCT’s zero delay; D [µm] is the total optical path traveled by the photons with respect to the OCT’s zero delay; and lc [µm] is the coherence length. Essentially, a Class I photon travels straight, allowing only a slight deviation within lc. We define Class II photons as photons that do not travel in a straight line before being detected by the OCT, which satisfy
| (2) |
Finally, we define those photons undetectable by the OCT system as Class III photons.
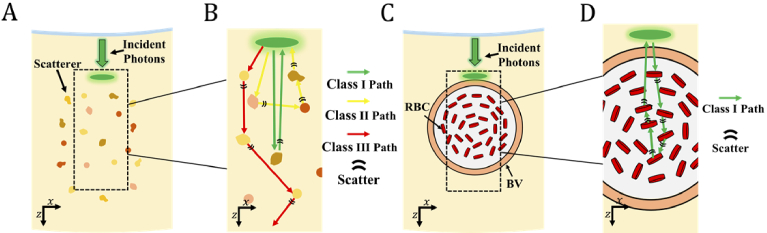
Fig. 1(A) & 1B illustrate OCT imaging in a weakly scattering tissue (e.g. µs < 100 cm-1 and 0.7 < g < 0.9) using a low NA (e.g. < 0.2). Fig. 1(A) shows a global illustration of tissue with optical properties within the NIR spectral range. The OCT sample arm focuses light on a spot in the tissue (illustrated by the green oval), which creates an A-line at that location. Due to the low NA, incident photons (green arrow) are nearly perpendicular to the tissue surface. Since the focus spot creates a conjugate point with the sample arm detector, it also acts as a geometric projection of the detector itself [42]. Only photons collected within the spot and the solid angle defined by the illumination NA will contribute to the A-line.
Fig. 1.
(A) Illustration of OCT illumination of a weakly scattering medium. Incident photons (green arrow) create a focal spot (green oval) and detection aperture in the tissue; (B) Magnified illustration of the highlighted region in panel A, showing the paths of Class I (green arrow), Class II (yellow arrow), and Class III photons (red arrow); (C) Illustration of vis-OCT illumination of a retinal blood vessel (RBC) containing red blood cells (RBC); (D) Magnified illustration of the highlighted region in panel C, showing the paths of Class I photons (green arrow).
Fig. 1(B) is a magnified illustration of Fig. 1(A) in the black-dashed box. The green, yellow, and red arrows respectively illustrate representative paths of Class I, Class II, and Class III photons. The black bands represent scattering events. The Class I photon travels deeply into the tissue, scatters once, reverses direction, and returns along almost the same path in the z-direction (also referred to as backscattering). The Class II photons are scattered multiple times and travel significantly along the x-direction before returning to the detector. The Class III photons are scattered multiple times deeply in the tissue and do not return to the detector. Under the conditions of µs < 100 cm-1 and 0.7 < < 0.9, photons can travel tens or hundreds of m along the -direction after each scattering event. Therefore, multiply scattered photons are increasingly likely to be Class III rather than Class II photons since they will travel too far from the detector before being absorbed by tissue or escaping the tissue. Meanwhile, most detected photons are likely to be Class I photons (green arrow in Fig. 1(B) since they do not have the opportunity to travel outside the detection region.
When most photons are Class I and single scattered, the OCT A-line can be modeled by the Beer-Lambert Law [43]
| (3) |
where [arbitrary unit] is the A-line intensity; z [mm] is the depth in the tissue; and the coefficient 2 in the exponential term indicates round trip in tissue. Eq. 3 has been thoroughly derived and experimentally validated for Class I photons [6]. Vis-OCT imaging of blood represents a special scenario that deviates from the assumptions described in Fig. 1(A) & 1B. The reported µs for oxygenated and deoxygenated blood states are > 3000 cm-1 and the W-scaled µs are near 1000 cm-1 [9]. Both these µs values are over an order of magnitude greater than µs values (< 100 cm-1) typical of most tissues within NIR spectral range. Furthermore, blood is more highly forward scattering ( 0.98) than most tissues (0.7 < < 0.9). Assuming normal incidence of light on a vessel (Fig. 1(C), photons can be multiply scattered and still satisfy the Class I condition. Fig. 1(D) illustrates such a path following the green arrow. We hypothesize that the path shown in Fig. 1(D) is a common, if not dominant, detection scenario in blood imaging using vis-OCT. A Class I photon that travels deeper than its single scatter assumption is equivalent to reducing its µs in Eq. 3. Previously, Thrane et al. developed a model for OCT incorporating multiple scattering using the extended Huygens-Fresnel [44] principle, which Almasian et al. verified in silica beads with µs up to 97 cm-1 and g up to 0.9. Their theoretical model predicted a reduction in the OCT measured µs, which is dependent on g, numerical aperture, and location of the tissue relative to the focal plane [5]. Here, we account for the reduction in µs by rewriting the Beer-Lambert Law as
| (4) |
where SSF [dimensionless] is the scattering scaling factor, which is < 1 and scales µs to account for the increased detection of photons deeper in tissue. The SSF is a generalized scaling factor and incorporates any other reductions of µs, including W.
1.2. Vis-OCT oximetry
Oxygenated and deoxygenated blood have distinct wavelength-dependent and , allowing estimation of sO2. An STFT [45] can reconstruct spectrally-dependent A-lines, which can be modeled by
| (5) |
where [nm] is the central wavelength of the selected STFT sub-band; sO2 [dimensionless, between 0 and 1] is the oxygen saturation in blood; the subscripts HbO2 and Hb denote oxygenated or deoxygenated hemoglobin, respectively; and SSF [dimensionless] is the scattering scaling factor. We used 21 STFT sub-bands ranging from 528 nm to 588 nm equidistant in wavenumber, with an average full-width-at-half-max (FWHM) bandwidth of 11 nm.
2. Methods
2.1. MC simulation parameters
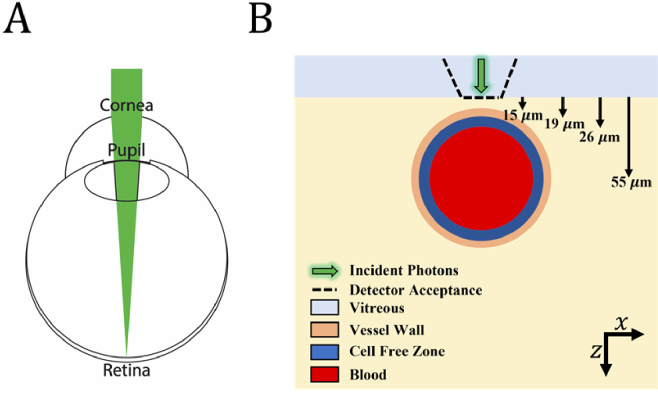
We simulated vis-OCT detection and reconstruction in a retinal blood vessel using MC simulation [8,27,35,38,46–50]. Fig. 2(A) shows the beam incident on the cornea, after which light is focused onto the retina. Fig. 2(B) shows a cross-sectional view of the multi-layered 3D model of a blood vessel embedded in the retina. We modeled the blood vessel using an infinitely long cylinder located 55 µm below the vitreous-retina interface. The vessel has three concentric layers: blood, cell-free zone (CFZ) [33,34], and the vessel wall. The CFZ is a thin layer consisting primarily of plasma between the blood and the vessel wall. It arises from the difference in viscosity between RBCs and plasma and is described by the Fahraeus Lindqvist (FL) effect [51]. The CFZ has been previously observed in OCT images [52] and is noticeable in our vis-OCT data. Table 1 summarizes the optical and geometrical parameters. We extracted the properties of the retina [27,48], vessel wall [27], and CFZ [53] from the literature. We used the theoretical optical properties of blood previously derived by Faber et al. [12,27]. To increase the speed of our simulation, we used the average µa and µs between 520 nm and 600 nm (center wavelength 560 nm). Although there is still uncertainty in the exact values of µa, µs, and g [9], our values are well within the reported range [9–11,27–29]. To account for correlated optical interactions between densely packed RBCs, we scaled blood’s µs using the packing factor , where H is hematocrit [dimensionless]. Assuming a hematocrit of 45% [54], we have W = 0.3025.
Fig. 2.
(A) Illustration of the beam incident on the cornea. (B) Illustration of tissue and imaging geometry in Monte Carlo simulation. Downward arrows (from left to right) highlight the interface depths of the vessel wall, cell-free zone, and blood, respectively; the fourth arrow highlights the depth of the vessel center.
Table 1. Optical properties of tissues used in Monte Carlo simulation.
| g [dimensionless] | Thickness [ ] | |||
|---|---|---|---|---|
| Retina | 319 | 9 | 0.97 | NA |
| Vessel Wall | 284 | 4 | 0.84 | 4 |
| Cell Free Zone | 0.8 | 0.4 | 0.7 | 6 |
| Blood | 3415.5 | 176.1 | 0.984 | 68 |
2.2. MC simulation algorithm
MC simulation of photon propagation in biological tissue has been widely reported [8,27,35,38,46–50,55]. We followed the algorithm of simulating photon transport in multi-layered tissues (MCML) in 3D [38]. Briefly, we launch an infinitely narrow photon beam towards the retina and blood vessel, as illustrated in Fig 2. Each photon packet’s launching position is at the vitreous-retina interface (Fig. 2(B) at the lateral center of the vessel. The initial direction vector is along the z-axis. Upon tissue entry, we generated the step size ( ) following the Poisson distribution
| (6) |
where and [dimensionless] is a random variable following a uniform distribution between 0 and 1. After traveling a distance s, the photon packet interacts with tissue and deposits a fraction of its weight. At each interaction location, the photon packet is scattered by an angle relative to its current propagation direction determined by the Henyey-Greenstein phase function [55]
| (7) |
At the interface between two media, the photon packet either reflects or transmits with probabilities according to Fresnel’s equations [56]. Upon entering a new tissue region, is adjusted accordingly. The simulation continues until the photon packet exits the retina into the vitreous or the optical path distance traveled is greater than 2000 m, well beyond the depth of the blood vessel.
If the photon packet exits the retina into the vitreous, we recorded the remaining weight of the photon packet, the optical pathlength traveled within the tissue, the total number of scattering events in all tissue regions, the total number of scattering events in blood, the exiting position, and the exit angle. We simulated 1010 photon packets for each A-line. We implemented the simulation in MATLAB 2020 using parallel computing on a PC with a 3.4-GHz Intel Core i7-6800 K CPU and 64-GB RAM. The simulation of an A-line took approximately 120 hours to complete.
2.3. Photon detection
To simulate OCT detection, we geometrically filtered photons exiting the retina [50] (black-dashed lines in Fig. 2(B). We determined photon acceptance aperture and angle according to the NA of the light incident on the retina. We tested the NA value from 0.015 to 0.112, which follows the optical properties of normal human eyes [57]. We calculated the NA as
| (8) |
where n [dimensionless] 1.35 is the refractive index; D [cm] is the diameter of the collimated beam incident on the cornea; f [cm] 1.8 cm is the focal length of a normal eye [58]; and is the acceptance angle with respect to normal incidence. We used the NA to calculate the focal spot beam waist
| (9) |
where = 560 nm is the central wavelength of the vis-OCT probing light. For simplicity, we detect photons using a uniform circle with a radius of w. In the results, we use an NA = 0.05, equivalent to a 2.9° acceptance angle and a detection diameter of 7.0 m unless otherwise specified.
2.4. Vis-OCT A-line reconstruction
We reconstructed simulated vis-OCT A-lines using the recorded photon weights and optical path distances in the simulation. We only used photons detected under the acceptance conditions. Adopting the methods in Kirillin et al. [50], we reconstructed the OCT A-line as
| (10) |
where [dimensionless] is the photon weight; [cm] is the optical path distance; and [µm] is the axial resolution. We note that our Monte Carlo simulation does not interfere sample arm and reference arm electric fields as in a real OCT system, which measures the square root of the A-line intensity [40,59]. Therefore, the simulated A-line is assumed to be directly proportional to A-line intensity and does not need to be squared. We set the distance between adjacent z positions as 1 m and used an axial resolution of 9 m defined by the of the STFT sub-band window centered at 558 nm with an FWHM bandwidth of 11 nm [40]. We used this sub-band window size for spectroscopic A-line reconstruction in our experimental studies.
2.5. Experimental measurements of ex vivo blood samples
We used the vis-OCT system operating from 510 to 610 nm described by Beckmann et al. [60] to image ex vivo blood samples in phantom vessels. The imaging objective in the sample arm had an NA of 0.05 [61], consistent with our simulation and human imaging. Briefly, we constructed a vessel phantom by pulling a glass capillary tube to have an inner diameter of 200 m and embedded and stabilized the tube in a plastic well. To reduce the influence of specular reflections, we added immersion oil to the well until the tube was covered. We prepared whole bovine blood (Quadfive, Ryegate, MT) of hematocrit 45% of oxygen levels ranging from 45% to > 99%. To oxygenate the blood, we added a constant stream of pure oxygen and stirred the blood with a magnetic stir bar. To deoxygenate the blood, we added sodium dithionite [62] to the solution and stirred. We repeated these processes until reaching the desired oxygen level. We monitored blood’s partial pressure of oxygen (pO2), partial pressure of carbon dioxide (pCO2), pH, and temperature using a blood-gas analyzer (Rapidlab 248, Siemens Healthcare Diagnostics, Malvern, PA) and estimated the corresponding sO2 [63]. Before loading the tube with blood, we flushed it with a phosphate-buffered saline and heparin solution to reduce clotting or sedimentation. Finally, we loaded the tube with blood and flowed it at 0.3 mm/s using a syringe pump (Fusion 100, Chemyx, Inc. Stafford, TX). We aligned the tube to be in focus and near the system zero-delay and illuminated it with 1.20 mW of power. Finally, we acquired data consisting of 512 A-lines × 256 B-scans with imaging range 1 mm × 1 mm at a 25 kHz A-line rate.
2.6. Experimental measurement of human retinal vessels
For human imaging, we used the system described by Rubinoff et al. [64]. We used Eq. 8 to estimate an NA of 0.05 in the retina, similar to the simulation and ex vivo measurements. All human imaging procedures were approved by Northwestern Institutional Review Board (IRB) and adhered to the Tenets of Helsinki. We illuminated the retina with 250 W of power and acquired human retinal images consisting of 8192 A-lines × 16 B-scans repeated across a 3.8 mm field of view at a 25 kHz A-line rate.
3. Results
3.1. Contribution from multiple forward scattering in vis-OCT blood signal
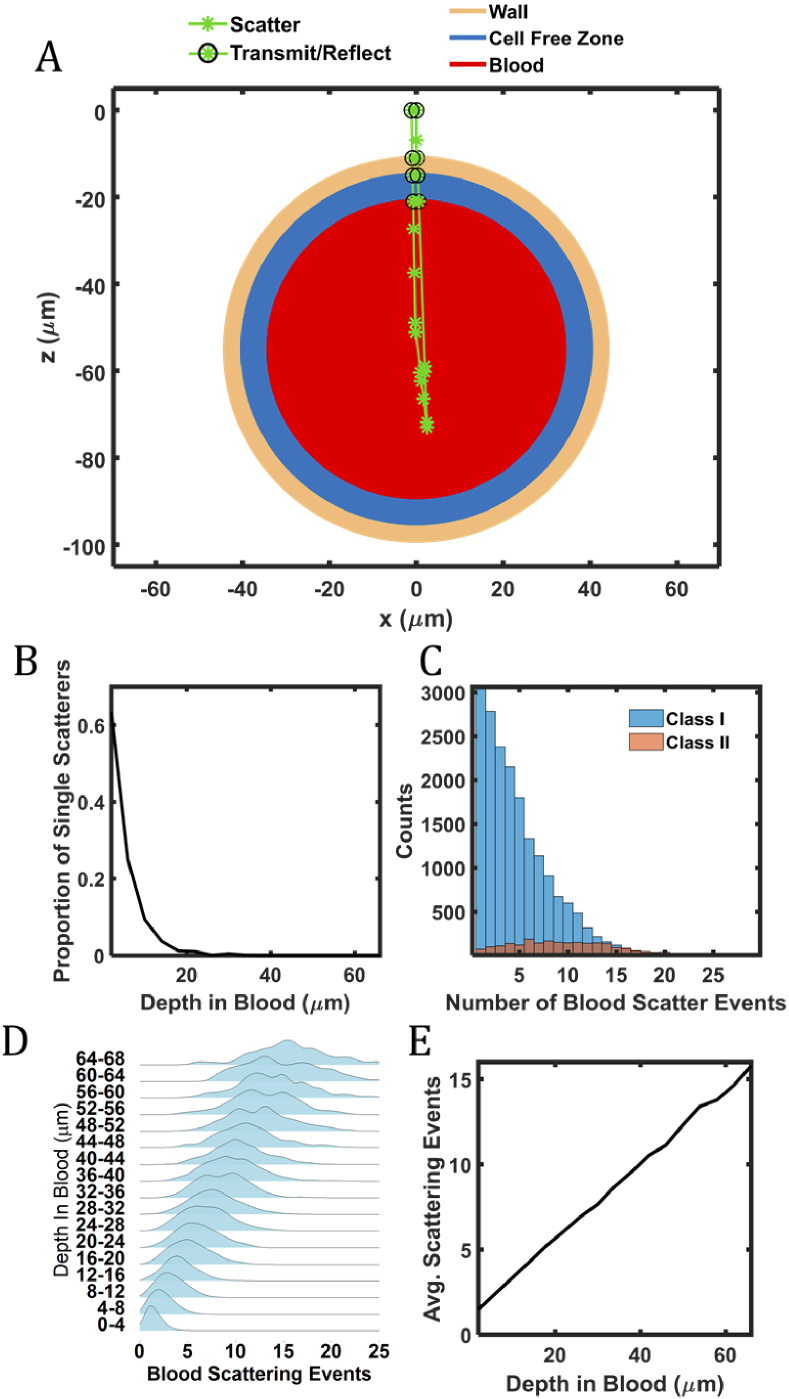
We investigated how blood’s scattering properties influence the detection of photons in vis-OCT. Fig. 3(A) plots a detected photon packet path from our MC simulation. The concentric rings plot the outer boundaries of each vessel layer. The photon packet launched from the origin followed the path of the green line. The green asterisk (*) highlights a scattering event, and a circled asterisk highlights a transmission or reflection across tissue regions. The photon packet in Fig. 3(A) was scattered 11 times inside the blood vessel. Notably, the photon packet travels mainly along the -axis, consistent with a high scattering anisotropy (g = 0.987). This allows the photon packet to backscatter to nearly the same x-position as it launched, similar to the illustration in Fig. 1(D). Despite the multiple scattering events, we classified this photon packet to be Class I. Based on the optical properties shown in Table 1, the calculated MFP in blood is 8.5 m; however, the photon packet travels 60 m into the vessel (Fig. 3(A).
Fig. 3.
(A) Simulated photon packet path (green line) and scattering events (green stars) in the blood vessel; (B) Proportions of detected singly-scattered photon packets; (C) Histogram showing the number of scattering events of the detected Class I and Class II photons; (D) Distributions of the number of scattering events at different depths in blood; (D) The average number of scattering events at different depths in blood.
To assess whether the multiple scattering observed in Fig. 3(A) was a frequent occurrence, we measured the proportion of all detected singly scattered photons packets that entered the blood region (Fig. 3(B). Within the first 10 m in blood, about 50% of photon packets are singly scattered, which is consistent with the predicted MFP near 8.5 m. The proportion drops rapidly, where almost no detected photons are singly scattered after 17 m into the blood region (2 MFPs). Considering that measurements deeper than 8.5 m are necessary to provide sufficient attenuation contrast, it is reasonable to assume that retinal oximetry measurements are dominated by multiply scattered photons (excluding capillaries that may not generate multiple scattering due to low RBC counts).
Fig. 3(C) plots the detected Class I and Class II photons that entered the blood region. To improve the precision of the photon packet classification, we used = 1.4 m, the estimated vis-OCT full band resolution, rather than = 9 m, the STFT resolution. As shown in Fig. 3(C), Class I photons dominate. Fig. 3(B) & 3C collectively demonstrate that most detected photons are both Class I and multiply scattered photons. This observation is further emphasized by Fig. 3(D), which plots the fitted histograms of scattering events in blood from detected photons for different depths. The histograms are normalized with respect to their maximum values to show detail. The distributions show that, other than at the shallowest depths, photons are always multiple scattered. The average value of scattering events increases, and their distributions broaden as photon packets propagate deeper. Fig. 3(E) shows that the average value of scattering events is always > 1 and increases linearly with depth. Such a linear increase is consistent with the notion that a photon packet travels nearly along the same direction after each scattering event. The slope of this line corresponds to 1 blood scattering event for a photon step of 8.9 m, consistent with the calculated MFP.
3.2. Measuring the SSF value
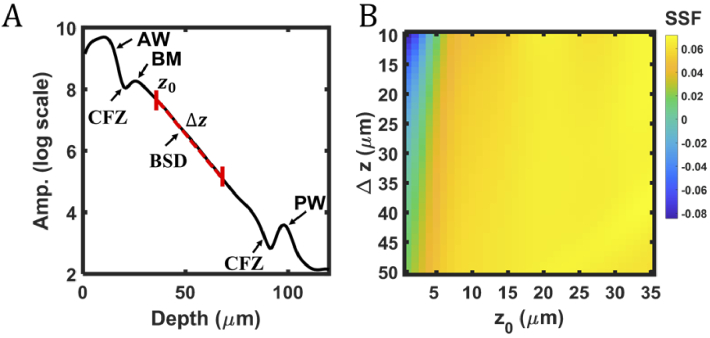
Fig. 4(A) plots the simulated A-line on a natural logarithm scale (referred to as ‘log’). and illustrates the depth selection procedure for SSF measurement. From left to right, the first peak represents the anterior wall (AW) of the vessel, which is slightly convolved with the retinal tissue above it. Beneath the AW is a valley representing the cell-free zone (CFZ). The valley is smaller than expected from a completely ‘scattering-free’ region due to the limited 9- m axial resolution. Beneath the CFZ is the blood maximum (BM), representing the start of blood signal decay (BSD) in the A-line. The distinct peak at the BM is collectively contributed by the finite MFP in blood, the size of the CFZ, and the limited 9- m axial resolution. The depth location of BM in the A-line is about 10 m deeper than the physical start of the vessel lumen and about 20 m deeper than the AW peak. The blood signal decay (BSD) follows the BM and is consistent with log-scale decay described by the Beer-Lambert law [43]. When measuring the optical properties of blood in vivo, it is critical to start at least from the BM rather than assuming BSD occurs at the boundary of the AW and vessel lumen. Finally, the last peak represents the posterior wall (PW) of the vessel.
Fig. 4.
(A) A simulated A-line at the center of the vessel, showing the anterior wall (AW), cell-free zone (CFZ), blood maximum (BM), blood signal decay (BSD), and posterior wall (PW); The red-dashed line highlights measurement depth range starting at and ranging ; (B) Measured SSF values from A-line in the panel A as a function of different and .
To measure the scattering coefficient, we modeled the BSD using a modified Eq. 5
| (11) |
We include only the oxygenated coefficients since the simulated sO2 was 100%. The term ‘avg’ indicates that simulation used optical properties that were the average value between 520 nm and 600 nm. . Although there are a handful of ways to extract from this equation, we elected to compute a depth-average of Eq. 11, which we empirically found robust against noise [65]. The starting measurement depth is and the depth range is . The full region of measurement is highlighted by the red dashed line. We first normalized by its amplitude at , which shifted the coordinate system to = 0. The average intensity becomes
| (12) |
Dividing by , we are left only with the linear combination of and . By subtracting , whose value is from the literature, we are left with , which can be compared with the literature µs value used in the simulation. The SSF can be calculated as
| (13) |
Fig. 4(B) shows the SSF under various combinations of and , where = 0 at the start of the vessel lumen. For between 0 µm and 5 µm, SSF 0, which is caused by choosing a depth before BM and is physically impossible. At 10 µm, the approximate location of BM, SSF = 0.05-0.06, with slight variation for different z. For between 11 µm and 25 µm, SSF = 0.060-0.068. For z0 > 25 µm, SSF is slightly greater than 0.07, which may be biased by the CFZ near the PW. Therefore, we selected = 17 m and = 33 m, a range where the SSF = 0.064. The measured SSF is approximately 5-fold smaller than the literature packing factor W = 0.3025. Here, = 0.06 = 222 cm-1, which is similar to the absorption coefficient = 174 cm-1.
3.3. Influence of the number of scattering events on SSF
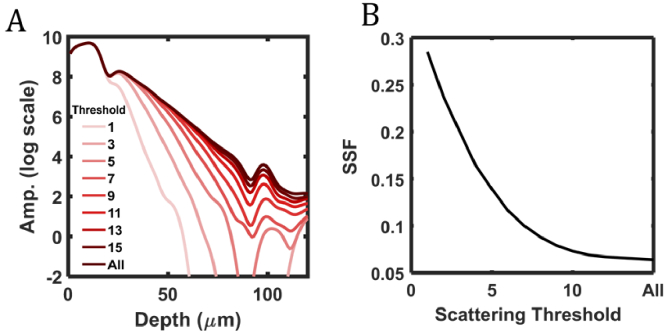
To understand how multiple scattering influences SSF, we set a graded threshold to the number of detected scattering events in blood. If a photon packet that entered the blood region is scattered more times than the set threshold, it was not included in the simulated A-line. Fig. 5(A) shows the simulated A-line for different scattering thresholds. The different shades of red plot different scattering threshold levels. The darkest shade has no threshold and collects photon packets from all scattering events (same as Fig. 4(A). A-line amplitude decays slower with higher threshold levels, consistent with the notion that increased multiple scattering reduces SSF. Specifically, when the threshold level is 1, the A-line is reconstructed by single-scattered Class I photon packets and decays within 20 m in blood. As sO2 calculation fits A-lines beyond 20 m in blood, multiply scattered photons are required for accurate sO2 measurement in vivo.
Fig. 5.
(A) Simulated A-line at the center of the vessel after thresholding the number of detected scattering events in blood. Lighter shades indicate a lower threshold of detected scattering events; (B) The SSF value as a function of detected scattering threshold.
Additionally, it becomes clear that multiple scattering enables deeper photon penetration necessary for visualizing the PW. The PW becomes weak when the threshold level is less than 7 and invisible when the threshold level is less than 3. This suggests that multiple forward scattering also facilitates the visualization of the PW, a landmark commonly used in vis-OCT oximetry to indirectly measure [30]. Fig. 5(B) shows the relationship between SSF and the scattering threshold level, which decays approximately exponentially with the scattering threshold, asymptotically approaching 0.064 after threshold > 15. Thresholding 7 scattering events gives SSF = 0.116 and thresholding 2 scattering events gives SSF = 0.285, approaching the set = 0.3025. We measured SSF = 0.424 when thresholding 1 scattering event; we did not include this data point due to insufficient signal-to-noise-ratio along the measured depths.
3.4. Influence of numerical aperture on SSF
As described in photon packet detection in our MC simulation, the detection NA acts as a spatial filter for photon scattering events. The detection aperture (radius) and angle limit an existing photon packet's position and propagation direction. Therefore, the detection criteria can potentially influence the measured SSF.
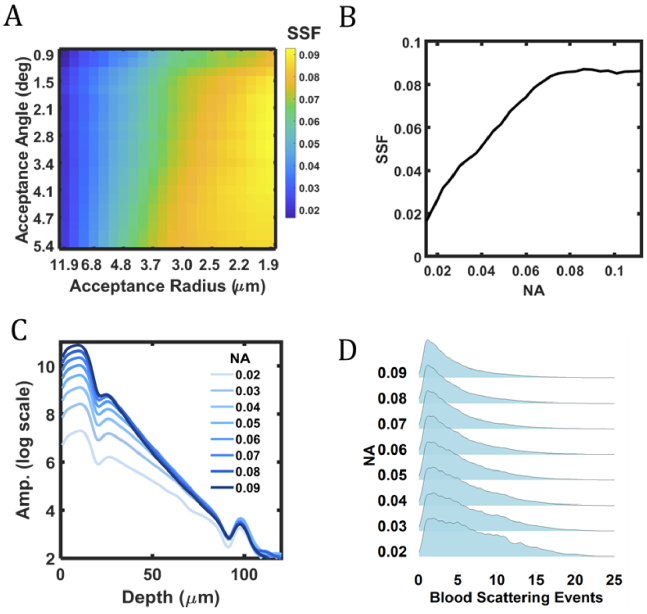
We examined the relationship between NA and SFF for = 17 m and = 33 m based on the conclusion from the above section. The tested NA’s are 0.015 to 0.112, which are based on physically reasonable imaging NA’s in the human eye. In OCT, retinal imaging NA is almost always less than the maximum possible NA (e.g. 0.2 [57]), since researchers must consider limiting factors like reduced depth-of-focus, aberrations, and eye dilation [42]. Therefore, we varied the acceptance radius from 1.9 µm to 11.9 µm and varied the acceptance angle from 0.9° to 5.4°. We found that SSF varied between 0.02 to 0.09 (Fig. 6(A).
Fig. 6.
(A) The SSF values as a function of optical detection radius and angle; (B) SSF as a function of numerical aperture (NA), which is the diagonal of the matrix in the panel A; (C) Simulated A-line at center of vessel for different NAs; lighter shades indicate lower NA; (D) Normalized distributions of scattering events in blood for different NAs.
Fig. 6(B) plots the SSF values for physically possible NA values, which are along the diagonal of the matrix plotted in Fig. 6(A), and shows that SSF increases with increased NA. However, the relationship between NA and SSF is asymptotic near an NA of 0.08 (we extended the simulation to a maximum NA of 0.11 to validate the asymptote). For all the tested NA values, SSF is always less than 0.1, which is still less than one third of the literature value = 0.3025. Fig. 6(C) plots the simulated A-line under different NA values. As NA increases, the amplitudes corresponding to AW and BM increase with respect to PW, which increases the slope of the blood decay and leads to an increased SSF. Conceptually, photons backscattered at shallower tissue depths do not travel far from the detection radius, making their detection more sensitive to acceptance angle rather than acceptance radius. Since the tissue exit angle of photons is depth-independent and stochastic, increased acceptance angles will result in increased numbers of detected photons from shallower depths (depths near 25 µm in Fig. 6(C). Meanwhile, photons backscattered from deeper depths can travel farther from the detection radius and are filtered by both acceptance angle and radius. Unlike shallower-traveling photons, deeper-traveling photons experience the inverse relationship between acceptance radius and acceptance angle when varying NA. Therefore, the total number of photons detected from deeper depths vary less with changing NA (depths near 75 µm in Fig. 6(C). Hence, the relative difference between the number of accepted photons at shallower and deeper depths explains the observed change in SSF, despite no change in the optical properties of blood. Eventually, the SSF will plateau at higher NA’s, when the acceptance radius becomes small enough, such that photons propagating at all depths are primarily filtered by acceptance radius.
Fig. 6(D) plots the fitted histograms of scattering events in blood from detected photon packets for different NA values, where each histogram is normalized by its respective maximum value. Fig. 6(D) confirms our previous hypothesis of increased detection of multiply scattered photon packets in Fig. 6(A)–6(C), where the histogram broadens with reduced NA values. Since the optical properties of blood remain unchanged, this difference is contributed by the changing detection criteria associated with NA.
It is important to note that this simulation presents a simplified view of the influence of OCT detection on SSF. Other variables, including the Gaussian beam profile, longitudinal chromatic aberrations, lateral chromatic aberrations, defocusing, eye geometry, oblique incidence, etc., will collectively influence the illumination and detection criteria as well [66]. However, the above simulation on the relationship between acceptance aperture and angle and SSF establishes a critical foundation for multiple scattering analysis in OCT. Such a relationship suggests no ‘one-size-fits-all’ SSF value exists.
3.5. Ex vivo experimental results
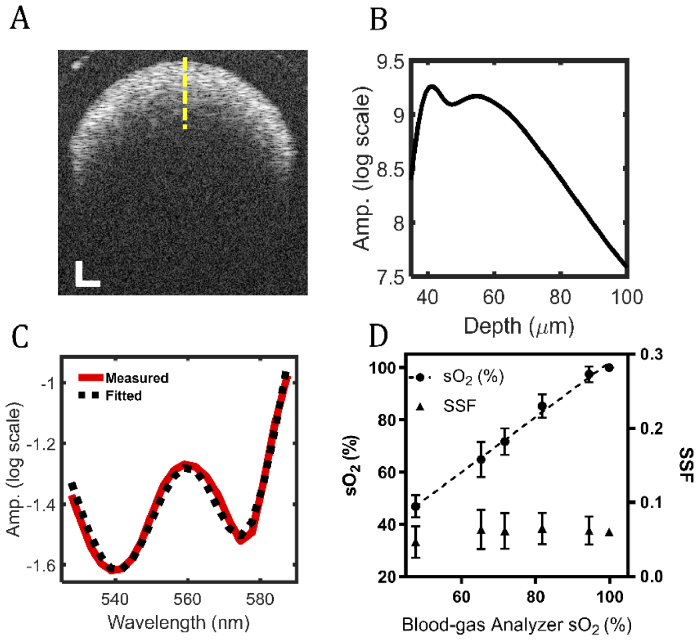
Fig. 7 plots experimental vis-OCT measurements of ex vivo blood phantoms. All A-line reconstruction included correction for roll-off and background biases as previously reported [65,67]. Fig. 7(A) shows a representative B-scan image of the phantom with fully oxygenated (sO2 = 100%) blood at a hematocrit of 45%, the same as our simulation. The yellow dashed line highlights the location of the A-line plotted in Fig. 7(B). The A-line is an average of STFT A-lines from 528 nm – 588 nm (central band centered at 558 nm). In Fig. 7(B), there is a clear delineation between the AW (40 m depth) and BM (57 m depth), corresponding to the CFZ.
Fig. 7.
(A) vis-OCT B-scan of fully oxygenated blood in a tube phantom; (B) A vis-OCT A-line at the center of tube phantom (yellow-dashed line) in the panel A; (C) Measured attenuation spectrum of fully oxygenated blood; (D) Measured sO2 and SSF values at different pre-set oxygenation levels.
Fig. 7(C) plots a least-squares fit of the measured attenuation spectrum of fully oxygenated blood (red line) to its theoretical attenuation spectrum (black-dashed line). We performed least-squares fitting using Eq. 5 to measure sO2 using the ratio of the oxygen-dependent coefficients [65] and estimate the SSF. The fitting (R2 = 0.98) in Fig. 7(C) yields sO2 = 100%, = 205 cm-1, and SSF = 0.06, which agrees with the simulated SSF for fully oxygenated blood.
We measured sO2 and SSF from five sO2 levels between 40% and 100%. We bootstrapped 100 measurements for each level by shuffling each dataset and randomly selecting 50 B-scans. Fig. 7(D) shows the mean and SD of measured sO2 (circles) and SSF (triangles). The black dashed line shows the linear best fit relationship ( ) between the blood-gas machine measurements and vis-OCT measurements, indicating excellent agreement between these two independent measurements. The average SSF is 0.060 +/- 0.021, and the average spectroscopic fit R2 is 0.99. The agreement between simulated and experimentally measured SSF values suggests that our work does not contradict the previously suggested packing factor in whole blood [9] but, instead, adds an additional correction for vis-OCT oximetry.
3.6. In vivo experimental results
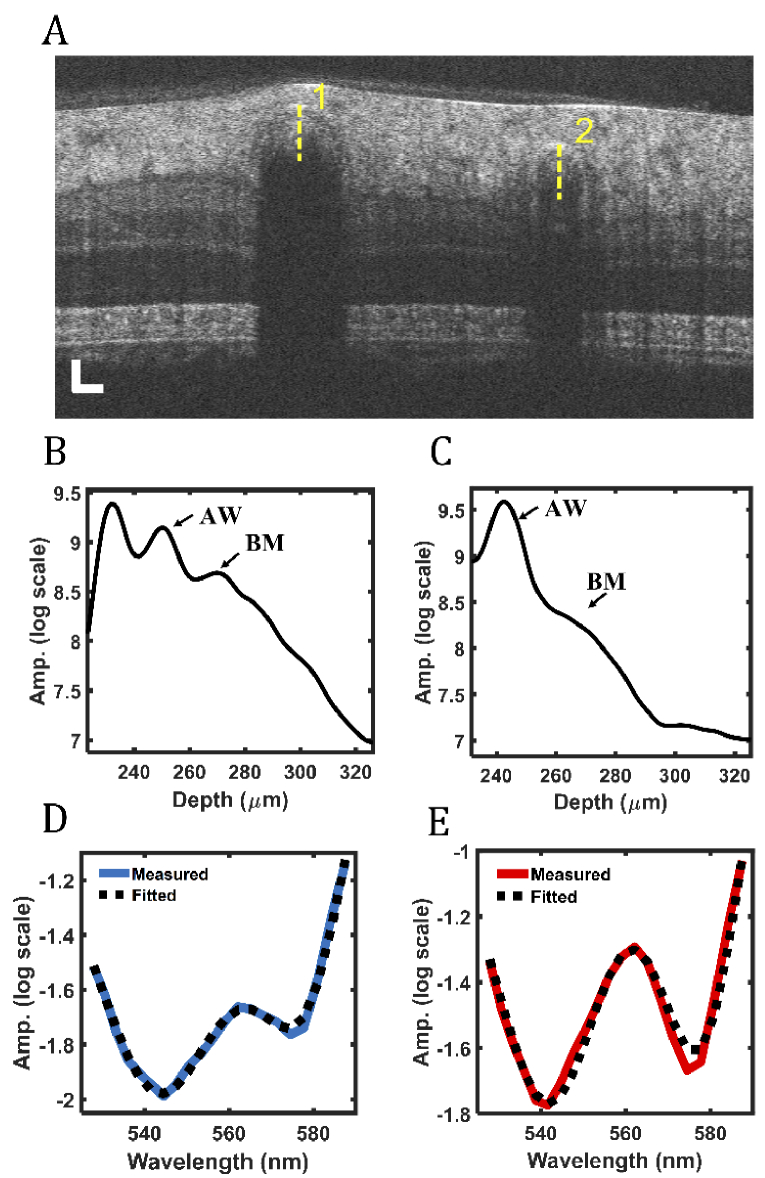
We validated SSF measurement in vis-OCT imaging of human retinas. Fig. 8(A) shows a B-scan image from a 23-year-old male volunteer. We investigated one major vein and one major artery, as highlighted by 1 and 2, respectively. The yellow dashed lines highlight the locations of A-lines plotted in Fig. 8(B) & 8C. The A-lines are an average of STFT A-lines from 528 nm – 588 nm. The vein plotted in Fig. 8(B) clearly delineated the AW and BM, similar to the simulated A-line (Fig. 4(A) and ex vivo A-line (Fig. 7(B). In the artery plotted in Fig. 8(C), this delineation is less obvious, and there is a change in slope near 260 m depth where the BM is typically located, which can be caused by higher, pulsatile blood flow in arteries leading to less precise spatial averaging. We also observe a small valley near the center of the vessel in Fig. 8(C), which may also be associated with more turbulent flow patterns in arteries.
Fig. 8.
(A) Vis-OCT B-scan image of a human retina, where a vein is labeled by 1 and an artery is labeled by 2; (B) Vis-OCT A-line of the vein from the highlighted position in the panel A; (C) Vis-OCT A-line of the artery from the highlighted position in the panel (A); (D) Measured attenuation spectrum from the highlighted vein in the panel A; (E) Measured attenuation spectrum from the highlighted artery in the panel A.
We calculated sO2 and SSF by fitting the wavelength-dependent attenuation spectrum with the theoretical spectrum [65]. The measured SSF agreed with our simulated and ex vivo experimental results. Fig. 8(D) shows a least-squares fit of the attenuation spectrum measured in the vein. The best fit yields sO2 = 59% (R2 = 0.99) and SSF = 0.07. Fig. 8(E) shows the fitting results for the artery, where sO2 = 100% (R2 = 0.97) and SSF = 0.07.
4. Discussion and conclusion
Accurate vis-OCT oximetry remains challenging because of systemic uncertainties introduced by multiple scattering. This work establishes a new correction factor SSF to account for multiply forward scattered photons in blood. Using MC simulation, we found that SSF is near 0.06, significantly smaller than the reported packing factor (W = 0.3025) [9,30,54]. Documented photon packets’ trajectories indicate that most detected photon packets belong to Class I, meaning they are ballistic photon packets and return to the detector with a small deviation from their incident axis. We found that these Class I photon packets were scattered multiple times, which is only possible if they are primarily forward scattered. We further investigated how different NAs influence the measured SSF. We found that physically reasonable NA values in the human retinal imaging yield SSF values between 0.02 and 0.09, suggesting that NA substantially impacts the measured SSF. As a result, vis-OCT should not use rigid, a priori models for retinal oximetry, especially with different hardware designs and imaging of different eyes.
We imaged ex vivo bovine blood phantoms using vis-OCT as the first validation of our simulation findings. After correcting systemic biases from the background and roll-off, we measured sO2 and SSF and compared vis-OCT measurements with blood-oxygen analyzer measurements. We found that the average SSF was 0.060 +/- 0.021, almost identical to the simulated results. We further performed vis-OCT sO2 measurements in the human retina and found that SSF was 0.06 and measured sO2 values consistent with physiological ranges for arteries and veins. This work is the first comprehensive investigation and validation of blood’s attenuation spectrum in vis-OCT using simulation, ex vivo phantom and human retinal imaging.
Using the packing factor to scale the scattering coefficient in our MC simulation resulted in SSF values in excellent agreement with experimental data. As suggested in the literature, the packing factor is the result of correlated scatterings among densely packed RBCs [9,28,68,69]. As RBC concentration increases, coherent interferences can affect the far-field scattered field, which is nonlinearly correlated with RBC density and is likely dependent on the orientations of individual RBCs. While MC simulation does not directly account for orientation-dependent scattering, it can replicate their statistical influence by scaling the input by W. Furthermore, previous experimental tests of blood’s scattering coefficient were performed using an integration sphere [10,11,28,46,70], which does not spatially filter detected photons as vis-OCT does. Our SSF combines the influence of scattering effects from blood hemodynamics (e.g., packing factor) and spatial filtering by the imaging modality (e.g., acceptance aperture and angle) on the effective measured by vis-OCT.
One limitation in our simulation is the assumption of blood as a homogenous medium. In reality, RBC packing density and orientations are affected by blood flow, blood velocity, vessel size, and incident angle [11,49,71–73]. These factors can alter scattering cross-section and directionality, changing the optical properties assumed in this work. Although significant spatial averaging may suppress these variations, researchers should carefully monitor the variability of SSF to ensure a suitable oximetry model. Additionally, factors outside of light-tissue interaction such as the confocal function and roll-off may impact the measured attenuation, particularly if they are spectrally dependent. Since we are using relatively low NAs in this study, the depth of focus (Rayleigh length = 71 m at NA = 0.05) is sufficiently long to have a negligible influence on the results. In addition, in clinical imaging, the focal plane of the human retina is not known a priori, and strong motions and chromatic aberrations make its correction nontrivial.
We investigated a suite of parameters influencing vis-OCT detection and concluded that a combination of low NA and multiple forward scattering causes a significant reduction of the measured scattering coefficient of blood. This enables the detection of ballistic photons penetrating deep into retinal vessels and absorption-dominated spectroscopic measurements. In the future, researchers should use these conclusions to inform parameters in sO2 models.
Funding
National Institutes of Health10.13039/100000002 (R01EY019949, R01EY026078, R01EY029121, T32GM142604, U01EY033001).
Disclosures
R. Fang, None; I. Rubinoff, None; H F. Zhang, Opticent Inc, which did not support this work
Data Availability
Data underlying the results presented in this paper are not yet publicly available but may be obtained from the authors upon request.
References
- 1.Schmitt J. M., “Optical coherence tomography (OCT): a review,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1205–1215 (1999). 10.1109/2944.796348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wojtkowski M., “High-speed optical coherence tomography: basics and applications,” Appl. Opt. 49(16), D30–D61 (2010). 10.1364/AO.49.000D30 [DOI] [PubMed] [Google Scholar]
- 4.Fujimoto J. G., Drexler W., Schuman J. S., Hitzenberger C. K., “Optical coherence tomography (OCT) in ophthalmology: introduction,” Opt. Express 17(5), 3978–3979 (2009). 10.1364/OE.17.003978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Almasian M., Bosschaart N., van Leeuwen T. G., Faber D. J., “Validation of quantitative attenuation and backscattering coefficient measurements by optical coherence tomography in the concentration-dependent and multiple scattering regime,” J. Biomed. Opt 20(12), 121314 (2015). 10.1117/1.JBO.20.12.121314 [DOI] [PubMed] [Google Scholar]
- 6.Gong P., Almasian M., Van Soest G., De Bruin D. M., Van Leeuwen T. G., Sampson D. D., Faber D. J., “Parametric imaging of attenuation by optical coherence tomography: review of models, methods, and clinical translation,” J. Biomed. Opt. 25(04), 1 (2020). 10.1117/1.JBO.25.4.040901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu S., Sotomi Y., Eggermont J., Nakazawa G., Torii S., Ijichi T., Onuma Y., Serruys P. W., Lelieveldt B. P., Dijkstra J., “Tissue characterization with depth-resolved attenuation coefficient and backscatter term in intravascular optical coherence tomography images,” J. Biomed. Opt 22(09), 1 (2017). 10.1117/1.JBO.22.9.096004 [DOI] [PubMed] [Google Scholar]
- 8.Smithies D. J., Lindmo T., Chen Z., Nelson J. S., Milner T. E., “Signal attenuation and localization in optical coherence tomography studied by Monte Carlo simulation,” Phys. Med. Biol. 43(10), 3025–3044 (1998). 10.1088/0031-9155/43/10/024 [DOI] [PubMed] [Google Scholar]
- 9.Bosschaart N., Edelman G. J., Aalders M. C., van Leeuwen T. G., Faber D. J., “A literature review and novel theoretical approach on the optical properties of whole blood,” Lasers Med. Sci. 29(2), 453–479 (2014). 10.1007/s10103-013-1446-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Friebel M., Helfmann J., Netz U. J., Meinke M. C., “Influence of oxygen saturation on the optical scattering properties of human red blood cells in the spectral range 250 to 2000nm,” J. Biomed. Opt. 14(3), 034001 (2009). 10.1117/1.3127200 [DOI] [PubMed] [Google Scholar]
- 11.Roggan A., Friebel M., Dörschel K., Hahn A., Mueller G. J., “Optical properties of circulating human blood in the wavelength range 400-2500 nm,” J. Biomed. Opt. 4(1), 36–46 (1999). 10.1117/1.429919 [DOI] [PubMed] [Google Scholar]
- 12.Faber D. J., Aalders M. C. G., Mik E. G., Hooper B. A., van Gemert M. J. C., van Leeuwen T. G., “Oxygen saturation-dependent absorption and scattering of blood,” Phys. Rev. Lett. 93(2), 028102 (2004). 10.1103/PhysRevLett.93.028102 [DOI] [PubMed] [Google Scholar]
- 13.Robles F. E., Wilson C., Grant G., Wax A., “Molecular imaging true-colour spectroscopic optical coherence tomography,” Nat. Photonics 5(12), 744–747 (2011). 10.1038/nphoton.2011.257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shu X., Beckmann L., Zhang H. F., “Visible-light optical coherence tomography: a review,” J. Biomed. Opt. 22(12), 121707 (2017). 10.1117/1.JBO.22.12.121707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Veenstra C., Kruitwagen S., Groener D., Petersen W., Steenbergen W., Bosschaart N., “Quantification of total haemoglobin concentrations in human whole blood by spectroscopic visible-light optical coherence tomography,” Sci. Rep. 9(1), 15115 (2019). 10.1038/s41598-019-51721-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lu C. W., Lee C. K., Tsai M. T., Wang Y. M., Yang C. C., “Measurement of the hemoglobin oxygen saturation level with spectroscopic spectral-domain optical coherence tomography,” Opt. Lett. 33(5), 416–418 (2008). 10.1364/OL.33.000416 [DOI] [PubMed] [Google Scholar]
- 17.Oldenburg A. L., Xu C. Y., Boppart S. A., “Spectroscopic optical coherence tomography and microscopy,” IEEE J. Select. Topics Quantum Electron. 13(6), 1629–1640 (2007). 10.1109/JSTQE.2007.910292 [DOI] [Google Scholar]
- 18.Linsenmeier R. A., Zhang H. F., “Retinal oxygen: from animals to humans,” Prog. Retinal Eye Res. 58, 115–151 (2017). 10.1016/j.preteyeres.2017.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu W. Z., Wang S. J., Soetikno B., Yi J., Zhang K. V., Chen S. Y., Linsenmeier R. A., Sorenson C. M., Sheibani N., Zhang H. F., “Increased retinal oxygen metabolism precedes microvascular alterations in type 1 diabetic mice,” Invest. Ophthalmol. Visual Sci. 58(2), 981 (2017). 10.1167/iovs.16-20600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen S. Y., Yi J., Liu W. Z., Backman V., Zhang H. F., “Monte Carlo Investigation of Optical Coherence Tomography Retinal Oximetry,” IEEE Trans. Biomed. Eng. 62(9), 2308–2315 (2015). 10.1109/TBME.2015.2424689 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen S., Yi J., Zhang H. F., “Measuring oxygen saturation in retinal and choroidal circulations in rats using visible light optical coherence tomography angiography,” Biomed. Opt. Express 6(8), 2840–2853 (2015). 10.1364/BOE.6.002840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yi J., Liu W., Chen S., Backman V., Sheibani N., Sorenson C. M., Fawzi A. A., Linsenmeier R. A., Zhang H. F., “Visible light optical coherence tomography measures retinal oxygen metabolic response to systemic oxygenation,” Light: Sci. Appl. 4(9), e334 (2015). 10.1038/lsa.2015.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pi S., Camino A., Wei X., Simonett J., Cepurna W., Huang D., Morrison J. C., Jia Y., “Rodent retinal circulation organization and oxygen metabolism revealed by visible-light optical coherence tomography,” Biomed. Opt. Express 9(11), 5851–5862 (2018). 10.1364/BOE.9.005851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pi S., Camino A., Cepurna W., Wei X., Zhang M., Huang D., Morrison J., Jia Y., “Automated spectroscopic retinal oximetry with visible-light optical coherence tomography,” Biomed. Opt. Express 9(5), 2056–2067 (2018). 10.1364/BOE.9.002056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chen S., Shu X., Nesper P. L., Liu W., Fawzi A. A., Zhang H. F., “Retinal oximetry in humans using visible-light optical coherence tomography,” Biomed. Opt. Express 8(3), 1415–1429 (2017). 10.1364/BOE.8.001415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pi S., Hormel T. T., Wei X., Cepurna W., Wang B., Morrison J. C., Jia Y., “Retinal capillary oximetry with visible light optical coherence tomography,” Proc. Natl. Acad. Sci. U.S.A. 117(21), 11658–11666 (2020). 10.1073/pnas.1918546117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Faber D. J., Mik E. G., Aalders M. C., van Leeuwen T. G., “Toward assessment of blood oxygen saturation by spectroscopic optical coherence tomography,” Opt. Lett. 30(9), 1015–1017 (2005). 10.1364/OL.30.001015 [DOI] [PubMed] [Google Scholar]
- 28.Meinke M., Müller G., Helfmann J., Friebel M., “Empirical model functions to calculate hematocrit-dependent optical properties of human blood,” Appl. Opt. 46(10), 1742–1753 (2007). 10.1364/AO.46.001742 [DOI] [PubMed] [Google Scholar]
- 29.Zijlstra W. G., Buursma A., van Assendelft O. W., Visible and Near Infrared Absorption Spectra of Human and Animal Haemoglobin: Determination and Application (VSP, 2000). [Google Scholar]
- 30.Yi J., Wei Q., Liu W., Backman V., Zhang H. F., “Visible-light optical coherence tomography for retinal oximetry,” Opt. Lett. 38(11), 1796–1798 (2013). 10.1364/OL.38.001796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Song W., Shao W., Yi W., Liu R., Desai M., Ness S., Yi J., “Visible light optical coherence tomography angiography (vis-OCTA) facilitates local microvascular oximetry in the human retina,” Biomed. Opt. Express 11(7), 4037–4051 (2020). 10.1364/BOE.395843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chong S. P., Merkle C. W., Leahy C., Radhakrishnan H., Srinivasan V. J., “Quantitative microvascular hemoglobin mapping using visible light spectroscopic optical coherence tomography,” Biomed. Opt. Express 6(4), 1429–1450 (2015). 10.1364/BOE.6.001429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chong S. P., Merkle C. W., Radhakrishnan H., Leahy C., Dubra A., Sulai Y. N., Srinivasan V. J., “Optical coherence imaging of microvascular oxygenation and hemodynamics,” in CLEO: Applications and Technology , (Optical Society of America, 2014), ATh1O. 2. [Google Scholar]
- 34.Liu R., Song W., Backman V., Yi J., “Quantitative quality-control metrics for in vivo oximetry in small vessels by visible light optical coherence tomography angiography,” Biomed. Opt. Express 10(2), 465–486 (2019). 10.1364/BOE.10.000465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yao G., Wang L. V., “Monte Carlo simulation of an optical coherence tomography signal in homogeneous turbid media,” Phys. Med. Biol. 44(9), 2307–2320 (1999). 10.1088/0031-9155/44/9/316 [DOI] [PubMed] [Google Scholar]
- 36.Rubinoff I., Kuranov R. V., Zhang H. F., “Intrinsic spectrally-dependent background in spectroscopic visible-light optical coherence tomography,” Biomed. Opt. Express 12(1), 110–124 (2021). 10.1364/BOE.410011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yuan E., Si P., Winetraub Y., Shevidi S., de la Zerda A., “A spectral demixing model for triplex in vivo imaging of optical coherence tomography contrast agents,” Acs Photonics 7(4), 893–900 (2020). 10.1021/acsphotonics.9b01819 [DOI] [Google Scholar]
- 38.Wang L., Jacques S. L., Zheng L., “MCML—Monte Carlo modeling of light transport in multi-layered tissues,” Comput. Methods Programs in Biomed. 47(2), 131–146 (1995). 10.1016/0169-2607(95)01640-F [DOI] [PubMed] [Google Scholar]
- 39.Yust B. G., Mimun L. C., Sardar D. K., “Optical absorption and scattering of bovine cornea, lens, and retina in the near-infrared region,” Lasers Med. Sci. 27(2), 413–422 (2012). 10.1007/s10103-011-0927-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Aumann S., Donner S., Fischer J., Müller F., “Optical coherence tomography (OCT): principle and technical realization,” High Resolution Imaging in Microscopy and Ophthalmol. 59–85 (2019). [PubMed]
- 41.Farsiu S., Christofferson J., Eriksson B., Milanfar P., Friedlander B., Shakouri A., Nowak R., “Statistical detection and imaging of objects hidden in turbid media using ballistic photons,” Appl. Opt. 46(23), 5805–5822 (2007). 10.1364/AO.46.005805 [DOI] [PubMed] [Google Scholar]
- 42.Pedrotti F. L., Pedrotti L. M., Pedrotti L. S., Introduction to optics (Cambridge University Press, 2017). [Google Scholar]
- 43.Swinehart D. F., “The beer-lambert law,” J. Chem. Educ. 39(7), 333 (1962). 10.1021/ed039p333 [DOI] [Google Scholar]
- 44.Thrane L., Yura H. T., Andersen P. E., “Analysis of optical coherence tomography systems based on the extended Huygens–Fresnel principle,” J. Opt. Soc. Am. A 17(3), 484–490 (2000). 10.1364/JOSAA.17.000484 [DOI] [PubMed] [Google Scholar]
- 45.Durak L., Arikan O., “Short-time Fourier transform: two fundamental properties and an optimal implementation,” IEEE Trans. Signal Process. 51(5), 1231–1242 (2003). 10.1109/TSP.2003.810293 [DOI] [Google Scholar]
- 46.Friebel M., Roggan A., Müller G. J., Meinke M. C., “Determination of optical properties of human blood in the spectral range 250 to 1100 nm using Monte Carlo simulations with hematocrit-dependent effective scattering phase functions,” J. Biomed. Opt. 11(3), 034021 (2006). 10.1117/1.2203659 [DOI] [PubMed] [Google Scholar]
- 47.Nilsson H., Nilsson G. E., “Monte Carlo simulations of light interaction with blood vessels in human skin in the red-wavelength region,” in Optical Diagnostics of Biological Fluids III , (International Society for Optics and Photonics, 1998), 44–53. [Google Scholar]
- 48.Hammer M., Roggan A., Schweitzer D., Muller G., “Optical properties of ocular fundus tissues-an in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation,” Phys. Med. Biol. 40(6), 963–978 (1995). 10.1088/0031-9155/40/6/001 [DOI] [PubMed] [Google Scholar]
- 49.Sakota D., Takatani S., “Quantitative analysis of optical properties of flowing blood using a photon-cell interactive Monte Carlo code: effects of red blood cells’ orientation on light scattering,” J. Biomed. Opt. 17(5), 057007 (2012). 10.1117/1.JBO.17.5.057007 [DOI] [PubMed] [Google Scholar]
- 50.Kirillin M., Meglinski I., Kuzmin V., Sergeeva E., Myllylä R., “Simulation of optical coherence tomography images by Monte Carlo modeling based on polarization vector approach,” Opt. Express 18(21), 21714–21724 (2010). 10.1364/OE.18.021714 [DOI] [PubMed] [Google Scholar]
- 51.Goldsmith H. L., Cokelet G. R., Gaehtgens P., “Robin Fahraeus: evolution of his concepts in cardiovascular physiology,” Am. J. Physiol.-Heart and Circulatory Physiol. 257(3), H1005–H1015 (1989). 10.1152/ajpheart.1989.257.3.H1005 [DOI] [PubMed] [Google Scholar]
- 52.Lauri J., Bykov A., Fabritius T., “Quantification of cell-free layer thickness and cell distribution of blood by optical coherence tomography,” J. Biomed. Opt. 21(4), 040501 (2016). 10.1117/1.JBO.21.4.040501 [DOI] [PubMed] [Google Scholar]
- 53.Meinke M. C., Müller G. J., Helfmann J., Friebel M., “Optical properties of platelets and blood plasma and their influence on the optical behavior of whole blood in the visible to near infrared wavelength range,” J. Biomed. Opt. 12(1), 014024 (2007). 10.1117/1.2435177 [DOI] [PubMed] [Google Scholar]
- 54.Billett H. H., “Hemoglobin and hematocrit,” Clinical Methods: The History, Physical, and Laboratory Examinations , 3rd edition (Butterworth, 1990). [PubMed] [Google Scholar]
- 55.Toublanc D., “Henyey–Greenstein and Mie phase functions in Monte Carlo radiative transfer computations,” Appl. Opt. 35(18), 3270–3274 (1996). 10.1364/AO.35.003270 [DOI] [PubMed] [Google Scholar]
- 56.Skaar J., “Fresnel equations and the refractive index of active media,” Phys. Rev. E 73(2), 026605 (2006). 10.1103/PhysRevE.73.026605 [DOI] [PubMed] [Google Scholar]
- 57.Atchison D. A., Smith G., Smith G., Optics of the Human Eye (Butterworth-Heinemann Oxford, 2000), Vol. 2. [Google Scholar]
- 58.Van Norren D., Tiemeijer L., “Spectral reflectance of the human eye,” Vision Res. 26(2), 313–320 (1986). 10.1016/0042-6989(86)90028-3 [DOI] [PubMed] [Google Scholar]
- 59.Izatt J. A., Choma M. A., “Theory of Optical Coherence Tomography,” in Optical Coherence Tomography: Technology and Applications , Drexler W., Fujimoto J. G., eds. (Springer Berlin Heidelberg, 2008), pp. 47–72. [Google Scholar]
- 60.Zhang X., Beckmann L., Miller D. A., Shao G., Cai Z., Sun C., Sheibani N., Liu X., Schuman J., Johnson M., “In vivo imaging of Schlemm's canal and limbal vascular network in mouse using visible-light OCT,” Invest. Ophthalmol. Visual Sci. 61(2), 23 (2020). 10.1167/iovs.61.2.23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.ThorLabs , “400 to 700 nm Wavelength Range,” (2022), retrieved https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=2910&pn=LSM03-VIS#.
- 62.Kuranov R. V., Qiu J., McElroy A. B., Estrada A., Salvaggio A., Kiel J., Dunn A. K., Duong T. Q., Milner T. E., “Depth-resolved blood oxygen saturation measurement by dual-wavelength photothermal (DWP) optical coherence tomography,” Biomed. Opt. Express 2(3), 491 (2011). 10.1364/BOE.2.000491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kelman G. R., “Digital computer procedure for the conversion of PCO2, into blood CO2 content,” Respir. Physiol. 3(1), 111–115 (1967). 10.1016/0034-5687(67)90028-X [DOI] [PubMed] [Google Scholar]
- 64.Rubinoff I., Kuranov R. V., Ghassabi Z., Wang Y., Beckmann L., Miller D. A., Tayebi B., Wollstein G., Ishikawa H., Schuman J. S., Zhang H. F., “Adaptive spectroscopic visible-light optical coherence tomography for human retinal oximetry,” bioRxiv (2021). [DOI] [PMC free article] [PubMed]
- 65.Ian Rubinoff R. V. K., Ghassabi Zeinab, Wang Yuanbo, Beckmann Lisa, Miller David A., Tayebi Behnam, Wollstein Gadi, Ishikawa Hiroshi, Schuman Joel S., Zhang Hao F., “Adaptive spectroscopic visible-light optical coherence tomography for human retinal oximetry,” bioRxiv (2021). [DOI] [PMC free article] [PubMed]
- 66.Pan Y., Lankenou E., Welzel J., Birngruber R., Engelhardt R., “Optical coherence-gated imaging of biological tissues,” IEEE J. Sel. Top. Quantum Electron. 2(4), 1029–1034 (1996). 10.1109/2944.577332 [DOI] [Google Scholar]
- 67.Rubinoff I., Soetikno B., Miller D. A., Rischall I., Fawzi A., Kuranov R., Zhang H. F., “Spectrally dependent roll-off in visible-light optical coherence tomography,” Opt. Lett. 45(9), 2680–2683 (2020). 10.1364/OL.389240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Twersky V., “Absorption and multiple scattering by biological suspensions,” J. Opt. Soc. Am. 60(8), 1084–1093 (1970). 10.1364/JOSA.60.001084 [DOI] [PubMed] [Google Scholar]
- 69.Ishiniaru A., Kuga Y., “Attenuation constant of a coherent field in a dense distribution of particles,” J. Opt. Soc. Am. 72(10), 1317–1320 (1982). 10.1364/JOSA.72.001317 [DOI] [Google Scholar]
- 70.Yaroslavsky A. N., Yaroslavsky I. V., Goldbach T., Schwarzmaier H.-J., “Optical properties of blood in the near-infrared spectral range,” in Optical Diagnostics of Living Cells and Biofluids , (International Society for Optics and Photonics, 1996), 314–324. [Google Scholar]
- 71.Friebel M., Helfmann J., Müller G. J., Meinke M. C., “Influence of shear rate on the optical properties of human blood in the spectral range 250 to 1100 nm,” J. Biomed. Opt. 12(5), 054005 (2007). 10.1117/1.2799154 [DOI] [PubMed] [Google Scholar]
- 72.Steenbergen W., Kolkman R., de Mul F., “Light-scattering properties of undiluted human blood subjected to simple shear,” J. Opt. Soc. Am. A 16(12), 2959–2967 (1999). 10.1364/JOSAA.16.002959 [DOI] [PubMed] [Google Scholar]
- 73.Enejder A. M., Swartling J., Aruna P., Andersson-Engels S., “Influence of cell shape and aggregate formation on the optical properties of flowing whole blood,” Appl. Opt. 42(7), 1384–1394 (2003). 10.1364/AO.42.001384 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not yet publicly available but may be obtained from the authors upon request.