Abstract
Microscopy with ultraviolet surface excitation (MUSE) is increasingly studied for intraoperative assessment of tumor margins during breast-conserving surgery to reduce the re-excision rate. Here we report a two-step classification approach using texture analysis of MUSE images to automate the margin detection. A study dataset consisting of MUSE images from 66 human breast tissues was constructed for model training and validation. Features extracted using six texture analysis methods were investigated for tissue characterization, and a support vector machine was trained for binary classification of image patches within a full image based on selected feature subsets. A weighted majority voting strategy classified a sample as tumor or normal. Using the eight most predictive features ranked by the maximum relevance minimum redundancy and Laplacian scores methods has achieved a sample classification accuracy of 92.4% and 93.0%, respectively. Local binary pattern alone has achieved an accuracy of 90.3%.
1. Introduction
Breast cancer is the second most common cancer and the second leading cause of death among women in the United States (U.S.). Breast-conserving surgery (BCS, or lumpectomy) followed by whole-breast irradiation therapy is a treatment option for early-stage patients. In 2022, it is estimated that there will be 287,850 women with newly diagnosed invasive breast cancer or ductal carcinoma in situ (DCIS) in the U.S., [1] of whom more than a half choose to undergo BCS [2–5]. Compared to women who have negative margins (no tumor at the surface of the excised specimen), women with positive surgical margins (cancer cells at the surface of the specimen) after BCS have significantly increased risk of local recurrence [6–11]. Therefore, additional surgery is recommended to achieve negative margins. Additional surgery can be associated with more surgical complications, worse cosmesis, additional discomfort, psychological stress, time and financial burdens to patients and their caregivers [12–14]. The contemporary national re-excision rates for BCS have decreased since the publication of the 2014 Society of Surgical Oncology and American Society for Radiation Oncology (SSO-ASTRO) guidelines that recommends re-excision surgery for positive margins only for invasive cancer, but it remains substantial (14% to 18%) [5]. One major reason why patients have positive margins after BCS is that intraoperative margin evaluation is typically not available.
Gross examination of an excised lumpectomy specimen is simple and rapid and can be either performed by an on-site pathologist or surgeon. However, it is subjective and has low sensitivity, and thus does not reduce re-excision rates [15]. Current margin assessment technologies, including 2D mammography, digital breast tomosynthesis, frozen section, imprint cytology, and MarginProbe, have been studied for intraoperative margin assessment [16]. Emerging technologies, such as intelligent knife (i-Knife), bioimpedance spectroscopy (ClearEdge), micro-computed tomography (micro-CT), diffuse reflectance spectroscopy (DRS), spatial frequency domain imaging (SFDI), optical coherence tomography (OCT), photoacoustic tomography (PAT), light-sheet microscopy, and MUSE, have been developed and investigated for this purpose [16,17]. However, no single tool has demonstrated the ability to detect positive margins effectively in a timely and inexpensive manner.
Among these technologies, MUSE can easily achieve a spatial resolution sufficient to visualize cell nuclei at the specimen surface and sharp contrasts with a low magnification objective (4x), [18] providing considerable information about tissue surface status which is highly desirable for detecting positive margins. Additionally, MUSE has cost-effective settings that are affordable for most hospitals. A few studies have used MUSE to image excised breast tissues, [19–21] but these studies mainly concentrated on generating virtual H&E images from the MUSE images for visual interpretation. However, virtual H&E images do not present exact morphological features that are familiar to pathologists and visual assessment of such images is subjective. To overcome these limitations, automated classification algorithms that can extract important features from MUSE margin images and make objective diagnosis decisions are highly desired for intraoperative margin assessment.
Tumor is characterized as uncontrolled cell growth and division, which exhibit special patterns and features, such as heterogeneity, compared to normal tissues. Texture analysis (TA) achieves quantifications of these patterns and features and thus has been widely used in oncological applications, such as radiomics, histology, SFDI, optical coherence microscopy (OCM), and fluorescence imaging [22–26]. During BCS, the surgeon’s decision to take additional tissue from the lumpectomy cavity is predicated on whether there are cancer cells at the surface of a lumpectomy specimen. Therefore, a binary or two-category classification of a margin as either positive or negative is sufficient. In this study, we report a two-step approach for automated detection of cancer cells at the surface of breast tumor specimens using TA of MUSE images. In the first step, a full MUSE image of one surface (or margin) of a tissue specimen is divided into many small patches and texture features are extracted from each patch using different TA methods, including first-order methods, [27] gray-level run length matrix (GLRLM), [28] gray-level co-occurrence matrix (GLCM), [29] Gabor filtering, [30] local binary pattern (LBP), [31] and fractal measures (fractal dimension, lacunarity) [32,33]. A support vector machine (SVM) is trained to be a patch classifier using the extracted texture features [34]. In the second step, a decision fusion technique predicts the margin as positive or negative based on the classification results of all patches within the tissue image.
2. Materials and methods
2.1. Breast tissue specimens
A total of 66 fresh human breast specimens from lumpectomy, mastectomy, and breast reconstruction surgeries were collected from the Medical College of Wisconsin (MCW) Tissue Bank for study. All tissue samples were de-identified and the study was approved by the MCW Institutional Review Board (IRB) and Institutional Biosafety Committee (IBC). Tissues were grossly examined and procured by the Tissue Bank staff before imaging. Tissue histology, including tumor subtype, grade, and biomarker profile, was also provided. A summary of tissue histological types is presented in Table 1. Use of ductal carcinoma in situ (DCIS) as the sole preoperative diagnosis was restricted by the Tissue Bank IRB protocol and thus not included in the current study.
Table 1. Summary of sample types.
| Category | Sample case/type | Sample number | |
|---|---|---|---|
| Tumor | Invasive ductal carcinoma (IDC) | 33 | |
| Invasive lobular carcinoma (ILC) | 9 | ||
|
|
|||
| Normal | Adipose-rich normal | 3 | |
| Fibrous/glandular-rich normal | 21 | ||
|
| |||
| Total | 66 | ||
2.2. Acquisition of MUSE images
A commercial inverted fluorescence microscope was converted into a MUSE imaging system to image the surfaces of the fresh ex vivo human breast specimens. A detailed description of the imaging system and imaging protocol can be found in a previous publication [21]. In brief, a deep-ultraviolet LED at 285-nm was used for fluorescence excitation. A 4X apochromatic long working distance objective lens with a numerical aperture of 0.13 and a cooled color camera with no filter were used for fluorescence image collection. Propidium iodide (PI), which fluoresces in the yellow-to-red spectral range, was selected for cell nuclear staining because of its high efficiency in binding to DNA. Eosin Y (EY) stains cytoplasm and connective tissue which emits fluorescence in the green-to-yellow spectral range. Stained tissues were imaged from one side by the MUSE system using tiling scan. After MUSE imaging, the tissues were returned to the Tissue Bank for routine hematoxylin and eosin (H&E) processing. Because of surface irregularities of the specimens, our histotechnologist was instructed to cut as superficial as possible so H&E image could match up with the MUSE image to the greatest extent. An experienced breast pathologist reviewed the digitalized H&E whole slide image and provided the diagnosis. Image sequences acquired from each sample were stitched to form a full tissue surface image after background correction.
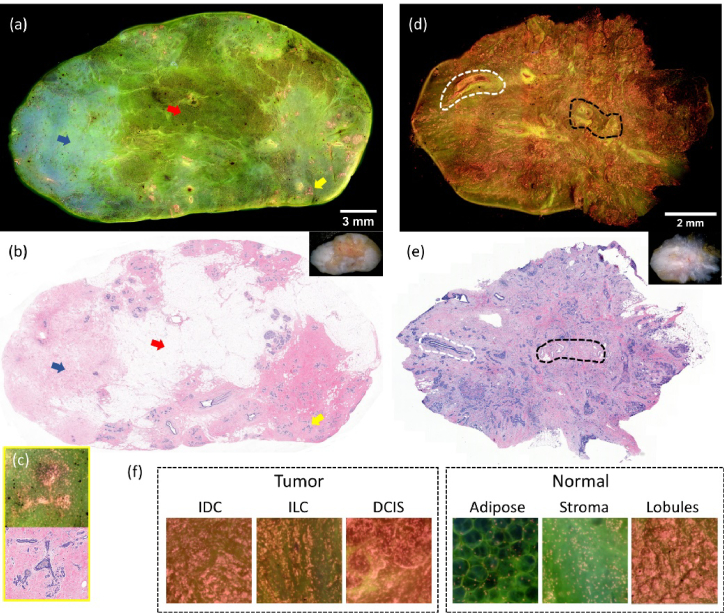
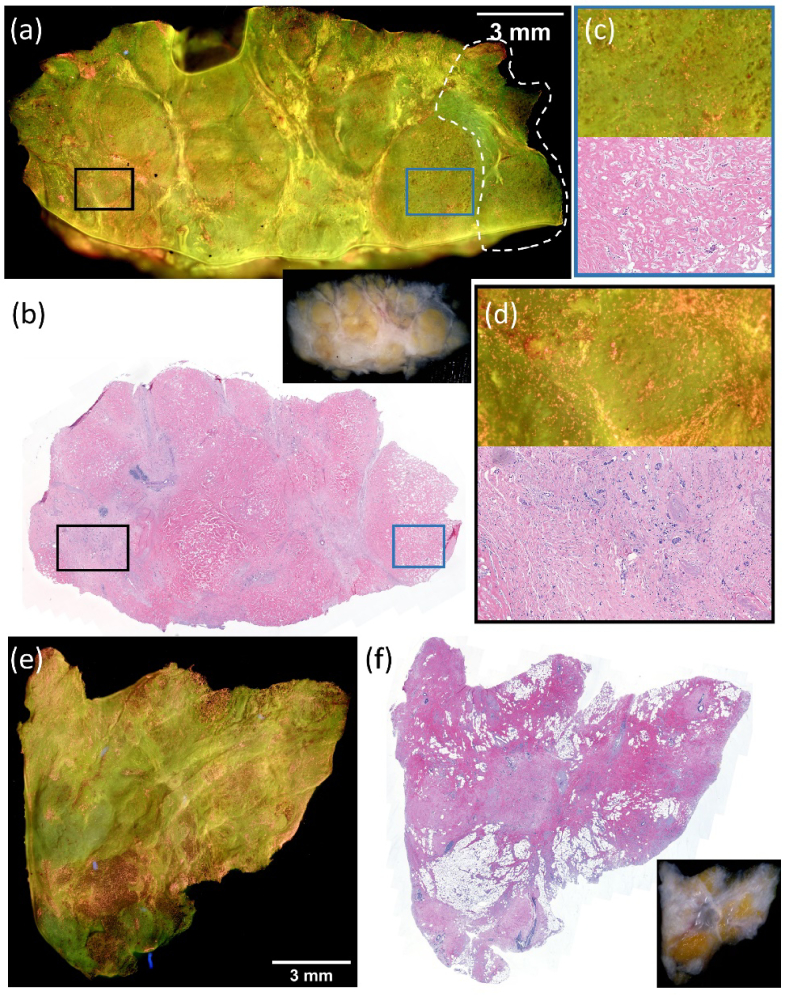
Two examples of MUSE images with corresponding H&E images are shown in Fig. 1. Most areas of the normal tissue in the MUSE image (Fig. 1(a)) show green, indicating low cell nuclei density. The adipose and fibrous stroma sites correlate well between the MUSE and the H&E images (Fig. 1(b)). Lobules have clustered foci of dense nuclei comprising glands and they distribute across the sample. Disparities between MUSE and H&E images are attributed to differences in depth: the H&E slides were obtained 0-200 µm below the tissue surface due to block trimming while the MUSE images were from the top surface only (about 20 µm). The tumor sample shows a high density of cell nuclei which appear yellow-to-red in the MUSE image (Fig. 1(d)). Normal structures such as ducts and blood vessels are easily identifiable in both the MUSE image (Fig. 1(d)) and H&E image (Fig. 1(e)). Enlarged images of several typical regions from various tissue samples are presented in Fig. 1(f). Tumor cells in the invasive ductal carcinoma (IDC) and invasive lobular carcinoma (ILC) images exhibit infiltrative patterns and show a high cell nuclei density. The DCIS image shows round-shaped, expanded patterns. Adipose and stroma have low cell nuclei density and appear mostly green. Lobules have high nuclei density, similar to tumor cells, but their cells distribute in a more regular pattern as compared to tumors.
Fig. 1.
Two representative examples and fluorescence image patches of typical breast tissue types. The MUSE image (a) and H&E image (b) of a normal (tumor-free) sample (∼31 × 15 mm2 size). Fibrous stroma indicated by blue arrows, adipose indicated by red arrows, and lobules indicated by yellow arrows match in the two images. Zoomed-in images of lobules pointed by the yellow arrows are shown at the lower left corner (c). The MUSE image (d) and H&E image (e) of a tumor sample (∼12 × 9 mm2 size) from an IDC grade 2, ER/PR+, HER2- case. Tumor cells appear with variable cellularity in fibrosis tissue and interspersed benign elements, such as the blood vessels highlighted by the black dashed line and ducts enclosed by the white dashed line. (f) Typical image patches of different tissue types cropped from various specimens.
2.3. Tissue labeling and dataset construction
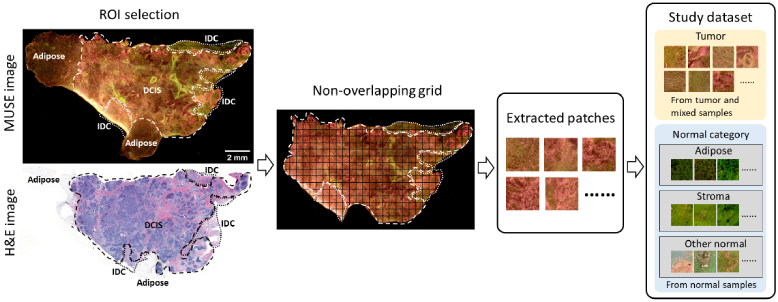
The automated tumor detection is based on the ability to identify and locate a small amount of cancer cells in MUSE images. The workflow for tissue labeling and image dataset construction is illustrated in Fig. 2. To achieve a high resolution in detecting positive margins, a full MUSE image from a tissue surface is divided into many small patches for texture analysis. The H&E image of the same tissue side as the MUSE image is used as the ground truth for region-of-interest (ROI) selection. All normal patches are extracted from purely normal samples. For tumor and mixed samples (samples with both tumor and normal tissue), only tumor regions are selected for analysis. Non-overlapping grids with 400 × 400 pixels or 0.51 × 0.51mm2 are used for patch extraction. The selection of patch size is a trade-off between the necessity of covering adequate tissue textural and morphological differences and the requirement for reasonable resolution for cancer detection. Low-quality patches, such as those caused by obvious out-of-focus, air bubbles, artifacts, large areas of background, and specimen boundaries, are excluded in the analysis. Each extracted patch is manually assigned a label from four classes: tumor, adipose, stroma, and other normal, based on the diagnosis outlined in the corresponding H&E image. Stroma class consists of mostly fibrous stroma, and the other normal class comprises benign adenosis, lobules, blood vessels, ducts, and other normal structures.
Fig. 2.
The workflow for construction of the MUSE image patch dataset illustrated using a mixed malignant specimen with mostly DCIS and some IDC on the edge. The H&E image is used as the ground truth guiding the selection of regions-of-interest (ROIs) in the MUSE image. DCIS is enclosed by dashed lines and IDC is enclosed by dot lines. All normal regions from malignant samples are excluded for analysis. A non-overlapping grid with 400 × 400 pixels (or 0.51 × 0.51 mm2 on the tissue surface) is used for patch extraction. Selected patches are labeled as tumor, adipose, stroma, or other normal.
2.4. Feature extraction and analysis
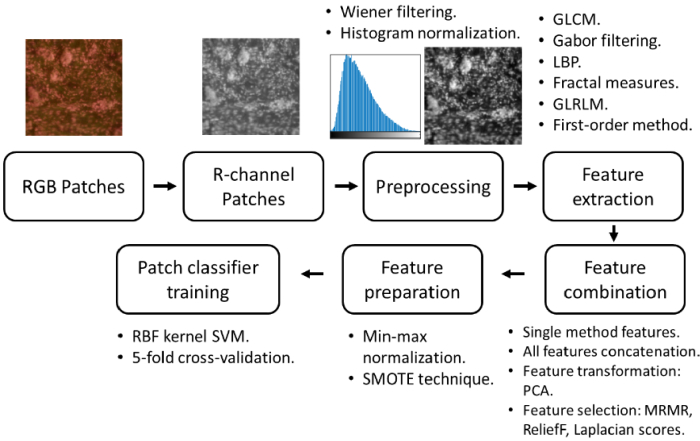
The workflow of feature extraction for patch classifier training is shown in Fig. 3. Because cell nuclei density, morphology, and distribution patterns are the major biomarkers contributing to the texture formation of MUSE images, only the red (R) channel of a color patch is used for analysis. Preprocessing steps include noise reduction and intensity normalization. A 2-dimensional adaptive Wiener filter is applied to remove additive noises from an R channel patch image [35]. A neighborhood of 3 × 3 pixels is used to estimate the local mean and standard deviation. The intensity normalization is used to rescale the R channel patch to the dynamic range of 0-255 (8 bits). Six gray-level TA methods, including the first-order methods, gray-level run length matrix (GLRLM), gray-level co-occurrence matrix (GLCM), Gabor filtering, local binary pattern (LBP), and fractal measures (fractal dimension and lacunarity), are used for characterizing patch textures [27–30,32,33,36,37]. Feature extraction time is an important factor that determines the overall speed of the model. Therefore, feature extraction time is recorded for each TA method. Whether there is a significant difference between normal and tumor patches for each feature is evaluated by the Wilcoxon rank-sum test (Mann-Whitney U-test). Linear dependencies between the TA features were evaluated by Pearson’s correlation coefficients calculated between all features. The visualization of patches in the study dataset on a 2-dimensional space can be achieved using the t-distributed stochastic neighbor embedding (t-SNE) algorithm on the extracted texture features [38].
Fig. 3.
The workflow for quantitative feature extraction and patch classifier training. The red (R) channel of an RGB color patch is used for feature extraction. Preprocessing operations, including Wiener filtering for noise reduction and histogram normalization, are performed prior to the feature extraction. Gray-level TA methods, including GLCM, Gabor filtering, LBP, fractal measures (fractal dimension and lacunarity), GLRLM, and first-order method, are used to obtain features for patch texture characterization. Several different feature subsets are tested. Then, min-max normalization is applied to rescale the selected features and the SMOTE technique is applied for minor class synthesis in the feature space to handle the data imbalance issue. Finally, the Radial Basis Function (RBF) kernel support vector machine (SVM) is trained as the patch classifier. 5-fold cross-validation is used during the process.
2.4.1. First-order methods
The first-order methods consider the probability distribution of a particular pixel intensity only and ignore the spatial relationships between pixels. Commonly used metrics are image statistics, including mean, variance, skewness, kurtosis, and entropy, that can be used as the first-order method features and calculated from the gray-level image histogram [27]. Therefore, the first-order method features are also called histogram features.
2.4.2. Gray-level run length matrix (GLRLM) method
GLRLM is a typical second-order method that considers the occurrence of gray level intensity combinations. The term “run” refers to a set of same intensity pixels that are consecutive in a specific direction. Run length is the number of pixels belonging to that run [28]. For a given direction, a GLRLM matrix can be constructed by recording the distribution of run lengths for each pixel intensity. Many metrics can be calculated from the GLRLM matrix, such as short run emphasis (SRE), low gray-level run emphasis (LGRE), and short run low gray-level emphasis (SRLGE) [39]. For each R channel patch image, four GLRLM matrix are obtained for the directions of 0°, 45°, 90°, and 135°. Eleven metrics are calculated from each GLRLM matrix. After that, the same type of metrics are averaged over the four directions to achieve a rotation-invariant texture representation. The eleven averaged metrics are used as the GLRLM features.
2.4.3. Gray-level co-occurrence matrix (GLCM) method
GLCM method applies a co-occurrence matrix to assess the spatial relations of each pixel intensity within an image [29]. For a given direction and displacement, a GLCM matrix can be obtained for texture representation. A GLCM matrix can be sparse if the image has a high bit-depth. Gray-level quantization is usually applied to address this issue and to reduce the load of computations. Typical Haralick features, such as contrast, correlation, energy, and homogeneity, can be calculated from the GLCM matrix [36]. In this study, the R channel image is quantized to 16 levels and a displacement value of 3 is used. Similar to the GLRLM method, matrices for four directions of 0°, 45°, 90°, and 135° are calculated. The four averaged Haralick features are obtained as the GLCM features.
2.4.4. Gabor filtering method
Gabor filtering mimics the perception in visual systems of humans and primates [40]. A Gabor filter is a complex function that enables local Fourier analysis by modulating sine and cosine functions with a Gaussian window [30]. Gabor filtering method performs convolutions on an image with Gabor filters from the pre-selected filter bank. In this study, wavelengths of 2, 3, 4, 5 pixel/cycle and orientations of 0°, 45°, 90°, 135° are combined to generate sixteen Gabor filters. The mean intensity of the filtered image is used as the feature. Averaging of features over the four orientations for each wavelength is operated to achieve rotation-invariance. Therefore, a total of four features are extracted for each R channel patch by Gabor filtering.
2.4.5. Local binary pattern (LBP) method
LBP method compares the intensity of each pixel with a given number of neighboring pixels [31]. The neighboring pixels are circularly distributed around the pixel at a fixed distance. A binary code is assigned to the pixel based on intensity comparisons. A histogram of codes of pixels within an image can be used as features. Several variants of LBP are proposed to improve the performance of the original LBP algorithm. The uniform rotation invariant LBP is used in this study [37]. The number of neighboring pixels is set to twelve and the distance between central and neighboring pixels is set to three. Linear interpolation was used for neighboring pixel computation. L2 normalization is applied to reduce numerical values in the feature histogram [41]. Fourteen textures are extracted for each patch using the LBP method.
2.4.6. Fractal measures
Studies have investigated the relationship between fractal geometry and carcinogenesis [42,43]. Fractal dimension and lacunarity are estimated on the R channel patch as fractal measures. Fractal dimension is a measure of structural complexity and self-similarity over a range of scales. Because fractal dimension does not encode all information necessary for texture characterization, lacunarity that measures the deviation of geometrical subjects from translational invariance is usually used to provide supplemental information to the fractal dimension. In this study, the differential box-counting method and the gliding-box method are used for the estimation of fractal dimension and lacunarity, respectively [32,33].
Overall, a total of forty features are extracted from each R channel patch by the six gray-level TA methods, as summarized in Table 2. Detailed explanations of these features can be found in the supplementary material. First-order methods are easy to implement without complicated calculations. GLRLM, GLCM, and LBP are statistical approaches that are based on the spatial distribution of pixel intensities. Fractal measures are driven by the development of fractal geometry. Other than focusing on fine-scale details and encoding regional variations, Gabor filtering provides global structure information of an image. The selection of these methods is motivated by representing the textures of tissues from various perspectives, which increases the chance of identifying underlying differences between normal and tumor tissues.
Table 2. Summary of texture features for tissue characterization.
| Texture descriptor | Extracted features | Number of features |
|---|---|---|
| First-order methods | Mean, variance, skewness, kurtosis, entropy | 5 |
| GLRLM | Short run emphasis (SRE), long run emphasis (LRE), low gray-level run emphasis (LGRE), etc. | 11 |
| GLCM | Contrast, correlation, energy, homogeneity | 4 |
| Gabor filtering | NA | 4 |
| LBP | 14 | |
| Fractal measures | Fractal dimension, lacunarity | 2 |
|
| ||
| Total | 40 | |
2.5. Patch-level classification
As shown in Fig. 3, a radial basis function (RBF) kernel SVM is trained to be the patch classifier. Several different feature subsets from the MUSE image patches are investigated for patch-level classification. First, each single TA method using only its own features is evaluated. Second, feature transformation, a process transforming existing features to new features, using principal component analysis (PCA) is assessed [44]. The selection of the number of transformed features from all six TA methods is determined by the criteria that the features selected after transformation can explain at least 95% of total variances. Third, feature selection by maximum relevance minimum redundancy (MRMR), ReliefF, and Laplacian score (LS) methods is studied [45–47]. Finally, classifications on all forty features were implemented. Because the features have different scales and an RBF kernel SVM infers using Euclidean distance, the min-max normalization is applied to rescale features to a range of 0 to 1 before classifier training. Additionally, in order to prevent data leakage, the min-max normalization is performed on the training data only. The test data undergo the same rescaling transformations as the training data at the test step. Because there are less chances of obtaining certain tissue types, such as ILC, due to their natural rarity, the study dataset is expected to be imbalanced. Training a classifier on an imbalanced dataset without appropriate handling tends to mislead the model biased toward the majority class. The synthetic minority over-sampling technique (SMOTE) is applied to address the data imbalance issue [48]. SMOTE technique synthesizes minor tissue types in the feature space and achieves a “balanced” dataset for the training purpose. The 5-fold cross-validation is used for the classification process. The 66 samples are randomly partitioned into five groups of equal or close sizes. One group is used as a test set and the other four are used as a training set. Patches extracted from the same sample are bundled up, which means they are either all in the training set or test set. This training and test process is repeated five times until each group is used as a test set exactly once. Five different random sample partitions are conducted to reduce potential partition bias caused by the limited number of samples. A total of 25 training and test processes are executed. A trained patch classifier outputs the posterior probabilities for tumor and normal predictions. Because a binary classification problem is considered, a patch is classified as tumor if the posterior probability for tumor prediction is above 0.5 and otherwise as normal. The sensitivity, specificity, and accuracy in differentiating positive from normal patches are reported as the performance metrics. The area under the curve (AUC) value of receiver operating characteristic (ROC) curve is also included for performance quantification. Classification of the MUSE image dataset using the previously-proposed nuclear-to-cytoplasm ratio (N/C) alone is also performed as the baseline method [21].
2.6. Margin-level classification
A weighted majority voting method was used for the decision fusion of margin-level predictions [49]. An illustration of the margin-level classification process is shown in Fig. 4. The model input is a full MUSE image of a whole margin which is simulated with one surface of a breast tissue specimen. A non-overlapping grid divides the MUSE image into patches of 400 × 400 pixels and preserves all patch locations. After invalid patches, such as dark backgrounds, are excluded, the trained patch classifier predicts class labels and posterior probabilities for all valid patches. The patch-level classification results can be displayed as a colored heatmap which indicates where tumors are likely located. The decision fusion method focuses on the most discriminative patches with high prediction confidence, for example, a posterior probability above 75%. Given the estimated posterior probabilities of tumor prediction for all patches in margin i where denotes the total number of valid patches, a decision fusion method determines the margin label as tumor (+1) or normal (-1). The decision fusion process selects patches with high confidence and assigns patch weights according to posterior probabilities :
| (1) |
Fig. 4.
The process for margin-level binary prediction (tumor vs. normal). A MUSE image of a full tissue surface is divided into many patches of 400 × 400 pixels in size by a non-overlapping gird. A trained patch classifier predicts the class of each patch with posterior probabilities as the confidence scores. Based on patch-level classification results, a decision fusion method decides the binary label of tumor or normal for the full margin.
The weighting scheme incorporates the patches with high discriminative power either for tumor or normal into the fused margin-level decision for the margin where is the sign function with a value of +1 or -1:
| (2) |
Because margin assessment is a binary classification problem, the probabilities for tumor and normal predictions are complementary with a sum of one for the same patch. In practice, each patch is assigned two weights the same as its posterior probability values for both tumor and normal prediction. The tumor predictive score is the weighted sum of all included patches for tumor prediction, and similarly, the normal predictive score is the weighted sum of all included patches for normal prediction. The margin label is predicted by comparing the tumor predictive score with the normal predictive score. If the patch classifier is balanced, the decision fusion treats two predictive scores equally, which suggests predicting the sample to be tumor if the tumor predictive score is higher than the normal predictive score, and vice versa. However, if the patch classifier appears highly biased after an observation of sensitivity and specificity, adjustments either on patch-level classification thresholds or margin-level predictive score weights can be determined using the ROC curves to correct the bias. The 5-fold cross-validation is utilized in this process, and the identical five sample partitions are tested regarding sample partition bias. Any patch from the test MUSE image is therefore isolated from the patch classifier training process.
3. Results
3.1. Image dataset and feature analysis
A total of 3,666 low-quality patches were discarded and 36,128 patches from 66 samples were labeled for the patch-level study dataset construction. The patch discarding rate is 9.2%. A summary of the patch distribution in the constructed study dataset is presented in Table 3. The dataset is imbalanced as expected. Stroma class makes up for 37.71% of all patches, which is the highest among the normal types. Tumor class accounts for 30.71% of all patches. In terms of binary categories, nearly 70% of patches are normal and the rest are tumor. The distribution of patch classes confirms the necessity of appropriate measures to handle the data imbalance issue.
Table 3. Summary of patches in the study dataset.
| Normal |
Tumor | Total | |||
|---|---|---|---|---|---|
| Adipose | Stroma | Other normal | |||
| Patch number | 6,685 | 13,624 | 4,724 | 11,095 | 36,128 |
| Percentage | 18.50% | 37.71% | 13.08% | 30.71% | 100% |
The Wilcoxon rank-sum test is a nonparametric statistical method that requires no normal distribution assumption, but the condition that the two distributions having similar shapes is still preferred. P-values of all features are less than 0.05 between tumor and normal patches, indicating that there are significant differences between tumor and normal tissues using the selected features. However, it should be noted that patches extracted from the same sample are not independent and a limited number of samples were included in this study. The assumption that patches are randomly sampled from normal and tumor populations may not be fulfilled due to the interpatient bias. A delicate statistical model with more tissue samples should address this issue in a future study.
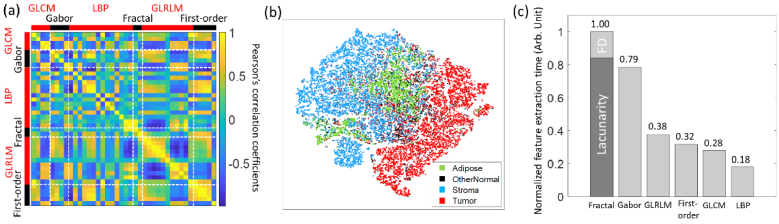
The results of feature analysis are shown in Fig. 5. Pearson’s correlation coefficients were calculated between each pair of features and are displayed in Fig. 5(a). High levels of internal correlations among GLRLM and first-order features are observed. High correlations among GLRLM features may be because the features are all based on intuitive reasoning [39]. LBP method exhibits a moderate-to-low level of internal correlations, which matches its mechanism that LBP histogram describes the distribution of local texture information. Generally, LBP and fractal measures show low levels of correlations with other methods. Although there is no absolute connection between linear correlation and discriminative power, it is reasonable to assume that the selection of a feature subset with little correlation is likely to yield better classification performance. The results suggest that LBP features are more likely to contain highly discriminative information for the classification. A 2-dimensional visualization of all patches in the study dataset using the t-SNE algorithm is shown in Fig. 5(b). The t-SNE algorithm is a nonlinear dimensionality reduction method that embeds the texture features from a 40-dimensional space to a 2-dimensional space with respect to similarities between different patches in the feature space. Similar tissue patches in the high dimensional feature space appear close in the t-SNE visualization. Most adipose and stroma patches cluster together forming a normal-majority cluster with a clear boundary to another cluster of tumor patches. Some other normal type patches intersperse among the tumor patches. Although there is no guarantee that a cluster in the t-SNE plot corresponds to a cluster in the feature space due to the high versatility of the t-SNE algorithm itself, the observation still implies a possible separability of tumor from normal patches in a different dimensional feature space. A comparison of feature extraction time is plotted in Fig. 5(c). Considering that actual feature extraction time depends on many factors, for instance, tissue image size and computational power, a normalized time is reported. Estimating lacunarity using binary gliding box method is relatively time-consuming. Despite that obtaining a fractal dimension takes a shorter time, fractal measures are still the slowest method. Gabor filtering contains many convolution calculations that make it the second slowest method. LBP is the fastest among the six texture extraction methods, which takes only 18% of the total time required by the fractal measures.
Fig. 5.
Results of texture feature analysis. (a) Pearson’s linear correlation between extracted features. High intra-method correlations are observed among the GLRLM and first-order method features. LBP shows moderate-to-low level of intra-method correlations. Overall, LBP and fractal measures have of the lowest inter-method correlations with other methods. (b) Visualization of all patches in the study dataset in a 2-dimensional space via the t-SNE algorithm. Most normal patches (adipose and stroma) cluster together and show a clear boundary to tumor patches. Some other normal patches intersperse among the tumor cluster. (c) Normalized texture feature extraction time. FD denotes fractal dimension. LBP is the most time-efficient method among the six TA techniques included in this study.
3.2. Patch-level
The sensitivities, specificities, accuracies, and AUCs of patch-level classification obtained using features of individual TA methods, combined features of different TA methods, and the baseline N/C method are summarized in Table 4. The performance of each individual TA method varies. GLRLM achieved the highest accuracy, but the model is biased in favor of specificity. Gabor filtering yielded the lowest performance while LBP gave the most balanced results (sensitivity of 86.23% and specificity of 86.44%). The low performance of Gabor filtering (the lowest AUC value of 0.910) might be caused by its lack of representation of fine-scale details. The method names for the feature transformation or selection consist of a feature selection method and a number of the most predictable features ranked by that method. Three numbers of features (8, 10, and 15) ranked by MRMR, ReliefF, and LS feature selection methods have been evaluated. The reported performance metrics in Table 4 are means across the five sample partitions and the standard deviations are shown in the parentheses. A lower standard deviation implies that the model is more stable. In each partition, the four performance metrics are the means over five folds during the cross-validation process.
Table 4. Results of patch-level binary classification.
| Method | Sensitivity | Specificity | Accuracy | AUC | |
|---|---|---|---|---|---|
| Baseline | N/C | 84.55% (0.57%) | 83.97% (1.12%) | 84.60% (0.35%) | 0.922 (0.003) |
|
| |||||
| Individual methods | GLCM | 83.68% (0.48%) | 87.83% (0.10%) | 86.97% (0.53%) | 0.935 (0.005) |
| Gabor | 82.18% (0.83%) | 83.97% (1.95%) | 84.08% (0.66%) | 0.910 (0.005) | |
| LBP | 86.23% (0.61%) | 86.44% (4.06%) | 86.97% (2.42%) | 0.926 (0.020) | |
| Fractal | 90.41% (0.41%) | 81.63% (1.48%) | 84.79% (0.55%) | 0.936 (0.005) | |
| GLRLM | 84.61% (0.47%) | 89.18% (1.39%) | 88.30% (0.49%) | 0.942 (0.003) | |
| First order | 87.22% (0.45%) | 85.57% (1.06%) | 86.47% (0.38%) | 0.930 (0.004) | |
|
| |||||
| Feature transformation or selection | PCA | 85.84% (0.91%) | 89.87% (1.31%) | 89.13% (0.52%) | 0.943 (0.003) |
| MRMR-8 | 87.72% (0.35%) | 88.20% (1.36%) | 88.60% (0.72%) | 0.940 (0.006) | |
| MRMR-10 | 87.04% (0.67%) | 88.94% (1.41%) | 88.92% (0.87%) | 0.941 (0.010) | |
| MRMR-15 | 85.99% (0.35%) | 90.11% (1.40%) | 89.39% (0.71%) | 0.945 (0.005) | |
| ReliefF-8 | 86.34% (0.52%) | 82.86% (2.32%) | 84.62% (1.02%) | 0.917 (0.007) | |
| ReliefF-10 | 86.77% (0.87%) | 87.83% (1.74%) | 87.99% (0.59%) | 0.939 (0.002) | |
| ReliefF-15 | 86.53% (0.45%) | 90.28% (1.44%) | 89.66% (0.62%) | 0.950 (0.004) | |
| LS-8 | 86.61% (0.39%) | 91.12% (1.35%) | 90.27% (0.53%) | 0.950 (0.003) | |
| LS-10 | 86.44% (0.68%) | 90.66% (2.44%) | 89.85% (1.32%) | 0.950 (0.005) | |
| LS-15 | 86.13% (0.52%) | 90.53% (2.56%) | 89.67% (1.48%) | 0.949 (0.007) | |
|
| |||||
| All features | 86.25% (0.70%) | 90.25% (2.57%) | 89.52% (0.14%) | 0.949 (0.007) | |
Most individual TA methods, all feature selection methods except ReliefF-8, and PCA show improved performance over the baseline N/C method. The highest accuracy of 90.27% and the highest AUC value of 0.950 with the minimum standard deviation were achieved using eight features selected by the LS method (LS-8). However, the sensitivity of 86.61% is lower than the specificity of 91.12%, which suggests the model is slightly biased and it generates more accurate predictions for normal than tumor patches. Using eight features selected by the MRMR method gives a nearly balanced result for the sensitivity of 87.72% and the specificity of 88.20%, even though the accuracy of 88.60% is slightly lower than that of the LS method and the AUC value of 0.940 is not the top-tier. Both MRMR and LS methods outperformed the ReliefF method overall, particularly when the number of features is low. Feature transformation using PCA reached a sensitivity lower than that obtained with the three feature selection methods (MRMR, ReliefF and LS). Seven of the forty transformed features explained higher than 95% variances for all experiments. Because the PCA algorithm focuses on obtaining maximum variance and a higher variance does not necessarily represent a higher discriminative power, it is reasonable that transformed features are not superior to ranked features. The concatenation of all forty features performs similarly to the PCA method, which may be caused by some dependencies and redundancies between features. Nevertheless, there is no obvious sign of overfitting, either. In this study, the feature dimensionality of forty is not too high compared to the number of patches during training and overfitting is likely to happen when feature dimensionality is comparable to or even higher than the number of training samples. Finally, since LBP features can be extracted in a shorter time (Fig. 5(c)), LBP can be potentially used alone for tissue texture characterization in time-sensitive scenarios such as intraoperative margin assessment.
3.3. Margin-level
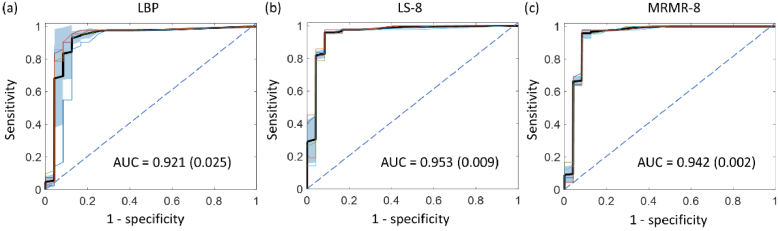
The margin-level classification was performed by using decision fusion on patch-level classification results and the top three feature subsets were investigated. The first feature set consisted of the most predictive eight features ranked by the MRMR method or MRMR-8 because it achieved the most balanced performance other than LBP at the patch-level. The second feature set was similar, but the features were selected by the LS method because of its highest accuracy and AUC value at patch-level. The third feature set included fourteen features extracted by the LBP method as it is the most promising one for high-speed desired applications. The decision fusion performances were evaluated by ROC curves and the results are shown in Fig. 6. LBP alone got the AUC value of 0.921. The highest AUC value of 0.953 was obtained using the LS-8 method and the MRMR-8 method reached a slightly lower AUC value (0.942). Both LS-8 and MRMR-8 exhibit fewer variations among different sample partitions while LBP shows larger differences between curves of different partitions. Future studies with more samples may be needed to determine whether LBP is less stable than LS and MRMR.
Fig. 6.
ROC curves of sample-level classification using LBP (a), LS-8 (b), and MRMR-8 (c) features. Each thin colored curve is the ROC curve of one individual sample partition. Thick black curves represent the ROC curves averaged over the 5 sample partitions. Areas denoting standard deviations are in light blue shadows. The means and standard deviations (in parentheses) of the AUC are also presented.
Assuming that the patch classifier is balanced, the decision criterion becomes a comparison of two predictive scores. The sensitivities, specificities, and accuracies of the three feature subsets are summarized in Table 5. Similarly, all values are means across the five sample partitions and the standard deviations are in the parentheses. The highest performance was achieved by the LS-8 method, with an averaged sensitivity, specificity, and accuracy of 93.81%, 91.67%, and 93.03%, respectively. In two out of the five sample partitions, there were two false positives (FPs) and two false negatives (FNs). There were three false negatively misclassified sample in the other three sample partitions. Interestingly, the bias between sensitivity and specificity of LS at patch-level classification did not significantly deteriorate margin-level predictions. MRMR-8 reported 2 FPs and 3 FNs in all sample partitions and reached similar mean metrics as the LS method. LBP method resulted in 2 FPs and 4 FNs in four sample partitions but 4 FPs and 4 FNs in one sample partition, but the three performance metrics are all higher than 90%, which suggests that LBP alone is an excellent method for time-sensitive scenarios. However, MRMR-8 or LS-8 may be selected if higher classification accuracy is necessary.
Table 5. Results of margin-level binary classification.
| Method | Sensitivity | Specificity | Accuracy |
|---|---|---|---|
| LBP | 90.48% (0.00%) | 90.00% (3.34%) | 90.30% (1.21%) |
| MRMR-8 | 92.86% (0.00%) | 91.67% (0.00%) | 92.42% (0.00%) |
| LS-8 | 93.81% (1.17%) | 91.67% (0.00%) | 93.03% (0.74%) |
4. Discussion
4.1. Significance
This study demonstrates the feasibility of identifying breast tumors in MUSE images of ex vivo surgical tissues using TA in an automated manner. Compared to the N/C method, adoption of texture features increased the binary classification accuracy from less than 85% to around 90% at patch-level. The decision fusion technique achieved high sensitivity and specificity for margin-level tumor detection. Most other MUSE studies focused on generating virtual H&E images by color mapping or deep learning, which needs to be reviewed by a pathologist. Moreover, because of limited sample sizes for visual assessment training and different contrasts from traditional H&E slides, interpreting images captured by the MUSE modality tends to encounter more ambiguities and uncertainties. Therefore, a computer-aided algorithm enabling automated tumor detection objectively and repeatably is desired to overcome those disadvantages and provide an alternative approach to MUSE image evaluation. This study aims to fulfill this clinical need. A trained classification model can potentially either be used for assisting visual assessment or functioning alone for diagnosis. The ability to evaluate the margin status of an excised lumpectomy specimen accurately and rapidly will allow the surgeon to decide whether shaving additional tissue from the surgical cavity is necessary to achieve negative margins during breast-conserving surgery, thus reducing the re-excision rate and associated pain and financial burden to the patients. In addition, accurate negative margin status information would prevent unnecessary shaving of additional tissue, which could impact cosmesis
4.2. Feature selection comparison
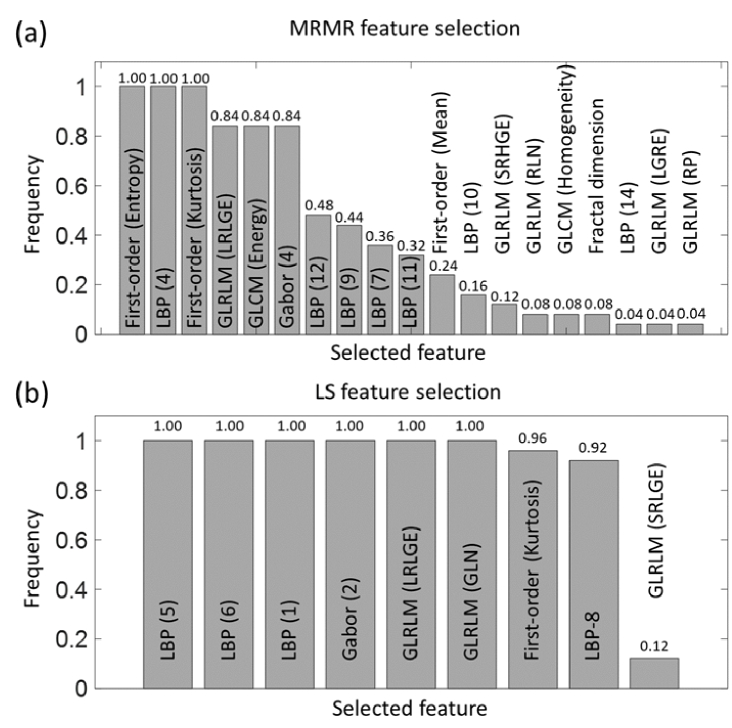
MRMR is a supervised filter method that ranks features with the objective of minimizing redundancies among between features and maximizing relevance between features and class labels using mutual information or F-statistic as the measure. LS is an unsupervised filter method that evaluates the importance of features by the power of preserving sample locality. Despite their comparable classification performances, MRMR and LS may be different in exact feature selection. To answer this question, frequencies of selected features were calculated and plotted in Fig. 7 for LS and MRMR. The frequency is defined as the ratio of times being selected among the eight features over the total rounds of the patch classifier training process. A frequency of one means that the feature was always selected to form the eight-feature subset for patch classifier training. It is observed that LS produced a stable feature selection subset while MRMR selected diverse features from a wide range. Six features and three features were always selected by LS and MRMR, respectively. Through the 25 training processes (five sample partitions and 5-fold cross-validation per partition), the total number of features involved was nine for LS and nineteen for MRMR. LBP features were frequently selected by both methods. Particularly, three out of the six consistently selected features of LS and one out of the three “always” selected features were from LBP. This comparison indicates that there are no unique ways to select a feature subset to achieve certain classification results. Additionally, the feature range of MRMR covered all six TA techniques while LS did not use any feature from GLCM and fractal measures. Therefore, it is reasonable to assume that excluding GLCM and fractal measures will not significantly decrease the performance, which can help reducing the feature extraction time.
Fig. 7.
The frequencies of features being selected by MRMR method (a) and LS method (b). Eight features were selected in each training/test round. Because five different sample partitions were tested and a 5-fold cross validation was used on each partition, a total of 25 rounds were performed. List of acronyms of statistics obtained by GLRLM method: LRLGE (long run low gray-level emphasis), SRHGE (short run high gray-level emphasis), RLN (run length nonuniformity), LGRE (low gray-level run emphasis), RP (run percentage), GLN (gray-level nonuniformity), SRLGE (short run low gray-level emphasis).
4.3. Misclassified samples
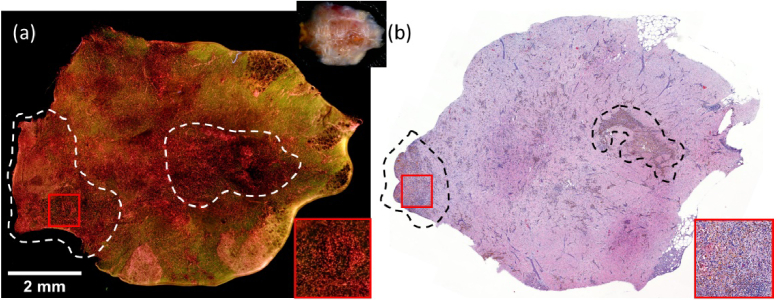
Inspection of misclassified samples helps to understand the situations when the developed classification model makes wrong decisions. Three representative incorrectly-predicted samples, two FNs and one FP, are shown in Fig. 8 and Fig. 9, respectively. The first FN sample shown in Fig. 8(a)-(d) was acquired from an IDC patient who received neoadjuvant therapy. Histopathology diagnosis reported a low residual tumor cellularity of 5% in this case. The MUSE image appears mostly green due to EY fluorescence emissions from fibrosis tissue, and cell nuclei in pink can be seen at various locations but largely in low density, such as the area enclosed by the blue box. An enlarged image of the blue box (Fig. 8(c)) clearly reveals sparse cell nuclei in dense fibrosis tissue, which match well with the corresponding H&E image. Some areas exhibit slightly higher nuclei density, such as the area enclosed by the black box with the zoomed-in image in Fig. 8(d). The low percentage of malignant cells secondary to the cancer treatment received prior to surgery can cause different textural and morphological patterns in the MUSE image. The second FN sample shown in Fig. 8(e), f was obtained from an ILC case, which exhibits relatively lower cellularity than the other eight ILC specimens. The FP sample shown in Fig. 9 contains large portions of hemosiderin depositions and fibrosis. Hemosiderin is an iron-storage complex that is consistent with biopsy sites and tracts. Both the MUSE and H&E images present fine-grained textures resembling high-density tumor cells to some extent. However, histopathology diagnosis did not find tumor cells on the H&E image.
Fig. 8.
Examples of two false-negatively misclassified samples. The first sample (20 × 11 mm2) is from a grade 2, ER/PR+, HER2- IDC case. A picture of the specimen is shown at the center. (a) The MUSE image and (b) H&E image of the sample. A small portion of tissue indicated by the dashed line on the right side in (a) was lost during the formalin-fixed paraffin-embedded (FFPE) process. Therefore, this area is not reflected on the H&E image in (b). The patient had received neoadjuvant therapy and a tumor cellularity of 5% following therapy was reported. (c) Zoomed-in area enclosed by blue boxes shows sparse cell nuclei in dense fibrosis tissue. (d) Zoomed-in area enclosed by black boxes shows slightly higher nuclei density. The second sample (12.5 × 12 mm2) is from a grade 2, ER/PR+, HER2- ILC case. A picture of the specimen is shown at the lower right corner. (e) The MUSE image and (f) H&E image of the sample.
Fig. 9.
A false positively misclassified sample (∼10 × 7 mm2 size). The MUSE image in (a) and the H&E image in (b) exhibit much hemosiderin and fibrosis, which usually exists in the track of a biopsy. A picture of the specimen is shown at the upper right position of (a). Areas with the highest concentration of hemosiderin are enclosed by dashed lines in both (a) and (b). Zoomed-in details of the region highlighted by the red boxes are displayed at the lower right corner in the two images. The histopathology diagnosis on (b) did not find any tumor cell.
It should be noted that there are no other treatment samples or high-hemosiderin-concentration samples imaged in this study. It is expected that a model may perform poorly on such “rare” samples due to inadequate training. Since 5-fold cross validation was utilized in this study, the patch classifiers used for the prediction of these two samples had not been trained with any similar samples. Therefore, a large sample size with an adequate number of each tissue type should decrease the odds of such misclassifications.
4.4. Limitations
There are several limitations in this study. First, the sample size is relatively small and a future study with a much larger number of samples is necessary to confirm the performance of the developed TA and classification algorithm. While the distribution among histologic subtypes in our samples reflects the natural distribution of breast cancers, the small sample size of ILC samples may impose an increased risk of biased sampling in real ILC domain, which can reduce the diagnostic accuracy for ILC. A larger diversity of tissue types can also help to improve the robustness and accuracy of the TA algorithm in assessing less-common tissue types. Second, some bias and errors might be introduced during the dataset construction process. Most tissue samples contained mixed tissue types and the label assigned to each patch may represent a portion of the area within the patch only. For instance, a tumor patch may include some normal regions and the extracted texture features are the averages of the whole patch area. The selection of a patch size considered multiple factors, including spatial resolution, data labeling workload, and computational efficiency. Empirically, a size of 400 × 400 pixels (∼0.51 × 0.51 mm2) was selected for a reasonable compromise between good spatial sensitivity for tumor detection while preserving distinctive visual patterns of different classes for texture analysis. However, the optimal patch size is yet to be determined and better classification results may be possible. Third, the ground-truth diagnosis is interpretated by one pathologist only (JMJ). While a study by Elmore JG, et al [50]. reported a concordance of invasive breast carcinoma diagnosis of 96% (95% confidence interval: 94-97%) among pathologists, a future study involving more pathologists may reduce possible bias in the ground-truth. Finally, the performances of the TA algorithm may be improved in multiple ways. For example, the numbers of features used for analysis were pre-decided empirically. Using some validated criteria for feature selection may help in identifying the optimal feature subset for analysis. Considering the linear correlations between texture features, feature decorrelation and data whitening techniques may be employed to improve the classification performances. Moreover, the color information of images has not been explored and only the R channel was included in the analysis. In addition to these limitations, future work should also involve the acceleration of computational efficiency, particularly if multiple TA methods are used, to enhance the clinical usability of the MUSE technology and TA models for intraoperative margin detection. Patch-level classification and margin-level decision fusion are rapid. Currently, the texture feature extraction, which is the most time-consuming step in the process, takes about 13 seconds and 126 seconds per cm2 for LBP alone, and LS feature section methods, respectively. The experiment was carried out on a laptop with an AMD Ryzen 5 4600H CPU (6 cores, 12 threads, 3.0 GHz clock-speed) and 2x 16 GB dual-channel memory (DDR4 3200 MHz). It is expected that a new generation desktop CPU such as Intel Core i-7 12700 or even a graphics processing unit (GPU) will significantly reduce the computational time of the proposed approach.
5. Conclusion
Our long-term goal is to develop a MUSE imaging system to reduce the re-excision rate of BCS. In this report, we present the preliminary results of automated breast tumor detection in MUSE images of ex vivo breast surgical tissues obtained using TA methods. The proposed TA methods consist of two steps, the patch-level classification and margin-level decision fusion. At the patch-level classification step, six TA methods were utilized to extract quantitative features based on cell nuclei pattern and morphology as the tumor biomarker. Construction of feature subsets from each individual TA method, feature transformation, and feature selection were evaluated for patch-level classifier training and test. At the margin-level decision fusion step, a simple weighted majority voting strategy selects high discriminative patches from patch-level classification results and predicts the sample class as tumor or normal based on the selected patches. Experiments on 66 fresh human breast tissues showed excellent sensitivity and specificity of the proposed method for both patch-level classification and margin-level decision fusion. The results demonstrate the feasibility of automated intraoperative margin assessment by combining MUSE and the automated TA algorithm for tumor margin assessment during breast-conserving surgeries.
Acknowledgments
Authors thank the Medical College of Wisconsin Tissue Bank for providing de-identified human breast tissue specimens.
Funding
Marquette University10.13039/100012793 (Startup grant to Bing Yu); Medical College of Wisconsin10.13039/100008980 (We Care Fund); GHR Foundation10.13039/100015595.
Disclosures
The authors have no conflicts of interest to claim.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (995.3KB, pdf) for supporting content.
References
- 1.Siegel R. L., Miller K. D., Fuchs H. E., Jemal A., “Cancer statistics, 2022,” CA: Cancer J. Clin. 72, 72–77 (2022). 10.3322/caac.21708. [DOI] [PubMed] [Google Scholar]
- 2.Nash R., Goodman M., Lin C. C., Freedman R. A., Dominici L. S., Ward K., Jemal A., “State variation in the receipt of a contralateral prophylactic mastectomy among women who received a diagnosis of invasive unilateral early-stage breast cancer in the United States, 2004-2012,” JAMA Surg. 152(7), 648–657 (2017). 10.1001/jamasurg.2017.0115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wong S. M., Freedman R. A., Sagara Y., Aydogan F., Barry W. T., Golshan M., “growing use of contralateral prophylactic mastectomy despite no improvement in long-term survival for invasive breast cancer,” Ann. Surg. 265(3), 581–589 (2017). 10.1097/SLA.0000000000001698 [DOI] [PubMed] [Google Scholar]
- 4.Kummerow K. L., Du L., Penson D. F., Shyr Y., Hooks M. A., “Nationwide trends in mastectomy for early-stage breast cancer,” JAMA Surg. 150(1), 9–16 (2015). 10.1001/jamasurg.2014.2895 [DOI] [PubMed] [Google Scholar]
- 5.Kantor O., Pesce C., Kopkash K., Barrera E., Winchester D. J., Kuchta K., Yao K., “Impact of the Society of Surgical Oncology-American Society for Radiation Oncology margin guidelines on breast-conserving surgery and mastectomy trends,” J Am. Coll. Surg. 229(1), 104–114 (2019). 10.1016/j.jamcollsurg.2019.02.051 [DOI] [PubMed] [Google Scholar]
- 6.G. Early Breast Cancer Trialists’ Collaborative , Correa C., McGale P., Taylor C., Wang Y., Clarke M., Davies C., Peto R., Bijker N., Solin L., Darby S., “Overview of the randomized trials of radiotherapy in ductal carcinoma in situ of the breast,” J Natl. Cancer Inst. Monogr. 2010(41), 162–177 (2010). 10.1093/jncimonographs/lgq039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marinovich M. L., Azizi L., Macaskill P., Irwig L., Morrow M., Solin L. J., Houssami N., “The association of surgical margins and local recurrence in women with ductal carcinoma in situ treated with breast-conserving therapy: a meta-analysis,” Ann. Surg. Oncol. 23(12), 3811–3821 (2016). 10.1245/s10434-016-5446-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Donker M., Litiere S., Werutsky G., Julien J. P., Fentiman I. S., Agresti R., Rouanet P., de Lara C. T., Bartelink H., Duez N., Rutgers E. J., Bijker N., “Breast-conserving treatment with or without radiotherapy in ductal carcinoma In Situ: 15-year recurrence rates and outcome after a recurrence, from the EORTC 10853 randomized phase III trial,” J Clin. Oncol. 31(32), 4054–4059 (2013). 10.1200/JCO.2013.49.5077 [DOI] [PubMed] [Google Scholar]
- 9.Houssami N., Macaskill P., Marinovich M. L., Morrow M., “The association of surgical margins and local recurrence in women with early-stage invasive breast cancer treated with breast-conserving therapy: a meta-analysis,” Ann. Surg. Oncol. 21(3), 717–730 (2014). 10.1245/s10434-014-3480-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wazer D. E., Schmidt-Ullrich R. K., Ruthazer R., Schmid C. H., Graham R., Safaii H., Rothschild J., McGrath J., Erban J. K., “Factors determining outcome for breast-conserving irradiation with margin-directed dose escalation to the tumor bed,” Int. J Radiat. Oncol. Biol. Phys. 40(4), 851–858 (1998). 10.1016/S0360-3016(97)00861-4 [DOI] [PubMed] [Google Scholar]
- 11.Mansfield C. M., Komarnicky L. T., Schwartz G. F., Rosenberg A. L., Krishnan L., Jewell W. R., Rosato F. E., Moses M. L., Haghbin M., Taylor J., “Ten-year results in 1070 patients with stages I and II breast cancer treated by conservative surgery and radiation therapy,” Cancer 75(9), 2328–2336 (1995). [DOI] [PubMed] [Google Scholar]
- 12.King T. A., Sakr R., Patil S., Gurevich I., Stempel M., Sampson M., Morrow M., “Clinical management factors contribute to the decision for contralateral prophylactic mastectomy,” J Clin. Oncol. 29(16), 2158–2164 (2011). 10.1200/JCO.2010.29.4041 [DOI] [PubMed] [Google Scholar]
- 13.Olsen M. A., Nickel K. B., Margenthaler J. A., Wallace A. E., Mines D., Miller J. P., Fraser V. J., Warren D. K., “Increased Risk of Surgical Site Infection Among Breast-Conserving Surgery Re-excisions,” Ann. Surg. Oncol. 22(6), 2003–2009 (2015). 10.1245/s10434-014-4200-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Greenup R. A., Peppercorn J., Worni M., Hwang E. S., “Cost implications of the SSO-ASTRO consensus guideline on margins for breast-conserving surgery with whole breast irradiation in stage I and II invasive breast cancer,” Ann. Surg. Oncol. 21(5), 1512–1514 (2014). 10.1245/s10434-014-3605-x [DOI] [PubMed] [Google Scholar]
- 15.Nunez A., Jones V., Schulz-Costello K., Schmolze D., “Accuracy of gross intraoperative margin assessment for breast cancer: experience since the SSO-ASTRO margin consensus guidelines,” Sci. Rep. 10(1), 1–9 (2020). 10.1038/s41598-019-56847-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maloney B. W., McClatchy D. M., Pogue B. W., Paulsen K. D., Wells W. A., Barth R. J., “Review of methods for intraoperative margin detection for breast conserving surgery,” J Biomed. Opt. 23(10), 1–19 (2018). 10.1117/1.JBO.23.10.100901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schwarz J., Schmidt H., “Technology for intraoperative margin assessment in breast cancer,” Ann. Surg. Oncol. 27(7), 2278–2287 (2020). 10.1245/s10434-020-08483-w [DOI] [PubMed] [Google Scholar]
- 18.Fereidouni F., Harmany Z. T., Tian M., Todd A., Kintner J. A., McPherson J. D., Borowsky A. D., Bishop J., Lechpammer M., Demos S. G., Levenson R., “Microscopy with ultraviolet surface excitation for rapid slide-free histology,” Nat. Biomed. Eng. 1(12), 957–966 (2017). 10.1038/s41551-017-0165-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yoshitake T., Giacomelli M. G., Quintana L. M., Vardeh H., Cahill L. C., Faulkner-Jones B. E., Connolly J. L., Do D., Fujimoto J. G., “Rapid histopathological imaging of skin and breast cancer surgical specimens using immersion microscopy with ultraviolet surface excitation,” Sci. Rep. 8, 1–12 (2018). 10.1038/s41598-018-22264-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Xie W., Chen Y., Wang Y., Wei L., Yin C., Glaser A. K., Fauver M. E., Seibel E. J., Dintzis S. M., Vaughan J. C., “Microscopy with ultraviolet surface excitation for wide-area pathology of breast surgical margins,” J. Biomed. Opt. 24, 026501 (2019). 10.1117/1.JBO.24.2.026501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lu T., Jorns J. M., Patton M., Fisher R., Emmrich A., Doehring T., Schmidt T. G., Ye D. H., Yen T., Yu B., “Rapid assessment of breast tumor margins using deep ultraviolet fluorescence scanning microscopy,” J. Biomed. Opt. 25(12), 126501 (2020). 10.1117/1.JBO.25.12.126501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Parekh V., Jacobs M. A., “Radiomics: a new application from established techniques,” Expert Rev. Precis. Med. Drug Dev. 1(2), 207–226 (2016). 10.1080/23808993.2016.1164013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kather J. N., Weis C.-A., Bianconi F., Melchers S. M., Schad L. R., Gaiser T., Marx A., Zöllner F. G., “Multi-class texture analysis in colorectal cancer histology,” Sci. Rep. 6(1), 27988 (2016). 10.1038/srep27988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Streeter S. S., Maloney B. W., McClatchy D. M., Jermyn M., Pogue B. W., Rizzo E. J., Wells W. A., Paulsen K. D., “Structured light imaging for breast-conserving surgery, part II: texture analysis and classification,” J. Biomed. Opt. 24(09), 1 (2019). 10.1117/1.JBO.24.9.096003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wan S., Lee H.-C., Huang X., Xu T., Xu T., Zeng X., Zhang Z., Sheikine Y., Connolly J. L., Fujimoto J. G., “Integrated local binary pattern texture features for classification of breast tissue imaged by optical coherence microscopy,” Med. Image Anal. 38, 104–116 (2017). 10.1016/j.media.2017.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Leiloglou M., Chalau V., Kedrzycki M. S., Thiruchelvam P., Darzi A., Leff D. R., Elson D. S., “Tissue texture extraction in indocyanine green fluorescence imaging for breast-conserving surgery,” J. Phys. D: Appl. Phys. 54(19), 194005 (2021). 10.1088/1361-6463/abe571 [DOI] [Google Scholar]
- 27.Bevk M., Kononenko I., “A statistical approach to texture description of medical images: a preliminary study,” in Proceedings of 15th IEEE Symposium on Computer-Based Medical Systems (CBMS 2002), (IEEE, 2002), 239–244. [Google Scholar]
- 28.Galloway M. M., “Texture analysis using gray level run lengths,” Comput. graph. image process. 4(2), 172–179 (1975). 10.1016/S0146-664X(75)80008-6 [DOI] [Google Scholar]
- 29.Haralick R. M., Shanmugam K., Dinstein I. H., “Textural features for image classification,” IEEE Trans. Syst., Man, Cybern. SMC-3(6), 610–621 (1973). 10.1109/TSMC.1973.4309314 [DOI] [Google Scholar]
- 30.Fogel I., Sagi D., “Gabor filters as texture discriminator,” Biol. Cybern. 61(2), 103–113 (1989). 10.1007/BF00204594 [DOI] [Google Scholar]
- 31.Ojala T., Pietikäinen M., Harwood D., “A comparative study of texture measures with classification based on featured distributions,” Pattern recognition 29(1), 51–59 (1996). 10.1016/0031-3203(95)00067-4 [DOI] [Google Scholar]
- 32.Sarkar N., Chaudhuri B. B., “An efficient differential box-counting approach to compute fractal dimension of image,” IEEE Trans. Syst., Man, Cybern. 24(1), 115–120 (1994). 10.1109/21.259692 [DOI] [Google Scholar]
- 33.Allain C., Cloitre M., “Characterizing the lacunarity of random and deterministic fractal sets,” Phys. Rev. A 44(6), 3552–3558 (1991). 10.1103/PhysRevA.44.3552 [DOI] [PubMed] [Google Scholar]
- 34.Bishop C. M., Nasrabadi N. M., Pattern Recognition and Machine Learning (Springer, 2006), Vol. 4. [Google Scholar]
- 35.Lim J. S., “Two-dimensional signal and image processing,” Englewood Cliffs (1990).
- 36.Haralick R. M., “Statistical and structural approaches to texture,” Proc. IEEE 67(5), 786–804 (1979). 10.1109/PROC.1979.11328 [DOI] [Google Scholar]
- 37.Ojala T., Pietikainen M., Maenpaa T., “Multiresolution gray-scale and rotation invariant texture classification with local binary patterns,” IEEE Trans. Pattern Anal. Machine Intell. 24(7), 971–987 (2002). 10.1109/TPAMI.2002.1017623 [DOI] [Google Scholar]
- 38.Van der Maaten L., Hinton G., “Visualizing data using t-SNE,” Journal of Machine Learning Research 9(2605), 2579–2605 (2008). [Google Scholar]
- 39.Tang X., “Texture information in run-length matrices,” IEEE Trans. on Image Process. 7(11), 1602–1609 (1998). 10.1109/83.725367 [DOI] [PubMed] [Google Scholar]
- 40.Serre T., Wolf L., Poggio T., “Object recognition with features inspired by visual cortex,” in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05), (IEEE, 2005), 994–1000. [Google Scholar]
- 41.Dalal N., Triggs B., “Histograms of oriented gradients for human detection,” in 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR'05), (IEEE, 2005), 886–893. [Google Scholar]
- 42.Baish J. W., Jain R. K., “Fractals and cancer,” Cancer Res. 60, 3683–3688 (2000). [PubMed] [Google Scholar]
- 43.Bizzarri M., Giuliani A., Cucina A., D’Anselmi F., Soto A. M., Sonnenschein C., “Fractal analysis in a systems biology approach to cancer,” in Seminars in Cancer Biology (Elsevier, 2011), 175–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Abdi H., Williams L. J., “Principal component analysis,” WIREs Comp Stat 2(4), 433–459 (2010). 10.1002/wics.101 [DOI] [Google Scholar]
- 45.Ding C., Peng H., “Minimum redundancy feature selection from microarray gene expression data,” J. Bioinf. Comput. Biol. 03(02), 185–205 (2005). 10.1142/S0219720005001004 [DOI] [PubMed] [Google Scholar]
- 46.Kononenko I., Šimec E., Robnik-Šikonja M., “Overcoming the myopia of inductive learning algorithms with RELIEFF,” Appl. Intell. 7(1), 39–55 (1997). 10.1023/A:1008280620621 [DOI] [Google Scholar]
- 47.He X., Cai D., Niyogi P., “Laplacian score for feature selection,” Advances in Neural Information Processing Systems 18, 1 (2005). [Google Scholar]
- 48.Chawla N. V., Bowyer K. W., Hall L. O., Kegelmeyer W. P., “SMOTE: synthetic minority over-sampling technique,” J. Artif. Intell. Res. 16, 321–357 (2002). 10.1613/jair.953 [DOI] [Google Scholar]
- 49.To T., Gheshlaghi S. H., Ye D. H., “Deep learning for breast cancer classification of deep ultraviolet fluorescence images toward intra-operative margin assessment,” in The 44th IEEE Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC’22, (IEEE, 2022). [DOI] [PubMed] [Google Scholar]
- 50.Elmore J. G., Longton G. M., Carney P. A., Geller B. M., Onega T., Tosteson A. N., Nelson H. D., Pepe M. S., Allison K. H., Schnitt S. J., “Diagnostic concordance among pathologists interpreting breast biopsy specimens,” Jama 313(11), 1122–1132 (2015). 10.1001/jama.2015.1405 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.