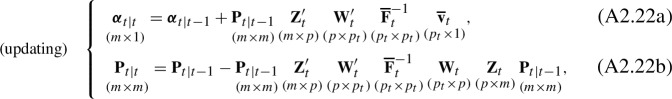Nowcasting Japan’s GDP

Abstract

This paper backtests a nowcast of Japan’s real GDP growth. It has three contributions: (i) use of genuine real-time data, (ii) implementation of a new method for the revision analysis that relates the revision of the nowcast to not only new observations but also data revisions, and (iii) a benchmarking of the nowcast to a market consensus forecast at monthly forecasting horizons. Our nowcast’s forecast accuracy is comparable to that of the consensus at most, but not all, monthly horizons. Our revision analysis of the March 2011 earthquake finds the nowcast reacting to a steep post-quake decline in car production. In contrast, the consensus hardly budged, most likely because the decline was correctly viewed as temporary. The onset of COVID-19 triggers the consensus to take a precipitous descent. The nowcast, despite timely red flags from “soft” (i.e., survey-based) indicators, does not respond immediately in full, because it took a month or more for “hard” (i.e., non-survey-based) indicators to register sharply reduced economic activities.

Introduction and summary

Many key economic variables, most notably GDP, are published with considerable delay. Inferring their current value from other indicator variables that are more frequently or more promptly observed is called nowcasting. This paper backtests a nowcast of Japan’s quarterly real GDP growth.

The literature on nowcasting for the USA, the UK, and the Euro-area countries has been surveyed by Bańbura et al. (2013) and, more recently, by Bok et al. (2018). The standard statistical model employed in the literature is the dynamic factor model. The model is particularly suitable for nowcasting because, when cast in a state-space form, it provides a natural way to handle data with mixed frequencies. Our GDP nowcast utilizes the model of Mariano and Murasawa (2003), a dynamic factor model designed for handling monthly and quarterly frequencies.

The paper has three contributions. As forcefully argued by Croushore (2011), the real-time nature of the backtest requires us to collect all past vintages of each indicator variable, which is a major undertaking because coverage of Japan by available off-the-shelf vintage sources is quite limited.1 The paper’s first contribution, relative to the literature on nowcasting Japan’s GDP (to be reviewed in Sect. 2), is that it is the first real-time backtest for Japan with a standard set of monthly and quarterly indicators, 19 in number, typically considered in the literature for other countries.2

The paper’s second contribution is that it implements an extension, recently developed by Hayashi and Tachi (2021), of the revision analysis of how a nowcast for a fixed target date evolves in time in response to various data releases and changes in the model parameters.3 A data release typically entails not only new observations of the indicator variable but also data revisions. In the existing revision analysis, only the effect of new observations can be broken down into contributions from individual variables.4 The new method allows us to do the breakdown for data revisions and parameter changes as well. This revision analysis is applied to three episodes of disasters, the Lehman crisis, the 2011 earthquake, and the COVID-19 voluntary lockdown of 2020.

The paper’s third contribution is a benchmarking of the nowcast to a market consensus forecast, which has not been done in previous studies for Japan. The consensus forecast paired with nowcasts in most US studies is quarterly, while our consensus forecast is monthly.5 Since our consensus growth forecast is for the current and subsequent quarters, it is possible to compare our nowcast of a given quarterly growth with the consensus at monthly forecasting horizons. The horizon ranges from $-1$ month when forecasts are as of 1 month after the quarter but before the “flash” (the first official estimate) released about 6 weeks after the quarter, to 11 months before the quarter’s end.

A summary of the paper’s results is as follows. Our nowcast’s RMSE (root mean squared error) is comparable to that of the consensus at most, but not all, monthly horizons. Our revision analysis of the Lehman crisis finds the GDP nowcast to be revised down substantially when a string of negative data releases brings about parameter changes. For the March 2011 earthquake, our nowcast of the 2011:Q1 to Q2 growth reacts to a steep decline in car production following the quake. In contrast, the consensus hardly budged, most likely because the decline was correctly viewed as temporary. The onset of COVID-19 triggers the consensus to take a precipitous descent. The nowcast, despite timely red flags from “soft” (i.e., survey-based) indicators, does not respond immediately in full, because it took a month or more for “hard” (i.e., non-survey-based) indicators to register sharply reduced economic activities. In all these episodes, the data-revisions effect cannot be ignored when compared to the new-observations effect for indicator variables with data revisions.

The organization of the paper is as follows. The next section is a brief survey of the literature on nowcasting Japan’s GDP. Section 3 quickly reviews the language of real-time data by an example of just two indicator variables. Section 4 reviews the Mariano and Murasawa (2003) model. Section 5 describes the real-time database that we constructed from primary sources. It is followed by an explanation of the structure of the monthly multi-horizon consensus forecast in Sect. 6. Sections 7 and 8 report our results on the multi-horizon RMSE comparison and on the revision analysis of the three disasters. Section 9 consists of a brief conclusion and an agenda for future research.

Brief review on nowcasting Japan’s GDP

There exist only a handful of papers on nowcasting Japan’s real GDP. There are two studies, Hara and Yamane (2013) and Chikamatsu et al. (2021), that use the bridge equation/MIDAS (mixed-data sampling) approach.6 The former does not conduct a backtest because forecast error calculation is in-sample, based on parameter values estimated on the full sample. The latter is not a real-time backtest either because, although the forecast error calculation is out-of-sample, the data are only “pseudo” real-time in that past vintages are assumed to be equal to the most recent vintage. This assumption is appropriate for “soft” (survey-based) indicators, but not for “hard” (non-survey-based) indicators such as GDP and IIP (the index of industrial production) whose initial values get revised in subsequent data releases.

More relevant to us are Urasawa (2014) and Bragoli (2017), both of which, like our paper, use mixed-frequency dynamic factor models. Their real-time backtests are constrained due to the limited coverage of Japan by available off-the-shelf vintage sources. The backtesting period in Urasawa (2014), 2012:Q2-2013:Q2, is very short, due most likely to the difficulty of obtaining pre-2012 vintages. The set of indicator variables consists of only six variables including real GDP.

The backtesting period in Bragoli (2017) is 2005–2015. The set of indicators for her “Model A” has 18 variables, but her model A backtest is only pseudo real-time. The variable set for her genuine real-time backtest has eleven variables, but only five of them are hard indicators. Past vintages of those variables, which she obtains from the OECD real-time database, misses a number of data releases because at most one data release per month is recorded in that database. Her benchmark forecast is not a consensus forecast by market economists; it is a model-based quarterly forecast by a private research institute.

The language of real-time data

A vintage of a variable is the time-series provided in a data release. The revision matrix of the variable is a matrix whose columns are vintages of the variable. To illustrate, Table 1 has the revision matrix for Japan’s GDP growth. Take, for example, the time series in the column labeled “2009/5/20.” It is the vintage released on that day. The reference point indicates the end-of-quarter month. For example, the March 2009 entry of $-16.49$ is the annualized quarterly GDP growth in percent from 2008:Q4 to 2009:Q1 (whose end-of-quarter month is March 2009). By construction, each row collects growth estimates for the same period from different data releases. Its first or left-most non-empty element is the “flash” (first official) estimate, indicated in italics. For example, the flash estimate of the 2008:Q4 to 2009:Q1 growth is $-16.49\%$ from the 2009/5/20 vintage.

Table 1.

Revision matrix for Japan’s GDP growth

Reference point	Vintages (data releases)
	...	2009/5/20	...	2011/5/19	...	2020/6/8	2020/8/3	2020/8/17
March 1990	...	0.61	...	$-1.91$	...	$-2.85$	$-2.85$	$-2.85$
June 1990	...	9.95	...	12.42	...	10.45	10.45	10.45
$⋮$		$⋮$		$⋮$		$⋮$	$⋮$	$⋮$
March 2009		$-16.49$	...	$-20.20$	...	$-19.61$	$-19.61$	$-19.62$
$⋮$				$⋮$		$⋮$	$⋮$	$⋮$
March 2020					...	$-2.27$	$-2.24$	$-2.49$
June 2020								$-32.56$

Annualized quarterly growth rate of seasonally adjusted real GDP in percent. That is, if t is the month indicated by the reference point, the GDP growth rate for t equals $400\times [log(Y_t)-log(Y_{t-3})]$ where $Y_t$ is the level of real GDP for the quarter whose end-of-quarter month is t. The “flash” (i.e., the first preliminary) estimates, which are released about 6 weeks after the conclusion of the quarter, are in italics

Three features of the table are noteworthy. First, Japan’s GDP estimates are revised substantially, particularly in the first two years after the initial release.7 Second, it takes about six weeks (as opposed to four for the USA) for the flash to be released. Third, the COVID-19 voluntary lockdown in the first half of 2020 has produced a jaw-dropping flash estimate, released on 2020/8/17, of $-32.56\%$ per year for June 2020.8

A real-time database is a collection of revision matrices, one for each variable in the set of indicator variables. The sample as of the vantage point v is a collection of latest vintages available as of date v for the set of variables. The sample may be of mixed frequencies. To illustrate, Table 2 shows two samples for just two indicator variables: IIP (the index of industrial production), which is monthly, and GDP, which is quarterly, for Japan.

Table 2.

Two samples from real-time data

Sample as of	July 6, 2020		August 7, 2020
Variable name	IIP	GDP	IIP	GDP
Vintage	2020/6/30	2020/6/8	2020/7/31	2020/8/3
January 1990	$-0.87$		$-0.87$
February 1990	0.87		0.87
March 1990	1.90	$-2.85$	1.90	$-2.85$
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
February 2020	$-0.30$		$-0.30$
March 2020	$-3.79$	$-2.27$	$-3.79$	$-2.24$
April 2020	$-10.33$		$-10.33$
May 2020	$-8.83$		$-9.33$
June 2020			2.63

Growth rates in percent. The GDP growth rate is an annualized quarterly growth rate, defined as 400 times the quarterly difference in logs. The IIP growth rate is the monthly growth rate, defined as 100 times the monthly difference in logs

Regarding the table’s first sample, which is as of the vantage point of July 6, 2020, and which is shortly after the end of 2020:Q2, the latest vintage of IIP is imported from the revision matrix for IIP (the IIP revision matrix not shown here). It is from a data release on 2020/6/30. For GDP, as seen from Table 1, the latest release as of July 6, 2020 is on 2020/6/8. Because GDP is quarterly, values are missing for months that are not the last month of a quarter. The second sample is as of August 7, 2020, which is about 1 month after the end of 2020:Q2. For GDP, the latest vintage is 2020/8/3.9 For IIP, it is 2020/7/31. The second sample differs from the first sample in two respects. First, there is a new observation: $2.63\%$ for IIP growth for June 2020 (from May to June 2020). Second, a data revision occurs: for IIP, the May 2020 value was revised from $-8.83\%$ in the 2020/6/30 vintage to $-9.33\%$ in the 2020/7/31 vintage; for GDP, the March 2020 value was revised from $-2.27\%$ to $-2.24\%$.

To construct a real-time database from which the sample can be derived, one needs to collect all past vintages. An alternative is pseudo real-time data, which obtains if values in all vintages are assumed to be equal to those in the latest vintage. For example, in Table 1, for each row, all values are set equal to the value in the right-most column. Therefore, provided that all past data release dates are known, a pseudo real-time database can be constructed from a single vintage. However, as forcefully argued by Croushore (2011), use of pseudo real-time data is inappropriate for real-time backtesting because the forecast is given the benefit of hindsight. This is particularly so if the forecast is to be benchmarked to market forecasts.

The Mariano–Murasawa model

This section reviews the mixed-frequency dynamic factor model of Mariano and Murasawa (2003). We start out with a refresher on state-space models because a dynamic factor model is a particular state-space model with a small number of state variables.

The canonical state-space model

The notation, with minor modifications, borrows from Durbin and Koopman (2012). There is a set of p observable variables, called the observation vector ${\mathbf{y}}_t$, which are related to m unobservable state variables assembled in the state vector ${\mathit{\alpha }}_t$, by the observation equation:10

$$\begin{array}{c}\hfill \text{(observation equation)}\underset{(p\times 1)}{{\mathbf{y}}_t}=\underset{(p\times 1)}{\mathbf{d}}+\underset{(p\times m)}{\mathbf{Z}}\underset{(m\times 1)}{{\mathit{\alpha }}_t}.\end{array}$$ 1

The state vector ${\mathit{\alpha }}_t$ obeys the state equation:

$$\begin{array}{cc}& \text{(state equation)}\underset{(m\times 1)}{{\mathit{\alpha }}_t}=\underset{(m\times m)}{\mathbf{T}}\underset{(m\times 1)}{{\mathit{\alpha }}_{t-1}}+\underset{(m\times r)}{\mathbf{R}}\underset{(r\times 1)}{{\mathit{\eta }}_t},\{{\mathit{\eta }}_t\}\text{white noise with}{\mathit{\eta }}_t\hfill \\ \hfill & \sim \mathcal{N}(\mathbf{0},\underset{(r\times r)}{\mathbf{Q}}).\hfill \end{array}$$ 2

$(\mathbf{d},\mathbf{Z},\mathbf{T},\mathbf{R},\mathbf{Q})$ are called the system matrices.

Write the sample as of the vantage point v as $({\mathbf{y}}_1,\dots ,{\mathbf{y}}_n)$ where ${\mathbf{y}}_n$ is the latest observation as of v. In Table 2 example, for $v=$ July 6, 2020, we have: $t=1$ for January 1990 and $t=n$ for May 2020. The standard apparatus of Kalman filtering and smoothing can be used to compute ${\mathit{\alpha }}_{t|n}$, defined as ${\mathit{\alpha }}_{t|n}\equiv \text{E}({\mathit{\alpha }}_t|{\mathbf{y}}_1,\dots ,{\mathbf{y}}_n)$, given the parameter value. If, as illustrated in Table 2, the sample is littered with missing values, there is a well-known procedure for accommodating them. “Appendix 2” describes the procedure and proves its validity.

With ${\{{\mathit{\alpha }}_{t|n}\}}_{t=1}^n$ in hand, we can compute the nowcast as follows. Suppose that the value of variable j for the target date t, $y_{\mathit{jt}}$, is missing. Its nowcast is the expected value of $y_{\mathit{jt}}$ conditional on the sample. Computing it involves either interpolation or extrapolation.

1. Suppose $t\le n$, so the target date t falls within the sample period. The observation equation (1) implies that the nowcast of $y_{\mathit{jt}}$ is the j-th element of $\mathbf{d}+\mathbf{Z}{\mathit{\alpha }}_{t|n}$.

2. Suppose, instead, that $t>n$. Compute ${\mathit{\alpha }}_{t|n}$ by operating on a recursion starting with ${\mathit{\alpha }}_{n|n}$. The recursion is obtained by taking the expectation, conditional on the sample, of the state equation (2):

   $$\begin{array}{c}\hfill {\mathit{\alpha }}_{s|n}=\mathbf{T}{\mathit{\alpha }}_{s-1|n},s=n+1,n+2,\dots ,t.\end{array}$$ 3

   The nowcast of $y_{\mathit{jt}}$ is again given by the j-th element of $\mathbf{d}+\mathbf{Z}{\mathit{\alpha }}_{t|n}$.

The GDP nowcast is the nowcast of $y_{\mathit{jt}}$ for j corresponding to GDP.

The Mariano–Murasawa (2003) monthly quarterly model

The Mariano–Murasawa model obtains if the system matrices of the state-space model are properly specialized. The unit time interval is a month. Assume, for now, that all indicator variables including GDP are observable monthly. The observation of the j-th variable for month t is $y_{\mathit{jt}}^{\ast }$. It is related to two unobservable common factors $(f_t^{(1)},f_t^{(2)})$ and an observation error $u_{\mathit{jt}}$ (also called the specific factor):11

$$\begin{array}{c}\hfill y_{\mathit{jt}}^{\ast }={\mu }_j^{\ast }+{\beta }_j^{(1)}{f}_t^{(1)}+{\beta }_j^{(2)}{f}_t^{(2)}+u_{\mathit{jt}},j=1,2,\dots ,p.\end{array}$$ 4

Those factors follow first-order autoregressions:

$$\begin{array}{cc}\hfill f_t^{(i)}=& {\varphi }_f^{(i)}{f}_{t-1}^{(i)}+{\zeta }_t^{(i)},i=1,2,\hfill \end{array}$$ 5

$$\begin{array}{cc}\hfill u_{\mathit{jt}}=& {\varphi }_j{u}_{j,t-1}+{\xi }_{\mathit{jt}},\text{Var}({\xi }_{\mathit{jt}})={\sigma }_j^2,j=1,2,\dots ,p.\hfill \end{array}$$ 6

The shocks to those autoregressions are jointly normally distributed, serially uncorrelated and uncorrelated with each other. Without loss of generality, the variance of the shock to the unobservable common factor, ${\zeta }_t^{(i)}$, is normalized to unity. The model parameters are:

$$\begin{array}{cc}& ({\mu }_1^{\ast },{\mu }_2^{\ast },\dots ,{\mu }_p^{\ast },{\beta }_1^{(1)},{\beta }_2^{(1)},\dots ,{\beta }_p^{(1)},{\beta }_1^{(2)},{\beta }_2^{(2)},\dots ,{\beta }_p^{(2)},{\varphi }_f^{(1)},{\varphi }_f^{(2)},\hfill \\ \hfill & {\varphi }_1,{\varphi }_2,\dots ,{\varphi }_p,{\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2).\hfill \end{array}$$

They are $5p+2$ in number. In our specification below, $p=19$, so there are 97 parameters.

Now assume that what is observable for variable j, $y_{\mathit{jt}}$, is temporally aggregated, as in

$$\begin{array}{cc}\hfill y_{\mathit{jt}}\equiv & {\omega }_{j0}{y}_{\mathit{jt}}^{\ast }+{\omega }_{j1}{y}_{j,t-1}^{\ast }+\cdots +{\omega }_{j,{\ell }_j}{y}_{j,t-{\ell }_j}^{\ast }\hfill \\ \hfill =& \sum _{s=0}^{{\ell }_j}{\omega }_{\mathit{js}}{y}_{j,t-s}^{\ast },j=1,2,\dots ,p.\hfill \end{array}$$ 7

The weights $({\omega }_{j0},\dots ,{\omega }_{j,{\ell }_j})$ can depend on the variable j. Examples include:

8

9

10

The “level” weights (9) obtain if the variable j is a quarterly variable that takes the average over the three constituent months. The “growth rate” weights (10) require some explanation. Let $y_{\mathit{jt}}^{\ast }$ be the monthly growth rate of variable j from month $t-1$ to t, and let $y_{\mathit{jt}}$ be the quarterly growth rate which is the log difference in the 3-month average of the variable from the previous 3-month period (months $t-5$, $t-4$, and $t-3$) to the current 3-month period (months $t-2$, $t-1$, and t). As Mariano and Murasawa (2003) noted, we have:

$$\begin{array}{c}\hfill y_{\mathit{jt}}\approx \frac{1}{3}{y}_{\mathit{jt}}^{\ast }+\frac{2}{3}{y}_{j,t-1}^{\ast }+y_{j,t-2}^{\ast }+\frac{2}{3}{y}_{j,t-3}^{\ast }+\frac{1}{3}{y}_{j,t-4}^{\ast },\end{array}$$ 11

with the weights as given in (10). This will be the aggregation weights for quarterly real GDP growth.

To derive the observation equation after temporal aggregation, substitute the j-th observation equation in (4) into (7) to obtain

$$\begin{array}{c}\hfill y_{\mathit{jt}}={\mu }_j+{\beta }_j^{(1)}\sum _{s=0}^{{\ell }_j}{\omega }_{\mathit{js}}{f}_{t-s}^{(1)}+{\beta }_j^{(2)}\sum _{s=0}^{{\ell }_j}{\omega }_{\mathit{js}}{f}_{t-s}^{(2)}+\sum _{s=0}^{{\ell }_j}{\omega }_{\mathit{js}}{u}_{j,t-s},j=1,2,\dots ,p,\end{array}$$ 12

where

$$\begin{array}{c}\hfill {\mu }_j\equiv ({\omega }_{j0}+\cdots +{\omega }_{j,{\ell }_j}){\mu }_j^{\ast }.\end{array}$$ 13

This is the observation equation in the Mariano–Murasawa model. The system matrices in a state-space representation of the model are in “Appendix 1.”

The real-time database

This section is a summary description of our real-time database.12

The indicator variables

The set of indicator variables is composed of 19 monthly and quarterly variables listed in the “name” column of Table 3. It is a standard set of variables used in many nowcasting studies and followed by market participants.13 All non-survey-based (i.e., “hard”) indicators are seasonally adjusted at the source, except for two variables ($j=7,8$) which are seasonally adjusted by us. We do not include financial indicators such as stock prices and interest rates, because most nowcasting studies report their limited contribution to nowcasting performance.14

Table 3.

The indicator variables

Variable no. (j)	Name	Original unit	Trans-formation	Approx. days between end of reference period and release date
1	Monthly earnings	Index	$\mathrm{\Delta }log$	34
2	Capacity utilization	Index	$\mathrm{\Delta }$	45
3	Construction orders	Yen	$\mathrm{\Delta }log$	30
4	Housing starts	Housing units	$\mathrm{\Delta }log$	30
5	Machinery orders	Yen	$\mathrm{\Delta }log$	42
6	Unemployment	#persons	$\mathrm{\Delta }$	29
7	Passenger car production	#vehicles	$\mathrm{\Delta }log$	29
8	Vehicle sales	#vehicles	$\mathrm{\Delta }log$	2
9	Exports	Yen	$\mathrm{\Delta }log$	21
10	Imports	Yen	$\mathrm{\Delta }log$	21
11	IIP (Index of Industrial Production)	Index	$\mathrm{\Delta }log$	29
12	Tertiary Industry Index	Index	$\mathrm{\Delta }log$	45
13	Retail Sales Index	Index	$\mathrm{\Delta }log$	29
14	Economy Watchers’ Survey	Index	$\mathrm{\Delta }$	9
15	Local Business Outlook Survey	Index	$\mathrm{\Delta }$	$-$ 1
16	Consumer Confidence Survey	Index	$\mathrm{\Delta }$	8
17	Tankan Survey	Index	$\mathrm{\Delta }$	$-$ 3
18	Large Firms Survey	Index	None	$-$ 17
19	Real GDP	Constant yen	$\mathrm{\Delta }log$	46

The frequency is monthly for the first 16 indicators ($j=1,2,\dots ,16$) and quarterly for $j=17,18,19$. The last column reports the publication lag in days between the end of the reference period and the time of the first data release. It can be negative if the data release occurs before the end of the reference period. For example, the result of the Tankan survey for the fourth quarter is released in mid-December

The set includes five “soft” indicators derived from surveys ($j=14,\dots ,18$). They are diffusion indices about business conditions.15 We follow the suggestion of Vermeulen (2012) to take the logistic transformation of these diffusion indexes.16 Respondents for the Economy Watchers’ Survey ($j=14$) and the Consumer Confidence Survey ($j=16$) are individuals. The Tankan Survey ($j=17$) covers a wide cross section of firms. For the Local Business Outlook survey ($j=15$) and the Large Firms Survey ($j=18$), the respondents are small-to-medium sized firms in the former survey and large firms in the latter. It is reasonably clear from the questionnaire that the Tankan survey is about the level of business conditions while the Large Firms Survey is about the change.

Many of the indicators appear to have trends. Following most other nowcasting studies, we take the first difference (or the first log difference as the case may be) for those indicators. The “transformation” column of Table 3 shows how we transformed the original monthly and quarterly time series before feeding them to the Mariano–Murasawa dynamic factor model. In particular, the real GDP growth rate is a log difference.

The last column reports the publication lag in days between the end of the reference period and the time of the first data release. For all monthly indicators, the publication lag is shorter than that for GDP of 46 days.

Temporal aggregation weights

The set of indicators includes three quarterly variables ($j=17,18,19$). We need to specify the vector of aggregation weights $({\omega }_{j0},\dots ,{\omega }_{j,{\ell }_j})$, defined in (7), that converts underlying monthly values into quarterly values.

• We have already indicated in Sect. 4.2 that the weights for real GDP ($j=19$), which aggregates monthly growth rates to quarterly growth rates, should be the “growth rate” weights (10).

• The weights for the Large Firms Survey ($j=18$) should be the same as those for real GDP, because the “change” in the questionnaire refers to the change from the previous quarter to the current quarter.

• Regarding the Tankan survey ($j=17$), we interpret “the current business condition” in the questionnaire to be about the current month.17 So if we take the first difference in Tankan’s (quarterly) diffusion index, it is a 3-month change from the previous survey. Since a 3-month change (stated at a monthly rate) is the average of the most recent three successive monthly changes, the “level” weights are appropriate.

The ESP forecast

As the benchmark forecast against which our nowcast is made to compete, we consider the ESP forecast, a monthly market consensus forecast compiled by the JCER (Japan Center for Economic Research).18 It is a survey that solicits approximately forty prominent professional forecasters for their forecasts of quarterly GDP growth and other macro variables over several successive quarters. The respondents are required to turn in their forecasts early in the month. The JCER then publishes the mean forecast in their monthly report.

The structure of the monthly ESP survey can be seen from Table 4. Forecasts of current and subsequent GDP growth at given points in time are in the columns of the table. For example, look at the column corresponding to the May 2020 report whose survey deadline is May 11, 2020. Its March 2020 entry of $-4.74\%$ is the ESP consensus forecast, as of May 11, of the annualized real GDP growth from 2019:Q4 to 2020:Q1 (whose end-of-quarter month is March 2020). It is the last forecast for March 2020 before the flash (first official estimate) was released on 2020/5/18. The June 2020 entry of $-23.99\%$ is the consensus forecast, formed on May 11, of the 2020:Q1 to Q2 growth. The other entries of the column are longer-horizon forecasts formed on the same date.

Table 4.

Real GDP growth forecasts in the ESP survey

End-of-quarter month	Deadline for professional forecasters
	Feb. 5, 2020	Mar. 10, 2020	Apr. 8, 2020	May 11, 2020	June 11, 2020	July 6, 2020	Aug. 7, 2020
December 2019	$-4.13$
March 2020	0.33	$-2.93$	$-4.14$	$-4.74$
June 2020	1.53	2.28	$-11.74$	$-23.99$	$-26.16$	$-26.83$	$-30.91$
September 2020	1.49	2.86	4.98	7.92	8.66	8.99	12.45
December 2020	0.64	0.97	3.83	5.27	4.71	4.59	4.60
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$

Annualized quarterly growth rates in percent. The source is the ESP survey published by JCER (Japan Center for Economic Research). The real GDP growth rate reported in the ESP survey is the rate of change in percent. The GDP growth rate here has been converted from the rate of change to the log difference. The conversion formula is $100\times log(1+z/100)$ where z is the ESP consensus forecast in annualized percent as originally published by JCER

The staggered structure of the ESP forecast means that each row of the table records the evolution of the forecast for a fixed target end-of-quarter month over several successive monthly horizons. Consider, for example, the 2020:Q1 to Q2 growth as the fixed target. The evolution of its nowcast is in the row for June 2020 (the ending month of 2020:Q2). The right-most entry of $-30.91\%$ is the consensus forecast, as of August 7, of the 2020:Q1 to Q2 growth (whose flash turned out to be, as shown in Table 1, the jaw-dropping $-32.56\%$ released on 2020/8/17). We say that its horizon in months is $-1$ because the vantage point, which is the survey deadline of August 7, is approximately 1 month after the conclusion of the quarter (of 2020:Q2). The entry of $-26.83\%$ to the left of it has a horizon of 0 because its vantage point of July 6 is shortly after the quarter’s end. Similarly, the forecast of $1.53\%$ in the February 2020 entry of the June 2020 row has a horizon of 5 months. This row shows that the forecasters became aware of the devastating effect of COVID-19 sometime between March 10 (whose horizon is 4 months) and April 8, 2020 (whose horizon is 3 months).

Results from multi-horizon RMSE comparison

This section reports a comparison of our nowcast with the ESP consensus forecast in terms of the root mean squared error (RMSE). For the target GDP growth that goes into the RMSE calculation, we will consider two measures: the flash (the first official GDP estimate) and the “final” which we define as the official estimate released two years after flash. For example, as can be read off from Table 1, the flash for the 2008:Q4 to 2009:Q1 growth is $-16.49\%$ released on 2009/5/20 and the final is $-20.20\%$ released on 2011/5/19.

Preliminaries

We have described in Sect. 4 how to compute our nowcast from the sample given the model parameters. We set the sample size to 20 years (240 months) in size. We follow the practice of the New York Fed Staff nowcast to revise the parameter vector at the beginning of every quarter. Parameter estimation is by maximum likelihood. See “Appendix 2” for the evaluation of the Gaussian likelihood function with missing values, and “Appendix 3” for details on the numerical optimization algorithm.

As assumed in the observation equations (4) or (12), the number of common factors is two. The information criteria of Bai and Ng (2002) for determining the number of factors is not directly applicable here because they do not accommodate mixed frequencies. Andreou et al. (2019), which allows for mixed frequencies, is not applicable either, because the aggregation weights are not the same across quarterly variables in our model. Given these constraints, we proceed as follows. We apply the $I{C}_{p1}$, $I{C}_{p2}$ and $I{C}_{p3}$ information criteria of Bai and Ng (2002) on a balanced panel of the monthly indicators ($j=1,2,\dots ,16$) listed in Table 3, with the maximum number of common factors set to 5.19 The number of common factors selected by $I{C}_{p1}$ is the maximum of 5, while the number selected by $I{C}_{p2}$ and $I{C}_{p3}$ is 1. We assume the common factors to be two in number, to allow for an additional factor that affects the three quarterly indicators ($j=17,18,19$) but not the monthly indicators ($j=1,2,\dots ,16$).

Availability of vintages determines the backtesting period for the RMSE calculation. We take the earliest GDP target end-of-quarter month to be March 2008. That is, the earliest GDP growth to forecast is from 2007:Q4 to 2008:Q1. It is an earliest time when vintage time series of most indicator variables are available. The backtesting period’s latest target end-of-quarter month is March 2020 (i.e., the latest GDP growth to forecast is from 2019:Q4 to 2020:Q1), because the final (the GDP estimate released two years after the flash) for 2020:Q2 is not yet available at this time of writing (of June 2022).

We define the RMSE for forecasting horizon k as

$$\begin{array}{cc}\hfill RMS{E}_k\equiv & \sqrt{\frac{1}{\#\mathcal{R}}\sum _{t\in \mathcal{R}}{(y_t-{\widehat{y}}_{t|v_k(t)})}^2},\hfill \\ \hfill \mathcal{R}\equiv & \{\text{March 2008},\text{June 2008},\dots ,\text{March 2020}\},\hfill \end{array}$$ 14

where $\mathcal{R}$, a collection of target end-of-quarter months, is the backtesting period, “$\#\mathcal{R}$” is the cardinality (the number of elements) of $\mathcal{R}$ (which is 49), $y_t$ is the target quarterly real GDP growth to forecast for the quarter ending in month t, ${\widehat{y}}_{t|v}$ is the forecast (be it the nowcast or the ESP consensus forecast) of $y_t$ as of vantage point v, and $v_k(t)$ is the vantage point whose horizon relative to t is about k months (so ${\widehat{y}}_{t|v_k(t)}$ is the k-month ahead forecast of $y_t$). This $v_k(t)$ is taken from the ESP survey. For example, as seen from Table 4’s row for $t=$ June 2020 (corresponding to the 2020:Q1 to Q2 growth), we have $v_k(t)$ = August 7 if $k=-1$, July 6 if $k=0$, and February 5 if $k=5$.20

Accuracy comparison of our nowcast with the consensus at short horizons

Table 5 reports the RMSE given by (14) at short horizons, $k=0$ (shortly after the conclusion of the quarter) and $k=-1$ (1 month after), for our nowcast and the ESP consensus forecast. The first two columns of numbers show that, when the GDP growth measure $y_t$ is the final, our nowcast slightly outperforms (i.e., the RMSE is smaller than) the consensus at $k=0$ but not at $k=-1$. However, as the Diebold-Mariano (Diebold and Mariano (1995)) t-value indicates, the difference is not statistically significant.

Table 5.

RMSE comparison, nowcast versus consensus

Backtesting period ($\mathcal{R}$)	Pre-COVID $\mathcal{R}=${March 2008,..., March 2020}				COVID $\mathcal{R}=${June 2020,..., March 2022}
GDP growth measure	Final		Flash		Flash
Horizon (k)	$k=0$	$k=-1$	$k=0$	$k=-1$	$k=0$	$k=-1$
RMSE for Nowcast	3.36	2.93	2.78	2.09	4.05	3.96
RMSE for Consensus	3.40	2.79	2.19	1.31	4.46	2.14
t-value for the difference	$-0.11$	0.40	1.65	2.78	–	–

The RMSE calculated by (14) where the target real GDP growth ($y_t$) is an annualized log difference in percent. That is, $y_t\equiv 400\times [log(Y_t)-log(Y_{t-3})]$ where $Y_t$ is the level of real GDP for the quarter whose ending month is t. The GDP growth measure is either the “flash” (the first preliminary estimate released by the Cabinet Office about 6 weeks after the conclusion of the ending quarter) or the “final” (the revised GDP estimate released 2 years after the flash). “Nowcast” refers to our dynamic factor model-based nowcast of real GDP growth. “Consensus” refers to the ESP consensus forecast. For both the ESP forecast and the GDP release by the Cabinet Office, the growth rate is the annualized rate of change by the formula $100\times \left[{\left(\frac{Y_t}{Y_{t-3}}\right)}^4,-,1\right]$. To be consistent with how $y_t$ is defined, we convert the annualized rate of change to the annualized log difference in percent. The conversion formula is $100\times log(1+z/100)$ where z is the annualized rate of change in percent. The estimate of the long-run variance, which is needed to calculate the Diebold–Mariano (Diebold and Mariano 1995) t statistic, includes up to third-order autocovariances. The Mariano–Diebold t statistic is not reported for the COVID period because of the small sample size

As the middle columns of the table show, the consensus forecast beats the nowcast when the GDP growth measure is the flash. At the shortest horizon ($k=-1$), the difference is statistically significant. A possible explanation of the consensus’s superiority is that it is optimized to the flash.21 Shortly after the end of the quarter, it may be possible for the professional forecasters to guess the government’s preliminary estimate of the underlying demand components of GDP that would go into the official calculation of the flash. This is particularly true for $k=-1$. Consider, for example, a Q1 to Q2 growth. As illustrated in Table 2, the vantage point with $k=-1$ is in early August, slightly more than a month after the last month (June) of the ending quarter but before the release of the flash (thanks to the six-week lag). By then, for a large number of key monthly indicators in addition to those in our set of indicators, their June values are already out. Those additional indicators may be useful at $k=-1$.22

We note in passing that GDP nowcasting for Japan exhibits less forecast accuracy than reported elsewhere for the USA and the Euro Area. Our nowcast’s RMSE for the final GDP growth measure at the shortest horizon ($k=-1$) is $2.93\%$ per year, or $0.73\%$ per quarter. The target real GDP measure in the real-time backtesting for the USA in Bańbura et al. (2013) is the most recent revision, similar to our “final” measure here. Their RMSE, if the vantage point is in the middle of the first month following the end of the quarter, is about $0.5\%$ per quarter. The RMSE for Euro Area GDP in Table V of Bańbura and Modugno (2014) for a similar vantage point is, somewhat puzzlingly, as low as $0.2\%$.23 In contrast, the RMSE for Japan’s real GDP growth in Bragoli (2017) is slightly higher than ours, about $0.8\%$ per quarter (which can be read off from her Figure 2).

The backtesting period (the $\mathcal{R}$ in (14)) does not include the COVID-19 end-of-quarter months from June 2020 on because for those months the “final” GDP growth estimate is not yet available at this time of writing (of June 2022). However, the “flash” is available for those months. The last two columns of Table 5 contain the RMSE comparison if the backtesting period is composed of end-of-quarter target months from June 2020 through March 2022. Not surprisingly, the forecast accuracy is relatively poor under COVID. As in the pre-COVID backtesting period, the consensus forecast is significantly more accurate at the shortest horizon ($k=-1$), but somewhat surprisingly, our nowcast outperforms the consensus at $k=0$.

RMSE comparison at longer horizons

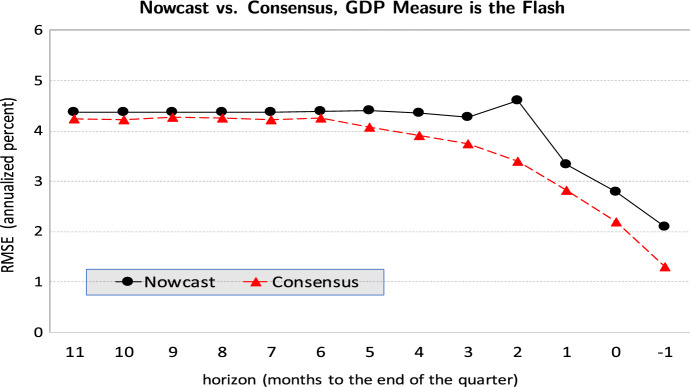
Figure 1 shows the RMSE profile (the plot of $RMS{E}_k$ against horizons $k=-1,0,1,\dots ,11$) for our nowcast and the consensus forecast. The measure of the target real GDP growth $y_t$ is the final here. Two notable features about the figure are:

• For the consensus forecast, the forecast accuracy as measured by RMSE steadily improves as horizon k gets shorter. That is, the RMSE profile is monotonically declining. This is what one would expect.

• The forecast accuracy of our nowcast is about as good as that of the consensus forecast at most monthly horizons, except at $k=2$ and $k=3$ where the profile has a hump.

To anticipate, the revision analysis of the next section will show that the hump is largely due to the nowcast’s large forecast error for the 2011:Q1 to Q2 target growth made during the days ensuing the March 2011 earthquake.

Fig. 1.

Nowcast versus consensus, GDP measure is the final. Notes: The RMSE calculated by (14) where the target real GDP growth ($y_t$) is an annualized log difference in percent. That is, $y_t\equiv 400\times [log(Y_t)-log(Y_{t-3})]$ where $Y_t$ is the level of real GDP for the quarter whose end-of-quarter month is t. The measure of GDP growth is the “final” (the revised GDP estimate released 2 years after the “flash” (the first official estimate) which in turn is released about 6 weeks after the end of the quarter). “Nowcast” refers to our dynamic factor model-based nowcast of real GDP growth. “Consensus” refers to the ESP consensus forecast. For both the ESP forecast and the GDP release by the Cabinet Office, the growth rate is the annualized rate of change by the formula $100\times \left[{\left(\frac{Y_t}{Y_{t-3}}\right)}^4,-,1\right]$. To be consistent with how $y_t$ is defined, we convert the annualized rate of change to the annualized log difference in percent. The conversion formula is $100\times log(1+z/100)$ where z is the annualized rate of change in percent

The next figure (Fig. 2) differs from Fig. 1 in that the measure of the target GDP growth is the flash rather than the final. Reflecting the fact that revisions subsequent to the flash are large for Japan, the RMSE is substantially lower for both forecasts and for all horizons. The profile for the consensus lies significantly below that for the nowcast at the short end of the horizon, the fact we already noted for Table 5.

Fig. 2.

Nowcast versus consensus, GDP measure is the flash. Notes: The RMSE calculated by (14) where the measure of the target real GDP growth ($y_t$) is the “flash” (the first preliminary estimate released about 6 weeks after the end of the ending quarter). See footnote to Fig. 1 for how the growth rate is calculated

A revision analysis of three disasters

In the revision analysis, the interest is how the nowcast ${\widehat{y}}_{t|v}$ of the target variable $y_t$ for a fixed given target end-of-quarter month t evolves as the vantage point v progresses in time. This section carries out the revision analysis for three choices of the target month t associated with three disasters: the Lehman crisis, the March 2011 earthquake and the ensuing Fukushima Daiichi nuclear disaster, and the COVID-19 voluntary lockdown of 2020.

The new-observations and data-revisions effects in the revision analysis

The nowcast ${\widehat{y}}_{t|v}$ is a function of the sample as of v and the parameter vector. Consider an interval $(v^{\prime },v^{\prime \prime }]$ defined by two successive vantage points $v^{\prime }$ and $v^{\prime \prime }$. Since, as illustrated in Table 2, new observations and data revisions constitute the difference in the sample between the two endpoints $v^{\prime }$ and $v^{\prime \prime }$ of the interval, the nowcast change over the interval, ${\widehat{y}}_{t|v^{\prime \prime }}-{\widehat{y}}_{t|v^{\prime }}$, is composed of three effects: the new-observations, data-revisions, and parameter-revisions effects. In the existing revision analysis, only the new-observations effect is broken down into contributions from individual indicator variables. The method of Hayashi and Tachi (2021) allows one to break down the other two effects as well.24

In the revision analysis below, we follow the practice of using a bar graph to show a breakdown. That is, for each interval $(v^{\prime },v^{\prime \prime }]$, the height of the bar equals ${\widehat{y}}_{t|v^{\prime \prime }}-{\widehat{y}}_{t|v^{\prime }}$. The bar is made up of segments representing the breakdown. To prevent the bar graph from becoming exceedingly cluttered, we aggregate the set of indicator variables into two groups: “hard” variables ($j=1,2,\dots ,13,19$, see Table 3 for the identity of those variables) and “soft” (i.e., survey-based) variables ($j=14,\dots ,18$). The contribution from the hard variables as a whole will be divided between the new-observations and data-revisions effects. For the soft variables, the data-revisions effect should be zero or close to zero because surveys involve no data revisions (except for occasional seasonal re-adjustment due to increased lengths of each vintage). For this reason, we won’t make the new-observations vs data-revisions distinction for the soft variables. We could, but will not, break down the parameter-revisions effect to maintain the readability of the bar graph. Therefore, the bar will have a 4-way makeup, consisting of four segments to be labeled as: “Hard, new observations,” “Hard, data revisions,” “Soft,” and “Parameter revisions.”25

The Lehman crisis

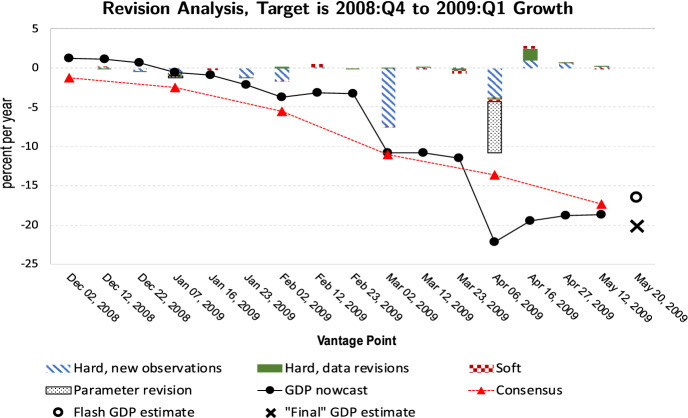
The first episode for our revision analysis is the Lehman crisis. We take the fixed target end-of-quarter month t to be March 2009 (so the target growth $y_t$ is from 2008:Q4 to 2009:Q1) when the real GDP growth registered the (then) postwar low.

Figure 3 displays the result. The hollow circle and the “x” at the right of the figure are the two measures of target GDP growth, the flash (released on 2009/5/20) and the final (released two years later, on 2011/5/19). Their difference is large: the flash was $-16.49\%$ per year which was revised down to $-20.20\%$ in two years. The filled-in circle tracks the evolution of the nowcast ${\widehat{y}}_{t|v}$ as the vantage point v proceeds in time. We consider 16 vantage points varying from $v=$ December 2, 2008 to $v=$ May 12, 2009, forming 15 intervals. Each interval is about 10 days wide. Included in those vantage points are monthly ESP vantage points. The filled-in triangle tracks the evolution of the consensus over those ESP vantage points.

Fig. 3.

Revision analysis, target is 2008:Q4 to 2009:Q1 growth. Notes: The target real GDP growth is from 2008:Q4 to 2009:Q1. The growth rate is annualized and is defined as 400 times the quarterly log difference. The two measures of the target GDP growth—the “flash” (i.e., the first preliminary estimate) and the “final” (the revised estimate 2 years after the flash)—are shown at the right of the figure. “Nowcast” refers to our dynamic factor model-based nowcast of the real GDP growth. The height of a bar in the bar graph equals the change in the nowcast from the previous vantage point to the current. Each bar is divided into four segments. The “Hard, new observations” segment measures the new-observations effect from the “hard” (non-survey-based) variables as a whole. The “Hard, data revisions” is the data-revisions effect from the “hard” variables as a whole. “Soft” is the sum of the new-observations and data-revisions effects from the five survey-based indicators. “Parameter revision” is the parameter-revisions effect through all 19 indicator variables. “Consensus” refers to the ESP forecast converted to log differences. The conversion formula is $100\times log(1+z/100)$ where z is the annualized rate of change in percent as reported in the ESP report

A notable feature of Fig. 3 is the sharp downward revision of the nowcast ${\widehat{y}}_{t|v}$ at $v=$ April 6, 2009. The makeup of the bar for the interval from March 23 to April 6 shows that the major contributor is the parameter revision on April 1, 2009. Many monthly indicators as of April 1 show negative growth over several consecutive months since the end of the previous year. Having seen this, our dynamic factor model decides that the underlying common factors must have been negative and persistent with no turnarounds during 2009:Q1.26 The newly found persistence in the common factors forces the model to lower the nowcast of the 2008:Q4 to 2009:Q1 growth. However, at the shortest end of the horizon (at $k=-1$ or $v=$ May 12), the nowcast almost matches the consensus, as data releases after April 6 start reporting positive changes.

The data-revisions effect represented by the “Hard, data revisions” segment is relatively minor, except at the April 6 to April 16 interval. Over this interval, there were data releases on Capacity Utilization and IIP with substantial data revisions.

The earthquake of March 11, 2011

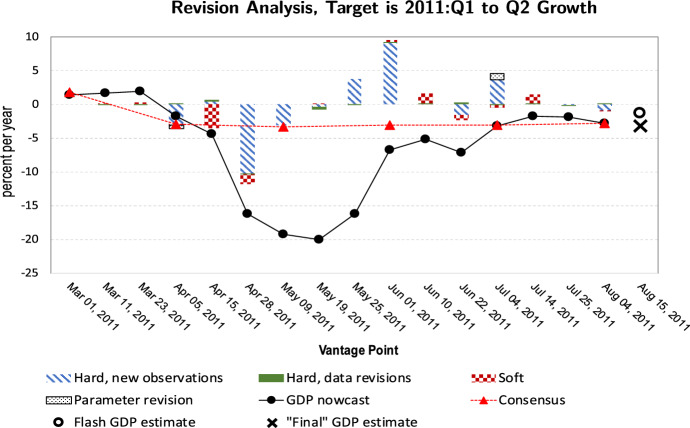
The next figure (Fig. 4) covers the earthquake of March 11, 2011, and the ensuing nuclear accident at the Fukushima Daiichi. The target growth $y_t$ is from 2011:Q1 to Q2, or $t=$ June 2011.

Fig. 4.

Revision analysis, target is 2011:Q1 to Q2 growth. Notes: The target real GDP growth is from 2011:Q1 to Q2. See note to Fig. 3 for other details

The figure’s striking feature is the nowcast’s large U-shaped movement. As can be seen from the 4-way makeup of the bars between April 28 and June 1, 2011, the main driver is the hard indicator variables. This segment during this period was dominated by data releases on IIP and Passenger Car Production that report sharp February to March drops and quick rebounds for April. For example, Passenger Car Production showed a February to March decline of $62\%$ (according to the 2011/4/28 release) followed by a $40\%$ increase from March to April (according to the 2011/5/31 release).

The gyration for automobile-related indicators is widely attributed to the well-publicized disruption of the domestic supply chain. The same is probably true for many other components of IIP. The nowcast, unaware that the gyration was a responses to the temporary shock due to the earthquake, obliges by fully responding to it. In contrast, the consensus hardly budged, most likely because the forecasters dismissed those monthly movements as temporary, with no implication for the second-quarter GDP. However, as in the Lehman episode, with subsequent data releases of positive changes coming in, the nowcast caught up with the consensus at short horizons.

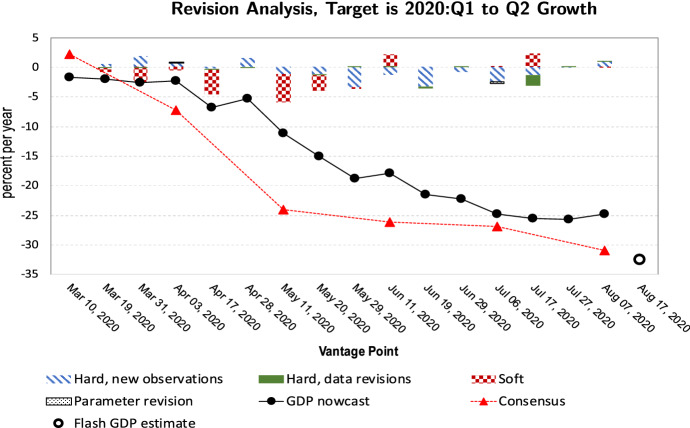
The COVID-19 voluntary lockdown of 2020

The residents in Japan were requested (but not required) to stay home during the second quarter of 2020. The flash estimate of the 2020:Q1 to Q2 growth was, as seen from Table 1, the jaw-dropping $-32.56\%$ per year. Figure 5 shows that while both the nowcast and the consensus took a precipitous fall, the nowcast lagged behind. As seen from the “Soft” segment of the bar graph, the soft indicators provided timely red flags, but the nowcast failed to respond in full because it took a month or more for the hard indicators to reflect the devastating impact of the lockdown.27 In particular, for the interval from March 19 to March 31, the negative effect from the soft variables is nearly offset by the hard variables. This is mainly due to the IIP release on 2020/3/31 reporting a positive change from January to February. However, as in the earlier two episodes, the nowcast started narrowing the difference with the consensus, this time because the hard indicators ceased sending conflicting signs.

Fig. 5.

Revision analysis, target is 2020:Q1 to Q2 growth. Notes: The “final” GDP estimate, to be released in August 2022, is not yet available at the time of this writing

At the shortest horizon ($k=-1$ or at $v=$ August 7, 2020), the consensus’s forecast error is smaller than the nowcast’s if the GDP growth measure is the flash. It is possible, however, that the consensus’s superiority will vanish if the growth measure is the final (to be released in August 2022).

The mean data-revisions effect

The “Hard, data revisions” segment of the bar graph gets thin if data revisions are infrequent for many of the hard variables. To adjust for the dilution due to the infrequency, we here consider, for each hard variable, the mean data-revisions effect, defined as the absolute value of the data-revisions effect averaged over those intervals where there is a data revision for the variable.28 Define the mean new-observations effect similarly. Table 6 displays the ratio of the mean data-revisions effect to the mean new-observations effect. The entry “n.a.” indicates that there are no data revisions in any of the 15 intervals of the episode.

Table 6.

The mean data-revisions effect for “Hard” variables

Variable name	Episodes
	Lehman crisis, target growth is 2008:Q4 to 2009:Q1	March 2011 quake, target growth is 2011:Q1 to Q2	COVID lockdown, target growth is 2020:Q1 to Q2
Monthly earnings	0.25	0.06	0.15
Capacity utilization	1.96	0.15	0.33
Construction orders	0.09	n.a.	n.a.
Housing starts	n.a.	n.a.	n.a.
Machinery orders	0.00	0.66	0.04
Unemployment	0.30	0.04	n.a.
Passenger car production	0.03	0.00	0.04
Vehicle sales	0.38	n.a.	n.a.
Exports	0.00	0.01	0.01
Imports	0.01	0.00	0.01
IIP	0.05	0.05	0.10
Tertiary Industry Index	0.11	0.11	0.38
Retail Sales Index	0.34	0.11	0.05
Real GDP	6.47	0.39	0.11

The ratio of the mean data-revisions effect to the mean new-observations effect. The mean data-revisions effect is defined as the mean absolute value of the data-revisions effect conditional on data revisions (see footnote 28 for a precise definition). The mean new-observations effect is defined similarly, as the mean absolute value of the new-observations effect conditional on new observations

The takeaway from the table is that the data-revisions effect cannot be ignored for GDP, Capacity Utilization, and other staple indicators. It can even be a dominant factor. The ratio for GDP for the Lehman crisis means the data-revisions effect is 6.47 times as large as the new-observations effect. The 15 intervals for this episode covers the period from December 2, 2008, to May 12, 2009 (see Fig. 3). There are three GDP releases during this period. One of them (released on 2009/2/16) has a flash estimate (for December 2008, or the 2008:Q3 to Q4 growth) and all three of them include quite substantial data revisions.

Concluding remarks

Our conclusion is that the model-based nowcasting is a useful complement to market forecasts. Thanks to its transparency and daily updatability, it provides a real-time stringent check on existing forecasts. The check is stringent because our nowcast performs as well as the market consensus at most forecasting horizons. It is true that the consensus is a better predictor of the flash GDP growth estimate at very short horizons, but we find it significant that the consensus’s advantage disappears after a series of revisions about GDP.

The results from our revision analysis of the three disasters point to various directions along which the nowcast’s performance might be improved.

• Since Bańbura et al. (2013), which found higher frequency indicators not helping to improve forecast accuracy, most nowcasting studies, including ours, chose the unit time interval to be a month. Our nowcast’s delayed response to the onset of COVID, shown in Fig. 5, should be mitigated if higher-frequency indicators (such as the Japanese equivalent of the weekly initial claims data from the U.S. Bureau of Labor Statistics) or even their monthly aggregates are included.

• Our nowcast’s over-reaction to the gyration in car production in the aftermath of the March 2011 earthquake arises because our dynamic factor model is linear. Very recently, several studies for the US GDP and the Euro-area GDP have shown that nowcasting performance improves if the model incorporates nonlinearities such as the stochastic volatility, Markov regime switching, fat tails, or combinations thereof.29 Our nowcast’s over-reaction would not have occurred if the model assumed the specific factor for car production to be more volatile or less persistent during the crisis. It remains an open question whether those nonlinearities can trick the model into behaving this way.

• The large and concentrated parameter-revisions effect, shown in Fig. 3, would not have occurred and the nowcast’s evolution would have been less jagged with Markov switching and perhaps with the stochastic volatility.

Extending the dynamic factor model along these lines is left for future research.

Appendix 1. System matrices with temporal aggregation

In this appendix, we represent the temporally aggregated Mariano–Murasawa model as the state-space model (1) and (2) by choosing the system matrices appropriately.

Because the common factor appears in all observation equations, it is useful to define ${\tilde{\mathit{\omega }}}_j$, whose length doesn’t depend on j, as

$$\begin{array}{c}\hfill \underset{1+{\ell }_{max}\text{elements}}{\underbrace{{\tilde{\mathit{\omega }}}_j^{\prime }}}\equiv (\underset{1+{\ell }_j\text{elements}}{\underbrace{{\mathit{\omega }}_j^{\prime }}},\underset{{\ell }_{max}-{\ell }_j\text{elements}}{\underbrace{0,\dots ,0}}),{\ell }_{max}\equiv max\{{\ell }_1,\dots ,{\ell }_p\}.\end{array}$$ A1.1

Then, (12) can be rewritten as

$$\begin{array}{cc}\hfill y_{\mathit{jt}}& ={\mu }_j+{\beta }_j^{(1)}{\tilde{\mathit{\omega }}}_j^{\prime }\left[\begin{array}{c}{f}_t^{(1)}\\ f_{t-1}^{(1)}\\ ⋮\\ f_{t-{\ell }_{max}}^{(1)}\end{array}\right]+{\beta }_j^{(2)}{\tilde{\mathit{\omega }}}_j^{\prime }\left[\begin{array}{c}{f}_t^{(2)}\\ f_{t-1}^{(2)}\\ ⋮\\ f_{t-{\ell }_{max}}^{(2)}\end{array}\right]+{\mathit{\omega }}_j^{\prime }\left[\begin{array}{c}{u}_{\mathit{jt}}\\ u_{j,t-1}\\ ⋮\\ u_{j,t-{\ell }_j}\end{array}\right]\hfill \\ \hfill & ={\mu }_j+{\beta }_j^{(1)}{\tilde{\mathit{\omega }}}_j^{\prime }{\mathbf{f}}_t^{(1)}+{\beta }_j^{(2)}{\tilde{\mathit{\omega }}}_j^{\prime }{\mathbf{f}}_t^{(2)}+{\mathit{\omega }}_j^{\prime }{\mathbf{u}}_t^{(j)},j=1,2,\dots ,p,\hfill \end{array}$$ A1.2

where

$$\begin{array}{c}\hfill \underset{((1+{\ell }_{max})\times 1)}{{\mathbf{f}}_t^{(1)}}\equiv \left[\begin{array}{c}{f}_t^{(1)}\\ f_{t-1}^{(1)}\\ ⋮\\ f_{t-{\ell }_{max}}^{(1)}\end{array}\right],\underset{((1+{\ell }_{max})\times 1)}{{\mathbf{f}}_t^{(2)}}\equiv \left[\begin{array}{c}{f}_t^{(2)}\\ f_{t-1}^{(2)}\\ ⋮\\ f_{t-{\ell }_{max}}^{(2)}\end{array}\right],\underset{((1+{\ell }_j)\times 1)}{{\mathbf{u}}_t^{(j)}}\equiv \left[\begin{array}{c}{u}_{\mathit{jt}}\\ u_{j,t-1}\\ ⋮\\ u_{j,t-{\ell }_j}\end{array}\right].\end{array}$$ A1.3

The model can be represented as the state-space model (1) and (2). The m, the ${\mathit{\alpha }}_t$, the r, and the ${\mathit{\eta }}_t$ are

$$\begin{array}{c}\hfill m=2(1+{\ell }_{max})+\sum _{j=1}^p(1+{\ell }_j),\underset{(m\times 1)}{{\mathit{\alpha }}_t}\equiv \left[\begin{array}{c}{\mathbf{f}}_t^{(1)}\\ {\mathbf{f}}_t^{(2)}\\ {\mathbf{u}}_t^{(1)}\\ {\mathbf{u}}_t^{(2)}\\ ⋮\\ {\mathbf{u}}_t^{(p)}\end{array}\right],r=2+p,\underset{(r\times 1)}{{\mathit{\eta }}_t}\equiv \left[\begin{array}{c}{\zeta }_t^{(1)}\\ {\zeta }_t^{(2)}\\ \underset{(p\times 1)}{{\mathit{\xi }}_t}\end{array}\right].\\ \hfill \end{array}$$ A1.4

The system matrices are as follows. Start with the observation equations (1). We can write the p temporally aggregated equations (A1.2) as (1) if we choose

$$\begin{array}{c}\hfill \underset{(p\times 1)}{\mathbf{d}}\equiv \left[\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ⋮\\ {\mu }_p\end{array}\right],\underset{(p\times m)}{\mathbf{Z}}\equiv \left[\begin{array}{cc}\underset{(p\times 2(1+{\ell }_{max}))}{\underbrace{\begin{array}{c}({\beta }_1^{(1)},{\beta }_1^{(2)})\otimes {\tilde{\mathit{\omega }}}_1^{\prime }\\ ({\beta }_2^{(1)},{\beta }_2^{(2)})\otimes {\tilde{\mathit{\omega }}}_2^{\prime }\\ ⋮\\ ({\beta }_p^{(1)},{\beta }_p^{(2)})\otimes {\tilde{\mathit{\omega }}}_p^{\prime }\end{array}}}& \begin{array}{c}\underset{(p\times {\sum }_{j=1}^p(1+{\ell }_j))}{\underbrace{\text{diag}({\mathit{\omega }}_1^{\prime },{\mathit{\omega }}_2^{\prime },\dots ,{\mathit{\omega }}_p^{\prime })}}\end{array}\end{array}\right].\\ \hfill \end{array}$$ A1.5

Next, turn to the state equations (2). The augmented dynamics of ${\mathbf{f}}_t^{(i)}\equiv {(f_t^{(i)},\dots ,f_{t-{\ell }_{max}}^{(i)})}^{\prime }$ ($i=1,2$) implied by (5) can be written as

$$\begin{array}{c}\hfill \underset{((1+{\ell }_{max})\times 1)}{{\mathbf{f}}_t^{(i)}}=\underset{((1+{\ell }_{max})\times (1+{\ell }_{max}))}{{\mathbf{{\rm Y}}}_1({\varphi }_f^{(i)},{\ell }_{max})}\underset{((1+{\ell }_{max})\times 1)}{{\mathbf{f}}_{t-1}^{(i)}}+\begin{array}{c}\left(\left[\begin{array}{c}{\zeta }_t^{(i)}\\ 0\\ ⋮\\ 0\end{array}\right],\right\}\end{array}{\ell }_{max}\text{elements}{,}^{i=1,2,}\\ \hfill \end{array}$$ A1.6

where

$$\begin{array}{c}\hfill \underset{((1+\ell )\times (1+\ell ))}{{\mathbf{{\rm Y}}}_1(\theta ,\ell )}\equiv \left[\begin{array}{c}\underset{1+\ell \text{elements}}{\underbrace{\begin{array}{ccccc}\theta & 0& 0& \cdots & 0\end{array}}}\\ \begin{array}{ccccc}& & {\mathbf{I}}_{\ell }& & \underset{(\ell \times 1)}{\mathbf{0}}\end{array}\end{array}\right],{\mathbf{{\rm Y}}}_1(\theta ,\ell )=\theta \text{if}\ell =0.\end{array}$$ A1.7

Similarly, the augmented dynamics of ${\mathbf{u}}_t^{(j)}\equiv {(u_{\mathit{jt}},\dots ,u_{j,t-{\ell }_j})}^{\prime }$ implied by (6) can be written as

$$\begin{array}{c}\hfill \underset{((1+{\ell }_j)\times 1)}{{\mathbf{u}}_t^{(j)}}={\mathbf{{\rm Y}}}_1({\varphi }_j,{\ell }_j)\underset{((1+{\ell }_j)\times 1)}{{\mathbf{u}}_{t-1}^{(j)}}+\begin{array}{c}\left(\left[\begin{array}{c}{\xi }_{\mathit{jt}}\\ 0\\ ⋮\\ 0\end{array}\right],\right\}\end{array}{\ell }_j\text{elements}{,}^{j=1,2,\dots ,p.}\\ \hfill \end{array}$$ A1.8

Therefore, the dynamics of ${\mathit{\alpha }}_t$, which collects ${\mathbf{f}}_t^{(1)}$, ${\mathbf{f}}_t^{(2)}$, and ${\mathbf{u}}_t^{(j)}$ ($j=1,2,\dots ,p$), can be written as (2) with

$$\begin{array}{cc}\hfill \underset{(m\times m)}{\mathbf{T}}\equiv & \text{diag}(\underset{((1+{\ell }_{max})\times (1+{\ell }_{max}))}{{\mathbf{{\rm Y}}}_1({\varphi }_f^{(1)},{\ell }_{max})},\underset{((1+{\ell }_{max})\times (1+{\ell }_{max}))}{{\mathbf{{\rm Y}}}_1({\varphi }_f^{(2)},{\ell }_{max})},\underset{((1+{\ell }_1)\times (1+{\ell }_1))}{{\mathbf{{\rm Y}}}_1({\varphi }_1,{\ell }_1)},\dots ,\underset{((1+{\ell }_p)\times (1+{\ell }_p))}{{\mathbf{{\rm Y}}}_1({\varphi }_p,{\ell }_p)}),\hfill \\ \hfill r=& 2+p,\underset{(m\times r)}{\mathbf{R}}\equiv \text{diag}({\mathbf{I}}_2\otimes {\mathbf{e}}_{{\ell }_{max}},{\mathbf{e}}_{{\ell }_1},\dots ,{\mathbf{e}}_{{\ell }_p}),\underset{(r\times r)}{\mathbf{Q}}\equiv \text{diag}({\mathbf{I}}_2,{\sigma }_1^2,\dots ,{\sigma }_p^2),\hfill \\ \hfill \end{array}$$ A1.9

where

$$\begin{array}{c}\hfill \underset{((1+\ell )\times 1)}{{\mathbf{e}}_{\ell }}\equiv \begin{array}{c}\left(\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right],\right\}\end{array}\ell \text{elements.}{}^{,{\mathbf{e}}_{\ell }=1\text{if}\ell =0.}\end{array}$$ A1.10

Appendix 2. Adaptation to missing values

This appendix shows how state-space models can be modified to accommodate missing values. Standard textbooks (Section 3.4.7 of Harvey (1990) and Section 4.10 of Durbin and Koopman (2012)) provide a procedure for adapting Kalman filtering/smoothing and the likelihood function to missing values. However, (as far as we are aware) there is available no full derivation of the procedure. Mariano and Murasawa (2003) provide only a sketch of it. The description in Camacho and Perez-Quiros (2010) is more detailed, but it does not provide a proof of the validity of the procedure. This appendix provides a proof.

2.1. The case of no missing values

The material for the case of no missing values is entirely standard. We will present relevant formulas without derivation. Those formulas will be modified later on to accommodate missing values.

The state-space model is

$$\begin{array}{cc}\hfill \text{(observation equation)}\underset{(p\times 1)}{{\mathbf{y}}_t}& =\underset{(p\times 1)}{{\mathbf{d}}_t}+\underset{(p\times m)}{{\mathbf{Z}}_t}\underset{(m\times 1)}{{\mathit{\alpha }}_t}+\underset{(p\times 1)}{{\mathit{\epsilon }}_t},\{{\mathit{\epsilon }}_t\}\hfill \\ \hfill & \text{white noise with}{\mathit{\epsilon }}_t\sim \mathcal{N}(\mathbf{0},\underset{(p\times p)}{{\mathbf{H}}_t}),\hfill \end{array}$$ A2.1

$$\begin{array}{cc}\hfill \text{(state equation)}\underset{(m\times 1)}{{\mathit{\alpha }}_t}& =\underset{(m\times m)}{{\mathbf{T}}_t}\underset{(m\times 1)}{{\mathit{\alpha }}_{t-1}}+\underset{(m\times r)}{{\mathbf{R}}_t}\underset{(r\times 1)}{{\mathit{\eta }}_t},\{{\mathit{\eta }}_t\}\hfill \\ \hfill & \text{white noise with}{\mathit{\eta }}_t\sim \mathcal{N}(\mathbf{0},\underset{(r\times r)}{{\mathbf{Q}}_t}),\hfill \end{array}$$ A2.2

where ${\mathit{\epsilon }}_t$ is the vector of observation errors. The system matrices, $({\mathbf{d}}_t,{\mathbf{Z}}_t,{\mathbf{H}}_t,{\mathbf{T}}_t,{\mathbf{R}}_t,{\mathbf{Q}}_t)$, are subscripted by t to allow them to possibly depend deterministically on time. For the unobservable state vector ${\mathit{\alpha }}_t$, define its prediction ${\mathit{\alpha }}_{t|\tau }$ and its prediction error variance ${\mathbf{P}}_{t|\tau }$ as30

$$\begin{array}{cc}& \underset{(m\times 1)}{{\mathit{\alpha }}_{t|\tau }}\equiv \text{E}({\mathit{\alpha }}_t|{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{\tau })\text{so, for example,}\underset{(m\times 1)}{{\mathit{\alpha }}_{t|t-1}}\equiv \text{E}({\mathit{\alpha }}_t|{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{t-1}),\hfill \end{array}$$ A2.3

$$\begin{array}{cc}& \underset{(m\times m)}{{\mathbf{P}}_{t|\tau }}\equiv \text{Var}({\mathit{\alpha }}_t|{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{\tau })\text{so, for example,}\underset{(m\times m)}{{\mathbf{P}}_{t|t-1}}\equiv \text{Var}({\mathit{\alpha }}_t|{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{t-1}).\hfill \\ \hfill \end{array}$$ A2.4

The Kalman filtering recursion is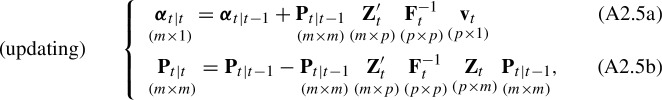

where

$$\begin{array}{cc}\hfill \underset{(p\times 1)}{{\mathbf{v}}_t}& \equiv \underset{(p\times 1)}{{\mathbf{y}}_t}-\underset{\text{one-period-ahead prediction of}{\mathbf{y}}_t}{\underbrace{({\mathbf{d}}_t+{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1}),}}\hfill \end{array}$$ A2.6

$$\begin{array}{cc}\hfill \underset{(p\times p)}{{\mathbf{F}}_t}& \equiv \underset{(p\times m)}{{\mathbf{Z}}_t}\underset{(m\times m)}{{\mathbf{P}}_{t|t-1}}\underset{(m\times p)}{{\mathbf{Z}}_t^{\prime }}+\underset{(p\times p)}{{\mathbf{H}}_t}.\hfill \end{array}$$ A2.7

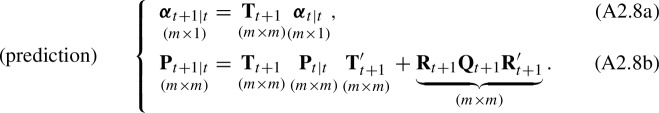A by-product of this recursion is ${\{{\mathit{\alpha }}_{t|t},{\mathbf{P}}_{t|t}\}}_{t=1}^n$ which will be useful in Kalman smoothing below. To kick off the recursion, the initial value, $({\mathit{\alpha }}_{1|0},{\mathbf{P}}_{1|0})$, needs to be provided. A popular choice, if the matrices $({\mathbf{T}}_t,{\mathbf{R}}_t)$ are time-invariant, is the unconditional mean and variance of the state vector:31

$$\begin{array}{c}\hfill {\mathit{\alpha }}_{1|0}=\mathbf{0},\text{vec}({\mathbf{P}}_{1|0})={\left(\mathbf{I},-,\mathbf{T},\otimes ,\mathbf{T}\right)}^{-1}\text{vec}(\mathbf{R}\mathbf{Q}{\mathbf{R}}^{\prime }).\end{array}$$ A2.9

The likelihood of the sample $({\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_n)$ can be readily derived by what is called the prediction error formula:

$$\begin{array}{c}\hfill logL=-\frac{1}{2}\sum _{t=1}^n[plog(2\pi )+log|{\mathbf{F}}_t|+{\mathbf{v}}_t^{\prime }{\mathbf{F}}_t^{-1}{\mathbf{v}}_t].\end{array}$$ A2.10

Kalman smoothing is a recursion for generating 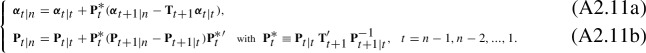$\{{\mathit{\alpha }}_{t|n},{\mathbf{P}}_{t|n}\}$ ($t=n-1,n-2,\dots 1$).

The recursion proceeds backward from $t=n$, taking the sequence ${\{{\mathit{\alpha }}_{t|t},{\mathbf{P}}_{t|t},{\mathbf{P}}_{t|t-1}\}}_{t=1}^n$ (which are, as noted above, available from Kalman filtering) as given.

2.2. Accommodating missing values

We now show how the above formulas can be modified to accommodate missing values in ${\mathbf{y}}_t$. Data for nowcasting necessarily include missing cases due to mixed frequencies. The textbook procedure for accommodating missing values, which we follow in this paper, has (to our knowledge) not been shown to produce the correct likelihood function.32 The key idea is to replace missing values by some noise that is totally unrelated to the system. Clearly, the state equation (A2.2), which is about the unobservable state vector, is not affected. What is affected is the observation equation (A2.1).

Allow some elements of ${\mathbf{y}}_t$ to be unobservable. Let $p_t$ ($\le p$) be the number of observed elements and ${\mathbf{S}}_t$ be the selection matrix. Here is an example. $p=3$ and the first and third elements of ${\mathbf{y}}_t$ are missing. Then $p_t=1$ and

$$\begin{array}{c}\hfill \underset{(3\times 3)}{{\mathbf{S}}_t}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right],\text{so}\underset{(3\times 1)}{\underbrace{{\mathbf{S}}_t{\mathbf{y}}_t}}=\left[\begin{array}{c}0\\ y_{2t}\\ 0\end{array}\right].\end{array}$$

${\mathbf{S}}_t{\mathbf{y}}_t$ is observable, but is not jointly normal. Consider the observation vector, $\underset{(p\times 1)}{{\tilde{\mathbf{y}}}_t}$, in which zeros are replaced by some noise that is normally distributed:

$$\begin{array}{c}\hfill \underset{(p\times 1)}{{\tilde{\mathbf{y}}}_t}\equiv \underset{(p\times 1)}{\underbrace{{\mathbf{S}}_t{\mathbf{y}}_t}}+\underset{(p\times p)}{\underbrace{({\mathbf{I}}_p-{\mathbf{S}}_t)}}\underset{(p\times 1)}{{\mathbf{e}}_t},{\mathbf{e}}_t\sim \mathcal{N}(\mathbf{0},{\sigma }_e^2·{\mathbf{I}}_p)\end{array}$$ A2.12

The noise ${\mathbf{e}}_t$ is assumed to be independent of the model’s shocks (${\mathit{\epsilon }}_s,{\mathit{\eta }}_s$) for all (t, s). In the above example,

$$\begin{array}{c}\hfill \underset{(3\times 1)}{\underbrace{{\mathbf{S}}_t{\mathbf{y}}_t}}=\left[\begin{array}{c}0\\ y_{2t}\\ 0\end{array}\right],\text{but}\underset{(3\times 1)}{\underbrace{{\mathbf{S}}_t{\mathbf{y}}_t}}+\underset{(3\times 3)}{\underbrace{(\mathbf{I}-{\mathbf{S}}_t)}}\underset{(3\times 1)}{{\mathbf{e}}_t}=\left[\begin{array}{c}{e}_{1t}\\ y_{2t}\\ e_{3t}\end{array}\right].\end{array}$$

Substitute (A2.1) into (A2.12) to obtain the observation equation with missing values:

$$\begin{array}{cc}& \text{(observation equation)}{\tilde{\mathbf{y}}}_t=\underset{(p\times 1)}{{\tilde{\mathbf{d}}}_t}+\underset{(p\times m)}{{\tilde{\mathbf{Z}}}_t}\underset{(m\times 1)}{{\mathit{\alpha }}_t}+\underset{(p\times 1)}{{\tilde{\mathit{\epsilon }}}_t},\{{\tilde{\mathit{\epsilon }}}_t\}\hfill \\ \hfill & \text{white noise with}{\tilde{\mathit{\epsilon }}}_t\sim \mathcal{N}(\mathbf{0},\underset{(p\times p)}{{\tilde{\mathbf{H}}}_t}),\hfill \end{array}$$ A2.13

where

$$\begin{array}{cc}\hfill \underset{(p\times 1)}{{\tilde{\mathbf{d}}}_t}\equiv & \underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times 1)}{{\mathbf{d}}_t},\underset{(p\times m)}{{\tilde{\mathbf{Z}}}_t}\equiv \underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times m)}{{\mathbf{Z}}_t},\underset{(p\times 1)}{{\tilde{\mathit{\epsilon }}}_t}\equiv \underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times 1)}{{\mathit{\epsilon }}_t}+\underset{(p\times p)}{\underbrace{({\mathbf{I}}_p-{\mathbf{S}}_t)}}\underset{(p\times 1)}{{\mathbf{e}}_t},\hfill \\ \hfill \underset{(p\times p)}{\widetilde{{\mathbf{H}}_t}}\equiv & \underset{(p\times p)}{\underbrace{\underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times p)}{{\mathbf{H}}_t}\underset{(p\times p)}{{\mathbf{S}}_t}}}+{\sigma }_e^2·\underset{(p\times p)}{\underbrace{({\mathbf{I}}_p-{\mathbf{S}}_t)}}.\hfill \end{array}$$ A2.14

The observation equation is now (A2.13) rather than (A2.1). In the above Kalman filtering equations, the prediction equations, (A2.8a) and (A2.8b), are not affected by missing values. To adapt the updating equations, (A2.5a) and (A2.5b), to missing values, (i) replace “${\mathbf{y}}_t$” by “${\tilde{\mathbf{y}}}_t$”, “${\mathbf{d}}_t$” by “${\tilde{\mathbf{d}}}_t$”, “${\mathbf{Z}}_t$” by “${\tilde{\mathbf{Z}}}_t$”, and “${\mathbf{H}}_t$” by “${\tilde{\mathbf{H}}}_t$” in (A2.5a) and (A2.5b), and then (ii) substitute (A2.12) and (A2.14) for ${\tilde{\mathbf{y}}}_t$, ${\tilde{\mathbf{d}}}_t$, ${\tilde{\mathbf{Z}}}_t$, and ${\tilde{\mathbf{H}}}_t$. This results in 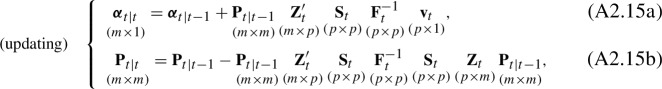where

$$\begin{array}{cc}\hfill \underset{(p\times 1)}{{\mathbf{v}}_t}& =\underset{\text{observation vector}}{\underbrace{{\mathbf{S}}_t{\mathbf{y}}_t+(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t}}-\underset{\text{one-period-ahead predictor}}{\underbrace{{\mathbf{S}}_t({\mathbf{d}}_t+{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})}}\hfill \end{array}$$ A2.16

$$\begin{array}{cc}\hfill \underset{(p\times p)}{{\mathbf{F}}_t}& =\underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times m)}{{\mathbf{Z}}_t}\underset{(m\times m)}{{\mathbf{P}}_{t|t-1}}\underset{(m\times p)}{{\mathbf{Z}}_t^{\prime }}\underset{(p\times p)}{{\mathbf{S}}_t}+\underset{(p\times p)}{{\mathbf{S}}_t}\underset{(p\times p)}{{\mathbf{H}}_t}\underset{(p\times p)}{{\mathbf{S}}_t}+{\sigma }_e^2·\underset{(p\times p)}{\underbrace{({\mathbf{I}}_p-{\mathbf{S}}_t)}}.\hfill \end{array}$$ A2.17

We show that ${\mathbf{e}}_t$ and ${\sigma }_e^2$ can be eliminated from Kalman filtering. We do this in three steps.

• Given ${\mathbf{S}}_t$, choose a permutation matrix ${\mathbf{C}}_t$, an identity matrix with its rows resequenced in some order, such that

  $$\begin{array}{c}\hfill \underset{(p\times p)}{{\mathbf{C}}_t}\underset{(p\times p)}{{\mathbf{S}}_t}=\begin{array}{cc}\left[\begin{array}{c}\underset{(p_t\times p)}{{\mathbf{W}}_t}\\ \underset{((p-p_t)\times p)}{\mathbf{0}}\end{array}\right]& \begin{array}{c}\}{p}_t\text{rows}\hfill \\ \hfill \\ \}p-p_t\text{rows,}\hfill \end{array}\end{array}\end{array}$$ A2.18

  where ${\mathbf{W}}_t$ is a subset of rows from ${\mathbf{I}}_p$. Permutation matrices are unitary matrices (so ${\mathbf{C}}_t{\mathbf{C}}_t^{\prime }=\mathbf{I}$). Other well-known properties are:

  1. $$\begin{array}{c}\hfill {\mathbf{C}}_t(\mathbf{I}-{\mathbf{S}}_t)=\begin{array}{cc}\left[\begin{array}{c}\underset{(p_t\times p)}{\mathbf{0}}\\ \\ \underset{((p-p_t)\times p)}{{\mathbf{U}}_t}\end{array}\right]& \begin{array}{c}\}{p}_t\text{rows}\hfill \\ \hfill \\ \}p-p_t\text{rows,}\hfill \end{array}\end{array}\end{array}$$

     where ${\mathbf{U}}_t$ is the remaining subset of rows from ${\mathbf{I}}_p$ not included in ${\mathbf{W}}_t$.
  2. (A2.18) and (a) immediately imply

     $$\begin{array}{c}\hfill {\mathbf{C}}_t=\left[\begin{array}{c}{\mathbf{W}}_t\\ {\mathbf{U}}_t\end{array}\right].\end{array}$$
  3. ${\mathbf{W}}_t{\mathbf{W}}_t^{\prime }=\mathbf{I}$, ${\mathbf{W}}_t{\mathbf{U}}_t^{\prime }=\underset{(p_t\times (p-p_t))}{\mathbf{0}}$, and ${\mathbf{U}}_t{\mathbf{U}}_t^{\prime }=\mathbf{I}$, because ${\mathbf{C}}_t$ is a unitary matrix.

  The above matrix ${\mathbf{W}}_t$ is a “compression matrix” because it extracts from ${\mathbf{y}}_t$ only non-missing elements. In the above example with $\underset{(3\times 3)}{{\mathbf{S}}_t}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right],$

  $$\begin{array}{c}\hfill {\mathbf{C}}_t=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right],{\mathbf{W}}_t=\left[\begin{array}{ccc}0& 1& 0\end{array}\right],{\mathbf{U}}_t=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\end{array}\right],{\mathbf{W}}_t{\mathbf{y}}_t=[y_{2t}].\end{array}$$
• Structure of ${\mathbf{F}}_t$. From (A2.17),

  $$\begin{array}{c}\hfill {\mathbf{C}}_t{\mathbf{F}}_t{\mathbf{C}}_t^{\prime }=\underset{\text{(A)}}{\underbrace{{\mathbf{C}}_t{\mathbf{S}}_t\left({\mathbf{Z}}_t,{\mathbf{P}}_{t|t-1},{\mathbf{Z}}_t^{\prime },+,{\mathbf{H}}_t\right){\mathbf{S}}_t{\mathbf{C}}_t^{\prime }}}+{\sigma }_e^2\underset{\text{(B)}}{\underbrace{{\mathbf{C}}_t(\mathbf{I}-{\mathbf{S}}_t){\mathbf{C}}_t^{\prime }.}}\end{array}$$

  $$\begin{array}{cc}\hfill \text{(A)}& =\left[\begin{array}{c}{\mathbf{W}}_t\\ \mathbf{0}\end{array}\right]\left({\mathbf{Z}}_t,{\mathbf{P}}_{t|t-1},{\mathbf{Z}}_t^{\prime },+,{\mathbf{H}}_t\right)\left[\begin{array}{cc}{\mathbf{W}}_t^{\prime }& \mathbf{0}\end{array}\right](\mathrm{by}(\mathrm{A}2.18))\hfill \\ \hfill & =\left[\begin{array}{cc}\underset{(p_t\times p_t)}{{\overline{\mathbf{F}}}_t}& \underset{(p_t\times (p-p_t))}{\mathbf{0}}\\ \underset{((p-p_t)\times p_t)}{\mathbf{0}}& \underset{((p-p_t)\times (p-p_t))}{\mathbf{0}}\end{array}\right],\hfill \end{array}$$

  where

  $$\begin{array}{c}\hfill \underset{(p_t\times p_t)}{{\overline{\mathbf{F}}}_t}\equiv \underset{(p_t\times p)}{{\mathbf{W}}_t}\underset{(p\times m)}{{\mathbf{Z}}_t}\underset{(m\times m)}{{\mathbf{P}}_{t|t-1}}\underset{(m\times p)}{{\mathbf{Z}}_t^{\prime }}\underset{(p\times p_t)}{{\mathbf{W}}_t^{\prime }}+\underset{(p_t\times p)}{{\mathbf{W}}_t}\underset{(p\times p)}{{\mathbf{H}}_t}\underset{(p\times p_t)}{{\mathbf{W}}_t^{\prime }}.\end{array}$$ A2.19

  $$\begin{array}{cc}\hfill \text{(B)}& =\left[\begin{array}{c}\mathbf{0}\\ {\mathbf{U}}_t\end{array}\right]\left[\begin{array}{cc}{\mathbf{W}}_t^{\prime }& {\mathbf{U}}_t^{\prime }\end{array}\right]\text{(by (a) and (b))}\hfill \\ \hfill & =\left[\begin{array}{cc}\underset{(p_t\times p_t)}{\mathbf{0}}& \underset{(p_t\times (p-p_t))}{\mathbf{0}}\\ \underset{((p-p_t)\times p_t)}{\mathbf{0}}& {\mathbf{I}}_{p-p_t}\end{array}\right]\text{(by (c))}.\hfill \end{array}$$

  Therefore,

  $$\begin{array}{c}\hfill {\mathbf{C}}_t{\mathbf{F}}_t{\mathbf{C}}_t^{\prime }={\mathbf{D}}_t\text{with}{\mathbf{D}}_t\equiv \left[\begin{array}{cc}\underset{(p_t\times p_t)}{{\overline{\mathbf{F}}}_t}& \underset{(p_t\times (p-p_t))}{\mathbf{0}}\\ \underset{((p-p_t)\times p_t)}{\mathbf{0}}& {\sigma }_e^2{\mathbf{I}}_{p-p_t}\end{array}\right],\end{array}$$

  so

  $$\begin{array}{c}\hfill {\mathbf{F}}_t^{-1}={\mathbf{C}}_t^{\prime }{\mathbf{D}}_t^{-1}{\mathbf{C}}_t\text{with}{\mathbf{D}}_t^{-1}=\left[\begin{array}{cc}\underset{(p_t\times p_t)}{{\overline{\mathbf{F}}}_t^{-1}}& \underset{(p_t\times (p-p_t))}{\mathbf{0}}\\ \underset{((p-p_t)\times p_t)}{\mathbf{0}}& \frac{1}{{\sigma }_e^2}{\mathbf{I}}_{p-p_t}\end{array}\right].\end{array}$$ A2.20

  Given this expression (A2.20) about the structure of ${\mathbf{F}}_t$, and using (A2.18) and (a), we can easily derive the following:

  $$\begin{array}{cc}& {\mathbf{S}}_t{\mathbf{F}}_t^{-1}{\mathbf{S}}_t=\underset{(p\times p_t)}{\underbrace{{\mathbf{W}}_t^{\prime }}}\underset{(p_t\times p_t)}{\underbrace{{\overline{\mathbf{F}}}_t^{-1}}}\underset{(p_t\times p)}{\underbrace{{\mathbf{W}}_t}},\hfill \end{array}$$ A2.21a

  $$\begin{array}{cc}& {\mathbf{S}}_t{\mathbf{F}}_t^{-1}(\mathbf{I}-{\mathbf{S}}_t)=\underset{(p\times p)}{\mathbf{0}},\hfill \end{array}$$ A2.21b

  $$\begin{array}{cc}& (\mathbf{I}-{\mathbf{S}}_t){\mathbf{F}}_t^{-1}(\mathbf{I}-{\mathbf{S}}_t)=\frac{1}{{\sigma }_e^2}\underset{(p\times (p-p_t))}{\underbrace{{\mathbf{U}}_t^{\prime }}}\underset{((p-p_t)\times p)}{\underbrace{{\mathbf{U}}_t}}.\hfill \end{array}$$ A2.21c
• We show below that the updating equations (A2.15a) and (A2.15b) with (A2.16) and (A2.17) become with

  $$\begin{array}{c}\hfill \underset{(p_t\times 1)}{{\overline{\mathbf{v}}}_t}\equiv {\mathbf{W}}_t{\mathbf{y}}_t-{\mathbf{W}}_t{\mathbf{d}}_t-{\mathbf{W}}_t{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1}\end{array}$$ A2.23

  and ${\overline{\mathbf{F}}}_t$ given by (A2.19).

Proof

(A2.15b) becomes (A2.22b) because of (A2.21a). (A2.15a) becomes (A2.22a) because

$$\begin{array}{cc}\hfill {\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}{\mathbf{v}}_t& ={\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}[{\mathbf{S}}_t{\mathbf{y}}_t+(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t-{\mathbf{S}}_t({\mathbf{d}}_t+{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})]\text{(by}(\mathrm{A}2.16))\hfill \\ \hfill & ={\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}{\mathbf{S}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})+{\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t\hfill \\ \hfill & ={\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}{\mathbf{S}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})\text{(by}(\mathrm{A}2.21\mathrm{b}))\hfill \\ \hfill & ={\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{W}}_t^{\prime }{\overline{\mathbf{F}}}_t^{-1}{\mathbf{W}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})\text{(by}(\mathrm{A}2.21\mathrm{a}))\hfill \\ \hfill & ={\mathbf{P}}_{t|t-1}{\mathbf{Z}}_t^{\prime }{\mathbf{W}}_t^{\prime }{\overline{\mathbf{F}}}_t^{-1}{\overline{\mathbf{v}}}_t.\text{(by}(\mathrm{A}2.23))\hfill \end{array}$$

• Mechanically, to modify the original updating equations, (A2.5a) and (A2.5b) with (A2.6) and (A2.7), to missing values, all we need to do is replace “${\mathbf{y}}_t$” by “${\mathbf{W}}_t{\mathbf{y}}_t$”, “${\mathbf{d}}_t$” by “${\mathbf{W}}_t{\mathbf{d}}_t$”, “${\mathbf{Z}}_t$” by “${\mathbf{W}}_t{\mathbf{Z}}_t$”, and “${\mathbf{H}}_t$” by “${\mathbf{W}}_t{\mathbf{H}}_t{\mathbf{W}}_t^{\prime }$.” This point is made, without proof, in Section 3.4.7 of Harvey (1990) and Section 4.10 of Durbin and Koopman (2012).

The likelihood function, (A2.10), is written in terms of ${\mathbf{v}}_t$ and ${\mathbf{F}}_t$. Below we rewrite it in terms of ${\overline{\mathbf{v}}}_t$ and ${\overline{\mathbf{F}}}_t$.

• Show: $log|{\mathbf{F}}_t|=log\left|\overline{{\mathbf{F}}_t}\right|+(p-p_t)log({\sigma }_e^2)$.

Proof

$$\begin{array}{cc}\hfill log|{\mathbf{F}}_t|& =-log|{\mathbf{F}}_t^{-1}|\hfill \\ \hfill & =-log\left|{\mathbf{C}}_t^{\prime },,\text{diag},(,{{\overline{\mathbf{F}}}_t}^{-1},,,\frac{1}{{\sigma }_e^2},,{\mathbf{I}}_{p-p_t},,),,{\mathbf{C}}_t\right|\text{(by}(\mathrm{A}2.20))\hfill \\ \hfill & =-log\left|\text{diag},(,{{\overline{\mathbf{F}}}_t}^{-1},,,\frac{1}{{\sigma }_e^2},,{\mathbf{I}}_{p-p_t},,),\right||{\mathbf{C}}_t^{\prime }{\mathbf{C}}_t|\hfill \\ \hfill & =-log\left|\text{diag},(,{{\overline{\mathbf{F}}}_t}^{-1},,,\frac{1}{{\sigma }_e^2},,{\mathbf{I}}_{p-p_t},,),\right|\text{(because}{\mathbf{C}}_t\text{is a unitary matrix)}\hfill \\ \hfill & =-log\left|{{\overline{\mathbf{F}}}_t}^{-1}\right|+(p-p_t)log({\sigma }_e^2)\hfill \\ \hfill & =log\left|{\overline{\mathbf{F}}}_t\right|+(p-p_t)log({\sigma }_e^2).\hfill \end{array}$$

• Rewrite ${\mathbf{v}}_t^{\prime }{\mathbf{F}}_t^{-1}{\mathbf{v}}_t$ in (A2.10).

  $$\begin{array}{cc}\hfill {\mathbf{v}}_t^{\prime }{\mathbf{F}}_t^{-1}{\mathbf{v}}_t& =[{\mathbf{S}}_t{\mathbf{y}}_t-{\mathbf{S}}_t{\mathbf{d}}_t-{\mathbf{S}}_t{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1}+(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t{]}^{\prime }\hfill \\ \hfill & {\mathbf{F}}_t^{-1}[{\mathbf{S}}_t{\mathbf{y}}_t-{\mathbf{S}}_t{\mathbf{d}}_t-{\mathbf{S}}_t{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1}+(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t]\text{(by}(\mathrm{A}2.16))\hfill \\ \hfill & ={[{\mathbf{S}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})+({\mathbf{I}}_p-{\mathbf{S}}_t){\mathbf{e}}_t]}^{\prime }\hfill \\ \hfill & {\mathbf{F}}_t^{-1}[{\mathbf{S}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})+({\mathbf{I}}_p-{\mathbf{S}}_t){\mathbf{e}}_t]\hfill \\ \hfill & =\underset{\text{(1)}}{\underbrace{{({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})}^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}{\mathbf{S}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})}}\hfill \\ \hfill & +2\underset{\text{(2)}}{\underbrace{{({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})}^{\prime }{\mathbf{S}}_t{\mathbf{F}}_t^{-1}({\mathbf{I}}_p-{\mathbf{S}}_t){\mathbf{e}}_t}}+\underset{\text{(3)}}{\underbrace{{\mathbf{e}}_t^{\prime }(\mathbf{I}-{\mathbf{S}}_t){\mathbf{F}}_t^{-1}(\mathbf{I}-{\mathbf{S}}_t){\mathbf{e}}_t}}.\hfill \end{array}$$

  By (A2.21a),

  $$\begin{array}{c}\hfill \text{(1)}={({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})}^{\prime }{\mathbf{W}}_t^{\prime }{\overline{\mathbf{F}}}_t^{-1}{\mathbf{W}}_t({\mathbf{y}}_t-{\mathbf{d}}_t-{\mathbf{Z}}_t{\mathit{\alpha }}_{t|t-1})={\overline{\mathbf{v}}}_t^{\prime }{\overline{\mathbf{F}}}_t^{-1}{\overline{\mathbf{v}}}_t,\end{array}$$ A2.24

  where ${\overline{\mathbf{v}}}_t$ is defined in (A2.23). By (A2.21b), the term (2) vanishes. By (A2.21c),

  $$\begin{array}{c}\hfill \text{(3)}=\frac{1}{{\sigma }_e^2}{\mathbf{e}}_t^{\prime }{\mathbf{U}}_t^{\prime }{\mathbf{U}}_t{\mathbf{e}}_t.\end{array}$$ A2.25
• So the likelihood function (A2.10) becomes

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill logL=& -\frac{1}{2}\sum _{t=1}^n\underset{\text{depends on model parameters but not on}({\sigma }_e^2,{\mathbf{e}}_t)}{\underbrace{[plog(2\pi )+log|{\overline{\mathbf{F}}}_t|+{\overline{\mathbf{v}}}_t^{\prime }{\overline{\mathbf{F}}}_t^{-1}{\overline{\mathbf{v}}}_t]}}\hfill \\ \hfill & -\frac{1}{2}\sum _{t=1}^n\underset{\text{depends on}({\sigma }_e^2,{\mathbf{e}}_t)\text{but not on model parameters}}{\underbrace{[(p-p_t)log({\sigma }_e^2)+\frac{1}{{\sigma }_e^2}{\mathbf{e}}_t^{\prime }{\mathbf{U}}_t^{\prime }{\mathbf{U}}_t{\mathbf{e}}_t]}}.\hfill \end{array}\end{array}$$ A2.26

  Since the second summation does not depend on the model parameters, the maximum likelihood estimate of the model parameters can be obtained by maximizing the first summation.

• Again, mechanically, all we need to do to adapt the likelihood function (A2.10) to missing cases is replace “${\mathbf{v}}_t$” by “${\overline{\mathbf{v}}}_t$” and “${\mathbf{F}}_t$” by “${\overline{\mathbf{F}}}_t$.”

Appendix 3. Details on numerical maximization of the likelihood function

A detailed description of our estimation procedure is as follows. The model parameters are: $({\mathit{\mu }}^{\ast },{\mathit{\beta }}^{(1)},{\mathit{\beta }}^{(2)},{\varphi }_f^{(1)},{\varphi }_f^{(2)},{\varphi }_1,{\varphi }_2,\dots ,{\varphi }_p,{\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2)$ where ${\mathit{\mu }}^{\ast }=({\mu }_1^{\ast },\dots ,{\mu }_p^{\ast })$ and ${\mathit{\beta }}^{(i)}=({\beta }_1^{(i)},\dots ,{\beta }_p^{(i)})$, $i=1,2$. ${\mathit{\mu }}^{\ast }$ is estimated as follows. We first estimate ${\mu }_j$ ($j=1,2,\dots ,p)$ by the sample mean of $y_{\mathit{jt}}$. ${\mathit{\mu }}^{\ast }$ is then recovered by the relation (13). The remaining parameters are estimated by maximum likelihood. The procedure for obtaining the initial parameter value, similar to the one in Giannone et al. (2008), is as follows. (i) Using monthly series only, extract two leading factors by the principal component analysis . (ii) The common factors’ AR(1) parameters $({\varphi }_f^{(1)},{\varphi }_f^{(2)})$ are estimated from the factors thus obtained, $({\beta }_j^{(1)},{\beta }_j^{(2)})$ ($j=1,2,\dots ,p$) from regressing $y_{\mathit{jt}}$ on the common factors, and the remaining parameters from the OLS residuals. (iii) Estimate the model’s common factors from the whole sample including both monthly and quarterly series by Kalman filtering and smoothing. (iv) Redo (ii), this time with the estimate of the common factors obtained from (iii). This last step produces our initial parameter values.

Maximization of the likelihood function starting with this initial parameter value is done on the programming language R using its “ucminf” package. The package stops when the line length of its line search is close to zero. The parameter estimate is then passed on to the BFGS option of R’s “optim” package, which for all cases resulted in convergence.

Funding

The research reported here was supported by grants-in-aid from the Ministry of Education, Culture, Sports, Science, and Technology of the Japanese government (Grant Number 16K03595(C)).

Declarations

Conflict of interest

The authors have no conflict of interest to report.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.