Machine learning and comorbidity network analysis for hospitalized patients with COVID-19 in a city in Southern Brazil

Abstract

The large amount of data generated during the COVID-19 pandemic requires advanced tools for the long-term prediction of risk factors associated with COVID-19 mortality with higher accuracy. Machine learning (ML) methods directly address this topic and are essential tools to guide public health interventions. Here, we used ML to investigate the importance of demographic and clinical variables on COVID-19 mortality. We also analyzed how comorbidity networks are structured according to age groups. We conducted a retrospective study of COVID-19 mortality with hospitalized patients from Londrina, Parana, Brazil, registered in the database for severe acute respiratory infections (SIVEP-Gripe), from January 2021 to February 2022. We tested four ML models to predict the COVID-19 outcome: Logistic Regression, Support Vector Machine, Random Forest, and XGBoost. We also constructed a comorbidity network to investigate the impact of co-occurring comorbidities on COVID-19 mortality. Our study comprised 8358 hospitalized patients, of whom 2792 (33.40%) died. The XGBoost model achieved excellent performance (ROC-AUC = 0.90). Both permutation method and SHAP values highlighted the importance of age, ventilatory support status, and intensive care unit admission as key features in predicting COVID-19 outcomes. The comorbidity networks for old deceased patients are denser than those for young patients. In addition, the co-occurrence of heart disease and diabetes may be the most important combination to predict COVID-19 mortality, regardless of age and sex. This work presents a valuable combination of machine learning and comorbidity network analysis to predict COVID-19 outcomes. Reliable evidence on this topic is crucial for guiding the post-pandemic response and assisting in COVID-19 care planning and provision.

1. Introduction

Coronaviruses are RNA viruses able to infect both animals and humans (Yang & Leibowitz, 2015). The coronavirus disease 2019 (COVID-19) is caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) (Lu et al., 2020), and it first broke out in Wuhan, China, in December 2019. The emergence of new and more transmissible SARS-CoV-2 lineages made this virus rapidly spread worldwide, with a disproportional burden on healthcare systems, especially in Brazil (Li et al., 2021; The Lancet, 2020).

Although the second year of the pandemic in Brazil, 2021, was marked by the advance of vaccination campaigns against COVID-19, April 2021 was a grim milestone: Brazil registered more than 4249 fatalities and surpassed the total number of deaths since the pandemic began in 2020, reaching the deadliest moment of the whole pandemic in the country (Castro et al., 2021). Therefore, understanding the underlying conditions that confer higher susceptibility to the disease with accurate prediction models and quantifying the impact of co-occurring comorbidities in COVID-19 mortality are essential to foster health policies with reliable evidence.

The large amount of COVID-19-related data enabled the application of Machine Learning (ML) algorithms to predict or identify people most likely susceptible to the disease (Aktar et al., 2021; Baqui et al., 2021; De Souza et al., 2021; Khedr et al., 2020; Mason et al., 2021). ML is a branch of artificial intelligence that concentrates on prediction by finding generalizable predictive patterns. ML methods for COVID-19 have been applied at three different scales: (i) molecular (to infer protein structures and genomic regions associated with SARS-CoV-2 infectivity); (ii) clinical (to support diagnosis from medical images and the need for invasive devices); and (iii) societal (to forecast the number cases given different policy choices) (Bullock et al., 2020). Compared to classical statistical methods, which focus on inference, ML methods make minimal assumptions about the data-generated distributions, can handle complicated non-linear interactions, and perform better for high-dimensional data (Bzdok et al., 2018).

Along with machine learning techniques to predict the profile of hospitalized patients and the outcome, several works have attempted to evaluate the contribution of comorbidities through a network approach (Espinosa et al., 2020; Gili et al., 2021; Khedr et al., 2020; Mason et al., 2021). Comorbidity network analysis is a graph-theoretic approach to study associations from disease co-occurrence data. This approach can elicit how frequently two diseases appear together within an individual and help us detect the underlying combination of comorbidities among severe cases of COVID-19.

This study explored the Brazilian SIVEP-Gripe (Sistema de Informação de Vigilância Epidemiológica da Gripe) dataset for hospitalized patients in Londrina, Paraná, from January 2021 to February 2022. Londrina had an estimated population of 580,870 inhabitants in 2021 (IBGE, 2022), and is the fourth most populous city in Southern Brazil. We employed a machine learning technique to explore the importance of demographic and clinical features to predict COVID-19 outcomes and comorbidity network analysis to evaluate the density and structure of these networks stratified by age groups. This paper contributes to the literature by presenting the importance of demographic and clinical features on COVID-19 mortality through a combination of machine learning to predict COVID-19 outcomes and comorbidity network analysis to infer diseases most likely to co-occur in hospitalized patients. Such evidence is also crucial for guiding the public health response at the local level and assisting in COVID-19 care planning and provision.

2. Methods

2.1. Study design, settings, and participants

We used the SIVEP-Gripe dataset for hospitalized patients from January 2021 to February 2022 in Londrina, Parana, Brazil. This dataset aims to strengthen epidemiological surveillance of respiratory viruses, including SARS-CoV-2. Public and private Brazilian hospitals must report severe acute respiratory syndrome-related deaths, even for those not hospitalized (Ministério da Saúde, 2022). Here, we considered only hospitalized patients with positive real-time PCR or serological tests for SARS-CoV-2.

2.2. Variables

The variables considered in this study were sex (male and female), age group (0–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70–79, 80+), ventilation support (invasive, non-invasive, absent), hospital legal status (public, private, and non-profit institution), intensive care unit (ICU) admission (yes or no), municipality of residence (Londrina or other), comorbidities, and symptoms.

2.3. Statistical analysis for categorical variables

The descriptive statistics included all categorical variables in SIVEP-Gripe dataset. Regarding the variables sex, age group, ventilatory support, ICU, municipality of residence, and hospital legal status, we conducted simple and multiple binary logistic regression models to assess the death risk for hospitalized patients. The association of each variable with COVID-19 outcome was retrieved using the Chi-square test. Regarding comorbidities and symptoms, the association with COVID-19 outcome was assessed for each variable without a reference category. P-values were obtained from Chi-square test. Odds ratio (OR) and 95% confidence intervals were reported for all categorical variables. The statistical analysis was performed using R software v4.0.2 (R Core Team, 2018).

2.4. Machine learning analysis

The outcome prediction task was formulated as a binary classification problem, with 0 representing recovery and 1 representing death of a given hospitalized patient. We tested four different ML models to predict the COVID-19 outcome: Logistic Regression, Support Vector Machine (SVM), Random Forest, and Extreme Gradient Boosting (XGBoost). This analysis was employed using the Scikit-learn v1.0.2 (Buitinck et al., 2013, pp. 108–122) and XGBoost v1.5.2 (Chen & Guestrin, 2016) python (Rossum & Drake, 2009) libraries.

We considered 8358 patients and 34 features, including sex, age group, municipality of residence, ventilation support, hospital legal status, ICU admission, comorbidities, and symptoms. Variables with more than two categories were represented by a set of dummy variables, with one variable for each category. To reduce data dimension, improve the estimator's accuracy, and boost the model performance, we employed a tree-based feature selection algorithm to discard irrelevant features based on their impurity estimate before splitting the dataset into training and testing sets (Ferri et al., 2001).

The dataset is unbalanced regarding the outcome: 66.60% of survived and 33.40% of deceased patients, respectively. To define the training and test sets that best represent the population studied, we conducted stratified sampling to split the dataset into 70% (5850 patients) to train and 30% (2508 patients) to test the models. We evaluated the performance of each model with the training dataset with k-fold cross-validation, with k varying from 2 to 10. For each k-fold and model, we computed Matthew's Correlation Coefficient (MCC) score to evaluate the model performance. To tune hyperparameters in the final ML model, we employed k-fold cross-validation with 5 folds. We used the area under the receiver-operating characteristic curve (AUC-ROC) as the model score metric.

To retrieve the importance of variables on explaining the model, we adopted the permutation and SHAP (Shapley Additive exPlanations) techniques. In the permutation approach, the relationship between a given feature and the target is broken via a random shuffle. The drop in the model score indicates how much the model depends on that feature (Breiman, 2001). On the other hand, the essence of SHAP is to measure the feature contribution of each individual to the outcome and whether the feature has a positive or negative impact on predictions (Lundberg & Lee, 2017). We performed a Principal Component Analysis (PCA) with two dimensions to examine how patients are clustered based on SHAP values.

2.5. Comorbidity network analysis

The SIVEP-Gripe dataset accrues information about 12 comorbidities: asthma, diabetes, Downs syndrome, heart disease, hematological disease, hepatic disease, immunosuppression, kidney disease, lung disease, neurological disease, obesity, and puerperal. Missing information about comorbidity was interpreted as the absence of comorbidities. The presence or absence of each comorbidity was used to perform the comorbidity network analysis. The dataset was further divided into survivors and deceased groups. Only those comorbidities present in at least 20 patients in each group were maintained (puerperal and Down's syndrome variables were discarded).

We conducted the network analysis from a rectangular presence-absence matrix where rows and columns represent comorbidities and patients, respectively. In this matrix, each entry is either one or zero if the comorbidity is present or absent in a given patient.

We employed a probabilistic model for analyzing comorbidity co-occurrence. This approach was initially proposed to estimate the co-occurrence of species in different sites to infer if species association is negative, positive, or random (Veech, 2012). Our work translated species and sites to comorbidities and patients, respectively. Moreover, we used this model to determine if the co-occurrence of two comorbidities is significantly greater than the expected (positive association).

The probability mass function of co-occurrence uses a random sampling with replacement represented by the hypergeometric distribution, which is implemented in the cooccur R package (Griffith et al., 2016). Briefly, we calculated the conditional probability of selecting a patient with the comorbidity $x$ given that it already has the comorbidity $y$. Let $N_x$ be the total number of patients with the comorbidity $x$, $N_y$ the total number of patients with comorbidity $y$, and $N$ the total number where both $x$ and $y$ could occur. The probability that $x$ and $y$ co-occur at exactly $j$ number of patients, for $j=\mathit{1}$ to $N_x$ patients, was given by:

$$P_j=\frac{\left(\begin{array}{l}{N}_x\\ j\end{array}\right)\times \left(\begin{array}{l}N-N_x\\ N_y-j\end{array}\right)}{\left(\begin{array}{l}N\\ N_y\end{array}\right)}$$ (1)

From the probability mass function shown in equation (1), we are interested in the upper tail of the distribution to retrieve positively associated comorbidities ($\alpha =\mathit{0.05}$). During the calculation, only patients sharing at least one morbidity were used to compute the probability of association with the R package cooccur v1.3 (Griffith et al., 2016).

The weighted undirected network was generated using igraph package (Csardi & Nepusz, 2006). Each node represents a comorbidity, and the edges connect them if their association is positive and higher than that expected by chance considering a significance level of 0.05. We also used igraph to compute the network density – the proportion of possible connections that are actually present – for each age group. The network density provides a metric of how many comorbidities are connected, given all possible connections. Therefore, the lower the density, the sparser the network (graph matrix with many zeros). To predict a confidence interval for the estimative, we performed 500 simulations to retrieve the network density for each age group. Briefly, for each iteration, we randomly sampled 60% of patients from the presence/absence matrix (without replacement), generated the comorbidity network, and then estimated the average network density with an associated error.

3. Results

This study included 8358 hospitalized patients in Londrina, from January 2021 to February 2022, of whom 5556 (66.60%) survived and 2792 (33.40%) deceased (Table 1 ). The risk of death was higher for patients admitted to ICU (OR = 10.8, IC 95% [9.663; 12.088], p-value < 0.001) and submitted to invasive ventilatory support (OR = 60.714, IC 95% [47.198; 79.326], p-value < 0.001). The differential death risk by sex had low statistical support (OR = 1.091, IC 95% [0.995; 1.197], p-value = 0.067), considering the significance level of 0.05. The increasing age was also associated with higher risk of death. Moreover, patients residing outside Londrina city had a 13% greater chance of death than those diagnosed with COVID-19 living in Londrina and reported at the same municipality (OR = 1.13, IC 95% [1.029; 1.243], p-value = 0.011).

Table 1.

Demographic and clinical information of survivors and deceased hospitalized patients with COVID-19. The ODDs ratio was calculated using the first “name” of each variable as the comparison base. Data are n (% of patients in each category in relation to survivors and deceased).

Variable	Survivors n (%)	Deceased n (%)	Odds Ratio (CI 95%)	P value
Total	5566 (66.59)	2792 (33.41)
Sex
Female	2413 (67.7)	1151 (32.3)
Male	3153 (65.77)	1641 (34.23)	1.091 [0.995; 1.197]	0.067
Age Group
0–9	52 (94.55)	3 (5.45)
10–19	51 (94.44)	3 (5.56)	1.02 [0.181; 5.732]	<0.001
20–29	333 (90.49)	35 (9.51)	1.822 [0.626; 7.748]	<0.001
30–39	790 (86.72)	121 (13.28)	2.655 [0.958; 11.023]	<0.001
40–49	1089 (80.91)	257 (19.09)	4.091 [1.491; 16.895]	<0.001
50–59	1291 (72.32)	494 (27.68)	6.633 [2.429; 27.332]	<0.001
60–69	910 (58.79)	638 (41.21)	12.152 [4.452; 50.072]	<0.001
70–79	689 (49.82)	694 (50.18)	17.459 [6.392; 71.956]	<0.001
80+	361 (39.76)	547 (60.24)	26.264 [9.58; 108.453]	<0.001
Ventilatory Support
no support	1275 (94.87)	69 (5.13)
non-invasive	3703 (82.4)	791 (17.6)	3.947 [3.085; 5.132]	<0.001
invasive	588 (23.34)	1931 (76.66)	60.714 [47.198; 79.326]	<0.001
ICU
No	3943 (88.43)	516 (11.57)
Yes	1623 (41.63)	2276 (58.37)	10.8 [9.663; 12.088]	<0.001
Municipality of residence
Londrina	3610 (67.59)	1731 (32.41)
Other	1956 (64.83)	1061 (35.17)	1.131 [1.029; 1.243]	0.011
Hospital Legal Status
Public	2892 (63.93)	1632 (36.07)
Private	1123 (71.03)	458 (28.97)	0.725 [0.639; 0.822]	<0.001
Non-profit institution	1551 (68.84)	702 (31.16)	0.804 [0.720; 0.896]	<0.001

Table 2 displays the coexisting conditions, odds ratio, and the most frequent symptoms and comorbidities among hospitalized COVID-19. Diabetes, heart disease, and obesity were the more prevalent comorbidities. The most common clinical presentation of patients with COVID-19 was shortness of breath (80%), SpO₂ <95% (79%), respiratory discomfort (71%), cough (57%), and fever (43%).

Table 2.

Coexisting conditions and Odds Ratio among hospitalized patients in Londrina, Parana – Brazil. Data are n (% of survivors or deceased in comorbidities and symptoms).

		Survivors n (%)	Deceased n (%)		Odds Ratio (CI 95%)	P value
Total		5566 (66.59)	2792 (33.41)
Comorbidities
Asthma	142 (2.55)		77 (2.76)	1.083 [0.818; 1.435]		0.611
Diabetes	1102 (19.8)		942 (33.74)	2.063 [1.862; 2.285]		<0.001
Downs syndrome	15 (0.27)		5 (0.18)	0.664 [0.241; 1.829]		0.487
Heart disease	1733 (31.14)		1592 (57.02)	2.934 [2.671; 3.223]		<0.001
Hematological disease	19 (0.34)		27 (0.97)	2.851 [1.582; 5.136]		<0.001
Hepatic disease	43 (0.77)		36 (1.29)	1.678 [1.075; 2.618]		0.030
Immunosuppression	108 (1.94)		107 (3.83)	2.014 [1.535; 2.642]		<0.001
Kidney disease	138 (2.48)		223 (7.99)	3.414 [2.747; 4.243]		<0.001
Lung disease	135 (2.43)		223 (7.99)	3.492 [2.806; 4.346]		<0.001
Neurological disease	217 (3.9)		285 (10.21)	2.802 [2.334; 3.364]		<0.001
Obesity	857 (15.4)		600 (21.49)	1.504 [1.339; 1.689]		<0.001
Other comorbidities	1973 (35.45)		1623 (58.13)	2.528 [2.304; 2.775]		<0.001
Puerpera	17 (0.31)		3 (0.11)	0.351 [0.103; 1.199]		0.097
Symptoms
Abdominal pain	249 (4.47)		122 (4.37)	0.976 [0.782; 1.218]		0.866
Another symptom	2244 (40.32)		1026 (36.75)	0.860 [0.783; 0.945]		0.002
Cough	3388 (60.87)		1409 (50.47)	0.655 [0.598; 0.718]		<0.001
Diarrhea	627 (11.26)		252 (9.03)	0.782 [0.670; 0.911]		0.002
Fatigue	2116 (38.02)		1039 (37.21)	0.966 [0.880; 1.061]		0.488
Fever	2502 (44.95)		1054 (37.75)	0.743 [0.677; 0.815]		<0.001
Ophthalmic loss	410 (7.37)		106 (3.80)	0.496 [0.399; 0.618]		<0.001
Respiratory discomfort	3634 (65.29)		2271 (81.34)	2.317 [2.076; 2.587]		<0.001
SpO2 <95%	4111 (73.86)		2485 (89.00)	2.865 [2.509; 3.272]		<0.001
Shortness of breath	4287 (77.02)		2397 (85.85)	1.810 [1.600; 2.048]		<0.001
Sore throat	606 (10.89)		227 (8.13)	0.724 [0.617; 0.850]		<0.001
Taste of loss	400 (7.19)		116 (4.15)	0.560 [0.453; 0.692]		<0.001
Vomit	387 (6.95)		168 (6.02)	0.857 [0.711; 1.033]		0.113

3.1. Machine learning modeling and interpretability

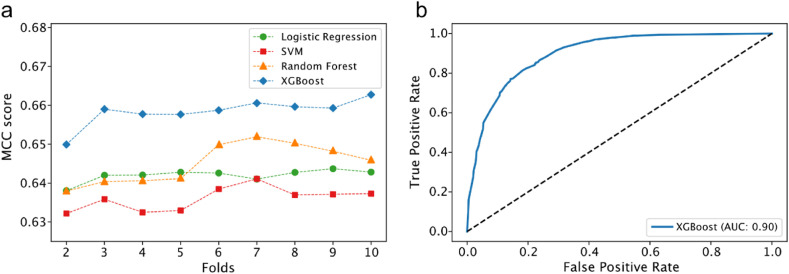
Considering different ML algorithms to predict COVID-19 outcomes, the XGBoost model outperforms the others based on the MCC score, a robust metric to evaluate binary predictors (Chicco & Jurman, 2020), regardless of the k chosen (see methods for more details). The accuracy, precision, and recall of the model were 0.81, 0.75, and 0.75, respectively. This model achieved an excellent performance of AUC-ROC = 0.90 (Fig. 1 b) and was used for downstream analyses. XGBoost is a supervised-learning ensemble algorithm that sequentially builds decision trees to provide accurate results while avoiding overfitting – it combines the result of many models to make a prediction.

Fig. 1.

Model evaluation and ROC curve. a) comparison of Matthews Correlation Coefficient (MCC) for different machine learning algorithms and b) ROC curve for XGBoost model. SVM stands for Support Vector Machine.

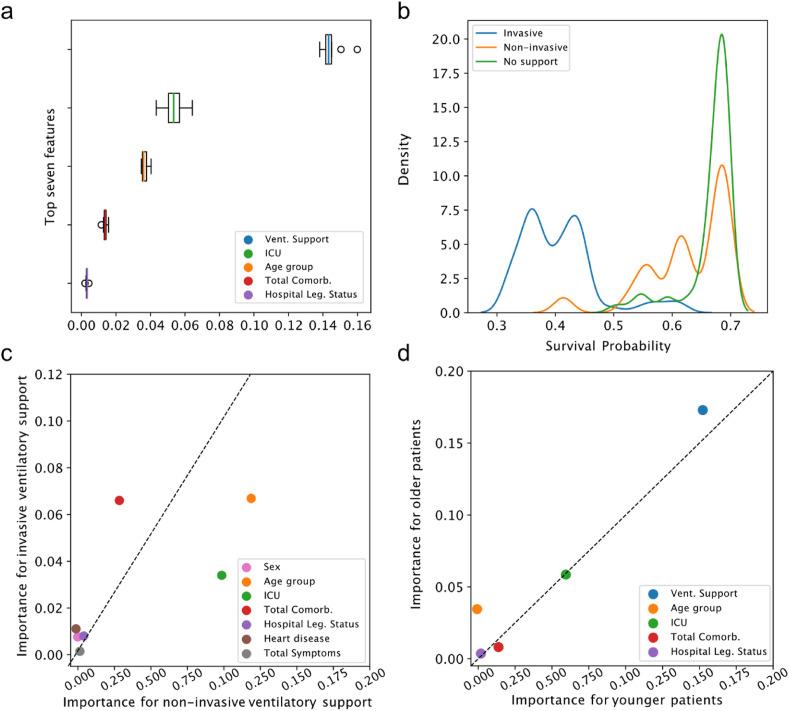
When exploring the feature importance for model's prediction using the permutation method, we observed that the three most important variables were those associated with severe prognosis: ventilatory support status (absent, invasive, and non-invasive), ICU admission, and age (Fig. 2 a). Regarding the density of hospitalized cases concerning the ventilatory support status, we noticed that patients without intervention or with non-invasive intervention have a probability distribution heavily skewed for higher survival probabilities – the opposite for those under invasive intervention (Fig. 2b). For hospitalized patients, invasive ventilatory support accounts for 69.15% of COVID-19 deaths, and the death risk is 60.71-fold the risk of a patient without ventilatory support (Table 1).

Fig. 2.

Relative feature importance to predict COVID-19 outcome in hospitalized patients. a) boxplot showing the distribution of the top seven estimated feature importance for those features with at least one simulated value higher than zero. b) survival probability distribution for ventilatory support status – ranging from 0 (death) to 1 (recovery) estimated using the XGBoost algorithm. c) relative importance of invasive and non-invasive ventilatory support for predicting COVID-19 mortality. d) relative importance for old (age ≥ 60 years) and young (<60 years) individuals. Dotted line represents the expected identical contribution for those analyzed variables. Values deviating from this line represent a differential contribution.

We evaluated the relative feature importance controlling by ventilatory support usage (non-invasive and invasive) and age (below and over 60 years old) (Fig. 2c and d). Considering patients with mechanical ventilation intervention, the number of comorbidities is crucial for patients under invasive intervention. On the other hand, ICU admission and age group are the most critical features for patients under non-invasive mechanical ventilation to predict COVID-19 outcomes (Fig. 2c). Regarding age dichotomization, we observed a slight deviation from the expected equal contribution for both groups (Fig. 2d). As expected, the ventilatory support status shows higher relative importance for older patients than for younger (Fig. 2d).

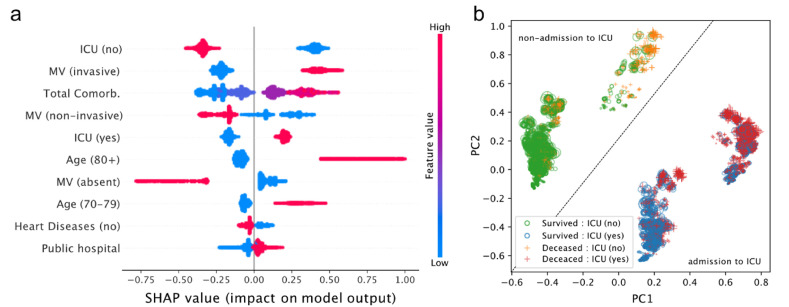
We also computed the SHAP values to further improve the model interpretability (Fig. 3 ). The three main features that most impact COVID-19 outcome prediction are non-admission to ICU, invasive ventilation, and the total number of comorbidities (Fig. 3a). Compared with other features, the absence of ventilatory support has a higher impact on predicting survival. On the other hand, ages above 80 years old contributes the most to predict death (Fig. 3a).

Fig. 3.

SHAP (Shapley Additive exPlanations) analysis. a) Dot chart with top 10 feature directionality impact. Each point is a SHAP value for an individual in a given feature. Positive SHAP values indicate impact to predict death and negative SHAP values indicate impact to predict survival outcome. b) Principal Component Analysis of SHAP values. The symbol size is proportional to the number of comorbidities in a given patient. MV stands for Mechanical Ventilation.

We also explored the grouping profile of all patients in the dataset based on SHAP values (Fig. 3b). After the dimensionality reduction through PCA, we observed four well-defined groups. It is possible to draw a diagonal line and divide the groups according to the ICU admission status: the two groups above the diagonal line represent non-admitted patients, while the ones below represent admitted patients. Negative PC1 values mostly indicate patients who survived, were not admitted to the ICU, but had a relatively high number of comorbidities (Fig. 3b). Negative PC2 values highlight survived patients who were admitted to ICU. Deceased patients admitted to the ICU with a high number of comorbidities tend to have high and positive PC1 values.

3.2. Age-adjusted comorbidity network for COVID-19 hospitalized patients

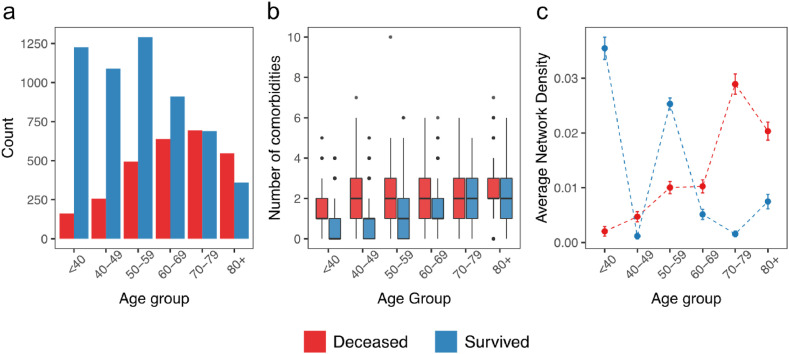
From the 8358 hospitalized cases explored in this work, 6006 patients (71.86%) harbored at least one comorbidity. Patients under 60 comprise the highest proportion of surviving patients (Fig. 4 a). The median value of comorbidities per patient varies according to age group. This number is lower in survived patients up to 70 years old than in deceased ones (Fig. 4b).

Fig. 4.

Age groups and comorbidity distribution. a) age group distribution. b) boxplot with the comorbidity number for deceased and surviving patients. c) average network density over 500 permutations of individuals per each age group. All density estimations differ (p-value < 0.001; t-test).

To further investigate the impact of comorbidities on COVID-19 outcomes, we constructed a comorbidity network from twelve comorbidities, adopting a probabilistic approach (Griffith et al., 2016; Veech, 2012) (see Methods for more details). For each age group, we computed the network density. Using our dataset, we observed that the COVID-19 comorbidity network is sparse (density <0.04). When comparing different age groups, all simulated density differs from survivals and deceased without overlapping confidence intervals (Fig. 4c). Moreover, while the network density for deceased people increases with age, the density tends to decrease for survivors (Fig. 4c).

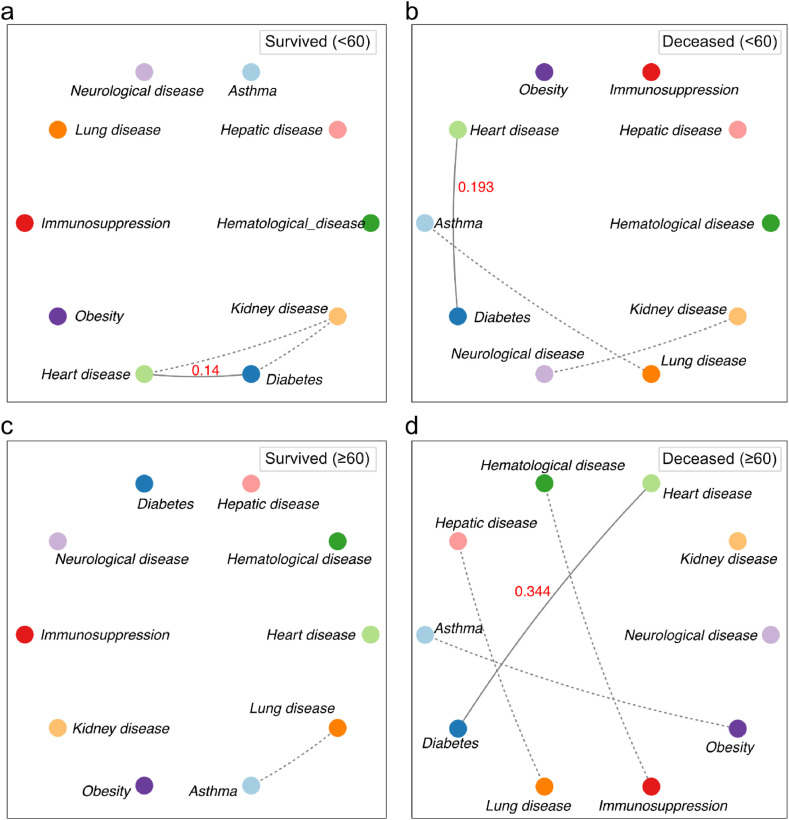
We also constructed the comorbidity network using 60 years old as a reference age for deceased and survived people. The network for surviving patients under 60 years old contains a triad composed by diabetes, kidney disease, and heart disease (Fig. 5 a). Considering the network for deceased patients in the same age group, there are three connections, but not in a triad form (Fig. 5b). Diabetes is positively associated with heart disease (probability = 0.193), but kidney disease links to neurological diseases. Finally, we observed the expected association between asthma and lung disease.

Fig. 5.

Comorbidity network for old (≥60 years) and young (<60 years) patients according to outcome. In the networks, each node represents a disease and the edges the significant associations between the co-occurrence of comorbidities (p-value < 0.05). Dotted edges represent associations with a probability of occurrence less than 0.1. Solid edges represent associations with a probability of occurrence greater than 0.1 (red numbers).

Regarding old patients (≥60 years old), the network for deceased patients is much denser than that for survivors. The only connection in the network for old surviving patients is between asthma and lung disease (Fig. 5c). However, we observed four connections for deceased patients – the denser network than all others (Fig. 5d). Diabetes and heart disease co-occur with an associated probability of 0.344, the highest compared to the network of survived individuals.

4. Discussion

This study employed a machine learning technique to investigate the importance of demographic and clinical variables on COVID-19 mortality among hospitalized patients in the fourth most populous city in Southern Brazil. We also analyzed how comorbidity networks were structured according to age groups. We conducted this study with 8358 hospitalized patients diagnosed with COVID-19 between January 2021 and February 2022.

The XGBoost model adopted here achieved an excellent performance (AUC-ROC = 0.90) and revealed the strong influence of ventilatory status, ICU admission, and age group on predicting COVID-19 outcome. These findings agree quantitatively with those observed from the odds ratio analysis: the death risk is much higher for old patients, admitted to ICU and submitted to ventilatory support (Table 1). Another study has also shown a higher risk of COVID-19 death among hospitalized patients who fit the characteristics listed, even in a well-resourced healthcare system (King et al., 2020). However, early diagnosis and intubation can dramatically decrease the chances of dying from COVID-19 (Zirpe et al., 2021), reinforcing the need for high-performance models to predict COVID-19 outcomes and analyze which characteristics are associated with mortality from the disease.

Model explainability is an essential topic in machine learning. In this paper, we tried to address this problem using the permutation technique and SHAP values obtained from the XGBoost model. Overall, we highlight the importance of ventilatory support, ICU admission, and age group status. In addition, two other relevant features were the number of comorbidities and the legal hospital status (public, private, or non-profitable). The SHAP analysis revealed that invasive ventilatory support, ICU admission, age above 70 years, and public hospital admission are the key subcategories associated with COVID-19 death. These results are consistent with recent findings on intensified death due to increased ICU experience, invasive mechanical ventilation requirement, and demographic discrepancies (Bastos et al., 2020; Chang et al., 2021; Lim et al., 2021). Therefore, Brazilian public authorities may benefit from this information for individual case management and overall resource planning.

Regarding the influence of comorbidities on COVID-19 outcomes, age plays a more important role than the total number of comorbidities (Ge et al., 2021; Khedr et al., 2020). Here, instead of considering the raw number of comorbidities, we also explored the comorbidity network stratified by age groups. The density of comorbidity networks for surviving young patients is higher than those for surviving older adults (Fig. 4). The rationale for this result is that most hospitalized young people already have more comorbidities. Moreover, mechanical ventilation or ICU admission may be unnecessary for older adults without comorbidities (Richardson et al., 2020), reducing the death risk.

According to the network density simulations, the comorbidity network density for deceased hospitalized patients tends to increase with age, while the network density for survived patients tends to decrease. We observed that diabetes and heart diseases usually co-occur with a high probability compared with other connections. Heart failure tends to increase in patients with diabetes who contract COVID-19, leading to severe outcomes (Freaney et al., 2020; Li et al., 2020). Therefore, our results suggest that the interplay of heart disease and diabetes may be an essential predictor of COVID-19 outcomes. This result agrees with those that observed that patients with diabetes and cardiovascular diseases have a higher death risk when infected with SARS-CoV-2 than those only with diabetes or heart disease alone (Hebbard et al., 2021; Li et al., 2020).

Although this paper combines ML and comorbidity network analysis to predict COVID-19 outcomes, there are some limitations. Firstly, we were unable to include the vaccination status for hospitalized patients. This feature would likely be an essential predictor, since studies in Londrina have already proven its effectiveness in reducing COVID-19 case-fatality rates (Passarelli-Araujo et al., 2022). Secondly, considering the unreported information about comorbidities in a given patient as absent may bias the comorbidity network to be less dense than expected. Thirdly, we considered hospitalized patients, discarding those asymptomatic individuals that could highlight other important patterns such as the hospitalization propensity. Monitoring COVID-19 outbreaks and incorporating vaccination status into the approach presented here will be critical to progress in our understanding about the demographic and clinical impacts of COVID-19.

5. Conclusion

In this paper, we have combined COVID-19 outcome prediction using ML, and the comorbidity association using network analysis. We also noted that this applied framework could help predict or classify other diseases' impacts using similar data as long as the a model is appropriately trained. We emphasized in this paper that analyzing comorbidity networks may be more relevant than focusing only on the prevalence of comorbidity to predict COVID-19 outcomes. Moreover, as the dataset continues to be accrued, it will become possible to better test hypotheses regarding gender and age-related comorbidity relationships in COVID-19. Altogether, this work provides insights for individual case management and reinforces the main contributors to COVID-19-related death that must be focused on to avoid long-standing clinical impacts.

CRediT author statement

Hemanoel Passarelli-Araujo: Conceptualization, Formal analysis, Investigation, Methodology, Visualization, Writing- Original draft. Hisrael Passarelli-Araujo: Data curation, Writing- Original draft. Mariana R. Urbano: Resources, Project administration. Rodrigo R. Pescim: Supervision, Writing – Review & Editing.

Institutional review board statement

This study was approved by the local Research Ethics Committee (Reference number: 50261221.3.0000.5231).

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.