Summary
Stable and fast-responding ionic current is a prerequisite for reliable measurements of small objects with a nanopore. Here, we report on the interference of ion diffusion kinetics at liquid-electrode interfaces in nanopore sensing. Using platinum as electrodes, we observed a slow and large decrease in the ionic current through a nanopore in a salt solution suggestive of the considerable influence of the growing impedance at the liquid-metal interfaces via Cottrell diffusion. When detecting nanoparticles, the resistive pulses became weaker following the steady increase in the resistance at the partially polarizable electrodes. The interfacial impedance was also demonstrated to couple with the nanopore chip capacitance thereby degraded the temporal resolution of the ionic current measurements in a time-varying manner. These findings can be useful for choosing the suitable size and material of electrodes for the single-particle and -molecule analyses by ionic current.
Subject areas: Sensor, Electrochemical engineering, Nanomaterials
Graphical abstract

Highlights
-
•
Ag/AgCl electrodes enable reliable resistive pulse detections of nanoparticles
-
•
Pt electrodes induce ionic current decay by time via the Cottrell diffusion
-
•
Cottrell diffusion deteriorates the nanopore sensor temporal resolution
Sensor; Electrochemical engineering; Nanomaterials.
Introduction
Nanopore is a powerful tool for analyzing biological samples at a single-molecule level (Xue et al., 2020; Hu et al., 2020; He et al., 2021; Fried et al., 2021). It is a conductometer that detects a temporal change of the ion flow in a nanoscale conduit upon translocation of an object via ionic current measurements (Henriquez et al., 2004), the simple mechanism of which has been demonstrated to enable a versatile sensor for identifying miscellaneous analytes from cells to genomes (Xue et al., 2020; Hu et al., 2020; He et al., 2021; Fried et al., 2021; Henriquez et al., 2004; Sun and Morgan, 2010). Being electrochemical in nature, meanwhile, the electrical current generally reflects the dynamic phenomena at the electrode-liquid interfaces (Zhang et al., 2006; Gao et al., 2019). Specifically, the application of voltage perturbs the local ion distribution by overconsuming reactants for the electrochemical reactions, which induces subsequent ion motions in the bulk to relax the acute ion concentration gradient near the electrode surface (Pletcher et al., 2011). This Cottrell diffusion causes a gradual decrease in the ionic current over time, whose characteristics provide rich information concerning the properties of ions in chronoamperometry (Messerschmitt et al., 2014; Lee et al., 2018). However, little effort has been devoted to investigate its relevance to the nanopore sensing (Zhang et al., 2006), where the time-course change in the impedance outside the pore may cause critical effects on the temporal resolution of the ionic current measurements for detecting small molecules and particles (Plesa et al., 2013, 2015; Tsutsui et al., 2021). In the present study, therefore, we explored this issue by comparing resistive pulse measurements of nanoparticles using multiple kinds of electrodes (Figure 1).
Figure 1.
Schematic model depicting nanopore sensing of single-nanoparticles
The ionic current Iion flowing through a nanopore in a SiNx membrane is measured in a phosphate buffered saline containing various concentrations of NaCl under the applied voltage Vb. Transient drops in Iion upon electrophoretic translocation of the negatively charged polymeric nanobeads were recorded using two different electrodes, Ag/AgCl and Pt. Inset is a scanning electron micrograph of a 300 nm diameter pore in a 40 nm thick SiNx membrane used for the resistive pulse measurements.
Results
Resistive pulse measurements using Ag/AgCl electrodes
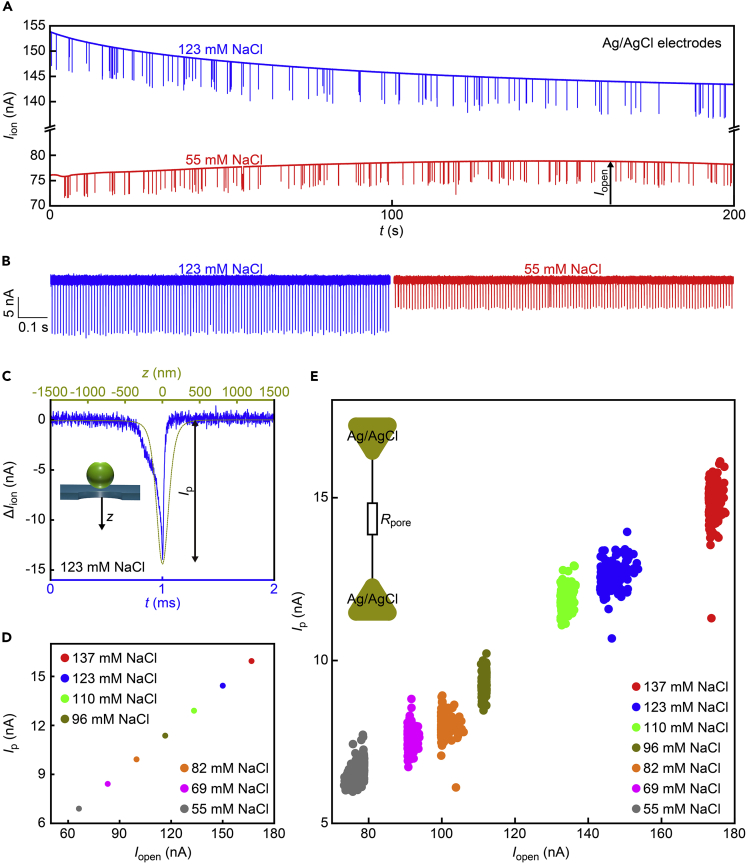
A nanopore of diameter 300 nm in a 40-nm thick SiNx membrane was used to detect 178-nm-sized polymeric beads in phosphate buffered saline at a concentration of 109 particles/mL (zeta potential of −37 to −30 mV in the electrolyte buffer of pH 7.6 containing 55 to 137 mM NaCl as measured by a zeta sizer) by recording the ionic current Iion under the applied voltage Vb (Vb is 0.4 V unless otherwise noted). We start with a case of Ag/AgCl, which is a typical compound used in nanopore measurements (Wang et al., 2022; Mojtabavi et al., 2022). It provided a persistent current flow with slow ups and downs (Figure 2A) associated with concentration fluctuations of reactants and products via their adsorption and precipitation at the surface under the electrochemical reactions in chloride solutions (Pletcher et al., 2011). In the meantime, resistive pulses were observed as the polymer nanoparticles passed through the pore by electrophoresis. These signals showed little variations in their heights (Figure 2B) representative of the narrow size distributions of the synthetic nanobeads (varying by less than 11% from the average particle diameter of 178 nm as confirmed by a dynamic light scattering method). There are also no notable changes in the pulse-like waveforms with time for the entire range of the salt concentration conditions tested, which suggested minor influence of the ion diffusion at the solution-electrode interfaces on the resistive pulse sensing.
Figure 2.
Open pore and blockade current characteristics observed with Ag/AgCl electrodes
(A) Partial ionic current traces recorded in a dilute suspension of 186 nm-sized polymeric nanobeads in phosphate buffered saline containing 123 mM (blue) and 55 mM (red) NaCl using a 300 nm-sized SiNx nanopore with Ag/AgCl electrodes under the transmembrane voltage Vb of 0.4 V.
(B) Resistive pulses of equal heights detected in the 123 mM (blue) and 55 mM (red) NaCl solutions. The open pore current is offset to zero.
(C) A magnified view of a resistive pulse in 123 mM NaCl (blue) compared with a simulated ionic signal for a 170 nm particle passing through a 300 nm diameter channel (dark yellow). The open pore current is offset to zero. z denotes the position of the particle center.
(D) The resistive pulse height Ip versus the open pore current Iopen obtained by the finite element simulations of the particle translocation in aqueous solutions of various NaCl concentrations.
(E) Experimental Ip under various salt concentration conditions plotted as a function of the open pore current Iopen at the moment when the resistive pulses were detected. Inset is an equivalent circuit model of the nanopore. There is no additional impedance at the solution/electrode interfaces due to the electrochemical nature of Ag/AgCl in the chloride solution.
To verify the accuracy of the single-particle measurements, we theoretically estimated the ionic blockade current by the polymeric sphere (Figure S1) (Tsutsui et al., 2019; Liao et al., 2020). Finite element calculations based on coupled Poisson-Nernst Planck and Navier Stokes equations predicted a drop in Iion (ΔIion) by approximately 15 nA when a 170-nm-sized particle was moved along the pore axis under the salt concentration of 123 mM NaCl (Figure 2C). The experimental ΔIion - t traces revealed similar features except the asymmetric signal line-shapes demonstrating the relatively slow motions at the nanopore orifice due to the hydrodynamic dragging under the electroosmotic flow (water flows in a direction opposite to the electrophoresis of the negatively charged particles in the SiNx nanopore for its negative native charge on the wall surface) (van Dorp et al., 2009; Firnkes et al., 2010). Moreover, the simulations indicated a linear rise in the resistive pulse height Ip with the open pore current Iopen (Figure 2D), which is in fair agreement with the experimental observations (Figure 2E). It can be interpreted by the fact that the electrolyte concentrations affect the homogeneous resistivity of the solution (1/ρ) including the open volume in the partially occluded nanopore by the particle. This in turn provides a transmission line circuit model of the fluidic system as a simple resistor of the resistance Rpore = ρ(4L/πdpore2 + 1/dpore) at the nanopore (Garaj et al., 2010; Kowalczyk et al., 2011) with negligible contributions of the electrodes (apart from the slight change in Ip in response to the time-course decrease in Iopen by less than 10% ascribable to the small yet finite effects of the resistance at the electrolyte solution-Ag/AgCl interfaces (Figure S2)).
Cottrell diffusion observed in Pt/nanopore/Pt systems
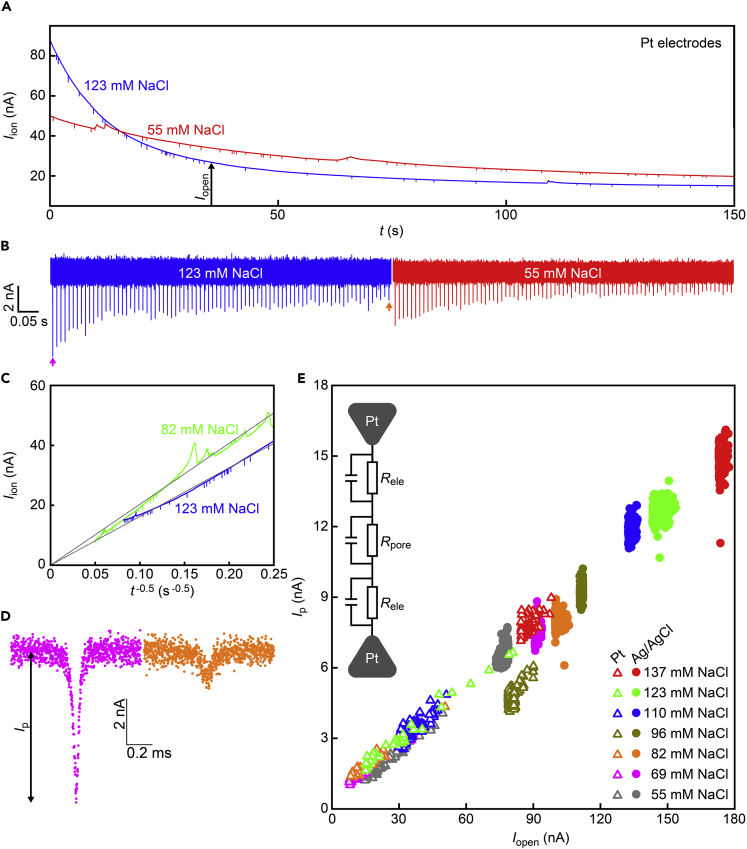
Measuring the polymeric beads using the same nanopore but with platinum electrodes instead of Ag/AgCl, we found quite different ionic current characteristics showing a large decrease in Iopen over time (Figure 3A). Furthermore, while the nanoparticles still could be detected, the resistive pulses became steadily weaker along the diminishing open pore current (Figures 3B–3E). Here, what is different in platinum from Ag/AgCl is the electrochemical reactions in the chloride solution involving no precipitation/adsorption of the reactants. In such a case, the Faraday current is expected to diminish monotonically rather than stay stable at a certain level, as the non-equilibrium ion concentration gradients at the voltage-biased electrode surface tend to be flattened by time via the diffusive motions of ions in the bulk solution (Plesa et al., 2015). In the case of parallel plate electrodes without a nanopore membrane, Fick’s law describes the time-dependent Faraday current to behave as Iion = nFAD0.5c/(πt)0.5, where F is the Faraday constant, A is the water-touching electrode area, D and c are the diffusion constant and the concentration of ions, and n is the number of electrons worked in the electrochemical reaction (Plesa et al., 2015). Indeed, the deep Iopen drop was found to occur as t−0.5 (Figure 3C) thereby manifested that the transmembrane ionic current is limited by the ion diffusion at the electrodes. More quantitatively, tentatively assuming water dissociation reactions on Pt surfaces in the pH7.6 buffer (van der Niet et al., 2013; Jaksic et al., 1993), we obtain D of 7.0 × 10−8 m2/s from the t−0.5 fitting (solid line in Figure 3C) with the electrode area of 2.7 × 10−5 m2. While this value is close to the diffusion constants of H+ and OH− at ambient conditions (Lee and Rasaiah, 2011; Holz et al., 2000), it should also be pointed out that Vb is lower than the voltage required for initiating Faraday electrolysis of water. Further efforts should thus be devoted to shed light on the electrochemical reactions responsible for the nanopore ionic current in the Pt/nanopore/Pt system.
Figure 3.
Time-varying Faraday current and resistive pulses in a Pt-nanopore-Pt setup
(A) Partial Iion traces in 123 (blue) and 55 mM (red) NaCl solutions recorded using a 300 nm-sized nanopore with Pt electrodes under Vb of 0.4 V. Large spike-like features are presumably due to charging/discharging.
(B) Resistive pulses of varying heights observed in 123 (blue) and 55 mM (red) NaCl.
(C) The ionic current curves displayed as a function of t−0.5. Gray lines are linear fitting to the data.
(D) Resistive pulses observed at the beginning (pink arrow in (b)) and the end (orange arrow in (b)) of one measurement.
(E) The measured Ip with Pt (open triangles) and Ag/AgCl (filled circles) plotted with respect to Iopen at the moment when the resistive pulses appeared. Inset is a circuit model of the Pt-nanopore-Pt system with impedance at the solution/electrode interfaces serially connected to the resistance at the pore.
Electrode material and electrolyte dependence of Cottrell behaviors
Extending the experiments to different electrode materials (Figure 4A), we obtained stable ionic current as well as uniform height resistive pulses of the polystyrene nanoparticles with Ti (Figure 4B). This demonstrates that Ti is equally useful to Ag/AgCl for nanopore sensing owing presumably to its dissolution reactions under the electric potential difference (Baehre et al., 2016). In case of Ag, the open pore current as well as the resistive pulse heights tended to become lower over time. It is naturally ascribed to the absence of AgCl for the precipitation/adsorption-mediated electrochemical reactions that led the Cottrell diffusion to become observable in the ionic current traces. Au also displayed similar behavior due to its electrochemically inert properties.
Figure 4.
Electrode material and electrolyte dependence of the ionic current characteristics
(A) Iion traces recorded using a 300 nm nanopore under 0.4 V with different metal electrodes: Ag/AgCl (red), Ti (greed), Ag (blue), and Au (dark yellow. Dashed lines are fitting with Iion∼t−0.5.
(B) Resistive pulses obtained for the 178 nm nanobeads within 15 min with various electrodes.
(C) Ionic current traces recorded in aqueous solutions of ferrocyanide using a 300 nm-sized nanopore with platinum electrodes under the transmembrane voltage of 0.4 V. Blue curve is the result in the water solution containing potassium hexacyanoferrate(III) (K3[Fe(CN)6]) and potassium hexacyanoferrate(II) trihydrate (K4[Fe(CN)6]) at 0.1 V while red curve is the result in the solution containing only K3[Fe(CN)6] at 0.1 M. The ionic current is plotted against t−0.5. A stable ionic current was observed with Fe(CN)64−/Fe(CN)63− due to the redox reaction at the platinum electrodes. In contrast, the absence of reactants with only K3[Fe(CN)6] led to diffusion-limited ionic current manifested by the decay in Iion by t−0.5 (dashed line is a fit with Iion∼t−0.5).
(D) Resistive pulse measurements of the 178 nm-sized polystyrene beads in the solution of 0.1 M Fe(CN)64−/Fe(CN)63−. No notable features suggestive of particle translocation were observed due presumably to aggregation of the polymeric beads.
Moreover, we tested salts other than NaCl. In case of a mixture aqueous solution of K3Fe(CN)6 and K4Fe(CN)6 (Figure 4C), the redox reactions involving precipitations (Luo et al., 2017), similar to those occurring at the Ag/AgCl electrodes in chloride solutions, provided stable ionic current even with Pt electrodes though not applicable for the resistive pulse detections (Figure 4D) perhaps due to the aggregation of the polystyrene nanobeads via the electrostatic interactions with the multivalent ions in the solution. On the other hand, a Cottrell behavior was observed when replacing the solution with the one containing only K3Fe(CN)6 since the redox reactions cannot take place without K4Fe(CN)6. These results were consistent to validate the pronounced roles of the electrochemical ion diffusion on the nanopore sensing.
Roles of electrode material on nanopore sensor temporal resolution
How about its impact on the nanopore sensing? The resistive pulses were already explained to become smaller over time (Figure 3D). To be more quantitative, we plotted the signal heights with respect to the open pore current. They revealed a proportionality between Ip and Iopen even for the data in a single measurement under a specific salt concentration condition (Figure 3E), which implies a direct relevance of the impedance at the solution/platinum interfaces on the ionic blockade current. Interestingly, the Ag/AgCl results were also in line with the linear dependence. Nevertheless, it should be noted that the underlying mechanisms are completely different. In the Ag/AgCl measurements, we changed the resistivity of the whole nanopore system by the salt concentration conditions that affected Ip and Iopen on the same footing (Henriquez et al., 2004). On the other hand, the ion diffusion at the voltage-biased platinum yielded local impedance at the liquid-electrode interfaces. In this sense, Ip is expected to scale with Iopen2 when assuming a serially connected resistor of resistance Rele at the two electrodes. It thus requires further analyses to explain the linear dependence observed in Figure 3E.
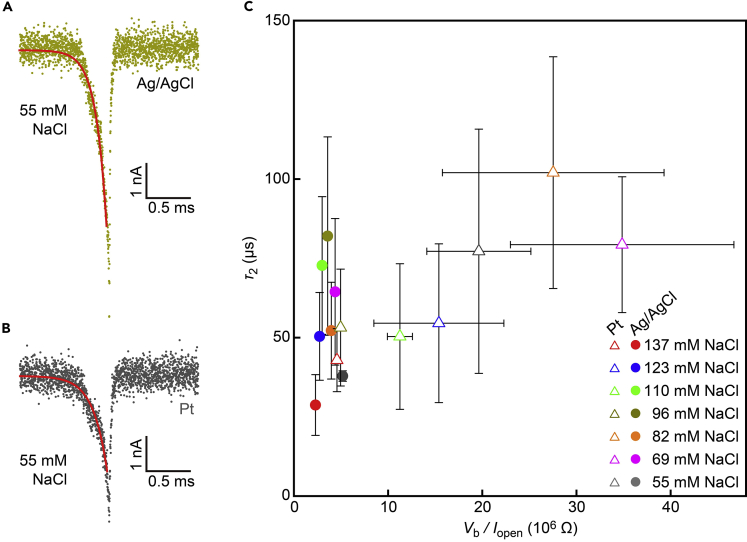
In fact, we found significant blunting of the resistive pulse waveforms via interplay between the resistance and capacitance (Tsutsui et al., 2018). Its effect was examined by fitting the tails with ΔIion ∼ exp(-t/τ1), where τ1 = RC is the time constant of a parallel RC circuit model assumed (Figures 5A and 5B). This expression is valid unless the translocation motions of the nanoparticles exiting the nanopore are much faster than the RC-mediated temporal resolution of the ionic current measurements. The signal pattern analysis revealed a linear relationship between τ1 and the resistance of the nanopore system, R = Vb/Iopen (Figure 5C; see also Figure S3), in the whole resistive pulse data including those recorded with not only Ag/AgCl but also Pt electrodes. The relationship as a whole implied the direct relevance of the time-varying Rele to the temporal resolution of nanopore sensors (note that τ1 scales linearly with R even within the data acquired under a certain salt concentration condition). In this context, it is noticeable that similar trends were reported when varying solution resistance at external regions of nanopores by integrating microchannels on membranes (Kishimoto et al., 2020). The τ1 – R dependence thus indicates the major contribution of Rele to alter the out-of-pore resistance contributing to the signal retardation. It is speculated that this gave rise to the linear Ip - Iopen dependence in Figure 3E.
Figure 5.
Impedance-limited temporal resolution of the nanopore sensing
(A and B) Typical resistive pulses recorded for the 186 nm-sized nanobeads in 55 mM NaCl solutions with Ag/AgCl (A) and Pt (B) electrodes under Vb of 0.4 V. Sky blue curves are the exponential fits by Iion ∼ -exp(-t/τ1) at the signal tails.
(C) τ1 versus Vb/Iopen scatter plots. Open triangles and filled circles are the data obtained with Pt and Ag/AgCl electrodes, respectively. Error bars denote the standard deviations. Dashed line is a linear fit to the whole plots. Inset is a refined equivalent circuit explaining the overall dependence of τ1 on the nanopore resistance.
In contrast, the curvatures at the left-half of the resistive pulses, which reflects the motions of the nanoparticles at the nanopore entrance, demonstrated a non-trivial manner. While the RC retardation is expected to be equally effective to blunt the signals at the onsets and the tails, the time constant τ2 (assessed by the exponential fits as shown in Figures 6A and 6B) revealed only faint dependence on R (Figure 6C). This is in part due to the considerable scattering in the pulse onset line-shapes reflecting the stochastic nature of the nanoparticles drawn into the nanopore at random angles (which is not the case after escaping the pore where the inertial effects tend to regulate their translocation motions) (Tsutsui et al., 2019). Another thing is the slow electrophoretic motions of the polymeric beads at the orifice (note that τ2 is relatively longer than τ1) allowing the ionic current to catch up with the change in their positions, hence obscuring the trait of the RC retardation.
Figure 6.
Resistive pulse onset line-shapes
(A and B) Resistive pulses recorded using Ag/AgCl (a) and Pt (b) with fit curves in red by Iion ∼ 1-exp(t/τ2).
(C) τ2 versus Vb/Iopen scatter plots shown by open triangles and filled circles for the data obtained with Pt and Ag/AgCl electrodes, respectively. Error bars denote the standard deviations.
Influence of electrode ion diffusion on particle translocation dynamics
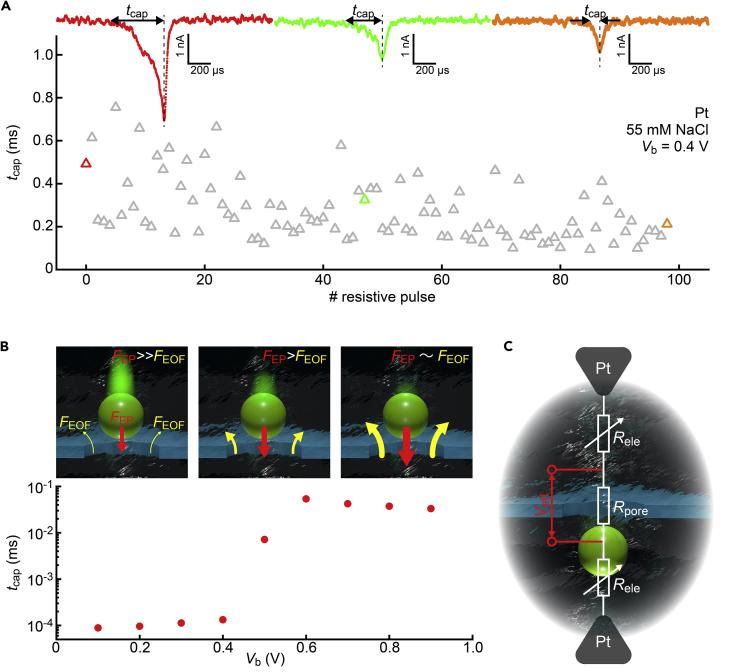
It is also noticeable that τ2 is electrode-material dependent. In the case of Ag/AgCl, we could find a tendency where τ2 becomes longer with R when decreasing the salt concentrations (Figure S4). Considering that the resistive pulse onsets mostly represent the translocation dynamics at the orifice rather than the RC effects, it can be explained by the slower motions of the polymeric particles under the more effective electroosmotic flow in the diluter electrolyte solution imposing stronger hydrodynamic drag forces to push them back (Figure S5) (Tsutsui et al., 2021; Firnkes et al., 2010; Xu et al., 2021). This is different for the results obtained with Pt, where τ2, or equivalently the time tcap for the nanobeads to be drawn into the nanopore (Figure 7A), scatters more and tends to become gradually shorter by time within the data collected under a constant salt concentration condition.
Figure 7.
Transmembrane voltage-dependent particle capture dynamics
(A) The width tcap at the first half of the resistive pulses obtained with the Pt-nanopore-Pt setup representing the time required for the particles to be electrophoretically drawn into the nanopore. The resistive pulses correspond to the data displayed as red, green, and orange triangles.
(B) Change in tcap with Vb observed in the resistive pulse measurements using Ag/AgCl electrodes in 55 mM NaCl solution. tcap increases steadily when increasing Vb from 0.1 to 0.6 V signifying a more rapid increase in the electroosmotic forces FEOF than the electrophoretic counterpart (FEP). The sketches depict the relative strength of the electrophoretic and hydrodynamic drag forces on the particles at the nanopore orifice under different transmembrane voltages.
(C) A circuit model explaining the time-varying electric potential difference at the nanopore Veff due to the growing impedance at the solution/Pt interfaces.
Since it is hard to imagine a gradual decrease in the mobility of the polymer spheres or ionic strength of the electrolyte buffer during the resistive pulse measurements, physical mechanisms other than the RC coupling should be responsible for the τ2 (tcap) characteristics. What largely determines the particle motions at the orifice is the balance between the counteracting electrophoretic and hydrodynamic drag forces (Tsutsui et al., 2021; Firnkes et al., 2010; Xu et al., 2021; Stein et al., 2010). As these forces both become stronger with the transmembrane voltage, it gives non-straightforward Vb dependence of the translocation dynamics (Bacri et al., 2011). For the present system, increasing voltage led to a monotonic elongation of tcap manifesting a more rapid increase in the hydrodynamic drag force compared to the electrophoretic counterpart (Figure 7B; see also Figure S6 that explains why tcap increases rapidly at above 0.4 V) (Tsutsui et al., 2021), i.e. faster translocation under lower Vb (here, Ag/AgCl was used to avoid the influence of the ion diffusion at the solution/electrode interfaces). Analogous discussion can be made to explain the plots in Figures 6C and 7A. At the beginning of the measurement with Pt electrodes, the impedance at the solution/electrode interfaces was low so that a large portion of Vb was focused at the nanopore. Later, however, the Cottrell diffusion steadily enlarged the interfacial resistance Rele at the electrodes. When it became comparable to Rpore, the voltage started to drop largely at the electrodes. As a consequence, the electric potential difference Veff across the nanopore became weaker over time (Figure 7C). Concurrently, it led to shorter tcap by the altered balance between the electrophoretic and hydrodynamic drag forces. In contrast to Pt, the low electrode impedance at the solution-Ag/AgCl interfaces led to Veff ∼ Vb, and hence relatively long τ2 due to the electroosmotic flow-derived slow motions of the nanoparticles at the nanopore entrance (with the aforementioned influence of the ionic strength as shown in Figure S4). Although it is not possible to quantify the effect of the interfacial impedance on the translocation dynamics of the nanoparticles due to the uncertainty in the time-evolved resistance distributions between the electrodes and the membrane, the above results elucidate another outcome of the electrode ion diffusion to vary the translocation motions of analytes.
Discussion
The present findings prove the important roles of electrode materials in nanopore sensing. Ag/AgCl is confirmed to be particularly useful to obtain persistent ionic current in a chloride solution for reliable resistive pulse detections of particles and molecules. Unlike the non-polarizable electrodes, electrochemical reactions at the platinum surfaces involve no precipitation/adsorption of reactants, and so induce growing interfacial impedance. This Cottrell diffusion-derived resistance was demonstrated to substantially degrade the temporal resolution of the ionic current measurements as well as to change the translocation dynamics of analytes in a time-varying manner, which would be fatal to discriminate analytes such as viruses (Arima et al., 2020) and proteins (Houghtaling et al., 2018, 2019) by the difference in the ionic signal waveforms. Yet, electrochemistry predicts a way to make such electrodes still useful by employing large electrode surface area with high ionic strength for mitigating the impedance increase to allow resistive pulse sensing for a certain period of time before it becomes comparable to the resistance at a nanopore. Conversely, it also cautions that care should be taken when utilizing microfabricated electrodes that may augment the electrode ion diffusion interference even with Ag/AgCl (Chia et al., 2019).
Limitations of the study
We note that the present work studied the roles of electrode materials for only 300 nm diameter nanopores. Considering that smaller nanopores possess larger Rpore, the roles of the Cottrell diffusion may change as the voltage division at Rele would become smaller. On contrary, the choice of electrode materials is predicted to become more important when using micropores where smaller pore resistance gives rise to more pronounced influence of Rele on the ionic current characteristics. Further efforts should be devoted to clarify this point.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, peptides, and recombinant proteins | ||
| Phosphate buffered saline | Nippon Gene | Cat#: 314-90185 |
| Polystyrene beads | Polysciences | Cat#: 08216-15 |
| Potassium ferricyanide K3Fe(CN)6 | Fujifilm Wako Chemicals | Cat#: 167-03722 |
| Potassium ferricyanide K4Fe(CN)6 | Fujifilm Wako Chemicals | Cat#: 161-03742 |
Resource availability
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Makusu Tsutsui (tsutsui@sanken.osaka-u.ac.jp).
Materials availability
This study did not generate new unique reagents.
Method details
Fabrication of micro- and nanopores
A 4-inch silicon wafer both sides of the surfaces covered with the low-pressure chemical vapor deposition-grown SiNx layers of 50 nm thickness was purchased from Electronics & Materials Co. and used as substrates after dicing into 30 mm × 30 mm pieces with a dicer. SiNx at one side of the substrate was partially removed by reactive ion etching through a metal mask, which created an approximately 1 mm square area of Si. The Si surface was then exposed to KOH aq. and heated to 80°C for deep wet etching. This formed a trench with a 40 nm-thick SiNx membrane at the bottom (due to thinning of the SiNx by about 10 nm during the wet etching). On the SiNx membrane, an electron beam resist ZEP520A (Zeon) was spin-coated. After baking at 180°C, a circle of diameter 300 nm was delineated by an electron beam lithography. Developing the pattern, the substrate was treated with the reactive ion etching to open a nanopore, where the residual resist layer served as a mask. Finally, the nanopore chip was immersed in N,N Dimethylformamide overnight to dissolve the resist followed by rinsing with ethanol and acetone.
Resistive pulse measurements
Polymer blocks were prepared by curing PDMS precursor (Sylgard184, Dow) and baking at 80°C for 5 h. The blocks were adhered on both sides of the nanopore chip by activating the surfaces with oxygen plasma. Three holes were punched in the blocks that served as inlet and outlet of sample solution as well as a place to put the electrode, either a Ag/AgCl or Pt rod of diameter 0.8 mm, for the ionic current measurements. After filling the pore with dilute suspension of nominally 200 nm-sized carboxylated polystyrene nanobeads (Polysciences) in diluted phosphate buffered saline, the voltage Vb was applied to one of the electrodes and the output ionic current was measured through the other electrode at 1 MHz using a custom-designed current amplifier and a digitizer (NI-5922, NI).
Data analyses
Resistive pulses were extracted from the raw ionic current curves by first offsetting the open pore current to zero. This was implemented by subtracting the linearly-fit components in every 0.5 s region. The pulse signals were then identified by searching local minima of the ionic current using a threshold level of −1 nA. Subsequently, the ionic current data of 5 milliseconds before and after each minimal point were saved. The resistive pulses obtained in this way were then fit by exponential functions to deduce τ1 and τ2. All the computational tasks were performed by codes written in Python.
Finite element simulations
Ionic blockade current and electroosmotic flow velocity in a nanopore were simulated with coupled Poisson-Nernst-Planck and Navier-Stokes equations using AC/DC, Chemical Reaction Engineering, and Computational Fluid Dynamics (CFD) modules in COMSOL. We defined a 25 μm diameter and 40 nm thick SiNx disk with a hole of 150 nm radius at the center in a cylindrical coordinate system. The nanopore was filled with NaCl solution of dynamic viscosity of η = 10−3 Pa s. Surface charge density of polystyrene beads and nanopore wall surface was set according to the zeta potential measured using a zeta-sizer (Malvern Panalytical). The permittivity of SiNx and water was assumed to be the same as that of the bulk.
Acknowledgments
A part of this work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 22H01926.
Author contributions
Conceptualization, M. Tsutsui and M. Taniguchi; Methodology, I.W.L., S.K., and M. Tsutsui; Investigation, I.W.L., S.K., and M. Tsutsui; Writing- Original Draft, M. Tsutsui; Writing – Review & Editing, M. Tsutsui; Funding Acquisition, M. Tsutsui; Resources, M. Tsutsui.
Declaration of interests
The authors declare no competing interests.
Published: October 21, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.isci.2022.105073.
Supporting Citations
The following references appear in the Supplemental information: Ermann et al., 2018; Yukimoto et al., 2013.
Supplemental information
Data and code availability
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
This paper does not report original code.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
References
- Arima A., Tsutsui M., Yoshida T., Tatematsu K., Yamazaki T., Yokota K., Kuroda S., Washio T., Baba Y., Kawai T. Digital pathology platform for respiratory tract infection diagnosis via multiplex single-particle detections. ACS Sens. 2020;5:3398–3403. doi: 10.1021/acssensors.0c01564. [DOI] [PubMed] [Google Scholar]
- Bacri L., Oukhaled A.G., Schiedt B., Patriarche G., Bourhis E., Gierak J., Pelta J., Auvray L. Dynamics of colloids in single solid-state nanopores. J. Phys. Chem. B. 2011;115:2890–2898. doi: 10.1021/jp200326w. [DOI] [PubMed] [Google Scholar]
- Baehre D., Ernst A., Weißhaar K., Natter H., Stolpe M., Busch R. Electrochemical dissolution behavior of titanium and titanium-based alloys in different electrolytes. Procedia CIRP. 2016;42:137–142. [Google Scholar]
- Chia C., Jeffrey S.S., Howe R.T. Anomalous hysteresis and current fluctuations in cyclic voltammograms at microelectrodes due to Ag leaching from Ag/AgCl electrodes. Electrochem. Commun. 2019;105:106499. [Google Scholar]
- Ermann N., Hanikel N., Wang V., Chen K., Weckman N.E., Keyser U.F. Promoting single-file DNA translocations through nanopores using electro-osmotic flow. J. Chem. Phys. 2018;149:163311. doi: 10.1063/1.5031010. [DOI] [PubMed] [Google Scholar]
- Firnkes M., Pedone D., Knezevic J., Döblinger M., Rant U. Electrically facilitated translocations of proteins through silicon nitride nanopores: conjoint and competitive action of diffusion, electrophoresis, and electroosmosis. Nano Lett. 2010;10:2162–2167. doi: 10.1021/nl100861c. [DOI] [PubMed] [Google Scholar]
- Fried J.P., Swett J.L., Nadappuram B.P., Mol J.A., Edel J.B., Ivanov A.P., Yates J.R. In situ solid-state nanopore fabrication. Chem. Soc. Rev. 2021;50:4974–4992. doi: 10.1039/d0cs00924e. [DOI] [PubMed] [Google Scholar]
- Gao R., Lin Y., Ying Y.L., Hu Y.X., Xu S.W., Ruan L.Q., Yu R.J., Li Y.J., Li H.W., Cui L.F., Long Y.T. Wireless nanopore electrodes for analysis of single entities. Nat. Protoc. 2019;14:2015–2035. doi: 10.1038/s41596-019-0171-5. [DOI] [PubMed] [Google Scholar]
- Garaj S., Hubbard W., Reina A., Kong J., Branton D., Golovchenko J.A. Graphene as a subnanometre trans-electrode membrane. Nature. 2010;467:190–193. doi: 10.1038/nature09379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y., Tsutsui M., Zhou Y., Miao X.-S. Solid-state nanopore systems: from materials to applications. NPG Asia Mater. 2021;13:48. [Google Scholar]
- Henriquez R.R., Ito T., Sun L., Crooks R.M. The resurgence of Coulter counting for analyzing nanoscale objects. Analyst. 2004;129:478–482. doi: 10.1039/b404251b. [DOI] [PubMed] [Google Scholar]
- Holz M., Heil S.R., Sacco A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMRPFG measurements. Phys. Chem. Chem. Phys. 2000;2:4740–4742. [Google Scholar]
- Houghtaling J., List J., Mayer M. Nanopore-based, rapid characterization of individual amyloid particles in solution: concepts, challenges and prospects. Small. 2018;14:1802412. doi: 10.1002/smll.201802412. [DOI] [PubMed] [Google Scholar]
- Houghtaling J., Ying C., Eggenberger O.M., Fennouri A., Nandivada S., Acharjee M., Li J., Hall A.R., Mayer M. Estimation of shape, volume, and dipole moment of individual proteins freely translocating a synthetic nanopore. ACS Nano. 2019;13:5231–5242. doi: 10.1021/acsnano.8b09555. [DOI] [PubMed] [Google Scholar]
- Hu Z., Huo M., Ying Y., Long Y. Biological nanopore approach for single-molecule protein sequencing. Angew. Chem. 2020;133:14862–14873. doi: 10.1002/anie.202013462. [DOI] [PubMed] [Google Scholar]
- Jaksic M., Johansen B., Tunold R. Electrochemical behaviour of platinum in alkaline and acidic solutions of heavy and regular water. Int. J. Hydrogen Energy. 1993;18:817–837. [Google Scholar]
- Kishimoto S., Murayama S., Tsutsui M., Taniguchi M. Crucial role of out-of-pore resistance on temporal response of ionic current in nanopore sensors. ACS Sens. 2020;5:1597–1603. doi: 10.1021/acssensors.0c00014. [DOI] [PubMed] [Google Scholar]
- Kowalczyk S.W., Grosberg A.Y., Rabin Y., Dekker C. Modeling the conductance and DNA blockade of solid-state nanopores. Nanotechnology. 2011;22:315101. doi: 10.1088/0957-4484/22/31/315101. [DOI] [PubMed] [Google Scholar]
- Lee G.-Y., Park J.-H., Chang Y.W., Cho S., Kang M.-J., Pyun J.-C. Chronoamperometry-based redox cycling for application to immunoassays. ACS Sens. 2018;3:106–112. doi: 10.1021/acssensors.7b00681. [DOI] [PubMed] [Google Scholar]
- Lee S.H., Rasaiah J.C. Proton transfer and the mobilities of the H+ and OH- ions from studies of a dissociating model for water. J. Chem. Phys. 2011;135:124505. doi: 10.1063/1.3632990. [DOI] [PubMed] [Google Scholar]
- Liao C., Antaw F., Wuethrich A., Anderson W., Trau M. Configurable miniaturized 3D pores for robust single-nanoparticle analysis. Small Struct. 2020;1:2070006. [Google Scholar]
- Luo J., Sam A., Hu B., DeBruler C., Wei X., Wang W., Liu T.L. Unraveling pH dependent cycling stability of ferricyanide/ferrocyanide in redox flow batteries. Nano Energy. 2017;42:215–221. [Google Scholar]
- Messerschmitt F., Kubicek M., Schweiger S., Rupp J.L. Memristor kinetics and diffusion characteristics for mixed anionic-electronic SrTiO3-δ bits: the memristor-based Cottrell analysis connecting material to device performance. Adv. Funct. Mater. 2014;24:7448–7460. [Google Scholar]
- Mojtabavi M., Tsai W.-Y., Vahid-Mohammadi A., Zhang T., Gogotsi Y., Balke N., Wanunu M. Ionically active MXene nanopore actuators. Small. 2022;18:2105857. doi: 10.1002/smll.202105857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plesa C., Kowalczyk S.W., Zinsmeester R., Grosberg A.Y., Rabin Y., Dekker C. Fast translocation of proteins through solid-state nanopores. Nano Lett. 2013;13:658–663. doi: 10.1021/nl3042678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plesa C., Ruitenberg J.W., Witteveen M.J., Dekker C. Detection of individual proteins bound along DNA using solid-state nanopores. Nano Lett. 2015;15:3153–3158. doi: 10.1021/acs.nanolett.5b00249. [DOI] [PubMed] [Google Scholar]
- Pletcher D., Greef R., Peat R., Peter L.M., Robinson J. Woodhead Publishing Limited; 2011. Instrumental Methods in Electrochemistry. [Google Scholar]
- Stein D., Deurvorst Z., van der Heyden F.H.J., Koopmans W.J.A., Gabel A., Dekker C. Electrokinetic concentration of DNA polymers in nanofluidic channels. Nano Lett. 2010;10:765–772. doi: 10.1021/nl902228p. [DOI] [PubMed] [Google Scholar]
- Sun T., Morgan H. Single-cell microfluidic impedance cytometry: a review. Microfluid. Nanofluid. 2010;8:423–443. [Google Scholar]
- Tsutsui M., Yokota K., Arima A., Tonomura W., Taniguchi M., Washio T., Kawai T. Temporal resolution of ionic current blockade in solid-state nanopores. ACS Appl. Mater. Interfaces. 2018;10:34751–34757. doi: 10.1021/acsami.8b11819. [DOI] [PubMed] [Google Scholar]
- Tsutsui M., Yokota K., Arima A., He Y., Kawai T. Solid-state nanopore time-of-flight mass spectrometer. ACS Sens. 2019;4:2974–2979. doi: 10.1021/acssensors.9b01470. [DOI] [PubMed] [Google Scholar]
- Tsutsui M., Ryuzaki S., Yokota K., He Y., Washio T., Tamada K., Kawai T. Field effect control of translocation dynamics in surround-gate nanopores. Commun. Mater. 2021;2:29. [Google Scholar]
- van der Niet M.J., Garcia-Araez N., Hernández J., Feliu J.M., Koper M.T. Water dissociation on well-defined platinum surfaces: the electrochemical perspective. Catal. Today. 2013;202:105–113. [Google Scholar]
- van Dorp S., Keyser U.F., Dekker N.H., Dekker C., Lemay S.G. Origin of the electrophoretic force on DNA in solid-state nanopores. Nat. Phys. 2009;5:347–351. [Google Scholar]
- Wang D., Wang Y., Li H., Han Y., Hu P., Ma K., Sheves M., Jin Y. Photoactivated bacteriorhodopsin/SiNx nanopore-based biological nanofluidic generator with single-protein sensitivity. ACS Nano. 2022;16:1589–1599. doi: 10.1021/acsnano.1c10255. [DOI] [PubMed] [Google Scholar]
- Xu C., Liu Y., Xiong T., Wu F., Yu P., Wang J., Mao L. Dynamic behavior of charged particles at the nanopipette orifice. ACS Sens. 2021;6:2330–2338. doi: 10.1021/acssensors.1c00418. [DOI] [PubMed] [Google Scholar]
- Xue L., Yamazaki H., Ren R., Wanunu M., Ivanov A.P., Edel J.B. Solid-state nanopore sensors. Nat. Rev. Mater. 2020;5:931–951. [Google Scholar]
- Yukimoto N., Tsutsui M., He Y., Shintaku H., Tanaka S., Kawano S., Kawai T., Taniguchi M. Tracking single-particle dynamics via combined optical and electrical sensing. Sci. Rep. 2013;3:1855. doi: 10.1038/srep01855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Zhang B., White H.S. Electrochemistry of nanopore electrodes in low ionic strength solutions. J. Phys. Chem. B. 2006;110:1768–1774. doi: 10.1021/jp054704c. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
This paper does not report original code.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.