Charge Induced Disorder Controls the Thermal Conductivity of Entropy Stabilized Oxides

Abstract

Manipulating a crystalline material’s configurational entropy though the introduction of unique atomic species can produce novel materials with desirable mechanical and electrical properties. From a thermal transport perspective, large differences between elemental properties such as mass and interatomic force can reduce the rate at which phonons carry heat and thus reduce the thermal conductivity. Recent advances in materials synthesis have enabled the fabrication of entropy-stabilized ceramics, opening the door for understanding the implications of extreme disorder on thermal transport. Measuring the structural, mechanical, and thermal properties of single-crystal entropy stabilized oxides, we show that local ionic charge disorder can effectively reduce thermal conductivity without compromising mechanical stiffness. These materials demonstrate similar thermal conductivities to their amorphous counterparts, in agreement with the theoretical minimum limit, resulting in this class of material possessing the highest ratio of elastic modulus to thermal conductivity of any isotropic crystal.

High entropy alloys (HEAs), consisting of five or more approximately equimolar compositions of elements,[1,2] have proven to exhibit unique physical properties such as high hardness,[3] thermal stability,[4] structural stability,[5] as well as corrosion, oxidation, and wear While resistance.[6–8] While microstructure and mechanical properties have been extensively studied, thermal properties, such as heat capacity and thermal conductivity, have been given far less attention.[9–11] Although the random distribution of atomic configurations in HEAs are appealing for understanding the role of configurational disorder on thermal transport, insight is limited by the significant electronic contribution that arises from the metallic nature of most HEAs, which can obscure insight into the lattice thermal conductivity. When nonmetal constituents comprise a disordered solid solution, the dynamics of thermal transport becomes dominated by phonons. However, only recently was the concept of entropy stabilization realized in ceramics,[12] allowing for an ideal platform to study the role of mass and interatomic force disorder beyond what has been previously accessible. Since the conception of these ceramics, high entropy oxides have demonstrated the capability for superionic mobility[13] and thermochemical water splitting.[14] Furthermore, high configurational entropy can be highly beneficial to the development of thermoelectric properties.[15] Understanding the general implications of extreme configurational entropy on the lattice thermal conductivity would greatly benefit the design of high entropy materials for use in such applications.

To this end, we study the thermal properties of a new class of mixed oxides analogous to their HEA metallic counterparts, entropy stabilized oxides (ESOs), characterized by their high configurational entropy that leads to structural and chemical stabilization through a local minimization of Gibbs free energy.[12] Each ESO forms a single phase, single crystal rocksalt structure having a fixed oxygen anion sublattice; between each oxygen atom pair sits a cation randomly selected among the equiprobable distribution of 5 or 6 unique elements. The ESOs (see Table I) include J14 (Mg_xNi_xCu_xCo_xZn_xO, x = 0.2), and five 6-cation oxides made up of the J14 composition plus an additional cation to include Sc (J30), Sb (J31), Sn (J34), Cr (J35), and Ge (J36). We show that ESOs possess amorphous-like thermal conductivities that, in contrast to analytical theory, drop by a factor of two when adding an additional cation species to a 5-cation crystal, regardless of the mass added. Using extended X-ray absorption fine structure, we isolate the mechanism of this reduction to atomic level disorder resulting from charge differences among the ions. This local atomic disorder manifests itself in an observable distortion of the oxygen sublattice while pre serving long range crystallographic order measured with X-ray diffraction. This finding is further corroborated by molecular dynamics simulations that account for differences among interatomic forces through electrostatic interactions based on Bader charges taken from density functional theory calculations.

TABLE I.

Thermal and physical properties of ESOs at room temperature. Compositions and measured properties include film thickness (d), thermal conductivity (κ), volumetric heat capacity (C_v), and elastic modulus (E).

Name	Composition	d (nm)	$\kappa \left(\frac{\text{W}}{\text{mK}}\right)$	${\text{C}}_{\text{v}}\left(\frac{\text{MJ}}{{\text{m}}^3\text{K}}\right)$	E (GPa)
J14	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_x{\text{Zn}}_x\text{O}$, x = 0.2	114 ± 2	2.95 ± 0.25	3.01 ± 0.49	152.0 ± 10.6
J30	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_x{\text{Zn}}_x{\text{Sc}}_x\text{O}$, x = 0.167	149 ± 4	1.68 ± 0.13	3.37 ± 0.42	236.7 ± 15.9
J31	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_x{\text{Zn}}_x{\text{Sb}}_x\text{O}$, x = 0.167	117 ± 6	1.41 ± 0.17	3.29 ± 0.54	158.4 ± 10.9
J34	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_x{\text{Zn}}_x{\text{Sn}}_x\text{O}$, x = 0.167	118 ± 2	1.44 ± 0.10	3.29 ± 0.44	180.8 ± 17.9
J35	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_{x}Z{\text{n}}_x{\text{Cr}}_x\text{O}$, x = 0.167	109 ± 8	1.64 ± 0.24	3.96 ± 0.75	151.0 ± 9.2
J36	${\text{Mg}}_x{\text{Ni}}_x{\text{Cu}}_x{\text{Co}}_x{\text{Zn}}_x{\text{Ge}}_x\text{O}$, x = 0.167	109 ± 3	1.60 ± 0.14	3.55 ± 0.48	229.9 ± 21.2

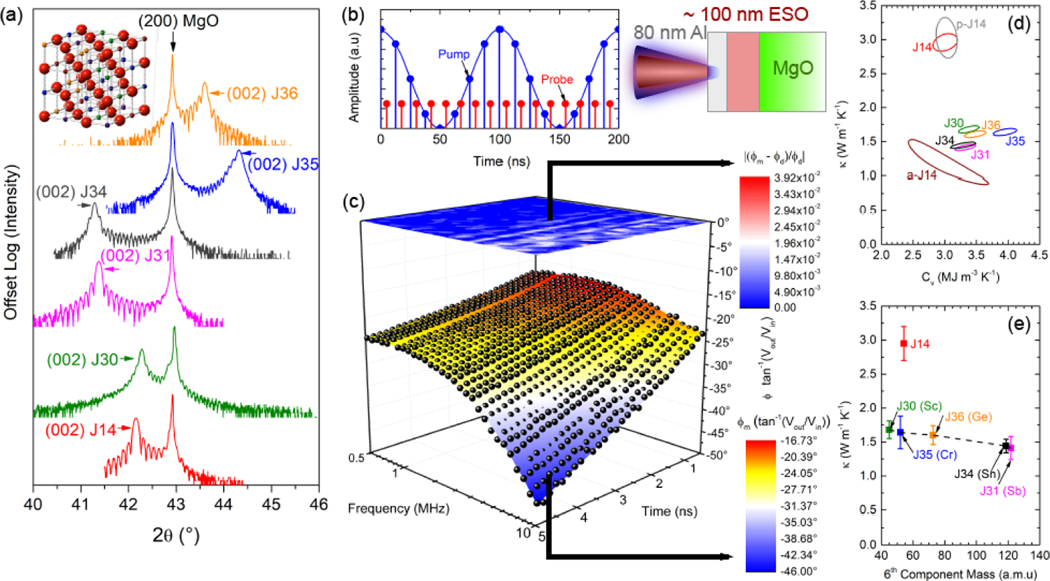
ESO thin films were grown epitaxially on MgO substrates using pulsed laser deposition. Because the ESOs are pinned in-plane to the MgO substrate, their in-plane lattice parameters match that of MgO at 4.21 Å, whereas the out-of-plane lattice parameters vary slightly based on composition. Crystal structures were characterized using X-ray diffraction (XRD). Figure 1(a) shows the 2θ-ω XRD scan around the (200) MgO substrate peak. Lower (higher) 2θ indicates larger (smaller) out of-plane lattice parameters. Thermal characterization was performed using a combined time- and frequency-domain thermoreflectance technique (see Methods) to simultaneously measure the thermal conductivity (κ) and volumetric heat capacity (C_v) of the thin-film ESO samples by modulating the pump heating event over a range of frequencies large enough to decouple thermal diffusivity from thermal effusivity. A schematic of the experiment and the sample geometry is shown in Fig. 1(b). The resulting best-fit surface model and data are shown in Fig. 1(c) for J14, along with the normalized residuals, for the phase as a function of delay time and modulation frequency. From this, we follow the procedure outlined by Wang et al.[16] to determine the 95% confidence interval of fitted thermal conductivity and heat capacity based on the 2 standard deviation difference from the minimum normalized residual. Figure 1(d) shows the results for J14 and all 6-component ESOs, where contour lines indicate the combinations of κ and C_v corresponding to a 95% confidence interval.

FIG. 1.

Structural and Thermal Characterization. (a) 2θ-ω X-ray diffraction scan around the (200) MgO substrate peak. Inset shows J14 crystal structure with red anions representing oxygen and cation cites occupied by a random distribution of five distinct elements. (b) Schematic for TDTR/FDTR experiment: sample is 80 nm Aluminum on a ~100 nm ESO film grown on an MgO substrate. Laser heating by a modulated pulsed pump is detected by a probe by locking into the pump modulation frequency; the modulation frequency is varied and the probe is delayed in time relative to the pump, creating a time and frequency space to which to fit a thermal model. (c) Combined TDTR/FDTR experimental phase data ($\varphi ={\tan }^{-1}\left(V_{\text{out}}/V_{\text{in}}\right)$) and surface fit for J 14 at room temperature (symbols), together with the best-fit thermal model and resulting normalized residuals $\left(\left|\left({\varphi }_{\text{m}}-{\varphi }_{\text{d}}\right)/{\varphi }_{\text{d}}\right|\right)$. (d) Contour of deviation sum as functions of κ and C_v all thin film samples, as determined by the 95% confidence interval in the normalized residuals. Sample compositions are provided in Table I. (e) κ vs. 6th-cation atomic mass for 6-cation ESOs. For reference, κ of J14 is also shown at it’s average cation mass.

There is a strong reduction in thermal conductivity between J14 and all 6-cation oxides; variation in κ among the latter are within 20% of one another and follow an expected decreasing trend with heavier average cation mass, as shown in Fig. 1(e). Accounting for uncertainties arising from film thicknesses and thermal properties does not explain this reduction from 5- to 6-cations. This finding suggests that there is an enhanced level of phonon scattering intrinsic to the 6-cation oxides compared to J14 that is dictating the observed reduction in thermal conductivity. Furthermore, a 105 nm polycrystalline J14 sample (p-J14) was fabricated on an amorphous SiO₂ (a-SiO₂) substrate; grain sizes were on the order of 50–100 nm as determined by atomic force microscopy (AFM). Grain boundaries typically scatter phonons on the order of the grain size,[17, 18] which would reduce the thermal conductivity of p-J14 relative to single crystal J14. Because the substrate is a-SiO₂ in this case, heat capacity and thermal conductivity cannot be decoupled (see Supporting Information for details). However, if we assume that the heat capacity is that of J14, the thermal conductivity is, within uncertainty, equal to that of J14. This indicates that phonon scattering at grain boundaries negligibly affects the thermal conductivity, suggesting that the phonons contributing most strongly to thermal transport in J14 have mean free paths smaller than this average grain size. Moreover, this result indicates that even with additional external scattering mechanisms, the thermal conductivity of J14 does not reduce to those of the 6-cation oxides. To understand the significance of this reduction in thermal conductivity, we measure a 78 nm amorphous J14 (a-J14) film grown on a-SiO₂. Again assuming the same heat capacity as J14, the thermal conductivity of a-J14 is 1.16±0.16, almost a third of that of J14, and within 20% of the thermal conductivity of J31. This amorphous thermal conductivity is typically assumed to be the minimum limit to the intrinsic thermal conductivity of a solid.[19]

Reduced crystalline thermal conductivity approaching the amorphous limit is an attractive property to several applications, including thermoelectric power generation[20] and thermal barrier coatings,[21] where crystalline materials allow for the desirable electronic properties and temperature stability necessary for extreme environments. Such reduction is often achieved via nanostructuring with defects and/or interfaces, the latter of which resulted in the lowest thermal conductivity measured in a fully dense solid at 0.05 W m⁻¹ K⁻¹ for WSe₂ in the cross-plane direction,[22] a 30× reduction over the c-axis thermal conductivity of single-crystal WSe₂. For macroscale applications in which films inevitably become large enough that grains of varying orientations form, thermal conductivity reduction in one crystallographic direction does not have significant benefit. Thus, for isotropic crystals, such reduction is typically achieved via increasing compositional disorder,[23] which can lead to mass mismatch, atomic radii mismatch, and local atomic strain that results in additional phonon scattering. For example, mixed crystals with controlled disorder were shown to have thermal conductivities that approach their minimum limit.[19] Similarly, unary and binary compound superatomic crystals were shown to have amorphous-like thermal conductivities when orientational disorder is present.[24] On the other hand, many complex crystals such as the cubic I-V-V1₂ semiconductor AgSbTe₂ have intrinsically glass-like thermal conductivities[25] attributed to extreme nanoscale domains with different orderings on the cation sublattice.[26]

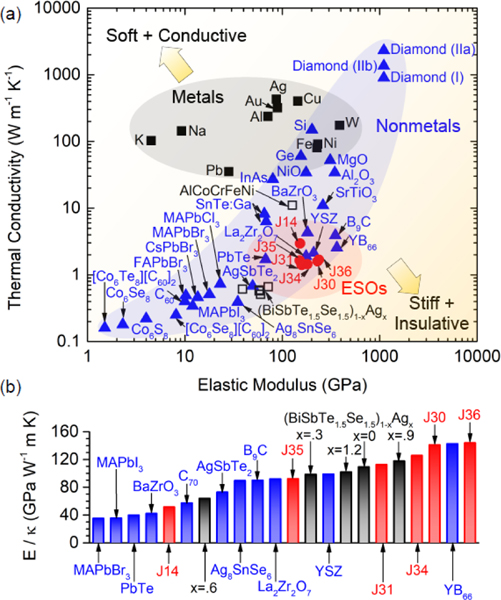
Regardless of the mechanism, a thermal conductivity reduction generally comes at the expense of a crystal’s stiffness, as determined by its elastic modulus. This is shown in Fig. 2(a), where thermal conductivity is plotted as a function of elastic modulus for a wide array of isotropic crystals. Whereas metals can maintain a relatively high thermal conductivity due to contribution from electron transport, phonons are the dominant heat carriers in nonmetals; reduction of elastic modulus is indicative of a reduction in phonon group velocity and energies, resulting in a lowered thermal conductivity. As shown in Fig. 2(a), the regime of simultaneously stiff and insulative crystals is unpopulated, despite the need in practical applications such as thermal barrier coatings. We show that ESOs, whose elastic modulus is measured with contact resonance atomic force microscopy (CR-AFM), represent a step towards filling this void. In fact, in Fig. 2(b) we quantify the ratio of elastic modulus to thermal conductivity (E/κ) to show that ESOs fall in line with the highest E/κ crystals at room temperature, surpassing prominent thermal barrier coating materials such as zirconates BaZrO₃, and La₂Zr₂O₇ and the most commonly used Y₂O₃-stabilized ZrO₂ (YSZ).[27] By comparison, HEAs have elastic moduli falling anywhere from 20 to 180 GPa,[28] while thermal conductivities generally fall in the range of >10 W m⁻¹ K⁻¹,[28] The general metallic nature of most HEAs mean that they will have relatively large contributions from electrons to thermal conductivity. However, recent developments in HEAs for use in thermoelectric applications[11, 29], have demonstrated that HEAs can have thermal conductivities as low as 0.5 W m⁻¹ K⁻¹ at room temperature.[11] Because E/ κ ($\propto 1/C\tau$, where C is heat capacity and $\tau$ is phonon scattering time) is indicative of the phonon scattering rate, the high ratios observed for the ESOs demonstrate the use of entropy stabilization with multiple components to reduce phonon scattering times rather than velocities, which opens the door to unique combinations of properties, in this case simultaneously high elastic modulus and near-minimum thermal conductivity.

FIG. 2.

Thermal and elastic properties of crystals. (a) Thermal conductivity (κ) vs. elastic modulus (E ) for a wide range of isotropic crystal s at room temperature. Material s are grouped into metals (squares) and nonmetals (triangles), the former having the subset of high entropy alloys (open squares) and the latter having the subset of ESOs (circles). (b) Ratio of E to κ for the highest-ratio crystals from (a). A table of data and references can be found in the Supporting Information.

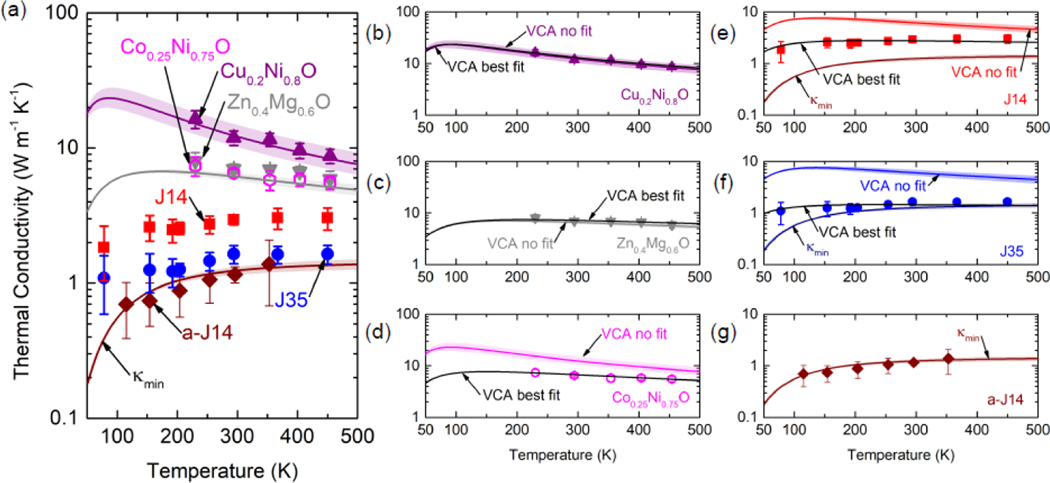
To better understand this reduction in thermal conductivity from 5- to 6-cations, we measure the thermal conductivities of J 14 and J35 over a temperature range of 78 – 450 K, presented in Fig. 3(a). J14 and J35 have nearly identical average mass, thickness, and sound speed, making the two ideal candidates to compare. A similar reduction in thermal conductivity is observed in J35 compared to J14 at all temperatures tested. Unlike typical crystalline materials’ thermal conductivity trends with temperature, both J14 and J35 display trends indicative of amorphous materials, having increasing thermal conductivities with temperature. To put this into perspective, we measure the thermal conductivity of a-J14 to show this characteristic amorphous thermal conductivity relation with temperature, revealing that J35 shows similar magnitudes of thermal conductivity to those of a-J14 at comparable temperatures. Furthermore, we measure 2-cation oxides of ${\text{Cu}}_{0.2}{\text{Ni}}_{0.8}\text{O}$, ${\text{Zn}}_{0.4}{\text{Mg}}_{0.6}\text{O}$, ${\text{Co}}_{0.25}{\text{Ni}}_{0.75}\text{O}$ at 230 – 450 K to show the characteristic Umklapp scattering trend ($\propto 1/T$) expected in crystalline materials and enhanced thermal conductivity relative to J14/J35. Qualitatively, the addition of cations results in greater deviation from a perfect crystal, which reduces thermal conductivity through increased phonon scattering. We model this phonon scattering to estimate the thermal conductivity as a function of temperature using the virtual crystal approximation (VCA)[30], details and assumptions for which are provided in the Supporting Information.

FIG. 3.

(a) Thermal conductivity vs. temperature. Purple and gray lines depict VCA models without fitting parameters for Cu_0.2Ni_0.80 and Zn_0.4Mg_0.60, while maroon line is the minimum thermal conductivity model for J14 ($k_{\min }$); shaded regions indicate uncertainties in the model. Thermal conductivity data is shown together with VCA models with and without adjustable parameters for (b) ${\text{Cu}}_{0.2}{\text{Ni}}_{0.8}\text{O}$, (c) ${\text{Zn}}_{0.4}{\text{Mg}}_{0.6}\text{O}$, (d) ${\text{Co}}_{0.25}{\text{Ni}}_{0.75}\text{O}$, (e) J14 (f) J35, and (g) a-J14.

Assessing the VCA as a predictive model, Fig. 3 shows that it accurately describes the thermal conductivity relation with temperature for both (b) ${\text{Cu}}_{0.2}{\text{Ni}}_{0.8}\text{O}$ and (c) ${\text{Zn}}_{0.4}{\text{Mg}}_{0.6}\text{O}$ when considering only mass disorder as the phonon-defect scattering process. The VCA, while capturing the Umklapp scattering temperature trend observed experimentally, does not accurately predict the magnitude of thermal conductivity for (d) ${\text{Co}}_{0.25}{\text{Ni}}_{0.75}\text{O}$, owing to the nearly identical mass of Co and Ni, suggesting the need to include additional phonon scattering due to variations in the interatomic force constants (IFCs). For the purposes of the VCA analytical model, we treat the IFC scattering rate coefficient and the Grüneisen parameter, which affects normal scattering rates, as fitting parameters. With these adjustable parameters, the VCA can accurately capture the measured thermal conductivity, as depicted in Fig. 3(d). Addition of these fitting terms proves to make a negligible difference for (b) ${\text{Cu}}_{0.2}{\text{Ni}}_{0.8}\text{O}$ and (c) ${\text{Zn}}_{0.4}{\text{Mg}}_{0.6}\text{O}$. Overall, the VCA captures the thermal conductivity of these 2-cation oxides with reasonable agreement to experiment.

When applied to 5- and 6-component ESOs, the VCA lacks predictive capability in both magnitude and temperature trend; this is shown in Fig. 3(e) and (f) for J14 and J35, respectively. In fact, the VCA predicts that J14 and J35 should have higher thermal conductivities than both ${\text{Zn}}_{0.4}{\text{Mg}}_{0.6}\text{O}$ and ${\text{Co}}_{0.25}{\text{Ni}}_{0.75}\text{O}$ due their virtual crystal’s average mass having a smaller weighted difference with constituent masses than do the 2-component oxides. Indeed, a saturation of phonon scattering from mass disorder limits the thermal conductivity reduction achievable with an increasing number of components.[31] A similar argument can be made regarding additional terms describing disorder scattering in the VCA, which are likewise defined by the difference between average and constituent properties. While fitting parameters allow for better agreement between the VCA and experimental thermal conductivities, no combination of Grüneisen parameter and IFC scattering rate can capture the amorphous-like temperature trend. However, this amorphous-like trend has been observed in a variety of complex crystalline systems.[23] In such cases, the minimum thermal conductivity (κ_min) model[19] can be invoked to lend insight into experimental findings. We show in Fig. 3(g) that ${\kappa }_{\text{min}}$, as defined for J14 based on sound speed derived from CR-AFM, agrees well with experimental thermal conductivities for a-J14 and reasonably captures J35’s thermal conductivity.

That the VCA fails to capture the trend in thermal conductivity of J14 and J35 may be interpreted by recent developments by Seyf et al.,[32] who hypothesize that non-propagating modes (diffusons) can comprise the majority of vibrational modes contributing to thermal conductivity when disorder becomes large. This manifests itself in amorphous-like thermal conductivity trends with temperature. Moreover, we do not observe any statistically significant size effects in thermal conductivity for the samples tested here (see Supporting Information), further supporting the idea that either diffusons or short mean-free-path phonons/propagons dominate thermal transport in these systems. An alternative interpretation, however, is that if the VCA is valid, the temperature-independent Rayleigh scattering may be large enough to overwhelm Umklapp scattering. Indeed, if we remove Umklapp scattering from the VCA model, we can reasonably emulate the thermal conductivity as a function of temperature, suggesting that Rayleigh scattering is the dominant phonon scattering mechanism dictating thermal conductivity (see Supporting Information). Finally, although strong anharmonic phonon scattering has been shown to arise due to large mass disorder,[33] the thermal expansion coefficient for the ESOs are measured via temperature-dependent XRD to be ~1.2 – 1.4×10⁻⁵/°C,in agreement with constituent oxides $\text{MgO}$[34] and $\text{NiO}$,[35] suggesting anharmonic scattering is not abnormally strong in the ESOs. Therefore, the temperature-independent nature of the mechanism causing reduction in thermal conductivity in ESOs, in particular that driving down 5- to 6-cation thermal conductivities, suggests strong Rayleigh scattering resulting from IFC disorder. The best-fit VCA models reveal that IFC disorder-induced scattering must be ~2.8× higher in J35 than in J14 to account for the difference in thermal conductivities between the two. We emphasize that J14 and J35 have approximately the same average mass. Additionally, we systematically increase mass disorder among 6-component oxides via increasing 6^th-cation mass (Fig. 1(f)) to conclude that while this increase leads to a reduction in thermal conductivity, the variation is less than 20%, far from the level of reduction needed to explain the difference from that of J14. Therefore, we hypothesize that there is a strong IFC disorder mechanism driving the enhanced reduction in thermal conductivity. Such a mechanism should be observable via differences in the local structure within the unit cell of J14 and J35.

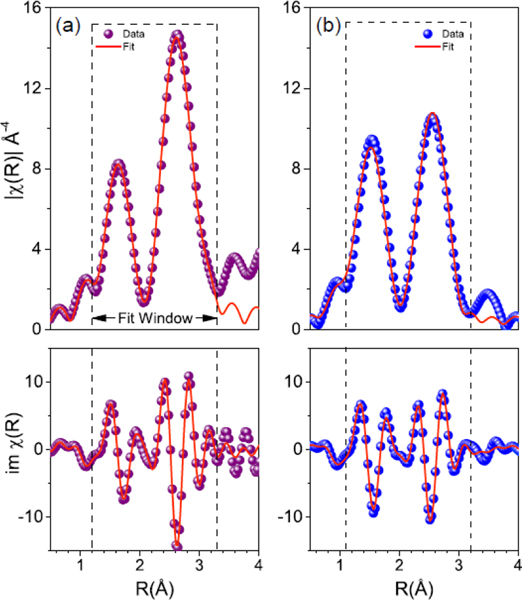
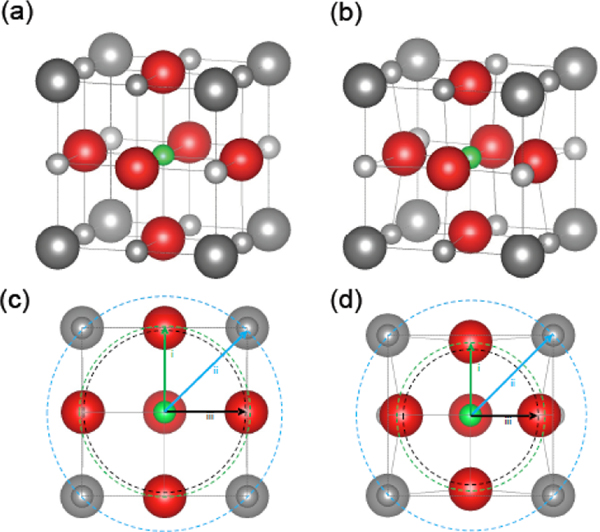
To test this hypothesis, we use extended X-ray absorption fine structure (EXAFS)[36–39] to observe changes in the local coordination environment about Co absorbers in J14 and J35. While XRD revealed crystallographic order, EXAFS allows for an atomic-level probe of the local crystal structure needed for determination of any observable quantity that would reveal such IFC disorder. Figure 4 shows fits to the phase-uncorrected, self-absorption corrected magnitude and imaginary part of the real space function $\chi (R)$ for (a) J14 and (b) J35, obtained by taking the Fourier transform of the EXAFS spectra, $k^2\chi (k)$, using a Keiser-Bessel window in the range of 3.75 – 10 Å^−l. Each $\chi (R)$ is consistent with a typical metal-oxide system, where the first and second peaks correspond to scattering between the absorber and atoms in the first and second coordination shells, respectively. Figure 5 illustrates the modified unit cell for both (a) J14 and (b) J35 compositions extracted by EXAFS. For J14, we find an expected distortion of the Co octahedra that coincides with the observed lattice parameters of the tetragonal unit cell, a = 4.21 Å and c = 4.29 Å. By the second coordination shell, or absorber-metal scattering paths, we find that the half-path length agrees with observed lattice parameters within less than 1%. The addition of a 6th component, as is the case in J35, appears to dramatically change the absorber octahedra such that a geometric extension no longer aligns to the lattice parameters. J35 exhibits a tetragonally compressed unit cell, with a = 4.21 Å and c = 4.08 Å. Half scattering path lengths between the Co absorber and the six nearest neighboring oxygen atoms suggest a highly compressed octahedra with 4 planar oxygens at 1.93 Å and 2 axial oxygens at 1.96 Å. Again, comparing the half scattering path length of the next nearest neighbors agrees with observed lattice parameters to within 1%. These EXAFS results largely align with our hypothesis from the thermal measurements in that a large strain is present in the 6-component ESOs such that the oxygen atoms are displaced from their ideal coordination positions. Such strong oxygen sublattice distortion is the indicator that IFC disorder is greatly enhanced in J35 relative to J14. This strong IFC disorder is promoted by charge compensation among cations to preserve charge neutrality when a 6^th cation is added.[40]

FIG. 4.

Local structure determination. Extended X-ray absorption fine structure data and models about cobalt for (a) J14 and (b) J35. Model and best fit model are shown for the magnitude (top) and imaginary portion of the real space function χ (R) as a function of radius away from the cobalt absorber (R).

FIG. 5.

Modified local structure of J14 and J35. Illustration depicting local structural changes about the cobalt species in (a) J14 and (b) J35. A comparison of the changes as a result of adding the 6th cation can be viewed by unit cell cross section along the (200) plane, as shown in (c) and (d) for J14 and J35 respectively. The lowercase roman numerals mark the coordination shell radius for i. nearest neighbor anion, ii. next nearest neighbor anion, and iii. nearest neighbor cation. In both cases, the nearest neighbor cation shell radius corresponds to one-half the face diagonal of the unit cell parameters, as determined through XRD.

The attribution of thermal conductivity reduction in ESOs to interatomic force disorder is further supported by molecular dynamics simulations (see Supporting Information) in which IFC disorder is modeled by electrostatic point charges in the interatomic potential based on Bader charges from density functional theory calculations. These simulations reveal that accounting for differences in interatomic forces homogeneously through adjustment of average properties, analogous to the VCA, cannot capture magnitude or trend in thermal conductivity, whereas heterogeneous integration of mass and charge disorder accurately captures the reduction in thermal conductivity observed between J14 and 6-cation oxides, reducing the thermal conductivity by a factor of almost two, in agreement with experiment. Moreover, in these simulations we decouple mass and charge disorder to show that the latter is responsible for the strong reduction in thermal conductivity measured. Taken together, the experiment and simulation reveal that entropy-stabilized oxides can have a uniquely low thermal conductivity while maintaining a relatively high elastic modulus, made possible through highly disordered interatomic forces resulting from charge disorder among ionic bonds. These results provide an example of the broader aspect of entropy stabilization as a means to create materials with unique thermophysical properties that could be highly beneficial to thermoelectric and thermal barrier coating applications.

Experimental Section

Time- and Frequency-Domain Thermoreflectance:

We use a combined time- and frequency-domain thermoreflectance (TDTR and FDTR) method, which is an optical pump-probe technique, to simultaneously measure the thermal conductivity and volumetric heat capacity of the thin-film ESO samples. This approach is based on the concept of varying the modulation frequency of the heating event to change the measurement property from thermal effusivity to thermal diffusivity, thereby decoupling thermal conductivity from volumetric heat capacity, allowing for a unique measurement of both quantities.[41–43] We extend the approach by Wei et al.[43] to incorporate TDTR phase data over a range of frequencies sufficient for FDTR, so as to combine the benefits of multifrequency TDTR and FDTR for thermal property measurement. This development provides a robust approach for measuring both the heat capacity and thermal conductivity of thin films.

Using the output of a pulsed Ti:Sapphire oscillator emanating 200 fs pulses at a repetition rate of 80 MHz, we divide the beam into two paths, a pump path and a probe path. The pump is used to heat a sample of interest, which has an 80 nm aluminum layer of aluminum deposited on it to serve as a transducer to convert the optical energy to thermal energy. The probe is used to measure the in-phase and out-of-phase change in thermoreflectance resulting from the pump-induced heating at time delays ranging from 200 ps to 6 ns and modulation frequencies ranging from 500 kHz to 10 MHz. A lock-in amplifier is used to ensure data collection at a given modulation frequency and improve signal-to-noise ratios. The number of data points collected are chosen such that they are sufficient for TDTR at a given frequency and pulsed-pulsed FDTR at a given probe time delay. Using a multilayer, radially symmetric thermal model incorporating both time delay and modulation frequency information directly extending from TDTR analysis procedures,[44–46] we use a surface fitting method to minimize the residuals between a time- and frequency-dependent thermal model with experimental data by varying three thermal parameters: ESO volumetric heat capacity (C_v), ESO thermal conductivity (κ), and Al/ESO thermal boundary conductance ($G_{\text{Al}/\text{ESO}}$). The ESO/MgO thermal boundary conductance ($G_{\text{ESO}/\text{MgO}}$) can in principle be set as a fitting parameter as well. However, in practice we are generally insensitive to this parameter, such that doing so gives us no additional benefit or physically meaningful information. Further details on the combined TDTR/FDTR approach and its comparison to the alternative methods to simultaneously measure C_v and κ can be found in the Supporting Information.

Extended X-ray Absorption Fine Structure:

Extended x-ray absorption fine structure (EXAFS) spectra were collected at beamline 10-BM-B at the Advanced Photon Source, Argonne National Laboratory (Lemont, IL). The Co K-edge was measured in fluorescence mode using a 4-element Vortex detector, elevated 30° above the sample. Measurement parameters varied by region of interest, determined by signal at higher k values up to re ~12 Å, as described elsewhere.[47] Individual scattering paths from Co absorbers are generated in J14 and J35 using FEFF6,[48] and fit to $\chi (R)$ using Artemis.[49] All EXAFS related uncertainty values were generated though the least squares output from fitting results.

Quantitatively, we obtain local structural information of the first and second nearest neighbors by fitting a theoretical model to the uncorrected $\chi (R)$ between ~l-3.1 Å using a Kaiser-Bessel window, including all scattering path lengths that fall within this range. The structural model used for fits is based on information obtained though X-ray diffraction, shown in Fig. 1(a), exhibiting a single phase, tetragonally strained rocksalt structure pinned in-plane to the MgO substrate. Each fit generally contains four fitting parameters: amplitude reduction factor $S_0^2$, inner potential energy shift $E_0$, half scattering path distance R, and EXAFS Debye-Waller factor ${\sigma }^2$. The resulting best-fit values for which are listed in Table S2 (see Supporting Information).

Contact Resonance Atomic Force Microscopy:

Contact resonance atomic force microscopy (CR-AFM) measurements were performed on a MultiMode 8 AFM (Bruker, Santa Barbara, CA, USA) equipped with a lock-in amplifier (Signal Recovery AMETEK, Oak Ridge, TN, USA) for CR frequency measurements. The AFM probes used were integrated PPP-SEIH silicon tips (Nanosensors, Neuchatel, Switzerland) with the first two free resonance frequencies at 102.0 kHz and 637.9 kHz and cantilever spring constant of 6.9 N/m. The same load of 84 nN was applied on the tip-sample contact in all the measurements to directly observe the stiffness response of the second CR frequency shift within a fix frequency range from 900.0 kHz to 1,200.0 kHz with a step of 50 Hz. A lock-in detection technique was used to measure the change in the CR frequency during these sweeps. A set of five measurements were made on each material, with two sets of measurements on sapphire bracketing the measurements on the ESO test materials. This measurement cycle with sapphire as reference was to confirm that the tip did not sustain wear or damage during measurements. Indeed, no significant deviations were observed in the measured CR frequencies on sapphire and all the measurements were used in the subsequent analysis. Besides these CR-AFM of the second eigenmode, a separate set of measurements were performed on all the materials studied with frequency sweeps over a larger range (100.0 kHz to 1,200.0 kHz, step 100 Hz) to observe both first and second CR frequencies. From these measurements, it was confirmed that the cantilever is well described by a spring coupled-clamped beam model with the tip located at the end of the beam.[50,51] By using this beam model, the frequencies measured on each material were normalized to the first free resonance of the cantilever and used to calculate the normalized contact stiffnesses. With the assumption of a Hertz contact geometry, these contact stiffnesses and the indentation moduli of the reference and AFM tip were used to determine the indentation modulus of a given material.[50–52] For each material, the measured second CR frequencies were used to calculate a weighted average and uncertainty of this average with the weights given by the uncertainties of the measured frequencies (the half width at the half height of the resonance peak). The uncertainty for each determined elastic modulus was calculated then by adding in quadrature the independent uncertainties from the first free-resonance of the cantilever and the second CR frequencies on the tested ESO sample and on the reference material, respectively.[51] The substrate contribution to the calculated elastic moduli was found negligible for the contact geometry, film thickness, applied loads, and materials involved in these measurements. Disclaimer: Certain commercial equipment, instruments, or materials are identified in this document. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products identified are necessarily the best available for the purpose.