Automatic counting of retinal ganglion cells in the entire mouse retina based on improved YOLOv5

Abstract

Glaucoma is characterized by the progressive loss of retinal ganglion cells (RGCs), although the pathogenic mechanism remains largely unknown. To study the mechanism and assess RGC degradation, mouse models are often used to simulate human glaucoma and specific markers are used to label and quantify RGCs. However, manually counting RGCs is time-consuming and prone to distortion due to subjective bias. Furthermore, semi-automated counting methods can produce significant differences due to different parameters, thereby failing objective evaluation. Here, to improve counting accuracy and efficiency, we developed an automated algorithm based on the improved YOLOv5 model, which uses five channels instead of one, with a squeeze-and-excitation block added. The complete number of RGCs in an intact mouse retina was obtained by dividing the retina into small overlapping areas and counting, and then merging the divided areas using a non-maximum suppression algorithm. The automated quantification results showed very strong correlation (mean Pearson correlation coefficient of 0.993) with manual counting. Importantly, the model achieved an average precision of 0.981. Furthermore, the graphics processing unit (GPU) calculation time for each retina was less than 1 min. The developed software has been uploaded online as a free and convenient tool for studies using mouse models of glaucoma, which should help elucidate disease pathogenesis and potential therapeutics.

INTRODUCTION

Glaucoma describes a group of diseases characterized by optic papillary atrophy and depression, visual field loss, and hypoplasia (Casson et al., 2012). It is caused by intraocular pressure (IOP)-associated optic neuropathy with loss of retinal ganglion cells (RGCs) (Berkelaar et al., 1994). By the time glaucoma presents with typical visual field defects, such as blurred or lost vision, the loss of RGCs may already be as high as 50%. Thus, apparent changes in the number of RGCs provide the basis for early glaucoma diagnosis (Balendra et al., 2015).

To study the mechanisms underpinning glaucoma, various animal models, especially mouse models, have been developed to mimic the features of the disease. However, to determine the progression of retinal glaucoma, it is necessary to quantify the number of RGCs. A variety of techniques (Mead & Tomarev, 2016) have been used for RGC labeling with neuronal markers, such as β III-tubulin (Jiang et al., 2015), or immunolabeling with RGC-specific markers, such as BRN3A (Nadal-Nicolás et al., 2009), RNA-binding protein with multiple scattering (RBPMS) (Rodriguez et al., 2014), or γ-synuclein.

However, after using the appropriate markers, the total number of RGCs must be estimated by manual counting. Not only is this a time-consuming process, but it is also susceptible to subjective bias. Long hours of work can tire taggers, resulting in counting errors. To overcome this issue, several software programs with automatic RGC labeling have been developed, which have the advantages of fast detection speed, high detection accuracy, good objectivity, and RGC degeneration assessment. Geeraerts et al. (2016) developed a freely available ImageJ-based (Abràmoff et al., 2004; Collins, 2007) script to semi-automatically quantify RGCs in entire retinal flat-mounts after immunostaining with RGC-specific transcription factor BRN3A, although the process requires manual parameter adjustment. Guymer et al. (2020) developed automated software to count immunolabeled RGCs accurately and efficiently, with the ability to batch processing images and perform whole-retinal analysis to generate isodensity maps. However, this software cannot effectively detect RGCs with low contrast and brightness.

The key to accurate measurements of the entire RGC population is efficient processing of RGC-specific immunolabeled images. Ideally, the image background should be a single light color, and the RGCs should have high brightness and distinct edges (Figure 1A). However, image quality can be affected by various factors, such as operator experience and experimental procedures (Figure 1B–E), giving rise to the following issues:

Figure 1.

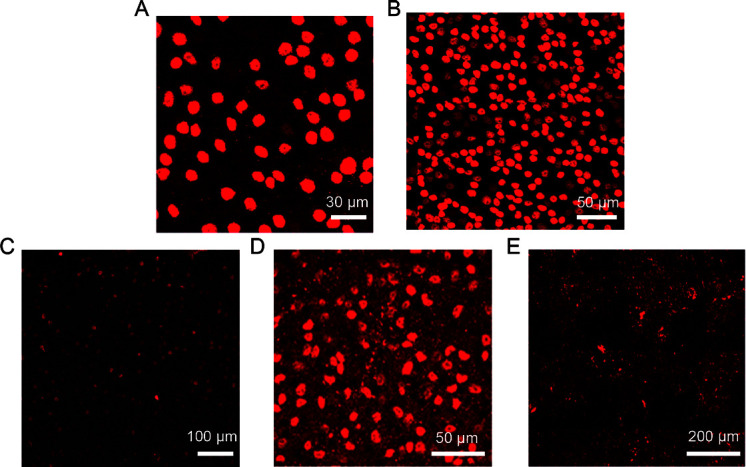
Examples of ideal and real images of mouse RGCs

A: Ideal RGC image. Scale bar: 30 μm. B: Image with densely distributed RGCs. Scale bar: 50 μm. C: Image with blurred RGCs. Scale bar: 100 μm. D: Image with high noise. Scale bar: 50 μm. E: Stitched RGC image with obvious stitching lines. Scale bar: 200 μm.

(1) Small and densely clustered RGCs

As shown in Figure 1B, RGCs are typically very small (about 15×15 pixels) and are distributed throughout the retina (distance of ≤20 pixels between cells). In addition, many RGCs overlap with each other and are not positioned on the same horizontal plane, resulting in lower image contrast and brightness of some RGCs, as shown in Figure 1C.

(2) Complicated retinal background

Other factors may lead to low-quality and noisy images, as shown in Figure 1D. When images of the entire retina are captured using confocal microscopy, images from multiple fields of view need to be stitched into one complete retinal image, which can result in obviously stitched edges, as shown in Figure 1E.

(3) Large image pixels

Whole retinal images are more than 8 000×8 000 pixels in size and contain more than 30 000 RGCs. Thus, both manual detection and recognition algorithm detection require a great deal of time.

As one of the most widely used artificial intelligence technologies, deep learning (Schmidhuber, 2015) allows computers to automatically learn pattern features and integrate feature learning into models to reduce incompleteness caused by artificially designed features. Machine learning algorithms use manually designed features that consider how each feature describes the object or image to be classified. Therefore, the performance of deep learning algorithms is more efficient than machine learning.

There are many ways to develop deep learning algorithms for real-time object detection. There are various popular CNN-based object detectors, e.g., retinaNet (Lin et al., 2017), faster-rcnn (Ren et al., 2017), and YOLO (Bochkovskiy et al., 2020; Jocher et al., 2020; Redmon & Farhadi, 2017, 2018).

To address the RGC recognition problem, we developed a deep learning model based on YOLOv5 (Jocher et al., 2020). The model can effectively identify RGCs with low brightness and contrast without being affected by background noise. In the case of graphics processing unit (GPU) computing, an 8 000×8 000 pixel image can be detected in less than 1 min. Furthermore, combined with the proposed deep learning model, we developed an automatic recognition software tool for counting BRN3A-labeled RGCs in whole-mount mouse retinas, which can process images in batches to generate RGC heat maps (Wilkinson & Friendly, 2009), and export results in comma-separated value (CSV) format. Our work has the following innovations:

(1) As RGCs are not at the same level under a biological microscope, a five-channel rather than a single-channel input was used to ensure that the RGCs can be collected at different focal lengths.

(2) A squeeze-and-excitation (SE) block (Hu et al., 2020) was added to the original network to detect blurred cells and increase detection accuracy.

(3) The developed software is fully automated and open source for convenient and cooperative use, which should help deepen our understanding of glaucoma and drug development.

MATERIALS AND METHODS

Network architecture

The basic detector (Figure 2) is divided into three parts. The first part performs feature extraction, and consists of convolution, batch normalization, activation function (Gulcehre et al., 2016), SE block (Hu et al., 2020) (details in next section), and cross-stage partial (CSP) structures (Wang et al., 2020). Convolution is critical for extracting image features through deep learning. Batch normalization (Ioffe & Szegedy, 2015) can accelerate model convergence and alleviate gradient disappearance, to a certain extent, making the training of deep network models easier and more stable. Activation function introduces nonlinear changes into the neural network to strengthen its learning ability. Here, we combined convolution, batch normalization, and activation function (i.e., CBL module) to increase expression ability. The CSP structure contains the CBL module and multiple convolutions, which can effectively solve gradient information repetition in the backbone of the convolutional neural network and integrate gradient changes into the feature map from beginning to end, thereby reducing model parameters.

Figure 2.

Illustration of the network architecture pipeline

The second part performs feature description, using PANet to aggregate upsampling, CBL module, and CSP structure (Wang et al., 2019). As a new feature pyramid network structure, PANet can enhance the bottom-up path during feature extraction, thereby enhancing the semantic and location information of the feature pyramid and effectively utilizing feature information.

The third part performs detection and consists of three bounding box priors (i.e., “anchors”) (Redmon & Farhadi, 2017). Each feature point predicts three bounding boxes to detect regions of interest of different sizes, finally outputting the prediction boxes and classes.

Squeeze-and-excitation block

In the first part of feature extraction, a SE block (Hu et al., 2020) was added to the CBL module of the basic model. The SE block achieved characteristic channel responses by increasing interdependence between channels. Squeeze obtained the global compression features of the current feature map by performing adaptive average pooling on the feature map layer. The activation function obtained the weight of each channel in the feature map, with the weighted feature map then used as the input of the next network layer. This significantly improved performance at a small computational cost. The SE block structure is depicted in Figure 3. Unlike the original description of the SE block, SiLU (Ramachandran et al., 2018) was used instead of ReLU (Howard et al., 2017) (Supplementary Figures S1, S2), as ReLU neuronal weights may not be updated.

Figure 3.

Squeeze-and-excitation block (Hu et al., 2020)

Training data pre-processing

We used five-channel rather than single-channel input images (see Section 3 dataset for detailed description). As the images were too large to be input into the detection network (Van Etten, 2018), each image was divided into smaller 512×512 pixel images with 20% overlaps. If no RGC was found in the small image, it was treated as the background. Adding all backgrounds to the training set would result in missed detections, whereas not adding backgrounds would result in false detections (Supplementary Figure S3). Thus, we added one-fifth of the background images to the training set in addition to all small images with RGCs.

Training data augmentation

As RGCs exhibit characteristic rotation invariance, we adopted the following data augmentations: rotation from [–10°,10°], translation from [–10, 10] for x and y, random zoom from [0.5, 1.5], and vertical and horizontal flip. In addition, mosaic data augmentation was used (Bochkovskiy et al., 2020). Four images were randomly sampled each time from the overall data, then randomly cropped and spliced to synthesize new images (Supplementary Figures S4, S5).

Inference

Given the large size of the whole retinal images, we constructed 512×512 sliding windows (with 20% overlapping areas) from top to bottom and left to right to detect RGCs in each window. Efficient non-maximum suppression (NMS) (Neubeck & Van Gool, 2006) of detection results for each sliding window was used to eliminate duplicate counts. All results were merged via the relative position of each sliding window in the retinal image, with NMS again used to suppress duplicate counts in the overlapping areas (Figure 4).

Figure 4.

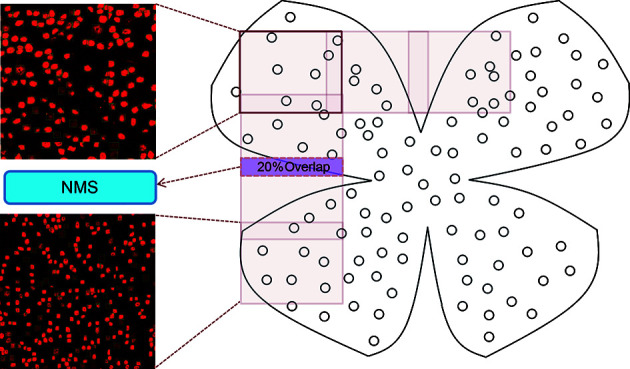
Inference for whole retina

Animals

The experimental mice were maintained under 12-h light/12-h dark cycles in the animal facility of the Sichuan Provincial People’s Hospital. All handling and care procedures followed the guidelines of the Association for Research in Vision and Ophthalmology (ARVO) for the use of animals in research. All experimental protocols were approved by the Animal Care and Use Committee of the Sichuan Provincial People’s Hospital (approval No.: 2016-36).

Whole-mount immunostaining of mouse RGCs

Adult C57B6J mice (3–12 months) were euthanized by cervical dislocation after anesthesia. The eyeballs were enucleated and fixed in 4% paraformaldehyde (PFA) and phosphate-buffered saline (PBS) for 20 min on ice. The sclera and retinal pigment epithelium (RPE) were peeled from the retina, which was then cut into four quadrants and fixed for an additional 12 h. After cryoprotection in 30% sucrose for 2 h, the retina was permeabilized and blocked with 5% normal donkey serum containing 0.5% Triton X-100 for 1 h at room temperature, followed by immunostaining with mouse anti-BRN3A primary antibodies (Abcam, USA, 1:200 dilution) for 3 d at 4 °C (Figure 5) and Alex488 or 594-conjugated donkey anti-mouse secondary antibodies (ThermoFisher, USA, 1:300 dilution). Fluorescent signals were acquired using a Zeiss LSM900 confocal microscope (Zeiss, Germany).

Figure 5.

RGC image acquisition process

Mouse eyeballs were removed and fixed in 4% PFA at 4 °C overnight. Retina was dissected, permeabilized with 0.5% Triton X-100, and incubated with BRN3A antibody at 4 °C for 3 d. Retina was then incubated with Alexa 488 or 594-conjugated anti-mouse secondary antibodies for 4 h at room temperature. Finally, images of each retina were acquired on a Zeiss LSM 900 confocal microscope.

Generation of glaucoma mouse models

The glaucoma mouse model was generated by inducing ganglion cell death using N-methyl-D-aspartate (NMDA), as described previously (Lam et al., 1999; Li et al., 1999). Briefly, 1 µL of NMDA (Sigma, USA) in PBS was injected into the intravitreal space of adult mice with a microsyringe (Hamilton, USA) through the pars plana, as per previous study (Yang et al., 2021). NMDA triggers RGC death through excessive stimulation of glutamate receptors. RGC death is attributed to NMDA excitotoxicity in several retinal diseases (Evangelho et al., 2019; Kuehn et al., 2005; Kwon et al., 2009) and progressive loss of RGCs is a characteristic feature of glaucoma. The mice were sacrificed by cervical dislocation 1, 2, or 3 d after injection with NMDA, representing different stages of RGC loss.

Data source

RGC images were acquired as described in the Methods section. As RGCs are not on the same horizontal plane in the retina, we selected five different image acquisition positions perpendicular to the Z axis of the microscope platform to ensure that most RGCs were clearly presented in the five images.

Our dataset contained 14 complete retinal images, including 10 from healthy mice (termed “normal” or “NOR”) and four from mice with RGC degeneration (termed “degenerative” or “DEG”), as summarized in Table 1. The size of each retinal image was 8 000×8 000 pixels, and all RGCs in each image were marked by experienced researchers. The manual marking error between different researchers was within 5%. Eleven images (eight normal and three degenerative images) were used as the training and validation dataset and three images (one degenerative and two normal images) were used as the test dataset. Following the training data preprocessing described in Section 2, 11 complete retinal images were divided into 2 237 small images (512×512 pixels) by manually labeling RGCs, which were divided into training and validation sets according to a 9:1 ratio. The other three complete retinas were used to compare the neural network output and manually labeled results.

Table 1. Complete retinal data.

	Manual marking	Pixel size	Health status
RGCs-T1 (train)	42 649	9 267×9 268	Normal
RGCs-T2 (train)	36 591	10 188×9 267	Normal
RGCs-T3 (train)	39 295	9 728×9 728	Normal
RGCs-T4 (train)	44 270	9 728×10 188	Normal
RGCs-T5 (train)	28 850	8 807×9 268	Normal
RGCs-T6 (train)	43 809	9 747×9 747	Normal
RGCs-T7 (train)	50 985	8 806×9 267	Normal
RGCs-T8 (train)	3 393	8 807×8 346	Degenerative
RGCs-T9 (train)	5 187	8 396×8 397	Degenerative
RGCs-T10 (train)	3 120	7 885×7 885	Degenerative
RGCs-T11 (train)	40 941	8 806×8 345	Normal
RGCs-D1 (test)	4 418	7 885×7 885	Degenerative
RGCs-N1 (test)	36 468	9 267×8 346	Normal
RGCs-N2(test)	43 473	8 806×8 346	Normal

Our algorithm was based on the PyTorch framework, and the experiment was carried out using the Ubuntu system on a 2.50 GHz Intel(R) Xeon(R) E5-2678 v3 CPU with a GTX TITAN XP GPU and 64 Gb RAM. For the neural networks, the learning rate was 0.0001 and batch size was eight.

Statistical evaluation metrics

We used three statistical evaluation metrics commonly used in medicine and average precision (AP), which is commonly used in object detection.

The Pearson correlation coefficient (Puth et al., 2014), defined as the covariance of two variables divided by the product of their standard deviations, is used to reflect the degree of linear correlation between two variables. Usually expressed as r or 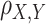, the higher the absolute value of r, the stronger the correlation.

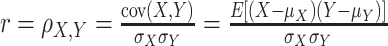1

where, given the variables 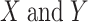, 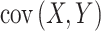is the covariance; are the standard deviations of 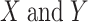, respectively; 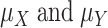are the means of 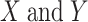, respectively; and E is the expectation.

The statistical measure r-squared (r²) represents the proportion of variance for a dependent variable explained by an independent variable or variables in a regression model. While correlation explains the strength of the relationship between an independent and dependent variable, r² explains the extent to which the variance of one variable explains the variance of a second variable.

Bland-Altman plots (Myles & Cui, 2007) can quantify the consistency between two quantitative measurements by establishing consistency limits, which are calculated using the mean and standard deviation of the difference between two measurements.

AP metrics

In deep learning, precision refers to the fraction of relevant instances among retrieved instances, while recall is the fraction of the total relevant instances retrieved. A precision-recall (PR) curve is simply a graph with precision values on the y-axis and recall values on the x-axis. The area enclosed by the PR curve and x- and y-axes, i.e., AP, is a widely used evaluation index in object detection. Precision and recall are calculated as follows:

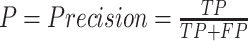2

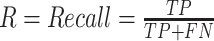3

where TP indicates true positives, FP indicates false positives, and FN indicates false negatives.

The area under the PR curve, i.e., AP, is calculated as follows:

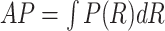4

where the integral is replaced with the sum at every position.

RESULTS

Accuracy and speed of new automatic RGC counting algorithm

After training, we selected the model weight with the best verification result to test the network. The whole retinal image was divided into smaller images (512×512 pixels), with a step of 400×400 pixels and adjacent small images overlapping by 20%. We synthesized the results as described in Section 2.3. The whole image could be counted in less than 1 min. We fused the five-channel input image into an RGB (red, green, blue model) image to display the result, with red representing the retina and RGCs and green representing the detection box (Figure 6). The detection results of two small images (512×512 pixels) are shown in Figure 6A, B. As indicated by the arrow, we did not consider the RGCs if half of the cell appeared on the boundary, as incomplete RGCs would be displayed and detected on adjacent small images. The results for the whole retina and partial enlargement of the retina are shown in Figure 6C, D, respectively.

Figure 6.

Curated examples of model on our test set, with confidence threshold of 0.3 used for display

A, B: Detection results of two small images with 512×512 pixels. C: Result of whole retinal image. Inset is enlarged and shown in D. D: Local area detection result. E: Original retinal image is shown in C. Arrows indicate that parts of the cell bodies on the edges are cut off.

Our test contained three complete retinal images, including two normal images (RGCs-N1 and RGCs-N2, respectively) and one degenerative image (RGCs-D1). We output the network detection results of each image.

Compared with the manual detection results, the error of automatic detection was less than 5% (Table 2), and there was a significant difference in the number of RGCs between normal and degenerative mice. Both manual labeling and automatic detection identified more than 20 000 RGCs in normal mice, but less than 10 000 RGCs in degenerative mice, which could serve as a reference in future studies.

Table 2. Calculation results of test images.

	Automatic counting	Total time (s)	Manual marking	Error (%)
RGCs-N1	37 516	44.9	36 468	2.87
RGCs-N2	43 244	53.4	43 473	0.53
RGCs-D1	4 279	6.5	4 418	3.14

For detailed statistical analysis, each retinal image was divided into multiple smaller images according to spatial area to compare the accuracy of spatial distribution and density of cells. Based on image size, the three test retinal images were divided into 317, 296, and 267 smaller images, respectively.

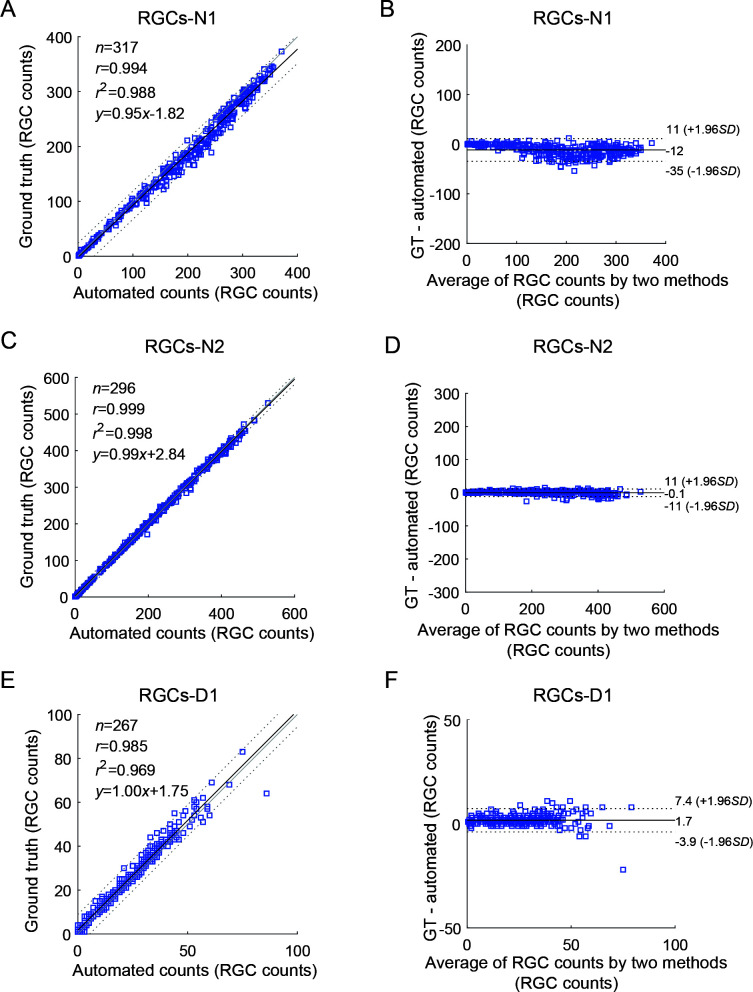
Linear regression analysis was used to simulate the relationship between ground truth and automatic RGC counts, and a Bland-Altman plot was used to investigate the consistency between these two variables (Table 3). Linear regression analysis showed good agreement between the automated counts and ground truth ((y=0.95x–1.82, Pearson r=0.994, n=317 frames), (y=0.99x+2.84, Pearson r=0.999, n=296 frames), (y=1.00x+1.75, Pearson r=0.985, n=267 frames) for N1, N2, and D1 retinal images, respectively) (Figure 7). The Bland-Altman plots of BRN3A-labeled retinal images (given the larger bias [–35, 11], [–11, 11], [–3.9, 7.4]) indicated no difference between automated and manual counting.

Table 3. Statistical evaluation metrics for test images.

	r	r2	95% confidence interval of average error
RGCs-N1	0.994	0.988	[-35, 11]
RGCs-N2	0.999	0.998	[-11, 11]
RGCs-D1	0.985	0.969	[-3.9, 7.4]
Mean	0.993	0.985	None

Figure 7.

Linear regression analysis and Bland-Altman plots of ground truth (GT) versus automated counts

First and second lines represent results of the two test images, respectively. A, C, E: Comparison of linear relationship between algorithm and real results. Continuous line is the best-fit line, and adjacent dotted lines represent 95% confidence intervals. B, D, F: Bland-Altman plot. Dotted lines indicate 1.96 SD region or 95% confidence interval. RGCs-N1, RGCs-N2, and RGCs-D1: Retinal ganglion cells in normal mouse 1, normal mouse 2, and degenerative mouse 1, respectively.

For object detection, we used AP to measure network performance (Table 4). In our computing environment, mean frames per second (FPS) was 40.6 and mean AP was 0.981, demonstrating high network calculation accuracy and speed.

Table 4. Evaluation of object detection for test images.

	FPS (GPU)	AP
RGCs-N1	41.8	0.989
RGCs-N2	39.3	0.985
RGCs-D1	40.8	0.970
Mean	40.6	0.981

To verify its effectiveness, we compared our method with other commonly used object-detection algorithms, as shown in Table 5. We tested faster-rcnn (Ren et al., 2017) and retinaNet (Lin et al., 2017) in the mmdetection (Chen et al., 2019) framework, and found that they were not suitable for working with dense images containing more than 200 RGCs. The YOLOv5 model builds four versions of network model according to the number of different blocks, i.e., s, m, l, and x, which were all tested. Although our method was slower than YOLOv5-l (40.6 FPS vs 41.1 FPS), the AP (0.981) was higher.

Table 5. Comparison of deep learning algorithms.

Model	FPS (GPU)	AP
RetinaNet	22.4	0.630
Faster-rcnn	20.6	0.452
YOLOv5-s	60.9	0.926
YOLOv5-m	45.0	0.924
YOLOv5-l	41.1	0.922
YOLOv5-x	28.2	0.923
Our Work	40.6	0.981

Performance of new algorithm compared to existing counting methods

We compared our approach with existing RGC counting methods, including the freely available ImageJ-based script developed by Cross et al. (2020), the machine learning script based on CellProfiler open-source software developed by Dordea et al. (2016), and the automated deep learning method used to quantify RBPMS-stained RGCs established by Masin et al. (2021). As shown in Figure 8, the methods proposed by Cross et al. (2020) and Masin et al. (2021) were unable to detect low-contrast RGCs, while the method proposed by Dordea et al. (2016) failed to separate RGCs in contact with each other. In contrast, our approach used deep learning to avoid these problems and achieve high counting accuracy.

Figure 8.

Comparison of RGC counting methods

A: Counting result using Cross et al. (2020) method. B: Counting result using Dordea et al. (2016) method. C: Counting result using Masin et al. (2021) method. D: Counting result using our method.

We used the same data and statistical methods for testing. The number of RGCs obtained by the different methods is shown in Table 6. Our method achieved the lowest error rate and highest calculation accuracy (error rates of 2.97%, 0.53%, and 3.14% for N1, N2, and D1, respectively). We split the three test images according to image size and performed linear regression analysis (Table 7). Both our approach and that of Masin et al. (2021) fit well, although our method showed better correlation ((y=0.95x−1.82, Pearson r=0.994, n=317 frames), (y=0.99x+2.84, Pearson r=0.999, n=296 frames), (y=1.00x+1.75, Pearson r=0.985, n=267 frames) for N1, N2 and D1, respectively).

Table 6. Quantitative comparisons of different RGC counting methods for test images.

	Manual marking	Dordea et al. method	Cross et al. method	Masin el al. method	Our method
RGCs-N1	36 468	48 934 (34.1%)	31 321 (14.1%)	31 671 (13.1%)	37 516 (2.97%)
RGCs-N2	43 473	45 989 (5.79%)	30 617 (29.5%)	40 800 (6.15%)	43 244 (0.53%)
RGCs-D1	4 418	7 160 (62.0%)	8 240 (86.5%)	3 953 (10.5%)	4 279 (3.14%)

Table 7. Linear regression analysis of test images.

	Dordea et al. method	Cross et al. method	Masin el al. method	Our method
RGCs-N1	y=0.6x+48.7 r=0.994	y=1.56x–69 r=0.898	y=1.09x–2.71 r=0.991	y=0.95x–1.82 r=0.994
RGCs-N2	y=1.01x+7.43 r=0.837	y=2.28x–149 r=0.927	y=1.00x–0.21 r=0.997	y=0.99x+2.84 r=0.999
RGCs-D1	y=0.44x+8.84 r=0.505	y=0.61x–3.46 r=0.597	y=1.04x+0.23 r=0.979	y=1.00x+1.75 r=0.985

We designed ablation experiments (Table 8) to demonstrate the validity of our model. We used YOLOv5-m as the baseline and added two improvements. Incorporating the SE block in the CBL module of the basic model increased the AP on the test set from 0.924 to 0.926, demonstrating that the SE block was effective. In addition, using five-channel rather than single-channel input further increased the AP on the test set to 0.981.

Table 8. Ablation experiments.

YOLOv5-m	CBL_SE	5-channels	AP
√			0.924
√	√		0.926
√	√	√	0.981

User friendly features of the software

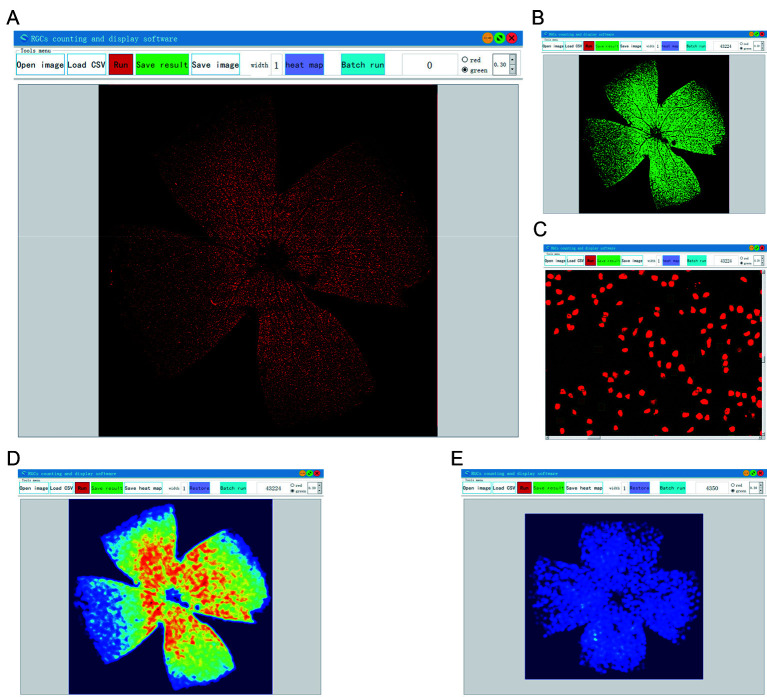
To facilitate operation of the algorithm and display, modify, and analyze the results, we developed an automatic RGC labeling software based on C++ and Qt5. Our proposed recognition algorithm was integrated into the software, and the detection results are shown in Figure 9. Users can zoom in and out to display the results (Supplementary Figure S6), and the report can be manually refined. The software can also process images in batches, display RGC heat maps, and export results in CSV format. Of the five columns in the report, the first two columns represent the coordinates of the upper left corner of each rectangular box in the whole image, the third and fourth columns list the widths and heights, respectively, and the fifth column provides the confidence values of the detection box.

Figure 9.

Automated software for RGC labeling

A: Import the image. Image can be zoomed in and out with the mouse to view details or outlines. B: Algorithm results. Click “Run” button. After a short wait, number of calculated RGCs can be seen in the upper right corner of the screen. Positions of each RGC are displayed in a green or red rectangular box on the image. The cut-off points for each detected RGC can be adjusted in the software to determine results. The cut-off point is 0.6 by default. C: Partial enlargement of entire retinal image. D, E: Heat map, which can visualize density function to represent density of dots in a map, enabling perception of point density independent of the zoom factor.

A heat map was generated based on the RGC labeling results (Figure 9). Figure 9D shows the density distribution of RGCs in normal mice and Figure 9E shows the distribution of RGCs in degenerative mice. Differences in quantity and spatial distribution between normal and degenerative retinas are easily seen in the heat map.

DISCUSSION

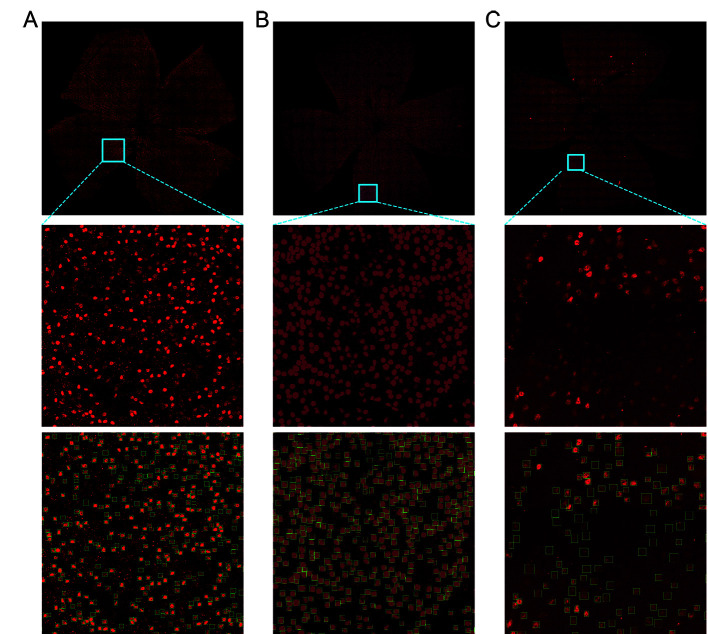
Our newly developed automatic RGC counting algorithm showed good performance for poor-quality retinal images, including noisy and low-contrast RGCs in RGCs-N1 and high-density RGCs in RGCs-N2. To explore the limitations of our algorithm, we labeled and tested a retina (RGCs-N3) with obvious stitching lines and a high proportion of low-contrast RGCs with blurred edges. The image and results are shown in Figure 10 and Table 9, respectively. The test results showed that the accuracy of our algorithm depended on the edge information of the RGCs. If the edge information was weak, the effect of the algorithm worsened. Blurred RGC edges were generally caused by inconsistent staining. The better the image quality, the more accurate the algorithm. However, the algorithm was not effective at detecting RGCs localized within a large area with high background staining (Figure 11).

Figure 10.

Test results for poor-quality images

A: Retinal image (RGCs-N1) with high noise and low contrast RGCs. B: Retinal image (RGCs-N2) with dense RGCs. C: Retinal image (RGCs-N3) with obvious stitching lines and large proportion of RGCs with blurred edges and low contrast. Insets in top panels are enlarged and shown in middle panels, respectively. Test results of middle panels are shown in bottom panels, respectively.

Table 9. Limitation analysis experiments.

	Manual marking	Automatic counting	Error (%)	AP
RGCs-N1	36 468	37 516	2.87	0.989
RGCs-N2	43 473	43 244	0.53	0.985
RGCs-D2	39 296	37 736	3.96	0.945

Figure 11.

Test result for retinal image with noise and blurred-edge RGCs

A: Retinal image with high noise and blurred-edge RGCs. B: Inset in A is enlarged and shown in upper panel. C: Test results of image shown in B. D, E: Insets in B, C are enlarged and shown in D, E, respectively.

Automatic RGC counting still faces many challenges. Due to their layering, certain RGCs in an image are always blurred, increasing the difficulty of counting. Other issues, such as labeling RGCs by different techniques, small and dense RGCs, or poor image quality caused by manual operation, require better methods in the future.

To address the time-consuming problem of manual RGC counting in mouse models, we developed an improved YOLOv5 algorithm through the analysis of RGC characteristics. Although we focused on RGC counting, our proposed method could be used in other fields, e.g., red blood cell and lymphocyte counting. Replacing manual counting with automated counting algorithms should greatly reduce the burden on researchers. This development direction is also the direction for the expansion of our algorithm and software in the future.

When studying mouse models of glaucoma, it is important to determine the progression of RGC loss by counting these cells throughout the retina. Manual and semi-automatic methods are susceptible to observer-dependent factors and can be time-consuming and inaccurate. To solve these challenges, we adopted a deep learning approach, improved the YOLOv5 network, and developed an open-source RGC recognition software tool. Our automated RGC counting software demonstrated high accuracy, speed, and objectivity. RGC degeneration could also be analyzed by combining the generated RGC heat maps. Our software provides a convenient tool to accurately assess RGC loss in mouse models of glaucoma, which has important implications for exploring the potential mechanisms and treatments of glaucoma.

COMPETING INTERESTS

The authors declare that they have no competing interests.

SUPPLEMENTARY DATA

Supplementary data to this article can be found online.

Funding Statement

This work was supported by the National Natural Science Foundation of China (61405028 to J.Z., 81770935 to H.B.Z.), Fundamental Research Funds for the Central Universities (University of Electronic Science and Technology of China) (ZYGX2019J053 to J.Z.), and Department of Science and Technology of Sichuan Province, China (2020YJ0445 to H.B.Z.)