Abstract
Background and Aims
Trees interconnected through functional root grafts can exchange resources, but the effect of exchange on trees remains under debate. A mechanistic understanding of resource exchange via functional root grafts will help understand their ecological implications for tree water exchange for individual trees, groups of trees and forest stands.
Methods
To identify the main patterns qualitatively describing the movement of sap between grafted trees, we reviewed the available literature on root grafting in woody plants that focus on tree allometry and resource translocation via root grafts. We then extended the BETTINA model, which simulates mangrove (Avicennia germinans) tree growth on the individual tree scale, to synthesize the available empirical information. Using allometric data from a field study in mangrove stands, we simulated potential water exchange and analysed movement patterns between grafted trees.
Key Results
In the simulations, relative water exchange ranged between −9.17 and 20.3 %, and was driven by gradients of water potential, i.e. differences in tree size and water availability. Moreover, the exchange of water through root grafts alters the water balance of trees and their feedback with the soil: grafted trees that receive water from their neighbours reduce their water uptake.
Conclusions
Our individual-tree modelling study is a first theoretical attempt to quantify root graft-mediated water exchange between trees. Our findings indicate that functional root grafts represent a vector of hydraulic redistribution, helping to maintain the water balance of grafted trees. This non-invasive approach can serve as a basis for designing empirical studies to better understand the role of grafted root interaction networks on a broader scale.
Keywords: Agent-based model, Avicennia germinans, BETTINA model, conceptual model, La Mancha Lagoon, mangroves, natural root grafting, tree–tree interaction, water exchange
INTRODUCTION
Functional and non-functional natural root grafts are unions of roots, which can share resources (functional root grafts) when cambium, xylem and phloem of both roots fuse, but can also form mere physical connections without resource exchange when tissues do not merge (non-functional grafts). As early as 1966, Graham and Bormann (1966) listed 150 species that exhibit natural root grafts. Even though this census has not yet been extended, research continues to determine the ecological significance of root grafts for the individual tree and the stand. A topical discussion is whether root grafts are of parasitic or symbiotic nature, and will thus have negative or positive effects on the connected trees. Root grafts can serve as vectors of pathogen transmission (Appel, 1994; Baric et al., 2008), which can lead to the spread of diseases such as oak wilt (Blaedow and Juzwik, 2010; Juzwik et al., 2010). On the other hand, they improve tree stability due to an increased anchorage area (Basnet et al., 1993). When functional, root grafts can facilitate exchange of resources such as water and nutrients (Bormann, 1966; Fraser et al., 2006; Bader and Leuzinger, 2019), with some authors (e.g. Bormann, 1966; Lev-Yadun, 2011) arguing that the connection of trees through root grafts is a cooperative strategy, where resource exchange compensates for temporal or spatial deficits (Vovides et al., 2021). Thus, root grafting might change the competition for resources between trees: if stronger individuals lose resources to weaker ones, their benefits might be reduced, but concurrently resilience for a whole population increases, thus stabilizing forest stands.
Although water exchange through root grafts has been documented (Stone and Stone, 1975; Bader and Leuzinger, 2019) and osmotic processes have been identified as driving mechanisms (Bader and Leuzinger, 2019), the quantification and direction of water translocation have not yet been determined and the net benefit individual trees could get from root graft resource translocation remains unclear. As the main component of plant cells, water has several physical and biochemical functions; it is a vector of nutrient transport and of reactions in biochemical processes (Schubert, 2011). A significant change in water availability could have a major impact on a tree. The gain or loss of water through root grafts may play a crucial role in the competition for resources and the development of forest structures, and should thus inform on the net cost/benefit of grafting in terms of tree–tree interactions.
The evidence of resource exchange between grafted trees is usually indirect. The response of the receiver tree (e.g. increasing growth or re-sprouting) to experimental treatments such as girdling (Bormann, 1966) or defoliation (Baret and DesRochers, 2011; Salomón et al., 2016), is used as an indicator for resource translocation. However, without direct measurements, it is challenging to quantify such exchange. Moreover, unstandardized empirical studies lead to variable and sometimes contradictory results.
The application of process-oriented models describing the behaviour of individual trees offers an opportunity to overcome the challenges to investigating root grafts, and allows the systematic test of hypotheses developed from empirical studies. A process-oriented approach further allows us to gain a fundamental mechanistic understanding and provides a projection of the potential response of the trees in a wider range of environmental changes than non-process-oriented models (Grimm and Berger, 2016). The BETTINA model (Peters et al., 2014, 2018) is such a process-oriented, single-tree model that has previously been applied to quantify water fluxes from the root zone to the canopy of trees (Bathmann et al., 2020; Peters et al., 2021) or as the representation of a tree in agent-based forest stand models (Peters et al., 2018; Bathmann et al., 2020). BETTINA describes explicitly the growth and allometry of trees in response to resource availability. The implementation of root connections between neighbouring trees in this model could help quantify water exchange and compare water uptake and availability of non-grafted and grafted trees under different environmental conditions.
In this study we aim to gain a mechanistic understanding of the impact that root graft-mediated water translocation has on tree water balance. Since there are no empirical studies quantifying resource exchange in situ, we first review the current state of knowledge. Thereby, we identify empirically observed, qualitative patterns of water exchange. These patterns suggest that the exchange is driven by water potential gradients, similar to water transport within trees. We implement this process into the BETTINA model in order to estimate water exchange. To verify the model and thus the underlying hypothesis, we use inventory data of root graft connected tree networks obtained in a mangrove forest bordering the central Gulf Coast of Mexico, where water limitation is driven by a salinity gradient. We thus seek to replicate the qualitative patterns reported in the literature and, beyond that, to answer the following research questions:
How much water could approximately be exchanged between connected trees?
What determines the direction and amount of exchanged water?
How does the exchange influence the water balance of the connected trees?
The study is a milestone on the future challenge to understand the consequences of processes occurring at the tree level on stand-level dynamics.
REVIEW
We reviewed 63 empirical studies on root grafting in woody plants (see details in Supplementary Data Methods S1), with the earliest published in 1934. By focusing on studies comparing tree allometric changes, growth rates and the response of trees grafted to other standing trees or living stumps to certain treatments, we draw conclusions about the exchange of resources and the translocation direction.
Methods used to verify the transmission of substances
Nearly half of the reviewed studies (44 %) measured or traced the translocation of substances through root grafts from one tree to another (Supplementary Data Fig. S1a), whereby the methodologies used to assess translocation differ considerably (Supplementary Data Table S1a, Fig. S1b). Initially, studies aimed to prove a direct exchange of substances by injecting and tracking dye or isotopes (e.g. Bormann and Graham, 1959; Schultz, 1963; Bormann, 1966). These studies are often invasive (require felling) and time consuming as care must be taken during the injection to avoid embolism. While a great proportion of the reviewed studies confirmed the exchange of substances indirectly by applying a treatment to one tree and observing the response of the suspected grafted neighbour (e.g. Jones and Bretz, 1958; Fraser et al., 2006; Juzwik et al., 2010; Baret and DesRochers, 2011), they focused on whether or not substances were translocated, and the quantification of resource transfer remains little understood. Thus, the ecological significance of the exchange for donor and receiver remains an open question.
Tree allometry and growth rates of grafted and non-grafted trees
A topical discussion on the effects of root grafting in trees is the difficulty in discerning whether increased growth is a short-term effect from altered competition regimes (i.e. increase in light availability due to the neighbour’s crown felling) and increased below-ground resources (Bormann, 1966; Eis, 1972) or whether the effect can be sustained in the long term. Hence, the observation of changes in tree allometry and crown positions of grafted and non-grafted trees can provide indirect assessment of the effect of root grafts on tree fitness through resource exchange. Several authors found that grafted trees tend to be bigger than non-grafted ones (Basnet et al., 1993; Gaspard and DesRochers, 2020), including their height (Basnet et al., 1993), stem diameter (Yli-Vakkuri, 1953) and root system (Gaspard and DesRochers, 2020). Nonetheless, it remains unclear whether this effect is a result of benefits derived from being grafted or due to the fact that larger trees have higher grafting probabilities due to their larger root systems (Gaspard and DesRochers, 2020). The differences in tree allometry could also be related to other factors such as local environmental conditions, tree age or even graft age, rather than to grafting alone. Additionally, differences were apparent between grafted and non-grafted trees when comparing height–stem diameter and crown–stem radius ratios, with generally lower ratios observed for grafted than for non-grafted trees (Basnet et al., 1993; Gaspard and DesRochers, 2020). A recent study, relating slenderness (i.e. height–stem radius ratio) to diameter at breast height, showed that grafted trees of the same size class are more slender, suggesting that by sharing anchoring root systems, grafted trees increase their mechanical stability (Vovides et al., 2021).
The occurrence of grafted trees has also been further associated with their position within the forest canopy (which can be described by crown classes, i.e. dominant, co-dominant or suppressed, or overtopped; Bechtold, 2003). Although natural root grafts have been observed in trees of all crown classes (Schultz, 1963; Eis, 1972; Baret and DesRochers, 2011), grafted trees tend to be dominant or co-dominant (Schultz, 1963; Külla and Lõhmus, 1999). Moreover, living stumps are more often associated with dominant or co-dominant rather than with suppressed trees (Schultz, 1963). This could be explained by the fact that the support of a living stump is energetically costly (Tarroux et al., 2010), and thus unlikely to be supported by small trees. Still, the effect of root grafting on growth is not fully understood. For example, Tarroux and DesRochers (2011) observed no significant differences in growth rates of grafted and non-grafted trees in natural stands of jack pine. However, they found found that trees that later developed root grafts had higher annual growth rates and were either dominant or co-dominant before grafting compared to those that remained non-grafted. After graft formation, the size of grafted trees equilibrated (Tarroux and DesRochers, 2011; Quer et al., 2020). Similarly, no clear effect of living stumps on the adjacent tree has been demonstrated: while Fraser et al. (2007) and Schultz (1963) did not observe a positive effect of living stumps on growth of the adjacent tree, Tarroux et al. (2010) described a negative effect on growth rates of the stump while Bormann (1966) and Dosen and Iyer (1979) reported increased growth rates of one tree after felling its grafted neighbour.
Coping with stress
Despite no clear effect of grafting over tree growth has been established, experiments carried out to confirm the existence of stress relief mechanisms in grafted trees show that fluctuations in nutrient, mineral and water supply caused by stress can be compensated for by the connection to a healthy or non-stressed tree (see approaches and specific studies in Table 1). Studies with experimental treatments and on naturally occurring events (i.e. during budworm outbreaks) showed that grafted trees suffer less under the threats compared to non-grafted trees (Fraser et al., 2006; Adonsou et al., 2016b; Salomón et al., 2016). This suggests that grafted trees exchange resources, compensating for spatial and temporal variations in their availability. Furthermore, the benefit a grafted tree received was greater when the grafted neighbour was dominant, and thus the advantage of grafting was found to be dependent on the size or crown class of the grafted trees (Baret and DesRochers, 2011). To the best of our knowledge, there are no studies comparing growth or tree performance between grafting and non-grafting species.
Table 1.
Summary of findings on how grafted trees cope with stress, triggered either by experiments or by natural events.
| Treatment | Key findings | Reference |
|---|---|---|
| Girdling (Experiment, tree level) | - Girdled suppressed tree kept growing below the girdle - Effect on adjacent dominant tree was negligible |
Bormann (1966) |
| Defoliation (Caterpillar and budworm outbreaks, stand level) | - Radial growth of grafted trees was less reduced compared to non-grafted trees |
Adonsou et al. (2016b) Salomón et al. (2016) |
| Defoliation (Experiment, tree level) | - Compensatory photosynthesis in the adjacent tree retaining its leaves - Effect of defoliation was greater when defoliated tree is dominant compared to a suppressed tree - Compensatory effect under good moisture conditions was negligible |
Baret and DesRochers (2011) |
| Drought stress (Experiment, tree level) | - Stressed ramets connected to a watered neighbour could maintain their stomatal conductance and net photosynthesis | Adonsou et al. (2016a) |
| Drought stress (Climate-growth analysis, stand level) | - Growth of grafted trees not significantly affected by warm conditions (indicating drought stress), while growth of non-grafted trees was reduced | Adonsou et al. (2016b) |
| Shading (Experiment, tree level) | - Total non-structural carbohydrate concentration in roots of shaded grafted trees was less reduced than in the roots of shaded non-grafted trees - Tendency for greater relative stem growth and lower crown recession in shaded grafted trees compared to shaded non-grafted trees |
Fraser et al. (2006) |
Flow direction, mechanisms and quantity of exchange
Herbicides, dyes and isotopes have been used to study the direction of resource translocation. The exchange was observed from dominant to suppressed trees (Eis, 1972; Shepperd, 1993) and from living stumps to the grafted living neighbour (Bormann, 1966; Wood, 1970; Bader and Leuzinger, 2019), and no or low transfer was described between trees of the same crown class (Eis, 1972).
The potential amount of water a graft can translocate has been assessed with outflow trials. By applying a fixed tension gradient (0.15 or 0.18 bar m–1) to excavated root grafts of different sizes and shapes of Pinus resinosa, Stone and Stone (1975) reported outflow rates ranging between 0.8 and 202 mL h−1 on a single graft arm. Further, flow has been found to follow the grain of wood, preventing trees from using the entire root system of their grafted neighbour (Bormann, 1966). However, lateral cross-grain movement has been observed from a stump to the adjacent living tree (Bormann, 1966; Wood, 1970). The direction of water exchange between a tree and a living stump was investigated in more detail by Bader and Leuzinger (2019), who observed an inverse coupling of diurnal sap flow and stem water potential patterns: at night, when transpiration in the trees approached zero, sap flow in the living stump increased, whereas during daytime, water movement in the stump decreased. The authors suggest that water movement in the stump is driven by osmotic processes, as transpiration streams were unlikely. A similar but less severe pattern has been observed during days with high precipitation or low vapour pressure deficit (Bader and Leuzinger, 2019). The direction of flow occurred from an irrigated tree to a tree with a dry soil matrix in clonal plants (Adonsou et al., 2016a), suggesting that movement of sap through root grafts is controlled by the transpiration pull, following the water potential gradient. In this context, translocation of materials between two or more trees appears to be bi-directional (Eis, 1972; Adonsou et al., 2016a), indicating that crown classes of connected trees, their health status and soil moisture content can be factors influencing the direction and rate of exchange.
Summary and synthesis of the literature review
Several studies have investigated the translocation of substances such as water (or dye) and carbohydrates through root grafts but the underlying mechanisms are not yet fully understood. Moreover, the translocation of materials could not always be detected (e.g. Jelínková et al., 2012; O’Neal and Davis, 2015) even if a graft was functional. As the studies focused on the identification of substances and the effect on grafted trees, to the extent of our knowledge, no quantification of translocated substances is available. Our review suggests that the exchange of water between the trees is controlled by transpirational pull (e.g. Bormann, 1966; Bader and Leuzinger, 2019), whereas translocation of other substances such as carbohydrates (Fraser et al., 2006) or herbicides (Shepperd, 1993) occurs from sources to sinks.
While grafted trees can compensate for stress through the transfer of substances (Fraser et al., 2006; Adonsou et al., 2016a), a consistent effect on growth has not been clearly demonstrated. The observed presence of dominant or co-dominant trees in groups of grafted trees (Schultz, 1963; Külla and Lõhmus, 1999) could be either due to the increased probability of grafting for large trees (Tarroux and DesRochers, 2011; Quer et al., 2020) or due to a positive effect on growth through the translocation of materials between trees (Bormann, 1966; Dosen and Iyer, 1979).
The reviewed studies focused mainly on individual trees and on pairs of grafted trees. However, root grafts can connect several trees (De La Rue, 1934; Bormann and Graham, 1959; Gordon, 1974; O’Neal and Davis, 2015; Vovides et al., 2021), with as many as 11 trees within a group reported in the literature (De La Rue, 1934). The group size and connectivity of trees might influence the translocation of resources. Thus, investigating grafted trees as groups and their relationship to environmental conditions could provide new insights into the nature of root grafting.
Based on the review, we propose four patterns describing water movement between connected trees:
P1: Between trees of similar size no or only marginal exchange exists
P2: Translocation of water takes place from the bigger to the smaller tree
P3: Translocation of water takes place from the tree growing in watered soil to that in dry soil
P4: The amount of water a tree receives relative to its own uptake (i.e. compensatory effect) is higher if the partner tree is larger
If water exchange between grafted trees is mainly driven by transpirational pull and thus water potential gradients, we expect to reproduce those patterns using a model where water uptake and movement is a function of water potential gradients.
MATERIALS AND METHODS
We extended an individual-tree model (BETTINA model, Peters et al., 2014, 2018, 2021), which simulates plant architecture development as a function of resource availability, to propose a process-based approach where water exchange is allowed between individual trees based on water potential differences. The model is applied using allometric mangrove tree parameters (i.e. stem diameter, tree height, and crown and root system radius) and porewater salinity, which contribute to differential water potentials between trees, allowing water to move following water potential gradients. In this way, we were able to quantify water exchange between individual trees and to verify if the proposed water exchange patterns (P1–P4) emerge from the simulation experiments.
Model description
The present study focuses on water movement, i.e. plant water uptake and water exchange, and therefore growth dynamics are kept static. The fundamental principle of water flow in BETTINA is a water potential difference and water will always flow from the higher to the lower water potential. The water potential difference between the stomata (transpiration) and the porewater drives tree water uptake. The model neglects high-resolution stem diameter variations, leading to an attenuation of the daily amplitude of the daily cycle and a phase shift between maximum solar radiation and maximum water uptake as in the hydraulic models presented by De Swaef et al. (2015). Water potential is composed of a gravimetric potential (height above/below reference level), the gas phase in the leaf (air humidity), soil osmotic potential (proportional to the molar concentration of dissolved ions in the water), soil matrix potential (due to adhesive capillary forces in unsaturated soils) and xylem pressure potential. The gravimetric potential arises from differences between roots and leaves, while the leaf level gas phase is represented by a species-specific minimum leaf water potential (Peters et al., 2014). In our model, we assume a saturated soil matrix, and thus the soil matrix potential has no effect on water flow and the porewater potential is defined by the salt content in the water. Hence, the boundaries of the model trees are defined by the minimum leaf water potential and the gravimetric potential at the leaf level as well as the porewater potential at the root level (Supplementary Data Methods S2 provide a detailed description of water uptake in the model).
Water flow along the potential gradient is controlled by flow resistances at the root surface and within the xylem of the tree (Fig. 1A). With Darcy’s law, xylem resistance is dependent on allometric measures (flow path length, cross-section of conducting wood) and hydraulic conductivities as estimated for various species at different sites (for mangroves, e.g. Melcher et al., 2001; Hao et al., 2009). According to pipe model theory (Shinozaki et al., 1964) we assume xylem hydraulic conductivities and the cross-section of conducting wood are constant along the vertical flow path. Consequently, the potential drop along the flow path is linear. Root system and stem geometry are inversely proportional to root surface and xylem resistance, respectively, while the flow path along the tree is proportional to xylem resistance.
Fig. 1.
Graphical representation of (A) a non-grafted model tree (left) and (B) a pair of grafted model trees (right) including the resistance at the root surface (Rro) and the xylem resistances at the root, stem and crown (Rxy,ro, Rxy,st, Rxy,cr, respectively) as well as the water potential around the root system (ψO) and at the leaves (ψL). The resistances are grouped according to their field of action in relation to potentially grafted roots as below- and above-graft resistance (Rbg, Rag). Blue arrows indicate the flow streams through and between the trees. ABS is the amount of water absorbed from the soil, AVAIL is the amount of water available for growth and maintenance, AWG is the absolute water gain, i.e. the water translocated between connected trees, and RGW is the relative water gain, i.e. the proportion of AWG in AVAILng. Indices indicate the graft status: root grafted (rg) or non-grafted (ng). For non-grafted trees, ABS equals AVAIL. The grey shading of the soil gives a fictitious gradient in the osmotic potential, determined by the salinity of the pore water.
For this study, we implemented an extension to the BETTINA model allowing trees to graft at the roots, with water translocation between grafted trees being driven by the water potential differences between them (Fig. 1B). Anatomical studies of functional root grafts suggest that involved roots develop a joined vascular system (Bormann, 1966; Rao, 1966; Eis, 1972). The wood anatomy of the root graft can present a higher complexity due to multiple axes of tracheid orientation (Bormann, 1966), which might decrease the hydraulic conductivity within the graft. Stone and Stone (1975), however, found no significant difference in relative hydraulic conductivity between root grafts and non-grafted root segments. To the best of our knowledge, theirs is the only study investigating conductivity in grafts. With this, we assume hydraulic conductivity in the grafted roots is to the hydraulic system of the grafted trees. The position of the grafted root segment in the model tree is located at the base of the tree, such that the acting resistances are divided into above-graft and below-graft resistance (Fig. 1B). In the model, each pair is connected only by one root graft. However, because multiple root grafts can occur in nature, it is defined that one model graft can represent several real grafts. This is achieved by a stem-diameter-dependent cross-sectional area, where larger trees have larger model grafts, which could represent several root grafts.
Applying the electronic–hydraulic analogy, a set of linear equations can be set up and solved to obtain the values for absorbed, available and exchanged water (see Supplementary Data Methods S2 for details). Whereas in the BETTINA model the amount of water absorbed from the soil (ABS) equals the amount of water available (AVAIL) to the tree for growth and maintenance (Fig. 1A), those values differ for grafted trees. The difference between AVAIL and ABS is the absolute water gain (AWG). If water is translocated away from the tree (water loss), this value is negative. With this modelling approach, the water balance of the tree changes as a function of the amount of water flowing through grafted roots and the water absorbed from the soil. Depending on the below- and above-graft resistances as well as the potential gradients, the water uptake of a grafted tree differs from that of a non-grafted tree with the same size and architecture. In the case of mangroves, the water uptake of trees can increase or decrease the salinization of the soil as more or less freshwater is extracted by the tree (Bathmann et al., 2020). This feedback effect on water availability was not taken into account in this study, i.e. salinity was considered constant.
A group of grafted trees can be considered as a unit, hereafter referred to as ‘groups’, where the sum of water translocated between trees within a group is zero [the amount of water that one tree receives equals the amount its partner(s) donates, eqn 1]. Yet, trees that lose water might compensate for the loss by pulling more water from the soil, depending on the water potential gradient. However, the sum of water absorbed by all trees of a group equals the sum of water available to those trees for growth and maintenance (eqn 2):
| 1 |
| 2 |
where is the number of trees in a group.
Model application
Here, we present an analytical application example to test whether the previously defined patterns (P1–P4) can be explained with the hydraulic mechanisms as implemented in the model. Furthermore, we investigated which characteristics, tree-specific or environmental attributes, determine the direction and amount of exchange through root grafts and what influence this has on the water balance of a tree.
Data
Four allometric measures and two hydraulic parameters were required to feed into the model application. For the allometric measures, we used biometric data from grafted and non-grafted black mangrove trees (Avicennia germinans L.). The data were obtained from five 30 × 30-m permanent plots located around the La Mancha Lagoon in Veracruz, Mexico (Vovides et al., 2014, 2016). This data set contains tree position (x, y coordinates), stem diameter, stem height and crown radius as well as the graft status, i.e. grafted or non-grafted, and if present the respective partners of each tree (Vovides et al., 2021).
In the original BETTINA model, the root system radius, which was not recorded, has two functional consequences (Peters et al., 2014, 2021). (1) For the description of the axial (xylem) flow resistance it is a part of the definition of the flow path length from the fine roots to the leaves. In this application, the root system radius is assumed to equal the crown radius. (2) Further, the root system radius defines the fine root surface andm with this, scales the root surface resistance. From the assumption of the BETTINA model to keep the resistances in equilibrium (Peters et al., 2014), we fixed the value of fine root resistance equal to the entire xylem resistance of the tree. Therefore, fine root permeability – one of the required hydraulic parameters – is obsolete for this study. The consequence of these assumptions largely affects the realism of the proportions of above- and below-graft resistance. The second parameter, hydraulic conductivity of the xylem, was set to 1.04e-7 kg s−1 m−1 Pa−1 (Sobrado, 2001). Additionally, for the description of xylem resistance in the grafted roots, we set the radius of the grafted roots to 25 % of the average stem radius of the involved trees. The effect of assumptions regarding root system radius and the hydraulic parameters as well as the resistance distribution among the model tree on water exchange was assessed with sensitivity analysis (see Supplementary Data Methods S3 and S4). As a result, the assumptions we made were assumed to be sufficient for the scope of this study as the influence on water exchange was subordinate compared to other parameters.
In the model, porewater salinity controls water availability via the osmotic potential. Higher salinity corresponds to a lower (more negative) potential, resulting in a more restricted water availability (Ball and Farquhar, 1984; Munns and Tester, 2008). The basic porewater salinity in the case study was set to 35 ppt and is considered to be the mean salinity of porewater under the respective tree. The water potential at the leaf end of the flow path must be lower than the osmotic potential to induce a flow towards the canopy. The minimum leaf water potential at noon was set to −7.86 MPa (Peters et al., 2021). This adds to the height potential of the canopy above the ground level.
Setups and scenarios
The effect of tree size and environmental conditions (i.e. porewater salinity, which reduces water availability) was investigated in two setups with two scenarios each (Fig. 2). While the setups define the structure of grafted tree groups, scenarios define the porewater salinity distribution. With this design we aim to be able to recognize the effect of tree attributes independent of environmental conditions on resource exchange.
Fig. 2.
Schematic representation of setups (rows) and scenarios (columns). Circles represent trees and lines show the connection of trees through root grafts. Colours indicate porewater salinity. In the homogeneous scenario, all trees have a fixed porewater salinity of 35 ppt, and in the heterogeneous scenario, porewater salinity ranges between 35 and 40 ppt.
In the first setup, we created fictitious pairs of interacting trees, hereafter named ‘Fictitious Grafting’. For this, all trees of one study plot are combined with one another. This site comprises 47 black mangrove trees, resulting in 2209 (the product of 47 × 47) pairs of grafted trees. Hereafter, trees of these pairs are named T1 and T2. The distance between them was set to 2.3 m, which equals the average distance between trees in this study plot. Each pair occurs twice with every tree once being the focal tree. In the second setup, named ‘Observed Grafting’, we used all grafted trees as well as their actual connections and distances observed in the field. Trees that are connected to each other are referred to as a group. These groups consist of two to nine members. While ‘Fictitious Grafting’ allows decoupled analysis of the effect of environmental and tree parameters on water exchange without considering the number of trees and links in a group, ‘Observed Grafting’ mirrors actual group structures observed in a mangrove forest and quantifies the amount of water that could be exchanged through root grafting.
Within these setups, two scenarios define the porewater salinity distribution (Fig. 2). In the first, hereafter named homogeneous scenario, the porewater salinity distribution is homogeneous, i.e. all trees have the same salinity of 35 ppt. In the second scenario, hereafter named heterogeneous scenario, the distribution is heterogeneous and ranged between 35 and 40 ppt. In ‘Fictitious Grafting’, the porewater salinity is set to 35 and 40 ppt for trees T1 and T2, respectively, where T2 has drought stress. In ‘Observed Grafting’, porewater salinity was randomly assigned and 20 repetitions were performed.
Statistical analysis
All statistical analyses were done with R (R Core Team, 2020). Considered model outputs were the water available to the tree without root grafts (AVAILng, non-grafted) and with root grafts (AVAILrg, grafted), absolute (AWG, eqn 3) and relative (RWG, eqn 4) water gain of grafted trees (negative values indicate water loss) as well as the summed relative water gain of a group (RWGgroup, eqn 5; Fig. 1).
| 3 |
| 4 |
| 5 |
where is the number of trees in a group. AVAILng was calculated for all trees and served as a baseline so that water exchange could be considered in relation to it.
The effect of tree size, i.e. stem height, stem radius and crown radius, on AVAILng and AWG was assessed using Spearman’s rank correlation (cor.test function; R Core Team, 2020; see Supplementary Data Table S2 for autocorrelation of geometry parameters). is a non-parametric measure to describe a monotonic relationship between two variables (Hedderich and Sachs, 2020).
In the case of grafted trees, the geometry parameters were considered as the log-transformed ratios of the respective parameters :
| 6 |
and are the parameter values of the focal tree and its adjacent partner and is the number of partners. A negative indicates higher geometry values of the focal tree compared to the adjacent partner, and vice versa for positive . indicates equal sizes. The log-transformation removes the skewness of the geometry ratios.
The distributions of RWG and RWGgroup were compared using skewness of distributions (‘e1071’ package; Meyer et al., 2019). The variance in AWG and RWG which is a result of scenario differences (homogeneous vs. heterogeneous) in the ‘Fictitious Grafting’ setup was determined using the intra-class correlation coefficient (ICC; Nakagawa et al., 2017).
RESULTS
Setup 1: ‘Fictitious Grafting’
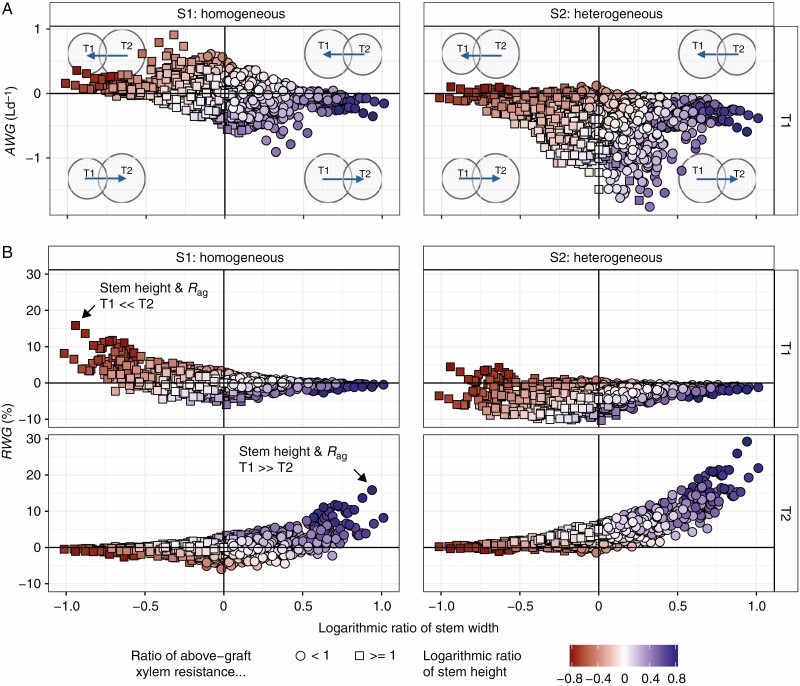
For trees without root grafts, water uptake was slightly higher under low salinity (35 ppt: 14.6 L d−1) than under high salinity (40 ppt: 13.3 L d−1), with a high variation between trees of different sizes (total range: 1.75–37.1 L d−1). Generally, water uptake was positively correlated with all three aspects of size, i.e. stem radius (ρ = 0.90), tree height (ρ = 0.34) and crown radius (ρ = 0.40, Table 2). Root grafting led to a slight redistribution of water under a homogeneous porewater salinity distribution (AWG per tree up to ± 0.91 L d−1; Fig. 3A). Differences in porewater salinity conditions of the two trees shifted this flux in favour of the more stressed tree T2, leading to an AWG of T2 between −0.12 and 1.8 L d−1 (and vice versa for T1; Fig. 3A).
Table 2.
Spearman correlation coefficient assessing the effect of model parameters on water uptake of non-grafted trees (AVAILng) and absolute water gain of grafted trees (AWG).
| Setup—scenario | n | Stem height | Stem radius | Crown radius | Porewater salinity | |
|---|---|---|---|---|---|---|
| AVAIL ng | F – homogeneous | 47 | 0.34 | 0.90 | 0.40 | – |
| AWG | F – homogeneous | 2209 | −0.78 | −0.38 | −0.08 | – |
| F – heterogeneous | 2209 | −0.51 | −0.25 | −0.04 | – | |
| O – homogeneous | 112 | −0.61 | −0.30 | 0.12 | – | |
| O – heterogeneous | 2240 | −0.43 | −0.25 | 0.07 | 0.68 |
The effect on AWG is determined by the logarithmic ratio of parameters of grafted trees (eqn 6). ‘F’: Fictitious Grafting setup, ‘O’: Observed Grafting setup, ‘n’ number of trees. Bold values are statistically significant at P < 0.05.
Fig. 3.
Calculated water flow patterns of trees T1 and T2 in setup ‘Fictitious Grafting’ as (A) absolute water gain (AWG) of tree T1 (L d–1) and (B) relative water gain (RWG) of trees T1 and T2 (percentage of water uptake of the non-grafted tree version). Pictograms in A represent trees T1 and T2, whereby the size of the circle indicates which tree is greater or smaller in stem radius, and the arrow indicates the direction of water flow. Ratios of biometric measures are logarithmic and given from the perspective of T1. That is, if the respective value is greater than 0, this parameter is greater for T1 than for T2.
The presence of salinity differences between trees explained 63 % of the variance of AWG (ICC = 0.63). Within each scenario, AWG was negatively correlated with the ratio of geometry parameters, i.e. stem height, stem and crown radii; nevertheless, the correlations were less strong in the heterogeneous scenario (Table 2, Supplementary Data Fig. S2). In the homogeneous scenario, water moved from the larger to the smaller tree, and the amount of exchanged water increased with increasing differences in tree geometry. This validated the empirical pattern P2, that is that water flows from the bigger to the smaller tree. Moreover, if trees are quite similar in size, there is little or no exchange, which replicates the empirical pattern P1. In the heterogeneous scenario, water exchange was mainly driven by the differences in porewater salinity and water tended to flow from the tree with lower to that with higher porewater salinity, i.e. from T1 to T2, corresponding to the empirical pattern P3.
Although in the model the amount that one tree receives equals the amount that the other loses, the results showed a high variation in the proportion of exchanged water in the total water uptake of the trees (RWG). Because a large tree has higher water uptake than a small tree, the amount of exchanged water corresponds to a larger portion of the water available for growth of the smaller tree compared to the large tree. With the homogeneous salinity distribution, RWG varied between −6.0 and 15.8 % (Fig. 3B). That is, a high relative water gain for the small tree corresponded to a low relative water loss for the large tree. RWG in the heterogeneous setup was almost twice as high as in the homogenous setup (RWG: −10.3 and 29.2 %; Fig. 3B). Further, relative water gain was higher than relative water loss, leading to skewed distributions (Fig. 4). If water translocation was only determined by differences in size, the distributions of RWG of both trees were equal and right-skewed (i.e. leaning in favour of T2). In cases where the larger tree is growing under more benign conditions, a larger size difference between the grafted trees promotes the compensatory effect of the root graft as the positive RWG increases. This validates empirical pattern P4. That effect caused different distributions of RWG for T1 and T2 (Fig. 4), with a negative and positive average RWG for T1 (−3.3 %, left-skewed) and T2 (4.1 %, right-skewed), respectively. That is, there were more trees with a relatively high water gain than trees with a relatively high loss.
Fig. 4.
Density estimates of relative water gain (RWG) of trees T1 and T2, setup ‘Fictitious Grafting’. In scenario S1, both trees have a porewater salinity of 35 ppt. In scenario S2, trees T1 and T2 have a porewater salinity of 35 and 40 ppt, respectively.
Setup 2: ‘Observed Grafting’
Water availability of trees without root grafts ranged between 0.86 and 76.1 L d−1, whereby the average daily uptake is slightly lower for trees with high salinity (40 ppt: 20.2 L) compared to trees with low salinity (35 ppt: 21.2 L).
Similar to ‘Fictitious Grafting’, the variation of AWG and RWG with the heterogeneous salinity distribution (AWG: −2.1 to 2.2 L, RWG: −9.5 to 19.1 %) was approximately twice as high as with the homogeneous salinity distribution (AWG: −1.0 to 1.2 L, RWG: −4.5 to 9.1 %). Moreover, AWG in actually grafted groups (‘Observed Grafting’) was slightly higher than between fictitious pairs as there are more complex combinations of trees. Groups consist of up to nine members, with many of the groups (55 %) still having two members. Hence, a tree can have more than two connections (Fig. 5). As in the ‘Fictitious Grafting’ setup, AWG is mainly influenced by the ratio of stem heights and, if salinity varies, by porewater salinity (Table 2). Nonetheless, the Spearman correlations were less strong than in ‘Fictitious Grafting’.
Fig. 5.
Schematic representation of three groups consisting of two, three and six grafted trees. The numbers indicate the absolute (AWG) and relative (RWG) water gain, respectively. The colour indicates the RWG (%). Both calculated with the homogeneous salinity distribution (i.e. scenario S1). Setup ‘Observed Grafting’.
Relating AWG to the cross-sectional area of the grafted roots results in flow velocities of up to 0.36 m d–1 (Supplementary Data Fig. S3). In both setups, barely more than half of the grafted trees had more water available than their non-grafted counterparts. In the homogeneous scenario, it was 55.4 % of the trees and in the heterogeneous scenario it was 52.9 %. Nonetheless, trees that receive water have up to 5.3 % (homogeneous) and 10.3 % (heterogeneous) more water available than their non-grafted version (i.e. AVAILrg > AVAILng). At the same time, their water absorption from the soil matrix was reduced (i.e. ABSrg < ABSng), by up to 3.8 % (homogeneous) and 8.7 % (heterogeneous).
The effect of higher water gain than loss became more evident at the group level: RWGgroup ranged between −2.8 and 10.9 % and −6.1 and 21.5 %, and was positive in 60.6 and 65.0 % of the groups in the homogeneous and heterogeneous scenario, respectively (Fig. 6B).
Fig. 6.
Density estimate of relative water gain (RWG) for (A) individual trees and (B) groups, shown as absolute values. The colour indicates whether the tree gained or lost water, i.e. had more water available than it absorbed. The values give the skewness of the distribution of RWG. Setup ‘Observed Grafting’.
DISCUSSION
Despite recent studies providing evidence of resource exchange between grafted trees (e.g. Bader and Leuzinger, 2019), the direction and quantity of exchange amongst pairs and groups of trees have not yet been determined. Such knowledge would increase our understanding of the mechanisms regulating resource-mediated interactions and whether these represent adaptive cooperative interactions or another vector of competition (Lev-Yadun, 2011). In this study, process-oriented modelling allowed us to test potential patterns of resource exchange identified from the available empirical literature and enabled the first estimate of water exchange rates and their implications for water uptake.
The conducted literature review revealed four empirical patterns (P1–P4) of water movement between grafted trees, which suggested that inter-tree water movement is driven by water potential gradients similar to water movement within trees (Richards and Caldwell, 1987). The model application clearly reproduced those empirical patterns: there was no water exchange between trees of the same size (P1) as no water potential gradient between the trees existed. However, when grafted trees differed in sizes, water flowed from the bigger to the smaller tree (P2) and when tested under heterogeneous water availability scenarios, water exchange occurred from the tree with higher to that with lower water availability (P3), which can superimpose P2. That is, if water is a limiting factor on the root–soil matrix of the bigger tree, the bigger tree will have a higher negative water potential, reducing the amount of water translocated to the smaller tree or even reversing the flow direction. The amount of water a tree received relative to its own uptake was higher the larger the size difference to the donor tree (P4) and with heterogeneous water availability the effect was enhanced. Similar to water potential differences in the soil matrix, a difference in minimum leaf water potential also affected the water exchange (not shown here): water flows from the tree with the higher (i.e. less negative) to that with the lower leaf water potential as described for hydraulic redistribution within individual plants (Burgess et al., 1998; Oliveira et al., 2014). The model results align with the only available study observing signals of water movement in a tree–stump–stump setup, where water exchange was driven by either transpiration of the tree or by osmotic potential differences between the root systems (Bader and Leuzinger, 2019). It is noteworthy that, while the overall flow pattern between a standing tree and a stump is from stump to tree (Bader and Leuzinger, 2019), the direction could be more dynamic for pairs or groups of living trees, as water potential gradients between trees can be more dynamic, reflecting individual traits as well as local conditions at the root–soil and leaf–atmosphere continuum, respectively (Lin and Sternberg, 1992; Suárez and Sobrado, 2000).
The range of water exchange between grafted mangroves observed with the simulations (−2.1 and 2.2 L d−1, observed – heterogeneous) was within the range of 0.02 and 4.8 L d−1 reported by Stone and Stone (1975) as the potential flow through root grafts of different size of Pinus resinosa. The agreement of modelled total tree water uptake with empirical values was discussed in Peters et al. (2021). These consistencies indicate that our extended model can provide a reliable first quantification of water exchange between grafted mangrove trees.
Root-graft mediated water exchange is an as yet unrecognized vector of hydraulic redistribution (HR) between different trees co-existing in forest stands. In saline ecosystems such as mangroves, the passive root water transport from wetter to drier soil layers (Richards and Caldwell, 1987) supports the dilution of salt in the soil column (Hao et al., 2009) and is known to be mediated by foliar water uptake (Schreel et al., 2019), which induces a reverse flow that could facilitate root-graft-mediated exchange. Simulated flow velocities through grafts, i.e. water exchange divided by root graft cross-sectional area, were up to 0.36 m d–1 (Supplementary Data Fig. S3), which is within the range of mycorrhiza-mediated HR between large pines and their seedlings (Warren et al., 2008). As HR might be more conservative in sandy or saline soils (Yoder and Nowak, 1999; Bazihizina et al., 2017), root-graft-mediated water exchange provides an additional path to compensate for heterogeneities as well as can have relevant implications to reduce water stress in trees and maintain optimal water balance. When trees go through temporal drought, grafted trees will probably experience less stress than non-grafted trees (Adonsou et al., 2016a, b), which could partially explain the higher grafting frequency with increasing salinity (Vovides et al., 2021) or at sites with higher sand content in terrestrial forests (Tarroux and DesRochers, 2010) as sand is less efficient in maintaining soil moisture (Passioura, 1988).
In the model, root grafts contributed to increases and decreases to both soil water uptake and the amount of water available for growth and maintenance. Due to the altered soil water potential gradient, trees that received water from their adjacent tree(s) lowered their water uptake and at the same time had more water available compared to the non-grafted tree version. For trees that lost water the effect was reversed. Plant–soil feedbacks, for example, between tree water uptake and soil salinity and thus water accessibility are a recognized driver in shaping mangrove ecosystems (Wimmler et al., 2021). Considering the complex plant–soil feedback mechanisms leading to heterogeneous water availability as, for example, investigated for mangroves (Bathmann et al., 2020, 2021), the increased water extraction at sites with more accessible water due to root grafting may lead to a mitigating effect to such inequalities.
This study does not come without limitations. For instance, the implemented model assumed xylem conductivity and minimum leaf water potential to be constant and equal for all trees, but these parameters can vary depending on the species, growth form and environmental conditions (Hao et al., 2009, Rodriguez-Dominguez and Brodribb, 2020), while both hydraulic and allometric relationships also change with increasing porewater salinity (Suárez and Sobrado, 2000; Sobrado, 2001; Peters et al., 2014). Nevertheless, varying hydraulic parameters without having more empirical knowledge on their relationship to tree size, age and environmental conditions would have added more uncertainty to the analysis. Adding complexity to process-oriented models will require simultaneous validation with empirical studies in such a way that an optimal model includes all essential processes without adding a level of complexity that reduces model reliability (Grimm et al., 2005). Furthermore, although trees can often graft in groups of two or more grafted members (Bormann and Graham, 1959; Gordon, 1974; Vovides et al., 2021), and our results suggest that groups with more than two members could receive greater benefits from resource exchange, the influence of group structure on water translocation remains unclear. This is due to a lack of empirical knowledge addressing group formation, and to the fact that the empirical data set used in this study (Vovides et al., 2021) had only two large groups (with seven and nine trees each).
Although model parameterization and tree data from the La Mancha Lagoon describe mangrove trees, the observed patterns and driving mechanisms of water exchange can be transferred to terrestrial trees as well. In both systems, i.e. terrestrial and coastal, water transport in trees is driven by water potential gradients (Richards and Caldwell, 1987). Quantification of water exchange between terrestrial trees can be achieved by including the soil matrix water potential on the water uptake process in the BETTINA model and parameterizing hydraulic properties.
We chose a static model application to uncover key patterns in water exchange through functional root grafts and to estimate their potential contribution to total water uptake. The presented example does not cover dynamic processes such as tree growth and thus does not explain how root grafting might alter tree and forest structure development. However, the tendency of higher relative water gains for the smaller, receiving tree suggests that functional root grafts can have a positive effect on growth for the receiver tree while the negative effect for the donor is negligible. This could explain the convergence of tree sizes (Tarroux and DesRochers, 2011; Quer et al., 2020), which is likely to occur faster if environmental conditions are heterogeneous. Future work should, therefore, focus on dynamic processes, including plant–soil feedbacks and HR, to uncover the role of water exchange under varying conditions for tree and stand development. Nonetheless, the model presents a non-invasive approach that could support the design and interpretation of empirical studies, for example by reproducing characteristic group structures observed under different environmental conditions (Vovides et al., 2021). Moreover, the model lays the foundation to understand the effect of root grafting on the stand scale and test hypotheses on its evolutionary significance, which might extend or question known concepts of cooperation and competition in tree populations.
SUPPLEMENTARY DATA
Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Figure S1: Overview of empirical studies. Figure S2: Visualization of the monotonic relationship between the absolute water gain and the ratios of tree geometry parameters. Figure S3: Water flow velocity in grafted roots in the ‘Observed Grafting’ setup. Table S1: Overview of methods used to study resource transmission between root grafted trees. Table S2: Correlation coefficients of tree geometry parameters. Methods S1: Methodology for the review of empirical studies. Methods S2: Detailed model description. Methods S3: Sensitivity analysis of the model. Methods S4: Theoretical exploration of flow resistances.
ACKNOWLEDGEMENTS
We thank J. Bathmann from the Helmholtz Centre for Environmental Research Leipzig for helpful discussions and the anonymous reviewers for their comments and contributions to improve this work. The data and codes used in this study are publicly available on https://github.com/mcwimm/RootGraftsMatter.
Contributor Information
Marie-Christin Wimmler, Faculty of Environmental Sciences, Department of Forest Sciences, Chair of Forest Biometrics and Systems Analysis, Technische Universität Dresden, 01062 Dresden, Germany.
Alejandra G Vovides, School of Geographical and Earth Sciences, University of Glasgow, Glasgow, UK.
Ronny Peters, Faculty of Environmental Sciences, Department of Forest Sciences, Chair of Forest Biometrics and Systems Analysis, Technische Universität Dresden, 01062 Dresden, Germany.
Marc Walther, Faculty of Environmental Sciences, Department of Forest Sciences, Chair of Forest Biometrics and Systems Analysis, Technische Universität Dresden, 01062 Dresden, Germany.
Nadezhda Nadezhdina, Institute of Forest Botany, Dendrology and Geobiocenology, Mendel University in Brno, Brno, Czech Republic.
Uta Berger, Faculty of Environmental Sciences, Department of Forest Sciences, Chair of Forest Biometrics and Systems Analysis, Technische Universität Dresden, 01062 Dresden, Germany.
FUNDING
This research was financed by the Volkswagen Foundation (Volkswagen Stiftung, Project No. 94 844) and partially financed by the MOMENTS project (Natural Environment Research Council [NERC], UK grant No. NE/P014127/1).
LITERATURE CITED
- Adonsou KE, Desrochers A, Tremblay F.. 2016a. Physiological integration of connected balsam poplar ramets. Tree Physiology 36: 797–806. doi: 10.1093/treephys/tpv142. [DOI] [PubMed] [Google Scholar]
- Adonsou KE, Drobyshev I, DesRochers A, Tremblay F.. 2016b. Root connections affect radial growth of balsam poplar trees. Trees 30: 1775–1783. doi: 10.1007/s00468-016-1409-2. [DOI] [Google Scholar]
- Appel DN. 1994. Identification and control of oak wilt in Texas urban forests. Journal of Arboriculture 20: 250–258. [Google Scholar]
- Bader MK-F, Leuzinger S.. 2019. Hydraulic coupling of a leafless kauri tree remnant to conspecific hosts. iScience 19: 1238–1247. doi: 10.1016/j.isci.2019.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball MC, Farquhar GD.. 1984. Photosynthetic and stomatal responses of two Mangrove species, Aegiceras corniculatum and Avicennia marina, to long term salinity and humidity conditions. Plant Physiology 74: 1–6. doi: 10.1104/pp.74.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baret M, DesRochers A.. 2011. Root connections can trigger physiological responses to defoliation in nondefoliated aspen suckers. Botany 89: 753–761. doi: 10.1139/b11-062. [DOI] [Google Scholar]
- Baric S, Kerschbamer C, Vigl J, Dalla Via J.. 2008. Translocation of apple proliferation phytoplasma via natural root grafts – a case study. European Journal of Plant Pathology 121: 207–211. [Google Scholar]
- Basnet K, Scatena FN, Likens GE, Lugo AE.. 1993. Ecological consequences of root grafting in Tabonuco (Dacryodes excelsa) trees in the Luquillo Experimental Forest, Puerto Rico. Biotropica 25: 28–35. doi: 10.2307/2388976. [DOI] [Google Scholar]
- Bathmann J, Peters R, Naumov D, Fischer T, Berger U, Walther M.. 2020. The MANgrove–GroundwAter feedback model (MANGA) – describing belowground competition based on first principles. Ecological Modelling 420: 108973. doi: 10.1016/j.ecolmodel.2020.108973. [DOI] [Google Scholar]
- Bathmann J, Peters R, Reef R, Berger U, Walther M, Lovelock CE.. 2021. Modelling mangrove forest structure and species composition over tidal inundation gradients: the feedback between plant water use and porewater salinity in an arid mangrove ecosystem. Agricultural and Forest Meteorology 308–309: 108547. [Google Scholar]
- Bazihizina N, Veneklaas EJ, Barrett-Lennard EG, Colmer TD.. 2017. Hydraulic redistribution: limitations for plants in saline soils. Plant, Cell & Environment 40: 2437–2446. doi: 10.1111/pce.13020. [DOI] [PubMed] [Google Scholar]
- Bechtold WA. 2003. Crown position and light exposure classification-an alternative to field-assigned crown class. Northern Journal of Applied Forest 20: 154–160. [Google Scholar]
- Blaedow RA, Juzwik J.. 2010. Spatial and temporal distribution of Ceratocystis fagacearum in roots and root grafts of Oak wilt affected Red Oaks. Arboriculture & Urban Forestry 36: 28–34. [Google Scholar]
- Bormann FH. 1966. The structure, function, and ecological significance of root grafts in Pinus strobus. Ecological Monographs 36: 1–26. doi: 10.2307/1948486. [DOI] [Google Scholar]
- Bormann FH, Graham BF.. 1959. The occurrence of natural root grafting in Eastern White Pine, Pinus Strobus L., and its ecological implications. Ecology 40: 677–691. doi: 10.2307/1929820. [DOI] [Google Scholar]
- Burgess SSO, Adams MA, Turner NC, Ong CK.. 1998. The redistribution of soil water by tree root systems. Oecologia 115: 306–311. doi: 10.1007/s004420050521. [DOI] [PubMed] [Google Scholar]
- De La Rue C. 1934. Root grafting in trees. American Journal of Botany 21: 121–126. [Google Scholar]
- De Swaef T, De Schepper V, Vandegehuchte MW, Steppe K.. 2015. Stem diameter variations as a versatile research tool in ecophysiology. Tree Physiology 35: 1047–1061. doi: 10.1093/treephys/tpv080. [DOI] [PubMed] [Google Scholar]
- Dosen RC, Iyer JG.. 1979. Effect of grafted roots of stumps on the growth of a thinned red pine plantation. Tree Planters’ Notes 30: 19–21. [Google Scholar]
- Eis S. 1972. Root grafts and their silvicultural implications. Canadian Journal of Forest Research 2: 111–120. doi: 10.1139/x72-022. [DOI] [Google Scholar]
- Fraser EC, Lieffers VJ, Landhäusser SM.. 2006. Carbohydrate transfer through root grafts to support shaded trees. Tree Physiology 26: 1019–1023. doi: 10.1093/treephys/26.8.1019. [DOI] [PubMed] [Google Scholar]
- Fraser EC, Lieffers VJ, Landhäusser SM.. 2007. The persistence and function of living roots on lodgepole pine snags and stumps grafted to living trees. Annals of Forest Science 64: 31–36. doi: 10.1051/forest:2006085. [DOI] [Google Scholar]
- Gaspard DT, DesRochers A.. 2020. Natural root grafting in hybrid poplar clones. Trees - Structure and Function 34: 881–890. [Google Scholar]
- Gordon DE. 1974. The importance of root grafting in the spread of phytophthora root rot in an immature stand of Port-Orford-cedar. Portland: Oregon State University. https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/3t945w349. [Google Scholar]
- Graham BF, Bormann FH.. 1966. Natural root grafts. The Botanical Review 32: 255–292. doi: 10.1007/bf02858662. [DOI] [Google Scholar]
- Grimm V, Berger U.. 2016. Robustness analysis: deconstructing computational models for ecological theory and applications. Ecological Modelling 326: 162–167. doi: 10.1016/j.ecolmodel.2015.07.018. [DOI] [Google Scholar]
- Grimm V, Revilla E, Berger U, et al. 2005. Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310: 987–991. doi: 10.1126/science.1116681. [DOI] [PubMed] [Google Scholar]
- Hao G-Y, Jones TJ, Luton C, et al. 2009. Hydraulic redistribution in dwarf Rhizophora mangle trees driven by interstitial soil water salinity gradients: impacts on hydraulic architecture and gas exchange. Tree Physiology 29: 697–705. doi: 10.1093/treephys/tpp005. [DOI] [PubMed] [Google Scholar]
- Hedderich J, Sachs L.. 2020. Angewandte Statistik. Methodensammlung mit R. Berlin: Springer-Verlag. [Google Scholar]
- Jelínková H, Tremblay F, Desrochers A.. 2012. Herbivore-simulated induction of defenses in clonal networks of trembling aspen (Populus tremuloides). Tree Physiology 32: 1348–1356. doi: 10.1093/treephys/tps094. [DOI] [PubMed] [Google Scholar]
- Jones TW, Bretz TW.. 1958. Experimental oak wilt control in Missouri. Research Bulletin 657. [Google Scholar]
- Juzwik J, O’Brien J, Evenson C, Castillo P, Mahal G.. 2010. Controlling spread of the Oak wilt pathogen (Ceratocystis fagaceorum) in a Minnesota urban forest park reserve. Arboriculture and Urban Forestry 36: 171–178. [Google Scholar]
- Külla T, Lõhmus K.. 1999. Influence of cultivation method on root grafting in Norway spruce (Picea abies (L.) Karst.). Plant and Soil 217: 91–100. [Google Scholar]
- Lev-Yadun S. 2011. Why should trees have natural root grafts? Tree Physiology 31: 575–578. doi: 10.1093/treephys/tpr061. [DOI] [PubMed] [Google Scholar]
- Lin G, Sternberg LS.. 1992. Comparative study of water uptake and photosynthetic gas exchange between scrub and fringe red mangroves, Rhizophora mangle L. Oecologia 90: 399–403. [DOI] [PubMed] [Google Scholar]
- Melcher PJ, Goldstein G, Meinzer FC, et al. 2001. Water relations of coastal and estuarine Rhizophora mangle: xylem pressure potential and dynamics of embolism formation. Oecologia 126: 182–192. doi: 10.1007/s004420000519. [DOI] [PubMed] [Google Scholar]
- Meyer D, Dimitriadou E, Hornik K, Weingessel A, Leisch F.. 2019. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. https://CRAN.R-project.org/package=e1071 [Google Scholar]
- Munns R, Tester M.. 2008. Mechanisms of salinity tolerance. Annual Review of Plant Biology 59: 651–681. doi: 10.1146/annurev.arplant.59.032607.092911. [DOI] [PubMed] [Google Scholar]
- Nakagawa S, Johnson PCD, Schielzeth H.. 2017. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of the Royal Society Interface 14: 20170213. doi: 10.1098/rsif.2017.0213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveira RS, Christoffersen BO, de V. Barros F, et al. 2014. Changing precipitation regimes and the water and carbon economies of trees. Theoretical and Experimental Plant Physiology 26: 65–82. [Google Scholar]
- O’Neal ES, Davis DD.. 2015. Intraspecific root grafts and clonal growth within Ailanthus altissima stands influence Verticillium nonalfalfae transmission. Plant Disease 99: 1070–1077. doi: 10.1094/PDIS-07-14-0722-RE. [DOI] [PubMed] [Google Scholar]
- Passioura JB. 1988. Water transport in and to roots. Annual Review of Plant Physiology and Plant Molecular Biology 39: 245–265. doi: 10.1146/annurev.pp.39.060188.001333. [DOI] [Google Scholar]
- Peters R, Lovelock C, López-Portillo J, et al. 2021. Partial canopy loss of mangrove trees: mitigating water scarcity by physical adaptation and feedback on porewater salinity. Estuarine, Coastal and Shelf Science 248: 106797. doi: 10.1016/j.ecss.2020.106797. [DOI] [Google Scholar]
- Peters R, Olagoke A, Berger U.. 2018. A new mechanistic theory of self-thinning: adaptive behaviour of plants explains the shape and slope of self-thinning trajectories. Ecological Modelling 390: 1–9. doi: 10.1016/j.ecolmodel.2018.10.005. [DOI] [Google Scholar]
- Peters R, Vovides AG, Luna S, Grüters U, Berger U.. 2014. Changes in allometric relations of mangrove trees due to resource availability – a new mechanistic modelling approach. Ecological Modelling 283: 53–61. doi: 10.1016/j.ecolmodel.2014.04.001. [DOI] [Google Scholar]
- Quer E, Baldy V, DesRochers A.. 2020. Forest ecology and management ecological drivers of root grafting in balsam fir natural stands. Forest Ecology and Management 475: 118388. doi: 10.1016/j.foreco.2020.118388. [DOI] [Google Scholar]
- R Core Team. 2020. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rao AN. 1966. Developmental anatomy of natural root grafts in Ficus Globosa. Australian Journal of Botany 14: 269–276. [Google Scholar]
- Richards JH, Caldwell MM.. 1987. Hydraulic lift: substantial nocturnal water transport between soil layers by Artemisia tridentata roots. Oecologia (Berlin) 73: 486–489. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Dominguez CM, Brodribb TJ.. 2020. Declining root water transport drives stomatal closure in olive under moderate water stress. New Phytologist 225: 126–134. [DOI] [PubMed] [Google Scholar]
- Salomón RL, Tarroux E, DesRochers A.. 2016. Natural root grafting in Picea mariana to cope with spruce budworm outbreaks. Canadian Journal of Forest Research 46: 1059–1066. doi: 10.1139/cjfr-2016-0121. [DOI] [Google Scholar]
- Schreel JDM, Van de Wal BAE, Hervé-Fernandez P, Boeckx P, Steppe K.. 2019. Hydraulic redistribution of foliar absorbed water causes turgor-driven growth in mangrove seedlings. Plant, Cell & Environment 42: 2437–2447. doi: 10.1111/pce.13556. [DOI] [PubMed] [Google Scholar]
- Schubert S. 2011. Pflanzenernährung: Grundwissen Bachelor. Stuttgart: Eugen Ulmer KG. [Google Scholar]
- Schultz RP. 1963. Occurrence of stump callusing in second-growth Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco). Master's Thesis, Portland: Oregon State University. https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/6d56zz98c. [Google Scholar]
- Shepperd WD. 1993. Initial growth, development, and clonal dynamics of regenerated aspen in the Rocky Mountains. U.S. Department of Agriculture, Forest Service, Rocky Mountain Forest and Range Experiment Station; RM-312. [Google Scholar]
- Shinozaki K, Yoda K, Hozumi K, Kira T.. 1964. A quantitative analysis of plant form - the pipe model theory II. Further evidence of the theory and its application in forest ecology. Japanese Journal of Ecology 14: 133–139. [Google Scholar]
- Sobrado MA. 2001. Hydraulic properties of a mangrove Avicennia germinans as affected by NaCl. Biologia Plantarum 44: 435–438. doi: 10.1023/a:1012479718305. [DOI] [Google Scholar]
- Stone J, Stone E.. 1975. The communal root system of red pine: water conduction through root grafts. Forest Science 21: 255–261. [Google Scholar]
- Suárez N, Sobrado MA.. 2000. Adjustments in leaf water relations of mangrove (Avicennia germinans) seedlings grown in a salinity gradient. Tree Physiology 20: 277–282. doi: 10.1093/treephys/20.4.277. [DOI] [PubMed] [Google Scholar]
- Tarroux E, DesRochers A.. 2011. Effect of natural root grafting on growth response of jack pine (Pinus banksiana; Pinaceae). American Journal of Botany 98: 967–974. doi: 10.3732/ajb.1000261. [DOI] [PubMed] [Google Scholar]
- Tarroux E, DesRochers A, Krause C.. 2010. Effect of natural root grafting on growth response of jack pine (Pinus banksiana) after commercial thinning. Forest Ecology and Management 260: 526–535. doi: 10.1016/j.foreco.2010.05.008. [DOI] [Google Scholar]
- Vovides AG, Marín-Castro B, Barradas G, Berger U, López-Portillo J.. 2016. A simple and cost-effective method for cable root detection and extension measurement in estuary wetland forests. Estuarine, Coastal and Shelf Science 183: 117–122. doi: 10.1016/j.ecss.2016.10.029. [DOI] [Google Scholar]
- Vovides AG, Vogt J, Kollert A, et al. 2014. Morphological plasticity in mangrove trees: salinity-related changes in the allometry of Avicennia germinans. Trees 28: 1413–1425. [Google Scholar]
- Vovides AG, Wimmler M-C, Schrewe F, et al. 2021. Roots of cooperation: can root graft networks benefit trees under stress?. Communications Biology, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren JM, Brooks JR, Meinzer FC, Eberhart JL.. 2008. Hydraulic redistribution of water from Pinus ponderosa trees to seedlings: evidence for an ectomycorrhizal pathway. New Phytologist 178: 382–394. doi: 10.1111/j.1469-8137.2008.02377.x. [DOI] [PubMed] [Google Scholar]
- Wimmler M-C, Bathmann J, Peters R, et al. 2021. Plant–soil feedbacks in mangrove ecosystems: establishing links between empirical and modelling studies. Trees 35: 1423–1438. [Google Scholar]
- Wood JP. 1970. Root grafting in Pinus Radiata D.Don. Master’s thesis, Australian National University. https://openresearch-repository.anu.edu.au/handle/1885/143227. [Google Scholar]
- Yli-Vakkuri P. 1953. Untersuchungen über Organische Wurzelverbindungenzwischen Bäumen in Kiefernbeständen. Acta Forestalia Fennica. Suomen metsätieteellinen seura (SMS) - The Finnish Society of Forest Science. http://hdl.handle.net/10138/17996 [Google Scholar]
- Yoder CK, Nowak RS.. 1999. Hydraulic lift among native plant species in the Mojave Desert. Plant and Soil 215: 93–102. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.