Comparative studies of AlphaFold, RoseTTAFold and Modeller: a case study involving the use of G-protein-coupled receptors

Abstract

Neural network (NN)-based protein modeling methods have improved significantly in recent years. Although the overall accuracy of the two non-homology-based modeling methods, AlphaFold and RoseTTAFold, is outstanding, their performance for specific protein families has remained unexamined. G-protein-coupled receptor (GPCR) proteins are particularly interesting since they are involved in numerous pathways. This work directly compares the performance of these novel deep learning-based protein modeling methods for GPCRs with the most widely used template-based software—Modeller. We collected the experimentally determined structures of 73 GPCRs from the Protein Data Bank. The official AlphaFold repository and RoseTTAFold web service were used with default settings to predict five structures of each protein sequence. The predicted models were then aligned with the experimentally solved structures and evaluated by the root-mean-square deviation (RMSD) metric. If only looking at each program’s top-scored structure, Modeller had the smallest average modeling RMSD of 2.17 Å, which is better than AlphaFold’s 5.53 Å and RoseTTAFold’s 6.28 Å, probably since Modeller already included many known structures as templates. However, the NN-based methods (AlphaFold and RoseTTAFold) outperformed Modeller in 21 and 15 out of the 73 cases with the top-scored model, respectively, where no good templates were available for Modeller. The larger RMSD values generated by the NN-based methods were primarily due to the differences in loop prediction compared to the crystal structures.

Introduction

Protein modeling

Protein structure prediction, or protein modeling, is one of the most challenging problems in structural biology (i.e. whether we can determine a 3D structure based on an amino acid sequence without physical experiments). Laboratory experiments based on different branches of science, including X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy, need to be conducted to determine the structure of a protein. The performance of such experiments in terms of time consumption, resolution and environment preparation has continuously improved. For example, the improved cryogenic electron microscopy method [1] allows researchers to obtain protein structures with a better resolution and in a more dynamic environment.

Although a massive amount of experimental effort has been exerted to solve structures, the structures of many protein sequences remain unknown. Hence, accurate computational modeling methods are desired, as they can potentially reduce experimental costs. To evaluate such computational modeling methods, the Critical Assessment of Structure Prediction (CASP, https://predictioncenter.org/) competition releases a set of sequences of unreported structures every 2 years to allow the application of state-of-the-art algorithms providing predictions and assessing the advances in modeling by comparing reported structures and predictions.

Neural network-based modeling of G-protein-coupled receptors

There are two main approaches for modern protein modeling: template-based and neural network (NN)-based. Template-based modeling (TBM), including threading and homology modeling, is a popular computational modeling method that has been used for decades. TBM utilizes available structures as templates to generate structure models. Software packages for TBM, such as Modeller [2] and Phyre2 [3], predict accurate structures when good templates are available. One issue with TBM is that the suitability of the obtained model depends on the selected template. If there is no known structure resembling the target protein domain, TBM fails to generate an accurate model. Some deep learning methods have been used to aid TBM in sequence-template alignment to produce better results [4].

NN-based algorithms for protein modeling have recently achieved substantial success. Deep learning was already used to generate models in the 13th CASP (CASP13) [4–6]. In CASP14, held in 2020, DeepMind structure prediction with AlphaFold [7] achieved an astonishingly high prediction accuracy for the assessment dataset, notably outperforming the other modeling methods. AlphaFold used a deep neural network with special attention modules designed for folding constraints, and the neural network was trained with self-supervised data from the Protein Data Bank (PDB, https://www.rcsb.org/). Subsequently, RoseTTAFold [8] was developed based on inspiration from AlphaFold. RoseTTAFold was designed as a three-track neural network with attention. Its accuracy approached that of AlphaFold in CASP14. Its results showed high consistency with the results of physical experiments and could help solve structures with molecular replacement (MR) methods [8].

With the enormous progress in deep learning-based algorithms, whether the predicted models are accurate enough to be leveraged by researchers has been discussed. To evaluate this issue, we tested the algorithms on G-protein-coupled receptors (GPCRs). GPCRs are the most important group of membrane receptor proteins in eukaryotes. These cell surface receptors receive messages informing cells about the presence or absence of life-sustaining substances in the environment, thus participating in numerous biological pathways in the human body. GPCRs play a crucial role in modern medicine, as many marketed drugs act by binding to them. Thus, understanding their structures is of primary interest in academia and business. In addition, GPCRs are challenging to solve based on NMR spectroscopy and X-ray crystallography for several reasons (e.g. complex sample preparation) [9]. This further increases the supply–demand gap in GPCR structure knowledge. Although dozens of GPCR structures are available by now [10], most of the GPCR structures are still unknown.

Because of the importance of GPCRs and the difficulty of modeling their urgently needed structures, we believe that the performance of GPCR structure prediction is a significant indicator of the advancement of protein modeling methods. We tested the novel NN-based AlphaFold and RoseTTAFold modeling methods on a collection of solved GPCRs in PDB. We used the root-mean-square deviation (RMSD) metric on the backbone alpha-carbons to estimate the accuracy of the predictions. Comparing the two NN-based methods, we found that AlphaFold showed a better performance with the top-scored model accuracy, whereas RoseTTAFold showed a smaller modeling variance of RMSDs. We further compared the modeling RMSDs of NN-based methods with that of the commonly used template-based method—Modeller. We also examined several cases to determine which modeling method can produce superior results and observe where and why modeling errors occurred.

Results

We first present a comparison of the results between AlphaFold and RoseTTAFold. Then, we compare these two deep learning-based methods and Modeller. Finally, we briefly examine several modeling cases.

The best AlphaFold models generally match closely to crystal structures; the RoseTTAFold generally gives more similar models among the top models

To compare both NN-based methods, we calculated the averages of the RMSD of the top-scored model (t_i) as well as the minimum distance between the experimentally solved structures from PDB and the top five scoring protein structures (5-model minimum, m_i), the 5-model average (μ_i) and the 5-model variance (σ_i²) among all the GPCR structures collected. The results are shown in Table 1. The definitions of the variables in the table can be found in the Materials and Methods section.

Table 1.

Basic statistics of the models generated by the two deep learning-based modeling algorithms

	AlphaFold	RoseTTAFold
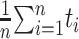
	5.527	6.284
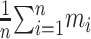
	4.623	5.444
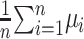
	6.035	6.231
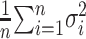
	2.730	1.627

Note: m_i, μ_i, and σ_i² represent the 5-model minimum, the 5-model average and the 5-model variance, respectively, and t_i represents the RMSD of the top-scored model. n = 73 is the size of the dataset. The values are in angstroms (Å).

The average m_i (5-model minimum) and t_i (RMSD of the top-scored model) of AlphaFold were better than those of RoseTTAFold. In contrast, the average σ_i² (5-model variance) of RoseTTAFold was 1 Å less than that of AlphaFold, and the two methods’ average μ_i (5-model average) differed by no >0.3 Å (Table 1). This indicates that AlphaFold tends to generate more diverse models than RoseTTAFold. The average modeling variances (σ_i²) of both methods are shown to be >1.5 Å, indicating a possibility of obtaining a noticeably worse model. Still, users can trust the ranking offered by the methods. Within the dataset of 73 GPCRs, there were 16 cases where AlphaFold’s top-ranked model was precisely the best (RMSD equals m_i), and 15 cases for RoseTTAFold. Moreover, the average difference between the RMSD of the top-scored model and the best model (in the top five models) was below 1 Å for both methods, suggesting that the top-ranked models displayed good fidelity.

Template-based methods are still better if good templates are available

For the 73 proteins in the dataset, 44 templates chosen by Modeller were the structure of the exact PDB entry (of the target protein), and 61 templates’ sequences attained 100% identity with the modeling sequence. Therefore, it would be no surprise that most Modeller models would have a smaller RMSD with an average of 2.17 Å. Comparatively, AlphaFold’s and RoseTTAFold’s t_i averages were 5.53 and 6.28 Å, respectively. Figure 1 shows a box plot of the RMSD of the three modeling methods for the selected dataset.

Figure 1.

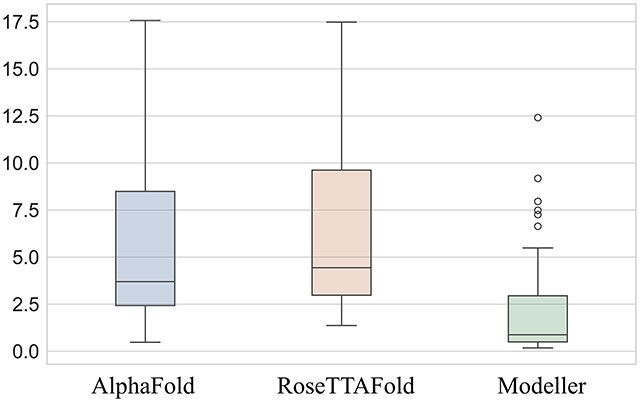
Box plot of the RMSDs of each method. Box plots of AlphaFold, RoseTTAFold and Modeller are shown from left to right, respectively. The RMSD values of AlphaFold and RoseTTAFold are the top-scored models (t_i).

The averages of the difference between t_i (the RMSD of the top-scored model) of AlphaFold and RoseTTAFold and the RMSD of the Modeller model are 3.36 and 4.12 Å, respectively. The positive results indicate that Modeller models are more accurate than the NN-based methods. Nevertheless, the NN-based methods’ models could sometimes achieve higher accuracy. AlphaFold’s best model’s RMSD (μ_i) was smaller than Modeller’s (δ_i) in 21 out of the 73 cases, whereas this was 15 cases with RoseTTAFold. In addition, the top-scored models of AlphaFold and RoseTTAFold showed better accuracy compared to Modeller with 18 and 14 cases, respectively. We noted that the average sequence identity of Modeller’s templates for the previously mentioned 18 cases is 73%, and 65% for the 14 cases. These numbers are lower than the average sequence identity of 96% of the templates over the entire dataset, indicating the NN-based methods performed better than Modeller, where no good templates were available.

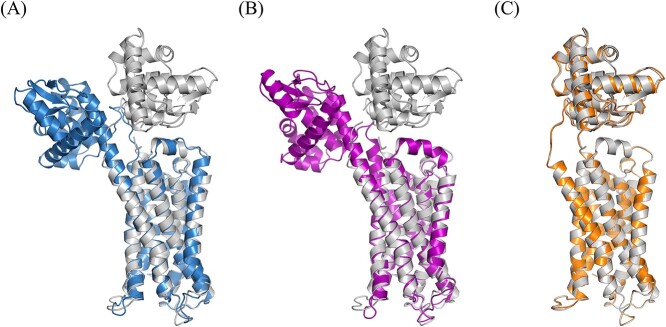
Case study of PDB entry 3PBL

One of the GPCRs in the dataset is an X-ray crystallography-solved human dopamine D3 receptor [6] with PDB code 3PBL. This receptor plays a crucial role in the nervous system and is a drug target for treating Parkinson’s disease, schizophrenia and drug addiction [11]. The structure of 3PBL was solved and deposited into PDB by Chien et al. in 2010. It is composed of 481 amino acids, of which 432 are solved, with 20 alpha-helices and three beta-sheets. The structure of 3PBL consisted of two main parts: the dopamine D3 receptor and the T4-lysozyme (T4L) that was added for stability during crystallization.

The RMSD of the AlphaFold top-scored model was 11.77 Å, and that of RoseTTAFold was 12.18 Å. The RMSD of the Modeller model was 0.42 Å, which was smaller than the other two models by >10 Å. We present the alignment results aligning the 7-TM (7-Transmembrane) part in Figure 2 to determine where the modeling errors occurred. The Modeller model was nearly identical to the crystal structure because it used the exact structure as its template. We noted that the AlphaFold model deviated from the crystal structure, not in the receptor region itself but in the T4L region. If we considered aligning only the 7-TM part, the RMSD dropped to 1.67 Å. Aligning only the T4L part led to an RMSD of 1.58 Å, meaning that the generated model is also accurate in this domain. This implied that the modeling error of the NN-based methods occurred at the junction between the receptor and the stabilizing protein domain. The same situation happened when the RoseTTAFold model was employed. Here, Modeller performed better than the AlphaFold and RoseTTAFold; the major determining factors appeared to rely on the template chosen by Modeller and the relatively poor ability of the NN-based methods to model the junctional loop area between the receptor and T4L.

Figure 2.

The alignment results of the three methods for dopamine D3 receptor in complex with (PDB: 3PBL). The solved crystal structure is grey; the modeling results are in other colors. (A) The alignment result of the AlphaFold model and the PDB structure. (B) The alignment result of the RoseTTAFold model and the PDB structure. (C) The alignment result of the Modeller model and the PDB structure.

Case study of PDB entry 6WJC and 5CXV

PDB entry 6WJC [12] is the crystal structure of an M1 muscarinic acetylcholine receptor (M₁AChR) in complex with muscarinic toxin 7 (MT7) binding to atropine. M₁AChR regulates nervous system functions and is a potential drug target for neurological disorders [13]. The original resolution of the solved structure is 2.55 Å, determined by Maeda et al. in 2020. This crystal structure possesses 21 alpha-helices, three beta-sheets, and a typical trans-membrane protein section. It is worth mentioning that PDB has another record, 5CXV [14], which is the same receptor bound to a different ligand, tiotropium. Despite binding to other ligands, the two PDB entries are of the same solved region, including the receptor and a stabilizing T4L. The amino acid sequences of 6WJC and 5CXV are nearly the same. The only difference is the sequence of 5CXV has 16 extra amino acids at the beginning of the sequence and a replacement of arginine by serine at the 121st position of 6WJC’s sequence. Here, we show the modeling result of AlphaFold and RoseTTAFold alone on both entries. The AlphaFold 5-model-average RMSD for 6WJC reached 3.70 Å, better than that of RoseTTAFold. Nevertheless, we observed the opposite result for 5CXV, in which RoseTTAFold achieved a better RMSD. The results are shown in Table 2.

Table 2.

The 5-model-average RMSDs of the NN-based methods for PDB entries 6WJC and 5CXV

	AlphaFold	RoseTTAFold
6WJC	3.698	4.122
5CXV	5.460	4.380

Note: The better results are indicated in bold. For PDB entry 6WJC, the average RMSD of AlphaFold’s model was smaller. However, for PDB entry 5CXV of nearly the same sequence, RoseTTAFold’s RMSDs are smaller. The values are in angstroms (Å).

Since the sequences of the two entries were nearly identical, a natural question was where the disagreement on the better modeling method originated. First, we noted that there existed modeling variance with the predicted models. AlphaFold’s RMSDs scaled from 2.27 to 4.65 Å for 6WJC, while all were >5 Å for 5CXV. This affected the comparison results against RoseTTAFold as the latter’s RSMDs were 4–5 Å for both entries. Second, the solved positions of the amino acids in the original structure were not exact. The structures of both entries had a resolution exceeding 2.5 Å, which was half the scale of the RMSD values. Third, even though the structures were determined with high precision, the different binding states of the protein might still cause a difference. 6WJC stored the protein in an M₁AChR-MT7 complex binding to the orthosteric antagonist atropine, while 5CXV is the toxin-free protein binding to the inverse agonist tiotropium. The differences between the two structures are described in 6WJC’s paper. We verified a difference by aligning the structures of 5CXV and 6WJC and found a structural difference of 2 Å RMSD. This revealed one shortcoming of the modeling methods: they do not explicitly consider the target protein’s environment. Recent NN-based methods produce structures with variance because of randomness or different neural network parameter weights, which might consider the environment implicitly, not because of the target protein status. The modeling algorithm must also consider the environment to provide more accurate predictions.

Case study of PDB entry 5NM4—the highest resolution structure

The structure with the highest resolution (1.70 Å) among all solved GPCR records in our dataset is the PDB entry 5NM4, a structure of the adenosine A_2A receptor (A_2AR) [15]. A_2AR is related to various diseases, including attention deficit hyperactivity disorder (ADHD) and Parkinson’s, and is a primary caffeine target [16]. The crystal structure was determined in which A_2AR is fused with apocytochrome b562 (bRIL), binding to the antagonistic chemical substance ZM241385. The structure record included A_2AR and the bRIL domains consisting of 433 amino acids.

The RMSD of the five AlphaFold models of 5NM4 ranged from 1.42 to 1.63 Å, and RoseTTAFold 1.34 to 1.41 Å, compared with the RMSD of the Modeller model of 5.04 Å. The alignment result is shown in Figure S2 in Supplementary Materials. This is an example from the collected dataset where the NN-based methods outperformed Modeller. The selected template used by Modeller is the structure of PDB entry 5UIG [17], the same receptor but bound to an antagonistic compound, Cmpd-1. Theoretically, a template-based method would not perform well due to (i) insufficient closely related templates and (ii) inadequate information related to the loop structures. 5NM4 had relatively short loop regions of 25 non-missing amino acids, implying most of it was formed by secondary structures. Thus, the relatively poor performance of Modeller might simply be due to being misinformed by 5UIG’s structure. Although not comparing the exact PDB entry 5NM4, the paper of 5UIG has explained the structural deviation of the A_2AR-BRIL-ZM241385 and the A_2AR-BRIL-Cmpd-1 complex, which contributed to the modeling bias of Modeller.

Case study of PDB entry 5W0P—the case with the most loops

Non-secondary structure regions (loops) cause most of the differences between templates and targets and are thus harder to model with template-based methods. Loops are hard to model because of their irregularity, meaning that it would be interesting to see how the three methods compared when using a structure with the most amino acids in loops in the dataset—PDB entry 5W0P [18]. The structure of 5W0P has 262 non-missing amino acids in the loop regions, storing a crystalized structure of T4L-fused rhodopsin bound to arrestin with a resolution of 3.3 Å. Rhodopsin is a primary photoreceptor molecule [19] that is of great importance in understanding the functioning of our vision and is a potential biomarker for neurodegenerative diseases [20].

For the results with 5W0P, the RMSDs of the RoseTTAFold models ranged from 4.36 to 4.76 Å. The Modeller model has a relatively small RMSD of 2.64 Å because it used the exact structure of 5W0P as its template. AlphaFold’s prediction demonstrated poor accuracy in this case, with its RMSDs ranging from 12.94 to 15.30 Å. To understand the reason for the bad accuracy of AlphaFold, we inspected partial structure alignments. AlphaFold, RoseTTAFold and Modeller exhibited 2.53, 1.73 and 1.09 Å RMSD on the 7-TM region. Although the relative order of the performance of the three methods remained the same, the RMSD difference was smaller, meaning that the major RMSD difference was not raised from the non-junction-loop sections. Rather, the difference came from the error cumulation of loop modeling. We noted that a small modeling error in a loop segment could cause the overall RMSD to grow dramatically. For example, Figure 3 shows the overlapping structures of the three methods and the experimental structure of 5W0P, only aligning one of the loop segments (residue number −4 to 3 in the experimentally solved PDB file). Although the RMSD of AlphaFold on the loop segment is only 1.29, there is a notable misalignment between its prediction and the experimental structure compared to those of RoseTTAFold and Modeller.

Figure 3.

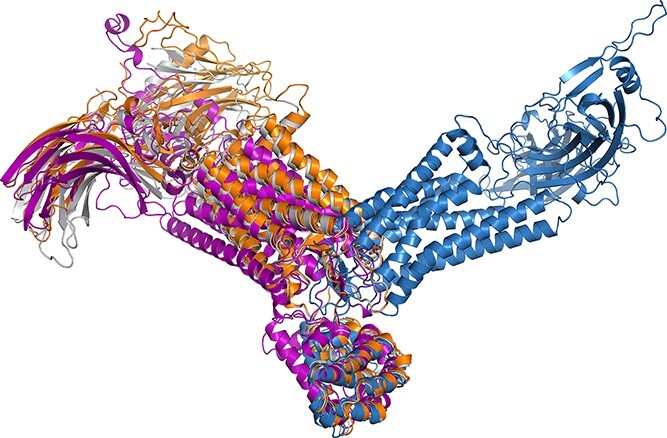
The alignment result of the three methods for PDB 5W0P on a specific loop section. The residue number of the loop section ranged from −4 to 3 in the experimentally solved PDB file. The solved crystal structure is shown in grey; the modeling result of AlphaFold, RoseTTAFold and Modeller are shown in blue, purple and orange, respectively. It is obvious that the structure of AlphaFold’s model deviated from other aligned structures.

Discussion

The analysis in this paper was performed based only on the RMSD metric for simplicity. Other metrics (e.g. TM score [21], global distance test (GDT) score [22] or local distance difference test (lDDT) score [23]) could also be used (with their difference explained in [24]). In addition, we only selected the crystal structures with the best resolution; whether those GPCRs we chose can best represent known GPCR sequences remains an open question. This study provides an overview of the performance of modern NN-based methods for GPCR proteins by showing the accuracy of AlphaFold and RoseTTAFold according to the average RMSD. We tried to provide a perspective on whether researchers can use the models of these methods without additional refinement.

The accuracy of the models of the two NN-based methods has limitations compared with Modeller’s despite outperforming the latter in some cases. We further inspected the cases where AlphaFold and RoseTTAFold both had a significant modeling error (>10 Å RMSD) and found that the error arose from poor modeling accuracy at the junctional loop regions, similar to that described in the case study of PDB entry 3PBL. These cases indicated that the NN-based methods also suffered from erroneous loop modeling. In addition, we examined 12 cases where both AlphaFold’s and RoseTTAFold’s top-scored RMSDs were considerably greater (>8 Å) than Modeller’s, and 14 cases where the difference between RMSDs of the three methods was small (<3 Å), and we noticed that there was a positive correlation between the average RMSD of the loop segments and the overall RMSD (see Table C in Supplementary Materials). A previous review [25] on the current status of protein modeling based on machine learning indicated that AlphaFold performed well on non-loop segments but poorly on loop regions. This result agreed with our case study, suggesting that the model is accurate for non-loop regions but inaccurate otherwise. Still, from the statistics numbers, we noted that the NN-based methods offered better predictions for the cases in which Modeller had no good templates. This suggests that the NN-based methods can be more helpful for predicting structures of unusual sequences.

The analysis in the RoseTTAFold paper [8] also tested its modeling performance on GPCRs. As the algorithm did not have information on the protein state (i.e. active/inactive), an additional method [26] might still be required to select the best structures from those generated for both active and inactive states. This shows that accurate protein modeling, especially for complex proteins, may require extra information regarding the environmental condition of the protein. A new version of AlphaFold [27] is being developed as this paper is being prepared, improving modeling accuracy for multimeric proteins.

Materials and methods

Metric

We used the RMSD metric to evaluate the performance of the predictions, which is calculated as follows:

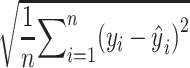where 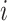iterates through n amino acids under consideration, and y_i and ŷ_i represent the coordinates of the ith amino acid’s alpha-carbon position in the first and second structures under comparison, respectively, in the 3D space. The smaller the RMSD value is, the closer the crystal structure and prediction are to each other.

Let n = 73 be the number of collected GPCRs. We define

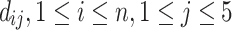as the RMSD between the jth-ranked model and the experimentally solved structure of the ith protein. We noted that the RMSDs introduced in this work were post-clipping values calculated within the segments where Modeller’s models were present. We define t_i to be the RMSD of the top-ranked model, namely, d_i₁, and the 5-model average

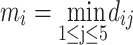as the minimal RMSD of the five models for the ith protein. We also define the 5-model average and the 5-model variance as follows:

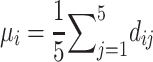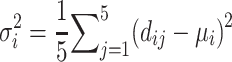Data pipeline

GPCR data collection

We collected the amino acid sequences in FASTA format and the corresponding PDB structure for 75 distinct GPCR proteins available in the PDB as our dataset to evaluate the modeling methods. Records of two proteins were removed due to failure of metric calculation (see below the section describing the post-modeling clipping process). The GPCRs were collected via manual searches and were all distinct. They could belong to the same family but not the same subtype. The resolutions of the solved structures were below 4.1 and 3.2 Å if entry 5UZ7 was excluded. The complete list of the GPCRs can be found in the Supplementary Materials.

Model generation

We input the collected FASTA sequence files into the modeling utilities. We only considered running the utilities with their default settings to test the most straightforward usage scenarios. For AlphaFold, we downloaded the open-source repository on GitHub (https://github.com/deepmind/alphafold, version 2.0.0) and ran it in a local GPU environment. For RoseTTAFold, we requested the Robetta web server (https://robetta.bakerlab.org/) from 11 September 2021 to 5 October 2021 and chose RoseTTAFold as the algorithm for generating the initial model structure. For TBM with Modeller, we used the Modweb (https://modbase.compbio.ucsf.edu/modweb/) web server from 30 September 2021 to 2 October 2021 to output the predictions. The AlphaFold pipeline output five trained structure prediction models for each input sequence that are ranked by the algorithm’s confidence. The Robetta web server also sampled five ranked models for each target. Modweb produced one or more models for a single target (based on different templates), and we picked the first one shown on the results webpage for use. All the predicted structures were collected in PDB format.

Residue alignment

The predicted models were then aligned with the experimentally solved structures using TM-align [28] (https://zhanggroup.org/TM-align/), which also calculated the alignment score and RMSD used in this study. Protein alignment programs, including TM-align, align residues according to alignment scoring. The same amino acid residue in the two proteins in an alignment may not be matched, leading to a biased comparison of RMSD between models. Fortunately, TM-align provides an alignment file argument that allows users to specify residues to be paired. We created an alignment file for each target protein to force the same-residue pairing. Each file contained two sequences: the predicted model and the experimentally solved structure in FASTA format. The problem of missing residues in the experimentally solved structures was also addressed here with the alignment files. For a solved structure with no missing residues, the two sequences were the same; for those with missing residues, we padded dashes at the missing positions in the sequences, which were skipped in TM alignment.

Post-modeling clipping

Modeller’s server only generated models for the regions of higher confidence in its predictions, so the output structures were shortened. We clipped the predicted structures obtained via the NN-based methods and experimentally solved structures by selecting residues in the PDB files to conduct a fair comparison when Modeller’s models were involved. The alignment files used by TM-align were also clipped. PDB entries 5UZ7 and 7D77 were removed from the dataset after clipping because there were no overlapping regions between the Modeller-predicted structure and the non-missing part of the experimentally solved structure for comparison. The ranges of the partial sequences obtained after clipping are listed in the Supplementary Materials.

Visualization

The open-source PyMOL system (https://pymol.org/2/) was used for visualization, and the TM-align extension for PyMOL was used to allow the results of the TM-align alignment to be viewed.

Key Points

• Recent improvements in neural network-based protein modeling methods raised the question of whether the models predicted are accurate enough and can be used for drug discovery.

• We explored the modeling performance of a commonly used template-based method (Modeller) and current neural network-based methods (AlphaFold and RoseTTAFold) based on G-protein-coupled receptor (GPCR) proteins, which are of great pharmaceutical importance.

• Our statistics show that the template-based protein modeling method is better if good templates are available.

• Our case studies indicate that modeling loops remain difficult by using NN-based methods. Also, information regarding environmental conditions is required for more accurate structure prediction.

Author Biographies

Chien Lee is a master’s student at the Department of Computer Science and Information Engineering, National Taiwan University.

Bo-Han Su is a postdoc at the Department of Computer Science and Information Engineering, National Taiwan University. His research interests include biomolecular simulation, computer-aided drug discovery and design, and cheminformatics.

Yufeng Jane Tseng is a professor at the Department of Computer Science and Information Engineering, National Taiwan University. Her research interests include computational chemistry, toxicology, bioinformatics, cheminformatics and health informatics.

Data availability

The data underlying this article are available in the article and its online supplementary materials.

Funding

This work was supported by the Taiwan Ministry of Science and Technology (MOST 109-2627-M-002-003-, MOST 110-2320-B-002-038- and MOST 111-2119-M-033-001-); the Taiwan Food and Drug Administration (MOHW110-FDA-D-114-000611 and MOHW111-FDA-D-114-000611); National Taiwan University (NTU-CC-110L890803, NTU-110L8809, NTU-CC-111L890203 and NTU-111L8809) and Toxic and Chemical Substances Bureau, Environmental Protection Administration, Executive Yuan, R.O.C. (110A022).