Abstract
A 2-dimensional multicomponent ion transport model based on Nernst-Planck (NP) equation and electroneutrality assumption is developed for an electrodialysis (ED) cell operated in the ohmic regime. The flow in channels are assumed incompressible, isothermal, and laminar. Donnan equilibrium and flux continuity are considered at ion-exchange membrane (IEM)-solution interfaces. To account for tortuosity effects inside membranes, effective ionic diffusion coefficients are calculated using membranes water volume fractions. The developed multicomponent model is used to elucidate the effects of feed solution properties, cell properties, system hydrodynamics, operational conditions, and membrane properties on selective divalent ion removal in the cell.
The results indicate that the selective removal of divalent ions improves with decreasing the cell length, imposed potential, and ionic strength of feed water. Enhanced mixing in spacer-filled cell also promotes selective divalent ion removal. Higher concentrations of fixed charges on the membranes results in greater selectivity toward divalent ions at short cell length and low imposed potentials. With equal concentrations of fixed charges, membranes with high water content are less favorable for selective divalent ion removal. The developed framework enables the optimum selection of cell design, IEMs, spacer design, and operational conditions to selectively remove ions from multicomponent solutions.
Keywords: Electrodialysis, Ion transport modeling, Multicomponent solution, Selective ion removal, Scale precipitation
Graphical abstract
Highlights
-
•
A 2-dimensional model is developed for electrodialysis of multicomponent solutions.
-
•
Parameters affecting selectivity of divalent ion removal are investigated.
-
•
Feed water composition and salinity affect the selectivity toward divalent ion.
-
•
Using spacer and lowering cell length and potential improve divalent ion removal.
-
•
Membrane with high fixed charges and low water uptake favors divalent ion transport.
1. Introduction
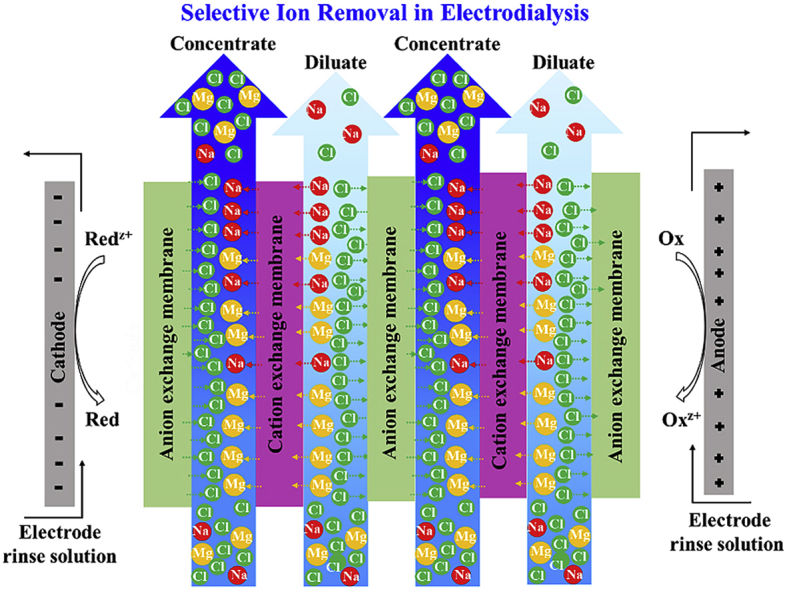
Brackish and produced waters are increasingly considered as potential sources of industrial, agricultural, and drinking waters. Scale formation due to mineral deposition from these saline waters is a major concern in many industries and chemical processes including oil and gas [1], power plants [2], and membrane desalination processes [3]. Seawater, brackish water, and oil and gas produced water are typically dominated by Na+ and Cl− ions [[4], [5], [6]]. Often, however, low concentrations of other ions e.g., Ba2+, Sr2+, Mg2+, Ca2+, SO42−, and HCO3−/CO32− are of primary concern for scale [[7], [8], [9]]. The selective removal of scale precipitating ions can be critical in allowing cost effective treatment processes that enable the industrial use of brackish water and seawater, as well as the reuse and recycling of waste streams e.g., produced water. The beneficial reuse of saline waste streams also helps avoid the environmental impacts associated with disposal [10]. Electrodialysis (ED) is an electro-membrane desalination technique that can potentially be used for selective removal of scale precipitating ions from saline water. An ED stack contains a series of cation and anion exchange membranes (CEM and AEM, respectively) placed in an altering arrangement between two electrodes. Feed water flows in the channels between the ion exchange membranes (IEMs). Due to the existence of an electric field perpendicular to the flow, ionic species migrate toward opposite-signed electrodes. The selective permeation of ions through IEMs results in decrease of ionic concentration in one channel, diluate, and increase of concentrations in the adjacent compartments, concentrates.
At equal concentrations of two ionic species, the ionic charge number and mobility play the key roles in selective removal in ED. A greater charge results in larger partitioning at the membrane-solution interfaces while the higher mobility results in greater transport in the boundary layers and inside the membranes. The molecular weight and the size of the species possibly can affect their selective transport through the membranes [11,12]. The ionic fluxes and partitioning depend on their concentrations as well. Thus, feed water chemistry and operational conditions, affecting the boundary layer concentrations, impact the selective removal in ED.
Moreover, several preparation and modification methods are developed to fabricate permselective IEMs that not only exhibit low permeability toward co-ions but they demonstrate selectivity toward different counterions [12]. The preparation techniques and the principles of selective ion transport through permselective IEMs are comprehensively reviewed by Luo et al. [12]. Such permselective membranes can be used in ED to further improve selective removal of specific ions from multicomponent solutions.
A number of experimental and theoretical studies have investigated the selective ion removal from various solutions with ED. Indusekhar et al. [13] used ED with a NO3−-specific AEM for selective removal of NO3−. NO3−-specific AEMs were prepared by amination of chloromethylated polysulphone with secondary and tertiary amines. At neutral pH, no selectivity was observed between NO3− and Cl− removals in ED, while with increasing or decreasing the pH, selective removal of NO3− enhanced. Elmidaoui et al. [14] studied the selective NO3− removal from groundwater with ED and achieved satisfactory water quality. Kabay et al. [11] conducted experiments with an ED stack containing ten cells at 5 and 10 V in a recycling batch mode to investigate the selective removal from binary and ternary aqueous solutions of Na+, K+, Ca2+, Mg2+, Cl−, NO3−, and SO42− ions. At 5 V, they observed higher ion removal from solutions containing monovalent counterions than those containing divalent counterions. However, the counterions effect on ion removal was negligible at 10 V. Sadrzadeh et al. [15] studied operational effects on selective removal of Na+, Cu2+, Zn2+, Pb2+, and Cr3+ from water in an ED cell. The impacts of concentration (100, 500, and 1000 mg/l), temperature (25, 40, and 60 °C), flow rate (0.07, 0.7, and 1.2 mL/s), and voltage (10, 20, and 30 V) on separation efficiency were investigated. In single electrolyte solutions, the separation percentages of all ions increased by enhancing the concentration, temperature, and voltage while increasing the flowrate had an adverse impact. The concentration effect disappeared beyond 500 (mg/l). In ED of multicomponent feed solutions at optimum operational condition, the separation percentage of monovalent ions were greater than multivalent ions. Xu et al. [16] investigated selective arsenic and monovalent ion removal in ED using monovalent permselective AEM. The AEM showed high selectivity toward monovalent anions over a wide spectrum of imposed current densities. However, the transport of multivalent cations through monovalent permselective CEM increased at higher cell potential. Nie et al. [17,18] evaluated the effects of various operational parameters including temperature (15–30 °C), flow rates (0.6–1.2 m3/h), the initial volumetric ratio of the concentrate (VC) to diluate (VD) streams (0.6–1), and the current density (5.9–1.38 A/m2) on selective transport of Li+ over Mg2+ in ED with monovalent permselective IEMs. The results indicated that the selective removal of Li+ ions improved at lower temperatures and higher current densities and flow rates. At VC to VD ratio of 0.8–1, the transport of both Li+ and Mg2+ were high. 95.3% of Li+ recovery was reached under the optimum operating conditions.
According to the experimental observations, ion properties, cell hydrodynamics, and membrane properties impact the selective removal of ions in ED. Kim et al. [19] studied competitive transport of cations in ED of an aqueous K+-Ca2+-Cl− ternary system with modeling approach. A one-dimensional model based on the Nernst-Planck (NP) equation assuming electroneutrality was developed and analytically solved to investigate the boundary layer effects on selective ion transport across the CEM. The co-ion transport through the membrane was neglected and the transport of cations inside the CEM was determined by trial-and-error. The one-dimensional model was further extended to two dimensions by dividing the cell length into control volumes and solving one-dimensional model for each. The modeling results indicated higher Ca2+ transport through the membranes at ohmic regime while K+ permeation became significant at non-ohmic regime. However, the developed model did not consider co-ion transport through the membranes and effects of solution composition on selective removal of cations.
Galama et al. [20] conducted ED experiments on ternary salt solutions of NaCl + Na2SO4 and synthetic North Sea water to investigate the selective removal of ions. They further developed a multicomponent ion transport model using NP equation, electroneutrality assumption, and local Donnan equilibrium at the membrane-solution interface. The correlation between diffusion coefficients of ions inside membranes and in solution was identified empirically, and found to be depended upon current for divalent ions in AEMs. Diffusion boundary layers (DBLs) were assumed stagnant with constant thickness along the cell. A uniform ion concentration was considered in the concentrate channel. Also, membranes were assumed to be ideal and no co-ion transport was considered through the membranes. Their results indicated that the selective removal of divalent ions in ED increased at lower operating current densities. However, the economical operation of ED at such small current densities required the development of less expensive IEMs.
Fíla and Bouzek [21] and Moshtarikhah et al. [22] employed the NP equation assuming electroneutrality within the electrochemical cells to model multicomponent ion transport i. The Schlögl’s flow equation was employed to describe the solution velocity inside Nafion membranes while in DBLs outside the IEMs, the convective ion transport was neglected. Thicknesses of DBLs were assumed constant and Donnan equilibrium was considered at the IEM-solution interface. The models developed in both studies failed to account for hydrodynamic effects inside the channel.
In the current effort, a multicomponent 2-dimensional ion transport model is developed using the NP equation, Navier-Stokes (NS) equation, continuity, and molar mass balance in a spacer-free and spacer-filled cell [23,24]. Electroneutrality is assumed inside channels and membranes and Donnan equilibrium is considered at the IEMs-solution interfaces [25,26]. The model accounts for co-ion transport through the membranes and calculates the development of DBLs along the cell with no limitation for the thicknesses of these layers. The current framework is an expansion of developed model for binary solutions [27].
The developed multicomponent model is used to investigate the effects of feed water ionic strength, feed water composition, imposed potential, cell length, spacers, membrane fixed charges concentrations, and membrane water volume fraction (ϕw) on selective divalent ion removal in ED of the aqueous Na+-Mg2+-Ba2+-SO42−-Cl− quinary solution. The quinary system under study contains the major ions of most saline waters (Na+ and Cl−) and several of the scale precipitating components (Mg2+, Ba2+, and SO42−) as examples. Note that the developed model can be employed for any multicomponent solutions and the quinary system under study here, serves as an example of a system that contains divalent and monovalent anions and cations. This study elucidates the sensitivity of selectivity in ED to each parameter and provides a guideline for optimization of design, material, and operational conditions. It is also useful to narrow the choices that might be used to experimentally explore selectivity in ED and to design such experiments.
2. Modeling framework
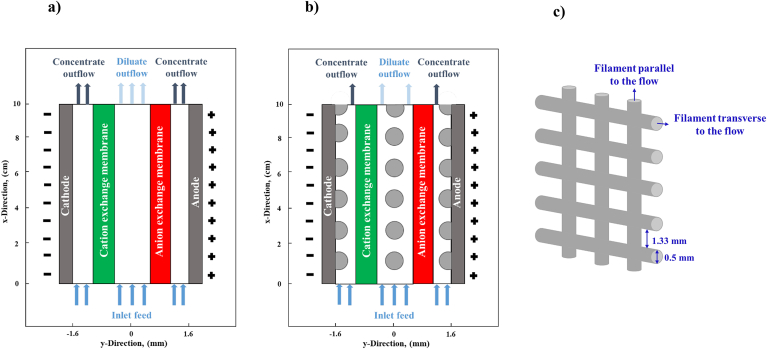
As indicated in Fig. 1a and b, both spacer-free and spacer-filled cells contain concentrate channels, a CEM, a diluate channel, an AEM, and a hypothetical cathode and an anode respectively placed in the leftmost and rightmost boundaries to represent the potential imposed upon a single cell. Table 1 contains the range of model input parameters. The reported [28,29] fixed charge concentrations and water volume fractions for CR61-CMP and AR103-QDP (Ionics Inc., USA) are used as modeling parameters for, respectively, CEM and AEM. However, the sensitivity of selectivity to membrane properties is investigated through changing the membranes fixed charge concentrations and water volume fractions in the ranges reported in Table 1.
Fig. 1.
a) A schematic of the spacer-free cell, b) A schematic of the spacer-filled cell, c) A schematic of the spacer net.
Table 1.
ED cell properties.
| Parameter | Value | Unit |
|---|---|---|
| Channel width (WCh) | 1 | [mm] |
| Channel length (L) | 2–10 | [cm] |
| Membrane width (WM) | 0.6 | [mm] |
| Spacer filament diameter | 0.5 | [mm] |
| Number of spacer filaments in the channel | 74 | – |
| Temperature | 298.15 | [K] |
| Flow inlet velocity (V0) | 0.06 | [m/s] |
| Cell potential | 0.3–1.3 | [V] |
| Na+ Diffusion coefficient in channels | 1.3 × 10−9 | [m2/s] |
| Mg2+ Diffusion coefficient in channels | 7.1 × 10−10 | [m2/s] |
| Ba2+ Diffusion coefficient in channels | 8.5 × 10−10 | [m2/s] |
| Cl− Diffusion coefficient in channels | 2 × 10−9 | [m2/s] |
| SO42− Diffusion coefficient in channels | 1.1 × 10−9 | [m2/s] |
| CR61-CMP fixed charges concentration (cF,CR61-CMP) [28,29] | 3210 | [mol/m3(absorbed water)] |
| AR103-QDP fixed charges concentration (cF,AR103-QDP) [28,29] | 3580 | [mol/m3(absorbed water)] |
| CR61-CMP water volume fraction (ϕw,CR61-CMP) [28,29] | 0.5 | Lw/Lsp |
| AR103-QDP water volume fraction (ϕw,AR103-QDP) [28,29] | 0.4 | Lw/Lsp |
| CEM fixed charges concentration (cF,CEM) | 1600–3210 | [mol/m3(absorbed water)] |
| AEM fixed charges concentration (cF,AEM) | 1809–3580 | [mol/m3(absorbed water)] |
| CEM water volume fraction (ϕw,CEM) | 0.4–0.6 | Lw/Lsp |
| AEM water volume fraction (ϕw,AEM) | 0.3–0.5 | Lw/Lsp |
The concentrations and ionic strength (Is) of the feed water are presented in Table 2. The ionic strength of saline water, defined as Eq. (1), represents the total concentrations of ions in water.
| (1) |
Table 2.
Ionic inlet concentration of the feed water.
| Components | Inlet concentrations, mol/m3 Feed Is = 1779 mol/m3 |
Inlet concentrations, mol/m3 Feed Is = 593 mol/m3 |
|---|---|---|
| Na+ | 1000.0 | 333.3 |
| Mg2+ | 250.0 | 83.3 |
| Ba2+ | 7.1 | 2.4 |
| Cl− | 1500.0 | 500.0 |
| SO42− | 7.1 | 2.4 |
Here, zi and ci are the charge number and concentration of species i, respectively. The investigated ionic strengths are based on the average salinity range of seawater and oil and gas produced water [[4], [5], [6]]. Such ionic strengths and compositions are chosen to explore the sensitivity of the preferential removal of scale precipitating ions to total salinity and chemistry of feed water. Due to the minor water dissociation and pH changes within the ohmic regime, salt precipitation is considered to be negligible in this study.
The porosity of the spacer-filled channel is set to 85%, which is associated with the mesh size of 1.33 mm and filament dimeter of 0.5 mm, as shown in Fig. 1c. In our 2-D model, the impacts of spacer filaments parallel to the flow are neglected. The model accounts for co-ion transport, while neglecting osmosis water transport through IEMs. The flow in channels moves upward in the positive x-direction and assumed to be isothermal and incompressible. An electric field in the y-direction, perpendicular to the flow, is considered in the cell.
The ionic transport occurs due to diffusion, electromigration, and convection and the fluxes are calculated using the NP equation [23] as
| (2) |
where j denotes compartments in the cell which can be channel (c) or membrane (m); Ni j, Di j, ci j, and Mi j are, respectively, the molar flux, diffusion coefficient, concentration, and mobility of species i in the compartment j; zi is the charge number of species i (+1, +2, +2, −1, −2 for Na+, Mg2+, Ba2+, Cl−, and SO42−, respectively); F is the Faraday constant (9.6 × 104 C/mol); Ø j denotes the potential in compartment j; and V j is the flow velocity in compartment j.
The mobility of species i in compartment j, Mij, relates to its diffusion coefficient via Nernst-Einstein equation [23] as
| (3) |
here, R, and T are the universal gas constant (8.314 J/mol.K) and temperature, respectively. To account for tortuosity effects inside membranes, effective diffusion coefficients of species i in membranes, Di m, are calculated based on the diffusion coefficients in solutions inside channels, Di c, and water volume fractions of membranes as described in Eq. (4) [29].
| (4) |
The electroneutrality which is assumed to hold in channels and IEMs are described as Eqs. (5), (6)), respectively. Note that electroneutrality inside membranes includes the concentration of membranes fixed charges.
| (5) |
| (6) |
here, cic, ci m are the concentration of species i in channels and inside membranes, respectively; zF is the charge number of fixed charge groups of IEMs. For ED cell operated in the ohmic regime, due to minor thicknesses of electric double layers formed at IEMs-solution interfaces, electroneutrality is considered to hold everywhere in the cell. The sharp changes in concentrations and potentials at the membrane-solution interfaces are calculated assuming local Donnan equilibrium [30]. Once the current reaches the limiting value (limiting current density), Poisson’s equation should replace the assumption of electroneutrality due to increases in thicknesses of space charge regions in DBLs [31]. Commercial ED plants, however, are conventionally operated at 80% of the limiting current values [32]. Hence, the focus of our study is developing ion transport model at ohmic regime (below limiting current density) in which local Donnan equilibrium and electroneutrality are appropriate assumptions [31].
In IEMs, the flow velocity, Vm, is assumed zero, eliminating the convection term in the NP equation. In channels, the NS equations are solved to obtain the velocity profile, Vc. The calculated Reynolds numbers using the inlet flow velocity and hydraulic diameter of channels suggest laminar flow for both spacer-free and spacer-filled channels. Boundary conditions used to solve the NS equation include no-slip condition on surface of membranes and spacer filaments; symmetry for the leftmost and rightmost boundaries of concentrate channels; normal inlet velocity; and zero pressure at the channel outlets. The details on flow modeling are provided elsewhere [27].
Substituting the NP equation and velocity profiles in molar balance equation results in N equations which are solved together with electroneutrality assumptions to calculate N+1 unknowns (concentrations of N species and the electric field).
The current density at each compartment, I j, is described using Faraday’s law as
| (7) |
3. Constituent boundary conditions
The boundary conditions for the molar balances include the continuity of ionic fluxes and current density along with Donnan equilibrium [25,26] at IEMs-solution interfaces as described in Eqs. (8), (9), (10).
| (8) |
| (9) |
| (10) |
Where Ni c, I c, Ø c are, respectively, molar fluxes of species i, current densities, and potential in channels; Ni m, I m, and Ø m are, respectively, molar fluxes of species i, current densities, and the potential in membranes; and is the unit vector normal to the area.
4. Numerical method and mesh structure
COMSOL Multiphysics 5.4 software with Electrochemistry module is used to solve the set of equations with assigned boundary conditions using the finite element method. Laminar Flow interface with linear discretization of velocity and pressure is used to calculate velocity profile in channels. Tertiary Current Distribution, Nernst-Planck interface with quadratic discretization of the concentration and potential is employed for mass transport computation. In spacer-filled cell, the spacer filaments are assumed to be non-conductive with no mass transport and flow through them. The MUMPS solver is used for solving the set of equations.
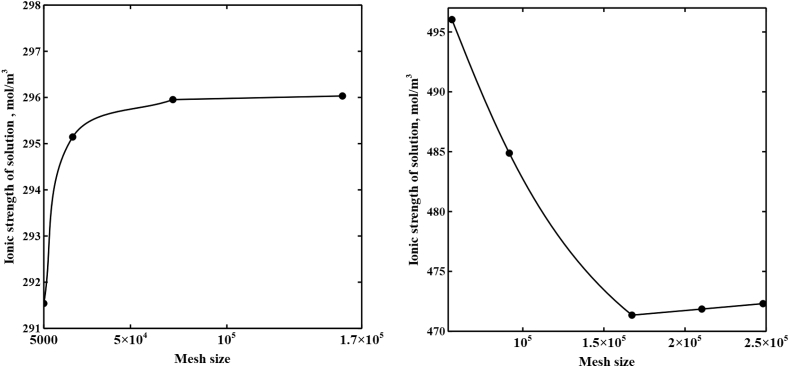
A rectangular mesh is defined for a spacer-free cell with smaller element size in the boundaries adjacent to IEM-solution interfaces. In a spacer-filled cell, a hybrid unstructured mesh is set with triangular elements outside the boundaries and quadrilateral elements inside the membrane-solution and spacer filaments-solution boundaries. A smaller element size is chosen at these boundaries to capture the sharp concentration, potential, and velocity changes. To reach mesh-independent results for both spacer-free and spacer-filled cells, a number of mesh refinement steps are taken and the mesh sizes are set to numbers beyond which no significance changes are observed in the calculated results. Fig. 2a and b demonstrate the ionic strength of the solution at CEM-solution interface in the diluate channel outlet for each mesh refinement step. The total number of elements are set to 160,000 and 167,289 for spacer-free and spacer-filled cells, respectively.
Fig. 2.
The ionic strength of the solution at the CEM-solution interface at the diluate channel outlet at different mesh size. a) spacer-free cell and b) spacer-filled cell.
5. Results and discussion
Higher total ion removal is achieved by increasing the cell length and potential due to the increases in residence time and electrical driving forces. However, the selective ion removal may not necessarily increase with cell length and potential since it can also be affected by other parameters e.g., membrane properties, composition of the feed water, and ion properties. The ion removal percentage, the relative ion percentage removal, and the relative ion mass removal, defined as Eqs. (11), (12), (13)), are used to evaluate the effects of various parameters on selectivity.
| (11) |
| (12) |
| (13) |
Where ci, cross-avg and ci, feed are, respectively, the horizontal cross-sectional average concentration and feed water concentration of species i in the diluate channel; cj,cross-avg and cj,feed are, respectively, the horizontal cross-sectional average concentration and feed water concentration of species j in the diluate channel. The increases in relative percentage removal and relative ion mass removal of species j to i demonstrate the enhanced selectivity toward removal of species j.
Due to the higher charge of divalent ions, Donnan equilibrium at IEMs-solution interfaces drives larger partition coefficients for divalent ions compared to monovalent ions. However, diffusion and electromigration fluxes of divalent ions are generally smaller due to their lower diffusion coefficients and concentrations. Thus, any parameters that increase Donnan potential drops at the interface and decreases fluxes of divalent ions in DBLs results in increases of monovalent ions concentrations and consequently, reduction of selectivity toward divalent ions. Note that the concentration of fixed charges and water volume fractions of the CEM and AEM are, respectively, set to reported values for CR61-CMP and AR103-QDP, as presented in Table 1, except for simulations that specifically change these parameters.
5.1. Cell length effects
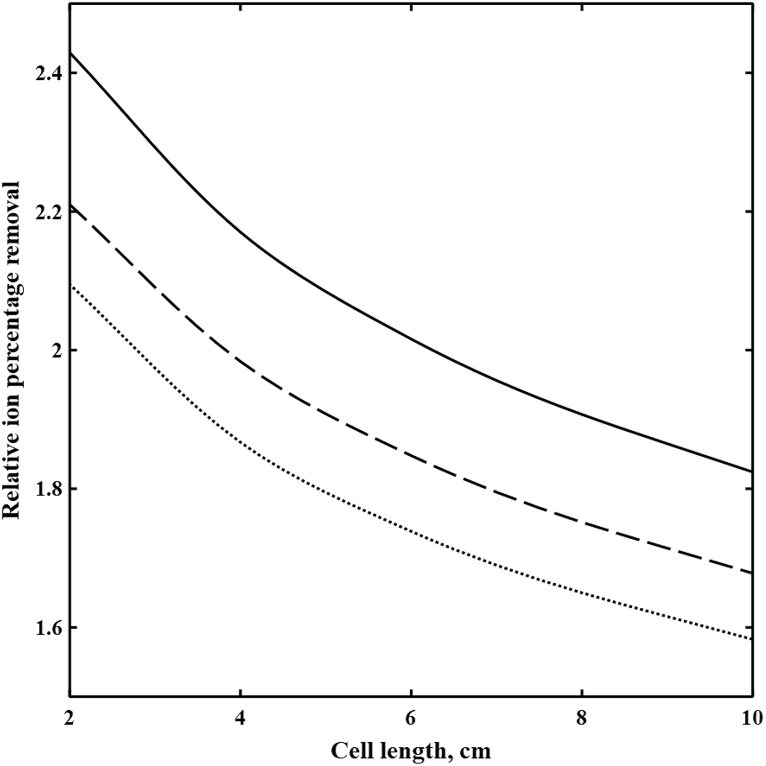
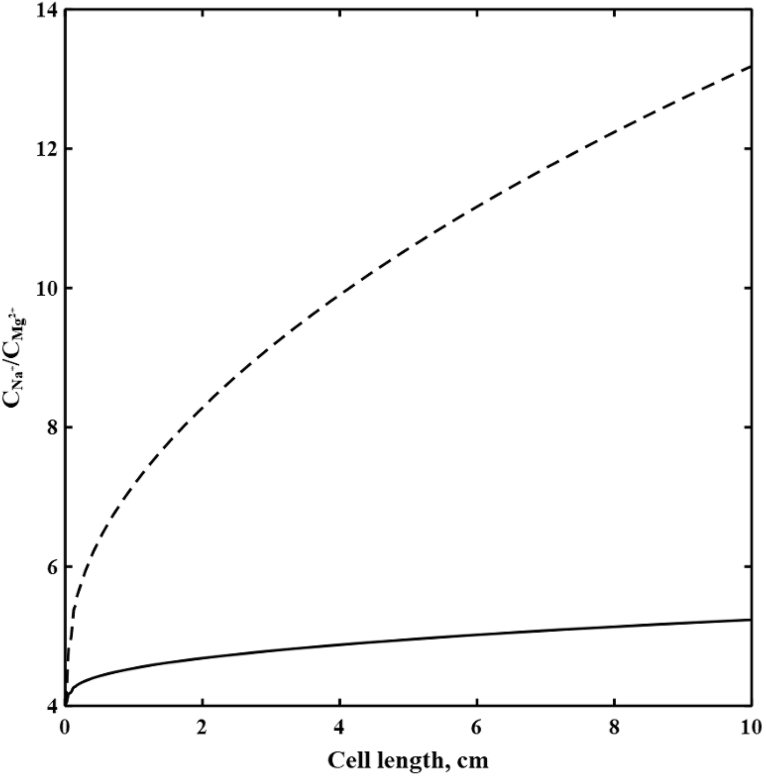
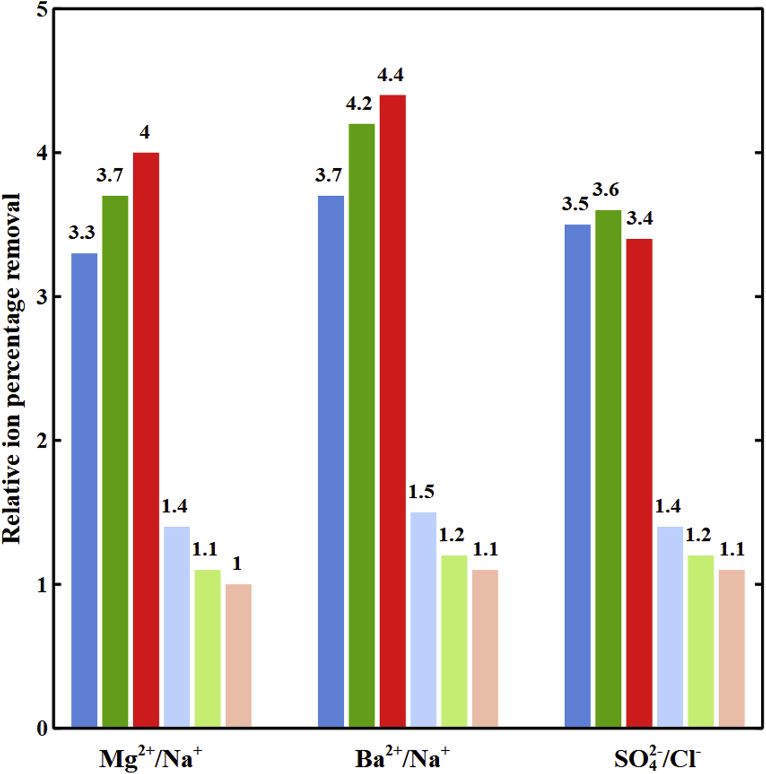
Fig. 3 demonstrates decreases in relative percentage removal of divalent to monovalent ions i.e., (Ba2+, Na+), (Mg2+, Na+), and (SO42−, Cl−) by increasing the cell length in the diluate channel of spacer-free cell at 1.3 V and feed ionic strength of 1779 mol/m3. Due to the higher partitioning at the interface and lower fluxes of divalent ions, the ratio of monovalent to divalent ions concentrations in DBLs continuously grow along the cell. Fig. 4 demonstrates such increases in Na+ to Mg2+ concentrations ratios with the cell length at 0.3 and 1.3 V. Thus, selective removals of divalent ions decrease with increasing length due to the continuous depletion of their concentrations in DBLs. Such result suggests that an optimum design might be multiple stages of short cell length.
Fig. 3.
The relative ion percentage removal versus cell length in the diluate channel of the spacer-free cell at V = 1.3 V, feed Is = 1779 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) Ba2+/Na+, (
) Ba2+/Na+, ( ) Mg2+/Na+, and (
) Mg2+/Na+, and ( ) SO42−/Cl−.
) SO42−/Cl−.
Fig. 4.
The concentration ratio of Na+ to Mg2+ at CEM-solution interface versus the cell length in the diluate channel of the spacer-free cell for feed Is = 1779 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) at V = 0.3 V and (
) at V = 0.3 V and ( ) at V = 1.3 V.
) at V = 1.3 V.
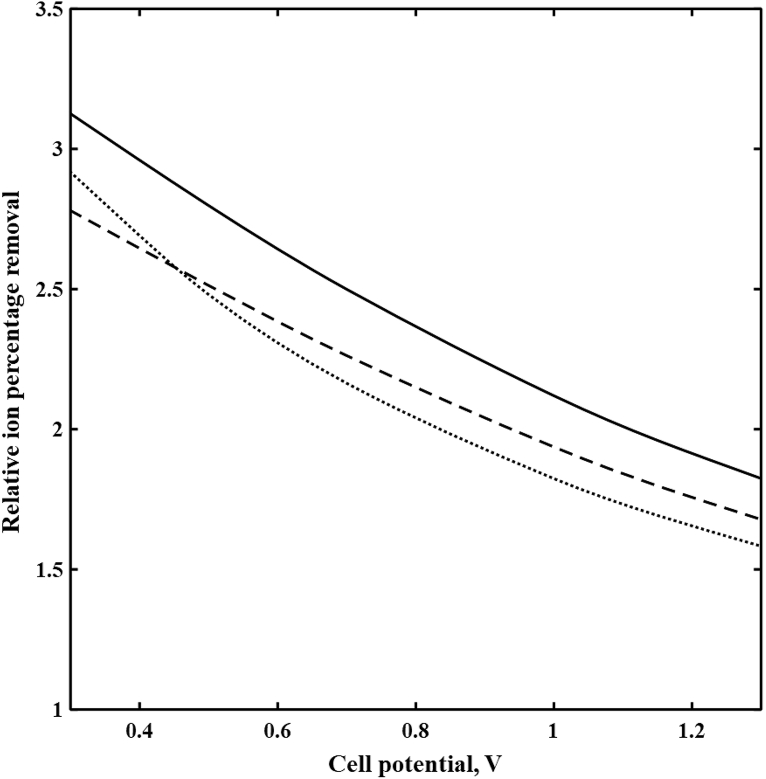
5.2. Imposed potential effects
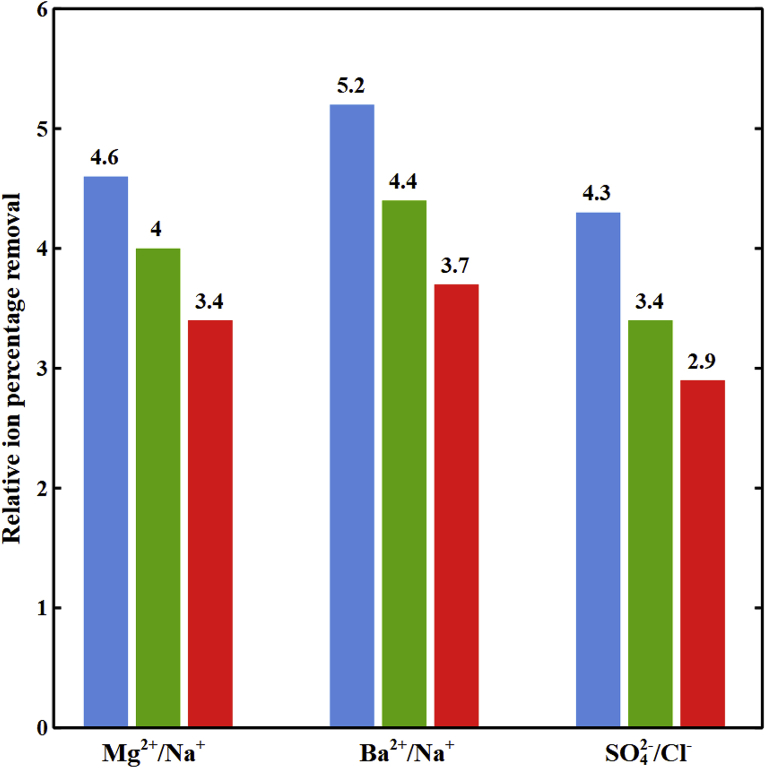
Fig. 5 shows the decrease of relative ion percentage removal of (Ba2+, Na+), (Mg2+, Na+), and (SO42−, Cl−) with the cell potential in the diluate channel of the spacer-free cell for a length of 10 cm and feed ionic strength of 1779 mol/m3. Increasing the imposed potential enhances Donnan potential drops and electromigration fluxes in the cell. As discussed earlier, greater Donnan potential drops provide higher partitioning for divalent ions at the interface. However, increases in electromigration fluxes are more significant for monovalent ions due to their greater diffusion coefficients and concentration. Thus, monovalent to divalent ion concentration ratios in DBLs increase at higher imposed potentials as shown in Fig. 4 for Na+ to Mg2+. This results in a decrease in selectivity toward divalent ions at higher imposed potentials.
Fig. 5.
The relative ion percentage removal versus imposed potential in the diluate channel of the spacer-free cell at L = 10 cm, feed Is = 1779 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) Ba2+/Na+, (
) Ba2+/Na+, ( ) Mg2+/Na+, and (
) Mg2+/Na+, and ( ) SO42−/Cl−.
) SO42−/Cl−.
5.3. Feed water ionic strength effects
Fig. 6 indicates the comparison between relative ion percentage removals of (Ba2+, Na+), (Mg2+, Na+), and (SO42−, Cl−) in the diluate channel of the spacer-free cell for feed ionic strengths of 1779 and 593 mol/m3, at the cell length of 2 cm, and imposed potential of 0.3 V. Donnan potential drops are higher for feed water with lower ionic strength, resulting in greater partitioning for divalent ions at IEMs-solution interfaces. Thus, at low cell length and imposed potential, the selective divalent ion removal is greater for feed water with lower ionic strength. However, due to the greater depletion of divalent ions in DBLs, the loss in selectivity with increasing the imposed potential and cell length is more significant for feed water with lower ionic strength.
Fig. 6.
The relative ion percentage removal with ionic strength in the diluate channel of the spacer-free cell at L = 2 cm, V = 0.3 V, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) Feed Is = 1778 mol/m3 and (
) Feed Is = 1778 mol/m3 and ( ) feed Is = 593 mol/m3.
) feed Is = 593 mol/m3.
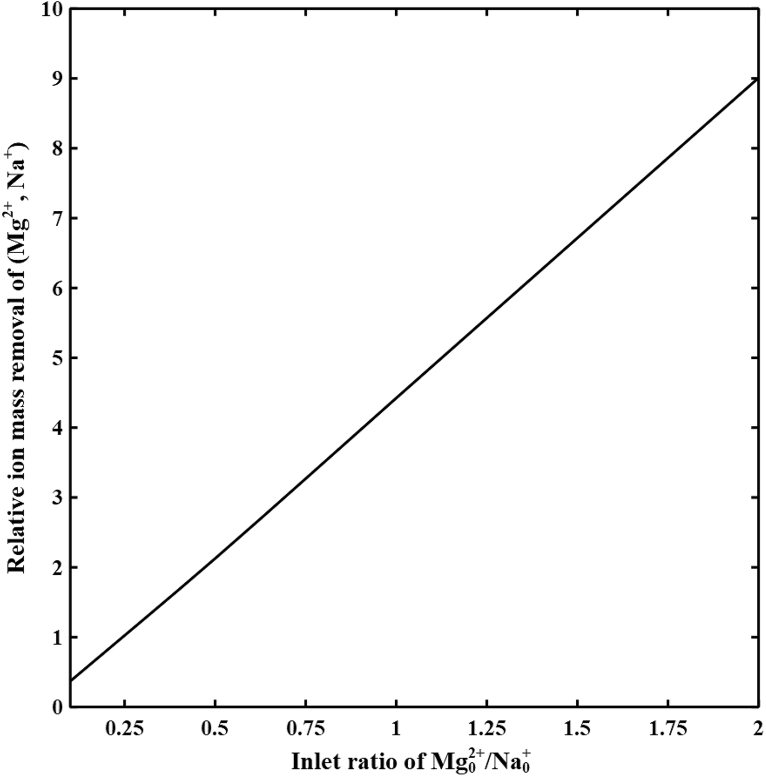
5.4. Inlet concentration effects
Fig. 7 shows the relative ion mass removal of (Mg2+, Na+) in the diluate channel of the spacer-free cell for the feed water with ionic strength of 593 mol/m3, Mg2+ to Na+ concentration ratio ranges from 0.1 to 2, at cell length of 2 cm, and imposed potential of 0.3 V. The Mg2+ removal is higher for feed water with greater Mg2+ to Na+ concentration ratio. Increasing the inlet concentration of divalent ions compensates for their lower diffusion coefficients thus, increasing their fluxes in the channel. Increases in divalent ion fluxes together with strong partitioning at the IEMs-solution interfaces result in higher selectivity toward divalent ions. For equal inlet concentration of both ions, the Mg2+ removal is more than four times greater than that of the Na+. Experimental observations also demonstrated higher selectivity toward divalent ions by increasing their concentrations in the feed water [33].
Fig. 7.
The relative ion mass removal of Mg2+/Na+ versus inlet concentration ratio Mg02+/Na0+ in the diluate channel of the spacer-free cell at V = 0.3 V, L = 2 cm, feed Is = 593 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp.
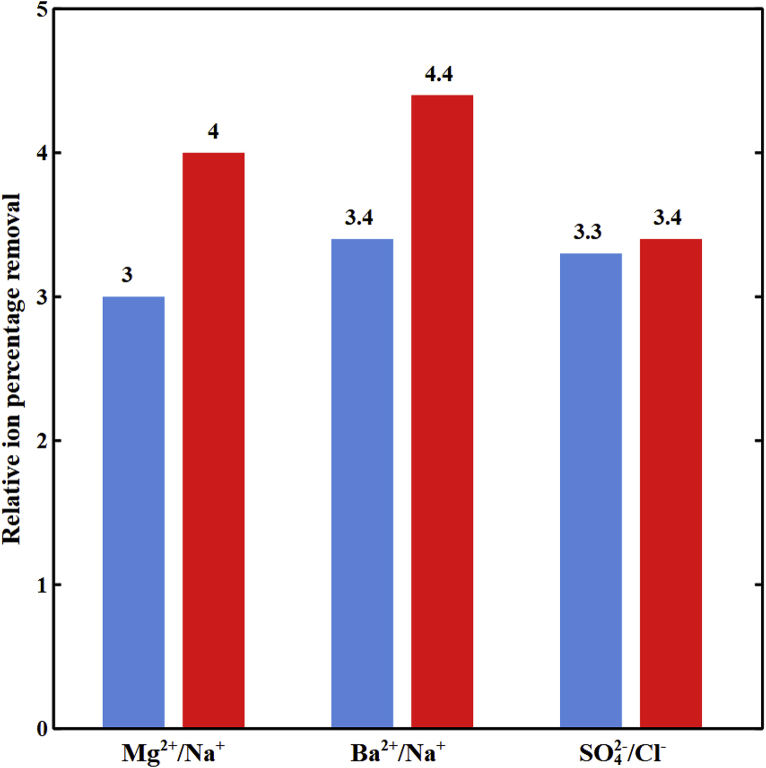
5.5. Spacer effects
In Fig. 8, divalent to monovalent relative ion percentage removals are compared for the spacer-free and spacer-filled cells for feed water with ionic strength of 593 mol/m3, cell lengths of 2 and 10 cm, and imposed potentials of 0.3 and 1.3 V. The enhanced cross-channel mixing in the spacer-filled cell lowers the divalent ion depletion at the IEMs-solution interfaces. The high concentration of divalent ions in DBLs of the spacer-filled channel relative to those of the spacer-free cell results in greater selective removal.
Fig. 8.
The variation of relative ion percentage removal in the diluate channel with feed Is = 593 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) Spacer-free cell at V = 0.3 V and L = 2 cm, (
) Spacer-free cell at V = 0.3 V and L = 2 cm, ( ) spacer-filled cell at V = 0.3 V and L = 2 cm, (
) spacer-filled cell at V = 0.3 V and L = 2 cm, ( ) spacer-free cell at V = 1.3 V and L = 10 cm, (
) spacer-free cell at V = 1.3 V and L = 10 cm, ( ) spacer-filled cell at V = 1.3 V and L = 10 cm.
) spacer-filled cell at V = 1.3 V and L = 10 cm.
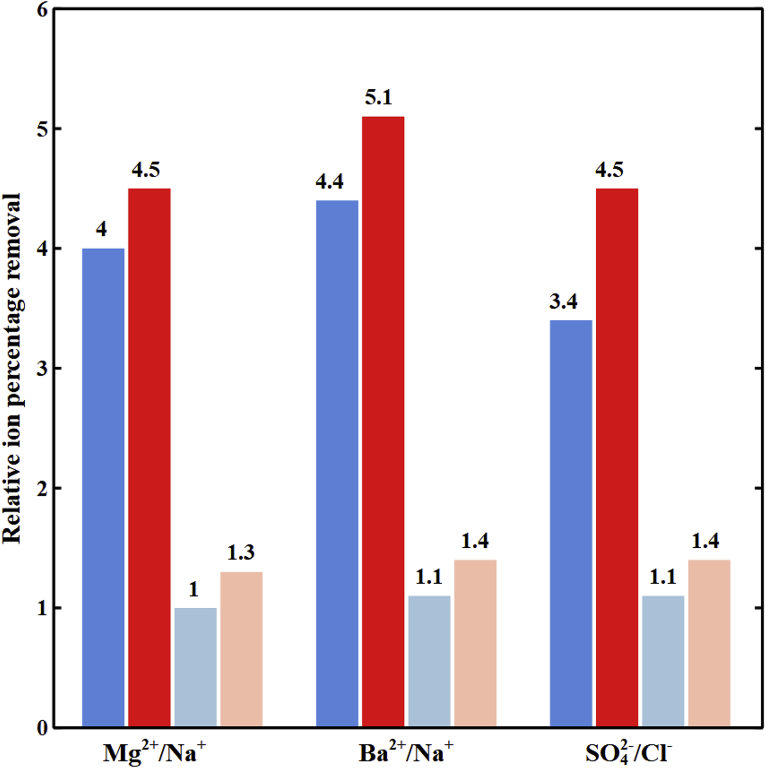
5.6. Membrane’s fixed charge concentration effects
Fig. 9 shows the relative ion percentage removal of divalent to monovalent ions in the diluate channel of the spacer-free cell with CEM fixed charge concentration (cF,CEM) of 1600, 2400, and 3210 mol/m3, AEM fixed charge concentration (cFAEM) of 1810, 2690, and 3580 mol/m3, cell lengths of 2 and 10 cm, imposed potentials of 0.3 and 1.3 V, and feed water ionic strength of 593 mol/m3. Increasing the concentration of fixed charges on the membranes enhances Donnan potential drops at the IEM-solution interfaces thus, increasing the selective divalent ion removal at the cell length of 2 cm and imposed potential of 0.3 V. Such results are consistent with experimental measurements conducted by Balster et al. [33] which demonstrated that increasing the fixed charge concentrations improves the divalent ions transport through the membranes. Hence, IEMs with higher charge density (greater IEC and lower water content) and high conductivity are preferred for selective divalent ion removal. However, due to the greater depletion of divalent ions in DBLs, losses in selectivity toward divalent ions by increasing the cell length and imposed potential is greater when using membranes with high concentrations of fixed charges.
Fig. 9.
The variation of relative ion percentage removal with membrane fixed charges concentration in the diluate channel of the spacer-free cell for feed Is = 593 mol/m3, ϕw,CEM = 0.5 Lw/Lsp, and ϕw,AEM = 0.4 Lw/Lsp. ( ) cF,CEM = 1600 mol/m3 and cF,AEM = 1809 mol/m3 at L = 2 cm and V = 0.3 V, (
) cF,CEM = 1600 mol/m3 and cF,AEM = 1809 mol/m3 at L = 2 cm and V = 0.3 V, ( ) cF,CEM = 2400 mol/m3 and cF,AEM = 2689 mol/m3 at L = 2 cm and V = 0.3 V, (
) cF,CEM = 2400 mol/m3 and cF,AEM = 2689 mol/m3 at L = 2 cm and V = 0.3 V, ( ) cF,CEM = 3210 mol/m3 and cF,AEM = 3580 mol/m3 at L = 2 cm and V = 0.3 V, (
) cF,CEM = 3210 mol/m3 and cF,AEM = 3580 mol/m3 at L = 2 cm and V = 0.3 V, ( ) cF,CEM = 1600 mol/m3 and cF,AEM = 1809 mol/m3 at L = 10 cm and V = 1.3 V, (
) cF,CEM = 1600 mol/m3 and cF,AEM = 1809 mol/m3 at L = 10 cm and V = 1.3 V, ( ) cF,CEM = 2400 mol/m3 and cF,AEM = 2689 mol/m3 at L = 10 cm and V = 1.3 V, (
) cF,CEM = 2400 mol/m3 and cF,AEM = 2689 mol/m3 at L = 10 cm and V = 1.3 V, ( ) cF,CEM = 3210 mol/m3 and cF,AEM = 3580 mol/m3 at L = 10 cm and V = 1.3 V.
) cF,CEM = 3210 mol/m3 and cF,AEM = 3580 mol/m3 at L = 10 cm and V = 1.3 V.
5.7. Membrane’s water content effects
The membrane water volume fraction defined as the volume of the absorbed water (Lw) to volume of the swollen polymer (Lsp) affects the selectivity in ED. Fig. 10 shows the relative ion percentage removals of divalent to monovalent ions in the diluate channel of the spacer-free cell with AEM water volume fraction (ϕw,AEM) of 0.3, 0.4, and 0.5 Lw/Lsp, CEM water volume fraction (ϕw,CEM) of 0.4, 0.5, and 0.6 Lw/Lsp, cell length of 2 cm, imposed potential of 0.3 V, and feed ionic strength of 593 mol/m3. Effective diffusion coefficients of ions and consequently, their fluxes, are higher in membranes with greater water volume fractions. Membrane’s water content effects are more significant for monovalent ions due to their greater diffusion coefficients, resulting in higher increases in their fluxes compared to divalent ions. Thus, the selective removals of divalent ions decrease by increasing the water volume fractions of the membranes. The experimentally determined [33] higher divalent ion fluxes through the membranes for IEMs with greater charge density (lower water content) is consistent with these modeling results.
Fig. 10.
The variation of relative ion percentage removal in the diluate channel of the spacer-free cell with respect to membrane water volume fraction at L = 2 cm, V = 0.3 V, feed Is = 593 mol/m3, cF,CEM = 3210 mol/m3, and cF,AEM = 3580 mol/m3( ) ϕw,CEM = 0.4 Lw/Lsp and ϕw,AEM = 0.3 Lw/Lsp, (
) ϕw,CEM = 0.4 Lw/Lsp and ϕw,AEM = 0.3 Lw/Lsp, ( ) ϕw,CEM = 0.5 Lw/Lsp and ϕw,AEM = 0.4 Lw/Lsp, (
) ϕw,CEM = 0.5 Lw/Lsp and ϕw,AEM = 0.4 Lw/Lsp, ( ) ϕw,CEM = 0.6 Lw/Lsp and ϕw,AEM = 0.5 Lw/Lsp.
) ϕw,CEM = 0.6 Lw/Lsp and ϕw,AEM = 0.5 Lw/Lsp.
5.8. Optimizing the ED cell properties
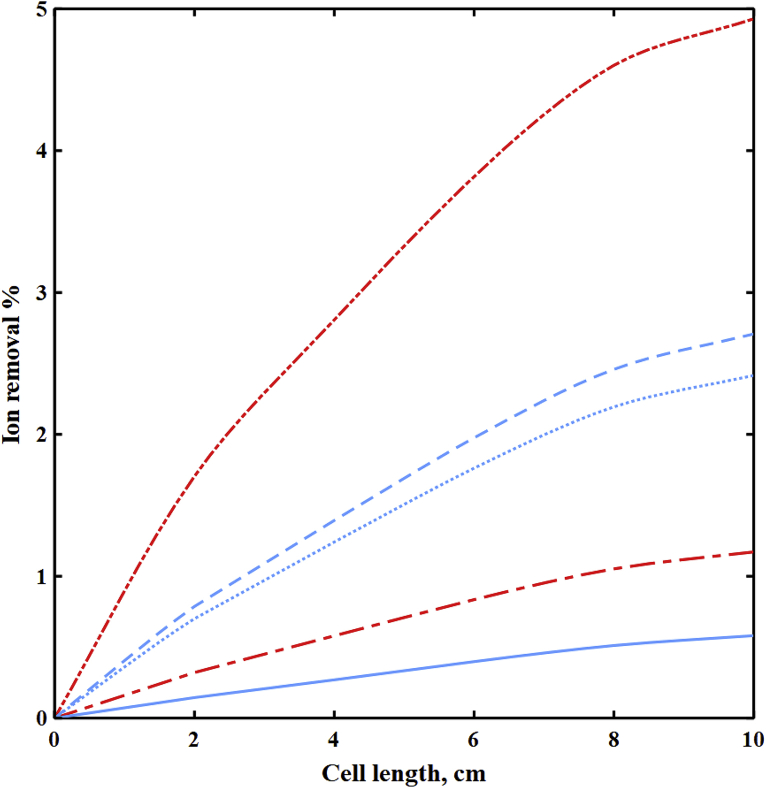
To reach maximum selectivity, the cell dimensions, membrane chemical structure, and operating conditions should be optimized with respect to the properties of the feed water and target ion. However, the parameters that can improve selectivity in ED may have adverse impacts on overall performance as defined by total reductions in ionic strength. Decreasing the cell length and imposing low potential promote selectivity toward divalent ions but result in a reduction of overall ion removal efficiency. Fig. 11 shows the ion removal percentages along the cell in the diluate channel of the spacer-filled cell at 0.3 V, feed water ionic strength of 593 mol/m3, cF,CEM of 3210 mol/m3, cF,AEM of 3580 mol/m3, ϕw,CEM of 0.4 Lw/Lsp, and ϕw,AEM of 0.3 Lw/Lsp. The ion removal percentages are greater for divalent ions, demonstrating higher selectivity toward them. However, the low removal percentages for all ions demonstrate that the overall ion removal and the separation efficiency are low in the cell. However, depending upon the chemical composition, even small absolute removal rates of divalent ions may provide substantial benefits for eliminating scaling. To minimize required surface area of membranes and maximize total ion removal in the cell, higher imposed potentials are preferred.
Fig. 11.
The ion removal percentages versus cell length in the diluate channel of the spacer-filled cell at V = 0.3 V, feed Is = 593 mol/m3, cF,CEM = 3210 mol/m3, cF,AEM = 3580 mol/m3, ϕw,CEM = 0.4 Lw/Lsp, and ϕw,AEM = 0.3 Lw/Lsp. ( ) Na+, (
) Na+, ( ) Mg2+, (
) Mg2+, ( ) Ba2+, (
) Ba2+, ( ) Cl−, and (
) Cl−, and ( ) SO42−.
) SO42−.
Optimization of membranes and spacers are significantly affected by cell dimensions and feed water properties. Membranes with high concentration of fixed charges provide greater divalent ion removal at small cell length; while membranes with lower concentration of fixed charges are superior in sustaining the divalent ion selectivity for longer cells. For high salinity feed water with high divalent ion concentration, the depletion of divalent ions in DBLs are minor thus, the spacer impacts on selectivity are small. For such feed waters, a more open spacer mesh can be employed, reducing the energy requirements for pumping fluid through the cell.
6. Conclusion
A 2-dimensional mathematical model is developed for multicomponent ion transport in a spacer-free and spacer-filled ED cell operating in the ohmic regime. The model is used to investigate the effects of feed water properties, cell hydrodynamics, and membrane properties on selective removal of divalent ions from the aqueous Na+-Mg2+-Ba2+-SO42−-Cl− quinary solution.
The selective divalent ion removal in diluate channels of both spacer-free and spacer-filled cells decreases by increasing the feed water ionic strength, cell potential, and cell length. Increasing the concentration of divalent ions in feed water improves their selective removal in the cell. Enhanced mixing in the spacer-filled channel results in higher divalent ion removals. Furthermore, increasing the fixed charge concentrations of the membrane while keeping the water content constant, enhances the selective divalent ion removal at low cell length and imposed potential. Increasing water volume fraction of IEM enhances the effective ionic diffusion coefficients inside the membranes. This results in greater monovalent ion fluxes through membranes and reduction in selectivity of the process towards divalent ions.
The developed multicomponent model can be used to optimize the effective parameters and reach maximum selectivity in the cell for any particular saline feed waters. It remains difficult, however, to develop conditions sufficiently selective that can eliminate the problems of scale precipitating ions present at low concentrations without incorporating a design of multiple stages each operated at optimum conditions to maximize selectivity.
Acknowledgment
The authors gratefully acknowledge the financial support of the Maddox Foundation and the Donovan Maddox Distinguished Engineering Chair Endowment.
References
- 1.Moghadasi J., Sharif A., Müuller-Steinhagen H., Jamialahmadi M. Prediction of scale formation problems in oil reservoirs and production equipment due to injection of incompatible waters. Dev. Chem. Eng. Miner. Process. 2006;14(3-4):545–566. [Google Scholar]
- 2.Ferguson R.J., Ferguson B.R. Association of Water Technologies; Reno, NV, USA: 2010. The Chemistry of Strontium and Barium Scales. [Google Scholar]
- 3.Honarparvar S., Zhang X., Chen T., Na C., Reible D. Modeling technologies for desalination of brackish water—toward a sustainable water supply. Curr. Opin. Chem. Eng. 2019;26:104–111. [Google Scholar]
- 4.Brennan S.T., Lowenstein T.K., Horita J. Seawater chemistry and the advent of biocalcification. Geology. 2004;32(6):473–476. [Google Scholar]
- 5.Igunnu E.T., Chen G.Z. Produced water treatment technologies. Int. J. Low Carbon Technol. 2012;9(3):157–177. [Google Scholar]
- 6.Sverdrup H.U., Johnson M.W., Fleming R.H. Prentice-Hall; New York: 1942. The Oceans: Their Physics, Chemistry, and General Biology. [Google Scholar]
- 7.Honarparvar S., Saravi S.H., Reible D., Chen C.-C. Comprehensive thermodynamic modeling of saline water with electrolyte NRTL model: a study on aqueous Ba2+-Na+-Cl−-SO42− quaternary system. Fluid Phase Equilib. 2017;447:29–38. [Google Scholar]
- 8.Honarparvar S., Saravi S.H., Reible D., Chen C.-C. Comprehensive thermodynamic modeling of saline water with electrolyte NRTL model: a study of aqueous Sr2+-Na+-Cl−-SO42− quaternary system. Fluid Phase Equilib. 2018;470:221–231. [Google Scholar]
- 9.Xiao J.J., Kan A.T., Tomson M.B. The role of calcium phosphino-polycarboxylate complexation in Inhibiting BaSO4 precipitation from brine. Adv. Cryst. Growth Inhib. Technol. 2000:165–185. [Google Scholar]
- 10.Reible D.D., Honarparvar S., Chen C.-C., Illangasekare T.H., MacDonell M. Environmental Technology in the Oil Industry. Springer; 2016. Environmental impacts of hydraulic fracturing; pp. 199–219. [Google Scholar]
- 11.Kabay N., Kahveci H., İpek Ö., Yüksel M. Separation of monovalent and divalent ions from ternary mixtures by electrodialysis. Desalination. 2006;198(1–3):74–83. [Google Scholar]
- 12.Luo T., Abdu S., Wessling M. Selectivity of ion exchange membranes: a review. J. Membr. Sci. 2018;555:429–454. [Google Scholar]
- 13.Indusekhar V., Trivedi G., Shah B. Removal of nitrate by electrodialysis. Desalination. 1991;84(1–3):213–221. [Google Scholar]
- 14.Elmidaoui F.E.A., Sahli M.M., Chay L., Elabbassi H., Hafsi M., Largeteau D. Pollution of nitrate in Moroccan ground water: removal by electrodialysis. Desalination. 2001;136(1–3):325–332. [Google Scholar]
- 15.Sadrzadeh M., Razmi A., Mohammadi T. Separation of monovalent, divalent and trivalent ions from wastewater at various operating conditions using electrodialysis. Desalination. 2007;205(1–3):53–61. [Google Scholar]
- 16.Xu P., Capito M., Cath T.Y. Selective removal of arsenic and monovalent ions from brackish water reverse osmosis concentrate. J. Hazard Mater. 2013;260:885–891. doi: 10.1016/j.jhazmat.2013.06.038. [DOI] [PubMed] [Google Scholar]
- 17.Nie X.-Y., Sun S.-Y., Sun Z., Song X., Yu J.-G. Ion-fractionation of lithium ions from magnesium ions by electrodialysis using monovalent selective ion-exchange membranes. Desalination. 2017;403:128–135. [Google Scholar]
- 18.Nie X.-Y., Sun S.-Y., Song X., Yu J.-G. Further investigation into lithium recovery from salt lake brines with different feed characteristics by electrodialysis. J. Membr. Sci. 2017;530:185–191. [Google Scholar]
- 19.Kim Y., Walker W.S., Lawler D.F. Competitive separation of di-vs. mono-valent cations in electrodialysis: effects of the boundary layer properties. Water Res. 2012;46(7):2042–2056. doi: 10.1016/j.watres.2012.01.004. [DOI] [PubMed] [Google Scholar]
- 20.Galama A., Daubaras G., Burheim O., Rijnaarts H., Post J. Seawater electrodialysis with preferential removal of divalent ions. J. Membr. Sci. 2014;452:219–228. [Google Scholar]
- 21.Fila V., Bouzek K. A mathematical model of multiple ion transport across an ion-selective membrane under current load conditions. J. Appl. Electrochem. 2003;33(8):675–684. [Google Scholar]
- 22.Moshtarikhah S., Oppers N., de Groot M., Keurentjes J., Schouten J., van der Schaaf J. Nernst–Planck modeling of multicomponent ion transport in a Nafion membrane at high current density. J. Appl. Electrochem. 2017;47(1):51–62. [Google Scholar]
- 23.Koryta J., Dvořák J., Kavan L. John Wiley & Sons Inc; 1993. Principles of Electrochemistry. [Google Scholar]
- 24.Bird R.B., Stewart W.E., Lightfoot E.N. John Wiley & Sons; 2007. Transport Phenomena. [Google Scholar]
- 25.Donnan F.G. The theory of membrane equilibria. Chem. Rev. 1924;1(1):73–90. [Google Scholar]
- 26.Prausnitz J.M., Lichtenthaler R.N., de Azevedo E.G. Pearson Education; 1998. Molecular Thermodynamics of Fluid-phase Equilibria. [Google Scholar]
- 27.Honarparvar S. Texas Tech University; 2019. Thermodynamic Modeling and Management of the Saline Water. PhD dissertation. [Google Scholar]
- 28.Kamcev J., Paul D.R., Freeman B.D. Ion activity coefficients in ion exchange polymers: applicability of Manning’s counterion condensation theory. Macromolecules. 2015;48(21):8011–8024. [Google Scholar]
- 29.Kamcev J., Paul D.R., Manning G.S., Freeman B.D. Predicting salt permeability coefficients in highly swollen, highly charged ion exchange membranes. ACS Appl. Mater. Interfaces. 2017;9(4):4044–4056. doi: 10.1021/acsami.6b14902. [DOI] [PubMed] [Google Scholar]
- 30.Nikonenko N.D.P.V., Belova E.I., Sistat P., Huguet P., Pourcelly G., Larchet C. Intensive current transfer in membrane systems: modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 2010;160(1–2):101–123. doi: 10.1016/j.cis.2010.08.001. [DOI] [PubMed] [Google Scholar]
- 31.Urtenov M.A.-K., Kirillova E.V., Seidova N.M., Nikonenko V.V. Decoupling of the Nernst−planck and Poisson equations. Application to a membrane system at overlimiting currents. J. Phys. Chem. B. 2007;111(51):14208–14222. doi: 10.1021/jp073103d. [DOI] [PubMed] [Google Scholar]
- 32.Turek M. Optimization of electrodialytic desalination in diluted solutions. Desalination. 2003;153(1–3):383–387. [Google Scholar]
- 33.Balster J., Krupenko O., Pünt I., Stamatialis D., Wessling M. Preparation and characterisation of monovalent ion selective cation exchange membranes based on sulphonated poly (ether ether ketone) J. Membr. Sci. 2005;263(1–2):137–145. [Google Scholar]