Countermovement Jump and Squat Jump Force-Time Curve Analysis in Control and Fatigue Conditions

Abstract

Hughes, S, Warmenhoven, J, Haff, GG, Chapman, DW, and Nimphius, S. Countermovement jump and squat jump force-time curve analysis in control and fatigue conditions. J Strength Cond Res 36(10): 2752–2761, 2022—This study aimed to reanalyze previously published discrete force data from countermovement jumps (CMJs) and squat jumps (SJs) using statistical parametric mapping (SPM), a statistical method that enables analysis of data in its native, complete state. Statistical parametric mapping analysis of 1-dimensional (1D) force-time curves was compared with previous zero-dimensional (0D) analysis of peak force to assess sensitivity of 1D analysis. Thirty-two subjects completed CMJs and SJs at baseline, 15 minutes, 1, 24, and 48 hours following fatigue and control conditions in a pseudo random cross-over design. Absolute (CMJ_ABS/SJ_ABS) and time-normalized (CMJ_NORM/SJ_NORM) force-time data were analyzed using SPM 2-way repeated measures analysis of variance with significance accepted at α = 0.05. The SPM indicated a magnitude of difference between force-time data with main effects for time (p < 0.001) and interaction (p < 0.001) observed in CMJ_ABS, SJ_ABS, and SJ_NORM, whereas previously published 0D analysis reported no 2-way interaction in CMJ and SJ peak force. This exploratory research demonstrates the strength of SPM to identify changes between entire movement force-time curves. Continued development and use of SPM analysis techniques could present the opportunity for refined assessment of athlete fatigue and readiness with the analysis of complete force-time curves.

Introduction

Jump tasks, such as the squat jump (SJ) and countermovement jump (CMJ), have been frequently researched (6,13) and are commonly used as monitoring tools in elite sports (41). The appeal of jump testing stems from the relationship between measures of jump performance and commonly desired traits associated with sport performance such as strength (44) and speed (25,44) including the ability to distinguish between athlete competitive levels in sports such as soccer, American football, ice hockey, rugby league, Australian rules football, and weightlifting (4,5,24,37). These factors coupled with the simplicity, reliability, and familiarity of jump assessments in athletes (6,7,41) have likely driven its usage in elite sports. Typically, when jumping tasks are used as fatigue monitoring tools, changes in one or more discrete variables (e.g., jump height, peak power, relative peak power, relative power, mean power, peak velocity, peak force, mean force, rate of force development, eccentric/concentric time, flight time/eccentric time, and flight time/contraction time) are used to determine a fatigue response or readiness for the next training stimuli (6). These metrics are either measured or calculated from ground reaction force (GRF) data collected with a force plate, displacement-time data collected with a linear position transducer, or contact and flight times recorded with a contact mat.

Variable selection likely has an effect on the sensitivity of detecting readiness or fatigue as few variables have provided consistent results (6). Mechanisms of fatigue are influenced by the method of fatigue inducement and are confounded by subject motivation, psychological status, muscle activation pattern, intensity, duration, and the continuous or intermittent nature of the task (2). Therefore, variable selection combined with the method of fatigue inducement may play a role in these reported inconsistencies. Two other factors often not discussed include (1) use of only discrete variables to describe a continuous movement and (2) the number of trials performed. One-dimensional (1D) statistical procedures address these factors by allowing analysis of continuous nature time-series data (31) and analysis of numerous trials which may influence the effectiveness of jumps as a fatigue monitoring tool (6,7).

The force-time curves of CMJ and SJ consist of hundreds or thousands of data points per second and to facilitate analysis of these force-time curves individual zero-dimensional (0D) data points are selected from specific phases (e.g., peak concentric force) or averaged across multiple jumps. In addition, 0D data can be derived from calculations of a limited number of points from a particular region of the curve (e.g., flight time to contraction time ratio) (31,32); however, 0D analysis characteristically involves the removal of data from the force-time curve as opposed to statistical analysis on all data between movement onset and offset. Although 0D data can assist with the simplicity of statistical analyses, it has been suggested that in comparison with the assessment of the continuous force-time curve (e.g., 1D analysis), the use of discrete variables (e.g., 0D analysis) derived from continuous data is a reductionist approach that limits insights into a motor skill (28). The removal of data or the selection of individual 0D points for analysis may reduce the sensitivity of jump testing and potentially introduce bias into the analysis and interpretation of data (31,32), further supporting the potential benefit of 1D analysis methods. Furthermore, the normalization of time to a stance or phase as is common in biomechanical research can change the ability for even 1D analysis to observe temporal changes (28). Thus, evaluations using absolute data aligned at movement onset or offset versus a more refined normalization (interpolating cubic spline) should be explored.

It has been previously suggested that jumping movement patterns are altered by fatigue (1,12,23) and result in timing variations in jump phases even where little difference is observed in jump height (8). Furthermore, elite athletes demonstrate alterations in muscle recruitment and movement proficiency to maintain performance when fatigued (11,36,38). The ability to alter muscle recruitment may be dependent on the skill level, however, as mixed results have been observed in nonelite populations (3,38). This phenomenon may be explained by the dynamical systems theory where multiple joints and muscles (or degrees of freedom) emerge with different movement solutions used to complete desired movements. This may occur specifically when the preferred muscles used in a prior movement strategy are fatigued (21) or injured (40), and it has been suggested that movement reorganization enables the maintenance of tasks through increased variations in skill execution (16,21). Changes in jump force-time and power-time curves in response to strength or power training have been reported in the literature (9,10). The change in the phases of the force-time curve likely indicates joint-based changes that summate to adaptations at the system center of mass (COM) as expressed by force-time curves. Therefore, movement alterations in response to fatigue, injury, physical capacity, or training specificity may present as variations in the shape of the force-time curve despite equal impulses. Statistical analysis of variables calculated from 2 or more 0D variables has been undertaken to quantify changes in the force-time curve shape with promising results (8,12,18). Ratios such as eccentric/concentric time, flight time/eccentric time, flight time/contraction time, duration of jump phases, and eccentric/concentric power in relation to time have been explored; however, 1D analysis could assess the complete GRF trace without the need to remove data or use ratios that may mask changes because of opposing shifts of the numerator and denominator. Consequently, force-time curve analysis may provide greater insight than 0D variables alone (12).

Statistical parametric mapping (SPM) measures spatiotemporal changes to smooth continuum data such as force-time curves or angular-time curves. Traditionally used in 3D functional neuroimaging, its use in biomechanical analyses allows the presentation of data in its native, complete state and reduces the likelihood of analysis bias resulting from the selection of 0D variables (31,32). The purpose of the current study was to determine if SPM analysis of force-time curves would be suitably sensitive to show changes in CMJ and SJ GRF traces between control and fatigue conditions in an exploratory extension of commonly assessed discrete variables (18). A secondary purpose was to examine the effect of 2 methods of data preparation for 1D SPM analysis. The first method applied absolute data (CMJ_ABS and SJ_ABS), aligned at a traditional offset (toe off). For each trial, an exact duration before toe off was included to standardize total data points across all trials. This method was compared with a time normalization of data that included more temporally matched phases of movement (CMJ_NORM and SJ_NORM). It was envisaged that use of SPM could provide a more sensitive method for coaches and scientists to assess changes in temporal-based or magnitude-based changes of the force-time curve at any point of athlete movement.

Methods

Experimental Approach to the Problem

A within-group pseudo random cross-over design was used to compare multiple performance tests across time and model fatigue in response to a randomly assigned seated control or repeated sprint cycle exercise condition. Ground reaction force data were collected during CMJ and SJ as part of a previously published battery of assessments that included a neuromuscular fatigue questionnaire, Stroop task, postural sway, isometric midthigh pull, and 10 seconds maximal cycle (18). Subjects attended 7 laboratory testing sessions, a familiarization session and 2 intervention blocks (fatigue and control) of 3 consecutive days. As part of the aforementioned testing battery, 2 sets of 3 SJs and CMJs were completed by each subject before control or fatigue conditions as well as at 15 minutes, 1, 24, and 48 hours after each condition (Figure 1). Subjects were provided 10-seconds rest between jump repetitions and 45-seconds rest between each set with the collected jumps' GRF time series data forming the data used for analysis in this study.

Figure 1.

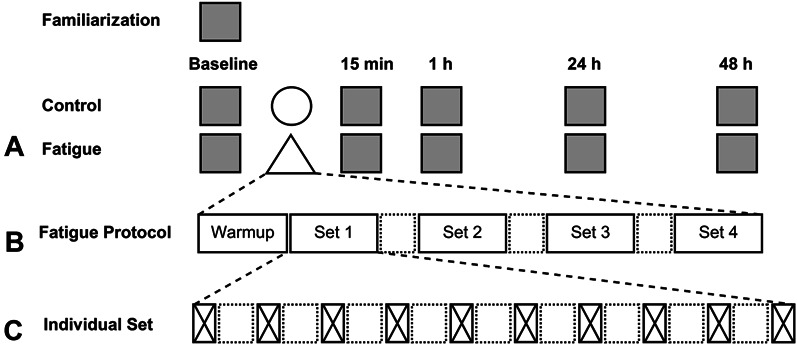
Study protocol overview. A) CMJ and SJ testing occurred at multiple time points (gray squares) as part of a previously published data set (18) with control protocol (circle) and fatigue condition (triangle). B) Fatigue condition consisting of 4 sprint sets interspersed with 90 seconds active recovery (dashed square). C) Sprint set breakdown consisting of 10 × 6 seconds sprints (crossed rectangle) with 30 seconds active recovery (dashed square). CMJ = countermovement jump; SJ = squat jump.

Subjects

Thirty-two physically active subjects (24 men: 27.8 ± 7.6 years; 81.4 ± 11.1 kg and 8 women: 24.5 ± 3.5 years; 69.0 ± 14.1 kg; SD) with a history of at least 6 months of resistance training were recruited and completed all testing sessions. Subjects were asked to avoid any strenuous exercise 24 hours before testing and during the 24 and 48 hours follow-up assessment period. Each subject was provided with a standardized meal (CHO = 1–1.5 g·kg⁻¹; protein = 0.3 g·kg⁻¹, fat = 0.28–0.47 g·kg⁻¹) that was consumed 2 hours before all testing sessions and a 600 ml bottle (618 kJ) of Gatorade sports drink (PepsiCo, New York, NY) during testing sessions. Subjects were instructed to avoid consumption of coffee the morning of testing sessions and were requested to maintain their current nutrition intake throughout the study. Each subject was provided with a written outline of the risks and benefits of study and given verbal instructions on how to perform all tasks. After an opportunity to answer any specific questions, written informed consent was obtained from all subjects. The study was approved by the Edith Cowan University institutional review board (Approval # 16284) which follows the ethical guidelines set by the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.

Procedures

Squat Jump and Countermovement Jump

The methodology for the SJ and CMJ were previously described (18). In brief, all jumps were completed on dual force platforms (9286BA, Kistler, Winterthur, Switzerland) sampling at 1,000 Hz, and vertical GRF was analyzed using Templo Jump Analysis Software (Version 2016.1.404, Contemplas GmbH, Kempten, Germany). Subjects completed 2 sets of 3 body weight SJ and CMJ with arms restricted by a lightweight (0.4 kg) aluminum bar held across the shoulders. The SJ repetitions were completed before CMJ with subjects instructed to jump as high as possible with external cues of “push off the ground as hard and as fast as possible” provided. For the SJ, subjects were instructed to maintain an isometric squat with an estimated 90° knee bend for 3 seconds before jumping vertically. Any trials with a GRF reduction >5% were discarded and repeated. The CMJ consisted of a self-selected countermovement before a maximal vertical jump.

Data Processing

One subject was removed because of competitive sport participation <24 hours before baseline resulting in 31 subjects. The force-time data were exported from Templo software with all trials from 31 subjects included in the SPM analysis. The unfiltered 1,000 Hz data from each force platform was combined and aligned at the point of toe off using a custom PowerShell script (Microsoft Corporation, Redmond, WA, version.NET 4.5) with the first force value <20 N used to align data and an additional 10 ms of data retained to capture the point where force ≤0 N. Force-time curves were then divided by individual body mass in newtons to account for differences in body mass between subjects. Movement onset was defined as the point where normalized body mass reached ≤0.97 with an additional 10 ms of data retained to the left of the force-time curve. Because of individual subjects' movement timing, total movement duration between movement onset and toe off ranged between 530–1,186 ms in CMJ and 294–727 ms in SJ. Absolute data (CMJ_ABS and SJ_ABS) consisted of all jumps aligned at toe off with 1,186 and 727 data points included before the point of toe off for CMJ and SJ, respectively. To remove the need to distort the time dimension of CMJ_ABS and SJ_ABS force-time curves, shorter duration trials included a longer weighing phase to provide the 1,186 and 727 data points for analysis. This resulted in some misalignment of jump phases between trials, with longer movement duration trials entering the unweighting (CMJ) or propulsive (SJ) phase, whereas shorter trials were still in the weighing phase. Importantly, SPM analysis assesses clusters of change; however, because of the potential that changes in the force-time curve may present at specific jump phases, linear length normalization (17,42) was used to normalize contraction durations and more closely align jump phases between subjects (CMJ_NORM and SJ_NORM). Thus, CMJ_ABS and SJ_ABS data were trimmed from movement onset to toe off and resampled through an interpolating cubic spline resulting in curves with a common time duration of 1,186 and 727 ms in CMJ_NORM and SJ_NORM, respectively.

Statistical Analyses

All statistical analysis were completed in the Enthought Canopy distribution of Python (Enthought, Inc., Austin, TX, version 1.7.4.3348) using open source package “spm1d” located at http://www.spm1d.org/ (33). Statistical parametric mapping was used to compare changes in CMJ and SJ force-time curves following a fatigue and control protocol with 2 approaches: (a) time intact and aligned at toe off point (CMJ_ABS and SJ_ABS) and (b) time normalized by linear length normalization (CMJ_NORM and SJ_NORM). A SPM 2-way (condition × time) repeated measures analysis of variance (ANOVA) was used for each jump and time analysis approach resulting in CMJ_ABS, CMJ_NORM, SJ_ABS, and SJ_NORM data with α = 0.05. Although the current method of ANOVA post-hoc analysis using the SPM T-test and Bonferroni correction is likely too simple (30), where an interaction effect was seen, post-hoc analysis was completed to further explore the capability of SPM analysis method for future hypothesis generation. For post-hoc analyses, the alpha value was set at α/12 for the number of post-hoc tests with 2-tailed inference analysis. The scalar output statistics (SPM{F} and SPM{T}) were calculated separately at each individual data point and are referred to as a statistical parametric map with the calculation of the SPM{F} and SPM{T} indicating the magnitude of the difference between data. Where the scalar output statistic crossed the critical threshold ({F} and {T}), the null hypothesis was rejected. Because of smoothness of force-time curves and the inter-dependence of neighboring points, multiple adjacent points of the SPM{F} or SPM{T} curve often exceeded the critical threshold and are referred to as “suprathreshold clusters” as exampled in Figure 2.

Figure 2.

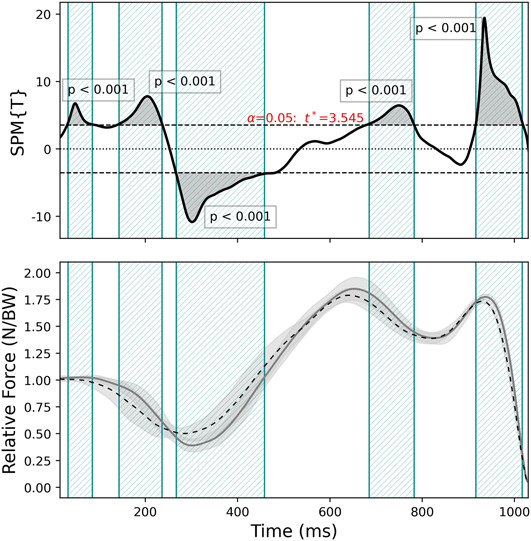
Example SPM t-test. Top—inference curve with suprathreshold clusters (shaded), critical threshold (t statistic) as a function of time represented by the dashed line that indicates the random field theory thresholds for significance (α = 0.05) and p-values that indicate the likelihood that a random process of temporal smoothness would be expected to produce a suprathreshold cluster of the observed size. Bottom—CMJ force-time curve for control (solid line) and fatigue (dashed line) conditions with SD cloud (shaded). CMJ = countermovement jump; SPM = statistical parametric mapping.

Results

Two-way repeated measures ANOVA analysis displayed suprathreshold clusters exceeding the critical threshold in CMJ_ABS, SJ_ABS, and SJ_NORM for both time and interaction (Table 1) with CMJ_NORM displaying suprathreshold clusters for time alone. No clusters exceeded the critical threshold in the main effect of condition for any analysis. Large suprathreshold clusters were observed close to toe off in CMJ_ABS, SJ_ABS, and SJ_NORM but were absent in CMJ_NORM (Figure 3).

Table 1.

Results of SPM 2-way repeated measure ANOVA presenting the suprathreshold cluster locations for each jump type and condition.^*†

	Time				Interaction
	%	ms	p	{F}	%	ms	p	{F}
CMJABS	—	599–673	<0.001	5.22	—	1,128–1,163	<0.001	5.22
	—	856–980	<0.001	5.22
	—	1,088–1,170	<0.001	5.22
SJABS	—	395–475	<0.001	5.08	—	652–706	<0.001	5.08
	—	636–711	<0.001	5.08
CMJNORM	21–37	—	<0.001	5.08
	51–74	—	<0.001	5.08
	88–94	—	<0.001	5.08
	98.6–98.9	—	<0.05	5.08
SJNORM	77–96	—	<0.001	4.91	86–94	—	<0.001	4.91

^*CMJ = countermovement jump; ANOVA = analysis of variance; SPM = statistical parametric mapping; SJ = squat jump.

^†The start and finish locations of suprathreshold clusters are provided as milliseconds for absolute analyses and as a percentage of the total movement duration for normalized analyses. Probability value (p) and critical threshold ({F}) are stated.

Figure 3.

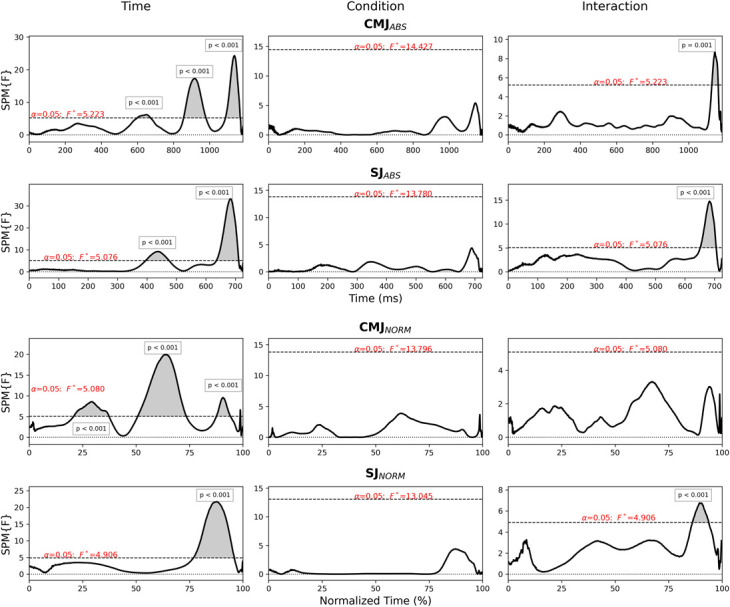
SPM 2-way repeated measures ANOVA results for CMJ_ABS, CMJ_NORM, SJ_ABS, and SJ_NORM as labeled. Inference curves with suprathreshold clusters (shaded) for time (column 1), condition (column 2), and interaction (column 3) with critical threshold (dashed line). ANOVA = analysis of variance; CMJ = countermovement jump; SJ = squat jump; SPM = statistical parametric mapping.

Post-hoc analysis was used to compare the differences between baseline and subsequent time points (15 minutes, 1, 24, and 48 hours) for control and fatigue conditions that demonstrated a significant interaction effect. Because of the 2-tailed analysis, suprathreshold clusters could cross the critical threshold ({T}) in a positive or negative direction. Suprathreshold clusters crossing the critical threshold represent a difference between the baseline and post-condition time point. Positive suprathreshold clusters represent a reduction in force when compared with the baseline force-time curve, and negative suprathreshold clusters represent an increase in force when compared with the baseline. The average and SD of phases has been provided in milliseconds for absolute analyses with normalized analysis data presented as a percent of movement. The critical threshold and p values are provided in each figure.

Alterations in the force-time curve were present at multiple time points when compared with baseline in CMJ_ABS (Figure 4). The average unweighting, braking, and propulsion phase in the fatigue condition occurred at 341 ± 117 ms, 669 ± 91 ms, and 872 ± 51 ms, respectively. Large positive suprathreshold clusters were present in 15 minutes (240–317 ms, 832–994 ms, and 1,096–1,170 ms) and 1 hour (229–354 ms, 843–1,007 ms, and 1,092–1,173 ms) time points with a small cluster at 24 hours (1,137.9–1,138.1 ms). A suprathreshold cluster at 1 hour postfatigue (570–730 ms) was in a negative direction. In the CMJ_ABS control condition, the unweighting, braking, and propulsion phase occurred at 356 ± 115 ms, 679 ± 92 ms, and 877 ± 52 ms. Positive clusters were present at 15 minutes (886–970 ms and 1,116–1,151 ms), 1 hour (861–965 ms and 1,113–1,165 ms), 24 hours (896–952 ms), and 48 hours (902–942 ms) with negative changes observed at 1 hour (550–667 ms) and 24 hours (589–638 ms) postcontrol condition (Figure 4).

Figure 4.

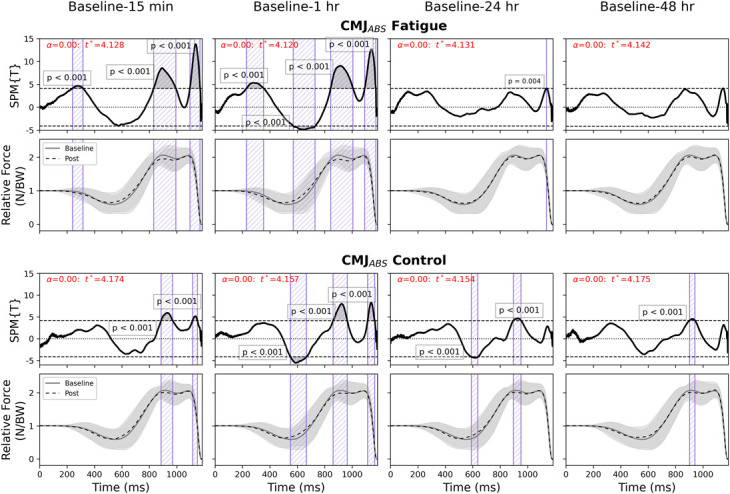
Follow-up SPM T-test with Bonferroni correction comparison between baseline and later time points in CMJ_ABS fatigue and control condition. Rows 1 and 3—inference curves with suprathreshold clusters (shaded) and critical threshold (dashed line). Rows 2 and 4—CMJ mean force for baseline (solid line) and postcondition time points (dashed line) with SD cloud (shaded) standardized to body mass in newtons. CMJ = countermovement jump; SPM = statistical parametric mapping.

In response to the fatigue intervention, changes were observed at all time points in SJ_ABS. (Figure 5). The average propulsion phase in the fatigue condition occurred at 313 ± 132 ms. Larger suprathreshold clusters were present at 15 minutes (425–448 ms, 633–713 ms, and 725–726 ms) and 1 hour time points (400–496 ms and 642–711 ms), decreasing at 24 hours (429–450 ms) and 48 hours (687–697 ms). In the control condition, the average propulsion phase occurred at 309 ± 130 ms. Comparisons between baseline SJ_ABS and later time points displayed changes in force-time curves at 15 minutes (352–463 ms and 568–616 ms), 1 hour (331–470 ms, 537–636 ms, and 669–707 ms), 24 hours (331–445 ms and 537–669 ms), and 48 hours (292–293 ms, 294–417 ms, and 536–667 ms) (Figure 5). Visual analysis showed a consistent pattern across all SJ_ABS control time points where positive suprathreshold clusters were present at the onset of force production leading into negative suprathreshold clusters at peak force production. This represented reduced force production shortly after movement onset with an increase in peak force when compared with baseline trials.

Figure 5.

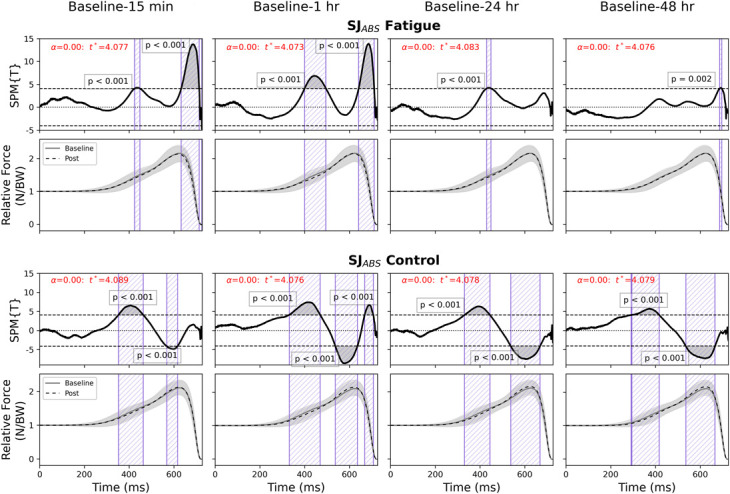
Follow-up SPM T-test with Bonferroni correction comparison between baseline and later time points in SJ_ABS fatigue and control condition. Rows 1 and 3—inference curves with suprathreshold clusters (shaded) and critical threshold (dashed line). Rows 2 and 4—SJ mean force for baseline (solid line) and postcondition time points (dashed line) with SD cloud (shaded) standardized to body mass in newtons. SJ = squat jump; SPM = statistical parametric mapping.

SJ_NORM time normalization (Figure 6) provided a standardized propulsion phase, with all movement onset occurring at 0%. The SJ_NORM conditions presented similar statistical parametric map shapes to SJ_ABS, specifically with respect to positive and negative clusters. However, large magnitude clusters observed midway through the SJ_ABS GRF traces presented earlier in the SJ_NORM conditions with a reduction in cluster magnitude.

Figure 6.

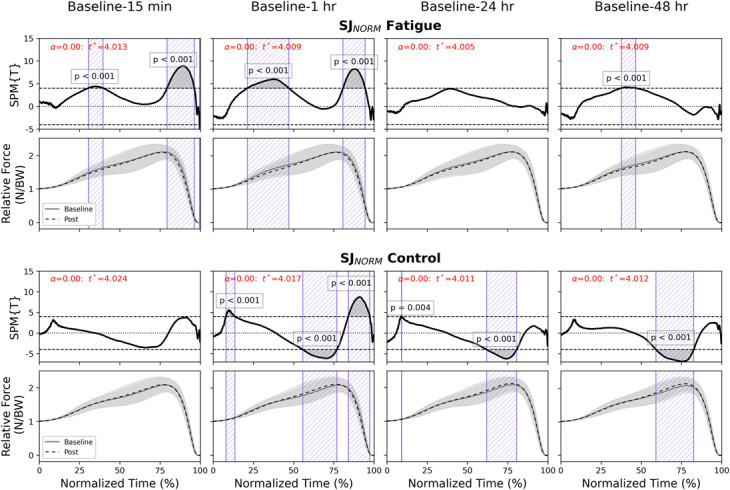
Follow-up SPM T-test with Bonferroni correction comparison between baseline and later time points in SJ_NORM fatigue and control condition. Rows 1 and 3—inference curves with suprathreshold clusters (shaded) and critical threshold (dashed line). Rows 2 and 4—SJ mean force for baseline (solid line) and postcondition time points (dashed line) with SD cloud (shaded) standardized to body mass in newtons. SPM = statistical parametric mapping; SJ = squat jump.

Discussion

The use of SPM analysis for this study enabled assessment of the entire force-time curve, enhancing visual inspection of phases and transition between phases. Because of timing variations between subjects' force-time curves, an explicit identification of phases could not be provided in Figures 4–5. SPM analysis of a single individual could improve identification of phases, enabling greater identification of changes relative to phases and thus demonstrating further practical utility of SPM for evaluating differences within whole movement cycles. To improve comprehension of the discussion, the unweighting, braking, and propulsion phases (27) have been referenced relative to the average phase onset of the force-time curves provided.

Initial analysis supports the ability of SPM techniques to measure change in CMJ and SJ force-time curves because of observed interaction effects for CMJ_ABS, SJ_ABS, and SJ_NORM as well as the main effects of time (Figure 3). Although post-hoc testing demonstrated changes in both fatigue and control conditions, larger suprathreshold clusters observed in the fatigue condition indicated greater changes in force postfatigue, specifically at 15 minutes and 1 hour time points. When compared with baseline, the SJ fatigue trials demonstrated lower force development throughout the movement represented by force decrements midway through the propulsion phase and a reduction in peak force, although these changes had largely dissipated by 24 hours. However, improvements in peak force were observed in comparison with baseline in SJ control trials. Although post-hoc analysis was not completed for CMJ or SJ main effects of condition, visual inspection of 2-way repeated measures ANOVA analysis shows the existence of clusters between 650 and 700 ms in SJ conditions and 900–1,100 and 1,100–1,186 ms in CMJ_ABS. Despite this, the low number of conditions resulted in critical thresholds {F} threefold higher than those in the main effects of time and interaction, impacting statistical significance.

Consistent with the previous literature (27), changes in force observed during the CMJ braking phase coincided with changes in the unweighting phase. These associated changes are because of equal net impulses being maintained between the 2 phases (27), with the decreased net impulse observed during unweighting suggesting that subjects reduced vertical displacement during this phase. The early net impulse reductions resulted in a concomitant reduction in the braking phase, explaining the depressed breaking force and leading to a reduction in elastic energy storage potential of the muscle-tendon units (27). Furthermore, 15 minutes and 1 hour CMJ_ABS fatigue trials showed significant earlier movement onset representing a longer movement duration than at baseline which could be indicative of several potential mechanisms. When fatigued, it is expected that subjects would experience reduced force production and control. This could potentially result in a prolonged movement duration and a reduction in negative COM displacement after movement onset, presenting as decreased force reduction during CMJ unweighting. The altered force-time duration could also be a demonstration of the dynamic movement theory representing the application of alternative movement patterns to achieve the desired outcome (3). Although the control condition did see a small magnitude reduction in unweighting, the warm-up provided before the 15 minutes test battery was potentially insufficient to reduce stiffness from sitting stationary on the cycle ergometer for the duration of the control condition and may have led to the observed decrements despite the absence of fatigue inducement.

For suprathreshold clusters to exceed the critical threshold, clusters of change must occur at similar segments of the force-time curve across multiple trials. If force changes are restricted to specific phases of a curve, large SDs in phase timing may reduce suprathreshold clusters in non-normalized data. Previously reported differences in jump pattern between (19) and within individuals (22) supports the use of normalization techniques during analysis to reduce the affect jump timing may have on phase alignment and the likelihood of clusters crossing the critical threshold. The interpolation technique used in this research led to improved alignment of phases; however, areas closest to the original point of alignment (toe off) were lengthened in shorter jump trials, reducing the magnitude of clusters between peak force and toe off. Because of this, the diminished cluster magnitude observed during the late propulsion phase of CMJ_NORM, resulted in nonsignificant findings in interaction and an inability to complete post-hoc testing (30). Although a similar trend occurred in SJ_NORM, significance was maintained with post-hoc tests showing a mirrored reduction in suprathreshold clusters near toe off when compared with SJ_ABS. Potentially, the greater movement complexity of the CMJ, specifically regarding the interplay between the 3 phases, may have played a role in the larger reduction in cluster magnitude after normalization.

This study provides an extended analysis of previous data with an initial aim to compare 1D SPM analysis with traditional 0D analysis methods commonly used in fatigue assessment. By providing the mean force-time curve (CMJ_ABS) at each time point for a single subject (Figure 7), we sought to highlight the potential changes in a force-time curve that can occur in response to fatigue. Differences observed in the force-time curve between 400 and 600 ms may be concealed when conducting discrete variable analysis as these changes are not exclusively constrained to maxima or minima. Previous 0D analysis of this data set (18) reported no 2-way interaction in relative peak force of CMJ or SJ (Table 2), a contrasting result to SPM analysis. Despite this result, significant differences between control and fatigue conditions were reported in 2 SJ (velocity and FT:CT ratio) and 3 CMJ (jump height, velocity, and FT:CT ratio) variables. Thus, 0D analysis may be useful to measure a desired performance outcome of a jump, i.e., velocity or jump height, whereas SPM can provide deeper analytical information on the movement strategy by presenting information relative to the entire movement. This includes areas between phases that may be overlooked in discrete assessment. Although the selection and analysis of multiple discrete variables spanning the entire movement may be an attractive alternative to SPM analysis, the issue of selection bias, the required multiple comparison corrections, and possibility that changes are not constrained to chosen discrete data points make SPM practically more useful to statistically assess changes across the whole movement.

Figure 7.

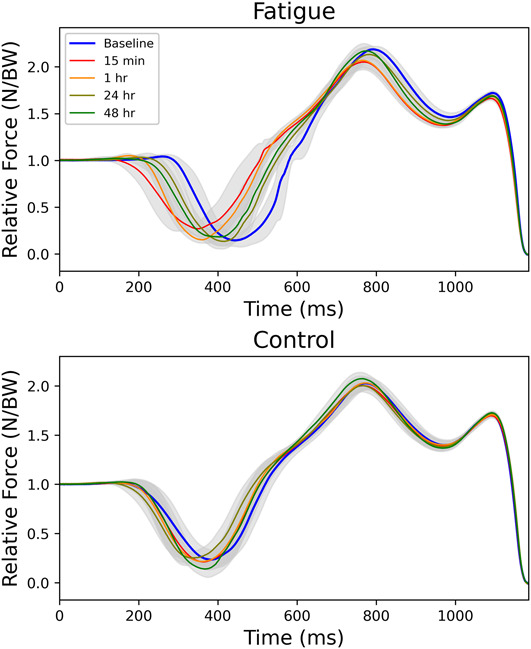
Mean CMJ_ABS force-time curve of a single subject in fatigue and control conditions. The mean CMJ_ABS force curve (solid line) at each time point with SD cloud (shaded) standardized to body mass in newtons. CMJ = countermovement jump.

Table 2.

Comparison of 1D and 0D 2-way repeated measures ANOVA analyses of a single data set.^*†

Two-way ANOVA	Result	Practical implications
1D—SPM analysis
CMJ and SJ relative force	Significant difference	Allows for analysis of the “how” of the jump provides potential movement strategy changes
0D—discrete analysis (18)
CMJ and SJ relative force(18)	No significant difference
CMJ height, FT:CT ratio, and velocity	Significant difference	Allows for analysis of the “what” of the jump, can miss strategy changes but provides clear outcome-based performance measures
SJ FT:CT ratio and velocity	Significant difference

^*CMJ = countermovement jump; ANOVA = analysis of variance; SPM = statistical parametric mapping; SJ = squat jump.

^†0D analysis previously published in Hughes et al. (18).

Discrete variables calculated from ratios of movement time, force, or power magnitude provide a proxy measure of changes to movement timing with previous research using these ratios to demonstrate fatigue (8,12). Cormack et al. (8) observed altered flight time to contraction time ratio up to 2 days after elite competition despite little changes in jump height performance, whereas the ratio of mean eccentric + concentric power to jump duration was more sensitive than peak power output, mean power output, and peak force 24 hours after fatigue (12). The observed changes in discrete variables using ratios of time, force, or power may provide support for the dynamical systems theory and the notion that different movement solutions occur to maintain a desired “performance” metric such as jump height or power output. Legg et al. (23) suggested that altering CMJ mechanics assisted with maintenance of jump height while in a fatigued state, with changes in dip magnitude observed midseason despite no change in jump height.

The current study contributes to the 1D analysis literature (29,42,45) of force-time curves by providing initial analysis of CMJ and SJ patterns using SPM. The greater sensitivity to force data reported in this research suggests that SPM could prove advantageous in fatigue assessment and understanding the readiness of an athlete to train or compete, a key component highly sought after by strength and conditioning professionals and sport scientists.

Changes in force-time curves across an entire CMJ have been explored (9,10,20,26,35), although rarely after fatigue inducement. In addition to a paucity of fatigue-related research, several analysis techniques were not appropriate 1D analysis methods. Gathercole et al. (14,15) have specifically looked at changes in relative force and power traces after fatigue; however, no statistical analysis was completed on these data. Visual analysis suggested longer movement durations in CMJ traces after acute fatigue (12,15) consistent with this research, with shortened durations after adaptation to chronic training (15). One-dimensional techniques such as functional data analysis (FDA) and SPM have been used to analyze force-time curves (43) with SPM providing parametric analysis and FDA using curve fitting, smoothing, and registration before nonparametric analysis. Although they differ in implementation, FDA analysis performed without curve fitting, smoothing, and registration has shown comparable results with SPM. Force-time data can also be analyzed using statistical nonparametric mapping which has provided almost identical results to FDA analysis (43).

Despite the potential benefits explored in this research, the current study is not without limitations. The complexity of the initial study design, requiring SPM 2-way repeated measures ANOVA analysis may be a limitation of this research. Post-hoc analysis of SPM 2-way repeated measures ANOVA is currently too simplistic (30) because it assumes that post-hoc tests are independent and involves separate smoothness assessments for each post-hoc test. As a result, the post-hoc analysis in this study should be interpreted with caution and in line with current guidelines post-analysis was not completed if it disagreed with initial ANOVA analysis (30). Furthermore, the large variation in jumping patterns between subjects also provides an obstacle to using SPM analysis methods. Wu et al.'s research suggested subject variation was the most significant contributor to CMJ variations after fatigue (45). Visual analysis of individual subjects, such as that in Figure 7, supports a variable response to fatigue by subjects. A critique of the style of analysis used in this research is that subject variations in the timing of jump phases, specifically in the CMJ, can potentially result in a mismatch of jump phases. Aligning the force-time curve at toe off ensures the final propulsion phase is aligned; however, as evidenced by the SD of phases, unweighting and braking phases found at the beginning and middle of the jump are less aligned. The linear interpolation method applied as part of the CMJ_NORM and SJ_NORM analysis partially corrected for this; however, in the CMJ_NORM analysis, it was less effective. In this instance, using linear interpolation to closer align early phases of the jump resulted in a reduced alignment at the points near toe off and reduced significance. Jump patterns are often highly variable with phases affected by multiple variables such as jumping experience or motor skill and training history (9,39). Consequently, an improved method of phase alignment may be required to reduce limitations of this method. Landmark or continuous registration techniques may provide an improved method of normalization for this research (34). These techniques transform curves to align specific features and reduce phase variation. Specific landmarks used in landmark or continuous registration often consist of maxima, minima, or zero crossings with landmarks such as onset of unweighting phase, minimum of unweighting phase, end of braking phase, maximum of propulsion phase, and end of propulsion phase being potentially useful for analysis of the CMJ force trace. However, to achieve use of landmark or continuous registration techniques consistently across the literature, it is incumbent on researchers to clearly define and agree to 0D landmarks.

Unimodal and bimodal peak variation reported within individual subjects (19,22) may also make cross sectional analysis of GRF traces problematic. A potential improvement would be the use of single subject analysis to reduce the magnitude of change from the required normalization or to remove the need for it entirely by increasing uniform jump characteristics across data collection. Fewer large variations in jump characteristics (phase timing and force application) may increase suprathreshold clusters as data from a single subject (such as in Figure 7) could provide greater consistency in control force traces making differences because of fatigue more apparent. To compare 2 time points using a SPM T-Test, as little as 6–12 jumps may be required for a single individual, although this will be dependent on the SD between force-time curves. If comparing multiple time points and multiple conditions of a single subject in a similar design to this study, a greater number of jumps would be required.

Practical Applications

Because of the low load required, daily or weekly jump testing is a viable method for assessing training or taper status around training blocks and competition; however, the analysis of discrete variables taken from a single point in the jump may miss changes elsewhere in the movement. Because strength and conditioning professionals, coaches and movement science specialists consider movement cues relative to whole movements and not relative to discrete points, analysis of the complete movement ensures identified differences are considered within the movement in its entirety. Practically, SPM analysis can provide important information relating to an athlete's movement strategy, expressed through a variation in the force-time curve, a key objective of coaches, movement science specialists and strength and conditioning coaches. The significant changes in force-time curves observed at multiple time points suggests that 1D analysis can detect differences throughout the force trace and may provide a method to assess athlete fatigue and readiness to perform. Although this research focused on athlete fatigue, the statistical assessment of movement strategy changes throughout lower-limb injury rehabilitation would be desirable for many professionals and may be a further avenue of interest. This research affirms the need for case study analysis on an individual experienced in jumping to ascertain if greater uniformity in jumping characteristics would demonstrate greater sensitivity than the current data set of 31 subjects. Furthermore, case study analysis could also compare 1D and 0D analysis to determine if single subject analysis provides greater sensitivity to fatigue than traditional 0D analysis methods. Continued development of this analysis technique could provide the ability to assess athlete fatigue and readiness to train by comparing daily pretraining efforts to previous nonfatigued efforts and providing an immediate analysis of athlete condition.