Abstract
The growth of hybrid nanofluids can be connected to their enhanced thermal performance as pertains to the dynamics of automobile coolant among others. In addition to that, the thermal characteristics of water-based nanofluids carrying three different types of nanoparticles are incredible. Keeping in view this new idea, the current investigation explores ternary hybrid nanofluid flow over a stretching sheet. Joule heating and viscous dissipation are addressed in the heat equation. Three distinct kinds of nanoparticles, namely, magnesium oxide, copper, and MWCNTs, are suspended in water to form a ternary hybrid nanofluid with the combination MgO–Cu–MWCNTs–H2O. To stabilize the flow of the ternary hybrid nanofluid, transverse magnetic and electric fields have been considered in the fluid model. The production of entropy has been analyzed for the modeled problem. A comparative study for ternary, hybrid, and traditional nanofluids has also been carried out by sketching statistical charts. The equations that govern the problem are shifted to dimension-free format by employing transformable variables, and then they are solved by the homotopy analysis method (HAM). It has been revealed in this work that the flow of fluid opposes by magnetic parameter and supports by electric field the volumetric fraction of ternary hybrid nanofluid, while thermal profiles are gained by the growing values of these parameters. Boosting values of the electric field, magnetic parameters, and Eckert number support the Bejan number and oppose the production of entropy. Statistically, it has been established in this work that a ternary hybrid nanofluid has a higher thermal conductivity than hybrid or traditional nanofluids.
1. Introduction
The exclusion of extraneous heat from different manufacturing procedures, transmission systems, and power plant equipment has been very challenging. Fluids that are based upon thermal flow such as ethylene glycol, water, and oils, etc. are termed as base fluid. These fluids have low thermal conductance that restrains their performance in different applications at the industrial level. The thermal conductance of these fluids can be enhanced by spreading solid particles as also proposed by Jawad et al.1 These particles are, for example, carbon, silver, magnesium oxide, copper oxide, alumina, titanium oxide, and graphene, etc. Such a combination of the base fluid and solid nanoparticles is termed as nanofluid. For its numerous applications in industry and engineering, nanofluid is a wide subject of deliberation for engineers and scientists. This type of material contains nanosized particles in the base fluid. Nanofluids normally have enhanced thermal conductance as necessary for various heat transmission systems. Algehyne et al.2 inspected MHD radiative nanofluid flow with a modified Buongiorno model past a curved slippery surface. It has also been observed that nanofluids could replace the prevailing cooling system in various areas of engineering such as transportation, electronics, energy, and manufacturing processes as discussed by Sajid and Ali.3 In this work it is revealed that the heat transfer efficiency is enhanced for both plates of the channel respectively by 7.10% (at the upper plate) and 4.11% (at the lower plate). Rasool et al.4 discussed numerically the EMHD nanofluid flow over a Riga plate placed horizontally in a permeable medium. Wakif et al.5 explored nanofluid flow past an isothermal stretching surface using a modified Buongiorno model. Shah et al.6 studied the heat transfer rate for gold blood nanoparticles using thermal radiation. The authors have considered the fluid flow in a channel with suction as well as injection effects on both plates of the channel.
With the passage of time, investigators came to know that the suspension of two different kinds of nanoparticles in a pure fluid such as engine oil, ethylene glycol, and water enhances the thermal characteristics of the base fluid. Such fluids are termed as hybrid nanofluids. These fluids have different applications in industry and engineering such as coolant in machines and manufacturing processes, heated pipes, ventilation processes, heat exchanger, automotive industry, ships, biomedicines, cooling of the nuclear system, and cooling of refrigeration systems, etc. Shah et al.7 deliberated thermal augmented EMHD micropolar hybrid nanofluid flow on a horizontal surface. Islam et al.8 surveyed the thermal flow for micropolar hybrid nanofluid (GO + Cu + H2O) flow amid two plates. The efficiency of hybrid nanofluid has been analyzed by Khashi’ie et al.9 with nanoparticles of copper and alumina in a base fluid taken as water. The entropy production along with heat transmission for a MHD hybrid nanofluid (Al2O3 + Cu + H2O) flow was examined by Perveen et al.10 using different flow conditions. Bhatti et al.11 investigated numerically hybrid nanofluid flow through an elastic circular and non-Darcy medium. A comparative analysis was conducted in this study in the absence of nanoparticles.
Recently scientists and researchers have developed a new class of nanofluid by suspending three unlike types of nanoparticles in the pure fluid. This innovative class of nanofluid is called a ternary hybrid nanofluid. The higher demand for the cooling agent in the combination of high thermal capability at the industrial level has attracted researchers to modify the existing nanofluid, as a result of which trihybrid nanofluid has been introduced with enhanced thermal characteristics. With this thinking, further experimental investigations have been conducted to enhance further the thermal characteristics of an existing hybrid nanofluid by suspending three unlike kinds of solid nanoparticles in pure fluid, leading to the ternary hybrid nanofluid. Sang et al.12 used CNTs and carbonate nanoparticles to enhance the thermal conductivity and specific heat for solar power systems. Mousavi et al.13 examined the dynamics of a trihybrid nanofluid by suspending magnesium oxide, copper oxide, and titanium oxide in water. Sahoo and Kumar et al.14 tried to promote an innovative correlation to improve the viscosity of trihybrid nanofluid. From the outcome of their work, it was revealed that the dynamic viscosity was enhanced and declined for augmentation in volume fraction and temperature, respectively. The density property of different nanofluids was introduced by employing equilibrium molecular dynamic simulations as investigated by Abbasi et al.,15 and it was highlighted in this work that the density of nanofluid is influenced significantly by the shape and size of nanoparticles.
Fluid flows due to stretching sheets have received considerable attention of scientists due to their applications in the fields of engineering and industry. These applications include hot rolling, extrusion of the sheet, shrink wrapping, bundle wrapping, manufacturing of foam, purification of crude oil, and electronic devices cooling, etc. Due to the stretching surface, the boundary layer flow plays a vital role in the production of paper, fabrication of glass, and the nuclear reactor, etc. The revolutionary work was initiated by Sakiadis16,17 in 1961 by presenting the idea of boundary layer flow past a stretching surface. Afterward, Crane18 extended this idea and determined the exact solution for the stretching sheet. Since then, various investigators have comprehended the idea of stretching sheets for different flows. Khan et al.19 applied the curved stretching sheet to optimize the entropy generation for a nanofluid. The authors of this investigation have addressed the impact of various flow conditions upon the flow system and have revealed that thermal flow has an upsurge with a hike in Brownian motion and thermophoretic parameters, while entropy generation is augmented with larger values of the curvature parameter. The production of entropy has also been minimized by Hayat et al.20 with the help of a stretching sheet by using Darcy-Forchheimer nanoparticles with slip conditions. Raza et al.21 investigated the creation of irreversibility by considering the nonlinear thermally radiative flow of a nanofluid upon the curved stretching surface. In this work, the curvilinear coordinate system was implemented to tackle the governing equations. Rasool et al.22 scrutinized the irreversibility and chemically reactive MHD fluid flow over a nonlinear stretched sheet. Hayat et al.23,24 discussed separately the axisymmetric MHD fluid flow over a stretched cylinder and between two sheets. Naseem et al.25 used the influence of magnetic effects upon bioconvective nanofluid flow over a stretching surface. Shafiq et al.26 inspected MHD squeezing fluid flow upon a stretched surface using non-Darcy phenomenon.
The irreversibility analysis is used to investigate the efficiency of different thermo-dynamical systems in engineering, industrial, and biomedical phenomenon. The production of entropy in a mechanical system is based upon the second law of thermodynamics. The optimization of entropy is employed to enhance the effectiveness of the thermo-dynamical system. The entropy is normally caused by the occurrence of molecular vibration, Joule heating, thermal radiation, chemical reaction, and force of resistance to a fluid’s motion, etc. Principally Bejan27,28 initiated theoretically the concept of production of irreversibility problems. Afterward, numerous studies were conducted by different researchers with the main focus on the optimization of entropy production for different flow systems. Ahmad et al.29 inspected convective flow of a power-law fluid over a vertical plate by using effects of Brownian motion as well as thermophoresis to the flow system. It was noticed in this study that Bejan number was reduced and entropy production was increased with higher values of the radiation parameter. Khan et al.30 examined the creation of irreversibility for the rotary motion of Casson nanofluid upon a spinning and stretched cylinder. The authors of this study highlighted that flow of fluid was enhanced and concentration had declined with augmentation in Reynolds number. The entropy was also noticed to be enhanced with advanced values of radiation parameter and Brinkman number. Habib et al.31 used the finite difference method to solve the modeled problem for entropy generation and thermal flow analysis in the power-law fluid and noticed that higher values of magnetic parameters enhanced the entropy of the flow system. Shashikumar et al.32 inspected the thermal flow and entropy production for MHD Williamson fluid flow passing through a microchannel.
The irreversibility phenomenon that converts the work performed by fluid particles by employing a shared force into thermal energy is termed as viscous dissipation. It alters the thermal diffusion by acting as a source of energy and affects thermal flow rate. Various studies have been conducted by incorporating the effects of viscous dissipation for fluid flow problems. To control the heat transmission rate for fluid flow past a stretched sheet, Bataller33 used a variable heat source with viscous dissipation and observed that thermal profiles were supported by Eckert number, radiation, and dissipation parameters. Zaydan et al.34 inspected EMHD dissipative fluid flow past a heated Riga plate using a heat source. Khan et al.35 analyzed nanofluid flow over a spinning needle employing viscous dissipation and magnetic effects to the flow system. It was depicted in this analysis that the flow characteristics of nanofluid were opposed by a volumetric fraction and magnetic field, whereas thermal flow was supported by upper values of Brownian motion and Eckert number. Bhatti et al.36 settled mathematically a model for naturally convective EMHD fluid flow through a microchannel consisting of non-Darcy permeable medium with influence of viscous dissipation. Shafiq et al.37 investigated analytically a stretched surface with the impact of viscous dissipation. Khan et al.38 investigated thermal flow optimization for micropolar fluid flow upon a needle using bioconvective and viscous dissipation effects upon the flow system. Gul et al.39 inspected thermal analysis for electroosmotic flow with viscous dissipation through a vertical tube. Abbas et al.40 deliberated mathematically nanofluid flow subject to viscous dissipation and other flow conditions.
From the cited literature it was revealed that plenty of investigations have been conducted to improve thermal conductivity of a pure fluid by suspending two different kinds of nanoparticles in it, but very few investigations have yet been conducted for ternary hybrid nanofluids. The novelty of current work is described in the following list:
Three different types of nanoparticles namely magnesium oxide, copper, and MWCNTs are suspended in the base fluid (water) to form ternary hybrid nanofluid.
The new combination MgO-Cu-MWCNTs-H2O has been used for the first time in the current work. This new combination helps in environmental purification and other appliances that require cooling.
For stabilization of the flow of a trihybrid nanofluid, the transverse magnetic and electric fields have been considered in the fluid model.
The main focus of this work is to analyze the thermal efficiency of ternary hybrid nanofluids and to carry out a comparative study for ternary, hybrid, and traditional nanofluids. This comparison will be expressed with the help of statistical charts.
The production of entropy has also been analyzed for the modeled problem.
Heat transfer enhancement is the main objective of the suggested model. The core objective of the current work is to show that ternary hybrid nanofluids can more reliably enhance heat transfer. Entropy and Bejan number affect the proposed model under the impact of numerous factors.
According to the above objectives, possible research questions that can arise in the minds of the readers are the following:
• Who cautions about this problem and why?
• What have others done?
• How can you demonstrate that your solution is a good one?
2. Problem Formulation
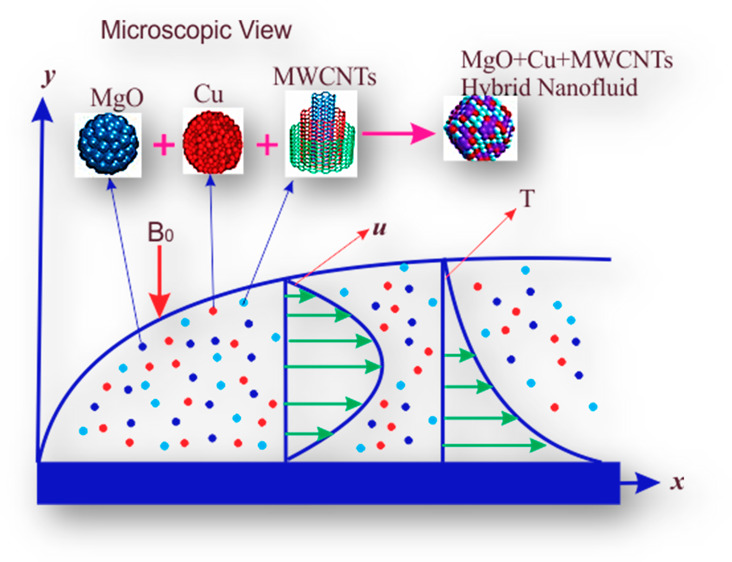
Two-dimensional flow of the ternary hybrid nanofluid past a stretching surface containing MgO, Cu, and MWCNTs nanoparticles has been considered (Figure 1). The transverse magnetic and electric fields stabilize the ternary hybrid nanofluid flow. Additionally, the Joule heating and viscous dissipation effects are used in the energy equations. Lorentz force is used as a resistive force to streamline the flow regime signified by J⃗ × B⃗ such that J⃗ is the current density and B⃗ is the magnetic field effect. Furthermore, J⃗ is defined by the Ohm law J⃗ = σ(V⃗ × B⃗ + E⃗) where E⃗ is used for electric field and σ is used for the electrical conductivity.
Figure 1.
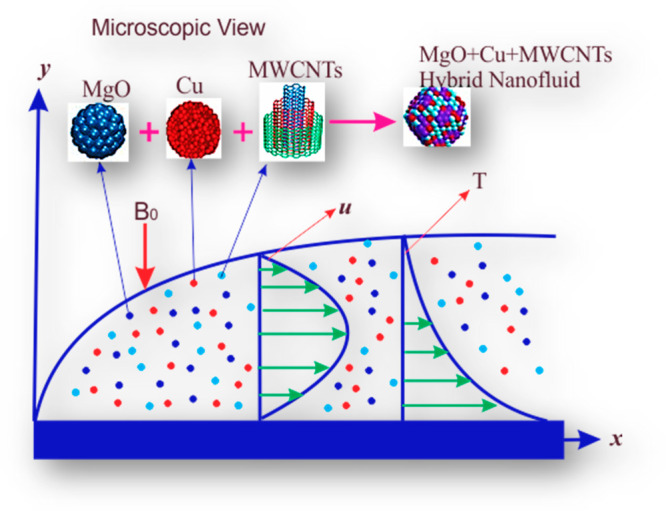
Geometrical view of the flow problem.
The equations that governed the flow problem can be stated mathematically as41
| 1 |
| 2 |
| 3 |
The conditions at the boundaries are41
| 4 |
Above u and v depict flow elements along the direction of x and y-axes and ρthnf represents ternary hybrid nanofluid density, μthnf, υthnf, αthnf, (ρcp)thnf and σthnf are the dynamic viscosity, kinematic viscosity, thermal diffusivity, heat capacitance, and electrical conductivity of the ternary hybrid nanofluid, whereas E0 is the strength of the electric field while B0 is magnetic strength.
It is to be noticed that the thermophysical characteristics of the ternary fluid are displayed as42,43
| 5 |
| 6 |
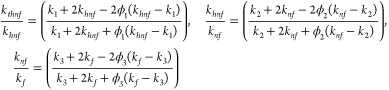 |
7 |
| 8 |
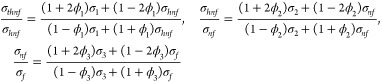 |
9 |
The set of dimensionless variables is43
| 10 |
Utilizing eqs 10 in eqs 1–3) we have
| 11 |
| 12 |
The related conditions at boundaries are
| 13 |
In eqs 11 and 12 Pr is Prandtl number, M is magnetic factor, E is electric field parameter, and Ec is Eckert, these factors are defined mathematically as
| 14 |
2.1. Physical Quantities
In the current investigation the main quantities of interest are expressed mathematically as follows:
| 15 |
Using eq 10 to eq 15 we have the modified format of the above quantities as follows:
| 16 |
3. Entropy Rate
In order to calculate the production of entropy in the current investigation, following the concept as presented by Bejan44 and Hayat et al.,45 the volumetric rate of dimensional entropy production can be expressed mathematically as
| 17 |
Incorporating eq 10 in eq 17 we have
| 18 |
Here 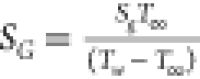 is the entropy production rate and
is the entropy production rate and 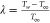 is the temperature difference parameter.
is the temperature difference parameter.
4. Bejan Number
The ratio of entropy produced due to heat transmission to total entropy of the flow system produced is the Bejan number. Mathematically it can be described as
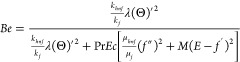 |
19 |
5. Method of Solution
For a solution of nonlinear differential equations various solution techniques have been used by different researchers. HAM46,47 is one of such techniques employed for the solution of nonlinear differential equations. Mathematica software is used to fulfill this aim. This method requires some initial guesses and values of linear operators which are discussed in the following lines.
| 20 |
| 21 |
such that
| 22 |
where NF̑ and NΘ̑ are described as
| 23 |
| 24 |
For eqs 6 and 7 the zeroth-order system is described as
| 25 |
| 26 |
Related boundary conditions are
| 27 |
For ζ = 0, ζ = 1 we have
| 28 |
The Taylor’s series expansion of F̑(η;ζ) and Θ̑(η;ζ) about ζ = 0 is expressed as
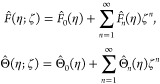 |
29 |
| 30 |
Subjected conditions are
| 31 |
Now
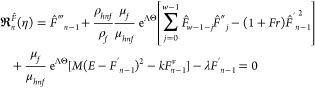 |
32 |
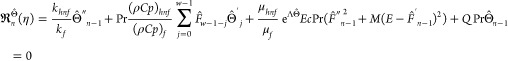 |
33 |
While
| 34 |
6. Discussion of Results
The current study explores a trihybrid nanofluid over a stretching sheet. Magnesium oxide, copper, and MWCNTs are suspended in the base fluid (water) to form a ternary hybrid nanofluid with a combination MgO-Cu-MWCNTs-H2O. In order to stabilize the flow of ternary hybrid nanofluid, the transverse magnetic and electric fields have been considered in the fluid model. The production of entropy has been analyzed for the modeled problem. A comparative study for ternary, hybrid, and traditional nanofluids has also been carried out by sketching statistical charts. After seeking the HAM solution of the problem, different graphical views have been obtained for various parameters which have been encountered during the process of nondimensionalization. In the following lines, some discussion has been carried out for explaining these graphical views theoretically with impact upon velocity, temperature, entropy, and Bejan number.
6.1. Variations in Velocity
The flow of fluid in response to variations in different parameters is discussed in Figures 2–4. From Figure 2, it is observed that when ϕ1 = ϕ2 = ϕ3 = 0.01, λ = 0.2, E = 0.2, and Ec = 1.0, then for variations in the magnetic parameter M, velocity profiles decline. Actually, the Lorentz force generates in the fluid flow system with higher values of M which maximizes the resistive force. Therefore, the velocity of ternary hybrid nanofluid decays due to resistance in fluid motion. Figure 3 presents the contribution of electric field E to velocity profiles f′(η) when M = 0.1, Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2. Since growth in E conveys a drop in the resistive forces to fluid flow and causes an enhancement in the velocity profiles for ternary, hybrid, and traditional nanofluids as portrayed in Figure 3. The effects of nanoparticles of magnesium oxide (MgO), copper (Cu), and MWCNTs upon velocity f′(η) are depicted in Figure 4. Since with augmentation in the values of solid nanoparticles the dense behavior of a fluid is enhanced, due to which resistive forces to motion are created, and declines velocity.
Figure 2.
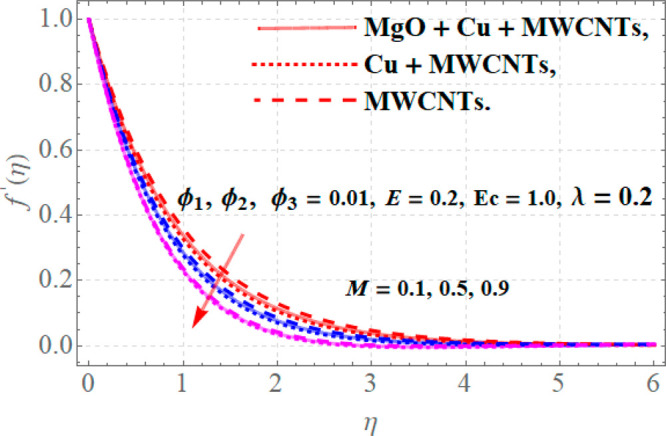
Velocity profiles versus variations in magnetic parameter M.
Figure 4.
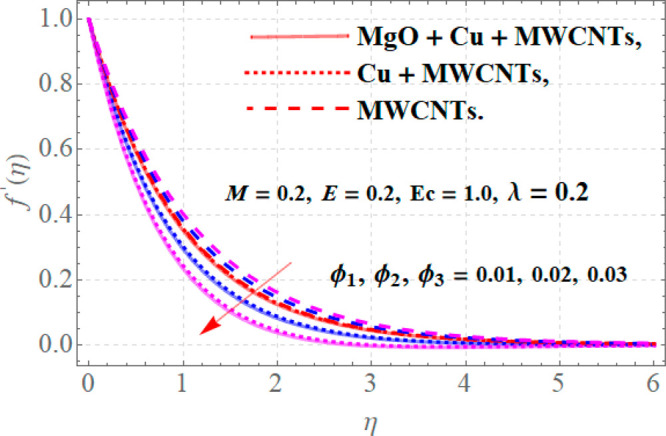
Velocity profiles versus variations in solid nanoparticles ϕ1, ϕ2, ϕ3.
Figure 3.
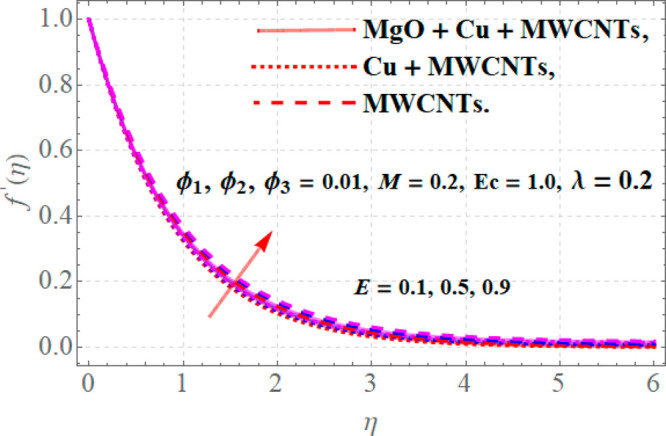
Velocity profiles versus variations in electric field parameter E.
6.2. Variations in Temperature
The influence of different parameters upon profiles of temperature θ(η) is presented in Figures 5–7. From Figure 5 it is noticed that for a growth in magnetic parameter (M) with E = 0.2, Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2, the thermal flow is boosted. Physically, for higher values of M there are much stronger resistive forces in the fluid motion that generate more energy dissipation and ultimately enhance the temperature. The electric field E acts as an increasing agent for the thermal field, as maximum thermal diffusivity takes place for higher values of E. Hence augmentation in E corresponds to a growth in thermal profiles when M = 0.2, Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2 as depicted in Figure 6. The influence of higher values of Eckert number (Ec) upon thermal field is portrayed in Figure 7 for fixed values of M = 0.2, Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2. Actually, for greater values of Ec, maximum heat energy transports from a region of higher thermal flow to a region of lower one due to which more heat transfer occurs. In this phenomenon the thermal profiles of a fluid increase as portrayed in Figure 7.
Figure 5.
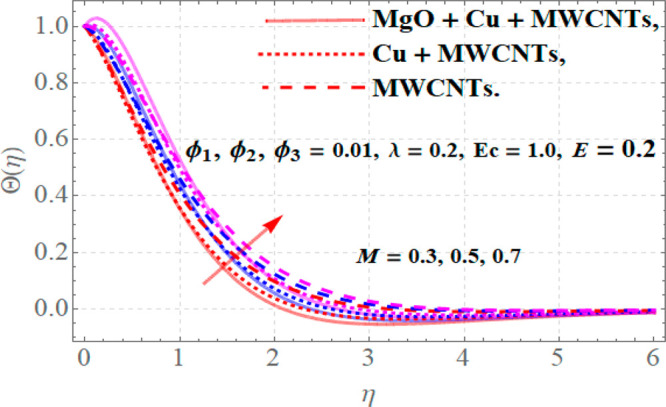
Temperature profiles versus variations in magnetic parameter M.
Figure 7.
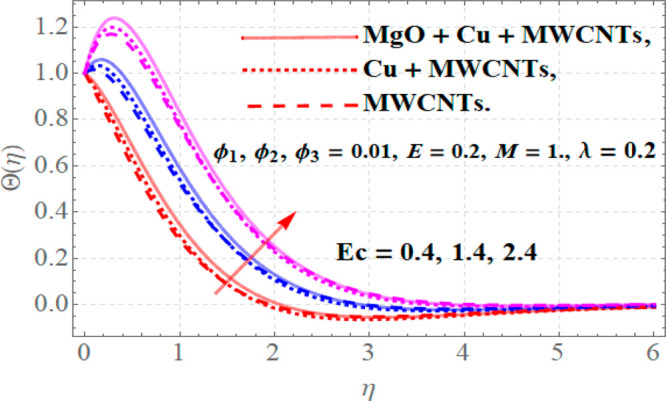
Temperature profiles versus variations in Eckert number Ec.
Figure 6.
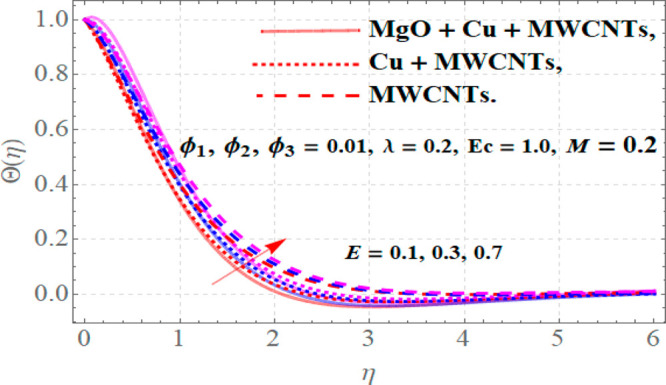
Temperature profiles versus variations in electric field parameter E.
6.3. Rate of Entropy Generation and Bejan Number
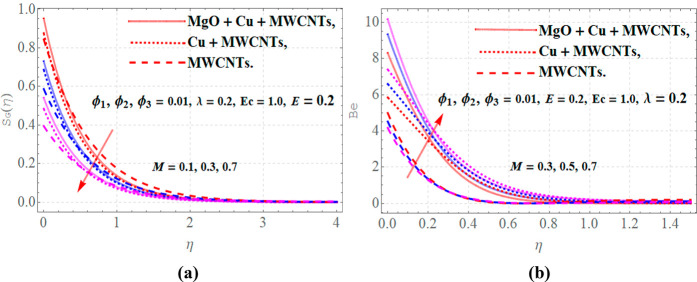
The impact upon entropy and Bejan number in response of variation in different factors is presented in Figures 8–11. The effect of magnetic parameter (M) over entropy and Bejan number is presented in Figure 8(a,b). Physically higher values of M offer more resistance to moving particles of the ternary hybrid nanofluid; this resistance disturbs the order of flow pattern and generates more entropy as depicted in Figure 8a. A reverse impact of higher values of M upon Bejan number is observed as depicted in Figure 8b with parameter values of E = 0.2,Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2.
Figure 8.
(a) Entropy and (b) Bejan number versus variations in magnetic parameter M.
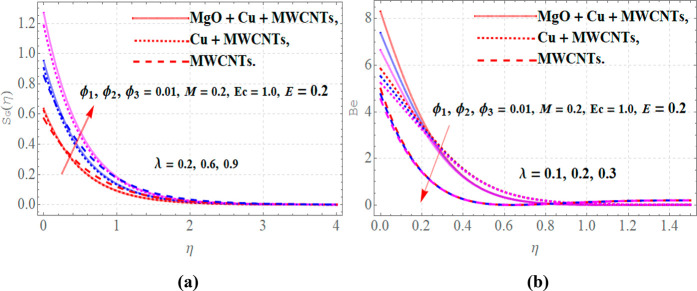
Figure 11.
(a) Entropy and (b) Bejan number versus variations in λ.
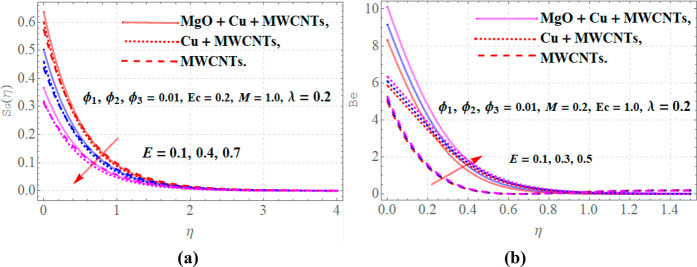
Figure 9 panels a and b portray the influence of electric parameters (E) upon the generation of entropy and Bejan number. From these figure, it is obvious that higher values of E decay entropy while the Bejan number increases, when M = 0.2, Ec = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2.
Figure 9.
(a) Entropy and (b) Bejan number versus variations in electric parameter E.
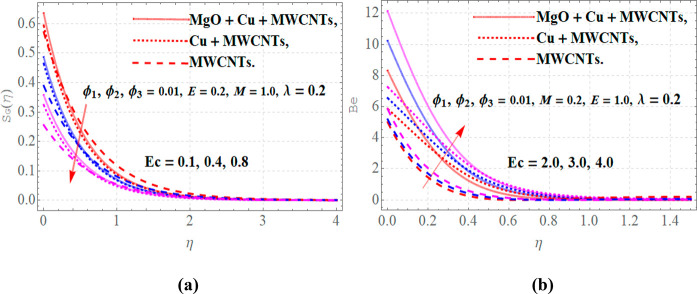
Figure 10 panels a and b reveal that augmenting values of Eckert number Ec decrease the values of entropy for E = 0.2, M = 1.0, ϕ1 = ϕ2 = ϕ3 = 0.01, and λ = 0.2, whereas for the growth in Ec the values of the Bejan number increase.
Figure 10.
(a) Entropy and (b) Bejan number versus variations in Eckert number Ec.
Figure 11 panels a and b portray that augmenting values of temperature difference parameter λ boost the values of entropy generation for E = 0.2, M = 0.2, ϕ1 = ϕ2 = ϕ3 = 0.01, and Ec = 1.0, whereas for the same range of these parameters the Bejan number decays for higher values of λ as depicted in Figure 11b.
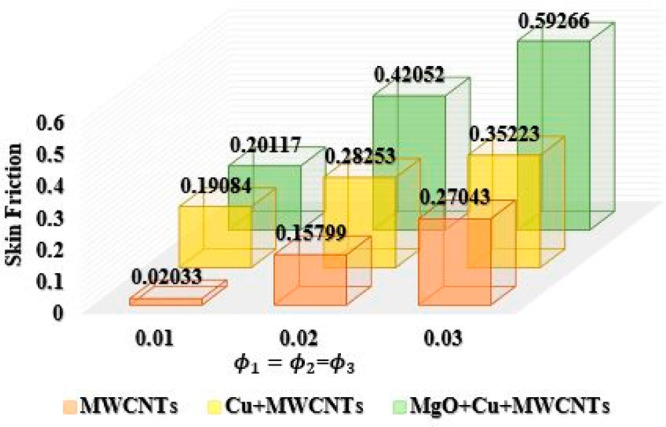
In Chart 1 the values of ternary hybrid nanofluid have been calculated for skin friction in response to variations in electric field parameters E with ϕ1 = ϕ2 = ϕ3 = 0.01 and M = 0.2. It has been noticed that for a variation in the values of E from 0.2 to 0.6 the values of skin friction coefficient vary from 0.52416 to 0.90166 for MWCNTs nanoparticles. The values of skin friction vary from 0.62528 to 0.99642 for Cu + MWCNTs nanoparticles, whereas for the same range of E for the ternary hybrid nanoparticles MgO + Cu + MWCNTs, the skin friction coefficient varies from 0.844944 to 1.144808. Hence an increasing trend has been observed in skin friction coefficient in response to variation in E from 0.2 to 0.6 and is much better in the case of ternary hybrid nanoparticles.
Chart 1. : Comparison of Ternary Hybrid Nanofluid for Skin Friction Using Electric Field Parameter E.
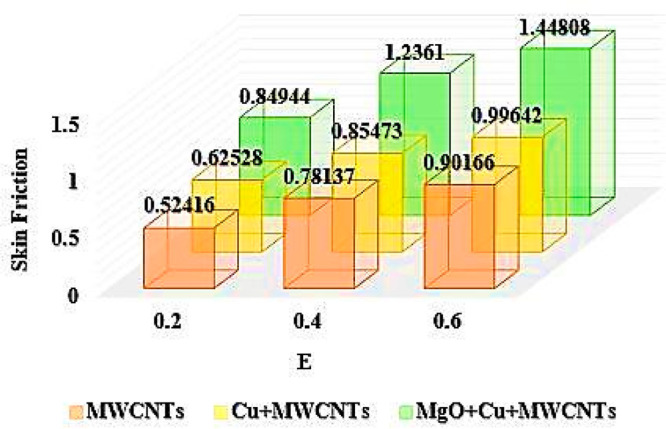
In Chart 2 the values of the ternary hybrid nanofluid have been calculated for skin friction in response of variations in magnetic parameters M with ϕ1 = ϕ2 = ϕ3 = 0.01 and E = 0.2. It has been noticed that, for variations in values of M from 0.2 to0.6 the values of skin friction coefficient varies from 0.27043 to 0.22012 for MWCNTs nanoparticles, these values of skin friction vary from 0.35223 to 0.29251 for Cu + MWCNTs nanoparticles , whereas, on the same range of M for ternary hybrid nanoparticles MgO + Cu + MWCNTs, the variations in skin friction coefficient are from 0.37266 to 0.36263. A decaying trend has been observed in the skin friction coefficient in response to variations in M from 0.2 to 0.6.
Chart 2. : Comparison of Ternary Hybrid Nanofluid for Skin Friction Using Magnetic Parameter M.
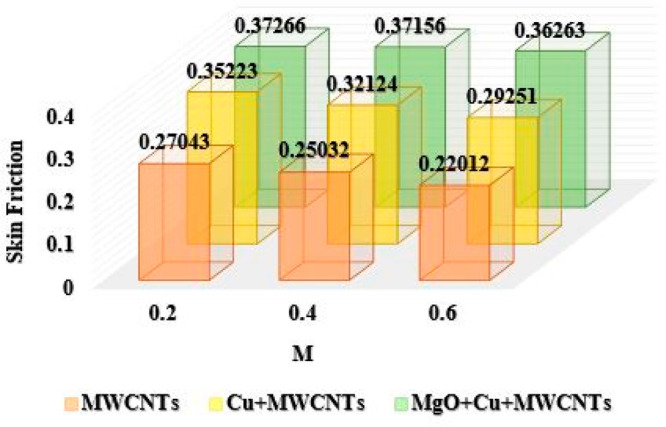
In Chart 3 the values of the ternary hybrid nanofluid have been calculated for skin friction in response of variations in volumetric fraction ϕ1, ϕ2, ϕ3 with M = 0.4, and E = 0.2. It has been observed that for variations in the values of ϕ1, ϕ2, ϕ3 from 0.01 to 0.03, the values of skin friction coefficient vary from 0.02033 to 0.27043 for MWCNTs nanoparticles and from 0.19084 to 0.35223 for Cu + MWCNTs nanoparticles, whereas on the same range of ϕ1, ϕ2, ϕ3 for ternary hybrid nanoparticles MgO + Cu + MWCNTs, the variations in skin friction coefficient are from 0.20117 to 0.59266. An enhancing behavior has been observed in the skin friction coefficient in response to variations in ϕ1, ϕ2, ϕ3 from 0.01 to0.03.
Chart 3. : Comparison of Ternary Hybrid Nanofluid for Skin Friction Using Parameters ϕ1, ϕ2, ϕ3.
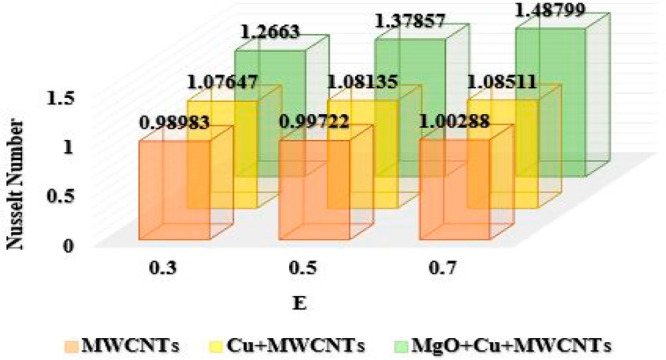
In Chart 4 the variations in Nusselt number have been depicted in response to augmenting values of electric field parameter E when ϕ1 = ϕ2 = ϕ3 = 0.01, Ec = 1, Pr = 6.2, and M = 0.2. It has been noticed that for variations in electric field parameter E from the range 0.3 to 0.7, the rate of transfer of heat augments from 0.98983 to 1.00288 for MWCNT nanoparticles. These values of heat transmission rate vary from 1.07647 to 1.08511 for Cu + MWCNTs nanoparticles, whereas on the same range of E for MgO + Cu + MWCNTs nanoparticles, the variations in Nusselt number are from 1.26630 to 1.48799. An enhancing behavior has been observed in Nusselt number in response to variations in E from 0.3 to 0.7. Moreover, the maximum heat transfer rate has been observed in the case of ternary hybrid nanofluid which is the main motivation in the current work.
Chart 4. : Comparison of Ternary Hybrid Nanofluid for Nusselt Number Using Electric Field Parameter E.
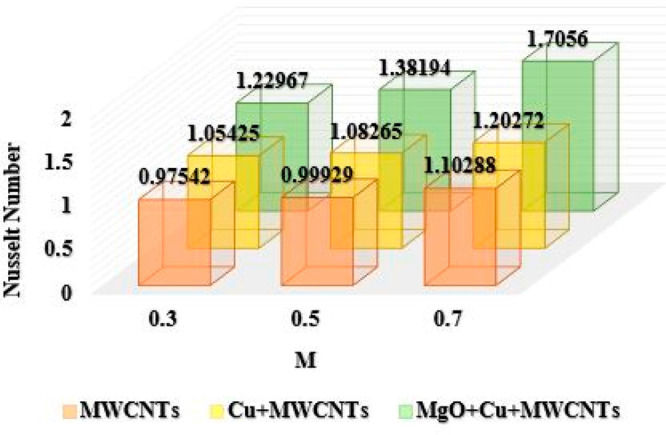
In Chart 5 the variations in Nusselt number are presented in response to augmenting values of the magnetic parameter M when ϕ1 = ϕ2 = ϕ3 = 0.01, Ec = 1, Pr = 6.2, and E = 0.2. For variations in E from a range 0.3 to 0.7, the Nusselt number varies from 0.97542 to 1.10288 for MWCNT nanoparticles, these variations in Nusselt number are from 1.05425 to1.20272 for Cu + MWCNTs nanoparticles, whereas on the same range of magnetic parameter for MgO + Cu + MWCNTs nanoparticles, the variations in Nusselt number are from 1.22967 to 1.70560. Once again an augmenting behavior has been noticed in Nusselt number.
Chart 5. : Comparison of Ternary Hybrid Nanofluid for Nusselt Number Using the Parameter M.
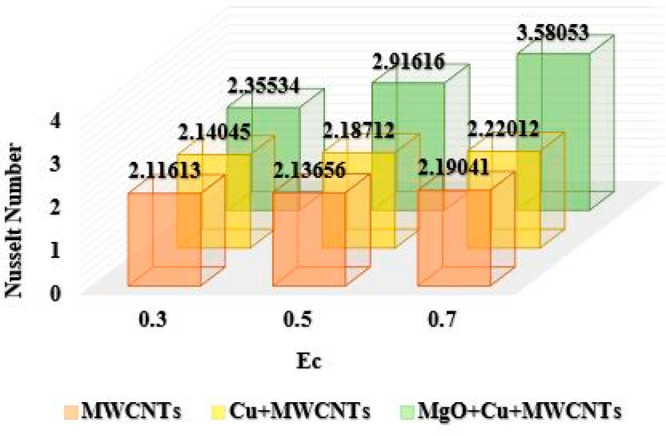
In Chart 6 the variations in Nusselt number are portrayed in the reaction of augmenting values of Eckert number Ec when ϕ1 = ϕ2 = ϕ3 = 0.01, M = E = 0.2, and Pr = 6.2. The value of Nusselt number changes from 2.11613 to 2.19041 for MWCNT nanoparticles, when Ec varies from 0.3 to 0.7. For the same range of Ec, the Nusselt number changes from 2.14045 to 2.22012 for Cu + MWCNTs nanoparticles. It has also been observed that for MgO + Cu + MWCNTs nanoparticles the Nusselt number varies from 2.35534 to 3.58053 when Ec varies from 0.3 to 0.7. In this case, a huge change has been observed in Nusselt number in the case of the ternary hybrid nanofluid.
Chart 6. : Comparison of Ternary Hybrid Nanofluid for Nusselt Number Using the Parameter Ec.
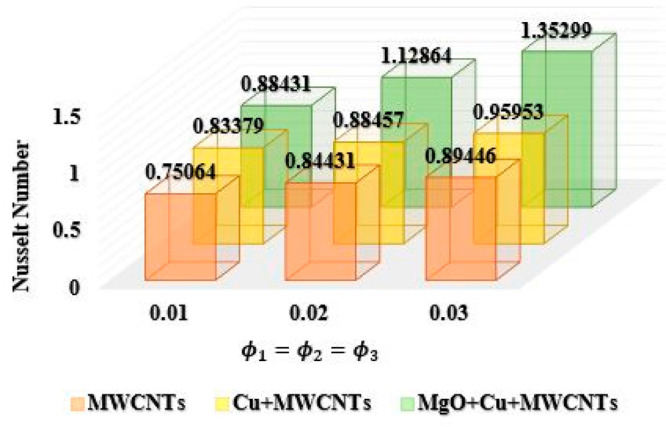
In Chart 7 the variations in Nusselt number are depicted in response to augmenting values of volume fraction of nanoparticles ϕ1, ϕ2, ϕ3 when Ec = 1, M = E = 0.2, and Pr = 6.2. The value of the Nusselt number changes from 0.75064 to 0.89446 for MWCNT nanoparticles, when ϕ1 = ϕ2 = ϕ3 varies from 0.01 to 0.03. For the same range of ϕ1 = ϕ2 = ϕ3, the Nusselt number varies from 0.83379 to 0.95953 for Cu + MWCNTs nanoparticles. It has also been observed that for MgO + Cu + MWCNTs nanoparticles, the Nusselt number varies from 0.88431 to1.35299 when ϕ1 = ϕ2 = ϕ3 varies from 0.01 to 0.03. Again an augmentation in heat transfer rate has been noticed for the ternary hybrid nanofluid.
Chart 7. : Comparison of Ternary Hybrid Nanofluid for Nusselt Number Using ϕ1,ϕ2,ϕ3.
7. Conclusions
The current study investigates ternary hybrid nanofluid flow over a stretching sheet with some flow conditions. Magnesium oxide, copper, and MWCNTs are suspended in the base fluid (water) to form a ternary hybrid nanofluid with a combination MgO–Cu–MWCNTs–H2O. In order to stabilize the flow of ternary hybrid nanofluid, the transverse magnetic and electric fields have been considered in the fluid model. The production of entropy has been analyzed for the modeled problem. A comparative study for ternary, hybrid, and traditional nanofluids has also been carried out by sketching statistical charts. After complete insight of the investigation the following points have been observed:
Flow of fluid decays for growth in the magnetic parameter and volumetric fraction of ternary hybrid nanofluid.
Higher values of the electric field parameter support the fluid motion for all types of nanoparticles.
For growth in the magnetic parameter, there is much stronger resistive force in the fluid motion that generates more energy dissipation and ultimately enhances the temperature of the fluid. Thermal profiles are also supported by augmentation in the electric field parameter.
For a growth in Eckert number, maximum heat diffusivity takes place that augments the thermal profiles of the ternary hybrid nanofluid.
Augmenting values of the magnetic parameter, electric field factor, and Eckert number support the expansion in the Bejan number and oppose the production of entropy. Whereas augmentation in temperature difference parameter enhances the production of irreversibility and decays the Bejan number.
With the help of statistical chart, it has established that skin friction coefficient augments with growing values of electric field parameter and volumetric fractions of solid nanoparticles, whereas it decays with growth in magnetic parameter.
Thermal flow rate grows up more rapidly with variations of different substantial parameters in the case of ternary hybrid nanofluid MgO + Cu + MWCNTs as compared to hybrid nanofluid Cu + MWCNTs or traditional nanofluid MWCNTs. Therefore, the ternary hybrid nanofluid has the highest thermal conductivity than hybrid or traditional nanofluids.
In the future the influence of mixed convection, Brownian motion, and thermophoresis effects will be added with inclusion of a concentration equation.
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code 22UQU4331317DSR79.
The authors declare no competing financial interest.
References
- Jawad M.; Saeed A.; Gul T.; Khan A. The magnetohydrodynamic flow of a nanofluid over a curved exponentially stretching surface. Heat Trans 2021, 50, 5356–5379. 10.1002/htj.22127. [DOI] [Google Scholar]
- Algehyne E. A.; Wakif A.; Rasool G.; Saeed A.; Ghouli Z. Significance of Darcy-Forchheimer and Lorentz forces on radiative alumina-water nanofluid flows over a slippery curved geometry under multiple convective constraints: a renovated Buongiorno’s model with validated thermophysical correlations. Waves Random Complex Media 2022, 1–30. 10.1080/17455030.2022.2074570. [DOI] [Google Scholar]
- Sajid M. U.; Ali H. M. Thermal conductivity of hybrid nanofluids: a critical review. Int. J. Heat Mass Transf, 2018, 126, 211–234. 10.1016/j.ijheatmasstransfer.2018.05.021. [DOI] [Google Scholar]
- Rasool G.; Shah N. A.; El-Zahar E. R.; Wakif A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022, 1–20. 10.1080/17455030.2022.2074571. [DOI] [Google Scholar]
- Wakif A.; Zaydan M.; Alshomrani A. S.; Muhammad T.; Sehaqui R. New insights into the dynamics of alumina-(60% ethylene glycol+ 40% water) over an isothermal stretching sheet using a renovated Buongiorno’s approach: A numerical GDQLLM analysis. Int. Commun. Heat Mass Transf 2022, 133, 105937. 10.1016/j.icheatmasstransfer.2022.105937. [DOI] [Google Scholar]
- Shah Z.; Khan A.; Khan W.; Alam M. K.; Islam S.; Kumam P.; Thounthong P. Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Comput. Methods Programs Biomed 2020, 186, 105197. 10.1016/j.cmpb.2019.105197. [DOI] [PubMed] [Google Scholar]
- Shah N. A.; Wakif A.; El-Zahar E. R.; Ahmad S.; Yook S. J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG),(40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. 10.1016/j.csite.2022.102046. [DOI] [Google Scholar]
- Islam S.; Khan A.; Deebani W.; Bonyah E.; Alreshidi N. A.; Shah Z. Influences of Hall current and radiation on MHD micropolar non-Newtonian hybrid nanofluid flow between two surfaces. AIP Adv. 2020, 10, 055015. 10.1063/1.5145298. [DOI] [Google Scholar]
- Khashi’ie N. S.; Waini I.; Arifin N. M.; Pop I. Unsteady squeezing flow of Cu-Al2O3/water hybrid nanofluid in a horizontal channel with magnetic field. Sci. Rep. 2021, 11, 1–11. 10.1038/s41598-021-93644-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parveen N.; Awais M.; Awan S. E.; Khan W. U.; He Y.; Malik M. Y. Entropy Generation Analysis and Radiated Heat Transfer in MHD (Al2O3-Cu/Water) Hybrid Nanofluid Flow. Micromachines 2021, 12, 887. 10.3390/mi12080887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatti M. M.; Ellahi R.; Doranehgard M. H. Numerical study on the hybrid nanofluid (Co3O4-Go/H2O) flow over a circular elastic surface with non-Darcy medium: Application in solar energy. J. Mol. Liq. 2022, 361, 119655. 10.1016/j.molliq.2022.119655. [DOI] [Google Scholar]
- Sang L.; Ai W.; Wu Y.; Ma C. Enhanced specific heat and thermal conductivity of ternary carbonate nanofluids with carbon nanotubes for solar power applications. Int. J. Energy Res. 2020, 44, 334–343. 10.1002/er.4923. [DOI] [Google Scholar]
- Mousavi S. M.; Esmaeilzadeh F.; Wang X. P. Effects of temperature and particles volume concentration on the thermophysical properties and the rheological behavior of CuO/MgO/TiO 2 aqueous ternary hybrid nanofluid. J. Therm. Anal. Calori. 2019, 137, 879–901. 10.1007/s10973-019-08006-0. [DOI] [Google Scholar]
- Sahoo R. R.; Kumar V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int. Commun. Heat Mass Transf 2020, 111, 104451. 10.1016/j.icheatmasstransfer.2019.104451. [DOI] [Google Scholar]
- Abbasi M.; Heyhat M. M.; Rajabpour A. Study of the effects of particle shape and base fluid type on density of nanofluids using ternary mixture formula: A molecular dynamics simulation. J. Mol. Liq. 2020, 305, 112831. 10.1016/j.molliq.2020.112831. [DOI] [Google Scholar]
- Sakiadis B. C. Boundary layer behaviour on continuous solid surface: I. The boundary layer on a continuous moving surface. AIChE J. 1961, 7, 26–28. 10.1002/aic.690070108. [DOI] [Google Scholar]
- Sakiadis B. C. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AIChE J. 1961, 7, 221–225. 10.1002/aic.690070211. [DOI] [Google Scholar]
- Crane L. J. Flow past a stretching plate.. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar]
- Khan S. A.; Hayat T.; Alsaedi A. Entropy optimization in passive and active flow of liquid hydrogen based nanoliquid transport by a curved stretching sheet. Int. Commun. Heat Mass Transf 2020, 119, 104890. 10.1016/j.icheatmasstransfer.2020.104890. [DOI] [Google Scholar]
- Hayat T.; Qayyum S.; Alsaedi A.; Ahmad B. Entropy generation minimization: Darcy-Forchheimer nanofluid flow due to curved stretching sheet with partial slip. Int. Commun. Heat Mass Transf 2020, 111, 104445. 10.1016/j.icheatmasstransfer.2019.104445. [DOI] [Google Scholar]
- Raza R.; Mabood F.; Naz R. Entropy analysis of non-linear radiative flow of Carreau liquid over curved stretching sheet. Int. Commun. Heat Mass Transf 2020, 119, 104975. 10.1016/j.icheatmasstransfer.2020.104975. [DOI] [Google Scholar]
- Rasool G.; Zhang T.; Chamkha A. J.; Shafiq A.; Tlili I.; Shahzadi G. Entropy generation and consequences of binary chemical reaction on MHD Darcy-Forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy 2020, 22, 18. 10.3390/e22010018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayat T.; Shafiq A.; Alsaedi A. MHD axisymmetric flow of third grade fluid by a stretching cylinder. Alex. Eng. J. 2015, 54, 205–212. 10.1016/j.aej.2015.03.013. [DOI] [Google Scholar]
- Hayat T.; Shafiq A.; Alsaedi A.; Awais M. MHD axisymmetric flow of third grade fluid between stretching sheets with heat transfer. Comput. Fluids 2013, 86, 103–108. 10.1016/j.compfluid.2013.07.003. [DOI] [Google Scholar]
- Naseem F.; Shafiq A.; Zhao L.; Naseem A. MHD biconvective flow of Powell Eyring nanofluid over stretched surface. Aip Adv. 2017, 7, 065013. 10.1063/1.4983014. [DOI] [Google Scholar]
- Shafiq A.; ÇOlak A. B.; Sindhu T. N.; Muhammad T. Optimization of Darcy-Forchheimer squeezing flow in nonlinear stratified fluid under convective conditions with artificial neural network. Heat Transfer Res. 2022, 53, 67–89. 10.1615/HeatTransRes.2021041018. [DOI] [Google Scholar]
- Bejan A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. 10.1016/0360-5442(80)90091-2. [DOI] [Google Scholar]
- Bejan A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. 10.1063/1.362674. [DOI] [Google Scholar]
- Ahmad S.; Ullah H.; Hayat T.; Alhodaly M. S. Time-dependent power-law nanofluid with entropy generation. Phys. Scr. 2021, 96, 025208. 10.1088/1402-4896/abcc9d. [DOI] [Google Scholar]
- Khan A.; Shah Z.; Alzahrani E.; Islam S. Entropy generation and thermal analysis for rotary motion of hydromagnetic Casson nanofluid past a rotating cylinder with Joule heating effect. Int. Commun. Heat Mass Transf 2020, 119, 104979. 10.1016/j.icheatmasstransfer.2020.104979. [DOI] [Google Scholar]
- Ullah H.; Hayat T.; Ahmad S.; Alhodaly M. S. Entropy generation and heat transfer analysis in power-law fluid flow: Finite difference method. Int. Commun. Heat Mass Transf 2021, 122, 105111. 10.1016/j.icheatmasstransfer.2021.105111. [DOI] [Google Scholar]
- Shashikumar N. S.; Madhu M.; Sindhu S.; Gireesha B. J.; Kishan N. Thermal analysis of MHD Williamson fluid flow through a microchannel. Int. Commun. Heat Mass Transf 2021, 127, 105582. 10.1016/j.icheatmasstransfer.2021.105582. [DOI] [Google Scholar]
- Bataller R. C. Viscoelastic fluid flow and heat transfer over a stretching sheet under the effects of a non-uniform heat source, viscous dissipation and thermal radiation. Int. Commun. Heat Mass Transf 2007, 50, 3152–3162. 10.1016/j.ijheatmasstransfer.2007.01.003. [DOI] [Google Scholar]
- Zaydan M.; Hamad N. H.; Wakif A.; Dawar A.; Sehaqui R. Generalized differential quadrature analysis of electro-magneto-hydrodynamic dissipative flows over a heated Riga plate in the presence of a space-dependent heat source: the case for strong suction effect. Heat Trans 2022, 51, 2063–2078. 10.1002/htj.22388. [DOI] [Google Scholar]
- Khan A.; Kumam W.; Khan I.; Saeed A.; Gul T.; Kumam P.; Ali I. Chemically reactive nanofluid flow past a thin moving needle with viscous dissipation, magnetic effects and hall current. PLoS One 2021, 16, e0249264. 10.1371/journal.pone.0249264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatti M. M.; Bég O. A.; Ellahi R.; Abbas T. Natural convection non-Newtonian EMHD dissipative flow through a microchannel containing a non-Darcy porous medium: Homotopy perturbation method study. Qual. Theory Dyn. Syst 2022, 21, 1–27. [Google Scholar]
- Shafiq A.; Rashidi M. M.; Hammouch Z.; Khan I. Analytical investigation of stagnation point flow of Williamson liquid with melting phenomenon. Phys. Scr. 2019, 94, 035204. 10.1088/1402-4896/aaf548. [DOI] [Google Scholar]
- Khan A.; Saeed A.; Tassaddiq A.; Gul T.; Mukhtar S.; Kumam P.; Ali I.; Kumam W. Bio-convective micropolar nanofluid flow over thin moving needle subject to Arrhenius activation energy, viscous dissipation and binary chemical reaction. Case Stud. Therm. Eng., 2021, 25, 100989. 10.1016/j.csite.2021.100989. [DOI] [Google Scholar]
- Gul F.; Maqbool K.; Mann A. B. Thermal analysis of electroosmotic flow in a vertical ciliated tube with viscous dissipation and heat source effects. J. Therm. Anal. Calorim. 2021, 143, 2111–2123. 10.1007/s10973-020-09702-y. [DOI] [Google Scholar]
- Abbas S. Z.; Khan W. A.; Sun H.; Ali M.; Irfan M.; Shahzed M.; Sultan F. Mathematical modeling and analysis of Cross nanofluid flow subjected to entropy generation. Appl. Nanosci. 2020, 10, 3149–3160. 10.1007/s13204-019-01039-9. [DOI] [Google Scholar]
- Hayat T.; Khan S. A.; Alsaedi A.; Fardoun H. M. Heat transportation in electro-magnetohydrodynamic flow of Darcy-Forchheimer viscous fluid with irreversibility analysis. Phys. Scr. 2020, 95, 105214. 10.1088/1402-4896/abb7aa. [DOI] [Google Scholar]
- Nazir U.; Sohail M.; Hafeez M. B.; Krawczuk M. Significant production of thermal energy in partially ionized hyperbolic tangent material based on ternary hybrid nanomaterials. Energies 2021, 14, 6911. 10.3390/en14216911. [DOI] [Google Scholar]
- Manjunatha S.; Puneeth V.; Gireesha B. J.; Chamkha A. Theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. J. Appl. Comput. Mech. 2022, 8, 1279–1286. [Google Scholar]
- Bejan A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transfer 1979, 101, 718–725. 10.1115/1.3451063. [DOI] [Google Scholar]
- Hayat T.; Khan S. A.; Alsaedi A.; Fardoun H. M. Heat transportation in electro-magnetohydrodynamic flow of Darcy-Forchheimer viscous fluid with irreversibility analysis. Phys. Scr. 2020, 95, 105214. 10.1088/1402-4896/abb7aa. [DOI] [Google Scholar]
- Liao S. J. Explicit totally analytic approximate solution for Blasius viscous flow problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. 10.1016/S0020-7462(98)00056-0. [DOI] [Google Scholar]
- Liao S. J. An optimal homotopy analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer Simul. 2010, 15, 2003–2016. 10.1016/j.cnsns.2009.09.002. [DOI] [Google Scholar]