Abstract
Intent recognition is a data-driven alternative to expert-crafted rules for triggering transitions between pre-programmed activity modes of a powered leg prosthesis. Movement-related signals from prosthesis sensors detected prior to movement completion are used to predict the upcoming activity. Usually, training data comprised of labeled examples of each activity are necessary; however, the process of collecting a sufficiently large and rich training dataset from an amputee population is tedious. In addition, covariate shift can have detrimental effects on a controller’s prediction accuracy if the classifier’s learned representation of movement intention is not robust enough. Our objective was to develop and evaluate techniques to learn robust representations of movement intention using data augmentation and deep neural networks. In an offline analysis of data collected from four amputee subjects across three days each, we demonstrate that our approach produced realistic synthetic sensor data that helped reduce error rates when training and testing on different days and different users. Our novel approach introduces an effective and generalizable strategy for augmenting wearable robotics sensor data, challenging a pre-existing notion that rehabilitation robotics can only derive limited benefit from state-of-the-art deep learning techniques typically requiring more vast amounts of data.
Index Terms—: data augmentation, deep learning, intent recognition, prosthesis control, signal processing
I. Introduction
Advances in wearable sensing have enabled access to a vast collection of kinematic, kinetic, and muscle activity patterns during locomotion from both healthy and gait-impaired individuals. These patterns, when aggregated across individuals and experimental conditions, have been useful for not only assessing walking behavior but also developing human-machine interfaces for controlling wearable assistive devices such as powered leg prostheses. In powered lower-limb prosthetics, movement-related signals detected before movement completion can be used to train a pattern classification algorithm. The algorithm predicts the upcoming activity to modulate assistance from the device on a step-by-step basis (e.g. at heel contact and toe off) with a technique called intent recognition [1], [2].
Intent recognition is a machine learning-based alternative to using threshold-based rules to trigger transitions between pre-programmed prosthesis activity modes such as level-ground and ascending/descending stairs and ramps. Intent recognition has already enabled amputees to safely, seamlessly, and intuitively transition between these modes [3] but labeled examples of these activities are required to train this type of controller. Collecting training data from a gait-impaired population is tedious and challenges the long-term clinical viability of intent recognition. During a typical training session, a subject walks on the device for up to 3–4 hours under supervision by clinical and research teams who ensure subject safety and comfort [4], [5].
User safety may be compromised by some prediction errors that cause substantial gait perturbations so minimizing the number of misclassified steps is an ongoing area of improvement for intent recognition [6]–[8]. Therefore, improving the long-term stability and generalizability of intent recognition-based classifiers without increasing the training burden represents a major improvement towards clinical viability. Ideally, experienced users should be able to walk with the prosthesis while performing activities of daily living over long durations after the initial training data collection. Novice users should also able to walk with the prosthesis using a classifier pre-trained on other users (after which classifier adaptation could provide additional personalization) [9].
Misclassifications occur when the trained classifier does not generalize well to new patterns at prediction time. Poor generalization (i.e. covariate shift) between days or users can be attributed to factors such as differences in device configuration (e.g. prosthetic alignment, socket comfort), task conditions (e.g. speed, step length), user characteristics (e.g. residual limb length, muscle strength), or the environment (e.g. stair height, level of distraction). Although these factors cannot be perfectly anticipated, solutions designed to mitigate their adverse effects could greatly improve intent recognition functionality by reducing error rates over long durations and for novice users.
Existing approaches to improve generalizability have mostly relied on online adaptation or experimental dataset expansion. In online adaptation, the system estimates the activity mode of the previous gait cycle to automatically label incoming data. Adaptation, though promising, is a gradual process that still requires an adequately performing initial classifier [10]. Intuitively, the classifier could also be improved by experimentally collecting more training data to provide better coverage of the input space. Using prior knowledge in how the predicted movements could be performed, the experimental protocol can be designed to target plausible sources of variability to improve classifier generalizability [11], [12].
The experimental protocol is commonly completed as semi-continuous circuits designed to maximize the number of transitions collected [10]. However, examples of transitional steps (e.g. level-ground to stairs) are still sparse compared to steady-state steps (e.g. level-ground walking) as a natural consequence of a circuit-based protocol. In addition to circuits completed in the laboratory, collecting additional data in more ecological settings (e.g. with spontaneous transitions, distractions) and with natural gait variability (e.g. in cadence, angle of approach) can encourage learning invariance to factors unrelated to the activity label [12]. Although these strategies may provide some benefit, there are practical limitations to just collecting more experimental training data.
Even with experimental dataset expansion, classifiers are effectively only trained on a sparsely sampled subset (relative to the set of all probable prosthesis configurations for a given activity) of the sensor data, which lie in a high-dimensional space. Therefore, we questioned whether we could learn the underlying generative model (i.e. true data distribution) of the multivariate time-series sensor data recorded from a powered leg prosthesis for several different walking activities. If successful, we could use the model to generate an arbitrary number of synthetic examples of sensor data which are similar to, but not mere copies of, the experimental training data. Ideally, synthetic examples would reflect plausible sources of variability and could supplement the limited experimental data.
Synthesizing images, sound, and text using deep generative models has been very successful [13]–[15]. However, deep generative modeling is not commonly applied to multivariate time-series data from sensors used in wearable robotics. Therefore, we developed and validated techniques for training deep generative models of multivariate sensor data using only tens or hundreds of experimentally-collected training examples by first applying data augmentation techniques including shifting, scaling, and additive random noise. We applied our approach to improve the generalizability of an existing intent recognition paradigm across days and across users [5]. Using the generative model yielded more robust representations of movement intention which effectively replaced an additional session of experimental training data collection.
To our knowledge, this study represents the first attempt to apply generative modeling to improve control of a wearable assistive device. The main contributions of our work include a flexible pipeline for training a deep generative model which synthesizes realistic sensor data and an initial demonstration of its effectiveness in mitigating some adverse effects of covariate shift. First, we describe the experimental protocol and training dataset and explain the intent recognition paradigm. Second, we detail the data processing steps for training a generative model of prosthesis sensor data. Lastly, we present offline classification results to highlight the ways in which combining data augmentation with a deep generative model can improve the generalizability and functionality of a state-of-the-art intent recognition paradigm without increasing the training burden.
II. Methods
A. Experimental protocol
Four individuals with a unilateral transfemoral amputation (Table 1) were recruited and gave written informed consent to participate in the study, which was approved by the Northwestern Institutional Review Board. Subjects were fitted with a powered knee-ankle prosthesis designed by Vanderbilt University [16] and had prior experience (at least 10 hours) with the device. The device is controlled using a finite-state based impedance control system, described in detail in [4]. Briefly, it uses an impedance-based model to specify reference joint torques throughout the gait cycle and vary the mechanical response of the prosthesis for stance and swing phases across different activity modes including level-ground walking, ramp ascent/descent, stair ascent/descent, and standing.
TABLE I:
Subject Characteristics
| TF1 | TF2 | TF3 | TF4 | |
|---|---|---|---|---|
| Sex | Male | Male | Female | Female |
| Age | 61 years | 69 years | 51 years | 32 years |
| Time post-amputation | 48 years | 42 years | 29 years | 18 years |
| Height | 180 cm | 175 cm | 165 cm | 172 cm |
| Weight | 84 kg | 86 kg | 66 kg | 70 kg |
| Etiology | Trauma (Left) | Trauma (Right) | Trauma (Right) | Cancer (Right) |
| Prescribed knee | Ossur Mauch | Ottobock C-Leg | Ossur Rheo XC | Ottobock C-Leg |
| Day 1-Day 2 | 3 weeks | 10 weeks | 2 weeks | 16 weeks |
| Day 1-Day 3 | 18 weeks | 20 weeks | 7 weeks | 21 weeks |
The prosthesis is pre-programmed to function in these six activity modes and uses a variety of device-embedded sensors (Table 2, in units after applying scaling factors) to record movement-related signals. These sensor signals are used to both trigger transitions between states and predict the upcoming activity using intent recognition. Each mode except for standing was subdivided into four states (early-to mid-stance, late-stance, swing flexion, swing extension); standing was subdivided into two states (load on, load off). Mode transitions occurred 90 ms after one of four gait event-related state transitions: heel contact, mid-stance, toe-off, or mid-swing. Previous work has shown that triggering changes only at these points in the gait cycle enables seamless and natural transitions between prosthesis modes [5], [10].
TABLE II:
Prosthesis Sensor Channels
| 1. Knee angle (deg) | 10. Shank Gx (deg/s) |
| 2. Knee velocity (deg/s) | 11. Shank Gy (deg/s) |
| 3. Knee motor current (Nm) | 12. Shank Gz (deg/s) |
| 4. Ankle angle (deg) | 13. Shank inclination angle (deg) |
| 5. Ankle velocity (deg/s) | 14. Thigh inclination angle (deg) |
| 6. Ankle motor current (Nm) | 15. Knee reference torque (Nm) |
| 7. Shank Ax (g) | 16. Ankle reference torque (Nm) |
| 8. Shank Ay (g) | 17. Axial load (normalized by body weight) |
| 9. Shank Az (g) |
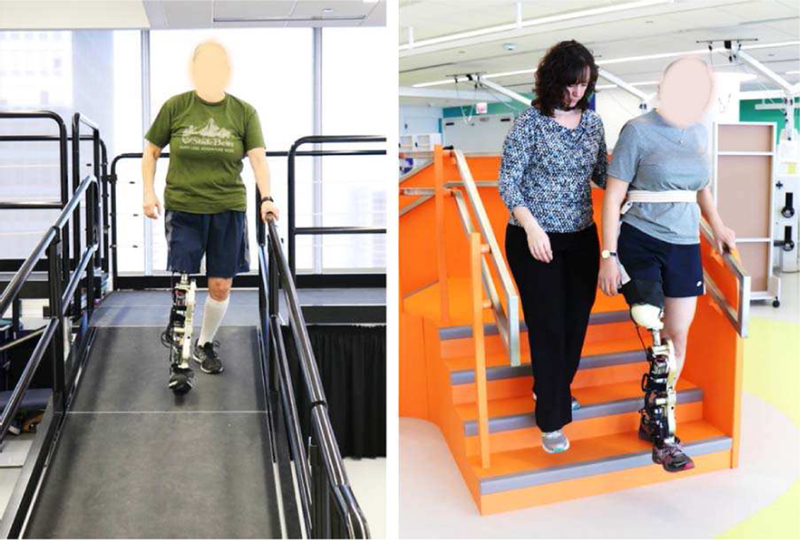
We used a mode-specific classification scheme [5] to predict whether the prosthesis should remain in the same mode or switch to a different mode. Eight mode-specific classifiers were selectively activated depending on the current mode and triggered gait event. For example, the heel contact level-ground walking classifier (HCLW) was active when heel contact was triggered in level-ground walking mode and predicted whether the prosthesis should remain in level-ground walking mode or transition to ramp descent or to stair descent mode for the upcoming stance phase. Training data were collected from subjects on three separate days separated by at least 7 weeks depending on subject availability (Figure 1, Table 1).
Fig. 1. Training data collection.
(Left) Collecting ramp descent training data from a subject in the ambulation laboratory with a circuit-based protocol. (Right) Collecting stair descent training data from another subject in a therapy gym which more closely resembles community ambulation.
On each day, subjects were instructed to perform several locomotor activities including level-ground walking, ascending/descending stairs and a 10° ramp, and transitions between these activities in the form of a circuit in an ambulation laboratory. A single circuit trial consisted of traversing the following ordered series of terrain in both directions (level-ground to stair ascent to level-ground to ramp descent to level-ground, and level-ground to ramp ascent to level-ground to stair descent to level-ground). Circuit A and circuit B distinguished trials using 6-step and 5-step staircases, respectively.
1). Day 1 protocol:
Ten trials each of circuit A and circuit B, 10 trials of level-ground walking (speed and heading varied trial-by-trial), 10 trials each of ascending/descending a 2-step staircase from standing, and 5 trials each of ascending/descending a 4-step staircase (different step height) from standing.
2). Day 2 protocol:
Seven trials each of circuit A and circuit B, 10 trials of level-ground walking (speed, direction, step length, and step width varied trial-by-trial), 10 trials each of ascending/descending a 2-step staircase (different step height from Day 1) from standing, and 5 trials each of ascending/descending the 4-step staircase from Day 1 with trial-by-trial variation in upper extremity support (i.e. one hand, both hands, no hands).
3). Day 3 protocol:
Two trials each of circuit A and circuit B and the following in a therapy gym in the rehabilitation hospital: 10 trials of level-ground walking (speed, heading, step length, step width, stops, starts, sudden turns varied trial-by-trial), 5 trials each of ascending/descending a 10° ramp and a 14° ramp (cadence, upper extremity support, step length, approach varied trial-by-trial), 10 trials each of ascending/descending a 4-step staircase (different step height from Days 1 and 2), a trial of ascending/descending 4 flights of stairs with varied number of steps, and 5 trials each of ascending/descending a 2-step staircase with trial-by-trial variation in upper extremity support.
Task variability was intentionally embedded in the training data by instructing subjects to vary speed, cadence, step length, step width, upper extremity support on stairs, and angle of approach. Environmental variability was embedded by using staircases with different step heights and varied number of even- or odd-numbered steps, and ramps with different grade. Data were also collected from more ecological settings where spontaneous and minimally constrained maneuvers were more highly encouraged compared to circuits in the laboratory. Characteristics of the training data are summarized in Table 3. We excluded the traditional toe off (TO), standing toe off (STO), and standing heel contact (SHC) classifiers because they usually have more training examples and achieve lower error rates than the other classifiers [5], [10]. The ramp ascent class was merged with level-ground walking in the HCLW classifier because previous studies have shown that sharing impedance parameters between these modes has negligible effect on prosthesis function but improves classification accuracy [17].
TABLE III:
Number of Experimental Examples (Mean ± S.D.) in Training Data for Mode-Specific Classifiers
| Train, Individual (Day 1) | Train, Pooled (Day 1) | Train, Individual (Day 1, Day 2) | Train, Pooled (Day 1, Day 2) | Test, Individual (Day 3) | |||
|---|---|---|---|---|---|---|---|
|
1. Heel contact level-ground walking (HCLW) Active in level-ground walking (LW) mode |
From LW to | LW | 592 ± 154 | 1775 ± 154 | 1327 ± 205 | 3980 ± 205 | 664 ± 112 |
| RD | 19 ± 1 | 56 ± 1 | 41 ± 2 | 122 ± 2 | 25 ± 1 | ||
| SD | 46 ± 8 | 137 ±8 | 80 ± 6 | 239 ± 6 | 36 ±1 | ||
|
2. Heel contact ramp descent (HCRD) Active in ramp descent (RD) mode |
From RD to | RD | 65 ± 14 | 195 ± 14 | 139 ± 27 | 417 ± 27 | 54 ± 11 |
| LW | 19 ± 1 | 56 ± 1 | 41 ± 3 | 122 ± 3 | 25 ± 2 | ||
|
3. Heel contact stair descent (HCSD) Active in stair descent (SD) mode |
From SD to | SD | 50 ± 3 | 149 ± 3 | 94 ± 3 | 281 ± 3 | 44 ± 2 |
| LW | 34 ± 8 | 101 ± 8 | 56 ± 7 | 168 ± 7 | 29 ± 4 | ||
|
4. Mid-stance (MST) Active in stair descent (SD) mode |
From SD to | SD | 83 ± 6 | 248 ± 6 | 149 ± 7 | 446 ± 7 | 72 ± 4 |
| LW | 12 ± 1 | 35 ± 1 | 24 ± 1 | 72 ± 1 | 7 ± 3 | ||
|
5. Mid-swing (MSW) Active in stair ascent (SA) mode |
From SA to | SA | 76 ± 14 | 227 ± 14 | 146 ± 21 | 437 ± 21 | 72 ± 4 |
| LW | 10 ± 1 | 29 ± 1 | 22 ± 2 | 67 ± 2 | 8 ± 3 |
B. Problem formulation
In this study, we formulated the problem of improving model generalizability from the perspective of learning a generative model of the prosthesis sensor signals. Learning the true high-dimensional data distribution is intractable so we use deep neural networks to learn a model approximating the true data distribution. Our working assumption is that the sensor data for each mode-specific classifier lie on or near a lower-dimensional “motion manifold” [18] which represents a subspace of plausible movement sequences preceding a user-initiated step while performing a certain locomotor activity. In other words, we assume that the relationship between movement intention and this motion manifold is preserved despite noise and variability in the measured sensor data.
We hypothesized that a deep generative model would learn robust representations of movement intention which are more invariant to sources of task, environmental, and subject -related variability and provide better generalization in the presence of covariate shift. If successful, our model should generate realistic synthetic sensor data that improve intent recognition classification accuracy. Guided by our working assumption, we build off previous work describing autoencoders [19] to learn a concise representation of our sensor data by jointly learning an encoder and decoder. The encoder maps data samples to a lower-dimensional latent space whereas the decoder maps the encoding from the latent space back to the original data space.
Some desirable properties of latent space models include expressivity (i.e. real examples can be reconstructed), realism (i.e. any point in latent space represents a plausible example, even ones not found in the training data), and smoothness (i.e. closeness in latent space implies similarity in input space). The autoencoder (i.e. encoder-decoder), a type of latent space model, is trained to reconstruct its input. Because large covariate shifts in the sensor data at prediction time cannot always be reasonably anticipated based off the training data or synthetic data, we also sought a method for aligning the motion manifolds between the training and testing data. To accomplish these goals, we combined several key training and architectural choices into our autoencoder model, including:
1). Denoising:
To make the decoding task more difficult, the input sensor data can be corrupted before being fed to the encoder and the decoder is trained to recover the uncorrupted sensor data. Additive white Gaussian noise is commonly used and forces the autoencoder to learn more robust representations which are preserved in the presence of task-invariant noise [20].
2). Regularization:
To encourage more concise representations of the input data, the latent space can be constrained to match a prior distribution (e.g. multivariate normal distribution). Methods for shaping the distribution of the latent space to match an arbitrary prior generally include variational and adversarial approaches. Variational approaches minimize the Kullback-Leibler divergence between the latent space and prior distributions, Alternatively, adversarial approaches formulate a minimax problem using a discriminator model which is trained to correctly distinguish latent space samples from the encoded latent space and the prior. In opposition, the encoder is updated such that the discriminator cannot correctly distinguish its encodings from the prior. Previous studies primarily in the domain of image generation have shown that adversarial approaches may lead to more expressive encoder models than variational approaches [21].
3). Semi-supervision:
To enable the model to align the motion manifolds without the true class label (as is the case at test time), the encoder should also predict its own class label (i.e. pseudo-label [22]) from the input sensor data. The predicted label can be combined with the latent representation before being fed to the decoder [21]. The latent space encoding and pseudo-label can be regarded as the “style” and “content,” respectively, of the input. Conditioning the decoder on the pseudo-label encourages the encoder to pay attention to class-discriminative information in the input sensor data, allows conditional generation of synthetic data using the trained generative model, and acts as a mild form of regularization by giving the network an auxiliary task [23].
C. Training data
Data from the 17 prosthesis sensor channels were recorded at 1 kHz and segmented into 300 ms windows beginning 210 ms before the gait event and ending 90 ms after the gait event. Windows were downsampled by a factor of 5 for computational efficiency yielding input tensors of shape (60, 17). The signs of shank accelerometer and gyroscope channels were flipped appropriately to account for side of amputation. Data augmentation can combat overfitting by injecting prior knowledge about the class-invariant sources of variability in the data to provide better coverage of the input space, especially when the training data are sparse in a high-dimensional space.
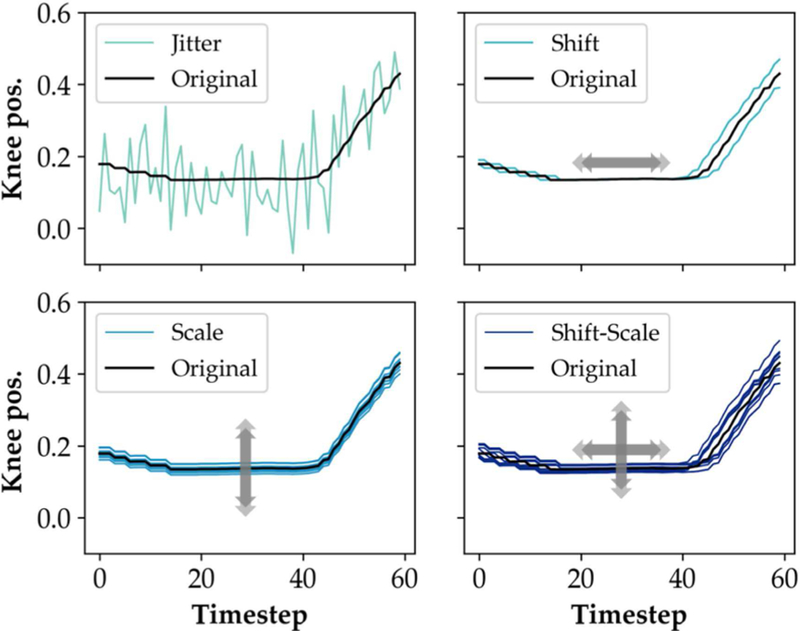
Applying label-preserving transformations such as scaling, shifting, rotation, and jitter (i.e. additive random noise) can improve the generalizability of deep neural networks for image classification [24]. In the domain of human activity recognition using wearable sensors, applying analogous transformations for data augmentation not only preserved class labels but also improved binary classification accuracy for detecting Parkinson’s disease symptoms using a single wearable accelerometer [25]. Similarly, we applied global (i.e. across all channels for all time steps) transformations consisting of 2 additional shifted copies (±10 ms relative to the original window), 8 additional scaled copies (the original window was multiplied by a scaling factor sampled from a uniform distribution between 0.95 and 1.05 on a per channel basis), and 10 shifted-scaled copies (5 scaled copies for each of the shifted copies) (Figure 2) for combined 20-fold data augmentation.
Fig. 2. Global data augmentation using transformations based on prior knowledge.
(Top left) Jitter by additive zero-centered Gaussian noise (σ = 0.1) for training the denoising autoencoder. (Top right) Two shifted copies at ± 10 ms relative to the original window account for variation in event detection timing. (Bottom left) Eight scaled copies multiplied by a uniformly sampled scaling factor account for baseline shift. (Bottom right) Ten combined shifted-scaled copies.
We used these shifting and scaling transformations to encourage the model to learn latent representations which were more robust to slight differences in timing of event detection and signal magnitude, respectively. The time shift was bounded by the range of ±10 ms because 10 ms represented the smallest allowable window increment for our embedded controller. The typical deviation in the signal magnitude (averaged across all channels) during trials where the subject performed standing only was about 10 percent. Therefore, we bounded the scaling factor by the range of 1 ± 0.05 to be more conservative about preserving the activity label. The ground truth label for each window recorded by the key fob was converted to a one-hot encoded vector (e.g. [1, 0, 0] for class 1) to make the categorical data accessible to a neural network.
After temporal down-sampling and data augmentation, the sensor data were normalized to the range [−1,1] to accelerate training and reduce the likelihood of the neural network converging unfavorably on local minima. To mitigate the effects of atypical channels in otherwise typical examples in the training data, we used quantile normalization. We calculated the median, absolute minimum, and absolute maximum values from each window on a per channel basis. Next, the 2nd, 50th, and 98th percentiles of the median, absolute minimum, and absolute maximum values were calculated based on the training data only. Windows in the training and testing data were normalized on a per channel basis by subtracting the 50th percentile and dividing by the range between the 2nd and 98th percentiles. Extreme values were clipped above and below the 98th and 2nd percentiles, respectively.
To mitigate the effects of class imbalance, we performed random resampling with replacement of the minority classes such that the number of instances of each minority class was at least half the number of instances of the majority class. Classes were not fully rebalanced in order to preserve the notion of a majority class, which we suspected would help in training a robust and discriminative classifier. Prior to training, each mode-specific classifier was required to have at least 10,000 total instances while preserving the rebalanced class proportions; otherwise, additional copies were created by applying additive zero-centered Gaussian noise (σ = 0.1) after augmenting and resampling the experimental data.
D. Implementation
1). Model architecture:
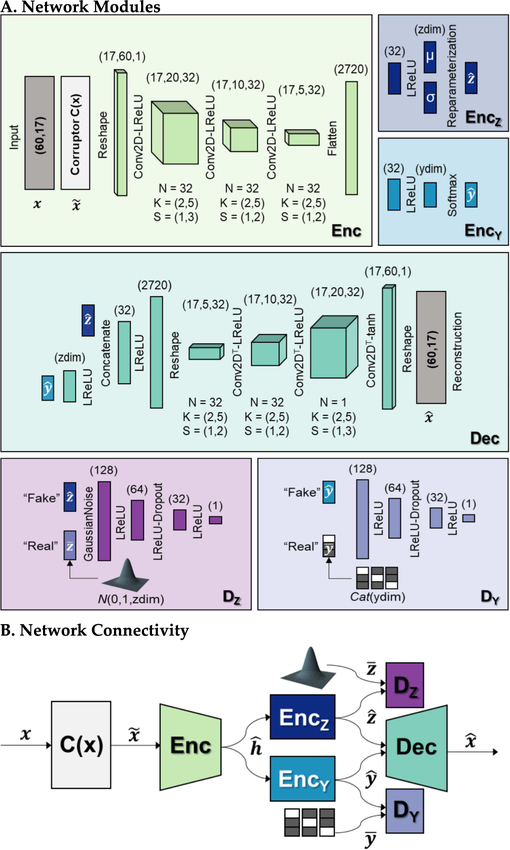
The overall architecture is depicted in Figure 3. Autoencoders consist of two learnable models, an encoder and a decoder, which we implement with deep convolutional neural networks. In a semi-supervised setting, the encoder also performs the auxiliary task of classification. Therefore, we subdivide the encoder into three modules: Enc, EncZ, and EncY.
Fig. 3. Proposed deep generative model, a semi-supervised denoising adversarial autoencoder.
(A) Individual modules with output dimensions listed in parentheses above each layer. N is the number of convolution kernels, K is the kernel size, S is the stride length, LReLU represents the leaky ReLU activation, and tanh represents the hyperbolic tangent activation. The latent space dimensionality (zdim) was set to 10. “Real” samples for the latent space and label discriminators were sampled from a multivariate standard normal distribution and a categorical distribution (Cat), respectively. (B) Overall schematic of network connectivity.
Base encoder (Enc):
The base encoder consists of an input layer for the multivariate time series (x), a corruptor layer (C) which applies additive zero-centered Gaussian noise (σ = 0.1), a sequence of three strided convolution layers, and a flattening layer to convert the output of the convolution layers into a fixed length 2720-dimensional hidden feature vector . We used two-dimensional kernels in order to combine movement-related information across sensor channels, and temporal downsampling (by a combined factor of 12) to encourage learning condensed, time-invariant latent representations. Enc had 20,896 total parameters.
Latent encoder (EncZ):
The latent encoder maps the hidden feature vector to a latent code in a 10-dimensional subspace. First, there is a linear layer with 32 units and L1 weight regularization (λ = 10−8) to encourage compression of the learned representation. Next, we apply the “reparameterization trick” used in traditional variational autoencoders [26] to backpropagate gradients through a Gaussian sampling layer. We sample ϵ ~ N(0, I) where I is the 10-dimensional identity matrix and then compute . μ and σ are linear layers with 10 units each representing the reparameterized mean and standard deviation of the stochastic latent code, respectively. For numerical stability, we actually learn the log variance of the latent code and compute σ by exponentiating. The mean and log variance layers have L2 activity regularization (λ = 10−8) to bias the latent code towards the standard multivariate normal distribution. EncZ had 87,732 total parameters.
Classifier (EncY ):
The classifier maps the hidden feature vector to a class prediction (y). EncY has a linear layer with 32 units and L1 weight regularization (λ = 10−8) to encourage compression of the learned representation. We use the softmax activation function to convert the predictions into class probabilities. EncY had 87,138 or 87,171 total parameters for two or three predicted classes, respectively.
The decoder (Dec) uses the latent code conditioned on the class probabilities for its reconstruction . In order to equalize the contribution of the latent representation and class information , we added a linear layer with 10 units before concatenation. Next, there was a linear layer with 32 units followed by a sequence of three strided transposed convolution layers which undo the convolution operations of the encoder in order to generate samples with the same dimensionality as the input. The last convolution layer has a hyperbolic tangent activation to constrain outputs to the range [−1, 1]. To maximize the capacity of the decoder, we did not include weight or activity regularization in any layers. To generate synthetic samples, we provide Dec with an arbitrary number of latent code samples from the prior distribution and corresponding class labels. Dec had 111,327 and 111,337 total parameters for two or three predicted classes, respectively.
Adversarial regularization was implemented with two discriminators: DZ and DY.
Latent space discriminator (DZ):
The latent space discriminator learns to differentiate between latent codes from the latent encoder and samples from the prior distribution . The input layer is followed by a layer which applies additive zero-centered Gaussian noise (σ = 0.1) as a form of instance noise [27] to prevent overfitting. DZ consists of a sequence of three linear layers (128, 64, and 32 units) and L2 weight regularization (λ = 10−8) to prevent overfitting. The output layer has 1 unit without an activation function. There is a dropout layer [28] with dropout rate of 0.2 following the 64-unit hidden layer. When trained to convergence, DZ assigns equal likelihood to latent codes from the encoder and from the prior distribution (i.e. the distribution of should approximate a multivariate standard normal distribution). DZ had 11,777 total parameters.
Label discriminator (DY):
The label discriminator learns to differentiate between classifier predictions and samples from a categorical distribution . This model has similar architecture to the latent space discriminator. When trained to convergence, DY assigns equal likelihood to predictions by the encoder and a categorical distribution (i.e. the classifier should make high confidence predictions in a single class). DY had 10,753 or 10,881 total parameters for two or three predicted classes, respectively.
2). Hyperparameters:
All networks were trained using the stochastic gradient descent solver Adam [29] (α = 0.0001, β1 = 0.5) with a mini-batch size of 128. We used leaky ReLU activations [30] (α = 0.2) as our default activation function in all cases (except the last convolution layer in Dec) because it can accelerate the convergence of stochastic gradient descent. The weights of all dense and convolution layers except the last convolution layer in Dec were initialized with He uniform variance scaling [31] because they preceded a leaky ReLU activation. The weights of the last convolution layer in Dec were initialized using Xavier uniform distribution [32] because they preceded a hyperbolic tangent activation. To provide smooth, non-saturating gradients for the discriminators, we used the least-squares generative adversarial network (LSGAN) loss function [33] formulation.
3). Training:
We used stratified sampling to form mini-batches of training data where the class proportions matched the overall class distribution after resampling. Next, training progressed iteratively in three phases:
Reconstruction:
Enc, EncZ, EncY and Dec were trained to minimize the reconstruction loss [equation (1)].
| (1) |
Regularization:
DZ and DY were trained to discriminate between samples from the prior and categorical distributions (“real) and samples from the encoder (“fake”). To encourage diversity in the generated samples, we also used one-sided label smoothing [34] to prevent the discriminators from being overconfident in their predictions of whether samples were “real” or “fake.” Target values for “real” samples were smoothed to a uniform distribution between 0.9 and 1.1 and target values for “fake” samples were smoothed to a uniform distribution between −0.1 and 0.1. DZ and DY were trained to minimize the LSGAN loss according to equations (2) and (3). Next, DZ and DY were made untrainable and the encoder modules were trained to fool the discriminator (i.e. the target values for “fake” samples from the encoder were flipped and set to 1). Enc, EncZ, and EncY were then trained to minimize the adversarial LSGAN loss according to equation (4).
| (2) |
| (3) |
| (4) |
| (5) |
Semi-supervised classification:
Enc and EncY were trained to predict the class by passing in the multivariate time series input (x) and its corresponding ground truth one-hot encodings (y) to minimize categorical cross entropy loss [equation (5)].
The loss weights (λrecon, λadv, and λclass) reflect the relative importance of the different functions of the denoising semi-supervised adversarial autoencoder and were determined by experimenting with different values. We found setting λrecon = 1, λadv = 0.01, and λclass = 0.01 enabled the model to strike a desirable compromise between high quality generated samples, accurate predictions, and a dense latent space approximating a standard multivariate Gaussian distribution. Experimentally, we found that losses began stabilizing after training for 10–20 epochs; therefore, we trained all models for 30 epochs to increase the likelihood of converging on a desirable solution for the generative model. Models were implemented in Keras using the Tensorflow backend on a laptop computer (Intel Core i7–7700, 2.80 GHz, 16 GB RAM) with GPU (4GB Nvidia GeForce GTX 1050) running Windows. Mode-specific generative models could be trained on the order of minutes to hours depending on the number of empirical training examples.
E. Evaluation
Our primary goal was to identify methods that could improve the long-term stability and generalizability of intent recognition-based classifiers while minimizing the training burden. We calculated offline classification error rates in the presence of covariate shift in the sensor signals across days and across users. Our secondary goal was to determine whether more advanced techniques using deep generative models were practical to implement and provided benefits that would out-weigh the cost of added computational complexity.
Data from the Day 3 protocol, which most closely resembled community ambulation, were used to test the control system. Error rates were calculated by dividing the number of incorrect decisions by the total number of decisions. We performed analyses for both individual (i.e. the training data came from the same user for the testing data) and pooled (i.e. the training data did not include any data from the user for the testing data) user configurations. Requiring only one visit to the ambulation laboratory to collect training data is preferable from a practical standpoint so we used data from our Day 1 protocol (“one-day baseline”) as a benchmark. To determine the expected lower bound on the error rate when testing on Day 3, we performed leave-one-out (LOO) cross-validation on the Day 3 data. In other words, we iterated through each example from Day 3, training a classifier using all the data except for one example and predicting the label of the excluded example.
For comparison, we evaluated error rates for several strategies designed to improve robustness to covariate shift:
Additional experimental training data (“two-day baseline”)
Training data collected on Day 2 were combined with Day 1.
Global augmentation (generative model not required)
Twenty-fold global augmentation (2 shifted, 8 scaled, and 10 shifted-scaled copies) was applied to the one-day and two-day baselines (data quantity equivalent to 21 and 42 training sessions after augmentation, respectively).
Specific augmentation by reconstruction and by sampling
After applying global augmentation to the one-day baseline, we constructed three additional sets of training data by applying specific augmentation by reconstruction (data quantity equivalent to 42 training sessions), by sampling (data quantity equivalent to 42 training sessions), and by both reconstruction and sampling (data quantity equivalent to 63 training sessions). To augment by reconstruction, we passed the globally augmented one-day baseline through the trained autoencoder . To augment by sampling, we passed latent codes sampled from a 10-dimensional standard normal distribution and corresponding desired class labels (with quantity and class proportions matching the globally augmented one-day baseline) through the decoder.
Manifold alignment using the latent space
We use the trained encoder to align training and testing data in the latent space, which we expected to represent movement intention robustly despite noise and variability in the measured sensor signals. Testing data is aligned by the trained autoencoder using its latent code and pseudo-label prediction . We suspected this strategy would be most beneficial when covariate shift fell outside the range found in the training data and could not be mitigated simply by bolstering the training data with augmented samples that resembled the experimental training data.
Classification using a deep convolutional neural network
For the above strategies, we used an a priori linear discriminant classifier with heuristic features (mean, standard deviation, maximum, minimum, initial value, final value) [5] extracted from the experimental, globally augmented, specifically augmented, or aligned event windows. We used principal components analysis to reduce the feature set to 50 dimensions when the number of original number of features (102) exceeded the number of training examples. As an alternative, we used Enc-EncY (referred to as convolutional neural network, CNN) directly on the input time series for classification.
Given the stochastic nature of training neural networks (e.g. weight initialization, sampling, dropout), we trained each mode-specific classification model five times for both user configurations (i.e. individual and pooled) for each subject. We report the lowest error rate achieved (from epoch 15 and afterwards) from the top three out of the five runs for each of the strategies above, representing a form of early stopping to avoid suboptimal solutions due to model overfitting. The overall error rate was computed by aggregating across the five mode-specific classifiers (HCLW, HCRD, HCSD, MST, and MSW from Table 3). Qualitatively, we inspected generated sensor signals for a variety of sensor types for both individual and pooled configurations across all subjects.
F. Analyses
Statistical analyses were performed using Minitab (Minitab, Inc., version 19.1.1) to compare the effect of different data augmentation strategies on overall error rate. To determine statistical significance, we used a linear mixed-effects model with error rate as the continuous response variable, subject as a random factor, strategy as a categorical fixed factor, and user configuration as a categorical fixed factor. Data were normalized using a Box-Cox log transformation. The interaction term between strategy and user configuration was not found to be significant (F2,12 = 0.43, p = 0.660); thus, the term was removed from the model.
Practically, we were primarily interested in evaluating how well generative model-based strategies trained on only one session (totaling about 3–4 hours) of experimental training data performed compared to the lowest achievable error rates when using one session or two sessions (totaling about 6–8 hours) of experimental training data without training a deep neural network. Therefore, we performed two-tailed multiple comparisons (p- value adjusted by Bonferroni correction for 3 pairwise comparisons) between global augmentation of the one-day baseline, global augmentation of the two-day baseline, and the best performing generative model-based strategy using only one experimental session (specific augmentation by reconstruction of the globally augmented one-day baseline).
III. RESULTS
We compared different strategies for mitigating the adverse effects of covariate shift across days and across users on a state-of-the-art intent recognition paradigm. We hypothesized that applying global augmentation techniques (i.e. shifting, scaling, additive Gaussian noise) to just one day of empirical training data would enable us to train a deep generative model which learns robust, low-dimensional representations of movement intention that improve model generalizability. First, we evaluated data augmentation strategies that did not require training a deep generative model. Second, we determined the extent to which our generative modeling approach was adaptable to synthesize realistic sensor data for different modalities, activities, and individuals. Lastly, we evaluated the potential benefit of methods relying on the trained generative model for both individual and pooled user configurations.
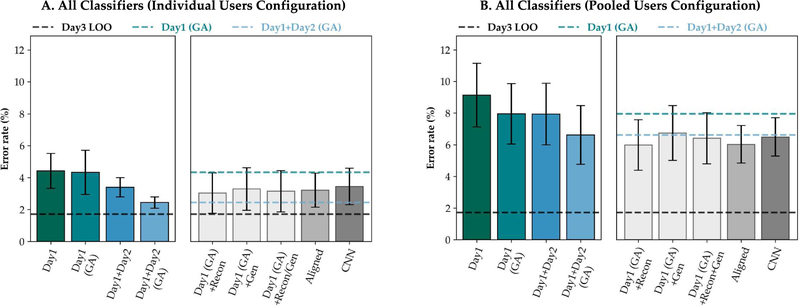
A. Additional experimental data and global augmentation improve generalizability without training a generative model
To quantify the performance of techniques that do not require training a generative model, we evaluated including a second day of experimental data and adding copies of the empirical data which have been shifted, scaled, and jittered. Adding a second day of empirical data to the baseline training dataset generally reduced error rates. Adding the second day reduced overall error rates (mean ± standard deviation) from 4.42 ± 2.19% to 3.40 ± 1.21% (24% reduction) and from 9.14 ± 4.02% to 7.94 ± 3.89% (13% reduction) for individual and pooled configurations, respectively (Figure 4A and Figure 4B, left). However, the mid-stance and mid-swing classifiers (not shown separately) did not benefit as much from the additional training session. Global augmentation of one-day and two-day baseline data generally reduced error rates further without drastically affecting its standard deviation for both user configurations. Also, the overall error rates for global augmentation of the one-day baseline (7.96 ± 3.82%) and including a second day of empirical data (7.94 ± 3.89%) were approximately equal for the pooled user configuration (Figure 4B, left). However, the difference between global augmentation of the one-day and two-day baseline data was not statistically significant (t(7) = −2.52, adjusted p-value = 0.066). Error rates for the pooled user configuration were significantly higher than the individual user configuration (t(11) = 7.63, adjusted p-value < 10−6).
Fig. 4. Overall offline error rates (mean ± standard error) for individual and pooled user configurations.
(A) Individual user configuration. (B) Pooled user configuration. Data from one or two experimental sessions were globally augmented (GA) (left panels). Globally augmented one-day basline data were combined with synthetic examples from specific augmentation by reconstruction (Recon) and/or by sampling (Gen) using the trained autoencoder (right panels). Other generative model-based strategies included manifold alignment (Aligned) and classification using the encoder (CNN). Dashed lines represent the globally augmented one-day and two-day baselines and the Day 3 leave-one-out (LOO) cross-validation benchmark.
B. Proposed generative model produces realistic multivariate sensor data without customization
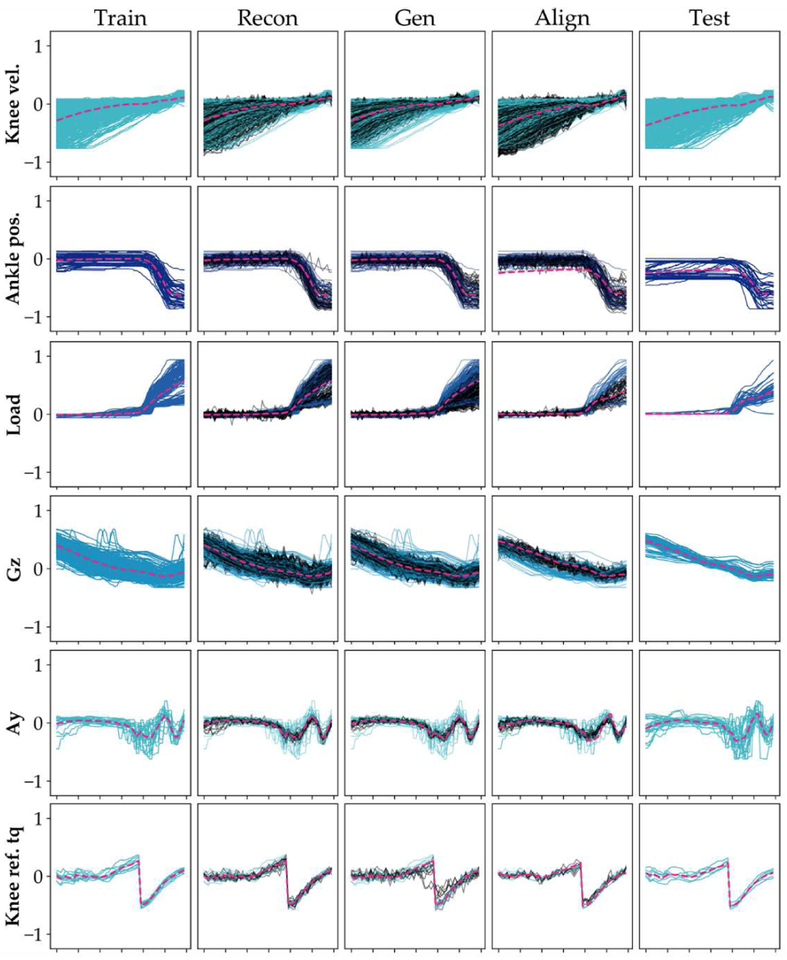
To determine the capacity of our generative model to synthesize high-quality sensor data for all channels, activities, and individuals without fundamentally modifying its architecture or hyperparameters, we examined the generated sensor data for each mode-specific classifier. After a few epochs of training, reconstructed samples began to be centered around the mean channel values as a result of the relatively high importance placed on the reconstruction loss; however, the generated data lacked diversity. As training progressed, the distribution of the latent space converged upon the multivariate standard normal distribution and synthetic samples became more diverse as a consequence. After training converged, the generative model could produce realistic synthetic sensor signals for both monotonic and non-monotonic channels with different signal-to-noise ratios and various waveform shapes (Figure 5).
Fig. 5. Representative signals (normalized) using different generative model-based strategies.
(Top to bottom) Knee velocity from TF3 (individual user) in level-ground mode for HCLW, ankle position from TF2 (individual user) in ramp descent mode for HCRD, load from TF1 (pooled users) in stair descent mode for HCSD, Gz for TF4 (pooled users) in stair ascent for MSW, Ay for TF2 (individual user) for level-ground mode for HCRD, knee reference torque for TF1 (individual user) for level-ground mode for MSW. In columns 1–4, colored traces represent samples from the corresponding training data. In column 5, colored traces represent the corresponding test data. Black traces in columns 2–4 represent artificial sensor data generated using specific augmentation by reconstruction (Recon), specific augmentation by sampling (Gen), or manifold alignment (Align). The dashed pink lines represent the mean of the training data for columns 1–3 and the mean of the testing data for columns 4–5.
As an example of the effectiveness of the manifold alignment strategy, the baseline shift in the ankle position and timing variability in the knee velocity at testing were mitigated (Figure 5, rows 1–2, column 4). Matching the latent space to a multivariate standard normal distribution also enabled the model to generate realistic samples for the load cell which were representative of test signals but not found in the empirical or globally augmented training data (Figure 5, row 3, column 3). Upon inspection, we found that the trained generative model could successfully synthesize realistic-looking sensor data for all mode-specific classifiers and for all sensor channels for all subjects without the need for additional tuning.
C. Generative model-based strategies functionally replace a second day of empirical training data
To compare generative model-based strategies, we computed error rates for specific augmentation by reconstruction and by sampling, manifold alignment, and classification with the encoder. Specific augmentation consistently reduced error rates for all classifiers compared to the globally augmented one-day baseline for both user configurations (Figure 4A and Figure 4B, right). However, specific augmentation by reconstruction was generally more effective than specific augmentation by sampling. Overall error rates for specific augmentation by reconstruction were reduced to 3.03 ± 2.54% (from 4.33 ± 2.76%, 30% reduction from globally augmented one-day baseline) and to 5.98 ± 3.19% (from 7.96 ± 3.82%, 25% reduction from globally augmented one-day baseline) for individual and pooled configurations, respectively. There was a statistically significant improvement when using specific augmentation by reconstruction (t(7) = −2.93, adjusted p-value = 0.028). In most cases, training datasets created using specific augmentation also resulted in lower error rates than the two-day baseline. However, variability in the error rates for specific augmentation was still higher than the two-day baseline for the individual configuration (Figure 4A, right). Manifold alignment and classification using the encoder achieved overall error rates similar to the other generative model-based strategies and were at or below the two-day baseline. However, these two strategies still had higher error rates than the globally augmented one-day baseline for the mid-stance and mid-swing classifiers in the individual user configuration (not shown separately). There was no statistically significant difference between overall error rates for global augmentation of the two-day baseline and the best performing generative model-based strategy (t(7) = −0.41, adjusted p-value = 1.00).
IV. Discussion
Our overall objective was to develop and evaluate novel strategies to mitigate the adverse effects of covariate shift across days and across users on intent recognition without increasing the training burden. Previous work had shown that bolstering the training data by collecting additional experimental data can improve generalizability [12] but the quantity and quality of data needed for improvement remained unclear. We hypothesized that training a deep generative model would enable learning more robust representations of movement intention and provide an alternative strategy for improving generalizability of a state-of-the-art intent recognition model. There had been few previous attempts to train deep neural networks using sensor data from wearable assistive devices for impaired populations. The limited amount of training data had been considered a major bottleneck to learning robust models which do not collapse to merely overfitting a small training dataset. Altogether, our findings suggest that applying techniques in deep learning to the control of wearable assistive device robotics is not only attainable but also advantageous.
We first amplified empirical prosthesis sensor data using prior knowledge by applying shifting, scaling, and additive random noise to embed invariance to slight differences in event detection timing, small shifts in the channel baselines, and random sensor noise, respectively. These label-preserving transformations provided small but consistent reductions in the error rates, suggesting that they are a beneficial offline pre-processing step even when applied globally. Our findings also suggest that collecting additional empirical data and applying global augmentation are complementary approaches that can improve model performance without necessarily training a deep neural network or generative model. Perhaps more importantly, we found that data augmentation was required to train our deep generative model because the number of trainable model parameters (in the hundreds of thousands) exceeded the number of empirical examples for some mode-specific models (in the tens and hundreds) by several orders of magnitude.
We developed methods for training a semi-supervised denoising adversarial autoencoder (a deep generative model) using relatively small empirical training datasets each collected from one visit lasting up to 3–4 hours. The generative model was highly expressive and synthesized realistic prosthesis sensor data for all channels, activities, and individuals using the same architecture and hyperparameters, suggesting that our novel approach has broad scope. In some cases, the mid-stance and mid-swing classifiers did not benefit as much from our data augmentation strategies. These two classifiers predicted the transition from stair descent or stair ascent to level-ground walking, respectively, for staircases with an odd number of steps and tended to have not only the most severe class imbalance but also the fewest examples of transitions. The poorer performance of these classifiers suggests there may be a critical lower bound on the number of experimental repetitions of a movement needed to train a robust model, especially because transitions are inherently more variable movements.
We found that generative model-based strategies including specific augmentation, manifold alignment, and classification with a neural network performed better than the one-day baseline, even with global augmentation. Overall error rates for the generative model-based strategies were generally as low or lower than adding a second day of empirical training data, effectively precluding the need for a second visit to the ambulation laboratory. In the laboratory, clinicians can instruct subjects to vary repetitions of a movement in order to embed meaningful task variability into the training data. However, this type of instruction can be mentally fatiguing for subjects. Our findings showed that generative-model based strategies may not only provide substantial and clinically meaningful reductions in the offline error rate but also potentially simplify the training protocol. By exploiting the generative model to implicitly identify plausible patterns of variability offline, we could generate rich and realistic synthetic sensor data that would be more challenging to collect experimentally.
In contrast to multilayer perceptron neural networks used for intent recognition [35], [36], we implemented classification using a convolutional neural network. Convolutional neural networks have become more prevalent for activity recognition based on wearable sensor data because they can learn robust representations of movement intention directly from the multivariate time series without feature engineering [37]. However, we found that when the deep generative model was first used to perform specific augmentation or manifold alignment offline, error rates using a simpler a priori linear discriminant classifier with heuristic features were not substantially different from the convolutional neural network classifier. We show that a state-of-the-art intent recognition model can be improved by simply performing offline data augmentation without fundamentally modifying the existing training or prediction pipeline or incurring additional online computational costs on an embedded system.
Limitations and future work
The findings of our study are limited by a few factors. First, there were only four amputee subjects, which led to large between-subject variability in the error rates in some cases. Therefore, due to our small sample size the results of our statistical analyses should be interpreted cautiously. However, we expect both error rates and their variability to decrease as the training data becomes richer with more training sessions and subjects. We did not consider training on or performing specific augmentation on the two-day baseline but expect error rates to decrease further because even global augmentation of the two-day baseline was generally beneficial. Nonetheless, generative model-based strategies consistently reduced error rates for the pooled subject configuration despite differences in height, weight, prescribed device, and walking style.
We also did not report online error rates, which would likely be higher than our reported offline error rates. However, previous online results have shown a strong correlation with offline error rates for lower limb powered prosthesis controllers [3]. Our findings are limited by only using the a priori linear discriminant classifier with heuristic features; however, our previous work using this feature-classifier combination has shown comparable performance with other methods including a support vector machine and a multilayer perceptron with single hidden layer [35]. Online evaluation with more individuals in more diverse ambulation environments including at-home and across longer durations will be necessary to determine the true benefit provided by our proposed approach.
The best approach to collecting training data for a powered leg intent recognition system remains unclear despite a precedence for using an in-lab protocol for which the majority of the training data are collected in the form of circuits [10]. The number of activities completed is generally limited by practicality because the protocol can be mentally and physically fatiguing. There were some differences between the Day 1, Day 2, and Day 3 protocols and the number of repetitions and types of task and environmental variability were chosen arbitrarily. However, further analyses beyond our comparison are necessary to determine the optimal quantity, type, and quality of empirical training data (e.g. disproportionate collection of transitions, shorter sessions spanning more days).
Although we developed a working pipeline to successfully train our chosen deep generative model, the design space consisting of pre-processing steps, architectural choices, and hyperparameters is still very large. We attempted to identify the most important design decisions but did not truly optimize them by performing a sensitivity analysis. We found class rebalancing critically affected overall model convergence because training the classifier updated the encoder parameters. However, the amount of global augmentation and the minimum total number of training samples were less critical and should be minimized to reduce pre-processing and training times. We also found that forcing the autoencoder to denoise led to more robust latent representations and reconstructions; however, the amount of corruption was not tuned. We found that prioritizing the reconstruction loss over the adversarial and classification losses was important for overall model performance but did not perform a sensitivity analysis on the non-reconstruction losses. We also did not optimize the dimensionality of the latent space but observed that using a low-dimensional space was sufficient for providing expressivity to the generative model. Less than 10-dimensional latent spaces performed poorly but much higher-dimensional latent spaces led to latent discriminator overfitting, which deteriorated overall model performance.
Generative adversarial networks are notoriously difficult to train because they pose a minimax problem which makes them more prone to non-convergence, mode collapse, and vanishing gradients when the discriminator overpowers the generator. Initially, we encountered similar challenges but incorporating several key regularization methods greatly improved the stability and performance of our model. We found that using the least-squares loss provided non-vanishing gradients (compared to the traditional generative adversarial network loss function [38]). Adding instance noise to the latent code samples for the latent discriminator and incorporating one-sided label smoothing effectively regularized the discriminator and prevented mode collapse. With time-series data, using networks which explicitly handle sequential information such as recurrent neural networks was a natural choice; however, we found that convolutional neural networks provided sufficient performance and required much less computation time.
In this study, we applied deep generative modeling to a specific intent recognition paradigm for controlling a powered leg prosthesis. Recently, several preliminary studies have used deep generative models in other domains to synthesize data for health applications including medical monitoring [39], electroencephalography [40], accelerometry [41], and movement kinematics [42] for classification problems. We believe our proposed framework is generic enough to solve many problems for which the desired output is a synthetic multivariate time-series (even heterogeneous modalities) and empirical training data are limited. For instance, the decoder could be conditioned on any supplementary information (e.g. height, weight, home prosthesis, side of amputation, etc.) in addition to the activity mode. Without any fundamental changes, we could also use our approach to synthesize the EMG envelope for controlling an upper limb prosthesis with pattern recognition. We could also selectively generate less prevalent samples by decoding from the tails of a multivariate normal prior distribution or even use the model to generate examples of mislabeled steps (which are invaluable for training a system for online adaptation but uncomfortable for subjects).
V. Conclusion
We developed and validated techniques for applying data augmentation and deep generative models to prosthesis sensor data to learn representations of movement intention which are more robust to covariate shift across days and across users. In an offline analysis of data collected from four amputee subjects with different characteristics across several weeks to months, using the generative model provided clinical benefit by functionally replacing a second session of training data collection in the laboratory. Our approach to generative modeling also successfully synthesized rich sensor data for all channels, activities, and individuals using the same architecture and hyperparameters. We expect our promising results to impact how training data for controlling wearable assistive devices are collected and to catalyze the further expansion of deep learning techniques into rehabilitation robotics.
Acknowledgments
This work was supported by the National Institutes of Health (R01 HD079428-05) and National Science Foundation (NRI Award 1526534).
References
- [1].Varol HA, Sup F, and Goldfarb M, “Multiclass Real-Time Intent Recognition of a Powered Lower Limb Prosthesis,” IEEE Trans. Biomed. Eng, vol. 57, no. 3, pp. 542–551, Mar. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Huang H, Zhang F, Hargrove LJ, Dou Z, Rogers DR, and Englehart KB, “Continuous Locomotion-Mode Identification for Prosthetic Legs Based on Neuromuscular–Mechanical Fusion,” IEEE Trans. Biomed. Eng, vol. 58, no. 10, pp. 2867–2875, Oct. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hargrove LJ et al. , “Intuitive Control of a Powered Prosthetic Leg During Ambulation,” JAMA, vol. 313, no. 22, p. 2244, Jun. 2015. [DOI] [PubMed] [Google Scholar]
- [4].Simon AM et al. , “Configuring a powered knee and ankle prosthesis for transfemoral amputees within five specific ambulation modes.,” PLoS One, vol. 9, no. 6, p. e99387, Jan. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Simon AM et al. , “Delaying Ambulation Mode Transition Decisions Improves Accuracy of a Flexible Control System for Powered Knee-Ankle Prosthesis.,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 25, no. 8, pp. 1164–1171, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Zhao H, Reher J, Horn J, Paredes V, and Ames A, “Realization of stair ascent and motion transitions on prostheses utilizing optimization-based control and intent recognition,” in 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), 2015, pp. 265–270. [Google Scholar]
- [7].Stolyarov R, Burnett G, and Herr H, “Translational Motion Tracking of Leg Joints for Enhanced Prediction of Walking Tasks,” IEEE Trans. Biomed. Eng, vol. 65, no. 4, pp. 763–769, Apr. 2018. [DOI] [PubMed] [Google Scholar]
- [8].Liu M, Zhang F, and Huang HH, “An Adaptive Classification Strategy for Reliable Locomotion Mode Recognition,” Sensors, vol. 17, no. 9, p. 2020, Sep. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Young AJ and Hargrove LJ, “A Classification Method for User-Independent Intent Recognition for Transfemoral Amputees Using Powered Lower Limb Prostheses,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 24, no. 2, pp. 217–225, Feb. 2016. [DOI] [PubMed] [Google Scholar]
- [10].Spanias JA, Simon AM, Finucane SB, Perreault EJ, and Hargrove LJ, “Online adaptive neural control of a robotic lower limb prosthesis,” J. Neural Eng., vol. 15, no. 1, p. 016015, Feb. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kazemimoghadam M, Li W, and Fey NP, “Continuous Classification of Locomotor Transitions Performed Under Altered Cutting Style, Complexity and Anticipation,” in 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), 2018, pp. 972–977. [Google Scholar]
- [12].Simon AM, Seyforth EA, and Hargrove LJ, “Across-Day Lower Limb Pattern Recognition Performance of a Powered Knee-Ankle Prosthesis,” in 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), 2018, pp. 242–247. [Google Scholar]
- [13].Radford A, Metz L, and Chintala S, “Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks,” Nov. 2015. [Google Scholar]
- [14].van den Oord A et al. , “WaveNet: A Generative Model for Raw Audio,” Sep. 2016. [Google Scholar]
- [15].Serban IV, Sordoni A, Bengio Y, Courville A, and Pineau J, “Building End-To-End Dialogue Systems Using Generative Hierarchical Neural Network Models,” Jul. 2015. [Google Scholar]
- [16].Sup F, Varol HA, Mitchell J, Withrow TJ, and Goldfarb M, “Preliminary Evaluations of a Self-Contained Anthropomorphic Transfemoral Prosthesis,” IEEE/ASME Trans. Mechatronics, vol. 14, no. 6, pp. 667–676, Dec. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Young AJ, Simon AM, and Hargrove LJ, “An intent recognition strategy for transfemoral amputee ambulation across different locomotion modes,” in 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2013, vol. 2013, pp. 1587–1590. [DOI] [PubMed] [Google Scholar]
- [18].Holden D, Saito J, Komura T, and Joyce T, “Learning motion manifolds with convolutional autoencoders,” in SIGGRAPH ASIA 2015 Technical Briefs on - SA ‘15, 2015, pp. 1–4. [Google Scholar]
- [19].Hinton GE, Krizhevsky A, and Wang SD, “Transforming Auto-Encoders,” Springer, Berlin, Heidelberg, 2011, pp. 44–51. [Google Scholar]
- [20].Vincent P, Larochelle H, Bengio Y, and Manzagol P-A, “Extracting and composing robust features with denoising autoencoders,” in Proceedings of the 25th international conference on Machine learning - ICML ‘08, 2008, pp. 1096–1103. [Google Scholar]
- [21].Makhzani A, Shlens J, Jaitly N, Goodfellow I, and Frey B, “Adversarial Autoencoders,” Nov. 2015. [Google Scholar]
- [22].Lee D-H, “Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks,” in ICML Workshop: Challenges in Representation Learning, 2013. [Google Scholar]
- [23].Odena A, Olah C, and Shlens J, “Conditional Image Synthesis With Auxiliary Classifier GANs,” Oct. 2016. [Google Scholar]
- [24].Perez L and Wang J, “The Effectiveness of Data Augmentation in Image Classification using Deep Learning,” Dec. 2017. [Google Scholar]
- [25].Um TT et al. , “Data Augmentation of Wearable Sensor Data for Parkinson’s Disease Monitoring using Convolutional Neural Networks *,” vol. 17. [Google Scholar]
- [26].Kingma DP and Welling M, “Auto-Encoding Variational Bayes,” Dec. 2013. [Google Scholar]
- [27].Mescheder L, Geiger A, and Nowozin S, “Which Training Methods for GANs do actually Converge?,” Jan. 2018. [Google Scholar]
- [28].Hinton G, “Dropout?: A Simple Way to Prevent Neural Networks from Overfitting,” vol. 15, pp. 1929–1958, 2014. [Google Scholar]
- [29].Kingma DP and Ba J, “Adam: A Method for Stochastic Optimization,” Dec. 2014. [Google Scholar]
- [30].Maas AL, Hannun AY, and Ng AY, “Rectifier Nonlinearities Improve Neural Network Acoustic Models,” 2013. [Google Scholar]
- [31].He K, Zhang X, Ren S, and Sun J, “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification,” Feb. 2015. [Google Scholar]
- [32].Glorot X and Bengio Y, “Understanding the difficulty of training deep feedforward neural networks,” in Proceedings of the 13th International Conference On Artificial Intelligence and Statistics, 2010, vol. 9, pp. 249–256. [Google Scholar]
- [33].Mao X, Li Q, Xie H, Lau RYK, Wang Z, and Smolley SP, “Least Squares Generative Adversarial Networks,” Nov. 2016. [DOI] [PubMed] [Google Scholar]
- [34].Salimans T, Goodfellow I, Zaremba W, Cheung V, Radford A, and Chen X, “Improved Techniques for Training GANs,” Jun. 2016. [Google Scholar]
- [35].Hu B, Rouse E, and Hargrove L, “Fusion of Bilateral Lower-Limb Neuromechanical Signals Improves Prediction of Locomotor Activities,” Front. Robot. AI, vol. 5, p. 78, Jun. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Woodward RB, Spanias JA, and Hargrove LJ, “User intent prediction with a scaled conjugate gradient trained artificial neural network for lower limb amputees using a powered prosthesis,” in 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2016, vol. 2016, pp. 6405–6408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Su B-Y, Wang J, Liu S-Q, Sheng M, Jiang J, and Xiang K, “A CNN-Based Method for Intent Recognition Using Inertial Measurement Units and Intelligent Lower Limb Prosthesis,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 27, no. 5, pp. 1032–1042, May 2019. [DOI] [PubMed] [Google Scholar]
- [38].Goodfellow IJ et al. , “Generative Adversarial Networks,” Jun. 2014. [Google Scholar]
- [39].Esteban C, Hyland SL, and Rätsch G, “Real-valued (Medical) Time Series Generation with Recurrent Conditional GANs,” Jun. 2017. [Google Scholar]
- [40].Luo Y and Lu B-L, “EEG Data Augmentation for Emotion Recognition Using a Conditional Wasserstein GAN,” in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2018, pp. 2535–2538. [DOI] [PubMed] [Google Scholar]
- [41].Norgaard S, Saeedi R, Sasani K, and Gebremedhin AH, “Synthetic Sensor Data Generation for Health Applications: A Supervised Deep Learning Approach,” in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2018, pp. 1164–1167. [DOI] [PubMed] [Google Scholar]
- [42].Li L and Vakanski A, “Generative Adversarial Networks for Generation and Classification of Physical Rehabilitation Movement Episodes.,” Int. J. Mach. Learn. Comput, vol. 8, no. 5, pp. 428–436, Oct. 2018. [PMC free article] [PubMed] [Google Scholar]