Strong isoprene emission response to temperature in tundra vegetation

Significance

How ecosystem–atmosphere exchange of reactive hydrocarbons, biogenic volatile organic compounds (BVOCs), responds to climate change may provide important feedbacks on the regional climate. We combined direct measurements with model predictions of ecosystem-scale fluxes of isoprene—the most emitted BVOC worldwide—from two contrasting tundra sites, to characterize their temperature response. The continuous time series provide clear evidence that tundra vegetation will substantially boost its isoprene emissions in response to rising temperatures and allow for improvement of models that currently underestimate the temperature dependence of high-latitude isoprene emissions. These insights have implications for the atmosphere in a high-latitude region where climate is changing more than anywhere else on our planet.

Abstract

Emissions of biogenic volatile organic compounds (BVOCs) are a crucial component of biosphere–atmosphere interactions. In northern latitudes, climate change is amplified by feedback processes in which BVOCs have a recognized, yet poorly quantified role, mainly due to a lack of measurements and concomitant modeling gaps. Hence, current Earth system models mostly rely on temperature responses measured on vegetation from lower latitudes, rendering their predictions highly uncertain. Here, we show how tundra isoprene emissions respond vigorously to temperature increases, compared to model results. Our unique dataset of direct eddy covariance ecosystem-level isoprene measurements in two contrasting ecosystems exhibited Q₁₀ (the factor by which the emission rate increases with a 10 °C rise in temperature) temperature coefficients of up to 20.8, that is, 3.5 times the Q₁₀ of 5.9 derived from the equivalent model calculations. Crude estimates using the observed temperature responses indicate that tundra vegetation could enhance their isoprene emissions by up to 41% (87%)—that is, 46% (55%) more than estimated by models—with a 2 °C (4 °C) warming. Our results demonstrate that tundra vegetation possesses the potential to substantially boost its isoprene emissions in response to future rising temperatures, at rates that exceed the current Earth system model predictions.

The northern high latitudes are warming at two to three times the global average rates (1), and this can have consequences on a vast number of ecosystem responses, including ecosystem–atmosphere gas exchange, which affects atmospheric composition. Isoprene is the most emitted biogenic volatile organic compound (BVOC) across the globe (2), as well as in many Arctic and subarctic tundra ecosystems (3–6). Beyond having key ecological roles (7), BVOCs exert a principal control over the oxidative capacity of the troposphere (8) and can ultimately shape the climate (9, 10), particularly in the comparatively thinly populated high latitudes where human pollution is not prevalent (11).

Substantial measurement and modeling deficits remain concerning tundra BVOC emissions and their role in Arctic climate feedbacks. BVOC contributions to tropospheric ozone or secondary organic aerosol (SOA) budgets may either increase or counteract Arctic amplification (12), depending on, e.g., the efficiency of BVOC species at forming SOA. Regardless, these mechanisms are poorly accounted for due to the lack of data to improve our understanding of the present-day and future Arctic climate.

Field measurements of BVOCs from tundra sites are still scant, owing primarily to the instrumental challenges associated with harsh environments and limited infrastructure but also due to a perceived low emission potential as a result of low plant biomass, short growing seasons, and cold temperatures (13). Hence, our current model predictions are based on emission responses observed on vegetation from lower latitudes (14) or studies carried out over short periods of time or using sporadic sampling across the growing season. Furthermore, typical measurements with enclosure techniques result in undesired side effects and may lead to sampling errors when upscaling from a small number of enclosures to whole ecosystem fluxes. This leaves our estimates of present and future high-latitude biogenic emissions highly uncertain. Nevertheless, recent studies suggest an intense temperature response of isoprene emissions by tundra vegetation (5, 6, 15–18).

We measured ecosystem-scale isoprene fluxes with the eddy covariance technique at two ecosystems in Scandinavia. Eddy covariance is a direct flux measurement that overcomes the unwanted artifacts of enclosures and enables round-the-clock measurements of undisturbed vegetation for months, resulting in abundant data collected under a variety of naturally occurring environmental conditions. Thus, our measurements form an unprecedented, unique dataset of tundra isoprene fluxes that span the entire growing season at two contrasting sites: a peatland area with discontinuous permafrost near the town of Abisko (Sweden, 385 m above sea level [asl]) in 2018 and an alpine tundra area near the town of Finse (Norway, 1,222 m asl) in 2019.

Results and Discussion

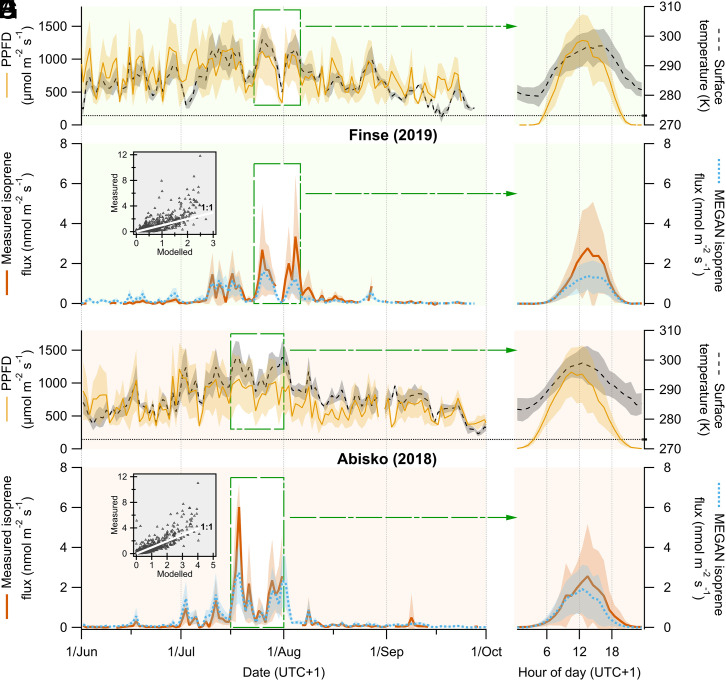
Both ecosystems exhibited similar seasonal variations in isoprene emissions, which started to intensify in June and were highest during July and the beginning of August (Fig. 1 C and G). Emission magnitudes at both sites were also comparable, with individual midday emission peaks in the range of 2 to 6 nmol m⁻² s⁻¹, occasionally reaching up to 10 to 11 nmol m⁻² s⁻¹, during the period of largest emissions. Indeed, the diel patterns during the period of maximum emission at both sites were alike in terms of the quantity and timing of the maximum hourly emissions, occurring between 13:00 and 14:00 h (UTC + 1) and averaging 2.6 ± 0.5 and 2.8 ± 0.4 nmol m⁻² s⁻¹ (mean ± SE) at Abisko and Finse, respectively (Fig. 1 D and H).

Fig. 1.

PPFD, vegetation surface temperature, and measured and modeled isoprene fluxes for (A–D) Finse and (E–H) Abisko. (Left) The time series of daytime averages between 1 June and 30 September, for which all data points, when PPFD ≥ 300 µmol m⁻² s⁻¹ during each day, were averaged (e.g., in the case of measured isoprene, 0 ≤ n ≤ 27 for Finse and 0 ≤ n ≤ 31 for Abisko), resulting in one average data point per day. The green dashed squares behind the traces indicate the time periods of ∼2 wk around the end of July, when isoprene emissions were highest at each site, that were included in the calculation of the diel cycles of hourly averages shown in Right. To calculate the diel cycles of temperature, PPFD, and modeled isoprene, only data points with available concurrent measured isoprene fluxes were used (n = 403 for Finse and n = 575 for Abisko). The trace shading indicates the SDs of daily daytime averages (Left) and hourly averages (Right). The horizontal dotted lines on the temperature axis (A, B, E, and F) indicate the temperature of 0 °C (=273.15 K). Insets in C and G are scatterplots showing the relationship between measured and modeled isoprene fluxes and include a white solid 1:1 identity line as a reference.

The Model of Emissions of Gases and Aerosols from Nature (MEGAN, version 2.1) (2) is the BVOC emission algorithm probably most widely implemented in state-of-the-art Earth system models (ESM) (19). We ran a single-point version of MEGAN at both our field sites using MEGAN’s default values for all parameters, including the default ecosystem isoprene emission factor (EF = 1,600 µg m⁻² h⁻¹) that MEGAN assigns to Arctic C₃ plants. Given the large differences between air and leaf temperature found in the tundra biome (20), in the model we prescribed the leaf temperature to equal the vegetation surface temperature that we measured at our field sites with infrared radiometers (Materials and Methods). In a broad sense, the isoprene emissions predicted by MEGAN matched the magnitudes of our observed fluxes (Fig. 1 C and G). At Finse, the season-long daily average (±SE) emission was 17 ± 4 µmol m⁻² d⁻¹, while MEGAN underestimated this by 18.5% (14 ± 3 µmol m⁻² d⁻¹; P < 0.05, n = 24 hourly averages, two-tailed Wilcoxon signed rank test for paired data, for the difference between measured and modeled emissions), and at Abisko, the difference was not statistically significant (18 ± 4 µmol m⁻² d⁻¹ for both measured and predicted fluxes, respectively). Notwithstanding, there were some noteworthy discrepancies. First, the predicted emissions outside of the peak growing season were generally higher than the measured emissions, whereas the real emissions observed at the peak growing season exceeded MEGAN’s predictions. Second, the modeled emissions for Abisko described a diel pattern that was close to the measured one but somewhat advanced in time, particularly in the afternoon, when predicted emissions declined earlier than those measured (Fig. 1H).

We leveraged our observed isoprene fluxes to establish what the MEGAN ecosystem EFs should be for our sites, using two sets of data that excluded fluxes measured when photosynthetic photon flux density (PPFD) was below 400 and 1,000 µmol m⁻² s⁻¹, respectively (Materials and Methods and SI Appendix, Tables S1 and S2). The season-long average EF for Finse was ∼1,990 µg m⁻² h⁻¹ (the averages ± 95% CI for each set of data were 2,009 ± 108 and 1,959 ± 139 µg m⁻² h⁻¹, respectively) and 1,290 µg m⁻² h⁻¹ (1,362 ± 74 and 1,212 ± 76 µg m⁻² h⁻¹, respectively) for Abisko, which corroborate that the MEGAN default (1,600 µg m⁻² h⁻¹) is reasonable for these ecosystems. The value for Finse confirms that MEGAN would need a higher EF than the default to better reproduce the measured fluxes in Finse (Fig. 1C). This higher seasonal value was caused mainly by the months of July and particularly August, when the monthly EF surpassed 3,000 µg m⁻² h⁻¹ because the original MEGAN fluxes were lower than observed (Fig. 1B). In contrast, the month of June saw lower fluxes than the model predicted, and thus, the EF was considerably lower as well. The seasonal EF for Abisko was lower than MEGAN’s default throughout, but it was very close to the default EF in the peak growing season when both measured and modeled fluxes matched decently well (Fig. 1H).

The magnitude of the MEGAN emissions depends heavily on the landscape average EF used because the calculated emissions result from the product of this fixed parameter and a few emission activity factors that incorporate the effect of environmental (e.g., leaf temperature) and developmental (e.g., leaf age) variables into the calculation. In our ensuing analysis, we assessed the temperature response of the observed isoprene emissions and compared it to model predictions. Therefore, the pertinent data to evaluate were the relative changes in isoprene emission rates as a function of vegetation temperature. For each site, we selected the periods when PPFD was not limiting (at least 1,000 µmol m⁻² s⁻¹) to circumvent potential interferences of the light response on that of temperature. Then we separately set our measured emissions and those modeled by MEGAN to equal 1 at 30 °C (=303.15 K) and scaled the rest of the fluxes relative to that reference flux at 30 °C. To achieve this, we divided each emission data point by the emission rate at 30 °C, thus obtaining a dimensionless quantity, analogous to MEGAN’s temperature activity factor (γ_T) for light-dependent emissions (2) (Fig. 2). Such a normalized emission, γ_T, disregards both the absolute magnitude of the observed emissions and of the MEGAN EF used, allowing for direct comparison of the temperature response of measured and modeled fluxes.

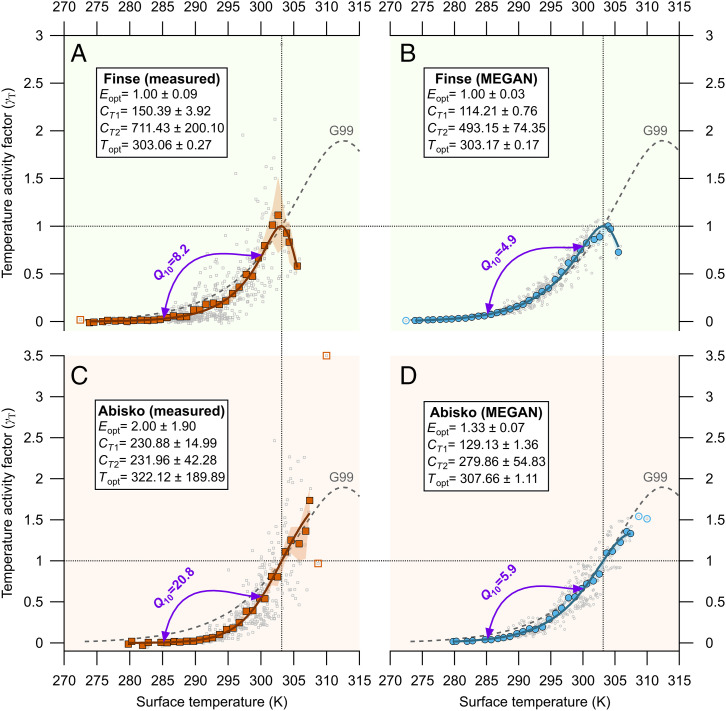
Fig. 2.

(A and C) Measured (square symbols) and (B and D) modeled (circle symbols) isoprene temperature activity factors (γ_T) plotted against the measured vegetation surface temperature for Finse, Norway (A and B), and Abisko, Sweden (C and D). The temperature emission activity factors here are essentially measured and modeled fluxes normalized to 1 at 30 °C (=303.15 K), as indicated by the dotted horizontal lines at γ_T = 1 and dotted vertical lines at T = 303.15 K. The small gray open symbols depict the individual temperature activity factors derived from the individual 30-min fluxes (n = 599 for Finse and n = 432 for Abisko) that passed the eddy covariance quality criteria and were not limited by available sunlight (PPFD ≥ 1,000 µmol m⁻² s⁻¹). Note that only MEGAN-simulated fluxes that corresponded with an available measured flux, and vice versa, were used in this comparison. The bigger, closed colored symbols represent the averages of the 1 K bins, and their shading represents their SE. These bin averages were fitted to Eq. 1 (Materials and Methods) with an unconstrained orthogonal distance regression weighted by the SE of each bin average. The open colored symbols represent bins that contained a single data value and were excluded from the fit. The text boxes show the fitting results (coefficient ± SD) for the empirical parameters of Eq. 1, and the solid line shows the fit line for each subplot. The purple arrow lines indicate the two temperatures (285.15 and 300.15 K) used to calculate the Q₁₀ values shown above each arrow (Eq. 2). For reference, the gray dashed line in each plot reproduces the standard G99 response curve (Materials and Methods), which between those temperatures has a Q₁₀ of 3.66.

Fig. 2 displays the newly determined γ_T values and their relationships to the vegetation surface temperature at each site, for either observed or modeled fluxes. We further grouped the individual γ_T values into 1 K bins to fit to the algorithm with which MEGAN models the isoprene emission temperature response (Eq. 1). The individual γ_T values differed significantly between the observed (n_o) and modeled (n_m) datasets for selected temperature ranges at each site (P < 0.05, one-tailed Wilcoxon signed rank test for paired data, 2 ≤ n_o = n_m ≤ 42 for each bin in Finse, 2 ≤ n_o = n_m ≤ 34 in Abisko). At Finse, the temperature bins with significantly different observed and modeled γ_T values were 278 to 298 K, whereas at Abisko, they were 285 to 300 K. Within these temperature ranges, the observed γ_T values were smaller than the modeled ones. Naturally, γ_T values at temperatures close to 303.15 K were not significantly different, because both the observed and modeled datasets had been normalized to 1 at that temperature.

We then calculated the Q₁₀ coefficient—the factor by which the emission rate increases with a 10 °C rise in temperature—between 285.15 and 300.15 K, using our fitted temperature curves (Eq. 2). Our flux measurements revealed Q₁₀ values of 8.2 for Finse and 20.8 for Abisko, which indicate strong temperature dependencies, much higher (1.7× to 3.5×) than those of the MEGAN simulations that were 4.9 and 5.9, respectively (Fig. 2). These results are consistent with the lower observed isoprene emissions early in the season, concurrent with colder temperatures, compared to the MEGAN predictions. Furthermore, these results are also consistent with the underprediction of real fluxes we observed later in the season, when temperatures reached their highest (Fig. 1 A and E), as was previously insinuated by a few days of measurements in the Alaskan tundra (21). These appreciable Q₁₀ coefficients highlight the unique, intense response of tundra isoprene emissions to temperature and are consistent with recent observations in diverse tundra ecosystems, where heaths and fens produced Q₁₀ values of 10 to 22 in reaction to either short- or long-term changes in temperature (5, 16, 17). These high values contrast with those of the MEGAN results, which match those of most biogenic VOC emission models. The latter range between 3 and 6, due to the synergistic interactions of the metabolic processes underlying isoprene emissions, which each have Q₁₀ ∼ 2, similar to all biochemical reactions in general (22, 23).

Vegetation development, phenology, could interact with isoprene emissions and their temperature responses. For instance, high temperatures might coincide with fully mature vegetation with high isoprene emission capacity, and low temperatures occur at a time of lower emission capacity. It is known that the isoprene emission capacity of temperate zone plants changes across the season, independently of instantaneous light and temperature conditions (24). In fact, MEGAN includes an adjustment for these developmental effects using the leaf age activity factor, which involves assigning a fractional value of the EF to each age category (e.g., newly developed leaves are assumed to emit 0.05 times the amount of mature, fully expanded leaves) and deriving the proportions of the different age categories from the evolution of leaf area index (LAI). However, the MEGAN results for our sites indicated that the weighted average leaf age activity factor varied by less than 0.6% (ranging between 0.994 and 0.999). Hence, our MEGAN model results did not include any compensation for phenology effects, other than the amount of emitting foliage according to the LAI. Regarding our isoprene flux measurements, we compared the monthly emission temperature responses and did not observe any obvious difference between months (SI Appendix, Figs. S3 and S4).

The optimal temperature (T_opt) of the isoprene response function for Finse was remarkably similar between our measurements and the modeled MEGAN results, including the pronounced decrease in emissions at temperatures beyond T_opt (Fig. 2 A and B). In MEGAN, T_opt depends linearly on the temperatures of the previous 240 h. The lower T_opt value we observed, compared to the G99 temperature response curve (25) (Materials and Methods), may be a consequence of the low temperatures experienced by the vegetation in Finse. In Abisko, even though vegetation temperatures covered a warmer range, we did not observe a decline in emissions, indicative of an optimal temperature for emission, within the observed temperatures (Fig. 2C). However, the fitted T_opt values for both sites are relatively uncertain because the number of available isoprene emission observations in the warmest segment of the temperature range is insufficient to draw robust conclusions. For example, in Finse, there were only 11 data points at 303.15 K or above. For Abisko, only 19 data points were recorded at or over 305.15 K, and the fitted T_opt is far beyond the temperatures registered on site. More field measurements are needed to populate these relationships with data collected under warmer temperatures to truly evaluate whether these fitted T_opt values are realistic.

We can use our fitted temperature response curves for a “back-of-the-envelope” estimation of how much isoprene emissions would intensify at our field sites in a future warmer climate based on the temperature response of isoprene emission. Taking the temperatures of the individual data points used in Fig. 2 (i.e., measured surface temperatures when PPFD ≥ 1,000 µmol m⁻² s⁻¹), we used separately the observed (Fig. 2 A and C) and modeled (Fig. 2 B and D) response curves with their fitted parameters for each site to derive the isoprene normalized emission at each single temperature data point (n = 599 for Finse and n = 432 for Abisko). Adding all of them up yielded a pair of season-aggregate normalized emissions for each site. We repeated the same calculation but adding 2 °C (4 °C) (1, 26) to each temperature. This rudimentary estimate revealed that a 2 °C (4 °C) rise in surface temperature would multiply isoprene emissions by 1.32 (1.63) in Finse and by 1.41 (1.87) in Abisko. The curves obtained from MEGAN’s predictions also projected enhanced emissions, although at lower levels: a factor of 1.26 (1.5) for Finse and 1.28 (1.56) for Abisko. In other words, our measured temperature response curves amplify the emissions by 23% (26%) in Finse and 46% (55%) in Abisko compared to what the MEGAN response curve would dictate.

While our results address temperature responses, multiple additional factors will also play a role in shaping future isoprene emissions. For example, as the climate continues to warm, the temperature response curves will most likely change, displaying higher optimal temperatures for isoprene emissions, together with higher maximum normalized emission capacities, as plants acclimate to a hotter environment, in a process that can develop in a matter of days (14, 24). Furthermore, warming-induced changes in the phenology, composition, and biomass of vegetation (1, 27, 28) can also contribute indirectly to modifying the BVOC blend of high-latitude ecosystems, as indicated by experimental warming treatments (29, 30). In addition, highly uncertain future precipitation regimes (31), increased herbivory (32), and more frequent defoliating insect outbreaks (33, 34) that result from milder winter conditions under global warming will also play a role in defining high-latitude BVOC emissions in the coming decades. Nevertheless, our results demonstrate that tundra vegetation possesses the potential to substantially boost its isoprene emissions in response to rising temperatures, at rates that exceed the current ESM predictions. The next generation of BVOC emission models embedded into ESM should take this strong response into account to improve their predictive capability, particularly considering the potential repercussions, for the regional atmospheric chemistry, of the likely large increases in tundra isoprene emissions to the clean background atmosphere of the unpolluted high-latitude environments.

Materials and Methods

Field Sites.

Our measurement campaigns took place at two Scandinavian sites, one located in oroarctic tundra and the other in subarctic peatland.

Abisko Stordalen measurement site (68° 21.35′ N, 19° 2.71′ E) is located in the Stordalen mire complex in Swedish Lapland, near the village of Abisko (Ábeskovvu). The mire complex also houses the Abisko-Stordalen station (SE-Sto) of the ICOS (Integrated Carbon Observation System) network, measuring CO₂ and CH₄ fluxes along with several auxiliary parameters on a continuous basis (35). The mean annual air temperature at Abisko weather station was −0.8 °C (1961 to 1990), and the annual average precipitation was 304 mm (1961 to 1990) (36). The mire complex consists of various microforms, defined by their topography, permafrost status, hydrology, nutrient status, and pH. A large part of the mire consists of raised permafrost plateau, with ombrotrophic features, while other parts are partially or fully thawed or shallow ponds, lakes, and streams. The fluxes analyzed here originate from ombrotrophic permafrost plateau, especially in western wind directions, with a significant contribution from wetter thaw features, especially in eastern wind sector (35). The vegetation on the permafrost plateau is dominated by Empetrum hermaphroditum, Betula nana, Rubus chamaemorus, Eriophorum vaginatum, Dicranum elongatum, and Sphagnum fuscum. The wet areas are characterized by E. vaginatum, Carex rotundata, Sphagnum balticum, Drepanucladus schulzei, and Politrichum jensenii (35, 37).

Finse is an oroarctic site located at 1,222 m asl on the Hardangarvidda mountain plateau in southern central Norway (60° 35.63′ N, 7° 31.61′ E). Mean annual air temperature (1961 to 1990) was −2 °C with an average annual precipitation of 1,030 mm. The ecosystem can be described as low-alpine tundra, with a heterogeneous mix of fens, lichen, heaths, snow beds, and open water bodies. The vegetation cover is dominated by lichens and heaths on wind-exposed ridges, narrow zones of dwarf shrub heath on the lee sides below the ridges, bands of willows (Salix spp.) along streams and rivers, and moss-dominated snow beds. Vascular plant species commonly found at the site include E. hermaphroditum, Salix herbacea and other Salix spp., Eriophorum angustifolium, and Carex spp. Frequent bryophytes in the area include Ptilidium ciliare and Polytrichum juniperinum, and usual lichens include Alectoria ochroleuca, Nephromopsis nivalis, and Cetraria islandica. The ecosystem is not generally water-limited, as snow melt and runoff from the nearby glacier and headwaters sustain throughout the growing season. Snow accumulates and melts out extremely variably, with exposed ridges almost snow-free year round and depressions accumulating several meters of snow and typically melting out in July. Multiyear comparisons of CO₂ fluxes indicate a small carbon sink function of the ecosystem and show that 2019 was a relatively normal year considering the carbon balance.

Eddy Covariance Measurements.

At both sites (Abisko, 1 June 2018 to 19 October 2018; Finse, 13 May 2019 to 25 September 2019), we conducted direct isoprene flux measurements at the ecosystem scale with the same proton transfer reaction–time of flight–mass spectrometer (PTR–ToF–MS; model PTR-TOF 1000ultra, Ionicon Analytik) housed in a hut built for this purpose. A detailed description of the settings and calibration of the PTR–ToF–MS, the processing of the raw data, and the calculation of fluxes is available from a virtually identical experimental setup described elsewhere (16), and we refer the reader to that. In short, sample air was drawn from a nearby micrometeorological mast (at a height of 4.4 m in Finse and 2.1 m in Abisko) through a heated PFA (perfluoroalkoxy) line (1/4 in. inner diameter, 3/8 in. outer diameter) inlet that was kept at a slightly more elevated temperature than ambient to minimize VOC and water condensation onto the inlet walls. The PTR–ToF–MS was calibrated monthly by diluting a gas standard containing several VOCs with nitrogen to perform a multistep calibration. In the PTR–ToF–MS mass spectra, isoprene was detected at the protonated mass-to-charge ratio of 69.07, as expected for hydronium ion protonation (38).

The 10 Hz raw data generated by the PTR–ToF–MS were processed first to obtain mixing ratios (39) and subsequently, in combination with three-dimensional wind information captured with an ultrasonic anemometer mounted on the same mast, isoprene fluxes in 30-min intervals (40). Every night, we assessed the background signal of the instrument by measuring VOC-scrubbed air. This “zero air” would compensate for any change in the baseline of the PTR-MS signal, but even if not, a change in baseline would have relatively little effect on the computed eddy covariance fluxes. The reason is that the average signal of each half-hour period is subtracted from the 10 Hz signal of that period to obtain the signal fluctuations from the average signal (Reynolds averaging) (41). That fluctuating part is then used to calculate the covariance of fluctuations of the vertical wind and VOC signals to obtain the turbulent flux (40). In addition, the ambient humidity was indirectly taken into account in the process of calculating the isoprene mixing ratios because the signal of isoprene ions was normalized by the sum of the signals of the PTR–ToF–MS primary ion (hydronium ions, H₃O⁺) and the first cluster of the hydronium ions with a water molecule [H₃O⁺(H₂O)]. The water cluster can also ionize the isoprene molecules inside the drift tube of the PTR–ToF–MS at a similar rate to the primary ion, and the abundance of this cluster in the drift tube is proportional to the ambient humidity in sampled air (42). Thus, we expect relatively little effect from the varying levels of ambient humidity on our data. The next quality control step consisted in excluding flux data points that failed the stationarity test (43) (result higher than 30%), which resulted in 20.4 and 11.6% of the isoprene fluxes being discarded from Finse and Abisko, respectively. We also calculated the random error (RE) of each of the 30-min eddy covariance fluxes by computing the SD of the covariance function between isoprene mixing ratios and vertical wind speed, at regions far away from the true lag between those signals (e.g., time lag of −180 to −160 s and +160 to +180 s) (44). With the RE, we can derive the limit of detection (LoD) of the fluxes (e.g., LoD = 2 × RE). However, we did not exclude any flux data points that were below the LoD to avoid biasing the computation of the flux averages shown in Figs. 1 and 2. In general, the fluxes below the LoD were typically those close to zero: at any time of day at the beginning and end of the season and, during the peak season, at moments of the day when solar radiation or temperature were not enough to induce isoprene emission. The final processing step involved spectral corrections to account for possible losses of high-frequency turbulence contributions to the fluxes, following an empirical method (45) that compares an attenuated (isoprene) to an unattenuated (temperature measured by the ultrasonic anemometer) signal. The experimental data were then fitted to a Gaussian function [a sigma function (45) for the Finse data and a modification of it (46) for Abisko, which best fitted the experimental data in each case] to derive the cospectral transfer function used to correct the isoprene flux data. The footprint of the measured isoprene fluxes was estimated with a two-dimensional model (16, 47) (SI Appendix, Fig. S1).

Surface Temperature and PPFD Measurements.

We retrieved the vegetation surface temperature with research-grade infrared radiometers (SI-111 in Abisko and SI-411 in Finse, both from Apogee Instruments), mounted on the eddy covariance mast, that measured noninvasively the vegetation surface temperature integrated over its field of view (4.8 and 12.4 m² in Abisko and Finse, respectively). These measurements of surface temperature constitute the best approximation of the temperature actually experienced by the tundra vegetation, which is known to be one of the main drivers of isoprene emissions. Furthermore, when attempting to understand and model biogenic isoprene emissions, it is important to work with surface temperature, rather than air temperature, because it has been shown that solar radiation can warm Arctic plants several degrees above the temperature of the surrounding air (16, 48, 49). The portion of the solar radiation that plants can capture to fuel photosynthesis (i.e., PPFD) was measured at both sites with quantum sensors: Apogee SQ110 in Abisko and LI-190 (LI-COR Biosciences) in Finse.

MEGAN Emission Model.

We used a single-point version of MEGAN (version 2.1) (2) to model the expected isoprene emissions at our tundra sites. MEGAN emissions are based on a simple mechanistic model that considers the major environmental and developmental variables that drive emission rates, namely, light, temperature, soil moisture, atmospheric CO₂ concentration, leaf age, and LAI. Each of the environmental variables determines a dimensionless activity factor that modulates the emissions calculated from a fixed canopy EF, which depends on the BVOC species and the plant functional type (PFT) concerned. For our study, we used MEGAN’s default isoprene landscape EF for PFT 12 (Arctic C₃ grass), with a value of 1,600 µg m⁻² h⁻¹, and considered isoprene emission to be entirely light-dependent, as MEGAN does by default (2). For the leaf age activity factor, we used the default values of the leaf age coefficients for each of the fractions of the canopy (A_new = 0.05, A_gro = 0.6, A_mat = 1, and A_old = 0.9 for new, growing, mature, and senescing leaves, respectively). These leaf age fractions are calculated by MEGAN based on the LAI evolution along the growing season. We obtained the fraction of vegetation cover and a daily LAI value for our tundra sites from the ERA5 reanalysis (50). In Finse, the fraction of soil covered by vegetation was set to 0.91, and LAI ranged between 0.9 m² m⁻² before the growing season and 1.3 m² m⁻² at the peak of the growing season. In Abisko, the vegetation cover fraction was 0.84, and LAI ranged between 0.78 and 1.22 m² m⁻². We excluded any potential effect of soil moisture (51, 52) or CO₂ inhibition (53) on isoprene emissions from the model as we expect they are negligible for this study. MEGAN includes a canopy radiative transfer model to account for light attenuation within a five-layer canopy with sun and shade leaf components and can calculate the leaf temperature from the air temperature and the leaf energy balance. We ran MEGAN for our tundra sites using the PPFD measured by us in situ. Given the short stature of the tundra vegetation and the great disparity between air and vegetation temperatures found in Arctic ecosystems (16, 48, 49, 54), we forced the model to set the leaf temperature equal to our measured vegetation surface temperature, instead of using leaf temperatures calculated with its leaf energy balance model. In addition, MEGAN’s light and temperature activity factors account for the past conditions (using the moving average of the last 24 h and the last 10 d) to model the response to light and temperature. We used the default values for all of the parameters involved in the calculation of the MEGAN light and temperature activity factors (2).

Additionally, we determined the MEGAN isoprene EFs for each field site based on our observed fluxes. We started by calculating the MEGAN dimensionless emission activity factor for each half-hour by dividing the modeled isoprene fluxes by MEGAN’s default ecosystem EF, then using these newly calculated activity factors as divisors of the observed fluxes, thus obtaining an EF estimate for each half-hour data point. The last step consisted of averaging the half-hourly EFs. We excluded the fluxes with small negative values (i.e., essentially, flux values that fluctuated around zero in moments with very low emission of isoprene) because they produced unreasonable numbers that would bias the average EFs. We calculated two sets of EFs for each site to assess how robust the estimated values are depending on the number of data points involved: one set using flux data when PPFD was at least 1,000 µmol m⁻² s⁻¹ and another set with the PPFD threshold at 400 µmol m⁻² s⁻¹. In both cases, lower irradiance levels were excluded to avoid interference from low light conditions. The resulting EFs are found in SI Appendix, Tables S1 and S2, and each set of EFs includes the average EF for the entire measurement season and an EF for each month separately because isoprene EFs are known to vary along the year in diverse ecosystems (24).

Isoprene Temperature Response.

The influence of leaf temperature on isoprene emission is simulated in MEGAN with the equation outlined by Guenther et al. (25):

$${\gamma }_{\text{T}}=\frac{E_{\text{opt}}·C_{T2}·e^{C_{T1}·x}}{C_{T2}-C_{T1}·(1-e^{C_{T2}·x})}, x=\frac{\frac{1}{T_{\text{opt}}}-\frac{1}{T}}{R},$$ [1]

where γ_T is a scalar representing the nondimensional response of isoprene and other light-dependent emissions to temperature (i.e., temperature activity factor), E_opt is the maximum normalized emission capacity at the optimum temperature T_opt (K), C_T1 (kJ mol⁻¹) and C_T2 (kJ mol⁻¹) are empirical parameters, T is the current temperature (K), and R is the ideal gas constant (=0.008314 kJ K⁻¹ mol⁻¹). The constant values recommended in Guenther et al. (25) for the parameters are E_opt = 1.9, T_opt = 312.5 K, C_T1 = 95 kJ mol⁻¹, and C_T2 = 230 kJ mol⁻¹. Using these constant values results in a response curve—which we refer to as G99 here—that increases exponentially with temperature until it reaches the maximum E_opt = 1.9 at T_opt = 312.5 K and then declines as leaf temperatures become too hot for isoprene synthesis. This G99 curve is nearly equivalent to that originally presented by Guenther et al. (55) that has been used extensively over the years to simulate the response of isoprene emission to changes in temperature on a time scale of seconds to minutes (24). Because the temperature conditions of the past few hours and days have an influence on the plant’s capacity of emitting isoprene, MEGAN implemented additional algorithms that calculate the variable values of E_opt and T_opt based on past conditions to account for this temperature history effect. Thus, in practice, the temperature response simulated by MEGAN can deviate substantially from the G99 curve (14, 24).

For our analysis of the temperature response of isoprene emissions, we considered the tundra vegetation as a big leaf (16, 51, 56) using the leaf-level algorithm of Eq. 1. We fitted Eq. 1 to a selection of our measured and modeled isoprene fluxes after normalizing them to equal 1 at 30 °C, thus converting the fluxes effectively into dimensionless temperature activity factors (γ_T; Fig. 2). The selected fluxes consisted of only those that were not limited by the amount of available light (PPFD of at least 1,000 µmol m⁻² s⁻¹) to minimize the confounding effect of light on the temperature response. The light response of isoprene emission for most previously studied plants typically saturates at higher PPFD levels, and our data revealed that this was the case at our sites as well (SI Appendix, Fig. S2).

To illustrate the dependence of the isoprene emissions on the vegetation temperature, we calculated the unitless Q₁₀ coefficient, defined as the ratio of the emission rate at one temperature to that of a temperature 10 K lower, as

$$Q_{10}={\left(\frac{E_2}{E_1}\right)}^{10/\left(T_2-T_1\right)},$$ [2]

where E₁ and E₂ are the emission rates at temperatures T₁ and T₂, respectively. Note that although the Q₁₀ coefficient expresses the ratio of emission rates between two temperatures that differ by 10 K, the temperatures T₁ and T₂ in Eq. 2 need not be 10 K apart to calculate the Q₁₀ coefficient using Eq. 2. Instead, T₁ and T₂ can span any range that is most relevant to the dataset being investigated. In our case, we chose T₁ = 285.15 K and T₂ = 300.15 K, which is the range where there were statistically significant differences between the measured and modeled temperature activity factors (see the Results and Discussion section and Fig. 2).

Data Availability

Measured isoprene fluxes with their RE, modeled isoprene fluxes, and environmental conditions (PPFD, air and vegetation surface temperatures, and averages of PPFD and temperatures for the past 24 and 240 h) have been deposited in Zenodo (https://doi.org/10.5281/zenodo.6340239) (57).