Abstract
Mathematical modeling of the relationship between the functional activity and the structural wiring of the brain has largely been undertaken using non-linear and biophysically detailed mathematical models with regionally varying parameters. While this approach provides us a rich repertoire of multistable dynamics that can be displayed by the brain, it is computationally demanding. Moreover, although neuronal dynamics at the microscopic level are nonlinear and chaotic, it is unclear if such detailed nonlinear models are required to capture the emergent meso-(regional population ensemble) and macro-scale (whole brain) behavior, which is largely deterministic and reproducible across individuals. Indeed, recent modeling effort based on spectral graph theory has shown that an analytical model without regionally varying parameters and without multistable dynamics can capture the empirical magnetoencephalography frequency spectra and the spatial patterns of the alpha and beta frequency bands accurately.
In this work, we demonstrate an improved hierarchical, linearized, and analytic spectral graph theory-based model that can capture the frequency spectra obtained from magnetoencephalography recordings of resting healthy subjects. We reformulated the spectral graph theory model in line with classical neural mass models, therefore providing more biologically interpretable parameters, especially at the local scale. We demonstrated that this model performs better than the original model when comparing the spectral correlation of modeled frequency spectra and that obtained from the magnetoencephalography recordings. This model also performs equally well in predicting the spatial patterns of the empirical alpha and beta frequency bands.
Keywords: Brain activity, Connectomes, Magnetoencephalography, Spectral graph theory
1. Introduction
How the brain exhibits dynamic functional activity with a static anatomical structural wiring, and how the structural and functional alterations are associated with neurological diseases (Fornito et al., 2015) has been a long-standing open question in the field of neuroscience. Functional activity in the gray matter regions can be measured non-invasively using functional magnetic resonance imaging (fMRI), electroencephalography (EEG), and magnetoencephalography (MEG). The connections between the gray matter regions, or the structural wiring, is estimated using diffusion tensor imaging (DTI) from MRI. One way of investigating the relationship between the functional activity and the structural wiring is by exploring a macroscopic graph with the gray matter regions as the nodes and the weights of the edges determined by the extent of connectivity of the white matter fibers between the nodes. Subsequently, various graph theoretic and modeling approaches have been undertaken to determine the functional-structural relationships and how they are altered in various neurological diseases.
Graph theoretic approaches have been widely used to evaluate statistical measures of relationships between functional and structural connectivity (Abdelnour et al., 2018; 2014; Achard et al., 2006; Bullmore and Sporns, 2009; Ghosh et al., 2008; Hermundstad et al., 2013; van den Heuvel et al., 2009; Honey et al., 2009; Park and Friston, 2013; Rubinov et al., 2009; Strogatz, 2001). However, they do not take into account any details of neural physiology (Mišić et al., 2015) and therefore are limited in their capability to develop a mechanistic understanding.
On the other hand, detailed computational modeling approaches have been undertaken to incorporate neural activity, such as neural mass (David and Friston, 2003; Muldoon et al., 2016) and mean field modeling (Boustani and Destexhe, 2009; Destexhe and Sejnowski, 2009; Wilson and Cowan, 1973), where neural assemblies and connections among them are modeled. Such computational models are non-linear and require several time consuming simulations to obtain the structure-function relationships. Although neuronal dynamics at the microscopic level (single neurons) are nonlinear and chaotic, it is unclear if such detailed nonlinear models are required to capture the emergent meso-(regional population ensemble) and macro-scale (whole brain) behavior, which is largely deterministic and reproducible across individuals (Fox and Raichle, 2007; Nozari et al., 2020). Indeed, it has been suggested that brain-wide neural activity can be independent of microscopic local activity of individual neurons (Abdelnour et al., 2014; Destexhe and Sejnowski, 2009; Mišić et al., 2015; 2014; Robinson et al., 2005; Shimizu and Haken, 1983), and instead may be regulated by long-range structural connectivity (Abdelnour et al., 2015; Deco et al., 2012; Jirsa et al., 2002; Nakagawa et al., 2014). Based on this hypothesis, Raj and colleagues had earlier developed a hierarchical, linear, analytic spectral graph theory model (SGM) which could accurately capture empirical MEG spectra and spatial distribution of alpha and beta frequency bands (Raj et al., 2020).
SGM provides a closed-form solution of brain oscillations in the form of steady state frequency response obtained from the eigendecomposition of a graph Laplacian, based on spectral graph theory (Auffarth, 2007; Kondor and Lafferty, 2002; Larsen et al., 2006; Ng et al., 2001). This model incorporates the structural connectome and long-range axonal conduction delays, and provides a set of frequency-rich spectra which can be directly compared to the empirical MEG wideband spectra obtained after source reconstruction of MEG signals. Moreover, since the analytical solution to this SGM model can be obtained in a closed-form, no time-consuming simulations are required. The model is parameterized by a small set of global parameters : the neural gains, time constants, conduction velocity, and macroscopic coupling. These model parameters admit physical interpretations and can be potentially controlled by neuromodulation (Shine et al., 2018). Most importantly for downstream applications, SGM model inference is highly feasible in comparison to other methods, and it is the only model whose inference can be realized from empirical regional power spectra rather than from functional correlation structures like functional connectivity (FC). Finally, the spectral graph model is conceptually attractive because it places the graph explicitly at the center of the model, a counter-point to coupled Neural Mass Models (NMMs), where the effect of the graph comes about only indirectly as coupling coefficients between local neural masses.
The previously published SGM had local model elements derived from a control theory viewpoint, due to which the local parameters and gain terms lacked classical interpretability in terms of extant NMMs. Here, we reformulate the SGM local model from bottom-up, in line with classical neural masses. We thoroughly explore the inference of this modified model on real MEG data, and show that the modified model is essentially equivalent to the original SGM, and displays a small but significantly more favorable fit to real MEG regional power spectra. Thus, the new model keeps the key strengths of the original, while providing more biologically interpretable parameters, especially at the local scale. This modified SGM (M-SGM) has an excellent ability to capture the spatial patterns of empirical alpha and beta frequency bands, requiring only 5–10 graph eigenmodes to do so.
2. Methods
2.1. M-SGM
We hierarchically model the local cortical mesoscopic and long-range macroscopic signals for each brain region, where the regions are obtained using the Desikan–Killiany atlas (Desikan et al., 2006). We then solve the model equations to obtain a closed-form solution in the Fourier frequency domain. This provides us frequency rich spectra which is an estimate of the source-reconstructed MEG spectra.
Notation All the vectors and matrices are written in boldface and the scalars are written in normal font. The frequency f of a signal is specified in Hertz and the corresponding angular frequency ω = 2πf is used to obtain the Fourier transforms. The connectivity matrix is defined as C = cjk, where cjk is the connectivity strength between regions j and k, normalized by the row degree.
2.1.1. Mesoscopic model
For every region k out of the total N regions, we model the local excitatory signal xe,k, local inhibitory signal xi,k as well as the long range excitatory signal xk where the global connections are incorporated. The local signals are modeled using an analytical and linearized form of neural mass equations. We write a set of differential equations for evolution of xe,k and xi,k due to decay of individual signals with a fixed neural gain, coupling of excitatory and inhibitory signals, and input white Gaussian noise. Letting fe(t) and fi(t) denote the ensemble average neural impulse response functions, the equations for xe,k and xi,k are:
| (1) |
| (2) |
where, ⋆ stands for convolution, p(t) is input noise, parameters gee, gii, gei are neural gain terms, and parameters τe, τi are characteristic time constants. These are global parameters and are the same for every region k. Here, the ensemble average neural impulse response functions fe(t) and fi(t) below are assumed to be Gamma-shaped:
| (3) |
| (4) |
2.1.2. Macroscopic model
A similar equation is written for the macroscopic signal xk, for every kth region, accounting for long-range excitatory corticocortical connections for the pyramidal cells. The evolution of xk is assumed as a sum of decay due to individual signals with a fixed excitatory neural gain, incoming signals from all other connected regions determined by the white matter connections, and the input signal xe,k(t) + xi,k(t) determined from Eqs. (1), (2). The equation for xk is:
| (5) |
where, τG is the graph characteristic time constant, α is the global coupling constant, cjk are elements of the connectivity matrix determined from DTI followed by tractography, is the delay in signals reaching from the jth to the kth region, υ is the cortico-cortical fiber conduction speed with which the signals are transmitted. The delay is calculated as djk/υ, where djk is the distance between regions j and k.
These set of equations are parameterized by 8 global parameters: excitatory time constant τe, inhibitory time constant τi, macroscopic graph time constant τG, excitatory neural gain gee, inhibitory neural gain gii, alternating population neural gain gei, global couping constant α, and conduction speed υ. The neural gain gee is kept as 1 to ensure parameter identifiability. We estimate the 7 global parameters using an optimization procedure described in the next section.
2.1.3. Model solution in the Fourier domain
Since the above equations are linear, we can obtain a closed-form solution in the Fourier domain as demonstrated below. The Fourier transform is taken at angular frequency ω which is equal to 2πf, where f is the frequency in Hertz. The Fourier transform of the Eqs. (1) and (2) will be the following, where and :
| (6) |
| (7) |
Here, P(ω) is the Fourier transform of the input Gaussian noise p(t) which we assume to be identically distributed for both the excitatory and inhibitory local populations for each region, and the Fourier transforms of the ensemble average neural response functions are:
| (8) |
| (9) |
On solving the above Eqs. (6) and (7), we get the following expressions for Xe(ω) and Xi(ω):
| (10) |
| (11) |
Then, the transfer functions He(ω) and Hi(ω) can be separated out and we get:
| (12) |
| (13) |
The total neural population is:
| (14) |
thus, Hlocal(ω) = He(ω) + Hi(ω). In order to obtain a Fourier response of the macroscopic signal, we first re-write Eq. (5) in the vector form as:
| (15) |
We similarly take a Fourier response of the macroscopic signal and obtain the following as the Fourier transform of Eq. (15), where :
| (16) |
where, . Note that each element in the matrix C is normalized already by the row degree. The above equation can be re-arranged as:
| (17) |
Here, we define the complex Laplacian matrix:
| (18) |
where, I is the identity matrix of size N × N. The eigen-decomposition of this complex Laplacian matrix is:
| (19) |
where, U (ω) are the eigenvectors and Λ(ω) = diag([λ1(ω), …, λN(ω)]) consist of the eigenvalues λ1(ω), …, λN(ω), at angular frequency ω. The macroscopic response Eq. (17) can be written as:
| (20) |
By using the eigen-decomposition of the Laplacian matrix, the above equation can be re-written as:
| (21) |
where, uk(ω) are the eigenvectors from U(ω) and λk (ω) are the eigen-values from Λ(ω) obtained by the eigen-decomposition of the complex Laplacian matrix obtained in Eq. (19). Eq. (21) is the closed-form steady state solution of the macroscopic signals at a specific angular frequency ω. We use this modeled spectra to compare against empirical MEG spectra and subsequently estimate model parameters. In M-SGM, we also included the cortical as well as subcortical region eigenvalues in calculation of the modeled spectra, unlike in SGM where only cortical eigenvalues were included. In addition, we performed whitening of the input noise term after calculating the modeled spectra in M-SGM, while it was whitened before calculating the modeled spectra in the original SGM.
2.1.4. Mesoscopic model in SGM
In the original SGM (Raj, Cai, Xie, Palacios, Owen, Mukherjee, Nagarajan, 2020), the mesoscopic model equations were:
| (22) |
| (23) |
Writing in terms of transfer functions gives Xe(ω) = He(ω)P(ω) and Xi(ω) = Hi(ω)P(ω). To account for coupling in SGM, an additional transfer function was introduced:
| (24) |
The net transfer function then was:
| (25) |
The main difference is in how the excitatory and inhibitory populations were coupled in M-SGM versus SGM.
2.2. Dataset description
The dataset used for this work is the same as the one used for the previous SGM work (Xie et al., 2020). For this dataset, MEG, anatomical MRI, and diffusion MRI was collected for 36 healthy adult subjects (23 males, 13 females; 26 left-handed, 10 right-handed; mean age 21.75 years, age range 7–51 years). All study procedures were approved by the institutional review board at the University of California at San Francisco (UCSF) and are in accordance with the ethics standards of the Helsinki Declaration of 1975 as revised in 2008. MEG recordings were collected while the subjects were resting and had eyes closed. MRI followed by tractography was used to generate the connectivity matrices. MEG recordings were downsampled to 600 Hz, followed by a bandpass filtering of the signals between 2 and 45 Hz using firls in MATLAB (The Mathworks, 2020) and generation of the frequency spectra for every region of interest using the pmtm algorithm in MAT-LAB (The Mathworks, 2020). Data collection procedure has already been described previously (Raj et al., 2020) and are summarized below.
2.3. MRI
A 3 Tesla TIM Trio MR scanner (Siemens, Erlangen, Germany) was used to perform MRI using a 32-channel phased-array radiofrequency head coil. High-resolution MRI of each subject’s brain was collected using an axial 3D magnetization prepared rapid-acquisition gradient-echo (MPRAGE) T1-weighted sequence (echo time [TE] = 1.64 ms, repetition time [TR] = 2530 ms, TI = 1200 ms, flip angle of 7°) with a 256-mm field of view (FOV), and 160 1.0-mm contiguous partitions at a 256 × 256 matrix. Whole-brain diffusion weighted images were collected at b = 1000 s/mm2 with 30 directions using 2-mm voxel resolution in-plane and through-plane.
2.4. MEG data
MEG recordings were acquired at UCSF using a 275-channel CTF Omega 2000 whole-head MEG system from VSM MedTech (Coquitlam, BC, Canada). All subjects were instructed to keep their eyes closed for 5 min while their MEGs were recorded at a sampling frequency of 1200 Hz.
2.5. Region parcellations
The T1-weighted images were parcellated into 68 cortical regions and 18 subcortical regions using the Desikan–Killiany atlas available in the FreeSurfer software (Fischl et al., 2002). To do this, the subject specific T1-weighted images were back-projected to the atlas using affine registration, as described in the previous studies (Abdelnour et al., 2014; Owen et al., 2013).
2.6. Structural connectivity networks
Different structural connectivity networks were reconstructed with the same Desikan–Killiany parcellations. Firstly, openly available diffusion MRI data was obtained from the MGH-USC Human Connectome Project to create an average template connectome. As in previous studies (Abdelnour et al., 2014; Owen et al., 2013), subject specific structural connectivity was computed on diffusion MRI data: Bedpostx was used to determine the orientation of brain fibers in conjunction with FLIRT, as implemented in the FSL software (Jenkinson et al., 2012). In order to determine the elements of the adjacency matrix, tractography was performed using probtrackx2. 4000 streamlines were initiated from each seed voxel corresponding to a cortical or subcortical gray matter structure and how many of these streamlines reached a target gray matter structure was tracked. The weighted connection between the two structures ci,j, was defined as the number of streamlines initiated by voxels in region i that reach any voxel within region j, normalized by the sum of the source and target region volumes Afterwards, connection strengths were averaged between both directions (ci,j and cj,i) to form undirected edges. To determine the geographic location of an edge, the top 95% of nonzero voxels by streamline count were computed for both edge directions. The consensus edge was defined as the union between both post-threshold sets.
2.7. MEG processing and source reconstruction
MEG recordings were downsampled from 1200 Hz to 600 Hz, then digitally filtered to remove DC offset and any other noisy artifact out-side of the 1 to 160 Hz bandpass range. Since MEG data are in sensor space, meaning they represent the signal observable from sensors placed outside the head, this data needed to be “inverted” in order to infer the neuronal activity that had generated the observed signal by solving the so-called inverse problem. Adaptive spatial filtering algorithms were used from the NUTMEG software tool written in house (Dalal et al., 2004). To prepare for source localization, all MEG sensor locations were co-registered to each subject’s anatomical MRI scans. The lead field (forward model) for each subject was calculated in NUTMEG using a multiple local-spheres head model (three-orientation lead field) and an 8 mm voxel grid which generated more than 5000 dipole sources, all sources were normalized to have a norm of 1. Finally, the MEG recordings were projected into source space using a beamformer spatial filter. Only the sources belonging to the 68 cortical regions were selected to be averaged around the centroid. All dipole sources were labeled based on the Desikan–Killiany parcellations, then sources within a 20 mm radial distance to the centroid of each brain region were extracted, the average time course of each region’s extracted sources served as empirical resting-state data for our proposed model.
2.8. Model parameter estimation
Modeled spectra was converted into power spectral density (PSD) by calculating the absolute value of the frequency response and both modeled and empirical MEG spectra were converted to to dB scale by taking 20 log10() of the PSD. Pearson’s r between modeled PSD and the empirical PSD was used as a goodness of fit metric for estimating model parameters. Pearson’s r was calculated for comparing spectra for each of the regions, and then they were averaged over all the 68 cortical regions. This average Pearson’s r was the objective function for optimization and used for estimating the model parameters. We used a dual annealing optimization procedure in Python and performed parameter optimization both for the M-SGM and the original SGM (Xiang et al., 1997). Parameter initial guesses and bounds are specified in Table 1. The bounds were the same as that in the original study. The dual annealing optimization was performed for three different initial guesses, and the parameter set leading to maximum Pearson’s correlation coefficient was chosen for each subject. The dual annealing settings were: maxiter = 500. All the other settings were the same as default. In the python implementation of this algorithm, one can check the success of convergence by checking the status of the final optimized results, which is an output of the optimizer. We checked this output for all the subjects for both the models to make sure the optimization was successful.
Table 1.
M-SGM parameter values, initial guesses, and bounds for parameter estimation.
| Name | Symbol | Initial value 1 | Initial value 2 | Initial value 3 | Lower/upper bound for optimization |
|---|---|---|---|---|---|
| Excitatory time constant | τ e | 0.012 s | 0.018 s | 0.006 s | [0.005 s, 0.02 s] |
| Inhibitory time constant | τ i | 0.005 s | 0.01 s | 0.018 s | [0.005 s, 0.02 s] |
| Long-range connectivity coupling constant | α | 1 | 0.5 | 0.1 | [0.1, 1] |
| Transmission velocity | υ | 5 m/s | 10 m/s | 18 m/s | [5 m/s, 20 m/s] |
| Alternating population gain | g ei | 4 | 2 | 1 | [0.5, 5] |
| Inhibitory gain | g ii | 1 | 2 | 4 | [0.5, 5] |
| Graph time constant | τ G | 0.006 s | 0.01 s | 0.018 s | [0.005 s, 0.02 s] |
| Excitatory gain | g ee | n/a | n/a | n/a | n/a |
3. Results
3.1. M-SGM fits MEG spectra better
The local mesoscopic model specified in Eqs. (1) and (2) is a modification of the original SGM (Raj, Cai, Xie, Palacios, Owen, Mukherjee, Nagarajan, 2020). Here, we have introduced asymmetry in the two equations by including the term for alternating populations. In the original SGM, the equations for excitatory and inhibitory signals were identical and the alternating population’s transfer function was modeled separately. Therefore, we compare the performance of the two models. We estimated parameters for both the models and then compared the modeled spectra. In particular, we compared the Pearson’s r between the empirical MEG spectra and the modeled spectra in both the cases for the same set of subjects, as shown in Fig. 1A. M-SGM has a statistically significantly higher Pearson’s r than SGM, based on a one-sided paired t-test of the Fisher’s z-transformed Pearson’s r (t-statistic = 12.10, p-value = 2.30e–14). Moreover, Pearson’s r was higher when M-SGM was used instead of SGM for almost every subject, as shown by the blue lines connecting subject-wise points corresponding to the two models.
Fig. 1.
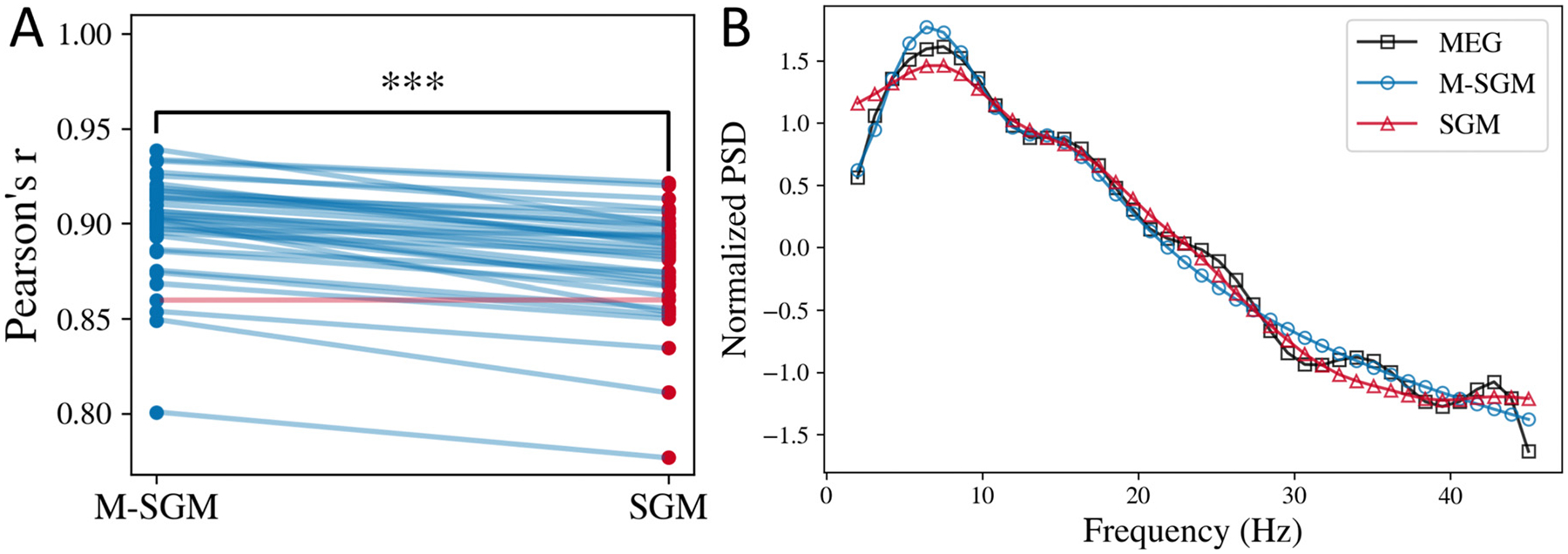
Modified SGM fits MEG spectra better. A: Comparison of average Pearson’s r for the modified versus the original SGM. Each line is joining the Pearson’s r corresponding to a specific subject. The line is in blue color if M-SGM’s Pearson’s r is higher than SGM’s Pearson’s r for that subject, and it is in red for vice versa. In this plot, each line other than one is in blue, implying for most subjects, M-SGM’s Pearson’s r was higher than SGM’s Pearson’s r. B: Average normalized power spectral density (PSD) obtained from MEG, M-SGM, and original SGM.
As seen in Fig. 1B, the average normalized power spectral density predicted by both the original and the modified SGM fit well with the empirical MEG spectra recorded. Both the models can exhibit a primary alpha peak and a secondary beta peak, however, they cannot generate the smaller peaks observed in the MEG spectra at higher frequencies. It is also to be noted that we only estimate the shape of the spectra, not the scale. Therefore, we used Pearson’s r as a metric for the goodness of fit. The scale can be adjusted by scaling the noise term P(ω) appropriately, which will be a part of the future work.
3.2. Both M-SGM and SGM predict alpha and beta spatial distributions
We also wanted to investigate if the eigenmodes (for every k) can capture the spatial distribution of the empirical alpha and beta frequency bands, as was shown for the original SGM. To this end, we sorted the modeled spectral eigenmodes according to their spatial correlation with the empirical alpha and beta bands spatial distribution, respectively. Here, we generated the spatial distribution of alpha and beta bands by summing the MEG spectra from frequencies 8–12 Hz and 13–25 Hz, respectively. The spatial correlation was defined as the Pearson’s r between the regional distribution of the summed alpha and beta spatial distribution and the model predicted eigenmodes which were also summed within the respective frequency bands. After sorting the eigenmodes, we summed the first few eigenmodes that lead to a peak in the spatial correlation. We used these sorted and summed eigenmodes as predictors of the alpha and the beta band activity.
Figs. 2 and 3 demonstrates the spatial correlation of the eigenmodes. As seen in Figs. 2B and 3B, the spatial correlation peaks with a subset of eigenmodes and then decreases again, and is similar for both the M-SGM and the SGM. The black curve in both the cases represent the average of the spatial correlations. Fig. 2A demonstrates the regional distribution of the empirical MEG spectra in the cortical region and that predicted by M-SGM, specifically its sum of top eigenmodes (where the top eigenmodes are those whose sum lead to the maximum spatial correlation) in the alpha band, for two different subjects whose spatial correlations are shaded in blue and brown in Fig. 2B, respectively. The Pearson’s r for Fig. 2A are 0.66 and 0.62 for the left and right columns, respectively. The modeled alpha power spatial distribution is prominent in the posterior regions, which strongly accords with the MEG literature, where alpha peak is well-known to be strongly posterior during rest and eyes closed situations. Based on a one-sided paired t-test between the maximum Pearson’s r obtained from M-SGM and those obtained from SGM, there was no significant difference, with a p-value of 0.799 (t-statistic = −0.85). Both M-SGM and SGM performed similarly in predicting the alpha frequency band’s spatial distribution.
Fig. 2.
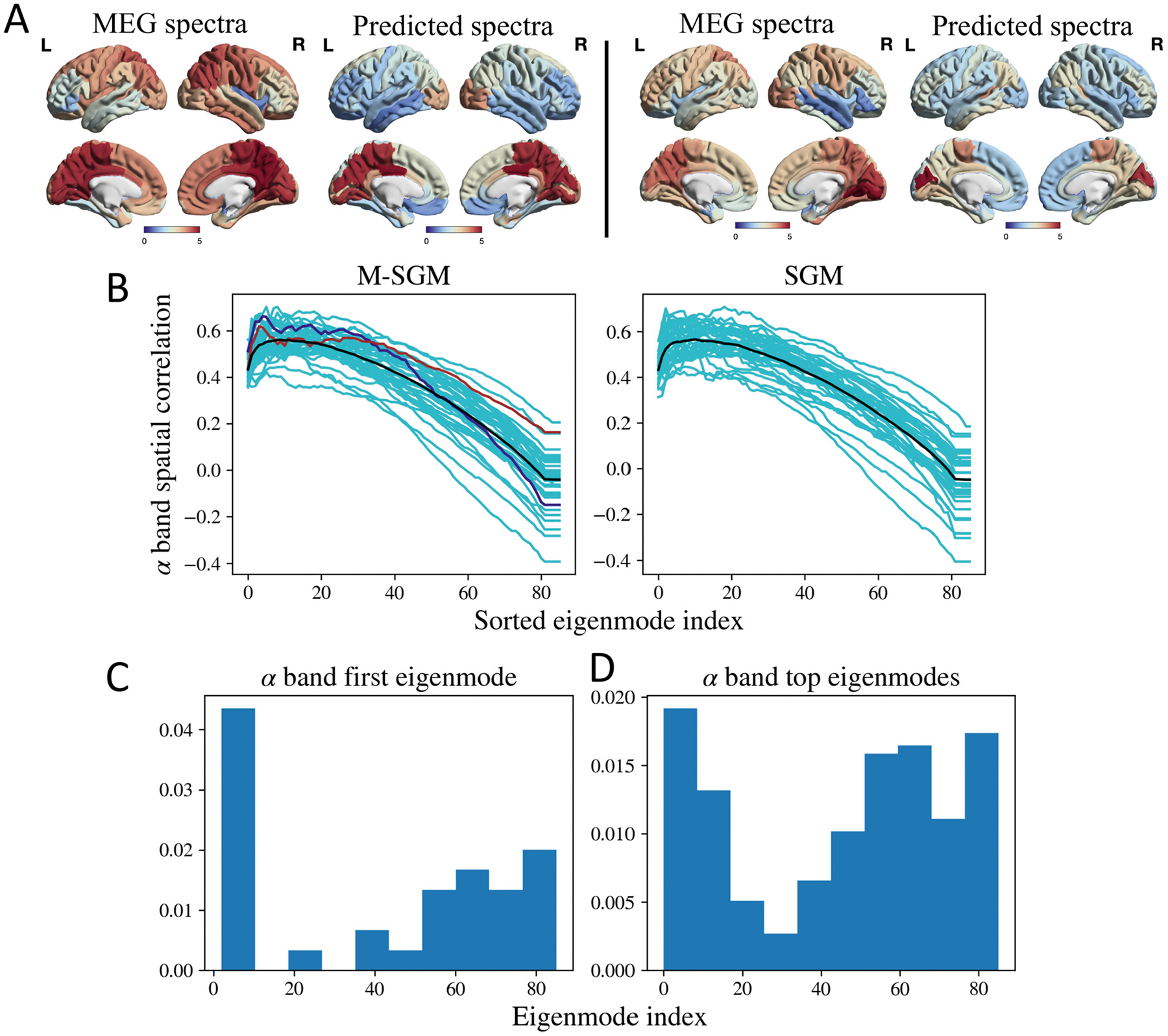
A: Left: MEG spectra and sum of top eigenmodes in the alpha band for a specific subject, shaded in blue in B. The Pearson’s r was 0.66. Right: MEG spectra and sum of top eigenmodes for a different subject, shaded in brown in B. The Pearson’s r was 0.62. B: Spatial correlations for alpha frequency band. The cyan lines correspond to subject-specific spatial correlations obtained as more eigenmodes are added. The black line corresponds to the average of the spatial correlations. The blue and brown lines correspond to two subjects whose spatial distribution has been demonstrated in A. P-value based on a one-sided paired t-test of the maximum Pearson’s r between M-SGM and SGM gave p = 0.799. No statistically significant difference was found between the two. C: Histogram of first eigenmode with maximum spatial correlation with the alpha frequency band. D: Histogram of the top eigenmodes whose summation leads to maximum spatial correlation with the alpha frequency band. Brain surface renderings were generated using BrainNet Viewer (Xia et al., 2013) in MATLAB (The Mathworks, 2020).
Fig. 3.
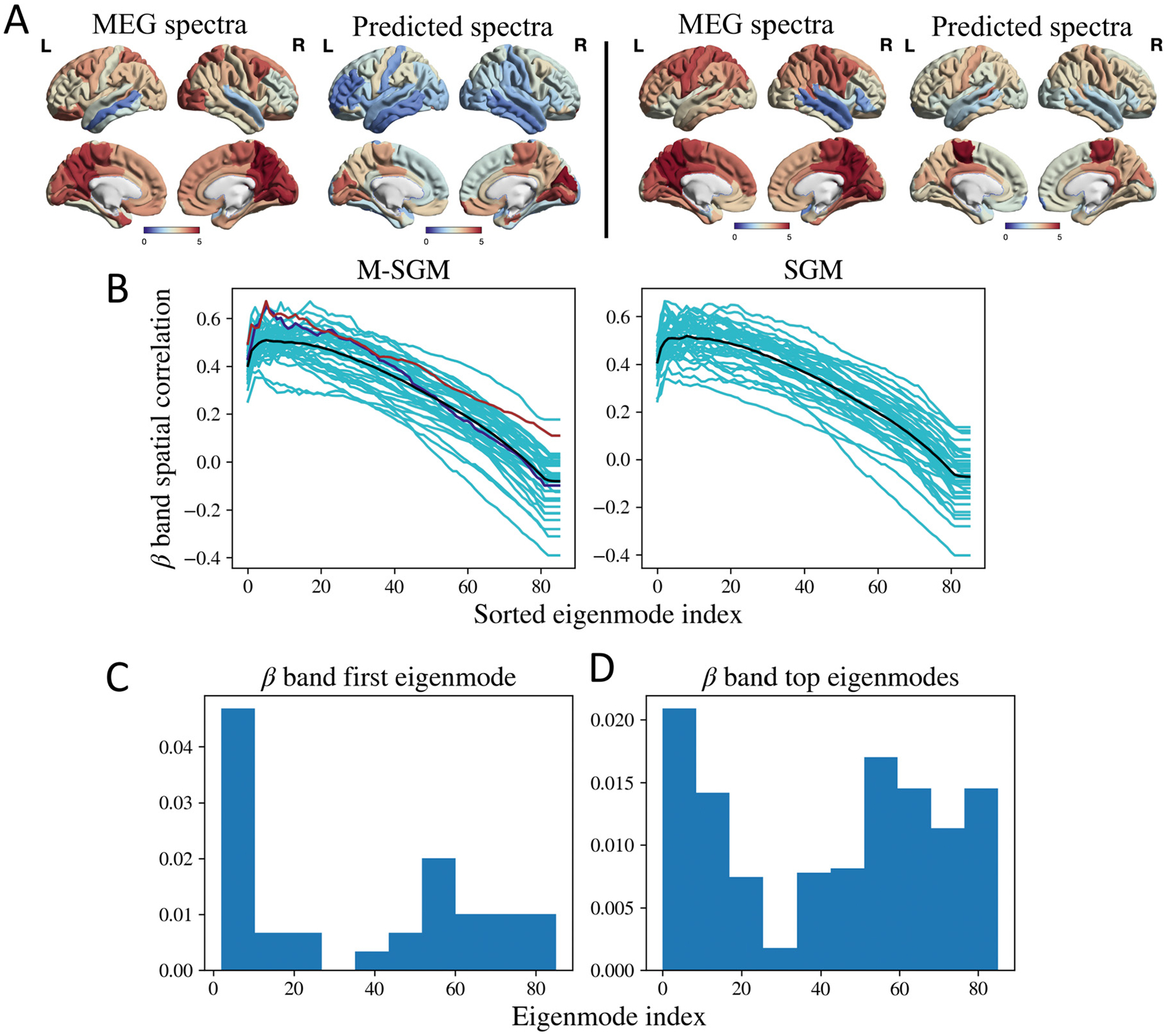
A: Left: MEG spectra and sum of top eigenmodes in the beta band for a specific subject, shaded in blue in B. The Pearson’s r was 0.65. Right: MEG spectra and sum of top eigenmodes for a different subject, shaded in brown in B. The Pearson’s r was 0.67. B: Spatial correlations for beta frequency band. The cyan lines correspond to subject-specific spatial correlations obtained as more eigenmodes are added. The black line corresponds to the average of the spatial correlations. The blue and brown lines correspond to two subjects whose spatial distribution has been demonstrated in A. P-value based on a one-sided paired t-test of the maximum Pearson’s r between M-SGM and SGM gave p = 0.873. The maximum Pearson’s r of M-SGM is statistically not different from that of SGM for the beta band. C: Histogram of first eigenmode with maximum spatial correlation with the beta frequency band. D: Histogram of the top eigenmodes whose summation leads to maximum spatial correlation with the beta frequency band. Brain surface renderings were generated using BrainNet Viewer (Xia et al., 2013) in MATLAB (The Mathworks, 2020).
Fig. 3A demonstrates the regional distribution of the empirical MEG spectra and sum of top eigenmodes in the beta band, for two different subjects whose spatial correlations are shaded in blue and brown in Fig. 3B, respectively. The Pearson’s r for Fig. 3A are 0.65 and 0.67 for the left and right columns, respectively. Based on a one-sided paired t-test between the maximum Pearson’s r obtained from M-SGM versus those obtained from SGM, no statistically significant difference was found between the two, with a p-value of 0.873 (t-statistic = −1.16). Both M-SGM and SGM performed similarly in predicting the beta frequency band’s spatial distribution.
In order to explore which graph eigenmodes most contribute to the summed model in above figures, we plot in Figs. 2C, D and 3C, D histograms of the eigenmode index of each participating eigenmode. We show both the single most-maximally contributing eigenmode, as well as all eigenmodes that appear up to the peak observed in Figs. 2B and 3B. We also observed that neither the first eigenmode with maximum spatial correlation, nor the top eigenmodes whose sum lead to the maximum spatial correlation, are necessarily those that appear as the first few eigenmodes as ordered by their eigenvalue.
4. Discussions
In this work, we demonstrated that a biophysical linearized spectral graph model can generate frequency-rich spectra that accurately match the empirical MEG spectra, with an overall accuracy higher than that of the original SGM (Raj, Cai, Xie, Palacios, Owen, Mukherjee, Nagarajan, 2020). SGM contained local model elements derived from a control theory viewpoint, due to which the local parameters and gain terms lacked classical interpretability in terms of extant neural mass models. The current reformulation brings the M-SGM in line with classical neural masses. In M-SGM, we have introduced an asymmetry in the excitatory and inhibitory population equations due to the alternating populations term. This asymmetry is the key distinguishing feature between M-SGM and SGM, and is the reason why the M-SGM is biophysically more realistic. Numerous non-linear models currently adopt Wilson-Cowan model type formulation at the mesoscopic scale as a biologically more realistic and interpretable model, involving coupled excitatory and inhibitory populations (Destexhe and Sejnowski, 2009; Kilpatrick, 2013). This coupling/interaction between excitatory and inhibitory populations is more explicitly defined in M-SGM, bringing it in alignment with the larger literature on Wilson–Cowan models. The primary difference between Wilson–Cowan models and M-SGM is that the coupling expression in M-SGM is linear while it is non-linear in the former. In M-SGM, we also included the cortical as well as subcortical region eigenvalues in calculation of the modeled spectra, unlike in SGM where only cortical eigenvalues were included.
This modified model retains all the attractive features of the original SGM: it is hierarchical, analytic, graph-based, and is parameterized by a parsimonious set of biophysically interpretable global parameters: the neural gains, time constants, conduction velocity, and macroscopic coupling. These model parameters admit physical interpretations and can be potentially controlled by neuromodulation (Shine et al., 2018). Due to its closed-form analytical solution in terms of frequency responses, the M-SGM can be fitted directly to regional MEG power spectra, without requiring any time-consuming simulations or numerical integration.
M-SGM has an excellent ability to capture the spatial patterns of empirical alpha and beta frequency bands, requiring only 5–10 graph eigenmodes to do so. To our knowledge, the presented SGM and M-SGM are the only models currently available that can simultaneously predict both the regional spectra as well as the spatial distribution of the empirical alpha and beta band activity. In the latter task there was no difference in performance between M-SGM and the original SGM. We see that quantitatively, the modified SGM’s modeled spectra captures the MEG spectra better than the original SGM, but its ability to predict the spatial distribution of the empirical alpha and beta frequency bands is no different from that of the original SGM. Please recall, the parameter optimization was done to maximize spectral fits only. A potential future study will involve incorporating both spectral as well as spatial correlations to obtain optimal model parameters. Even though the quantitative performance is only better when comparing spectral correlations, it is to be noted that this modified local mesoscopic model is biophysically similar in formulation to the nonlinear neural mass models.
4.1. No natural ordering of eigenmodes
Surprisingly, in our analysis of which graph eigenmodes most contribute to the summation in the M-SGM (Figs. 2C, D and 3C, D), we found that the eigenmodes that maximally contribute to the spatial patterning of alpha or beta power are not necessarily those that appear as the first few eigenmodes as ordered by their eigenvalue. Although our results clearly indicate that the first few eigenmodes have the highest frequency of participation, almost all eigenmodes exhibit some ability to participate in the model summation. That the “natural ordering” of eigenmodes (i.e. in increasing order of eigenvalue) is not reflected in fitted M-SGM, at least as far as predicting band-limited spatial patterns, is intriguing. Previous eigendecomposition models on graphs have found a strong natural ordering. E.g. Abdelnour et al. report that only the first few Laplacian eigenmodes (with smallest eigenvalues) are required to resemble empirical functional connectivity of resting state BOLD fMRI (Abdelnour et al., 2018; 2021); similar results were reported by Atasoy and others (Atasoy et al., 2016; Preti and De Ville, 2019; Xie et al., 2021). Other studies involve a series expansion of the graph adjacency or Laplacian matrices (Becker et al., 2018; Deslauriers-Gauthier et al., 2020; Glomb et al., 2020; Robinson et al., 2016; Tewarie et al., 2020), which also amount to weighting the first natural eigenvectors more heavily in the summation. This difference between ordering of eigenmodes in M-SGM versus previous works might reflect the different context here: MEG rather than fMRI, and modeling of spectral power instead of functional connectivity. It is also possible that since our M-SGM model has far more expressability and a richer repertoire of wideband activity spectrum, the model parameters are capable of tuning a wider range of eigenmodes. This aspect was also noted in a recent thorough exposition of complex Laplacian eigenmodes (Xie et al., 2021). Whether there is a natural ordering of eigenmodes that account for observed functional activity patterns or not remains an open question. The ability of the brain’s connectome to engage a wide range of eigenmodes might be an important feature of realistic and rich brain behavior - an aspect that merits a deeper future exploration.
4.2. Relationship to other work
Due to their parsimony a key feature of this and the original SGM is that parameter inference is far more tractable than various non-linear modeling approaches such as The Virtual Brain (Ritter et al., 2013), where multiple refinement steps are required for inference of a larger set of free parameters. While SGM and M-SGM cannot yield a repertoire of dynamical solutions that the detailed non-linear modeling counter-parts can, it is unclear if incorporating such non-linearities are required at the macroscopic scale (Nozari et al., 2020). In comparison to methods based on coupled NMMs, the inference of SGM and M-SGM model parameters can be realized directly from empirical wideband regional power spectra rather than from functional correlation structures like FC. Indeed, cutting edge tools like The Virtual Brain do not attempt to fit to empirical wideband power spectra, relying instead on capturing the second-order correlation structures of brain activity after filtering out high-frequency signals or removing the carrier frequency and retaining only the (slowly-varying) Hilbert amplitude envelope. The latter aspect was analyzed elegantly using a linearized coupled NMM by Tewarie et al. (2019); however their model is only accessible via numerical integration and time series simulations, unlike ours.
Another point to note is that there are different interpretations of the eigenmodes. In M-SGM, SGM and its subsequent extension, the eigenmodes were obtained from the eigen-decomposition of the complex-valued Laplacian matrix, taking into account the global coupling and conduction speed (Raj et al., 2020; Xie et al., 2021). Previous works have been based on obtaining the eigenvectors of a real-valued Laplacian obtained from the structural connectome (Abdelnour et al., 2018; 2021; Atasoy et al., 2016; Becker et al., 2018; Deslauriers-Gauthier et al., 2020; Glomb et al., 2020; Preti and De Ville, 2019; Tewarie et al., 2020) or by eigen-decomposition of the solution to the Helmholtz equation on a curved cortical surface using neural field theory (Robinson et al., 2016).
4.3. Limitations, potential applications, and future work
By design, the model’s frequency spectra can exhibit two peaks at most, whereas empirical MEG spectra (see Fig. 1A) have higher frequency peaks than alpha and beta. Although it is possible to generate those higher beta or gamma peak as a primary peak by varying the local time constants, additional peaks cannot be generated using the current model under plausible parameter regimes. In the future, we will extend the model to capture the peaks in the higher beta and gamma regions as well - this will require additional local population coupling and complexity. However, we note that our current model is already fully capable of reproducing the secular frequency fall-off seen in empirical spectra, e.g. the hypothesized 1/fα behavior. Future work will also involve including spatial correlation in addition to spectral correlation in the cost function for model parameter estimation, as well as exploring region-specific model parameters to incorporate spatial heterogeneity better.
This model can be extended to investigate various aspects of functional brain activity. Firstly, this work can be extended to investigate temporal state changes in the functional activity. One way would be by introducing a temporal component to the model parameters. Secondly, this work can also be extended to investigate functional activity in different brain states such as sleep, task-focused, and unconscious. As mentioned earlier, we also plan to extend this model to generate peaks in the higher beta and gamma regions of the modeled spectra. Future work will also involve ensuring that the system is stable with the estimated parameters, using adaptive gain control.
This modeling approach can be used to investigate underlying biophysical mechanisms involved in different neurological diseases, as well. For example, we recently estimated regionally varying local model parameters for empirical MEG spectra collected for healthy and Alzheimer’s disease subjects. We then found that the excitatory and inhibitory parameters were differentially distributed for the healthy versus the Alzheimer’s disease subjects, indicating an excitatory/inhibitory imbalance (unpublished data). Such investigations can be extended to various other neurological diseases as well. Lastly, it will be of interest to extend this model to include other modalities such as fMRI and EEG, as well. In these biomedical applications, the parsimony and inferrability of the SGM model will prove to be critical assets, especially in comparison with current high-dimensional and non-linear models.
Acknowledgments
This work was supported by NIH grants R01NS092802, R01NS183412, R01AG062196, R01AG072753, R01EB022717, R01DC013979, R01NS100440, R01DC176960, R01DC017091, UCOP-MRP-17-454755 and an industry research contract from Ricoh MEG Inc. The template Human Connectome Project (HCP) connectome used in the preparation of this work were obtained from the MGH-USC HCP database (https://ida.loni.usc.edu/login.jsp). The HCP project’s MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga and Van Wedeen; U01MH093765) is supported by the NIH Blueprint Initiative for Neuroscience Research Grant; the National Institutes of Health grant P41EB015896; and the Instrumentation Grants S10RR023043, 1S10RR023401, 1S10RR019307. Collectively, the HCP is the result of efforts of co-investigators from the University of Southern California, Martinos Center at Massachusetts General Hospital (MGH), Washington University, and the University of Minnesota. Additionally, we would like to acknowledge Kamalini G. Ranasinghe for helping with generating the brain surface renderings.
Footnotes
Declaration of Competing Interest
Authors declare that they have no conflict of interest.
Credit authorship contribution statement
Parul Verma: Methodology, Software, Formal analysis, Writing – original draft. Srikantan Nagarajan: Conceptualization, Methodology, Writing – review & editing, Supervision, Funding acquisition. Ashish Raj: Conceptualization, Methodology, Writing – review & editing, Supervision, Funding acquisition.
Data availability
The code and processed datasets (processed connectivity and distance matrices, and the MEG spectra) used in this work are available at https://github.com/Raj-Lab-UCSF/spectrome-revisited and are based on the original SGM repository (Xie et al., 2020).
References
- Abdelnour F, Dayan M, Devinsky O, Thesen T, Raj A, 2018. Functional brain connectivity is predictable from anatomic network’s Laplacian eigen-structure. NeuroImage 172, 728–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abdelnour F, Dayan M, Devinsky O, Thesen T, Raj A, 2021. Algebraic relationship between the structural network’s Laplacian and functional network’s adjacency matrix is preserved in temporal lobe epilepsy subjects. NeuroImage 228, 117705. [DOI] [PubMed] [Google Scholar]
- Abdelnour F, Raj A, Dayan M, Devinsky O, Thesen T, 2015. Estimating function from structure in epileptics using graph diffusion model. In: 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), pp. 466–469. [Google Scholar]
- Abdelnour F, Voss HU, Raj A, 2014. Network diffusion accurately models the relationship between structural and functional brain connectivity networks. NeuroImage 90, 335–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E, 2006. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci 26 (1), 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atasoy S, Donnelly I, Pearson J, 2016. Human brain networks function in connectome-specific harmonic waves. Nat. Commun 7 (1), 10340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auffarth B, 2007. Spectral Graph Clustering. Universitat de Barcelona, Course Report for Technicas Avanzadas de Aprendizaj, at Universitat Politecnica de Catalunya. [Google Scholar]
- Becker CO, Pequito S, Pappas GJ, Miller MB, Grafton ST, Bassett DS, Preciado VM, 2018. Spectral mapping of brain functional connectivity from diffusion imaging. Sci. Rep 8 (1), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boustani SE, Destexhe A, 2009. A master equation formalism for macroscopic modeling of asynchronous irregular activity states. Neural Comput. 21 (1), 46–100. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O, 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci 10 (3), 186–198. [DOI] [PubMed] [Google Scholar]
- Dalal SS, Zumer JM, Agrawal V, Hild KE, Sekihara K, Nagarajan SS, 2004. Nutmeg: a neuromagnetic source reconstruction toolbox. Neurol. Clin. Neurophysiol 2004, 52. [PMC free article] [PubMed] [Google Scholar]
- David O, Friston KJ, 2003. A neural mass model for MEG/EEG:: coupling and neuronal dynamics. NeuroImage 20 (3), 1743–1755. [DOI] [PubMed] [Google Scholar]
- Deco G, Senden M, Jirsa V, 2012. How anatomy shapes dynamics: a semi-analytical study of the brain at rest by a simple spin model. Front. Comput. Neurosci 6, 68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, et al. , 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage 31 (3), 968–980. [DOI] [PubMed] [Google Scholar]
- Deslauriers-Gauthier S, Zucchelli M, Frigo M, Deriche R, 2020. A unified framework for multimodal structure-function mapping based on eigenmodes. Med. Image Anal 66, 101799. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Sejnowski TJ, 2009. The Wilson–Cowan model, 36 years later. Biol. Cybern 101 (1), 1–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM, 2002. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron 33 (3), 341–355. [DOI] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Breakspear M, 2015. The connectomics of brain disorders. Nat. Rev. Neurosci 16 (3), 159–172. [DOI] [PubMed] [Google Scholar]
- Fox MD, Raichle ME, 2007. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci 8 (9), 700–711. [DOI] [PubMed] [Google Scholar]
- Ghosh A, Rho Y, McIntosh AR, Kötter R, Jirsa VK, 2008. Cortical network dynamics with time delays reveals functional connectivity in the resting brain. Cogn. Neurodyn 2 (2), 115–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glomb K, Queralt JR, Pascucci D, Defferrard M, Tourbier S, Carboni M, Rubega M, Vulliemoz S, Plomp G, Hagmann P, 2020. Connectome spectral analysis to track EEG task dynamics on a subsecond scale. NeuroImage 221, 117137. [DOI] [PubMed] [Google Scholar]
- Hermundstad AM, Bassett DS, Brown KS, Aminoff EM, Clewett D, Freeman S, Frithsen A, Johnson A, Tipper CM, Miller MB, et al. , 2013. Structural foundations of resting-state and task-based functional connectivity in the human brain. Proc. Natl. Acad. Sci 110 (15), 6169–6174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Mandl RCW, Kahn RS, Pol HEH, 2009. Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum. Brain Mapp 30 (10), 3127–3141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P, 2009. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci 106 (6), 2035–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM, 2012. Fsl. NeuroImage 62 (2), 782–790. 20 YEARS OF fMRI [DOI] [PubMed] [Google Scholar]
- Jirsa VK, Jantzen KJ, Fuchs A, Kelso JAS, 2002. Spatiotemporal forward solution of the EEG and MEG using network modeling. IEEE Trans. Med. Imaging 21 (5), 493–504. [DOI] [PubMed] [Google Scholar]
- Kilpatrick ZP, 2013. Wilson–Cowan Model. Springer New York, New York, NY, pp. 1–5. [Google Scholar]
- Kondor RI, Lafferty J, 2002. Diffusion kernels on graphs and other discrete structures. In: Proceedings of the 19th International Conference on Machine Learning, vol. 2002, pp. 315–322. [Google Scholar]
- Larsen R, Nielsen M, Sporring J, 2006. Medical image computing and computer-assisted intervention–MICCAI 2006. In: 9th International Conference, Copenhagen, Denmark, October 1–6, 2006, Proceedings, Part I, vol. 4190. Springer. [Google Scholar]
- Mišić B, Betzel RF, Nematzadeh A, Goni J, Griffa A, Hagmann P, Flammini A, Ahn Y-Y, Sporns O, 2015. Cooperative and competitive spreading dynamics on the human connectome. Neuron 86 (6), 1518–1529. [DOI] [PubMed] [Google Scholar]
- Mišić B, Sporns O, McIntosh AR, 2014. Communication efficiency and congestion of signal traffic in large-scale brain networks. PLoS Comput. Biol 10 (1), E1003427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muldoon SF, Pasqualetti F, Gu S, Cieslak M, Grafton ST, Vettel JM, Bassett DS, 2016. Stimulation-based control of dynamic brain networks. PLoS Comput. Biol 12 (9), 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagawa TT, Woolrich M, Luckhoo H, Joensson M, Mohseni H, Kringelbach ML, Jirsa V, Deco G, 2014. How delays matter in an oscillatory whole-brain spiking-neuron network model for MEG alpha-rhythms at rest. NeuroImage 87, 383–394. [DOI] [PubMed] [Google Scholar]
- Ng A, Jordan M, Weiss Y, 2001. On spectral clustering: analysis and an algorithm. Adv. Neural Inf. Process. Syst 14, 849–856. [Google Scholar]
- Nozari E, Stiso J, Caciagli L, Cornblath EJ, He X, Bertolero MA, Mahadevan AS, Pappas GJ, Bassett DS, 2020. Is the brain macroscopically linear? A system identification of resting state dynamics. arXiv preprint arXiv:2012.12351. [Google Scholar]
- Owen JP, Li Y-O, Ziv E, Strominger Z, Gold J, Bukhpun P, Wakahiro M, Friedman EJ, Sherr EH, Mukherjee P, 2013. The structural connectome of the human brain in agenesis of the corpus callosum. NeuroImage 70, 340–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H-J, Friston K, 2013. Structural and functional brain networks: from connections to cognition. Science 342 (6158), 1238411. [DOI] [PubMed] [Google Scholar]
- Preti MG, De Ville DV, 2019. Decoupling of brain function from structure reveals regional behavioral specialization in humans. Nat. Commun 10 (1), 1–7. https://www.nature.com/articles/s41467-019-12765-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A, Cai C, Xie X, Palacios E, Owen J, Mukherjee P, Nagarajan S, 2020. Spectral graph theory of brain oscillations. Hum. Brain Mapp 41 (11), 2980–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritter P, Schirner M, McIntosh AR, Jirsa VK, 2013. the virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connect. 3 (2), 121–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson PA, Rennie CJ, Rowe DL, O’Connor SC, Gordon E, 2005. Multiscale brain modelling. Philos. Trans. R. Soc. B 360 (1457), 1043–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson PA, Zhao X, Aquino KM, Griffiths JD, Sarkar S, Mehta-Pandejee G, 2016. Eigenmodes of brain activity: neural field theory predictions and comparison with experiment. NeuroImage 142, 79–98. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O, van Leeuwen C, Breakspear M, 2009. Symbiotic relationship between brain structure and dynamics. BMC Neurosci. 10 (1), 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimizu H, Haken H, 1983. Co-operative dynamics in organelles. J. Theor. Biol 104 (2), 261–273. [DOI] [PubMed] [Google Scholar]
- Shine JM, Aburn MJ, Breakspear M, Poldrack RA, 2018. The modulation of neural gain facilitates a transition between functional segregation and integration in the brain. Elife 7, E31130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strogatz SH, 2001. Exploring complex networks. Nature 410 (6825), 268–276. [DOI] [PubMed] [Google Scholar]
- Tewarie P, Abeysuriya R, Byrne A, O’Neill GC, Sotiropoulos SN, Brookes MJ, Coombes S, 2019. How do spatially distinct frequency specific MEG networks emerge from one underlying structural connectome? The role of the structural eigenmodes. NeuroImage 186, 211–220. [DOI] [PubMed] [Google Scholar]
- Tewarie P, Prasse B, Meier JM, Santos F, Douw L, Schoonheim MM, Stam CJ, Mieghem PSV, Hillebrand A, 2020. Mapping functional brain networks from the structural connectome: relating the series expansion and eigenmode approaches. NeuroImage 216, 116805. [DOI] [PubMed] [Google Scholar]
- The Mathworks Inc., 2020., Natick, Massachusetts. MATLAB version 9.8.0.1451342 (R2020a) Update 5. [Google Scholar]
- Wilson HR, Cowan JD, 1973. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13 (2), 55–80. [DOI] [PubMed] [Google Scholar]
- Xia M, Wang J, He Y, 2013. BrainNet viewer: a network visualization tool for human brain connectomics. PLoS One 8 (7), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang Y, Sun DY, Fan W, Gong XG, 1997. Generalized simulated annealing algorithm and its application to the Thomson model. Phys. Lett. A 233 (3), 216–220. [Google Scholar]
- Xie X, Cai C, Damasceno PF, Nagarajan SS, Raj A, 2021. Emergence of canonical functional networks from the structural connectome. NeuroImage 237, 118190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie XH, Stanley M, Damasceno PF, 2020. Raj-lab-UCSF/spectrome: Spectral graph model of neural dynamics on connectomes.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The code and processed datasets (processed connectivity and distance matrices, and the MEG spectra) used in this work are available at https://github.com/Raj-Lab-UCSF/spectrome-revisited and are based on the original SGM repository (Xie et al., 2020).


