Assessing dengue infection risk in the southern region of Taiwan: implications for control

SUMMARY

Dengue, one of the most important mosquito-borne diseases, is a major international public health concern. This study aimed to assess potential dengue infection risk from Aedes aegypti in Kaohsiung and the implications for vector control. Here we investigated the impact of dengue transmission on human infection risk using a well-established dengue–mosquito–human transmission dynamics model. A basic reproduction number (R₀)-based probabilistic risk model was also developed to estimate dengue infection risk. Our findings confirm that the effect of biting rate plays a crucial role in shaping R₀ estimates. We demonstrated that there was 50% risk probability for increased dengue incidence rates exceeding 0·5–0·8 wk⁻¹ for temperatures ranging from 26°C to 32°C. We further demonstrated that the weekly increased dengue incidence rate can be decreased to zero if vector control efficiencies reach 30–80% at temperatures of 19–32°C. We conclude that our analysis on dengue infection risk and control implications in Kaohsiung provide crucial information for policy-making on disease control.

INTRODUCTION

Recently, Bhatt et al. [1] estimated that there were nearly 390 million [95% credible interval (CrI) 284–528] dengue infections annually in 2010, of which up to 96 million (95% CrI 67–136) developed clinical or subclinical symptoms with different levels of severity. On the other hand, Asia bore 67 (95% CrI 47–94) million apparent infections (~70%) of this burden [1]. The high disease prevalence, lack of a registered vaccine or other prophylactic measures, and absence of specific treatment make dengue fever a great threat to public health globally [2]. The viruses and their predominant mosquito vector, Aedes aegypti (yellow fever mosquito), are endemic to most of the tropical and subtropical regions of the world [3].

Southern Taiwan is located in a tropical region with relatively high temperature and relative humidity (RH) year-round, forming an ideal condition for the growth of the vector of dengue fever, i.e. mosquito. Historical epidemics of dengue in Taiwan have been documented in 1902, 1915, and 1922 in Penghu Islet; in southern regions of Taiwan in 1924, 1927, and 1931; and throughout the island during 1942–1943 [4]. The most well known dengue outbreaks in Taiwan have varied since 1987 in that the prevalence has been higher in southern Taiwan [4]. In general, dengue epidemics have occurred in Taiwan annually for the past decade and the largest epidemic occurred in southern Taiwan in 2002 with 52 imported and 5336 indigenous cases that peaked around September–December [5, 6].

Patterns of dengue infection vary over time owing to the effects of extrinsic, e.g. climate [3, 7–9] and intrinsic, e.g. predictor–prey dynamics between the pathogen and the host population [9–11], and immunity and viral factors [12, 13]. Incidence patterns reflect the complex interactions of all these factors. Wu et al. [14] indicated that weather variability such as monthly maximum and minimum temperatures, rainfall, and RH are identified as meaningful and significant indicators for the increasing occurrence of dengue fever in the Taiwan region. Chen et al. [15] indicated that warmer temperature with 3-month lag, elevated humidity with high mosquito density increased the transmission rate of dengue fever infection in southern Taiwan. Lambrechts et al. [7] revealed that short-term temperature fluctuations had significant impact on dengue virus transmission by female A. aegypti.

The dynamics in mosquito–human dengue transmission is a complex process involving many potentially important factors. For vector-borne diseases, the vectorial capacity (V) or the basic reproduction number (R₀) is usually used to characterize the key components involved in vector–human transmission dynamics [7, 16–18]. V captures key parameters of an insect's role in pathogen transmission, whereas R₀ characterizes the number of secondary cases generated by a primary infectious case via the vectors in an entirely susceptible population [19]. R₀ can be determined by a range of entomological and epidemiological parameters [7, 9, 16–18, 20]. Moreover, R₀ is a key epidemiological determinant that provides an index of transmission intensity and establishes threshold criteria for control practices [16].

The key factors used to determine V and R₀ include vector density, vector biting rate, vector survival probability, extrinsic incubation period (EIP) of the parasite within the mosquito, transmission coefficients between vector and human, and recovery rate of hosts from infection. In infinite human populations, heterogeneous biting increases R₀ because humans who are bitten most often are also most likely to become infected and then, by infecting a large number of mosquitoes, amplify transmission [10]. On the other hand, temperature fluctuations have important impacts on the time whenever mosquitoes become infectious and hence impact on R₀ and V [7, 20].

It is recognized that the interactions between coupled mosquito−human population dynamics and dengue transmission play an important role in the development of dengue fever. A variety of mathematical and computational models have been proposed for elucidating the nonlinear transmission dynamics and for enhancing our understanding of the within-host spread of diseases [13, 17, 18, 21–24].

The incidence of dengue fever in Taiwan varies widely from year to year, showing nearly a tenfold difference between years, indicating that the presence of non-stationarity and nonlinearity exists in incidence data. Hence, the transmission and population dynamics of dengue fever in southern Taiwan are poorly understood. The purpose of this study was to develop a R₀-based probabilistic risk framework by incorporating the dynamic model of vector–human dengue transmission to predict dengue infection risk in southern Taiwan. To examine the dengue population dynamics and potential risk of infection, a well-established mathematical model of dengue transmission was adopted to study the potential impact of dengue transmission on infection risk. The implications on the dengue vector control were also discussed.

MATERIALS AND METHODS

Study data

Here we used the city of Kaohsiung, a major dengue epidemic area, located on the southwestern coast of Taiwan (22° 48′ N to 23° 47′ N, 120° 176′ E to 121° 05′ E) as a study area. Kaohsiung is the second largest metropolitan area with a typical tropical climate. Thus, Kaohsiung is a densely populated region (~2·78 million persons within a total area of 3000 km²) with very high suitability for dengue transmission and can provide adequate data for setting the model parameters.

All monthly confirmed dengue cases were provided by the Taiwan Center of Disease Control (Taiwan CDC; http://www.cdc.gov.tw) for the period 2004–2009 including indigenous and imported cases. Monthly dengue incidence rates per 100 000 population were estimated from monthly confirmed dengue cases over the specific year-end population size. The monthly maximum, mean, and minimum temperatures in Kaohsiung during 2004–2009 were used. Here the monthly minimum and maximum temperatures are defined as the monthly average of the daily minimum and maximum temperatures, respectively. The time-series temperature profiles were adopted from the Center Weather Bureau, Taiwan (http://www.cwb.gov.tw/V7/index.htm).

Dengue−mosquito−human transmission model

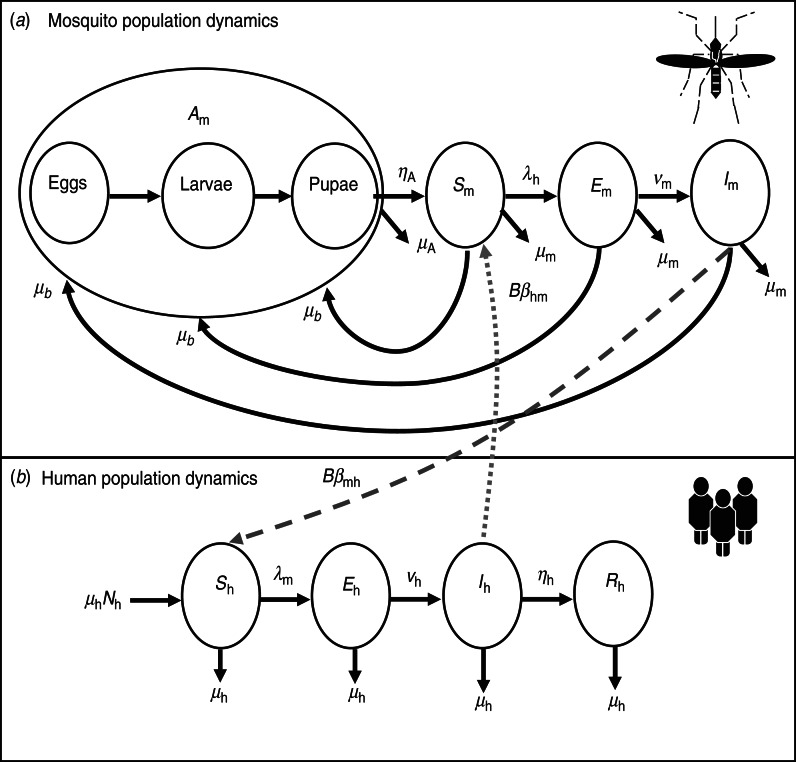
By studying a model of dengue−mosquito−human transmission dynamics built on past well-developed models [13, 17, 18, 22–24], we explored the consequences of vector–host interactions involving in two levels: (i) mosquito population dynamics and (ii) human population dynamics. The essential features of the present model are depicted in Figure 1. The system of ordinary differential equations corresponding to the model in Figure 1 is listed in Table 1 [equations (T1)–(T8)].

Fig. 1.

Mosquito–human dengue transmission model describing the interaction of (a) mosquito population and (b) human population dynamics in the present study.

Table 1.

Summary of governing equations for dynamic model of mosquito–human dengue transmission (Fig. 1) and basic reproduction numbers

Equations		Meaning
Mosquito population dynamics
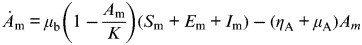	(T1)	Aquatic phase
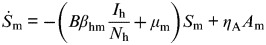	(T2)	Susceptible mosquito
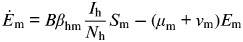	(T3)	Exposed mosquito
İm = νmEm − μmIm	(T4)	Infected mosquito
Human population dynamics
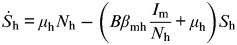	(T5)	Susceptible human
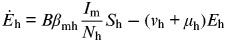	(T6)	Exposed human
İh = vhEh − (ηh + μh)Ih	(T7)	Infected human
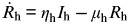	(T8)	Resistant human
Basic reproduction number (R0)*
R02=Rmh × Rhm	(T9)	Aggregated R0
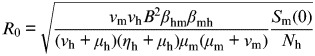	(T10)	Basic reproduction number
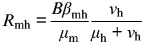	(T11)	R0 from mosquito to human
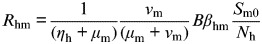	(T12)	R0 from human to mosquito

μ_h, Human mortality rate (d⁻¹); N_h, total human population; B, biting rate (d⁻¹); β_mh, transmission probability from vector to host per bite (bite⁻¹); ν_h, intrinsic incubation rate (d⁻¹); η_h, mean viraemic rate (d⁻¹); μ_b, number of eggs at each deposit per capita (d⁻¹); K, maximal capacity of larvae; η_A, average aquatic transition rate (d⁻¹); μ_A, average aquatic mortality rate (d⁻¹); β_hm, transmission probability from host to vector per bite (bite⁻¹); μ_m, average mortality rate for mosquito in adult stage (d⁻¹); ν_m, extrinsic incubation rate (d⁻¹); S_m(0), initial value of susceptible mosquitoes.

^*Adopted from Dumont et al. [25].

Figure 1 depicts the dengue transmission dynamics characterized specifically in terms of the biting rate of mosquitoes and the transmission probabilities following a bite. Briefly, the mosquito's life cycle is divided into an aquatic phase (A_m) and adult female stages (Fig. 1a). The immature period of the aquatic phase is divided into eggs, larvae, and pupae. Adult female mosquitoes may be (i) uninfected and susceptible (S_m); (ii) exposed and carrying dengue viruses but not yet capable of transmitting dengue (E_m); or (iii) carrying the viruses and fully infectious (I_m).

The aquatic phase converts to the adult female stage at an average transition rate η_A (d⁻¹). Parsimoniously, we used aquatic phase (A_m) to represent the immature period and assumed that aquatic phase and all adult stages suffer the average mortality rate of μ_A and μ_m (d⁻¹), respectively. Moreover, it is assumed that adult female mosquitoes lay eggs at the same average rate μ_b (d⁻¹). Uninfected adult female mosquitoes acquire infection at a rate dependent on the force of infection (λ_h, d⁻¹) and the extrinsic incubation rate (ν_m, d⁻¹). The force of infection resulting from humans (λ_h) depends on the biting rate of mosquitoes (B, d⁻¹), the transmission probability from host to vector per bite (β_hm, bite⁻¹), and the infected humans (I_h). Thus λ_h can be expressed as Bβ_hmI_h/N_h where N_h is the total human population.

The susceptible-exposed-infectious-recovery (SEIR) model was used to simulate the demographic dynamics of the human population dengue transmission in Kaohsiung with an assumption of equal birth and mortality rate μ_h (d⁻¹) (Fig. 1b). Susceptible individuals (S_h) acquire infection at the force of infection rate (λ_m, d⁻¹), that depends on the biting rate of mosquitoes (B), the transmission probability from vector to host per bite (β_mh, bite⁻¹), and the infected mosquitoes (I_m). Therefore, λ_m can be written as Bβ_mhI_m/N_m, where N_m is the total mosquito population. The exposed humans (E_h) acquire infection at a rate ν_h (d⁻¹) depending on the duration of the intrinsic incubation period. Most infected individuals (I_h) recover at a rate η_h (d⁻¹) into a resistant compartment (R_h).

Studying the force of infection rates of λ_h and λ_m, biting rate is seen as the most crucial parameter needing to be estimated. Barbazan et al. [20] indicated that the daily biting rate can be calculated from the duration of the gonotrophic cycle (GC) as B = 1/GC, where GC is the time spent in digesting a bloodmeal and for eggs to reach maturity between two bloodmeals. Focks et al. [26] used enzyme kinetics to determine the temperature-dependent gonotrophic development rate (i.e. 1/GC). Here we analogized the temperature-dependent gonotrophic rate as the biting rate based on the GC concept. In doing so, the temperature-dependent biting rate has the form as [26],

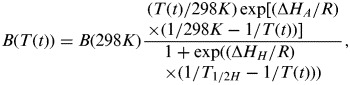(1)

where B(T(t)) is the biting rate per mosquito (d⁻¹) at temperature T (K) on day t, B(298 K) is the biting rate at 298 K (d⁻¹), T is temperature (K), T_½H is the temperature (K) when half of the enzyme is deactivated from high temperature, ΔH_A and ΔH_H are the thermodynamic enthalpy changes (cal mol⁻¹), and R is the universal gas constant (1·987 cal mol⁻¹ K⁻¹).

R₀ estimations

R₀ in dengue−mosquito−human dynamics is the product of the number of infectious mosquitoes generated during the infectious period of a primary infectious human (R_mh) and the number of infectious humans generated by the proportion of infectious mosquitoes surviving the extrinsic incubation period (R_hm) as R₀² = R_mh × R_hm [18, 25, 27]. The equations of R₀ are summarized in Table 1 [equations (T9)–(T12)]. When R₀ > 1 it implies that the epidemic is spreading within a population and incidence is increasing, whereas R₀ < 1 means the disease is dying out. An average R₀ of 1 means the disease is endemically in equilibrium within the population.

R₀-based probabilistic risk model

To develop a R₀-based risk model, a conditional probability distribution function (pdf) describing the relationship between R₀ and the increased dengue incidence rate has to be constructed. Massad et al. [18, 27] developed a model that can be used to calculate the increased dengue incidence rate (λ_d, wk⁻¹) that is a function of R₀, where λ_d is the rate constant describing the increase in dengue cases over 1 week under an exponential growth condition,

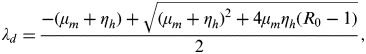(2)

where μ_m is the average mosquito mortality rate (wk⁻¹) and η_h is the mean viraemic rate (wk⁻¹).

Given the λ_d estimates from equation (2) based on the probability distribution of R₀ by incorporating Kaohsiung-specific μ_m and η_h values, a conditional pdf of P(λ_d|R₀) describing the R₀−increased dengue incidence rate profile can then be reconstructed by a four-parameter Hill equation as

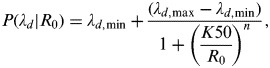(3)

where λ_d,min and λ_d,max are the minimum and maximum values of λ_d, K50 is the R₀ at half value of λ_d,max, and n is the fitted Hill coefficient.

The risk of increased dengue incidence rate can be calculated by a joint probability function describing the probability of a dengue outbreak in a susceptible population based on R₀ driven by dengue−mosquito−human interactions. This can be expressed mathematically as,

(4)

where R(λ_d) is the risk of an increase in dengue cases and P(R₀) is the pdf of R₀.

Sensitivity and uncertainty analyses

A sensitivity analysis was performed by Pearson correlation statistics to investigate the parameter contributions in R₀. The TableCurve 2D package (AISN Software Inc., USA) and Statistica v. 6 (Statsoft Inc., USA) were used to perform model-fitting techniques and statistical analyses. A Monte Carlo (MC) technique was implemented to quantify the uncertainty and its impact on the estimation of expected risk. A MC simulation was also performed with 10 000 iterations to generate 2·5 and 97·5 percentiles as the 95% CI for all fitted models. Crystal Ball software v. 2000.2 (Decisioneering Inc., USA) was employed to implement MC simulation. Model simulations were performed by using Berkeley Madonna v. 8.0.1. (http://www.berkeleymadonna.com)

RESULTS

Dengue transmission dynamics

This study summed all observation values from various studies and then calculated the weighted mean and standard deviation (s.d.) of specific parameters based on different sample sizes (i.e. weights) of the respective studies. Nevertheless, the underlying distributions of these mean values were unknown. Thus we used a lognormal (LN) probability function to generate likelihood estimates performed by MC simulation. The demographic data of the human population from Kaohsiung were incorporated into the model. Model parameterization of mosquito parameters was based on published literature related to the experiments on A. aegypti. Table 2 summarizes the parameter values and initial conditions used in the present model.

Table 2.

Point values and probability distribution [LN(a, b) = Lognormal distribution with geometric mean a and geometric standard deviation b] of parameter values and initial values used in the model

Symbol	Meaning	Distribution/point value
Mosquito parameter
μAa	Average mortality rate of aquatic phase (d−1)	LN(0·07, 2·29)
ηAa	Average maturation rate from aquatic phase to adult (d−1)	LN(0·004, 5·07)
μma	Average mortality rate for mosquito in adult stage (d−1)	LN(0·04, 1·38)
νmb	Extrinsic incubation rate (d−1)	LN(0·08, 1·11)
Bc	Biting rate (d−1)	LN(0·46, 1·50)
βmhd	Transmission probability from vector to host per bite (bite−1)	LN(0·71, 1·16)
μbe	Number of eggs at each deposit per capita (d−1)	6
Human parameter
βhmf	Transmission probability from host to vector per bite (bite−1)	LN(0·71, 1·16)
ηhg	Mean viraemic rate (d−1)	LN(0·24, 1·38)
νhh	Intrinsic incubation rate (d−1)	LN(0·04, 1·17)
μhi	Human mortality rate (d−1)	LN(2·96 × 10−8, 1·00)
Initial values used in the model
Nh	Total human population in Kaohsiung	2 759 160
Eh(0), Ih(0)	Exposed, infected human	1
Rh(0)	Resistant human	0
me	Female mosquitoes per human	6
ke	Number of larvae per human	3
Am(0)e	Aquatic phase: k × Nh	8 277 480
Sm(0)e	Susceptible mosquitoes: m × Nh	16 554 960
Em(0), Im(0)	Exposed, infected mosquitoes	0
Ke	Maximal capacity of larvae: k × Nh	8 277 480

^aEstimate based on Yang et al. [11].

^bEstimate based on Halstead [28].

^cEsitmate based on Pinho et al. [29].

^dEstimate based on Newton & Reiter [24].

^eEstimate based on Dumont et al. [25].

^fEstimate based on Rosen et al. [30] and Watts et al. [31].

^gEstimate based on Harn [32].

^hEstimate based on Hsieh & Ma [33].

ⁱAdopted from the Department of Statistics, Ministry of the Interior, ROC.

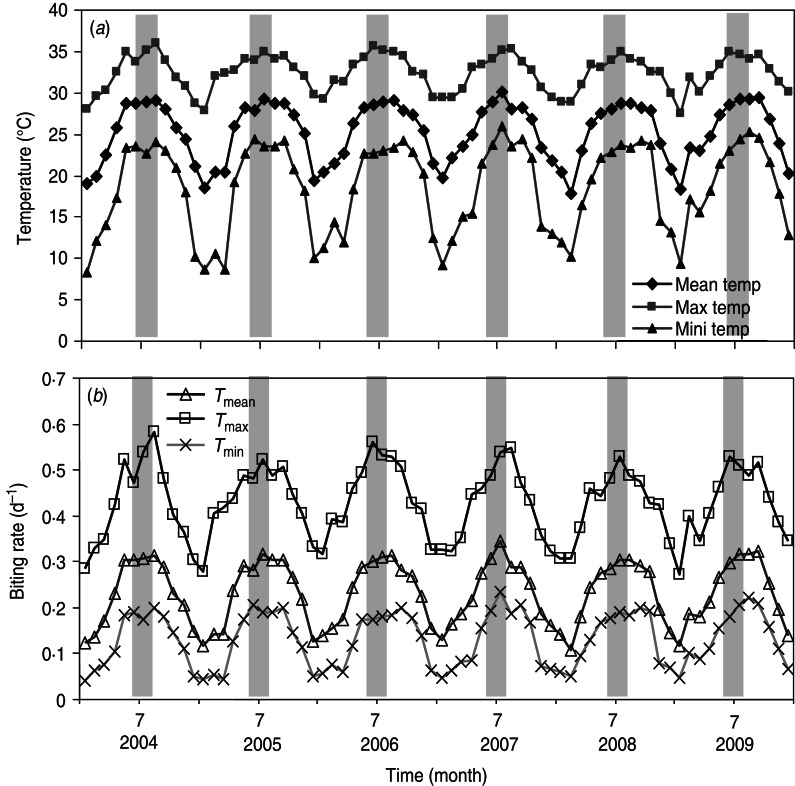
By examining the major factor that influences R₀, we performed the sensitivity analysis on R₀ in equation (T10) (Table 1). We found statistically significant evidence that ~63% of the biting rate effect is associated with R₀. Given that the crucial factor in R₀ is the biting rate, we estimated the biting rates [equation (1)] based on the time-series of monthly maximum (T_max), mean (T_mean), and minimum (T_min) temperatures (Fig. 2a). Figure 2b shows the estimated time-series of temperature-specific biting rates for 2004–2009. The mean biting rates were 0·13 ± 0·06 (mean ± s.d., N = 72), 0·23 ± 0·07, and 0·43 ± 0·08 d⁻¹ for T_min, T_mean, and T_max temperature regimens, respectively (Fig. 3a).

Fig. 2.

(a) Time-series of monthly maximum, mean, and minimum temperature, and (b) mean biting rates varied according to T_min, T_mean, and T_max in Kaohsiung during 2004–2009.

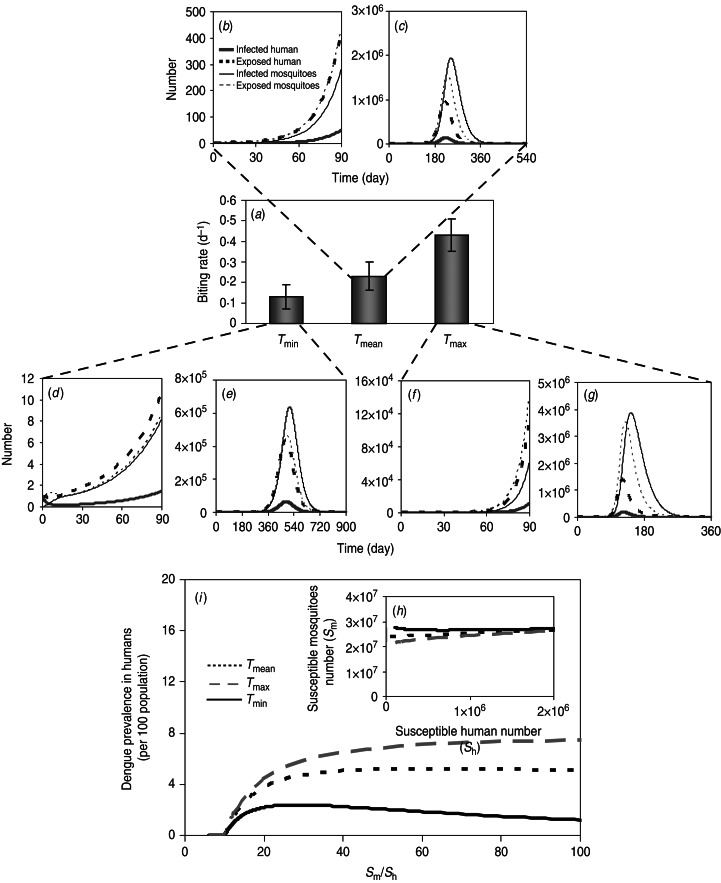
Fig. 3.

Simulation of mosquito–human population dynamics estimated by (a) temperature regimen-specific mean biting rate. The number of human and dengue populations based on mosquito–human dengue transmission model during 90 days (b, d, f) and at equilibrium (c, e, g), respectively, at T_min, T_mean, and T_max. (h) Relationship between the number of susceptible humans and number of susceptible mosquitoes. (i) Relationship between dengue prevalence in humans and ratio of susceptible mosquitoes to humans.

Our results indicated that a higher biting rate (e.g. T_max) results in a higher R₀ and the fraction of infected mosquitoes or human individuals in the population is higher, and thus there are more secondary (or later) infections (Fig. 3b, d, f), leading to higher dengue prevalence occurring over the timescale of nearly 6–12 months (Fig. 3c, e, g). However, the prevalence will eventually settle towards equilibrium with most of the human population having experienced infection (Fig. 3c, e, g).

To understand the relationship between dengue prevalence in humans and susceptible mosquitoes or humans, we considered that dengue dynamics varied with the ratio of susceptible mosquitoes to humans (S_m/S_h) (Fig. 3 h, i). The critical value of S_m/S_h was ~10, the point where an epidemic was just possible at three temperature regimens, indicating that above this point the equilibrium of dengue prevalence rapidly increased to their asymptotic values (Fig. 3i).

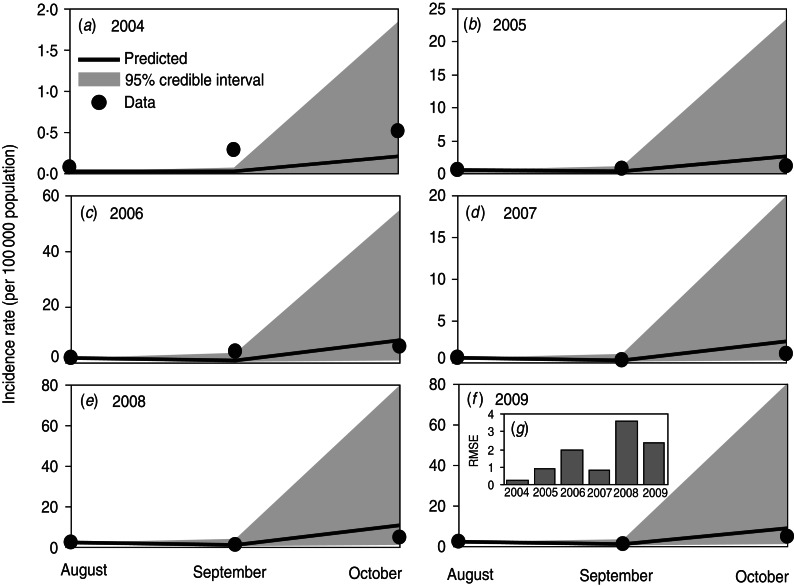
The dengue incidence rates during the summer season (August–October) in 2004–2009 were validated against the model simulations (Fig. 4a–f). This study calculated root-mean-squared errors (RMSEs) to examine the model's predictability of dengue cases. The lower RMSE values indicate higher precise predictions in comparison with observations. The results indicated that the predictions were in apparent agreement with the observed data (RMSEs were 0·22, 0·92, 2·00, 0·84, 3·63, and 2·36/100 000 populations from 2004 to 2009, respectively) (Fig. 4g). Despite the simplicity of the model, we found a fair quantitative agreement between model predictions and observed data. Overall, the present model captures the transmission dynamics of the dengue incidence rate in Kaohsiung during the summer season during 2004–2009.

Fig. 4.

(a–f) Comparison of dengue incidence rate (per 100 000 population) during summer (August–October) for 2004–2009 by mosquito–human–dengue transmission model with 95% credible intervals. (g) Root-mean-squared error (RMSE) calculated between predictions and observed data in Kaohsiung.

Dengue infection risk estimates

The temperature-specific R₀ values due to dengue−mosquito−human dynamics were calculated based on equations (T9)–(T12) (Table 1). A LN distribution was used to generate log-likelihood estimates of 95% CIs for R₀, indicating that median R₀ estimates were 1·77 (95% CI 0·67–4·81), 3·22 (95% CI 1·44–6·99), and 6·08 (95% CI 2·81–12·65), respectively, corresponding to T_min, T_mean, and T_max regimens.

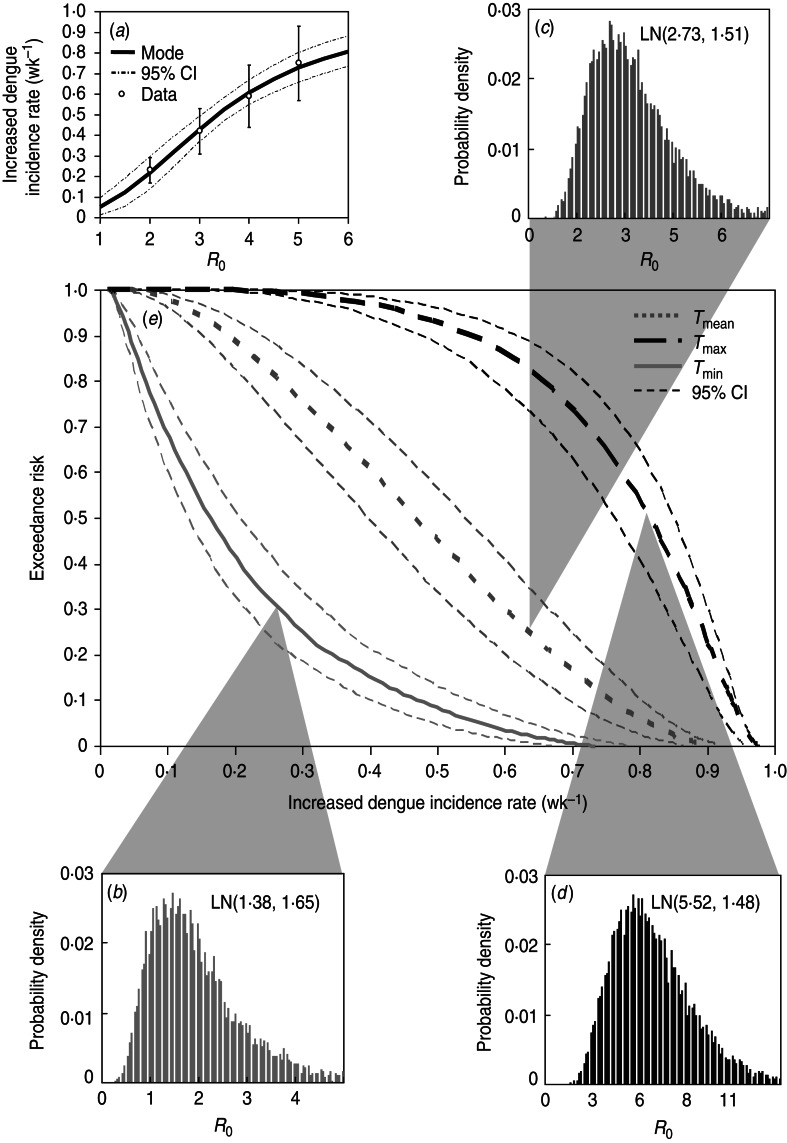
A four-parameter Hill equation was best fitted to the data calculated from equation (2) to depict the relationship between increased dengue incidence rate and R₀ in Kaohsiung with four fitted parameters of λ_d,min = 0·01 wk⁻¹, λ_d,max = 0·99 wk⁻¹, K50 = 3·36 ± 0·07, and n = 2·55 ± 0·18 (r² = 0·99) (Fig. 5a). Given the reconstructed Hill model-based conditional pdf describing the dose–response relationship of P(λ_d|R₀)(Fig. 5a) and the temperature regimen-specific R₀ distributions (Fig. 5b–d), the exceedance risk probabilities of dengue infection at T_min, T_mean, and T_max can then be estimated followed by equation (4) (Fig. 5e).

Fig. 5.

(a) Reconstructed dose–response profile describing the relationship between R₀ estimates and increased dengue incidence rate (wk⁻¹). (b–d) Temperature regimen-specific R₀ distributions described by the lognormal function of LN(geometric mean, geometric standard deviation). (e) Exceedance risk profiles of increased dengue incidence rate (wk⁻¹) estimate based on R₀ distributions at T_min, T_mean, and T_max.

Table 3 summarizes the estimates of increased dengue incidence rate at exceedance risks of 0·1, 0·5, and 0·9 at T_min, T_mean, and T_max. We found that there were 90% and 10% risk probabilities for average increased dengue incidence rates exceeding 0·04 and 0·47, 0·19 and 0·76, and 0·54 and 0·93 wk⁻¹ at T_min, T_mean, and T_max, respectively (Table 3). Generally, our results predicted that there was a 50% risk probability for increased dengue incidence rates exceeding 0·47 and 0·81 wk⁻¹ at T_min and T_max, respectively, in Kaohsiung.

Table 3.

Estimates of increase in number of dengue cases (wk⁻¹) (median with 95% confidence intervals) at exceedance risk of 0·1, 0·5, and 0·9 in Kaohsiung varied according to T_min, T_mean, and T_max

Exceedance risk
0·1	0·5	0·9
Tmax
0·93 (0·91–0·94)	0·81 (0·76–0·85)	0·54 (0·47–0·61)
Tmean
0·76 (0·70–0·80)	0·47 (0·39–0·54)	0·19 (0·15–0·24)
Tmin
0·47 (0·40–0·54)	0·16 (0·13–0·21)	0·04 (0·03–0·05)

Control applications

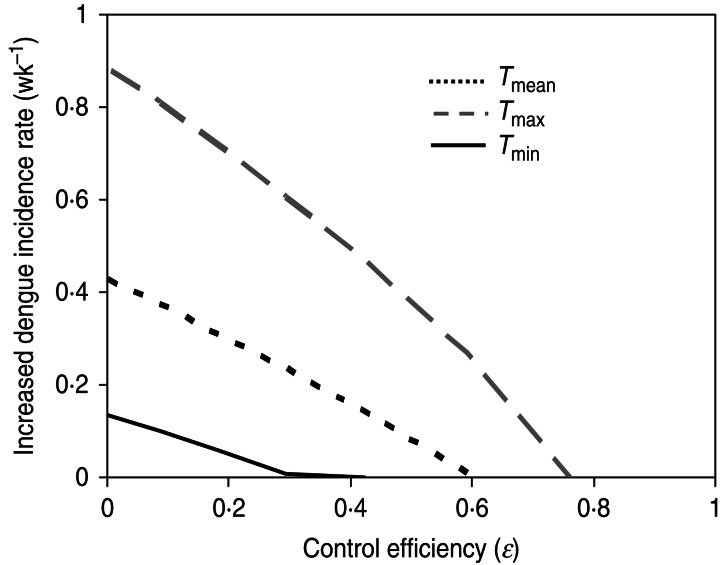
To apply our study to vector control, we used the reduction of mosquito numbers as the parsimonious vector control measure. We defined ε as the control efficiency describing the proportional reduction in the parasite's basic reproduction number due to elimination of susceptible mosquitoes as ε = 1−R_0C/R₀, where R_0C is the basic reproduction number of the mosquitoes after vector control by eliminating susceptible mosquitoes. The results indicated that the weekly increased dengue incidence rate can be decreased to zero if the control efficiencies almost reach 0·3, 0·6, and 0·78, at T_min, T_mean, and T_max, respectively (Fig. 6). Our vector control application also implies that R₀ is a linear function of the number of adult mosquitoes, and therefore, if the only effect of vector control is to eliminate the density of mosquitoes then ε will be equal to the proportional reduction in that density.

Fig. 6.

Relationship between weekly increased dengue incidence rate (wk⁻¹) and the control efficiency varied according to T_min, T_mean, and T_max.

DISCUSSION

Modelling perspectives

Our analysis reveals several features of dengue fever risk prediction in Kaohsiung. The major findings are: (i) the effect of biting rate plays a crucial role in shaping R₀ estimates, (ii) the mean biting rates (±s.d.) were 0·13 ± 0·06, 0·23 ± 0·07, and 0·43 ± 0·08 d⁻¹ at T_min, T_mean, and T_max, respectively, (iii) R₀ estimates were 1·77 (95% CI 0·67–4·81), 3·22 (95% CI 1·44–6·99), and 6·08 (95% CI 2·81–12·65), respectively, corresponding to T_min, T_mean, and T_max regimens, (iv) the Hill equation can best describe the relationship between dengue cases increasing rate and R₀, and (v) there was 50% risk of increased dengue incidence rate that exceeded 0·47 wk⁻¹ at T_mean.

Generally, our average R₀ estimates during 2004–2009 are in agreement with the published data of 2·23 (95% CI 1·47–3·00) in Singapore during 2005 [33], 3·09 (95% CI 2·34–3·84) in Colima, Mexico during 2002 [16], and 5·10 (95% CI 2·61–10) in Brazil during 2006–2007 [17]. In view of R₀ formulation [Table 1, equation (T10)], the ratio of initial susceptible mosquitoes and the total human population is vital in determining both R₀ and the dynamics of infection. It implies that R₀ increases with the number of mosquitoes, and decreases with the number of humans. Thus for a successful spread and invasion of dengue infection, a sufficiently large ratio of mosquitoes to humans must be reached, which can be described mathematically by

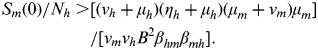Based on the S_m(0)/N_h ratio, the prevalence and proportion of seropositives in the human population along with maximum disease prevalence can also be estimated [21]. Moreover, R₀ also captures key components of the role of mosquitoes in pathogen transmission, which is mainly influenced by environmental, ecological, behavioural, and molecular factors [10, 16]. Generally, the extrinsic incubation rate of many vector-borne pathogens is also known to be temperature sensitive [10].

Thus R₀ is influenced by environmental temperature [34]. Beserra et al. [35] indicated that the favourable temperature for A. aegypti development was between 21°C and 29°C, whereas for dengue longevity and fecundity, the temperature was between 22°C and 30°C. Thus climatic conditions are important predictors of dengue amplification due to the tight relationship between mosquito development from egg to biting adult, survival rate at each life stage, and temperature-dependent feeding behaviour [11, 20].

We usually used constant temperature-based experimental data to derive vector-borne disease parameter values [34]. Moreover, the averaged weekly/monthly temperature was also usually used in combination with constant-temperature disease parameters for constructing the relationship between climatic factors and vector-borne disease incidence for mathematical modelling purposes. In fact, temperature fluctuated throughout the day, therefore, mosquitoes and their pathogens do not simply experience mean conditions. In our study, we assessed the effect of temperature range on the potential for dengue fever transmission by female A. aegypti at T_min, T_mean, and T_max defined by time-series dynamics of measured temperature.

Although the present model has captured the transmission dynamics of dengue incidence rate along with the risk prediction in southern Taiwan during the summer season for 2004–2009, there are potential limitations of our study that warrant discussion. Limiting data acquisition of daily or weekly confirmed dengue cases resulted in monthly dengue incidence rate estimates. Important limiting assumptions of the models are that there is no vertical transmission of dengue virus in A. aegypti. On the other hand, the mosquitoes never recover from the infection since their infective period ends with their death. Moreover, the model considered only one serotype of dengue virus. In light of the biting rate used in our study, we propose that biting rate can be converted from gonotrophic cycle (i.e. biting rate = 1/gonotrophic cycle) in that all mosquitoes are assumed to become infected at the same first bloodmeal and only bite a human during the gonotrophic cycle.

Mathematical models have long been recognized as useful tools for exploring complicated relationships that underlie infectious disease transmission [19, 21]. The accuracy of the predictions obtained from mathematical modelling depends on the accuracy of the estimated parameters used in the model. To this end, good parameter estimates are needed to understand and model the potential spread of dengue fever while the interpretation of data from experimental infection studies provides validation of mathematical model predictions for different dengue fever infection scenarios. The complexity of the model is determined by the purpose of the study and the amount of information in the dataset. On the other hand, it is not advantageous to use a more complex model when a simpler model provides an adequate fit to the data. Undoubtedly, many factors influence the relationship between mosquito and human population dynamics.

Implications on dengue vector control

Under the circumstance without existence of licensed vaccine or dedicated therapy for dengue containment, the most promising strategies to control the disease involve targeting the predominant mosquito vector, A. aegypti [18]. The best existing methods of control such as mosquito control with chemical sprays and treated bed nets can reduce the burden of disease substantially and can even eliminate the disease in some epidemic regions [36].

The reduction in adult density depends upon the present form of the density-dependent function regulating mosquito populations [37]. Burattini et al. [22] indicated that even a marked fall in the size of adult mosquito populations may not be sufficient to stop ongoing dengue epidemics. Yet, they showed that the mixed strategy of adulticide and larvicide methods seem to be very effective in reducing the number of cases in the first weeks after implementing control measures.

The major vector control measures may include chemical spray (e.g. pesticide), treated bed net (i.e. inducing adult mosquitoes to lay eggs on the net with water below, therefore growing and being trapped when the larvae become adult mosquitoes), and genetic modification (e.g. parasitic microbe Wolbachia endosymbiotic in the A. aegypti mosquitoes to inhibit the replications of dengue virus [38]). In this study, we only provide common examples of vector control. In addition to chemical control strategies, there are many control measures that can be used to reduce dengue prevalence without much cost where only notification of public health policy is required, such as reducing human–vector contact and removing water storage containers. Specifically, removing water storage containers is the most effective way to eliminate A. aegypti since A. aegypti breed primarily in man-made containers in Asia. On the other hand, reducing contact between humans and the vector can be simply achieved by wearing long trousers and long-sleeved shirts or staying indoors with the windows closed. These control strategies can sufficiently control a dengue outbreak and produce savings on the government's budget. However, cost-effective analysis should be considered to determine the optimal control strategy in future research.

Much work will need to be done on risk assessment, community engagement, and regulatory protocols [13, 39]. Moreover, potentially direct and indirect effects on the abundance of other species and on ecosystem services should be considered [7, 11]. Recently, Luz et al. [13] suggested that vector control policies of dengue may need to be reassessed based on continuous larval control only. The ability to successfully predict dengue incidence is generally believed to depend on how well we can predict vector abundance. Notably, because humans are the primary dengue host, human behaviour may be as important as vector abundance for accurate forecasts of pathogen amplification and dengue infection risk [40].

In conclusion, dengue continues to impose a substantial burden on human health. We reconstructed a well-developed dengue−mosquito−human population transmission model and re-analysed dengue epidemiology to predict the risk of an increase in dengue fever cases in the southern region of Taiwan. Given that local surveillance data of climatic factors and dengue cases were obtainable, the well-developed population transmission model could easily be used to estimate dengue prevalence in a specific city or country. We also recognize that ecology of infectious diseases in natural populations is ultimately complex [19, 36]. However, we anticipate that our present parsimonious model of dengue−mosquito–human population dynamics in a homogeneous, constant environment can be used to determine what is required to eliminate Aedes mosquitoes. Most importantly, the conclusion from this study, combined with recent estimates of the critical parameters in the laboratory, is that this present approach could provide a method for estimating the risk of dengue fever and guide improvements in vector control methods or other disease control strategies.

DECLARATION OF INTEREST

None.