COVID-19 medical waste transportation risk evaluation integrating type-2 fuzzy total interpretive structural modeling and Bayesian network

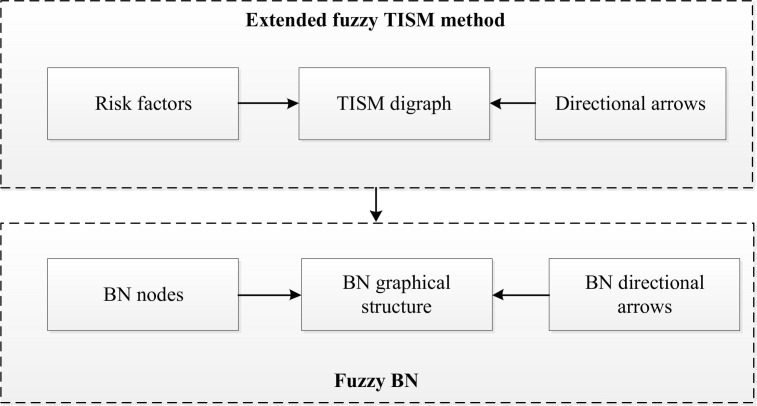
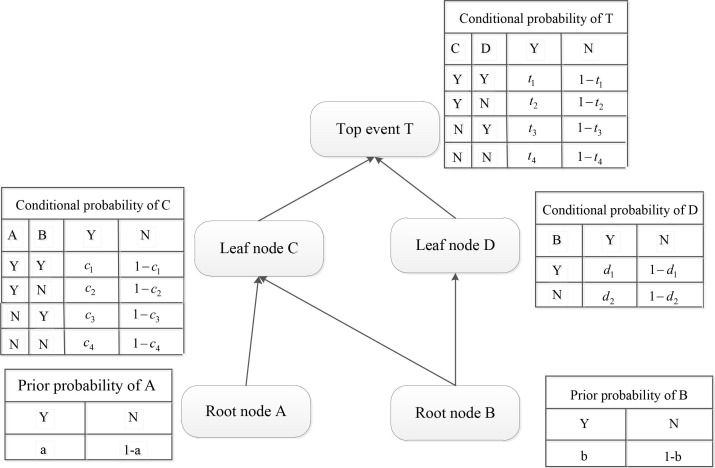
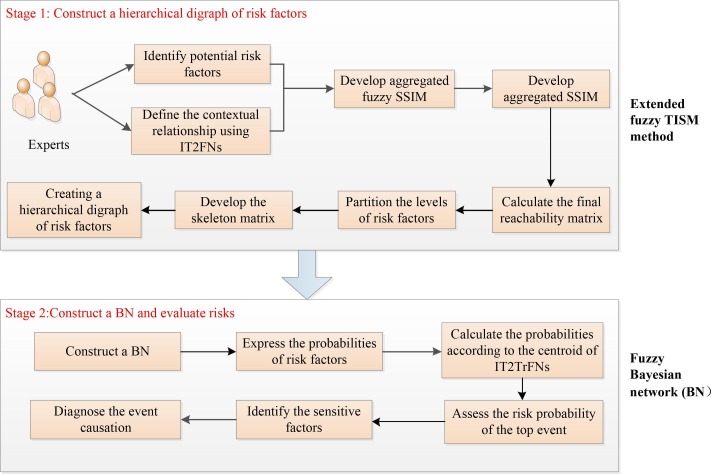
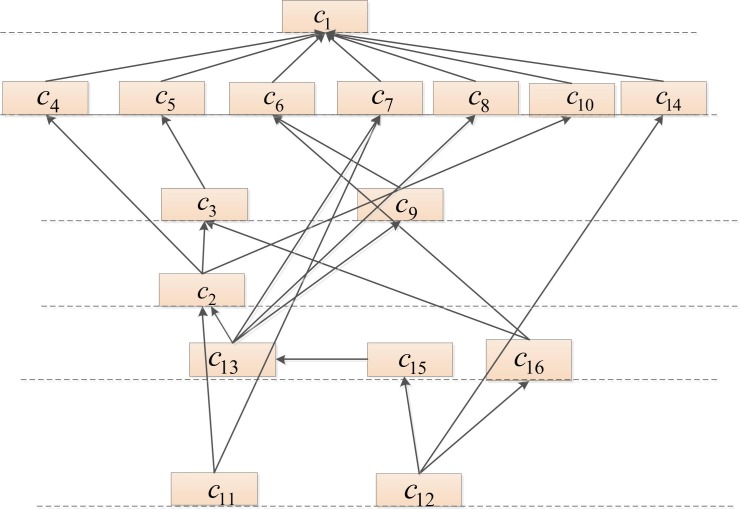
Abstract

With the amount of medical waste rapidly increasing since the corona virus disease 2019 (COVID-19) pandemic, medical waste treatment risk evaluation has become an important task. The transportation of medical waste is an essential process of medical waste treatment. This paper aims to develop an integrated model to evaluate COVID-19 medical waste transportation risk by integrating an extended type-2 fuzzy total interpretive structural model (TISM) with a Bayesian network (BN). First, an interval type-2 fuzzy based transportation risk rating scale is introduced to help experts express uncertain evaluation information, in which a new double alpha-cut method is developed for the defuzzification of the interval type-2 fuzzy numbers (IT2FNs). Second, TISM is combined with IT2FNs to construct a hierarchical structural model of COVID-19 medical waste transportation risk factors under a high uncertain environment; a new bidirectional extraction method is proposed to describe the hierarchy of risk factors more reasonably and accurately. Third, the BN is integrated with IT2FNs to make a comprehensive medical waste transportation risk evaluation, including identifying the sensitive factors and diagnosing the event's causation. Then, a case study of COVID-19 medical waste transportation is displayed to demonstrate the effectiveness of the proposed model. Further, a comparison of the proposed model with the traditional TISM and BN model is conducted to stress the advantages of the proposed model.

1. Introduction

Medical waste, often known as health care waste, is created during a variety of medical procedures, including diagnosis, treatment, human or animal vaccination, and biological testing (Yong, et al., 2009). The corona virus disease 2019 (COVID-19) has produced a sharp rise in medical waste globally. Since corona virus has a high degree of spatial infectious, latent and viral, the tremendous increase in medical waste is a vital transmission medium for the virus and thus poses severe and new challenges to medical waste management (Chen et al., 2021, Zhao et al., 2022). Current research on COVID-19 medical waste mainly focuses on the selection of waste disposal techniques (Manupati, et al., 2021), sustainable production and waste management policies (Ahmad et al., 2021, Singh et al., 2022, Torkashvand et al., 2021), and the vehicle routing problem (Eren and Tuzkaya, 2021, Govindan et al., 2021). However, safe transportation within the medical waste treatment process is an essential problem in medical waste management (Kumar, et al., 2015). To our extent, no research considers the risks of COVID-19 medical waste transportation. The risks of medical waste transportation process will cause enormous loss of life and property, harm the environment and soil, and even affect social stability (Kumar, et al., 2015). For example, the rebound of the pandemic that broke out in Nanjing in July 2020 was caused by the improper handling of the protective clothing by airport staff after cleaning the cabin. Therefore, to avoid such incidents, identifying and evaluating the potential risk factors in the transportation process is a crucial issue that needs to be paid attention to.

Since the occurrence of COVID-19 is sudden and historical data is insufficient, the evaluation of risks requires the support of experts in related fields. Some researchers have used fuzzy set theory to deal with the inadequate data in the context of COVID-19 pandemic, indicating that the fuzzy set theory is effective and feasible (Karmaker et al., 2021, Mardani et al., 2020, Sharma et al., 2020). The fuzzy set theory proposed by L. A. Zadeh (1965) is an extensive used tool to handle ambiguous and confusing real-world problems, which can evaluate experts' subjective and inaccurate assessments. Type-1 fuzzy sets are used widely to model imprecise information in literature (Liu, 2011, Maniram Kumar et al., 2018, Sayyadi Tooranloo and Ayatollah, 2016). Nevertheless, uncertainties are inherent in handling words in a natural language, as the same words have various meanings for different persons (Boukezzoula and Coquin, 2020). To describe the different opinions about the same word, Zadeh (1975) proposed the type-2 fuzzy sets (T2FS). However, it has a relatively heavy computational burden in the actual application process (Xiaohong and Yingming, 2021). Thus, Mendel and John (2002) suggested the interval type-2 fuzzy sets (IT2FSs) as a reduced version of the T2FS. It's worth noting that the IT2FS is a particular instance of the T2FS, and its calculation is significantly easier than the T2FS. Therefore, it has been extensively utilized in many fields, such as maritime transportation (Celik and Akyuz, 2016, Pelin and Emre, 2021), green supplier selection (Wu, et al., 2019) and waste site selection (Hong, et al., 2021).

COVID-19 medical waste transportation process involves multiple risk factors since COVID-19 has a high degree of spatial infectious, latent and viral. Understanding the interactions between risk factors can help to control risks (Schulte, et al., 2012). Considering the interaction relationships between the risk factors related to COVID-19, total interpretative structural modeling (TISM) and decision making trial and evaluation laboratory (DEMATEL) are commonly used (Karmaker et al., 2021, Lakshmi Priyadarsini and Suresh, 2020, Sen et al., 2021). Sen, et al. (2021) applied DEMATEL to investigate the influential factors on COVID-19 related deaths and their effects on each other. Lakshmi Priyadarsini and Suresh (2020) introduced TISM to understand the interrelationship between and among the factors that affect the epidemiological characteristics of COVID-19. Karmaker, et al. (2021) used TISM to visualize the hierarchical structure of mutual relationships between/among the factors affecting supply chain sustainability in the context of COVID-19 pandemic. DEMATEL is a survey to help understand the complex relationship among selected factors, which is incapable of determining the hierarchical structure of complicated systems (Wang, et al., 2018). TISM is an enhanced version of interpretive structural modeling (ISM), proposed by Sushil (2012), which can identify the structural relationship between multiple factors and demonstrate direct and transitive relationships (Li, et al., 2019). Especially, Liao, et al. (2021) proposed a double alpha-cut-based consensus measurement method for HFLPRs, which has low computational complexity and high accuracy in handling fuzzy information. We refer to the idea and propose a new double alpha-cut method to convert the IT2FNs into numerical values of 0 or 1, by which we can establish a reachability matrix during the calculation of TISM under a high uncertain environment. After obtaining the reachability matrix, level extraction is used to determine the hierarchical relationships among risk factors. Two main widely used level extraction methods of TISM are up-type hierarchy method and down-type hierarchy method (Zhang, Huang et al., 2021), also known as result-first hierarchy extraction method and cause-first hierarchy extraction method. However, these two traditional extraction methods may have some inconsistencies in practice. So we propose a new hierarchical extraction method, called the bidirectional extraction method to help reflect the dialectical relationship between causes and results more realistic and effective.

As to quantify the risks of the COVID-19 medical waste transportation process, the Bayesian network (BN) provides a very important idea for the risk evaluation of systems composed of multiple risk factors. BN is popular to solve risk evaluation problems due to its ability to express dependencies among events, update probability based on new evidence and reasoning under uncertainty (Li, et al., 2018). Based on the hierarchical structure of risk factors obtained by TISM, BN is applied to describe uncertain and complex relationships among various factors quantitatively. Moreover, there has been a tendency in studies to combine fuzzy set theory with the BN considering the uncertain information during the evaluation process. For example, Ghasemi, et al. (2021) developed an approach for predicting human error probabilities of road tanker loading operation by using fuzzy set theory and BN. Yucesan, et al. (2021) use the fuzzy Bayesian network (FBN) to determine the occurrence probabilities of the failure modes and apply the model in an industrial kitchen equipment manufacturing facility. Guo, et al. (2020) combined the FBN with an improved similarity aggregation method to assess the storage tank accident risk, FBN is used to identify the critical events of the storage tank accident. Abbassinia, et al. (2020) developed a dynamic model of human error assessment in emergencies in the petrochemical industry based on FBN and fuzzy-AHP-TOPSIS method. Based on these studies, the BN based on the hierarchy of factors, is proposed to analyze risk factors and identify the sensitive factors for the medical waste transportation system. Moreover, the interval type-2 fuzzy numbers (IT2FNs) is used to calculate the prior probabilities of root nodes and the conditional probabilities of leaf nodes, which are the fuzzification of the linguistic expressions obtained from expert opinions.

Based on the abovementioned consideration, this paper proposes an extended fuzzy TISM method and maps the hierarchical structure model to BN. IT2FSs are applied to handle the subjective uncertainty of information when experts evaluate the COVID-19 medical waste transportation risk factors since the linguistic variables are more in line with the expression habits of experts. A double alpha-cut of IT2FNs and a new bidirectional extraction method are first combined with TISM method to construct the hierarchy diagram of risk factors under high uncertain environment. The BN is applied to model the objective uncertainties caused by probabilistic variations of risk factors and conduct a comprehensive risk analysis. It also provides a description of different risk factors and their interconnections through graphical representations. The contributions of this article are:

• (i).Experts evaluate the risk factors in the process of COVID-19 medical waste transportation by using IT2FNs, which has the capability of reflecting the subjectivity under uncertain environments.
• (ii).An extended fuzzy TISM method is proposed to analyze risk factors and interpret hierarchical relationships of risk factors in a complex and uncertain system.
• (iii).A new double alpha-cut is first combined with IT2FNs to convert IT2FNs into crisp numbers, which has low computational complexity and high accuracy in the calculation process.
• (iv).A new bidirectional extraction method is first proposed to construct the hierarchy diagram of risk factors in TISM, accurately reflecting the risk factors' levels.
• (v).The structural model of risk factors is transformed into a BN to quantitatively analyze the functions and interactions among risk factors. The IT2FSs are combined with BN to derive the prior probabilities and conditional probabilities of risk factors.

The rest of the paper is organized as follows. Section 2 briefly introduces some notions and properties about the IT2FS, TISM method and the BN. Section 3 describes the research methodology for the proposed risk evaluation framework. Section 4 introduces specific steps of the integrated model for COVID-19 medical waste transportation risk evaluation based on extended fuzzy TISM and fuzzy BN. Section 5 presents a case study in Nanjing concerning COVID-19 medical waste transportation process to emphasize the effectiveness of the proposed model. Section 6 conducts a comparison of our proposed model with traditional model. Section 7 provides a brief conclusion and future research directions.

2. Preliminaries

2.1. Interval type-2 fuzzy set

The interval type-2 fuzzy sets (IT2FSs) are used to express imprecise and uncertain evaluation information considering experts' psychological variables. A type-2 fuzzy set $\stackrel{\approx }{A}$ in the universe of discourse $X$ can be denoted by a type-2 membership function ${\mu }_{\stackrel{\approx }{A}}$ as follows:

$$\stackrel{\approx }{A}=\left\{\left(\left(x,\left(u\right)\right)\right)\right),{\mu }_{\stackrel{\approx }{A}}\left(x,\left(u\right)\right)\left|\forall x\in X,\forall u\in J_x\right)\subseteq \left(\left[0,\left(1\right]\right)\right\}$$ (1)

In which$J_x\subseteq \left[0,\left(1\right]\right)$, and $0⩽{\mu }_{\stackrel{\approx }{A}}\left(x,\left(u\right)\right)⩽1$ for all admissible $x$ and$u$. Furthermore, the type-2 fuzzy set $\stackrel{\approx }{A}$ can also be shown in the following form:

$$\stackrel{\approx }{A}={\int }_{x\in \chi }{\int }_{u\in J_x}{\mu }_{\stackrel{\approx }{A}}\left(x,\left(u\right)\right)/\left(x,\left(u\right)\right)$$ (2)

If all${\mu }_{\stackrel{\approx }{A}}\left(x,\left(u\right)\right)$ = 1, then $\stackrel{\approx }{A}$ is defined as an IT2FS. An IT2FS $\stackrel{\approx }{A}$ can be presented as a subset of type-2 fuzzy sets, which is defined as follows:

$$\stackrel{\approx }{A}={\int }_{x\in \chi }{\int }_{u\in J_x}1/\left(x,\left(u\right)\right)$$ (3)

Among these various types of fuzzy numbers, the interval type-2 trapezoidal fuzzy number (IT2TrFN) is one of the most widely used for describing uncertainty information (Hendiani et al., 2020, Jin et al., 2020, Liu, 2011, Xie et al., 2017).

Let $\stackrel{\approx }{A}=\left(A^U,A^L\right)=\left[\left(a_1^U,a_2^U,a_3^U,a_4^U;h_A^U\right),\left(a_1^L,a_2^L,a_3^L,a_4^L;h_A^L\right)\right]$ be an IT2TrFN, which can be denoted as Fig. 1 . Suppose that there are two IT2TrFNs as follows:

$${\stackrel{\approx }{A}}_1=\left[\left(a_{11}^U,a_{12}^U,a_{13}^U,a_{14}^U;h_{1A}^U\right),\left(a_{11}^L,a_{12}^L,a_{13}^L,a_{14}^L;h_{1A}^L\right)\right]$$

$${\stackrel{\approx }{A}}_2=\left[\left(a_{21}^U,a_{22}^U,a_{23}^U,a_{24}^U;h_{2A}^U\right),\left(a_{21}^L,a_{22}^L,a_{23}^L,a_{24}^L;h_{2A}^L\right)\right]$$

Fig. 1.

Interval type-2 trapezoidal fuzzy sets.

Mathematical operations between the IT2TrFNs are described as follows:

$$\begin{array}{c}{\stackrel{\approx }{A}}_1\oplus {\stackrel{\approx }{A}}_2=\left[\left(a_{11}^U+a_{21}^U,a_{12}^U+a_{22}^U,a_{13}^U+a_{23}^U,a_{14}^U+a_{24}^U;\min \left\{h_{1A}^U,\left(h_{2A}^U\right\}\right)\right)\right),\\ \left(\left(a_{11}^L+a_{21}^L,a_{12}^L+a_{22}^L,a_{13}^L+a_{23}^L,a_{14}^L+a_{24}^L;\min \left\{h_{1A}^L,\left(h_{2A}^L\right\}\right)\right)\right]\end{array}$$ (4)

$$\begin{array}{c}{\stackrel{\approx }{A}}_1-{\stackrel{\approx }{A}}_2=\left[\left(a_{11}^U-a_{24}^U,a_{12}^U-a_{23}^U,a_{13}^U-a_{22}^U,a_{14}^U-a_{21}^U;\min \left\{h_{1A}^U,\left(h_{2A}^U\right\}\right)\right),\right)\\ \left(\left(a_{11}^L-a_{24}^L,a_{12}^L-a_{23}^L,a_{13}^L-a_{22}^L,a_{14}^L-a_{21}^L;\min \left\{h_{1A}^L,\left(h_{2A}^L\right\}\right)\right)\right]\end{array}$$ (5)

$$\begin{array}{c}{\stackrel{\approx }{A}}_1\otimes {\stackrel{\approx }{A}}_2=\left[\left(a_{11}^U·a_{21}^U,a_{12}^U·a_{22}^U,a_{13}^U·a_{23}^U,a_{14}^U·a_{24}^U;\min \left\{h_{1A}^U,\left(h_{2A}^U\right\}\right)\right),\right)\\ \left(\left(a_{11}^L·a_{21}^L,a_{12}^L·a_{22}^L,a_{13}^L·a_{23}^L,a_{14}^L·a_{24}^L;\min \left\{h_{1A}^L,\left(h_{2A}^L\right\}\right)\right)\right]\end{array}$$ (6)

$$\begin{array}{c}k·{\stackrel{\approx }{A}}_1=\left[\left(k·a_{11}^U,k·a_{12}^U,k·a_{13}^U,k·a_{14}^U;h_{1A}^U\right),\right)\\ \left(\left(k·a_{11}^L,k·a_{12}^L,k·a_{13}^L,k·a_{14}^L;h_{1A}^L\right)\right]\end{array}$$ (7)

2.2. Total interpretive structural modeling

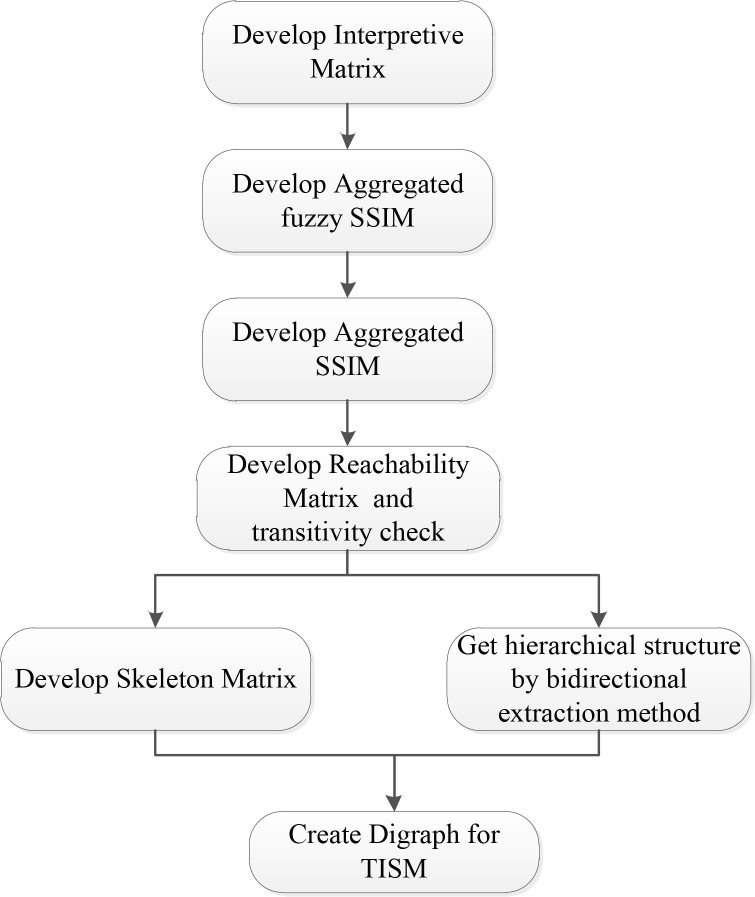
To explain the contextual direction and relationship between the elements in the pairwise comparison, Total Interpretive Structural Modeling (TISM) is proposed as an improved model of the ISM. TISM is used to model the factors for better comprehension of their interaction. Fig. 2 shows the flowchart and specific steps of TISM analysis:

Fig. 2.

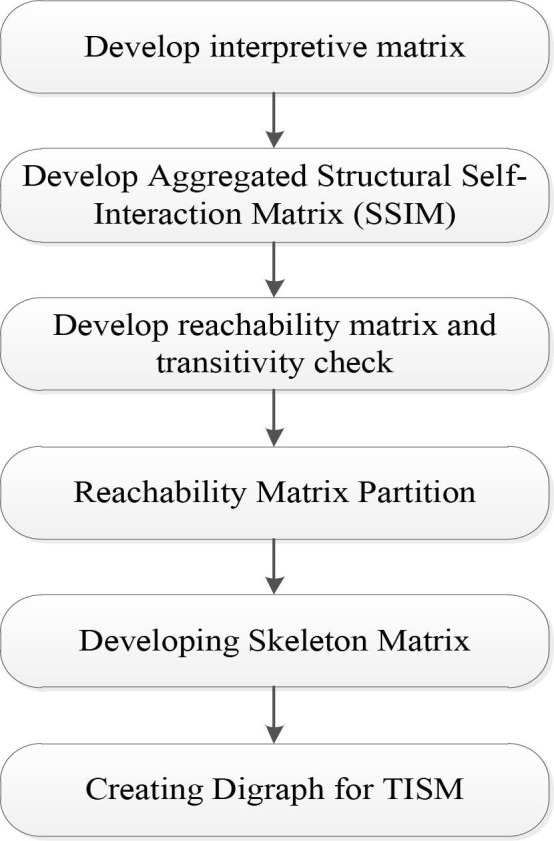
Specific steps of TISM.

Step 1: Developing Interpretive Matrix.

TISM (similar to ISM) starts with identifying the components and establishing their contextual relationships. Experts determine the connection between any two components depending on the context of each element.

Step 2: Develop Aggregated Structural Self-Interaction Matrix (SSIM).

V, A, X, and O are the four symbols that describe the relationships between any two elements under consideration. The aggregated SSIM is obtained by filling responses of a group of experts on the pairwise interaction matrix.

Step 3: Developing Reachability Matrix.

Convert the information in SSIM into 1 and 0 to construct the reachability matrix. Moreover, a transitivity check is required. The transitivity matrix is verified for the transitivity rule and modified as necessary until complete transitivity is achieved.

Step 4: Reachability Matrix Partition.

The next stage is to generate a digraph and extract a structural model when the transitivity check is completed. On sets and subsets of elements, relation partition and level partition may be used to partition the reachability matrix process (Warfield, 1974).

Step 5: Developing Skeleton Matrix.

After eliminating the transitivity, the reduction matrix is obtained by successfully removing the strongly connected elements in each level. Then the skeleton matrix is obtained by removing the leap-over binary relations among elements in the reduction matrix and the self-reaching binary relations.

Step 6: Creating Digraph for TISM.

The final TISM model shows all transitive and direct influential links according to the skeleton matrix. In addition, it is possible to analyze the proper justification behind the impact of one element on other elements.

2.3. Bayesian network

After obtaining the hierarchy diagram of risk factors, a Bayesian network (BN) is introduced to provide a flexible and robust graphical structure in a probabilistic approach, a directed acyclic graph composed of several nodes and the correlation between nodes (Bapin and Zarikas, 2019). The BN consists of two parts: one is the topological structure (which includes network nodes and directed links), and the other is the conditional probability table. The qualitative description element of the model is the topological structure, which consists of nodes displaying variables and directed arrows. A node from which a directed arrow is generated is called the parent node, while the other node to which the directed arrow is directed is called child node (Pristrom, et al., 2016). The Bayesian network's quantitative section concerns the probability tables of the system's variables. Probabilities, conditional probabilities, and their posterior probabilities are all included in the probability tables. Inference algorithms are based on the following equations (Mahadevan, et al., 2001):

The joint probability distribution of a set of variables $U\text{=}\left\{X_1,X_2\cdots X_n\right\}$ is represented as:

$$P\left(U\right)=\prod _{i=1}^{n}P\left(X_i\left|P_a\left(X_i\right)\right)\right)$$ (8)

where $P$ is the probability, $n$ represents number of nodes, $X_i$ represents the $i$ th node in the network, $P_a\left(X_i\right)$ is the parent set of the variable$X_i$. Then, the posterior (updated) probabilities can be calculated when new pieces of evidence $E$ on variables are given.

$$P\left(U\left|E\right)\right)=\frac{P\left(U,E\right)}{P\left(E\right)}=\frac{P\left(U,E\right)}{{\sum }_{U}P\left(U,E\right)}$$ (9)

3. Research methodology

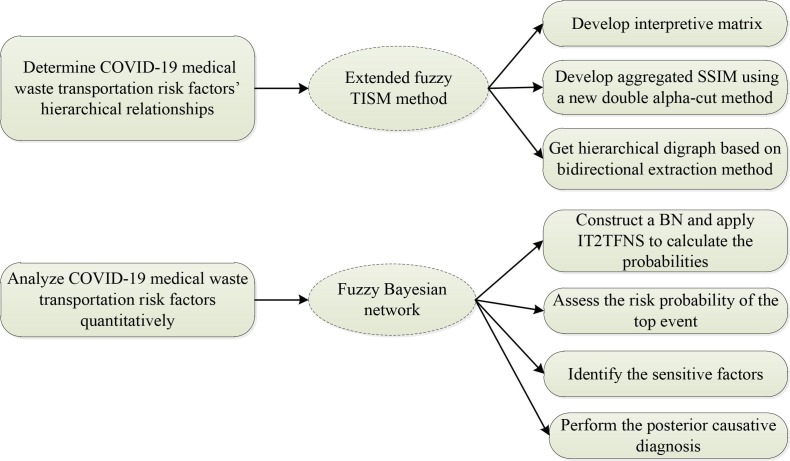
This section describes the research methodology for COVID-19 medical waste transportation risk evaluation from two aspects. First, COVID-19 medical waste is spatial infectious, latent and viral, which makes the transportation process contain multiple risk factors. An extended fuzzy TISM method is proposed to help understanding the interactions between/among risk factors and determine COVID-19 medical waste transportation risk factors’ hierarchical relationships. Second, considering the uncertainties caused by probabilistic variations of COVID-19 medical waste transportation risk factors, the probabilities of risk factors need to be quantified to control risk. The fuzzy BN is used to conduct a comprehensive risk analysis, including identifying the sensitive factors and diagnosing the event's causation. Fig. 3 is drawn to better presentation of the research methodology for COVID-19 medical waste transportation risk evaluation.

Fig. 3.

The framework of the research methodology.

3.1. Determination of risk factors' hierarchical relationships with extended fuzzy TISM method

To determine the COVID-19 medical waste transportation risk factors' hierarchical relationships, an extended fuzzy TISM method is proposed in this section. The traditional TISM is described in Section 2.2. During the TISM process, the double alpha-cut of IT2TrFNs is presented to convert the aggregated fuzzy SSIM into the aggregated SSIM. Moreover, a new bidirectional extraction method is also proposed to obtain a more reliable hierarchical structure. The detailed procedure for the extended fuzzy TISM is discussed as follows and the flow chart of TISM is drawn in Fig. 4 .

Fig. 4.

The flow chart of TISM.

3.1.1. Develop interpretive matrix

Let $E=\left\{e_1,e_2,\cdots e_h\right\}$ be the set of experts. Consider the risk factors$C=\left\{c_1,c_2,\cdots c_n\right\}$, where $c_l$ is the $l$ th factor, in which$l\text{=}1,2\cdots n$. Traditional risk evaluation is based on probabilistic risk assessment methods, which require the support of accurate probability distribution information of risk factors. However, COVID-19 medical waste transportation is complicated and it is challenging to grasp sufficient information on related risk factors. Experts with knowledge and experience in relevant domains are needed to deal with the problem of inadequate data. Therefore, we introduce IT2TrFNs, one of the most often utilized forms of fuzzy numbers, to represent uncertainty and ambiguity. Table 1 adopts a five-level linguistic term to express experts' evaluation (Abdullah and Najib, 2014).

Table 1.

The linguistic terms of IT2TrFNs.

Linguistic terms	IT2TrFNs
Very high influence(VH)	[(0.8,0.9,0.9,1.0;1),(0.85,0.9,0.9,0.95;0.9)]
High influence(H)	[(0.6,0.7,0.7,0.8;1),(0.65,0.7,0.7,0.75;0.9)]
Low influence (L)	[(0.4,0.5,0.5,0.6;1),(0.45,0.5,0.5,0.55;0.9)]
Very low influence (VL)	[(0.2,0.3,0.3,0.4;1),(0.25,0.3,0.3,0.35;0.9)]
No influence (No)	[(0,0.1,0.1,0.1;1),(0,0.1,0.1,0.05;0.9)]

The risk factors are linked in such a way that they either influence or are influenced by one another. The following four symbols V, A, X, and O (Sayali Sandbhor 2019) are used to show the direction of the links between the two risk factors $c_i$ and$c_j$.

• (i).V: To show a relationship from risk factor $c_i$ to risk factor $c_j$ but not vice versa; the relationship can be expressed as V followed by [Very high (VH), High (H), Low (L), Very low (VL)]. For example, V (VH) or V(H) or V(L) or V(VL).
• (ii).A: To show the relationship from risk factor $c_j$ to risk factor $c_i$ but not vice versa; the relationship can be expressed as A followed by [Very high (VH), High (H), Low (L), Very low (VL)].
• (iii).X: To show the relationship from risk factor $c_i$ to $c_j$ and risk factor $c_j$ to$c_i$; the relationship can be expressed as X followed by [Very high (VH), High (H), Low (L), Very low (VL)].
• (iv).O: To show no existence of a relationship between two risk factors; the relationship can be represented as O followed by [No influence (No)].

3.1.2. Develop aggregated SSIM using a new double alpha-cut method

• (i).Develop aggregated fuzzy SSIM

  The opinions of the $h$ experts on risk factors are collected. Then, the aggregated fuzzy SSIM $\stackrel{\approx }{M}$ is obtained according to Eq. (10).

(10)

• (ii).Develop aggregated fuzzy SSIM

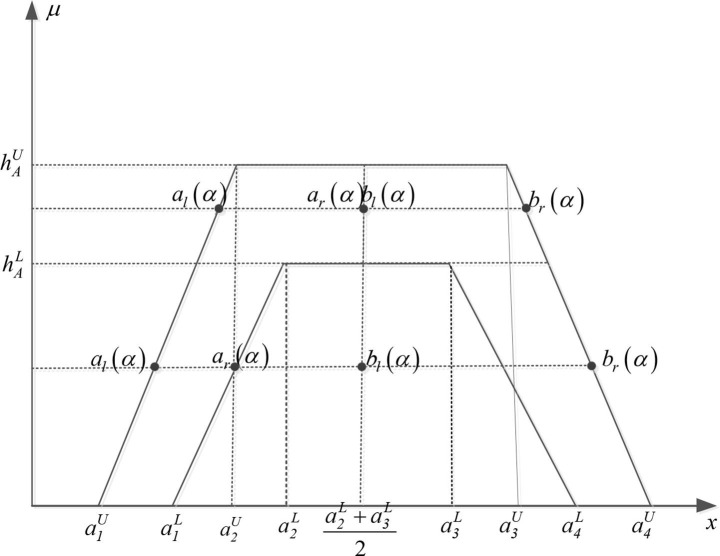
  To establish an aggregated SSIM, the alpha-cut method is a method to deal with uncertainty, by which we can decompose the membership function of a fuzzy set into intervals (Rouhparvar and Panahi, 2015). The concept of alpha level sets of fuzzy sets was initiated by Nguyen (1978), regarded as a simple and effective way to convert fuzzy numbers into crisp values (Dymova et al., 2015, Liao et al., 2021, Yang et al., 2020). The most commonly used alpha-cuts of IT2FS $\stackrel{\approx }{A}$ are presented as Eq. (11) (Dymova, et al., 2015). Where $a\left(\alpha \right)\in \left[a_l\left(\alpha \right),a_r\left(\alpha \right)\right],$ $b\left(\alpha \right)\in \left[b_l\left(\alpha \right),b_r\left(\alpha \right)\right]$ and$0⩽\alpha ⩽1$.

$$\stackrel{\approx }{A}\left(\alpha \right)=\left\{\left(x\right|{\underset{\_}{\mu }}_{\stackrel{\approx }{A}}\left(x\right)⩾\alpha ,{\overline{\mu }}_{\stackrel{\approx }{A}}\left(x\right)⩾\alpha \right\}=\left\{a\left(\alpha \right),b\left(\alpha \right)\right\}$$ (11)

To avoid the overlap of the left and right intervals of the alpha-cuts of a IT2TrFN$\stackrel{\approx }{A}=\left[\left(a_1^U,a_2^U,a_3^U,a_4^U;h_A^U\right),\left(a_1^L,a_2^L,a_3^L,a_4^L;h_A^L\right)\right]$, Yang, et al. (2020) make a modification of $a_r\left(\alpha \right)$ and$b_r\left(\alpha \right)$, which are defined as follows:

$$a_r\left(\alpha \right)\triangleq \left\{\begin{array}{c}{a}_r\left(\alpha \right),\alpha \in \left[0,h_A^L\right]\\ \frac{a_2^L+a_3^L}{2},\alpha \in \left[h_A^U,h_A^L\right]\end{array}\right)$$ (12)

$$b_r\left(\alpha \right)\triangleq \left\{\begin{array}{c}{b}_l\left(\alpha \right),\alpha \in \left[0,h_A^L\right]\\ \frac{a_2^L+a_3^L}{2},\alpha \in \left[h_A^U,h_A^L\right]\end{array}\right)$$ (13)

The lower ${\underset{\_}{\mu }}_{\stackrel{\approx }{A}}\left(x\right)$ and upper ${\overline{\mu }}_{\stackrel{\approx }{A}}\left(x\right)$ membership functions of IT2TrFNS are defined as follows:

$${\underset{\_}{\mu }}_{\stackrel{\approx }{A}}\left(x\right)=\left\{\begin{array}{c}\frac{\left(x-a_1^L\right)h_A^L}{a_2^L-a_1^L},a_1^L⩽x⩽a_2^L\\ h_A^L,a_2^L⩽x⩽a_3^L\\ \frac{\left(a_4^L-x\right)h_A^L}{a_4^L-a_3^L},a_3^L⩽x⩽a_4^L\\ 0,\text{otherwise}\end{array}\right)$$ (14)

$${\overline{\mu }}_{\stackrel{\approx }{A}}\left(x\right)=\left\{\begin{array}{c}\frac{\left(x-a_1^U\right)h_A^U}{a_2^U-a_1^U},a_1^U⩽x⩽a_2^U\\ h_A^U,a_2^U⩽x⩽a_3^U\\ \frac{\left(a_4^U-x\right)h_A^U}{a_4^U-a_3^U},a_3^U⩽x⩽a_4^U\\ 0,otherwise\end{array}\right)$$ (15)

The definition of the alpha-cuts of IT2TrFNs is depicted in Fig. 5 :

Fig. 5.

The alpha-cut of the IT2TrFNs.

A number of intermediate intervals could be obtained by cutting the membership functions by the alpha-cut. However, the widely used alpha-cuts of IT2TrFNs can only decompose the membership functions of a fuzzy set into intervals. As an important part of the TISM framework, the reachability matrix can help reflect the contextual relationships. To reach the reachability matrix with numerical values of 0 and 1, we refer to the idea of the double alpha-cut-based consensus measurement method in the study of Liao, et al. (2021) and propose a new double alpha-cut method to convert the IT2FNs in SSIM into crisp numbers. The specific steps are as follows:

The ${\alpha }^1$-cut set of IT2TrFN is defined as:

$${\mu }_{\stackrel{\approx }{A}}^{{\alpha }^1}=\left\{\left(x\right|{\overline{\mu }}_{\stackrel{\approx }{A}}\left(x\right)⩾{\alpha }^1,{\underset{\_}{\mu }}_{\stackrel{\approx }{A}}\left(x\right)⩾{\alpha }^1\right\}=\left\{a\left({\alpha }^1\right),b\left({\alpha }^1\right)\right\}$$ (16)

To demonstrate the characteristics of using double alpha-cut to deal with fuzzy information, a simple example is provided.

Example 1:Let an IT2TrFN${\stackrel{\approx }{A}}_1\text{=}\left[\left(0.1,0.3,0.4,0.5;1\right),\left(0.2,0.3,0.35,0.4;0.9\right)\right]$. The membership functions, which have the domain$U=\left[0,1\right]$,$a\left({\alpha }^1\right)\text{=}\left[0.3,0.475\right]$,$b\left({\alpha }^1\right)\text{=}\left[0.227,0.386\right]$ of${\alpha }^1$ = 0.25, ${\mu }_{{\stackrel{\approx }{A}}_1}^{0.25}$ is$\left\{\left[0.3,0.475\right],\left[0.227,0.386\right]\right\}$.

As we can see from Example 1, the ${\alpha }^1$-cut set ${\mu }_{\stackrel{\approx }{A}}^{{\alpha }^1}$ shows the distribution of the membership degrees corresponding to an IT2TrFN when $x$ is fixed as${\alpha }^1$. Then, the second alpha-cut, ${\alpha }^2$-cut set is introduced as follows:

$${\mu }_{\stackrel{\approx }{A}}^{{\alpha }^1,{\alpha }^2}=\left\{\begin{array}{c}0,\text{if}{a}_l\left({\alpha }^1\right)<{\alpha }^2,a_r\left({\alpha }^1\right)<{\alpha }^2,b_l\left({\alpha }^1\right)<{\alpha }^2,b_r\left({\alpha }^1\right)<{\alpha }^2\\ 1,others\end{array}\right)$$ (17)

Example 2: In Example 1, ${\mu }_{{\stackrel{\approx }{A}}_1}^{0.25}$ is$\left\{\left[a_l\left({\alpha }^1\right),a_r\left({\alpha }^1\right)\right]\text{=}\left[0.3,0.475\right],\left[b_l\left({\alpha }^1\right),b_r\left({\alpha }^1\right)\right]\text{=}\left[0.227,0.386\right]\right\}$. Let ${\alpha }^2$ be 0.1, 0.3 and 0.6 respectively. When${\alpha }^2$ = 0.1, both $a_l\left({\alpha }^1\right),a_r\left({\alpha }^1\right)$ and $b_l\left({\alpha }^1\right),b_r\left({\alpha }^1\right)$ are bigger than${\alpha }^2$, so ${\mu }_{{\stackrel{\approx }{A}}_1}^{0.25,0.1}$ is 1. When${\alpha }^2$ = 0.3, although$b_l\left({\alpha }^1\right)$ = 0.227 is smaller than 0.3, $a_l\left({\alpha }^1\right),a_r\left({\alpha }^1\right)$ and $b_r\left({\alpha }^1\right)$ is bigger than${\alpha }^2$. Hence, ${\mu }_{{\stackrel{\approx }{A}}_1}^{0.25,0.5}$ is 1 as well.${\alpha }^2$ = 0.6, because both $a_l\left({\alpha }^1\right),a_r\left({\alpha }^1\right)$ and $b_l\left({\alpha }^1\right),b_r\left({\alpha }^1\right)$ are smaller than${\alpha }^2$,${\mu }_{{\stackrel{\approx }{A}}_1}^{0.25,0.9}$ is 0.

Based on the double alpha-cut proposed above, the IT2TrNs are defuzzified into 0 or 1. In this way, convert the information in $\stackrel{\approx }{M}$ into 1 and 0 to construct the aggregated SSIM$M$.

$$M={\left[M_{\mathit{ij}}\right]}_{n\times n}=\left[\begin{array}{c}{M}_{11}{M}_{12}\cdots M_{1n}\\ M_{21}{M}_{22}\cdots M_{2n}\\ ⋮⋮\ddots ⋮\\ M_{n1}{M}_{n2}\cdots M_{\mathit{nn}}\end{array}\right]$$

$$M_{\mathit{ij}}\text{=}\left\{\begin{array}{c}0,{\mu }_{{\stackrel{\approx }{m}}_{\mathit{ij}}}^{{\alpha }^1,{\alpha }^2}\text{= 0}\\ 1,{\mu }_{{\stackrel{\approx }{m}}_{\mathit{ij}}}^{{\alpha }^1,{\alpha }^2}\text{= 1}\end{array}\right)$$ (18)

3.1.3. Get hierarchical digraph based on bidirectional extraction method

• (i).Developing Reachability Matrix and transitivity check

  Then, the aggregated SSIM matrix is turned into a reachability matrix. The final reachability is denoted as$N$. A transitivity check among pairs of risk factors should be done simultaneously to avoid unnecessary iteration. 1* implies the transitivity between selected pairs of risk factors, which are changed from 0 to 1. Then, the final reachability matrix $N$ is obtained according to Eqs. (19), (20) (Warfield, 1974).

Let $B$ be a multiplying matrix which is defined as follows, where $I$ is an identity matrix:

$$B=M+I$$ (19)

$$B^{k-1}\ne B^k=B^{k+1}=N$$ (20)

• (ii).Reachability Matrix Partition—Bidirectional extraction

  In this step, the final reachability matrix is partitioned at different levels. On the basis of the reachability matrix$N$, a reachability set$R$, an antecedent set $Q$ and an intersection set $G$ are obtained, where$G=R\cap Q$. $R$ is the column set of the $i$ th row in the reachable matrix $N$ containing the element 1, $Q$ is the set of rows with element 1 in the $i$ th column in the reachable matrix$N$. The result-first hierarchy extraction rule is$G\left(c_l\right)\text{=}R\left(c_l\right)$. The cause-first hierarchy extraction rule is$G\left(c_l\right)\text{=}Q\left(c_l\right)$. In a hierarchical diagram, the factors at the lowest level are the root causes and the factors at the top level are the output results. The factors at the middle level are the transition level, which are both causes and results. In order to keep all the root cause factors at the lowest level and the final result factors at the top level, this section defines a new bidirectional extraction method. The rotation extraction rule method is $G\left(c_l\right)\text{=}R\left(c_l\right)$ for the first iteration and $G\left(c_l\right)\text{=}Q\left(c_l\right)$ for the second iteration; the rest should be deduced by analogy.

• (iii).Developing Skeleton Matrix

  If there is a loop in the system, after the contraction processing is performed, all the forward edges of the contraction matrix obtained will be deleted. The resulting matrix is called the skeleton matrix. If the original matrix does not have loops, the skeleton matrix $S$ conforms to a simple algebraic formula.

$$S=N-{\left(N-I\right)}^2-I$$ (21)

• (iv).Creating Digraph for TISM

  After determining the levels of risk factors, use the factors' serial number and the directional arrow to construct the relationships between the risk factors. The final TISM model shows all transitive links and direct influential links. Arrows point from lower-level factors to upper-level. It means that the lower-level factors have an influence on the upper-level factors.

3.2. The risk evaluation and analysis based on the fuzzy BN

The fuzzy BN is applied to analyze COVID-19 medical waste transportation risk factors quantitatively. IT2FNs is combined with BN to model the objective uncertainties caused by probabilistic variations of risk factors. The prior probabilities and the conditional probabilities are calculated according to the centroid of IT2FNs. BN is introduced to provide a description of risk factors and their interactions with graphical representations and evaluate the risk probability quantitatively.

3.2.1. Construct a BN and apply IT2TFNS to calculate the probabilities

After obtaining the hierarchy diagram of risk factors, BN provides a graphical structure in a probabilistic approach based on the TISM digraph, including several nodes and the correlation between nodes. Netica software package, version 5.18, is utilized in this study to carry out the BN application, which is widely used in many studies (Fan et al., 2020, Fan et al., 2020, Sahin et al., 2019). Netica is practical software with an intuitive user interface that is great for BN applications. The most recent and quickest algorithms are utilized in conjunction with the networks to carry out various types of inference (Erkan, et al., 2021). The structure transformation of BN is shown in the Fig. 6 . The BN is composed of topological structure and conditional probability tables. Fig. 7 shows the particular example of BN with two root nodes, two leaf nodes and one top event.

Fig. 6.

Structure transformation of BN.

Fig. 7.

The particular example of BN.

To obtain the complete BN, experts are required to estimate the prior probabilities and conditional probabilities of nodes. In this paper, a five-level linguistic term is selected for expert expression, as shown in Table 1. To determine the probabilities of all nodes, the individual information of each expert should be aggregated firstly. For IT2FSs, a large variety of fuzzy power aggregation operators is suggested (Liu and Yu, 2014, Zhang, 2013). Among them, a traditional aggregation operator, named generalized weighted average (GWA) operator, is one of the most widely used operator for multiple attribute group decision making with fuzzy information (Chou and Cheng, 2012, Liu and Tang, 2016, Wang et al., 2016). It derives a group evaluation matrix based on the weights of each expert. The equation is shown below.

$$GWA\left({\stackrel{\approx }{o}}_1,{\stackrel{\approx }{o}}_2,\cdots ,{\stackrel{\approx }{o}}_h\right)={\left(\sum _{k=1}^h{\vartheta }_k{\stackrel{\approx }{o}}_k^{\lambda }\right)}^{1/\lambda }$$ (22)

where $\left({\stackrel{\approx }{o}}_1,{\stackrel{\approx }{o}}_2,\cdots ,{\stackrel{\approx }{o}}_h\right)$ represents the risk factors' probabilities evaluation provided by $h$ experts, ${\vartheta }_k$ represents the weights of the expert$e_k$. Drawing the experience of the literature (Liu, 2011), take$\lambda =1$. The aggregation can be described as the following form:

$$GWA\left({\stackrel{\approx }{o}}_1,{\stackrel{\approx }{o}}_2,\cdots ,{\stackrel{\approx }{o}}_h\right)=\sum _{k=1}^h{\vartheta }_k{\stackrel{\approx }{o}}^k\text{=}\left(\begin{array}{cccc}{\stackrel{\approx }{o}}_{11}& {\stackrel{\approx }{o}}_{12}& \cdots & {\stackrel{\approx }{o}}_{1n}\\ {\stackrel{\approx }{o}}_{21}& {\stackrel{\approx }{o}}_{22}& \cdots & {\stackrel{\approx }{o}}_{1n}\\ ⋮& ⋮& ⋮& ⋮\\ {\stackrel{\approx }{o}}_{m1}& {\stackrel{\approx }{o}}_{m2}& \cdots & {\stackrel{\approx }{o}}_{\mathit{mn}}\end{array}\right)$$ (23)

where.

$$\begin{array}{c}{\stackrel{\approx }{o}}_{\mathit{ij}}=\left[\left(o_{ij1}^U,o_{ij2}^U,o_{ij3}^U,o_{ij4}^U;\left(h_{\mathit{ij}}^U\right)\right)\right),\left(\left(o_{ij1}^L,o_{ij2}^L,o_{ij3}^L,o_{ij4}^L;\left(h_{\mathit{ij}}^L\right)\right)\right]\text{=}\left[\sum _{k=1}^h{\vartheta }_k\left({\stackrel{\approx }{o}}_{\mathit{ij}}^k\right)\right]\\ \text{=}\left[\left(\sum _{k=1}^h{\vartheta }_k{o}_{ij1}^{\mathit{kU}},\sum _{k=1}^h{\vartheta }_k{o}_{ij2}^{\mathit{kU}},\sum _{k=1}^h{\vartheta }_k{o}_{ij3}^{\mathit{kU}},\sum _{k=1}^h{\vartheta }_k{o}_{ij4}^{\mathit{kU}};\left(\sum _{k=1}^h{\vartheta }_k{o}_{\mathit{ij}}^{\mathit{kU}}\right)\right)\right),\\ \left(\left(\sum _{k=1}^h{\vartheta }_k{a}_{ij1}^{\mathit{kL}},\sum _{k=1}^h{\vartheta }_k{a}_{ij2}^{\mathit{kL}},\sum _{k=1}^h{\vartheta }_k{a}_{ij3}^{\mathit{kL}},\sum _{k=1}^h{\vartheta }_k{a}_{ij4}^{\mathit{kL}};\sum _{k=1}^h{\vartheta }_k\left(h_{\mathit{ij}}^{\mathit{kL}}\right)\right)\right]\end{array}$$ (24)

Next, the centroid of an IT2TrFN is applied to calculate the probabilities of the factors based on the aggregated evaluation information. Suppose the risk status of the risk factors are occurrence ($Y$) and non-occurrence ($N$), invite experts to give opinions on risk status $Y$ according to Table 1.. The prior probabilities and conditional probabilities of risk factors are calculated according to the following equations. For an IT2TrFN$\stackrel{\approx }{O}\text{=}\left[\left(o_1^U,o_2^U,o_3^U,o_4^U;h_O^U\right),\left(o_1^L,o_2^L,o_3^L,o_4^L;h_O^L\right)\right]$, ${\underset{\_}{\mu }}_{\stackrel{\approx }{O}}\left(x\right)$ and ${\overline{\mu }}_{\stackrel{\approx }{O}}\left(x\right)$ can be derived according to the Eqs. (14), (15). The centroid $C_{\stackrel{\approx }{O}}$ of an IT2TrFN $\stackrel{\approx }{O}$ is the union of the centroids of all its embedded type-1 fuzzy sets$O_e$. $c_l\left(\stackrel{\approx }{O}\right)$ and $c_r\left(\stackrel{\approx }{O}\right)$ represent the left and right endpoints of the centroid of an IT2TrFN$\stackrel{\approx }{O}$.

$$C_{\stackrel{\approx }{O}}=\cup {}_{\forall O_e}{c}_{\stackrel{\approx }{O}}\left(O_e\right)=\left\{c_l\left(\stackrel{\approx }{O}\right),\dots c_r\left(\stackrel{\approx }{O}\right)\right\}$$ (25)

Let $x_i\left(i=1,2,\cdots N\right)$ represents the discretization of an IT2TrFN, the specific calculation formulas of $c_l\left(\stackrel{\approx }{O}\right)$ and $c_r\left(\stackrel{\approx }{O}\right)$ are defined as Eqs. (26), (27). The prior probabilities of root nodes and the conditional probabilities of leaf nodes can be calculated according to Eq. (28). Then, apply the probabilities to the Netica software.

$$c_l\left(\stackrel{\approx }{O}\right)\text{=}\underset{\forall O_e}{\min }{c}_{\stackrel{\approx }{O}}\left(O_e\right)=\underset{\forall {\theta }_i\in \left[{\underset{\_}{\mu }}_{\stackrel{\approx }{O}}\left(x\right),{\overline{\mu }}_{\stackrel{\approx }{O}}\left(x\right)\right]}{\min }\left(\frac{{\sum }_{i=1}^N{x}_i{\theta }_i}{{\sum }_{i=1}^N{\theta }_i}\right)$$ (26)

$$c_r\left(\stackrel{\approx }{O}\right)\text{=}\underset{\forall O_e}{\max }{c}_{\stackrel{\approx }{O}}\left(O_e\right)=\underset{\forall {\theta }_i\in \left[{\underset{\_}{\mu }}_{\stackrel{\approx }{O}}\left(x\right),{\overline{\mu }}_{\stackrel{\approx }{O}}\left(x\right)\right]}{\max }\left(\frac{{\sum }_{i=1}^N{x}_i{\theta }_i}{{\sum }_{i=1}^N{\theta }_i}\right)$$ (27)

$$C\left(\stackrel{\approx }{O}\right)=\frac{c_l\left(\stackrel{\approx }{O}\right)\text{+}{c}_r\left(\stackrel{\approx }{O}\right)}{2}$$ (28)

3.2.2. Assess the risk probability of the top event$T$.

BN provides a description of risk factors and their interconnections by graphical representations. Risk factor(s) at the top level (level I) should be called top event(s)$T$. The risk probability of the top event $T$ can be calculated by inputting the prior probabilities and the conditional probabilities of the antecedent set$\left\{X_1,X_2,\cdots X_t\right\}$, as shown in Eq. (29).

$$P\left(T\right)=\sum P\left(X_1,X_2,\cdots X_t\right)P\left(T\left|X_1,X_2,\cdots X_t\right)\right)$$ (29)

where $P\left(T\right)$ represents the probability of the top event, $P\left(X_1,X_2,\cdots X_t\right)$ is the joint probability distribution of$X$, which is an antecedent set of $t$ risk factors. $P\left(T\left|X_1,X_2,\cdots X_t\right)\right)$ is the conditional probability distribution.

3.2.3. Identify the sensitive factors

Sensitivity is used to measure the degree of influence of changes in the state of each risk factor on the change in the state of the top event$T$. The sensitivity calculation can identify the risk factors that have a greater impact on the top event and should be controlled in the event development (Zhang, TerMaath, & Shields, et al., 2021). The equation is expressed as follows, where$i\in \left[1,t\right]$:

$$I_Y\left(X_i\right)=\frac{1}{2}\left[\frac{\left|P\left(\left(T=Y\right|X_i=Y\right)-P\left(T=Y\right)\right|}{P\left(T=Y\right)}\right]+\left[\frac{\left|P\left(\left(T=Y\right|X_i=N\right)-P\left(T=Y\right)\right|}{P\left(T=Y\right)}\right]$$ (30)

3.2.4. Perform the posterior causative diagnosis

According to Eq. (31), the posterior causative diagnosis is performed by backward inference of the BN, where $i\in \left[1,t\right]$. Suppose the top event $T$ is in the occurrence state$Y$, then calculate the posterior probability of each risk factor state (where $k$ is equal to $Y$ or $N$). The higher the posterior probability at the state $Y$ of risk factors, the higher the probability that these risk factors may cause the top event to be in the state$Y$. The posterior probability of each risk factor is ranked from largest to smallest. When the top event occurs, each risk factor is examined in turn.

$$P\left(\left(X_i=k\right|T=Y\right)=\frac{P\left(X_i=k\right)P\left(\left(T=Y\right|X_i=k\right)}{P\left(T=Y\right)}$$ (31)

4. The solution procedures for COVID-19 medical waste transportation risk

Based on the above research methodology for the medical waste transportation process, Section 4.1 presents the specific steps of the integrated risk evaluation model for COVID-19 medical waste transportation, which consists of three Stages as shown in Fig. 8 . Stage 1 is to identify risk factors and develop aggregated SSIM. Potential risk factors are identified and IT2FSs are applied to express the uncertainty in experts' evaluation. A new double alpha-cut of IT2FNs is first combined with TISM method to develop aggregated SSIM. Stage 2 is to construct a hierarchical digraph of risk factors. The type-2 fuzzy sets and a new bidirectional extraction method are combined with TISM method to construct the hierarchy diagram of risk factors. Stage 3 is to construct a BN and evaluate risks. The hierarchy diagram of risk factors is substituted into BN to describe the objective uncertainties caused by probabilistic variations of risk factors. The main characteristics of the integrated model are listed in Section 4.2.

Fig. 8.

The specific steps of the integrated risk evaluation model.

4.1. The specific steps of the integrated model

Stage 1: Identify risk factors and develop aggregated SSIM.

Step 1.1: Identify potential risk factors.

The first step is to recognize all potential risk factors of medical waste transportation. A set of risk factors is established as$C=\left\{c_1,c_2,\cdots c_n\right\}$. $E=\left\{e_1\right),e_2,\cdots \left(e_h\right\}$ represents $h$ experts who provide the evaluation of the risk factors' relationships.

Step 1.2: Define the contextual relationship between factors by IT2TFS.

The contextual relationship between factors $C=\left\{c_1,c_2,\cdots c_n\right\}$ is gathered from a group of $h$ experts$E=\left\{e_1,e_2,\cdots e_h\right\}$. The direction of the relationship between the two factors $c_i$ and $c_j$ can be denoted by the following four symbols V, A, X and O and the linguistic terms of IT2TrFNs. The evaluation matrix can be expressed as.

Step 1.3: Develop aggregated fuzzy SSIM.

The aggregated fuzzy SSIM matrix $\stackrel{\approx }{M}$ is obtained according to Eq. (10).

Step 1.4: Develop aggregated SSIM using the double alpha-cut of IT2TrFNs.

Then, the aggregated SSIM $M$ with crisp numbers can be obtained based on the double alpha-cut of IT2TrFNs, using Eq. (18).

Step 1.5: Calculate the final reachability matrix.

The final reachability $N$ is calculated by using Eqs. (19), (20). Then, a transitivity check among pairs of factors should be done simultaneously to avoid unnecessary iteration.

Step 1.6: Partition the levels of risk factors.

Based on the reachability matrix, the levels of factors are determined according to the bidirectional extraction method; the rule is $G\left(c_l\right)\text{=}R\left(c_l\right)$ for the first iteration,$G\left(c_l\right)\text{=}Q\left(c_l\right)$ for the second iteration and the rest be deduced by analogy.

Step 1.7: Develop the skeleton matrix.

If the original matrix does not have loops, the skeleton matrix can be obtained by using Eq. (21).

Step 1.8: Creating a hierarchical digraph of risk factors.

After determining the levels of risk factors, the final TISM uses a directional arrow to construct the relationship between the factors shown in the skeleton matrix. The hierarchical digraph of risk factors is created.

Stage2: Construct a BN and evaluate risks.

Step 2.1: Construct a BN.

After obtaining the hierarchy diagram of risk factors, the BN is constructed according to the transformation rules shown in Fig. 6.

Step 2.2: Express the probabilities of risk factors using IT2TrFNs.

After obtaining the hierarchical digraph, experts give evaluation opinions on the probabilities of risk factors by using the linguistic terms of IT2TrFNs shown in Table 1.

Step 2.3: Calculate the probabilities according to the centroid of IT2TrFNs.

The prior probabilities of root nodes and the conditional probabilities of leaf nodes are calculated according to the centroid of IT2TrFNs, using Eqs. (22), (23), (24), (25), (26), (27), (28).

Step 2.4: Assess the risk probability of the top event.

Based on the prior probabilities and conditional probabilities, the risk probability of the top event $T$ is obtained by using Eq. (29).

Step 2.5: Identify the sensitive factors.

Set the probability value of the node state $Y$ for each risk factor to 1 and 0 respectively, represents the occurrence and non-occurrence of each risk factor, record the probability value of the top event$T$. Then, calculate the sensitivity of each risk factor according to Eq.(30).

Step 2.6: Diagnose the event causation.

Set the probability of risk occurrence $Y$ of the top event $T$ as 1, and obtain the posterior probability of each node to diagnose the event causation by using Eq. (31).

4.2. The main characteristics of the integrated model

The integrated model for COVID-19 medical waste transportation based on extended fuzzy TISM and fuzzy BN has been described above. This model can help analyze the risk factors in the medical waste transportation process under high uncertain environment, identify the sensitive factors and diagnose the event causation. The main characteristics are summarized below:

• (i).The COVID-19 pandemic is an emergency without sufficient historical data. The evaluation of COVID-19 medical waste transportation risk requires the support of experts in related fields. The proposed model considers the ambiguous evaluation information expressed by experts; introduces the linguistic terms and corresponding IT2FNs to avoid the omission and distortion of evaluation information under uncertain environments.
• (ii).Considering the interaction relationships between/among risk factors, TISM is combined with IT2FSs to analyze the contextual relationships of risk factors under uncertain environment. Moreover, a new double alpha-cut is proposed to defuzzificate the IT2FNs in the process of constructing the aggregated SSIM to help obtain a hierarchical digraph of risk factors.
• (iii).A new bidirectional extraction method is first developed to partition the levels of risk factors in the process of TISM. The bidirectional extraction method can reflect the dialectical relationship between causes and results more realistic and effective.
• (iv).After obtaining the hierarchical digraph of risk factors by using the extended fuzzy TISM method, the digraph is transformed into a BN to make a comprehensive risk evaluation. Moreover, the prior probabilities and conditional probabilities of risk factors are expressed by IT2FNs.

5. Case study

In this section, a case study of the COVID-19 medical waste transportation process at Lukou international airport in Nanjing is proposed to demonstrate the effectiveness and advantages of the proposed model. The detailed description and the calculation process of the case are shown as follows:

5.1. The detailed description of the case in Nanjing

On July 20, 2022, 9 samples were found to be positive in a routine nucleic acid test conducted at Lukou international airport in Jiangning District, Nanjing, all of which were airport cleaners. As of 24:00 on July 25, this round of Nanjing epidemic has affected 5 provinces and 9 cities. As of 24:00 on July 27, Nanjing has reported a total of 153 local confirmed cases and 2 local asymptomatic infections. The new cases are mainly concentrated in Lukou Airport and surrounding areas, and many cluster outbreaks have been found.in the reported cases. The initial COVID-19 virus in Nanjing was caused by the cleaner who cleaned the cabin of the CA910. The handling of the protective clothing after work was not standardized, which caused the individual infection and spread among the cleaners. Some other airport workers were infected by contact with cleaners or the polluted environment. Since corona virus has a high degree of spatial infectious, latent and viral, handling the protective clothing can also be regarded as part of the medical waste transportation process. Therefore, we take this Nanjing epidemic as the background to assess the risk of medical waste transportation.

5.2. The calculation process of the case study

Stage 1: Identify risk factors and develop aggregated SSIM.

Step 1.1: Identify potential risk factors.

Three relevant experts $E=\left\{e_1\right),e_2,\left(e_3\right\}$ are invited to evaluate the risk factors' relationships. The three experts with different backgrounds and fields are selected to establish the expert group.

Table 2 shows the description of the three experts. Experts $e_1$ and $e_2$ are both from Zhongda Hospital Southeast University, $e_1$ is a doctor in the hospital's respiratory medicine department, $e_2$ is a supervisor of the hospital. Expert $e_3$ is a transportation worker responsible for the transportation of hospital medical waste. The three experts are suggested to give evaluation information in terms of linguistic terms, which is shown in Table 1.

Table 2.

The description of experts.

Experts ID	Position	Age	Working experience
$e_1$	Doctor	43	13
$e_2$	Supervisor	37	9
$e_3$	Transportation worker	35	10

COVID-19 medical waste must be transported by special employee and vehicles. Employee must take standard precautions as required, such as medical surgical masks, gloves and work clothes. Personnel entering the isolation ward to collect medical waste should take precautions according to the requirements of the employee entering the area. Therefore, possible risks are the risk of employee infection and the risk of inadequate personal protection of employee. At the same time, the storage of COVID-19 medical waste in the special area of medical institutions shall not be mixed with other medical waste and domestic waste, and should be marked with “highly infectious waste” identification signs and strict sealing measures should be adopted. Medical institutions should hand over the new crown medical waste to the medical waste disposal unit for disposal on the same day, specify the person responsible for management. According to the above transportation characteristics and the literature related to transportation risks, we can obtain 16 risk factors as shown in Table 3 .

Table 3.

The descriptions of risk factors.

number	Risk factors	Literature support
$c_1$	Employee infection risk	(Akpieyi et al., 2015, Kumar et al., 2015)
$c_2$	Low employee safety awareness	(Manupati, et al., 2021)
$c_3$	Improper operation by employee	(Huang et al., 2020, Kumar et al., 2015, Manupati et al., 2021)
$c_4$	Inadequate personal protection of employee	(Huang et al., 2020, Ouyang et al., 2021)
$c_5$	Improper disinfection of transfer tools	(Akpieyi et al., 2015, Manupati et al., 2021)
$c_6$	Unsafe handling equipment	(Huang et al., 2020, Kumar et al., 2015)
$c_7$	Unreasonable collection and transportation of medical waste containers	(Ouyang, et al., 2021)
$c_8$	Irregular construction of temporary storage sites for medical waste	(Taslimi, et al., 2020)
$c_9$	Unreasonable location of storage location	(Kumar et al., 2015, Taslimi et al., 2020)
$c_{10}$	Failure to conduct regular health checkups on relevant personnel	(Akpieyi et al., 2015, Manupati et al., 2021)
$c_{11}$	Insufficient technical training	(Ouyang et al., 2021, Song et al., 2020)
$c_{12}$	Lack of safety education	(Huang et al., 2020, Makan and Fadili, 2020)
$c_{13}$	Insufficient accountability system	(Makan and Fadili, 2020, Song et al., 2020)
$c_{14}$	Insufficient emergency response mechanism for safety management	(Huang et al., 2020, Makan and Fadili, 2020)
$c_{15}$	Insufficient supervision of collection and disposal	(Makan and Fadili, 2020)
$c_{16}$	Harsh processing environment	(Huang, et al., 2020)

Step 1.2: Define the contextual relationship between factors by IT2TFS.

Define the contextual relationship between factors by IT2TFS.

The relationship between the factors $C=\left\{c_1,c_2,\cdots c_{16}\right\}$ is gathered from a group of three experts. The evaluation matrix represents the direction of the relationship between the two factors $c_i$ and $c_j$ given by the expert$e_1$, which is shown in Table 4 .

Table 4.

The fuzzy SSIM matrix by expert$e_1$.

$e_1$	$c_{16}$	$c_{15}$	$c_{14}$	$c_{13}$	$c_{12}$	$c_{11}$	$c_{10}$	$c_9$	$c_8$	$c_7$	$c_6$	$c_5$	$c_4$	$c_3$	$c_2$
$c_2$	A(VL)	O(No)	A(H)	O(No)	O(No)	O(No)	A(H)	O(No)	A(L)	A(H)	A(VH)	A(VH)	A(VH)	A(L)	O(No)
$c_3$	O(No)	O(No)	O(No)	A(H)	A(VH)	A(L)	V(H)	O(No)	O(No)	V(L)	O(No)	V(H)	V(VH)	V(L)
$c_4$	O(No)	O(No)	O(No)	A(H)	A(H)	A(H)	O(No)	A(H)	O(No)	V(L)	O(No)	V(H)	O(No)
$c_5$	O(No)	A(H)	O(No)	A(H)	A(VH)	A(L)	O(No)	O(No)	O(No)	O(No)	O(No)	O(No)
$c_6$	O(No)	A(H)	O(No)	A(VH)	A(VH)	A(H)	O(No)	O(No)	O(No)	O(No)	O(No)
$c_7$	O(No)	O(No)	O(No)	O(No)	O(No)	O(No)	O(No)	A(L)	A(L)	O(No)
$c_8$	O(No)	A(VH)	O(No)	A(VH)	A(H)	A(H)	O(No)	O(No)	O(No)
$c_9$	O(No)	O(No)	O(No)	A(L)	A(H)	O(No)	O(No)	O(No)
$c_{10}$	O(No)	O(No)	O(No)	A(H)	A(H)	O(No)	O(No)
$c_{11}$	O(No)	O(No)	O(No)	A(L)	A(VH)	O(No)
$c_{12}$	O(No)	O(No)	O(No)	O(No)	O(No)
$c_{13}$	V(L)	V(L)	V(H)	O(No)
$c_{14}$	O(No)	A(H)	O(No)
$c_{15}$	O(No)	O(No)
$c_{16}$	O(No)

Step 1.3: Develop aggregated fuzzy SSIM.

The aggregated fuzzy SSIM matrix $\stackrel{\approx }{M}$ is obtained according to Eq. (10). Table A1 (see Appendix A) shows the detailed results.

Step 1.4: Develop aggregated SSIM using the double alpha-cut of IT2TrFNs.

The aggregated SSIM $M$ can be obtained based on the double alpha-cut of IT2TrFNs,using Eq. (18). Table A2 (see Appendix A) shows the detailed results.

Step 1.5: Calculate the final reachability matrix.

The final reachability $N$ is calculated by using Eqs. (19), (20). A transitivity check among pairs of factors should be done simultaneously to avoid unnecessary iteration. Table A3 (see Appendix A) presents the aggregated SSIM $M$ after transitivity check. Then, the final reachability $N$ is calculated by using Eqs. (19), (20) as shown in Table 5 .

Table 5.

The final reachability$N$.

	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$	$c_{11}$	$c_{12}$	$c_{13}$	$c_{14}$	$c_{15}$	$c_{16}$
$c_1$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_2$	1	0	1	1	1	0	0	0	0	1	0	0	0	0	0	0
$c_3$	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
$c_4$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_5$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_6$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_7$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_8$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_9$	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
$c_{10}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{11}$	1	1	1	1	1	0	1	0	0	1	0	0	0	0	0	0
$c_{12}$	1	1	1	1	1	1	1	1	1	1	0	0	1	1	1	1
$c_{13}$	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0
$c_{14}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{15}$	1	1	1	1	1	1	1	1	1	1	0	0	1	0	0	0
$c_{16}$	1	0	1	0	1	1	0	0	0	0	0	0	0	0	0	0

Step 1.6: Partition the levels of factors.

The levels of factors are determined according to the bidirectional extraction method. Table 6 presents the calculation steps of the bidirectional extraction method.

Table 6.

The bidirectional extraction.

Variables	Reachability set	Antecedent set	Intersection set	Level
(a):Iteration-1
$c_1$	1	1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16	1	1
$c_2$	1,2,3,4,5,10	2,11,12,13,15	2
$c_3$	1,3,5	2,3,11,12,13,15,16	3
$c_4$	1,4	2,4,11,12,13,15	4
$c_5$	1,5	2,3,5,11,12,13,15,16	5
$c_6$	1,6	6,9,12,13,15,16	6
$c_7$	1,7	7,11,12,13,15	7
$c_8$	1,8	8,12,13,15	8
$c_9$	1,6,9	9,12,13,15	9
$c_{10}$	1,10	2,10,11,12,13,15	10
$c_{11}$	1,2,3,4,5,7,10,11	11	11
$c_{12}$	1,2,3,4,5,6,7,8,9,10,12,13,14,15,16	12	12
$c_{13}$	1,2,3,4,5,6,7,8,9,10,13	12,13	13
$c_{14}$	1,14	12,14	14
$c_{15}$	1,2,3,4,5,6,7,8,9,10,13,15	12,13,15	13,15
$c_{16}$	1,3,5,6,16	12,16	16
(b):Iteration-2
$c_2$	2,3,4,5,10	2,11,12,13,15,16	2
$c_3$	3,5	2,3,11,12,13,15,16	3
$c_4$	4	2,4,11,12,13,15	4
$c_5$	5	2,3,5,11,12,13,15,16	5
$c_6$	6	6,9,12,13,15,16	6
$c_7$	7	7,11,12,13,15	7
$c_8$	8	8,12,13,15	8
$c_9$	6,9	9,12,13,15	9
$c_{10}$	10	2,10,11,12,13,15	10
$c_{11}$	2,3,4,5,7,10,11	11	11	II
$c_{12}$	2,3,4,5,6,7,8,9,10,12,13,14,15,16	12	12	II
$c_{13}$	2,3,4,5,6,7,8,9,10,13	12,13	13
$c_{14}$	14	12,14	14
$c_{15}$	2,3,4,5,6,7,8,9,10,13,15	12,13,15	13,15
$c_{16}$	3,5,6,16	12,16	16
(c):Iteration-3
$c_2$	2,3,4,5,10	2, 13,15,16	2
$c_3$	3,5	2,3,13,15,16	3
$c_4$	4	2,4,,13,15	4	III
$c_5$	5	2,3,5,13,15,16	5	III
$c_6$	6	6,9,,13,15,16	6	III
$c_7$	7	7,13,15	7	III
$c_8$	8	8,13,15	8	III
$c_9$	6,9	9,13,15	9
$c_{10}$	10	2,10,13,15	10	III
$c_{13}$	2,3,4,5,6,7,8,9,10,13	13	13
$c_{14}$	14	14	14	III
$c_{15}$	2,3,4,5,6,7,8,9,10,13	13,15	13
$c_{16}$	3,5,6,16	16	16
(d):Iteration-4
$c_2$	2,3,	2,13,15,16	2
$c_3$	3,	2,3,13,15,16	3
$c_9$	9	9,13,15	9
$c_{13}$	2,3,9,13	13	13	IV
$c_{15}$	2,3,9,13,15	13,15	13,15	IV
$c_{16}$	3, 16	16	16	IV
(e):Iteration-5
$c_2$	2,3,	2	2
$c_3$	3,	2,3,	3	V
$c_9$	9	9,	9	V
(f):Iteration-6
$c_2$	2	2	2	VI

Step 1.7: Develop the skeleton matrix.

If the original matrix does not have loops, the skeleton matrix $S$ in Table A4 (see Appendix A) is obtained according to Eq. (21).

Step 1.8: Creating a hierarchical digraph of risk factors.

The level of each risk factor is determined through bidirectional extraction. Element 1 in the skeleton matrix determines where the arrow is pointing. Based on Table 6 and Table A4, the final TISM model is described in Fig. 9 .

Fig. 9.

The final TISM digraph.

Step 2: Construct a BN and evaluate risks.

Step 2.1: Construct a BN.

The BN structure is obtained based on the final TISM digraph.

Step 2.2: Express the probabilities of risk factors using IT2TrFNs.

The final TISM digraph is transformed into BN according to the corresponding relationship in Fig. 6. After obtaining the BN graphical structure, experts give evaluation opinions on the risk factors by using linguistic terms shown in Table 1. $c_1$ (Employee infection risk) is the top event.

Step 2.3: Calculate the probabilities according to the centroid of IT2TrFNs.

The prior probabilities and conditional probabilities for each sub-indicator in the BN are determined by experts' evaluation. The average probability of fuzzy occurrence for each factor is calculated according to the centrality calculation of IT2FNs. The $c_{11}$ and $c_{12}$ need to calculate the prior probabilities because the two nodes belong to root nodes, the results are shown in Table 7 and Table 8 . The risk status of the risk factors are occurrence ($Y$) and non-occurrence ($N$), three experts are invited to give evaluation opinions on the risk status $Y$ of the root nodes $c_{11}$ and $c_{12}$ in the BN structure.

Table 7.

The evaluation of root nodes.

Root nodes	$e_1$	$e_2$	$e_3$
$c_{11}$	VH	VH	H
$c_{12}$	VH	H	H

Table 8.

The aggregated evaluation matrix of root nodes.

Root nodes	The aggregated evaluation
$c_{11}$	[(0.7333,0.8333,0.8333,0.9333;1.0),(0.7833,0.8333, 0.8333,0.8833;0.9)]
$c_{12}$	[(0.6667,0.7667,0.7667,0.8667;1.0),(0.7167,0.7667,0.7667,0.8167;0.9)]

Assuming that three experts are given the same weight, that is,${\vartheta }_k$ is assigned 1/3 in Eq. (23). The aggregated evaluation matrix is shown in the table below.

Based on the aggregated evaluation matrix, the prior probabilities of $c_{11}$ and $c_{12}$ are calculated according to Eqs. (25), (26), (27), (28), respectively as below:

$$P\left(c_{11}\right)=\left\{c_{11}=Y,c_{11}=N\right\}=\left\{0.8333,0.1667\right\}$$

$$P\left(c_{12}\right)=\left\{c_{12}=Y,c_{12}=N\right\}=\left\{0.7667,0.2333\right\}$$

In the same way, the conditional probabilities of other leaf nodes are calculated based on the expert's linguistic variable evaluation value.

Step 2.4: Assess the risk probability of the top event.

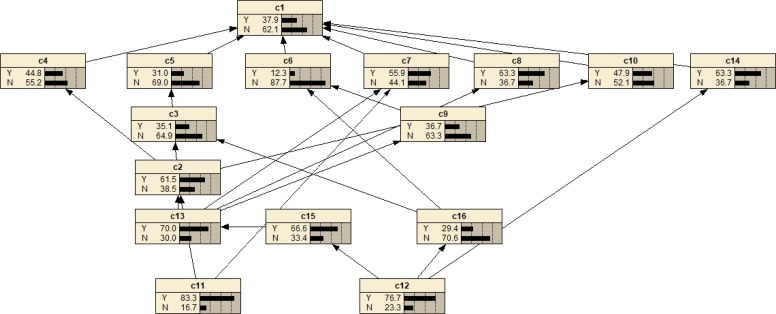
According to the prior probabilities of root nodes and conditional probabilities of leaf nodes, the BN is drawn on a visual interface in the Netica software. Through BN forward inference, the probability of occurrence for each risk factor is derived, and the calculation results are shown in Fig. 10 . The occurrence probability of the top event (medical waste transportation risk accident) is 0.379, which is relatively high. Therefore, it is necessary to study the causative factors leading to the top event $c_1$ to avoid the occurrence of larger accidents.

Fig. 10.

The occurrence probability of the top event.

Step 2.5: Identify the sensitive factors.

Based on the BN structure, risk factors $\left\{c_2,c_3,c_4\cdots c_{16}\right\}$ can be expressed as an antecedent set of variables$X_i\left(i\in 1,2\cdots 15\right)$. In Netica software, the state of each risk factors in antecedent set is set to 1 and 0 respectively, record the probability value of the top event$c_1$. The sensitivity of risk factors, which is the probability of top event $c_1$ when the factor occurs($Y$) minus the probability of $c_1$ when the factor does not occur ($N$). The results are shown in Table 9 .

Table 9.

The sensitivity of risk factors.

Risk factor	$P\left(T\text{=}Y\left|X_i=Y\right)\right)$	$P\left(T\text{=}Y\left|X_i=N\right)\right)$	$I_{T\text{=}Y}\left(X_i\right)$	Rank
$c_2$	0.452	0.267	0.185	3
$c_3$	0.454	0.345	0.109	5
$c_4$	0.548	0.242	0.306	1
$c_5$	0.542	0.306	0.236	2
$c_6$	0.488	0.364	0.124	4
$c_7$	0.409	0.342	0.067	8
$c_8$	0.386	0.368	0.018	11
$c_9$	0.389	0.374	0.015	14
$c_{10}$	0.4	0.356	0.044	10
$c_{11}$	0.396	0.295	0.101	6
$c_{12}$	0.383	0.367	0.016	13
$c_{13}$	0.404	0.32	0.084	7
$c_{14}$	0.385	0.369	0.016	12
$c_{15}$	0.381	0.379	0.002	15
$c_{16}$	0.416	0.364	0.052	9

In view of the findings, the top event $c_1$ (employee infection risk) increased obviously since the state of risk factors $c_4,c_5,c_2$ changed respectively. The sensitivity of risk factor $c_4$ is highest, which is 0.306. $c_4$ (Inadequate personal protection of employees) is the most sensitive factor, which means that $c_4$ is a crucial control risk factor in the transportation of medical waste. According to relevant news, the COVID-19 outbreak in Lukou international airport caused the employee infection by improper self-protection of the cleaning staff. Therefore, in the process of medical waste transportation and disposal, we should focus on controlling this risk factor, and minimize the possibility of this risk factor through control, to avoid the occurrence of employee infection.

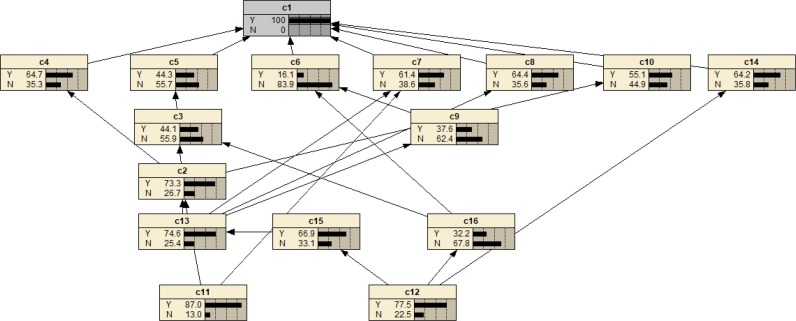
Step 2.6: Diagnose the event causation.

Set the occurrence probability of the top event $c_1$ as 1, and derive the posterior probability of each factor through BN backward inference, and the results are shown in Fig. 11 .

Fig. 11.

The event causation diagnosis.

It can be seen from Fig. 11 that the largest accident causal chains are $c_{12}\to c_{15}\to c_{13}\to c_2\to c_4\to c_1$ (Lack of safety education → Insufficient supervision of collection and disposal → Insufficient accountability system → Low employee safety awareness → Inadequate personal protection of employees → Employee infection risk) and $c_{11}\to c_2\to c_4\to c_1$ (Insufficient technical training → Low employee safety awareness → Inadequate personal protection of employees → Employee infection risk). The risk factors on the largest causal chains are important factors leading to the top event $T$ (Employee infection risk). Therefore, in the safety management of the medical waste transportation process, the above factors should be mainly controlled.

According to a report from Website of the Central Commission for Discipline Inspection and State Supervision Commission (https://www.ccdi.gov.cn/pln/202107/t20210728_142075.html), Lukou international airport had problems such as lack of supervision and unprofessional management; various measures for epidemic prevention and control have not been implemented in detail, resulting in the spread of the COVID-19 epidemic. Moreover, the airport had the problem of unprofessional management After the discovery of positive samples, the prevention and control management of relevant personnel at the airport was not in place, which led to the spread of the epidemic. The causal chains and critical factors identified by the proposed model are consistent with this report. Moreover, we also identified several other cause factors, such as lack of safety education and low employee safety awareness. The obtained results prove the feasibility and effectiveness of the proposed model and provide a reference for preventing the occurrence of similar accidents.

6. Comparisons analysis

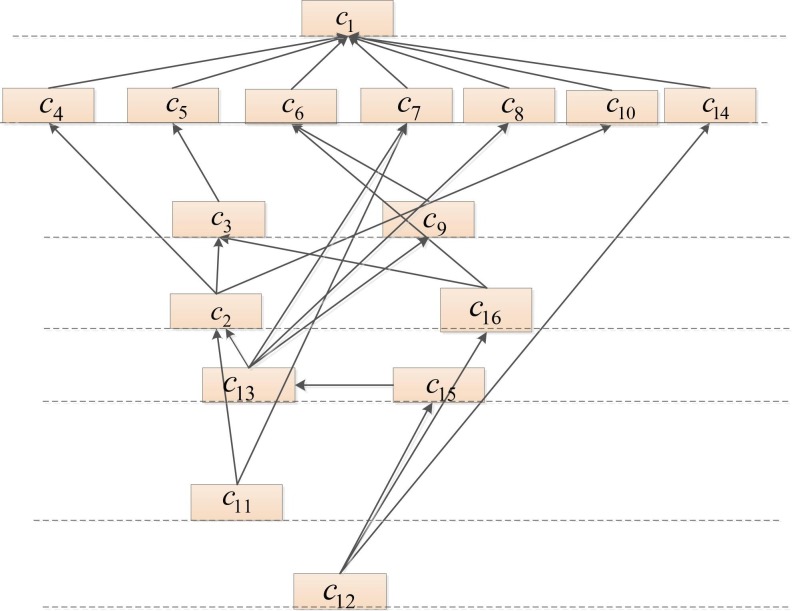
In this section, a comparison of our proposed model with traditional TISM and BN model is conducted. We substitute the data in the case study into the traditional TISM model. The level of each risk factor is determined through the result-first hierarchy extraction rule. The result-first hierarchy extraction rule is$G\left(c_l\right)\text{=}R\left(c_l\right)$. Fig. 12 shows the digraph obtained from traditional TISM.

Fig. 12.

The digraph obtained from traditional TISM.

Then the TISM digraph is transformed into BN to make comprehensive risk analysis. Referring from the traditional BN (Wang, et al., 2022), the prior and conditional probabilities of risk factors are given by the experience of experts, represented by crisp numbers. Calculate the average of the probabilities given by the three experts. For example, the conditional probabilities of $c_2$, the prior probabilities of $c_{11},c_{12}$ are depicted in Table 10 and Table 11 .

Table 10.

The prior probabilities of$c_{11},c_{12}$.

	$c_{11}$	$c_{12}$
$Y$	0.7	0.6
$N$	0.3	0.4

Table 11.

The conditional probabilities of$c_2$.

$c_{13}$	$c_{11}$	$Y$	$N$
$Y$	$Y$	0.767	0.233
$Y$	$N$	0.483	0.517
$N$	$Y$	0.35	0.65
$N$	$N$	0.216	0.784

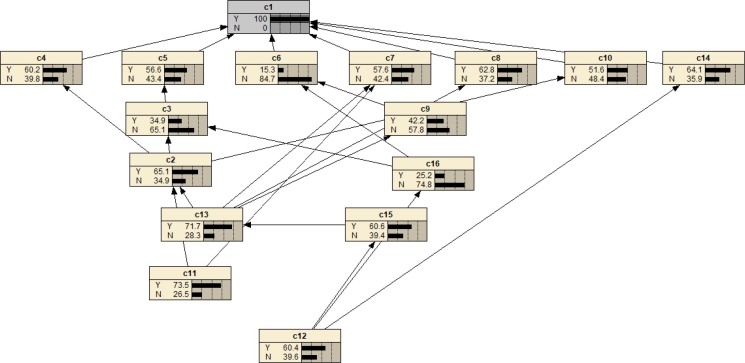
From Fig. 13 , we can conclude that the largest causal chains are $c_{12}\to c_{14}\to c_1$ (Lack of safety education → Insufficient emergency response mechanism for safety management → Employee infection risk). It can be seen that compared with the results obtained by the proposed model, many risk factors are lost in the accident causal chain obtained by the traditional BN model. The event causation diagnosis based on traditional BN is inconsistent with the mentioned factors in the report from Website of the Central Commission for Discipline Inspection and State Supervision Commission. The fuzzy BN proposed in this paper can provide a more complete and realistic accident causal chain because the IT2FNs can retain more uncertain information in the expert evaluation. At the same time, the hierarchical digraph obtained using traditional TISM has seven levels. $c_{12}$ and $c_{11}$ are both root factors, without being placed on the same level. It shows that the traditional hierarchical extraction method is not as effective as the bidirectional extraction method in reflecting the relationship between risk factors.

Fig. 13.

The event causation diagnosis based on traditional BN.

Therefore, the differences in results calculated by the traditional model and our proposed model are mainly in the following aspects. (i) In the practical BN application, the risk evaluation information is often uncertain and imprecise on account of the incomplete and inaccurate information, required knowledge and capability of experts. We combine the IT2FNs with TISM and BN, considering the uncertainty evaluation information, reflecting the relationship between/among risk factors more accurately. (ii) We propose a new hierarchical extraction method to conduct the hierarchy digraph. And the cause and effect elements are separated in the resulting hierarchy, making the hierarchical relationship between risk factors clearer. (iii) A new double alpha-cut is proposed to defuzzificate the IT2FNs in the process of constructing the aggregated SSIM to help obtain a hierarchical digraph of risk factors.

7. Conclusion

The risk identification and evaluation of COVID-19 medical waste transportation can effectively prevent potential infection accidents. IT2FNs are adopted to reflect the subjectivity under uncertain environments. The TISM is combined with IT2FNs to obtain a hierarchical digraph, which shows the relationships between risk factors, enhancing the understanding of complex accident systems and providing assistance in accident prevention. The hierarchical digraph obtained by fuzzy TISM is mapped to BN, assesses the occurrence probability of the top event using IT2TFS, identifies the sensitive factors and performs the posterior causative diagnosis. The feasibility of the integrated model is verified through the case study.

The case of COVID-19 medical waste transportation process in Nanjing selects 16 risk factors and constructs a hierarchical digraph based on the extended fuzzy TISM method. Then, the hierarchical digraph is transformed into BN, the prior probabilities of root nodes and conditional probabilities of leaf nodes are determined. The sensitive factors are identified by setting the occurrence probability of the risk factor to 1. The posterior probabilities of risk factors through BN backward inference is obtained by setting the occurrence probability of the top event as 1. The risk factor $c_4$ (0.306) is the most sensitive factor, also in the largest accident causal chains, which means $c_4$(inadequate personal protection of employees) is a crucial control risk factor in medical waste transportation process. The results can provide a reference for preventing the occurrence of similar accidents.

The limitations of the proposed model mainly include two aspects. (i) The integrated model does not consider the significance of experts, which means that we have ignored the influences of the relative weights of experts on risk evaluation. (ii) The integrated model is failed to describe the dynamic situations when experts' opinions change. Further, the integrated model will be extended to cover some generalized aggregation operators to calculate the different weights of experts under uncertain environment. Henceforth, we will introduce some dynamic simulation techniques to fit dynamic situations in application better.

CRediT authorship contribution statement

Jing Tang: Conceptualization, Methodology, Validation, Formal analysis, Writing – original draft, Visualization. Xinwang Liu: Writing – review & editing, Supervision, Project administration, Funding acquisition. Weizhong Wang: Methodology, Validation, Data curation, Writing – original draft, Visualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

In this appendix, we present detailed results about aggregated fuzzy SSIM matrix$\stackrel{\approx }{M}$, aggregated SSIM$M$, aggregated SSIM $M$ after transitivity check and the skeleton matrix $S$ of TISM method.

Table A1.

The aggregated fuzzy SSIM matrix$\stackrel{\approx }{M}$.

	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$	$c_{11}$	$c_{12}$	$c_{13}$	$c_{14}$	$c_{15}$	$c_{16}$
$c_1$	0	No	No	No	No	No	No	No	No	No	No	No	No	No	No	No
$c_2$	No	0	L	VH	H	No	L	No	No	H	No	No	No	No	No	No
$c_3$	L	No	0	No	H	No	L	No	No	No	No	No	No	No	No	No
$c_4$	VH	No	No	0	No	No	No	No	No	No	No	No	No	No	No	No
$c_5$	VH	No	No	No	0	No	No	No	No	No	No	No	No	No	No	No
$c_6$	VH	No	No	No	No	0	No	No	No	No	No	No	No	No	No	No
$c_7$	H	No	No	No	No	No	0	No	No	No	No	No	No	No	No	No
$c_8$	L	No	No	No	No	L	No	0	No	No	No	No	No	No	No	No
$c_9$	No	No	H	No	No	L	No	No	0	No	No	No	No	No	No	No
$c_{10}$	H	No	No	No	No	No	No	No	No	0	No	No	No	No	No	No
$c_{11}$	No	L	H	L	H	No	H	No	No	No	0	No	No	No	No	No
$c_{12}$	No	VH	H	VH	VH	No	H	H	H	VH	No	0	No	H	L	L
$c_{13}$	No	H	H	H	VH	No	VH	L	H	L	No	No	0	No	No	No
$c_{14}$	H	No	No	No	No	No	No	No	No	No	No	No	No	0	No	No
$c_{15}$	No	No	No	H	H	No	VH	No	No	No	No	No	H	No	0	No
$c_{16}$	VL	No	H	No	No	L	No	No	No	No	No	No	No	No	No	0

Table A2.

The aggregated SSIM$M$.

	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$	$c_{11}$	$c_{12}$	$c_{13}$	$c_{14}$	$c_{15}$	$c_{16}$
$c_1$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_2$	0	0	1	1	1	0	0	0	0	1	0	0	0	0	0	0
$c_3$	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
$c_4$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_5$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_6$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_7$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_8$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_9$	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
$c_{10}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{11}$	0	1	1	1	1	0	1	0	0	0	0	0	0	0	0	0
$c_{12}$	0	1	1	1	1	0	1	1	1	1	0	0	0	1	1	1
$c_{13}$	0	1	1	1	1	0	1	1	1	1	0	0	0	0	0	0
$c_{14}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{15}$	0	0	0	1	1	0	1	0	0	0	0	0	1	0	0	0
$c_{16}$	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0	0

Table A3.

The aggregated SSIM $M$ after transitivity check.

	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$	$c_{11}$	$c_{12}$	$c_{13}$	$c_{14}$	$c_{15}$	$c_{16}$
$c_1$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_2$	1*	0	1	1	1	0	0	0	0	1	0	0	0	0	0	0
$c_3$	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
$c_4$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_5$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_6$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_7$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_8$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_9$	1*	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
$c_{10}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{11}$	1*	1	1	1	1	0	1	0	0	0	0	0	0	0	0	0
$c_{12}$	1*	1	1	1	1	1*	1	1	1	1	0	0	0	1	1	1
$c_{13}$	1*	1	1	1	1	0	1	1	1	1	0	0	0	0	0	0
$c_{14}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{15}$	1*	0	0	1	1	0	1	0	0	0	0	0	1	0	0	0
$c_{16}$	1*	0	1	0	1*	1	0	0	0	0	0	0	0	0	0	0

Table A4.

The skeleton matrix$S$.

	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$	$c_{11}$	$c_{12}$	$c_{13}$	$c_{14}$	$c_{15}$	$c_{16}$
$c_1$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_2$	0	0	1	1	0	0	0	0	0	1	0	0	0	0	0	0
$c_3$	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
$c_4$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_5$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_6$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_7$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_8$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_9$	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
$c_{10}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{11}$	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0
$c_{12}$	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1
$c_{13}$	0	1	0	0	0	0	1	1	1	0	0	0	0	0	0	0
$c_{14}$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$c_{15}$	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0
$c_{16}$	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0	0

Data availability

Data will be made available on request.