Time Efficient Image Encryption-Decryption for Visible and COVID-19 X-ray Images Using Modified Chaos-Based Logistic Map

Abstract

In this pandemic situation, radiological images are the biggest source of information in healthcare and, at the same time, one of the foremost troublesome sources to analyze. Clinicians now-a-days must depend to a great extent on therapeutic image investigation performed by exhausted radiologists and some of the time analyzed and filtered themselves. Due to an overflow of patients, transmission of these medical data becomes frequent and maintaining confidentiality turns out to be one of the most important aspects of security along with integrity and availability. Chaos-based cryptography has proven a useful technique in the process of medical image encryption. The specialty of using chaotic maps in image security is its capability to increase the unpredictability and this causes the encryption robust. There are large number of literature available with chaotic map; however, most of these are not useful in low-precision devices due to their time-consuming nature. Taking into consideration of all these facts, a modified encryption technique is proposed for 2D COVID-19 images without compromising security. The novelty of the encryption procedure lies in the proposed design which is split into mainly three parts. In the first part, a variable length gray level code is used to generate the secret key to confuse the intruder and subsequently it is used as the initial parameter of both the chaotic maps. In the second part, one-stage image pixels are shuffled using the address code obtained from the sorting transformation of the first logistic map. In the final stage, a complete diffusion is applied for the whole image using the second chaotic map to counter differential and statistical attack. Algorithm validation is done by experimentation with visual image and COVID-19 X-ray images. In addition, a quantitative analysis is carried out to ensure a negligible data loss between the original and the decrypted image. The strength of the proposed method is tested by calculating the various security parameters like correlation coefficient, NPCR, UACI, and key sensitivity. Comparison analysis shows the effectiveness for the proposed method. Implementation statistics shows time efficiency and proves more security with better unpredictability.

Introduction

In this pandemic time, digital medical images are becoming increasingly vital in modern hospitals for detecting and treating diseases, and as a result, they are attracting greater attention. Medical images contain the patient’s diagnostic information and is stored and transmitted through networks. During this pandemic situation, with this advancement of technologies, the transmission and storage of medical information becomes fast and easy to share. If unauthorized accesses steal, view, or exploit these confidential photographs, disastrous accidents may occur. A hacker or a rogue database administrator, for example, could utilize the unauthorized photographs for personal gain, such as medical marketing and false insurance claims, posing a life-threatening risk. As a result, safeguarding medical pictures is critical. It is mandatory to provide a good secure mechanism for transmitting these digital images.

According to the National Laboratories WHO scientific guidelines, real-time polymerase chain reaction (RT-PCR) testing is the gold standard for validating the diagnosis of COVID-19. However, the RT-PCR test became inadequate, and showed high levels of false-negative results to confirm cases that were positive for COVID-19 [1–5]. In addition RT-PCR is a very time-consuming, complex manual process, and kits are currently lacking. Besides, the test is uncomfortable and invasive, and it complains of a nasopharyngeal swab. Therefore, medical imaging techniques such as chest X-rays and computed tomography (CT) have been regarded as powerful tools for detecting COVID-19 infection, especially in new cases of pregnant women and children [6–8]. Computer tomography employs a combination of X-rays and computer imaging permitting specialists to see the condition of organs, bones, blood vessels, and tissues. A CT check can be done on any portion of the body, and it may be a non-invasive, simple strategy to get the core rough image [9, 12].

The primary aim of medical image encryption is to keep the patient’s medical data secret. So, need of highly secure digital image transmitting system is essential. To fulfil this security, development of time efficient secured mechanism is required. Researchers are rigorously working on the development of a secure encryption technique. There are numbers of encryption algorithms that have already been proposed in the literature [10] Encryption using Hash-based BBS (HBBS) is used in CT coronavirus images (COVID-19), cyclic coding [11], DNA encryption [13], and image steganography model (EIS-SDT) [45].

Numerous studies on medical image encryption are based on chaos-based cryptography [14]. The efficiency of the chaos-based encryption techniques mainly depends on the two factors.

1. The generation of the external key used for the encryption technique.

2. The technique by which image pixel positions are scrambled.

Most of the discrete time chaotic systems use a logistic map, Henon map, tent map, and so on; however due to the small size of the key space, the encryption scheme exhibits low security and insufficient complexity [15]. The second factor of encryption is to confuse the relationship between cipher text and plain text. Most of the chaos-based encryption techniques use confusion and diffusion [16]. In the confusion stage, the pixels are scrambled and the positions are changed randomly. In general, row and column positions are confused and subsequently the pixel values are modified. XOR operation is used extensively in literatures to confuse the pixels followed by row and column transformation [17]. Another common method of confusion technique is sort transformation. In general, sort transformation is used in pixel shuffling where the image pixels are shuffled using sorting technique row-wise or column-wise [18]. Arnold transformation is another technique to shuffle the image to scramble the position of the image. But most of the techniques suffer from either time complexity or security issue.

Error metrics like MSE (mean square error), PSNR (peak signal-to-noise ratio), NPCR (number of pixel change rate), and UACI (unified average changing intensity) are the other most commonly used statistical analysis for checking efficiency of the encryption techniques used in the literature [19–21]. This paper develops a chaos-based encryption which is time efficient. Efficiency of the proposed method proves by correlation analysis. This analysis shows the pixel scrambling between original and cipher image. Further validation is done using other statistical parameters and key sensitivity analysis.

Contribution to the Proposed Work

This paper uses two logistic maps which are highly chaotic. Both the logistic maps are iterated by using the initial parameter obtained from the external key. The first logistic map is used to find the new positions by using sort transformation to get the pixels of the original image to be rearranged. In the confusion stage, sort transformation is used in the sequence generated by the logistic map . The whole image pixels are shuffled based on the new positions obtained from the first logistic map after transformation. In the diffusion stage, the second logistic map is used to manipulate the pixel value. At the final stage, the cipher image is produced. In the proposed technique, the unique approach is applied in the key generation stage. Both the logistic maps used possess the same external key which is a 4ⁿ-bit gray level code. In this technique, gray level code is used to confuse the attacker which is again further modified and used as an initial parameter for both the logistic maps. The two logistic maps and the 64-bit external gray level code help to form the encryption technique. The proposed approach is applied on several monochrome images with different sizes. The cipher images obtained as a result of encryption are analyzed in the following sections. The correlation coefficient for the original image and the cipher image are derived and the result shows the proposed algorithm has good encryption performance. A time analysis is carried out which proves the algorithm favors to be in practical uses.

Paper Organization

To validate the proposed logistic map algorithm, the following components were presented: (i) Scheme for both encryption and decryption is presented and (ii) encryption on COVID-19 X-ray images and visual images with different sizes are analyzed and their experimental results are discussed in detail. (iii) A comparison is done with other recent encryption schemes and it shows the effectiveness of the proposed method; (iv) key sensitivity and key space analysis have been carried out and finally in the last section a conclusion is provided.

Related Works

Chaos-Based Encryption Techniques

In a chaotic-based image encryption algorithm, the performance of the algorithm depends on the key and the design of the chaotic mapping. In order to achieve large key space and more security, 1D chaotic logistic maps are extensively used in cryptography. It has been seen that 1D logistic maps exhibit high key space and randomness in behavior and provides robustness against commonly known attacks [22–24]. In recent years, numerous encryption algorithms are proposed to ensure better security. A 1D chaotic logistic map with an external key is applied in encryption [25]. They developed an effective compression and encryption algorithm based on a chaotic system to overcome the weakness and reduce the correlation among the pixels [26]. [27] uses a hybrid chaotic map to encrypt the image. A hybrid chaotic map is the combination of a sine map, logistic map, and tent map. [28] proposes an image encryption scheme based on a public key cryptosystem and quantum logistic map in frequency domain. In some literature [29], they used discrete cosine transformation for converting the image into frequency domain and then encryption is done subsequently. Among the substitution technique, a cubic-logistic map [30] is another box substitution and a bifurcation technique is in usage for encryption. Renzhi Li et al. proposed a new chaotic map dependent on a constant variable logistic map with a haphazardly selected decimal [31]. In their paper [31], a two-dimensional logistic-adjusted-sine map (2D-LASM)–based chaotic algorithm is used to find better ergodicity and unpredictability. 2D-LASM is a 2D chaotic map which is used to convert a 1D sine map into phase plane 2D. Conversion from 1D map to 2D their approach is able to avoid possible attacks in an effective way [31].

Recently, in IOT era, tent maps are used to achieve good security and take significantly less time for in execution. Image encryption frameworks dependent on such chaotic map provide some better exhibitions. Using a tent map encryption algorithm, at first, the chaotic tent map is changed to produce chaotic key stream. This approach is more reasonable for image encryption and furthermore the key stream based on chaos is created by a 1D chaotic tent map [32]. Tent map methodology gives better executions as far as irregularity properties and security level.

Encryption strategy dependent on dynamic substitution boxes is also in literature. In a dynamic substitution box technique, [33] utilizes two chaotic maps. Pixel values are permuted row-wise and column-wise of the original plain text image via arbitrary successions. It is useful to minimize the correlation of the original image and arbitrary successions are also created by a 2D Burgers chaotic map.

There are many modifications experimented with a logistic map. In the article presented by [34], a logistic chaotic map is employed to generate dynamic substitution boxes. A chaotic fuzzy cellular neural network is used in a chaotic system which enhances the order of security in insecure lines and achieves high speed in execution [35]. [35] states that permutation provides security against many common attacks. Chaotic algorithms based on cellular automata and DNA exhibit dynamic structure of key space, very low correlation- coefficient, and high entropy by [37]. Entropy and S-AES make an algorithm more sensitive to changes and provide robustness against a plain-text attack [38].

Modification on chaos theory makes the encryption effective. [39] proposed a modified approach to add more security in chaos-based image encryption that employs a genetic algorithm to optimize correlation between adjacent pixels. In their proposed approach, they have used the rand function instead of a logistic map and the security of the proposed algorithm is evaluated by testing the impact of several attacks on it. [40] proposed another method which involves a 3D chaotic logistic map as well as DNA encoding and it is used for confusion and diffusion of image pixels. In addition, they [40] have used three symmetric keys at the initial condition of the logistic map, which enables the algorithm to provide more security. The 32-bit ASCII keys are used in symmetric keys, Chebyshev chaotic key, and prime key. Patel et al. first apply a 3D non-linear logistic chaotic map with three symmetric keys in order to generate initial conditions. These conditions are then used in image row and column permutation to create randomness in pixels. The third chaotic sequence generated by 3D map is used to generate key image. Diffusion of these random pixels is done using DNA encoding; further XOR logical operation is applied between DNA encoded input image and key image. Analysis parameters like NPCR, UACI, entropy, histogram, chi-square test, and correlation are calculated for the proposed algorithm and also compared with different existing encryption methods. In [41], a 1D logistic map is developed which suppresses the dynamic degradation of digital chaotic systems by using parameter variables and state variables to influence each other, and using sine function as feedback function to destroy the state space. The simulation results show that the improved logistic mapping with the proposed method has better randomness and higher complexity than the original logistic mapping. To prove the practicability and applicability of the improved chaotic map, they design a new image encryption algorithm, which is suitable for both color image and gray scale image. The numerical results indicate that the proposed algorithm has high encryption efficiency, good resistance to various attacks, and certain competitiveness with other encryption algorithms.

Motivation

Among the various literatures, it has been noticed that a 1D logistic map is a classical type and easy to implement. Due to its simple structure and having only few parameters, it exhibits low security. Many existing literatures as mentioned in Table 1 try to overcome this problem by exhibiting large number of steps in the encryption procedure and the same steps followed in the reverse order in decryption resulting more time complexity and higher cost. Keeping in mind to all these complexity issues, this paper proposed a method which follows limited number of steps. This method not only reduces the time complexity in encryption but also shows the randomness among pixels exhibiting better security in the cipher image.

Table 1.

A state-of-the-art framework of several contributions for proposed chaotic based encryption decryption paradigm

Serial no.	Schemes	Pixel scrambling technique	Chaotic map	Security parameters
				Correlation coefficient	NPCR	UACI	MSE	PSNR
1	[25]	Sorting	“Y”	“Y”	“Y”	“Y”	“Y”	“Y”
2	[26]	Arnold transform	“Y”	“Y”	“Y”	“Y”	“Y”	“Y”
3	[27]	Discrete wavelet transform	Y	Y	Y	Y	Y	Y
4	[28]	Position scrambling	Y	Y	−	−	−	−
5	[29]	DCT and Arnold transform	Y	−	−	−	−	Y
6	[30]	Substitution box (S-box).	Y	Y	−	−	Y	Y
7	[31]	Arnold transform	Y	Y	Y	Y	−	−
8	[33]	Substitution box (S-box).	Y	Y	Y	−	Y	Y
9	[34]	Substitution box (S-box).	Y	Y	Y	Y	Y	Y
10	[35]	Bit level permutation	Y	Y	Y	Y	−	−
11	[38]	Substitution box (S-box)	Y	Y	Y	Y	−	−

Materials and Methods

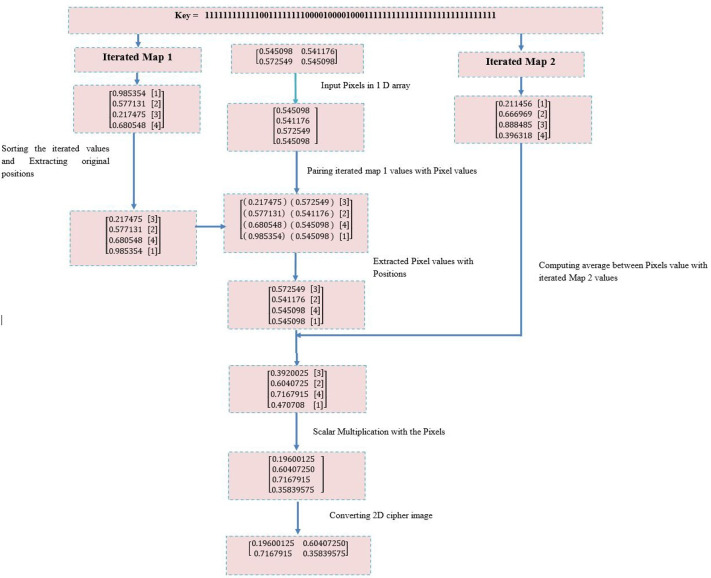
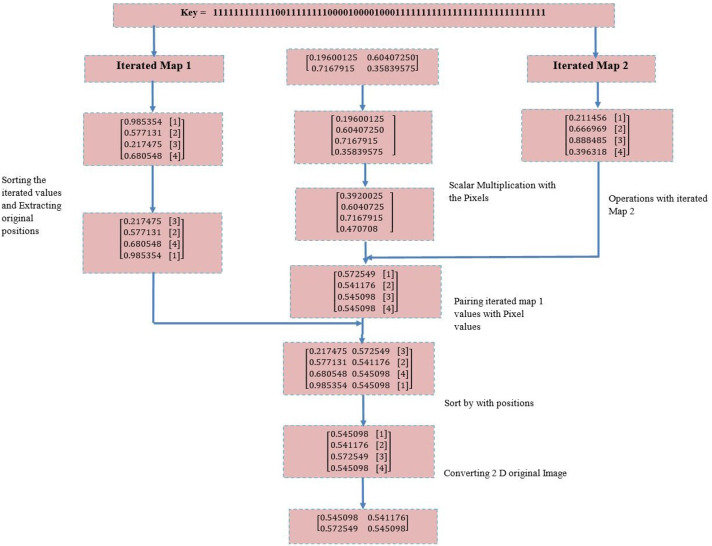
In this proposed work, two logistic maps are considered which are chaotic in nature. Two algorithms are proposed: One is for encryption and another is for decryption. This section discussed the approach in detail. Proposed encryption and decryption techniques are described with all numerical detail. Figure 1 illustrates the flow diagram for proposed approaches. The decryption process is usually the same as encryption which performed in reverse order. The main concern on decryption is its speed to recover the plain text. Figures 2 and 3 include an example matrix which demonstrate the proposed encryption procedure.

Fig. 1.

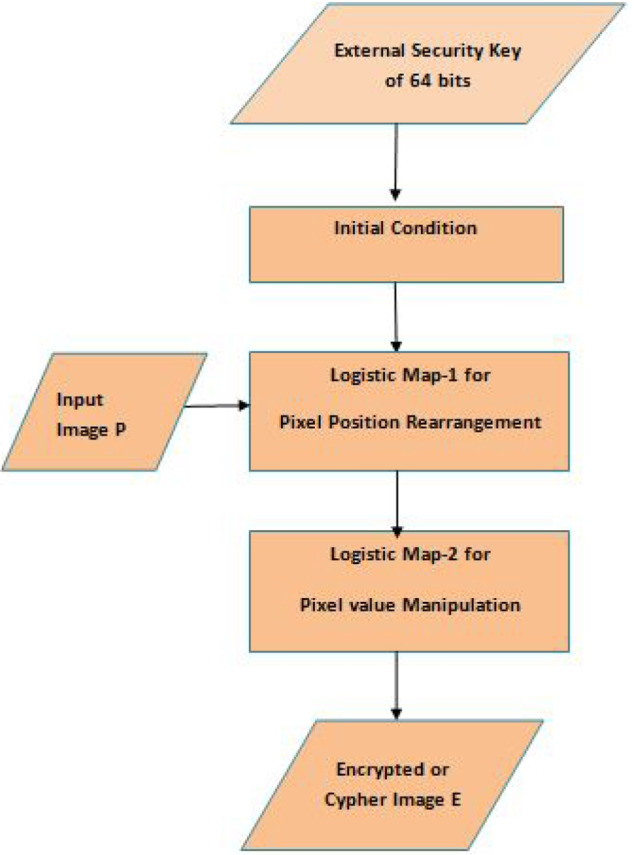
Flow chart of the proposed methodology

Fig. 2.

Sequence of steps of the proposed encryption procedure with a 2×2 matrix

Fig. 3.

Sequence of steps of the proposed decryption procedure with a 2×2 matrix

Algorithm Description

Proposed Encryption Approach

We consider the matrix as (a_ij)_m×n, and we rename the elements as b_j, where b_{(i− 1)n+j} = a_ij

• Step 1: Key GenerationTo generate a key, the receiver is sent a 4ⁿ (we have considered n = 3)-bit long secret gray code. The secret code is further divided into 4^n− 1 four-bit (this part may further be generalized) blocks.

  $$Key=\{G_1,,G_2,G_3,...,G_{4^{n-1}}\}$$

  where each G_i represents a four-bit gray code.

  In the next step, XOR operation is performed between G_i and G_i+ 1. The description for XOR operation is discussed below:

  Key_g=g_i : g_i = G_2i− 1 XOR G_2i where i = 1,2,....2^2n− 3

  Since each g_i is a four-bit binary code, that is the reason each key is converted into gray code Key_g with its equivalent binary conversion.

  The procedure can be represented as

  $$Ke{y}_b=\{k_{\mathit{ij}}:i=1,2,...,2^{2n-3},j=1,2,3,4\}$$

  where each gray level code g_i ={K_i1,K_i2,K_i3,K_i4}.
  Initial criterion parameter is evaluated by using Eq. 1:

  $$x_0=\frac{{\sum }_{i=1}^{2^{2n-3}}{\sum }_{j=1}^4{k}_{\mathit{ij}}{2}^{ij-1}}{4.2^{2n-3}}$$ 1

• Step 2: In this approach, two separate chaotic maps for encryption and decryption are considered. Both chaotic maps are iterated for m × m times. A chaotic system is extremely sensitive to initial condition so, in this encryption, the initial condition x₀ is calculated using Eq. 1.

  We consider logistic maps

  $$x_{j+1}^i=a^i{x}_j^i(1-x_j^i),i=1,2:j=0,1,2,...$$

  with two different control parameters having the same initial value as calculated from (1). We consider the set $B=\{(x_j^1,j,b_j):i=1,2,...,m\times m\}$, now we rearrange the elements in increasing order to get $x_{j_1}<x_{j_2}<...<x_{j_k}<..$. and the corresponding set is $B=\{(x_{j_k}^1,j_k,b_{j_k}):k=1,2,...,m\times m\}$

• Step 3: Rearranging the pixel value of the input image with the new position obtained and modify the same by evaluating the average with the iterated values of the second chaotic map $x_k^2$

• Step 4: The average value is further modified to get the encrypted image.

  $$b_{j_k}=b_{j_k}^{\prime }\mathit{if}{j}_k\mathit{is}\mathit{even}$$

  $$=p.b_{j_k}^{\prime },\mathit{if}{j}_k\mathit{is}\mathit{odd}$$

  The encrypted image is the matrix (c_ij)_m×n, where b_jk = c_x+ 1y+ 1 and k − 1 = nx + y

Proposed Decryption Algorithm

Decryption is the reverse process of encryption.

Step 1

Iterate the logistic map defined in Step 2 of the encryption algorithm.

Step 2

Pair the value of the 1st logistic map and each of its corresponding position B and sort the element of B with respect to the first element.

Step 3

Pixel values are manipulated by accomplishing the processes of the encryption technique in reversed manner to get the original pixel value.

Step 4

Sorted the stored and re-positioned the pixels.

During the whole encryption decryption process, pixels are shuffled depending on the values of the first logistic map. Furthermore, the pixels are modified in a spatial domain using the values of the second logistic map and finally the values are modified by using scalar multiplication. The decryption process is usually the same as encryption which performed in reverse order. During encryption and decryption, the main concern is its speed to recover the original image with negligible information loss, which is achieved through this technique.

Discussion

The developed algorithm can be applied on any of the format of the image like .Jpg and .tif. Here the encryption and decryption have been performed on the monochrome images which are freely available at http://sipi.usc.edu/database/. The algorithm is also experimented with lung images affected during COVID-19. The lung images are taken from a public dataset [42].

Work Done with Visible Images

Monochrome images available in the above database are of different size like 256 × 256, 512 × 512, and 1024 × 1024. In gray scale plot, the value range of intensities is divided into 0–255. In this algorithm, monochrome images are used for encryption and decryption. The benefits of processing such type of images are due to its simple in structure and faster to compute in comparison of color images. In addition, areas like medical imaging, remote sensing where maintaining confidentiality is utmost important, most of the sensors used in these areas produce gray scale images.

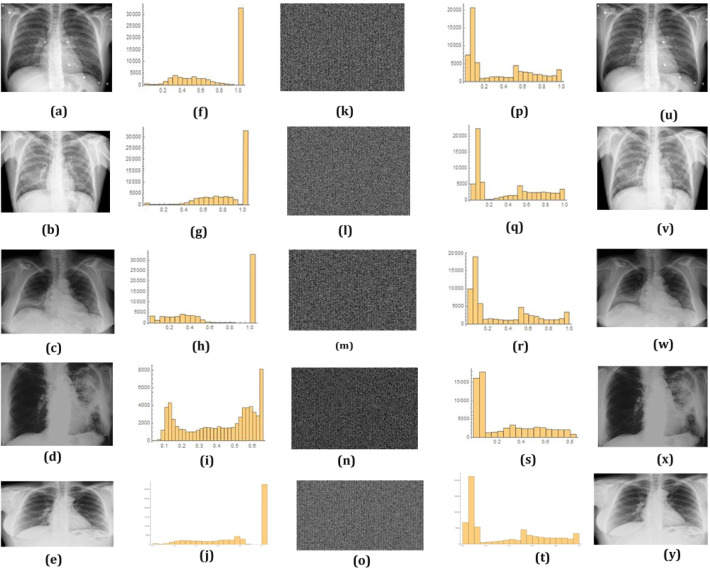
Figure 4 includes three visible images taken from a standard dataset. The proposed encryption algorithm is initially applied. Figure 4 (g),(h),(i) depicts the cipher image and Fig. 4 (m),(n),(o) depicts the de-cipher image. Figure 4 (d),(e),(f) are the image histograms for the original images and (j),(k),(l) are the corresponding image histogram of the cipher images. It is significantly noticeable from these results that the image histogram of the cipher image is completely different with the original images. Another major advantage is shown in the histograms of the cipher images that the histogram shows uniformity. Hence, it is very difficult to get any statistical attack on the proposed encryption algorithm.

Fig. 4.

a, b, and c are the visible images taken as input. d, e, and f are the histogram representation of the input images. g, h, and i are the respective encrypted images. j, k, and l are the histogram of encrypted images. m, n, and o are the respective cipher-text images

Work Done with COVID-19 Affected Lung Images

In the present scenario, the transmission of the radiological images is very much frequent to get consultation from various expert clinicians. Any medical data requires to maintain confidentiality for the sake of the patient. So, here the proposed encryption and decryption technique is also applied for medical image data available in the dataset [42]. Figure 5 shows five COVID-19 affected lung images in which the encryption and decryption is employed. The histogram results show that the algorithm is very much efficient to real-time COVID-19 X-ray images as well as for securing the medical images.

Fig. 5.

a, b, c, d, and e are the X-ray images affected with COVID-19 symptoms. f, g, h, i, and j are the histograms for these input images. k, l, m, n, and o are the corresponding cipher images. p, q, r, s, and t are image histogram for the cipher images and u, v, w, x, and y are the histogram drawn for decrypted images

The performance is plotted in time analysis for all input images and their detailed result is shown in Table 2. It has been noticed that for the images of sizes 256 × 256 and 512 × 512, the average time taken to complete encryption and decryption is around 3 s and 11 s respectively which is quite fast and is suitable for practical use in terms of time complexity. A detailed security analysis is carried out in the section of correlation coefficient analysis.

Table 2.

Correlation comparison analysis between the proposed technique with Pareek et al. (2006) [19]

Image name	Proposed method	[19]	Time taken in secs.
5.1.09	0.000499	0.000779	3.241
5.1.10	0.00262	− 0.007672	3.022
5.1.11	− 0.00067	− 0.004110	3.015
5.1.12	− 0.00430	− 0.011780	3.102
5.1.13	0.00337	− 0.017896	3.023
5.1.14	− 0.0001	− 0.008989	3.068
5.2.08	− 0.0035	− 0.006210	10.908
5.2.09	− 0.00017	− 0.006024	11.646
5.2.10	0.0045	− 0.001512	11.760
7.1.01	− 0.0002	− 0.000297	11.62
7.1.02	− 0.0011	− 0.001944	10.887
7.1.03	− 0.00155	− 0.006857	11.57
7.1.04	0.00224	− 0.006561	12.261
7.1.05	− 0.00220	− 0.011244	11.086
7.1.06	− 0.001129	− 0.002139	11.152
7.1.07	0.00049	− 0.006582	11.191
7.1.08	− 0.001218	0.001338	10.948
7.1.09	− 0.00036	− 0.002992	10.901
7.1.10	0.00064	0.006279	11.058

The proposed algorithm contains steps which manipulates pixel value and there is a chance of data loss during the process of decryption of the encrypted images. Data loss between the original image and the decrypted image is evaluated and obtained by using the image negative. The result is illustrated in Table 3. There is a negligible data loss found which shows that the proposed decryption algorithm is quite efficient to get the original data without incurring any data loss.

Table 3.

Data loss between the original image and the decrypted image available in USC-SIPI image database

Image	Data loss
Lena	1.259610298010027 ∗ 10− 11
5.1.09	1.254497547509281 ∗ 10− 11
5.1.10	1.298943765049021 ∗ 10− 11
5.1.13	1.163270868520527 ∗ 10− 11

Correlation Coefficient Analysis

Correlation coefficient is commonly used to determine the performance of the encryption technique and it provides the degree of similarity between two adjacent pixels of an image. Mathematically, the pixel correlation is given by Eq. (2). In Table 2, correlation coefficient is reported for a list of plain images and the cipher images. It has been observed that the result obtained for the cipher image is close to zero which indicates that the algorithm provides security over statistical attack. A comparison result is carried out with the algorithm referred in [19] and the result found that the pixels are distributed randomly and relatively less correlated and the values are competitive with those of other algorithms.

$$C_r=\frac{N{\sum }_{j=1}^N(x_j*y_j)-{\sum }_{j=1}^N{x}_j*{\sum }_{j=1}^N{y}_j}{\sqrt{(N{\sum }_{j=1}^N{x}_j^2-{({\sum }_{j=1}^N{x}_j)}^2)*(N{\sum }_{j=1}^N{y}_j^2-{({\sum }_{j=1}^N{y}_j)}^2)}}$$ 2

Furthermore, correlation coefficient is evaluated for the horizontal, vertical, and diagonal pixel. Correlation coefficient result is compared with the results of Cao et al. [43] which is shown in Table 4. The algorithm is applied to a random sample of pixel of size 30,000 and the result is captured in Table 3 and it shows that the encryption technique exhibits lower correlation coefficient compared to Cao et al. [43].

Table 4.

Correlation between the original image and the cipher image for the images referred in (Cao et al.) [43] and proposed algorithm

Lena image	(Cao et al.) [43]	Proposed algorithm
Horizontal	− 0.0008	− 0.0002167
Vertical	− 0.0013	0.0053385
Diagonal	0.0018	0.0006699

Figure 6 shows the correlation distribution between two adjacent pixels. Adjacency is taken as horizontally, vertically, and diagonally. The figure represents these three correlation diagrams for Fig. 4(a). From the diagram and quantity, it is observed that the adjacent pixels are highly correlated. However, the corresponding pixels in the encrypted image are much more scattered and therefore the correlation is weaker. Similarly, the diagonal and vertical pixels posses the similar property. The results demonstrate that the proposed image compression and encryption algorithm can resist any type of statistical analysis attack.

Fig. 6.

Correlation analysis: a, c, and e are horizontal, vertical, and diagonal adjacent pixels of the visible image 4(a). b, d, and f are the correlation diagram for the cipher-text image

Table 5 shows the result of the correlation coefficient obtained for the COVID-19 images shown in Fig. 5. The result is calculated for a random sample of pixel of size 30,000 and image size of 256 × 256. The correlation coefficient obtained in all horizontal, vertical, and diagonal direction shows that the technique is equally capable of exhibiting lower correlation coefficient in medical image data encryption.

Table 5.

Test result of the correlation coefficient analysis of the images a, b, c, d, and e in Figure 5 in horizontal, vertical, and diagonal adjacent pixels

Image name	Size	Horizontal	Vertical	Diagonal
a	256 × 256	0.007801	0.007780	0.007778
b	256 × 256	0.007039	0.007044	0.00706
c	256 × 256	0.002112	0.001885	0.001885
d	256 × 256	0.002112	0.001885	0.001013
e	256 × 256	0.007157	0.007185	0.007167

Differential Attack Analysis

An algorithm should be able to resist a differential attack. It is one of the most efficiently and commonly used methods by the attacker to come across significant information between the plain text and the cipher image. Indicators like NPCR (number of changing pixel rate) and UACI (unified averaged changed intensity) are used to quantify the ability of an encryption algorithm to test the effectiveness of being sensitive when the plain-text image is changed or modified during transmission or any stage by different attacks. NPCR determines the change rate in number of pixels between two ciphered images C1 and C2. The cipher-text image C2 is obtained from the plain-text image P2 which is a modified version of P1 and C1 is the cipher-text image obtained from P1. An effective cryptosystem yields close to 100 percent which indicates maximum resistance to differential attack.

The NPCR vlaue is obtained from the below equation

$$\begin{array}{ccc}& & NPCR=\frac{{\sum }_{i=1}^H{\sum }_{j=1}^{W}Z(a,b)}{H\ast W}\hfill \end{array}$$ 3

where

$\begin{array}{cc}\hfill \text{Z}(a,b)=1& \text{if}C1\ne C2\text{and}=0\hfill \\ \hfill & \text{if}C1=C2\text{and H is the height, W is the width.}\hfill \end{array}$  

A comparison is carried out among different schemes [16, 19, 44] and the values are furnished in Table 6. The NPCR value for the Lena image is obtained as 99.66 and the result is relatively satisfactory with those of other algorithms.

Table 6.

NPCR measure for different schemes

SL. no.	Schemes	NPCR
1	[44]	99.60
2	[16]	99.6506
3	[19]	99
4	Proposed	99.66

UACI (unified averaged changed intensity) is used to compute number of average changed intensity when applied two different keys generally two cipher-text image C1 and C2. The calculation of UACI is shown in Table 7 which is ranged between [33.1582,33.6992] and NPCR > 99.50 and this result shows the robustness of the proposed technique.

$$UACI=\sum \frac{CP1(i,j)-CP2(i,j)}{H\ast W\ast 255}$$ 4

where CP1 and CP2 are the two cipher-text image and H and W are the height and width of the image.

Table 7.

NPCR and UACI value for different visual images available in USC-SIPI image database

SL. no.	Image	NPCR	UACI
1	Leena	99.6632	33.6992
2	5.1.09	99.5214	33.5125
3	5.1.10	99.5523	33.5221
4	5.1.11	99.6016	33.1921
5	5.1.12	99.5437	32.9918
6	5.1.13	99.5219	33.1582

Key Sensitivity Analysis

A good encryption technique should ensure high sensitivity with respect to the secret key that is used throughout the algorithm [2, 34]. In this proposed approach, a 64-bit long gray level code is used and change of any bit results the change of the value of the key. To test the result, we have used the secret key:

$$\begin{array}{ccc}& & K1=11111111111100111111110000100001000\hfill \\ \hfill & & 11111111111111111111111111111\hfill \end{array}$$

Figure 7 includes the result for encryption and decryption. At next level, the secret key is manipulated in 11th (for key K2) and 12th position (for key K3).

$$\begin{array}{ccc}& & K2=1111111111010011111111000010000100011111\hfill \\ \hfill & & 111111111111111111111111\hfill \end{array}$$

Fig. 7.

Key sensitivity analysis: a original image. b Encrypted with key k1. c Decrypted with key k1

and

$$\begin{array}{ccc}& & K3=111111111100001111111100001000010001111\hfill \\ \hfill & & 1111111111111111111111111.\hfill \end{array}$$

The proposed approach is tested for decryption with the help of keys K2 and K3. Meanwhile, Fig. 8 shows the result when the decryption is accomplished using the keys K2 and K3. It can be concluded that even a single bit change in the secret key cannot be able to recover the original image and hence the exact key is required to decrypt the cipher image.

Fig. 8.

Key sensitivity analysis: a original image. b Decrypted with key k2. c Decrypted with key k3

Key sensitivity analysis is done with correlation coefficient. Correlation coefficient is calculated for all the keys K1, K2, and K3. This result is captured in Table 8 among the three groups of pixels in horizontal, vertical, and diagonal direction and the result shows that the correlation varies w.r.t keys sensitivity.

Table 8.

Correlation analysis among keys K1, K2, and K3

Key	Horizontal	Vertical	Diagonal
K1	− 0.00419078935	− 0.003866281	− 0.0060043
K2	− 0.006248	− 0.003165226	− 0.00124
K3	− 0.001690823	− 0.006999	− 0.003862

Key Space Analysis

In the proposed algorithm, the external key is a 4ⁿ-bit long gray level code and which can be a $2^{4^n}$ different combination of bits 0 and 1. The key is unpredictable and infeasible for any brute force attack not only due to it being longer in size but also its gray level code in nature. The initial value of the logistic maps used is derived from the secret key which is very much sensitive in nature and provides the encryption algorithm more security.

Performance analysis

The speed of the encryption and decryption algorithm is one of the most important features in today’s digital world. The algorithm is computed in the machine with the following software and hardware specifications: Windows 10 (64 bit) operating system is chosen with Wolfram Mathematica 11 kernel. Intel(R) Pentium(R) CPU @3.80 GHz with RAM of 8 GB memory. The computational algorithm consists of sorting and manipulating pixels of image and the time taken for the process is O(HIW) where H is the height and W is the width of the image and I is the number of iterations performed. The algorithm consists of very simple mathematical operations and hence the encryption and decryption time is very less which is illustrated in Table 2 for various input images.

Conclusion and Scope for Future Research

In this paper, another method of COVID-19 image encryption plot has been proposed which uses two chaotic map calculated guides and an external key of 4ⁿ-bit. The underlying conditions for both the logistic maps are inferred utilizing the external gray level secret key which is a combination of 0 or 1. The gray level secret key has increased the efficiency of the algorithm and also can able to protect the information from various types of attack. The algorithm’s efficiency has been measured not only by analyzing the security but also considering the time taken to complete both encryption and decryption. The security is calculated and compared with the algorithm proposed in the existing literature and found satisfactory results. The time complexity analysis also shows the algorithm’s compatibility in practical use.

Author Contribution

SB wrote the manuscript. MG, SB, and BC were involved in study design and performed the experiment. All authors have gone through the manuscript and approved the submitted version.

Data Availability

The visible images analyzed are freely available at http://sipi.usc.edu/database/. The proposed technique is also experimented with lung images affected during COVID-19. The lung images are taken from public dataset [42]. The datasets generated during and/or analyzed during the current study are also available from the corresponding author on reasonable request.

Declarations

Ethics Approval

This work does not require any ethical clearance or approval.

Competing Interests

The authors declare no competing interests.

Consent for Publication

Consent from all authors has been taken.

Consent to Participate

Consent has been taken from all participants (mentioned on author list).