Abstract
First-principles-based DFT calculations have been carried out to analyze the structural, mechanical, elastic anisotropic, Vickers hardness, electronic, optical, and thermodynamic properties of TlBO3 (B = Cr, Mn) for the first time. We determined the lattice parameters, which are in good agreement with the previous results. The Born criteria was ensured by the elastic constants, which also confirms the ductility of the solid. The elastic constants were also used to evaluate and analyze some related physical properties. The values of Vickers hardness were calculated to determine the hardness and relative application of both TlCrO3 and TlMnO3. Though the metallic characteristics were evaluated via the investigation of the electronic band structure and density of states, both TlCrO3 and TlMnO3 reveal semiconducting behavior under spin–orbit polarization with up-spin and down-spin configurations. Significant constants such as absorption, conductivity, reflectivity, dielectric, loss function, and refractive index were also considered and determined without spin and with spin. As a result, various possible electronic, optical, and optoelectronic applications were predicted. TlBO3 (B = Cr, Mn) was also found to be reliable for thermal barrier coating (TBC) as indicated by the evaluated values of thermal conductivity and Debye temperature.
Here, we have employed the density functional theory on TlBO3 (B = Cr, Mn) to study the structural, mechanical, electronic, optical, and thermal properties for the first time. Spin polarization causes a metallic-to-semiconducting transition.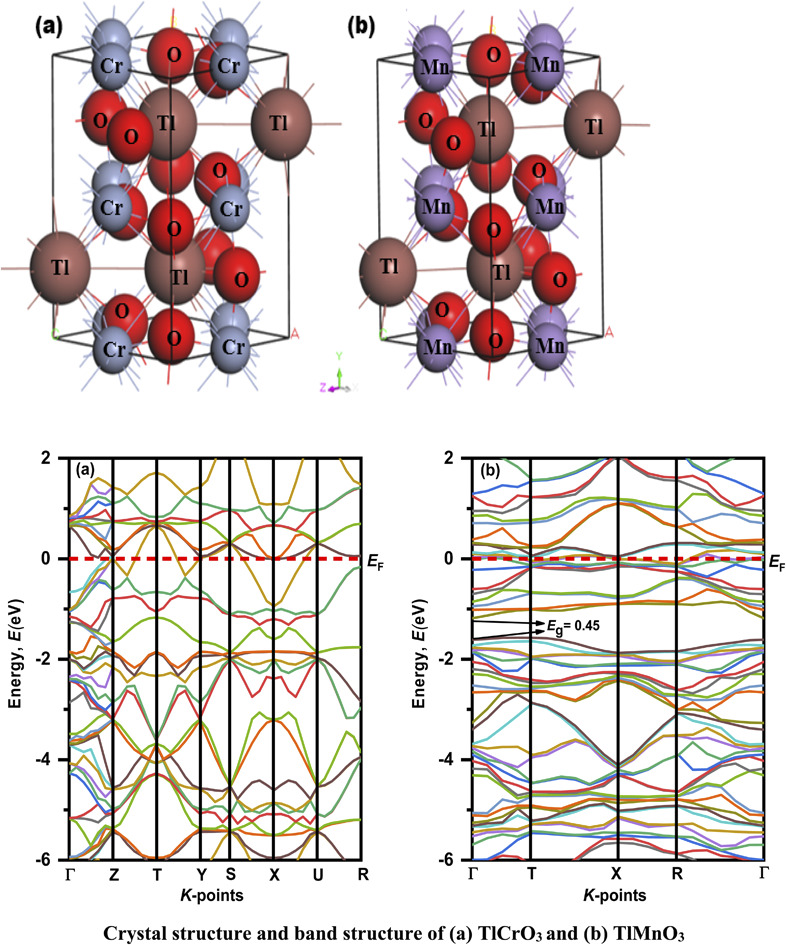
1. Introduction
Perovskite oxides (ABO3) are a point of interest for scientific researchers for their phase transformation and significant applications in modern technology.1–5 ABO3-structured perovskites have been extensively explored for metal-insulator transitions (MITs) correlated transition metal oxides.6–14 La1−xBxMnO3(B = Mn, Ca) perovskite magnates are well known to show MITs with ferromagnetic–paramagnetic transition.15 Perovskite materials are also found to be suitable for solid oxide fuel cells.16,17 ABO3 is considered as an ideal perovskite material, where A is a monovalent otherwise divalent cation situated on the edges of the crystal, and B is a tetravalent or pentavalent transition metal.18,19 Kim et al. discussed the structural distortion of ABO3-type perovskite owing to a disparity in the A–O and B–O bond distances.20 The physical properties of A cation on structural distortion are difficult to investigate, as Kim et al. agreed, because rare earth and yttrium ions bond to oxygen with parallel covalency. As a result, Tl(iii), a post-transition metal ion, is a decent choice for A cation in ABO3 perovskites due to its full occupation of the 4f and 5d orbitals ([XE] = 4f14 5d10 6s2 6p1) in comparison to rare-earth ions ([XE] = 4fn 5d0 6s0; 0 ≤ n ≤ 14). The transition metals in the B site of ABO3 perovskite make the material suitable for any application such as high-temperature superconductivity, colossal magnetoresistance (CMR), charge ordering, giant magnetoresistance (GMR), piezoelectricity, and ferroelectricity.21–24 ABO3 perovskite oxides are also interesting because of their use in the construction of infrared sensors, optoelectronic modulators, infrared detectors, microwave devices, and different electromechanical systems.25–28 Tl(iii) compounds such as TlFeO3 and TlCrO3 were formulated five decades back29 but lack in-depth investigation due to the difficulty of their preparation. Thus, it is exciting to further study TlBO3 (B = Cr, Mn)-structured perovskites.
ACrO3 (A = Sc, I, Tl, Bi)30–34 perovskite-type chromite is significantly different in its properties from isostructural chromite RCrO3 (R = rare earth elements), which can result from the distortion of the crystal structure (ScCrO3, InCrO3), chemical bonds (TlCrO3, BiCrO3) in these compounds, and the electronic structure of A3+.35 RCrO3 compounds have been found to exhibit spin reorientation transition, good oxygen-ion conduction (doped), and sensitivity toward methanol, ethanol, some gases, and humidity.36 R3+Mn3+O3 have also been investigated for their multiferroic properties in both perovskites and hexagonal modification37–42 and rich magnetic phases.41 RCrO3 (R = Gd, Tb, Er, Tm, Sn, and Y)43,44 has shown large polarization at a high temperature equivalent to the Neel temperature (TN) of the Cr subsystem, while LaCrO3 and CeCrO3 display high TN in RCrO3 structure type materials.45 Orthorhombic RMnO3 (R = Tb, Dy)37,46 are spiral magnets that display magnetoelectric (ME) coupling. DyFeO3 was investigated by Tokunaga et al. and found to be versatile with gigantic ME phenomena.47
Paul et al. analyzed ABO3 perovskites such as BiNiO3 or PbCrO3 (ref. 48) for MITs, and different investigations on A and B ions led to the proposition of two more candidates in this category, namely, TlMnO3 and InMnO3. Yi et al. synthesized TlCrO3 (ref. 31) and TlMnO3 (ref. 49) and investigated them with Mössbauer spectroscopy with high pressure (6 GPa) and high temperature (1500 K), and found separate structural and magnetic properties, where the absence of spin canting suggested that TlCrO3 has a non-trivial magnetic structure. Khalyavin et al. also studied the magnetic structure of TlMnO3 (ref. 50) under the same conditions of high temperature and pressure by applying the neutron diffraction technique and confirmed anisotropic exchange interactions that revealed that the Jahn–Teller distortion plays a key role in creating the magneto-crystalline anisotropy. Belik investigated manganese oxide-based Bi1−xYxMnO3 with high pressure and high temperature.51 R2O3–In2O3 systems were studied at normal pressure, and some ABO3 compounds were found that contained I3+ or Tl3+.52,53 With this criteria, Shannon synthesized some perovskites containing In and Tl such as InCrO3, TlCrO3, and TlFeO3.29Ab initio study was performed on many perovskites including BaMO3 (M = Pr, Th, U),54 SnTaO3,21 ACO3 (A = Ca, Sr),55 and SrHfO3.56 Z. Hasan et al. investigated the ABO3 type perovskite AMoO3,57 where A is Ca, Sr, SrBO3 (ref. 58) and B is Cr, Fe, and SrFeO3,59 with density functional theory (DFT) and found them to be mechanically stable at different pressures along with other physical properties. LnCrO3,60–62 which crystallizes in GdFeO3 and BiFeO3 with similar structured perovskites, were studied and found to have applications in thin-film devices. LaNiO3 reveals a metallic nature along with Pauli paramagnetism. LuNiO3 and YNiO3, on the other hand, display Curie–Weiss paramagnetism with antiferromagnetic order, which is below the TN.63 The TlNiO3 perovskite was synthesized under high pressure and a relative study was performed with TNiO3 (T = rare earth).64 According to Cao et al., chromium oxide-based CeCrO3,65 which is a rare earth orthochromite, shows magnetic properties and anti-ferromagnetism. LaCoO3 with ABO3 structure was studied for a lengthy period for its spin-state transition and electronic or ionic conductivity.66 Mn3+-based perovskite TlMnO3 has been described to have a triclinic crystal structure with a clear signature of Jahn–Teller distortion.49 Ding et al. investigated TlCrO3, InCrO3, and ScCrO3 with high pressure and high-temperature settings, which revealed the orthorhombic structure of these materials.67
In this study, further investigation of the ABO3 structure-based TlBO3 (B = Cr, Mn) is done, where Tl is a post-transition metal, Cr and Mn are transition metals, and O is a non-metal. ABO3 structure-based perovskite shows unique physical properties whose diverse types are used in modern technology, motivating us to properly analyze and uncover their physical properties. This paper studies the physical properties such as structural, mechanical, elastic anisotropic, electronic, thermal, Vickers hardness, and optical properties of TlCrO3 and TlMnO3 compounds using DFT-based CAmbridge Serial Total Energy Package (CASTEP). The main purpose of this investigation is to analyze the abovementioned physical properties of the perovskites that can be subjugated to different usages.
2. Computational methods
The investigation of various physical properties such as structural, electronic, mechanical, thermal and optical TlBO3 (B = Cr, Mn) were done with the most commonly used first-principles method. Density Functional Theory (DFT) with the periodic ambient condition along with generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional was employed68–70 using the Cambridge Serial Total Energy Package (CASTEP) code.71 The atomic calculations for Tl – 6s2 6p1, Cr – 3d5 4s1, Mn – 3d5 4s2, and O – 2s22p6 were executed. Brillouin zone k-points sampling was done using the Monkhorst–Pack scheme72 with 10 × 7 × 10 grid points for TlCrO3 and 7 × 5 × 7 grid points for TlMnO3. The plane-wave cut-off energy was 450 eV and 400 eV for TlCrO3 and TlMnO3, respectively. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization method, also known as the quasi-Newton method,73 was employed as a method of optimization of the crystal. The principles of convergence for the optimization were set to 1 × 10−5 eV per atom for total energy, 0.03 eV Å−1 for maximum force, and 0.05 GPa for maximum stress. The stress–strain method74 was used to attain the elastic stiffness constants of TlBO3 (B = Cr, Mn) using CASTEP. The Young's modulus, shear modulus, and Poisson's ratio presented in the 3D anisotropy models were obtained using the ELATE program.75 Lastly, the electronics properties were evaluated by setting the abovementioned parameters.
3. Results and discussion
3.1. Structural properties
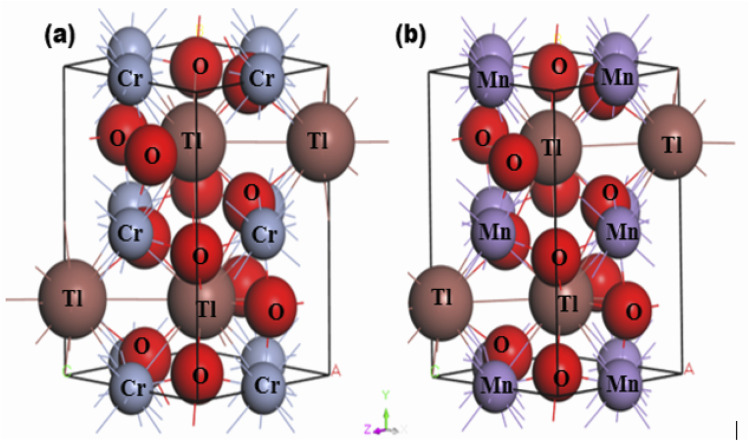
Both synthesized TlBO3 (B = Cr, Mn) perovskite materials share the same TlBO3 ionic structure but both share different crystal structure types. Fig. 1 illustrates the crystal structure of TlBO3 (B = Cr, Mn). TlCrO3 crystallizes in an orthorhombic structure in the space group Pnma (no. 62). In TlCrO3, the Tl site has 4c Wyckoff position (0.04617, 0.25, 0.98732), the Cr site has 4b Wyckoff position (0, 0, ½), and O has two sites, for the first one, the 4c Wyckoff position (0.4504, 0.25, 0.1050) and for the second, the 8d Wyckoff position (03 009, 0.0558, 0.6969).31 TlMnO3 crystalizes in the triclinic structure with the space group P1̄ (no. 2). In TlMnO3, Tl site has 2i (0.54745, 0.25794, 0.50994) and 2i (0.04935, 0.24233, 0.97513). The Mn atoms are positioned in 4 sites. Mn1, Mn2, Mn3, and Mn4 has 1d (1, 0.5, 0, 0), 1e (1, 0.5, 0.5, 0). 1b (1, 0, 0, 0.5), and 1g (1, 0, 0.5, 0.5), respectively. O atoms are positioned in 6 site O (1–6), which are in the numerical order as follows—2i (for all sites) Wyckoff position (0.9423, 0.2309, 0.3799); (0.4450, 0.2708, 0.1147); (0.2056, 0.5732, 0.2055); (0.8053, 0.0511, 0.8070); (0.2824, 0.4406, 0.6847); (0.6839, 0.9275, 0.2855), respectively.49 The optimized lattice parameters a, b, and c are presented in Table 1 along with the calculated unit cell volume V. The obtained results are associated with the former results and seems to be in good agreement with them, which shows our calculations to be reliable. It is noted that both materials share different crystals structures, but the calculated lattice constants and volumes are quite close.
Fig. 1. Crystal structures of (a) TlCrO3 and (b) TlMnO3.
Calculated lattice constants and unit cell volume of TlBO3 (B = Cr, Mn).
| Compound | Lattice constants (Å) | Volume (Å3) | Remarks | ||
|---|---|---|---|---|---|
| a | b | c | |||
| TlCrO3 (orthorhombic) | 5.433306 | 7.693412 | 5.434486 | 227.16511 | This work |
| 5.40318 | 7.64699 | 5.30196 | 219.06671 | Exp.31 | |
| 5.405 | 7.647 | 5.302 | 219.14245 | Exp.29 | |
| TlMnO3 (triclinic) | 5.457218 | 7.692286 | 5.463322 | 229.341717 | This work |
| 5.4248 | 7.9403 | 5.28650 | 227.713553 | Exp.49 | |
| 5.41987 | 7.9250 | 5.27683 | 226.652881 | Exp.50 | |
| LaCrO3 (orthorhombic) | 5.6139 | 7.8942 | 5.5702 | 246.856 | Exp.76 |
| LaMnO3 (orthorhombic) | 5.765 | 7.582 | 5.5702 | 237.302 | Exp.76 |
3.2. Elastic constants and mechanical properties
The elastic characteristics of a crystal define various features of the solid under symmetry conditions, as well as solid stability, bonding characteristics, elastic, and machinability.77 The elastic constants are produced from the first approach via the CASTEP module using a variety of uniform finite value distortions. After the optimization of the internal degrees of freedom, the stresses are therefore determined.78 The elastic constants for TlBO3 (B = Cr, Mn) were determined and are presented in Table 2. Nine elastic constants were calculated for orthorhombic TlCrO3 and twenty-one elastic constants were found for triclinic TlMnO3. No past results regarding elastic constants were found; thus, no relative investigation has been shown. The current outcomes (elastic constants) must adhere to the Born stability principles by describing the following relationships.
| C11 − C12 > 0, C44 > 0, and C11 + 2C12 > 0 | 1 |
Elastic constants, Cij (GPa) of TlBO3 (B = Cr, Mn).
| TlCrO3 (orthorhombic) | TlMnO3 (triclinic) | ||||
|---|---|---|---|---|---|
| C 11 | 298.487 | C 11 | 247.771 | C 23 | 144.011 |
| C 22 | 252.195 | C 22 | 219.456 | C 24 | −0.484 |
| C 33 | 298.712 | C 33 | 298.029 | C 25 | 1.908 |
| C 44 | 104.875 | C 44 | 87.156 | C 26 | −1.104 |
| C 55 | 42.099 | C 55 | 35.395 | C 34 | −3.159 |
| C 66 | 104.859 | C 66 | 74.132 | C 35 | 2.344 |
| C 12 | 150.459 | C 12 | 131.126 | C 36 | −0.291 |
| C 13 | 85.594 | C 13 | 110.109 | C 45 | −1.427 |
| C 23 | 150.071 | C 14 | −6.898 | C 46 | 1.183 |
| C 15 | 0.171 | C 56 | 1.436 | ||
| C 16 | −1.434 | ||||
The elastic constants calculated are positive (Table 2) and uphold the abovementioned stability criteria, which confirms the mechanical stability of TlBO3 (B = Cr, Mn). The material also satisfies generalized stability criteria for an orthorhombic crystal (TlCrO3),71,79,80 which is as follows.
| Cij > 0, (ij = 1–6); | 2 |
| [C11 + C22 + C33 + 2 (C12 + C13 + C23)] > 0; | 3 |
| [C11 + C22 − 2C12] > 0; | 4 |
| [C13 + C33 − 2C13] > 0; | 5 |
| [C22 + C33 − 2C23] > 0; | 6 |
The elastic constants of the compound in Table 2 agree with the above conditions, further confirming that the considered compound TlCrO3 is mechanically stable in the orthorhombic phase. For both the materials, the C44, C55, and C66 crudely agree with the distortions of the lattice angles (α, β, and γ). It can be concluded that γ is the maximum stable angle since the elastic constant C66 is larger than C44/C55 (Table 2), which is dependent on the changing tendencies of the lattice angles in the crystal.81 Here, C11 is connected with linear compression resistance in the x-direction and the value C11 is higher than C12, which indicates incompressibility near the a-axis, not near the b-axis. The density of the atom along the [100] direction is higher if compared with the direction of [011]. It is also seen that C44 > C66 for TlMnO3, which means higher shear deformation resistance along the [010] direction than the [110] direction, while for the TlCrO3 compound, this value is not so different. The shear component, C44 (TlCrO3) > C44 (TlMnO3), indicating higher resistance to shear deformation of TlCrO3 compared to TlMnO3. Furthermore, the value of C44 predicts the hardness of the material. Therefore, it assumes that the compound TlCrO3 should have higher hardness than TlMnO3. From Cauchy pressure (C12–C44) the metallic or non-metallic (ionic/covalent) features of the compounds are revealed. The materials will be a dominant covalent bond in nature if the Cauchy pressure shown in Table 3 is negative, which is not the case. Thus, both TlCrO3 and TlMnO3 have a dominant ionic bond in nature as the Cauchy pressure values are positive.
The estimated bulk modulus, BR (Reuss), BV (Voigt), B (Hill) (GPa), shear modulus, GR (Reuss), GV (Voigt), G (Hill) (GPa), Young's modulus, Y (GPa), Pugh's ratio, B/G, Poisson's ratio v, Cauchy pressure, C12–C44, and machinability index μM of TlBO3 (B = Cr, Mn).
| Elastic moduli and mechanical properties | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Compound | B R | B V | B | G R | G V | G | Y | B/G | v | C 12 –C 44 | μ M | Remarks |
| TlCrO3 (orthorhombic) | 179.92 | 180.18 | 180.05 | 68.39 | 81.25 | 74.82 | 197.12 | 2.41 | 0.32 | 45.58 | 1.72 | This work |
| TlMnO3 (triclinic) | 168.62 | 170.64 | 169.63 | 56.79 | 64.67 | 60.73 | 162.76 | 2.79 | 0.34 | 43.97 | 1.93 | This work |
| CeCoO3 (cubic) | 179.12 | 179.12 | 179.12 | 72.66 | 80.39 | 76.53 | 200.97 | 2.34 | 0.32 | 45.12 | 3.05 | Exp.92 |
| CeCuO3 (cubic) | 132.09 | 132.09 | 132.09 | 39.94 | 46.55 | 43.24 | 116.96 | 3.05 | 0.35 | 54.51 | 4.25 | Exp.92 |
Voigt–Reuss–Hill (VRH) approximations are employed to evaluate the polycrystalline elastic properties.82–84 Bulk modulus (BV) and shear modulus (GV) in Voigt approximation is expressed as follows.
| BV = 1/9 [(2(C11 + C12) + 4C13 + C33)]; | 7 |
| GV = 1/30 (C11 + C12 − 4C13 + 12C44 + 12C66); | 8 |
The Bulk modulus BR and shear modulus GR in the Reuss approximation is defined as follows.
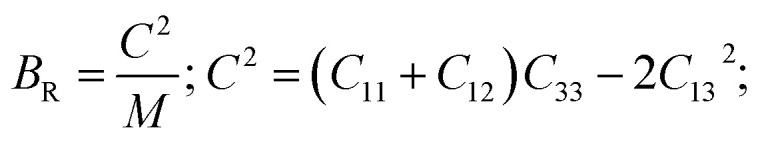 |
9 |
| M = C11 + C12 + 2C33 − 4C13; | 10 |
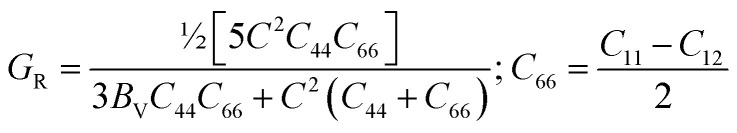 |
11 |
For Hill approximation, B and G, which are bulk and shear modulus, respectively, are calculated utilizing the following equations.
 |
12 |
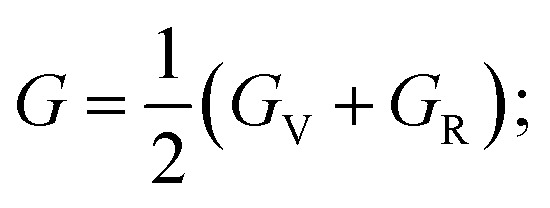 |
13 |
As we know, the elastic moduli bulk modulus B, shear modulus G, Young's modulus Y, and Poisson's v describe the mechanical performance of solids, which are calculated by VRH approximations.85–87B and G is then used to determine the Young's modulus Y and Poisson's ratio v via the following equations.88
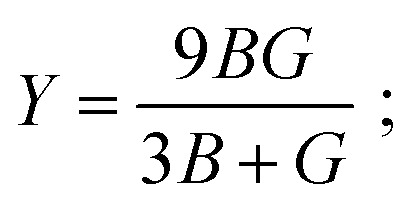 |
14 |
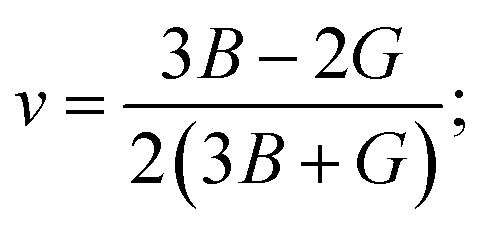 |
15 |
The resistance in contradiction to volume, shear, and longitudinal deformation is represented by bulk modulus B, shear modulus G, and Young's modulus Y, respectively. Y, G, and B of TlBO3 were determined for the first time in this investigation and are shown in Table 3. Pugh's ratio, depicted as B/G, in Table 3 demonstrates if a material is ductile or brittle,89 which is more than 1.75, indicating the ductile nature of both the materials; otherwise, it behaves in a brittle manner. Likewise, Poisson's ratio v is an additional parameter to determine the ductile or brittle nature of solids.90 The value should be more than 0.25 to be ductile and less to be brittle. As the value of v is more than 0.25, as shown in Table 3, it further confirms the result obtained from Pugh's ratio, suggesting that both TlCrO3 and TlMnO3 are ductile. Furthermore, the value of the Cauchy pressure (C11–C44) is positive, indicating the ductile nature of both materials; otherwise, it would be brittle if the value is negative.91
The machinability index μM describes the cutting capability of a compound, the maximum financial level of machine operation, and plastic strain, which is vital for industrial areas. It is determined as follows.
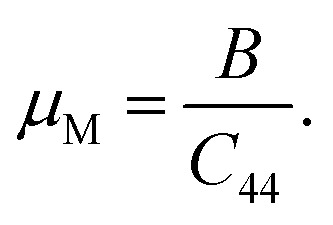 |
16 |
For both orthorhombic TlCrO3 and TlMnO3, the value of μM in Table 3 is more than 2, referring to improved lubricating characters and lesser frictions, which has significant applications in different fields.
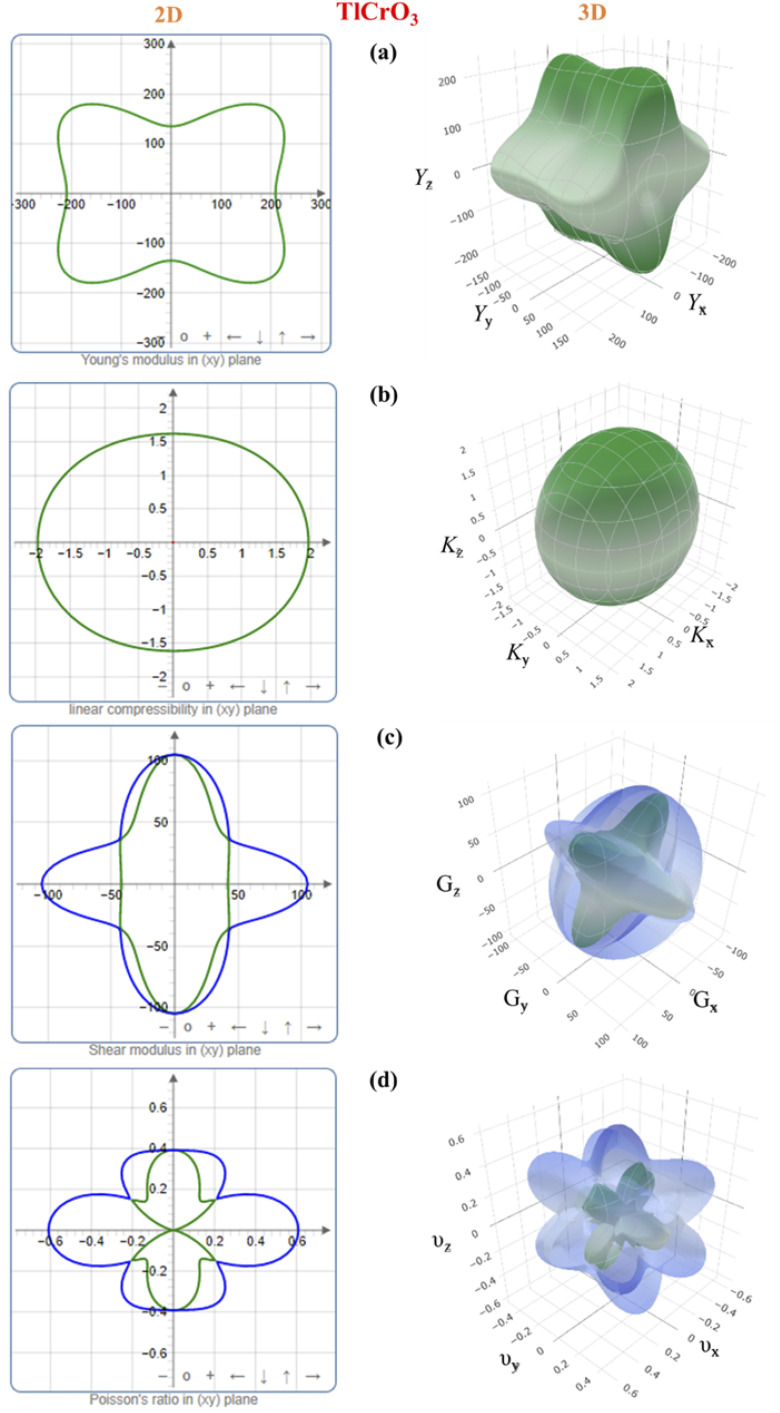
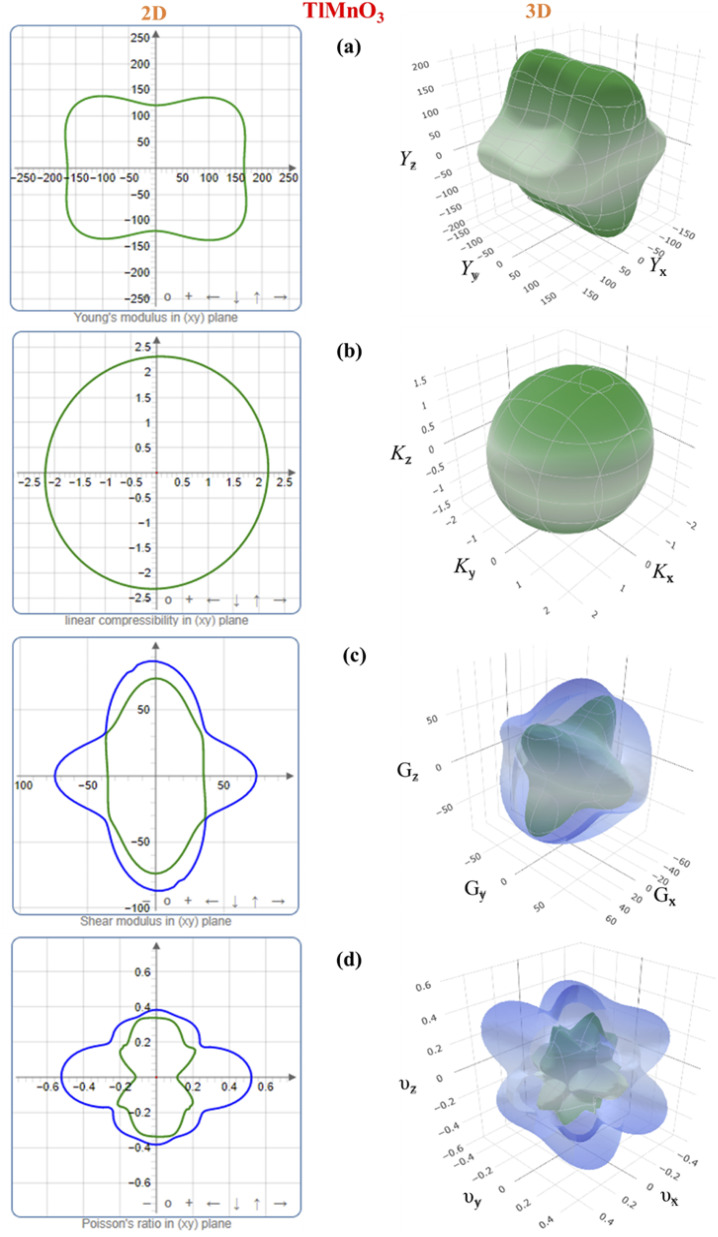
3.3. Elastic anisotropy
The microscopic activity of solids is developed by the amount of elastic anisotropy for single and polycrystalline materials.93 Therefore, the investigation of the outward directional dependence of the elastic tensor is important for the materials involved so that the mechanical resilience, degree of elastic anisotropy, and usage of material under peripheral stress can be heightened. In applied engineering sciences, these appearances will play an equally critical part in the design activities, clear interpretations, along with fundamental crystal physics.94 The Shivakumar Ranganathan model represents elastic anisotropy as follows.83
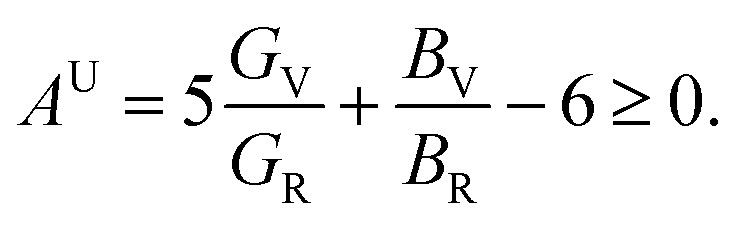 |
17 |
AU = 0 represents the isotropic performance, although the exemption from this (AU ≠ 0) replicates the anisotropic performance of materials. Therefore, the values of AU are estimated for orthorhombic TlCrO3 (∼0.941) and triclinic TlMnO3 (∼0.702), characterizing both materials as anisotropic. Furthermore, Chung and Buessum presented the conception of percent anisotropy modulus, AG (shear), and AB (bulk) as follows82 (in polycrystalline materials).
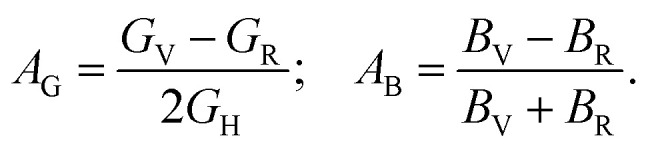 |
18 |
For AG = AB = 0, the solid materials represent elastic isotropy. Thus, in the present analysis, both TlCrO3 and TlMnO3 show anisotropic aspects. If we consider the directional requirement on the elastic tensor, TlMnO3 shows a higher degree of anisotropy. In addition, shear anisotropy is more prevalent as it seems to have a greater value (Table 4) for both the materials. In both the materials, TlBO3 (B = Cr, Mn) the bulk modulus is anisotropic, as we observed that BH ≠ BR ≠ BV. The value of AB in Table 4 illustrates that the bulk modulus of compounds is anisotropic and TlMnO3 is further anisotropic than TlCrO3, which shows negligible anisotropic character. Both compounds indicate anisotropic character (Table 4) in the measured shear anisotropic factors as well. The anisotropic shear pointers offer a valuation of the degree of anisotropy in the bonding of different planes between atoms. Along the {100}, {010}, and {001} shear planes, the shear anisotropic parameters are stated as follows.
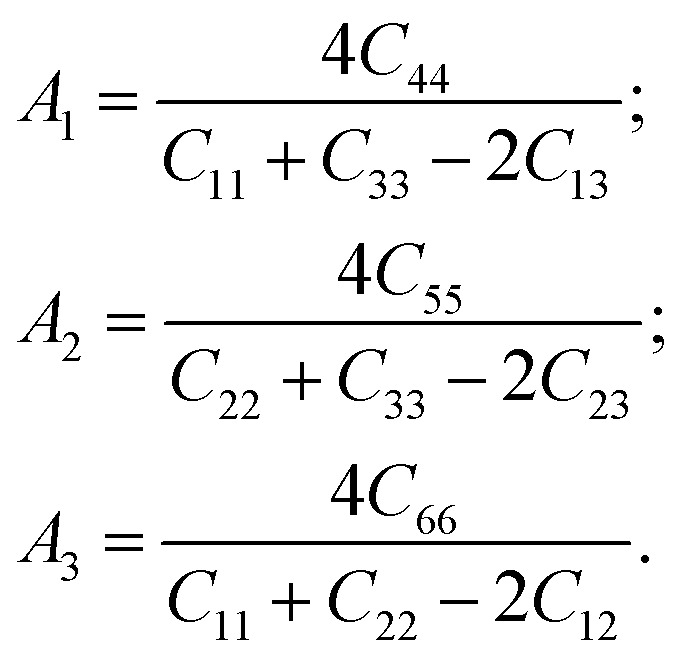 |
19 |
Calculated shear anisotropic factors, Ai (i = 1–3), Zener's anisotropy index (A), anisotropy in shear (AG), anisotropy in bulk modulus (AB), universal anisotropy index (AU), and equivalent Zener anisotropy (Aeq) of TlBO3 (B = Cr, Mn).
| Compound | Crystal system | A 1 | A 2 | A 3 | A | A G | A B | A U | A eq |
|---|---|---|---|---|---|---|---|---|---|
| TlCrO3 | Orthorhombic | 0.985 | 0.672 | 1.679 | 1.417 | 0.086 | 0.0007 | 0.941 | 2.3605 |
| TlMnO3 | Triclinic | 1.071 | 0.617 | 1.447 | 1.494 | 0.065 | 0.0059 | 0.702 | 2.1114 |
In the case of A1 = A2 = A3, the materials show isotropic nature or it measures the amount of elastic anisotropy exhibited by the crystal. Since A1, A2, and A3 are not equivalent (Table 4), both orthorhombic and triclinic materials display anisotropic character. The Zener anisotropy index (A) and the Zener anisotropy equivalent (Aeq) for both the compounds are calculated to achieve acceptable anisotropy as follows.95,96
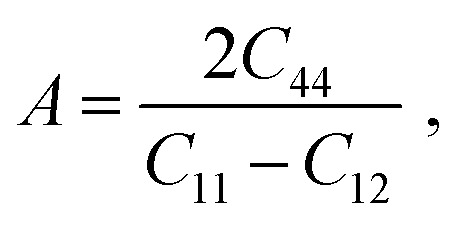 |
20 |
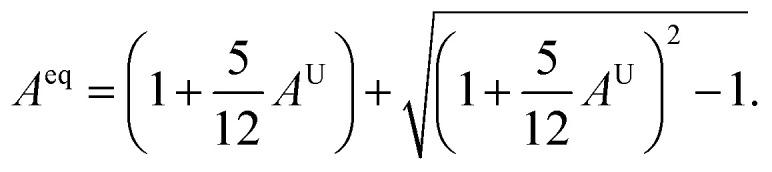 |
21 |
In Table 4, the values of A and Aeq confirm our previous analysis, reinstating that both the compounds have an anisotropic character. The anisotropy index A = 1 suggests the isotropic behavior of solid materials, and anisotropic natures are revealed for more or less than Uni (>1 or <1). The evaluated value of TlBO3 (B = Cr, Mn) shows both materials to be anisotropic, where TlCrO3 manifested a slightly higher degree of elastic anisotropy.
To further study the elastic anisotropy of both the materials, Young's modulus (Y), bulk modulus (K), shear modulus (G), and Poisson's ratio (v) elastic moduli were constructed for both TlCrO3 and TlMnO3 in Fig. 2 and 3 using ELATE code.75 3D and 2D models were used to identify the nature of anisotropy. If the 3D plots are entirely spherical and their projection on different planes is rounded, the materials are isotropic. The non-spherical shape in the 3D plots for both orthorhombic TlCrO3 and triclinic TlMnO3 signify the extent of anisotropy. As depicted in Fig. 2 and 3, the unconventionality between the 3D surface and the sphere for all the moduli suggests the elastic anisotropy characteristics for TlBO3 (B = Cr, Mn). This analysis displays good consistency with the results of all the anisotropy indexes discussed above. Furthermore, the 3D plot of different anisotropy moduli looks somewhat similar in Fig. 2 and 3 for both the compounds.
Fig. 2. 3D and 2D anisotropy contour plots of (a) Young's modulus, Y, (b) compressibility, K, (c) shear modulus, G, and (d) Poisson's ratio, v of TlCrO3.
Fig. 3. 3D and 2D anisotropy contour plots of (a) Young's modulus, Y, (b) compressibility, K, (c) shear modulus, G, and (d) Poisson's ratio, v of TlMnO3.
3.4. Vickers hardness
Vickers hardness is mainly associated with the resistance offered by the material to plastic deformation. The ability of a material to resist plastic deformation can also be estimated by it. Many important applications for practical devices can be predicted by understanding the hardness of a solid. Furthermore, a deep understanding of the mechanical behavior can be achieved through the relationship between elastic polycrystalline modules and hardness. Vickers hardness can be calculated for metallic compounds by the means of the equation found by Gou et al.97 If all the individual bond hardness are calculated, their geometric average can be used to evaluate the hardness of a multiband solid. It can be done using the following equations.98–100
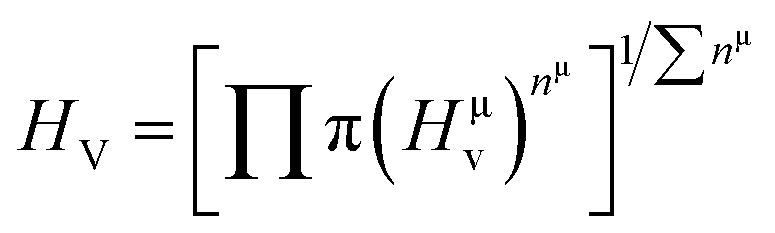 |
22 |
| Hμv = 740(Pμ − Pμ′)(υμb)−5/3; | 23 |
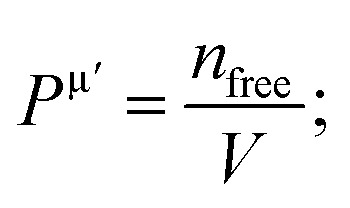 |
24 |
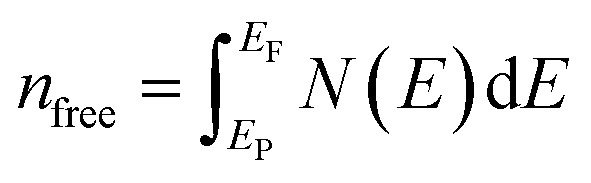 |
25 |
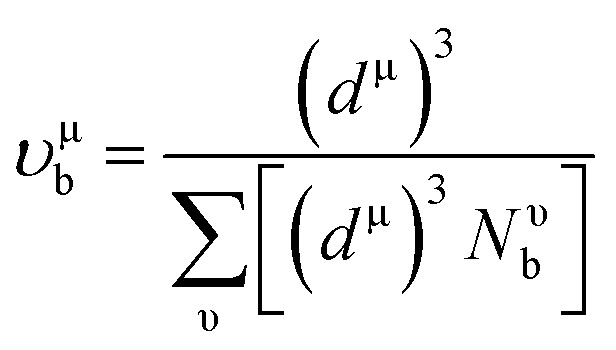 |
26 |
here, Pμ′ and Pμ is the Mulliken population and the metallic population of the μ-type bond, respectively, nfree is the number of free electrons between the first pseudo gap and Fermi level, V is called cell volume (Table 1), υμb is the volume of a bond of μ-type, (dμ)3 is the bond length of μ-type bond, and Nυb is the bond number of υ per unit volume.
The evaluated values of Vickers hardness of TlBO3 (B = Cr, Mn) are displayed in Table 5. It is clear from Table 5 that TlCrO3 is harder than TlMnO3. However, the overall observation of the values reveals both materials to have much lower hardness compared to diamond, considering the most rigid (Vickers hardness 70 to 150 GPa)101 material among all. As a result, both TlCrO3 and TlMnO3 indicate a flexible and soft nature, making them suitable for thin-film production. The hardness values are 8.729 GPa for TlCrO3 and 5.208 Gpa for TlMnO3, which is close to 2–8 GPa, values of many well-known MAX phase (M is transition metal, A is group 13–15 A element, X is C or N) materials.102
Theoretical hardness of TlBO3 (B = Cr, Mn).
| Compounds | Bond | n μ | d μ (Å) | P μ | P μ′ | v μ (Å3) | H μ (GPa) | H v (GPa) |
|---|---|---|---|---|---|---|---|---|
| TlCrO3 | O–Cr(i) | 8 | 1.9201 | 0.55 | 0.043743 | 9.43794 | 8.888 053 | 8.72858 |
| O–Cr(ii) | 8 | 1.92232 | 0.54 | 0.043743 | 9.47072 | 8.662 297 | ||
| O–Cr(iii) | 8 | 1.92342 | 0.54 | 0.043743 | 9.48698 | 8.637 555 | ||
| TlMnO3 | O–Mn(i) | 2 | 1.95981 | 0.36 | 0.071407 | 5.04956 | 14.36908 | 5.20793 |
| O–Mn(ii) | 2 | 1.96337 | 0.36 | 0.071407 | 5.07713 | 14.23928 | ||
| O–Mn(iii) | 2 | 1.96358 | 0.36 | 0.071407 | 5.07876 | 14.23167 | ||
| O–Mn(iv) | 2 | 1.96733 | 0.35 | 0.071407 | 5.10791 | 13.60809 | ||
| O–Mn(v) | 2 | 1.9818 | 0.35 | 0.071407 | 5.22145 | 13.1185 | ||
| O–Mn(vi) | 2 | 1.98243 | 0.35 | 0.071407 | 5.22643 | 13.09767 | ||
| O–Mn(vii) | 2 | 1.98378 | 0.35 | 0.071407 | 5.23711 | 13.05316 | ||
| O–Mn(viii) | 2 | 1.98532 | 0.34 | 0.071407 | 5.24932 | 12.53589 | ||
| O–Mn(ix) | 2 | 1.98597 | 0.32 | 0.071407 | 5.25448 | 11.58347 | ||
| O–Mn(x) | 2 | 1.98904 | 0.32 | 0.071407 | 5.27888 | 11.49435 | ||
| O–Mn(xi) | 2 | 1.99018 | 0.35 | 0.071407 | 5.28797 | 12.84463 | ||
| O–Mn(xii) | 2 | 1.99083 | 0.34 | 0.071407 | 5.29315 | 12.36337 | ||
| O–Tl(i) | 2 | 2.28171 | 0.1 | 0.071407 | 7.9688 | 0.665 542 | ||
| O–Tl(ii) | 2 | 2.30589 | 0.1 | 0.071407 | 8.22484 | 0.631 371 | ||
| O–Tl(iii) | 2 | 2.33132 | 0.14 | 0.071407 | 8.49997 | 1.433 789 | ||
| O–Tl(iv) | 2 | 2.36947 | 0.12 | 0.071407 | 8.92412 | 0.936 555 | ||
| O–Tl(v) | 2 | 2.39337 | 0.12 | 0.071407 | 9.19689 | 0.890 718 | ||
| O–Tl(vi) | 2 | 2.41888 | 0.11 | 0.071407 | 9.49411 | 0.670 893 |
3.5. Electronic properties
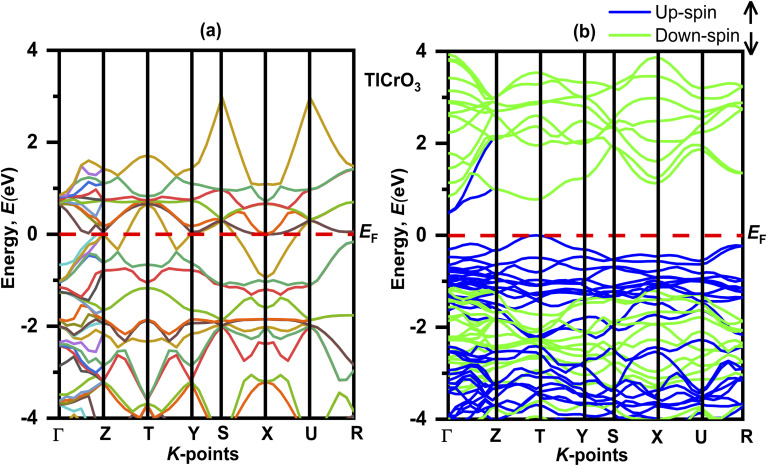
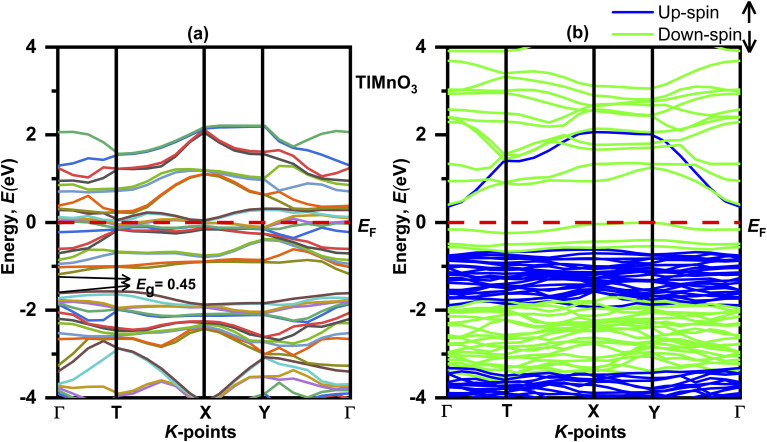
The electronic properties of the TlBO3 (B = Cr, Mn) perovskites were studied by measuring the band structure along with the total partial density of states (DOS). The electronic band structures without spin for both orthorhombic TlCrO3 and triclinic TlMnO3 are displayed in Fig. 4(a) and 5(a) correspondingly. The band structure with spin is displayed in Fig. 4(a) and 5(a). The straight (dotted) line at 0 eV in both Fig. 4 and 5 specifies the Fermi level (EF) separating the conduction band and the valence band. If the electronic band-structure of both the materials is compared, it is observed that for both materials, energy bands without spin display bulky scattering diagonally to the Fermi level (EF); the conduction and valence bands both are superimposed and displayed no bandgap, suggesting both materials to be metals. Moreover, the energy density of TlMnO3 along the Fermi level (EF) describes it to be more metallic than TlCrO3. The bandgap (Eg = 0.45) in Fig. 5(a) reveals possible semiconducting abilities in TlMnO3. Then again, the band structure with spin shows a dramatic transition from metallic to semiconductor for both TlCrO3 and TlMnO3, respectively, as no scattering of electrons can be seen along the Fermi level (EF) for both the solids. These results showed the material TlBO3 (B = Cr, Mn) switching from metallic to semiconductor nature. These are very much promising results that can be used to explain the metallic and optoelectronics properties, which may result from both Cr and Mn being magnetic atoms.103,104 No previous study on the density of states and band structure has been done.
Fig. 4. Electronic band structure of TlCrO3 (a) without spin and (b) with spin.
Fig. 5. Electronic band structure of TlMnO3 (a) without spin and (b) with spin.
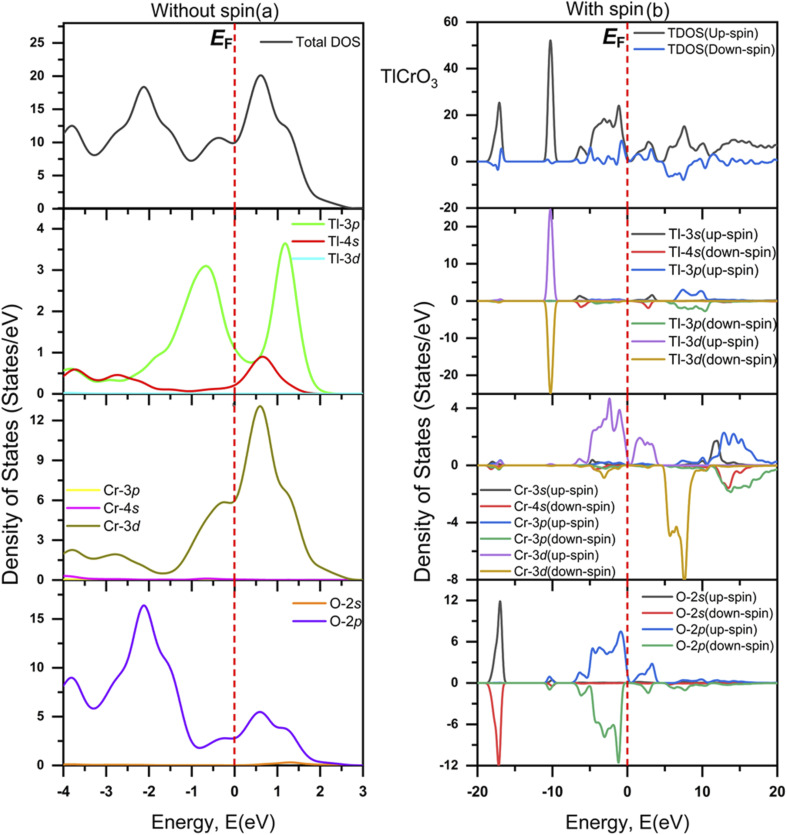
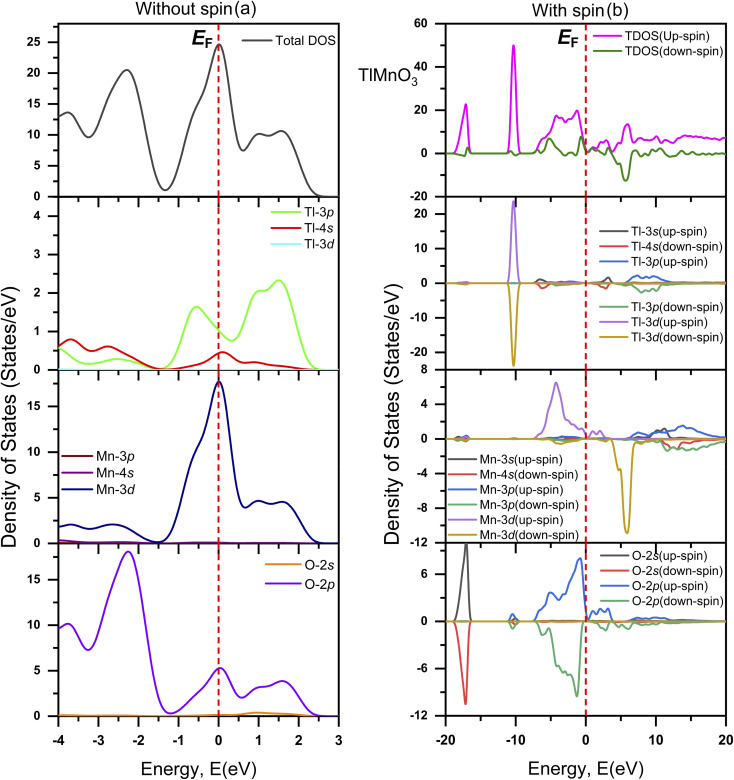
The evaluated total (TDOS) and partial density of states (PDOS) of TlCrO3 without spin and with spin along with atomic contributions of different orbitals around EF by the CASTEP code are displayed in Fig. 6(a) and (b), respectively. Also, the total (TDOS) and partial density of states (PDOS) of TlMnO3 without spin and with along with the atomic contributions of different orbitals around the Fermi level are displayed in Fig. 7(a) and (b), correspondingly. In Fig. 6(a) and 7(a), the EF of the TDOS without spin values are about 10 and 24 states/eV for TlCrO3 and TlMnO3, respectively. For both the materials, the Tl-3p orbital seems to be contribute to both the valence band and conduction band. TlCrO3 contributes to both bands in case of Tl-3p orbital at ∼−0.7 eV (∼3.3 states per eV) and ∼0.13 eV (3.7 states per eV). TlMnO3 contributes ∼−0.6 eV (∼1.7 states/eV) and ∼1.6 eV (∼2.4 states per eV). TlCrO3 contributes more to the formation of both the conduction and valence bands, resulting in less overlap of both the bands. As a result, TlCrO3 is less metallic. It can be observed from Fig. 6(a) and 7(a) that major contribution near the Fermi level (EF) is derived from Cr-3d and Mn-3d. Here, Cr-3d seems to contribute more to the formation of the conduction band at ∼0.6 eV. However, Mn-3d contributes along the Fermi level, making TlMnO3 more metallic. Both TlCrO3 and TlMnO3 compounds also have a fair contribution along with EF from the O-2p orbital. The orbitals also seem to have significant overlaps in energy without spin, which point toward hybridization and inclination to the creation of covalent bonding. The values of DOS are finite, which indicates TlBO3 (B = Cr, Mn) to be metallic. Moreover, the O-2p contributes to the creation of the valence band at ∼−2.1 eV (for TlCrO3) and ∼−2.2 eV (for TlMnO3) below the Fermi level (EF). Hence, both perovskite materials are metallic. Two TDOS peaks for TlMnO3 are found with close values at ∼−2.1 eV and 0.7 eV. TlMnO3 has the largest TDOS peak at EF, again confirming it to have more metallic characteristics. In case of density of states without spin that is displayed in Fig. 6(a) and with spin displayed in Fig. 6(b), the value of TDOS along the EF level is ∼10 eV and ∼2 (both up-spin and down-spin), respectively. For TlMnO3, the value of TDOS along the EF level is ∼24 in case of without spin (Fig. 7(a)) and ∼1 (both up-spin and down-spin) with spin (Fig. 7(b)).
Fig. 6. Total and partial DOS of TlCrO3 (a) without spin and (b) with spin.
Fig. 7. Total and partial DOS of TlMnO3 (a) without spin and (b) with spin.
3.6. Optical properties
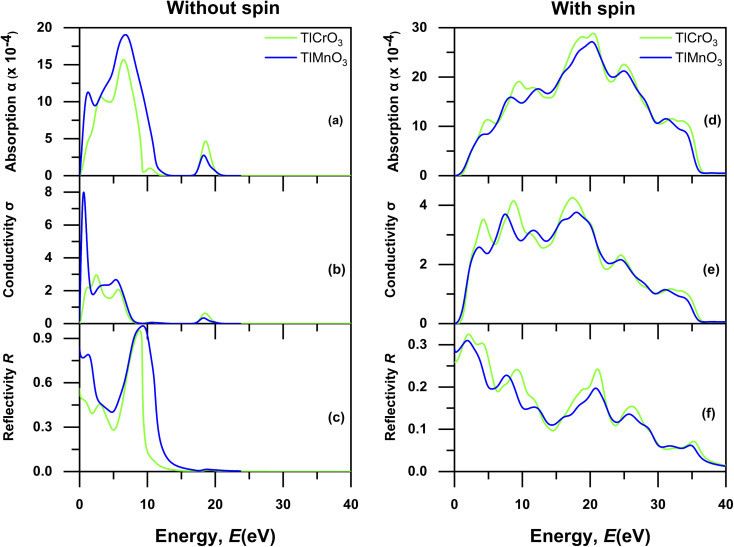
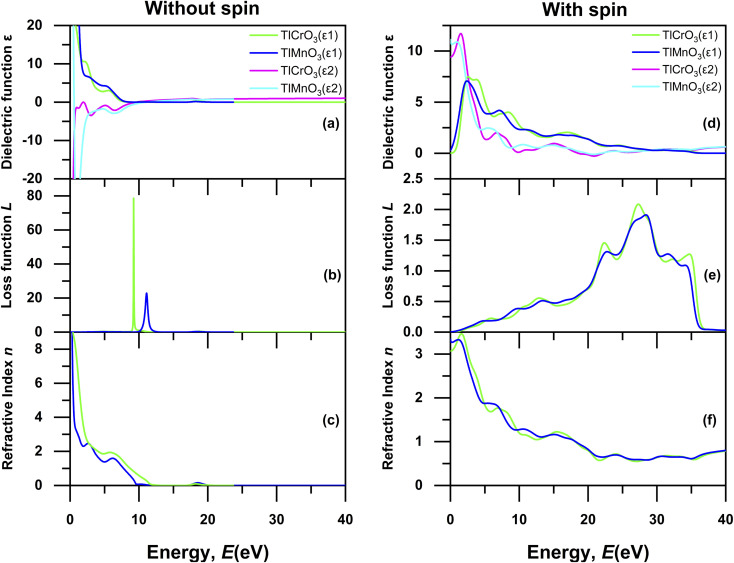
These properties are important for describing the response of solids to an electromagnetic wave and for exploring the potential of photovoltaic and optoelectronic devices. In this context, the performances of the materials to the infrared, visible, and ultraviolet light are particularly noteworthy. Various optical energy-dependent (frequency) parameters, which are the absorption co-efficient α(ω), conductivity σ(ω), reflectivity R(ω), the real part of dielectric function ε(ω), loss function L(ω), and the refractive index n(ω) are calculated for photon energies up to 50 eV with electric field polarization vectors along the [100] direction to analyze TlBO3 (B = Cr, Mn). Fig. 8 and 9 depicted the different optical properties. The absorption spectrum without spin and with spin is displayed in Fig. 8(a) and (d), which shows expansion at inferior energies from ∼0 to 15 eV in case of without spin due to transitions between close-lying energy levels, including the band. Absorption with spin shows a drastic change, which shows expansion of absorption from ∼2 eV to ∼36 eV. With spin, both materials exhibit possible application as photovoltaic cells.
Fig. 8. Energy-dependent absorption α(ω), conductivity σ(ω), and reflectivity R(ω) of TlBO3 (B = Cr, Mn) without spin (a–c) and with spin (d–f).
Fig. 9. Energy-dependent dielectric function ε(ω) (ε1 real and ε2 imaginary), loss function L(ω), and refractive index n(ω) of TlBO3 (B = Cr, Mn) without spin (a–c) and with spin (d–f).
The peaks associated with the interband transitions exist in the optical conductivity spectrum, which is presented in Fig. 8(b) (without spin) and 8(e) (with spin). A sharp edge can be seen for TlMnO3 near the UV region ∼2 eV and expansion can be seen for TlCrO3 near ∼4 eV in Fig. 8(b) without spin. However, in the case of with spin in Fig. 8(e), expansion can be seen in conductivity from 0 eV to ∼36 eV. This suggests the electrical conductivity in both the materials. Though the peak value is lower than that without spin, it shows a steady peak value rather than a sharp peak. The reflectivity is presented in Fig. 8(c) (without spin) and 8(e) (with spin) for both TlCrO3 and TlMnO3. The zero-frequency reflectivity (R(0)) in Fig. 8(c) is ∼0.47 and ∼0.71 for TlCrO3 and TlMnO3, respectively, but it decreases when evaluated with spin in Fig. 8(f). The zero-frequency reflectivity (R(0)) in Fig. 8(f) is only is ∼0.0.26 and ∼0.28 for TlCrO3 and TlMnO3, respectively. A minor peak in the high-energy region is produced for TlCrO3 due to interband carriers.
We considered the optical properties in the interband region. Dielectric function ε(ω) is generally measured by the interband along with interband optical transitions. For this investigation, we overlooked the indirect intraband transition as this comprises phonon with an inadequate scattering cross-section compared to that of direct transition; as a result, phonon scattering is not required to recollect the momentum. The ε(0) static dielectric constant is a significant optical parameter that is related to the semiconductor optical band gap and sometimes displays an opposite relationship with the values of the bandgap. Fig. 9(a) and (d) represent the energy loss function without spin and with spin, respectively, which means the loss of a fast-moving electron passing through the solid. The maximum energy loss of TlCrO3 and TlMnO3 in case of without spin occurs at ∼9 eV and ∼12 eV, respectively. The energy related to the peak is called the plasma peak and the related frequency is named plasma frequency. Moreover, if more energy compared to plasma frequency is generated, the investigated materials would develop transparency. Nevertheless, when the loss function of both the solids is evaluated with spin, the value of loss function is decreased and both display similar expansion from 0 eV to 40 eV. The optical property, viz., the refractive index, holds a significant role from the standpoint of applications such as solar cells, photonic crystals, and waveguides. The calculated values of the zero-frequency refractive index are ∼9 and ∼10 for the solids TlCrO3 and TlMnO3, respectively, as shown in Fig. 9(c) in case of without spin. As the frequency is increased more than 10 eV, the values of the refractive index decrease for both the materials, and slight non-linear nature can also be seen. In Fig. 9(f) with spin, the value of the refractive index decreases to ∼3 and ∼3.3 for TlCrO3 and TlMnO3, respectively.
3.7. Thermodynamic properties
The thermodynamic properties of TlBO3 (B = Cr, Mn) are significant to find different natures of the solids under different pressures and temperatures. Different variety of thermodynamic properties can be measured such as Debye temperature (θD), melting temperature (Tm), and minimum thermal conductivity (Kmin) using other properties such as density (ρ), longitudinal, transverse, and average sound velocities (vl, vt, and vm). The Debye temperature (θD) is evaluated as follows.105
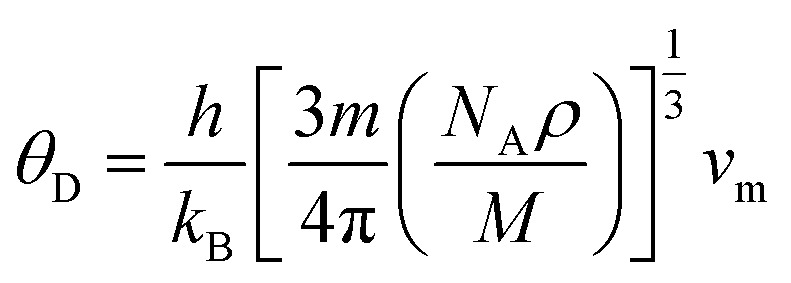 |
27 |
where h, kB, V, vm, and n is Planck's constant, Boltzmann constant, unit cell volume, average sound velocity, and the number of atoms in the unite cell, respectively. Here, vm can be evaluated by the equation
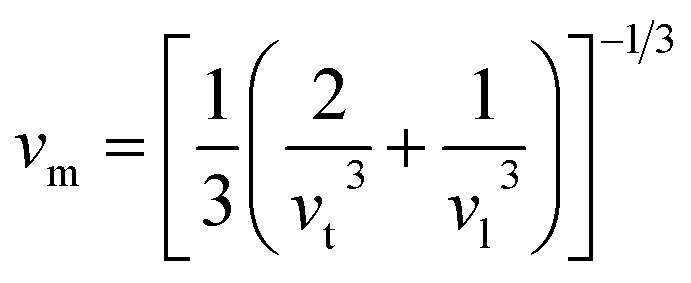 |
28 |
where vl is the transverse velocity and vt is the longitudinal sound velocity of the solids. vl and vt are evaluated by the formula below.
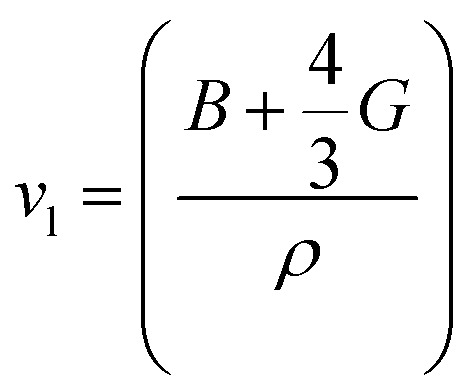 |
29 |
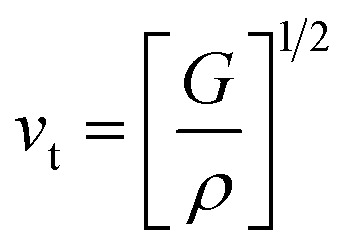 |
30 |
The melting temperature (Tm) is also determined to explore the possible application of the materials at high temperatures. The following equation is used to determine (Tm).106
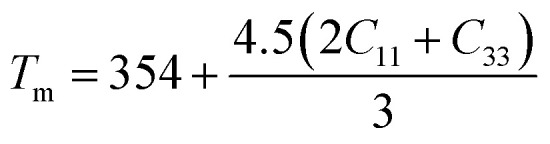 |
31 |
Thermal conductivity, an important parameter to investigate the heat conduction of both TlCrO3 and TlMnO3, was determined. The minimum thermal conductivity (Kmin) of a solid material is associated with temperature and will decrease to a certain value with a steady rise in temperature.107 Minimum thermal conductivity (Kmin) is calculated by Clarke formula.108
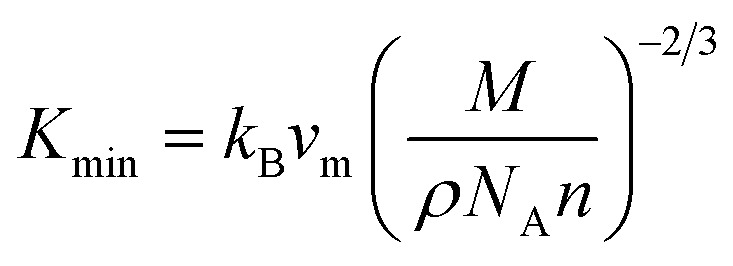 |
32 |
where M, n, and NA signify the molecular mass, atoms per molecule, and Avogadro's number, respectively. The calculated thermal properties θD,Tm, Kmin, vm, vt, and vl are presented in Table 6. The values of θD and Kmin for the title compounds are much lower than the commercialized thermal barrier coating (TBC) compound Y4Al12O9 (Kmin = 1.13 W m−1 K−1; θD = 564 K).109,110
The calculated density (ρ), longitudinal, transverse, and average sound velocities (vl, vt, and vm), Debye temperature (θD), melting temperature (Tm), and minimum thermal conductivity (Kmin) of the TlBO3 (B = Cr, Mn) compound.
| Compounds | Crystal systems | ρ (g cm−3) | v l (km s−1) | v t (km s−1) | v m (km s−1) | θ D (K) | T m (K) | K min (W m−1 K−1) |
|---|---|---|---|---|---|---|---|---|
| TlCrO3 | Orthorhombic | 8.898 | 4.319 | 2.772 | 3.045 | 403.5 | 1697.53 | 0.83 |
| TlMnO3 | Triclinic | 8.982 | 3.898 | 2.514 | 2.760 | 365.7 | 1544.35 | 0.75 |
4. Conclusions
The physical properties such as structural, mechanical, elastic anisotropic, Vickers hardness, electronic, optical, and thermodynamic properties of TlBO3 (B = Cr, Mn) structured perovskites were investigated for the first time using ab initio-based DFT calculations. Good agreement was obtained between the calculated values and the obtained elastic constants. Born criteria for both the materials was fulfilled, signifying that both solids are mechanically stable. Both materials are ductile, as defined by all the elastic moduli such as Cauchy pressure, Poisson's ratio, and Pugh's ratio. All the different methods employed for studying the anisotropy of TlBO3 (B = Cr, Mn) obtained the same results. The hardness calculations reveal that both solids are flexible, soft, and suitable for making a thin film. The Vickers hardness value is also very small compared to MAX phase materials. Both solids displayed a transition from metallic to semiconducting nature without spin and with spin configuration. The investigation of the optical properties of both TlCrO3 and TlMnO3 reveals various possible uses such as waveguides, ultralarge integration of integrated circuits, microelectronics, and the reduction of solar heating, where the investigation with spin study exposes both materials' better absorption and application in solar cells. The solids have lower values of θD and Kmin, which implies that they can be used as a thermal barrier coating (TBC) material. We hope that this investigation will help a researcher use these materials for different applications according to their physical properties and inspire scientists both experimentally and theoretically to discover this material in more depth in the future.
Data availability
All data needed to evaluate the conclusion of this study are presented in the paper. Additional data are available from the corresponding author upon reasonable request.
Author contributions
Wakil Hasan: methodology, data curation, formal analysis, writing original draft; Adeeb Mahamud Hossain: formal analysis, review-editing; Md. Rasheduzzaman: conceptualization, supervision, formal analysis, review-editing. Md. Atikur Rahman: validation, formal analysis, review-editing; Md. Mukter Hossain: formal analysis, review-editing; supervision, K. Rashel Mohammad: formal analysis, review-editing; Raihan Chowdhury: formal analysis, review-editing; Khandaker Monower Hossain: formal analysis, review-editing; M. Moazzam Hossen: formal analysis, review-editing; Md. Zahid Hasan: investigation, conceptualization, supervision, formal analysis, review-editing.
Conflicts of interest
The authors declare no conflict of interests.
Supplementary Material
Acknowledgments
Authors are grateful to the Department of Physics, Chittagong University of Engineering & Technology (CUET), Chattogram-4349 and Department of Physics, Pabna University of Science and Technology, Pabna-6600, Bangladesh, for providing the computing facilities for this work.
References
- MacChesney J. B. Jetzt J. J. Potter J. F. Williams H. J. Sherwood R. C. J. Am. Ceram. Soc. 1966;49:644–647. [Google Scholar]
- Lines M. E. Glass A. M. Burns G. Phys. Today. 1978;31:56–58. [Google Scholar]
- Banach G. Temmerman W. M. Phys. Rev. B: Condens. Matter Mater. Phys. 2004;69:054427. [Google Scholar]
- Mathi Jaya S. Jagadish R. Rao R. S. Asokamani R. Phys. Rev. B: Condens. Matter Mater. Phys. 1991;43:13274–13279. doi: 10.1103/physrevb.43.13274. [DOI] [PubMed] [Google Scholar]
- Mattheiss L. F. Phys. Rev. B: Solid State. 1972;5:290–306. [Google Scholar]
- Quackenbush N. F. Tashman J. W. Mundy J. A. Sallis S. Paik H. Misra R. Moyer J. A. Guo J.-H. Fischer D. A. Woicik J. C. Muller D. A. Schlom D. G. Piper L. F. J. Nano Lett. 2013;13:4857–4861. doi: 10.1021/nl402716d. [DOI] [PubMed] [Google Scholar]
- Dagotto E. Science. 2005;309:257–262. doi: 10.1126/science.1107559. [DOI] [PubMed] [Google Scholar]
- Boris A. V. Matiks Y. Benckiser E. Frano A. Popovich P. Hinkov V. Wochner P. Castro-Colin M. Detemple E. Malik V. K. Bernhard C. Prokscha T. Suter A. Salman Z. Morenzoni E. Cristiani G. Habermeier H.-U. Keimer B. Science. 2011;332:937–940. doi: 10.1126/science.1202647. [DOI] [PubMed] [Google Scholar]
- Kim T.-H. Angst M. Hu B. Jin R. Zhang X.-G. Wendelken J. F. Plummer E. W. Li A.-P. Proc. Natl. Acad. Sci. U. S. A. 2010;107:5272–5275. doi: 10.1073/pnas.1000655107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannetti C. Capone M. Fausti D. Fabrizio M. Parmigiani F. Mihailovic D. Adv. Phys. 2016;65:58–238. [Google Scholar]
- Imada M. Fujimori A. Tokura Y. Rev. Mod. Phys. 1998;70:1039–1263. [Google Scholar]
- Zaanen J. Sawatzky G. A. Allen J. W. Phys. Rev. Lett. 1985;55:418–421. doi: 10.1103/PhysRevLett.55.418. [DOI] [PubMed] [Google Scholar]
- Held K. Keller G. Eyert V. Vollhardt D. Anisimov V. I. Phys. Rev. Lett. 2001;86:5345–5348. doi: 10.1103/PhysRevLett.86.5345. [DOI] [PubMed] [Google Scholar]
- Shen Z. Dessau D. J. Phys. C: Solid State Phys. 1972;5:1253. [Google Scholar]
- Nakamura S. Nanba K. Iida S. J. Magn. Magn. Mater. 1998;177–181:884–885. [Google Scholar]
- Steele B. C. H. and Heinzel A., in Materials for Sustainable Energy, Co-Published with Macmillan Publishers Ltd, UK, 2010, pp. 224–231 [Google Scholar]
- Jacobson A. J. Chem. Mater. 2010;22:660–674. [Google Scholar]
- Wolfram T. and Ellialtioglu S., Electronic and optical properties of D-band perovskites, Cambridge University Press, Cambridge, UK, New York, 2006 [Google Scholar]
- Feng Z. Hu H. Cui S. Bai C. Solid State Commun. 2008;148:472–475. [Google Scholar]
- Kim S.-J. Demazeau G. Alonso J. A. Choy J.-H. J. Mater. Chem. 2001;11:487–492. [Google Scholar]
- Ali Z. Ahmad I. Khan I. Amin B. Intermetallics. 2012;31:287–291. [Google Scholar]
- Takeno S. Ohara R. Sano K. Kawakubo T. Surf. Interface Anal. 2003;35:29–35. [Google Scholar]
- Yoshino M. Solid State Ionics. 2000;127:109–123. [Google Scholar]
- Fang Z. Nagaosa N. Takahashi K. S. Asamitsu A. Mathieu R. Ogasawara T. Yamada H. Kawasaki M. Tokura Y. Terakura K. Science. 2003;302:92–95. doi: 10.1126/science.1089408. [DOI] [PubMed] [Google Scholar]
- Scott J. F. Science. 2007;315:954–959. doi: 10.1126/science.1129564. [DOI] [PubMed] [Google Scholar]
- Cross E. Nature. 2004;432:24–25. doi: 10.1038/nature03142. [DOI] [PubMed] [Google Scholar]
- Schneider T. Leduc D. Cardin J. Lupi C. Barreau N. Gundel H. Opt. Mater. 2007;29:1871–1877. [Google Scholar]
- Watton R. Ferroelectrics. 1989;91:87–108. [Google Scholar]
- Shannon R. D. Inorg. Chem. 1967;6:1474–1478. [Google Scholar]
- Belik A. A. Matsushita Y. Tanaka M. Takayama-Muromachi E. Chem. Mater. 2012;24:2197–2203. [Google Scholar]
- Yi W. Matsushita Y. Katsuya Y. Yamaura K. Tsujimoto Y. Presniakov I. A. Sobolev A. V. Glazkova Y. S. Lekina Y. O. Tsujii N. Nimori S. Takehana K. Imanaka Y. Belik A. A. Dalton Trans. 2015;44:10785–10794. doi: 10.1039/c4dt03823a. [DOI] [PubMed] [Google Scholar]
- Niitaka S. Solid State Ionics. 2004;172:557–559. [Google Scholar]
- Darie C. Goujon C. Bacia M. Klein H. Toulemonde P. Bordet P. Suard E. Solid State Sci. 2010;12:660–664. [Google Scholar]
- Belik A. A. Tsujii N. Suzuki H. Takayama-Muromachi E. Inorg. Chem. 2007;46:8746–8751. doi: 10.1021/ic701099f. [DOI] [PubMed] [Google Scholar]
- Sobolev A. V. Bokov A. V. Yi W. Belik A. A. Presniakov I. A. Glazkova I. S. J. Exp. Theor. Phys. 2019;129:896–902. [Google Scholar]
- Sardar K. Lees M. R. Kashtiban R. J. Sloan J. Walton R. I. Chem. Mater. 2011;23:48–56. [Google Scholar]
- Kimura T. Goto T. Shintani H. Ishizaka K. Arima T. Tokura Y. Nature. 2003;426:55–58. doi: 10.1038/nature02018. [DOI] [PubMed] [Google Scholar]
- Fiebig M. Lottermoser Th. Fröhlich D. Goltsev A. V. Pisarev R. V. Nature. 2002;419:818–820. doi: 10.1038/nature01077. [DOI] [PubMed] [Google Scholar]
- Kumagai Y. Belik A. A. Lilienblum M. Leo N. Fiebig M. Spaldin N. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2012;85:174422. [Google Scholar]
- Lee S. Pirogov A. Kang M. Jang K.-H. Yonemura M. Kamiyama T. Cheong S.-W. Gozzo F. Shin N. Kimura H. Noda Y. Park J.-G. Nature. 2008;451:805–808. doi: 10.1038/nature06507. [DOI] [PubMed] [Google Scholar]
- Tachibana M. Shimoyama T. Kawaji H. Atake T. Takayama-Muromachi E. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;75:144425. [Google Scholar]
- Yu Pomjakushin V. Kenzelmann M. Dönni A. Harris A. B. Nakajima T. Mitsuda S. Tachibana M. Keller L. Mesot J. Kitazawa H. Takayama-Muromachi E. New J. Phys. 2009;11:043019. [Google Scholar]
- Rajeswaran B. Khomskii D. I. Zvezdin A. K. Rao C. N. R. Sundaresan A. Phys. Rev. B: Condens. Matter Mater. Phys. 2012;86:214409. [Google Scholar]
- Serrao C. R. Kundu A. K. Krupanidhi S. B. Waghmare U. V. Rao C. N. R. Phys. Rev. B. 2005;72:220101. [Google Scholar]
- Zhou J.-S. Alonso J. A. Pomjakushin V. Goodenough J. B. Ren Y. Yan J.-Q. Cheng J.-G. Phys. Rev. B: Condens. Matter Mater. Phys. 2010;81:214115. [Google Scholar]
- Goto T. Kimura T. Lawes G. Ramirez A. P. Tokura Y. Phys. Rev. Lett. 2004;92:257201. doi: 10.1103/PhysRevLett.92.257201. [DOI] [PubMed] [Google Scholar]
- Tokunaga Y. Iguchi S. Arima T. Tokura Y. Phys. Rev. Lett. 2008;101:097205. doi: 10.1103/PhysRevLett.101.097205. [DOI] [PubMed] [Google Scholar]
- Paul A. Mukherjee A. Dasgupta I. Paramekanti A. Saha-Dasgupta T. Phys. Rev. Lett. 2019;122:016404. doi: 10.1103/PhysRevLett.122.016404. [DOI] [PubMed] [Google Scholar]
- Yi W. Kumagai Y. Spaldin N. A. Matsushita Y. Sato A. Presniakov I. A. Sobolev A. V. Glazkova Y. S. Belik A. A. Inorg. Chem. 2014;53:9800–9808. doi: 10.1021/ic501380m. [DOI] [PubMed] [Google Scholar]
- Khalyavin D. D. Manuel P. Yi W. Belik A. A. Phys. Rev. B. 2016;94:134412. [Google Scholar]
- Belik A. A. J. Solid State Chem. 2017;246:8–15. [Google Scholar]
- Keith M. L. Roy R. Am. Mineral. 1954;39:1–23. [Google Scholar]
- ROTH R. S. J. Res. Natl. Bur. Stand. 1957;58:75–88. [Google Scholar]
- Ali Z. Ahmad I. Reshak A. H. Phys. B. 2013;410:217–221. [Google Scholar]
- Ali Z. Ahmad I. J. Electron. Mater. 2013;42:438–444. [Google Scholar]
- Feng L. Liu Z. Liu Q. Phys. B. 2012;407:2009–2013. [Google Scholar]
- Rasheduzzaman M. Monower Hossain K. Z. Hasan M. Int. J. Mater. Res. 2020;111:1038–1046. [Google Scholar]
- Hasan M. Z. Rasheduzzaman M. Monower Hossain K. Chin. Phys. B. 2020;29:123101. [Google Scholar]
- Hasan Md. Z. Hossain K. M. Mitro S. K. Rasheduzzaman Md. Modak J. K. Rayhan M. A. Appl. Phys. A. 2021;127:36. [Google Scholar]
- Bertaut E. F. Delapalme A. Forrat F. Roult G. De Bergevin F. Pauthenet R. J. Appl. Phys. 1962;33:1123–1124. [Google Scholar]
- Shamir N. Shaked H. Shtrikman S. Phys. Rev. B: Condens. Matter Mater. Phys. 1981;24:6642–6651. [Google Scholar]
- Colin C. V. Pérez A. G. Bordet P. Goujon C. Darie C. Phys. Rev. B: Condens. Matter Mater. Phys. 2012;85:224103. [Google Scholar]
- Demazeau G. Marbeuf A. Pouchard M. Hagenmuller P. J. Solid State Chem. 1971;3:582–589. [Google Scholar]
- Kim S. J. Demazeau G. Alonso J. A. Largeteau A. Martinez-Lope J. M. Presniakov I. Choy J.-H. Solid State Commun. 2000;117:113–115. [Google Scholar]
- Cao Y. Cao S. Ren W. Feng Z. Yuan S. Kang B. Lu B. Zhang J. Appl. Phys. Lett. 2014;104:232405. [Google Scholar]
- Itoh M. Hashimoto J. Yamaguchi S. Tokura Y. Phys. B. 2000;281–282:510–511. [Google Scholar]
- Ding L. Manuel P. Khalyavin D. D. Orlandi F. Kumagai Y. Oba F. Yi W. Belik A. A. Phys. Rev. B. 2017;95:054432. [Google Scholar]
- Clark S. Segall M. Z. Kristallogr. 2005;220:567. [Google Scholar]
- Perdew J. P. Ruzsinszky A. Csonka G. I. Vydrov O. A. Scuseria G. E. Constantin L. A. Zhou X. Burke K. Phys. Rev. Lett. 2009;102:039902. doi: 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- Hohenberg P. Kohn W. Phys. Rev. 1964;136:B864–B871. [Google Scholar]
- Segall M. D. Lindan P. J. D. Probert M. J. Pickard C. J. Hasnip P. J. Clark S. J. Payne M. C. J. Phys.: Condens. Matter. 2002;14:2717–2744. [Google Scholar]
- Monkhorst H. J. Pack J. D. Phys. Rev. B: Solid State. 1976;13:5188–5192. [Google Scholar]
- Pfrommer B. G. Côté M. Louie S. G. Cohen M. L. J. Comput. Phys. 1997;131:233–240. [Google Scholar]
- Fan C.-Z. Zeng S.-Y. Li L.-X. Zhan Z.-J. Liu R.-P. Wang W.-K. Zhang P. Yao Y.-G. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;74:125118. [Google Scholar]
- Gaillac R. Pullumbi P. Coudert F.-X. J. Phys.: Condens. Matter. 2016;28:275201. doi: 10.1088/0953-8984/28/27/275201. [DOI] [PubMed] [Google Scholar]
- Li Y. R. Hou Z. T. Wang T. X. Li Y. Liu H. Y. Dai X. F. Liu G. D. J. Phys.: Conf. Ser. 2017;827:012015. [Google Scholar]
- Majumder R. Hossain M. M. Comput. Condens. Matter. 2019;21:e00402. [Google Scholar]
- Truesdell C. Bull. Am. Math. Soc. 1952;58:577–579. [Google Scholar]
- Wang J. Yip S. Phillpot S. R. Wolf D. Phys. Rev. Lett. 1993;71:4182–4185. doi: 10.1103/PhysRevLett.71.4182. [DOI] [PubMed] [Google Scholar]
- Wallace D. C., Thermodynamics of Crystals. XVIII u. 484 S. mit 57 Abb., John Wiley & Sons Ltd., Chichester, New York, Sydney, Tokio, Mexiko, 1972 [Google Scholar]
- Qin H. Yan B.-L. Zhong M. Jiang C.-L. Liu F.-S. Tang B. Liu Q.-J. Phys. B. 2019;552:151–158. [Google Scholar]
- Chung D. H. Buessem W. R. J. Appl. Phys. 1967;38:2010–2012. [Google Scholar]
- Gao X. Jiang Y. Zhou R. Feng J. J. Alloys Compd. 2014;587:819–826. [Google Scholar]
- Ravindran P. Fast L. Korzhavyi P. A. Johansson B. Wills J. Eriksson O. J. Appl. Phys. 1998;84:4891–4904. [Google Scholar]
- Voigt W., Lehrbuch Der Kristallphysik, Vieweg + Teubner Verlag, Wiesbaden, 1966 [Google Scholar]
- Reuss A. Z. Angew. Math. Mech. 1929;9:49–58. [Google Scholar]
- Hill R. Proc. Phys. Soc. A. 1952;65:349–354. [Google Scholar]
- Maibam J. Indrajit Sharma B. Bhattacharjee R. Thapa R. K. Brojen Singh R. K. Phys. B. 2011;406:4041–4045. [Google Scholar]
- Pugh S. F. Lond. Edinb. Dublin philos. mag. j. sci. 1954;45:823–843. [Google Scholar]
- Ali Md. L. Rahaman Md. Z. Int. J. Mod. Phys. B. 2018;32:1850121. [Google Scholar]
- Pettifor D. G. Mater. Sci. Technol. 1992;8:345–349. [Google Scholar]
- Ahmed T. Roknuzzaman M. Sultana A. Biswas A. Alam Md. S. Saiduzzaman M. Hossain K. M. Mater. Today Commun. 2021;29:102973. [Google Scholar]
- Rubel M. H. K. Hossain K. M. Mitro S. K. Rahaman M. M. Hadi M. A. Islam A. K. M. A. Mater. Today Commun. 2020;24:100935. [Google Scholar]
- Majumder R. Mitro S. K. Bairagi B. J. Alloys Compd. 2020;836:155395. [Google Scholar]
- Kube C. M. AIP Adv. 2016;6:095209. [Google Scholar]
- Gueddouh A. Bentria B. Lefkaier I. K. J. Magn. Magn. Mater. 2016;406:192–199. [Google Scholar]
- Gou H. Hou L. Zhang J. Gao F. Appl. Phys. Lett. 2008;92:241901. [Google Scholar]
- Gao F. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;73:132104. [Google Scholar]
- Ali M. A. Hadi M. A. Hossain M. M. Naqib S. H. Islam A. K. M. A. Phys. Status Solidi B. 2017;254:1700010. [Google Scholar]
- Chowdhury A. Ali M. A. Hossain M. M. Uddin M. M. Naqib S. H. Islam A. K. M. A. Phys. Status Solidi B. 2018;255:1700235. [Google Scholar]
- Kholil M. I. Ali M. S. Aftabuzzaman M. J. Alloys Compd. 2018;740:754–765. [Google Scholar]
- Barua P. Hossain M. M. Ali M. A. Uddin M. M. Naqib S. H. Islam A. K. M. A. J. Alloys Compd. 2019;770:523–534. [Google Scholar]
- Luo H. Zhu Z. Ma L. Xu S. Liu H. Qu J. Li Y. Wu G. J. Phys. D: Appl. Phys. 2007;40:7121–7127. [Google Scholar]
- Fruchart R. Roger A. Senateur J. P. J. Appl. Phys. 1969;40:1250–1257. [Google Scholar]
- Anderson O. L. J. Phys. Chem. Solids. 1963;24:909–917. [Google Scholar]
- Fine M. E. Brown L. D. Marcus H. L. Scr. Metall. 1984;18:951–956. [Google Scholar]
- Shen Y. Clarke D. R. Fuierer P. A. Appl. Phys. Lett. 2008;93:102907. [Google Scholar]
- Clarke D. R. Surf. Coat. Technol. 2003;163–164:67–74. [Google Scholar]
- Rubel M. H. K. Hadi M. A. Rahaman M. M. Ali M. S. Aftabuzzaman M. Parvin R. Islam A. K. M. A. Kumada N. Comput. Mater. Sci. 2017;138:160–165. [Google Scholar]
- Zhou Y. Xiang H. Lu X. Feng Z. Li Z. J. Adv. Ceram. 2015;4:83–93. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data needed to evaluate the conclusion of this study are presented in the paper. Additional data are available from the corresponding author upon reasonable request.