Detecting differential protein abundance by combining peptide level P-values

Abstract

The majority of methods for detecting differentially abundant proteins between samples in label-free LC-MS bottom-up proteomics experiments rely on statistically testing inferred protein abundances derived from peptide ionization intensities or averaging peptide level statistics. Here, we statistically test peptide ionization intensities directly and combine the resulting dependent P-values using the Empirical Brown’s Method (EBM), avoiding error introduced through the estimation of protein abundances or summarizing test statistics. We show that on a spike-in proteomics dataset, a peptide level approach using EBM outperforms differential abundance detection using a protein level approach and several analysis workflows, including MSstats. Additionally, we demonstrate the effectiveness of this approach by detecting enriched proteins from an activity-based protein profiling dataset.

Introduction

Drawing biological conclusions from proteomics measurements often involves comparing protein abundances between samples. The difference in abundance may be indicative of a physiological response to experimental variables, or in the case of targeted enrichment-based experiments, the difference may detect functionally similar or spatially related proteins. To identify differentially abundant proteins, high-throughput LC-MS is widely used to quantify protein or peptide ionization intensities that are used as an indirect measure of abundance that can be statistically compared between samples.

In bottom-up proteomics, proteins are enzymatically digested and the constituent peptide intensities are measured by LC-MS.¹ While peptides tend to ionize more readily than proteins, comparing protein abundances between samples becomes increasingly complex due to the difficulty of inferring protein abundance from multiple peptide intensities. Estimating relative protein abundances from the intensities of peptides from bottom-up LC-MS experiments has been a major effort of the proteomics community, resulting in a variety of methods that are commonly used to detect differentially abundant proteins.²

The techniques used for inferring protein abundances include selecting the most highly ionized peptides and averaging or summing their intensities³, comparing peptide ratios⁴, fitting regression-based models to predict protein abundances⁵, or aggregating peptide level statistics through summarization or median-based techniques.⁶ To statistically account for the variability in peptide intensity measurements due to preparation technique, instrumentation, or biological variance, experimental designs often incorporate multiple biological or technical replicates. Inference-based methods may be used to estimate protein abundances from peptide level intensities, which are then often transformed in an attempt to achieve homoscedastic error and statistically tested between samples to detect differentially abundant proteins. Peptide aggregation methods differ by obtaining an estimated test statistic at the protein level, often through averaging or otherwise measuring the central tendency of peptide level t-statistics that can be used to derive an estimated P-value for a particular protein.

The methods for inferring protein abundances are routinely used, but that does not preclude them from having limitations. Regression-based protein abundance predictions require training model parameters from known relative abundances and are specific to a certain instrument and conditions, making it difficult to adapt this methodology to label-free experiments. Methods based on averaging, summing, comparing ratios, or otherwise aggregating peptide intensities do not statistically account for the peptide level variance between sample replicates, thereby introducing error when inferring protein abundances that are tested for differential abundance. Statistical modeling approaches for detecting differentially abundant proteins have been implemented in R packages such as MSstats⁶, which perform a run-level summarization of peptide intensities to the protein level that is statistically tested for differential abundance with a linear mixed-effects model. Also operating on peptide level data, the PECA R package⁷ calculates t-statistics for each peptide which are then used to generate a median t-statistic used to derive a P-value for each protein. Similar to averaging peptide intensities before statistical testing, methods based on measuring a central tendency of test statistics at the peptide level do not statistically account for the variance of each peptide. A hierarchical Bayesian approach that does not perform the aggregation of peptide intensities or statistics prior to statistical testing has been applied in the mapDIA software.⁸ Such hierarchical Bayesian methods perform well when the number of differentially abundant proteins is relatively large enough to provide evidence of differential abundance, but lose sensitivity in comparisons with relatively few differentially abundant proteins. MSqRob⁵ is yet another method available as an R package that performs peptide modeling with robust ridge regression and an empirical Bayes shrinkage of protein-level errors to detect differentially abundant proteins.

We propose a method that directly detects differentially abundant proteins between samples while statistically accounting for peptide level variance that is applicable to any bottom-up proteomics LC-MS dataset. This is achieved by first performing a statistical test comparing peptide intensities to obtain a set of P-values for each peptide. P-values for peptides originating from the same protein are then grouped and combined using the Empirical Brown’s Method (EBM) for combining dependent P-values with empirically calculated covariance⁹, producing a single P-value for each protein (Figure 1). This method enables a statistical measure of differential protein abundance without introducing error by inferring protein abundances or averaging test statistics.

Figure 1.

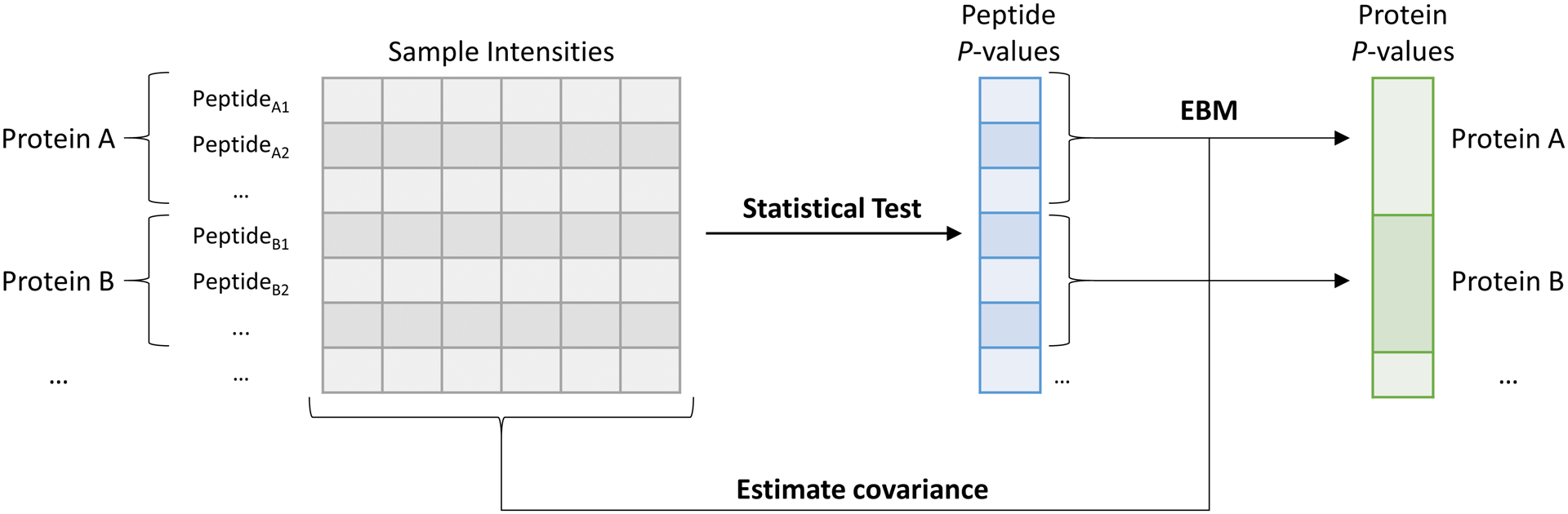
Application of the Empirical Brown’s Method (EBM) to peptide level data to determine differentially abundant proteins. Peptide intensities are statistically tested to obtain peptide level P-values and estimated covariance for peptides belonging to each protein is empirically calculated. Peptide level P-values and covariance estimates are then both used during P-value combination by EBM to obtain protein level P-values.

We compared EBM combination of peptide level P-values obtained from empirical Bayes models with corresponding protein level approaches using MaxQuant’s LFQ protein intensities^4,10. Additionally, we compared PECA’s averaging of peptide level moderated t-statistics and complete MSstats and MSqRob workflows to detect differentially abundant proteins. We show that peptide level P-value combination with EBM outperforms the other approaches on the publicly available Clinical Proteomic Tumor Analysis Consortium (CPTAC) label-free LC-MS data with known spike-in protein concentrations.¹¹ We also show the effectiveness of our approach on enriched activity-based protein profiling (ABPP) LC-MS data, where protein abundances are unknown.¹²

Materials and Methods

Combining P-values provides a means to test a single hypothesis with multiple contributing pieces of evidence. Fisher was the first to implement this approach when he introduced the combined probability test, which combines P-values from multiple independent tests into a single P-value.¹³ Fisher did this by recognizing multiple P-values from independent tests can be transformed to follow a chi-squared distribution with 2k degrees of freedom, where k is the number of independent tests performed. The combined P-value originates from the probability of observing a given set of transformed P-values given the null hypothesis that their distribution follows ${\chi }_{2k}^2$

$${\chi }_{2k}^2 ~ \sum _{i=1}^k-2log{P}_i$$ (1)

The assumption for independence between P-values is critical if the measured variables are positively dependent, which has been shown to result in an overestimated amount of evidence for rejection of the null hypothesis.¹⁴ This poses a problem in the often highly-correlated datasets of biological research, where dependence between measured variables may be due to a variety of biological factors and sample preparation techniques. Even further dependency is expected in LC-MS data from bottom-up proteomics, as peptides derived from the same protein have theoretically equivalent abundances under the assumption of complete enzymatic digestion.

To account for dependence between P-values, Brown extended Fisher’s method by scaling the chi-squared distribution appropriately to account for covariance between measured variables⁹

$$c{\chi }_{2f}^2 ~ \sum _{i=1}^k-2log{P}_i$$ (2)

where c and f are scaling factors defined by

$$f= \frac{E{\left[\psi \right]}^2}{var\left[\psi \right]} c= \frac{var\left[\psi \right]}{2E\left[\psi \right]}$$ (3)

and ψ is the statistic calculated from (2).

Due to computational complexity, initial implementations of Brown’s method estimated the covariance with polynomial approximations.¹⁵ With Poole’s development of calculating the covariance empirically from the data, this method became more feasible to apply to large datasets.¹⁴ Thus, Brown’s method with empirically calculated covariance takes into account the actual data used for statistical analysis in addition to multiple P-values that contribute evidence to a unified hypothesis to obtain a single P-value. Since its development, the empirical Brown’s method (EBM) has been applied to transcriptomic data to detect pathway-level changes in gene expression.¹⁶

Herein, we adapted EBM for combining P-values to LC-MS bottom-up proteomics datasets to detect differential protein abundance between samples. Peptides originating from a specific protein are first compared between samples by a statistical test to obtain P-values. Each peptide level test contributes evidence for rejection of the protein level null hypothesis that the originating protein is not more abundant in one sample compared to another. This set of P-values is then combined using Brown’s method with empirically calculated covariance, resulting in a single P-value indicative of the differential abundance of the protein. It is important to note that only P-values from one tail of the probability distribution can be combined, since different peptides from the same protein may be enriched in opposing samples, each resulting in significant P-values if a two-tailed test is used. This leaves ambiguity during P-value combination at the protein level as to which sample the protein is enriched in. As the peptide level P-values from a two-tailed test do not contribute evidence to the same protein level hypothesis, their combination is not indicative of protein level enrichment in a particular sample. Two individual one-tailed tests may be performed to detect an increase or decrease of protein abundance between two samples, but here we focus on detecting differentially abundant proteins between samples from spike-in and enriched experimental datasets.

Datasets for detecting differentially abundant proteins

CPTAC dataset:

We first tested the performance of detecting differentially abundant proteins using our EBM-based approach on the publicly-available LC-MS bottom-up proteomics datasets from the National Cancer Institute’s CPTAC study 6.¹¹ We analyzed the dataset originating from the LTQ Orbitrap at site 56 and compared peptide and protein level methods for detecting differential abundance between samples. The dataset contains three replicates for each sample, which consist of identical concentrations of yeast proteome spiked with varying concentrations of a mixture of 48 human proteins at equimolar concentrations (A: 0.25, B: 0.74, C: 2.22, D: 6.67, and E: 20 fmol/μl). As samples D and E have been shown to suffer from high ionization competition effects⁵, we compared the differential abundance between samples with the three lowest spike-in concentrations: A, B, and C.

MaxQuant was used for peptide-spectrum matching and ionization intensity calculations. The dataset from site 56 was loaded into MaxQuant version 1.6.3.4. Variable modifications were selected to include methionine oxidation, N-terminal protein acetylation, and glutamine to pyroglutamate conversion, while carbamidomethylation of cysteine was selected as a fixed modification. LFQ was enabled for quantification and match between runs was enabled. All other settings were left as the default values. The FASTA file for the Saccharomyces cerevisiae (strain ATCC 204508 / S288c) proteome was obtained from Uniprot¹⁷ and contains 6,721 reviewed proteins. The spike-in UPS FASTA sequences were obtained from the Sigma Aldrich website and contains 48 proteins. Both FASTA files were used in MaxQuant’s sequence search. Peptide intensities from MaxQuant’s peptides.txt file and protein level LFQ intensities from the proteinGroups.txt file were used for comparative analysis.

Activity-Based Protein Profiling dataset:

Enrichment of proteins is performed in a variety of experimental procedures where a specific protein or subgroup of proteins are concentrated from a biological sample. Activity-based protein profiling (ABPP) is a method of enriching functionally similar proteins from complex proteomes through the application of a small-molecule probe that mimics a protein binding partner, such as glutathione or vitamin B₁₂.^12,18 Modifications to the native molecule allow for irreversible binding and subsequent enrichment of protein binding partners. These modified molecules are termed activity-based probes (ABPs). Application of an ABP to a proteome allows for the enrichment of ABP-bound proteins, which are then subjected to bottom-up proteomics for identification of protein binding partners. However, non-specifically bound proteins are often carried through experimental protocol steps and detected in LC-MS experiments after enrichment, resulting in ambiguity between background proteins and those targeted by the ABP. To determine probe-targeted proteins, enriched samples must be statistically compared with an appropriate control.

To show the effectiveness of the peptide level approach on enrichment-based experiments, we analyzed an ABPP LC-MS dataset consisting of mouse liver lysate subjected to either a UV-activated glutathione-based ABP or an appropriate inactive control with three replicates for both conditions.¹² It is expected that samples subjected to the activated probe will bind to and enrich glutathione-binding proteins, while the control sample contains proteins that are non-specifically carried through the experimental enrichment steps. The control provides a background proteomic profile that the probed samples can be compared with to determine probe-enriched proteins. Raw LC-MS data used for this analysis is available at the PRIDE repository via ProteomeXchange with dataset identifier PXD006920.

MaxQuant parameters for peptide identification and LFQ calculation were selected to be the same as those used on the CPTAC study, except variable modifications were selected to only include methionine oxidation and N-terminal protein acetylation. The Mus musculus FASTA file used for the MaxQuant search was obtained from Uniprot and contains 22,286 genes.

Differential protein abundance analysis

Due to missing peptide intensities that are commonly present in proteomics data, pre-processing for missing peptides was performed. For each comparison between samples, peptides were selected for analysis if intensities were detected in at least 80% of the replicates for a specific sample. The corresponding comparative sample replicates were included for further analysis regardless of any missing intensities. For our analyses, this resulted in datasets where peptide intensities are present in all three replicates for at least one of the two samples being compared, but missing values may still remain.

A variety of methods and algorithms are available for imputing or removing missing values. However, careful consideration must be made when dealing with differentially abundant proteomics datasets, as peptides detected in one sample that are undetected in a comparative sample may indicate a differentially abundant protein. To deal with this, the imputeLCMD R package¹⁹ was used to impute missing values of peptides selected for comparison. Imputed values were drawn from a left-censored Gaussian distribution centered around the 0.01-th quantile of intensities in the sample with standard deviation equal to the median sample standard deviation. This approach was chosen due to the expectation of missing peptide intensities between samples with differentially abundant proteins and to prevent peptides detected near the limit of detection contributing significant P-values to the combined protein level P-value. This allowed for peptide abundance profiles that accounted for both present and missing data between replicates of selected peptides.

Peptide intensities were then log₂-transformed to normalize the error distributions. The lmfit and eBayes functions available through the limma R package²⁰ were then used to generate test statistics for each peptide between samples C-A, C-B, and B-A. The resulting statistics were used to generate t-distributions to obtain right and left-tailed P-values for each comparison. Peptide level P-values were then grouped based on protein identification from the leading razor protein in the peptides.txt MaxQuant output file and their P-values were combined using EBM. Proteins were limited to include only those with an average peptide level fold-change aligning with the tail from which the peptide level P-values originated from. Empirical calculation of the covariance was performed using both sets of sample replicates for each comparison.

Similar approaches were used to compare the EBM method with a protein level analysis. Protein level LFQ intensities were treated identically with the exception of EBM P-value combination. Additionally, PECA was used to compare proteins from peptide level intensities to calculate median modified t-statistics generated by the lmfit and eBayes functions in the limma R package using the same prepared peptide intensities as the EBM approach. Finally, we performed complete MSstats and MSqRob workflows using standard options directly on MaxQuant outputs for comparison. To ensure a balanced comparison of performance between methods, only proteins that were analyzed by all methods were included in the following comparisons.

Results and discussion

CPTAC

From the UPS mixture, 21, 24, and 27 spike-in proteins were analyzed by all methods for the B-A, C-A, and C-B comparisons respectively. For each method of differential abundance analysis and concentration comparison, the list of protein level P-values were compared for their detection of spike-in proteins using receiver operating characteristic (ROC) and precision-recall (PR) curves (Figure 2 a,b). Additionally, the area under the curve (AUC) was calculated for all ROC and PR curves (Figure 2 d).

Figure 2.

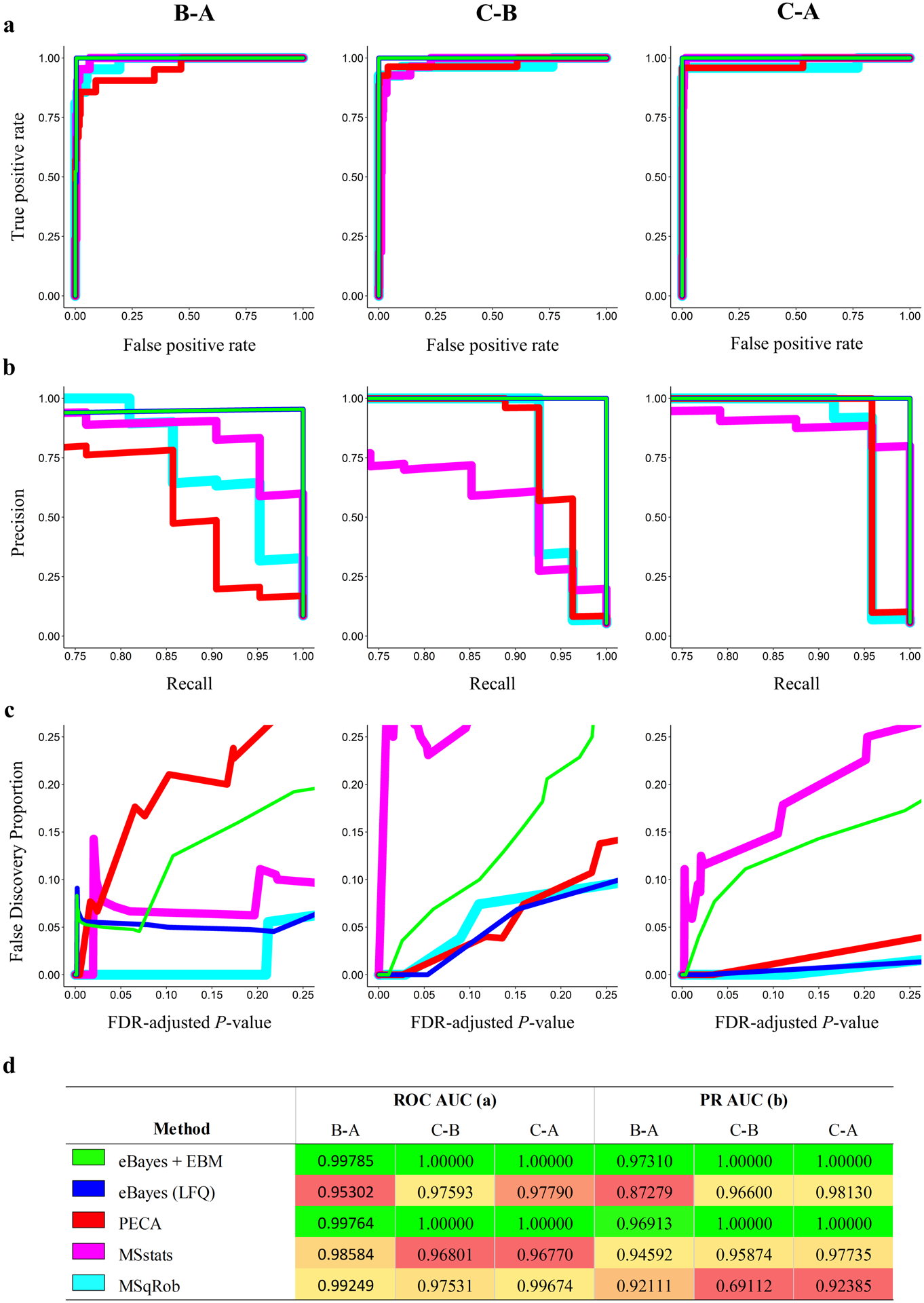
Comparison of methods for detecting differentially abundant proteins using (a) ROC curves, (b) PR curves, (c) FDP vs. predicted FDR-adjusted P-values, and (d) corresponding ROC and PR AUC values for each sample comparison. Colored lines (a, b, c) indicate the different methods compared for detection of spike in proteins as indicated in (d). Differences in line thickness are for visual aid only. Gradient coloring in (d) is specific to each sample comparison and method with green coloring indicating the highest AUC and red the lowest. Note that the axes for each metric (a-c) vary in range.

For the C-B and C-A comparisons, both eBayes + EBM and PECA performed exceptionally well at correctly ranking all spike-in proteins, resulting in AUC’s of 1.0 for both comparisons. The eBayes + EBM method marginally outperformed PECA in both ROC and PR AUC metrics for the minimally differentially abundant B-A comparison. In contrast, the eBayes and MSstats protein level approaches performed relatively poorly by AUC metrics. We note that while MSqRob performed moderately well by ROC metrics, it performed poorly at precise recall, particularly in the C-B comparison. Thus, the peptide level approaches performed exceptionally well at correctly ranking spike-in proteins in all sample comparisons and outperformed other methods by ROC and PR metrics.

For the practical purpose of detecting differentially abundant proteins between experimental samples where protein concentrations are unknown, it is important that the observed false discovery rate (FDR) be controlled while allowing for the detection of differentially abundant proteins. Therefore, we compared FDR-adjusted P-values (q-values)²¹ with the corresponding false discovery proportion (FDP) (Figure 2 c). While PECA performed nearly identically to the eBayes + EBM method by ROC and PR metrics, the q-values produced by the eBayes + EBM method reflected the FDP more accurately than all other methods in the practical FDR range of 0 to 0.25. This observation along with the corresponding ROC and PR metrics suggests the statistical combination of P-values using EBM is more effective at detecting differentially abundant proteins than the compared methods.

While eBayes + EBM performed exceptionally well, misclassification of a single yeast protein in the B-A comparison resulted in a sharp spike in the FDP that was also observed in the PECA and MSstats analyses. Upon inspection of the raw peptide level data of the misclassified LSM2_YEAST protein (Table 1), we identified that the peptide LDNISCTDEK was detected well above the limit of detection in all B samples but was not detected in any A samples. Missing value imputation near the limit of detection resulted in an extremely low P-value for this peptide. EBM combination of this P-value with the second insignificant P-value still resulted in a low protein level P-value in the same range of P-values as the UPS spike-in proteins. While this protein was misclassified as differentially abundant, such errors are difficult to avoid when the peptide intensities reflect likely differential abundance. Censoring of peptide level P-values or requiring more peptides per protein for EBM combination may be performed to possibly mitigate such errors, but these approaches may discard true positives from the analysis or artificially influence the final protein level P-value. Thus, we decided not to apply any of these approaches to correct similar misclassifications due to their potential trade-offs in performance.

Table 1.

Raw peptide intensity data and the corresponding eBayes + EBM analysis result of the misclassified LSM2_YEAST protein in the B-A comparison.

Peptide	A1	A2	A3	B1	B2	B3	eBayes P-values	EBM P-value
LDNISCTDEK	NA	NA	NA	154720	183280	226760	9.28E-06	8.77063E-05
NMVDTNLLQDATR	123440	133280	133870	117160	108710	164440	0.542
GTLQSVDQFLNLK	17387	NA	NA	NA	NA	17284	Dropped

As previously discussed, methods that implement aggregation of peptide intensities to obtain protein intensities prior to statistical testing do not accurately account for peptide level variance. While the LFQ method attempts to aggregate peptide level intensities appropriately to estimate protein abundance, it is prone to error due to heuristic methods of combining intensities. Analysis of the UPS spike-in protein TNFA_HUMAN in the C-B comparison provides an example of statistically testing estimated protein intensities that results in a P-value that does not meet a reasonable threshold for detection of differential abundance (Table 2). In contrast, by treating individual peptides statistically prior to EBM aggregation, eBayes + EBM is able to accurately detect the protein’s differential abundance. Although extreme, this example highlights the importance of peptide level approaches to differential abundance analysis.

Table 2.

Comparison of eBayes + EBM on raw peptide level data (top) with eBayes on protein level LFQ data (bottom) for the UPS spike-in TNFA_HUMAN protein in the C-B comparison.

Peptide	B1	B2	B3	C1	C2	C3	eBayes P-values	EBM P-value
IAVSYQTK	NA	57994	NA	107710	173680	433650	1.98E-03	1.48E-05
VNLLSAIK	123150	105160	100730	400480	339660	304580	7.11E-05
GQGCPSTHVLLTHTISR	83480	NA	NA	198220	NA	NA	Dropped
Protein	B1	B2	B3	C1	C2	C3	eBayes P-value
LFQ	925010	382610	NA	712230	731170	984080	0.062

While the eBayes + EBM analysis performed well at detecting differentially abundant proteins, it is important to consider the effect varying the number of peptides to be combined per protein has on the final protein level P-value. As the number of peptide level P-values to be combined by EBM varies with the number of peptides analyzed for each protein, the degrees of freedom for the chi-square statistic from which the protein level P-value originates may trend differently among proteins with different peptide coverage. Since varying the number of peptides used for analysis may influence the final protein level P-value, we investigated how different amounts of combined peptides per protein effect the protein level P-values obtained by EBM combination. To do this, we used Kendall’s method to test for correlation between protein level P-values and the number of peptides used to generate them for each spike-in yeast protein across all concentration comparisons. This yielded a significant but extremely weak positive correlation (P-value: 8.763e-07, τ: 0.0738). Additionally, figure 3 shows the protein level P-value distribution for varying numbers of contributing peptides. While significant, this weak correlation reveals little dependence between the number of combined peptides and the corresponding protein level P-values obtained by EBM combination.

Figure 3.

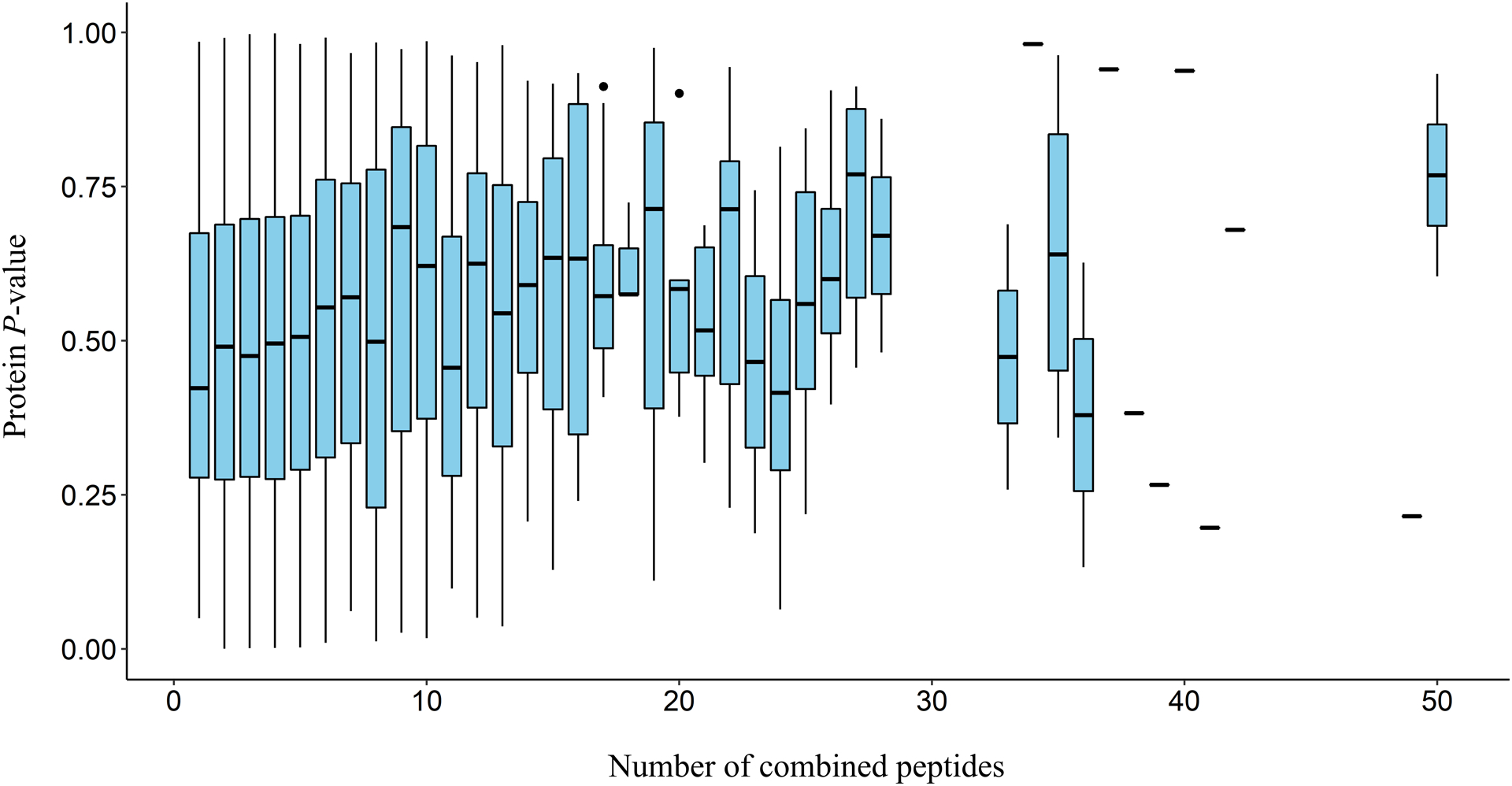
Boxplots of protein level P-value distributions produced by EBM combination for varying numbers of combined peptides for all yeast proteins across all comparisons. Missing boxplots indicate a lack of proteins detected with the specified number of peptides. Single horizontal lines outside of a boxplot indicate the P-value of a single analyzed protein.

Glutathione ABPP

To detect glutathione-binding proteins from experimental ABPP proteomics data, the eBayes + EBM peptide level approach used for the CPTAC datasets was replicated during the analysis of probed and control samples. While targets of the glutathione-based probe are expected to be annotated with glutathione-binding domains, comparisons between the probe and control can enable the discovery of proteins with unknown glutathione-binding functionality. To account for multiple hypothesis testing and P-value dependence, combined P-values were corrected with the BH FDR correction to obtain a set of FDR-adjusted P-values in a similar fashion to the CPTAC analysis. In addition to statistical significance, the average of the log₂ peptide level fold-changes for each protein was calculated to provide an approximate measure of relative protein abundance. The detection of statistically differentially abundant proteins below the 5% FDR cutoff with average log₂ peptide level fold-changes greater than 2.0 indicates significant enrichment of proteins with glutathione binding activity (Figure 4).

Figure 4.

Volcano plot of differentially abundant mouse proteins targeted by the glutathione activity-based probe. Proteins detected under a 5% FDR using the EBM + eBayes method with average log₂ peptide level fold-changes greater than 2.0 are labeled with protein identifiers, while dashed lines indicate FDR (adjusted P-value) and fold-change thresholds. Known glutathione-binding protein identifiers are highlighted green.

The majority of significantly enriched proteins are annotated as containing glutathione-binding domains¹⁷, indicating successful statistical detection of glutathione-binding proteins. Many of these proteins are glutathione S-transferases (GSTs) capable of transferring glutathione to target substrates. Other enriched proteins with annotated glutathione or derivative binding domains include elongation factor 1-gamma (EF1G) and lactoylglutathione lyase (LGUL). Proteins with unknown glutathione binding may be involved in glutathione metabolism or have an affinity for the glutathione probe. Many of these proteins are involved in fatty acid metabolism, including fatty acid binding protein in the liver (FABPL) and apolipoprotein A-I (APOA1) proteins. Targets specifically involved in the metabolism of coenzyme A derivatives, including bile acid-CoA:amino acid N-acyltransferase (BAAT) and alpha-methylacyl-CoA racemase (AMACR), are annotated to act on thiol-containing molecules similar to those found in glutathione conjugates¹⁷. As the majority of enriched proteins contain known glutathione binding domains, our analysis provides evidence of glutathione-binding activity by these proteins with previously unknown glutathione interaction. We include the results of comparative methods used in the CPTAC analysis in the supplementary information.

Conclusions

Detecting differentially abundant or enriched proteins between samples is critical for many proteomics experiments. With the rising focus on comparing protein abundances between complex samples such as those originating from the microbiome²², there is an increasing need for statistics-based methods that accurately identify enriched proteins from LC-MS bottom-up proteomics datasets. By applying EBM to peptide level statistics originating from a linear model with empirical Bayes moderation of errors, the inaccuracy introduced during inference of protein abundance or summarizing peptide level statistics in a heuristic manner can be avoided.

We have demonstrated that our method provides accurate detection of differentially abundant proteins on experimental datasets. Analysis of CPTAC data showed our P-value combination approach was able to detect spike-in proteins with better precise recall and accuracy when compared to analogous protein level analysis of LFQ intensities and other peptide level approaches. Additionally, analysis of enriched glutathione ABPP experimental LC-MS data revealed a high selectivity for known glutathione-binding proteins while identifying several potential unknown binding partners. Thus, our approach can be applied to a variety of enrichment-based experimental designs to detect enriched proteins, including activity-based protein profiling (ABPP), peroxidase-catalyzed proximity biotinylation (APEX)²³, and protein-specific enrichment. This approach may also be used to identify differentially abundant proteins in non-enrichment based proteomics experiments provided the combined peptide level P-values support the same protein level hypothesis. Thus, our approach implementing EBM combination of peptide level P-values is generally applicable to bottom-up mass-spectrometry proteomics experiments.