Thermodynamic coupling between neighboring binding sites in homo‐oligomeric ligand sensing proteins from mass resolved ligand‐dependent population distributions

Abstract

Homo‐oligomeric ligand‐activated proteins are ubiquitous in biology. The functions of such molecules are commonly regulated by allosteric coupling between ligand‐binding sites. Understanding the basis for this regulation requires both quantifying the free energy ΔG transduced between sites, and the structural basis by which it is transduced. We consider allostery in three variants of the model ring‐shaped homo‐oligomeric trp RNA‐binding attenuation protein (TRAP). First, we developed a nearest‐neighbor statistical thermodynamic binding model comprising microscopic free energies for ligand binding to isolated sites ΔG ₀, and for coupling between adjacent sites, ΔG _α . Using the resulting partition function (PF) we explored the effects of these parameters on simulated population distributions for the 2 ^N possible liganded states. We then experimentally monitored ligand‐dependent population shifts using conventional spectroscopic and calorimetric methods and using native mass spectrometry (MS). By resolving species with differing numbers of bound ligands by their mass, native MS revealed striking differences in their ligand‐dependent population shifts. Fitting the populations to a binding polynomial derived from the PF yielded coupling free energy terms corresponding to orders of magnitude differences in cooperativity. Uniquely, this approach predicts which of the possible 2 ^N liganded states are populated at different ligand concentrations, providing necessary insights into regulation. The combination of statistical thermodynamic modeling with native MS may provide the thermodynamic foundation for a meaningful understanding of the structure–thermodynamic linkage that drives cooperativity.

1. INTRODUCTION

1.1. Homotropic allostery is widespread in biology

Homotropic cooperativity describes a ubiquitous process in biological regulation. It arises commonly in proteins that form symmetric homo‐oligomeric assemblies whose biological activity is modified by ligands. ¹ , ² In such symmetric assemblies, even though the binding sites are identical, ligand‐binding affinities depend on the liganded state of the oligomeric protein; that is, the affinity K of a ligand for a receptor with no bound ligands will be different for a receptor that already has one or more bound ligands. ³ This difference in affinity arises through “allosteric” interactions between the ligand‐binding sites, which alter the free energy change upon additional ligand binding. ⁴ , ⁵ Such thermodynamic changes are most often associated with structural changes that accompany ligand binding, though changes in protein dynamics have also been implicated. ⁶ , ⁷ , ⁸ A large proportion of biological processes are regulated by oligomeric ligand‐binding proteins, from hemoglobin ⁹ to p97 ATPase. ¹⁰ , ¹¹ Therefore, to understand biological regulation we must first understand the linkage between ligand‐induced structural changes and changes to protein‐ligand free energy landscapes. ¹²

1.2. TRAP protein rings as models of homotropic allostery

We explore homotropic cooperativity in the homo‐oligomeric trp RNA‐binding attenuation protein (TRAP), which plays a central role in regulating tryptophan (Trp) production in Bacilli. ¹³ TRAP was originally identified in Bacillus subtilis (Bsu) as a 76‐residue protein that assembles into homo‐oligomeric complexes. Upon binding multiple Trp ligands, TRAP is activated to bind specific RNA sequences in the 5′ untranslated region of the trp operon mRNA. ¹⁴ , ¹⁵ Crystal structures of TRAP from Bsu, B. stearothermophilus (Bst), B. licheniformis, and B. halodurans (Bha) revealed undecameric (11mer) and dodecameric (12mer) rings with binding sites for Trp in the interfaces between each of the protomers (Figure 1a–c). Trp‐dependent sequence‐specific RNA recognition is achieved via base contacts from amino acids located on loops that are shown by NMR studies to be flexible in the absence of Trp and structured upon Trp binding ¹⁶ , ¹⁷ ; these loops thus mediate heterotropic Trp‐RNA cooperativity. The same loops that mediate RNA binding also are points of contact between neighboring Trp‐binding sites, providing a structural scaffolding for mediating site‐site interactions (Figure 1d).

FIGURE 1.

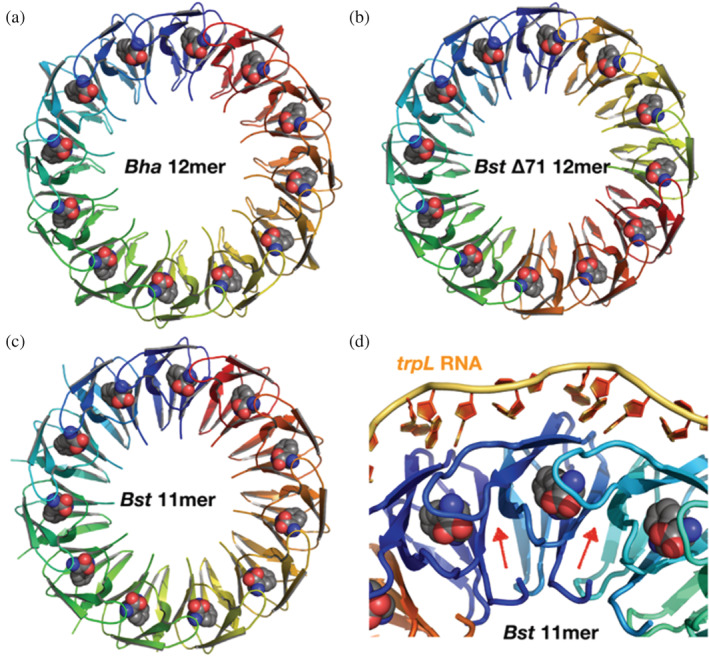
TRAP forms ring‐shaped homo‐oligomers to bind Trp and RNA. (a–c) Crystal structures of Trp‐bound TRAP revealed 12mers for Bha TRAP (a; 3zzl), and for an engineered Bst TRAP Δ71 (b; 3zzs), while wild‐type Bst TRAP crystallized as 11mers (c; 1qaw). Bound Trp ligands are shown as spheres. (d) Crystal structure of Bst TRAP bound to an idealized trp leader RNA (green; 1c9s). Protein loops (red arrows) that are disordered in Trp‐free TRAP and become structured upon Trp binding, participate in RNA recognition and mediate allosteric interactions between Trp‐binding sites. Each TRAP ring can adopt 2 ^N (=2,048 or 4,096) states with 0–N bound Trp where N equals 11 or 12. Measuring the populations of these states is required to quantify magnitude and mechanism of allostery. TRAP, trp RNA‐binding attenuation protein; Trp, tryptophan

1.3. Quantifying the detailed thermodynamics of ligand binding to homo‐oligomeric proteins is difficult

Experimentally, binding affinities are usually quantified by measuring ligand‐dependent changes in an observable that is proportional to the fraction of bound states Y; for example, a spectroscopic signal, or heat released upon binding. For binding a ligand L to its site on a macromolecule M to form an ML complex, $\mathrm{M}+\mathrm{L}\rightleftharpoons \mathrm{ML}$, Y has the familiar hyperbolic form $Y=\frac{\left[\mathrm{L}\right]}{\left[\mathrm{L}\right]+1/K}$. Here [L] is the free ligand concentration, and the equilibrium association constant K is related to the free energy difference between the free and bound states, ΔG = −RTln K. The population of the bound state is proportional to its Boltzmann probability, $p_{\text{bound}}\propto \exp \left(-\mathrm{\Delta }G/\mathit{RT}\right)$. So, measuring a signal proportional to Y at different ligand concentrations [L] yields K and the binding free energy ΔG.

For oligomeric macromolecules, the measured signal is averaged over multiple sites and configurations. For a dodecameric protein with 12 binding sites, there are 2¹² = 4,096 possible configurations with 0–12 bound ligands. If the binding sites are independent and have the same affinity K for the ligand (i.e., in the absence of cooperativity), the most likely configurations are those with the greatest statistical degeneracy: the populations of states with 0–12 bound ligands L follow a binomial distribution: $P\left(n,M,Y\right)=\frac{M!}{n!\left(M-n\right)!}{Y}^n{\left(1-Y\right)}^{M-n}$, where n is the number of bound ligands, M is the total number of sites; Y, the fraction of bound sites, is equivalent to the probability of sites being bound. ¹⁸ , ¹⁹ Thus, for example, when enough ligand is present so that on average one‐twelfth of all sites are occupied (Y = 1/12 = 0.083), states with one ligand bound are only slightly more abundant than those with none bound, or with two bound (0: 35%, 1: 38%, 2: 19%, 3: 6%) (Figure S1). If enough ligand is present to fill half of the sites (Y = 0.5), the most dominant states are those with six bound ligands because there are simply more ways to arrange 6 ligands on a 12‐site lattice, $\frac{M!}{n!\left(M-n\right)!}=\frac{12!}{6!6!}=924$. Under these conditions the states with 0–12 bound ligands are populated according to a normal distribution, with coefficients of 1:12:66:220:495:792:924:792:495:220:66:12:1 (Figure 2). The experimentally measured signal is thus the average over all liganded states and their configurations. Nevertheless, if the sites are identical and independent, and the signal is proportional to Y, we can determine K by measuring how it changes with [L].

FIGURE 2.

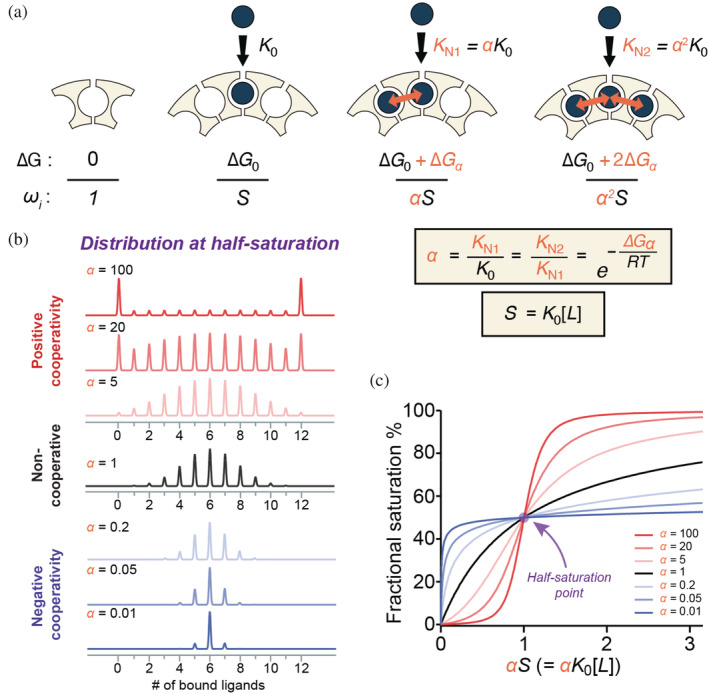
Nearest‐neighbor models can explain and predict population distributions for cooperative ligand binding to ring‐shaped oligomeric proteins. (a) In an NN model of cooperativity, four basic ligand‐binding modes can be described with two energy parameters: an intrinsic free energy change for binding to sites with no occupied neighbors (ΔG ₀), and a coupling free energy term contributed solely from each adjacent bound ligand (ΔG _α ). An empty site is defined as the reference state with ΔG ₀ = 0 and a statistical weight of 1. Binding to an isolated site is afforded a statistical weight ω = S = K ₀[L]. Cooperativity from one bound neighbor results in an association constant K _N1 = αK ₀, ω = αS, while binding to a site with two occupied neighbors is occurs with affinity K _N2 = α ² K ₀, and ω = α ² S. α values >1 indicate stronger binding to sites with occupied neighbors. The four liganded states are referred to in the text as 0, N0, N1 and N2, respectively. (b) Effect of NN cooperativity on simulated population distributions for dodecameric rings with 0–12 bound ligands at half‐saturation. Simulated populations for a non‐cooperative binding (α = 1, black), equivalent to non‐interacting sites, yield the expected binomial distribution. Population distributions arising from both positive (α > 1, red) and negative (α < 1, blue) cooperativity were simulated using a cyclic NN model. In the presence of stronger positive cooperativity the apo and holo populations dominate the distribution. In contrast, negative cooperativity favors states with half of the sites occupied. (c) Effects of NN cooperativity on fractional saturation of ligand‐binding sites. Positive cooperativity (red) generates sigmoidal binding curves, the non‐cooperative binding curve is hyperbolic (black), whereas negative cooperativity (blue) generates curves that are steeper at low concentration but shallow at high concentration. NN, nearest‐neighbor

Cooperativity implies that ligand‐binding events to otherwise identical sites occur with different affinities. Because affinities and free energy changes are linked, these differences result in altered population distributions. At the extreme of infinitely positive cooperativity, under conditions of half maximal saturation (Y = 0.5), instead of a normal distribution we would observe a strict bimodal distribution: half of the oligomers will be fully bound, and half will be empty. Thus, cooperativity makes some configurations more favorable than others; which states are more favored depends on the mechanism and magnitude of the cooperative interactions. Thus, the population distribution encodes rich information about cooperative mechanisms that is largely lost when convolved into the average metric Y.

A complicating factor in measuring population distributions is that cooperativity may distort the proportionality between the observable signal and fractional saturation Y. For example, in isothermal titration calorimetry (ITC) experiments, ligands may bind with differing affinities K _i , but also with different enthalpies ΔH _i ; this complicates the use of heat as a metric for quantifying populations. Likewise, if a ligand bound at a site allosterically favors structural shifts in neighboring binding sites, monitoring subsequent ligand‐binding events by circular dichroism (CD) might generate smaller structural changes and therefore lose proportionality to bound population. Thus, it can be difficult to determine populations of states from typical bulk‐averaged observables.

1.4. Native mass spectrometry can measure population distributions

Native mass spectrometry (MS) has the potential to distinguish allosteric mechanisms by more directly probing bound‐state distributions. ⁷ , ⁸ , ²⁰ , ²¹ , ²² Unlike measurements of average fractional saturation, native MS can directly probe the populations of states with different numbers of bound ligands. ²² The mass (and mass‐to‐charge ratios, m/z) of a macromolecular complex is exactly determined by the molecular weight of its constituents. Thus, for an ionized macromolecule with n bound ligands, the signal will appear at the m/z dictated by the mass of the components and the charge on the ion. This direct proportionality between signal and ligand occupancy thus makes native MS well suited to characterize populations of states for molecules with multiple binding sites.

1.5. Proper model selection is important

Finally, a severe confounding factor in understanding mechanisms of cooperativity is the selection of an appropriate model to extract thermodynamic parameters from binding data. In the absence of cooperativity, one may fit the signal change with the hyperbolic binding equation $\text{Δsignal}=\text{amplitude}\times \frac{\left[\mathrm{L}\right]}{\left[\mathrm{L}\right]+1/K}$ if the free ligand concentration is known or can be approximated, or the quadratic equation:

$$\text{Δsignal}=\text{amplitude}\times \frac{{\left[\mathrm{L}\right]}_{\mathrm{T}}+{\left[\mathrm{M}\right]}_{\mathrm{T}}+1/K-\sqrt{{\left({\left[\mathrm{L}\right]}_{\mathrm{T}}+{\left[\mathrm{M}\right]}_{\mathrm{T}}+1/K\right)}^2-4{\left[\mathrm{L}\right]}_{\mathrm{T}}{\left[\mathrm{M}\right]}_{\mathrm{T}}}}{2{\left[\mathrm{M}\right]}_{\mathrm{T}}},$$ (1)

if only total ligand and binding site concentrations [L]_T and [M]_T are known; amplitude is the proportionality between fractional saturation Y and the signal change. However, these equations are inappropriate for cooperative binding since they only include one equilibrium constant K. Cooperativity is plainly evident if binding curves cannot be adequately described by one of these equations.

Parsimonious approaches to data analysis demand adding only as many parameters as needed to produce a good fit to the binding data. A common approach is to use the Hill equation, which can generate sigmoidal binding curves but is uninformative about free energy differences between binding modes. ²³ Phenomenological multi‐site independent binding models can also produce cooperative binding curves as well as different apparent affinities, yielding free energy differences between phenomenological binding modes. ²⁴

However, to decipher cooperativity mechanisms, it is necessary to apply an appropriate physical binding model to the thermodynamic parameters. In the concerted Monod‐Wyman‐Changeux (MWC) model, all subunits of a homo‐oligomer are posited to simultaneously exchange between distinct structures with different affinities for the ligand binding. ²⁵ In the sequential Koshland‐Nemethy‐Filmer (KNF) model, each subunit independently undertakes conformational changes upon ligand binding, altering the binding affinity for subsequent binding events. ²⁶ While each of these models are able to reproduce cooperative binding curves, they are unable to clarify which of the 2 ^N  = 4,096 possible liganded configurations of a 12mer are more favorable, or how ligand‐binding events alter the free energies for other binding events.

1.6. Mechanistic insights from statistical thermodynamic models and native MS

Here, we explore the use of mechanistic nearest‐neighbor (NN) lattice‐based statistical thermodynamic models, along with native MS, to quantify and describe the cooperative behavior of three TRAP protein variants. We apply an NN model parametrized with the free energy of binding to isolated sites ΔG ₀, and a microscopic free energy for communication between sites ΔG _α . We iterate over all possible 2 ^N liganded configurations of TRAP rings to develop a statistical thermodynamic partition function (PF) that describes the ligand‐dependent probabilities of each of the 2 ^N possible states. We explore the effect of NN interaction energies on population distributions during simulated ligand titrations and examine the sensitivity of average site occupancy to the underlying population distributions.

We then measure Trp binding to TRAP variants using conventional bulk methods (CD, ITC), and using native MS. We find that native MS makes it possible to resolve and quantify states with 0–N bound ligands, thereby allowing measurement of the statistical thermodynamic PF. Fitting of the populations of states with different numbers of bound ligands to a binding polynomial derived from the PF allows quantification of the microscopic free energy transduced between adjacent ligand‐binding sites. This is the thermodynamic quantity required for a true understanding of structure–thermodynamic relationships in biological regulation.

2. RESULTS

2.1. Nearest‐neighbor statistical thermodynamic model can quantify cooperativity and provide mechanistic insights

A NN model posits that the thermodynamics of ligand binding to a site are influenced by the liganded states of the immediately adjacent sites. ⁵ Thus, the thermodynamics of binding to a given site can be parametrized using two microscopic free energy terms (ΔG ₀, ΔG _α , Figure 2a), corresponding to free energies for binding to sites with no bound neighbors, and thermodynamic contributions of interactions with occupied neighbors, respectively; ΔG _α  = 0 in the absence of cooperativity. Each of the N sites in the macromolecule can be classified as either: (a) empty, state‐0 (ΔG = 0, the reference state); (b) bound with no occupied neighbors, state‐N0 (ΔG ₀); (c) bound with one occupied neighbor, state‐N1 (ΔG ₀ + ΔG _α ); or (d) state‐N2 (ΔG ₀ + 2ΔG _α ), bound with two occupied neighbors. The corresponding microscopic ligand‐binding affinity constants for each state are $K_0=1$, $K_{\mathrm{N}0}=\exp \left(-\frac{\mathrm{\Delta }{G}_0}{\mathit{RT}}\right)$, $K_{\mathrm{N}1}=\exp \left(-\frac{\mathrm{\Delta }{G}_0+\mathrm{\Delta }{G}_{\alpha }}{\mathit{RT}}\right)$, and $K_{\mathrm{N}2}=\exp \left(-\frac{\mathrm{\Delta }{G}_0+2\mathrm{\Delta }{G}_{\alpha }}{\mathit{RT}}\right)$, respectively. In addition, it is convenient to quantify “cooperativity” by comparing the affinities for ligand binding in various modes, such that α = K _N1/K ₀ > 1 quantifies the fold increase in affinity afforded by having the first occupied neighbor, while α < 1 quantifies the fold decrease in affinity from negative cooperativity. Likewise, α ² is the fold change in affinity to a site with two bound neighbors, compared to none. An α = 10 means a ligand binds 10 times more tightly to a site with one occupied neighbor than to one with none, and 100 times more tightly to a site with two flanking neighbors; it also corresponds to a thermodynamic coupling between sites of ΔG _α  = −RTln 10 = −2.3RT, or −1.4 kcal mol⁻¹ at 298 K. With these parameters, NN models enable elaboration of a statistical partition function that enumerates the free energies and Boltzmann probabilities of all possible 2 ^N states by straightforward iteration and examination of their NN site occupancy. ⁵ , ³⁹

Application of an NN model to a cyclic homo‐dodecamer results in a partition function (PF) Ξ_NN with 38 unique energetic terms corresponding to the summed statistical weights ω _i for the 2¹² = 4,096 configurations:

$$\begin{array}{cc}{\mathrm{\Xi }}_{\mathrm{NN}}=& 1\hfill \\ & +S\left(12\right)\hfill \\ & +S^2\left(54+12\alpha \right)\hfill \\ & +S^3\left(12+96\alpha +12{\alpha }^2\right)\hfill \\ & +S^4\left(105+240\alpha +360{\alpha }^2+144{\alpha }^3+12{\alpha }^4\right)\hfill \\ & +S^5\left(36+240\alpha +360{\alpha }^2+144{\alpha }^3+12{\alpha }^4\right)\hfill \\ & +S^6\left(2+60\alpha +300{\alpha }^2+400{\alpha }^3+150{\alpha }^4+12{\alpha }^5\right)\\ & +S^7\left(36{\alpha }^2+240{\alpha }^3+360{\alpha }^4+144{\alpha }^5+12{\alpha }^6\right)\hfill \\ & +S^8\left(105{\alpha }^4+252{\alpha }^5+126{\alpha }^6+12{\alpha }^7\right)\hfill \\ & +S^9\left(112{\alpha }^6+96{\alpha }^7+12{\alpha }^8\right)\hfill \\ & +S^{10}\left(54{\alpha }^8+12{\alpha }^9\right)\hfill \\ & +S^{11}{\alpha }^{10}\left(12\right)\hfill \\ & +S^{12}{\alpha }^{12}\hfill \end{array}$$ (2)

Here, S = K ₀[L], where [L] is the free Trp concentration and K ₀ and α are as in Figure 2; generation of the PF was automated using itcsimlib. ⁵ Each row in Equation (2) corresponds to states with different numbers of bound ligands, from 0 to 12, with 1 assigned as the statistical weight of the state with zero bound ligands. For each term, the coefficients reflect the degeneracy of the energetic states. For example, there are 12 equivalent ways to configure 1 or 11 ligands on a 12‐mer. For two bound ligands, there are 12 ways to arrange them next to each other, with statistical weights modified by the cooperativity factor α, and 54 ways to arrange them in isolation, with no interaction term (Figure S3A). The exponent on the α terms reflects the number of NN interactions in that configuration, such that, for example, the half‐bound state with the 400α ³ term corresponds to configurations that arrange the six bound ligands with three pairs of interactions (e.g., Figure S3B).

With the NN partition function constructed it is possible to predict the effect of cooperativity on the populations of each of the 4,096 states in a ring‐shaped homo‐dodecameric proteins. As noted above, in the absence of cooperativity, at ligand concentrations that result in half of the sites being bound, the populations follow a binomial distribution (Figure 2b, black). Positive cooperativity increases the population of states with more bound ligands because they feature more NN interactions; this also results in more states with fewer sites bound, due to mass balance (Figure 2b, red; Figure S4A). In the case of strong positive cooperativity, apo and holo states dominate the population distribution, with intermediate states being lowly populated. In contrast, negative cooperativity has the opposite effect, favoring half‐bound configurations that spread out ligands over all available sites while minimizing NN interactions (Figure 2b, blue; Figure S4B).

In addition to providing details of the underlying populations, NN models can be used to compute bulk properties for comparison with experimental measurements (Figure 2c). A plot of fractional saturation versus free ligand concentration generates the expected hyperbolic curve in the absence of cooperativity (black). Positive cooperativity produces the expected sigmoidal curves (red) and negative cooperativity yields compressed saturation curves (blue). For reference, we also fit the trajectories with the Hill equation. This yielded Hill coefficients of ~8 and ~0.2 for α = 100, and 0.01, respectively. However, while α is directly related to the coupling‐free energy, the Hill coefficient is phenomenological and not mechanistically informative.

2.2. Cooperative Trp binding to multimers can be difficult to characterize using traditional bulk binding assays

To quantify Trp binding to oligomeric TRAP rings, we first used CD spectropolarimetry to measure its ellipticity at 228 nm, which reports on Trp binding (Figure 3a). ³¹ CD measurements were conducted at 25°C with ~24 μM TRAP (2 μM rings) over a range of Trp concentrations. Binding curves were fit with the binding quadratic (Equation (1)), yielding apparent dissociation constants (K _d,app = 1/K _app). The three TRAP variants yielded similar apparent Trp‐binding affinities of 3–14 μM (Table S1), consistent with previous findings. ²⁷ Under these conditions, cooperative binding of Trp to the TRAP variants is not evident.

FIGURE 3.

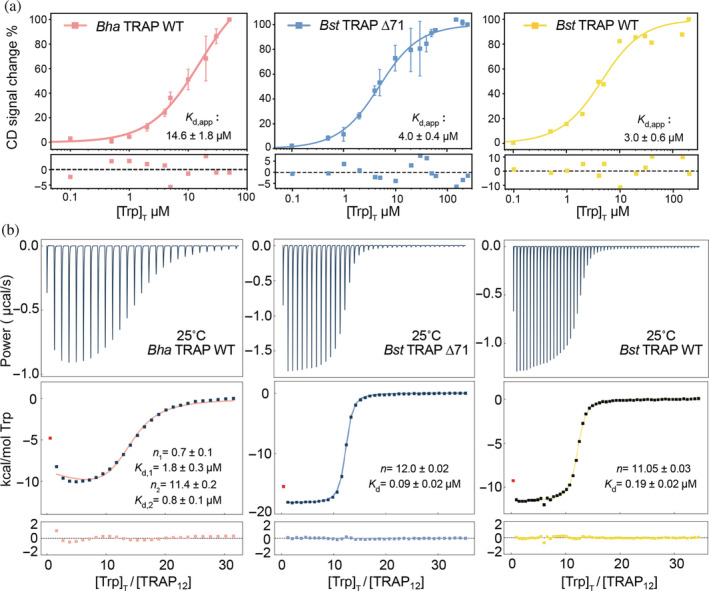
Bulk binding and phenomenological modeling provide limited information on cooperative ligand‐binding to dodecameric Bha TRAP and Bst TRAP Δ71 (left, middle), or undecameric wild‐type Bst TRAP (right). (a) The circular dichroism signal at 228 nm in 50 mM sodium phosphate buffer (pH = 8) was measured as a function of added Trp, and the data fit with the quadratic binding equation (Equation (1); Table S1). CD data were acquired by using 2 μM TRAP with increasing Trp concentration from 0 to 300 μM. The fitted parameters from CD suggest all three proteins exhibit similar μM‐binding affinity and homotropic cooperativity is not evident. (b) ITC experiments titrating Trp into TRAP at 25°C in buffer A (see Methods) were fit with quadratic independent site models (Table S2). Bst TRAP Δ71 (middle) and Bst TRAP (right) can be well fitted with one‐site binding model, in which 12mer Bst TRAP Δ71 (K _d = 0.09 ± 0.02 μM) has two‐times higher binding affinity than 11mer Bst TRAP (K _d = 0.19 ± 0.02 μM). The data for Bha TRAP (left) are better fit to a two‐sites binding model yielding parameters in which the first Trp binds with K _d of 1.8 ± 0.3 μM while the remaining 11 bind with a K _d of 0.8 ± 0.1 μM. CD, circular dichroism; TRAP, trp RNA‐binding attenuation protein

Homotropic cooperativity can alter thermodynamic parameters other than binding‐free energy (e.g., ΔH), so we also studied Trp binding to TRAP using isothermal titration calorimetry (ITC), which directly measures enthalpy changes resulting from ligand binding. The binding thermograms for Bst TRAP₁₂ Δ71 and Bst TRAP₁₁ could be well fit with single‐site (non‐cooperative) model, with comparable affinities (Figure 3b; Table S2). However, the binding thermogram for Bha TRAP₁₂ is biphasic (Figure 3b), indicative of thermodynamically inequivalent binding events. Fitting of the thermograms for Bha TRAP to a phenomenological two‐site binding model yielded parameters with an initial (n ≈ 1) ligand‐binding event of K _d,1 = 1.8 ± 0.3 μM, and subsequent ~11 binding events with K _d,2 = 0.8 ± 0.1 μM. Such parameters would suggest an arguably implausible binding model in which initial weaker binding of the first ligand fundamentally alters the structures of all other binding sites to favor binding, or alternatively, that all subsequent binding events occur in a defined sequential manner. These models describe drastically different modes of cooperativity but are indistinguishable by this method, which provides little insight into the mechanism by which thermodynamic communication occurs between sites.

2.3. Native MS enables quantification of TRAP states with different numbers of bound ligands

We used native MS to quantify populations of Trp_n‐TRAP_m states over a range of Trp concentrations for Bha TRAP₁₂, Bst TRAP₁₂ Δ71 and Bst TRAP₁₁ (Figure 4a). For each protein, titration samples were prepared in parallel by incubating the proteins in 400 mM ammonium acetate solutions with differing concentrations of Trp. For each oligomer, we obtained spectra with narrow charge distributions indicative of native structure. ⁴⁰ The most abundant charge states for each protein were 24+, 22+ and 21+ for Bha, Bst Δ71 and Bst TRAP, respectively. Recorded spectra provided baseline resolution of signals corresponding to different numbers of bound Trp. Double deconvolution of the m/z spectra to include proteoforms ³⁷ resulted in very clean zero‐charge mass spectra, and improved fits (Figure 4b; Figure S5). Spectra recorded in the absence of Trp contained signals corresponding to the apo oligomeric protein rings, and spectra at the highest Trp concentrations were dominated by the fully bound holo states, while intermediate states could be discerned at all non‐zero Trp concentrations. Thus, these spectra enable us to resolve and quantify populations of states corresponding to the ligand‐free apo states, the fully liganded holo states, and intermediate species with differing numbers of bound Trp ligands. These populations can be directly compared to the populations predicted by the NN model (Figure 2) and used to determine thermodynamic cooperativity parameters.

FIGURE 4.

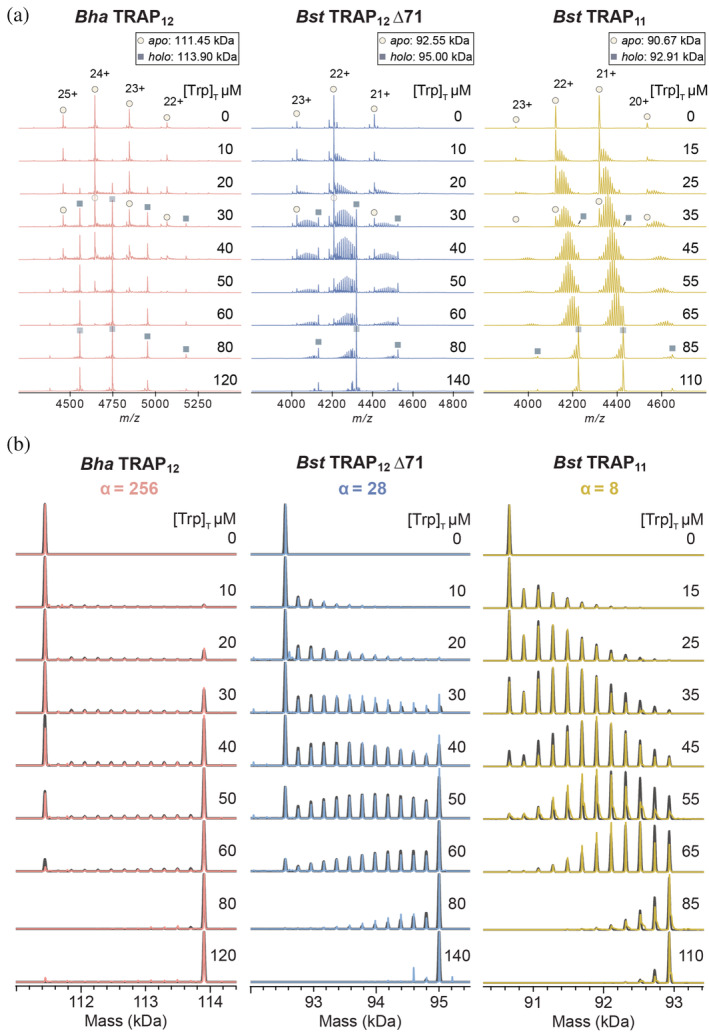
Population distributions measured by native MS reveal extents of homotropic cooperativity in ligand binding to 12mer Bha and Bst Δ71 TRAP (left, middle), and 11mer wild‐type Bst TRAP (right). (a) Native mass spectra of the three TRAP oligomers (6.0–7.4 μM; Table S3) titrated with 0–140 μM Trp. Increasing Trp in each titration shifts the Trp _n ‐TRAP populations from apo (Trp₀, circles) to holo (Trp_11/12, squares). Each Trp titration set with either Bha TRAP₁₂ (left), Bst TRAP₁₂ Δ71 (middle), or Bst TRAP₁₁ (right) features different population distributions, reflecting different degrees of cooperativity. (b) Deconvolved zero‐charge mass spectra for the three TRAP oligomers: Bha TRAP₁₂ (left), Bst TRAP₁₂ ∆71 (middle), or Bst TRAP₁₁ (right). Each experimental dataset (colored) is superimposed with a simulated mass spectrum obtained from best‐fit parameters to the nearest‐neighbor model (grey). Cooperativity is quantified by the parameter α, which is the ratio of the association constant for binding to sites with one bound neighbor, and no bound neighbors (K _N1/K ₀; Figure 2a). Bha TRAP₁₂ (left) shows the strongest cooperativity (α = 256, 1/K ₀ = 718 μM), with populations dominated by apo and holo rings. Cooperativity is moderate (α = 28, 1/K ₀ = 217 μM) in Bst TRAP₁₂ Δ71 (middle) and weak (α = 8, 1/K ₀ = 36 μM) in Bst TRAP₁₁ (right).TRAP, trp RNA‐binding attenuation protein

2.4. Differing extent of Trp‐Trp cooperativity is evident from population distributions in native MS titrations

Strikingly different population distributions were observed for Bha, Bst Δ71, and Bst TRAP in native MS titrations (Figure 4). For the Bha Trp _n ‐TRAP₁₂ titration, distributions were dominated by either Trp₀‐TRAP₁₂ (apo) or fully bound Trp₁₂‐TRAP₁₂ (holo) with minimal population of intermediate Trp _n ‐TRAP₁₂ states (Figure 4, left). Such a pattern is consistent with strong positive cooperativity (i.e., Figure 2b). Population distributions for Bst TRAP were similar to those previously described, ²⁰ with a high population of intermediate states consistent with weak cooperativity. The distributions for Bst TRAP Δ71 reflected an intermediate cooperativity between the Bst and Bha TRAP (Figure 4, middle). In contrast to the highly congruent CD and ITC titrations, the native MS titration data were quite divergent, implying distinctly different underlying thermodynamics.

Fitting of ligand‐dependent population distributions revealed strong cooperativity for Bha TRAP₁₂, moderate cooperativity for Bst TRAP₁₂ Δ71, and weak cooperativity for Bst TRAP₁₁. After correcting binding site concentrations using mass‐balance (see Section 5) the experimental Trp _n ‐TRAP₁₂ populations were fit with a binding polynomial corresponding to the NN model. For each dataset, we obtained good agreement between populations determined from integration of deconvoluted spectra, and those simulated from best‐fit thermodynamic parameters (Figure 4b, Table 1).

TABLE 1.

Best‐fit thermodynamic parameters for the NN model of Trp‐binding cooperativity for native MS titration data (room temperature ~ 25°C) ^a

Protein	ΔG N# (kcal mol−1)		1/K N# (μM) b		Cooperativity factor
	ΔG 0	ΔG 0 + ΔG α	1/K 0	1/(αK 0)	α
Bha TRAP12	−4.3 ± 0.1	−7.6 ± 0.2	720 ± 140	2.8 ± 0.8	256 ± 87
Bst TRAP12 ∆71	−5.00 ± 0.03	−7.0 ± 0.1	217 ± 13	7.8 ± 1.2	28 ± 5
Bst TRAP11	−6.1 ± 0.2	−7.3 ± 0.3	36 ± 12	4.4 ± 1.9	8 ± 5

Abbreviations: MS, mass spectrometry; NN, nearest‐neighbor; TRAP, trp RNA‐binding attenuation protein.

^a Thermodynamic parameters from global fitting of titration data to the nearest‐neighbor model, with free energy changes for binding to sites with 0, or 1 occupied neighbors ΔG _N0, and ΔG _N1 = ΔG ₀ + ΔG _α , respectively. Values are best fit parameters, while uncertainties are standard deviations from three datasets. Standard deviation was calculated between replicates.

^b Dissociation equilibrium constants are the reciprocal of the corresponding association equilibrium constants.

The best fit parameter values obtained from the NN model (Table 1) were consistent with expectations from inspection of the population distribution shifts in the native mass spectra (Figure 4). Cooperativity in Bst TRAP yielded a mild eight‐fold increase in affinity for sites with one neighbor compared to no neighbors, α = 8, consistent with prior findings. ²⁰ Bha TRAP exhibited remarkably strong cooperativity, with a 256‐fold higher affinity for sites with one occupied neighbors, consistent with the observation of low abundance for partially loaded states throughout the titration (e.g., Figure 2b). Fits for the engineered 12mer, Bst TRAP Δ71 revealed intermediate cooperativity, α = 28, consistent with the mixed population distributions of partially and fully loaded states (Figure 4). Thus, the native MS experiments, coupled with statistical thermodynamic modeling enabled an accurate description of the thermodynamics of Trp‐TRAP binding for variants with cooperativity values differing by a factor of 32 (=256 ÷ 8).

2.5. Microscopic parameters predict macroscopic behavior

Typical methods used for measuring bound fractions (e.g., CD, ITC) yield an average signal that is obtained from all extant micro‐states and populations, whereas the NN statistical thermodynamic models can define the populations of each individual micro‐state. To compare the bulk observable and predicted populations, we simulated macroscopic properties of population distributions of individual protein micro‐states over a range of ligand concentrations using the NN model and microscopic parameters obtained from fitting the native MS data (Figure 5a,b). These simulations show good agreement between the MS and solution experiments. Discrepancies were largest for the Bha TRAP data, whereas they were arguably within experimental error for Bst and Bst Δ71 TRAP.

FIGURE 5.

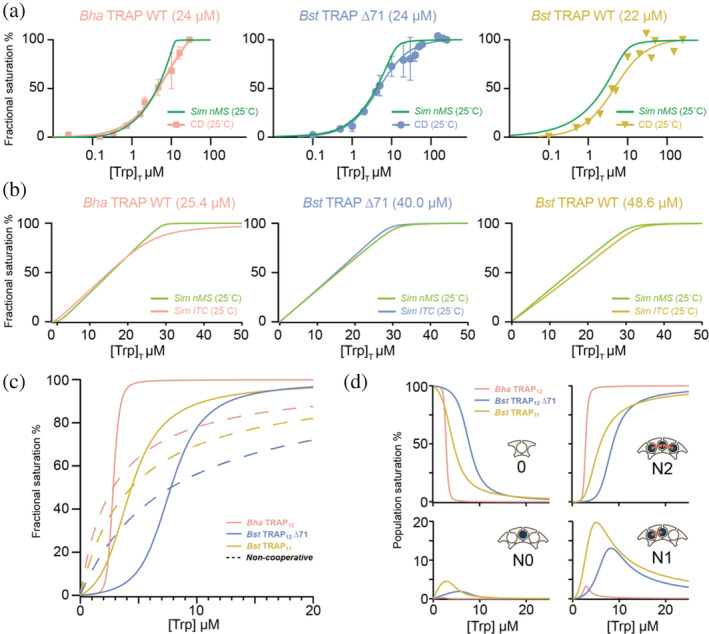
Prediction of macroscopic behavior from microscopic parameters from the NN cooperativity model. (a) Simulated native MS bound fraction from nearest‐neighbor parameters (green) and experimental CD signal change (at 228 nm) at the indicated Trp‐binding site concentrations. (b) Simulated native MS bound fraction nearest‐neighbor parameters (green) and computed ITC fractional saturation curves based on phenomenological model parameters ΔG and n (Table S2). Simulations used thermodynamic parameters from native MS at room temperature, and temperature and concentrations used in CD and ITC experiments. (c) Simulated mean site occupancy of TRAP proteins over a range of ligand concentrations [Trp]. Bha TRAP₁₂ (pink) features a sharp change from almost empty to near complete saturation over the range [Trp] of 2–3 μM. Bst TRAP₁₁ (yellow) and Bst TRAP₁₂ ∆71 (blue) have more gradual saturation curves due to their weaker cooperativity. Saturation curves with the same apparent K _D values in the absence of Trp‐Trp cooperativity are shown by dashed lines. (d) Population evolution for the four distinct nearest neighbor binding configurations as a function of [Trp]: (1) empty sites (0), (2) bound sites with no bound neighbors (N0), (3) bound sites with one bound neighbor (N1), and (4) bounds sites with two bound neighbors (N2). The strong cooperativity in Bha TRAP₁₂ (pink) makes N2 the most dominant bound configuration through the range of concentrations. Weaker cooperativity in Bst TRAP₁₁ (yellow) and Bst TRAP₁₂ ∆71 (blue) allows significant populations of N0, N1, and N2 states over the concentration range. The concentration of populations with adjacent bound ligands can be understood to affect the protein's regulatory response. CD, circular dichroism; ITC, isothermal titration calorimetry; MS, mass spectrometry; TRAP, trp RNA‐binding attenuation protein

Cooperative behavior in ligand binding is often recognized from sigmoidal isotherms that correlate fractional saturation and free ligand concentration. To approximate this behavior, we simulated fractional saturations over various free Trp concentrations [Trp] (Figure 5). The cellular concentration of TRAP protein rings in B. subtilis cells has been estimated at ~80 nM (0.9 μM Trp‐binding sites), ⁴¹ while cellular Trp concentrations have been measured in the low micromolar range. ⁴² Thus, simulations were performed with a binding site concentration of 1 μM and [Trp] to 20 μM. Compared to experimental titrations which monitor response to total ligand concentration (Figure 5), we see the expected sigmoidal curves predicted for positive cooperativity. Despite 20‐fold differences in intrinsic affinities K ₀, the apparent affinities fall in a relatively narrow range between ~2 and 8 μM, consistent with those measurements.

We briefly extended the analysis to consider the activation of TRAP for RNA binding. TRAP binds RNA in a Trp‐dependent manner, while several binding elements in a single ring are required to achieve high affinity RNA binding. ⁴³ , ⁴⁴ To approximate this behavior, we separately compute bulk saturation and the relative abundance of the four basic nearest‐neighbor states (empty sites 0, sites with no bound neighbors N0, sites with 1 bound neighbor N1, and sites with two bound neighbors N2) as a function of free ligand concentration [Trp] (Figure 5d). Consistent with the bulk parameters for Bha TRAP (Figure 5c), populations of empty sites drop off steeply in exchange for sites with two bound neighbors, whereas for Bst and Bst Δ71 TRAP states with one bound neighbor become significantly populated. This behavior can be expected to affect the trajectory of Trp‐dependent RNA binding.

3. DISCUSSION

3.1. Statistical thermodynamic nearest‐neighbor models can readily predict complex ligand behavior in cyclic oligomeric proteins

We used a statistical thermodynamic approach to model the binding of ligands to symmetric ring‐shaped homo‐oligomeric proteins. By applying NN circular lattice model, we generated partition functions corresponding to the 2 ^N possible liganded states of 12mer and 11mer TRAP rings (Equation (2)). In this model, the Trp‐binding sites are arranged on a rigid protein ring, while flexible loops gate access to the binding sites. In their flexible ligand‐free states, there is little structural coupling between adjacent sites. Binding of a Trp ligand rigidifies the loops that sandwich its site, resulting in structural, dynamic, and thermodynamic propagation to its adjacent sites (Figure 1d). The model thus enables probabilistic description of a statistically complex ensemble of liganded states using only two microscopic parameters: the intrinsic affinity of a site K ₀, and the site–site coupling term α. This parsimonious model allowed us to compute the probability distributions of these states as a function of ligand concentration for a range of cooperativity strengths (Figure 2). Population distributions of states with zero to n bound ligands are revealed to be much more sensitive to the underlying microscopic thermodynamic parameters than the bulk metric of fractional saturation. The ability to measure more directly those underlying population distributions can enable us to decipher mechanisms and magnitudes of cooperativity.

3.2. Native MS can directly quantify populations of states with 0 to n bound ligands, informing mechanistic binding models

For each of the homo‐oligomeric protein variants examined here, native MS enabled us to resolve and quantify populations of oligomers with 0 to n bound ligands (Figure 4). These data showed clear and distinct ligand concentration‐dependent population shifts, reminiscent of the population distributions simulated with NN statistical thermodynamic models. Population distributions in each titration series could be fit accurately with binding polynomial derived from this model, yielding thermodynamic parameters that quantify the affinity of a ligand for isolated sites, K ₀, and coupling terms that quantify the allosteric thermodynamic communication between sites ΔG _α (Table 1). For Bst TRAP this coupling energy was −1.2 ± 0.3 kcal mol⁻¹ interaction⁻¹, resulting in an eight‐fold higher affinity for binding sites with one occupied neighbor compared to isolated sites, while for Bha TRAP a stronger coupling energy of −3.3 ± 0.2 kcal mol⁻¹ interaction⁻¹ results in a 256‐fold higher affinity. In contrast, conventional ligand‐binding measurements by spectroscopic and calorimetric methods (Figure 3) failed to clearly distinguish magnitudes of allosteric coupling. Although the population distributions are strikingly different for the three proteins, bulk properties computed from these distributions were in fact similar, suggesting that the native MS measurements have the unique power to resolve underlying population shifts hidden when averaging over all micro‐states.

3.3. Implications for understanding of TRAP function

TRAP proteins have evolved to regulate expression of the trp operon in response to changing levels of free Trp. Although the TRAP protein sequence is highly conserved, ⁴⁵ disparities exist between proteins from organisms that inhabit vastly different environment conditions (i.e., Bst—a thermophile, Bha—a halophile), in the encoding of the transacting protein factor anti‐TRAP (AT), ⁴⁶ where the fully transcribed leader possesses sequences capable of preventing ribosome binding to the Shine‐Dalgarno sequence, ²⁹ and in their predominant oligomeric states. ⁴⁷ , ⁴⁸ In the three proteins studied here, two 12mers and an 11mer, we observed orders of magnitude differences in Trp‐Trp homotropic cooperativity. The origins of these differences merit additional characterization, but it is tempting to speculate that tighter packing of the otherwise isosteric protomers ²⁷ results in stronger coupling between sites. Nevertheless, apparent overall affinities of Trp for Bha and Bst TRAP were similar, possibly reflecting similarities in the fluctuating concentrations of Trp in bacterial cells.

3.4. Limitations

The combination of statistical thermodynamic modeling and native MS to extract and quantify allosteric parameters from the partition function is powerful but has limitations. The most obvious is that while NN mechanistic models can be readily envisioned for lattices in which NN interactions can be expected to be dominant, such as symmetric ring‐shaped proteins, it is less straightforward to develop such models for hetero‐oligomeric proteins, or homo‐oligomers with non‐cyclic symmetry elements (e.g., double‐rings like GroEL ⁴⁹ and the proteosome ⁵⁰ ). Another limitation has to do with the degeneracy of liganded states: for example, for the NN model, the populations of 12mers with six bound ligands convolve 924 individual configurations with the same mass distributed among six distinct statistical weights (Equation (2)); the abundance of species with six bound ligands does not distinguish between configurations. Thus, it is likely that other models of cooperativity, including MWC‐like mechanisms, could provide similar population distributions. Other limitations have to do with the measurements themselves: solution conditions suitable for high resolution native MS typically deviate from the physiological and from solution conditions typical for in vitro biochemical measurements; such deviations could result in context‐dependent populations. Moreover, even when native MS‐friendly solutions do not perturb populations of states, care must be taken to ensure that ion detection mirrors the populations of states in the solution, avoiding or correcting for differences in ionization efficiencies of different microstates, differences in transmission efficiencies of different ions through the mass spectrometer, or due to potential for dissociation of ligands during ionization and transmission. ²² , ⁵¹ , ⁵² The native MS measurements showed that purified TRAP proteins exhibit additional states, including double‐rings and numbers of protomers, and possessed proteoforms (Figures S7 and S8). These factors could introduce competing equilibria that complicate efforts to quantify major‐state populations in different bound states; of course, such factors would also skew traditional binding measurements that are simultaneously blind to their presence. Nevertheless, with rapidly improving technology for the analysis of proteins by native MS, its combination with statistical thermodynamic models has tremendous potential to advance our understanding of mechanisms of regulation.

4. CONCLUSIONS

Deciphering mechanisms of allosteric communication between ligand‐binding sites in oligomeric proteins is difficult. One serious challenge is that for most biophysical measurements the proportionality between the measured signal and populations of liganded states can be distorted by the very property of interest (i.e., allosteric coupling). As an analytical tool, native MS has the advantage that the signal does not suffer from this confounding effect—the mass unambiguously tells us the number of bound ligands. If the intensity of each signal is proportional to its population, we have an accurate measurement of the underlying distribution of states. Armed with such information, one is then in the position to design and test mechanistic models of site‐site communication. In favorable cases, the result can be an understanding of the thermodynamic quantities exchanged between binding sites. These microscopic thermodynamic parameters provide a genuine basis for establishing the structure–thermodynamic relationships responsible for thermodynamic coupling and biological regulation.

5. MATERIALS AND METHODS

5.1. Protein preparation

Three TRAP variants were prepared for these studies: Bha TRAP, which forms predominantly 12mers, Bst TRAP, which forms predominantly 11mers, and Bst TRAP‐Δ71, which forms predominantly 12mers. ²⁷ , ²⁸ Lacking genetically encoded Trp, and bearing only two tyrosines, the proteins share the same low protomer extinction coefficient (ε = 2,980 M⁻¹ cm⁻¹) at 280 nm as predicted using ProtParam (https://web.expasy.org/protparam/). Protein concentrations were determined using a Nanodrop 2000c spectrophotometer (Thermo Scientific) in droplet mode.

To produce Bha TRAP (WP_010897809.1), the coding region for the wild‐type protein, in the pET17b plasmid (Novagen), ²⁹ was modified by the insertion at the C‐terminus of sequences encoding the TEV protease cleavage site (ENLYFQ/G) followed by six histidine residues (a His‐tag); after removal of the His‐tag, the resulting protein consists of ENLYFQ on C‐terminus (Figure S2B). Proteins were expressed in Escherichia coli BL21(DE3) cells and grown at 37°C in LB. At mid‐log phase (OD₆₀₀ = 0.4–0.6), 0.5 mM IPTG (isopropyl β‐d‐1‐thiogalactopyranosid) was added for induction of protein expression. Cells were harvested by centrifugation at 5,000g for 5 min, resuspended in lysis buffer (500 mM NaCl, 20 mM NaPi, 100 mM imidazole, pH = 7.4, 1 mM benzamidine, 1 mM PMSF [phenylmethylsulfonyl fluoride]), and lysed in a French pressure cell at 10,000 psi. The lysate was centrifuged at 30,000g for 20 min and filtered (0.45 μm cellulose acetate filters, Advantec) before loading onto 1 mL HisTrap™ HP nickel column (GE Healthcare) on an AKTA fast protein liquid chromatography (FPLC) system. His‐tagged Bha TRAP WT protein was eluted with an imidazole gradient from 100 mM to 1 M in elution buffer (0.1–1 M imidazole, 500 mM NaCl, 20 mM NaPi, pH = 7.4). The pooled protein sample was dialyzed into buffer A (100 mM NaCl, 50 mM NaPO₄, pH 8.0) and treated with TEV protease at a mass ratio of 100:1 to cleave the C‐terminal His‐tag. The protease‐treated fraction was then reloaded onto the 1 ml HisTrap™ HP nickel column (GE Healthcare) and eluted with lysis buffer and the flow‐through fraction collected. To remove bound Trp, protein was denatured by dialysis for more than 6 hr at room temperature in a 3.5 kDa cut‐off dialysis tubing membrane (Spectrum Labs) against 6 M guanidinium hydrochloride (Gdn‐HCl) in buffer A. The fraction was then filtered using a 25 mm minisart® syringe filter (pore size: 0.2 μm, Sartorius) and further purified using reversed‐phase high‐performance liquid chromatography (RP‐HPLC) on a 250 × 10 mm Proto 300 C4 column (Higgins Analytical) as previously described. ³⁰ The resulting protein fractions were lyophilized and stored at −80°C until needed. The protein was refolded by dissolving the lyophilized pellet in 6 M Gdn‐HCl buffer A at a concentration of ~1 mg ml⁻¹, and gradually refolded by sequential dialysis against 3 M, 1.5 M, 0.75 M, and 0 M Gdn‐HCl in buffer A in 3.5 kDa cut‐off dialysis membrane (Spectrum Labs) for 12 hr per round at room temperature. The refolded protein was then purified by size‐exclusion chromatography using a Hiload™ 16/600 Superdex™ 75 pg column (Sigma‐Aldrich) in buffer A.

The gene of Bst TRAP WT (WP_033013997.1) and the C‐terminal‐five‐residue‐truncated Bst TRAP Δ71 were expressed from pET17b and pET9a vectors (Novagen, Inc.), respectively, as previously described. ²⁰ , ²⁷ The proteins were separately expressed in E. coli BL21(DE3) cells, grown at 37°C in LB, and induced at OD₆₀₀ = 0.4–0.6 with 0.5 mM IPTG. Cells were harvested by centrifugation, resuspended in lysis buffer B (100 mM K₂HPO₄, 50 mM KCl, 1 mM EDTA, pH = 8.0) plus 1 mM benzamidine and 1 mM PMSF (phenylmethylsulfonyl fluoride). The cells were broken in a French pressure cell at 10,000 psi. The lysate was clarified by centrifugation at 30,000g for 25 min. For every 5 ml of supernatant, 1 ml of 2% protamine sulfate was added. Then the lysate was stirred on ice for 30 min. The lysate was centrifuged at 30,000g for 25 min and the supernatant was heated to 80°C for 10 min followed by another centrifugation at 30,000g for 25 min. The supernatant was then dialyzed overnight against 50 mM Tris–HCl (pH = 8.0). Dialyzed proteins were loaded on Mono Q™ 10/100 GL column (GE Healthcare) in 50 mM Tris–HCl (pH 8.0). Proteins were eluted with a salt gradient from 0 to 1 M NaCl in 50 mM Tris–HCl (pH 8.0). The same protocol and buffers described above were used to remove Trp and refold proteins to obtain apo (ligand‐free) proteins, except that the 0.75 M Gdn‐HCl dialysis step was omitted during refolding, and that RP‐HPLC purified Bst TRAP Δ71 was refolded at 55°C instead of at room temperature.

5.2. Circular dichroism

Tryptophan binding to TRAP was measured by CD spectroscopy at 25°C using a JASCO model J‐715 spectropolarimeter with cell path length of 1 mm. Spectra were recorded between 226 nm and 230 nm using ~24 μM TRAP protomers (~2 μM ring) in 50 mM sodium phosphate buffer, pH 8.0, in the presence of increasing concentrations of Trp (0–300 μM). The change in CD signal at 228 nm, which shows the maximal difference between spectra of apo‐ and Trp‐liganded TRAP, was used as a measure of tryptophan binding. ³¹ The change in CD signal was fit with the quadratic single‐site binding equation (Equation (1)).

5.3. Isothermal titration calorimetry

RP‐HPLC‐purified, refolded, and SEC‐purified TRAP proteins were dialyzed extensively against buffer A. A stock solution of tryptophan was prepared by dissolving L‐Trp powder (Sigma Aldrich, 93,659) in the dialysate. Trp concentration was determined from its extinction coefficient at 280 nm of ε = 5,540 M⁻¹ cm⁻¹ using a Nanodrop 2000c spectrophotometer (Thermo Scientific) in droplet mode. The measured concentrations of Trp in the syringe and of TRAP protomers in the cell were 293 μM and 23 μM for Bha TRAP, 433 μM and 38 μM for Bst TRAP Δ71, and 645 μM and 74.7 μM for Bst TRAP WT, respectively. ITC thermograms were recorded on a MicroCal VP‐ITC (Malvern Instruments) at 25°C. A reference power of 30 μcal s⁻¹ and a stirring speed of 307 rpm were applied for all experiments. Deionized water was used in the reference cell. The software NITPIC was used to correct the baseline for each isotherm by iteratively optimizing the noise parameter wrmsd and then integrating the enthalpy at each titration point. ³² The integrated heats showed bimodal binding behavior for Bha TRAP, and single mode for Bst Δ71 and Bst TRAP. The integrated enthalpy data were then fit with two‐sites or one‐site binding models using itcsimlib. ⁵ TRAP oligomer concentrations were corrected assuming a stoichiometry of 1 Trp per protomer based on the fitted stoichiometry n; corrected concentrations were 25.4 μM for Bha TRAP, 40.0 μM for Bst TRAP Δ71, and 48.6 μM for Bst TRAP WT. Confidence intervals in fitted parameters were estimated from 200 bootstrapped samples.

5.4. Native mass spectrometry

Aliquots of purified proteins were dialyzed into 400 mM ammonium acetate (Sigma Aldrich, 431,311). For Bha TRAP and Bst TRAP Δ71, the pH was adjusted to pH 8 by adding ammonium hydroxide (~1 M NH₃ in H₂O, Sigma‐Aldrich). Dialyzed protein concentrations (~60 μM protomers) were measured as above (ε = 2,980 M⁻¹ cm⁻¹) at 280 nm using a Nanodrop 2000c spectrophotometer (Thermo Scientific) in droplet mode. The Trp was dissolved in 400 mM ammonium acetate and the Trp concentration was measured as above (ε = 5,540 M⁻¹ cm⁻¹) at 280 nm. ³³ Samples for each titration point were prepared freshly in parallel by mixing the dialyzed protein solutions with serial dilutions from a 1 M Trp stock solution to the indicated ligand concentrations (0–140 μM).

Native MS experiments were performed at room temperature (~25°C) on a Q Exactive Ultra‐High Mass Range (UHMR) Orbitrap mass spectrometer (Thermo Fisher Scientific) modified to allow for surface induced dissociation, similar to that previously described. ³⁴ Emitters were pulled from borosilicate filament capillaries (OD 1.0 mm, ID 0.78 mm, Sutter Instrument) in‐house on a P‐97 Flaming/Brown Micropipette Puller (Sutter Instrument) that is fitted with a thermometer placed near the heating element. The temperature near the heating element was stabilized below 30°C between each pull, and the same tip pulling parameters were used for each titration set. Each sample was loaded into an emitter using gel loading tips (Genesee Scientific, 0.5‐10 μl Ultra Micro Gel Tip) to avoid contamination, and then placed on a Nanospray Flex ion source (Thermo Fisher Scientific) equipped with a platinum wire to allow for static nano electrospray ionization. To obtain a stable total ion current, the spray voltage was initially ramped to about 1.4 kV and then gradually decreased to between 0.6–0.9 kV and held constant. For all measurements, the following instrument tune settings were kept constant: capillary temperature 250°C, Source DC Offset 21 V, S‐lens RF level 200, detector optimization to low m/z, ion transfer target high m/z, injection flatapole DC 5 V, inter flatapole lens 4 V, bent flatapole DC 2 V, transfer multipole DC 0 V, C‐trap entrance lens inject 1.8 V, HCD energy 1 V, HCD field gradient 200 V, and HCD cell pressure 4 (UHV Sensor ~3−4E‐10 mbar). For most emitters, spectra were collected at resolutions of 6,250, 12,500 and 25,000, as defined at 400 m/z. Each spectrum was obtained by averaging the same number of scans, and the injection time and averaged micro‐scans were fixed. For Bha TRAP and Bst TRAP Δ71, each titration point was recorded three times using different emitters. For Bst TRAP, two sets of spectra were obtained from different time points from a single emitter, and the third sample from a different emitter.

Data were manually examined using Xcalibur Qual Browser software (Thermo Fisher Scientific), and spectral deconvolution was carried out using UniDec. ³⁵ For quantification of Trp _n ‐TRAP _m populations, all spectra from each titration set were initially deconvolved using MetaUniDec V4.4 and then later each spectrum was reprocessed using UniDec V5.0.1 to allow for the double deconvolution approach to be used to produce deconvolved zero‐charge mass spectra where the proteoforms found in the apo TRAP spectrum from each titration are combined. ³⁶ , ³⁷ The titration spectra collected at a resolution of 12,500 were used for the final deconvolutions. Custom deconvolution parameters were used for each protein titration set. For all sets, UniDec parameters were adjusted to a narrow m/z range around the dominant oligomer charge state distribution, the charge range was set to less than 11 charges surrounding the most abundant charge state; mass sampling was set every 1 Da, FWHM (full width at half maximum) was set to 0.8 Th, peak shape function was set to split Gaussian/Lorentzian; artifact suppression, point smooth width and mass smooth width were set to 0; charge smooth width was set to 1.5, native charge offset range was set to ±6, and m/z to Mass transform was set to interpolate. A Mass List Window width of ±1,200 Da was used. A mass list for each protein was generated based on the protein mass, oligomeric state N, and 0 to N bound tryptophan. For Bst TRAP and Bst TRAP Δ71 this list consisted of the expected 11mer and 12mer oligomeric states, respectively, with variable Trp. For Bha TRAP, we found that in addition to the expected 12mer, minor overlapping signals from trace amounts of a 13mer were present, so the mass list was set to include those species. The respective deconvolved apo TRAP zero‐charge mass spectrum was used as the double deconvolution kernel file. The areas for each species in the deconvolved spectra were extracted, sum normalized, and used for the model fitting. The area extraction window was set to ±2 times the standard deviation. The standard deviation was determined based on the average FWHM of the deconvolved apo and holo peaks using the simplified equation where FWHM divided by 2.35 equals the standard deviation.

Accurate determination of protein concentration is complicated for TRAP proteins because they lack encoded Trp residues and have low extinction coefficients, while a 5–10% error in concentration translates to ±1 site for an 11–12 mer protein. Before thermodynamic analysis of the MS titration data, protein concentrations were corrected by fitting the bound fraction at each Trp concentration with the quadratic independent sites model; [L]_T was assumed to be accurate, while [M]_T and the apparent dissociation constant K _D were fit parameters. ²⁰ This fit yielded the binding site concentration [M]_T that was in general about 33% higher than initial estimated concentration (Table S3, Figure S6).

5.5. Fitting of population distributions with the NN model

Following TRAP concentration correction, experimental data obtained from native MS were fit using a NN model for 12 binding sites via itcsimlib ⁵, as described previously. ²⁰ Briefly, the relative abundance of Trp‐TRAP species (0–12 bound, 13 total liganded states) was determined from the integrated peak areas; because Trp binding in excess of the available sites is not observed, we did not consider the possibility of non‐specific binding of Trp to TRAP. To fit this population distribution, the NN model was parametrized with values for ΔG ₀ (intrinsic binding free energy) and ΔG _α (binding‐free energy with an occupied neighbor). A binding partition function that includes all possible Trp _n ‐TRAP₁₂ configurations (2¹² = 4,096) was generated using itcsimlib. The statistical thermodynamic probabilities of each configuration were then computed at each experimental ligand and binding site concentration. The probabilities of each of 4,096 configurations were summed and converted into the relative abundance of the 13 Trp‐TRAP species, permitting generation of a virtual titration dataset. Then the discrepancy between native MS experimental titration data and the virtual titration data was globally minimized by iteratively varying the parameters of ΔG ₀ and ΔG _α using a Powell ³⁸ gradient‐descent optimization algorithm. Uncertainties in fit parameters were obtained from the standard deviation of three independent experimental repeats.

5.6. Population simulations with NN models

Simulated population distributions for 12‐mer proteins were computed using NN statistical thermodynamic models, with the same ΔG _N2 = −7.5 kcal mol⁻¹ (binding‐free energy with two occupied neighbors) but varied NN cooperativity factor α, and therefore different ΔG ₀ (intrinsic binding free energy). ⁵ In the NN model, given ΔG ₀ and ΔG _α values, the statistical thermodynamic probability of each of Trp _n ‐TRAP₁₂ configuration (2¹² = 4,096), along with the probabilities of the four basic NN energy configurations (0, N0, N1, N2) were computed over a range of 280 ligand concentrations using itcsimlib. ⁵ From these trajectories we computed fractional saturation curves by summing the three ligand‐bound states, N0, N1, and N2, as a function of free ligand concentration [L] (Figure 2c; Figure S3). The relative abundance of species with 0–12 bound Trp was used to simulate Gaussian peak shapes for each state (Figure 2b). To obtain apparent Hill coefficients, the resulting trajectories were fit using the Hill equation, $Y=\frac{{\left[\mathrm{L}\right]}^h}{{\left[\mathrm{L}\right]}^h+K_{\mathrm{d},\mathrm{app}}^h}$, where h is the Hill coefficient and K _d,app is the apparent equilibrium dissociation constant.

AUTHOR CONTRIBUTIONS

Weicheng Li: Conceptualization (equal); formal analysis (equal); methodology (equal); software (equal); visualization (equal); writing – original draft (equal); writing – review and editing (equal). Andrew S. Norris: Conceptualization (equal); data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); validation (equal); visualization (equal); writing – review and editing (equal). Katie Lichtenthal: Conceptualization (equal); data curation (equal); investigation (equal); resources (equal); validation (equal). Skyler Kelly: Data curation (equal); investigation (equal); resources (equal). Elihu C. Ihms: Conceptualization (supporting); methodology (supporting); software (equal). Paul Gollnick: Conceptualization (equal); project administration (equal); resources (lead); supervision (equal). Mark P. Foster: Conceptualization (equal); data curation (equal); formal analysis (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (equal); software (equal); supervision (equal); validation (equal); visualization (equal); writing – review and editing (equal).

FUNDING INFORMATION

This work was supported by National Institutes of Health (NIH) grants R01 GM120923 (to Mark P. Foster and Paul Gollnick), R01 GM077234 (to Mark P. Foster and Paul Gollnick), and P41 GM128577 (to Vicki H. Wysocki).

Supporting information

Appendix S1 Supporting Information

Li W, Norris AS, Lichtenthal K, Kelly S, Ihms EC, Gollnick P, et al. Thermodynamic coupling between neighboring binding sites in homo‐oligomeric ligand sensing proteins from mass resolved ligand‐dependent population distributions. Protein Science. 2022;31(10):e4424. 10.1002/pro.4424

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.