Summary
The hippocampus is implicated in memory formation, and neurons in the hippocampus take part in replay sequences that have been proposed to reflect memory of explored space. By recording from large ensembles of hippocampal neurons as rats explored various tracks, we show that sustained replay appears after a single experience. Further, we found that with repeated experience in a novel environment, replay slows down, taking more time to traverse the same trajectory. This effect was dependent on experience, not passage of time, and was environment-specific. By investigating the slow gamma (25–50Hz) hover-and-jump dynamics within replays, we show that replay slows by adding more hover locations, increasing the resolution of the behavioral trajectory. We provide evidence that inhibition and cortical engagement both increase as replay slows. Thus, replays can reflect single experiences, and evolve with re-exposure, in a manner consistent with the encoding of greater detail into replay memories with experience.
eTOC blurb
By recording from large ensembles of hippocampal neurons as rats explored various tracks, Berners-Lee et al. find that sustained replay appears after a single experience. Further, with repeated experience on a novel track, replay slows down, taking more time to traverse the same trajectory.
Introduction
How quickly is the memory of a new place stored in the brain, and how is that memory modified upon re-exposure to the same place? These questions are particularly relevant for the hippocampus (HP), which is implicated in both the representation of space (O’Keefe and Nadel, 1978) and the formation of memory (Scoville and Milner, 1957; Morris et al., 1982). Hippocampal neurons are known as place cells because their responses are spatially localized within “place fields” as the animal moves around an environment. These place field responses have been a natural focus for questions about memory formation (Wilson and McNaughton, 1993; Mehta, Quirk and Wilson, 2000; Frank, Stanley and Brown, 2004). However, the interpretation of place field responses is complicated by the fact that the stimuli and behaviors associated with the place must be present for the place cell to generate the response. Here we consider instead a probe of memory in place cells that utilizes these cells’ remarkable capacity for activation outside of their place fields. Beginning just seconds after exploring space, HP place cells spike in sequences that depict the prior spatial experience on a speeded-up timescale (Nadasdy et al., 1999; Lee and Wilson, 2002; Foster and Wilson, 2006; Csicsvari et al., 2007; Karlsson and Frank, 2009; Gupta et al., 2010; but see Liu, Sibille and Dragoi, 2019 for an alternative perspective on the role of experience). This phenomenon, known as HP replay, offers an opportunity to monitor the development of place memories independently of the experiences during which they were encoded. We present here, to our knowledge, the first study of the rapid development of, and progressive changes to, the format of replay, in response to the repetition of individual experiences consisting of individual running laps along an initially novel linear track. Moreover, we differentiate between the various factors that might account for these changes such as the passage of time, or acquisition of experience in a different environment, or, the acquisition of experience in the current environment. Finally, we identify specific elements of replay associated with individual experiences, to reveal that the structure of replay is built up incrementally through the integration of distinct signatures of individual experiences.
There are reasons to expect that replays will develop rapidly in response to a novel environment. The HP is especially active in response to novelty (Larkin et al., 2014) and replay rates increase during and after exposure to a novel environment in a plasticity-dependent manner (Foster and Wilson, 2006; Cheng and Frank, 2008; Silva, Feng and Foster, 2015). However, even in experiments with novel environments, replays are usually studied only after animals have run dozens of trials. Where replay has been reported after a single trial (Foster and Wilson, 2006), the duration of the memory was not assessed beyond a minute-long stopping period. So, the one-trial development of lasting replay remains underexplored. Similarly, there are reasons to anticipate changes to replay upon re-exposure to the same places. Many aspects of HP activity change across laps on a novel track. More place fields appear on the track (Wilson and McNaughton, 1993), their shape changes (Mehta, Quirk and Wilson, 2000), neurons fire more (Frank, Stanley and Brown, 2004), coordination between HP place cells increases (Cheng and Frank, 2008), and compressed sequences of future positions emerge that align to the HP theta rhythm (~8Hz in the LFP) while the rat runs (termed “theta sequences”; Feng, Silva and Foster, 2015). Thus, with experience in a novel environment, there is increased activity, co-activity, and sequences during running that are on a timescale suitable for plasticity. However, whether the trajectory information depicted within replays changes due to experience has not been explored at an equally fine-grained temporal scale. For example, it is known that certain characteristics of replay can change day by day (Cheng and Frank, 2008), but it remains unknown whether and how replays change on a moment by moment basis. In particular, it remains to be determined whether, after re-exposure, replays repeat, replace or augment existing information contained within earlier replays.
Here we used high density tetrode recordings to monitor the spiking activity of up to hundreds of HP neurons simultaneously in freely moving rats exploring a novel environment, and measured the development of replay both upon initial exposure, and during repeated re-exposures. Our data reveal establishment of replay after a single experience, that can persist for at least an hour. We also find changes to replays after repeated experience, that augment the information in replay with representations of places that were not contained in the earlier replay patterns. In this way, replay memories evolve with experience, in a manner suggestive of the incorporation of greater detail with more experience.
Results
Replays appeared after a single experience
We analyzed data recorded from putative hippocampal (HP) neurons in 17 male Long-Evans rats as they ran back and forth on linear tracks, gaining different amounts of experience (number of rats in each experiment, and numbers of cells recorded simultaneously, listed in Table 1). To test whether replays occur after a single experience in a novel environment, we used the following behavioral design with four phases (Figure 1a): (I) Rats first rested on a familiar platform (Pre-rest; 29–64 minutes, mean 45) before (II) running 1–2 passes across a novel track (“Run 1”; 2 passes = 1 pass in each running direction = 1 lap). (III) They then rested again on the platform (“Rest”; 61–86 minutes, mean 71), after which (IV) they ran multiple passes on the track (“Run 2”; 40+ passes). Place fields were constructed from each cell’s spiking and the animal’s position, measured in phase II, using standard methods (Mehta, Barnes and Mcnaughton, 1997; Foster and Wilson, 2006; S Cheng and Frank, 2008; see Methods). Candidate replay events (lasting 100 – 500 ms) during either Pre-rest or Rest were detected as periods of elevated spiking across the population of recorded cells. Memoryless Bayesian position decoding was applied to each candidate replay event, using 2.5 cm position bins and 20 ms bins time bins (Figure 1b), again using standard methods (Davidson, Kloosterman and Wilson, 2009a; Silva, Feng and Foster, 2015) We constructed thresholds on two measures applied to each candidate event: the absolute weighted correlation between position and time during the event (which is a single score for each event using the posterior probabilities of all position-time combinations, see (Silva, Feng and Foster, 2015), and the maximum jump distance between the peak decoded position at successive time bins (also a single score for each event). For each of either Pre-Rest or Rest, we compared the number of candidate events passing both thresholds with a distribution of this same quantity based on 5000 shuffled data sets, generating a P value. Since any particular threshold value was arbitrary, we repeated this analysis for all combinations of all possible values of the two thresholds, to generate a matrix of P values for each rest period (eg Figure 1c).
Table 1.
Experiment details
| Experiment | Included data published previously | Included sessions not previously used in papers (in addition to any re-clusted or previously used data) | Figure | Sup. Figure | Rats | Sessions | HP PYR Neurons range (median) | Other Neurons range (median) |
|---|---|---|---|---|---|---|---|---|
| One lap | No | Yes | 1a–c, 4a–b | --- | 4 | 5 | 38–155 (133) | --- |
| Novel | Some data also used in (Feng, Silva and Foster, 2015; Silva, Feng and Foster, 2015) | Yes | 2, 3a–b, 5, 6. | 1, 4a–d, 5, 6, 7 | 7 | 39 | 21–115 (66) | --- |
| Familiar | Some data also used in (Pfeiffer and Foster, 2015) | Yes | 6a * | 2, 6 | 9 | 75 | 20–208 (101) | --- |
| Reward change | Data also used in (Ambrose, Pfeiffer and Foster, 2016) | No | --- | 3 | 6 | 38 | 55–208 (110.5) | --- |
| Remote | Re-clustered versions of data that was used in (Silva, Feng and Foster, 2015) | Yes | 3c–f | 4e | 8 | 20 | 16–112 (46.5) | --- |
| Remote w/rest | Same as “Remote” | Yes | 4c–d | 4f | 8 | 13 | 16–158 (46) | --- |
| Novel with Interneurons | Same as “Novel” | Yes | 7a–b | --- | 5 | 9 | 42–115 (74) | INT: 1–4 (1), 19 total |
| Grosmark et al. | (Grosmark, Long and Buzsaki, 2016) | No | 7c–d | --- | 4 | 5 | 48–120 (59) | INT: 13–20 (17), 82 total |
| Pre-frontal cortex | Data also used in (X Wu and Foster, 2014; Berners-Lee, Wu and Foster, 2021) | No | 7e | --- | 4 | 11 | 62–137 (79) | PFC: 7–25 (14), 158 total |
Combined with Novel
Figure 1. Replay after a single experience.
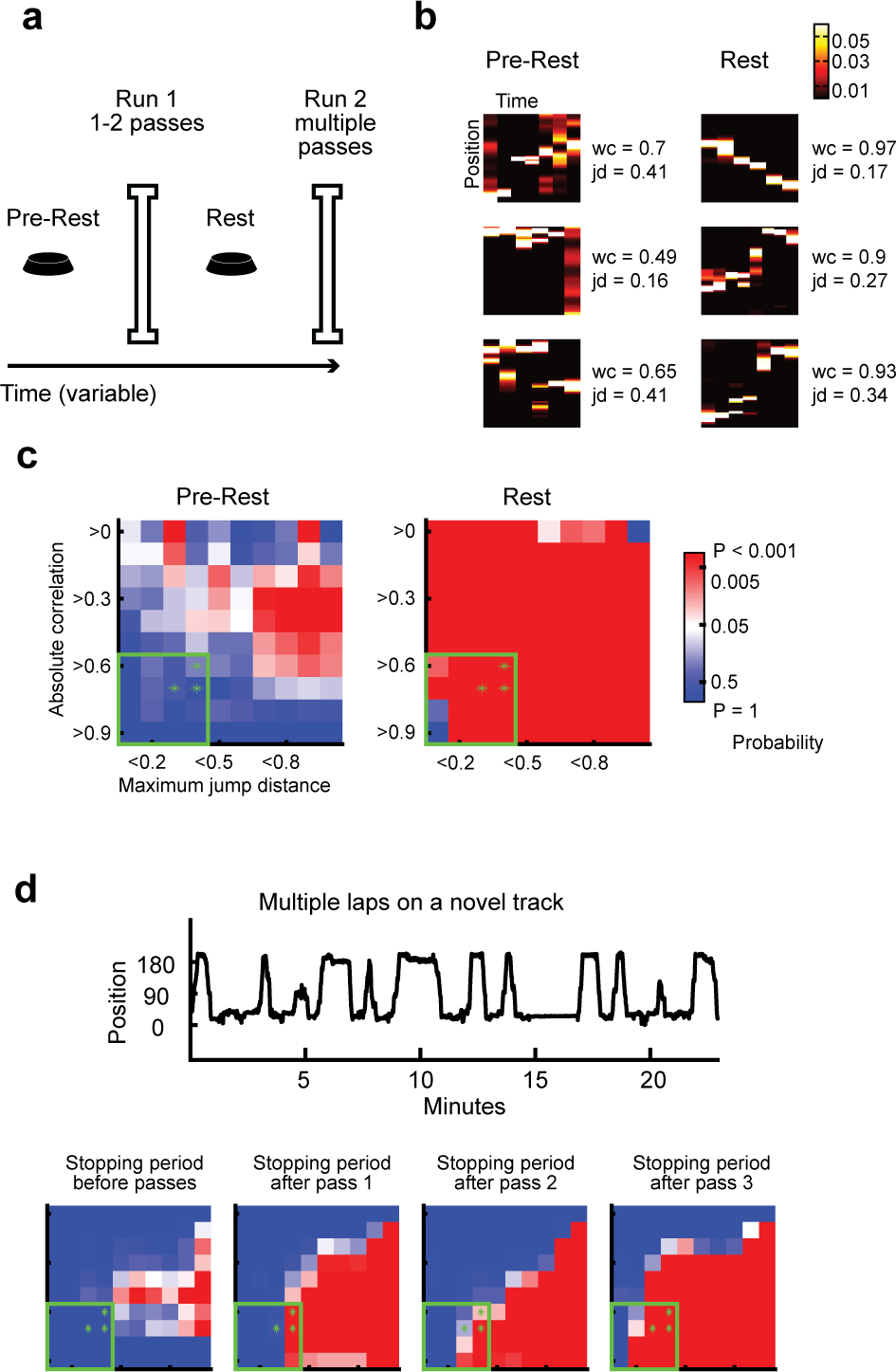
(a) Behavioral design: Rats rested on a small platform (Pre-rest) then ran 1–2 passes on a novel linear track (Run 1), then rested again on the platform (Rest), and subsequently ran on the same track for multiple passes (Run 2).
(b) From one example recording day, three replays during Pre-rest (left) and Rest (right), defined as follows: Of replays that crossed 40% of the track, replays were ranked by wc*(1-jd) and the top three were chosen. “wc” is absolute weighted correlation, “jd” is maximum jump distance (see Methods). Values for wc and jd shown on the right of each event.
(c) Significance matrices over parameter space generated by different combinations of wc and jd, over all recording days using the behavioral design of Figure 1a. Color bar shows probability values for all matrices in figure: blue values, insignificant (P > 0.05); red values, significant (P < 0.05); white, P = 0.05. P-values for the parameters denoted by the green asterisks, listed top-right to bottom-left: Pre-rest: P = 0.21, 0.73, 0.48; Rest: P = 2.0e-4, 2.0e-4, 2.0e-4. P-values cumulatively over all parameters in the green box: Pre-rest: P = 0.39; Rest: P = 2.0e-4. The selection of asterisk and box parameters followed that in (Silva, Feng and Foster, 2015)
(d) (Top) Alternative behavioral design: Example behavior from a recording session in which a rat ran multiple passes on a novel track (i.e. without the initial exposure depicted in Figure 1a). (Bottom) Significance matrices over all recording days using this behavioral design. P-values for asterisks, listed top-right to bottom-left : Stopping period prior to first pass: P = 1, 1, 1; Pass 1: P = 0.001, 2.0e-4, 0.6; Pass 2: P = 0.024, 8.0e-4, 0.13; Pass 3: P = 2.0e-4, 2.0e-4, 2.0e-4. Cumulative P-values for box: Stopping period prior to first pass: P = 1; Pass 1: P = 0.002; Pass 2: P = 0.006; Pass 3: P = 2.0e-4.
Visual comparison of the P value matrices for Pre-Rest and Rest periods (before and after the novel experience, respectively) revealed a much wider range of significant parameters in the post-experience Rest period (Figure 1c), and visualization of the highest scoring events from Pre-Rest suggested poor sequence quality compared to Rest (Figure 1b). We quantified these effects using a procedure described previously (Silva, Feng and Foster, 2015), which had established that random data, generated by the experimenter, produces significance in many regions of the P value matrix, thus exposing a danger of false positive results. The only reliably diagnostic part of the P value matrix (ie where random data did not produce significance) is a small region in the lower left corner, representing high correlations between position and time, concurrently with small steps between successively represented positions (green box, Figure 1c). We therefore applied this same analysis to our P value matrices, measuring mean P values across the diagnostic region, and also in the three particular edge cases close to the region border used in the previous study (green asterisks, Figure 1c). By all four measures, replay in the Pre-Rest period was not significant, while replay in the Rest period was highly significant. Thus, significant replay was detected during the >1 hour long Rest period, after only a single behavioral experience.
We also re-did these analyses equating either the number of events or time spent in both pre-rest and rest periods and still found that the pre-sleep period did not have a significant amount of replay (quadrant p-value matching the number of events P = 0.53, matching the time of the session P = 0.39) while there is still a significant amount of replay in post-sleep (P = 2.0 e-4 in each of the two control scenarios).
We also tested whether replays expressed on the track, known as local replays, appeared after single passes on a novel track. To do this we analyzed data from experiments where rats ran a full session (14+ passes) on a novel track. To enable comparison with the single lap study described above, for each stopping period on the track, we decoded replay as above but using spiking from only the immediately preceding or following lap to estimate place fields (preceding for passes >=1; following for the stopping period prior to the first pass). We did not observe replays when the rat was first placed on the track before exploring it (Figure 1d), however after only one pass across the track we observed a significant number of replays (Figure 1e). Thus, whether the rat remained in the same environment or was moved elsewhere, replays appeared after a single experience.
Replays slowed down with experience in a novel environment
Although replays appeared after a single lap, we hypothesized that the experience accrued over repeated passes might produce changes in replays on a novel track (Figure 2a). Indeed, replays were rapid when they appeared and then slowed across the first 14 passes, taking more time to make their way across the track (Figure 2a–c). Replays increased in duration across the first 14 passes (Figure 2d). Further, replays decreased in slope across the first 14 passes (Figure 2e). There were no changes in replay correlation or jump distance over this period (Figure S1a–b, all p ≥ 0.2) and any other significant changes we saw were unreliable (Figure S1c–l).
Figure 2. Replay slowed down across experience in a novel environment.
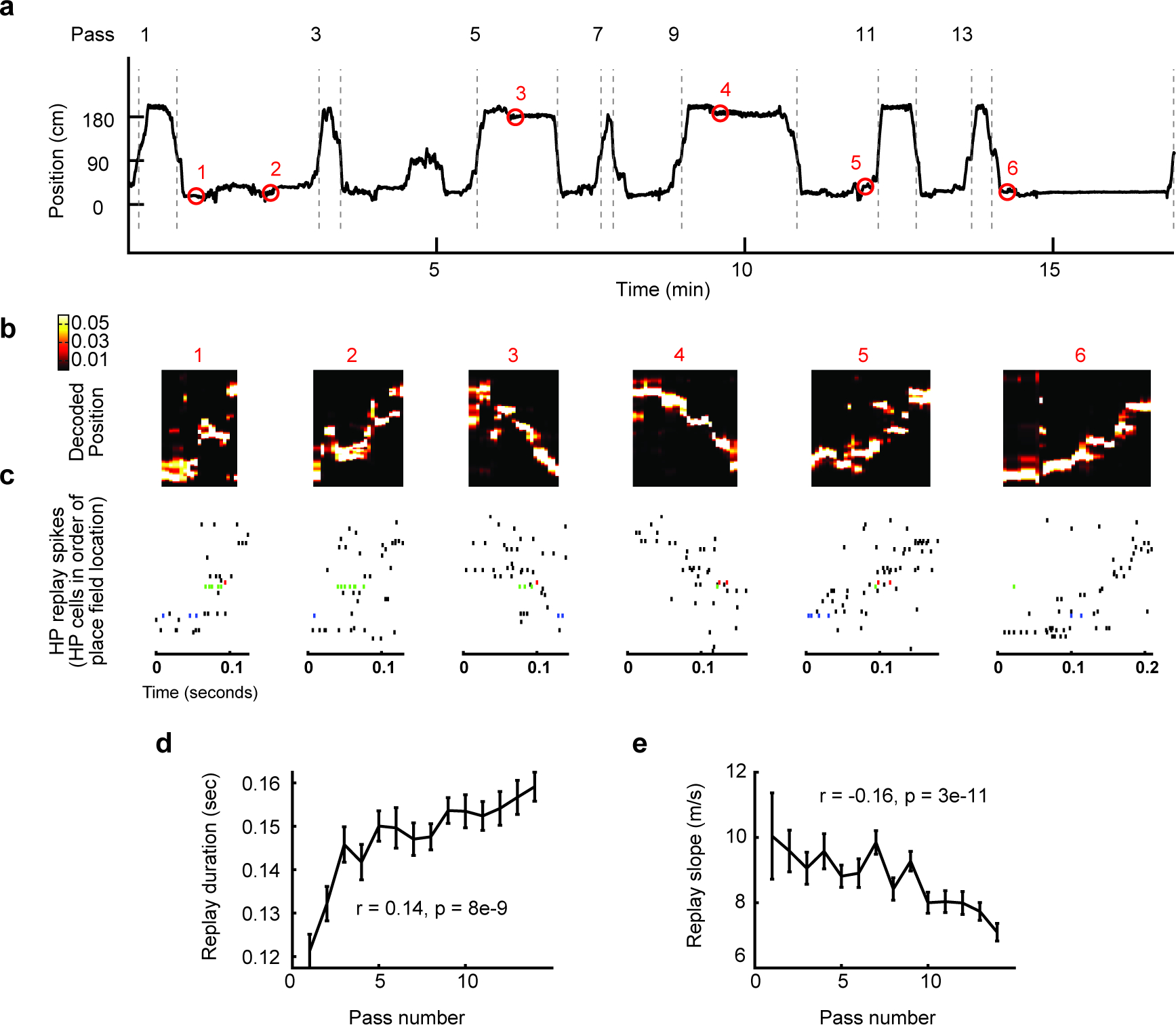
(a) Rat position (black line) as a function of time in one example recording session, in a novel environment. The first 15 passes and subsequent stopping periods are shown. Red circles indicate times and locations of replay events, highlighted in b.
(b) (Top) Decoded probability of position for the seven example replays in a. Colors indicate posterior probabilities, as in color bar (right). (Bottom) Matched with each replay, the spike rasters from all simultaneously recorded place cells, ordered by place field peak. Three neuron’s spikes are highlighted in blue, green and red.
(d) The duration of replay increased across the first 14 passes in novel environments (N = 1609, R = 0.14, P = 8e-9).
(e) The slope of replay decreased across the first 14 passes in novel environments (N = 1609, R = −0.054, p = 0.03). All error bars depict S.E.M., correlations are Pearson’s correlation values.
To test whether this effect was particular to novel environments, we also analyzed experiments where rats ran multiple-lap sessions on familiar tracks (defined as a track the rat had previously run at least one multiple-lap session). Changes in replay duration and slope were not observed on the familiar track, and the changes on the novel track were significantly greater than on the familiar (Figure S2). Additionally, we tested whether a novel change in the environment, such as a change in the reward landscape, could produce rapid replays. To test this we performed an experiment where rats ran on familiar track but the reward value had been changed on one end of the track, a manipulation that uniquely modulates reverse replays (Ambrose, Pfeiffer and Foster, 2016). This did not produce changes in duration or slope, and significantly differed from the effect of novelty (Figure S3).
Only local replays slowed down with experience
To test whether these changes in duration and speed on a novel track were unique to replays, we compared replays (Figure 3a, left) with non-replays (Figure 3a, right; defined as candidate events failing to pass the two thresholds that defined the green box in Figure 1c). Non-replay events did not slow down over passes, and differed significantly in this from replays (Figure 3b). Although non-replays exhibited a significant decrease in slope, the change across laps was significantly less than for replays (Figure S4). The significant change in slope in non-replays is likely due to our high criteria for replays. When we looked at only the non-replays with a weighted correlation of less than 0.4 and maximum jump distance of greater than 0.7 (the opposite quadrant to the green box in Figure 1) we found that they did not change in slope across passes (N = 355, R = −0.02, P = 0.7). Thus, replays of the current environment slowed down more than non-specific spike density events.
Figure 3. Slowing was specific to replay vs non-replay, and local replay vs remote.
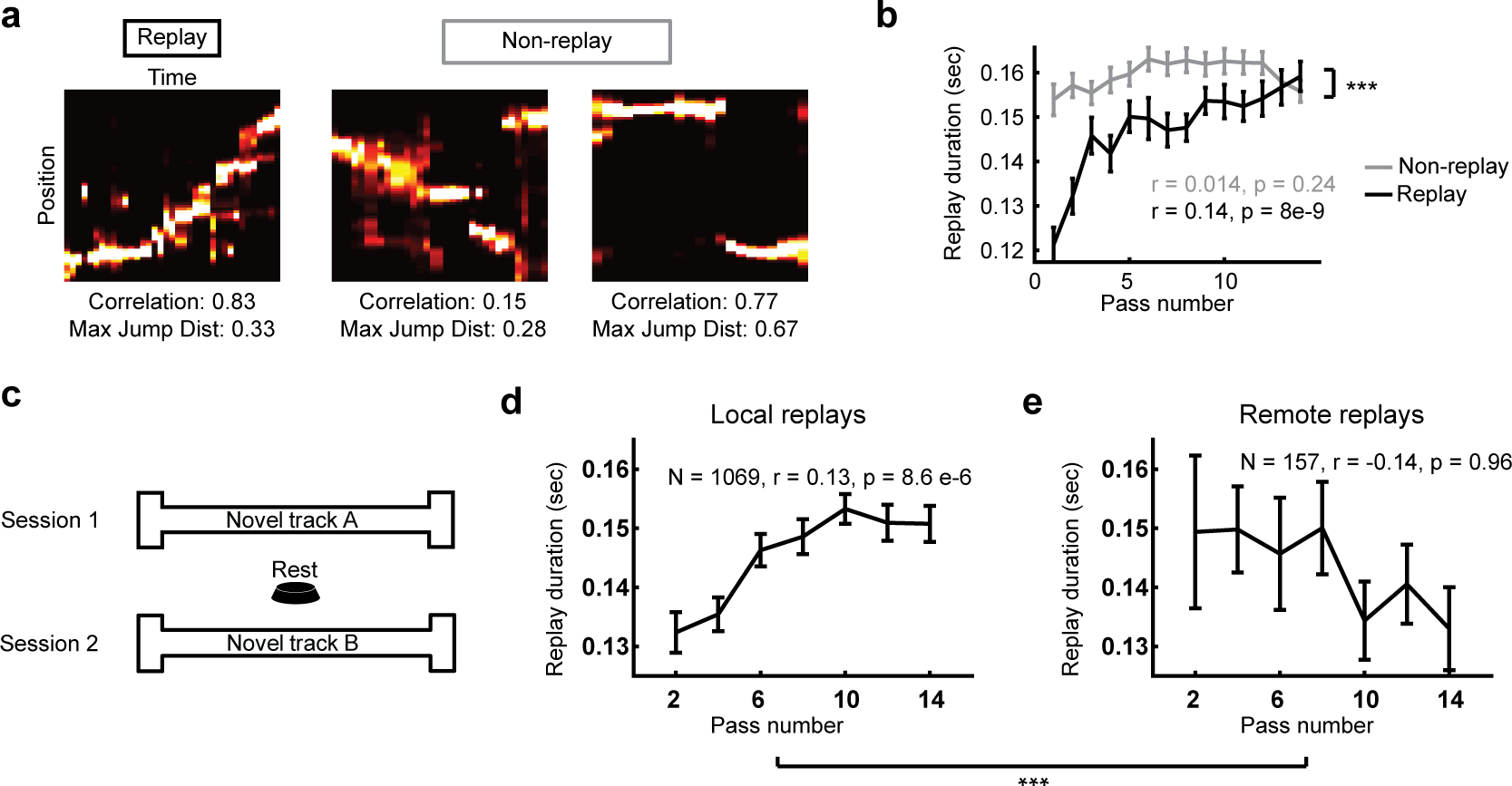
(a) Examples of a replay (left) and two non-replays (right; absolute weighted correlation > 0.6 and maximum jump distance < 40% of the track).
(b) The duration of replay across passes for all replays (black) and all non-replays (gray). Non-replays did not increase in duration (N = 6893, R = 0.014, P = 0.24). Two-way ANOVA between group and pass: main effect of group: F(1,8501) = 18.6, P = 1.7e-5, main effect of pass: F(1,8501) = 30.1, P = 3.3e-8, interaction: F(1,8501) = 10.9, P = 9.9e-4.
(c) Schematic of behavior for local vs non-local experiment: rats ran Session 1 on novel Track A, rested on a familiar platform, and then ran Session 2 on a different novel Track B.
(d) The duration of local replays increased with passes of the track (One-tail test: N = 1069, Duration: R = 0.13, P = 8.6e-6).
(e) The duration of remote replays of Track A did not increase with passes of Track B (One-tail test: N = 157, R = −0.14, P = 0.96). Two-way ANOVA local replay and remote replay: main effect of group P > 0.9, main effect of pass F(1,1225) = 5.3, P = 0.021, interaction: F(1,1225) = 10.3, P = 1.3e-3. Additionally, the duration of Track A replays at the end of session 1 was not different than at the beginning of session 2 (Session 1 local replays > 10 passes N = 856, Session 2 remote replays passes 1–4 N = 33; Wilcoxon rank-sum test, duration: P = 0.3). All data show mean ± S.E.M. Correlations are Pearson’s correlation values. *** P < 0.001, ** P < 0.02, * P < 0.05
To explore further the specificity of this effect, we tested whether remote replays of other environments slowed down while the rat gained experience in a new environment. To do this we analyzed data from experiments where we allowed rats to run on two different novel tracks (‘A’ and ‘B’, Figure 3c) with a rest session on a familiar platform in between. We found in this subset of data that local replays increased in duration (Figure 3d), and also, despite greater variability on trial 1, decreased significantly in speed (Figure S4). However, remote replays of Track A while the rat was on Track B did not slow down (Figure 3e, Figure S4), and comparison of local and remote replay revealed a significant difference (Figure 3e, Figure S4). Additionally, the duration and slope of Track B replays at the end of session 1 was not different than at the beginning of session 2. Thus, replays of the environment the animal was experiencing slowed down, while spike density events without trajectory information and replays of remote environments did not.
Time alone was not sufficient to slow replays down
We tested an alternative hypothesis of how replays slow down: an internal process put in motion by a novel experience that could also occur offline. We tested this for replay during a rest period following a single pass, and found that replays did not increase in duration during rest (Figure 4a,b). However, when the rat was placed back on the track that it had hitherto experienced only once, replay duration increased across passes, and this was significantly different to the preceding rest (Figure 4b). There was a corresponding trend for slope to decrease (Figure S4e). Additionally, we found a breakpoint in duration during the first pass of Run 2 when replay durations started to increase (Chow test, N = 508, duration: F = 14.3, P = 1.8e-4) that was significant compared to a shuffled distribution (P = 0.001). By contrast, neither the duration nor slope of replay changed between the end of Rest and the first four passes of Run 2 (Wilcoxon rank-sum test, Rest: N = 228, Run 2: N = 8, duration: P = 0.8, slope: P = 0.2). Thus, replays did not increase in duration after a single experience, but only with continued experience.
Figure 4. Slowing was due to experience not time.
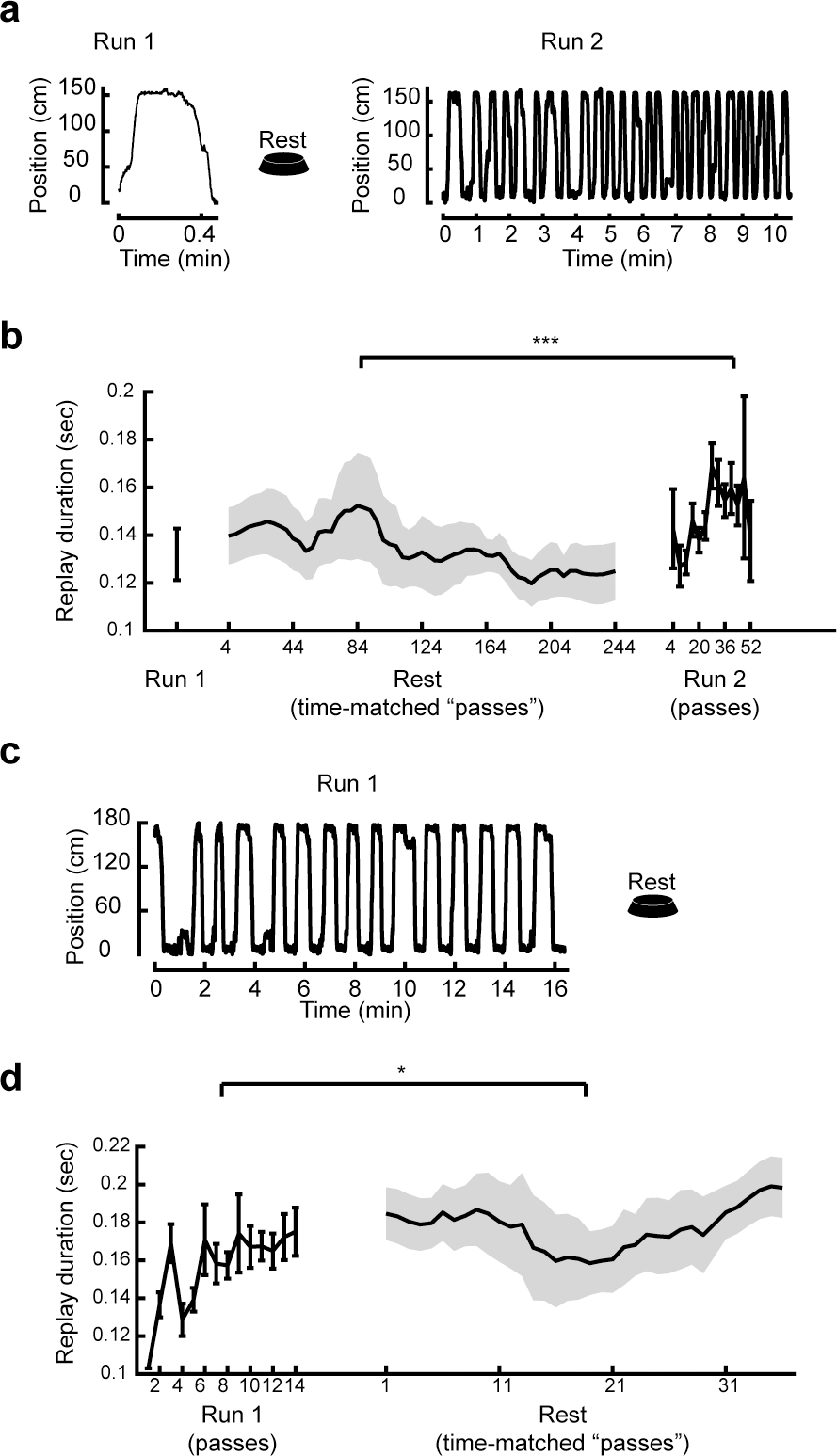
(a) Example behavior and (b) all data for replay durations during a single pass of a novel track, subsequent rest, and a second exposure to the track with multiple passes. Replays did not increase in duration during rest (One-tail test: N =228; Duration: R = −0.14, P = 0.98), c, P = 2.4e-4). Two-way ANOVA: main effect of group F(1,507) = 4.7, P = 0.03, main effect of pass F(1,507) = 9.9, P = 2.0e-3, interaction F(1,507) = 14.9, P = 1.3e-4.
(c) Example behavior and (d) all data for replay durations during, and in rest following, a multiple-pass session on a novel track. Replays of the novel track (Run 1) increased in duration with continued experience on the track (One-tail test: N = 216, Duration: R = 0.20, P = 0.0019), but did not continue to increase in duration during subsequent rest (One-tail test: N = 79, Duration: R = 0.054, P = 0.32). Two-way ANOVA: main effect of group: F(1,294) = 5.6, P = 0.019, main effect of pass: F(1,294) = 7.69, P = 5.9e-3, interaction: F(1,294) = 5.5, P = 0.020. All data show mean ± S.E.M. Correlations are Pearson’s correlation values. *** P < 0.001, ** P < 0.02, * P < 0.05
We further considered that replays could continue to slow down during offline periods, provided that sufficient experience had already been accrued. To test this, we analyzed replays that occurred during a rest session after a full session on a novel track (Figure 4c). Replays slowed down across passes on the novel track, but after being placed in a familiar rest box, replays did not slow down further, and the difference was significant (Figure 4d; Two-way ANOVA: main effect of group: F(1,294) = 5.6, P = 0.019, main effect of pass: F(1,294) = 7.69, P = 5.9e-3, interaction: F(1,294) = 5.5, P = 0.020). There was no change in the duration or slope of replays between the end of Run 1 and the first four passes of Rest (Wilcoxon rank-sum test, Run: N = 216, Rest: N = 15, duration P = 0.96, slope P = 0.84). Additionally, there was a significant breakpoint in the changing duration and slope of replays at the beginning of Rest (Chow test N = 295, duration: F = 5.5, P = 0.02, Monte-Carlo P = 0.026, slope: F = 3.9, P = 0.048, Monte-Carlo P = 0.048). Taken together, irrespective of the amount of experience a rat had in a novel environment, replays did not slow down with rest after a novel experience, only with additional continued experience.
Replays slowed down by adding more, smaller steps
Replays do not move smoothly across an environment, but instead “hover-and-jump” at the timescale of slow gamma (Pfeiffer and Foster, 2015; 25–50Hz; Figure 5a–b). We examined how hover-and-jump dynamics change with experience. We first replicated previous findings that replays exhibited hover-and-jump dynamics at the slow-gamma timescale (Figure 5c). We then found that multiple features of hover-and-jumps including the step duration, hover duration, jump duration, gamma frequency, gamma power, and gamma mean resultant vector (MRV) remained constant across experience (Figure S5). However, the number of steps that replays took increased across passes (Figure 5d) while the distance that each step covered (step size) decreased (Figure 5e; Figure S1). Hence, replays slowed down by using more, smaller steps along the track (Figure 5f).
Figure 5. Replays slowed down by adding more, smaller steps.
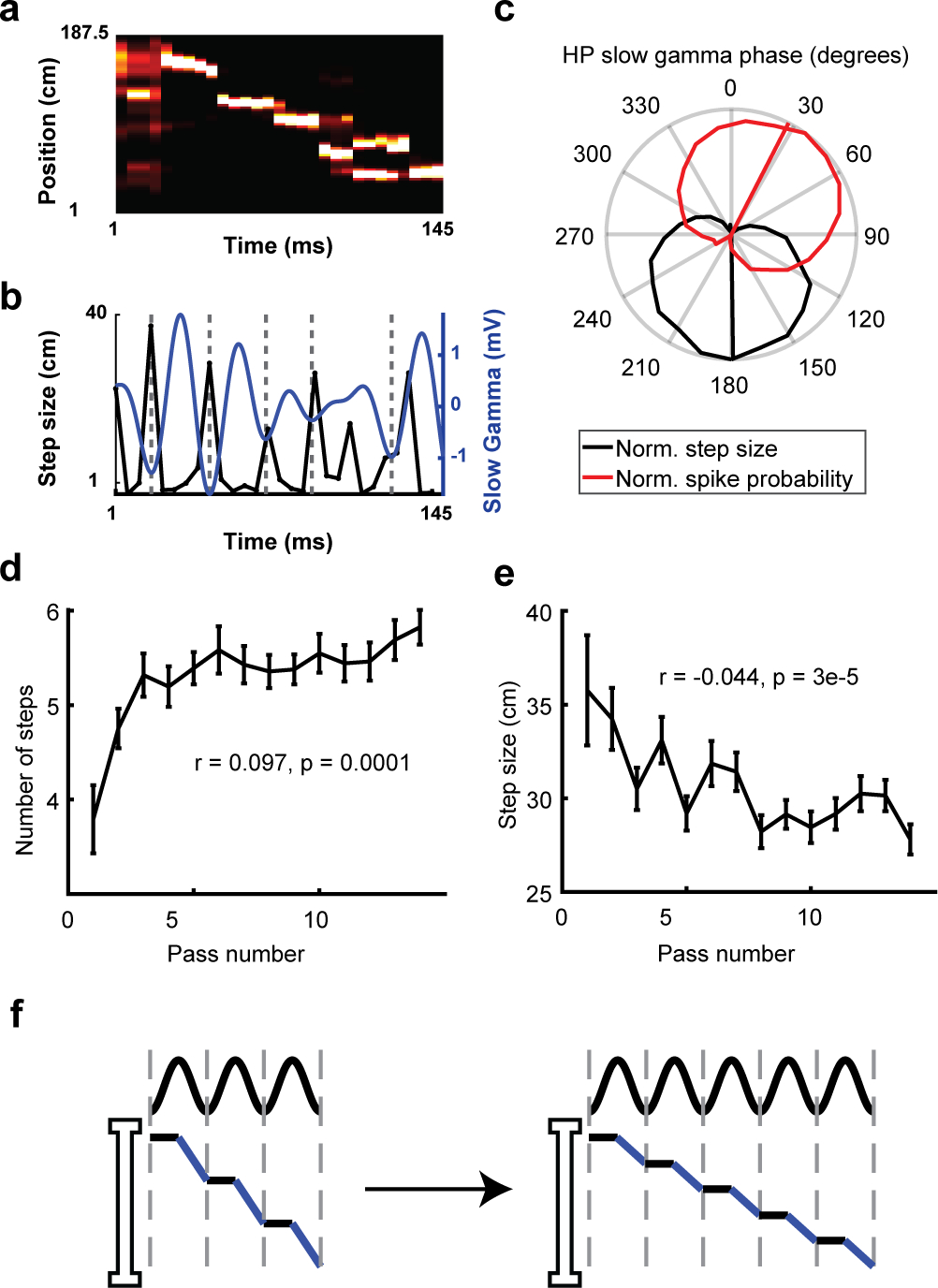
(a) An example replay on a novel track.
(b) Step size (left axis) and slow-gamma oscillation (LFP filtered in 25–50Hz band; right axis) signal during the replay in a.Troughs (180° phase) in the gamma trace indicated with dashed lines.
(c) Both the step size and spike probability of HP pyramidal neurons were locked to HP slow gamma (Rayleigh test, N = 841,115, Step size: Z = 316, P = 4.1e-233, Spike probability: Z = 5.5, P = 4.0e-3).
(d) Across passes of a novel environment, the number of steps in replays increased (N = 1609, R = 0.097, P = 1.0e-4)
(e) The step size (distance each step takes) decreased (N = 1609, R = −0.044, P = 3.0e-5).
(f) Schematic of replay slowing down with experience by adding more, smaller steps. All data show mean ± S.E.M. Correlations are Pearson’s correlation values.
Experience allowed for greater detail to be incorporated into replays
We next explored the way in which steps were added to replays with experience, using 117 sessions from 11 rats that ran novel or familiar tracks. First, we examined the distribution of places on the track where replays tended to hover. Having established that there are fewer hovers within replays in early laps, we wanted to see whether, when taken all together, replays tended to hover in fewer locations in early laps (instead of reducing the frequency of hovering equally across all locations in early laps). To consider all available evidence for possible hover locations, we used all candidate events, rather than only those that passed our previous criteria for replay. Events tended to hover in certain places on the track, creating a bumpy distribution of hover locations (Figure 6a). To make sure that this effect did not depend on inhomogeneities in the distribution of place fields, we performed an artificial place field population flattening procedure, a cell ID shuffle, and decoding of running periods and compared the distributions of those control procedures (Figure S6). Through these analyses we found that the tendency of replays to dwell in particular locations depended on the mapping of spikes to information but not on any chance variability in the fields we sampled or any spurious effect of Bayesian decoding interacting with inhomogeneous place fields.
Figure 6. Addition of hover locations.

(a) Hover location distributions (example session shown here) are a histogram built up of the hover locations from all candidate events (two example events in insert) Dotted lines on the histogram and circles on the track below mark the peaks in the hover location distribution on the track (see Methods).
(b) Equal quartiles of candidate events from the same example session sorted by time from early to late passes (passes 1–14) showing consistency in hover locations across experience.
(c) Correlation value across all sessions between the four equal quartile distributions of hover locations (mean across the six pairwise correlations) (line). Histogram of correlation value calculated in the same way from 1000 data shuffles (see Methods). Real value was significantly greater than shuffles (Mean correlation = 0.54, Monte-Carlo P = 0.001).
(d) The distributions of hover locations for passes 1–4 for one example session. Hover locations in the first pass shown by dashed red lines for each pass (peaks of histogram; see Methods).
(e) Number of unique hover locations for first pass of a novel environment (line), compared to histogram of the same quantity calculated from 1000 shuffled datasets, in each of which the number of first pass events is preserved but the events themselves are sampled randomly from all later passes of the same session. Real number was significantly lower than the shuffles (Monte-Carlo P = 0.022).
(f) Example three replays across Passes 1, 2, and 5 with a schematized version of hovers below, showing how unique hover locations build up across passes.
We next examined whether hover locations remained stable while replays slowed down across passes on novel tracks. To test this, we divided the first 14 passes of each novel session into four quartiles by time, such that each quartile had the same number of replays, and visualized the distribution of hover locations across these quartiles (Figure 6b). Across all sessions, the hover distributions were more similar across quartiles than a shuffle control in which the quadrants’ hover distributions were randomly circularly shifted (Figure 6c). Thus, although individual replays in early passes hovered at fewer locations, they were the same locations that later, slower replays would hover in.
We next wanted to test the hypothesis that unique hover locations were inserted over passes, consistent with the notion that detail was being added to replay as animals gained increasing experience. In this case, replays on the first pass should have exhibited only a subset of the final hover locations, with additional hover locations being inserted after later passes (Figure S7 “insertion hypothesis”). Alternatively, replays after the first pass, despite being individually shorter and containing fewer hover points, might have been capable as a population of sampling from all hover locations. This would imply that replay had the full capacity to access any of the final set of hover locations, and thus that no new learning occurred over passes (Figure S7; “sampling hypothesis”). To distinguish between these hypotheses, we tested whether there were fewer unique hover locations on the first pass of a novel track than one would expect by chance sampling. We compared the number of peaks of the first pass hover location distribution (Figure 6d, gray dotted lines) to the number of peaks of a distribution generated by randomly selecting replays from all subsequent passes, keeping the number of replays and the number of hovers consistent with the first pass. We found that the average of the real number of peaks in the first passes’ hover distribution was less than expected (Figure 6e; Monte-Carlo P = 0.022). Thus, new hover locations were inserted into replays due to the experience of running passes on the novel track (Figure 6).
Longer, later replays were associated with higher interneuron activity and greater PFC neuronal modulation
We have shown that replays cross the track rapidly with little experience in a novel environment, and then slow down with subsequent experience. Novelty affects many aspects of brain function and so there could be multiple candidate mechanisms at work (Palacios-Filardo and Mellor, 2019). We hypothesized that inhibition could be dampened during early replays, allowing for rapid pass between representations of position by HP pyramidal neurons. To test this, we analyzed HP interneurons recorded simultaneously with pyramidal neurons while rats ran on linear tracks (42–115 putative HP pyramidal neurons, median 74; 1–4 putative HP interneurons, median 1, total 19). We asked whether interneurons fired less during replays in early passes than in later passes (Figure 7a). Indeed, the population of HP interneurons tended to increase replay-related firing across passes (Figure 7b). Our interneuron yield was low, so to further test this theory we analyzed data from a publicly available dataset where rats ran on novel linear tracks and more interneurons were recorded (48–120 putative HP pyramidal neurons, median 59; 13–20 putative HP interneurons, median 17, total 82) (Grosmark, Long and Buzsaki, 2016). In this data set as well, interneurons increased their firing rate modulation to replays over passes (Figure 7c–d). Thus, across two datasets, we observed that interneurons were more modulated to replays in later passes than early passes.
Figure 7. Relationship to hippocampal inhibitory interneuron activity, and to prefrontal cortical unit activity.
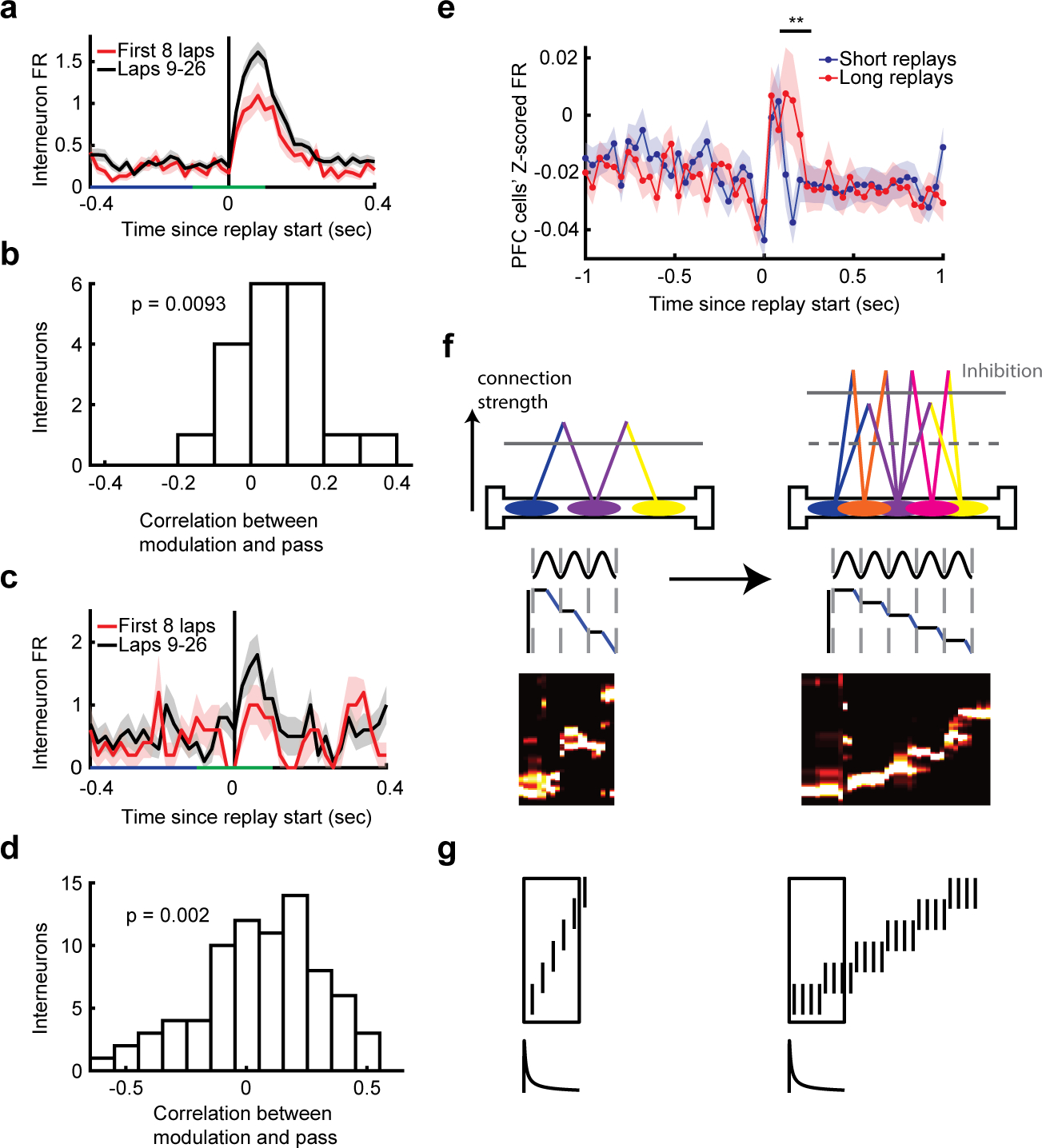
(a) Example HP interneuron firing rate centered on the start of replays in the first 8 passes (red) or passes 9–26 (black) in a novel environment. The modulation window is marked in green (m; −100 to 100 ms) and the baseline window is marked in blue (b; −400 to −100 ms).
(b) Correlation between modulation to replay (defined as [m+b]/[m−b]) and pass number, across all HP interneurons (N=19). The distribution of HP interneurons’ correlations was significantly greater than zero (one-sided Wilcoxon signed-rank test, N = 19, Z = 2.4, P = 9.3e-3).
(c) An example neuron from a separately recorded group of rats running on novel linear tracks (Grosmark et al., 2016) in the same format as in a.
(d) Correlation between modulation to replay (defined as [m+b]/[m−b]) and pass number, across all HP interneurons (N=82). The distribution of HP interneurons’ correlations was significantly greater than zero (one-sided Wilcoxon signed-rank test, N = 82, Z = 2.9, P = 2.0e-3).
(e)PFC neurons’ z-scored firing rate centered on the start of short (blue) or long (red) HP replay events (median split of the duration of replays). Data show mean ± S.E.M. One-sided Wilcoxon signed-rank test, 80–160 ms after replays, N = 158, 158, Z = −2.7, P = 3.5e-3; Two-way ANOVA between length of event and first 80 ms after replay compared to next 80 ms: Main effects P > 0.05, Interaction: F(1,1264) = 4.2, P = 0.04. (Replays of each arm separately: one-sided Wilcoxon signed-rank test, N = 158,158, 80–160 ms after replays: Arm 1 P = 0.097, Arm 2 P = 0.012, Arm 3 P = 4.0e-5.).
(f) Schematic of how experience changes replay. Left: early in a novel experience replays are rapid and short; interneurons are less modulated and connections between place cells are weak. Right: later in experience replays are slow and longer; interneurons are more active and connections between place cells are stronger.
(g) Replay can act as an eligibility trace for reinforcement learning. Left: upper schematic depicts a fast replay, as occurs early in training. Lower schematic depicts a decaying gain factor for synaptic plasticity, as might characterize, for example, a spike-time dependent plasticity rule for place cell inputs to a downstream neuron in the striatum. If plasticity is also modulated by a dopaminergic reward prediction error, the striatal neurons will learn a value function according to TD(λ), or, if the striatal neurons are also selective to action choice, action-values according to SARSA(λ). Right: as replay slows down, the window over which TD learning acts shrinks: this is equivalent to reducing λ, as is recommended as learning proceeds (see text for discussion). *** P < 0.001, ** P < 0.02, * P < 0.05
We also wanted to explore a possible consequence of having longer, slower replays in HP. Based on the idea that engaged cortical areas perform computation during HP replay (Buzsáki, 1996; Carr, Jadhav and Frank, 2011; Eichenbaum, 2017; Zielinski, Tang and Jadhav, 2020), we hypothesized that longer replays could give those cortical areas more computing time. We analyzed data from HP and prefrontal cortical (PFC) neurons recorded simultaneously in 11 sessions from four rats as they ran an asymmetric Y-maze and were rewarded for performing an alternation rule (62–137 putative HP pyramidal neurons, median 79, total 968; 7–25 PFC neurons, median 14, total 158) (X. Wu and Foster, 2014; Berners-Lee, Wu and Foster, 2021). We compared the z-scored firing rates of all PFC neurons during short replays and long replays and found that PFC neurons stayed modulated longer to longer events (Figure 7e).
Discussion
We have investigated how hippocampal (HP) replays appear and change in novel environments. We found that replays appeared after a single experience, while the animal was resting in either that same environment or a remote location. We then explored how replays change with subsequent experience and found that replays slowed down across passes on a novel linear track. We found that the only replays that slowed down were those of the environment that was actively being explored. They did so by adding hover locations, filling in details that had been absent in early, rapid replays. We also investigated HP interneurons and prefrontal cortical neurons recorded simultaneously with HP replay, providing clues as to the potential mechanisms and consequences of replay slowing down.
Our experiments focused on changes to the speed of replay across passes in the first session on a novel track. Previous work has explored changes in the occurrence of replay on the time-scale of days (Frank, Stanley and Brown, 2004; Cheng and Frank, 2008). Replays tend to occur more frequently with more experience in a novel environment but less as that environment becomes more familiar across days (O’Neill et al., 2008; Cheng and Frank, 2008). It is possible that the changes in the duration and speed of replay reported here for the first day on a novel track would reverse over subsequent days’ sessions on the same track, as suggested by recent data showing shortening durations and lengthening trajectories across sessions (Shin, Tang and Jadhav, 2019). Experiments where the duration and slope of replays is investigated in data recorded across days of the same, initially novel track would help determine how these changes occur at longer timescales.
To what kind of memory does this HP replay correspond? Episodic memory is one-trial learning by definition (Tulving, 1972), while with respect to retrieval, the memories can last a lifetime. We have demonstrated that replay exhibits this duality at least to some degree: it can be acquired from one experience (one lap), and retained for an extended period of time (at least one hour). A second feature of episodic memory is that the subject doesn’t merely recall information but “re-experiences” it, in a process that Tulving called “mental time travel” (Tulving, 2002). Replay exhibits an intriguing correspondence to this process, since the representation of current location moves to other locations while the animal is itself stationary.
These considerations support the explicit hypothesis made by others (Carr, Jadhav and Frank, 2011; Buzsáki, 2015) that replay represents a form of episodic memory retrieval. However, our results also point to a semantic aspect to replay, since information is added to the replay memory of the track upon subsequent re-exposures to it. This observation supports the idea of replay as a model of the world, as opposed to a record of individual experience, and this fits nicely with several other features of replay, including evidence that replay captures environmental topology, and that it can generate novel combinations of previous experiences (Gupta et al., 2010; Foster, 2017). Our results add the notion that there is a kind of “graceful improvement” to the model, so that “gist” information may be available early on even while the model is not complete. This is partially in line with recent computational suggestions that episodic memory may provide “gist”-like records of actually experienced behavioral experience that support an efficient mode of control under conditions of limited experience (Lengyel and Dayan, 2008; Gershman and Daw, 2017). On the other hand, the notion of incremental augmentation of initial memories suggests that there may not be such a sharp distinction between the proposed episodic and semantic modes of control as proposed in the models.
We note that application of a world model to decision-making is complicated by changes to the model that are unrelated to the world (in this case, temporal elongation that does not reflect spatial elongation). For example, choice-related quantities such as spatial distance, or temporally discounted prediction of future reward, that could in theory be mapped to time-within-replay, will be difficult to extract if these temporal relationships change. This difficulty is particularly acute if at the same moment some spatial trajectories can be in a “fast” replay state while others are “slow”, as suggested by our data. Using temporal surrogates to compare the two trajectories would be unreliable, and a global normalization strategy (such as modulation of values by a global neuromodulator) would fail to ameliorate the problem. However, there are at least two alternatives that might resolve this paradox. First, according to theoretical work, reverse replay can function as an eligibility trace in the context of temporal difference learning (specifically TD(λ); Cichosz, 1999; Reynolds, 2002), and so changes in the speed of replay effectively alter the window over which the eligibility trace is maintained (Figure 7g). It has been proposed that the eligibility trace should be extensive at the beginning of learning, and shrink as learning progresses (λ −> 0), to manage a changing bias-variance tradeoff (Watkins, 1989). This nicely matches the shift observed for replay (Figure 7g). Furthermore, replays tend to be reverse early in learning which also fits this proposal (Foster and Wilson, 2006). A second resolution involves reassessing more fundamentally the role of replay in memory. It is possible that the information content of replay is entirely restricted to the hover points, while the transitions between hover points correspond to a search process that does not explicitly encode information. According to this idea, temporal compression does not occur at all, since the hover locations are static (or possibly real-time) retrieval events, and the temporal relationship between them expressed by replay is not utilized. Rather, replay with multiple hover points would reflect a search process of transitioning between intermediary items in search of the desired memory item. Further research is required to distinguish between these alternatives.
What mechanism is responsible for the changes? We can ask first whether the changes in replay reflect a retrieval mechanism or an encoding one. Retrieval mechanisms might be expected to vary globally with changes in current behavioral state, such as anxiety or satiety, however our data suggest that replays of different speeds can be produced in the same behavioral state, depending rather on whether the environment is novel or familiar. Moreover, this dependence was shown to be a function of experience, rather than of the amount of intervening time, suggesting that the speed of replay is altered in a lasting way by some encoding process occurring at the time of experience, including at the times of repeated exposures to the same trajectory. Changes in the speed of replay appear to be driven only by environmental novelty, as we did not see changes in speed due to unpredicted reward changes. This result could be informative about potential mechanisms of replay slowing. “Common” novelty such as changes in local cues or objects in the environment is thought to engage a different circuit than “distinct” novelty that is achieved with a brand new environment (Duszkiewicz et al., 2019). Both cases affect HP neurons (Leutgeb et al., 2004; Larkin et al., 2014; Ambrose, Pfeiffer and Foster, 2016) and increase dopamine (O’Carroll et al., 2006; Takeuchi et al., 2016), however the former may involve ventral tegmental area while the latter may engage the locus coeruleus, both of which project to the HP (Takeuchi et al., 2016; Duszkiewicz et al., 2019). Thus, dopamine input from the locus coeruleus might be a potential mechanism at play and it would be fruitful to investigate the role either area plays in modulating HP replay speed. It would also be important to expand the tests of common novelty on replay speed from changes in reward to changes in barriers, local and distant cues, and objects.
The above considerations support an encoding explanation for replay speed changes, however this presents a conundrum. To add interstitial locations to a fast replay, the sequential relationships between locations in the fast replay must be undone, while the sequential relationships reflecting the new, more detailed sequences must be created. We propose a simple mechanism to support these changes (Figure 7f) depending on changes in inhibition from HP interneurons as well as the connection strengths between HP place cells that represent nearby locations on the track. In early passes, HP place cells may be weakly connected having had only a few chances to fire together while running, but inhibition is low. This low inhibition allows replays to jump between positions that are further away on the track. Across laps, more place cells come online and the strength between locations on the track increases. Increased inhibition in these later laps disallows large jumps between locations, but enough plasticity has occurred that replays can jump to each hover location. Simulation studies have shown that increased inhibitory activity reduces the number of place cells that reach the threshold to fire in replay (Malerba et al., 2016). This aspect of the proposed mechanism could be tested in future studies by subtly changing inhibitory drive during stopping periods in a novel environment to observe changes in replay speed, possibly uncovering the original, large jumps seen in earlier replay sequences.
Our results also have implications for attractor models of replay. The hover-and-jump steps and accompanying gamma rhythm have been proposed to reflect underlying attractor dynamics, with replays dwelling in the relatively low-energy hover locations (Pfeiffer and Foster, 2015). We found that the temporal aspects of individual hover-and-jump cycles, as well as the frequency of the associated gamma rhythm, did not change across experience. Rather, replays took more, smaller steps with more experience, and the HP was able to take variably sized steps between hover locations. Further, once a hover location appeared, it remained, but additional hover locations were inserted over subsequent laps. Together these data imply that existing attractors are stable, while new attractors are incorporated quickly, within as little as one trial, and whatever plasticity is required to establish the asymptotic properties of the attractor are completed within one trial, i.e. further experience is not required. As in the previous work that initially reported hover-and-jump dynamics in replay (Pfeiffer and Foster, 2015), we were not able to detect physical correlates of hover locations, such as spatially localized inhomogeneities in stimuli or behavior. However, we cannot rule out the possibility of such correlates, perhaps arising from behaviors that have been linked to place cell activity changes, such as head-scanning behavior or vicarious trial-and-error (Monaco et al., 2014; Redish, 2016). We also did not explore the origins of this gamma rhythm or its relationship with the number of ripple bouts (Oliva et al., 2018) and cannot rule out the notion that concatenated ripples are the root of these gamma-timescale step dynamics.
Recent work using optogenetic stimulation suggests that longer replays may benefit learning (Fernández-Ruiz et al., 2019). Here we have shown that replays naturally lengthen, and do so by incorporating increased detail about the experienced environment. Supporting the notion that these changes are functional, we have additionally observed increased recruitment of cortical neuronal activity as a consequence of replay lengthening. These changes suggest that the slowing down of HP replay leads to increased replay-related processing in downstream cortical circuits. Examination of the information content of these activations will likely shed further light on the function and significance of HP replay.
STAR Methods
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dr. David Foster (davidfoster@berkeley.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
This paper analyzes some existing, publicly available data. These accession numbers for the dataset are listed in the key resources table and in the references. Other data reported in this paper will be shared by the lead contact upon request.
Individual units were separated using custom clustering software (xclust2, M.A. Wilson). All analyses were performed using custom code written in MATLAB (Mathworks). Custom code has been deposited in a public repository: ZenodoDOI:10.5281/zenodo.6330850; https://zenodo.org/badge/latestdoi/466486266
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning. | Grosmark, A. D., Long, J. and Buzsaki, G. (2016) ‘Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning.’, CRCNS.org | DOI: http://dx.doi.org/10.6080/K0862DC5 |
| Experimental models: Organisms/strains | ||
| Male Long-Evans rats | Charles River | RRID:RGD_2308852 |
| Software and algorithms | ||
| MATLAB R2020b | MathWorks | RRID:SCR_001622 |
| Custom data processing and analysis code | This paper | Zenodo DOI: 10.5281/zenodo.6330850; https://zenodo.org/badge/latestdoi/466486266 |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
In this study, we recorded from a total of 17 male Long-Evans rats (Charles River) weighing 450–550 g, 10–20 weeks old. All procedures were approved by the Johns Hopkins University Animal Care and Use Committee and followed US National Institutes of Health animal use guidelines. Some of the data we presented were used in previous publications and re-analyzed here, outlined in Pre-training and behavior. Surgical implantation and tetrode adjustment and data acquisition was identical to prior studies (X. Wu and Foster, 2014; Silva, Feng and Foster, 2015; Ambrose, Pfeiffer and Foster, 2016). The methods for pre-training and behavior has also been published but is re-stated here. We also augmented this data with publicly available data from four rats (Grosmark and Buzsaki, 2016; Grosmark, Long and Buzsaki, 2016).
METHOD DETAILS
We habituated rats to daily handling and food deprived them to 85–90% of their baseline weight. We then pretrained them to run back and forth on a 1–1.8-m long, 6 cm wide, linear track to receive a liquid chocolate-flavored reward (Carnation). The tracks had a reward delivery well at each end. Following recovery from surgery, we food-deprived the rats again and retrained them on a training linear track with recording cables attached for approximately 2 days before recording sessions began. All data were collected using a Neuralynx data acquisition system. We tracked the rat’s position using two LED diodes (red and green) mounted on the micro-drive and an overhead camera capturing the behavior at 60 Hz.
We conducted several different experiments after pre-training, surgery and recovery. The different behavioral paradigms and the number of sessions and rats we used are outlined here and summarized in Table 1. To test whether replay appears and slows down after one lap (Figure 1a–c, Figure 4a–b) we conducted an experiment with four rats in five sessions whereby after resting in a rest box, the rat ran 1–2 passes (only one session had two passes) across a novel linear track after which he was placed back in the rest box, and subsequently placed back on the same track to run a full session (30+ min). Next, to test whether remote replays were affected by experience in a novel environment (Figure 3c–e) we conducted an experiment with 20 sessions from eight rats whereby rats ran a session on a novel linear track, and then ran a full session on a different novel track. To test whether replays slow down after a full run on a novel track (Figure 4c–d) we used 13 sessions from eight rats that ran a full session on a novel track and then rested in a familiar rest box. To test whether replays slow down in a novel environment (Figure 1d, Figure 2, Figure 3a–b, Figures 5–6, S1, S4, S6) we recorded 39 sessions from seven rats as they ran on a full session on a novel linear track (Silva, Feng and Foster, 2015). To test whether HP interneurons changed their modulation across passes (Figure 7a–b) we used nine of those novel sessions from five rats where interneurons were recorded. We augmented that analysis with a published publicly available dataset of rats running in five novel linear track sessions recorded from four rats (Grosmark and Buzsaki, 2016; Grosmark, Long and Buzsaki, 2016) (Figure 7c–d). To test whether cortical neurons responded differently to longer replays (Figure 8a) we used simultaneously recorded HP and prefrontal cortical neuron (PFC) data from 11 sessions from four rats as they ran on a novel asymmetric Y-maze and were rewarded for alternating between two arms while returning to a center arm (X. Wu and Foster, 2014). To test whether replays slowed down in familiar environments (Figure S2), we recorded from 78 sessions from nine rats as they ran on familiar linear tracks. To test whether replays changed their speed in response to a reward change in the environment (Figure S3), we used sessions two and three of a three session experiment where the second session had a change in the reward amount (4x or 0x) at one end (40 total sessions with six rats) (Ambrose, Pfeiffer and Foster, 2016). In session one, rats ran on a familiar track with equal reward at each end. In session two, one of the ends of the track had either 4x or 0x the amount of reward as the other side and as it had in session one. In session three the rewards were equal to each other and the amounts from session one. In analyses to test hover location distributions (Figure S6) we used 117 sessions from 11 rats as they ran on either novel or familiar tracks.
QUANTIFICATION AND STATISTICAL ANALYSIS
Calculating place fields
We used spikes from putative HP pyramidal neurons to create place fields in two ways: whole session fields and lap-by-lap fields. For both methods we binned the linear track into 2.5 cm bins and only used times when the speed of the rat exceeded 5 cm/sec. For each neuron, separately for each running direction, we divided the spikes evoked in each position bin by the occupancy in that bin and then smoothed this spike rate with a gaussian filter (radius = 20 bins, sigma = 2 bins). For whole session decoding, we used all the laps in the session to build the fields. For lap-by-lap decoding we used only the last 2 passes (1 lap) to build the fields. We used these lap-by-lap fields to perform lap-by-lap decoding whereby we decoded the candidate events at each stopping period using the fields from the most recent 2 (or 1 in the case of the first stopping period) passes across the track (described in decoding position within candidate events).
Identifying candidate events
We identified candidate events as HP putative pyramidal neuron spike density events. Spikes were binned into 1 ms bins and then smoothed with a gaussian filter (radius = 100 ms, sigma = 10 ms). For run epochs, we removed any spiking occurring when the rat was running (>5 cm/sec). We identified events that exceeded 3 standard deviations of the mean spike rate across the whole session (we defined the mean and standard deviation separately for each epoch). Events were clipped at the start and end when they returned to the mean. We removed events with durations less than 100 ms or more than 500 ms.
Decoding position within candidate events
As stated in Calculating place fields, we decoded candidate events using either using whole session fields or lap-by-lap fields. We also performed decoding with overlapping bins (20 ms window moving by 5 ms) and with non-overlapping bins (20 ms bins; Figure 1). We performed probability decoding to create a posterior probability of the animal’s position for each time bin, as described previously (Silva, Feng and Foster, 2015) by means of Bayesian decoding with a uniform prior over position and assuming independent rates and Poisson firing statistics for all neurons (Davidson, Kloosterman and Wilson, 2009b).
Structure of candidate events and replays
We assessed the structure of candidate events and replays using metrics described previously (Davidson, Kloosterman and Wilson, 2009b; Silva, Feng and Foster, 2015). (i) Weighted correlation: decoded probabilities (prob) were assigned as weights of position estimates to calculate the correlation coefficient between time (T) and decoded position (P):
where weighted covariance between time and decoded position is
and weighted means of time and decoded position are
(ii) We defined maximum jump distance as the maximum distance between peak decoded positions in neighboring decoded time windows for each candidate event normalized by the length of the track.
(iii) We defined track coverage as the range of weighted mean posterior probability estimates of position from the event divided by the length of the track.
(iv) We determined the decoded slope by calculating the likelihood R that the decoded candidate event (duration of n time bins) is along the fitted line with slope V and starting location ρ was calculated as the averaged decoded probability in a 30 cm vicinity along the fitted line:
where Δt is the moving step of the decoding time window (20 ms) and the value of d was empirically set to 25 cm for small local variations in slope. (For those time bins k when the fitted line would specify a location beyond the end of the track, the median probability of all possible locations was taken as the likelihood.) To determine the most likely slope for each candidate event, we densely sampled the parameter space of V and ρ to find the values that maximize R.
Testing the significance of the number of replays
To test whether the number of replays across passes or in rest after a single lap exceeded chance, we repeated analyses that were developed previously in the lab (Silva, Feng and Foster, 2015), re-stated here. Replays were defined as candidate events that obtained both strong weighted correlation and small maximum jump distance in the decoding (green asterisks in Figure 1c–d, top-right to bottom-left, weighted correlation > 0.6 and maximum jump distance < 0.4, weighted correlation > 0.7 and maximum jump distance < 0.4, weighted correlation > 0.7 and maximum jump distance < 0.3). To determine whether there was a significant number of replays under different conditions, we calculated the number of candidate events that passed both correlation and jump distance thresholds under all combinations, and compared them with the distribution of numbers from 5000 shuffled data sets that were generated through time shuffle (Davidson, Kloosterman and Wilson, 2009b), which was done by randomly shuffling the time-bins of each replay 5000 times. The Monte-Carlo P-value was calculated as (n + 1)/(r + 1), where r is the total number of shuffles and n is the number of shuffles that produce greater than or equal to the number of candidate events that meet the criteria compared to the actual data. We subsequently represented P-values under all combinations of the two thresholds in a color-coded matrix (significance matrix), where a P-value below 0.05 was considered significant and marked in red. We reported P-values at the green asterisks as well as the cumulative replays that fall into the entire quadrant highlighted by the green box (Figure 1c–d, weighted correlation > 0.6 and maximum jump distance < 0.4 to weighted correlation > 0.9 and maximum jump distance < 0.1).
Replays across laps and general statistics
A lap is defined as two passes across the track, and we broke down changes over experience into individual passes across the track. Significant replays are defined as those with weighted correlation > 0.6 and maximum jump distance < 0.4 unless otherwise noted (the two thresholds that defined the green box in Figure 1c). We assessed how aspects of replay changed across passes using Pearson’s correlation tests comparing the aspect of replay with the pass the replay occurred on, across all replays. In some analyses (Figure S1i–l) we first averaged the aspects of all replays in a given session for each pass before performing a Pearson’s correlation. For all two-way ANOVAs assessing different conditions across passes we designated the passes variable as “continuous” in MATLAB’s “anovan” function. All statistical tests are two-sided unless otherwise noted.
Rest session analyses
Rest sessions were divided into “pass” equivalents, each with a duration of the median pass time of the associated run session. The number of passes in the multi-lap experiment (Figure 4d) was capped at 14 passes. For visualization, data from the single-lap experiment (Figure 4b) was binned into four pass bins, but all stats in both experiments were performed without binning. For this data, replays during the rest between Run 1 and Run 2 were decoded with Run 1 place fields, and Run 2 replays were decoded for Run 2 place fields. We compared the durations and slopes of significant replays (weighted correlation > 0.6 and maximum jump distance < 0.4) across passes and epochs first by evaluating the Pearson’s correlation for each epoch, next by using a two-way ANOVA where “pass” was a continuous variable, and finally with a Chow test. The Chow test assessed whether replays changed differentially between the two sessions (run and rest) by asking whether the start of the second epoch was a significant breakpoint. We also performed a shuffle where the order of the replay was shuffled 1000 times to produce a distribution of Chow test statistics which we then compared to the real value using a Monte-Carlo test: (n + 1)/(r + 1), where r is the total number of shuffles and n is the number of shuffles that produce a Chow test statistic greater than or equal to the actual data.
Gamma and hover-jump analyses
Gamma analysis was similar to in Pfeiffer and Foster’s work (Pfeiffer and Foster, 2015), outlined again here. For each tetrode, we used the electrode with the highest theta single-to-noise ratio. For slow gamma analysis, we band-pass filtered the LFP between 25 and 50 Hz. To calculate power in the slow-gamma frequency during SWRs, we calculated the absolute value of the Hilbert transform of the filtered signal, smoothed it (Gaussian kernel, SD = 85 ms), and averaged the z-scored power across tetrodes. We determined the phase of each spike relative to the gamma oscillation on the tetrode from which the spike was recorded and used those phases to calculate the mean resultant vector. We defined the peak of the oscillation as 0°/360° and the mid-point of the descending phase as 90°. We defined the instantaneous gamma frequency as the reciprocal of the duration of each gamma cycle in the filtered signal.
We used the weighted mean posterior probability estimates of position as the decoded position. We defined hover-bins in a replay as those that had a difference of less than 5 cm between the previous time-bin and the current time-bin’s decoded position (analyses were repeated with 2.5 cm hover cutoff and findings were similar and significant), and we defined all other bins as jump-bins. We defined hovers as consecutive hover-bins and jumps as consecutive jump-bins. We defined the number of steps as the number of jumps in a replay and the step duration as the duration between when jumps in a replay started. We calculated the duration for each jump, hover and step in a replay so that we could assess how they changed across passes (Figure S5). For this analysis, when a replay started or ended with a hover, that hover was not included.
Hover locations and controls
We used the weighted mean posterior probability estimates of position as the decoded position. We generated each session’s hover location distribution by taking a histogram of all decoded positions during hovers from all candidate events (Figure 6a). To produce a flat distribution of place fields as a control, we computed the difference between the mean firing rate in each position bin (Figure S6b, black line) and the mean of firing rate across all the position bins. We then multiplied this bias vector with a matrix with the size of the population of place fields (Neuron # x position bin) of random numbers between 0 and 1 and added this biased noise to the place fields, while making sure that no position bin in a field fell below zero. We continued this until the maximum difference between the mean of each position bin and the mean of all position bins was less than or equal to 1e-4 (Figure S6b, red line). We then decoded candidate events with these artificially flattened fields and calculated a hover location distribution as described previously. We did this 100 times to obtain a distribution of artificially flattened hover location distributions. As another control, we also performed a cell ID shuffle, where the ID of each neuron’s place field was shuffled 100 times. We then compared the real hover location distribution with these alternatives by using a Pearson’s correlation for each of the 100 shuffles (Figure S6j). We also did a supplementary test of the number of peaks in the hover location distribution. We used MATLAB “findpeaks” function using a minimum peak prominence of 0.4 probability and a minimum peak distance of one tenth of the range of track positions. We did this for the real hover location distribution as well as the artificially flattened field distributions and assessed whether they were different using a Monte-Carlo test: (n + 1)/(r + 1), where r is the total number of shuffles and n is the number of shuffles that produced greater than or equal to the number of peaks in the hover location distribution in the actual data (Figure S6f). In addition, we performed another control whereby we decoded the running periods (anytime > 5cm/sec for longer than 100 ms) using the same time-sclae decoding analysis and compared the distribution of decoded positions (Figure S6i) with the flat field distribution (Figure S6k) by taking the Pearson’s correlation coefficient for each session.
Assessing how hover locations change across passes
To assess how hover locations changed across passes, we first divided the candidate events that occurred in the first fourteen passes up for each session into four groups of equal numbers of candidate events. We took a histogram of the decoded positions of hover bins from the events for each group and calculated the Pearson’s correlation R value across all pairs of these four groups and then took the mean of those R values. To create a chance distribution, we randomly circularly shifted the groups’ hover location distributions 1000 times for each session. We then compared the average of the sessions’ R values to the average of the sessions’ R values for each shuffle (Figure 6c) and tested the significance with a Monte-Carlo test: (n + 1)/(r + 1), where r is the total number of shuffles and n is the number of shuffles that produce greater than or equal to the average R value as in the actual data.
We then tested how likely it was to get a small number of peaks in the hover location distribution from candidate events that occurred on the first pass. The “first pass” was defined as the first pass that there was a candidate event (range: 1–2, first pass was pass 1 in 26 sessions and pass 2 in 8 sessions), excluding any sessions that did not have enough replays in other passes to create 1000 different distributions (5 of 39 sessions). The first pass had a candidate event in 76% of the sessions (26), but for the other 24% of sessions (8) in which the first event occurred on the second pass, we used the second pass as the “first pass.” We took a histogram of the decoded position for any hover bins from the first pass. To find the number of peaks, we used MATLAB’s “findpeaks” function using a minimum peak prominence of 1.5 bins and a minimum peak distance of one tenth of the range of track positions. To test whether this value was smaller than chance, we generated a distribution of shuffles by randomly choosing the same number of candidate events as occurred on the first pass from any of the subsequent passes. We also added a criterion that the number of bins that were spent hovering across these candidate events needed to equal the number in the true data. We generated a distribution of 1000 shuffles for each session and compared the average number of peaks across sessions to the average number of peaks for each of these shuffles (Figure 6f) using a Monte-Carlo test: (n + 1)/(r + 1), where r is the number of shuffles and n is the number of shuffles that produce a number of peaks that is less than or equal to the true number of peaks.
HP Interneuron and PFC analyses
For HP interneuron and PFC analyses we loosened our criteria for replay (to weighted correlation > 0.3 and maximum jump distance < 0.7). This presumably increased our false positive rate for replays but allowed us to study second order effects of HP interneuron and PFC’s responses to replays with more power by increasing the number of events.
Analyses for our interneuron data was identical to those used here with Grosmark et al.’s data (Grosmark, Long and Buzsaki, 2016). We binned the interneuron firing rate into 20 ms bins and computed a modulation window (m, from −100 ms to 100 ms) that we compared to a baseline window (b, from −400 ms to −100 ms) around the start of replays: (m−b)/(m+b). We calculated this modulation index for each replay and correlated it with the pass the replay occurred on (using the first 26 passes; Pearson’s correlation). We plotted the correlation of each HP interneuron in a histogram and performed a one-sided Wilcoxon signed-rank test to test whether the population had correlation values greater than zero.
We recorded PFC neurons alongside HP neurons as rats ran on an asymmetric Y-maze(X. Wu and Foster, 2014). Here, we decoded candidate events using 2-d fields (with a gaussian filter with radius 50 cm, sigma 5 cm; lap-by-lap decoding with 20 ms bins with 5 ms sliding window) and then projected the estimates of position into the three linear arms as defined by the experimenter. For each candidate event, we calculated the number of time-bins that the peak posterior of position was on each arm, and identified periods where the peak posterior position was on one arm for at least 50 ms. If only one arm had representation for over 50 ms, that event was designated as an event of that arm. If no arms had a representation for over 50 ms, the event was discarded. If two arms had a representation for over 50 ms, the event was cut into two events at the midpoint between when one arm’s representation ended and the next arm’s representation started. We binned each PFC neuron’s firing rate into 40 ms bins and z-scored this across time for each neuron. We split replays into two equal groups based on their duration. To visualize the difference between these groups we averaged the z-scored firing rate for each PFC neuron for each group of replays. We assessed the significance of the sustained modulation to long replays two ways. We used a two-way ANOVA to compare 0–80 ms after replays begin to 80–160 ms after, across short and long replays, to test whether PFC modulation was elevated for longer during long replays. We also used a one-sided Wilcoxon signed-rank to test the difference in firing rate across all neurons between the two groups in the 80–160 ms window after replay started. We repeated this test using only replays of each of the three arms as well.
Supplementary Material
Highlights.
Sustained replay appears after a single experience.
With repeated experience in a new place, replay slows down.
This effect was dependent on experience, not time, and was environment-specific.
Within hover-and-jump dynamics, replays slow down by adding more hover locations.
Acknowledgements
This work was supported by National Institutes of Health grant MH103325.
Footnotes
Declaration of Interests
Authors declare no competing financial interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ambrose RE, Pfeiffer BE and Foster DJ (2016) ‘Reverse Replay of Hippocampal Place Cells Is Uniquely Modulated by Changing Reward’, Neuron, 91(5), pp. 1–13. doi: 10.1016/j.neuron.2016.07.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berners-Lee A, Wu X and Foster DJ (2021) ‘Prefrontal cortical neurons are selective for non-local hippocampal representations during replay and behavior’, The Journal of Neuroscience, 41(April), p. JN-RM-1158–20. doi: 10.1523/JNEUROSCI.1158-20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G (1996) ‘The Hippocampo-Neocortical Dialogue’, Cerebral Cortex, 6(2), pp. 81–92. doi: 10.1093/cercor/6.2.81. [DOI] [PubMed] [Google Scholar]
- Buzsáki G (2015) ‘Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning’, Hippocampus, 25(10), pp. 1073–1188. doi: 10.1002/hipo.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr MF, Jadhav SP and Frank LM (2011) ‘Hippocampal replay in the awake state: a potential substrate for memory consolidation and retrieval.’, Nature neuroscience, 14(2), pp. 147–53. doi: 10.1038/nn.2732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng S and Frank LM (2008) ‘New Experiences Enhance Coordinated Neural Activity in the Hippocampus’, Neuron. 2008/01/25, 57(2), pp. 303–313. doi: 10.1016/j.neuron.2007.11.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cichosz P (1999) ‘An analysis of experience replay in temporal difference learning’, Cybernetics and Systems, 30(5), pp. 341–363. doi: 10.1080/019697299125127. [DOI] [Google Scholar]
- Csicsvari J et al. (2007) ‘Place-selective firing contributes to the reverse-order reactivation of CA1 pyramidal cells during sharp waves in open-field exploration’, European Journal of Neuroscience, 26(3), pp. 704–716. doi: 10.1111/j.1460-9568.2007.05684.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson TJ, Kloosterman F and Wilson MA (2009a) ‘Hippocampal replay of extended experience’, Neuron. 2009/08/28, 63(4), pp. 497–507. doi: S0896–6273(09)00582–0 [pii] 10.1016/j.neuron.2009.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson TJ, Kloosterman F and Wilson MA (2009b) ‘Hippocampal replay of extended experience’, Neuron. 2009/08/28, 63(4), pp. 497–507. doi: S0896–6273(09)00582–0 [pii] 10.1016/j.neuron.2009.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duszkiewicz AJ et al. (2019) ‘Novelty and Dopaminergic Modulation of Memory Persistence: A Tale of Two Systems’, Trends in Neurosciences, 42(2), pp. 102–114. doi: 10.1016/j.tins.2018.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum H (2017) ‘Prefrontal–hippocampal interactions in episodic memory’, Nature Reviews Neuroscience, 18(9), pp. 547–558. doi: 10.1038/nrn.2017.74. [DOI] [PubMed] [Google Scholar]
- Feng T, Silva D and Foster DJ (2015) ‘Dissociation between the Experience-Dependent Development of Hippocampal Theta Sequences and Single-Trial Phase Precession’, Journal of Neuroscience, 35(12), pp. 4890–4902. doi: 10.1523/JNEUROSCI.2614-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Ruiz A et al. (2019) ‘Long-duration hippocampal sharp wave ripples improve memory’, Science, 364(6445), pp. 1082–1086. doi: 10.1126/science.aax0758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster DJ (2017) ‘Replay Comes of Age’, Annual review of neuroscience, 40(1), pp. 581–602. doi: 10.1146/annurev-neuro-072116-031538. [DOI] [PubMed] [Google Scholar]
- Foster DJ and Wilson M. a. (2006) ‘Reverse replay of behavioural sequences in hippocampal place cells during the awake state’, Nature. 2006/02/14, 440(7084), pp. 680–683. doi: 10.1038/nature04587. [DOI] [PubMed] [Google Scholar]
- Frank LM, Stanley GB and Brown EN (2004) ‘Hippocampal Plasticity across Multiple Days of Exposure to Novel Environments’, Journal of Neuroscience, 24(35), pp. 7681–7689. doi: 10.1523/JNEUROSCI.1958-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershman SJ and Daw ND (2017) ‘Reinforcement Learning and Episodic Memory in Humans and Animals: An Integrative Framework’, Annual Review of Psychology, 68(1), pp. 101–128. doi: 10.1146/annurev-psych-122414-033625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosmark AD and Buzsaki G (2016) ‘Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences’, Science, 351(6280), pp. 1440–1443. doi: 10.1126/science.aad1935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosmark AD, Long J and Buzsaki G (2016) ‘Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning.’, CRCNS.org. doi: 10.6080/K0862DC5. [DOI] [Google Scholar]
- Gupta AS et al. (2010) ‘Hippocampal replay is not a simple function of experience.’, Neuron, 65(5), pp. 695–705. doi: 10.1016/j.neuron.2010.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MP and Frank LM (2009) ‘Awake replay of remote experiences in the hippocampus’, Nat Neurosci. 2009/06/16, 12(7), pp. 913–918. doi: 10.1038/nn.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkin MC et al. (2014) ‘Hippocampal output area CA1 broadcasts a generalized novelty signal during an object-place recognition task’, Hippocampus, 24(7), pp. 773–783. doi: 10.1002/hipo.22268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AK and Wilson MA (2002) ‘Memory of Sequential Experience in the Hippocampus during Slow Wave Sleep’, Neuron. 2002/12/24, 36(6), pp. 1183–1194. doi: 10.1016/S0896-6273(02)01096-6. [DOI] [PubMed] [Google Scholar]
- Lengyel M and Dayan P (2008) ‘Hippocampal Contributions to Control: The Third Way’, Advances in neural information processing systems, NeuRIPS, 20, pp. 889–896. Available at: http://cbl.eng.cam.ac.uk/pub/Public/Lengyel/Publications/lengyel08-suppl.pdf. [Google Scholar]
- Leutgeb S et al. (2004) ‘Distinct ensemble codes in hippocampal areas CA3 and CA1.’, Science (New York, N.Y.), 305(5688), pp. 1295–8. doi: 10.1126/science.1100265. [DOI] [PubMed] [Google Scholar]
- Liu K, Sibille J and Dragoi G (2019) ‘Preconfigured patterns are the primary driver of offline multi-neuronal sequence replay’, Hippocampus, 29(3), pp. 275–283. doi: 10.1002/hipo.23034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P et al. (2016) ‘Hippocampal CA1 Ripples as Inhibitory Transients’, PLOS Computational Biology. Edited by Blackwell KT, 12(4), p. e1004880. doi: 10.1371/journal.pcbi.1004880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Barnes CA and Mcnaughton BL (1997) ‘Experience-dependent, asymmetric expansion of hippocampal place fields’, Proceedings of the National Academy of Sciences of the United States of America, 94(16), pp. 8918–8921. doi: 10.1073/pnas.94.16.8918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Quirk MC and Wilson MA (2000) ‘Experience-Dependent Asymmetric Shape of Hippocampal Receptive Fields’, Neuron, 25(3), pp. 707–715. doi: 10.1016/S0896-6273(00)81072-7. [DOI] [PubMed] [Google Scholar]
- Monaco JD et al. (2014) ‘Attentive scanning behavior drives one-trial potentiation of hippocampal place fields.’, Nature neuroscience, 17(5), pp. 725–31. doi: 10.1038/nn.3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris RGM et al. (1982) ‘Place navigation impaired in rats with hippocampal lesions’, Nature, 297(5868), pp. 681–683. doi: 10.1038/297681a0. [DOI] [PubMed] [Google Scholar]
- Nádasdy Z et al. (1999) ‘Replay and Time Compression of Recurring Spike Sequences in the Hippocampus’, The Journal of Neuroscience. 1999/10/26, 19(21), pp. 9497–9507. doi: 10.1523/JNEUROSCI.19-21-09497.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Carroll CM et al. (2006) ‘Dopaminergic modulation of the persistence of one-trial hippocampus-dependent memory’, Learning & Memory, 13(6), pp. 760–769. doi: 10.1101/lm.321006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J and Nadel L (1978) The Hippocampus as a Cognitive Map. Oxford: Oxford University Press. doi: 10.1086/411699. [DOI] [Google Scholar]
- O’Neill J et al. (2008) ‘Reactivation of experience-dependent cell assembly patterns in the hippocampus.’, Nature neuroscience, 11(2), pp. 209–15. doi: 10.1038/nn2037. [DOI] [PubMed] [Google Scholar]
- Oliva A et al. (2018) ‘Origin of Gamma Frequency Power during Hippocampal Sharp-Wave Ripples’, Cell Reports, 25(7), pp. 1693–1700.e4. doi: 10.1016/j.celrep.2018.10.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palacios-Filardo J and Mellor JR (2019) ‘Neuromodulation of hippocampal long-term synaptic plasticity’, Current Opinion in Neurobiology, 54, pp. 37–43. doi: 10.1016/j.conb.2018.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer BE and Foster DJ (2015) ‘Autoassociative dynamics in the generation of sequences of hippocampal place cells.’, Science (New York, N.Y.), 349(6244), pp. 180–3. doi: 10.1126/science.aaa9633. [DOI] [PubMed] [Google Scholar]
- Redish AD (2016) ‘- in the oth’, Nature Reviews Neuroscience, 17(3), pp. 147–159. doi: 10.1038/nrn.2015.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds SI (2002) Experience Stack Reinforcement Learning for Off-Policy Control, Technical Report CSRP-02–1. The University of Birmingham. Available at: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.19.6979. [Google Scholar]
- Scoville WB and Milner B (1957) ‘Loss of Recent Memory After Bilateral Hippocampal Lesions’, Journal of Neurology, Neurosurgery & Psychiatry, 20(1), pp. 11–21. doi: 10.1136/jnnp.20.1.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin JD, Tang W and Jadhav SP (2019) ‘Dynamics of Awake Hippocampal-Prefrontal Replay for Spatial Learning and Memory-Guided Decision Making’, Neuron, 104(6), pp. 1110–1125.e7. doi: 10.1016/j.neuron.2019.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva D, Feng T and Foster DJ (2015) ‘Trajectory events across hippocampal place cells require previous experience’, Nature Neuroscience, 18(12), pp. 1772–1779. doi: 10.1038/nn.4151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeuchi T et al. (2016) ‘Locus coeruleus and dopaminergic consolidation of everyday memory’, Nature, 537(7620), pp. 357–362. doi: 10.1038/nature19325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulving E (1972) ‘Episodic and semantic memory’, in Tulving E and Donaldson W (eds) Organization of memory. New York and London: Academic Press, pp. 382–402. doi: 10.1016/B978-0-12-809324-5.21037-7. [DOI] [Google Scholar]
- Tulving E (2002) ‘Episodic Memory: From Mind to Brain’, Annual Review of Psychology, 53(1), pp. 1–25. doi: 10.1146/annurev.psych.53.100901.135114. [DOI] [PubMed] [Google Scholar]
- Watkins CJCH (1989) Learning from delayed rewards, PhD Thesis. Cambridge University. [Google Scholar]
- Wilson M. a and McNaughton BL (1993) ‘Dynamics of the hippocampal ensemble code for space.’, Science (New York, N.Y.), 261(5124), pp. 1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- Wu X and Foster DJ (2014) ‘Hippocampal Replay Captures the Unique Topological Structure of a Novel Environment’, Journal of Neuroscience, 34(19), pp. 6459–6469. doi: 10.1523/JNEUROSCI.3414-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X and Foster DJ (2014) ‘Hippocampal Replay Captures the Unique Topological Structure of a Novel Environment’, Journal of Neuroscience, 34(19), pp. 6459–6469. doi: 10.1523/JNEUROSCI.3414-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zielinski MC, Tang W and Jadhav SP (2020) ‘The role of replay and theta sequences in mediating hippocampal-prefrontal interactions for memory and cognition’, Hippocampus, 30(1), pp. 60–72. doi: 10.1002/hipo.22821. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This paper analyzes some existing, publicly available data. These accession numbers for the dataset are listed in the key resources table and in the references. Other data reported in this paper will be shared by the lead contact upon request.
Individual units were separated using custom clustering software (xclust2, M.A. Wilson). All analyses were performed using custom code written in MATLAB (Mathworks). Custom code has been deposited in a public repository: ZenodoDOI:10.5281/zenodo.6330850; https://zenodo.org/badge/latestdoi/466486266
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning. | Grosmark, A. D., Long, J. and Buzsaki, G. (2016) ‘Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning.’, CRCNS.org | DOI: http://dx.doi.org/10.6080/K0862DC5 |
| Experimental models: Organisms/strains | ||
| Male Long-Evans rats | Charles River | RRID:RGD_2308852 |
| Software and algorithms | ||
| MATLAB R2020b | MathWorks | RRID:SCR_001622 |
| Custom data processing and analysis code | This paper | Zenodo DOI: 10.5281/zenodo.6330850; https://zenodo.org/badge/latestdoi/466486266 |


