Abstract
Do cities accelerate COVID-19 transmission? Increased transmission arising from population density prompts spatial policies for financial support and containment, and poorer prospects for recovery. Using daily case counts from over 3,000 counties in the U.S. from February to September 2020, I estimate a compartmental transmission equation. Rational sheltering behavior plausibly varies by location, so I propose two instruments that exploit unanticipated variation in exposure to potential infection. In the first month of local infections, an additional log point of population density raises the expected transmission parameter estimate by around 3%. After the first month, the relation vanishes: density effects occur only in the outbreaks. Public transport, work-from-home jobs and income explain additional variation in transmission but do not account for the density effects. Consistent with location-varying optimal sheltering behavior, I document stronger mobility declines in denser areas, but only after the first month of infections. These results suggest that differences in transmission between cities and other places do not motivate spatial policies for recovery or containment, or poorer prospects after the pandemic.
Keywords: COVID-19 transmission, Cities, Population density, Sheltering choices, Instrumental variables
1. Introduction
Cities are plausible protagonists in the spread of the COVID-19 epidemic. High population densities imply frequent face-to-face interactions, crowding, and wide-ranging social networks. Moreover, cities were the hotbeds of many historical epidemics, including the plague and cholera. However, the evidence that links population density to contagion is mixed for the COVID-19 pandemic. Some studies report a graver incidence of COVID-19 in densely and more populated locations, such as Whittle and Diaz-Artiles (2020, for zip codes within New York), Stier et al. (2021, for U.S. cities) or Lin et al. (2020, for Chinese cities). Other studies report no significant impact of population density or only an impact on the local epidemic’s timing (e.g., Hamidi et al., 2020 and Heroy, 2020 for U.S. metropolitan areas and counties and Ribeiro et al., 2020 for Brazil), and a few studies report outright negative associations of population density and COVID-19 prevalence (such as Fang and Wahba, 2020 and Qiu et al., 2020 for China). The lack of consensus is not unique for COVID-19: the evidence on the role of population density is mixed for many modern day infectious diseases (Li et al., 2018).
It is important to understand whether densely populated areas propel transmission for at least two reasons. First, cities are the pinnacle of human proximity, and proximity becomes perilous during an infectious disease pandemic. Crowding, jobs that rely on close interaction, denser living arrangements, large face-to-face service industries and wider social networks – all found in cities – magnify fears of contagion. The consequences of population density in the current epidemic will likely persist over time. Labor markets have been transformed by structural investments, for instance, in teleworking infrastructure; habits have changed, such as the demand for services or commuting choices; and fears remain of the endemic pressure of the current virus and of future epidemics. The organization of cities and their labor markets during and after the recovery headline in academic discussions (Florida et al., 2020, Nathan and Overman, 2020 among many others) as well as policy advise (WHO, 2020, World Bank, 2020, UN, 2020). Evidence on the transmission risks of cities helps these debates. Second, and more acutely, estimates of urban transmission risk help to explain and predict the spread of the epidemic, as many CDCs expect sizable consequences of density for COVID-19 transmission. The U.S. CDC, for instance, has published a manual on the mitigation of transmission in densely populated areas,1 but lists population density as a parameter in need of identification for the Pandemic Planning Scenarios (September 2020). Relatedly, the U.S. and many European countries apply localized lockdowns and spatial non-pharmaceutical interventions (e.g., Chowdhury et al., 2020), and vaccination strategies may become more effective with spatial prioritizations (Grauer et al., 2020). The rationale for such policies, the contribution of densely populated cities to virus transmission, still has a thin evidence base.
This paper analyzes whether the speed of COVID-19 transmission varies systematically with population density. First, I conjecture that urban living affects transmission in two ways: directly, due to inevitable proximity and interaction in dense areas, and indirectly, as density affects people’s decisions to seek exposure or to stay home. I argue that possibly, higher infection rates may rationally incite more sheltering for people who live in denser areas. Then, I estimate transmission parameters from a fixed effects equation for infections in daily case data covering U.S. counties, which allows for time- and location-varying estimates of transmission parameters. The methodology employs two novel instrumental variables to isolate transmission parameters from the location-specific sheltering behavior that might influence the number of transmissions. The instruments are based on ex post local case statistics revisions and on unanticipated infections (conditional on the same-day information set). They both represent shocks to infection risk to which people could not adapt their exposure choices.
Areas of higher population density had significantly higher transmission rates, but only in the local onsets of the epidemic. Areas with an additional log point of density have around 0.03 higher transmission parameters- or San Francisco’s transmission parameter is 16% higher than that of a county of median density. After the first month of local infections, densely populated areas show no different transmission rates than other areas do. Correlated explanations for transmission risk, such as public transport use and work-from-home job shares, show significant impacts on transmission in the onset of infections too. However, they do not explain the impact of density on transmission estimates. In line with the conjectured behavioral responses, I show that location-specific sheltering responses arise: sheltering (staying home, avoiding work, transit and shops) is significantly more pronounced in densely populated areas after a month of local infections, and device-tracking mobility data reveal that people avoid destinations of high infections, relative to other destinations, in particular in dense areas.
This paper studies the local transmission of COVID-19, while most related literature studies cross-sectional variation the incidence of COVID-19. For instance, Stier et al. (2021), Ribeiro et al. (2020), Heroy, 2020, Wheaton and Kinsella Thompson, 2020, Carozzi et al. (2020), Glaeser et al. (2020) and Almagro and Orane-Hutchinson (2020) explain differences across cities, counties and neighborhoods in COVID-19 cases, case growth, testing rates or mortality. The conclusions about the role of density in COVID-19 related outcomes are mixed. There are two advantages to estimating transmission parameters. First, the transmission is estimated as the number of new cases arising out of previous cases, which avoids direct level comparisons between counties. The ratio of new cases to the preceding stock of infectious people is not necessarily influenced by local confounders such as an airport that introduces external patients, the quality of the local health infrastructure, or the climate. Moreover, instrumenting the infection rate with unanticipated infections relieves worries about such omitted variables, if those omitted variables are uncorrelated with the statistical revisions used as instrument. The transmission equation can be estimated in first differences and allows the introduction of state-day fixed effects. The detailed fixed effects allow controlling for county time-invariant factors such as an area’s affluency or education, and for localized time variant explanations, such as NPIs, identification rates or awareness of risks, when explaining the prevalence of COVID-19. As a second advantage, the methodology exploits the limited period of infectiousness for repeated observations of transmission, and takes no stance on which cross-section to select. Selecting a cross-section for cross-county level comparison is not necessarily neutral. As Fig. 4 in the Appendix shows for the data used in this paper, the cross-sectional correlations between population density and infection rates may be negative, neutral or positive, depending on the cross-section selected (both for cross-sections of calendar days and cross-sections in days since the first local case). As an additional contribution, the supporting analyses in this paper add to literature that relates sheltering choices and social distancing to people’s income, ethnicity, political preference, job types and means of transport (e.g., Engle et al., 2020, Brzezinski et al., 2020, Crowley et al., 2020). The results of this paper show that local geographical conditions, including population density, labor market characteristics and transport infrastructure, explain sheltering choices. Additionally, they show that sheltering has a more sophisticated geographical structure than documented so far: infection rates determine the choice where to travel, in addition to the choice whether to travel.
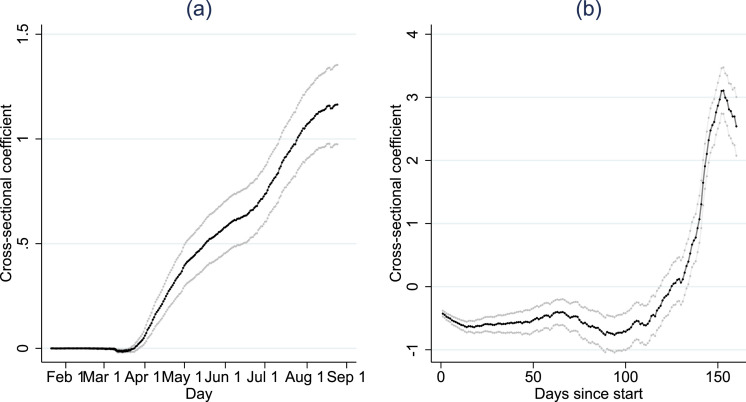
Fig. 4.
Cross-sectional relation between incidence and log population density.
Notes. The reported coefficient is the estimate of a cross-sectional regression of incidence (new cases per 100,000 cap) on log population density. Panel (a) reports the coefficients for cross-sections of calendar days. Panel (b) reports the coefficients for cross-sections of the number of days since a county developed 10 cases (i.e., the cross-section at 50 days since start compares all counties that experienced 50 days of local infections). The gray lines indicate (robust) 95.
2. Estimating transmission
To structure the analysis, I first fix ideas on how people choose sheltering behavior in the face fo infection risk, before laying out the methodology and data. The number of transmissions of COVID-19 in a city is plausibly the result of the intensity of interaction between its inhabitants. The intensity of interaction in a city, in turn, follows from the way the city is organized on the one hand (i.e. an environmental factor), and from how citizens respond to the expectation of being infected on the other hand (i.e. a behavioral factor). The formalization is highly stylized, portraying identical people and generic exposure behavior, as it is intended to develop to provide an intuition with the econometric methodology.
2.1. Rational exposure choices
Suppose that identical people in a city choose a level of exposure to infection . The term exposure is intended to capture all individual behavior that increases risks of infection, such as workplace travel, social visits, shopping, inviting guests, or less distancing within the home. People incur a benefit from exposure, such as showing up at work or enjoying social interactions, which they value at rate . Exposure has decreasing returns: the marginal benefit of exposure declines in the quantity of exposure. The overall benefit is , where a higher parameter (between 0 and 1) reflects more strongly decreasing returns from exposure. Exposure can also cause infection. An infection does damage to the person, for illness or inability to work due to isolation, for instance. The probability of being infected follows a standard epidemiological formulation, in which susceptible persons randomly interact with others who may be infectious but not (yet) isolated. For a susceptible person, the expected probability of acquiring an infection on a given day is . In this expression, is the expected share of infectious (but not isolated) individuals of group size out of all individuals . For simplicity, I assume that the number of isolated cases is small, such that approximates the potential number of interactions. People may develop an expectation of the current number of infectious individuals based on the number of positive tests. Due to test reporting delays and an imperfect prediction of how tests results relate to the current number of infectious people, the precise number is unknown when making an exposure choice, so people make decisions on their expectation of the infection rate, . The term is the transmission parameter, which is determined by the contact rate – a susceptible person’s share of daily interactions out of all possible interactions – and the probability of transmission within a possibly infectious interaction. The transmission parameter is a function of the environmental factors , such as the local population density or the city’s reliance on public transport, which facilitate or reduce transmission. It is also a function of the average choice of exposure of all other people in the city, . If others choose higher levels of exposure, such that there is more crowding and interaction, and less precautions, the probability of transmission is higher. The expected damage of exposure at level is the product of the infection probability and the damage, per unit of exposure: .
Every citizen optimizes the benefits of exposure net of costs: . Optimizing with respect to the decision of exposure, , gives the optimal exposure level as:
| (1) |
People choose higher levels of exposure if the ratio of damage to benefits is low; if the local expected infection rate is low; and if the local transmission parameter is lower. Hence, as infection rates rise, the reduction in travel may be stronger for people in denser areas (where is high). The average rate of exposure is the average of all individuals’ optimized exposure levels .2
This choice of exposure can be inserted into a standard compartmental (“SI” or “SIR”) model for infectious diseases, by allowing the transmission parameter to be affected by exposure choice, . In compartmental models, susceptible persons (of number ) can be infected by interactions with infectious persons (of number ). The infection equation relates the number of infections to the number of potential infectious interactions ( times ), multiplied by the transmission parameter, . In this setup, a standard infection equation of the form contains two channels by which the city organization affects transmission. First, reflects urban features such as the population density and transport infrastructure that directly moderate the probability of transmission for a given level of infectious people and exposure behavior. Second, the term is the exposure choice averaged across citizens: as more people relax caution, the transmission parameter rises. Urban features and their interaction with the expected local infection rates, , affect the choice to expose (Eq. (1)), thus indirectly affecting transmission parameters. As people anticipate higher infection rates, they will reduce exposure, hence limiting transmission. Following the exposure choice decision in (1), the degree of reduction in exposure can vary with the city’s population density or transport infrastructure, if those factors amplify transmission probabilities.
One might estimate the transmission parameter as the rate at which infectious people () cause new cases, and check whether the transmission varies systematically with density. However, that estimate is biased when people adapt their behavior to the anticipated local infection rates and to their urban environment summarized in . The transmission parameter depends on behavioral choices , and therefore on expected infection rates . Hence, the estimation suffers from endogeneity, as i) higher anticipated local infection rates lead people to adjust their exposure, and ii) the magnitude of adjustments may vary between locations according to their density, even if the infection rates are the same.
To analyze transmission in isolation of exposure and other behavioral responses, the estimates below exploit instrumental variables that correlate to the actual infection rates , but are plausibly unrelated to the infection rate expectations that determine the choice of exposure, . Hence, the moment conditions do not suffer from the endogeneity of . In supporting analyses, I also draw on phone-tracked movement data to examine whether different behavior measures of travel, exposure and sheltering (summarized in ), respond to local infection rates, and whether these differ with the density of population.
2.2. Estimating equation
The number of new infections is estimated as in a standard compartmental (“SIR”) model, in which infections are identified at time in location , denoted , arise as:
| (2) |
where is the number of potential pairs for interaction between infectious and susceptible people; is the transmission parameter that determines what share of interactions lead to infection; and is the time between the infection and the identification of the infection. For a comparison of the transmission parameter across different assumptions on the duration of infectiousness, I divide the term by the days of infectiousness (which relates the transmission parameter to the reproduction number Wallinga and Lipsitch, 2007, Lloyd, 2009).
In order to allow for spatial interactions in this model, I assume that people can acquire infections in other locations, proportional to outward commuting flow shares from an origin to destination , (e.g. Song et al., 2017).3 The potential for interaction is then replaced for a measures of infection rates average across destinations with commuting weight: , where is the population at the destination and is the relevant infection rate at the destination.
To infer whether (the log of) population density is structurally associated with the transmission parameter estimate , I introduce an interaction of the local log population density with the infectious measure. This identifies whether the rate of new case development out of interactions is faster in areas of high population density. Two modifications are required to validate this interpretation of the equation.
First, I estimate the infection equation in first differences and include fixed effects for the state-day combinations. First-differencing excludes time-invariant spatial confounders, such as a highly connected local labor market, climatic conditions or an airport that leads to external introductions of patients, from explaining the results.4 State-day fixed effects () absorb daily variation over counties within the same state, so the estimate is unaffected by developments in understanding of the virus and treatment and state-specific shocks, policies and interventions. As the fixed effects are time-varying, they may also account for national or state-specific variations in the quality of detection. This gives the following estimating equation, in which test whether population density affects the transmission parameter:
| (3) |
2.3. Instrumentation
The second methodological step addresses that behavioral responses affect the estimate of transmissions. In compartmental models, like in this context, is the product of the number of contacts per person per day, and the probability of transmission per contact. If people in high-density areas reduce their contacts, the estimate of from Eq. (3) reflects that a) density affects transmission directly (e.g. because of likely crowding) and b) density may make people more cautious when infection rates are high (i.e. population density encourages sheltering).
To separate the direct impact of density from its behavioral implications, I use an instrumentation strategy. The strategy exploits unanticipated variation in interactions with local infectious people, so that people did not have the opportunity to adjust their behavior. As a result, the possibility that people stay home or avoid work does not explain the estimated transmission rate.
The first instrumental variable is the ex post revision of infection rates. The daily reported county case numbers are often revised in the ensuing days, for instance due to updated medical records, miscommunications on the numbers, or changes to the location of registration. As revisions to case statistics are known only after the day that they describe, people cannot adjust their travel behavior on that day. I construct a county’s daily exposure to revisions as , where is the correction of the case numbers for county at day . The revision is calculated from the historical versions of the New York Times COVID-19 datasets, by comparing the local case numbers published on the day itself to local case numbers in the final dataset.
The data show revisions for 22,395 county-day combinations. As corrections are positive and negative, the average correction is small (1.6 cases) but the standard deviation is 31 across all county-day observations, and 139 across county-day observations that experienced a correction. Revisions occurred frequently across all periods of the pandemic, and on a daily basis the number of affected counties is just under 1,500.5 A concern could be that positive revisions typically occur when local cases are rising, in which case the instrument simply identifies outbreaks. This concern is minor: the directions is not explained by case numbers – 1,000 local cases in a day in a county increase the probability of the correction being positive by 5% () unconditionally, and by 0.1% () conditional on the state-day fixed effects.
The second instrument is the deviation of actual cases from the predictable cases, denoted “unpredicted cases”. The instrument exploits that on the day of travel or shelter choices, only the results of tests taken up to approximately two days before are available. Shocks to the number of people who test positive are unknown on that same day. I use the two-day lagged information on infection rates and impose the weekly trend to predict the contemporaneous infection rate, and subsequently I isolate deviations of the actual infection rate from that prediction. The prediction is: . The unpredicted share in the infection rate is , which is the error of the simple predictive equation. Consequently, I construct the instrument as .
2.4. Infectious time and detection delays
To quantify potential interactions with infectious people, two parameters are needed: the average number of days of infectiousness , and the number of days from infection to detection . The baseline results are derived under the assumptions of 5 days of infectiousness and 6 days to detection. This stems from the following observations (Siordia, 2020, Pung et al., 2020). Patients typically become infectious from the third day after infection but develops symptoms after 5 days. Infectiousness may last up to three weeks, but transmission typically occur in a shorter time frame: viral loads decline for after 7 days for the majority of patients; more severe cases are likely to lead to isolation; and transmission frequently occurs in the presymptomatic stage (He et al., 2020). Hence, the average time of infectiousness is plausibly less than 9 days. The number of infectious people on day is proxied as the number of people testing positive in the ensuing days, consistent with being infectious at : . The virus is generally detectable and likelier to be detected from the third day since infection, but on average no longer than nine days, as patients see viral loads decline or develop pneumonia.
From a statistical viewpoint, a model with fewer days of infectiousness than days to detection is desirable: otherwise, the new cases for a given day enter into the infectious rate measures for that same day (though it is biologically possible that when a patient infects another patient, the infector could be identified later than the infected). Lastly, the evolution of susceptible people requires specification. In the baseline results, I take to be the entire population. This assumption has little consequence: allowing for up to three times the number of positive cases to become permanently immune does not qualitatively change the results.
A full set of results that explores all combinations of assumptions on time of infectiousness and time to detection from 3 to 9 days is reported in a supplementary Appendix S1.
One concern is that a fixed number of days of infectiousness and of infection to detection may approximate the evolution of infections imprecisely. Many infections are detected upon the onset of symptoms, and some infections are detected much beyond the sixth day. In the results section, I examine how sensitive the results are to the assumption of fixed duration. I re-estimate the transmission equation based on a compartmental model in which infectiousness follows a composite exponential distribution, and compare the results. An added benefit of the compartmental model-based approach is that it provides a direct estimate of the number of infectious people, too, while in the fixed-duration model, the number of infectious is assumed proportional to the number of cases (subsequently) identified.
2.5. Data
Daily county COVID-19 case counts from January to September are from the New York Times Github repository. The counts include both laboratory-confirmed and probable cause cases compiled from reports from state and local health agencies. The case counts are based on clinical criteria and epidemiological linking in addition to laboratory-confirmed cases, following the Council of State and Territorial Epidemiologists protocol. These were the preferred estimates as the limits to test capacity severely underidentified the number of cases, and led official sources favor a broader definition. Still, cases plausibly go undetected, and rates of testing may differ per location. The rate of detection is likely not equal to one, but the main variables and both scale to the local rate of detection, and the fixed effects difference out state-day shocks. Hence, imperfect detection rates may affect the estimates in particular if the detection rates show both strong within-state differential trends and sharp breaks within days.6
The data on population density are drawn from the population counties the most recent 5-year American Community Surveys (ACS) of 2018. To check stability against definitions of density, I use three calculations: i) the number of people over area, ii) the number of people over built area,7 and iii) the number of houses over area. Selected covariates (public transport use shares among commuters, wages, unemployment health insurance coverage and occupation distributions) are drawn from the ACS in 2018 accessed through IPUMS (Ruggles et al., 2020). The share of work-from-home jobs is calculated as the (weighted) share of workers that have a job classified as teleworkable (Dingel and Neiman, 2020). Trip frequency changes are from the Google mobility reports (Google, 2020). Table 6 in Appendix A lists the full sample descriptives for the variables of the main analysis. The code used to collect, clean and merge the data is available from the website of the author.
3. Results
In the full sample, there is no evidence to suggest that the estimate of the transmission parameter varies with population density. Column 1 of Table 1 summarizes the baseline transmission parameter estimate: unconditionally on population density, an increase of one case in the 5-day mean infection rate leads to 1.2 new cases, on average. Columns 2 to 4 show that for any definition of population density, the interaction coefficient of density and exposure is insignificant.
Table 1.
Transmission equation (IV) conditioned on different definitions of population density.
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
|
|---|---|---|---|---|---|---|---|---|
| Full sample | 1st month after first 10 cases | |||||||
| 1.19*** | 1.34*** | 1.24*** | 1.27*** | 1.29*** | 1.09*** | 1.21*** | 1.08*** | |
| (0.08) | (0.29) | (0.16) | (0.28) | (0.07) | (0.14) | (0.11) | (0.12) | |
| log density | −0.02 | 0.03** | ||||||
| X | (0.05) | (0.01) | ||||||
| ln density | −2.01** | −1.37*** | ||||||
| (0.87) | (0.45) | |||||||
| log built density | −0.01 | 0.02* | ||||||
| X | (0.03) | (0.01) | ||||||
| log built density | −1.34** | −0.90*** | ||||||
| (0.62) | (0.30) | |||||||
| log house density | −0.01 | 0.03*** | ||||||
| X | (0.05) | (0.01) | ||||||
| log house density | −2.13** | −1.41*** | ||||||
| (0.98) | (0.45) | |||||||
| Observations | 583,301 | 583,301 | 577,393 | 582,656 | 87,146 | 87,146 | 86,449 | 87,056 |
| State-day fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Kleibergen Paap F | 146.5 | 72.28 | 19.31 | 37.97 | 132.5 | 63.39 | 48.74 | 60.44 |
| Hansen J | 1.329 | 3.190 | 3.202 | 3.823 | 3.520 | 3.579 | 3.634 | 3.591 |
| p-value | 0.249 | 0.203 | 0.202 | 0.148 | 0.0606 | 0.167 | 0.162 | 0.166 |
Notes. *** 0.01, ** 0.05, * 0.1. The dependent variable is the county-day level of cases. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. is the 6-day lagged 5-day average number of infected, weighted for each destination county with the origin-normalized commuting flows, multiplied with the origin population.
Consistent with the expectation that higher local infection rates invoke cautious behavior, the instrumentation to account for sheltering behavior leads to significantly higher estimates of transmission parameters by approximately 20%, see Appendix B. Across the results of Table 1, instrument tests show no concern for relevance or exogeneity. Appendix B examines the performance of the instruments in more detail. In the main specification, an additional corrected case is associated with 0.14 actual cases (), an additional unpredicted case is associated with 0.07 actual cases (), and the first-stage f-statistic is 146, demonstrating the instrument relevance also conditional on the fixed effects. The instruments are individually relevant, too. The exogeneity assumption suggests that the instruments should not affect travel of exposure choices. Appendix B confirms that the instruments do not predict observed measures of sheltering indexes, including homestaying, and work and recreation movements.
The process of transmissions looks different in the onset of the crisis. Columns 5 to 8 of Table 1 use observations on the first 30 daily observations (“1st month”) after a county has developed 10 cases. The data in the first month of infections does show a significant role for density: the transmission parameter estimate is roughly 0.03 higher for every log point of density. Alternatively interpreted, San Francisco’s predicted transmission parameter is approximately 16% higher than in a county of median population density. This magnitude is similar across definitions of density.
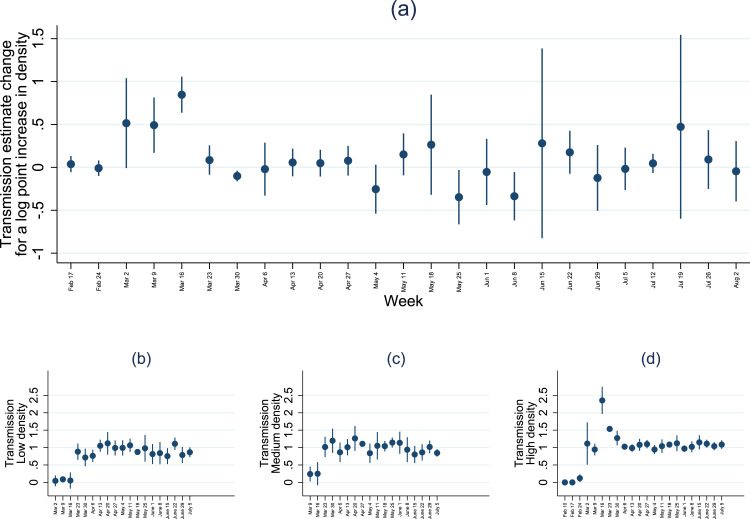
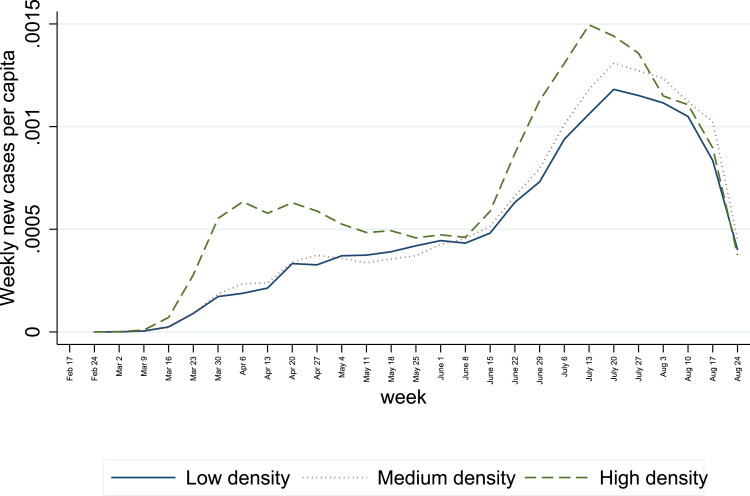
To further explore the time-varying role of transmission implied by the results of Table 1, I estimate the role of density by week, and I split the sample by three tertiles (of low, median and high population density) to estimate the weekly transmission by group of density.8
Fig. 1, panel (a), visualizes the weekly coefficient for the interaction between log population density and infectious rates. The coefficient is significant and positive in the earliest weeks of the outbreak, with an additional 0.8 points for every log unit of log density at the peak. The coefficient implies that the predicted transmission parameter in San Francisco is close to 5 times higher than in a county of median population density. The coefficient for the interaction is close to zero from April onward, suggesting that population density is not associated with faster transmissions. For illustration, if for three weeks the transmission parameter is 1.5 instead of 1, and assuming a reinfection period of 5 days, then the cumulative number of (ever) infected is 4.5 times higher in three weeks. Even if the transmission parameter is reverts to 1 after the initial three weeks, the aggregate number of infected is persistently higher after three weeks of elevated transmission parameters.
Fig. 1.
Weekly transmission estimates and population density.
Notes. The coefficients report the estimated transmission rate from exposure (6 days to detection, 5 days of infectiousness), with exposure instrumented by commuting-matrix based data revisions and unanticipated infections. The whiskers show 95% confidence intervals.
Fig. 1, panels (b) to (d) show weekly transmission parameter estimates for county groups of low, median and high population density. The largest transmission parameter estimates by far are reported for high-density counties in the week of March 16 onward. By the week of April 6th, the transmission parameter confidence intervals are around 1 for all density groups, if slightly lower in the least populated counties.9 The elevated estimates of transmission parameters coincide with a sharp rise in daily cases per capita in the most densely populated counties early on in the outbreak. For reference, Appendix C shows a plot of cumulative cases per capita for the three groups, showing an earlier rise in cases in densely populated areas. In the regression, the number of counties with non-zero cases contributing to identification rises sharply in the week of March 16, from 421 to 1,116. Moreover, the number of new cases rise quickly in the vicinity of New York City. However, the conclusions do not materially change when adding or dropping New York from the sample.
3.1. Covariates of density effects
Several of the culprits of infection risk identified in the emerging COVID-19 literature correlate closely with population density. Citizens of larger (and denser) cities rely more on crowdable public transport which is frequently linked to transmission (Tian et al., 2020, Hamidi and Hamidi, 2021). Urban areas host more service jobs that require physical interaction, but at the same time, urban areas also host higher income jobs that permit more precautions, less time on the job and in some cases spacier living conditions (a.o. Takagi et al., 2021, Almagro and Orane-Hutchinson, 2020). Relatedly, health insurance coverage may affect caution in choices for interaction. Unemployment, on the other hand, could reduce mobility. Finally, age structure could play a role in virology and mobility: children appear to be weaker spreaders of the virus, whilst elderly people suffer heavier infections (Dowd et al., 2020).10
The results in Table 2 shows the impact of population density on the transmission rate, when controlling for covariates suggested by the literature. As before, the log of population density is significant only in the first month of local infections (columns 4 to 6). Areas show higher transmission rates if they have higher health insurance coverage and higher shares of children, and if they have lower wages and lower unemployment. Public transport shares are linked to larger transmission in the long run, as are higher wages, lower shares of work-from-home job shares, and elderly and children. A sample standard deviation in increase in public transport use (16% point of commuters) is linked to a 0.04 points higher transmission; a sample standard deviation in work-from-home jobs (2% point of jobs) is linked to 0.13 points lower transmission; and a sample standard deviations in elderly and children are linked to 0.14 and 0.18 points higher rate transmission estimates.
Table 2.
Transmission equation (IV) conditioned on different urban covariates.
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
|---|---|---|---|---|---|---|
| Full sample | First month | |||||
| 1.24*** | −6.18 | −7.00 | 0.81*** | 6.63 | 8.52 | |
| (0.32) | (8.71) | (9.36) | (0.29) | (7.04) | (7.09) | |
| Interacted with.. | ||||||
| log density | −0.01 | −0.04 | 0.07** | 0.12*** | ||
| (0.06) | (0.07) | (0.03) | (0.01) | |||
| Public transport share | 0.25*** | 0.22*** | −0.01 | 0.07*** | ||
| (0.09) | (0.08) | (0.03) | (0.02) | |||
| Health insurance coverage | −0.46 | −0.05 | 2.15** | 2.03** | ||
| (1.24) | (1.11) | (0.88) | (0.92) | |||
| log average wage | 0.97* | 0.92* | −0.57*** | −0.62*** | ||
| (0.50) | (0.47) | (0.11) | (0.12) | |||
| Unemployment rate | −3.12 | −2.96 | −2.70* | −1.92*** | ||
| (5.09) | (4.96) | (1.54) | (0.56) | |||
| Proximity index of jobs | −0.51 | −0.39 | −0.87 | −1.11 | ||
| (2.01) | (2.12) | (1.01) | (1.01) | |||
| Work-from-home | −6.24* | −6.44* | 0.46 | 0.86 | ||
| Share of jobs | (3.40) | (3.44) | (1.27) | (1.18) | ||
| Share elderly (70) | 8.35*** | 8.98*** | −0.49 | 0.24 | ||
| (2.81) | (3.10) | (1.19) | (1.35) | |||
| Share children (18) | 5.65*** | 6.75*** | 3.93** | 4.42*** | ||
| (1.28) | (1.92) | (1.62) | (1.56) | |||
| Observations | 87,460 | 86,620 | 86,620 | 12,234 | 12,234 | 12,234 |
| State-day fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Interaction arguments | Yes | Yes | Yes | Yes | Yes | Yes |
Notes. *** 0.01, ** 0.05, * 0.1. The dependent variable is the county-day level of cases. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. is the 6-day lagged 5-day average number of infected, weighted for each destination county with the origin-normalized commuting flows, multiplied with the origin population. Public transport share (of all commuters), health insurance coverage, unemployment rate, work-from-home share of jobs (of all jobs), share elderly and share children are shares of population or subpart of population where indicated — ranging from 0 to 1, see descriptive statistics for details on covariates.
The conclusions on the role of density are unchanged when controlling for correlated factors. In the first month of infections, the contribution of density on transmission is in fact larger, rather than smaller, once confounding explanations are controlled for — the coefficient rises from 0.07 to 0.12 in this sample. A potential explanation is that high wage workers concentrate in cities, and higher wages are associated with lower transmission (0.10 points lower for a sample standard deviation).
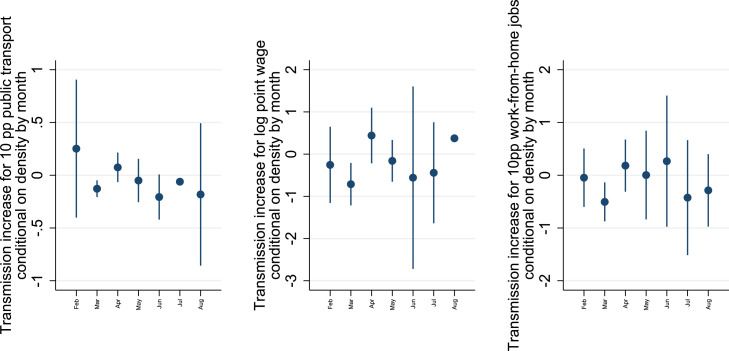
The large role of density in the initial outbreaks cannot be explained by the variables most correlated with density: public transport share in commutes, wages and work-from-home job shares. To analyze the contributions over time, Fig. 2 graphs estimates of the covariates’ contributions to transmission rate estimates by month, conditional on the month-varying impact of density on the transmission rate. The month March shows a negative conditional contribution to transmission for public transport use (0.17 points lower transmission per 10%p commuters in public transport), and high wages and work-from-home job shares (resp 0.7 point lower transmission for a log point in average wage and 0.4 point lower for 10%p in work-from-home job shares) - all significant at . The impact in March coincides with a stronger association of density with transmission in the same period (Fig. 1), so they do not explain the simultaneous peaks in transmission in large cities.11
Fig. 2.
Impact of public transport, wages and work-from-home job shares on the estimated transmission.
Notes. The coefficients report the monthly change estimated transmission rates with per 10 percentage point public transport user share, per log point wage, and per 10 percentage point the share of work-from-home jobs, by month. The reported coefficients are conditional on the impact of density on the estimated transmission rate. Instrumentation: commuting-matrix based data revisions and unanticipated infections. The whiskers show 95.
3.2. Relaxing the fixed duration assumption
The measures of infectious population used thus far rely on an assumption of a fixed duration of infectiousness and detection. When imposing more structure on the data, the fixed duration assumption can be relaxed for a more realistic development of infections to detection. In this subsection, I use the structure of a compartmental model with virological parameters. The compartmental model produces (convolutions of) exponential distributions of the number of infectious people since the day of their infection. Compared to a fixed duration model, the exponential model produces a skewed distribution of infectious people over the days since infection, which allows relatively many people to be infectious shortly after infection on the one hand, and allows a portion of cases to persist beyond the horizon of the fixed duration framework on the other hand. To check the robustness of the main estimates to assuming a fixed duration approach, I recover the numbers of infections and infectious people by day implied by an epidemiological model. Subsequently, I check whether the main results change when estimating the main regressions under the assumption that the epidemiological model is the (deterministic) data generating process.
I assume that infections follow a susceptible–exposed–infectious–removed (SEIR) compartmental framework (e.g., Lloyd, 2009). The dynamics are that interactions between susceptible and infectious (the potential is per head) produce new infections at a daily proportion , leading the infected to move from the susceptible () to the exposed compartment (). In the exposed stage, the infection is latent — people are infected but not infectious. The reason to include a latent stage is that for COVID19, infected persons do not become infectious instantly, and that the latent stage allows the number of days to detection and the number of days of infectiousness to differ, as in the fixed duration approach. From the exposed compartment, people become infectious at daily rate , moving into the infectious compartment . I assume that cases are identified at a constant daily rate from the infectious group. The assumption that latent patients are not detected allows the most likely day of detection to be the second day or later, rather than immediate detection. Infectious people are removed from the infectious compartment as they recover at daily rate , or if they are identified and isolated, at daily rate . I assume that in either case, the removed become effectively non-infectious. The movement through compartments is summarized by the following system:
| (4) |
This SEIR framework provides a probability distribution of the day of infection for every identified case, by connecting the day of identification to the model-implied probabilities of the corresponding day of infection. The SEIR equations also predict the quantity of people who are infectious on a given day. The distributions of infections and infectious people by day are constructed as follows. Of all infectious people, rate is tested positive daily. The cumulative inflow into the infectious compartment is the sum of previously exposed over the preceding days , turned infectious at proportion per day. The daily removal share from the infectious department is , such that the expected cases identified by day is: . Using to define infections at date , the pool of exposed at time is: . Using this expression for the size of the exposed compartment in the days preceding detection, the expected detection at time of a set of preceding infections is:
| (5) |
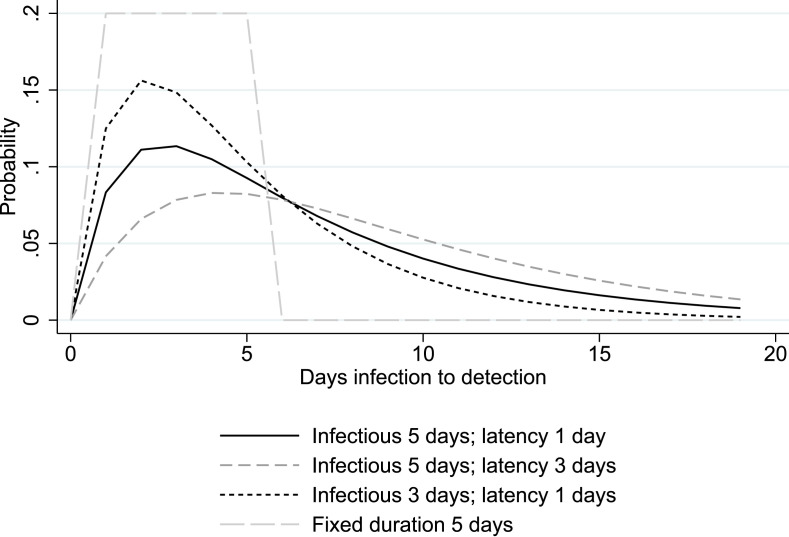
Hence in system (4), for a set of identified cases on a given day, the epidemiological parameters , , and produce an exponential distribution of the number of infections by preceding days. The density distribution is given by , where , and . A more detailed derivation is in Appendix D. Fig. 3 describes the probability distribution of days to detection for different assumptions of the parameters, which can be summarized by the mean number of days of infectiousness, , and the mean number of days of latency, . The SEIR model produces a convolution of exponential distributions, rather than a uniform distribution as under the fixed duration (of infectiousness of 5 days and 6 days to detection; the gray dashed line in the Figure). The probability density rises in the first days, as infected people go through the exposed stage and see increasing likelihood of detection, and declines in later days as infectious people are tested or recover. Shorter spans of infectiousness imply larger probabilities of detection earlier on, while longer latency leads to longer average duration to detection.
Fig. 3.
Distribution of the time between infection and detection.
Notes. Lines represent the probability distribution of days between infection and detection. The parameters of the SEIR model (rate of transition from exposed to infectious; rate of infectious to removed) are selected to be consistent with the mean duration reported in the legend.
Based on the quantity of positive tests per day, the SEIR-model implies a quantity of infections per day. First, I assign all identified cases (i.e., positive tests) to a day of infection according to the probability weight that follows from the parameters , , and . Then, I aggregate all the assigned cases from later detection by implied day of infection to approximate the number of infections on that day. Finally, to construct the number of infectious people by day, I use the SEIR model evolution on infectiousness since the day of infection, and aggregate the implied infectious people by day across all days of original infection.
The advantage of estimating a transmission equation based on model-implied infections is that it may account for more realistic disease dynamics. For instance, in the fixed duration model, the infectious impact of a short local peak is caused by five days of a large infectious compartment , and then vanishes, while realistically, the intensity may be high on day three and low but not absent by day seven. However, imposing a model structure on the daily infections has two downsides. First, it complicates the analysis of spatial processes. With a commuting or proximity matrix, the likelihood of a detected infection originating in another county can be formulated, but there will be a model-constructed spatial relation between infections and preceding infectiousness in the resulting dataset. Second, the instrumentation is less accurate. Every identified case has an infection probability distribution over the preceding days, while the instrument (the unanticipated or revised number of positive tests) is defined for a single day. As a consequence, the instrument is likely contain unanticipated test rates from both before and after the actual day of infection. In order to still make a comparison between estimates derived from a model data generating process on the one hand, and the assumption of fixed duration on the other, I show transmission equation estimates based on local transmission (i.e. within the county), noting that the case for exogeneity of the instruments is weaker when using model-implied infection rates.
Table 3 shows the results of estimating the within-county transmission equation during the first month12 of local infections implied by SEIR models. The columns represent different assumptions on the distributions of days of infectiousness and latency, as indicated in the first rows. For comparison, the estimates of the fixed duration model (of 5 days of infectiousness and 6 days to detection) for within county infections are reported in the first column. As before, the size of the infectious pool is scaled to its mean duration to foster comparability across the columns. Panel (a) reports coefficient estimates for the transmission equation. For comparable horizons of infectiousness and detection, the estimated coefficient is around 3% higher when using a SEIR data generating process. Allowing for shorter or longer periods of infectiousness or latency leads to minor changes in the coefficient. When moving to model-based infection rates, Hansen exogeneity tests frequently reject, as may be expected: in contrast to the fixed duration case, the definition of the instrumental variable is not strictly based on observations preceding the day of infection, so it is likely to predict the number of new infections directly. In panel b, the infectious rate measures are interacted with local population densities. As before, density is associated with a higher transmission coefficient. An additional unit of log density adds around 0.07 to the transmission coefficient. This contribution is comparable for all reported parameters on the SEIR model-based estimates, while it is just over 0.04 in the fixed duration model of similar parameters. Hence, the results based on infection rate estimates from epidemiological models suggest a similar, if slightly larger role for population density in the first month.
Table 3.
Transmission equation (IV) for different underlying epidemiological data generating processes.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Mean days of.. | ||||||
| Infectiousness | Fixed | 5 | 4 | 7 | 5 | 5 |
| Latency | duration | 1 | 1 | 1 | 2 | 3 |
| Panel a: transmission | ||||||
| 1.17*** | 1.208*** | 1.171*** | 1.273*** | 1.226*** | 1.247*** | |
| (0.062) | (0.0458) | (0.0430) | (0.0514) | (0.0511) | (0.0555) | |
| Observations | 81,594 | 81,594 | 81,594 | 81,594 | 81,594 | 81,594 |
| State-day FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Kleibergen Paap F | 252 | 113.3 | 129.1 | 97.04 | 103.9 | 96.38 |
| Hansen J | 3.15 | 4.410 | 4.433 | 4.357 | 4.403 | 4.392 |
| p-value | 0.116 | 0.0357 | 0.0352 | 0.0369 | 0.0359 | 0.0361 |
| Panel b: conditioned on density | ||||||
| 0.88*** | 0.711*** | 0.645*** | 0.825*** | 0.723*** | 0.748*** | |
| (0.055) | (0.178) | (0.174) | (0.190) | (0.193) | (0.207) | |
| x log density | 0.043*** | 0.0706*** | 0.0751*** | 0.0636** | 0.0714*** | 0.0705** |
| (0.0051) | (0.0247) | (0.0243) | (0.0266) | (0.0270) | (0.0291) | |
| Log density | −0.67* | −0.562* | −0.470* | −0.672** | −0.594* | −0.624* |
| (0.37) | (0.296) | (0.278) | (0.323) | (0.319) | (0.338) | |
| Observations | 81,594 | 81,594 | 81,594 | 81,594 | 81,594 | 81,594 |
| State-day FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Kleibergen Paap F | 44.2 | 10.74 | 11.68 | 9.599 | 10.11 | 9.569 |
| Hansen J | 2.87 | 4.280 | 4.286 | 4.255 | 4.292 | 4.296 |
| p-value | 0.24 | 0.118 | 0.117 | 0.119 | 0.117 | 0.117 |
Notes. *** 0.01, ** 0.05, * 0.1. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. In column 1, the dependent variable is the number of new cases detected at the county-day level andis the 6-day lagged 5-day average number of infected measured within the county. In columns 2–6, the dependent variable is the daily number of county infections implied by the SEIR model based on observed detections. is the pool of infectious as constructed according to the SEIR model. The durations of latency and infectiousness translate to SEIR parameters asandrespectively.
3.3. Mobility reductions
The argument that location determines how people respond to infection risk can be tested directly, too. I examine how changes in exposure (as used in the infection equation) drive changes in mobility. The mobility measure is the daily county-level percentage difference in phone-tracked trip frequency as compared to its frequency in the period January 3 to February 6, 2020. It is denoted . The infection rate used here is the commuting-flow weighted average infection rate across destinations, using 5 days of infectiousness and 6 days to detection as before: . When scaled with the number of susceptibles, the exposure rate is equal to the exposure level originally used. I estimate a variation of the transmission Eq. (3) to examine how mobility changes with exposure:
| (6) |
Note that as is determined before , there is no reverse causality. The outcome is measured in change relative to the county baseline mobility, so variation between counties in time-invariant mobility patterns do not explain the results. A county-level fixed effect accounts for the average exposure and trip decline of a county (as there is no potential for Nickell bias as there was in the transmission equation).13
The results in Table 4 show that counties with higher densities shelter more: when exposure rises, they show lower work trip frequency (per additional case per 1,000 capita, an additional log point in density is associated with 7 percentage point stronger decline, ), more home-staying (1.6 percentage point increase, ), and lower frequency in transit and retail and recreation (58 resp. 24 percentage points, ). There is no evidence of such a role of density in sheltering in the first month of local infections (columns 5 to 8). Counties with higher shares of work-from-home jobs and with lower average wages show more sheltering in the full sample, but less sheltering in the first month. Public transport is not associated with stronger sheltering responses in either period.
Table 4.
Mobility responses to exposure rates.
| Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
|---|---|---|---|---|---|---|---|---|
| Full sample |
First month |
|||||||
| Work | Home | Transit | Recreation | Work | Home | Transit | Recreation | |
| −537.10*** | 143.15** | −2,019.99*** | −1,296.94*** | 1,740.78** | −815.49** | 177.49 | 615.01 | |
| (132.48) | (55.64) | (632.63) | (291.45) | (845.23) | (404.84) | (1,947.74) | (1,054.93) | |
| Interacted with | ||||||||
| log density | −7.27*** | 1.63* | −58.16*** | −23.71*** | −13.17 | 4.68 | 4.61 | −32.96 |
| (2.23) | (0.86) | (10.76) | (6.06) | (10.84) | (3.55) | (33.06) | (21.26) | |
| Public transport | 0.06 | 0.00 | −11.41 | −0.40 | 2.62 | 4.52 | −5.13 | 25.55 |
| (2.53) | (1.19) | (16.02) | (10.40) | (7.11) | (3.59) | (25.05) | (15.48) | |
| log wage | 67.91*** | −23.13*** | 297.50*** | 169.14*** | −227.48** | 96.88*** | 0.90 | 28.15 |
| (15.57) | (6.24) | (82.30) | (37.57) | (100.35) | (35.99) | (229.81) | (126.38) | |
| Work-from-home | −410.14** | 267.53*** | −2,267.53*** | −1,023.23*** | 1,684.31** | −505.90** | −539.11 | −2,176.96** |
| jobs | (172.31) | (66.87) | (616.26) | (272.32) | (791.85) | (250.17) | (1,641.51) | (918.36) |
| Observations | 81,896 | 81,769 | 70,195 | 81,896 | 11,991 | 11,929 | 10,487 | 11,991 |
| R-squared | 0.96 | 0.96 | 0.85 | 0.94 | 0.96 | 0.96 | 0.92 | 0.96 |
| County fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| State-day fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
Notes. *** 0.01, ** 0.05, * 0.1. The dependent variable is the mobility index in the column-corresponding category. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. is the 6-day lagged 5-day average infection rate, weighted for each destination county with the origin-normalized commuting flows. “Public transport” is the share of commuters that uses public transport and “work-from-home jobs” is the county share of jobs classified as teleworkable, see descriptive statistics for details on covariates.
3.4. Destination choices
Do people avoid places with high rates of infections? The transmission rates are estimated based on infection rate measures that presume people travel between counties. In addition to changes in the general propensity to travel, phone movement data show changes in the destinations of travel. I use the PlaceIQ data on movement between counties (Couture et al., 2020) that record what share of the phones residing in a county has “pinged” (registered to a cell phone network) in another county over the previous two weeks. I estimate the regression equation with destination specific phone mobility:
| (7) |
The dependent variable pingshare is the share of phones residing in origin county that ping in destination county over the two weeks of period . As the phone-tracking data at any day is based on two weeks of historical data, I take two weeks preceding the first and 16th day of every month to avoid overlap in the time periods. The independent variable is the mean daily number of new cases per 1,000 inhabitants over the preceding two weeks in destination . The coefficient measures the association between infection rates in and the share of phones that recorded presence in over the period.
The specification contains fixed effects for origin–destination county pairs (), and for combinations of county of origin and day () that control for averages in trip volumes by pair, and for overall declines in travel by origin. The coefficient is identified by comparing whether trips from the same origin are lower to a specific destination relative to other destinations, when the destination’s infection rate rises relative to the other destinations.
Table 5, column 1, shows substantial reductions in visits to destinations with higher infection rates. The estimate in column 1 implies that an additional daily case per 10,000 inhabitants in the preceding two weeks in a destination is associated with a reduction of about 4 percentage points in the share of phones that moves to that area relative to other areas.
Column 2 shows that the reduction in trips for a given rise in destination infection rates is stronger for destinations of higher population density. An additional daily case per 10,000 inhabitants in the preceding fortnight leads to 1.4 percentage point additional reduction in phone movement, if a destination county is twice as dense (i.e. one additional log point). The regression in column 3 is restricted to observations in first the month after a destination develops the first case. In the first month of the local outbreak, the interaction coefficient is positive, implying that areas of higher density received comparatively more trips, rather than less trips. The evidence for sheltering behavior only after the first month of infections is consistent with earlier results.
The results in columns 4 and 5 examine whether trips between counties reduce more steeply, if they are connected by public transport. Public transport use in the American Community Survey (marked ACS in the Table) is only observed for a subset of all county pairs. The interaction between destination infection rates and the share of public transport users on the link is significantly negative, implying that mobility reduced more with rising infection rates for county pairs connected by public transport. As before, in the sample of observations in the first month after the destination developed infections, there is no such evidence. The higher coefficient estimates for the density-infection rate interaction is driven by selection in the ACS sample: repeating the original estimation of column 2 in the ACS sample in column 6 yields similarly elevated coefficients.
Taken together, these estimates suggest that phone movement towards infected areas declined, in particular towards dense areas. However, the decline is not present in the early stages of local outbreaks. Given the origin-time fixed effects in the estimating equation, the estimated decline in movement to affected counties is not explained by the reluctance to travel by people residing near outbreaks. Rather, the estimates reflect that people reduced their presence more substantially in heavily affected destinations, compared to their other destinations.
Table 5.
Share of phones by origin that are active in a destination county in the preceding two weeks.
| Share of phones active | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| in destination county | ACS |
||||||
| Full | 1st month | Full | 1st month | Full | 1st month | ||
| Cases per 1,000 cap | −0.41*** | 0.18* | −1.91*** | 74.47*** | −4.48 | 76.53*** | −0.44 |
| (daily over 2 weeks) | (0.03) | (0.10) | (0.43) | (7.87) | (35.84) | (8.01) | (36.43) |
| Interacted with | |||||||
| ln density destination | −0.14*** | 0.33*** | −13.43** | −0.49 | −13.78*** | −1.08 | |
| (0.03) | (0.09) | (1.04) | (4.28) | (1.06) | (4.37) | ||
| Public transport user | −9.75*** | −9.60 | |||||
| origin–destination | (3.64) | (14.92) | |||||
| Observations | 40,799,055 | 40,799,055 | 7,413,014 | 66,100 | 11,302 | 66,100 | 11,302 |
| Origin–destination FE | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Origin-time FE | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
Notes. *** 0.01, ** 0.05, * 0.1. Twoway (county and day) clustered standard errors in parentheses.
4. Discussion
The transmission of COVID-19 in the U.S. saw large differences across cities. Transmission risks associated with densely populated cities are critical to the recovery and future organization of cities and urban jobs. Moreover, urban transmission rates inform containment interventions and efficient vaccination strategies. The contribution of this article is to fit an infection equation to daily U.S. county level data and to examine whether the transmission varies structurally with the local population density. In doing so, the analysis proposes two instrumental variables to isolate behavioral responses from transmission estimates. It also explicitly documents such behavioral responses to potential infection.
The results show that population density links to faster transmission during the first month of local outbreaks, but not after. Plausible urban covariates to density (transport, incomes, work-from-home jobs) do not explain the result. The faster initial transmission in dense areas coincides with evidence of a delay in sheltering behavior: evidence for reduced mobility can only be found after the first month.
As such, cities may have kickstarted the spread of COVID-19. Their considerably higher initial transmission parameters may have caused higher infection levels within weeks. As dense area transmission speeds converged to but did not fall behind the transmission speeds of less dense areas, the higher infection rates may persist over time. The importance of early transmission suggests i) that the initial stages of the local outbreak are consequential for the gravity of COVID-19 impacts in later phases of the epidemic and ii) that later containment and recovery policies targeted at cities specifically find little motivation in the purported transmission risk, as the rates of transmission were not higher than elsewhere as the epidemic evolved.
The results are consistent with rational exposure choices that play a role in virus transmission — as conjectured when motivating the methodology and consistent with, e.g., Glaeser et al. (2020). Regressions with instrumented infectiousness measures show significantly higher transmission rates than OLS regressions do, which implies that the transmission from unanticipated exposure is higher than the transmission from exposure in general. General virus exposure also leads to increased levels of sheltering behavior, while unanticipated exposure does not. Auxiliary analyses show geographical aspects to sheltering. People from dense areas shelter more actively, and people actively avoid destinations with higher infection rates, in particular if the destination is more densely populated. Hence, the parameter for population density desired in the transmission equations of epidemiological planning scenarios plausibly depends on people’s choices to shelter.
The concentration of the role of density in early phases of outbreaks can have (at least) two explanations. First, denser, urban areas are generally hit earlier (see e.g. Fig. 7), and hence mechanically show higher case numbers when compared to other areas in a cross-section at a given point in time. Second, density could foster virus transmission, but as dense and urban areas develop a stronger behavioral response over time, their transmission rates gradually reduce towards the rates of other areas. In cross-sectional studies, it is often hard to differentiate the two explanations. Two new arguments may be found in this analysis that favor the second explanation. First, the results are based on virus transmission (connecting new cases to preceding infections), rather than on cross-sectional variation in the incidence of COVID-19. The transmission parameter does not depend on the level of infection rates or on the time since the virus was introduced. The transmission parameter is initially higher for larger cities, even for comparable times of introduction of the virus. Second, the fixed effects methodology controls comprehensively for state-day shocks, so differences in the understanding and containment effectiveness of the virus over time do not explain transmission estimates. Hence, differences in awareness or preparedness are less likely to explain differences in virus transmission when drawing comparisons between counties within a state-day combinations.
Fig. 7.
Development of new cases per capita among countries split by tertiles of population density.
There are several limitations to the results. The use of fixed effects may exclude groups of observations at different times if those groups have no within-variation, leading to a changing sample over time. Second, the set of covariates of density cannot be presumed exhaustive, such that other unobserved variables might explain the estimated impacts of density. Third, the population does not mix homogeneously, as the standard transmission equation presumes. The estimated transmission parameters may hence mask considerable variation in transmission within age groups or social groups. Fourth, the data are from a journalistic source that represents an ongoing data collection effort, and results may change as more data become available.
Footnotes
This paper has benefited from comments and help on data by Frank van Oort, Luc Coffeng, Joris Engbers and Daniel Arribas-Bel.
This stylized representation has immediate welfare implications. The aggregate welfare function is the sum of net benefits from exposure , where is the symmetric exposure choice and is the probability of infection per unit of exposure. The efficiency condition is . The first-order condition for the individual implies . Hence, the social costs of exposure are a factor higher than the private costs of exposure: the difference is the elasticity of the infection probability with respect to exposure choice. Hence, exposure is higher than socially optimal as the individual ignores the increased probability of others getting infected due to his/her own exposure choice.
The regressions in Supplementary Appendix S1 also explore the model performance when using within-county interactions or interaction measures based on phone movement. Commuting measures shows better fit in terms of Root Mean Squared Errors.
An augmented Pesaran test show no signs of residual serial correlation on the first-differenced series.
More information about variation in the instrument is visualized in Fig. 5 in the Appendix.
Mortality statistics might identify the long-run incidence more precisely, but they require sizable case-mix adjustment and have much larger variation in time-to-death (roughly 2 to 8 weeks according to the WHO), so they are less precise in identifying transmission. Testing rates are not generally reported precisely at the county level (HHS, 2020).
The built up land area share is calculated from the National Land Cover Database. It is calculated in QGIS as the share of pixels in each county polygon classified as “Developed Open Space”, “Developed Low Density”, “Developed Medium Density” ’or “Developed High Density” out of the total count of non-open water and non-perennial snow/ice pixels in the county polygon.
Less densely populated counties generally develop transmissions later; and conditional on state-day fixed effects, no transmission can be identified before March 2 in counties of medium or low population density.
Containment policy responses might also affect the estimates. In a supplementary Appendix S3, I explore the influence of non-pharmaceutical interventions on transmission rate estimates. The issuance of stay-at-home orders is linked to declines in the transmission rates, but only before summer. Other policies have no measurable impact conditional on the state-day fixed effects. The effect of a stay-at-home order on the transmission estimate shows an additional 0.01 point stronger reduction for every additional log point density. Hence, potential targeting of densely populated areas by containment policies may explain a part, but far from all of the reduction of their transmission estimates after the outbreaks.
Unreported direct monthly estimates of the impact of urban covariates on case development, and , show cross-sectional variation in case development unconditional on earlier exposure levels. Hence, they can be compared to studies that explain cross-sectional variation in infection rates. The results, however, depend on the selection of the time horizon: infection rates are positively associated with density per se early on, but negatively for cross-sections from June onward. For public transport use per se, the cross-sectional association with infection rates is negative in April but positive in May. These estimates and may not capture direct local transmission, as they do not measure moderation of the rate at which previous local infections predict new cases.
As before, there are no significant results with data after the first month of local infections.
In a supplementary Appendix S4 I verify that sheltering occurs as expected in the data. Regressions of trip change on infection rates, conditional on county and state-year fixed effects, show that one infection per 1,000 people is associated with 28% fewer workplaces trips (p=0.00), and similarly intuitive and significant results on transit, parks, shopping, recreation, and staying.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.euroecorev.2022.104283.
Appendix A. Data
A.1. Descriptive statistics
The cross-sectional relation between population density and COVID-19 incidence is frequently estimated using a regression equation of the form:
| (8) |
where measures the expected additional cases per 100,000 people per log point of density.
Table 6.
Descriptive statistics for variables used in the baseline results.
| Mean | Standard deviation | Count | |
|---|---|---|---|
| Case number revision | 1.65 | 30.85 | 484.,89 |
| Commute-weighted case number revisions | 2.28 | 24.76 | 605,963 |
| Census 2018 population | 102,127 | 327,220 | 728,186 |
| Change in cases | 8.65 | 67.02 | 726,264 |
| −0.00 | 291.66 | 602,609 | |
| Exposure to commute-weighted case number revisions | 1.15 | 62.45 | 590,057 |
| Exposure to commute-weighted unanticipated cases | 3.69 | 146.63 | 590,057 |
| Ln population density | 2.91 | 1.76 | 602,394 |
| Ln population density (built environment) | −0.01 | 2.63 | 719,896 |
| Ln house density | 3.02 | 1.67 | 727,088 |
| Public transport share of commuters | 0.15 | 0.29 | 727,418 |
| Ln mean wage | 10.15 | 0.18 | 727,418 |
| Work-from-home job share | 0.34 | 0.03 | 727,418 |
Notes. This table reports the full-sample statistics at the county-day level. The number of observations used varies by regression.
Fig. 4 plots the development of the relation between density and incidence for two types of cross-sections. Panel (a) shows the estimate of by calendar day. The coefficient reported in panel (b) reflects estimates in cross-sections of the day since the first case. The coefficient is identified for counties that experienced the same period of infections, even though the calendar date may differ. The comparison is hence between counties with similar periods of progression into the epidemic.
The cross-sectional coefficients do not deliver a uniform message. In calendar day cross-sections, the relation is significant and negative in early spring of 2020, but turns significant and positive as the pandemic progresses — suggesting that population density was briefly associated with lower infection rates, and then with higher infection rates. In cross-section of the number of days into local infections, the coefficient is negative at first, but turns positive later on — suggesting that population density predicted lower infection rates in the first months of a local outbreak, but higher infection rates in later stages of development.
A.2. Job context matching
In order to derive proximity indexes (and other job characteristics), I connect O*NET job context data on occupations to county-level estimates of the prevalence of those occupations. The county-level job requirements for proximity are approximated as the employment-weighted average of the context scores from O*NET. I use the 2018 crosswalk from the U.S. Census Bureau between the 2018 Census Code and the 2018 SOCcode. The hierarchical procedure is as follows: I merge based on the 6-digit crosswalk, then merge unmatched occupations on a 5-digit crosswalk, and then merge the remaining occupations on a 4-digit crosswalk. Using this, I merge 320 6-digit occupations, followed by 132 original 6-digit occupations on a 5-digit scheme, followed by 43 original 6-digit occupations on 4 digit scheme. The dataset supporting this paper also includes job context scores for exposure to infection, face to face discussion, exposure to contaminants and responsibility for others’ health and safety.
Appendix B. Diagnostics of the instrumental variable strategy
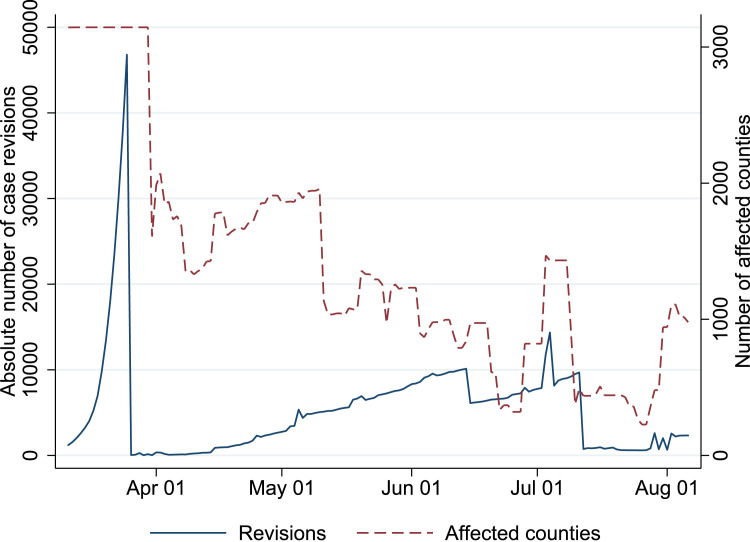
Figure Fig. 5 shows that considerable numbers of counties were affected by case count revisions every day. as argued in the main text, the revisions hsow little persistence over time by county. To illustrate the pattern of case count revisions, Figure Fig. 6 plots the daily revisions for three large counties.
Fig. 5.
Case number revisions and affected counties.
Notes. The solid blue shows that nationally aggregated absolute revisions of the COVID-19 cases, obtained by comparing the NYT case count at the day itself to case counts reported later on. The red dotted line shows the number of counties each day for which the commuting based exposure measure is affected by a case count revision.
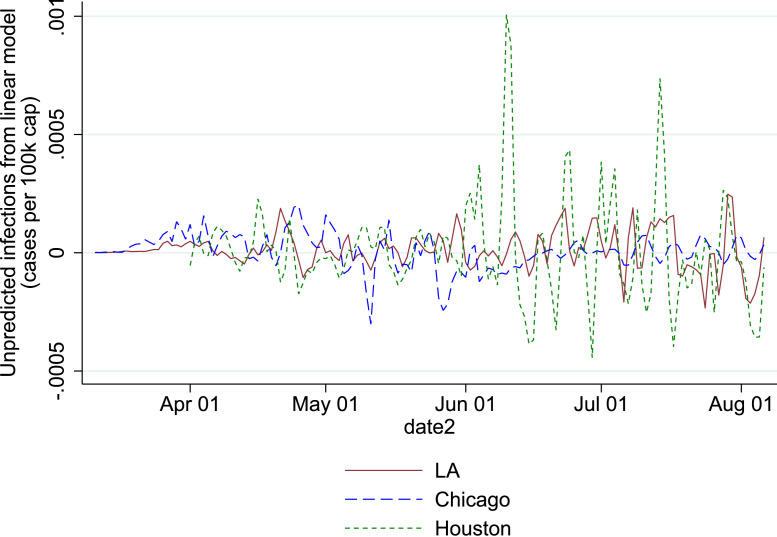
Fig. 6.
Development of unanticipated cases from weekly trend for three most populous counties.
Notes. The lines show the difference between the registered infectious rate and the predicted infectious rate, based on 2-day lagged weekly local trend. The three most populous counties are selected and referred to by their main city: Los Angeles County (Los Angeles), Cook County (Chicago) and Harris County (Houston).
To assess the relevance of the instruments, Table 7 regresses the preferred infectious rate (6 days lags in identification, 5 days of infectiousness, as described below) on the corresponding instruments. The infectious rate and the instruments are measured on the same scale, suggesting roughly one infection for every 5 revised cases, conditional on state-day fixed effects. Cases number revisions and unpredicted cases also show relevance conditional on the other instrument. From the F statistics, the revised cases number weighted by the commuting interactions is the instrument with highest relevance. After including the instruments constructed using commuting flows, the impact of the locally measured instruments is negative (columns 4 and 6), consistent with the better performance of commuting as interaction measures.
The instruments can be tested for exogeneity formally, as in Table 9, but the data also allow an informal test. The instrumentation needs to rule out that mobility and sheltering responses affect the transmission rate estimate. The informal requirement on the instrument is that it does not cause changes in mobility choice. The reasoning here is that revisions in the case numbers and deviations from the weekly infection rate trends are unforeseen, and do not contribute to mobility choices. Table 8 reports regressions to check whether the instrument set predicts changes in trip frequency to work, staying in the residence, presence on transit infrastructure, or higher shares of phones registering in the resident county. Conditional on the state-day fixed effects, the instruments show no significant association with any of the mobility measures.
Table 7.
First stage regressions: impact on exposure variable, conditional on fixed effects.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Revised cases (commuting) | 0.14*** | 0.16*** | 0.40*** | |||
| (0.01) | (0.01) | (0.13) | ||||
| Unpredicted cases (commuting) | 0.07*** | 0.07*** | 0.11* | |||
| (0.02) | (0.02) | (0.06) | ||||
| Revised cases (local) | 0.12*** | −0.22* | ||||
| (0.01) | (0.11) | |||||
| Unpredicted cases (local) | 0.30*** | −0.18 | ||||
| (0.07) | (0.19) | |||||
| Observations | 583,301 | 414,944 | 583,301 | 443,044 | 583,301 | 414,944 |
| State-day fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| F statistic | 146.5 | 144.3 | 213.4 | 67.66 | 18.95 | 206.6 |
Notes. *** 0.01, ** 0.05, * 0.1. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. Revised cases refer to ex post corrections in the count statistics. Unpredicted cases refer to the deviation in cases numbers from the two-day lagged weekly trend. Variables labeled “commuting” employ the between-county commuting flows as weights. Variables labeled “local” concern exposure within the county.
Table 9 shows the baseline transmission equation estimated in an OLS model and various instrumentations. The term takes the six day lag of five day infection rates from counties weighted by the commuting flows.
Table 8.
Impact of instruments on measures of mobility.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Workplace | Residence | Transit | Residential county pings | |
| Revised cases | −0.00015 | 0.000037 | 0.000083 | 0.000056 |
| (0.00038) | (0.00015) | (0.00047) | (0.000062) | |
| Unpredicted cases | −1.7e−06 | 0.000028 | 0.00013 | 0.000041 |
| (0.00030) | (0.00016) | (0.00067) | (0.000033) | |
| Observations | 112,130 | 55,554 | 47,335 | 213,808 |
| State-day fixed effects | Yes | Yes | Yes | Yes |
Notes. *** 0.01, ** 0.05, * 0.1. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. Revised cases refer tho ex post corrections in the count statistics. Unpredicted cases refer to the deviation in cases numbers from the two-day lagged weekly trend. Revised and unpredicted cases use the commuting flows to other counties to weigh the exposure.
The main set of instruments uses case number revisions and unanticipated cases from the same commuting-flow-weighted county set as the infectious rate variable. The instrumentation increases the transmission coefficient estimate by about 20%. The Kleibergen-Paap F statistics shows instrument relevance conditional on the state-day fixed effects. The Hansen J-test shows no signs of overidentification.
Columns 3 to 7 of Table 9 show the results using different instrument sets. Using only local case number revisions and unanticipated cases instead of those based on the commuting matrix, the coefficient is the unchanged. This is not entirely surprising, as there is a substantial correlation between the instruments created from the commuting matrix and those created from the local interactions only. The instrumentation based on case number revisions (columns 4 and 5) leads to slightly lower transmission estimates than the instrumentation based on unpredicted cases (columns 6 and 7). The Hansen J-test, accounting for the clustered nature of the standard errors, shows no overidentification when using instrument sets based on revisions and unanticipated infections. The J-test rejects when the local and commuting weighted revisions are introduced, and is close to rejection when the local and commuting weighted unanticipated infections are used.
Table 9.
OLS and IV estimates for the transmission rates: impacts on new cases.
| (1) | (2) | (3) | (4) | (6) | |
|---|---|---|---|---|---|
| 0.98*** | 1.19*** | 1.19*** | 1.12*** | 1.25*** | |
| (0.01) | (0.08) | (0.08) | (0.08) | (0.08) | |
| Observations | 583,510 | 583,301 | 414,944 | 583,301 | 583,301 |
| State-day fixed effects | Yes | Yes | Yes | Yes | Yes |
| Instruments used | |||||
| Revisions (commuting) | Yes | No | Yes | No | |
| Unpredicted (commuting) | Yes | No | No | Yes | |
| Revisions (local) | No | Yes | No | No | |
| Unpredicted (local) | No | Yes | No | No | |
| Kleibergen Paap F | 146.5 | 144.3 | 213.4 | 18.95 | |
| Hansen J | 1.329 | 1.168 | |||
| p-value | 0.249 | 0.280 | |||
| Endogeneity test -value | 0.00767 | 0.00524 | 0.108 | 0.00651 |
Notes. *** 0.01, ** 0.05, * 0.1. Estimated in first differences. Twoway (county and day) clustered standard errors in parentheses. is the 6-day lagged 5-day average number of infected, weighted for each destination county with the origin-normalized commuting flows, multiplied with the origin population.
Appendix C. Development of infected rates for low, medium and high density counties
See Fig. 7.
Appendix D. The distribution of days to detection and the number of infectious in the seir model
The number of identified cases per day is:
To get an intuition for the probability of being identified, I discuss the probability of an infected person for the first days of infection. It is helpful to define the ratio of the daily probability of remaining exposed to the daily probability of remaining in infectious as . The likelihood of being detected on the day of infection is zero. After one day, identification can happen if a person has moved from the exposed to infectious compartment, and is identified straight away. The probability is , the product of the detection rate and the rate of moving from exposed to infectious. In two days, there are two routes by which infected can evolve to detection: one day in exposed, or one day in infected, before being detected: . In three days, the probabilities across all routes sum to . The term is the likelihood of spending one day in the exposed compartment and one day in the infectious compartment. Note that it is not possible to move from infectious compartment back to exposed compartment. The general formulation for the likelihood of the possible routes from the day of infection to the day of detection, using the term to factor the geometric sequence , is: .
The aggregate probability mass to all routes of identification over all days to detection is:
| (9) |
The probability that an infection of date is detected at is, as in the main text:
| (10) |
The implied quantity of people in the infectious compartment at a given day can be constructed from the implied infections by day and the probability distribution of being infectious by day since infection. First, note that the probability distribution of being infectious after days since infection is proportional to the probability distribution of being detected. Suppose that observed detections over all days along with parameters , , and , imply a quantity of infections denoted by . Then, the pool of infectious people at day is .
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Data, code and auxiliary results.
References
- Almagro M., Orane-Hutchinson A. JUE insight: The Determinants of the Differential Exposure to COVID-19 in New York city and their evolution over time. J. Urban Econ. 2020 doi: 10.1016/j.jue.2020.103293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brzezinski A., Deiana G., Kecht V. The COVID-19 pandemic: Government versus community action across the United States. CEPR Covid Econ.: Vetted Real-Time Pap. 2020;7:115–156. [Google Scholar]
- Carozzi F., Provenzano S., Roth S. Institute of Labor Economics (IZA); 2020. Urban Density and COVID-19: Technical Report. [Google Scholar]
- Chowdhury R., Luhar S., Khan N., Choudhury S.R., Matin I., Franco O.H. Long-term strategies to control COVID-19 in low and middle-income countries: An options overview of community-based, non-pharmacological interventions. Eur. J. Epidemiol. 2020;35(8):743–748. doi: 10.1007/s10654-020-00660-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couture V., Dingel J., Green A., Handbury J., Williams K. 2020. Exposure indices derived from PlaceIQ movement data. https://github.com/COVIDExposureIndices/COVIDExposureIndices. [Google Scholar]
- Crowley F., Daly H., Doran J., Ryan G. COVID-19, social distancing, remote work and transport choice. CEPR Covid Econ.: Vetted Real-Time Pap. 2020;30 [Google Scholar]
- Dingel J.I., Neiman B. How many jobs can be done at home? J. Public Econ. 2020;189:1–8. doi: 10.1016/j.jpubeco.2020.104235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowd J.B., Andriano L., Brazel D.M., Rotondi V., Block P., Ding X., Liu Y., Mills M.C. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. 2020;117(18):9696–9698. doi: 10.1073/pnas.2004911117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engle S., Stromme J., Zhou A. Staying at home: Mobility effects of Covid-19. CEPR Covid Econ.: Vetted Real-Time Pap. 2020;4:86–102. [Google Scholar]
- Fang W., Wahba S. 2020. Urban density is not an enemy in the coronavirus fight: Evidence from China. World Bank Sustainable Cities blog, April 20, 2020. [Google Scholar]
- Florida R., Rodriguez-Pose A., Storper M. Cities in a post-COVID world. Pap. Evol. Econ. Geogr. 20.41. 2020 doi: 10.1177/00420980211018072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaeser E.L., Gorback C., Redding S.J. JUE insight: How much does COVID-19 increase with mobility? Evidence from new york and four other US cities. J. Urban Economics. 2020 doi: 10.1016/j.jue.2020.103292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Google, ., 2020. Google Mobility Reports retrieved from https://www.google.com/covid19/mobility/.
- Grauer J., Löwen H., Liebchen B. Strategic spatiotemporal vaccine distribution increases the survival rate in an infectious disease like covid-19. Nature. 2020;10(21594):1–10. doi: 10.1038/s41598-020-78447-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamidi S., Hamidi I. Subway ridership, crowding, or population density: Determinants of COVID-19 infection rates in New York City. Am. J. Prev. Med. 2021 doi: 10.1016/j.amepre.2020.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamidi S., Sabouri S., Ewing R. Does density aggravate the COVID-19 pandemic? Early findings and lessons for planners. J. Am. Plan. Assoc. 2020;86(4):495–509. [Google Scholar]
- He X., Lau E.H., Wu P., Deng X., Wang J., Hao X., Lau Y.C., Wong J.Y., Guan Y., Tan X., et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020;26(5):672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Heroy S. Metropolitan-scale COVID-19 outbreaks: How similar are they? ArXiv: Populat. Evol. 2020 [Google Scholar]
- Li R., Richmond P., Roehner B.M. Effect of population density on epidemics. Physica A. 2018;510(C):713–724. [Google Scholar]
- Lin C., Lau A.K., Fung J.C., Guo C., Chan J.W., Yeung D.W., Zhang Y., Bo Y., Hossain M.S., Zeng Y., et al. A mechanism-based parameterisation scheme to investigate the association between transmission rate of COVID-19 and meteorological factors on plains in China. Sci. Total Environ. 2020;737 doi: 10.1016/j.scitotenv.2020.140348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd A.L. Mathematical and Statistical Estimation Approaches in Epidemiology. Springer; 2009. Sensitivity of model-based epidemiological parameter estimation to model assumptions; pp. 123–141. [Google Scholar]
- Nathan M., Overman H. Will coronavirus cause a big city exodus? Environ. Plan. B: Urban Anal. City Sci. 2020;47(9):1537–1542. [Google Scholar]
- Pung R., Chiew C.J., Young B.E., Chin S., Chen M.I., Clapham H.E., Cook A.R., Maurer-Stroh S., Toh M.P., Poh C., et al. Investigation of three clusters of COVID-19 in Singapore: Implications for surveillance and response measures. Lancet. 2020 doi: 10.1016/S0140-6736(20)30528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu Y., Chen X., Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. J. Popul. Econ. 2020;33(4):1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribeiro H.V., Sunahara A.S., Sutton J., Perc M., Hanley Q.S. City size and the spreading of COVID-19 in Brazil. PLoS One. 2020;15(9) doi: 10.1371/journal.pone.0239699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggles S., Flood S., Meyer R.G.J.G.E., Pacas J., Sobek M. 2020. IPUMS USA: Version 10.0 [dataset] [Google Scholar]
- Siordia J.A., Jr. Epidemiology and clinical features of COVID-19: A review of current literature. J. Clin. Virol. 2020 doi: 10.1016/j.jcv.2020.104357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song L.-P., Zhang R.-P., Feng L.-P., Shi Q. Pattern dynamics of a spatial epidemic model with time delay. Appl. Math. Comput. 2017;292:390–399. [Google Scholar]
- Stier A.J., Berman M.G., Bettencourt L. Early pandemic COVID-19 case growth rates increase with city size. Nat. Partn. J. Urban Sustain. 2021;1(1):1–6. [Google Scholar]
- Takagi H., Kuno T., Yokoyama Y., Ueyama H., Matsushiro T., Hari Y., Ando T. Ethnicity/race and economics in COVID-19: Meta-regression of data from counties in the New York metropolitan area. J. Epidemiol. Community Health. 2021;75(2):205–206. doi: 10.1136/jech-2020-214820. [DOI] [PubMed] [Google Scholar]
- Tian H., Liu Y., Li Y., Wu C.-H., Chen B., Kraemer M.U., Li B., Cai J., Xu B., Yang Q., et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science. 2020;368(6491):638–642. doi: 10.1126/science.abb6105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- UN, 2020. UN Habitat: Covid-19 Policy and Programme Framework. Technical Report, Retrieved July 14 2020 from:.
- Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B: Biol. Sci. 2007;274(1609):599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheaton W.C., Kinsella Thompson A. 2020. The geography of COVID-19 growth in the US: Counties and metropolitan areas. Available at SSRN 3570540. [Google Scholar]
- Whittle R.S., Diaz-Artiles A. An ecological study of socioeconomic predictors in detection of COVID-19 cases across neighborhoods in New York City. BMC Med. 2020;18(1):1–17. doi: 10.1186/s12916-020-01731-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO R.S. World Health Organization 2019-nCoV Urban preparedness 2020(1); Geneva: 2020. Strengthening Preparedness for COVID-19 in Cities and Other Urban Settings: Interim Guidance for Local Authorities: Technical Report. [Google Scholar]
- World Bank R.S. Washington World Bank/Building Sustainable Cities and Communities; 2020. Urban and Disaster Risk Management Responses to COVID-19: Technical Report. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data, code and auxiliary results.