Protracted Indian monsoon droughts of the past millennium and their societal impacts

Significance

Severe and long-lasting droughts represent one of the greatest potential threats to human societies in the Indian subcontinent. While historical documentary sources from the region provide vivid accounts of catastrophic drought-related famines and mass mortality events, these accounts are fragmentary, and their veracity cannot always be confirmed. In this study, we have used the oxygen isotopes in speleothems from northeast India to reconstruct a history of Indian summer monsoon droughts over the past millennium with an unprecedented dating accuracy comparable in precision to historical records. Our reconstructed summer monsoon drought history is in striking synchrony with the historical evidence and provides important context against which the key geopolitical and societal changes and their links to climate can be assessed.

Abstract

Protracted droughts lasting years to decades constitute severe threats to human welfare across the Indian subcontinent. Such events are, however, rare during the instrumental period (ca. since 1871 CE). In contrast, the historic documentary evidence indicates the repeated occurrences of protracted droughts in the region during the preinstrumental period implying that either the instrumental observations underestimate the full spectrum of monsoon variability or the historic accounts overestimate the severity and duration of the past droughts. Here we present a temporally precise speleothem-based oxygen isotope reconstruction of the Indian summer monsoon precipitation variability from Mawmluh cave located in northeast India. Our data reveal that protracted droughts, embedded within multidecadal intervals of reduced monsoon rainfall, frequently occurred over the past millennium. These extreme events are in striking temporal synchrony with the historically documented droughts, famines, mass mortality events, and geopolitical changes in the Indian subcontinent. Our findings necessitate reconsideration of the region’s current water resources, sustainability, and mitigation policies that discount the possibility of protracted droughts in the future.

Spatially widespread multiyear failures of the Indian summer monsoon(ISM) potentially pose one of the most serious threats to human welfare and India’s vast monsoon-centric agriculture sector, which contributes ∼20% to its gross domestic product and employs nearly 60% of the workforce (1). However, such events have rarely occurred during the instrumental period (approximately the last 150 y). Various time series of the area-weighted rainfall such as the All India Summer Monsoon Rainfall (hereafter, AIR) (2) depict a monsoon system that appears to be remarkably stable over the instrumental period with rainfall oscillating biennially within a narrow range (±10% or ∼±1 SD of the long-term mean ∼900 mm) (3). There are sporadic aberrations in ISM rainfall manifesting as a 10 to 15% reduction in the AIR—a widely used metric for defining droughts (or “deficient rainfall”) over India (4). By this metric, India has experienced 27 droughts during the instrumental period, with only one instance of a 3-y consecutive drought (1985 to 1987 CE) (SI Appendix, Fig. S1A). Subcontinent-wide severe droughts or “monsoon failures” (>2 SDs departures in AIR) are rare, with only five such instances over the last 150 y, including the one in 1877 CE when the AIR fell ∼30% below the mean (SI Appendix, Fig. S1A) with devastating societal consequences (5). Instrumental observations also provide a hint to the quasi-oscillatory variability in ISM rainfall that appears to promote higher frequencies of droughts and pluvials over multidecadal periods of weaker and stronger monsoon, respectively (6). For example, ∼10 droughts occurred between the 1960s and 1990s, whereas only 4 droughts took place between the 1930s and 1960s (SI Appendix, Fig. S1B).

In contrast to the instrumental period, the historical documentary evidence and high-resolution proxy records paint a drastically different picture of ISM drought characteristics during the past millennium and beyond. For example, classical ancient Indian texts such as Arthshastra (ca. 150 CE) and Rigveda (ca. 1500 BCE) contain numerous accounts of continuous multiyear droughts and ensuing famines, some lasting for as long as 12 y (7). Periods of protracted droughts (defined here as droughts lasting more than three consecutive years and/or multidecadal periods with drought every other or every third year) are evident in the systematic compilations of historical droughts and famines that occurred between ∼1500 CE and 1900 CE (8–12) (SI Appendix, section 1). Reconstructions of ISM variability based on high-resolution proxy archives such as Himalayan ice cores (13), speleothems from central (14–17) and northern (18, 19) India, the Arabian Peninsula (20), Southeast Asia (21), and the gridded-tree-ring network over Asia (22–24) also indicate extended periods of droughts that broadly agree with the historic evidence of droughts and famines over the last 500 y.

Empirical and modeling considerations have alternately conceptualized ISM as a self-regulating coupled ocean–atmosphere system that tends to remain within a narrow range (3) or a system prone to abrupt nonlinear transitions between strong and weak states in response to changes in internal feedback mechanisms (16, 25). Understanding which of the two mechanisms, if either, will dictate the future behavior of ISM in a warming climate holds enormous societal implications. An extended record of ISM natural drought variability is, therefore, a vital estimate for assessing the true range of past climate variability and the degree to which it is represented in climate models. In this study, we have constructed a subannually resolved and precisely dated (average 1σ error ± 4 y) speleothem record from Mawmluh cave, located near the town of Cherrapunji (25°15′32″N, 91°42′45″E, 1,290 m above sea level) at the southern fringe of Meghalaya Plateau in northeast India (NEI) (SI Appendix, Fig. S2). Our data together with the historical evidence of droughts provide key insights into the ISM drought history over the past millennium (∼1080 to 1905 CE). Our new reconstruction represents a marked improvement over previous speleothem-based reconstructions from the region providing critical targets for climate models and a robust hydroclimatic context against which the key geopolitical and societal changes and their links to climate can be assessed.

Results and Discussion

Speleothem Paleoclimate Record.

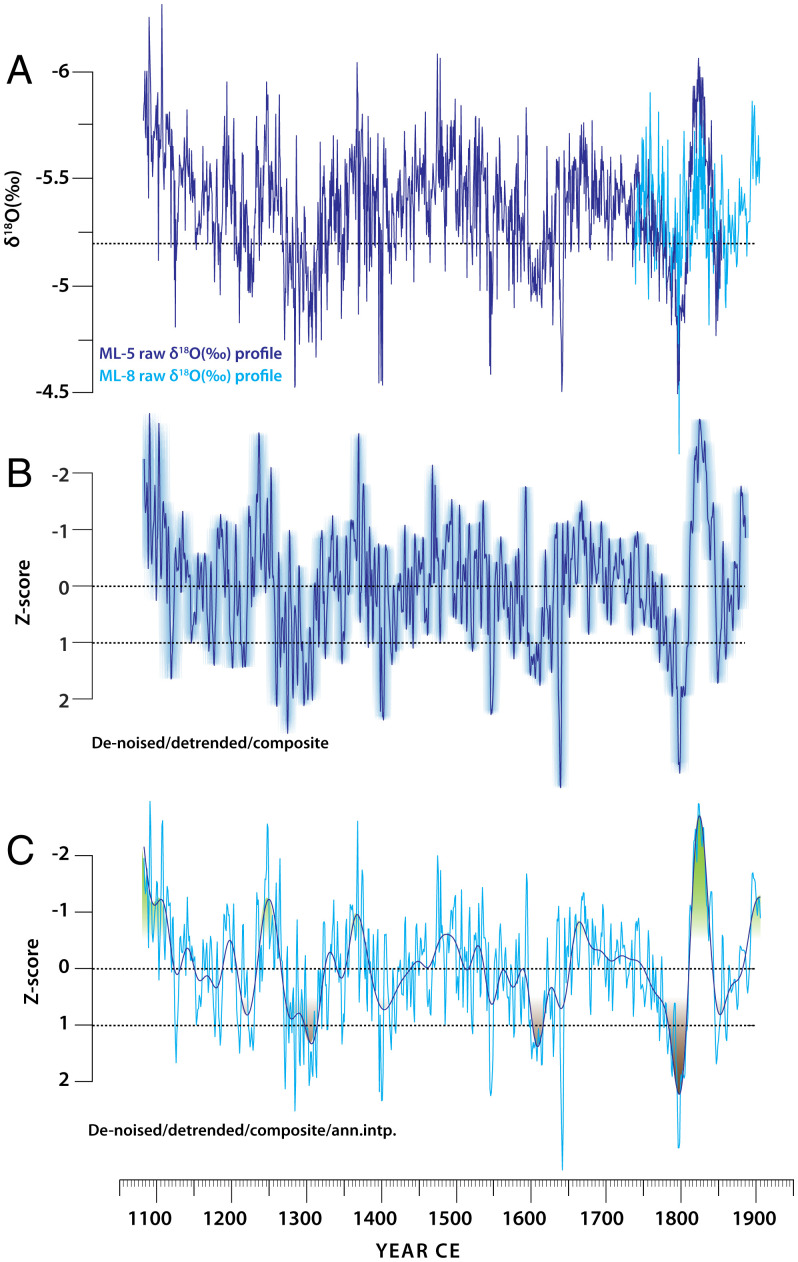
The paleoclimate record for this study is established by ∼1,545 paired measurements of stable oxygen (δ¹⁸O) and carbon (δ¹³C) isotope from two stalagmites (ML-5 and ML-8) from Mawmluh cave (25°15′32″N, 91°42′45″E, 1,290 m above the sea level) (SI Appendix, Table S1). The chronology is tightly constrained by 14 and 4 ²³⁰Th dates, respectively. The ML-5 and ML-8 samples have very high uranium concentrations (>600 parts per billion) and low detrital ²³²Th concentrations (∼62 to 250 parts per trillion) that allow us to obtain accurate ages with an average age uncertainty of ∼4 y (1σ) (SI Appendix, Table S2). The age model for each of the δ¹⁸O profiles was constructed by generating 2,000 age realizations using the COPRA (Construction of Proxy Record from Age models) age-modeling routine (26), and the median ages are used as final age models (SI Appendix, Fig. S3 and Materials and Methods). Statistically significant replication between the ML-5 and ML-8 δ¹⁸O profiles during their contemporaneous growth period (∼1739 and 1854 CE, n = 116, r = 0.33, P = 0.02, after accounting for serial autocorrelation in each time series) on their independent age models suggests that the records contain a common climate signal (SI Appendix, section 2 and Fig. S4). The ML-5 and ML-8 δ¹⁸O profiles were stacked together (hereafter, MAW) in such that the “composite” record consists of the ML-5 isotopic values until ca. 1854 and the ML-8 isotopic values afterward to 1906 CE. After stacking, the record was denoised and detrended (SI Appendix, Fig. S5; also see Materials and Methods) to yield a continuous record that spans from ∼1080 to 1906 CE with an average temporal resolution and age uncertainty of ∼0.6 and ∼4 y (1σ), respectively (Fig. 1).

Fig. 1.

Mawmluh cave speleothem δ¹⁸O records. (A) Raw δ¹⁸O profiles of ML-5 (indigo) and ML-8 (cyan) on their independent age models. The mean δ¹⁸O value is indicated by a horizontal dotted line. The ML-5 and ML-8 δ¹⁸O profiles were subsequently combined by stacking on a common age scale (see SI Appendix, Fig. S4 and Materials and Methods). (B) The denoised, detrended, and z-score-transformed MAW profile (indigo) is shown along with the 1σ age uncertainty based on the Monte Carlo results from COPRA (shaded) (26) (Materials and Methods). The median age was selected as the final age model (SI Appendix, Fig. S3 and Materials and Methods). The high-frequency (∼1 to 2 y) noise and long-term (>200 y) nonlinear trends were removed by using the ensemble empirical mode decomposition (55) and singular spectrum analysis (56) (SI Appendix, Fig. S5 and Materials and Methods). (C) Annually interpolated MAW profile (from B) on its median age (cyan) overlain by a 30-y low-pass Butterworth filter (indigo). Shades of brown and green delineate multidecadal periods of inferred droughts (z-score >1) and pluvial conditions (z-score <−1).

Proxy Interpretation.

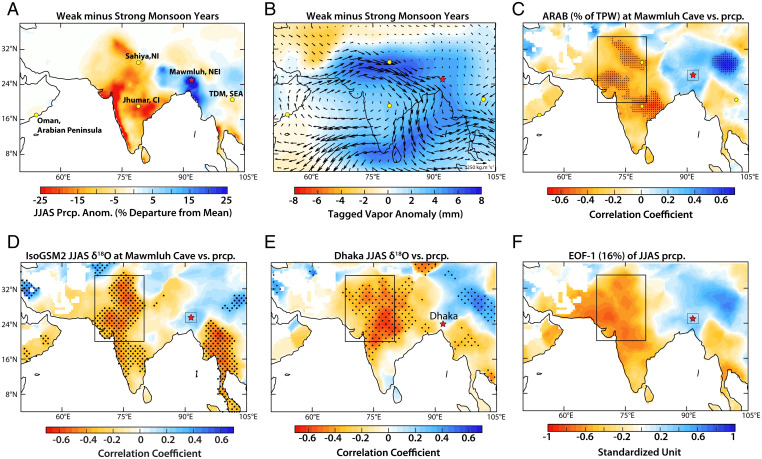
Mawmluh cave is located in one of the wettest places on Earth with an average annual precipitation of over ∼11,000 mm, with 70 to 80% of its annual precipitation falling during JJAS (June to September) (SI Appendix, Fig. S2) (27). On intraseasonal to interannual timescales, rainfall over NEI and the rest of the Indian subcontinent exhibits a quasi‐east–west precipitation dipole with anomalies of one sign over NEI and of an inverse sign over north, northwest, and central India (16, 27) (Fig. 2 A and F). Previously, we used an isotope-incorporated Global Spectral Model version 2 (IsoGSM2) with moisture-tagging capability (28) to show that changes in the relative moisture contributions from different moisture source regions drive much of the observed interannual variability in the oxygen isotope composition of precipitation (δ¹⁸O_p) and its amount over the Indian subcontinent (29). Our previous work indicates that during weak monsoon years the zonal moisture flux is anomalously enhanced across north India (with its core at ∼25°N) via a northward shifted low-level jet over the Arabian Sea and across continental India, which serves as a conduit for transporting moisture from the Arabian Sea/Red Sea moisture source region (hereafter, ARAB) over a large northwest–southeast trending region that extends from the Arabian Peninsula to Southeast Asia (Fig. 2 B and C). This zonal moisture flux exports ¹⁸O-enriched moisture from the Arabian Sea along the Indo-Gangetic plains to NEI, where Mawmluh cave is located. Consequently, during weak monsoon years, the relative contribution of moisture originating from the ARAB dominates over much of the Indian subcontinent, including over NEI, while moisture from the remote portion of the Indian Ocean has a greater influence during strong ISM years (29, 30). Indeed, time-series comparisons between the simulated δ¹⁸O_p and ARAB (i.e., percent fraction of total precipitable water (TPW) extracted from the grid cell nearest to Mawmluh cave show statistically significant negative and positive correlations with precipitation amount, respectively, over much of subcontinental India, approximately west of 85° E longitude (Fig. 2 B–F and SI Appendix, Fig. S6). These dynamical constraints, therefore, explain the intriguing situation that the δ¹⁸O_p of summer monsoon rainfall at NEI, despite being located at the opposite end of the precipitation dipole, reflects upstream changes in monsoon precipitation amount over north, northwest, and central India (∼15 to 28°N and 70 to 84°E) (via the moisture source effect rather than the “classical” amount effect). This line of reasoning is strongly supported by the strong positive correlation between the MAW δ¹⁸O record and the first principal component (PC1) of ∼15 tree ring width chronologies (31) from NEI in such that positive speleothem δ¹⁸O values (i.e., reflecting drier conditions over northwest/north/central India) covary with the higher values of PC1 (i.e., wetter conditions over NEI) and vice versa between 1700 and 1900 CE (SI Appendix, Fig. S7). Following this reasoning (fully described in ref. 29), we interpret temporal variations in the MAW δ¹⁸O record to be a sensitive indicator of precipitation variability over a broad region roughly west of 85°E longitude over subcontinental India.

Fig. 2.

Spatial patterns of climate field anomalies and proxy locations. (A and B) Spatial patterns of JJAS anomalies (weak monsoon minus strong monsoon years) from the monthly Climatic Research Unit (CRU) TS4.03 (57) and tagged Arabian Sea moisture (ARAB) anomalies are shown as fractions of total precipitable water (% TPW, shaded, from ref. 29) overlain by the vertically integrated moisture flux anomalies (black arrows) (28). (C) The inverse field correlations between the JJAS ARAB (% TPW) extracted from the grid points nearest to Mawmluh cave (small square) and precipitation amount at all other grid points (58). Note that the increased flux of ¹⁸O-enriched ARAB moisture over NEI India is associated with reduced rainfall over the rest of the Indian subcontinent. (D) Same as C, but for simulated JJAS precipitation oxygen isotope (δ¹⁸O_p) data extracted from the grid points nearest to Mawmluh cave (28) and precipitation amount (57). Note that the higher (lower) δ¹⁸O values over NEI are associated with reduced (increased) rainfall over the rest of the Indian subcontinent. (E) Same as D but for spatial correlations between the observed amount weighted JJAS δ¹⁸O_p at Dhaka and the precipitation amount at other grid points for the period from 2009 to 2016 (see ref. 29 for details). (F) The first Empirical Orthogonal Function (EOF) mode of normalized JJAS precipitation (57) over the region 38°N to 4°S and 50°W to 105°E. The EOF-1 (explained variance ∼16%) shows a precipitation dipole akin to the observed weak minus strong pattern of JJAS rainfall anomalies as in A. The locations of Mawmluh cave (red star), other cave records (yellow dots), and Dhaka (red star) are shown in different panels. Stippling in C–E indicates regions of significant correlations at the 95% significance level obtained after accounting for serial correlations in data at each grid point followed by the application of the FDR procedure (58) with a 5% threshold (Materials and Methods). FDR is the expected proportion of rejected hypotheses when the null hypothesis is true for those tests. Large black rectangles (∼20°N-35°N; 68°E-80°E and small squares ∼27°N-23°N; 90°E-94°E) in C–F demarcate the region where the JJAS precipitation amount is strongly and inversely correlated to the model-derived δ¹⁸O_p and tagged ARAB (% TPW) extracted from the grid cell nearest to Mawmluh cave. These time-series comparisons are shown in SI Appendix, Fig. S6.

The detrended z-score-transformed MAW δ¹⁸O profile exhibits prominent interannual and quasi-oscillatory multidecadal–centennial scale variability (Fig. 1C and SI Appendix, Fig. S8). The multidecadal episodes of inferred weaker and stronger ISM rainfall are highlighted by a 30-y low-pass filter. Embedded within the weaker episodes of ISM are sustained intervals with high z-score values (>1), which we interpret as drought-like conditions. An important caveat regarding this interpretation is that the memory effects in the overlying karst might lead to an overestimate of the duration of these episodes but an underestimate of their amplitude. Comparisons of the MAW δ¹⁸O profile with the existing high-resolution speleothem records of ISM from the north, central, and northeast India (14–19), the Arabian Peninsula (20), and southeast Asia (21) indicate broad similarities but also some differences (SI Appendix, Fig. S9). The latter is to be expected owing to the dating errors and the unique karst characteristics of each cave site that lead to the homogenization of meteoric waters to a varying degree. Notwithstanding, the general pattern of multidecadal to centennial timescale variability is similar across all records during the past millennium. More importantly, however, the inferred intervals of extreme droughts identified in the MAW record are also evident in other regional speleothem records (based on >90 percentile values of normalized and detrended time series of each record) (Fig. 3 and SI Appendix, Fig. S9). We note that some existing records from NEI do not have sufficiently high dating precision, temporal resolution, and robust chronological framework (16, 32–34), and therefore these records were excluded from this comparison.

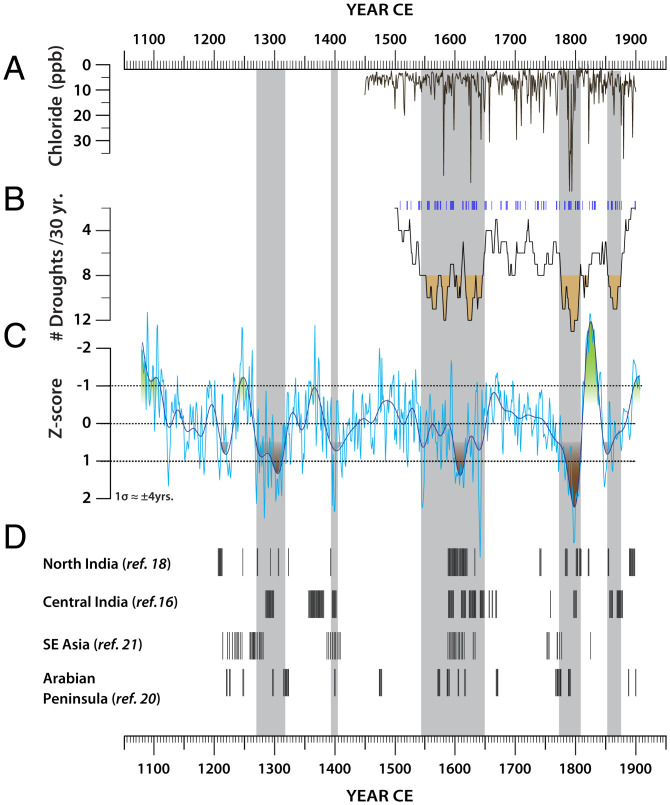
Fig. 3.

Comparison of the MAW record with historic data and other proxy records. (A) The chloride concentrations in Dasuopu ice core, Himalaya (black) (13). (B) Historic drought frequency in a 30-y moving average (black) (11). The drought frequency >8 is highlighted (shaded). Historic drought years are shown by vertical blue lines. (C) MAW δ¹⁸O record (this study, cyan) overlain a 30-y Butterworth low-pass filter (indigo). The dotted black line highlights the z-score values delineating several multidecadal periods of inferred droughts (z-score >1). (D) Vertical black lines show extreme dry events derived from the denoised, detrended, annually interpolated speleothem δ¹⁸O records (based on z-score thresholds >90% percentile ∼ >1.25) in each of the following records: Sahiya cave (30°36’N, 77°52’E) (18), north India; Jhumar/Dandak cave (18°52’N, 81°52’E) (15, 16), central India; Tham Doun Mai cave (20°45’N, 102°39’E) (21), Laos, Southeast Asia; and Oman cave (17°10’N, 54°18’E) (20), Arabian Peninsula (also see SI Appendix, Fig. S9 for a detailed comparison). The vertical bars (shaded) highlight intervals of multiyear droughts identified in the MAW record and historical drought compilations.

Hydroclimatic Extremes and Societal Changes.

The precise chronology of the MAW δ¹⁸O record allows a direct comparison with historically documented droughts and famines for the period between 1500 and 1900 CE (SI Appendix, section 1). Although the “drought” compilations (8–11) were constructed by painstakingly extracting information from a variety of documentary sources (SI Appendix, section 1), one important caveat exists that the drought chronology for the 1500s to 1770s is essentially that of famines (10). While famines typically result from a combination of societal, political, and environmental reasons, the vast majority of famines in India before the British period were ultimately caused by drought-induced harvest failures (35). It is, therefore, not unreasonable to assume that the droughts were the dominant reason for famines during the period between the 1500s and 1770s.

A comparison of the historic drought chronology with the MAW δ¹⁸O profile is highlighted by using a centered 30-y sliding mean of the drought recurrences as reported in ref. 11 (Fig. 3). For most portions between the 1500s and 1900s, the historic drought frequencies are similar to the instrumental period (averaging about four to eight droughts per 30 y). Notably, three multidecadal periods of high drought frequencies (approximately 8 to 14 droughts per 30 y) in the historical data (the 1560s–1640, 1780s–1810s, and 1850s–1870s) are in excellent temporal agreement with the inferred periods of weaker ISM inferred from our data (Fig. 3). Similarly, the periods of low drought frequencies indicated from historical evidence conform generally well with the pluvial conditions inferred from our MAW record. There are, however, also a few instances of apparent mismatch between the proxy and historical data. For example, the weak monsoon period from the 1550s to 1640s deduced from the historical drought compilations appears to be inflated compared to the proxy data (Fig. 3).

The period from the 1780s to 1810s stands out as an exceptional interval in both historical and proxy data. The historic drought compilations for this period principally draw their information almost exclusively from one East India Company report by F. C. Danvers, a British officer with the company. His report, in turn, was compiled from contemporary accounts of droughts and famines from various regions of the subcontinent. Danvers’ report—“A Century of Famines” (36), shows that there were at least 11 drought-related famines during this period, six of which, including the well-known Chalisa and Doji Bara or Skull Famines, occurred between ∼1782 and 1792 CE (Fig. 4), with a combined estimated death toll in the excess of 11 million, making it one of the deadliest decades in Indian history (8–11, 37). The z-score values in the MAW record between 1780 and 1810 CE are among the highest and occurred in striking temporal agreement with large positive δ¹⁸O excursions in other regional speleothem records and the largest chloride/dust spikes in the Himalayan ice core record (Fig. 3 and SI Appendix, Fig. S9), which are interpreted to reflect greater aridity and enhanced dust transport from the Indian peninsula (13) indicating severe drought conditions.

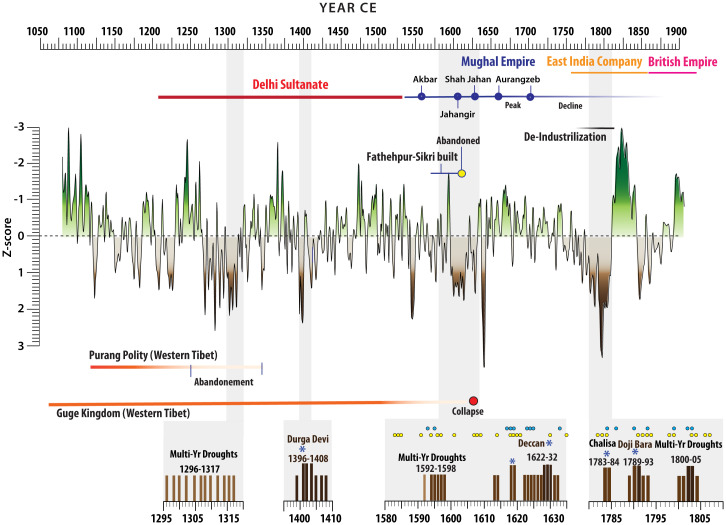
Fig. 4.

The MAW record, geopolitical context, and historic droughts. The interpolated MAW record (0.6 y, black) with multidecadal periods of inferred droughts (z-score >1, brown) and pluvial conditions (z-score <−1, green). The insets show historic droughts (light and dark brown bars) over the Indian subcontinent (11) (SI Appendix, section 1). The dark brown bars show the historic droughts reported with high reliability. The asterisks show the catastrophic droughts and famines associated with mass mortality events (also see SI Appendix, Fig. S10). Historic El Niño events are shown with yellow (52) and cyan (53) circles. The text associated with solid and varying saturation intensity-colored lines describes the various political/dynastic timelines and key events discussed in SI Appendix, section 1.

Mutually corroborating proxy and historical evidence for severe droughts in the late 18th and early 19th centuries sheds new light on the possible role of climate as a contributing factor that led to India’s deindustrialization between approximately the 1750s and 1860s (38) (Fig. 4 and SI Appendix, Fig. S10). At the peak of the Mughal Empire (ca. 1650 to 1700 CE) India was manufacturing and exporting ∼25% of the world’s textiles. However, by the middle of the 19th century, India had lost most of its export market, predominantly to the British Empire (SI Appendix, section 1). While the exact mechanisms of deindustrialization were complex and global in scope, it has been argued that the fragmentation of the Mughal Empire and reduced agricultural productivity severely limited the supply of grains, resulting in sharp rises in the prices and nominal wages in the cotton and weaving industry, which precipitated the first phase (ca. CE 1780s to 1810s) of deindustrialization (38). Our data place the early phase of deindustrialization into the most severe 30-y spell of weaker ISM of the entire past millennium, thus supporting the hypothesis that a drastic slump in agricultural productivity together with the fragmentation of the Mughal Empire sowed the seeds of India’s deindustrialization (Fig. 4 and SI Appendix, section 1 and Fig. S10).

The 1550s to 1640s stand out as another interval of strong coherence between the historical and proxy data. Within this near-century-long interval of weaker ISM, the MAW δ¹⁸O record indicates ∼25 y of sustained high z-score values (>1) between ∼1595 and 1620 CE that are coeval with the prominent dust and chloride spikes in the Himalayan ice core record (13) and with extreme positive δ¹⁸O excursions in the regional speleothem records (14–21) indicating severe drought conditions (Fig. 3). The drought compilations for this period extract information from textual documents composed in Farsi during the reigns of the prominent Mughal emperors such as Akbar (1556 to 1605 CE), Jehangir (1605 to 1628 CE), Shah Jahan (1628 to 1659 CE), and Aurangzeb (1659 to 1707 CE) (39). These court chronicles, for example, the Akbarnama (the book of Akbar) and Ain-I Akbari (the regulations of Akbar) provide vivid accounts of droughts and famines during this period, including the “Deccan Famine” (1630 to 1632 CE)—one of the most devastating mass mortality events in recorded Indian history (Fig. 4 and SI Appendix, section 1). This period also coincides (within age uncertainties) with the collapse of the Guge Kingdom in western Tibet (19) and with the abandonment of Fatehpur Sikri (40), one of the largest cities of its time that briefly served as the capital of the Mughal Empire (ca. 1571 to 1585 CE) under the reign of Akbar, before it was completely abandoned by 1610 CE (Fig. 4 and SI Appendix, section 1 and Fig. S10). Intense debates surround the circumstances under which the city was abandoned, with most historians attributing it to a range of political and military reasons, although extreme droughts and the ensuing loss of water supply to the city have also been proposed (40, 41). Our data support the latter suggestion as it places the abandonment phase of Fatehpur Sikri well within one of the driest multidecadal episodes (∼1580 to 1610 CE) of the past millennium (Fig. 4 and SI Appendix, Fig. S10).

Striking accordance between our data and the historic drought chronology indicates that the MAW record can be reliably used to extend back the ISM drought variability for periods where the historic information is fragmentary or unreliable. Our data reveal a prominent near-century-long interval of weaker ISM between the second half of the 13th and early 14th centuries, with peak drier conditions between ∼1290 and 1310 CE (Fig. 3). The scattered documentary evidence from this period indicates frequent multiyear droughts in northern India between ∼1296 and 1316 CE (e.g., refs. 11 and 42) under the reign of Alauddin Khilji, one of the several dynastic rulers of the “Delhi Sultanate” that preceded the Mughal Empire (Fig. 4). Additionally, fragmentary historic and archaeological evidence from western Tibet indicates important political, environmental, and social changes in the region. Between ∼950 and 1350 CE, western Tibet was under a confederacy rule by Purang, Guge, and Maryul polities (43). Historical sources speak of a gradual decline in the polity after ∼1200 CE with a complete collapse by ∼1350 CE (44). Although the historical documents describe this collapse primarily in political terms, archaeological evidence from the Sutlej Valley indicates settlement abandonment, a significant drop in the water table, and stranded major irrigation systems that are tentatively dated to the period CE 1250 and 1300 (15), coinciding within the period of severe weakening in the ISM (Fig. 4).

Extreme Droughts and Pluvials.

One notable feature of the MAW record is the presence of abrupt and extremely positive δ¹⁸O excursions (exceeding 2 or even 3 SDs) against the mean state of both weaker and stronger monsoon conditions (Fig. 4). We interpret these as episodes of “extreme” droughts. One such event in our record centered at ∼1400 CE occurred tantalizingly close to the “Durga Devi Famine”—one of the most widely referenced famines (1395 to 1408 CE) in the historic accounts (7–11) that struck large parts of western India (Fig. 4 and SI Appendix, section 1). Another event centered at ∼1640 CE constituting the largest positive δ¹⁸O excursion in our record, coincided with the so-called “Ming Dynasty drought” (∼1638 to 1641 CE) that affected large parts of northern China and India (22, 45). The closest modern analog of these extreme events is the drought of 1877 when the AIR fell more than 3 SDs against the backdrop of a stronger monsoon (SI Appendix, Fig. S1). The 1877 drought was a regional expression of a globally orchestrated period of climate anomalies that coincided with a strong El Niño, which immediately followed the preceding 6 y of strong La Niña conditions (5). We note here that the 1877 drought is, however, weakly expressed in our record, likely because a single season of ¹⁸O-enriched low rainfall amount may not be sufficient to skew the δ¹⁸O of speleothem to more positive values due to the mixing of meteoric waters in the overlying karst. In addition to extreme droughts, our record also contains evidence of the presence of extreme pluvial conditions. For example, the first half of the 19th century in our record is marked by an exceptional wet phase of ∼35 y (CE 1810 to 1845), which came on the heels of one of the driest ISM episodes (∼CE 1780s to 1810s) in our record (Figs. 3 and 4). We estimate that this extreme dry to extreme wet transition occurred well within less than a decade and may represent an extreme manifestation of abrupt nonlinear transitions in ISM in response to either changes in the internal feedback mechanisms or external forcing (16, 25).

ENSO and ISM Droughts.

Historic documentary and proxy evidence discussed above make an intriguing case that ISM can periodically “lock” into a drought-prone mode that may last for decades (15, 16). Understanding what climate dynamics triggered and sustained such extended periods of drought during the past millennium is vital to estimate the likelihood of their recurrence in the future. ISM droughts have been generally attributed to changes in the El Niño Southern Oscillation (ENSO) (46), sea surface temperature anomalies in the Indian (47), and Atlantic (48) Oceans, and internal dynamics (49). While detailed examinations of the potential causative mechanisms require coordinated proxy-modeling efforts that are outside the scope of this paper, here below we briefly explore the role of El Niño in causing the ISM droughts during the past millennium by cross-examining the historical and proxy-based reconstructions of ENSO with our record.

Time-series analysis of the MAW δ¹⁸O record in the frequency domain reveals intermittent but prominent periodicities in the interannual band of ENSO (∼2 to 8 y) (SI Appendix, Fig. S8) consistent with the similar spectral estimates detected from a temporally short (∼1960s to 2010s) but ultrahigh-resolution (∼0.1 y) speleothem record from Mawmluh cave (34). Intermittent presence of the ENSO band, particularly before the ∼1250s and after ∼1650s, is quite like the waxing and waning of the ENSO–ISM relationship observed during the instrumental period (50), and thus in the long-term context of our data the supposed “breakdown” of this relationship since the 1980s (51) is not that unusual. Furthermore, comparisons of the MAW record to a large array of tree-ring and coral-based reconstructions of ENSO (SI Appendix, Fig. S11) reveal no consistent relationship between the multidecadal periods of enhanced ENSO variance and ISM droughts, due in part to large divergence among the various ENSO reconstructions during the preindustrial period.

We also compared the historic droughts chronology (11) to two historic El Niño events chronologies constructed from textual documentary evidence from northern Peru (52), a region of heightened sensitivity to ENSO, and global multiproxy data blended with historical documentary sources for the period between 1525 and 1900 CE (53). Both chronologies show broad qualitative similarities in the evolution of El Niño activity but differ markedly in terms of the number of identified El Niño events (SI Appendix, Fig. S12). The chronology in ref. 52 likely underestimates El Niño events, as not all events result in precipitation extremes in northern Peru, whereas the latter chronology (53) is likely an overestimation because it includes some instances where the historic ISM droughts were used to denote El Niño events, which is problematic because not all summer monsoon droughts are caused by El Niño events over India (54). Notwithstanding these caveats, both chronologies show notable multidecadal scale peaks in El Niño activity centered in the 1640s, 1720s, 1800s, and ∼1880s. While the peaks in El Niño activity in the 1640s and 1800s correspond with the increased historical drought frequency (SI Appendix, Fig. S12), on an event-by-event basis comparison, only ∼20% and ∼50% of the historic droughts appear to have cooccurred with El Niño events as reported in refs. 52 and 53, respectively. These estimates of drought–El Niño association from historical sources are not unlike during the instrumental period, where less than 50% of the ISM droughts have cooccurred with the El Niño events (54) (SI Appendix, Fig. S1), suggesting that the ISM internal dynamics and/or other external forcing are equally, if not more important, causative mechanisms of protracted droughts during the past millennium (15, 54).

In summary, historical documentary and proxy evidence presented in this paper show that the ISM drought history during the past millennium was characterized by subdecadal to multidecadal periods of weaker ISM that contained protracted droughts. This view of the ISM system stands in stark contrast with the instrumental period, whose apparent stability might lead one to incorrectly surmise that neither protracted droughts nor frequently occurring droughts are intrinsic aspects of its variability. This seemingly reassuring but rather myopic view currently informs the region’s present-day water resource infrastructure and contingencies policies and discounts the possibility of protracted monsoon failures in the future (15–17). Recurrence of protracted droughts can easily overwhelm the adaptive capabilities of modern societies unless a longer-term and holistic understanding of monsoon variability is incorporated into drought management and mitigation planning.

Materials and Methods

Field Collection and Sample Preparation.

Mawmluh cave (25°15′ N, 91°42′ E, 1,290 m above sea level) is located near the town of Sohra (Cherrapunji) at the southern fringe of the Meghalaya Plateau, NEI. The cave is overlain by a total overburden of ∼30 to 100 m, consisting of limestone, sandstone, a 0.5- to 1-m-thick layer of coal, and a thin soil cover (<15 cm), which permits the short residence time of seasonal changes in precipitation (59). In most portions of the cave, relative humidity is >95%. The vegetation above the cave is sparse, mostly consisting of grasses, shrubs, and bushes. Only dolines hold remnants of forest, which today are held sacred. Two stalagmites—ML-5 (∼128.5 mm) and ML-8 (∼55.40 mm)—were collected ∼300 to 500 m from the cave’s entrance in February 2015. The cave’s ambient temperature and relative humidity (at the time of sample collection were ∼18.0 °C and 98%, respectively. A multiannual monitoring program, conducted between 2007 and 2014, characterizes the cave’s hydrochemistry and ventilation dynamics (59). The stalagmites were cut with a thin diamond blade along the growth axes and polished. Subsamples for ²³⁰Th dating (weighing typically between 200 and 300 µg) were obtained by drilling with a 0.5-mm carbide dental burr. An automated triaxial micro mill (New Wave Micromill) was used to obtain subsamples for stable isotopic analyses by continuously milling at 50-µm increments along the growth axis of ML-5 (between ∼18 and 128.5 mm with 0 being the top where the isotopic sampling was initiated) and at 100 µm for ML-8 (between 0 and 55.40 mm, with 0 being the top where the isotopic sampling was initiated) (SI Appendix, Table S1). Both ML-5 and ML-8 samples are characterized by the presence of thin (∼15 to 20 mm) whitish aragonitic layers (SI Appendix, Fig. S3). We discarded samples from this layer because the previous cave studies from the Mawmluh cave have shown that this distinctive layer was pervasively deposited over a large number of stalagmites, flowstones, and stalactites in the cave since the post-1950s, marking the onset of large-scale limestone mining operation above the Mawmluh cave, which resulted in extensive fracturing of bedrock and the rapid infiltration of meteoric waters into the cave. The oxygen and carbon isotopic values from this aragonite layer are in isotopic disequilibrium and not representative of the values expected from natural climate variability (59).

Stable Isotope Measurements.

The ML-5 and ML-8 isotope profiles consist of 1,286 and 259 stable isotope measurements, respectively (Fig. 1 and SI Appendix, Table S1 and Fig. S13). Subsamples for δ¹⁸O and δ¹³C analyses were measured using a Finnigan MAT 253 mass spectrometer coupled with an online carbonate preparation system (Kiel IV) at the Isotope Laboratory, Xi’an Jiaotong University, Xi’an, China. All results are reported per mil (‰) relative to the Vienna Pee Dee Belemnite (VPDB) standard. The long-term precision of the VPDB standard for the δ¹⁸O and δ¹³C was ∼0.08 ‰. Duplicate measurements of standards NBS19 and TTB1 show a long-term reproducibility of ∼0.1‰ (1σ) or better.

²³⁰Th Dating.

The chronological frameworks of ML-5 and ML-8 records were established by 14 and 4 ²³⁰Th dates, respectively (SI Appendix, Table S2). ²³⁰Th dating was performed at Xi’an Jiaotong University, China, by using Thermo Finnigan Neptune plus multicollector inductively coupled plasma mass spectrometers. We used standard chemistry procedures (60) to separate uranium and thorium. A triple-spike (²²⁹Th–²³³U–²³⁶U) isotope dilution method was used to correct instrumental fractionation and to determine U/Th isotopic ratios and concentrations (61). U and Th isotopes were measured on a MasCom multiplier behind the retarding potential quadrupole in the peak-jumping mode using standard procedures (61). Uncertainties in U/Th isotopic measurements were calculated offline at the 2σ level, including corrections for blanks, multiplier dark noise, abundance sensitivity, and contents of the same nuclides in spike solution. Corrected ²³⁰Th ages assume an initial ²³⁰Th/²³²Th atomic ratio of 4.4 ± 2.2 × 10⁻⁶ and a bulk earth ²³²Th/²³⁸U value of 3.8 for material at secular equilibrium (61).

Age Models and Composite Record.

The ML-5 and ML-8 age models and associated age uncertainties were modeled using the COPRA routine (26). We used 2,000 Monte Carlo age model realizations to account for the dating uncertainties and the median and the 2.5 and 97.5% quantile confidence limits were used in the final age model. ML-5 and ML-8 have a subannual temporal resolution, respectively. The ML-5 and ML-8 isotope profiles span from 1080 to 1854 CE and 1738 to 1906, respectively. The ML-8 isotope profiles were stacked with ML-5 at 1854.65 CE to derive the final composite MAW record with a subannual average resolution (SI Appendix, Fig. S3). Statistically significant replication between the ML-5 and ML-8 δ¹⁸O profiles during their contemporaneous growth period (∼1739 and 1854 CE, n = 116, r = 0.33, P = 0.02) on their independent age models allow us to generate a composite record by stacking the ML-5 and ML-8 δ¹⁸O profiles at ∼1854 CE. For the contemporaneous interval from 1739 to 1854 CE, the ML-5 sample was selected as the main record because of its higher age precision in comparison with ML-8. The portion from 1854 to 1906 CE is derived from ML-8 (SI Appendix, Fig. S4).

Statistical Analyses.

Denoising the composite record.

The composite MAW δ¹⁸O record exhibits prominent high-frequency oscillations (Fig. 1 and SI Appendix, Fig. S4) due to extremely high temporal resolution (mean ∼0.6 y) and the low water residence time in Mawmluh cave (59). This high-frequency signal likely reflects the mixed δ¹⁸O of meteoric waters from (mostly ISM) rainfall throughout the year. We removed this high frequency “noise” using the ensemble empirical mode decomposition (EEMD) algorithm (55), which is an adaptive data decomposition method for analyzing nonstationary and nonlinear time series. EEMD uses an ensemble distribution of data generated by adding white noise to the source data and then iteratively removes the highest frequency oscillatory components superimposed on lower frequency signals. We denoised the δ¹⁸O data by removing the first component of the EEMD decomposition (Fig. 1 and SI Appendix, Fig. S5). The lag-1 autocorrelation of the first EEMD component is −0.39, lag-2 is 0.12, and lag-3 is even smaller (0.03), indicative of characteristic white noise.

Trend removal of the denoised record.

To highlight the subdecadal to multidecadal variability, we used singular spectrum analysis (SSA) to remove the nonlinear trends (>200 y) from the denoised records (Fig. 1 and SI Appendix, Fig. S5). The SSA method decomposes time series into monotonic and oscillatory modes of variability (56). We detrended the composite record by removing the first component (i.e., the largest eigenvalue from an autocovariance matrix of SSA). The size of the embedded window was set to one-fifth the size of the length of the time series. The denoised and detrended time series was normalized by its mean and SD to produce z-scores and was interpolated to 0.6- and 1-y resolution (Fig. 1 and SI Appendix, Fig. S5) for better comparison with other time series. The 0.6-y interpolated version was used for the spectral and wavelet analysis.

Spectral and wavelet analysis.

Periodic variations in the denoised and detrended time series were assessed by the multitaper method (MTM) using a half-bandwidth parameter of 2 that represents the optimal compromise between spectral resolution and variance (62). Because interpolation procedures might introduce artifacts, potentially biasing derived frequencies, we also conducted a parallel analysis on uninterpolated denoised and detrended data using the Lomb–Scargle approach (63). The latter utilizes the unevenly spaced data and provides an independent check for any such artifacts. All power spectra were assessed only up to a conservative assessment of the Nyquist frequency (i.e., up to a frequency approximately twice the average sample frequency). We quantified the effect of age model errors by conducting MTM (62) and Lomb–Scargle (63) procedures on the 2,000 age model realizations from COPRA to obtain uncertainty bands for the estimated spectrum. Peaks were tested for significance relative to the null hypothesis of a globally red noise background, estimated empirically from the first-order autoregressive (AR-1) character of the data. We tested the significance of spectral peaks by comparing them against simulated 2,000 AR-1 nulls and estimating the 5 to 95% quantile of this distribution. Only spectra outside the AR-1 envelope are deemed significant. Wavelet analysis was performed using procedures described in ref. 64.

Strong and weak years composites.

The strong (1983, 1988, and 1994) and weak (1982, 1987, 2002, 2004, and 2009) ISM seasons as shown in Fig. 2 are defined as positive (negative) departures of 1 SD from the mean of all India rainfall (4).

Field and linear correlations and significance.

The statistical significance of field correlations is calculated using the false discovery rate (FDR) procedure (58) to control the proportion (q = 5%) of erroneously rejected null hypotheses using a MATLAB code (65), where q guarantees that 5% or fewer of the locations where the null hypothesis is rejected are false detections. The statistical significance of linear trends and correlation coefficients (95% confidence intervals and P values) reported in this paper, where appropriate, account for the autocorrelation of time series.

IsoGSM2.

We used an isotope-enabled general circulation climate model version 2 (IsoGSM2) (66) together with the moisture-tagging (29) simulation data to understand the dynamic controls of precipitation oxygen isotope (δ¹⁸O_p). The IsoGSM2 has been widely used for both modern and past climate and isotope simulations and agrees well with available δ¹⁸O_p observations in the Global Network of Isotopes in Precipitation (GNIP) on annual and seasonal time scales. The IsoGSM2 model has been extensively validated for the Indian monsoon domain (29). IsoGSM2 has a horizontal resolution of ∼200 km (T62) with 28 vertical levels. The model applies a global downscaling technique, which nudges temperature and wind speed (at scales larger than 1,000 km) toward the National Center for Environmental Prediction Reanalysis 2 (NCEP R2) (28, 67). The nudging (performed at every 6 h for all sigma levels) provides dynamical constraints to the simulated atmospheric circulation and is directly comparable with the observations. In IsoGSM, most isotopic fractionations are assumed to occur at thermodynamic equilibrium, except for open water evaporation, condensation in supersaturation conditions (vapor to ice), raindrop reevaporation, and air–rain isotopic exchange, where kinetic fractionation occurs. In the tracer mode, IsoGSM2 can track a given moisture mass back to its last time at sea level by setting the surface evaporative fractionation factor to 1 for the target region (and 0 for all other regions) and by turning off all the other isotopic fractionation in the atmosphere. The evaporated water is marked by its origin with a tag. The tagged vapor once added to the atmosphere is allowed to undergo the same atmospheric hydrological cycle as normal water vapor until it leaves the atmosphere as precipitation (67). The tagged simulation output (1979 to 2010) was generated at daily intervals and interpolated into 17 vertical pressure levels and monthly averaged (67).

Data, Materials, and Software Availability

The data used in this study are reported in SI Appendix, Tables S1 and S2 and have been deposited at the National Oceanic and Atmospheric Administration (NOAA), https://www.ncdc.noaa.gov/data-access/paleoclimatology-data (68). All other study data are included in the article and/or SI Appendix.