Abundant phosphorus expected for possible life in Enceladus’s ocean

Significance

Enceladus is one of the prime targets in the search for life in the solar system. Observations made by the Cassini spacecraft show that this small moon of Saturn has an ice-covered water ocean that erupts into space, forming a plume that contains almost all of the basic requirements of terrestrial life. However, the bioessential element phosphorus has yet to be found. Here, we perform geochemical modeling, constrained by Cassini data, to predict how much phosphorus could be present in the Enceladus ocean. These models suggest that Enceladus’s ocean should be relatively rich in dissolved phosphorus. This means that there can now be greater confidence that the ocean of Enceladus is habitable.

Abstract

Saturn’s moon Enceladus has a potentially habitable subsurface water ocean that contains canonical building blocks of life (organic and inorganic carbon, ammonia, possibly hydrogen sulfide) and chemical energy (disequilibria for methanogenesis). However, its habitability could be strongly affected by the unknown availability of phosphorus (P). Here, we perform thermodynamic and kinetic modeling that simulates P geochemistry based on recent insights into the geochemistry of the ocean–seafloor system on Enceladus. We find that aqueous P should predominantly exist as orthophosphate (e.g., HPO₄²⁻), and total dissolved inorganic P could reach 10⁻⁷ to 10⁻² mol/kg H₂O, generally increasing with lower pH and higher dissolved CO₂, but also depending upon dissolved ammonia and silica. Levels are much higher than <10⁻¹⁰ mol/kg H₂O from previous estimates and close to or higher than ∼10⁻⁶ mol/kg H₂O in modern Earth seawater. The high P concentration is primarily ascribed to a high (bi)carbonate concentration, which decreases the concentrations of multivalent cations via carbonate mineral formation, allowing phosphate to accumulate. Kinetic modeling of phosphate mineral dissolution suggests that geologically rapid release of P from seafloor weathering of a chondritic rocky core could supply millimoles of total dissolved P per kilogram of H₂O within 10⁵ y, much less than the likely age of Enceladus’s ocean (10⁸ to 10⁹ y). These results provide further evidence of habitable ocean conditions and show that any oceanic life would not be inhibited by low P availability.

The search for habitable worlds is usually guided by the presence of liquid water. Apart from Earth, water oceans also exist in the subsurface regions of some icy bodies (e.g., Enceladus, Europa, and Titan) in the outer solar system. The evidence for an ocean is strongest at Enceladus, where a water-rich plume erupts from a subsurface ocean (1, 2). Moreover, habitability is determined by other environmental factors, such as the availability of energy and CHNOPS elements (3). Data from the Cassini spacecraft indicate that Enceladus’s ocean likely satisfies most of these other requirements for life. For example, the abundance of molecular hydrogen that coexists with CO₂ in the plume suggests the availability of chemical energy that could support methanogens (4–6). Carbon dioxide and a variety of organic compounds, which can serve as carbon sources for microorganisms, are also abundant in the plume (4, 7–9). Detected ammonia (4) or organic amines (8), and tentatively detected hydrogen sulfide (9, 10), could provide biologically useable nitrogen and sulfur, respectively.

However, a notable ingredient for habitability that has eluded detection on Enceladus is phosphorus. In terrestrial life, phosphorus in the form of orthophosphate (PO₄³⁻ and its conjugate acids) participates in biological and prebiological reactions. For example, it forms kinetically stable, charged linkages in genetic molecules and phospholipids and is used to transfer metabolic energy primarily via adenosine triphosphate (11). Phosphorus is essential and its availability is often a limiting factor for biological productivity (12, 13). Because phosphate is yet to be detected in the Enceladus plume or in Saturn’s E Ring (14, 15), geochemical modeling is necessary to constrain the availability of this critical nutrient in Enceladus’s ocean. Existing models (16–18) predict a very low concentration of phosphate [<10⁻¹⁰ mol/kg H₂O or molal, vs. ∼10⁻⁶ molal in Earth’s oceans (19)], which challenges the current perception of Enceladus’s ocean as a habitable environment. However, those models are not based on the latest understanding of the geochemistry of the ocean–seafloor system on Enceladus (20–22). In addition to phosphate, reduced forms of phosphorus could be present and might support prebiotic chemistry. Examples include phosphine (PH₃) acquired from the solar nebula (23) or phosphite (HPO₃²⁻ and its conjugate acids) formed from aqueous alteration of accreted chondritic rocks (24). Neither of these forms of phosphorus have been identified at Enceladus (10), and it is unknown how stable these species would be in its ocean.

Here, we present thermodynamic and kinetic modeling results on the chemical speciation and solubility of phosphorus in Enceladus ocean water. Our results suggest the predominant stability of orthophosphate (vs. instability of reduced forms of P) and relatively high solubility in alkaline and carbonate-rich water.

Results and Discussion

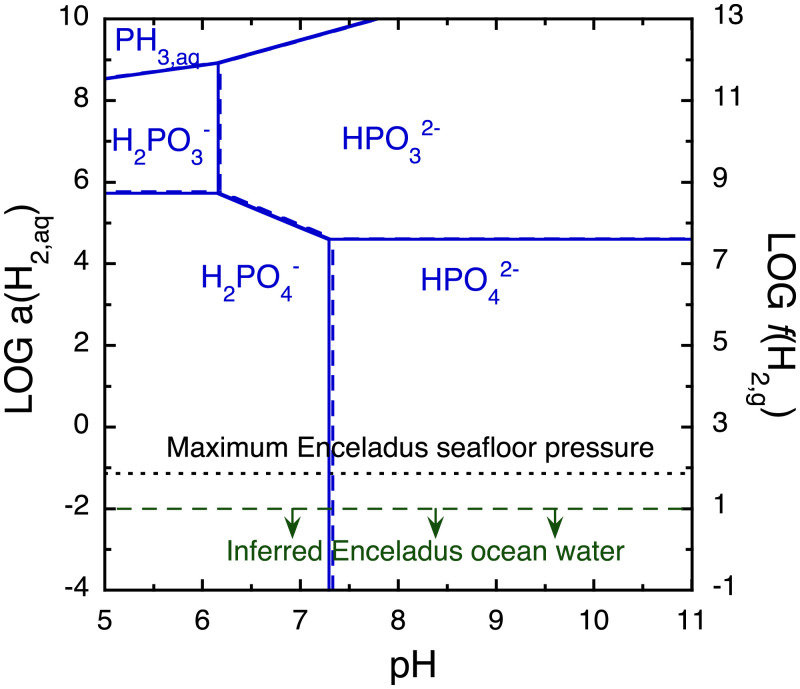
We begin by evaluating the thermodynamic stabilities of different forms of dissolved phosphorus on Enceladus. Fig. 1 shows the predominance regions of P species as a function of pH and equilibrium oxidation state at 0 °C. The redox state is represented by the activity of H₂, which is approximately equal to the molal concentration of H₂ in solutions that are not brines. The Enceladus ocean is thought to be relatively reducing because H₂ is abundant in the plume gas (4, 21). Nevertheless, oxidized P (in the form of phosphates) is likely to be the most stable form of phosphorus in the ocean, as presently constrained activities of H₂ are insufficient to favor reduced forms of P (including +III and −III oxidation states) at equilibrium (Fig. 1). Even in the most extreme scenario, where the H₂ activity is maximized by assuming that the H₂ fugacity is similar to the seafloor pressure [∼70 bars (21)], oxidized P(+V) should be the most stable form of P. Only low-level concentrations of reduced P species can be maintained outside of their predominance regions (SI Appendix, Fig. S1). Higher concentrations of metastable reduced P species might occur if they were delivered recently to the ocean from an exogenous source [e.g., a cometary impact (25)] or from iron phosphide corrosion deep in the rocky core (24). We regard the persistence of significantly unstable P species from the early history of Enceladus as unlikely if the ocean is relatively long-lived (≳100 My) (26–28) and hydrothermally processed (4, 22, 29). Assuming that thermodynamic stability is the chief determinant, then orthophosphate would be the most abundant form of P in the ocean of Enceladus.

Fig. 1.

Thermodynamically favored form of dissolved phosphorus as a function of pH and equilibrium oxidation state (as activity of dissolved hydrogen, or fugacity of hydrogen gas in bars) at 0 °C and 70 bars (1 bar for reference in dashed lines). Within its predominance region, the indicated species would have the highest activity out of all aqueous P species if equilibrium is reached. The observationally based upper limit on a(H_2,aq) (dashed green line) is from Waite et al. (4), and the theoretical upper limit on f(H_2,g) (dotted black line) is from Glein et al. (21). Diphosphate species do not appear in this plot since they constitute less than ∼0.1% of the equilibrium P budget for total P concentrations up to 100 mmolal (SI Appendix, Fig. S13).

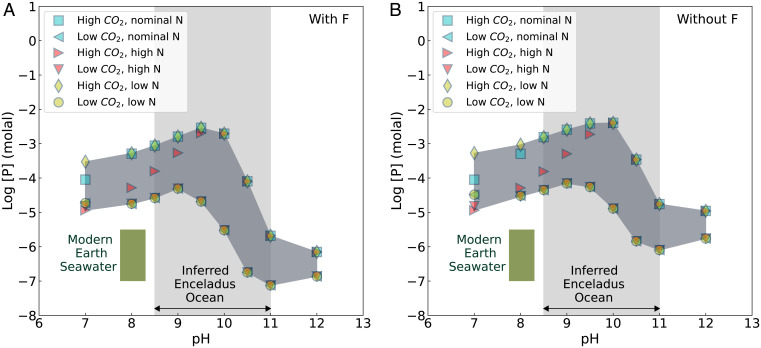
The next question is how much orthophosphate could be in the ocean? By mass balance, complete leaching of a chondritic inventory of phosphorus from Enceladus’s core into its ocean would result in up to ∼100 mmolal dissolved P (SI Appendix, Table S6). If interplanetary dust particles are more compositionally analogous to the rock component in the building blocks of Enceladus (which are unknown), then a modestly larger P inventory may be implied (30). However, total dissolution represents an upper limit, and more realistic estimates can be made by calculating the solubilities of phosphate minerals under Enceladus ocean conditions. The solubilities are constrained by the thermodynamic properties of minerals and aqueous species, and the conditions are constrained by Cassini observations (Methods and SI Appendix, section S1 and Table S2). The ocean pH is treated as the primary independent variable with a range, since there is some disagreement between published values (21). Application of the above constraints leads to predictions of the orthophosphate concentration (mainly as HPO₄²⁻) at equilibrium. We find that its concentration can reach up to several millimolal over a range of previously proposed pH values from 8.5 to 11 (14, 20, 22, 31, 32) (Fig. 2 and SI Appendix, Fig. S2). This relatively high level of dissolved P persists under a much broader range of environmental conditions (SI Appendix, section S3).

Fig. 2.

Predicted concentration of orthophosphate (mainly HPO₄²⁻) in Enceladus’s ocean depending on if (A) fluoride is sufficiently abundant or (B) there is insufficient fluoride in the ocean–seafloor system to affect the oceanic abundance of P. Variation of dissolved P is controlled by the solubility of the least soluble P-bearing minerals (SI Appendix, Fig. S3), which is largely affected by the variation of major cations (SI Appendix, Fig. S2). Symbols show different cases for the concentrations of total carbonate species and total ammonia (SI Appendix, Table S2). The inferred pH range of Enceladus ocean water (light gray shading) also comes from interpretations of Cassini data (14, 20, 22, 31, 32). The dark gray band indicates the range of P concentration that is implied by the present modeling of water–rock equilibrium. The P concentration of modern Earth seawater (olive green box) is from Berner and Berner (19).

Phosphorus concentration also depends on the amounts of inorganic carbon and ammonia (Fig. 2 and SI Appendix, Figs. S2, S4, S5, and S8). When inorganic carbon is abundant, it keeps divalent cations (Ca, Mg, Fe, etc.) in carbonate minerals (e.g., calcite, magnesite, dolomite, and siderite; SI Appendix, Fig. S3), which promotes leaching of P from phosphate minerals so that Enceladus ocean water can reach a state of saturation with respect to the most stable phosphate mineral. In addition, phosphorus concentration is found to be inversely related to the concentration of total ammonia (NH₃ + NH₄⁺) at pH values close to neutral (where NH₄⁺ predominates), reflecting solubility control by ammonium phosphates (e.g., struvite; SI Appendix, Fig. S3).

In contrast to dissolved carbonate species and ammonia, the H₂ activity, indicating the redox state of the system, and temperature have minor effects on P concentration in the modeled Enceladus ocean water (SI Appendix, Fig. S4 and S5). Although the bulk ocean is expected to be near 0 °C, it is strongly suspected that there is hydrothermal activity in Enceladus’s rocky core at elevated temperatures (>50 °C) (33). However, elevation of temperature has minimal effects on phosphorus concentration (SI Appendix, Fig. S7), and low-temperature water–rock reactions are expected to dominate the P budget in Enceladus’s ocean assuming that fluid flow at the seafloor is dominated by low-temperature transport, as on Earth (SI Appendix, section S5). In comparison to temperature, increasing concentration of dissolved silica appears to decrease the P concentration, particularly if the silica concentration can reach very high values and the pH is less than ∼9 (SI Appendix, Fig. S9).

Long-term phosphate burial on Earth is usually linked with fluorine via the formation of sparsely soluble fluorapatite [Ca₅(PO₄)₃F] or its precursor phases (34, 35). Lacking a measured value for the concentration of fluoride in Enceladus’s ocean from Cassini data (14, 15), we considered cases with and without fluorine in the chemical system (SI Appendix, sections S1 and S3.1 and Table S4). In the former case, sufficient fluoride would decrease the P concentration owing to the lower solubility of fluorapatite compared with other phosphate minerals, including OH- and Cl-apatites (Fig. 2A and SI Appendix, Fig. S3 and Table S3). However, given the relative abundances of fluorine and phosphorus in the solar system (36), even if all fluoride on Enceladus is in fluorapatite this mineral would only take up about 30% of the P budget derived from chondritic material. We do not assume that magmatic processes have produced rocks that are enriched in fluoride. Igneous differentiation would produce a metal inner core and lead to an enrichment in potassium in evolved magmas that could be emplaced at/near the seafloor. However, Enceladus’s moment of inertia factor (∼0.335) appears to be too large to permit the existence of a dense inner core (37), and the K/Na molar ratio in the ocean may be too small (⪅0.1) to support a significant enrichment of K at/near the seafloor. Because there is a lack of evidence for magmatic processes that could locally increase the F/P ratio, it seems unlikely for fluorapatite solubility to be the dominant control of P at Enceladus’s seafloor. The phosphate concentration in Fig. 2A can therefore be taken as a potential lower limit for Enceladus’s ocean. Nevertheless, in both cases dissolved phosphorus is inferred to reach concentrations higher than or at least similar to those in modern Earth seawater [10^−5.5 to 10⁻⁷ molal (19)] (Fig. 2 and SI Appendix, Fig. S2). It should be noted that we did not model the possible roles of organic phosphorus (38) or other reduced inorganic phosphorus species (39). If any metastable, reduced phosphorus is present in the Enceladus ocean, then the concentration of total dissolved phosphorus would be higher than our estimates.

The high concentration of phosphate up to 10⁻² molal is mainly caused by low concentrations of divalent cations in (bi)carbonate-rich and alkaline Enceladus ocean water (14, 21). The concentrations of these cations are limited by the precipitation of carbonate and phyllosilicate minerals (SI Appendix, Fig. S3). Consistent with these results, high concentrations of dissolved phosphate (as well as corresponding low concentrations of divalent cations together with similar Ca/Mg carbonate mineral precipitates) have been reported in alkaline and carbonate-rich lake waters on Earth (40–43). Moreover, the nearly linear relationship between log [total P] and log [total carbonate] in modern alkaline lakes (40, 41) is consistent with our model (SI Appendix, Fig. S8 and section S3.2). This resonates with the notion that modern alkaline, carbonate-rich waters may be analogous in major ion composition to Enceladus’s “soda ocean” (14, 31), although the analogy is imperfect since terrestrial soda lakes are in contact with an atmosphere and subject to locally enhanced evaporative concentration.

Soil science provides additional context that reinforces our finding that the chemistry of Enceladus’s ocean is primed to make phosphate minerals unusually soluble. The commonly used “Olsen method” for the analysis of phosphate in terrestrial soils is to extract it using a 0.5 M sodium bicarbonate solution at pH 8.5 (44). These conditions extract phosphate from minerals by removing calcium from the aqueous solution via carbonate mineral precipitation. This is the same application of Le Chatelier’s principle that yields abundant dissolved phosphate in our geochemical model of Enceladus’s ocean (SI Appendix, Figs. S2, S3 and S8). Indeed, the general conditions of the “Olsen method” are similar to those inferred for the ocean of Enceladus (pH ∼8.5 to 11, ∼0.01 to 0.1 molal HCO₃⁻ + CO₃²⁻) (14, 21).

The inference of a P-rich Enceladus ocean is also supported by laboratory experiments that demonstrate significant aqueous leaching of phosphate from the Murchison and Allende carbonaceous chondrites. In the most extensive study, Mautner and Sinaj (45) reported that phosphate is readily leached, and the extracted concentration increases with solid/solution ratio and starts to level off at ratios between 0.1 and 0.4 kg⋅L⁻¹. The equilibrium P concentration was found to be ∼0.15 mM at 20 °C and pH 7.4 to 7.9. This is relevant to Enceladus as the ocean water chemistry appears to be rock-buffered at a similarly high rock/water ratio of ∼0.3 to 1 kg⋅L⁻¹ (20), probably because Enceladus’s core is so porous (4, 29). While the experimental conditions of the previous leaching experiments do not exactly match Enceladus ocean conditions, they show that a relatively high concentration of dissolved phosphate can be obtained by simple water extraction of chondritic rock. Also, the consistency between results where the experiments and our model partially overlap at circumneutral pH (Fig. 2) can be seen as a successful empirical test of our model for chondritic systems.

Our results seem to be at odds with earlier simulations that predicted less than 10⁻¹⁰ molal orthophosphate (16, 17), which was found to be due to the extremely low solubility of whitlockite [β-Ca₃(PO₄)₂]. The large disagreement in P concentration is attributed to a substantial discrepancy of thermodynamic data for whitlockite between the equilibrium constant in the previous models [log K_sp = −50.98 at 25 °C for Ca₃(PO₄)₂ → 3Ca²⁺ + 2PO₄³⁻] (16, 17) and that from actual solubility experiments [log K_sp = −28.92 at 25 °C for the same reaction with solubility >10⁻⁴ molal P at circumneutral to alkaline pHs (46–48); SI Appendix, section S6]. We adopted the latter value because it is most consistent with the process that we are modeling—phosphate mineral equilibration with water. To gain additional insight, we forced the former equilibrium constant for β-whitlockite into our code and obtained extremely low solubilities of dissolved P (10⁻¹⁵ to 10⁻¹⁰ molal; SI Appendix, Fig. S10), similar to the results of previous models (16, 17). In this case, we also found that the P concentration is controlled by the solubility of whitlockite under a wide range of conditions; in these test runs, all other P minerals were extremely undersaturated, including merrillite, which was experimentally shown to be less soluble than whitlockite (48). Previous treatments overestimated the stability of whitlockite. The present model, incorporating the latest published constraints on Enceladus’s ocean water chemistry, as well as an internally consistent thermodynamic database that is tailored to P species and minerals (SI Appendix, Tables S1 and S3), should provide a more realistic representation of P availability that is determined by mineral solubility in Enceladus’s ocean.

Our estimates also differ from results that were based on scaling fluxes of the P cycle on the modern Earth to Enceladus (18). However, there are fundamental differences between Enceladus and Earth in terms of continuous production of “fresh” seafloor igneous rocks on Earth vs. the likely presence of unrecycled, already-altered rocks at the seafloor of Enceladus (20) and more carbonate-rich ocean water on Enceladus than on Earth (14) (SI Appendix, Fig. S8). One should note that removal of orthophosphate through surface adsorption onto ferrihydrite is a major P sink for oxidized modern Earth seawater (49), but this process may not be relevant to reduced ocean water on Enceladus. Green rust [e.g., Fe₆(OH)₁₂(CO₃,SO₄)] has been proposed as a major metastable phase in Fe(II)-rich early Earth seawater (50) and can remove phosphate (51). However, green rust is not thermodynamically stable and will eventually transform into more stable phases, e.g. greenalite or siderite (50, 52) (SI Appendix, section S4). Our geochemical model suggests favorable formation and persistence of carbonate minerals and phyllosilicates at Enceladus’s seafloor (SI Appendix, Fig. S3). Surfaces of these minerals will be net negatively charged because their points of zero charge are lower than the inferred pH of Enceladus ocean water (SI Appendix, Table S7). Consequently, there should not be significant adsorption of phosphate on mineral surfaces at Enceladus’s seafloor (53) (SI Appendix, section S4).

A liquid water ocean might have existed for tens of million to several billion years inside Enceladus (26–28). Given this potentially long history, dissolution of phosphates and other minerals can be expected to release considerable amounts of phosphorus (together with other dissolved constituents) into the ocean, perhaps allowing these minerals to equilibrate with the ocean. As an initial assessment, equilibrium seems plausible in terms of mass balance; i.e., only small quantities of secondary minerals need to be dissolved for their saturation states to be reached. For example, the total dissolution of core rock would release more than 100 mmolal P (SI Appendix, Table S6), but our simulations predicted no higher than millimolal levels of dissolved P at equilibrium (Fig. 2). This dissolved P inventory is equivalent to ∼1% of the core’s mass, or the P content in a subseafloor rock layer that is less than ∼0.5 km thick (for comparison, the radius of Enceladus’s core is thought to be around 190 km). Multivalent cations (Ca, Mg, Fe, and Si) affecting P solubility would similarly need only a thin layer of rock to exchange elements with the ocean. Because the required extents of rock exposure to ocean water are minimal, it appears that physical access of rock to water should not preclude equilibrium. Therefore, the actual equilibration period for P and its controlling metals should be much less than the complete serpentinization duration of Enceladus’s core (∼10⁸ y) (54, 55). However, phosphates and other minerals in rock would still need to dissolve at geologically sufficient rates for species concentrations in the ocean to reach equilibrium values.

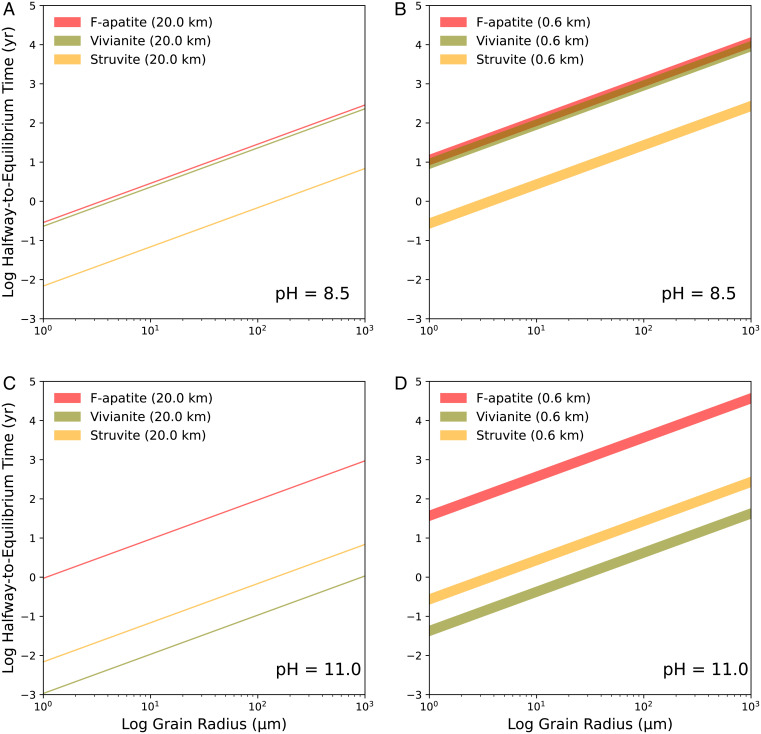
To further test if such equilibria can be reached at the present time, we estimated kinetic timescales of grain dissolution of relevant minerals on Enceladus. First, we calculated a halfway-to-equilibrium timescale for the dissolution of major phosphate minerals commonly observed in chondrites (56) (Methods and SI Appendix, Tables S4 and S5). These calculations assume that ocean water circulates through a porous and permeable subseafloor aquifer layer (0.6 to 20 km thick) of Enceladus’s core and phosphate mineral grains within this layer dissolve at rates based on laboratory studies. The results suggest that the half-time for dissolution of phosphate minerals to reach 1 mmolal in the Enceladus’s ocean is less than 10⁵ y (Fig. 3), much shorter than the expected lifetime of Enceladus’ ocean (10⁸ to 10⁹ y).

Fig. 3.

Amount of time that is required for the dissolution of P minerals to proceed halfway to equilibrium as defined by Eq. 6. into Enceladus’s ocean at 0 °C, as a function of the grain radius of P minerals and thickness of a permeable subseafloor layer [0.6 to 20 km (20, 78)]. Top and bottom panels correspond to limiting values of the observationally constrained pH range (14, 20, 22, 31, 32). Shaded areas indicate the dissolution timescale with a 20-km- (A and C) or 0.6-km- (B and D) thick permeable layer. The vertical extent of shading reflects variation in mineral surface area (i.e., decreasing grain size) as mineral dissolution proceeds (Methods). The equilibrium concentration of dissolved P is set to be 1 mmolal to illustrate a conservative case (Fig. 2 and SI Appendix, Fig. S2) with a relatively long timescale.

We performed a second set of kinetic calculations to determine whether the other minerals in our model would dissolve fast enough so that their equilibria can indirectly affect the phosphorus concentration. These simpler calculations for the total dissolution lifetime of spherical mineral grains can serve as an indicator of whether slow kinetics would inhibit the attainment of equilibrium (57). We find that these timescales are less than 10⁸ y even at 0 °C and may be much shorter than this if secondary silicates in Enceladus’s core are analogous to the very fine-grained matrix (<1 to ∼10 μm grain radii) (58) that is the dominant component of aqueously altered chondrites (SI Appendix, Fig. S12). The above findings jointly support (but of course do not guarantee) the assumption of equilibrium for phosphate, suggesting that the results in Fig. 2 and SI Appendix, Figs. S2 and S3 are applicable to present knowledge of Enceladus’s ocean. Note that there remains uncertainty as to whether merrillite would dissolve sufficiently fast to equilibrate with the ocean because rate data do not exist where it is predicted to be most stable (pH >9 to 10; SI Appendix, Figs. S3 and S11). However, the general trend in our kinetic analyses is that minerals with ionic salt structures dissolve relatively quickly (Fig. 3 and SI Appendix, Fig. S12). Merrillite [Ca_9.5Mg(PO₄)₇] can be expected to behave similarly. We also note that even deeper fluid circulation is plausible and may be linked to the prodigious heat output of Enceladus (29), but we chose to focus on shallower circulation because it is less difficult (less rocky material to flow through). On the other hand, if deep fluid circulation is sufficiently widespread and rapid enough to influence the ion composition of the ocean, then phosphate should reach equilibrium even faster because ocean water would have access to additional phosphate mineral grains.

Implications

Our finding that phosphate should be abundant in Enceladus’s ocean implies that another major component of habitability is likely to be satisfied there. Indeed, phosphate becomes limiting for the growth of terrestrial hydrogentrophic methanogens below ∼10⁻⁸ to 10⁻⁶ molal phosphate (59, 60), and this requirement can be easily satisfied by the inferred high phosphate levels in the Enceladus ocean (Fig. 2 and SI Appendix, Figs. S2, S4 and S5). If life exists in the Enceladus ocean, its activity could promote the bioavailability of phosphorus. For instance, life cannot only synthesize organic P and increase the concentration of total dissolved P but also recycle organic P in the ocean column (61, 62). Finding appreciable abundances of organic P-bearing species containing phosphate ester and particularly phosphoanhydride bonds would likely implicate biosynthesis, since a state of significant disequilibrium would be implied, given what we know about conditions in Enceladus’s ocean (SI Appendix, section S7). In addition, life’s activities can facilitate the process of reaching thermodynamic equilibria between water and minerals via ligand-promoted mineral dissolution (63, 64) or biologically mediated mineral precipitation (65).

Further analysis enables a deeper perspective on what could ultimately limit the habitability of Enceladus’s ocean. It does not appear to be CHNOPS elements or energy sources, if the tentative detection of H₂S (9, 10) and our predictions of phosphorus availability (Fig. 2) can be confirmed via either further analyses of Cassini Cosmic Dust Analyzer data or detection by future missions. Measurements of sodium phosphate salts would enable direct testing of our geochemical model predictions (Fig. 2 and SI Appendix, Fig. S8), and the oceanic concentration of P in relation to other biogenic elements would allow quantitative assessment of whether P or a different element is a limiting nutrient for putative life. We do not expect reduced P species to be found if the P–O–H system has reached redox equilibrium in Enceladus’s ocean (Fig. 1 and SI Appendix, Fig. S1). Our geochemical model can also be tested by making measurements of additional elements (Ca and Mg) that are expected to be controlled by mineral dissolution equilibria (16, 20) (SI Appendix, Figs. S2 and S3). By determining the ocean’s major ion chemistry, pH, and phosphate concentration, mineral saturation indices could be evaluated to constrain the seafloor mineralogy, including the most stable P-hosting phase. This would be valuable for advancing our understanding of the geochemical evolution of the ocean–seafloor system on Enceladus.

Cassini data show that molecular hydrogen (4) and organic compounds (7–10) represent substantial sources of electron donors for microbes including methanogens. The availability of electron acceptors (oxidants), however, is potentially limiting. Oxidant (O₂ and H₂O₂) production from radiolysis of water molecules is relatively slow on Enceladus, and there may be additional complications such as discontinuous transport of oxidants from the surface to the ocean or scavenging of reactive oxygen species by organic compounds in the ocean (66). The only abundantly available oxidant that has been observed is inorganic carbon in the form of carbonate species. This oxidant appears to be sufficient to allow hydrogenotrophic methanogenesis (CO_2,aq + 4 H_2,aq → CH_4,aq + 2 H₂O) that would provide enough energy to support methanogens (4–6). However, the potential to sustain metabolisms that rely on other oxidants may be more restricted on Enceladus.

An additional limiting factor for possible life may be transition metals. These are needed to catalyze biological redox reactions including methanogenesis (67), which uses nickel-based enzymes (68). The availability of transition metals in the Enceladus ocean may be scarce because of low solubilities of their mineral forms in alkaline, carbonate-rich, and reduced ocean water (e.g., iron, nickel, zinc, and molybdenum) (17, 31). If this effect is important, then the most habitable zone on Enceladus may be the water–rock interface where these elements are most accessible. Alternatively, there may be potential to mobilize metals via chelation in an organic-rich ocean (8). These considerations emphasize the next step of thinking beyond CHNOPS and also in terms of local environments as we more deeply probe the prospects for life in Enceladus’s ocean (69).

Methods

Dominant Form of Dissolved Phosphorus.

Equilibrium constants for the phosphorus Pourbaix diagram (Fig. 1) were computed with the code SUPCRT92b (70), using the most recently updated revised Helgeson–Kirkham–Flowers (HKF) equations-of-state parameters taken from the database of the Deep Earth Water model (71). Thermodynamic properties of aqueous phosphorus species correspond to 0 °C and 70 bars. Equilibrium boundaries between aqueous species were calculated using their Gibbs free energies of formation at the seafloor pressure ($\mathrm{\Delta }{G}_{f, P}^{\circ }$) and assuming equal activities of the two P species separated by each boundary. Values of $\mathrm{\Delta }{G}_{f, P}^{\circ }$ were calculated using standard Gibbs free energies of formation ($\mathrm{\Delta }{G}_f^{\circ }$) and other thermodynamic properties (standard partial molal entropy, volume, heat capacity, and a₁-a₄, c₁-c₂ and ω parameters) for the revised HKF equations of state for aqueous species, which are provided in SI Appendix, Table S1.

Numerical Simulation of Enceladus Ocean Chemistry.

Thermodynamic calculations were performed using the aqueous speciation, complexation, and solubility code EQ3NR (72), except for the temperature sensitivity tests which adopted output of EQ3NR at 0 °C as input of EQ6 for a heating simulation (SI Appendix, sections S1 and S3.5). EQ3NR determines which minerals should be present at equilibrium and assumes that enough rock is available to prevent complete dissolution of those minerals (SI Appendix, Fig. S3 and Table S6) during the process of reaching equilibrium. Previous reaction path modeling suggests that the currently constrained chemistry of Enceladus’s ocean is consistent with the results of chondrite alteration by CO₂-rich fluids at low water/rock mass ratios (between 1 and 3) (20). The thermodynamic database used in the present calculations was built using established data for aqueous species (73) and minerals (74–76). A large number of aqueous species and minerals of phosphorus were included in the database (SI Appendix, Tables S1 and S3), and we verified that white P at 25 °C is the reference state for all of their apparent Gibbs energies and enthalpies. While the present database is extensive, one should be mindful that it is possible that some unfamiliar P mineral could form in this potentially exotic extraterrestrial environment, but because of a lack of thermodynamic data it would not be represented by our model.

The Enceladus ocean chemistry model was parameterized based on current plume constraints on ocean composition; i.e., total concentrations of Cl⁻ and carbonate species, ratios of Na/K, H_2(aq)/CO_2(aq), and ΣNH₃/CO_2(aq), at 0 °C (SI Appendix, Table S2). This is the same type of approach as that used by Waite et al. (4), and it is extended here to include mineral equilibria. We adjusted the redox state of the system (e.g., log fO_2,g [oxygen fugacity]) to reproduce the observationally constrained H₂ molality (∼activity). Na⁺, as the dominant cation in the ocean, provides charge balance [the calculated strength varied from 0.08 to 0.49 molal; this is within the range of applicability of the extended Debye–Hückel equation that is used by EQ3NR to account for nonideal solution behavior of ions (72)]. For multivalent cations, we iterated the model to reach the levels with the lowest solubilities of their corresponding secondary minerals commonly observed in aqueously altered chondrites (usually carbonate or phyllosilicate minerals; SI Appendix, Table S4), e.g. magnesite (at lower pH) and talc (at higher pH) for Mg²⁺. This state of lowest solubility is equilibrium, where no alternative mineral is supersaturated. Silica concentration was nominally set to be at the solubility of quartz, consistent with recent estimates (20) (SI Appendix, sections S1 and S3.6). We found that no other silicate minerals were supersaturated in this chemical system. Due to a lack of knowledge on the fluorine abundance in Enceladus ocean water, we considered two endmember systems: one without and one with fluorine. The concentration of fluoride in the latter calculations was set to whichever is lower between the solubility of fluorite and the value for comparable leaching of F⁻ and Cl⁻ from rock of CI chondritic bulk composition (36). To estimate the concentration of dissolved phosphate over a wide range of pH values (7–12), we iterated the model to find the phosphate mineral of lowest solubility (SI Appendix, Figs. S2 and S3).

In addition to the above-mentioned simulations under the observationally constrained conditions, we tested the effects of key parameters (e.g., carbonate, ammonia, and temperature) on the equilibrium concentration of P in Enceladus’s ocean under a much broader range of environmental conditions (SI Appendix, sections S1 and S3). Note that organic nitrogen species (amines) and organic acids were not included as sources of additional ions in our model because the specific species and their concentrations are too uncertain. We also did not consider redox equilibration between C and N species (e.g., CO₂–CO, N₂–NH₃) because redox reactions are presumably kinetically inhibited in the cold bulk ocean of Enceladus. However, these exclusions do not affect the chemistries of carbonate and ammonia, which are determined by plume values in our geochemical model (SI Appendix, Table S2).

Our database corresponds to 1 bar total pressure because it is conventional for aqueous geochemical databases to tabulate equilibrium constants at this pressure for temperatures below 100 °C. In reality, maximum pressures in Enceladus’s ocean will be higher, ranging from 20 to 70 bars depending on the depth (21, 77). However, as shown in Fig. 1, pressures up to 70 bars have little influence on the aqueous speciation of phosphorus. Furthermore, the pressure effect on solubilities of P minerals is within a factor of 2.5 (SI Appendix, Fig. S6), much smaller than the effects of compositional changes (Fig. 2 and SI Appendix, Figs. S2, S4 and S5). More importantly, increased pressure makes P minerals more soluble (SI Appendix, section S2 and Fig. S6), supporting the availability of abundant P in Enceladus ocean water.

P-Releasing Kinetics during Alteration of the Enceladan Seafloor.

It is assumed that there is a porous and permeable layer directly below Enceladus’s seafloor where element exchange between rock and ocean water occurs. On Earth, this type of interaction occurs in the upper oceanic basement, and the thickness of this aquifer layer is ∼0.6 km (78). However, ocean water is likely to reach greater depths into the seafloor of Enceladus. Geochemical modeling indicates that the upper part of the rocky core has been significantly carbonated via interaction with CO₂-bearing ocean water down to a depth of at least ∼20 km below the seafloor (20). Geophysical modeling suggests that both cool and warm/hot fluids can be transported through the entire core (29, 79). Here, we consider a more conservative range of 0.6 to 20 km for the aquifer layer thickness to estimate upper limits on the timescale for phosphate minerals to equilibrate with ocean water.

The volume of the permeable subseafloor layer is

$$V_{\mathit{aquifer}}=\left(4/3\right)\times \pi \times \left(R_c{}^3-r^3\right)\text{,}$$ [1]

where R_c = core radius [∼190 km; Waite et al. (4); see also ref. (77)] and r = radius at the bottom of the permeable layer. Given ϕ = water-filled core porosity [∼27%; Waite et al. (4); see also ref. (29)], the fraction of this volume that is rock is 1 − ϕ. The mass of rock in the permeable layer is m_rock = ρ_rock × V_rock, where ρ_rock = rock density [∼3.0 g/cm³; Waite et al., (4)]. The corresponding mass of P in the rock is m_P = m_rock × c_P,rock, where c_P,rock represents the mass fraction of P in rock in Enceladus’s core, suggested to be similar to that in CI carbonaceous chondrites [920 ppm (36)]. We note that a different assumed carbonaceous chondrite analog of Enceladus rock would provide a similar abundance of P as this quantity exhibits little (<10%) variation among carbonaceous chondrites (80).

Assuming that all P in the permeable layer that interacts with the ocean is in a single host mineral (e.g., apatite, struvite, or vivianite), the total amount of P in this layer can be converted into a mineral volume (V_min; cubic meters) using available data of molar mass and mineral density (SI Appendix, Table S5). Further assuming that the mineral grains are spherical with x_grain as the radius, the total surface area (A) of P minerals is

$$A_{\mathit{min}}=3V_{\mathit{min}}/x_{\mathit{grain}}.$$ [2]

The grain size of P minerals in aqueously processed terrestrial and chondritic samples that may be relevant to Enceladus’s seafloor ranges from <10 to 100s of micrometers (65, 81). Here, we consider a wide range of grain size; i.e., 1 µm to 1 mm.

Dissolution kinetics of phosphate minerals were compiled from previous experimental results (SI Appendix, Table S5 and Fig. S11). The dissolution rate is defined as the amount of mineral that dissolves per unit surface area per second (R₊; moles of released P⋅m⁻²⋅s⁻¹). We adopted laboratory-based rates because they provide a useful starting point with well-characterized values. It is important to be aware that dissolution rates inferred from field measurements on Earth can be much different from those measured in the laboratory, owing to the complexity of geologic environments (82, 83). However, we do not (yet) understand the kinds of complexity that could change dissolution rates on Enceladus. In the laboratory, the dissolution rates of phosphate minerals are usually measured at 25 °C. According to the available activation energy values for dissolution reactions of fluorapatite and struvite (SI Appendix, Table S5), the dissolution rate at 0 °C is about five times less than that at 25 °C. This factor is applied to vivianite since dissolution rate data are not currently available for it at 0 °C. The net rate of dissolution of P minerals can be represented by

$$R_{\text{net}}=R_{+}(1-\frac{\mathit{[}\mathit{\text{P]}}}{{\mathit{[}\mathit{\text{P]}}}_{\mathit{\text{eq}}}}),$$ [3]

where [P] and [P]_eq are real-time and equilibrium concentrations of dissolved phosphate, respectively. This equation provides a simple accounting for the reverse reaction of precipitating the phosphate mineral of interest as the system approaches equilibrium (84). It is simplified by the assumption that the background electrolytes in Enceladus’s ocean (mainly NaCl) remain constant over the course of phosphate mineral dissolution, so that the ratio of concentrations in Eq. 3 is similar to the ratio of appropriate activities. From this first-order formulation, the P concentration (molal) in Enceladus’s ocean would evolve according to

$$\frac{d\mathit{[}\mathit{\text{P]}}}{dt}=\frac{A_{\text{min}}{R}_{+}}{m_{\text{ocean}}}(1-\frac{\mathit{[}\mathit{\text{P]}}}{{\mathit{[}\mathit{\text{P]}}}_{\mathit{\text{eq}}}}),$$ [4]

where A_min stands for the total surface area of phosphate minerals that exchange P with the ocean, as estimated above, and m_ocean refers to the mass of Enceladus’s ocean [∼2 $\times$ 10¹⁹ kg (77)]. For simplicity, assuming that A_min stays constant (i.e., the mineral grain radius does not significantly decrease during partial dissolution) and the initial concentration of orthophosphate in the ocean was zero, then the integrated rate equation would be

$$-{\left[P\right]}_{\mathit{\text{eq}}}\ln (1-\frac{\mathit{[}\mathit{\text{P]}}}{{\mathit{[}\mathit{\text{P]}}}_{\mathit{\text{eq}}}})=\frac{A_{\text{min}}{R}_{+}}{m_{\text{ocean}}}t.$$ [5]

The timescale (years) to reach halfway-to-equilibrium is then

$$t_{1/2}=\frac{-m_{\text{ocean}}{\mathit{[}\mathit{\text{P]}}}_{\mathit{\text{eq}}}}{A_{\text{min}}{R}_{+}}\ln (1-0.5).$$ [6]

On the other hand, A_min would decrease noticeably due to a high degree of P-mineral dissolution if the permeable layer of the core is very shallow (e.g., 0.6 km). To bound this effect, we considered the mass balance of P at an ocean concentration of [P] = [P]_eq/2. We calculated the mass of phosphate minerals that would dissolve into Enceladus’s ocean to reach this concentration, and then calculated the remaining mass of phosphate minerals in the aquifer layer (designated by m_P,1/2). The corresponding grain radius and total surface area of phosphate minerals in the aquifer layer are given by

$$\frac{m_{\text{P,0}}}{x_{\text{grain,0}}^3}=\frac{m_{\text{P,1/2}}}{x_{\text{grain,1/2}}^3}$$ [7]

and

$$\frac{A_{\text{min,0}}}{x_{\text{grain,0}}^2}=\frac{A_{\text{min,1/2}}}{x_{\text{grain,1/2}}^2},$$ [8]

where subscript 0 indicates the initial state of the system and subscript 1/2 refers to the halfway-to-equilibrium point. We used these equations to convert from m_P,1/2 to A_min,1/2 and evaluated Eq. 6 for the new smaller surface area. The resulting halfway-to-equilibrium time can serve as an upper limit (Fig. 3) as it is based on the minimum total surface area.

Above, we quantitatively evaluated the dissolution rates of phosphate minerals, as they are known to be important P-containing secondary phases in aqueously altered chondrites (SI Appendix, Table S4), and Enceladus’s core is thought to be heavily altered (i.e., hydrated). However, prior to the formation of phosphate minerals, there were probably anhydrous rocks on Enceladus perhaps like ordinary chondrites or other ultramafic rocks, such as peridotite. The implication is that some P could have been dispersed within olivine, and the majority of accreted P most likely resided in metal phosphides, such as schreibersite. It is notable that the dissolution rate of olivine minerals, e.g., forsterite, is experimentally shown to be faster than that of apatite at alkaline pHs relevant to Enceladus ocean water (85, 86). Metal phosphides are very reactive and if present inside Enceladus would dissolve in days (39). We conclude that the estimated timescales of P availability will be conservative not only to the attainment of equilibrium with secondary phosphates, but also with respect to the initial stage of aqueous alteration.

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.