Abstract
Introduction:
Multi-omics data integration facilitates collecting richer understanding and perceptions than separate omics data. Various promising integrative approaches have been utilized to analyze multi-omics data for biomedical applications, including disease prediction and disease subtypes, biomarker prediction, and others.
Methods:
In this paper, we introduce a multi-omics data integration method that is constructed using the combination of gene similarity network (GSN) based on uniform manifold approximation and projection (UMAP) and convolutional neural networks (CNNs). The method utilizes UMAP to embed gene expression, DNA methylation, and copy number alteration (CNA) to a lower dimension creating two-dimensional RGB images. Gene expression is used as a reference to construct the GSN and then integrate other omics data with the gene expression for better prediction. We used CNNs to predict the Gleason score levels of prostate cancer patients and the tumor stage in breast cancer patients.
Results:
The model proposed near perfection with accuracy above 99% with all other performance measurements at the same level. The proposed model outperformed the state-of-art iSOM-GSN model that constructs the GSN map based on the self-organizing map.
Conclusion:
The results show that UMAP as an embedding technique can better integrate multi-omics maps into the prediction model than SOM. The proposed model can also be applied to build a multi-omics prediction model for other types of cancer.
Keywords: Multi-omics data integration, deep learning, UMAP, data embedding, cancer
Introduction
The advancement in next-generation sequencing (NGS) technology has exponentially increased the amount of available biological data. NGS methods generate cost-effective enormous volumes of omics data, including genomic, transcriptomic, proteomic, and epigenomic data. This leads to delivering a more comprehensive understanding of the various properties of genes, proteins, or biomolecules. Multi-omics data provide multiple views with different feature sets for the same patients. Therefore, there is necessary to develop new approaches to handle large-scale data to integrate and analyze multi-omics data, and machine learning is playing a vital role in this task.1,2 Arjmand et al 1 discussed the importance of utilizing machine learning in multi-omics data integration in the prognosis, diagnosis, and treatment of cancer. Cai et al 2 listed the technology that has been used to measure each omic, the resultant data formats, and the corresponding analytical strategies. The analytics strategies may handle the data in earlier (data concatenation), middle, late stage of the prediction model. While concatenation treats the heterogeneous omics data similarly, the late stage strategy treats various omics independently. In the middle stage strategy, the model is built based on finding the relationships among the omic features, then integrate them in one prediction model that learns from the associations between the extracted relationships to mimic the actual biological associations. Some methods apply clustering based on a joint latent variable model to integrate multi-omics data to categorize cancer data into subtypes.3,4 In this work, we propose utilizing an embedding technique to merge various omics in the prediction model. The aim is to find the global association among discriminative features from the various omics data that works together in the cause or the progress of the diseases.
Data embedding techniques are used to map the data into lower dimensional approaches.5-8 Kohonen 5 suggested an artificial neural network named self-organizing map (SOM) to find spatial organized internal representations for higher-dimensional features. SOM topological information must be determined in advance. Hinton and Roweis 6 proposed using stochastic neighbor embedding (SNE) to locate the sample’s data points in a 2 or three-dimensional map. SNE struggles to capture the local structure of the data in a map, which is solved later by using the t-distributed variant, where the newer version is known as t-SNE. 7 UMAP is another dimensionality reduction and visualization method that is built on mathematical foundations related to the Laplacian eigenmaps. UMAP preserves more of the global structure than t-SNE with superior run time performance. 8
Argelaguet et al 9 proposed multi-omics factor analysis (MOFA), a Bayesian model that factorizes omics data to extract fundamental causes of variation in multi-omics data sets. Chalise and Fridley introduced iOmicsPASS, a network-based multi-omics integration method that provides a supervised evaluation of quantitative multi-omics data to calculate biological interaction scores. A shrunken gene-centroid algorithm is applied to the scores to discover predictive sub-networks for phenotypic groups. Chalise and Fridley introduced a clustering integration approach named intNMF for multi-omics data integration. The approach exploits non-negative matrix factorization (NMF) to classify disease subtypes of datasets consisting of DNA methylation, mRNA gene expression, and protein expression. The approach utilizes a separate set of clusters of multiple high-dimensional molecular data without the need for distributional assumptions. 10 Meng et al proposed a multivariate integration method called multiple co-inertia analysis (MCIA). The method applies a covariance optimization criterion to detect interactions and variations between multiple datasets by projecting the multiple datasets into the same dimensional space. 11 In another study by Lyu and Haque the high dimensional RNA-Seq data was embedded into a two-dimensional map to classify tumor types through a convolutional neural network. A heatmap was created for all the genes to confirm the association of top genes to tumor-specific pathways. 12
Fatima and Rueda introduced iSOM-GSN, which integrates multi-omics data of gene expression, gene CNA, and gene methylation by embedding the high dimensional multi-omics data into a lower two-dimensional grid. The embedding applies Kohonen’s self-organizing map (SOM) to gene expression data and merges them with other genomic features to enhance visualization and performance. Then, a convolutional neural network is applied to classify diseases types and status. 13 In addition, Alkhateeb et al introduced a prediction model of a 5-year interval survival of breast cancer InClust5 based on integrating multi-omics data that consists of gene expression, copy number alteration (CNA), and clinical features datasets using a deep learning model. It expands the iSOM-GSN model by exploiting a self-organizing map (SOM) to embed each omics data into a lower two-dimensional relational map instead of relying only on the gene expression map as in the iSOM-GSN model. Three convolutional neural networks are used to classify each map. The outputs of CNNs are fed to an integration layer that utilizes majority votes to predict the model’s output. 14 Another work involving SOM was introduced by Jansen et al and named SOMatic. SOMatic is a gene regulatory network that integrates scRNA-seq and scATAC-seq data by assembling a self-organizing map (SOM) for each dataset to distinguish genes and chromatin that might alter over time. Then, -means clustering accumulates the 2 SOMs data into meta-clusters to connect similar genes and corresponding genomic regions. 15
In another study, Zhou et al incorporated t-distributed stochastic neighbor embedding (t-SNE) and residual neural network (ResNet) to integrate multi-omics data, including gene expression, copy number alteration (CNA), and mRNA for Nottingham Prognostics Index (NPI) prediction in a cohort of breast cancer patients. t-SNE was applied separately to each omics data, then concatenated their maps before being fed to the residual neural network (ResNet). 16 This paper designs a GSN via UMAP to integrate multi-omics data for predictions of disease states. First, we apply UMAP to the gene expression omics to embed it into a lower dimension and create a template map to project other omics data into the template to enhance the performance. Then, all feature maps will feed a convolutional neural network for disease classification.
Materials and Methods
Datasets
In this work, 2 cancer data sets are investigated: TCGA Prostate Adenocarcinoma (PRCA) for patients’ classification based on Gleason scores 17 and the TCGA Breast Invasive Carcinoma (BRCA) 18 that explores the tumor stages. Both data sets contain 3 omics: gene expression, DNA methylation, and copy number alteration (CNA). The total number of samples for PRCA and BRCA is 499 and 570, respectively.
The PRCA is divided into 3 classes; 3 + 4, 4 + 3, and the combination of 4 + 5 and 5 + 4 as the same class due to the low number of samples in theses advance classes. The BRCA is divided into 3 classes: 2A, 2B, and 3A. We only considered the samples with the 3 omics, which reduced the number of samples to 387 and 392 patients for PRCA and BRCA, respectively. The distributions of samples in both datasets are listed in Table 1.
Table 1.
The distribution of samples among 2 datasets the Gleason score classes in the PRCA dataset and the tumor stage classes in the BRCA dataset.
| The PRCA data set |
The BRCA dataset |
||
|---|---|---|---|
| Number of samples | Gleason score class | Number of samples | Tumor stage |
| 147 | 3 + 4 | 179 | 2A |
| 101 | 4 +3 | 129 | 3B |
| 139 | 4 + 5 and 5 + 4 | 84 | 3A |
Pre-processing
We adopted the preprocessing steps in Fatima and Rueda. 13 First, the gene expression features were filtered to eliminate all those with less than 0.2% variance. As a result, the number of gene expression features went down from about 39 000 to 16 000. Then, all 3 omics data were normalized on an average scale, and genes that are not listed in HUGO format were eliminated. The last step was to substantially distinguish the mutated genes through the MutsigCV algorithm 14 ; it calculates False-discovery rates (q-values), then genes with q ⩽ 0.1 were identified as significantly mutated that yielded select 14 mutated genes from MutsigCV output for this study. These genes are listed in Table 2.
Table 2.
The top 14 selected genes using MutsigCV in the PRCA dataset.
| Gene | Gene Description |
|---|---|
| SPOP | SPOP (Speckle Type BTB/POZ Protein) is a Protein Coding gene. |
| FOXA1 | FOXA1 (Forkhead Box A1) is a Protein Coding gene. |
| CTNNB1 | CTNNB1 (Catenin Beta 1) is a Protein Coding gene. |
| CLPTM1L | Cleft Lip And Palate Transmembrane Protein 1-Like Protein is a Protein Coding gene. |
| DPYSL2 | DPYSL2 (Dihydropyrimidinase Like 2) is a Protein Coding gene. |
| NEIL1 | NEIL1 (Nei Like DNA Glycosylase 1) is a Protein Coding gene. |
| PITPNM2 | PITPNM2 (Phosphatidylinositol Transfer Protein Membrane Associated 2) is a Protein Coding gene. |
| ATM | Ataxia-telangiectasia (A-T) is a recessive disorder resulting from germline mutation of the A-T mutated (ATM) gene on chromosome 11q. |
| EMG1 | EMG1 (EMG1 N1-Specific Pseudouridine Methyltransferase) is a Protein Coding gene. |
| ETV3 | ETV3 (ETS Variant Transcription Factor 3) is a Protein Coding gene. |
| BRAF | BRAF (B-Raf Proto-Oncogene, Serine/Threonine Kinase) is a Protein Coding gene. |
| NKX3-1 | NKX3-1 (NK3 Homeobox 1) is a Protein Coding gene. |
| ZMYM3 | ZMYM3 (Zinc Finger MYM-Type Containing 3) is a Protein Coding gene. |
| SALL1 | SALL1 (Spalt Like Transcription Factor 1) is a Protein Coding gene. |
Proposed method
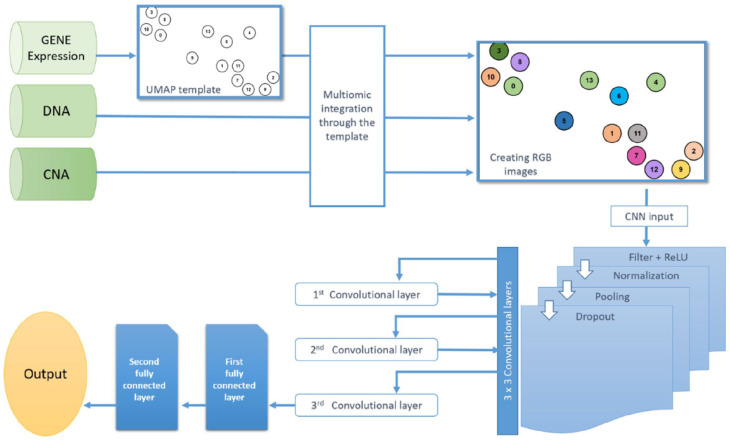
The workflow of our method is illustrated in Figure 1. It starts by generating a gene similarity network (GSN) via UMAP on gene expression omics to convert the high-dimensional gene expression omics to a two-dimensional map and create a feature template. Then, the template integrates all omics data and depicts each sample as a colored image filled in with all omics data. Finally, those images are fed to CNN for classification.
Figure 1.
Shows the workflow of the proposed method.
Uniform manifold approximation and projection (UMAP)
Uniform manifold approximation and projection is a dimension reduction method employing Riemannian geometry and algebraic topology theory. 8 UMAP utilizes the high dimensional data to build a fuzzy weighted graph illustrating the likelihood of connection of each pair of data points. Then, this graph is mapped into a lower dimensionality, creating a fuzzy graph similar to the high dimensional graph to preserve the local structure. UMAP assumes a uniform distribution of data on the Riemannian manifold, the approximation of the Riemannian metric is locally constant, and the manifold is locally connected. UMAP uses a radius to connect each data point with its neighbors that fall within the radius distance. The radius is a critical aspect of UMAP, where it might cause points to cluster in small and isolated clusters with a small radius or too large clusters with a large radius. UMAP overcomes this issue by selecting a local radius based on the distance between each point and its nearest neighbor. UMAP operates by building the weighted -neighborhood graph and then computing the low-dimensional layout of this graph.
Weighted K-neighborhood Graph
Assume the input dataset with dissimilarity metric for each and an input hyperparameter , we will compute and as follows:
| (1) |
is set to satisfy the following:
| (2) |
Where:
is - nearest neighbor for each point .
Now, we compute the weighted directed graph , where the vertices of are the dataset . By constructing the set of directed edges . The weight function w is computed as follows:
| (3) |
The adjacency matrix of undirected weighted graph B can be computed as:
| (4) |
Where:
A is the weighted adjacency matrix of D–, and “∘” is the Hadamard product.
Low-dimensional layout
A low-dimensional force-directed graph layout algorithm is employed in practice by UMAP.
The algorithm applies repulsive force at vertices and gravitational forces at edges. The gravitational force between 2 vertices and at coordinates is computed as the following:
| (5) |
Where: and are hyper-parameters.
The repulsive force is computed as the following:
| (6) |
Where:
is a constant number to avoid dividing by zero.
Gene similarity network and omics integration
We apply UMAP on the gene expression omics to build the GSN and visualize genes on a two-dimensional map. The two-dimensional map coordinates the genes based on their similarity and shows the connections between linked genes. The two-dimensional map is used as a template to integrate all omics data. The integration is done by creating a circular zone of chosen radius around genes points as depicted in Figure 2, then filling those zones with different colors related to omics’ type as shown in Figure 3. Each data sample would contribute to coloring the RGB palette if it only falls within a certain radius of a gene point. The red color (R) is donated for gene expression, the green (G) for DNA methylation, and the blue (B) for CNA.
Figure 2.
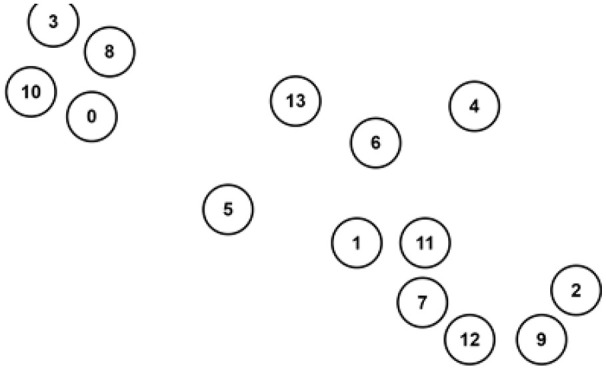
The template created by UMAP and gene expression.
Figure 3.
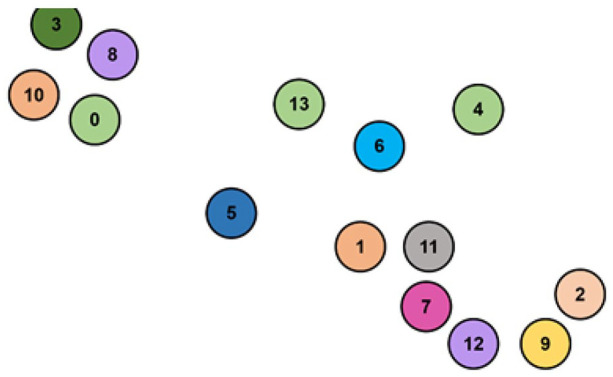
The integration of the 3 omics where the mixed (RGB) colors indicate the combination of their values.
Classification
CNNs are deep feed-forward neural networks that apply convolution operations as feature extraction from images. 19 In addition to the convolutional layers, CNNs consist of other layers that incorporate dropout regularization technique to enhance their performance. These layers include pooling layers, fully-connected layers, and classification layers. The architecture of our CNN is as follows:
First convolutional layer
It consists of 32 convolutional filters of size 3 × 3 with a rectified linear operator (ReLU), a Max-pooling layer of 2 × 2 size and 1 × 1 stride, a normalized layer, and a dropout layer of 20% ratio.
Second convolutional layer
It consists of 32 convolutional filters of size 3 × 3 with a rectified linear operator (ReLU), a Max-pooling layer of 2 × 2 size and 1 × 1 stride, a normalized layer, and a dropout layer of 50% ratio.
Third convolutional layer
It consists of 32 convolutional filters of size 3 × 3 with a rectified linear operator (ReLU), a Max-pooling layer of 2 × 2 size and 2 × 2 stride, a normalized layer, and a dropout layer of 50% ratio.
First fully connected layer
It consists of 128 neurons with a rectified linear operator (ReLU), a normalized layer, and a dropout layer of a 10% ratio.
Second fully connected layer
It is the prediction layer, and it consists of 3 neurons that feed their output to a Softmax layer to predict the classes based on their probabilities.
Experiments and Results
For this experiment, we applied the proposed model to both the PRCA and the BRCA data sets. We kept the default setting of UMAP’s neighbor, which is 15. Using grid-search, we set the learning rate to 0.07 and employed 1000 epochs which provided the best accuracy. The datasets samples are divided into 70% training pool and 30% testing pool. We also ran iSOM-GSN model 13 on the both data sets and kept the default parameter to compare it with the proposed method. The proposed method performed very well in the testing pool, where it achieved over 99% in all evaluation metrics, as in Table 3.
Table 3.
Performance evaluation of the proposed model and iSOM-GSN.
| The PRCA data set |
The BRCA data set |
|||
|---|---|---|---|---|
| Evaluation metric | Proposed model | iSOM-GSN | Proposed model | iSOM-GSN |
| Accuracy | 99.37% | 97.89% | 97.66% | 82.83% |
| Precision | 99.69% | 98.82% | 99.59% | 98.58% |
| Recall | 99.83% | 98.72% | 99.70% | 98.88% |
| F1-measure | 99.75% | 98.71% | 99.63% | 98.65% |
| AUC | 0.9992 | 0.9984 | 0.9982 | 0.9676 |
We used the following performance measurements as evaluation metrics:
| (7) |
| (8) |
| (9) |
| (10) |
Where:
is positive predictive value that is measured as equation (11):
| (11) |
Sensitivity or true positive rate (TPR) is defined as:
| (12) |
Specificity or true negative rate (TNR) is defined as:
| (13) |
is true positive, is false positive, is true negative, and is false negative.
The results illustrate the robustness of our model. For both data sets, the performance of the model almost scored near perfection in each evaluation metric. For the PRCA data set, the accuracy of the proposed model is 99.37%, while it is 97.89% for iSOM-GSN model. The area under the curve (AUC) is a robust overall performance measurement 20 ; it measures how the prediction model can classify both positive and negative classes. The proposed model scored 0.9992 of AUC compared to 0.9984 for the iSOM-GSN. Similarly, for the BRCA data set, the accuracy of the proposed model is 97.66%, while it is 82.83% for iSOM-GSN model. The proposed model scored 0.9982 of AUC compared to 0.9676 for i-SOM-GSN. The proposed model outperformed iSOM-GSN by 1% to 2% in the remaining performance measurements as seen in Table 3 for both data sets.
Discussion
Many previous studies depend on early data concatenation 21 or independent analysis of the late merging of the omics data in the prediction model. 14 Data embedding techniques try to extract the meaningful relationships using visual maps, then merge those relationships in the CNN model to find the global associations from the spatial representation of the omics. The model utilizes UMAP, which tries to find the global and local structure of the relationships among the features and represent it on a two-dimensional map. The model outperformed the state-of-art iSOM-GSN in predicting the cancer outcomes from 2 publicly available data sets. The first is Gleason score levels in prostate cancer, and the second is the tumor stage in breast cancer. The clinical reports may incorporate the multi-omics biomarkers to assist the physicians in prescribing the proper treatment.
Similar to iSOM-GSN, this work’s main limitation is that it can only integrate 3 omics because we are using the RGB coloring system. Another limitation of the current multi-omics data models is the lack of a large number of samples. Most of the current publicly available data sets contain a couple of hundreds of samples that may lead to insignificant results in the lower number of data sets’ samples.
Conclusion
Cancer has a heterogeneous nature, where there is always a necessity to find biomarkers for different subtype of cancer. 22 In this model, the GSN map was created using UMAP to merge patients’ samples with 3 omics, including Gene expression, DNA methylation, and CNA. The maps are colored using the samples values in the RGB coloring system. The embedded patients’ maps are fed into a deep learning prediction model consisting of several CNN levels. UMAP extracts the discriminative relationships between the features by mapping them into Laplacian eigenmaps. The model is applied to the PRCA and BRCA to predict the outcome of cancer, and it outperformed iSOM-GSN that is another embedding data integration model.
The integration happens at the middle stage of the machine learning model. While the genes were selected from the gene expression data to create the template, all omics have been used in coloring the two-dimensional maps. The future direction is to investigate more types of cancer and other complex diseases, and to enhance the embedding techniques to reach the ultimate modeling of the molecular-based analysis.
Footnotes
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: A.A. received financial support as a seed fund from the King Abdullah I School of Graduate Studies and Scientific Research at the Princess Sumaya University for Technology with grant number 2021/2022 –25 (16).
Declaration Of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author Contributions: BE and AA: made substantial contributions from the inception of the research idea to proposal development, data collection, analysis and interpretation of data, preparation of the manuscript, design, analysis of the study. HQ, LA: made substantial contributions in the analysis of the study, validation of the methods, and participated in the preparation of the manuscript for publication. BS participated in the analysis and the preparation of the manuscript for publication All authors read and approved the final version of the manuscript.
Availability of Data and Materials: Data related to this manuscript is available on the hand of corresponding author and will be obtained under a reasonable request.
References
- 1. Arjmand B, Hamidpour SK, Tayanloo-Beik A, et al. Machine learning: a new prospect in multi-omics data analysis of cancer. Front Genet. 2022;13:824451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Cai Z, Poulos RC, Liu J, Zhong Q. Machine learning for multi-omics data integration in cancer. Iscience. 2022;25:103798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Shen R, Olshen AB, Ladanyi M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics. 2009;25:2906-2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Mo Q, Wang S, Seshan VE, et al. Pattern discovery and cancer gene identification in integrated cancer genomic data. Proc Natl Acad Sci U S A. 2013;110:4245-4250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kohonen T. The self-organizing map. Proc IEEE. 1990;78:1464-1480. [Google Scholar]
- 6. Hinton GE, Roweis ST. Stochastic neighbor embedding. In: Becker S, Thrun S, Obermayer K, eds. Advances in neural information processing systems. Vol. 15. The MIT Press; 2002: 833-840. [Google Scholar]
- 7. Van der Maaten Laurens, Geoffrey H. Visualizing data using t-SNE. JMach Learn Research. 2008;9:11. [Google Scholar]
- 8. McInnes L, Healy J, Melville J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv preprint, arXiv:1802.03426, 2018. [Google Scholar]
- 9. Argelaguet R, Velten B, Arnol D, et al. Multi-omics factor analysis—a framework for unsupervised integration of multi-omics data sets. Mol Syst Biol Appl. 2019;14:22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Chalise P, Fridley BL. Integrative clustering of multi-level ‘omic data based on non-negative matrix factorization algorithm. PLoS One. 2017;12:e0176278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Meng C, Kuster B, Culhane AC, Gholami AM. A multivariate approach to the integration of multi-omics datasets. BMC Bioinform. 2014;15:162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lyu B, Haque A. Deep learning based tumor type classification using gene expression data. Paper presented at: 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics: ACM; 2018:89-96. [Google Scholar]
- 13. Fatima N, Rueda L. ISOM-GSN: an integrative approach for transforming multi-omic data into gene similarity networks via self-organizing maps. Bioinformatics. 2020;36:4248-4254. [DOI] [PubMed] [Google Scholar]
- 14. Alkhateeb A, Zhou L, Tabl AA, Rueda L. Deep Learning Approach for Breast Cancer InClust 5 Prediction based on Multiomics Data Integration. Paper presented at: 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics; September 21, 2020:1-6. [Google Scholar]
- 15. Jansen C, Ramirez RN, El-Ali NC, et al. Building gene regulatory networks from scATAC-seq and scRNA-seq using linked self organizing maps. PLoS Comput Biol. 2019;15:e1006555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Zhou L, Rueda M, Alkhateeb A. Classification of breast cancer nottingham prognostic index using high-dimensional embedding and residual neural network. Cancers. 2022;14:934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. National Cancer Institute. TGCA. cBioPortal for Cancer Genomics. 2013. Accessed July 2022. http://cbioportal.org/study/summary?id=prad_tcga
- 18. National Cancer Institute. TGCA. cBioPortal for Cancer Genomics. 2015. Accessed July 2022. http://cbioportal.org/study/summary?id=brca_tcga_pub2015
- 19. LeCun Y, Bengio Y. Convolutional networks for images, speech, and time series. In: Arbib MA, ed. The Handbook of Brain Theory and Neural Networks. Vol. 3361. MIT Press; 1995:1-14. [Google Scholar]
- 20. Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29-36. [DOI] [PubMed] [Google Scholar]
- 21. Schulte-Sasse R, Budach S, Hnisz D, Marsico A. Integration of multiomics data with graph convolutional networks to identify new cancer genes and their associated molecular mechanisms. Nat Mach Intell. 2021;3:513-526. [Google Scholar]
- 22. Lawrence MS, et al. Mutational heterogeneity in cancer and the search for new cancer-associated genes. Nature. 2013;499:214-218. [DOI] [PMC free article] [PubMed] [Google Scholar]