Guided interactive image segmentation using machine learning and color-based image set clustering

Abstract

Motivation

Over the last decades, image processing and analysis have become one of the key technologies in systems biology and medicine. The quantification of anatomical structures and dynamic processes in living systems is essential for understanding the complex underlying mechanisms and allows, i.e. the construction of spatio-temporal models that illuminate the interplay between architecture and function. Recently, deep learning significantly improved the performance of traditional image analysis in cases where imaging techniques provide large amounts of data. However, if only a few images are available or qualified annotations are expensive to produce, the applicability of deep learning is still limited.

Results

We present a novel approach that combines machine learning-based interactive image segmentation using supervoxels with a clustering method for the automated identification of similarly colored images in large image sets which enables a guided reuse of interactively trained classifiers. Our approach solves the problem of deteriorated segmentation and quantification accuracy when reusing trained classifiers which is due to significant color variability prevalent and often unavoidable in biological and medical images. This increase in efficiency improves the suitability of interactive segmentation for larger image sets, enabling efficient quantification or the rapid generation of training data for deep learning with minimal effort. The presented methods are applicable for almost any image type and represent a useful tool for image analysis tasks in general.

Availability and implementation

The presented methods are implemented in our image processing software TiQuant which is freely available at tiquant.hoehme.com.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Advances in imaging technology have led to a diversification of microscopy techniques enabling examination of a broad spectrum of biological questions and have thus contributed to the establishment of imaging and image analysis as one of the main pillars of bioscience. Optical microscopy in combination with (immuno)histochemical and immunofluorescent staining allows for the visualization of tissue and physiological entities. Therefore, these techniques are widely used (i) in medical diagnosis, e.g. using histological sections of tissue specimens or biopsies, as a means to distinguish physiological and pathological tissue architectures and (ii) in medical research to study tissue microarchitecture, e.g. using 3D volumetric confocal microscopy (Friebel et al., 2015; Hammad et al., 2014; Hoehme et al., 2010), and tissue-scale or intracellular processes, e.g. by time-resolved two-photon microscopy (Vartak et al., 2019). In many use cases, computer-aided image analysis is preceded by the detection or pixel-accurate segmentation of objects of interest. Detection asks for the location of an object in the image, e.g. using bounding boxes, while segmentation tries to capture the precise shape of the object. The most basic segmentation technique, manual pixel-accurate labeling, is time consuming, inconsistent and practically infeasible in many use cases, such as e.g. blood vessel segmentation in volumetric images. A multitude of (semi-)automatic image processing methods have been proposed, including e.g. intensity-thresholding and morphological operators (Friebel et al., 2015; Hammad et al., 2014; Hoehme et al., 2010), region-based methods (Lopez et al., 1999) or deformable models (McInerney and Terzopoulos, 1996). These methods are usually tailored towards a specific image setup (i.e. image dimensionality, magnification and staining) and/or object class (e.g. nuclei, blood vessels and necrotic tissue) and as such are typically limited in their applicability to differing use cases. Additionally, method parametrization to cope with image variability is often challenging and time consuming. More recently, shallow and deep machine learning methods were successfully applied to pixel-accurate image segmentation (Ciresan et al., 2012; Lucchi et al., 2012; Ren and Malik, 2003; Ronneberger et al., 2015). By learning object appearance from training examples, these methods allow for the incorporation of subtle expert knowledge, are less restricted regarding image or object class specifics and minimize parametrization complexity.

Deep learning proved to be an extremely powerful approach to improving performance across all image processing tasks (He et al., 2017; Krizhevsky et al., 2012; Long et al., 2015; Ronneberger et al., 2015). This is primarily due to its ability to operate directly on the input image and implicitly learn features of increasing complexity. The price of finding a suitable feature space in addition to the decision surface itself is a high demand for training data and long training times. By now, there is a large variety of specialized network architectures for segmentation of biomedical images and pre-trained models for standard targets such as nuclei or cells that can be applied directly if the images to be segmented are similar to images in the training set, or that can be tuned using transfer learning thereby reducing the amount of training data needed. However, the range of imaging systems and segmentation targets in the biomedical field is diverse so that often no suitable pre-trained models are available, image counts are in many cases very low and ground truth is usually not readily available and expensive to generate, which poses significant challenges for the applicability of deep learning methods. Furthermore, the development but also the training of deep learning models requires significant expert knowledge and is therefore difficult to achieve for untrained personnel. In contrast, traditional, so-called shallow, machine learning approaches such as random forests or support vector machines (SVMs), rely on handcrafted features. While this limits versatility, as engineered features need to represent the learning problem at hand, finding a decision surface in a restricted feature space greatly simplifies the learning task. Thereby, relatively few training examples and short training times are required, which makes these shallow methods eminently suitable for interactive segmentation.

A number of interactive segmentation approaches and software packages that utilize machine learning have been published in recent years. A supervoxel-based approach for segmentation of mitochondria in volumetric electron microscopy images was developed by Lucchi et al. (2012), though the published executable software and code encompassed only the supervoxel algorithm SLIC. SuRVos (Luengo et al., 2017) is a software for interactive segmentation of 3D images using a supervoxel-based hierarchy, which lays a focus on the segmentation of noisy, low-contrast electron microscopy datasets. The extendable software package Microscopy Image Browser (Belevich et al., 2016) allows for the processing of multidimensional datasets and features a selection of conventional processing algorithms, several region selection methods aiding manual segmentation, and methods for semi-automatic segmentation, including a supervoxel-based classification approach. FastER (Hilsenbeck et al., 2017) is designed specifically for cell segmentation in grayscale images, using features that are very fast to compute. The Fiji plugin Trainable Weka Segmentation (Arganda-Carreras et al., 2017) is a tool for pixel classification in 2D and 3D images using a broad range of features. Ilastik (Berg et al., 2019) provides a streamlined user interface with workflows for i.e. image segmentation, object classification and tracking as well as a sophisticated on-demand back end enabling processing of images with up to five dimensions that are larger than available RAM. Its segmentation workflow employs a random forest classifier for pixel classification from local features such as color, edgeness and texture at different scales.

Most of these interactive segmentation tools allow for the reuse of trained classifiers on new, unseen images. However, due to the variability of image appearance, even for sets of images that were acquired following a standard protocol, classifier reuse is usually a trial-and-error procedure and quickly becomes cumbersome for larger image sets. One of the main contributing factors to image quality variability is systematic discrepancies of coloration that can be attributed to minor deviations in the image acquisition process (e.g. sample preparation procedure, imaging settings and condition of the imaged subject). Since color information is used in various ways as a feature by all mentioned segmentation tools that target colored images, degraded prediction accuracy is to be expected for images with variable coloration.

We propose an approach that combines (i) interactive image segmentation from sparse annotations with (ii) the guided reuse of thereby trained classifiers on unseen images to enable efficient batch processing. (i) We formulate interactive pixel-accurate segmentation as a machine learning problem working on supervoxels, which are connected, homogeneously colored groups of voxels, using random forests or SVMs as classifiers. Dimensionality reduction through use of supervoxels, precomputation of supervoxel features and a convenient graphical user interface enable rapid, intuitive refinement of training annotations by iterative correction of classification errors or uncertainties. (ii) We introduce a color-based image clustering method that enables the automated grouping of image sets into subsets of similarly colored images. A corresponding number of so-called prototype images is identified which serve as eligible candidates for interactive training of classifiers for within-subset reuse. These new methods, that are applicable to 2D and 3D images, have been fully incorporated into our freely available image processing software TiQuant. The first version of TiQuant, released in 2014, included various processing methods specifically for liver tissue segmentation of 3D confocal micrographs, as well as the corresponding analysis functionality (Hammad et al., 2014; Friebel et al., 2015).

We evaluate the interactive image segmentation method as well as the color-based image clustering strategy to guide classifier reuse using a previously published image set consisting of 22 brightfield micrographs of mouse liver tissue with corresponding manual nuclei annotations (Hoehme et al., 2010). We show that the interactive approach outperforms a human annotator and a comparable state-of-the-art interactive segmentation software and that limiting classifier reuse to similarly colored images significantly improves performance compared to reuse on images of differing coloration, yielding results close to the level of a human annotator.

2 Materials and methods

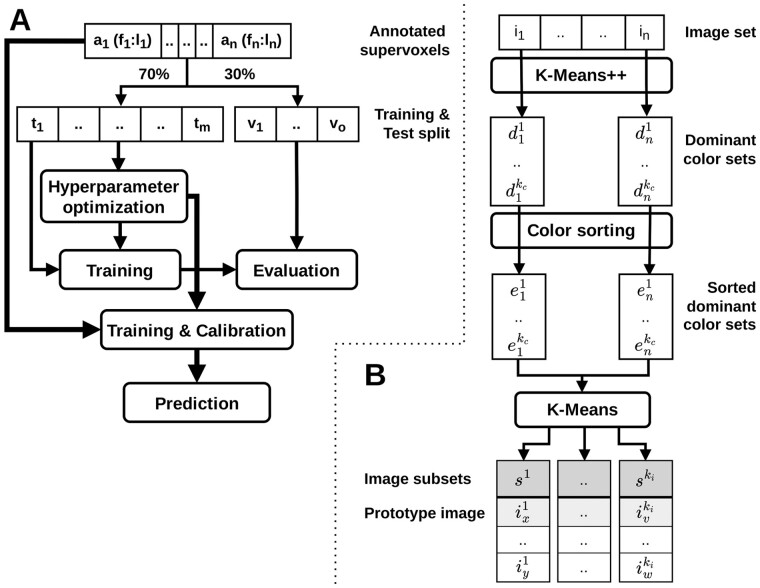
The general workflow of segmenting an image with our supervoxel-based approach is split into a preprocessing step and the interactive training, prediction and segmentation steps that require direct user intervention and must be iteratively repeated for refinement as needed to achieve a segmentation of desired quality (see Fig. 1A).

Fig. 1.

(A) Workflow of the supervoxel-based interactive image segmentation approach from a user perspective. The classifier training procedure is illustrated in detail in Figure 3A. (B) Workflow of guided reuse of interactively trained classifiers: The set of n images is grouped into m subsets of similarly colored images using our color-based image clustering method. For each subset a prototype image is identified, which is then interactively segmented. The resulting m trained classifiers are reused on the remaining images in their respective subsets. The color-based clustering algorithm is depicted in detail in Figure 3B

In the preprocessing step, the image is partitioned into similarly sized supervoxels and descriptive features are computed for them. A single parameter, the target supervoxel size, must be adjusted by the user to ensure supervoxels fit the objects of interest. This step is computationally expensive compared to the interactive steps because it scales with the number of pixels and superpixels. For example, on a modern computer, it takes ∼1 min to partition a 7.5k × 7.5k pixel image into 100k superpixels and 6 min to calculate all available features for them. However, this step is usually performed only once per image.

Subsequently, the user annotates exemplary fore- and background regions in the original image to generate a training database. A classifier is then fitted to the training data, and probability estimates for class membership are predicted for all supervoxels in the image. In the final step, a segmentation is generated based on these probability estimates, which can be refined through post-processing.

If segmentation quality is insufficient, the user can provide further training data, especially for regions that were poorly segmented. Thereby, high-quality segmentations can be generated quickly by iterative annotation refinement.

Trained classifiers can be used for the prediction on unseen images, eliminating the need for producing training data for every image. To guide the process of identifying training images and matching candidate images for classifier reuse, the images to be processed are grouped into similarly colored subsets using a two-stage clustering approach (see Fig. 1B).

2.1 Supervoxel initialization

The term supervoxel (respectively superpixel in 2D) was introduced by Ren and Malik (2003), who proposed oversegmentation, i.e. the process of partitioning an image into contiguous regions so that the objects of interest are themselves subdivided into distinct regions, as a preprocessing step to reduce image complexity while preserving most of the structure necessary for segmentation at the scale of interest. Supervoxels group voxels into visually meaningful building blocks of more or less similar size and compactness, depending on the chosen generative approach and parametrization. They reduce data dimensionality with minimal information loss, thereby greatly reducing the computational cost of subsequent processing steps, and they allow the computation of local features such as color histograms and texture descriptors. To date, a multitude of different supervoxel algorithms exists which can be categorized by their high-level approach, into e.g. graph-based, density-based and clustering-based algorithms (Stutz et al., 2018).

We use the SLIC0 variant of the clustering-based algorithm simple linear iterative clustering (SLIC) (Achanta et al., 2012), due to its comparatively strong performance regarding Boundary Recall and Undersegmentation Error (Stutz et al., 2018), and its memory and runtime efficiency (Achanta et al., 2012). Its iterative nature enables straightforward runtime restriction and provides direct control over the number of generated superpixels. SLIC is an adaptation of k-means clustering with two main distinctions: (i) The search space is reduced to a region proportional to the superpixel size, yielding a complexity linear in the number of pixels and independent of superpixel count. (ii) The weighted distance measure used combines color and spatial proximity, providing control over size and compactness of the resulting superpixels. The SLIC0 variant adaptively chooses the superpixel compactness, thereby reducing the free parameters to be adjusted to the number of superpixels, or the superpixel size, respectively. The SLIC0 algorithm was implemented as an ITK (Insight Toolkit) filter and extended to work in three dimensions. Examples of superpixel oversegmentations can be seen in Figure 2.

Fig. 2.

Illustration of supervoxel-based image segmentation procedure on an image of a cheetah (left) (photo by Behnam Ghorbani, published via Wikimedia Commons CC 4.0), and a 3D confocal micrograph of mouse liver tissue in which blood vessels were segmented (right). The capillaries in this imaging setup appear yellow–green and usually comprise an unstained lumen as well as few small, elongated nuclei colored blue, which typically belong to endothelial (sinusoidal) cells forming the capillary wall, immune cells residing in the lumen or other non-parenchymal cells. (1) Supervoxel outlines are shown in gray. (2) Training data for the background class is colored red in both instances, while the foreground class is colored blue in the left and white in the right example. Annotations were selected to represent the characteristic visual features of both classes. For example, annotations of capillaries comprise yellow-colored walls, lumen and enclosed cell nuclei, whereas the background annotations encompass unstained cytoplasm and nuclei of the parenchymal liver cells (blue), bile canaliculi (green) as well as regions close to capillaries to promote learning of exact boundaries. (3) Class membership probabilities in the prediction images are illustrated using a color mapping ranging from red (low probability of being foreground) over yellow to blue (high probability of being foreground). (4) The segmentation is visualized by a blue overlay on the left, and a yellow overlay on the right (A color version of this figure appears in the online version of this article.)

In brightfield and confocal microscopy, tissues or physiological entities are stained; accordingly, color, color gradients or boundaries, and local color patterns are the primary source of information for image interpretation. Therefore, the implemented supervoxel features comprise local and neighborhood color histograms, edge-ness over several spatial scales, as well as texture descriptors (detailed description in Supplementary Appendix), yielding a feature vector with a maximum of 138 entries. Feature categories can be disabled by the user to speed up processing.

2.2 Interactive training data generation

For training data generation, TiQuant provides a graphical user interface that allows visualization of and interaction with images. The user can draw directly on the image in order to denote exemplary regions for the classes to be segmented. Supervoxels in the annotated regions are collected and their feature vector together with the annotated class are written into a training database. For examples of how training data annotation is presented in the software, see Figure 2.

2.3 Supervoxel classification

Random forests (RF) and SVM are supported as classifiers to learn the class membership of supervoxels given their feature vectors. We included both classifiers to choose from as they were found to be the two best-performing classifier families when evaluated on a diverse set of learning problems (Fernández-Delgado et al., 2014). Furthermore, both classifier families are able to handle non-linear data and have few parameters, however, RFs are faster in regard to training and execution and are therefore set as default.

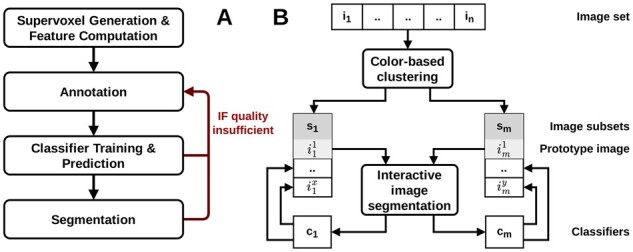
The user-supplied training data, which is summarized in the training database, are split into a training set and a test set in a 70:30 ratio to allow evaluation of classifier performance (see Fig. 3). Since training data can be relatively sparse, we use this skewed ratio to ensure a sufficiently large database for training, potentially at the expense of accuracy in assessing classifier performance. Furthermore, the training data are expected to be imbalanced, i.e. that classes are unevenly distributed. To account for this disparity, the initial training-test split, as well as splits performed during cross-validation, are done in a stratified fashion to preserve relative class frequencies. Moreover, in the training phase, the training samples are weighted, where the weight is inversely proportional to the class frequency, and appropriate scoring functions that are insensitive to imbalanced training data are used for classifier evaluation. The feature vectors computed during supervoxel initialization, described in detail in the Supplementary Information, are normalized by subtracting the mean and scaling to unit variance independently for each feature component to ensure comparable feature scales.

Fig. 3.

(A) Flowchart of the classifier training procedure. The set of annotated supervoxels is split in a 70:30 ratio into a training and test split. The RF or SVM classifier is trained on the training split after optional hyperparameter optimization and evaluated on the test split to allow the user to assess and compare classifier performance. The classifier employed for final prediction uses the optimized parametrization and is trained and calibrated on the entire original set of annotated superpixels. Figure 1A illustrates the integration of the training procedure into the interactive segmentation workflow. (B) Flowchart of the color-based image clustering algorithm. For each image, a characteristic set of the k_c most dominant RGB colors is determined by k-means clustering of the RGB pixel values using the k-means++ initialization scheme. To ensure comparability of these representative sets, their RGB entries are sorted by component-wise comparison of R/G/B values. Finally, k-means clustering is applied in the 3*k_c-dimensional space of sorted dominant color sets to group the corresponding n images into k_i subsets. For each of these subsets, a prototype image is identified, which is recommended for interactive segmentation. Figure 1B illustrates the integration of the color-based image clustering algorithm into the workflow of guided reuse of interactively trained classifiers

Prior to classifier training, hyperparameter optimization of the chosen RF or SVM classifier can optionally be performed to tune parameters that are not directly learned to the learning problem. In order to limit execution time while retaining the explorative quality of an exhaustive Grid Search, the optimization is done using Random Search, which tests a fixed number of parameter settings sampled from given distributions (Bergstra and Bengio, 2012). The search is performed on the training split with 5-fold cross-validation employing the balanced accuracy score (Brodersen et al., 2010) to evaluate classifier performance.

As an intermediate step, the (optionally) optimized classifier is trained on the training split and evaluated on the withheld test split to assess its performance. This allows the user to evaluate the suitability of the selected features and classifier, to compare different configurations and to determine whether additional training data are expected to improve performance.

Finally, to make efficient use of the sparse training data, the classifier is trained and calibrated on the entire user-supplied data corpus using the previously determined optimized parametrization. The resulting trained classifier is then used to predict the class membership probability estimates of all supervoxels of the image. Exemplary probability maps are shown in Figure 2. Classifier calibration is performed after training using 5-fold cross-validation to provide calibrated probabilistic estimates of class membership as output. In case of SVMs, Platt Scaling (Platt et al., 1999) is used for this purpose, fitting an additional sigmoid function to map SVM scores to probabilities. RFs, on the other hand, provide probabilistic estimates per default, which can be optionally calibrated using Platt Scaling or the non-parametric Isotonic Regression approach (Barlow, 1972). Empirical results show that SVMs and RFs are among the models that predict the best probabilities after calibration (Niculescu-Mizil and Caruana, 2005). The Brier score is used to evaluate classifier performance during calibration since it is a proper scoring rule that measures the accuracy of probabilistic predictions (Gneiting and Raftery, 2007).

2.4 Segmentation

The probabilistic estimates are mapped to a binary class membership by applying a threshold, which defaults to the value of 50%. Subsequently, the resulting segmentation can be post-processed using three optional filters. The first post-processing step allows for the removal of isolated foreground objects smaller than a specified minimal foreground object size, as well as filling of holes in foreground objects smaller than a minimal hole size. Additionally, a morphological closing operator followed by an opening operator can be applied to smooth surfaces. Specialized label set operators are used that work on the label image representation in which pixel values represent connected objects. These operators preserve the initial label assignment by not merging disconnected foreground objects (Beare and Jackway, 2011). Finally, the watershed algorithm may be applied in order to split wrongly connected objects such as nuclei (Malpica et al., 1998). Two exemplary segmentations are shown in Figure 2.

2.5 Color-based image clustering

A common but severe problem hampering efficient batch processing of a large number of images is visual heterogeneity of images due to varying imaging settings and conditions, or systematic visual changes during the imaged process. One approach to solve this problem is image normalization that aims to visually equalize images prior to segmentation and analysis.

There is a large number of normalization methods available today, typically aiming at normalizing the intensity distribution of images and/or improving the signal-to-noise ratio, such as variations of adaptive histogram equalization (Pizer et al., 1987), color deconvolution (Ruifrok and Johnston, 2001) or more recent deep learning-based methods (Litjens et al., 2017). However, the selection of a suitable method as well as its parameterization is non-trivial. Moreover, normalization methods can easily introduce systematic errors in subsequent image analysis if differences in visual appearance originally result from changes in tissue conditions to be analyzed. In this case, normalization could remove properties that actually should be quantified.

We propose a different method to overcome the problem of visual heterogeneity in microscopic images by automatically and robustly grouping images of a given dataset into visually homogeneous subsets. Thereby, we can not only guide the selection of training images but also facilitate classifier reuse leading to minimized manual annotation effort. The underlying assumption is that minor procedural discrepancies in the image acquisition process introduce systematic changes of coloring. Possible causes comprise slight variations between sample preparation sessions (e.g. affecting staining penetration depth, thus color saturation), minor deviations in imaging settings between imaging sessions (e.g. affecting brightness and contrast), as well as differing conditions of the imaged subjects (e.g. healthy vs. impaired tissue).

In a first step, images are analyzed for their dominant colors (see Fig. 3). This process, also known as palette design, is one of the two phases of color quantization, an operation used for e.g. image compression. It has been shown that k-means clustering is an effective method for this task (Celebi, 2009; Kasuga et al., 2000). In order to identify a set of the k_c most dominant colors of an image in RGB color space, each pixel’s RGB color vector is interpreted as a data point in 3D space. Instead of starting with fully random cluster centers the k-means++ initialization scheme (Arthur and Vassilvitskii, 2006) is used, as it has been demonstrated to improve effectiveness for this task (Celebi, 2009). Elkan's algorithm (Elkan, 2003), which is a faster variant of Lloyd’s algorithm (Lloyd, 1982), using the triangular inequality to avoid many distance calculations, is employed to cluster the RGB color data points.

Next, the entries of the dominant color sets are sorted, since their initial order is based on color prevalence, i.e. the number of pixels assigned to a respective color cluster. This ordering, however, is susceptible to changes in image composition, so that, e.g. the size or number of physiological entities influences the rank of the color cluster(s) they are assigned to. Sorting, which is done component-wise on the RGB vector entries, allows comparing the dominant color sets of different images.

Finally, the image set is partitioned into subsets with similar dominant color sets. Our approach extends previous work, in which color moments (Maheshwary and Srivastav, 2008) or histograms (Malakar and Mukherjee, 2013) were used as image descriptors for k-means-based image clustering. Each image is represented by its 3*k_c-dimensional sorted dominant color set. K-means clustering is applied to this set of data points yielding k_i clusters, minimizing the within-cluster variances of the sorted dominant color sets. The images with the smallest Euclidean distance to their respective cluster center are recommended training images for their image cluster.

3 Experiments

3.1 Validation

We validated our interactive segmentation and image set clustering method exemplarily on a set of 22 brightfield micrographs of mouse liver paraffin slices. These images were hand-labeled by a trained expert to automatically extract architectural and process parameters, which were used to parameterize a spatio-temporal tissue model of tissue regeneration after CCl₄ intoxication (Hoehme et al., 2010). Tissue slices were immunostained for BrdU positive nuclei to visualize proliferation and typically show a single liver lobule centered by a central vein. Image data were obtained for a control (t = 0) and at seven-time points after administration of CCl₄, which causes necrotic tissue damage in the area around the central vein. Over the observed time period, this damage regenerates and the lost cells are replenished by cell proliferation of the surviving liver cells.

We reuse this image set to validate our method as it is representative for many image segmentation tasks in a biomedical context, which are characterized by a small total number of available images and heterogeneous image appearance caused by variations in sample preparation, imaging settings or tissue conditions, or by various other possible technical problems like entrapped air, blurring or imperfect staining application.

A re-examination of the original nuclei annotations revealed several inaccuracies and inconsistencies (Fig. 4A). Therefore, two trained experts manually revised all 22 images thoroughly to define a gold standard nuclei annotation. The annotations represent each nucleus as a 2D pixel coordinate. As a measure for segmentation accuracy, we use the F₁ score, thereby considering both precision and recall. The number of true positives (tp), false positives (fp) and false negatives (fn) underlying the score are quantified based on an object-wise mapping of the gold standard to the respective segmentation. Specifically, a segmented nucleus is considered a tp if a gold standard nucleus (i.e. its 2D coordinate) lies within the segmented region. Accordingly, a segmented nucleus within which there is no gold standard nucleus is counted as a fp. A fn is registered if there is no segmented nucleus in the immediate neighborhood (kernel of size 1) of a gold standard nucleus. Based on the F₁ scores, we validate and compare the following methods: (i) original manual annotation (Fig. 4A), (ii) our superpixel-based interactive processing approach (Fig. 4B), (iii) intra- and (iv) inter-cluster reuse of interactively pre-trained classifiers as well as (v) the state-of-the-art tool ilastik (Berg et al., 2019) as a reference point.

Fig. 4.

Visualization of error classes from comparison with gold standard (GS): (A) Comparison of GS with the original manual segmentation created by a single human annotator: Correctly segmented nuclei (true positives: bright green); Incorrectly segmented nuclei (false positives: yellow); Nuclei that were falsely not segmented (false negatives: red). (B) Comparison of GS with a segmentation generated by our interactive segmentation tool: Coloring as in (A). Nuclei outlines in (A) were generated from 2D pixel coordinates provided by the annotator, while outlines in (B) were generated directly from the nuclei segmentation (A color version of this figure appears in the online version of this article.)

For validation of the superpixel-based approach, each image was partitioned into approximately 50k superpixels of target size 64 pixels (initially 8 × 8 pixels), and each superpixel was analyzed for all available features, comprising gradient magnitude, Laplacian of Gaussian, local and neighborhood color histograms as well as texture features.

In order to evaluate the suitability of our tool for interactive segmentation, appropriate training data was produced for each of the 22 images by annotation (following workflow Fig. 1A). Per image, a RF classifier was trained and calibrated after hyperparameter optimization was performed. The trained classifiers were applied to the respective image to predict class membership of all contained superpixels. The resulting segmentations were post-processed by removing objects smaller than three superpixels, smoothing of boundaries of segmented nuclei, and finally by applying the watershed algorithm to split up agglomerations of nuclei into individual objects.

Subsequently, to evaluate how well the trained classifiers generalize to unseen images and whether a restriction to images with similar coloration improves performance, we grouped the image set into k_i = 6 subsets. The number of clusters was determined experimentally using the Elbow method, a heuristic for determining the optimal number of clusters representing the majority of the variability in a dataset. The number of dominant color sets k_c = 4 was chosen manually to correspond with the different image compartments of relevant size (i.e. background, nuclei and two tissue compartments for healthy tissue/necrotic lesion or glutamine synthetase positive/negative zone, respectively). Per image subset the image with the smallest Euclidean distance to the image cluster center was selected as prototype image. The previously trained classifiers of these prototype images were applied (i) intra-cluster to all other images in the respective cluster and (ii) inter-cluster to all images not belonging to the respective cluster. Segmentation post-processing was done as described before.

We compare our approach with the established image processing software ilastik. For the results to be comparable, we used ilastik’s ‘Pixel Classification + Object Classification’ workflow. All 37 predefined features were selected for training. The training annotations created with our software were imported and an object size filter was used for segmentation post-processing.

The summarized results of the method validation are shown in Table 1, while a more detailed per image/cluster analysis is shown in the Supplementary Appendix  Figure S3. The best result was achieved with the fully interactive approach where dedicated training data were provided for each image. The original manual annotation produced comparable results to intra-cluster reuse of classifiers trained on prototype images, indicating that the restriction of classifier reuse to similarly colored images is able to produce human-grade results. However, as the increased variance for classifier reuse indicates, segmentation quality is less reliable. Reusing classifiers on images with differing coloration generally degrades segmentation quality greatly, as expected given the importance of color information. Fully interactive segmentation with ilastik, using dedicated training data for each image, performed slightly better than the pre-trained classifiers on intra-cluster images.

Table 1.

Comparison of different segmentation methods on 22 images

Method	F1 (median ± σ)
Manual	0.9021 ± 0.027
Interactive segmentation	0.9297 ± 0.013
Intra-cluster reuse	0.9018 ± 0.044
Inter-cluster reuse	0.6484 ± 0.245
Ilastik	0.9079 ± 0.022

Note: Bold indicates the best performance.

3.2 Runtime evaluation

A detailed discussion of aspects of computational performance is given in the Supplementary Appendix. The interactive processing steps training and prediction are independent of pixel count and linear in the number of supervoxels. For the segmentation step, runtime scales linear with image size and number of supervoxels. Exemplarily, execution times for an image with 100M pixels and 100k supervoxels are ∼2 and 9 min for supervoxel generation without and with feature generation. Training database generation, prediction and segmentation were completed in 5, 12 and 51 s, respectively. The analysis was done on an Intel Core i9-7900X with 10 logical cores at a 3.3 GHz clock speed with 64 GB RAM.

4 Discussion

Currently, interactive image segmentation often is the optimal image processing approach for applications where a detailed analysis of objects of interest is the aim, but only a few images are available, and/or training annotations are not provided. However, these seemingly specific conditions are fulfilled in many cases of biological and medical image processing where often pixel-accurate segmentations of physiological entities are required based on 2D or 3D images. This includes the counting and measuring of (sub-)cellular structures and vascular networks in tissue. Custom-made image processing solutions that target specific physiological entities imaged utilizing a specific technical setup are still a very common and widespread approach. Unfortunately, these solutions usually cause considerable development overhead compared to interactive solutions based on machine learning that can be easily adapted to new data through training. Moreover, custom-made solutions require profound expertise in image analysis techniques including knowledge of particular algorithms and the impact of parameter choices. In contrast, interactive image segmentation using machine learning from manual image annotations has a much flatter learning curve and greatly simplifies the process of quantifying the content of complex images enabling users to directly apply their expert knowledge of, for example, biological or medical entities in the analyzed images. The method described in this article, reduces the technical parameters virtually to zero. Only the size of the superpixels has to be set; however, it can be inferred from the size of the structures to be quantified.

Furthermore, interactive segmentation is also applicable for larger datasets consisting of many images, when no ground truth or appropriate pre-trained deep learning models are available. In this case, interactive image segmentation can be useful in producing training data for deep learning with significantly reduced manual effort and thus cost.

The presented supervoxel approach using the SLIC0 algorithm is especially suited as a basis for responsive, interactive segmentation not only because it is easy to use but also technically due to its dimensionality reduction characteristic, minimizing processing times and memory consumption. The latter effect is particularly pronounced if the objects of interest are highly resolved. On the other hand, the advantage diminishes if object size approaches those of single pixels. For objects with fluent boundaries or low-resolution images, the alignment of supervoxels to object boundaries can be suboptimal and traditional pixel-level segmentation methods might provide higher segmentation accuracy especially in boundary areas.

The features implemented in the presented work are designed for application to color images and might be less effective in representing learning problems formulated based on grayscale or binary images, for example, electron microscopy or X-ray, for which optimized features could be integrated.

Learning from annotations on single images and reusing these interactively trained classifiers for unseen images would further decrease manual effort. However, the downside of learning from such sparse annotations is a decreased generalizability which is especially deteriorating results in case of high color variations between the images to be quantified. We have demonstrated that limiting classifier reuse to similarly colored images significantly increases the average performance on a validation dataset and thus improves the suitability of interactive image segmentation for processing moderately sized image sets.

5 Conclusion

We present a novel approach that combines machine learning-based interactive image segmentation using supervoxels with a clustering method for the automated identification of similarly colored images in large image sets which enables a guided reuse of interactively trained classifiers. Our approach solves the problem of deteriorated segmentation and quantification accuracy when reusing trained classifiers which is due to significant color variability prevalent and often unavoidable in biological and medical images. We demonstrate that our interactive image segmentation approach achieves results superior to both manual annotations done by a human expert and also an exemplary popular interactive segmentation tool when dedicated training data are provided for each image (see Table 1). We show that by limiting classifier reuse to automatically identified images of similar color properties, segmentation accuracy is significantly improved compared to a traditional, non-discriminative reuse. In addition, our approach greatly reduces the necessary training effort. This increase in efficiency facilitates the quantification of much larger numbers of images thereby improving interactive image analysis for recent technological advances like high throughput microscopic imaging or high-resolution video microscopy (Ljosa et al., 2012). Additionally, the presented method can readily be used for a fast generation of training data for deep learning approaches. In summary, our approach opens up new fields of application for interactive image analysis especially in but not limited to a biological and medical context. The provided free software makes the presented methods easily and readily usable.

Data Availability

The software and image data underlying this article are available at https://tiquant.hoehme.com.