Robust Effects of Working Memory Demand during Naturalistic Language Comprehension in Language-Selective Cortex

Abstract

To understand language, we must infer structured meanings from real-time auditory or visual signals. Researchers have long focused on word-by-word structure building in working memory as a mechanism that might enable this feat. However, some have argued that language processing does not typically involve rich word-by-word structure building, and/or that apparent working memory effects are underlyingly driven by surprisal (how predictable a word is in context). Consistent with this alternative, some recent behavioral studies of naturalistic language processing that control for surprisal have not shown clear working memory effects. In this fMRI study, we investigate a range of theory-driven predictors of word-by-word working memory demand during naturalistic language comprehension in humans of both sexes under rigorous surprisal controls. In addition, we address a related debate about whether the working memory mechanisms involved in language comprehension are language specialized or domain general. To do so, in each participant, we functionally localize (1) the language-selective network and (2) the “multiple-demand” network, which supports working memory across domains. Results show robust surprisal-independent effects of memory demand in the language network and no effect of memory demand in the multiple-demand network. Our findings thus support the view that language comprehension involves computationally demanding word-by-word structure building operations in working memory, in addition to any prediction-related mechanisms. Further, these memory operations appear to be primarily conducted by the same neural resources that store linguistic knowledge, with no evidence of involvement of brain regions known to support working memory across domains.

SIGNIFICANCE STATEMENT This study uses fMRI to investigate signatures of working memory (WM) demand during naturalistic story listening, using a broad range of theoretically motivated estimates of WM demand. Results support a strong effect of WM demand in the brain that is distinct from effects of word predictability. Further, these WM demands register primarily in language-selective regions, rather than in “multiple-demand” regions that have previously been associated with WM in nonlinguistic domains. Our findings support a core role for WM in incremental language processing, using WM resources that are specialized for language.

Introduction

Language presents a major challenge for real-time information processing. Transient acoustic or visual signals must be translated into structured meaning representations very efficiently, at least fast enough to keep up with the perceptual stream (Christiansen and Chater, 2016). Understanding the mental algorithms that enable this feat is of interest to the study both of language and of other forms of cognition that rely on structured representations of sequences (Howard and Kahana, 2002; Botvinick, 2007). Language researchers have focused for decades on one plausible adaptation to the constraints of real-time language processing: working memory (WM). According to memory-based theories of linguistic complexity (e.g., Frazier and Fodor, 1978; Clifton and Frazier, 1989; Just and Carpenter, 1992; Gibson, 2000; Lewis and Vasishth, 2005; see Fig. 2), the main job of language-processing mechanisms is to rapidly construct (word-by-word) a structured representation of the unfolding sentence in WM, and incremental processing demand is thus driven by the difficulty of these WM operations.

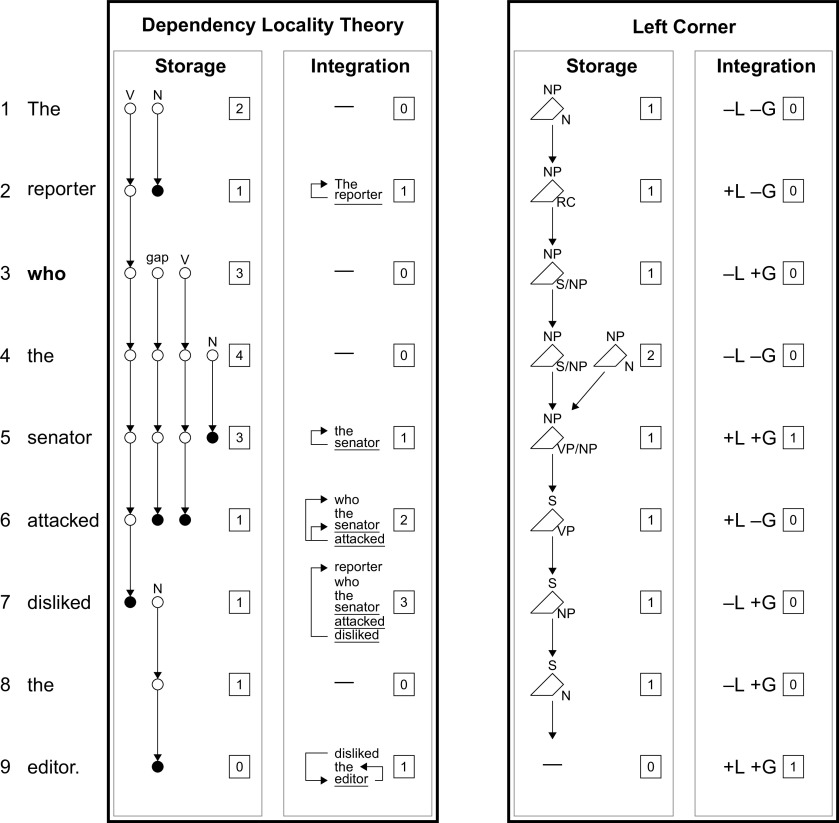
Figure 2.

Visualization of storage and integration and their associated costs in two of the three frameworks investigated here: the DLT (Gibson, 2000) versus left corner parsing theory (e.g., Rasmussen and Schuler, 2018). [The third framework—ACT-R (Lewis and Vasishth, 2005)—assumes a left corner parsing algorithm as in the figure above but differs in predicted processing costs, positing (1) no storage costs and (2) integration costs continuously weighted both by the recency of activation for the retrieval target and the degree of retrieval interference.] Costs are shown in boxes at each step. DLT walk-through: in the DLT, expected incomplete dependencies (open circles) are kept in WM and incur storage costs (SCs), whereas dependency construction (closed circles) requires retrieval from WM of the previously encountered item and incurs integration costs (ICs). DRs (effectively, nouns and verbs) that contribute to integration costs are underlined in the figure. At “The,” the processor hypothesizes and stores both an upcoming main verb for the sentence (V) and an upcoming noun complement (N). At “reporter,” the expected noun is encountered, contributing 1 DR and a dependency from “reporter” to “the,” which frees up memory. At “who,” the processor posits both a relative clause verb and a gap site, which is coreferent with “who,” and an additional noun complement is posited at “the.” The expected noun is observed at “senator,” contributing 1 DR and a dependency from “senator” to “the.” The awaited verb is observed at “attacked,” contributing 1 DR and two dependencies, one from “attacked” to “senator” and one from the implicit object gap to “who.” The latter spans 1 DR, increasing IC by 1. When “disliked” is encountered, an expected direct object is added to storage, and a subject dependency to “reporter” is constructed with an IC of 3 (the DR “disliked,” plus 2 intervening DRs). At the awaited object “editor,” the store is cleared and two dependencies are constructed (to “the” and “disliked”). Left corner walk-through: the memory store contains one or more incomplete derivation fragments (shown as polygons), each with an active sign (top) and an awaited sign (right) needed to complete the derivation. Storage cost is the number of derivation fragments currently in memory. Integration costs derive from binary lexical match (L) and grammatical match (G) decisions. Costs shown here index ends of multiword center embeddings (+L +G), where disjoint fragments are unified (though other cost definitions are possible, see below). At “the,” the processor posits a noun phrase (NP) awaiting a noun. There is nothing on the store, so both match decisions are negative. At “reporter,” the noun is encountered (+L) but the sentence is not complete (–G), and the active and awaited signs are updated to NP and relative clause (RC), respectively. At “who,” the processor updates its awaited category to S/NP [sentence (S) with gapped/relativized NP]. When “the” is encountered, it is analyzed neither as S/NP nor as a left child of an S/NP; thus, both match decisions are negative and a new derivation fragment is created in memory with active sign NP and awaited sign N. Lexical and grammatical matches occur at “senator,” unifying the two fragments in memory, and the awaited sign is updated to VP/NP [verb phrase (VP) with gapped NP, the missing unit of the RC]. The awaited VP (with gapped NP) is found at “attacked,” leading to a lexical match, and the awaited sign is updated to the missing VP of the main clause. The next two words (“disliked” and “the”) can be incorporated into the existing fragment, updating the awaited sign each time, and “editor” satisfies the awaited N, terminating the parse. Comparison: both approaches posit storage and integration (retrieval) mechanisms, but they differ in the details. For example, the DLT (but not left corner theory) posits a spike in integration cost at “attacked.” Differences in predictions between the two frameworks fall out from different claims about the role of WM in parsing.

This view has faced two major challenges. First, some have argued that typical sentence comprehension relies on representations that are shallower and more approximate than those assumed by word-by-word parsing models (Ferreira et al., 2002; Christiansen and MacDonald, 2009; Frank and Bod, 2011; Frank and Christiansen, 2018) and that standard experiment designs involving artificially constructed stimuli may exaggerate the influence of syntactic structure (Demberg and Keller, 2008). Second, surprisal theory has challenged the assumptions of memory-based theories by arguing that the main job of sentence processing mechanisms is not structure building in WM but rather probabilistic interpretation of the unfolding sentence (Hale, 2001; Levy, 2008), with processing demand determined by the information (quantified as surprisal, the negative log probability of a word in context) contributed by a word toward that interpretation. Surprisal theorists contend that surprisal can account for patterns that have been otherwise attributed to WM demand (Levy, 2008). Consistent with these objections, some recent naturalistic studies of language processing that control for surprisal have not yielded clear evidence of working memory effects (Demberg and Keller, 2008; van Schijndel and Schuler, 2013; Shain and Schuler, 2021; but see e.g., Brennan et al., 2016; Li and Hale, 2019; Stanojević et al., 2021).

To investigate the role of WM in typical language processing, we use data from a previous large-scale naturalistic functional magnetic resonance imaging (fMRI) study (Shain et al., 2020) to explore multiple existing theories of WM in language processing, under rigorous surprisal controls (van Schijndel and Linzen, 2018; Radford et al., 2019). We then evaluate the most robust of these on unseen data.

We additionally address a related ongoing debate about whether the WM resources used for language comprehension are domain general (e.g., Just and Carpenter, 1992) or specialized for language (e.g., Caplan and Waters, 1999; for review of this debate, see Discussion). To address this question, we consider two candidate brain networks, each functionally localized in individual participants: the language-selective (LANG) network (Fedorenko et al., 2011); and the domain-general multiple-demand (MD) network, which has been robustly implicated in domain-general working memory (Duncan et al., 2020), and which is therefore the most likely candidate domain-general brain network to support WM for language.

Results show strong, surprisal-independent influences of WM retrieval difficulty on human brain activity in the language network but not the MD network. We therefore argue (1) that a core function of human language processing is to compose representations in working memory based on structural cues, even for naturalistic materials during passive listening; and (2) that these operations are primarily implemented within language-selective cortex. Our study thus supports the view that typical language comprehension involves rich word-by-word structure building via computationally intensive memory operations and places these operations within the same neural circuits that store linguistic knowledge, in line with recent arguments against a separation between storage and computation in the brain (e.g., Hasson et al., 2015; Dasgupta and Gershman, 2021).

Materials and Methods

Except where otherwise noted below, we use the materials and methods of the study by Shain et al. (2020). At a high level, we analyze the influence of theory-driven measures of working memory load during auditory comprehension of naturalistic stories (Futrell et al., 2020) on activation levels in the LANG versus domain-general MD networks identified in each participant using an independent functional localizer. To control for regional variation in the hemodynamic response function (HRF), the HRF is estimated from data using continuous-time deconvolutional regression (CDR; Shain and Schuler, 2018, 2021) rather than assumed (e.g., Brennan et al., 2016; Bhattasali et al., 2019). Hypotheses are tested using generalization performance on held-out data.

In leveraging the fMRI blood oxygenation level-dependent (BOLD) signal (a measure of blood oxygen levels in the brain) to investigate language processing difficulty, we adopt the widely accepted view that “a spatially localized increase in the BOLD contrast directly and monotonically reflects an increase in neural activity” (Logothetis et al., 2001). To the extent that computational demand (e.g., from performing a difficult memory retrieval operation) results in the recruitment of a larger number of neurons, leading to a synchronous firing rate increase across a cell population, we can use the BOLD signal as a proxy for this increased demand.

Experimental design

Functional magnetic resonance imaging data were collected from seventy-eight native English speakers (30 males), aged 18–60 (mean ± SD, 25.8 ± 9; median ± semi-interquartile range, 23 ± 3). Each participant completed a passive story comprehension task, using materials from the stud by Futrell et al. (2020), and a functional localizer task designed to identify the language and MD networks and to ensure functionally comparable units of analysis across participants. The use of functional localization is motivated by established interindividual variability in the precise locations of functional areas (e.g., Frost and Goebel, 2012; Tahmasebi et al., 2012; Vázquez-Rodríguez et al., 2019)—including the LANG (e.g., Fedorenko et al., 2010) and MD (e.g., Fedorenko et al., 2013; Shashidhara et al., 2020) networks. Functional localization yields higher sensitivity and functional resolution compared with the traditional voxelwise group-averaging fMRI approach (e.g., Nieto-Castañón and Fedorenko, 2012) and is especially important given the proximity of the LANG and the MD networks in the left frontal cortex (for review, see Fedorenko and Blank, 2020). The localizer task contrasted sentences with perceptually similar controls (lists of pronounceable nonwords). Participant-specific functional regions of interest (fROIs) were identified by selecting the top 10% of voxels that were most responsive (to the target contrast; see below) for each participant within broad areal “masks” (derived from probabilistic atlases for the same contrasts, created from large numbers of individuals; for the description of the general approach, see Fedorenko et al., 2010), as described below.

Our focus on these functionally defined language and multiple-demand networks is motivated by extensive prior evidence that these networks constitute functionally distinct “natural kinds” in the human brain. First, a range of localizer tasks yield highly stable definitions of both the language network (Fedorenko et al., 2010, 2011; Scott et al., 2017; Malik-Moraleda et al., 2022) and the MD network (Fedorenko et al., 2013; Shashidhara et al., 2019; Diachek et al., 2020), definitions that map tightly onto networks independently identified by task-free (resting state) functional connectivity analysis (Vincent et al., 2008; Assem et al., 2020a; Braga et al., 2020). Second, the activity in these networks is strongly functionally dissociated, with statistically zero synchrony between them during both resting state and story comprehension (Blank et al., 2014; Malik-Moraleda et al., 2022). Third, the particular tasks that engage these networks show strong functional clustering: the language network responds more strongly to coherent language than perceptually matched control conditions and does not engage in a range of WM and cognitive control tasks, whereas the MD network responds less strongly to coherent language than perceptually matched controls and is highly responsive to diverse WM and cognitive control tasks (for review, see Fedorenko and Blank, 2020). Fourth, within individuals, the strength of task responses between different brain areas is highly correlated within the language network (Mahowald and Fedorenko, 2016) and the MD network (Assem et al., 2020b), but not between them (Mineroff et al., 2018). Fifth, distinct cognitive deficits follow damage to language versus MD regions. Some patients with global aphasia (complete or near complete loss of language) nonetheless retain the executive function, problem-solving, and logical inference skills necessary for solving arithmetic questions, playing chess, driving, and generating scientific hypotheses (for review, see Fedorenko and Varley, 2016). In contrast, damage to MD regions causes fluid intelligence deficits (Gläscher et al., 2010; Woolgar et al., 2010, 2018). Thus, there is strong prior reason to consider these networks as functional units and valid objects of study. Our localizer tasks simply provide an efficient method for identifying them in each individual, as needed for probing their responses during naturalistic language comprehension.

Relatedly, our assumption that the MD network is the most likely home for any domain-general WM resources involved in language comprehension follows from an extensive neuroscientific literature on WM across domains that most consistently identifies the specific frontal and parietal regions covered by our MD localizer masks. For example, a Neurosynth (Yarkoni et al., 2011) meta-analysis of the term “working memory” (https://neurosynth.org/analyses/terms/working%20memory/) finds 1091 papers with nearly 40,000 activation peaks, and the regions that are consistently associated with this term include regions that correspond anatomically to the MD network, including the parietal cortex, anterior cingulate/supplementary motor area, the insula, and regions in the dorsolateral prefrontal cortex. This finding derives from numerous individual studies that consistently associate our assumed frontal and parietal MD regions (or highly overlapping variants of them) with diverse WM tasks (e.g., Fedorenko et al., 2013; Hugdahl et al., 2015; Shashidhara et al., 2019; Assem et al., 2020a) and aligns strongly with results from multiple published meta-analyses (e.g., Rottschy et al., 2012; Nee et al., 2013; Emch et al., 2019; Kim, 2019; Wang et al., 2019). As acknowledged in the Discussion, some additional regions are also reported in studies of WM with less consistency, including within the thalamus, basal ganglia, hippocampus, and cerebellum. Although we leave possible involvement of such regions in language processing to future research, current evidence makes it a priori likely that the bulk of domain-general WM brain regions will be covered by our MD localizer masks.

Six left-hemisphere language fROIs were identified using the contrast sentences > nonwords: in the inferior frontal gyrus (IFG) and the orbital part of the IFG (IFGorb); in the middle frontal gyrus (MFG); in the anterior temporal cortex (AntTemp) and posterior Temp (PostTemp); and in the angular gyrus (AngG). This contrast targets higher-level aspects of language, to the exclusion of perceptual (speech/reading) and motor-articulatory processes (for review, see Fedorenko and Thompson-Schill, 2014; Fedorenko, 2020). This localizer has been extensively validated over the past decade across diverse parameters and shown to generalize across task (Fedorenko et al., 2010; Cheung et al., 2020), presentation modality (Fedorenko et al., 2010; Scott et al., 2017; Chen et al., 2021), language (Malik-Moraleda et al., 2022), and materials (Fedorenko et al., 2010; Cheung et al., 2020), including both coarser contrasts (e.g., between natural speech and an acoustically degraded control: Scott et al., 2017) and narrower contrasts (e.g., between lists of unconnected, real words and nonwords lists, or between sentences and lists of words; Fedorenko et al., 2010; Blank et al., 2016).

Ten multiple-demand fROIs were identified bilaterally using the contrast nonwords > sentences, which reliably localizes the MD network, as discussed below: in the posterior parietal cortex (PostPar), middle Par (MidPar), and anterior Par (AntPar); in the precentral gyrus (PrecG); in the superior frontal gyrus (SFG); in the MFG and the orbital part of the MFG (MFGorb); in the opercular part of the IFG (IFGop); in the anterior cingulate cortex and pre-supplementary motor cortex; and in the insula (Insula). This contrast targets regions that increase their response with the more effortful reading of nonwords compared with that of sentences. This “cognitive effort” contrast robustly engages the MD network and can reliably localize it (Fedorenko et al., 2013). Moreover, it generalizes across a wide array of stimuli and tasks, both linguistic and nonlinguistic, including, critically, standard contrasts targeting executive functions (e.g., Fedorenko et al., 2013; Shashidhara et al., 2019; Assem et al., 2020a). To verify that the use of a flipped language localizer contrast does not artificially suppress language processing-related effects in MD, we performed a follow-up analysis where the MD network was identified with a hard > easy contrast in a spatial working memory paradigm, which requires participants to keep track of more versus fewer spatial locations within a grid (e.g., Fedorenko et al., 2013) in the subset of participants (∼80%) who completed this task.

The critical task involved listening to auditorily presented passages from the Natural Stories corpus (Futrell et al., 2020). The materials are described extensively in the study by Futrell et al. (2020), but in brief, they consist of naturally occurring short narrative or nonfiction materials that were edited to overrepresent rare words and syntactic constructions without compromising perceived naturalness. The materials therefore expose participants to a diversity of syntactic constructions designed to tax the language-processing system within a naturalistic setting, including nonlocal coordination, parenthetical expressions, object relative clauses, passives, and cleft constructions. A subset of participants (n = 41) answered comprehension questions after each passage, and the remainder (n = 37) listened passively.

Full details about participants, stimuli, functional localization, data acquisition, and preprocessing are provided in the study by Shain et al. (2020).

Statistical analysis

This study uses CDR for all statistical analyses (Shain and Schuler, 2021). CDR uses machine learning to estimate continuous-time impulse response functions (IRFs) that describe the influence of observing an event (word) on a response (BOLD signal change) as a function of their distance in continuous time. When applied to fMRI, CDR-estimated IRFs represent the hemodynamic response function (Boynton et al., 1996) and can account for regional differences in response shape (Handwerker et al., 2004) directly from responses to naturalistic language stimuli, which are challenging to model using discrete-time techniques (Shain and Schuler, 2021). For model details, see the Model design subsection below.

Our analyses consider a range of both perceptual and linguistic variables as predictors. For motivation and implementation of each predictor, see the Control predictors and Critical predictors subsections below. As is often the case in naturalistic language, many of these variables are correlated to some extent (Fig. 1), especially variables that are implementation variants of each other (e.g., different definitions of surprisal or WM retrieval difficulty). We therefore use statistical tests that depend on the unique contribution of each predictor, regardless of its level of correlation with other predictors in the model. For testing procedures, see the Ablative statistical testing subsection below.

Figure 1.

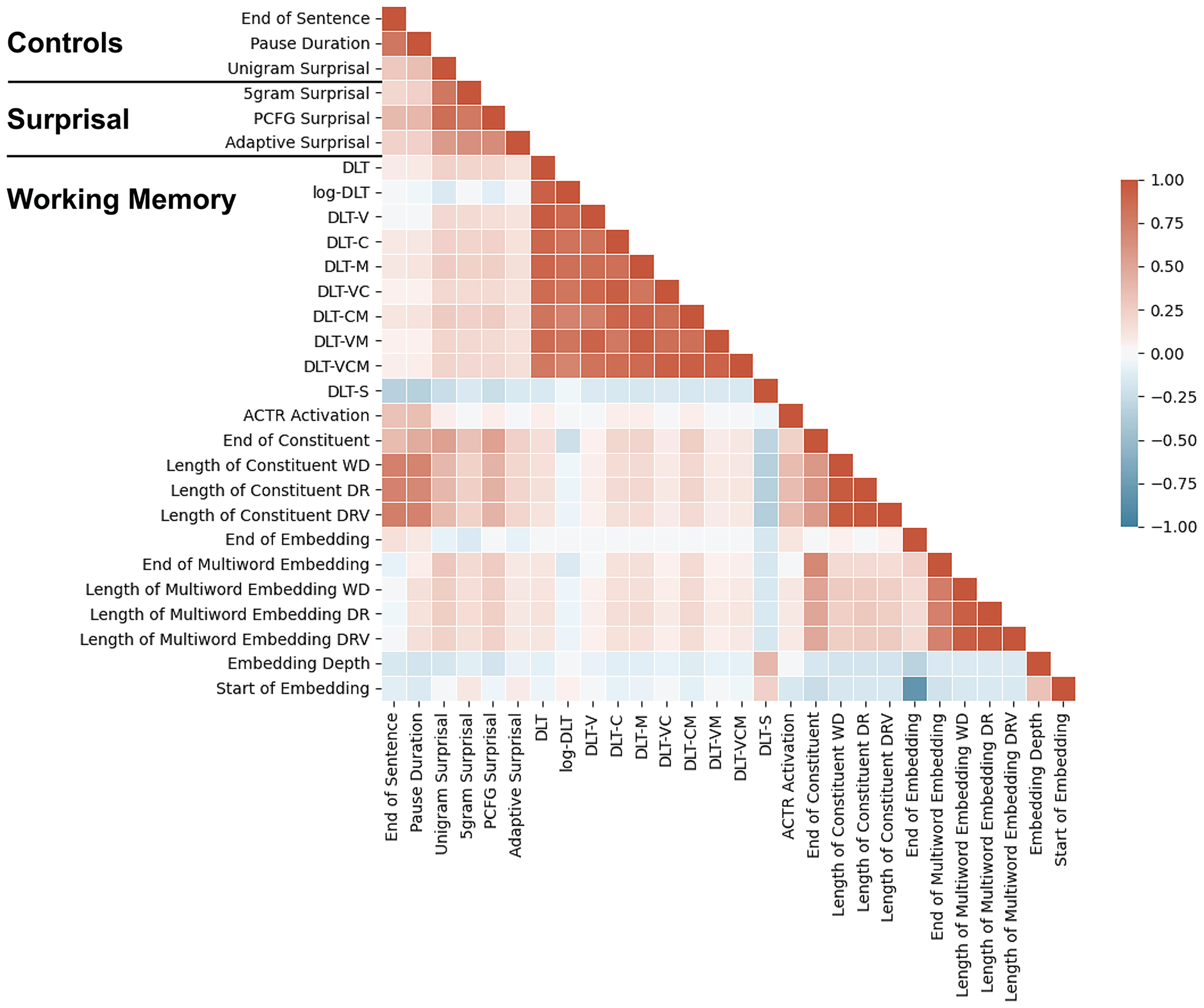
Pairwise Pearson correlations between all word-level predictors considered in our exploratory analyses.

Control predictors

We include all control predictors used in the study by Shain et al. (2020), namely the following.

Sound power.

Sound power is predicted with frame-by-frame root mean square energy of the audio stimuli computed using the Librosa software library (McFee et al., 2015).

TR number.

The repetition time (TR) number is an integer index of the current fMRI volume within the current scan.

Rate.

Rate is the deconvolutional intercept. A vector of one's time aligned with the word onsets of the audio stimuli. Rate captures influences of stimulus timing independent of stimulus properties (See e.g., Brennan et al., 2016; Shain and Schuler, 2018).

Frequency (unigram surprisal).

Corpus frequency of each word computed using a KenLM unigram model trained on Gigaword 3. For ease of comparison with surprisal, frequency is represented here on a surprisal scale (negative log probability), such that larger values index less frequent words (and thus greater expected processing cost).

Network.

The numeric predictor for network ID (0 for MD and 1 for LANG). This predictor is used only in models of combined responses from both networks.

Furthermore, because points of predicted retrieval cost may partially overlap with prosodic breaks between clauses, we include the following two prosodic controls.

End of sentence.

The end-of-sentence predictor is an indicator for whether a word terminates a sentence.

Pause duration.

Pause duration is the length (in milliseconds) of the pause following a word, as indicated by hand-corrected word alignments over the auditory stimuli. Words that are not followed by a pause take the value 0 ms.

We confirmed empirically that the pattern of significance reported in the study by Shain et al. (2020) holds in the presence of these additional controls.

In addition, inspired by evidence that word predictability strongly influences BOLD responses in the language network, we additionally include the following critical surprisal predictors from the study by Shain et al. (2020).

5-gram surprisal.

5-gram surprisal for each word in the stimulus is computed from a KenLM (Heafield et al., 2013) language model with default smoothing parameters trained on the Gigaword 3 corpus (Graff et al., 2007). 5-gram surprisal quantifies the predictability of words as the negative log probability of a word given the four words preceding it in context.

PCFG surprisal.

Lexicalized probabilistic context-free grammar (PCFG) surprisal is computed using the incremental left corner parser of van Schijndel et al. (2013) trained on a generalized categorial grammar (Nguyen et al., 2012) reannotation of Wall Street Journal sections 2 through 21 of the Penn Treebank (Marcus et al., 1993). Note that, like the 5-gram model, the PCFG model is fully lexicalized, in that it generates a distribution over the next word (e.g., rather than the next part-of-speech tag). The critical difference is that the PCFG model conditions this prediction only on its hypotheses about the phrase structure of a sentence, with no direct access to preceding words.

PCFG and 5-gram surprisal were investigated by Shain et al. (2020) because their interpretable structure permitted testing of hypotheses of interest in that study. However, their strength as language models has been outstripped by less interpretable but better performing incremental language models based on deep neural networks (e.g., Jozefowicz et al., 2016; Gulordava et al., 2018; Radford et al., 2019). In the present investigation, predictability effects are a control rather than an object of study, and we are therefore not bound by the same interpretability considerations. To strengthen the case for the independence of retrieval processes from prediction processes, we therefore additionally include the following predictability control.

Adaptive surprisal.

Adaptive surprisal is word surprisal as computed by the adaptive recurrent neural network (RNN) of van Schijndel and Linzen (2018). This network is equipped with a cognitively inspired mechanism that allows it to adjust its expectations to the local discourse context at inference time, rather than relying strictly on knowledge acquired during the training phase. Compared with strong baselines, results show both improved model perplexity and improved fit between model-generated surprisal estimates and measures of human reading times. Because the RNN can in principle learn both (1) the local word co-occurrence patterns exploited by 5-gram models and (2) the structural features exploited by PCFG models, it competes for variance in our regression models with the other surprisal predictors, whose effects are consequently attenuated relative to those in the study by Shain et al. (2020).

Models additionally included the mixed-effects random grouping factors Participant and fROI. We examine the responses for each network (LANG, MD) as a whole, which is reasonable given the strong evidence of functional integration among the regions of each network (e.g., Blank et al., 2014; Assem et al., 2020a,b; Braga et al., 2020), but we also examine each individual fROI separately for a richer characterization of the observed effects. Before regression, all predictors were rescaled by their SDs in the training set except Rate (which has no variance) and the indicators End of Sentence and Network. Reported effect sizes are therefore in standard units.

Critical predictors

Among the many prior theoretical and empirical investigations of working memory demand in sentence comprehension, we have identified three theoretical frameworks that are broad coverage (i.e., sufficiently articulated to predict word-by-word memory demand in arbitrary utterances) and implemented (i.e., accompanied by algorithms and software that can generate word-by-word memory predictors for our naturalistic English-language stimuli): the dependency locality theory (DLT; Gibson, 2000); ACT-R (Adaptive Control of Thought-Rational) sentence-processing theories (Lewis and Vasishth, 2005); and left corner parsing theories (Johnson-Laird, 1983; Resnik, 1992; van Schijndel et al., 2013; Rasmussen and Schuler, 2018). We set aside related work that does not define word-by-word measures of WM demand (e.g., Gordon et al., 2001, 2006; McElree et al., 2003). A step-through visualization of two of these frameworks, the DLT and left corner parsing theory, is provided in Figure 2.

At a high level, these theories all posit WM demands driven by the syntactic structure of sentences. In the DLT, the relevant structures are dependencies between words (e.g., between a verb and its subject). In ACT-R and left corner theories, the relevant structures are phrasal hierarchies of labeled, nested spans of words (syntax trees). The DLT and left corner theories hypothesize active maintenance in memory (and thus “storage” costs) from incomplete dependencies and incomplete phrase structures, respectively, whereas ACT-R posits no storage costs under the assumption that partial derivations live in a content-addressable memory store. All three frameworks posit “integration costs” driven by memory retrieval operations. In the DLT, retrieval is required to build dependencies, with cost proportional to the length of the dependency. In ACT-R and left corner theories, retrieval is required to unify representations in memory. Left corner theory is compatible with several notions of retrieval cost (explored below), whereas ACT-R assumes retrieval costs are governed by an interaction between continuous time activation decay mechanisms and similarity-based interference.

Prior work has investigated the empirical predictions of some of these theories using computer simulations (e.g., Lewis and Vasishth, 2005; Rasmussen and Schuler, 2018) and human behavioral responses to constructed stimuli (e.g., Grodner and Gibson, 2005; Bartek et al., 2011), and reported robust WM effects. Related work has also shown the effects of dependency length manipulations in measures of comprehension and online processing difficulty (e.g., Gibson et al., 1996; McElree et al., 2003; Van Dyke and Lewis, 2003; Makuuchi et al., 2009; Meyer et al., 2013). In light of these findings, evidence from more naturalistic human sentence-processing settings for working memory effects of any kind is surprisingly weak. Demberg and Keller (2008) report DLT integration cost effects in the Dundee eye-tracking corpus (Kennedy and Pynte, 2005), but only when the domain of analysis is restricted—overall DLT effects are actually negative (longer dependencies yield shorter reading times, a phenomenon known as “anti-locality” Konieczny, 2000). Van Schijndel and Schuler (2013) also report anti-locality effects in Dundee, even controlling for word predictability phenomena that have been invoked to explain anti-locality effects in other experiments (Konieczny, 2000; Vasishth and Lewis, 2006). It is therefore not yet settled how central syntactically related working memory involvement is to human sentence processing in general, rather than perhaps being driven by the stimuli and tasks commonly used in experiments designed to test these effects (Hasson and Honey, 2012; Campbell and Tyler, 2018; Hasson et al., 2018; Diachek et al., 2020). In the fMRI literature, few prior studies of naturalistic sentence processing have investigated syntactic working memory (although some of the syntactic predictors in the study by Brennan et al., 2016, especially syntactic node count, are amenable to a memory-based interpretation).

DLT predictors

The DLT posits two distinct sources of WM demand, integration cost and storage cost. Integration cost is computed as the number of discourse referents (DRs) that intervene in a backward-looking syntactic dependency, where “discourse referent” is operationalized, for simplicity, as any noun or finite verb. In addition, all the implementation variants of integration cost proposed by Shain et al. (2016) are considered.

Verbs.

Verbs (Vs) are more expensive. Nonfinite verbs receive a cost of 1 (instead of 0), and finite verbs receive a cost of 2 (instead of 1).

Coordination.

Coordination (C) is less expensive. Dependencies out of coordinate structures skip preceding conjuncts in the calculation of distance, and dependencies with intervening coordinate structures assign that structure a weight equal to that of its heaviest conjunct.

Modifier.

Exclude modifier (M) dependencies. Dependencies to preceding modifiers are ignored.

These variants are motivated by the following considerations. First, the reweighting in V is motivated by the possibility (1) that finite verbs may require more information-rich representations than nouns, especially tense and aspect (Binnick, 1991); and (2) that nonfinite verbs may still contribute eventualities to the discourse context, albeit with underspecified tense (Lowe, 2019). As in Gibson (2000), the precise weights are unknown, and the weights used here are simply heuristic approximations that instantiate a hypothetical overall pattern: nonfinite verbs contribute to retrieval cost, and finite verbs contribute more strongly than other classes.

Second, the discounting of coordinate structures under C is motivated by the possibility that conjuncts are incrementally integrated into a single representation of the overall coordinated phrase, and thus that their constituent nouns and verbs no longer compete as possible retrieval targets. Anecdotally, this possibility is illustrated by the following sentence: “Today I bought a cake, streamers, balloons, party hats, candy, and several gifts for my niece's birthday.”

In this example, the dependency from “for” to its modificand “bought” does not intuitively seem to induce a large processing cost, yet it spans six coordinated nouns, yielding an integration cost of 6, which is similar in magnitude to that of some of the most difficult dependencies explored in the study by Grodner and Gibson (2005). The C variant treats the entire coordinated direct object as one discourse referent, yielding an integration cost of 1.

Third, the discounting of preceding modifiers in M is motivated by the possibility that modifier semantics may be integrated early, alleviating the need to retrieve the modifier once the head word is encountered. Anecdotally, this possibility is illustrated by the following sentence: “(Yesterday,) my coworker, whose cousin drives a taxi in Chicago, sent me a list of all the best restaurants to try during my upcoming trip.”

The dependency between the verb “sent” and the subject “coworker” spans a finite verb and three nouns, yielding an integration cost of 4 (plus a cost of 1 for the discourse referent introduced by “sent”). If the sentence includes the pre-sentential modifier “Yesterday,” which, under the syntactic annotation used in this study, is also involved in a dependency with the main verb “sent” then the DLT predicts that it should double the structural integration cost at “sent” because the same set of discourse referents intervenes in two dependencies rather than one. Intuitively, this does not seem to be the case, possibly because the temporal information contributed by “Yesterday” may already be integrated with the incremental semantic representation of the sentence before “sent” is encountered, eliminating the need for an additional retrieval operation at that point. The +M modification instantiates this possibility.

The presence/absence of the three features above yields a total of eight variants, as follows: DLT, DLT-V (a version with the V feature), DLT-C, DLT-M, DLT-VC, DLT-VM, DLT-CM, and DLT-VCM. A superficial consequence of the variants with C and M features is that they tend to attenuate large integration costs. Thus, if they improve fit to human measures, it may simply be the case that the DLT in its original formulation overestimates the costs of long dependencies. To account for this possibility, this study additionally considers a log-transformed variant of (otherwise unmodified) DLT integration cost: DLT (log).

We additionally consider DLT storage cost (DLT-S), the number of awaited syntactic heads at a word that is required to form a grammatical utterance.

In our implementation, this includes dependencies arising via syntactic arguments (e.g., the object of a transitive verb), dependencies from modifiers to following modificands, dependencies from relative pronouns (e.g., who, what) to a gap site in the following relative clause, dependencies from conjunctions to following conjuncts, and dependencies from gap sites to following extraposed items. In all such cases, the existence of an obligatory upcoming syntactic head can be inferred from context. This is not the case for the remaining dependency types (e.g., from modifiers to preceding modificands, since the future appearance of a modifier is not required when the modificand is processed), and they are therefore treated as irrelevant to storage cost. Because storage cost does not assume a definition of distance (unlike integration cost), no additional variants of it are explored.

ACT-R predictor

The ACT-R model (Lewis and Vasishth, 2005) composes representations in memory through a content-addressable retrieval operation that is subject to similarity-based interference (Gordon et al., 2001; McElree et al., 2003; Van Dyke and Lewis, 2003), with memory representations that decay with time unless reactivated through retrieval. The decay function enforces a locality-like notion (retrievals triggered by long dependencies will on average cue targets that have decayed more), but this effect can be attenuated by intermediate retrievals of the target. Unlike the DLT, ACT-R has no notion of active maintenance in memory (items are simply retrieved as needed) and therefore does not predict a storage cost.

The originally proposed ACT-R parser (Lewis and Vasishth, 2005) is implemented using hand-crafted rules and is deployed on utterances constructed to be consistent with those rules. This implementation does not cover arbitrary sentences of English and cannot therefore be applied to our stimuli without extensive additional engineering of the parsing rules. However, a recently proposed modification to the ACT-R framework has a broad-coverage implementation and has already been applied to model reading time responses to the same set of stories (Dotlačil, 2021). It does so by moving the parsing rules from procedural to declarative memory, allowing the rules themselves to be retrieved and activated in the same manner as parse fragments. In this study, we use the same single ACT-R predictor used in Dotlačil (2021): in ACT-R target activation, the mean activation level of the top three most activated retrieval targets is cued by a word. Activation decays on both time and degree of similarity with retrieval competitors, and is therefore highest when the cue strongly identifies a recently activated target. ACT-R target activation is expected to be anticorrelated with retrieval difficulty. See Dotlačil (2021) and Lewis and Vasishth (2005) for details.

The Dotlačil (2021) implementation of ACT-R activation is the only representative we consider from an extensive theoretical and empirical literature on cue-based retrieval models of sentence processing (McElree et al., 2003; Van Dyke and Lewis, 2003; Lewis et al., 2006; Van Dyke and McElree, 2011; Van Dyke and Johns, 2012; Vasishth et al., 2019; Lissón et al., 2021), because of the lack of broad-coverage software implementation of these other models that would permit application to our naturalistic language stimuli.

Left corner predictors

Another line of research (Johnson-Laird, 1983; Resnik, 1992; van Schijndel et al., 2013; Rasmussen and Schuler, 2018) frames incremental sentence comprehension as left corner parsing (Rosenkrantz and Lewis, 1970) under a pushdown store implementation of working memory. Under this view, incomplete derivation fragments representing the hypothesized structure of the sentence are assembled word by word, with working memory required to (1) push new derivation fragments to the store, (2) retrieve and compose derivation fragments from the store, and (3) maintain incomplete derivation fragments in the store. For a detailed presentation of a recent instantiation of this framework, see Rasmussen and Schuler (2018). In principle, costs could be associated with any of the parse operations computed by left corner models, as well as (1) with DLT-like notions of storage (maintenance of multiple derivation fragments in the store) and (2) with ACT-R-like notions of retrieval and reactivation, since items in memory (corresponding to specific derivation fragments) are incrementally retrieved and updated. Unlike ACT-R, left corner frameworks do not necessarily enforce activation decay over time, and they do not inherently specify expected processing costs.

Full description of left corner parsing models of sentence comprehension is beyond the scope of this presentation (See e.g., Rasmussen and Schuler, 2018; Oh et al., 2021), which is restricted to the minimum details needed to define the predictors covered here. At a high level, phrasal structure derives from a sequence of lexical match (±L) and grammatical match (±G) decisions made at each word (for relations to equivalent terms in the prior parsing literature, see Oh et al., 2021). In terms of memory structures, the lexical decision depends on whether a new element (representing the current word and its hypothesized part of speech) matches current expectations about the upcoming syntactic category; if so, it is composed with the derivation at the front of the memory store (+L), and, if not, it is pushed to the store as a new derivation fragment (–L). Following the lexical decision, the grammatical decision depends on whether the two items at the front of the store can be composed (+G) or not (–G). In terms of phrasal structures, lexical matches index the ends of multiword constituents (+L at the end of a multiword constituent, –L otherwise), and grammatical match decisions index the ends of left-child (center-embedded) constituents (+G at the end of a left child, –G otherwise). These composition operations (+L and +G) instantiate the notion of syntactic integration as envisioned by, for example, the DLT, since structures are retrieved from memory and updated by these operations. They each may thus plausibly contribute a memory cost (Shain et al., 2016), leading to the following left corner predictors.

End of constituent (+L).

This is an indicator for whether a word terminates a multiword constituent (i.e. whether the parser generates a lexical match).

End of center embedding (+G).

This is an indicator for whether a word terminates a center embedding (left child) of one or more words (i.e. whether the parser generates a grammatical match).

End of multiword center embedding (+L, +G).

This is an indicator for whether a word terminates a multiword center embedding (i.e. whether the parser generates both a lexical match and a grammatical match).

In addition, the difficulty of retrieval operations could in principle be modulated by locality, possibly because of activation decay and/or interference, as argued by Lewis and Vasishth (2005). To account for this possibility, this study also explores distance-based left corner predictors.

Length of constituent (+L).

This encodes the distance from the most recent retrieval (including creation) of the derivation fragment at the front of the store when a word terminates a multiword constituent (otherwise, 0).

Length of multiword center embedding (+L, +G).

This encodes the distance from the most recent retrieval (including creation) of the derivation fragment at the front of the store when a word terminates a multiword center embedding (otherwise, 0).

The notion of distance must be defined, and three definitions are explored here. One simply counts the number of words [word distance (WD)]. However, this complicates comparison with the DLT, which then differs not only in its conception of memory usage (constructing dependencies vs retrieving/updating derivations in a pushdown store), but also in its notion of locality (the DLT defines locality in terms of nouns and finite verbs, rather than words). To enable direct comparison, DLT-like distance metrics are also used in the above left corner locality-based predictors—in particular, both using the original DLT definition of DRs, as well as the modified variant +V that reweights finite and nonfinite verbs (DRV). All three distance variants are explored for both distance-based left corner predictors.

Note that these left corner distance metrics more closely approximate ACT-R retrieval cost than DLT integration cost, because, as stressed by Lewis and Vasishth (2005), decay in ACT-R is determined by the recency with which an item in memory was previously activated, rather than overall dependency length. Left corner predictors can therefore be used to test one of the motivating insights of the ACT-R framework: the influence of reactivation on retrieval difficulty.

Note also that because the parser incrementally constructs expected dependencies between as-yet incomplete syntactic representations, at most two retrievals are cued per word (up to one for each of the lexical and grammatical decisions), no matter how many dependencies the word participates in. This property makes left corner parsing a highly efficient form of incremental processing, a feature that has been argued to support its psychological plausibility (Johnson-Laird, 1983; van Schijndel et al., 2013; Rasmussen and Schuler, 2018).

The aforementioned left corner predictors instantiate a notion of retrieval cost, but the left corner approach additionally supports measures of storage cost. In particular, the number of incomplete derivation fragments that must be held in memory (similar to the number of incomplete dependencies in DLT storage cost) can be read off the store depth of the parser state.

Embedding depth.

Embedding depth is the number of incomplete derivation fragments left on the store once a word has been processed.

This study additionally considers the possibility that pushing a new fragment to the store may incur a cost.

Start of embedding (–L–G).

This is an indicator for whether embedding depth increased from one word to the next.

As with retrieval-based predictors, the primary difference between left corner embedding depth and DLT storage cost is the efficiency with which the memory store is used by the parser. Because expected dependencies between incomplete syntactic derivations are constructed as soon as possible, a word can contribute at most one additional item to be maintained in memory (vis-a-vis DLT storage cost, which can in principle increase arbitrarily at words that introduce multiple incomplete dependencies). As mentioned above, ACT-R does not posit storage costs at all, and thus the investigation of such costs potentially stands to empirically differentiate ACT-R from DLT/left corner accounts.

Model design

Following Shain et al. (2020), we use CDR (Shain and Schuler, 2018, 2021) to infer the shape of the HRF from data (Boynton et al., 1996; Handwerker et al., 2004). We assumed the following two-parameter HRF kernel based on the widely used double-gamma canonical HRF (Lindquist et al., 2009):

$$h\left(x;\alpha ,\beta \right)=\frac{{\beta }^{\alpha }{x}^{\alpha -1}{e}^{\frac{-x}{\beta }}}{\Gamma \left(\alpha \right)}-\frac{1}{6}\frac{{\beta }^{\alpha +10}{x}^{\alpha +9}{e}^{\frac{-x}{\beta }}}{\Gamma \left(\alpha +10\right)},$$

where parameters α and β are fitted using black box variational Bayesian inference. Model implementation follows Shain et al. (2020), except in replacing improper uniform priors with normal priors, which have since been shown empirically to produce more reliable estimates of uncertainty (Shain and Schuler, 2021). Variational priors follow Shain and Schuler (2018).

The following CDR model specification was fitted to responses from each of the LANG and MD fROIs, where italics indicates predictors convolved using the fitted HRF and bold indicates predictors that were ablated for hypothesis tests, as follows: BOLD ∼ TRNumber + Rate + SoundPower + EndOfSentence + PauseDuration + Frequency + 5gramSurp + PCFGSurp + AdaptiveSurp + Pred1 + … + PredN + (TRNumber + Rate + SoundPower + EndOfSentence + PauseDuration + Frequency + 5gramSurp + PCFGSurp + AdaptiveSurp + Pred1 + … + PredN | fROI) + (1 | Participant).

In other words, models contain a linear coefficient for the index of the TR in the experiment, convolutions of the remaining predictors with the fitted HRF, by-fROI random variation in effect size and shape, and by-participant random variation in base response level. This model is used to test for significant effects of one or more critical predictors Pred1, …, PredN in each of the LANG and MD networks. To test for significant differences between LANG and MD in the effect sizes of critical predictors Pred1, …, PredN, we additionally fitted the following model to the combined responses from both LANG and MD, as follows: BOLD ∼ TRNumber + Rate + SoundPower + EndOfSentence + PauseDuration + Frequency + 5gramSurp + PCFGSurp + AdaptiveSurp + Pred1 + … + PredN + TRNumber:Network + Rate:Network + SoundPower:Network + EndOfSentence:Network + PauseDuration:Network + Frequency:Network + 5gramSurp:Network + PCFGSurp:Network + AdaptiveSurp:Network + Pred1:Network + … + PredN:Network + (1 | fROI) + (1 | Participant).

By-fROI random effects are simplified from the individual network models to improve model identifiability (Shain et al., 2020).

Ablative statistical testing

Following the study by Shain et al. (2020), we partition the fMRI data into training and evaluation sets by cycling TR numbers e into different bins of the partition with a different phase for each subject u:

$$\text{partition}\left(e;u\right)=⌊\frac{e+u}{30}⌋\mathrm{mod}2$$

assigning output 0 to the training set and 1 to the evaluation set. Model quality is quantified as the Pearson sample correlation, henceforth r, between model predictions on a dataset (training or evaluation) and the true response. Fixed effects are tested by paired permutation test (Demšar, 2006) of the difference in correlation (r_diff) that equals r_full – r_ablated, where r_full is the r of a model containing the fixed effect of interest, while r_ablated is the r of a model lacking it. Paired permutation testing requires an elementwise performance metric that can be permuted between the two models, whereas Pearson correlation is a global metric that applies to the entire prediction–response matrix. To address this, we exploit the fact that the sample correlation can be converted to an elementwise performance statistic as long as both variables are standardized (i.e., have sample mean 0 and sample SD 1):

$$\rho \left(X,Y\right)=\frac{1}{n-1}{\displaystyle \sum }_{i=1}^n\left(\frac{x_i-\overline{x}}{s_x}\right)\left(\frac{y_i-\overline{y}}{s_y}\right)=\frac{1}{n-1}{\displaystyle \sum }_{i=1}^n{x}_i{y}_i.$$

As a result, an elementwise performance metric can be derived as the elements of a Hadamard product between independently standardized prediction and response vectors. These products are then permuted in the usual way, using 10,000 resampling iterations. Each test involves a single ablated fixed effect, retaining all random effects in all models.

Exploratory and generalization analyses

Exploratory study is needed for the present general question about the nature of WM-dependent operations that support sentence comprehension because multiple broad-coverage theories of WM have been proposed in language processing, as discussed above, each making different predictions and/or compatible with multiple implementation variants, ruling out a single theory-neutral measure of word-by-word WM load. In addition, as discussed in the Introduction, prior naturalistic investigations of WM have yielded mixed results, motivating the use of a broad net to find WM measures that correlate with human processing difficulty. Exploratory analysis can therefore illuminate both the existence and kind of WM operations involved in human language comprehension.

However, exploring a broad space of predictors increases the false-positive rate, and thus the likelihood of spurious findings. To avoid this issue and enable testing of patterns discovered by exploratory analyses, we divide the analysis into exploratory (in-sample) and generalization (out-of-sample) phases. In the exploratory phase, single ablations are fitted to the training set for each critical variable (i.e., a model with a fixed effect for the variable and a model without one) and evaluated via in-sample permutation testing on the training set. This provides a significance test for the contribution of each individual variable to r_diff in the training set. This metric is used to select models from broad “families” of predictors for generalization-based testing, where the members of each family constitute implementation variants of the same underlying idea: DLT integration cost [DLT-(V)(C)(M)]; DLT storage cost (DLT-S); ACT-R target activation; left corner end of constituent (+L, plus length-weight variants +L-WD, +LDR, and +L-DRV); left corner end of center embedding (+G); left corner end of multiword center embedding (+L+G, plus length-weigted variants +L+G-WD, +L+G-DR, and +L+G-DRV); and left corner embedding depth (Embedding depth and Start of embedding).

Families are selected for generalization-based testing if they contain at least one member (1) whose effect estimate goes in the expected direction and (2) which is statistically significant following Bonferroni's correction on the training set. For families with multiple such members, only the best variant (in terms of exploratory r_diff) is selected for generalization-based testing. To perform the generalization tests, all predictors selected for generalization set evaluation are included as fixed effects in a model fitted to the training set, and all nested ablations of these predictors are also fitted to the same set. Fitted models are then used to generate predictions on the (unseen) evaluation set, using permutation testing to evaluate each ablative comparison in terms of out-of-sample r_diff. This analysis pipeline is schematized in Figure 3B.

Figure 3.

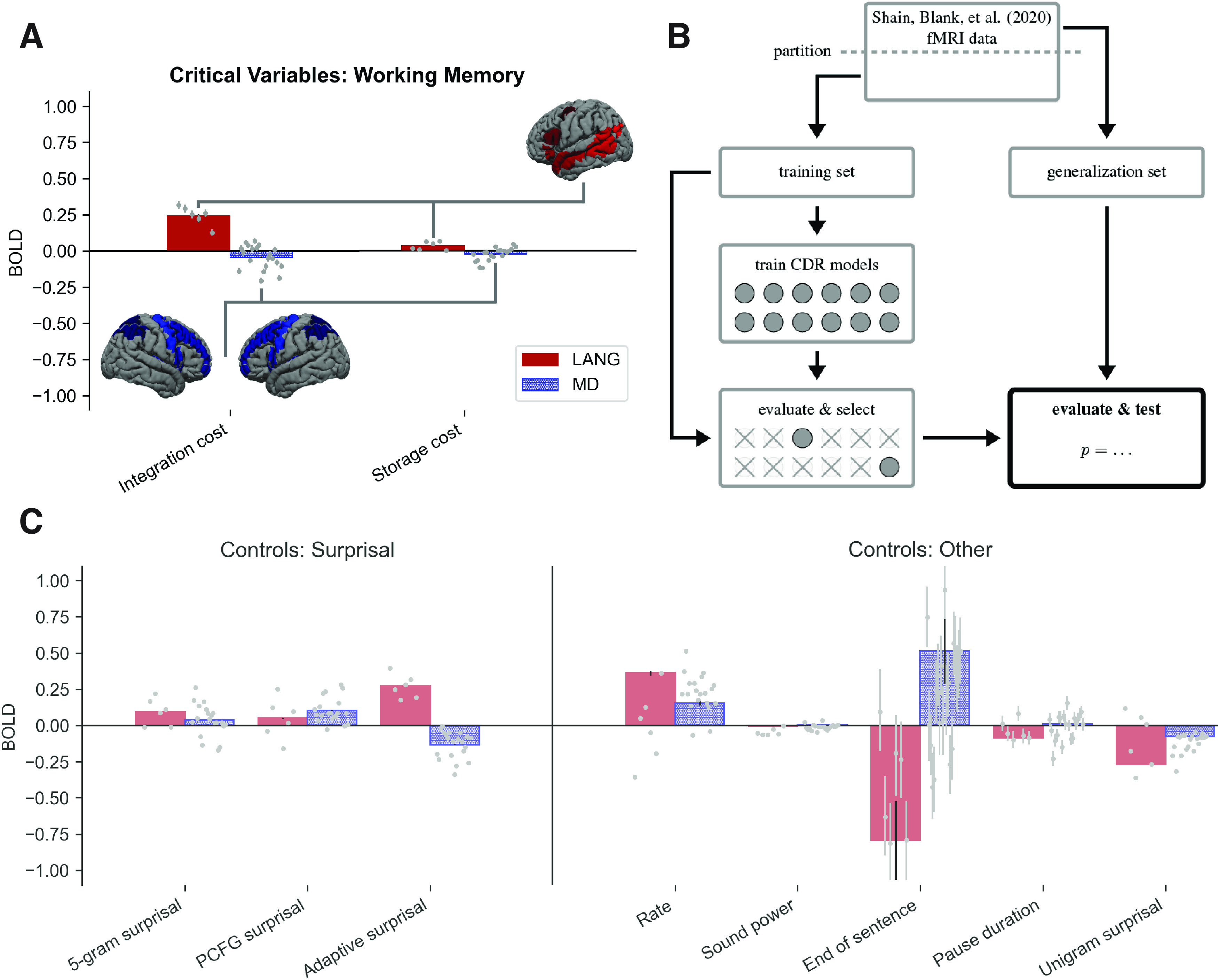
A, C, The critical working memory result (A), with reference estimates for surprisal variables and other controls shown in C. The LANG network shows a large positive estimate for integration cost (DLT-VCM, comparable to or larger than the surprisal effect) and a weak positive estimate for storage (DLT-S). The MD network estimates for both variables are weakly negative. fROIs individually replicate the critical DLT pattern and are plotted as points left-to-right in the following order (individual subplots by fROI are available on OSF: https://osf.io/ah429/): LANG: LIFGorb, LIFG, LMFG, LAntTemp, LPostTemp, LAngG; MD: LMFGorb, LMFG, LSFG, LIFGop, LPrecG, LmPFC, LInsula, LAntPar, LMidPar, LPostPar, RMFGorb, RMFG, RSFG, RIFGop, RPrecG, RmPFC, RInsula, RAntPar, RMidPar, and RpostPar (where L is left, R is right). (Note that estimates for the surprisal controls differ from those reported in the study by Shain et al. (2020). This is because models contain additional controls, especially adaptive surprisal, which overlaps with both of the other surprisal estimates and competes with them for variance. Surprisal effects are not tested because they are not relevant to our core claim.) Error bars show 95% Monte Carlo estimated variational Bayesian credible intervals. For reference, the group masks bounding the extent of the LANG and MD fROIs are shown projected onto the cortical surface. As explained in Materials and Methods, a small subset (10%) of voxels within each of these masks is selected in each participant based on the relevant localizer contrast. B, Schematic of analysis pipeline. fMRI data from the Study by Shain et al. (2020) are partitioned into training and generalization sets. The training set is used to train multiple CDR models, two for each of the memory variables explored in this study (a full model that contains the variable as a fixed effect and an ablated model that lacks it). Variables whose full model (1) contains estimates that go in the predicted direction and (2) significantly outperforms the ablated model on the training set are selected for the critical evaluation, which deploys the pretrained models to predict unseen responses in the generalization set and statistically evaluates the contribution of the selected variable to generalization performance.

Data availability

Data used in these analyses, including regressors, are available on OSF: https://osf.io/ah429/. Regressors were generated using the ModelBlocks repository: https://github.com/modelblocks/modelblocks-release. Code for reproducing the CDR regression analyses is public: https://github.com/coryshain/cdr. These experiments were not preregistered.

Results

Exploratory phase: do WM predictors explain LANG or MD network activity in the training set?

Effect estimates and in-sample significance tests from the exploratory analysis of each functional network are given in Table 1 (LANG) and Table 2 (MD).

Table 1.

LANG Exploratory results

Variable	Mean	2.5%	97.5%	r ablated	r full	r diff	p
DLT	0.085	0.073	0.096	0.1325	0.1334	0.0010	0.0318
DLT (log)	0.144	0.136	0.153	0.1323	0.1346	0.0024	0.0005
DLT-V	0.094	0.083	0.105	0.1326	0.1337	0.0011	0.0173
DLT-C	0.190	0.179	0.200	0.1324	0.1370	0.0046	0.0001
DLT-M	0.139	0.129	0.148	0.1329	0.1356	0.0027	0.0003
DLT-VC	0.239	0.228	0.250	0.1326	0.1386	0.0060	0.0001
DLT-VM	0.154	0.144	0.165	0.1329	0.1360	0.0031	0.0001
DLT-CM	0.231	0.221	0.242	0.1330	0.1402	0.0072	0.0001
DLT-VCM	0.267	0.256	0.277	0.1333	0.1417	0.0084	0.0001
DLT-S	0.065	0.061	0.068	0.1328	0.1352	0.0024	0.0001
ACT-R target activation	0.007	0.003	0.010	0.1330	0.1331	0.0000	0.7025
End of constituent	−0.061	−0.072	−0.051	0.1324	0.1326	0.0002	0.2850
Length of constituent (WD)	−0.076	−0.092	−0.059	0.1329	0.1333	0.0004	0.1430
Length of constituent (DR)	0.069	0.054	0.085	0.1324	0.1327	0.0003	0.2541
Length of constituent (DRV)	0.042	0.026	0.056	0.1326	0.1327	0.0001	0.6763
End of center embedding	0.137	0.134	0.141	0.1326	0.1338	0.0013	0.0206
End of multiword center embedding	0.026	0.013	0.038	0.1328	0.1328	0.0001	0.6458
Length of multiword center embedding (WD)	−0.042	−0.060	−0.026	0.1343	0.1345	0.0002	0.2484
Length of multiword center embedding (DR)	−0.015	−0.032	0.003	0.1332	0.1332	0.0000	0.6133
Length of multiword center embedding (DRV)	−0.039	−0.056	−0.022	0.1334	0.1337	0.0002	0.2306
Embedding depth	−0.035	−0.037	−0.032	0.1347	0.1355	0.0008	0.0293
Start of embedding	−0.118	−0.130	−0.106	0.1329	0.1335	0.0006	0.2979

V, C, and M suffixes denote the use of verb, coordination, and/or preceding modifier modifications to the original definition of DLT integration cost. Effect estimates with 95% credible intervals, correlation levels of full and ablated models on the training set, and significance by paired permutation test of the improvement in training set correlation are shown. Families of predictors are delineated by black horizontal lines. Variables that have the expected sign and are significant under 22-way Bonferroni's correction are shown in bold (note that the expected sign of ACT-R target activation is negative, since processing costs should be lower for more activated targets). r_diff is the difference in Pearson correlation between true and predicted responses from a model containing a fixed effect for the linguistic variable (r_full) to a model without one (r_ablated).

Table 2.

MD Exploratory results

Variable	Mean	2.5%	97.5%	r ablated	r full	r diff	p
DLT	0.003	−0.003	0.009	0.0812	0.0812	0.0000	0.9851
DLT (log)	−0.038	−0.043	−0.034	0.0819	0.0823	0.0003	0.0742
DLT-V	−0.001	−0.007	0.005	0.0810	0.0809	0.0000	1.0000
DLT-C	−0.042	−0.047	−0.037	0.0814	0.0820	0.0006	0.0122
DLT-M	−0.017	−0.022	−0.012	0.0818	0.0819	0.0001	0.5709
DLT-VC	−0.047	−0.052	−0.043	0.0810	0.0815	0.0006	0.0156
DLT-VM	−0.025	−0.030	−0.020	0.0813	0.0815	0.0002	0.3473
DLT-CM	−0.059	−0.063	−0.054	0.0819	0.0829	0.0011	0.0010
DLT-VCM	−0.062	−0.067	−0.058	0.0813	0.0824	0.0011	0.0012
DLT-S	−0.034	−0.036	−0.032	0.0817	0.0828	0.0011	0.0026
ACT-R target activation	0.020	0.019	0.022	0.0817	0.0825	0.0008	0.0047
End of constituent	0.032	0.027	0.037	0.0811	0.0811	0.0000	0.8994
Length of constituent (WD)	0.115	0.107	0.124	0.0813	0.0821	0.0008	0.0460
Length of constituent (DR)	0.051	0.043	0.059	0.0809	0.0812	0.0003	0.2344
Length of constituent (DRV)	0.075	0.067	0.082	0.0812	0.0816	0.0004	0.1388
End of center embedding	0.022	0.020	0.024	0.0818	0.0819	0.0001	0.5319
End of multiword center embedding	0.065	0.059	0.070	0.0810	0.0816	0.0005	0.0589
Length of multiword center embedding (WD)	0.009	0.003	0.015	0.0811	0.0811	0.0000	0.6645
Length of multiword center embedding (DR)	0.026	0.018	0.033	0.0813	0.0815	0.0002	0.2171
Length of multiword center embedding (DRV)	0.013	0.005	0.021	0.0810	0.0810	0.0000	0.6798
Embedding depth	0.005	0.004	0.006	0.0814	0.0814	0.0000	0.8179
Start of embedding	0.060	0.054	0.065	0.0811	0.0813	0.0002	0.4439

V, C, and M suffixes denote the use of verb, coordination, and/or preceding modifier modifications to the original definition of DLT integration cost. Effect estimates with 95% credible intervals, correlation levels of full and ablated models on the training set, and significance by paired permutation test of the improvement in training set correlation are shown. Families of predictors are delineated by horizontal lines. No variable both (1) has the expected sign (note that the expected sign of ACT-R target activation is negative, since processing costs should be lower for more activated targets) and (2) is significant under 22-way Bonferroni's correction. r_diff is the difference in Pearson correlation between true and predicted responses from a model containing a fixed effect for the linguistic variable (r_full) to a model without one (r_ablated).

The DLT predictors are broadly descriptive of language network activity: six of eight integration cost predictors and the DLT-S predictor yield both large significant increases in r_diff and comparatively large overall correlation with the true training response r_full. The strongest variant of DLT integration cost is DLT-VCM. Although the log-transformed raw DLT predictor provides substantially stronger fit than DLT on its own, consistent with the hypothesis that the DLT overestimates the cost of long dependencies, it is still weaker than most of the other DLT variants, suggesting that these variants are not improving fit merely by discounting the cost of long dependencies. None of the other families of WM predictors is clearly associated with language network activity.

No predictor is significant in MD with the expected sign. Two variants of DLT integration cost (DLT-M and DLT-VCM) are significant but have a negative sign, indicating that BOLD signal in MD decreases proportionally to integration difficulty. This outcome is not consistent with the empirical predictions of the hypothesis that MD supports WM for language comprehension, though it is possibly instead consistent with “vascular steal” (Lee et al., 1995; Harel et al., 2002) and/or inhibition (Shmuel et al., 2006) driven by WM load in other brain regions (e.g., LANG).

In follow-up analyses, we addressed possible influences of using the flipped language localizer contrast (nonwords > sentences) to define the MD network by instead localizing MD using a hard > easy contrast in a spatial WM task (Fedorenko et al., 2013). Results were unchanged: no predictor has a significant effect in the expected direction (see OSF for details: https://osf.io/ah429/).

These exploratory results have several implications. First, they support the existence of syntactically related WM load in the language network during naturalistic sentence comprehension. Second, they present a serious challenge to the hypothesis that WM for language relies primarily on the MD network—the most likely domain-general WM resource: despite casting a broad net over theoretically motivated WM measures and performing the testing in-sample, the MD network does not show systematic correlates of WM demand.

Based on these results, DLT-VCM and DLT-S are selected for evaluation on the (held-out) generalization set, to ensure that the reported patterns generalize. Models containing/ablating both predictors are fitted to the training set, and their contribution to r measures in the generalization set is used for evaluation and significance testing. Because the MD network does not register any clear signatures of WM effects, further generalization-based testing is unwarranted. MD models with the same structure as the full LANG network models are fitted simply to provide a direct comparison between estimates in the LANG versus MD networks.

These results also suggest that implementation variants in models of WM may influence alignment with measures of human language processing load: certain variants of the DLT are numerically stronger predictors of language network activity than the DLT as originally formulated, ACT-R theory, or left-corner parsing theory. This outcome warrants further investigation because, although the DLT does not commit to a parsing algorithm (Gibson, 2000), algorithmic-level theories like ACT-R and left corner parsing make empirical predictions that are in aggregate similar to those of the DLT (Lewis and Vasishth, 2005), and yet they are not in evidence (beyond surprisal) in human neuronal timecourses, at least not in brain regions identified by either of the independently validated MD localizer contrasts that we considered (nonwords > sentences and hard > easy spatial working memory). This result raises three key questions for future research. (1) Are the gains from DLT integration cost and its variants significant over other theoretical models of WM in sentence processing? If so, (2) which aspects of the DLT (e.g., linear effects of dependency locality, a privileged status for nouns and verbs) give rise to those gains, and (3) how might the critical constructs be incorporated into algorithmic level sentence processing models to enable them to capture those gains?

Generalization phase

Do WM predictors explain neural activity in the generalization set?

Effect sizes (HRF integrals) by predictor in each network from the full model are plotted in Figure 3A. As shown, the DLT-VCM effect is strongly positive and the DLT-S effect is weakly positive in LANG, but both effects are slightly negative in MD.

The critical generalization (out-of-sample) analyses of DLT effects in the language network are given in Table 3. As shown, the integration cost predictor (DLT-VCM) contributes significantly to generalization r_diff, both on its own and over the DLT-S predictor. Storage cost effects are significant in isolation (DLT-S is significant over “neither”) but fail to improve statistically on integration cost (DLT-S is not significant over DLT-VCM). Generalization-based tests of interactions of each of these predictors with network (a test of whether the LANG network exhibits a larger effect than the MD network) are significant for all comparisons, supporting a larger effect of each variable in the LANG network. In summary, the evidence from this study for DLT integration cost is strong, whereas the evidence for DLT storage cost is weaker (storage cost estimates are (1) positive, (2) significant by in-sample test, and (3) significantly larger by generalization-based tests than storage costs in MD; however, they do not pass the critical generalization-based test of difference from 0 in the presence of integration costs, and the existence of distinct storage costs is therefore not clearly supported by these results).

Table 3.

Critical comparison

	LANG (p)	Interaction with network (p)
DLT-VCM over neither	0.0001***	0.0001***
DLT-S over neither	0.0033***	0.0013**
DLT-VCM over DLT-S	0.0001***	0.0001***
DLT-S over DLT-VCM	0.3301	0.0007***

The p values that are significant under eight-way Bonferroni's correction (because eight comparisons are tested) are shown in bold. For the LANG network [LANG (p) column], integration cost (DLT-VCM) significantly improves network generalization r_diff both alone and over DLT-S, whereas DLT-S only contributes significantly to generalization r_diff in the absence of the DLT-VCM predictor (significant over “neither” but not over DLT-VCM). For the combined models [interaction with network (p) column], the interaction of each variable with network significantly contributes to generalization r_diff in all comparisons, supporting a significantly larger effect of both variables in the language network than in the MD network.

Thus, whatever storage costs may exist, they appear to be considerably fainter than integration costs (smaller effects, weaker and less consistent improvements to fit), and a higher-powered study may be needed to tease the two types of costs apart convincingly (or to reject the distinction). In this way, our study reflects a fairly mixed literature on storage costs in sentence processing, with some studies reporting effects (King and Kutas, 1995; Fiebach et al., 2002; Chen et al., 2005; Ristic et al., 2022) and others failing to find any (Hakes et al., 1976; Van Dyke and Lewis, 2003).

How well do models perform relative to ceiling?

Table 4 shows correlations between model predictions and true responses by network in both halves of the partition (training and evaluation), relative to a “ceiling” estimate of stimulus-driven correlation, computed as the correlation between (1) the responses in each region of each participant at each story exposure and (2) the average response of all other participants in that region, for that story. Consistent with prior studies (Blank and Fedorenko, 2017), the LANG network exhibits stronger language-driven synchronization across participants than the MD network (higher ceiling correlation). Our models also explain a greater share of that correlation in LANG versus MD, especially on the out-of-sample evaluation set (39% relative correlation for LANG vs 3% relative anticorrelation for MD).

Table 4.

Correlation r of full model predictions with the true response compared with a ceiling measure correlating the true response with the mean response of all other participants for a particular story/fROI

	LANG		MD		Combined
	r-Absolute	r-Relative	r-Absolute	r-Relative	r-Absolute	r-Relative
Ceiling	0.221	1.0	0.116	1.0	0.152	1.0
Model (train)	0.143	0.647	0.085	0.733	0.083	0.546
Model (evaluation)	0.086	0.389	−0.003	−0.026	0.048	0.316

The “r-Absolute” columns show absolute percent variance explained, while “r-Relative” columns show the ratio of r-absolute to the ceiling.

Are WM effects localized to a hub (or hubs) within the LANG network?

Estimates also show a spatially distributed positive effect of DLT integration cost across the regions of the LANG network (Fig. 3A, gray points) that systematically improves generalization quality (Table 5), significantly so in inferior frontal and temporal regions. This pattern indicates that all LANG fROIs are implicated to some extent in the processing costs associated with the DLT, rather than being focally restricted to one or two “syntax” regions. Storage cost effects are less clear: although numerically positive DLT-S estimates are found in all language regions (Fig. 3A), they do not systematically improve generalization quality (Table 5). No such pattern holds in MD: regional effects of both DLT variables cluster around 0 (Fig. 3A, gray points), and the sign of r_diff across regions is approximately at chance. These results converge to support strong, spatially distributed sensitivity in the language-selective network to WM retrieval difficulty.

Table 5.

Unique contributions of fixed effects for each of integration cost (DLT-VCM) and DLT-S to out-of-sample correlation improvement r_diff by language fROI (relative to ceiling performance in LANG of 0.221)

fROI	Network	DLT-VCM rdiff relative	DLT-S rdiff relative
IFGorb	LANG	0.038***	0.003
IFG	LANG	0.027*	−0.003
MFG	LANG	0.019	−0.003
AntTemp	LANG	0.062***	0.006
PostTemp	LANG	0.027*	0.006
AngG	LANG	0.002	−0.001

DLT-VCM improves correlation with the true response in all (six of six) LANG regions, but DLT-S improves correlation with the true response in only three of six LANG regions. Significance derived from an uncorrected paired permutation test of r_diff for each critical WM predictor within each fROI is shown by asterisks.

*p < 0.05,

**p < 0.01,

***p < 0.001.

Having shown evidence that WM demand is distributed throughout the language network, we asked whether different regions show these effects to different degrees. To do so, we fit a variant of the main model (a “fixed WM-only” model) differing only in that it lacks by-fROI random effects for the WM predictors DLT-VCM and DLT-S, enforcing the null hypothesis of identical WM effects across regions. This null model fits the test set significantly less well than the main model (r_diff relative = 0.008, p = 0.001), supporting the existence of quantitative differences in WM effects among the regions of the language network. The population effect of DLT-VCM is slightly smaller numerically in the fixed WM-only model (0.227 vs 0.245), likely reduced by the AngG fROI, which showed a smaller effect in the main model. To probe which regions primarily contribute to the gains of the main model over the fixed WM-only model (and therefore benefit most from allowing WM effects to vary by region), we assessed the difference in performance between the main model and the fixed WM-only model by fROI. This analysis shows which regions benefit most from relaxing the assumption of a uniform WM effect across fROIs (Table 6). The largest improvements are found in the inferior frontal fROIs, which also show the largest DLT-VCM effect sizes (Fig. 3A). Thus, although all language regions appear to participate in WM operations for syntactic structure building, they do so to different degrees, with the largest effects appearing in inferior frontal areas.

Table 6.

Unique contributions of random effects by fROI for the WM predictors DLT-VCM and DLT-S to out-of-sample correlation improvement r_diff by fROI (relative to ceiling performance in LANG of 0.221)

fROI	Network	rdiff-relative
IFGorb	LANG	0.012*
IFG	LANG	0.012*
MFG	LANG	0.008
AntTemp	LANG	0.001
PostTemp	LANG	0.006
AngG	LANG	−0.006

All regions but the AngG fROI show a numerical improvement, reaching significance in the inferior frontal fROIs. Significance derived from an uncorrected paired permutation test of r_diff for each critical WM predictor within each fROI is shown by asterisks.

*p < 0.05,

**p < 0.01,

***p < 0.001.

Are WM effects driven by item-level confounds?

Because the data partition of the study by Shain et al. (2020) distributes materials across the training and evaluation sets, it is possible that item-level confounds may have affected our results in ways that generalize to the test set. To address this possibility, in a follow-up analysis we repartition the data so that the training and generalization sets are approximately equal in size but contain nonoverlapping materials, and we rerun the critical analyses above. The result is unchanged: DLT-VCM and DLT-S estimates are positive with similar magnitudes to those reported in Figure 3A; DLT-VCM contributes significantly both on its own (p < 0.001) and in the presence of DLT-S (p < 0.001); and DLT-S contributes significantly in isolation (p < 0.004) but fails to contribute over DLT-VCM, even numerically (p = 1.0). The evidence from both analyses is consistent: WM retrieval difficulty registers in the language network, with little effect in the multiple-demand network. Effect estimates from this reanalysis are consistent with those in Figure 3 and are available on OSF: https://osf.io/ah429/.

Are WM effects driven by passage-level influences on word prediction?

Although the three predictors in our surprisal baseline insure against the possibility that WM effects in the LANG network are driven by sentence-internal patterns of word predictability, all three measures (5-gram surprisal, PCFG surprisal, and adaptive surprisal) are constrained to make predictions based solely on preceding information within the same sentence. What if these controls underestimate the role of extrasentential influences on word predictability (i.e., from preceding sentences in the same passage)? Adaptive surprisal partially mitigates this concern because the predictive model adapts to the local statistics of the passage after each sentence, although the prediction itself can only access intrasentential context. However, recent large-scale language models based on the Transformer architecture (Vaswani et al., 2017), especially the GPT-2 network (Radford et al., 2019), directly consider entire preceding passages in making next-word predictions and have been shown to correlate strongly with human sentence processing, both in their representational similarity to human brains (Schrimpf et al., 2021; Goldstein et al., 2022) and in the correlation between model-generated surprisal and measures of human comprehension difficulty (Wilcox et al., 2020). We therefore conduct a follow-up analysis in which we control for passage-level effects on word predictability by adding surprisal measures derived from GPT-2-XL (Radford et al., 2019) to our existing set of control variables and rerunning our critical confirmatory analyses on responses from the language network. GPT-2-XL is a 48-layer 1.5 billion-parameter decoder-only autoregressive transformer neural network model, which uses a byte-pair encoding tokenization (Sennrich et al., 2016) to represent unknown words as sequences of subword character sequences. GPT-2 bases its decisions on a context window of 1024 preceding words. In cases where the article length exceeded the length of the context window, the last 512 words of the previous context window were used as the first 512 words of the subsequent context window. Inclusion of GPT-2-XL surprisal has little effect on the estimated overall change in BOLD associated with an SD increase in integration cost (from 0.245 without GPT-2-XL surprisal in the baseline to 0.233 with it) and storage cost (from 0.035 without GPT-2-XL surprisal in the baseline to 0.057 with it), and our critical finding is unchanged: integration cost contributes significantly to model fit to the unseen test set, both over the baseline (p < 0.001) and over the baseline with an additional fixed effect for storage cost (p < 0.001). Given that our main finding holds in the presence of surprisal from a state-of-the-art passage-level transformer language model, it is unlikely that passage-level influences on word predictability explain the patterns we have attributed to WM demand.

Interestingly, we also found that storage costs are significant in the language network when GPT-2-XL surprisal is controlled for, both over the baseline (p < 0.001) and over the baseline with an additional fixed effect for integration cost (p < 0.002). Given that this pattern only emerged in follow-up analyses and did not hold in our main comparison, we draw no conclusion about the existence of storage costs and simply reiterate that our ensemble of results suggests that, should any such costs exist, their effect is considerably smaller than that of integration/retrieval costs (Fig. 3A), with inconsistent findings on whether they can be dissociated from integration costs.

Constraining the space of possible domain-general WM involvement in language comprehension

We have shown that the MD network shows no significant increase in activation in response to theory-driven estimates of WM demand for language processing and has a significantly weaker response to these measures than the LANG network in direct comparisons.

Notwithstanding, there are two possibilities that our present design cannot rule out: (1) that WM for language is implemented—in addition to the LANG network—by domain-general WM regions that are nonoverlapping with the MD network as we have defined it; and (2) that WM for language is implemented primarily in the language regions but also has a faint signature in the domain-general MD regions that we lack the power to detect. We consider possibility 1 to be implausible and possibility 2 to be of little consequence. Regarding possibility 1, the weight of prior evidence that the MD network primarily supports domain-general WM (see Materials and Methods) renders it highly likely that any putatively domain-general WM resources used for language comprehension will overlap substantially with the MD network. Although brain areas outside of the MD network have been associated with WM, including within the thalamus (Rottschy et al., 2012), basal ganglia (Emch et al., 2019), hippocampus (Olson et al., 2006), and cerebellum (Rottschy et al., 2012), these areas are less consistently identified in meta-analyses than the core MD areas, and their functional role in WM is debated (for the discussions of the role of the hippocampus in WM, see Baddeley and Warrington, 1970; Nadel and MacDonald, 1980; Shrager et al., 2008; Baddeley et al., 2010, 2011; Jeneson et al., 2010). We see no clear reason to expect domain-general WM during language comprehension (unlike most other domains in which WM has been studied) to fall primarily in areas like these, rather than the MD network.

Regarding B, our current testing protocol cannot provide evidence against (only fail to find evidence for) any MD involvement in WM for language. However, our results indicate that any such effects are so small (relative to the effects in the LANG network) as to be of no practical interest. The by-fROI WM effects in the MD network cluster tightly around 0, and the overall MD network effect for both WM variables is numerically negative, in stark contrast to the tightly clustered positive WM effects in the LANG network (Fig. 3A). Our large-scale (by fMRI standards) study (78 participants) is adequately powered to soundly reject the null hypothesis when applied to the language network (***p < 0.0001). Thus, if there is any WM burden sharing between the LANG and MD networks, the MD network contribution is tiny and is inadequate to rescue the hypothesis of primarily domain-general WM for language.

Discussion

The centrality of word-by-word structure-building operations in WM during language processing has been challenged by arguments that human language processing may be mostly approximate and shallow, especially in naturalistic settings (Frank and Bod, 2011), and that the main driver of language processing costs may be surprisal rather than WM demand (Levy, 2008). In this study, we analyzed a large publicly available dataset of fMRI responses to naturalistic stories (Shain et al., 2020) with respect to diverse theory-driven estimates of syntactically modulated WM demand (Gibson, 2000; Lewis and Vasishth, 2005; Rasmussen and Schuler, 2018) under rigorous controls for word predictability (Heafield et al., 2013; van Schijndel et al., 2013; van Schijndel and Linzen, 2018; Radford et al., 2019).

We additionally addressed a related debate about the domain specificity of WM resources for language. Some have argued that language processing relies primarily on a domain-general working memory resource (Wanner and Maratsos, 1978; King and Just, 1991; Just and Carpenter, 1992). This view draws support from evidence that individual differences in nonlinguistic WM capacity modulate linguistic processing (King and Just, 1991; Prat and Just, 2011; Slevc, 2011; Meyer et al., 2013; Payne et al., 2014; Nicenboim et al., 2015, 2016; but see Federmeier et al., 2020), from dual-task experiments supporting a shared pool of linguistic and nonlinguistic WM resources (Gordon et al., 2002; Fedorenko et al., 2006, 2007; Van Dyke and McElree, 2006), and from evidence that nonlinguistic WM training can facilitate sentence comprehension (Novick et al., 2014; Hsu and Novick, 2016; Hussey et al., 2017; Hsu et al., 2021). However, others have argued that language processing relies primarily on domain-specific working memory resources (Lewis, 1996; Waters and Caplan, 1996; Caplan and Waters, 1999). This view draws support from studies showing little relation between WM capacity and language processing (Waters and Caplan, 2004; Sprouse et al., 2012; Traxler et al., 2012) and from studies showing distinct patterns of brain activity for linguistic and nonlinguistic WM demand (Fiebach et al., 2001; Santi and Grodzinsky, 2007; Makuuchi et al., 2009; Glaser et al., 2013). To probe the nature of the computations in question, we examined neural responses in two functionally localized brain networks: the domain-specific LANG network (Fedorenko et al., 2011) and the domain-general MD network (Duncan, 2010), implicated in executive functions, including working memory.

Exploratory analyses of theories of WM load in sentence comprehension, which posit integration costs associated with retrieving representations from WM and/or storage costs associated with maintaining representations in WM, identified clear effects in the LANG network of integration cost and weaker effects of storage costs over rigorous surprisal controls. No WM measures reliably characterized responses in the MD network. Generalization tests on held-out data support both (1) integration costs (but not storage costs) in the LANG network, and (2) systematically larger effects of integration and storage costs in the LANG network than in the MD network. Further, integration costs are found across the different regions of the LANG network, supporting a broadly distributed WM system for language comprehension, rather than a spatially restricted “hub” or a set of hubs.

This pattern of results supports two broad inferences about the neural implementation of human sentence processing. First, our results support the widely held view that a core operation in human sentence processing is to encode and retrieve items in WM as required by the syntactic structure of sentences (Gibson, 2000; McElree et al., 2003; Lewis and Vasishth, 2005; Van Dyke and McElree, 2006; Rasmussen and Schuler, 2018), even in a naturalistic setting where behavioral evidence for such effects has been mixed in the presence of surprisal controls (Demberg and Keller, 2008; van Schijndel and Schuler, 2013; Shain and Schuler, 2018). And second, our results challenge prior arguments that the WM operations supporting language comprehension draw on primarily domain-general WM resources (Stowe et al., 1998; Fedorenko et al., 2006, 2007; Amici et al., 2007). Activity in the MD network—the most plausible candidate for implementing domain-general WM computations (Goldman-Rakic, 1988; Owen et al., 1990; Kimberg and Farah, 1993; Duncan and Owen, 2000; Prabhakaran et al., 2000; Cole and Schneider, 2007; Duncan, 2010; Gläscher et al., 2010; Rottschy et al., 2012; Camilleri et al., 2018; Assem et al., 2020a)—shows no association with any of the WM measures explored here and shows significantly weaker associations with critical WM predictors than does the LANG network. Our results thus support the hypothesis that the WM operations required for language comprehension are primarily conducted by the brain regions that store linguistic knowledge (Caplan and Waters, 1999; Fiebach et al., 2001; Fedorenko and Shain, 2021). This outcome accords with prior arguments that memory and computation are tightly integrated in the brain (Fitz et al., 2020; Dasgupta and Gershman, 2021) and that, for domains like language—supported by specialized brain circuits—general computations like WM may be preferentially carried out within those circuits (Fedorenko and Shain, 2021).

Our results also bear on ongoing debates about the degree of regional specialization for syntactic processing within the LANG network. According to some proposals, syntactic structure building is carried out focally in IFG (Hagoort, 2005, 2013; Friederici, 2017; Grodzinsky et al., 2021), whereas other proposals primarily locate syntactic structure building in the posterior temporal lobe (Pylkkänen, 2019; Matchin and Hickok, 2020). Nonetheless, effects for syntactic manipulations have been reported in other areas associated with language processing, including temporoparietal areas (Meyer et al., 2012, 2013) and anterior temporal areas (Mazoyer et al., 1993; Friederici et al., 2000; Humphries et al., 2006). The inferior frontal fROIs and anterior/posterior temporal fROIs all reach significance in our stringent out-of-sample test, with numerically positive contributions in all six fROIs. Thus, our results are most consistent with a spatially distributed burden of syntactic processing across the regions of the language network (Bates et al., 1995; Caplan et al., 1996; Wilson and Saygin, 2004; Blank et al., 2016; Toneva and Wehbe, 2019; Shain et al., 2020; for review, see Fedorenko et al., 2020). In particular, all language regions register a signature of syntactic structure building, contrary to prior arguments for the existence of one or two dedicated syntactic processing centers (Vandenberghe et al., 2002; Hagoort, 2005; Friederici et al., 2006; Bemis and Pylkkänen, 2011; Pallier et al., 2011; Tyler et al., 2011; Brennan et al., 2012; Matchin et al., 2017; Matchin and Hickok, 2020). In this way, they align with recent evidence from our group that the regions of the language network are all sensitive to linguistic information at many grain sizes, from subword level to phrase and sentence level, and are all sensitive to both manipulations of sentence structure and word meaning, with no region showing strong selectivity for the former over the latter (Blank et al., 2016; Fedorenko et al., 2016, 2020; Blank and Fedorenko, 2020; Shain et al., 2020, 2021; Regev et al., 2021). The presence of graded differences in the strength of WM effects between regions (the largest gains from WM predictors in the inferior frontal and anterior and posterior temporal areas, and the largest WM retrieval effects in the inferior frontal areas) suggests that within-network specialization may be a matter of degree rather than a kind of processing, at least when it comes to WM for incremental language comprehension.

The WM effects shown here are not explained by multiple strong measures of word predictability, which have repeatedly been shown in prior work to describe naturalistic human sentence processing responses across modalities, including behavioral (Demberg and Keller, 2008; Frank and Bod, 2011; Fossum and Levy, 2012; Smith and Levy, 2013; van Schijndel and Schuler, 2015; Aurnhammer and Frank, 2019; Shain, 2019), electrophysiological (Frank et al., 2015; Armeni et al., 2019; Heilbron et al., 2022), and fMRI (Brennan et al., 2016; Henderson et al., 2016; Willems et al., 2016; Lopopolo et al., 2017; Shain et al., 2020). In its strong form, surprisal theory (Hale, 2001; Levy, 2008) equates sentence comprehension with allocating activation among many possible interpretations of the unfolding sentence, in proportion to their probability given the currently observed string. Under such a view, structured representations are assumed to be available, and the primary work of comprehension is (probabilistically) selecting among them. However, according to integration-based theories (Gibson, 2000; Lewis and Vasishth, 2005) incremental effort is required to compute the available interpretations in the first place (i.e., by storing, retrieving, and updating representations in memory). By showing integration costs that are not well explained by word predictability, our study joins arguments in favor of complementary roles played by integration and prediction in language comprehension (Levy et al., 2013; Ferreira and Chantavarin, 2018). Strong word predictability controls are of course a perpetually moving target: we cannot rule out the possibility that some other current or future statistical language model might explain apparent WM effects. However, such an objection effectively renders surprisal theory unfalsifiable. We have attempted to address such concerns by drawing on the current state of the art in language modeling (“adaptive surprisal” and “GPT-2-XL surprisal”).

Notwithstanding, one recent variant of surprisal theory might offer an alternative explanation for our finding: lossy context surprisal (Futrell et al., 2021), which derives what we have termed integration costs as predictability effects by positing a memory store subject to a progressive noise function, whereby words are more likely to be forgotten the longer ago they occurred. Because dependencies can make words more predictable, forgetting renders words less predictable on average (and thus harder to process) when they terminate longer dependencies. Because lossy context surprisal currently lacks a broad-coverage implementation (Futrell et al., 2021), we cannot directly test its predictions for our study, and we leave further investigation to future work.

In conclusion, our study supports the existence of a distributed but domain-specific working memory resource that plays a core role in language comprehension, with no evidence of recruitment of domain-general working memory resources housed within the multiple-demand network.