Interfacing Motor Units in Nonhuman Primates Identifies a Principal Neural Component for Force Control Constrained by the Size Principle

Abstract

Motor units convert the last neural code of movement into muscle forces. The classic view of motor unit control is that the CNS sends common synaptic inputs to motoneuron pools and that motoneurons respond in an orderly fashion dictated by the size principle. This view, however, is in contrast with the large number of dimensions observed in motor cortex, which may allow individual and flexible control of motor units. Evidence for flexible control of motor units may be obtained by tracking motor units longitudinally during tasks with some level of behavioral variability. Here we identified and tracked populations of motor units in the brachioradialis muscle of two macaque monkeys during 10 sessions spanning >1 month with a broad range of rate of force development (1.8–38.6 N · m · s⁻¹). We found a very stable recruitment order and discharge characteristics of the motor units over sessions and contraction trials. The small deviations from orderly recruitment were fully predicted by the motor unit recruitment intervals, so that small shifts in recruitment thresholds happened only during contractions at a high rate of force development. Moreover, we also found that one component explained more than ∼50% of the motor unit discharge rate variance, and that the remaining components represented a time-shifted version of the first. In conclusion, our results show that the recruitment of motoneurons is determined by the interplay of the size principle and common input and that this recruitment scheme is not violated over time or by the speed of the contractions.

SIGNIFICANCE STATEMENT With a new noninvasive high-density electromyographic framework, we show the activity of motor unit ensembles in macaques during voluntary contractions. The discharge characteristics of brachioradialis motor units revealed a relatively fixed recruitment order and discharge characteristics across days and rate of force developments. These results were further confirmed through invasive axonal stimulation and recordings of intramuscular electromyographic activity from 16 arm muscles. The study shows for the first time the feasibility of longitudinal noninvasive motor unit interfacing and tracking of the same motor units in nonhuman primates.

Introduction

Theories of motor control are grounded on recording spinal motor unit activity during voluntary force contractions (Adrian and Bronk, 1929; De Luca and Erim, 1994; Kandel et al., 2000; Faisal et al., 2008). Accurate understanding of motor unit function reveals in a direct way the strategies used by the nervous system to control and coordinate muscle forces (Adrian and Bronk, 1929). Generation of force is believed to occur by a combination of recruitment and rate coding of spinal motor neurons. While it is often assumed that recruitment order and rate coding are determined by the size of motor neurons (Henneman, 1957; Duchateau and Enoka, 2011) and the common inputs that the motor neurons in a pool receive (De Luca and Erim, 1994), some studies have challenged this view by proposing a more flexible motor unit control (Harrison and Mortensen, 1962; Basmajian, 1963; Marshall et al., 2021). Although previous evidence supports the size principle during isometric contractions (Milner-Brown et al., 1973a; Desmedt and Godaux, 1977), these results have been challenged by the possibility that the motor cortex could provide independent input to spinal motoneurons. Moreover, it is still unclear whether the high correlations in motor unit output (Nordstrom et al., 1992; De Luca and Erim, 1994; Baker et al., 1999; Farina et al., 2014b) have a functional origin or represent a physiological epiphenomenon.

The current lack of definitive evidence for size principle and common input during recruitment with force modulation is because of technical limitations. Accurate measures of the recruitment order and common input necessitate multiple recordings from as many units as possible and the tracking of the same motor units across different days and across rates of muscle force development (Adrian and Bronk, 1929; Basmajian, 1963; Milner-Brown et al., 1973a, b; Desmedt and Godaux, 1977; Mantel and Lemon, 1987; Lemon et al., 1990; Olivier et al., 2001; Marshall et al., 2021). Currently, no studies tracked the same population of motor units in longitudinal experiments during voluntary tasks in nonhuman primates. Such tracking of the same population of neurons is crucial to infer functional behavior. This is even more important when testing intrinsic properties of motoneurons, such as those associated with the size principle. One way to identify motor unit activity during voluntary tasks is to insert percutaneous wire electrodes into muscles. However, these electrodes may yield limited signal quality and a limited number of detected motor units.

By tracking the behavior of the same motor neurons across multiple experimental sessions with a noninvasive neural interface consisting of high-density grids of electrodes placed on the muscle, we investigated for the first time the variability in motoneuron recruitment and discharge characteristics over a period of 1 month in two monkeys during voluntary contractions. The tracking of a relatively large population of spinal motor units during contractions at different rates of force development allowed us to define the neural strategies accomplished by the CNS to control muscle force. Moreover, it was possible to investigate the associations between recruitment of motoneurons and estimates of common synaptic inputs.

We found a very small day-to-day and trial-to-trial variability in recruitment order and rate coding, suggesting consistent control of the population of motoneuron ensembles. Moreover, with a factorization method we demonstrated that one common input component was sufficient to explain motor unit recruitment. The application of this approach in a primate species with a motor system closely similar to humans opens the future possibility of combining multiple single-motor unit measurements with invasive recordings from central pathways. This has the potential to yield substantial new insights into the anatomic source of common drive during different motor tasks.

Materials and Methods

Animals

Recordings were performed from two adult female awake behaving monkeys (Macaca mulatta; monkeys MI and MA; age, 6 years; weight, 6.2 and 6.7 kg, respectively). All animal procedures were performed under appropriate licenses issued by the UK Home Office in accordance with the Animals (Scientific Procedures) Act (1986) and were approved by the Animal Welfare and Ethical Review Board of Newcastle University.

Behavioral task

The monkeys were trained to perform an isometric elbow flexion task with their right arm. Monkey MA was also trained to perform this task with her left arm. The forearm was placed into a rigid plastic cast. This was three-dimensionally printed from a digital model of the forearm made using a laser scanner (Go!Scan, Creaform 3D), ensuring a close but comfortable fit. A further support held the upper arm; the supports were attached to the training cage to fix the elbow in 90° flexion, and the forearm in semipronation so that the radius and ulnar were oriented in a vertical plane. A load cell (model LC703-25, OMEGA Engineering) attached to the forearm cast registered elbow flexion torque. The force [in kilogram-force (kgF)] applied to the load cell was recorded as a voltage signal by a custom-designed task program. A calibration factor was determined that allowed for the conversion of the voltage signal back into kgF at a later stage. To determine the torque (in newtons per meter) produced by the animals, the recorded kilogram force was gravity corrected and converted into newtons and, second, was multiplied by the distance between the load cell sensor and the elbow pivot joint (0.08 m). The monkey initiated a trial by contracting elbow flexors to place the torque within a set window (1.648–3.295 N · m). This window was kept constant in all sessions and for both animals. The torque had to be held in this window for 1 s before releasing to obtain a food reward. Auditory cues were used to indicate to the monkey that the exerted force was within the required window, or else it was too high. Auditory feedback was also given to mark the end of the hold period. Recordings were collected from 10 sessions spanning 30 and 24 d for monkey MI and MA, respectively.

Surgical preparation

After behavioral training was complete, monkey MI underwent a sterile implant surgery. After initial sedation with ketamine (10 mg/kg, i.m.), anesthesia was induced with medetomidine (3 μg/kg, i.m.) and midazolam (0.3 mg/kg, i.m.). The animal was then intubated, and anesthesia was maintained using inhalation of sevoflurane (2.5–3.5% in 100% O₂) and intravenous infusion of alfentanil (0.4 μg/kg/min). Methylprednisolone was infused to reduce edema (5.4 mg/kg/h, i.v.). Blood oxygen saturation, heart rate, arterial blood pressure (using a noninvasive blood pressure cuff on the leg), core and peripheral temperatures, and end-tidal CO₂ were monitored throughout; ventilation was supported with a positive pressure ventilator. Hartmann's solution was infused to prevent dehydration (total infusion rate including drug solutions, 5–10 ml/kg/h). Body temperature was maintained at 37°C using a thermostatically controlled heating blanket and also a source of warmed air. Intraoperative prophylactic antibiotics (cefotaxime 20 mg/kg, i.v.) and analgesia (carprofen 5 mg/kg, s.c.) were given.

In monkey MI, nerve cuff electrodes (MicroProbes) were implanted around the median and deep radial nerves bilaterally and secured with the integral sutures. Each cuff contained eight contacts, arranged as two sets of four wires placed radially around the inner circumference. A plastic headpiece (model TECAPEEK MT CF30, Ensinger) was manufactured based on an MRI scan to fit the skull and was fixed using ceramic bone screws (Thomas Recording) and dental acrylic. Intramuscular electrodes comprising Teflon-insulated stainless steel wires were implanted in eight arm and forearm muscles bilaterally for gross electromyography (EMG) recording. Specifically, the muscles that were implanted with intramuscular electrodes corresponded to the following: deltoids, extensor carpi radialis, extensor digitorum communis, biceps brachii, brachialis, brachioradialis, flexor carpi radialis, and the flexor digitorum superficialis muscle. The EMG and nerve cuff wires were tunneled subcutaneously to connectors fixed to the headpiece. Nine weeks after the first implant surgery for monkey MI, several wires connected to the deep radial nerve cuffs bilaterally were found to be broken, and stimulation through these cuffs was no longer possible. Replacement cuffs (with three contacts each, organized radially around the inner circumference) were then implanted bilaterally on the radial nerve below the spiral groove in a further brief surgery, again with wires tunneled subcutaneously to the head. Monkey MA underwent the implant surgery at a later stage to monkey MI and so was implanted with the same three contact cuffs around the median and radial nerves, along with EMG electrodes in the same muscles and fitted headpiece. All recordings were subsequently collected using the three contact nerve cuffs.

Postoperative care included a full program of antibiotic (co-amoxiclav, dose as given above) and analgesics (meloxicam, 0.2 mg/kg, oral, plus a single dose of buprenorphine 0.02 mg/kg, i.m.).

Nerve cuff stimulation and recording

Biopolar current pulses (0.2 ms/phase) were delivered through the first and third contacts of the three contact radial cuffs with a biphasic constant current isolated stimulator (model DS4, Digitimer). Stimulus current was delivered at supramaximal intensity (monkey MI, 0.45 mA; monkey MA, 0.4 mA) and ramped down in decrements of 0.1 µA to threshold intensity. Left and right arms were stimulated in different sessions, following recordings of the motor task.

Electrophysiological recordings

Recordings were made from the brachioradialis muscle using a high-density surface EMG grid (model GR04MMI305, OT Bioelettronica) with 64 electrodes (spacing, 4 mm). A biadhesive foam strip with holes aligned to the matrix was placed on the grid, and the holes were filled with conductive paste (CC1, OT Bioelettronica). This assembly was then stuck to the skin over the muscle. To ensure good skin contact, the forearm was shaved and cleansed with alcohol wipes. The location of the grid on the skin was marked each day with permanent marker pen to ensure reproducible placement from session to session. Standard surface adhesive electrodes (Neuroline 720, Ambu A/S) were placed over the flexor and extensor tendons at the wrist to act as reference and ground; in the implanted animal (monkey MI), one of the unused nerve cuff electrodes was used as the ground. The surface grid electrode was connected to a custom-printed circuit board containing a 64-channel amplifier (gain, 192; bandwidth, 30 Hz to 2 kHz) and an analog-to-digital converter (model RHD2164, Intan Technologies). Digitized signals were sent over a serial peripheral interface cable to an RHD USB interface board (Intan Technologies). This allowed data to be captured to a computer hard disk (5000 samples/s) along with the elbow torque signal and digital markers signaling the phases of task performance and stimulus timing. Voluntary brachioradialis activity was recorded from the grid electrode during performance of the behavioral task (typically, 100 successful trials/session). Involuntary contractions were recorded by the intramuscular electrodes and the grid electrode during the radial nerve stimulation protocol.

Motor unit decomposition and analysis

The high-density EMG (HDEMG) recordings were digitally filtered offline with a 20–500 Hz Butterworth filter. Semiautomated MATLAB software extracted the area under the power spectrum and the amplitude of each of the 64 channels and highlighted the channels with poor signal-to-noise ratio for visual inspection and exclusion from subsequent analysis. After this procedure, the monopolar signals were used for the decomposition. Identification of the individual motor unit firings was accomplished through a previously proposed algorithm (Negro et al., 2016), modified for these large datasets to use a graphical processing unit running CUDA software (Nvidia).

Briefly, this algorithm takes advantage of the unique two-dimensional (2D) spatiotemporal features of individual motor unit action potentials to converge on an estimate of the motor unit spike trains. The decomposition blindly identifies the motor unit firings; only motor units with high silhouette measure (>0.92 SIL) are initially maintained. SIL represents a qualitative measure of decomposition accuracy that is comparable to the pulse-to-noise ratio, ranging from 0 to 1, where 1 indicates perfect clustering of the motor unit action potential. The blind source separation procedure leverages the high spatial and temporal dimensionality of motor unit action potentials. This information is used to converge in an iterative way in the unique time series representation of the firing times of the alpha motoneurons. We briefly describe here the general steps of decomposition. For a more detailed look into the details of high-density EMG decomposition, the technical and physiological details have been described previously (Farina and Holobar, 2016; Del Vecchio et al., 2020a)

The EMG signal corresponds to the filtering of the motoneuron action potential by the muscle tissue with some added noise. Therefore, it is possible to represent in a mathematical form the signal that is carried by each channel of a multidimensional arrays of EMG signals. The EMG signal can be described as a convolution of the motoneuron discharge timings (sources) by the muscle tissue (muscle unit action potentials). The sources (s) are the motoneuron axonal action potentials when reaching the muscle fibers and can be written as a Dirac δ function, as follows:

$$s_j(k)={\displaystyle {\sum }_r\delta (k-{\phi }_{jr})},$$ (1)

where φ_jr represents the spike times of the jth motor unit. We can then write the EMG signal in a matrix $\underset{¯}{\underset{¯}{x}}$ form (e.g., when recorded with multidimensional arrays such as the high-density EMG grids used in this study) as follows:

$$\underset{¯}{\underset{¯}{x}}(k)={\displaystyle {\sum }_{l=0}^{L-1}\underset{¯}{\underset{¯}{H}}}(1)s(k-1)+\underset{¯}{\underset{¯}{n}}(k),$$ (2)

where s (k) = [s₁ (k), s₂ (k),…, s_n (k)]^T represent the n motor unit discharge times that generate the EMG signal, and n is the noise to for each electrode. The matrix H (l) in Equation 2 contains the spatial information of the motor unit action potential and has size m × 1 with lth sample of motor unit action potentials for the n motor units and m channels (2D format, hereafter referred to as “2D motor unit waveform”). The high spatial sampling given by the 64 electrodes, further enhanced by extending the observation numbers (Farina and Holobar, 2016), allows the recovery of the sources in an iterative blind way with a function that maximizes the sparsity between each motor unit action potential (Fig. 1A). This process is obtained in a fully automatic and blind way; therefore, we can inspect the validity of decomposition by spike-triggered averaging. With spike-triggered averaging, it is also possible to retrieve by correlation analysis the information that is carried by the action potential (H) on different days, in a fully automatic way. By using 2D correlation analysis, it indeed is possible track motor unit waveform across weeks (Martinez-Valdes et al., 2017) and even months (Del Vecchio et al., 2019c). The motor unit tracking uses the information carried in H to compare two-dimensional cross-correlations across sessions and across all possible combinations of motor unit action potentials. The two-dimensional cross-correlation (called “2D correlation” hereafter) is comparable to a one-dimensional cross-correlation, but with a weighted average across the time–space features of the motor unit waveforms (Fig. 1). The output of the two-dimensional cross-correlation ranges from 0 to 1, where 1 indicates maximal similarity. For example, two randomly selected motor units have a two-dimensional cross-correlation of <0.3 (Del Vecchio and Farina, 2019).

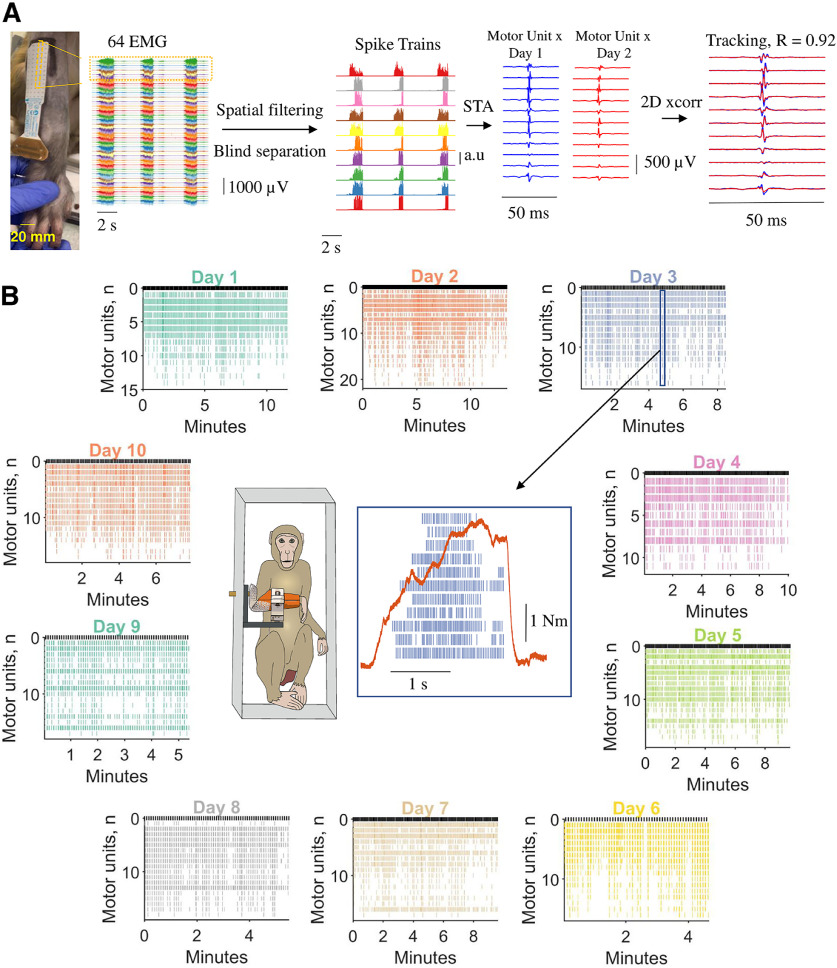
Figure 1.

Motor unit decomposition in awake behaving macaques, experimental framework, and analysis. A, From left to right, 64 monopolar EMG signals during three individual contractions. Each contraction lasted ∼2 s. The monopolar EMG signals were spatially filtered with a double-differential derivation. After this process, blind source separation identified the spike trains belonging to individual motor units. The spike trains for each motor unit were used to spike trigger the average 2D motor unit waveform. The 2D motor unit waveforms were used for the longitudinal tracking, through a 2D cross-correlation function. B, Monkey 1 (MI) individual motoneuron spike trains across the 10 d (color coded). Note that during the different days, we identified a relatively similar number of motor units. The center of the figure shows the experimental setup and an individual voluntary contraction (force signal in red) extracted from day 3. STA, Spike-triggered average. R represents the two-dimensional cross-correlation value.

Motor unit characteristics

We first displayed 2D correlation values for all motor units with R > 0.55 and with a total number of discharge timings (impulses) >100, and visually inspected the waveforms for potential errors. The unique combinations of motor unit waveforms that were preserved after this visual inspection stage had R > 0.70. From all the retained motor units, we computed the instantaneous discharge rate (inverse of the interspike interval) averaged across the hold period for all trials of the task on a given day. Synchronization of the motor unit pool was also assessed, as the magnitude of the cross-correlation between two equally sized groups of motor unit spike trains. The number of motor units in each group was randomly assigned for a total of 100 permutations. For each iteration, two random unique subsets of units were selected for each group (each group being half of the total number of the identified units during a specific contraction). The spike trains (binary signals) for each motor unit group were then summed and smoothed using a Hanning window with two corner frequencies of 40 and 2.5 Hz. We chose two cutoff frequencies because they retain most of the oscillatory activity of the motoneuron pool (40 Hz), and the low frequency is mainly associated to the neural drive that is responsible for force production (i.e., the correlation between a force signal and the low pass-filtered motor unit discharge timings are minimally distorted by the musculotendinous unit).

For the motor unit recruitment threshold estimates, we first looked at the recruitment order (in seconds) of the motor unit during the individual contractions. This was estimated by taking the time point when that unit was active for the first time. We then calculated the average recruitment threshold (in seconds) for all units across all contractions. Afterward, we labeled each unit from 1 to the maximum number of identified units in a specific contraction (i.e., a motor unit takes the value of 1 if it is the first recruited). Then we plotted the recruitment thresholds for each specific unit across all contractions. Because the labeling is not dependent on the average, if there is a correlation between the average recruitment threshold and the binarized recruitment threshold across all contractions, this relationship indicates the amount of flexibility in recruitment order obtained by the nervous system in a direct way.

We then computed the derivative of the motor unit recruitment times (i.e., the recruitment thresholds expressed as time instants). The recruitment time or threshold corresponded to the time of the first spike discharged by a given motor unit. After calculating these recruitment instants for all the motor units in each contraction, they were sorted from the smallest to the largest. The corresponding sorted vector comprised the ordered time instants of recruitment of each identified motor unit. We then computed the derivative of this vector and, therefore, obtained a second vector with elements corresponding to the time intervals separating the recruitment of consecutively detected units. The average of all the elements of this vector represented the average time separating the recruitment of motor units, and the inverse of this number corresponded to the estimated number of motor units recruited per unit of time. For example, if in one contraction there were three identified motor units, one recruited at 10 ms, one at 20 ms, and one at 35 ms, the time intervals separating the recruitment of successive units would be 10 ms (interval between the first and the second identified unit) and 15 ms (intervals between the second and the third). The average of the two intervals is 12.5 ms, and its inverse corresponds to 80 motor units/ms. It is evident that this measure is influenced by the number of detected motor units, which is a limitation of the approach. The number of motor units recruited per second represents an estimate of the efferent drive received by the population of motor units (i.e., a faster recruitment speed of motoneurons results in a faster rate of force development; Del Vecchio et al., 2019b; Dideriksen et al., 2020). We then associated for each contraction the variability in recruitment order, which was calculated as the SD of the binarized recruitment thresholds versus the motor unit recruitment speed (the first derivative of the recruitment thresholds). If there would be an association between these two variables, it would indicate that a faster recruitment (which could be because of higher synaptic input) is associated with a violation in the recruitment order.

Factorization of motor unit activities

We factorized the motor unit discharge timings with a non-negative matrix factorization (NNMF) method Lee and Seung (1999). This method can learn specific features in 2D images such as human face characteristics or sematic properties of a written text with the use of linear algebra. In the context of neural signals, we constrained this method to learn the unique components in the motor unit discharge rates that are responsible for force production. See Figure 5 for the overall architecture for this analysis.

Figure 5.

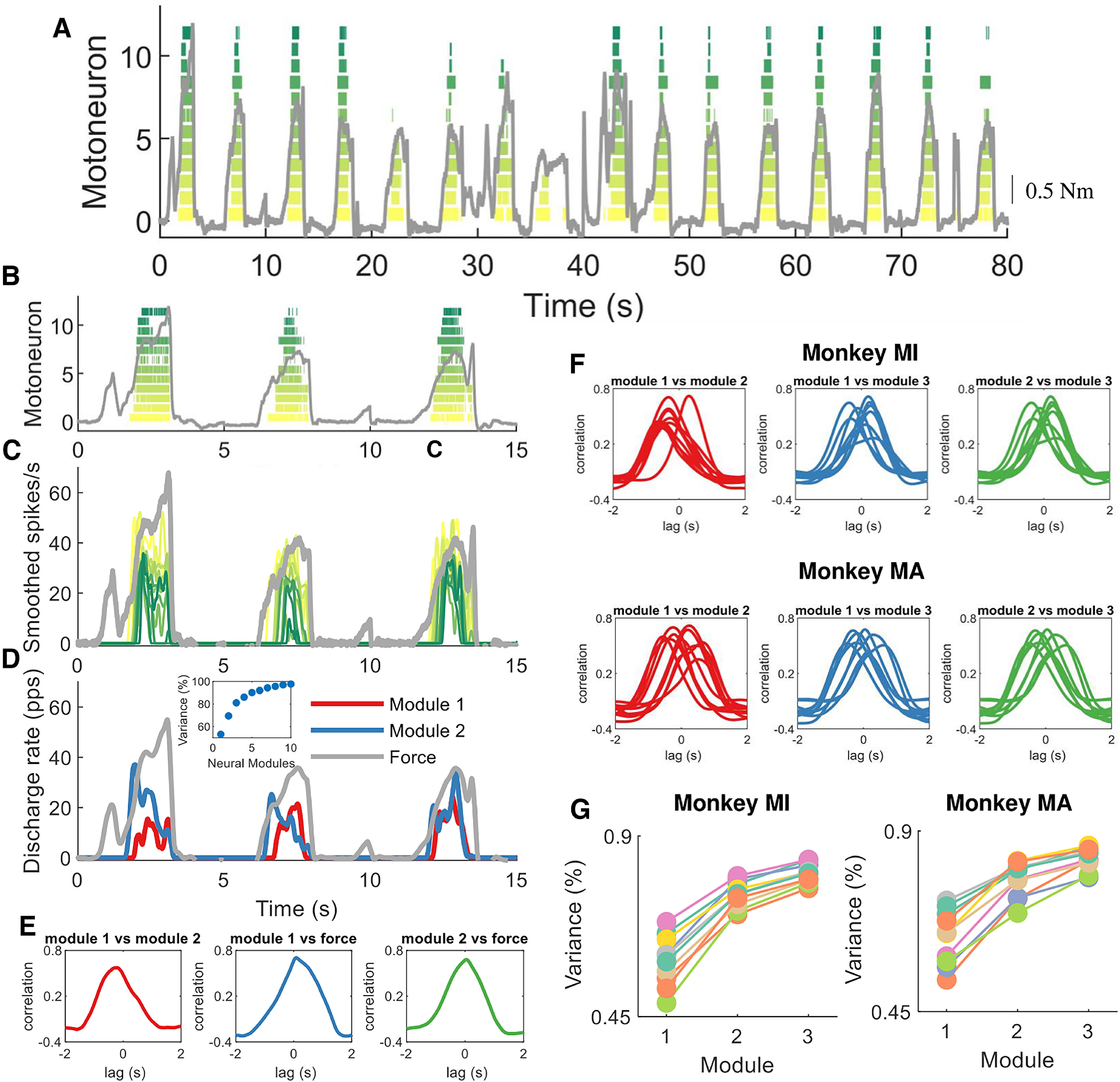
Encoding of muscle force by motor units. We aimed at decoding and encoding the temporal motor unit information into components by non-negative matrix factorization. A, Raster plot of 12 motor units during a subset of macaque voluntary isometric contractions (gray lines indicate the torque signal). Note the variability in peak forces and the rate of force developments. B–D, The first three contractions in A. C, The motor unit spike trains in B were convoluted with a 2.5 Hz Hanning window. Note the high correlation between the motor unit smoothed discharge rates and muscle force. D, We applied the reduction dimensionality technique non-negative matrix factorization. We constrained the model to learn the components in the motor unit discharge rates up to 10 factors. In this example, the two modules that together explained ∼80% of the variance are shown. Note that these two modules are highly correlated, and time shifted. The inset in D shows the reconstruction accuracy (variance percentage) of the neural modules with respect to the original signal (smoothed motor unit discharge rates). E, We applied cross-correlation analysis between the modules and muscle force. This example shows the correlation between the first module and the second module as well with voluntary force. F, The same method was then applied for the three modules in both monkeys. Note the high correlation across all days and for both monkeys. Moreover, there was always one module with a dominant component (the lag between the different modules was never zero). G, This indicates that there is only one component constrained by the size principle, since the motor unit recruitment thresholds are highly preserved across all contractions. The reconstruction accuracy (variance percentage) is explained across the 10 d for both monkeys.

The force level developed by a muscle is driven by the number of motor unit activation signals, which can be represented as time sequences of M-dimensional vectors, which correspond to the activation of the motoneurons m(t) in response to common and independent synaptic inputs arising from afferent and efferent volleys. Therefore, we can express the motoneuron behavior as combinations of N varying synaptic inputs that construct a specific motor unit firing characteristic, or neural module, expressed as {w_i(t)}_i=1, N, as follows:

$$m(t)={\displaystyle \sum _{i=1}^N{c}_i}{w}_i,$$

where c_i is a non-negative scaling coefficient of the ith neural module. We are interested in finding the w_i vectors within the low-frequency motor unit discharge rates. Because motor unit firing rates are non-negative, we can use NNMF (Lee and Seung, 1999) to constrain w_i to be non-negative. This procedure maximizes the interpretability of the data since the representation of the neural motor unit ensemble only includes additive and not subtractive combinations, therefore, having an output module with the same scale as the input signal. NNMF iteratively finds the non-negative factors W and H with an interactive procedure that minimize the residuals between D (the sources) and W * H, so that W * H is a lower-rank approximation of the firings of the individual motor units (D). The firing of the individual motor units is stored in a matrix with rows equal to the number of identified motor units and with columns having the duration of the recording. The motor units are initially stored as a function of Dirac δ, δ(k-φ_jr), and then low pass filtered at 2.5 Hz (see Fig. 6). NNMF is an iterative algorithm that starts with random initial values of W and H. Because the root mean square of D can have local minima, we performed up to 1000 iterations to converge to a representative reconstruction of D = W * H.

Figure 6.

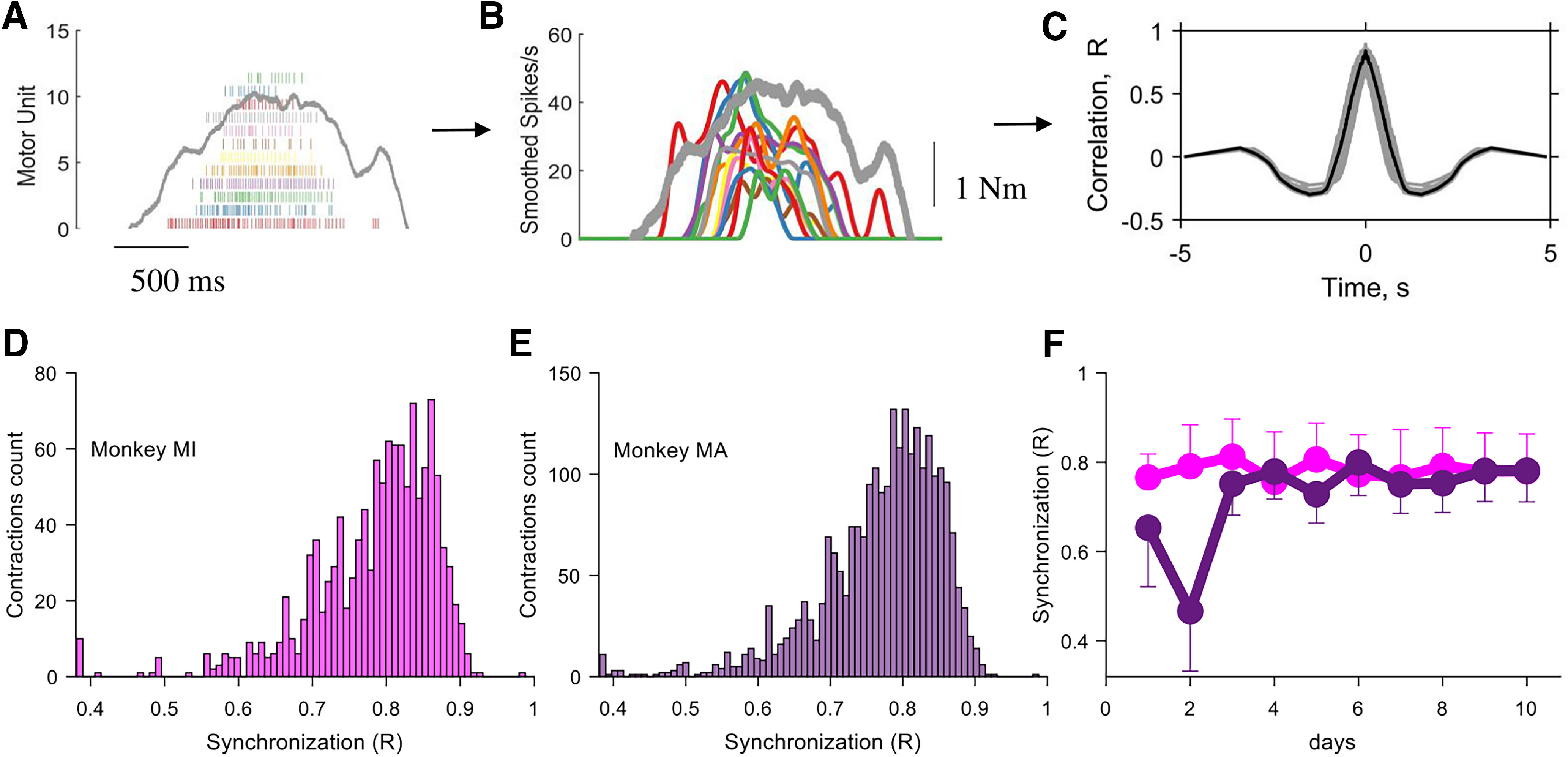
Motor unit synchronization across the different contractions for monkeys MI and MA (color coded). A–C, Pipeline for the estimate of motor unit synchronization for an individual contraction. A, Raster plot of 12 motor units (gray indicates the torque with the scale shown in B). B, The discharge timings of the motor units were filtered with a Hanning window of 200 ms. C, The synchronization value was obtained by performing the cross-correlation function between two groups of randomly permutated groups of motor units (number of permutations, 100). Note that the synchronization value was relatively high and comparable to what was observed in humans during rapid force contractions. D, E, Histogram of the synchronization value across the individual contractions for both monkeys. F, The synchronization value was stable across the 10 d (average and SD values for each day are shown). For monkey 2, the first 2 d resulted in a lower synchronization value because of a lower number of identified motor units, as shown previously. Note that the small variability in synchronization value in D and E was fully explained by the instantaneous discharge rate of the motor units, as previously shown (de la Rocha et al., 2007; Del Vecchio et al., 2019b).

We then evaluated the output of NNMF with different decoding–encoding functions. First, we constrained the number of factors equal to the number of identified motor units across a specific day. After this initial procedure, we consistently found that >10 factors explained 99% of the variance. The reconstruction accuracy (residual variance or variance explained) was calculated by computing the residuals (D – W * H) and then computing the deviation from the mean (R²). Second, we evaluated the decomposition by looking at the decoding–encoding of the individual neurons with the respect to the matrix W. This analysis was computed by performing the cross-correlation between the low pass-filtered motor unit discharge rates (D) and the individual neural modules (W) extracted by NNMF. The same method was applied on the gross EMG signals from the intramuscular electrode. After rectification and averaging, the average EMG signals for each day were processed by NNMF and the residual variance was calculated in the same way for the motor units [see Fig. 7, results and analysis of the intramuscular EMG (iEMG) signals]. All of the analyses were performed in MATLAB.

Figure 7.

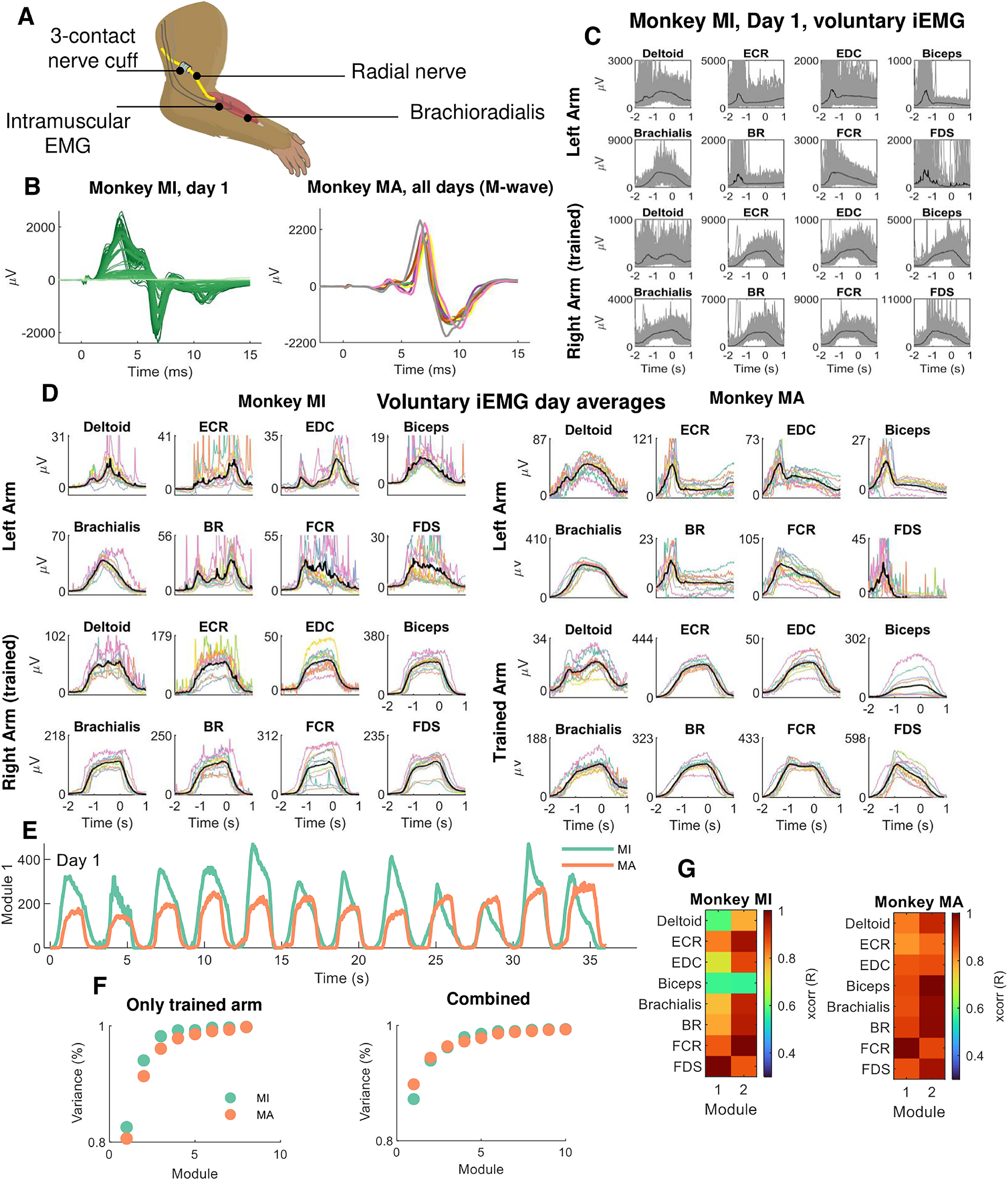
Neuromuscular implants in macaques. A, Both monkeys were implanted bilaterally with a nerve cuff around the median and radial nerves. Implanted intramuscular EMG signals recorded the gross myoelectric activity of 16 muscles bilaterally (8 muscles per side). B, During each experiment, the nerve cuff delivered stimulation pulses at supramaximal intensity (M-waves) and ramped down in small decrements of 0.1 µA. The left side of B (dark green lines) shows the iEMG recording sessions from supramaximal intensity to the smallest intensity (light green). On the right side of the panel, 12 M-waves obtained during the different days (color coded). C, The iEMG signals from the voluntary contractions during one experimental session. Individual contractions as well as the average (black line) are shown. Note the high intertrial variability in gross EMG responses. D, The average iEMG traces across days (color coded), for monkeys MI and MA. E, Non-negative matrix factorization analysis applied to the gross iEMG signals. The neural module that explained most of the variance is shown for each monkey. F, The reconstruction accuracy (variance percentage) of the components extracted by NNMF. Note that one component explained >80% of the variance. G, The cross-correlation of the first two modules for the respective muscles.

Statistics

Motor unit waveforms were compared via the 2D cross-correlation analysis with the MATLAB function xcorr2. The bivariate correlation level between the longitudinally tracked motor units discharge characteristics across the different days was computed with Pearson's correlation coefficient, and the p-value was corrected with Bonferroni's method. The same test was used for studying the association between the motor unit amplitude value and recruitment threshold. The neural module correlation values across days and muscles extracted from the motor units or intramuscular EMG signals corresponded to the output of the cross-correlation value (MATLAB function xcorr).

Results

Motor unit decomposition and tracking

We describe the strategies of control of macaque motor units and evaluate the performance of a new noninvasive neural interface framework to monitor the changes in the number and properties of longitudinally tracked units over 10 experimental days (gathered over 1 month) in two animals.

We decomposed spike trains of individual motor units from high-density EMG signals using blind source separation techniques (Fig. 1A; for details, see Materials and Methods). After this process, the spike trains belonging to each decomposed motor unit were used to estimate the average 2D waveform of the corresponding action potentials (Fig. 1A, one column of the recording grid). The motor unit waveforms were used to track the same motor unit with a 2D cross-correlation function (Del Vecchio and Farina, 2019; Del Vecchio et al., 2020b). Figure 1B shows the raster plot of all motor units across the 10 d for monkey MI. The y-axis in Figure 1B shows the total number of identified motoneurons across days (color coded). The middle panel of Figure 1B shows an example of force signal and raster plot of the motor units during a contraction.

On average, each recording session (one per day; total, 10 d) lasted 9.8 ± 2.5 min (monkey MI) and 8.6 ± 2.8 min (monkey MA). During these sessions, the monkeys performed on average 118.0 ± 30.1 (monkey MI) and 103.5 ± 33.9 (monkey MA) contractions, which were used for the subsequent EMG analyses. The monkeys were instructed to reach a target without specific training on the rate of force development. Therefore, we obtained a relatively large variance in the rate of force development and motor unit recruitment speeds across contractions. During these contractions, the rate of force development ranged widely, with an average ± SD of 6.44 ± 4.00 N · m · s⁻¹ (range, 1.86–38.66 N · m · s⁻¹). Moreover, the peak force obtained across days also showed high variability, spanning twofold maximum EMG amplitudes.

We identified a total of 389 motor units (monkey MI, 192; monkey MA, 197) in the individual recordings. Of these, only a subset (Fig. 2) could be tracked and reliably matched with a unit from ≥1 different days on the basis of a two-dimensional correlation coefficients R > 0.7 (for details, see Materials and Methods). The mean ± SD numbers of identified motor units for each experimental session were 19.2 ± 2.97 and 19.7 ± 2.4, for monkeys MI and MA, respectively. We were able to track on average 9.07 ± 1.06 and 8.13 ± 2.08 motor units across all 10 d. Figure 2 shows the total number of identified motor units on each day and the number of tracked motor units across sessions for the two monkeys. The top panel of Figure 2 shows examples of 2D and 3D motor unit waveforms as well as the total number of motor units across contractions and days (Fig. 2F–I, bottom). Figure 2F–I depicts the total number of motor units decomposed on each day for both monkeys. Figure 2G–I (right panels) shows the individual motor units that were tracked across the different days (all possible combinations). Note that the largest number of units in these bar plots correspond to the units recorded during the examined day, which are highlighted with a black-edged bar (Fig. 2G,I). The number of the tracked units across days was lower than the total number of identified motoneurons (on average, 19.45 vs 8.60) because small changes in the proportion of recruited motor units challenge the tracking procedure. We previously obtained a very similar result in humans (Del Vecchio and Farina, 2019) because of different target forces and day-to-day variability.

Figure 2.

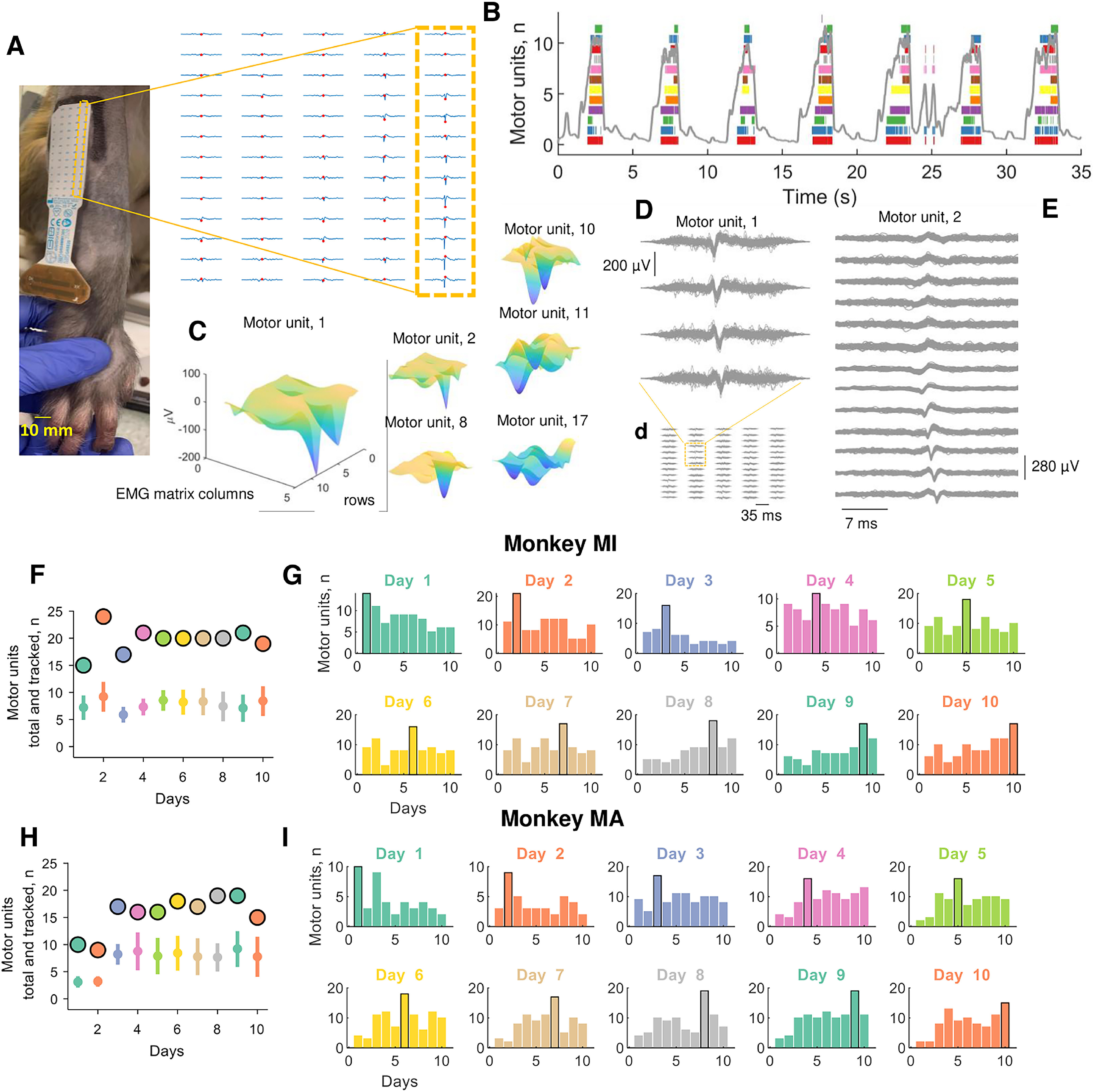
Motor unit action potentials and total numbers of identified and tracked motor units across the 10 d (color coded). A, Two-dimensional motor unit action potential propagating under the high-density EMG electrode array. The highlighted yellow inset shows the respective column and row of the high-density EMG matrix during the experiment on the brachioradialis muscle. B, Raster plot of 12 identified motor units (color coded) for seven representative contractions. C, Three-dimensional representation of the motor unit action potential in a specific time instant (highlighted with a red dot in A). Note that each action potential has a unique 3D signature that allows the independent component analysis to converge to the time series of discharge timings of the motor unit. D, Shimmer plots for two action potential waveforms. Each action potential was averaged across an individual contraction and then superimposed across all contractions for a specific day. Note the high similarity across channels for two representative motor units. The left side of the figure shows four EMG channels corresponding to the largest amplitude across the full 64 EMG electrodes, which are shown in d and a. On the right side, E shows a full representative column of the grid (13 monopolar EMG signals). F, H, The total number of identified motor units across the 10 d (black-edged circles) and tracked motor units (open circles with vertical line depicting the SD) for monkeys MI (F) and MA (H). G, I, Bar plot of the number of motor units that were successfully tracked across the 10 d (color coded). Note that the black-edged bar plot corresponds to the number of motor units that were identified at the respective day and used for tracking those motor units in the other days.

Despite the number of tracked motor units being lower than the number of identified motor units, the discharge characteristics of the tracked motor units was highly correlated across sessions over the full duration of the experiments (∼1 month), as described in the following section.

Motor unit identification validity

The motor unit action potential similarity across sessions was assessed with the 2D cross-correlation function (for details, see Materials and Methods). Because the motor unit action potential waveform and motor unit discharge characteristics are independent, we first computed quality measures of decomposition based on the action potential waveform, and successively we computed correlation measures between the firing characteristics of the tracked motor units (discharge rate and recruitment threshold across days).

The consistency of each motor unit action potential that was accepted to belong to the same cluster, was very high (silhouette measure averaged across all the identified motor units and the 10 d, 0.91 ± 0.01 and 0.92 ± 0.01, respectively, for monkeys MI and MA). Silhouette measures >0.9 have been associated with highly accurate decomposition with respect to intramuscular EMG signals (Negro et al., 2016). Moreover, the tracked units across sessions exhibited very high 2D correlation coefficients of the motor unit waveform (>0.7 for the tracked units) and similar discharge rates across the different days. Figure 2D shows the action potentials that were spike trigger averaged across the individual contractions (all the action potentials for a representative contraction were used to generate the motor unit action potential waveform, across all 64 channels). The variability in the action potential waveforms across contractions for the same day were minimal, with 2D correlation values of action potentials always >0.9. This indicates very high reliability in identifying the same motor unit across contractions.

Physiologic characteristics of macaque motor units

Figure 3 shows the discharge characteristics of the tracked motor units across and between days. The interday motor unit discharge rate variability was very low, at 3.51% and 5.41% for monkeys MI and MA, respectively. For monkey MI, the bivariate Pearson correlation coefficients between the average discharge rate across the different days were significant in all cases (p < 0.001 after Bonferroni's correction; Fig. 3A,B). Indeed, the absolute differences in discharge rate across the units over the different days (Fig. 3C) was very low (0.14 ± 3.45 spikes/s). For monkey MA, the results were similar, although with a smaller number of reliably decomposed motor units during the first 2 d (Fig. 2B), which resulted in poorer tracking performance during those 2 d (Fig. 3D,E). However, the lower number of motor units did not change the performance of the tracking algorithm and discharge characteristics of the units. There was a very small variability in discharge rate of the tracked units and corresponded to 0.09 ± 3.12 spikes/s, with an average discharge rate across the 10 d for all the identified motor units of 41.77 ± 1.46 and 38.42 ± 2.07 spikes/s, for monkeys MI and MA, respectively.

Figure 3.

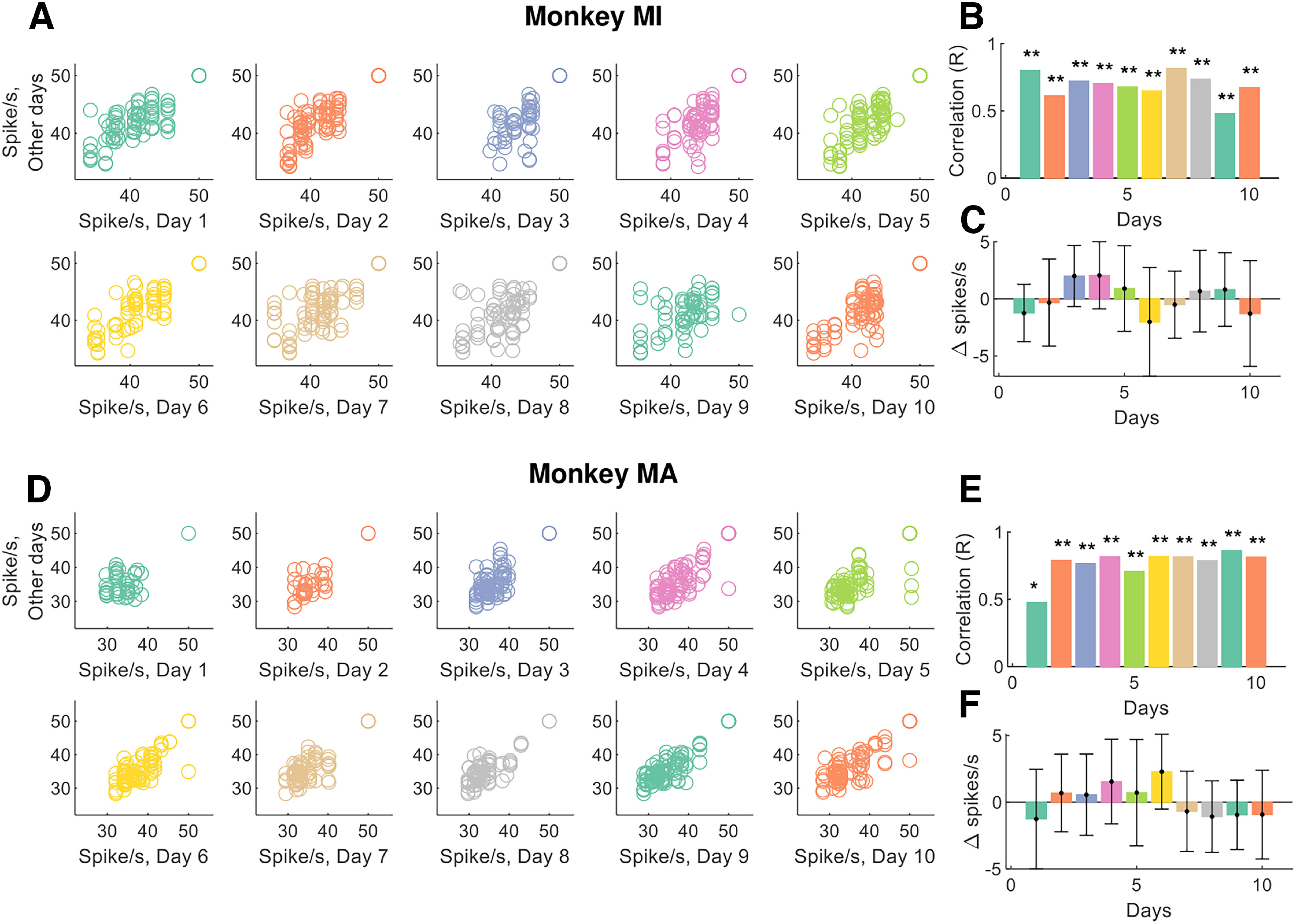
Motor unit discharge characteristics for the tracked motor units. A, The average instantaneous motor unit discharge rate was plotted for all tracked motor units at any given day. Note that some motor units may show different discharge rates because of changes in synaptic input. B, The day-to-day variability was very low (<6%), and this low variability is demonstrated by very high correlation values for the tracked motor units. C, The absolute variability in the discharge rate of the tracked motor units (i.e., the average motor unit discharge rate at day 1 minus the discharge rate of the same motor unit in the other days). Note that this correlation can be significant only if the motor units are tracked successfully, since the motor unit discharge rate shows high variability across the different units (see the figures below). D–F, The same plots as in A–C for monkey (MA). *p < 0.01, **p < 0.001.

The recruitment order across the 10 experimental sessions was occasionally violated for motor units with very close recruitment thresholds (Fig. 4A–D). In these cases, the occasional reversals of recruitment order were highly correlated with the speed of recruitment (and therefore with the rate of force development; Fig. 4D). With very fast recruitment, the difference in threshold between motor units with close recruitment threshold compresses to very small values so that the variability in synaptic input may likely explain the occasional reversals (that happened in a small range).

Figure 4.

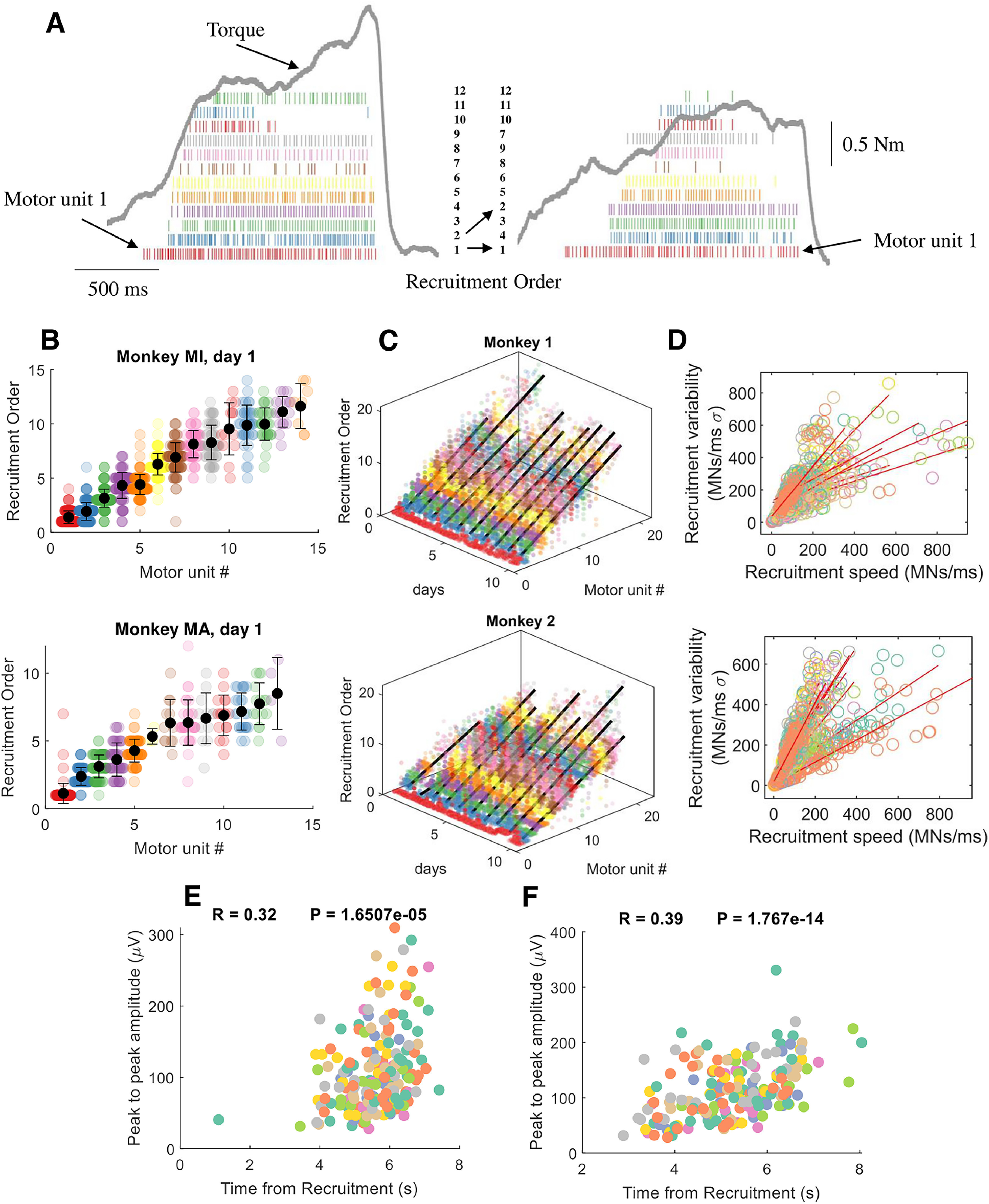
Motor unit recruitment thresholds and intervals across different contractions, motor units, and days. A, For each motor unit, we calculated the shifts in recruitment order with respect to the average recruitment threshold of that unit. The motor units in the two contractions in A are color coded with respect to the recruitment threshold in the first contraction. For example, it is possible to observe the shift in the recruitment order of 2 to 4 in the second contraction. However, these changes only happen for motor units with very similar thresholds. For example, the motor unit (1 in left panel; red), and the highest threshold motor unit (12; green) shows a consistent recruitment order. This can be well appreciated in the following figures when showing the motor unit recruitment order with respect to the average across the specific day. B, Swarm plots of the recruitment order across all motor units. We first computed the recruitment threshold as the first spike of the motor unit during a specific contraction. We then averaged the recruitment threshold across all contractions for the specific motor unit that was tracked across all contractions (each dot in the swarm plot represents the recruitment threshold of a motor unit in an individual contraction). The average recruitment threshold was then used to sort the recruitment interval of all motor units. Note that each motor unit shows a stable behavior across all contractions. C, Three-dimensional swarm plot for all the motor units across the 10 d. For both monkeys, the relationship between recruitment order and motor unit number was linear across the 10 experimental sessions spaced over a month (monkey MI, R = 0.88 ± 0.04; monkey MA, R = 0.88 ± 0.04; p < 0.00001). D, The variability in recruitment order across days and contractions was highly correlated with the recruitment speed of motoneurons. The recruitment speed of motoneurons is an estimate of supraspinal drive and corresponds to the time derivative of the first discharge timings of all motor units during an individual contraction. Each regression line in D shows the variability across contractions for a specific day. Note the high variability in recruitment speed, which indicates the variance in rate of force development across the contractions for a specific day. E, F, Recruitment threshold versus peak-to-peak amplitude of the motor units for monkey MI (E) and monkey MA (F). Each color represents 1 d, and the peak-to-peak amplitude is calculated after spike trigger averaging the high-density EMG signal from the firings of the individual units. The final peak-to-peak value corresponds to the average of the column with the highest activity in the electrode grid. The correlation coefficient is calculated after pooling all days and motor units.

The present results are in accordance with previous human and in vitro experiments indicating that motor units are recruited in a specific order. Moreover, the motor unit recruitment thresholds were positively correlated with the peak-to-peak amplitude of the corresponding motor unit action potentials (Fig. 4E,F). Although with important limitations, the action potential amplitude is associated with the size of the motor units (Milner-Brown et al., 1973a; Milner-Brown and Stein, 1975; Del Vecchio et al., 2017). As expected, the association between recruitment threshold and amplitude showed very high variability because the motor unit size is only one of the factors of influence of action potential amplitude, as previously discussed (Farina et al., 2014a; Del Vecchio et al., 2017). We therefore wanted to understand whether there are specific patterns in the motor unit discharge timings that control the recruitment and muscle force. We applied a non-negative matrix factorization analysis (Lee and Seung, 1999) to the motor unit discharge timings. Because of the large amount of motor unit data, we were able to discern the exact patterns common to all and to subgroups of motor units.

The non-negative matrix factorization revealed a principal component that explained ∼50% of the variance. There was a significant second factor that explained ∼25% of the variance. Interestingly, this second module was an undistorted, time-shifted version of the first component. We then performed correlation analysis between all the components (total, 10; see Materials and Methods) and looked at the specific weight distributions across the individual motor unit recruitment thresholds. We found that these components were consistently time shifted and with very high correlation values between each other (Fig. 5F). The temporal order of the modules depended on the motor units represented in each module. Modules representing mainly low-threshold units occurred earlier in time than modules representing higher-threshold units. The order in which the modules were extracted by NNMF depended on the variance explained by each module, which was determined by the relative number of low-threshold and high-threshold units detected by decomposition. Thus, the labeling of module 1 or 2 was not fixed in relation to the time of activation of the module. Figure 5F shows the cross-correlation value and time lag between the first two modules for various contractions. The time lags identified with this analysis were both positive and negative, according to the way the modules were extracted. In all cases, the modules occurring earlier in time represented threshold units lower than those in the other modules.

These results indicate that motor unit discharge rates during voluntary tasks in macaque monkeys are driven by one dominant command, which manifests in time-shifted form because of the progressive recruitment imposed by the size principle (Fig. 4). Because the motoneuron is a nonlinear system, the ensemble activity strongly indicates that these common fluctuations must originate from common input from cortical, afferents, or brainstem pathways. We provide strong evidence that a main component drives a pool of macaque brachioradialis motor units that is mediated by the recruitment order of the motor units.

Motor unit synchronization

It has been reported that the discharge timings of spinal motor units show very high synchronization values (De Luca and Erim, 1994), which are associated with the generation of muscle force (Feeney et al., 2018). Accordingly, we found high values of motor unit synchronization similar to what is typically observed in humans (Del Vecchio et al., 2019c). We analyzed synchronization in two frequency bandwidths: one that retains most of the information of the corticospinal pathways (0–40 Hz; Baker et al., 2003); and a narrowed one (0–5 Hz), which retains the information that is correlated to force generation (corresponding to the muscle low-pass filtering bandwidth, <5 Hz; Baldissera et al., 1998). The cross-correlation values for the low pass-filtered signals (5 Hz) at lag 0 was 0.78 ± 0.01 and 0.72 ± 0.10 for monkeys MI and MA, respectively. The values across the different bandwidths were consistently very high. These values also showed very small deviations across the contractions (1.55% and 2.30% for monkeys MI and MA; Fig. 6). Interestingly, the value of synchronization was in the highest portion of the range observed in humans (R = 0.5–0.8).

The high correlation further indicates that the motoneurons likely received a strong common excitatory synaptic input and that this input was stable across days (Fig. 6F).

Variability of motor commands are distributed within and between motor unit pools and have a common supraspinal origin

The previous results indicated that, despite a large range of values in rate of force development and motor unit recruitment discharge characteristics, the general motor control scheme shows high reliability in the recruitment order and neural output of brachioradialis motor units. We also monitored the activity of other muscles involved in the tasks to see whether the behavioral variability across trials and days observed in the motor units from HDEMG signals is also observed in the iEMG recordings. We implanted 16 iEMG electrodes into the muscles of the left and right arms (Fig. 7) and nerve cuffs around the median and radial nerves. The recordings from the iEMG signals were performed for the voluntary force contractions as well as for the involuntary stimulated contractions (Fig. 7A,B). We investigated the full bandwidth of efferent and afferent volleys with small changes of electric currents applied on the axon, until maximum efferent activation (Fig. 7B, M-wave).

The potentials evoked by electrical stimulation showed high reliability across days, with negligible deviations around the mean (Fig. 7B). This demonstrated stability of the recordings over days. On the other hand, the voluntary EMG amplitudes showed very high variability (Fig. 7C,D), with some muscles (including the brachioradialis) showing a twofold difference in maximal amplitude. This indicated relatively large variability in the way contractions were executed.

We then applied the same method for the identification of motor unit components (Fig. 5) to identify the neural modules within the muscles, as classically referred to as muscle synergies (D'Avella et al., 2003; Ivanenko et al., 2004; Tresch et al., 2006). We found one invariant neural component that explained more than ∼90% of the variance (Fig. 7E,F). This component was present either in the iEMG signals only from the trained limb or in the combined iEMG signals from both limbs (Fig. 7F). Figure 7G shows the module correlation distribution across all muscles. It can be seen that all muscles are highly correlated with the main dominant module, with the second module representing a distorted, time-shifted version of the first. This result further supports the role of a common input that is distributed between and within motor nuclei that are processed by the size principle and spinal cord circuitries, despite the large variability in the muscle activities.

Discussion

We have proposed a noninvasive method based on wearable sensors to monitor spinal motoneurons in nonhuman primates that surpasses previous invasive methods in terms of performance (number of motor units), accuracy, and the possibility to track units over time. With this method, we reveal an accurate representation of the strategies used by the nervous system to control motor units and muscle force. We reveal that despite the high number of dimensions observed in motor cortex, the control of muscle force results from fixed recruitment and the discharge rate of spinal motoneurons that are largely independent of time and contraction speed.

The condensed spatial dimensions given by the high-density grids allowed us to identify the same motor units in two macaque monkeys performing voluntary isometric contractions across several experimental sessions. The access to populations of motor units and their longitudinal tracking provides a framework to study the changes in the recruitment of spinal motoneurons and rate coding during voluntary tasks. With respect to intramuscular recordings, these noninvasive approaches provide stable signals even during fast contractions (Del Vecchio et al., 2019b), a greater number of decoded motor units (Negro et al., 2016), and the possibility to track the same motor units over multiple experimental sessions across days (Martinez-Valdes et al., 2017) and weeks (Del Vecchio and Farina, 2019). These approaches have been developed and extensively validated in humans (Negro et al., 2016; Del Vecchio and Farina, 2019; Del Vecchio et al., 2019a). Here, for the first time, we show a noninvasive framework for decoding and longitudinally tracking relatively large populations of spinal motor neurons in behaving monkeys.

We found relatively high motor unit discharge rates in macaque monkeys (41.7 ± 1.4 and 38.4 ± 2.0 spikes/s for monkeys MI and MA, respectively, across the 10 d). These discharge rates were higher than those observed in isometric contractions at low and moderate forces in humans (<50% of maximal voluntary force, <30 spikes/s; Del Vecchio et al., 2019a). Conversely, when related to fast human isometric contractions of the tibialis anterior muscle, the observed rates are similar (40.09 and 42.85 spikes/s, for the nonhuman and human motor units, respectively; Del Vecchio et al., 2019b).

The discharge timings of the motor units represent the neural code that generates muscle force. Recordings of motor unit activity during voluntary force contractions allow us to test the recruitment of motor units by the CNS in a detailed way, clarifying current debates in motor control. It has been debated for decades whether the common motoneuron fluctuations observed at the motor unit level are an epiphenomenon or have a functional origin. Similarly, the Henneman's size principle has been constantly under investigation, because of the lack of in vivo evidence with contractions at different rates of force development (Harrison and Mortensen, 1962; Basmajian, 1963; Stephens et al., 1978; Duchateau and Enoka, 2011; Dean et al., 2014; Marshall et al., 2021). These problems arise because of the lack of adequate methods.

Previous evidence showed that motoneurons are recruited according to the size principle (Henneman, 1957). This implies that for a given synaptic input, motoneurons are recruited according to intrinsic properties (De Luca and Erim, 1994). However, some current and previous studies suggest a flexible control of spinal motor units in the mammalian nervous system (Basmajian, 1963; Marshall et al., 2021), so that a strict recruitment order is seen as a special case of a flexible control. According to this view, it is conceivable that variability in recruitment may occur over multiple experimental sessions where the monkeys are instructed to reach a target force level according to a broad range of contraction speeds. Contrary to this idea, we found a consistent recruitment order of motor units that was maintained across contractions and days (Fig. 4).

There are some reports showing violations of the size principle in humans (Nardone et al., 1989) which have been associated with the nature of the task. For example, Nardone et al. (1989) reported a selective recruitment of high-threshold motor units during lengthening muscle contractions. However, several other investigators failed in identifying differences in recruitment order when comparing lengthening and shortening contractions during a vast range of experiments (Garland et al., 1996; Søgaard et al., 1996; Kossev and Christova, 1998; Stotz and Bawa, 2001; but for a complete detailed discussion, see Heckman and Enoka, 2012). A recent work in macaques, recording motor unit activity during several voluntary movements at different joint lengths, showed results partly different from those of the present study (Marshall et al., 2021). Although the methods and behavioral tasks in the two studies differ, we cannot exclude the possibility that some motoneurons innervating the same muscle may receive more than one common input. Alterations in joint length indeed involve different synergistic activations of muscles so that motoneurons may receive multiple common inputs (Desmedt and Godaux, 1981). In the present study, we show a consistent recruitment order in the brachioradialis muscle during a one-dimensional motor task. Marshall and colleagues recorded from the shoulder muscles during different motor tasks and joint angles. Desmedt and Godaux (1981) recorded from the same motor units in two synergistic muscles during tasks at different joint angles and found some violations in recruitment order but for a very small proportion of motor units. Similarly, in human intercostal muscles, recruitment of the motor units is dictated by a principle of neuromechanical matching, rather than by the size principle, so that the neural drive is higher in the muscles with the greatest mechanical advantage for inspiration (Butler and Gandevia, 2008). These examples indicate that the observation of the size principle of recruitment during natural tasks is necessarily linked to the presence of common synaptic input to the analyzed group of neurons. When inputs to motoneurons are nonuniform, the intrinsic excitability of each neuron plays a relatively smaller role in recruitment. Accordingly, the recording of motoneuron activity in fish showed that the size principle is dictated by the strength of synaptic currents and not by intrinsic motoneuron properties (i.e., input resistance; Gabriel et al., 2011). There are reports showing that at higher swimming speeds there is a preferential synaptic input current to larger motoneurons (Kishore et al., 2014).

Here we showed that the neural drive to the muscle is highly structured in a hierarchical fashion. We found strong associations between hierarchy and behavior, so that for a given common input signal, the motoneurons behave synchronously once they reach their threshold to discharge, likely dictated by the intrinsic motoneuron properties. Our results are in strong accordance with simulations suggesting that the spinal cord decodes inputs from descending pathways by modulating the recruitment and derecruitment of motoneurons (Watanabe and Kohn, 2015). The factorization analysis applied to individual motor unit discharge timings and gross intramuscular EMG signals from the trained and untrained limb revealed that one component explained >80% of the variance. The motor unit findings revealed that this component is filtered by size principle. Our results demonstrate the interplay between common synaptic input and size principle. While in some task conditions more than one component may be observed (i.e., more than one common input; Del Vecchio et al., 2022), we believe that the projection of inputs to motoneurons is strongly constrained by delivering common components to groups of motoneurons, rather than controlling motoneurons that are fully flexible and independent of each other (Formento et al., 2021; Marshall et al., 2021).

In conclusion, we presented a new noninvasive framework to decode populations of single spinal neural cells in macaque monkeys, which allows us to move from simple measures of behavior (force) to the inputs that determine that behavior. In addition to being noninvasive, this framework identifies the same motor units across months over the full force range. This is critical since inferring the patterns of motor behavior by random sampling of a small population of active units may be inadequate (Milner-Brown et al., 1973a; Mantel and Lemon, 1987; Lemon et al., 1990; Lee et al., 2011; Marshall et al., 2021). We anticipate that this approach may find further utility when combined with invasive recordings of central motor circuits, which can provide direct access to the various putative sources of a common drive (Witham et al., 2007; Williams et al., 2010; Soteropoulos et al., 2012).