Abstract
Electrical manipulation of spins is essential to design state-of-the-art spintronic devices and commonly relies on the spin current injected from a second heavy-metal material. The fact that chiral antiferromagnets produce spin current inspires us to explore the magnetization switching of chiral spins using self-generated spin torque. Here, we demonstrate the electric switching of noncollinear antiferromagnetic state in Mn3Sn by observing a crossover from conventional spin-orbit torque to the self-generated spin torque when increasing the MgO thickness in Ta/MgO/Mn3Sn polycrystalline films. The spin current injection from the Ta layer can be controlled and even blocked by varying the MgO thickness, but the switching sustains even at a large MgO thickness. Furthermore, the switching polarity reverses when the MgO thickness exceeds around 3 nm, which cannot be explained by the spin-orbit torque scenario due to spin current injection from the Ta layer. Evident current-induced switching is also observed in MgO/Mn3Sn and Ti/Mn3Sn bilayers, where external injection of spin Hall current to Mn3Sn is negligible. The inter-grain spin-transfer torque induced by spin-polarized current explains the experimental observations. Our findings provide an alternative pathway for electrical manipulation of non-collinear antiferromagnetic state without resorting to the conventional bilayer structure.
Subject terms: Spintronics, Magnetic properties and materials
Under an applied current, chiral antiferromagnets, such as Mn3Sn, can produce a spin-polarized current. Here, by varying the thickness of a buffering layer, the authors show that this spin-polarized current can drive self-induced switching in polycrystalline Mn3Sn.
Introduction
Recently Mn3X (X = Sn, Ge, Ga, Rh, Ir, Pt) based non-collinear antiferromagnets (AFMs) have attracted significant attention1–8 due to their large anomalous Hall1,2,4,5, anomalous Nernst6, and magneto-optical Kerr8 effects and importantly, all these effects are accessible via a moderate magnetic field. In addition, these non-collinear AFMs also host a wide range of exotic phenomena from magnetic Weyl fermions9,10, to ferroic ordering of cluster octupole moment11, spin-polarized current12,13, and magnetic spin Hall effect14. These exciting findings show that the chiral-spin structure and the resultant Berry curvature affect profoundly the charge and spin transport properties and make the Mn3X-based AFMs not only appealing for fundamental studies of the interplay between magnetism and topological electronic states15,16 but also promising for AFM-based spintronics17–23.
For practical applications, it is important to prepare thin films using commonly available deposition techniques such as sputtering and demonstrate the possibility of electrical manipulation of the non-collinear AFM state, both of which have been reported by several groups recenly24–32. Notably, Tsai et al.31 have demonstrated deterministic switching of the AFM state of Mn3Sn polycrystalline films in Mn3Sn/heavy metal (HM) bilayers with a bias field applied in the current direction, and showed that the sign of Hall voltage change caused by the AFM state switching is determined by both the relative directions of the current and bias field and the sign of spin Hall angle of the HM layer. The polycrystalline film consists of crystal grains with different orientations, and the AFM state switching was found to occur mainly when the kagome plane is perpendicular to the current and parallel to the polarization direction of the spin current injected from the HM layer, which is also confirmed by Takeuchi et al.32 in epitaxial Mn3Sn/HM bilayers. In addition, Takeuchi et al.32 have observed field-free chiral-spin rotation of non-collinear AFM state in the epitaxial bilayer, and found that the threshold current density for spin rotation is much smaller when the spin current polarization is perpendicular to the kagome plane as compared to the in-plane configuration. Both findings corroborate the spin-orbit torque (SOT) scenario, i.e., the injection of spin Hall current from the adjacent HM layer is responsible for the magnetization switching or chiral-spin rotation. The realization of spin manipulation in AFM/HM bilayers will certainly facilitate its integration with the ferromagnet (FM)-based spin-orbitronics as both employ the same bilayer structure. However, apart from externally injected spin current, the non-collinear spin structure can also produce transverse spin current and longitudinal spin-polarized currents inside the AFM itself12–14. These self-generated spin currents are equally important in electrical manipulation of the non-collinear AFM states, particularly in polycrystalline samples, but their roles are unrevealed in previous studies31,32.
Here we demonstrate current-induced deterministic switching of AFM state in Ta/MgO/Mn3Sn/MgO/Ta multilayers in which the thickness of MgO is varied from 0 to 6 nm to control spin current injection from the Ta layer. Clear current-induced switching is observed at all MgO thicknesses investigated, and interestingly, the switching polarity reverses when the MgO layer is sufficiently thick (>~3 nm). Our results demonstrate that there are two competing mechanisms causing the switching, one is the SOT from the spin current injected from the Ta layer and the other is the inter-grain spin-transfer torque (IGSTT) due to the spin current from neighboring grains. Current-induced switching is also observed in samples with MgO or Ti seed layer, which further confirms the existence of self-generated spin current in Mn3Sn, in particular in the case of MgO seed layer, the top, and bottom interfaces are symmetrical. We argue that, unlike FMs, polycrystalline Mn3Sn possesses sharp domain walls defined by the grain boundaries due to large magnetocrystalline anisotropy in the kagome plane, which makes the IGSTT an efficient mechanism for manipulating the AFM state of individual crystallites. We corroborate our argument with the magnetic properties of polycrystalline Mn3Sn films and magneto-optical Kerr effect (MOKE) imaging of current-induced switching of the crystal grains. Furthermore, the removal of the thick HM layer that was used in previous studies significantly increases the anomalous Hall effect (AHE) signal by more than one order of magnitude, making it more appealing for energy-efficient device applications. Accurate control of grain size and its distribution may provide an effective knob to tune the switching characteristics that is more suitable for emerging applications such as neuromorphic computing.
Results
Structural and magnetic properties
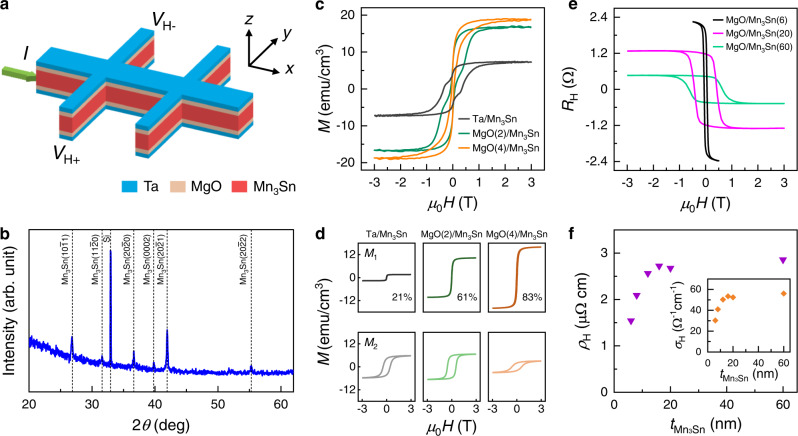
The current-induced switching experiments are performed on sputter-deposited multilayers (Fig. 1a): Ta(2)/MgO(tMgO)/Mn3Sn()/MgO(tMgO)/Ta(1.5) (the numbers inside the parentheses indicate the layer thickness in nm). All the samples are fabricated on Si/SiO2 substrates. Here, tMgO and denote the thickness of MgO and Mn3Sn, respectively. The bottom Ta(2) and top Ta(1.5) layers are the seed and capping layers, respectively, and at the same time, the bottom Ta(2) also functions as a spin current injector. The bottom MgO layer with a thickness ranging from 0 to 6 nm is added to control the amount of spin current injection into the Mn3Sn layer, where tMgO = 0 corresponds to Ta/Mn3Sn/Ta. To make the layer structure as symmetric as possible, we keep the thickness of the bottom and top MgO layers the same. The Ta(1.5) capping layer is presumably oxidized in ambience and can hardly contribute to spin current generation (hereafter MgO/Ta(1.5) is omitted for simplicity). Before we conduct the current-induced switching experiments, we first characterize the structural, magnetic, and transport properties of the multilayers.
Fig. 1. Structural and magnetic properties.
a Schematic of the Hall bar device used in electrical measurement. Current is applied along x-direction, and Hall voltage is measured from two Hall probes VH+ and VH- in y-direction. b XRD pattern of a Ta(2)/MgO(2)/Mn3Sn(60) coupon film. c M-H loops for Ta/MgO(tMgO)/Mn3Sn, tMgO = 0, 2, 4 nm at 300 K, with the magnetic field along out-of-plane direction. d Decomposed sub-loops of the M-H loops in c. e Field dependence of Hall resistance RH for Ta/MgO/Mn3Sn() with = 6, 20, 60 nm at 300 K. f Extracted anomalous Hall resistivity ρH as a function of . Inset: anomalous Hall conductivity σH as a function of .
Figure 1b shows the X-ray diffraction (XRD) pattern of a sputter-deposited Mn3Sn film with a thickness of 60 nm. As can be seen, multiple peaks corresponding to (), (), (), (), (), and () planes of D019 phase Mn3Sn are observed, confirming the polycrystalline structure in sputter-deposited Mn3Sn24. The peak positions remain the same for samples with different MgO thickness of 0, 2, and 4 nm (see Supplementary Information S1), suggesting that the insertion of MgO layer does not affect the crystalline structure of Mn3Sn. We further characterize the magnetic properties of Mn3Sn with or without the MgO insertion layer using a superconducting quantum interference device (SQUID) magnetometer. Figure 1c shows the M-H curves measured at room temperature with an out-of-plane magnetic field. As can be seen, both the saturation magnetization Ms and the shape of M-H loops change with the insertion of MgO layer. Although the Ms increases from 7 emu/cm3 at tMgO = 0 to 16 emu/cm3 at tMgO = 2 nm, and 19 emu/cm3 at tMgO = 4 nm, they are all on the same order of the saturation magnetization reported for polycrystalline Mn3Sn films at 300 K28,33,34. The M-H loop apparently consists of two sub-loops with different saturation magnetization and coercivity. As detailed in Supplementary Information S2, the M-H loop can be decomposed into two main components using the relation . Here, Ms is the total saturation magnetization, is the weightage of individual component, indicates how responsive each component is to an applied field, and Hci is the coercivity. The ± sign indicates the backward and forward sweeping curves, respectively. Figure 1d shows the decomposed M-H loops for the samples whose total M-H loops are shown in Fig. 1c. Based on the XRD data and the fact that the easy axis of Mn3Sn is in the kagome plane, we can establish the following correlation: and , , and planes. As can be seen from Fig. 1d, the MgO underlayer promotes the formation of () and () planes, both of which have their kagome plane perpendicular to the substrate. It should be noted that there should also be a small contribution from the plane due to the out-of-kagome plane component, but it is difficult to separate it from the diamagnetic contributions from the substrate. The above results show that polycrystalline Mn3Sn films can be considered as consisting of magnetically weakly coupled crystal grains with different orientations. The grain boundary functions as an atomically sharp domain wall which makes the IGSTT more important in non-collinear AFM than in its ferromagnetic counterpart.
Next, we study the transport properties by patterning the Mn3Sn stacks into Hall bar devices (Methods for details). Figure 1e shows the anomalous Hall resistance RH of Ta/MgO/Mn3Sn with varying Mn3Sn thickness of 6, 20, 60 nm and a fixed MgO thickness of 2 nm. As can be seen, the RH increases with decreasing the Mn3Sn thickness due to both the increase of longitudinal resistance and enhancement of crystalline orientation alignment (Fig. 1e). The latter can be inferred from the decrease of coercivity when the thickness decreases. By fitting the longitudinal resistance as a function of , we obtain the resistivity of Mn3Sn and Ta as 225.9 and 680.6 µΩ cm, respectively (see Supplementary Information S3). Using these values, we can calculate the anomalous Hall resistivity (ρH) and conductivity (σH) as a function of , and the results are shown in Fig. 1f. As can be seen, although ρH decreases with decreasing the thickness, it maintains a sizable value down to 6 nm below which the AHE becomes diminishingly small at room temperature. In contrast, the AHE for Ta/Mn3Sn disappears when is below 12 nm (See Supplementary Information S3), presumably caused by the interdiffusion of Ta into Mn3Sn. Therefore, although our original intention was to use the MgO to suppress the spin current flow from the Ta layer to Mn3Sn, it turned out that it also improves the magnetic properties, possibly due to the reduced interdiffusion at the Ta/Mn3Sn interface. It is worth noting that, although Mn3Sn is an AFM, the RH shown in Fig. 1e is comparable to that of typical HM/FM bilayers with a similar thickness, due to its large AHE induced by the Berry phase4.
Current-induced switching in Mn3Sn
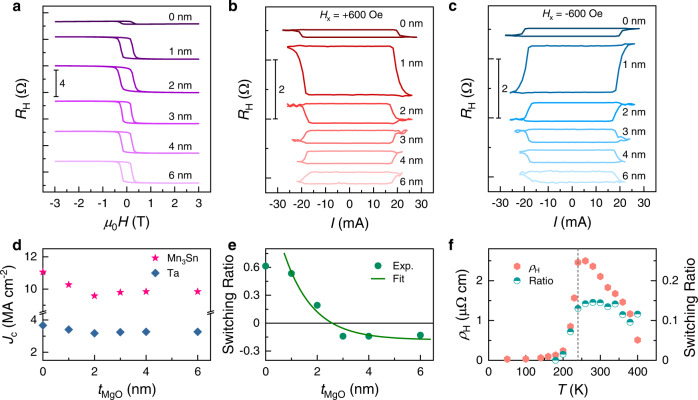
Current-induced switching measurements are performed for Ta/MgO/Mn3Sn with different tMgO. Current pulses with a constant pulse width of 5 ms but varying amplitude are applied along the longitudinal direction, i.e., x-direction, of the Hall bar. In-between two adjacent writing pulses, the AFM state of Mn3Sn is read by current pulses with the same duration as that of the writing pulses but at a much smaller amplitude of 1 mA. Figure 2a shows the field-dependent Hall resistance of Ta/MgO/Mn3Sn with a fixed Mn3Sn thickness of 12 nm but varying tMgO from 0 to 6 nm. The extracted anomalous Hall resistivity ρH is 0.28 µΩ cm at tMgO = 0, but it increases quickly to 2.13 µΩ cm at tMgO = 1 nm, and 2.56 µΩ cm at tMgO = 2 nm, after which it maintains a constant value of ~2.09 µΩ cm. Again, the large enhancement from tMgO = 0 to 1 nm can be accounted for by the change in crystalline orientation induced by the MgO layer.
Fig. 2. AHE and current-induced switching in Mn3Sn with varying MgO thickness.
a Field dependence of Hall resistance of Ta(2)/MgO(tMgO)/Mn3Sn(12) at varying tMgO from 0 to 6 nm. b, c Current dependence of Hall resistance of Ta(2)/MgO(tMgO)/Mn3Sn(12) at varying tMgO from 0 to 6 nm with an in-plane assistant field of +600 Oe and −600 Oe, respectively. d, e Extracted critical current density Jc and switching ratio as a function of tMgO. The solid-line in e is an exponential fitting. f Anomalous Hall resistivity ρH and switching ratio of Ta(2)/MgO(2)/Mn3Sn(12) as a function of temperature.
Figure 2b, c show the Hall resistance RH as a function of pulsed current amplitude I in an applied longitudinal field Hx of +600 Oe and −600 Oe, respectively, for six Ta/MgO/Mn3Sn samples with different tMgO. We observe current-induced switching behavior for all the samples, which exhibit opposite switching polarity of RH upon reversing either the current or applied field direction. The switching of AFM state in Ta/Mn3Sn (tMgO = 0) is consistent with previous reports on W/Mn3Sn and Ta/Mn3Sn based on the SOT scenario31,32. However, interestingly, the switching also occurs even with an MgO insertion layer between Ta and Mn3Sn. In addition, it can be noticed that the switching polarity of Mn3Sn suddenly changes when tMgO increases to ~3 nm and beyond. Figure 2d shows the extracted switching current density in the Ta and Mn3Sn layer based on current distribution in each layer. The switching current density in the Ta layer is around 3.2 × 106 A cm−2, comparable with those of previous reports, whereas the role of the spin current in the Mn3Sn layer will be discussed shortly.
The SR, i.e., the ratio between the current and field switched Hall resistance, is shown in Fig. 2e as a function of tMgO. The change of sign at tMgO = 3 nm is due to the change of switching polarity. We can see that the SR is positive and decreases monotonically from 61% to nearly zero at tMgO = 2.5 nm (as comparison, the previously reported W/Mn3Sn device has a SR of ~25%)31. After the polarity reverses at around 3 nm, the SR becomes almost constant at ~14% till tMgO = 6 nm. The solid-line in Fig. 2e is the fitted switching ratio (SR) according to , from which we can see that the SR consists of two components, one is negative with a constant amplitude and the other is an exponentially decaying contribution with a decay length of ~1.1 nm. The results point clearly to the fact that, in addition to the spin current from the Ta layer which should decrease exponentially with tMgO, there must be another mechanism originated from the spin current or spin-polarized current inside the Mn3Sn layer, which is independent of the MgO thickness. Similar results are also observed for devices with different Mn3Sn thickness (see Supplementary Information S3). In addition, we have also confirmed from temperature-dependent measurement that the switching only occurs in the temperature region in which Mn3Sn is in the non-collinear AFM phase (Fig. 2f, Supplementary Information S4). The SR begins decreasing around 240 K, which is the transition temperature from the AFM phase to a spiral spin structure24,35.
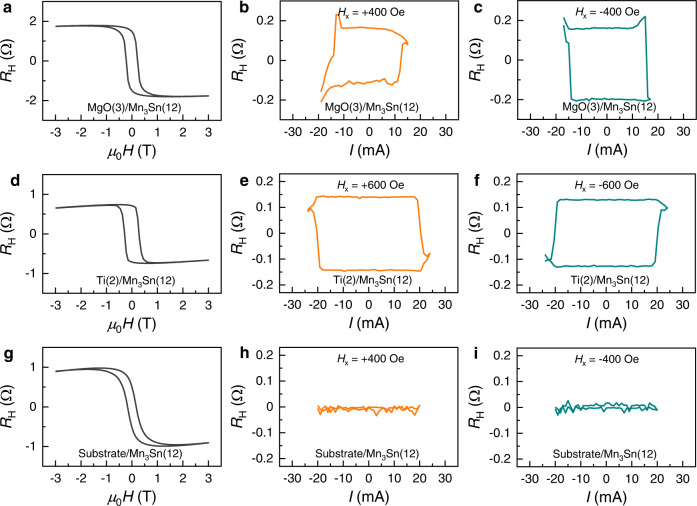
Furthermore, we performed current-induced switching in MgO(3)/Mn3Sn(12) and Ti(2)/Mn3Sn(12) (both are also covered with the MgO/Ta capping layers), where the Ta seed layer is replaced by MgO or Ti layer with negligible spin Hall angle. In both cases, external injection of spin Hall current to Mn3Sn is negligible. As shown in Fig. 3a, d, both MgO(3)/Mn3Sn(12) and Ti(2)/Mn3Sn(12) show evident AHE with ρH of 2.16 µΩ cm and 0.94 µΩ cm, respectively. The former is comparable with the AHE in Ta/MgO/Mn3Sn while the latter is half the value. As shown in the current dependence of Hall resistance displayed in Fig. 3b, c,e, f, deterministic current-induced switching is also observed in both structures with an SR ~11% and 20%, respectively. It is interesting to note that the switching polarity of Ti/Mn3Sn is the same as that of Ta/Mn3Sn but opposite of Ta/MgO/Mn3Sn with a thick MgO spacer and MgO/Mn3Sn. Put the switching polarity aside (which will be discussed later), the results indeed suggest that it is possible to manipulate the AFM state of polycrystalline Mn3Sn without an extra spin Hall layer but using the self-generated spin-polarized current. Besides, we also performed current-induced switching in Mn3Sn directly deposited on Si/SiO2 substrate (Fig. 3h, i). The much smaller remanence in its AHE loop (Fig. 3g) compared to other structures above indicates that grain size and its orientation in Si/SiO2/Mn3Sn can be quite different compared to other samples, resulting in negligible current-induced switching.
Fig. 3. AHE and current-induced switching in Mn3Sn with MgO, Ti seed layer or directly grown on substrate.
a, d, g Field dependence of Hall resistance of MgO(3)/Mn3Sn(12), Ti(2)/Mn3Sn(12), and Substrate/Mn3Sn(12), respectively. b, e, h Current dependence of Hall resistance of MgO(3)/Mn3Sn(12), Ti(2)/Mn3Sn(12), and Substrate/Mn3Sn(12) with a positive in-plane assistant field , respectively. c, f, i Current dependence of Hall resistance of MgO(3)/Mn3Sn(12), Ti(2)/Mn3Sn(12), and Substrate/Mn3Sn(12) with a negative , respectively.
MOKE imaging of current-induced switching
The low SR suggests that the switching of Mn3Sn does not necessarily follow the two dominant mechanisms in SOT-based switching of HM/FM bilayers36–41, i.e., coherent rotation (for small device)36,37,40 or domain wall nucleation and propagation (for large device)38–41. In order to gain insight, we perform scanning MOKE imaging of the current-induced switching process. Here, we employ the polar mode MOKE to probe the magnetic state in Mn3Sn (see Methods). A pulsed current with an amplitude larger than the threshold current and a pulse width of 5 ms is injected along the longitudinal direction of the Hall bar device. An in-plane field Hx along the current direction is also applied to assist the switching. Figure 4a, b show the switching of Ta(2)/MgO(2)/Mn3Sn(12) after the injection of a −25 mA pulsed current (upper panel) and 25 mA (lower panel) at Hx of +460 Oe and −460 Oe, respectively. The MOKE image of the Hall bar changes from light gray to dark gray (Hx = +460 Oe) and from dark gray to light gray (Hx = −460 Oe) when the current changes from −25 mA to +25 mA, which indicates the switching of AFM state in Mn3Sn. The light gray and dark gray images correspond to positive and negative anomalous Hall resistance8. It should be noted that it is difficult to estimate the SR from the MOKE image due to the limited spatial resolution of MOKE imaging. Consistent with the electrical measurement results, the reversal of switching polarity is also observed via MOKE imaging in samples with thick MgO layer, as can be seen from the MOKE images of Ta(2)/MgO(4)/Mn3Sn(12) in Fig. 4c, d, respectively. In addition, we also perform the current-sweeping measurements. However, for both structures, we do not see clear domain wall nucleation and propagation from the MOKE images as reported for field-induced switching in single-crystal Mn3Sn8. Instead, with increasing the current, the AFM state reverses gradually in localized areas across the sample (see Supplementary Information S5), resulting in graduate change of the MOKE image contrast. The results imply that the magnetic state reversal begins and ends with some of the crystallites instead of the entire sample, which explains why the SR is low. Furthermore, the switching becomes more non-uniform in the tMgO = 4 nm sample as compared to the tMgO = 2 nm sample (Fig. 4a, b), which is in good agreement with the electrical transport measurements.
Fig. 4. MOKE images showing current-induced switching in Mn3Sn.
a, b The images of Ta(2)/MgO(2)/Mn3Sn(12) after application of a longitudinal current pulse with an amplitude of −25 mA (upper panel) and 25 mA (lower panel) in an longitudinal field of +460 Oe and −460 Oe, respectively. c, d The MOKE images of Ta(2)/MgO(4)/Mn3Sn(12) after application of a longitudinal current with an amplitude of −22 mA (upper panel) and 22 mA (lower panel) in a longitudinal field of +600 Oe and −600 Oe, respectively.
Discussion
The aforementioned results suggest that in addition to the external spin current from the Ta layer, there is another spin current source contributing to the spin dynamics of a particular grain in polycrystalline Mn3Sn, which is from neighboring grains with misaligned spin sublattices. If we focus on a particular crystalline grain in Ta/MgO/Mn3Sn, the dynamics of the magnetization vector mξ(ξ = A, B, C) of each kagome sublattice can be described by the Landau-Lifshitz-Gilbert-Slonczewski (LLGS) equation
| 1 |
where , and are the gyromagnetic ratio and Gilbert damping constant, , Ici, si, and are the spin polarization/spin current angle of Mn3Sn or spin Hall angle (θSH) of Ta, charge current, spin polarization direction, and spin injection efficiency of ith spin current source which includes both the Ta layer and neighboring Mn3Sn grains, respectively, Ms and are the magnetization and volume of the crystal grain to be switched, is the reduced Planck constant, e is the electron charge, and Hξ, eff is the effective field which can be calculated from the total magnetic energy density of the three sublattices31,32,42–45. Equation (1) is obtained by eliminating the time-dependent term at the right-hand-side of the standard LLGS equation45. The dynamic spin configuration of Mn3Sn under external stimulus can be obtained by numerically solving the coupled LLGS equations. However, in order to gain a fundamental insight without resorting to micromagnetic modeling, we may examine qualitatively how the ground state of Mn3Sn will be affected by the spin currents based on symmetry analysis43,46. In this regard, the magnetic state of Mn3Sn may be represented by an average magnetization vector and two staggered order parameters and . When the in-plane anisotropy is sufficiently large, the out-of-kagome plane component is very small, then n1 and n2 may be parameterized by φ as and , where φ is the azimuthal angle from the easy axis direction of mC. For a single domain state without any external stimulus, the equilibrium states are given by φ = 0 and π, respectively. The corresponding magnetization vectors are m = (−1, 0, 0) and m = (1, 0, 0), respectively, with a magnitude of the order of , where K is the anisotropy constant and J0 is the homogeneous exchange coupling energy. There are three equivalent easy axis directions with the other two pointing at , respectively. When an external field H is applied in the kagome plane, the magnetization will be aligned with the external field direction, when H exceeds the coercivity which is on the order of a few hundreds of Oe.
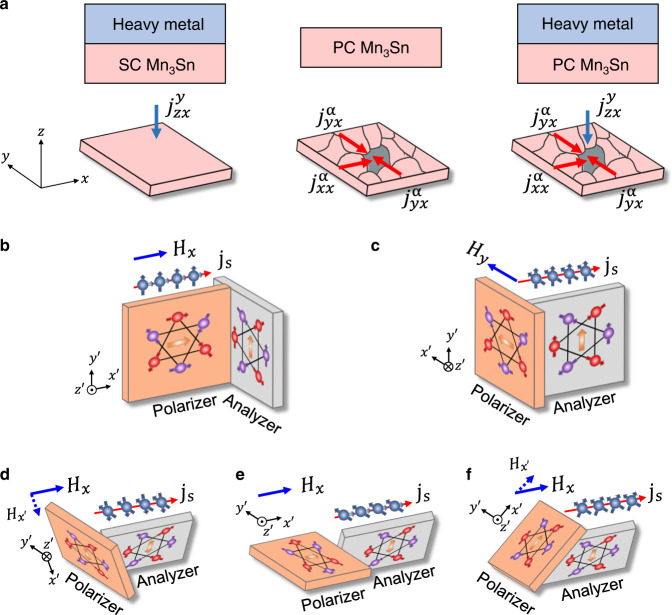
With the approximated ground state, we now discuss qualitatively the effect of spin current by replacing mξ in Eq. (1) with the average moment m. Without losing generality, we consider three types of structures as illustrated in Fig. 5a, namely, (i) HM/SC-Mn3Sn, (ii) PC-Mn3Sn, and (iii) HM/PC-Mn3Sn. Here, SC and PC denote single-crystal and polycrystal, respectively. In case (i), we only need to consider the spin current injected from the HM layer with the spin polarization sHM = (0, ±1, 0) (hereafter, we ignore the ± sign as it is dependent on the sign of spin Hall angle of the HM layer and current direction), and therefore, . As revealed by the previous studies31,32,43,44, the effect of spin current on the AFM state depends on the direction of sHM with respect to the kagome plane; binary switching occurs when sHM is in the kogome plane, whereas spin rotation dominates when sHM is perpendicular to the kagome plane. Based on Eq. (1), field-free switching will occur when the kagome plane is parallel to the xy-plane as there is always a finite projection of sHM on one or more of the three easy axes. However, such a switching cannot be detected by the AHE in the present measurement configuration as the Hall voltage probes are along y axis. The configuration which allows for both magnetization switching and AHE detection is when the kagome plane is parallel to the yz-plane. In this case, however, a longitudinal bias field Hx is required to break the symmetry, same as the SOT-based switching in HM/FM bilayers31,32. When the kagome lattice is in the zx-plane, there will be no deterministic switching as sHM is perpendicular to the kagome plane.
Fig. 5. Schematics of SOT and IGSTT-based switching.
a Three different structures for current-induced switching: heavy metal /single-crystalline (SC) Mn3Sn, polycrystalline (PC) Mn3Sn, and heavy metal /polycrystalline Mn3Sn. b–f Schematic of IGSTT-based switching. The polarizer (left grain) denotes the grain which provides spin-polarized current, whereas the analyzer (right grain) denotes the grain whose magnetic state is to be switched. : spin current flows in β direction with a polarization along α, induced by a charge current in γ direction. The x′y′z′ coordinate system is the local coordinate system attached to the polarizer such that x′y′ are always in the kagome plane, and z′ is along the c-axis of the polarizer.
Next, we consider case (ii), which consists of only a single-layer polycrystalline film. In this case, only has the contributions from the neighboring grains (to facilitate discussion, hereafter we refer to the neighboring grains as polarizer and the grains to be switched as analyzer). For ultrathin films, we may assume that there is only a single grain in the thickness direction. Furthermore, the average effects of spin current transverse to the charge current should be largely canceled out based on symmetry considerations. Therefore, only longitudinal spin current or spin-polarized current is considered to possibly contribute to switching. For a collinear ferromagnet, the equilibrium polarization of spin-polarized current is generally parallel with the local magnetization direction. However, recent studies suggest that transverse polarization also exists47. For the present case, the longitudinal or spin-polarized current plays the dominant role. According to J. Železný, et al.12, with the presence of spin-orbit interaction, the spin-polarized current emanating from the polarizer contains both a transverse and a longitudinal polarization. As revealed by XRD and magnetic measurements, the crystalline grains in polycrystalline Mn3Sn may be divided into three groups based on their kagome plane orientation with respect to the substrate: (i) and , (ii) , and , and (iii) . Grains with orientation do not contribute to the measured AHE signal and therefore, it cannot be analyzer. In general, when the charge current passes through the polarizer, spin current with both transverse and longitudinal polarization is generated. In the case of configurations shown in Fig. 5b, c, only spin current with transverse polarization plays a role in switching, because the longitudinal spin polarization is perpendicular to the kagome plane. Here, the primed coordinate system is the local coordinate system attached to the polarizer such that and are always in the kagome plane, which is to be differentiated from the global coordinate system shown in Fig. 5a. In the configuration shown in Fig. 5b, an assistant field is used to align m of the polarizer along x-direction. In this case the spin current from the polarizer may be written as js = (note x and are in the same direction in this case)12. By convention, we use to denote the spin current flowing in direction with a polarization along , induced by a charge current in direction. When the spin-polarized current enters the analyzer, spins with transverse polarization , will lead to magnetization switching due to the STT. The switching polarity should depend on the delicate balance of the spin-polarized current from neighboring grains. On the other hand, in the configuration shown in Fig. 5c, the polarizer and analyzer inter-change their roles, in which STT-based switching is also possible when an assistant field is applied in y direction (See Supplementary Information S9). However, as the spin polarization in the two cases may be different in amplitude, the ratio of switched regions can differ significantly in the two cases. In actual samples, the polarizer and analyzer are not necessarily always perpendicular to each other as revealed by both XRD and SQUID results. Figure 5d–f show three possible configurations which can lead to both magnetization switching and detectable AHE. Unlike cases in Fig. 5b, c, it is difficult to decompose js into spin current with longitudinal and transverse polarizations in the local coordinates as the kagome planes of the polarizer and analyzer do not form a right-angle. In these cases, depending on the exact kagome plane orientation of the polarizer and analyzer, spin currents with both transverse and longitudinal spin polarization may cause the switching of the magnetization. In the current measurement configuration, phenomenologically the AHE signal is proportional to the vertical component of the net magnetization in the kagome plane. Therefore, the configurations shown in Fig. 5d–f would lead to switching with a polarity opposite to that of Fig. 5b, c.
As discussed earlier, the texture of polycrystalline Mn3Sn is well reflected in its M-H loop. From the decomposition of M-H curves as shown in Fig. 1d, we find that in the case of Ta/MgO(tMgO)/Mn3Sn, the contribution from group (i) grains increases with increasing the MgO thickness, indicating that MgO seed layer facilitates the formation of group (i) grains and the switching in MgO/Mn3Sn might be dominated by the configuration in Fig. 5b, c. In addition, as shown in Supplementary Information S2, the M-H loop for Ti(2)/Mn3Sn(60) is very similar to that of Ta/MgO(2)/Mn3Sn, at which sign reversal has not occurred yet, i.e., the switching polarity is the same for Ta/Mn3Sn, Ti/Mn3Sn, and Ta/MgO(2)/Mn3Sn. The XRD profiles and temperature-dependent AHE of Mn3Sn in different structures further suggest that there are mostly group (ii) and (iii) grains in Ti/Mn3Sn (Supplementary Information S1 and S7). Therefore, the switching configurations in Fig. 5d–f may become dominant in Ti/Mn3Sn. At this stage, however, a quantitative analysis of the switching polarity would be difficult considering the random distribution of the crystalline orientation of the grains.
Lastly, case (iii) is a combination of case (i) and (ii), which represents most of the experimental configurations including the Ta/MgO/Mn3Sn trilayers of present study when the MgO is thin. However, when the MgO is thick, we will have case (ii). The effects of the SOT (due to externally injected spin current) and STT (due to self-generated spin-polarized current) can either add up or partially cancel out, depending on the spin Hall angle of HM and crystallite orientations. In the present case, it seems that they cancel out partially at small tMgO due to opposite sign. This explains why the switching polarity reverses at large tMgO when the SOT effect is mostly suppressed.
As mentioned above, from MOKE images for Ta(2)/MgO(4)/Mn3Sn(12) in Fig. 4c, d, we can see that the switched areas are discrete and more non-uniformly distributed than Ta(2)/MgO(2)/Mn3Sn(12) case. This is consistent with the inter-grain STT switching scenario as the switching occurs only when a pair of neighboring grains have specific configurations as one shown in Fig. 5b–f. However, it is not quite possible to determine the exact crystalline orientations of individual grains from the MOKE images due to limited spatial resolution of MOKE imaging. To support this scenario, we further examined the crystalline structure using transmission electron microscopy (TEM). From the cross-sectional TEM images in Fig. 6a, b, the Mn3Sn grain size ranges from 10 nm to 40 nm. Figure 6c displays the high-resolution (HR) cross-sectional TEM image for Ta/MgO(4)/Mn3Sn, from which the structure for each layer is clearly seen. Despite the post-annealing at 450 °C, there is no apparent intermixing of Mn3Sn with Ta layer due to the MgO insertion layer, and the crystalline texture for Mn3Sn layer is visible. By performing fast Fourier transform for the Mn3Sn layer in Fig. 6c, we obtained the corresponding electron diffraction pattern as shown in Fig. 6d. Based on the distances of the spots to the center, we further obtained the interplane spacings and the corresponding crystalline planes, as marked near each spot. The crystalline planes determined from TEM images is consistent with the XRD measurement. Multiple planes are detected in the small imaging area with width of ~37 nm, indicating the existence of grains with different crystalline planes in the lateral direction of the sample. In addition, the twin spots observed in Fig. 6d further confirm the grains existence and imply the existence of grain boundaries in the form of twin boundaries48–50. A recent study also finds that there exist multiple grains in polycrystalline Mn3Sn and individual grain is like a domain with specific crystalline and magnetic orientation. The magnetic state in each grain switches independently due to the grain boundary51. A combination of in-situ TEM and spin-dependent scanning tunneling microscopy may be able to obtain more insights, which is out of the scope of this study.
Fig. 6. TEM images of Mn3Sn.
a, b Cross-sectional TEM images of Ta/Mn3Sn and Ta/MgO(4)/Mn3Sn, respectively. c HR cross-sectional TEM image of Ta/MgO(4)/Mn3Sn. d Electron diffraction pattern of the Mn3Sn layer in c.
The random distribution of crystal grain orientation and large size distribution may pose a challenge in applications where the device size has to be very small, e.g., non-volatile memory. In this regard, some of the techniques that have been developed for high-density magnetic recording media may be used to reduce the grain size and improve its size distribution. In addition, templated seed layer or grain boundary materials may be employed to control the crystalline orientations. On the other hand, nonuniformity in grain size distribution may also be exploited for emerging applications where gradual instead of abrupt switching is required, such as neuromorphic computing. One other limitation is incomplete switching, which is also reported in the other studies on HM/Mn3Sn systems31,32,51. From the current-induced switching in different structures, we find that the SR overall presents a positive correlation with the AHE remanence RH(H=0)/RAHE (as shown in Supplementary Information S10) which is an indicator of the degree of texturing of the non-collinear AFM film. Therefore, further studies may be required to produce well-textured films with desirable grain orientation/size for current-induced switching. The active switching region may be reduced to contain only a few or ultimately two grains, thereby allowing to gain further insights into the switching mechanism and enhance the switching efficiency.
Before we conclude, it is worth mentioning that the proposed mechanism is different from previous reports on magnetization switching of single-layer FM or AFM which treat the single-layer largely homogeneous in terms of the magnetic order parameter. The mechanisms proposed in these early works include spin current with spin polarization transverse to the magnetization52,53, AHE-induced surface spins with spin polarization rotation in FM54, asymmetric absorption of internally generated spin Hall current in ferrimagnet55, and current-induced internal staggered SOT due to local inversion asymmetry of spin sublattices in collinear AFM17,19,56. However, all these mechanisms cannot account for the results obtained in this study. In addition, the interface-related effect such as Rashba effect is not likely to play an important role here, as in samples of Ta/MgO/Mn3Sn/MgO/Ta and MgO/Mn3Sn/MgO/Ta, we always kept the bottom and upper MgO layer the same thickness to minimize structural asymmetry. If there is any significant Rashba effect between MgO and Mn3Sn interface, the effects from upper and lower interfaces will be largely canceled out. The interface-related effect also fails to account for the negligible switching in substrate/Mn3Sn/MgO/Ta, as structural asymmetry is more prominent in this structure. Furthermore, a previous study has excluded the interface effect in current-induced switching of Mn3Sn by inserting a Cu layer between Mn3Sn and heavy metal layer57. Previous studies also suggest negligible charge-spin conversion at Ti/ferromagnetic interface58,59. In addition, as shown in Supplementary Information S8, the same switching polarity and similar level of SR in Ti/Mn3Sn/Ti symmetric structure with Ti/Mn3Sn further attests that the switching is not induced by interface effect. After the submission of this manuscript, several theoretical and experimental works have been published, which support the spin current generation and grain-based switching mechanism discussed in this study13,51,60.
In conclusion, we have demonstrated that current-induced AFM state switching is possible in single-layer Mn3Sn polycrystalline films via the inter-grain spin-transfer torque. As it does not require a heavy metal layer, the current shunting effect is significantly suppressed, which leads to a large anomalous Hall signal. Our results shed light on the crucial role of IGSTT in current-driven dynamics of polycrystalline non-collinear AFMs, which reveals the presence of self-generated spin current in non-collinear AFM. The IGSTT may be used to realize devices such as inter-grain spin valve and tunnel junctions. We shall point out that the IGSTT has been studied before in a different context as a possible mechanism in magnetization reversal of heat-assisted magnetic recording, in which the magnetic grains are separated by oxide and the spin-polarized current is generated by heat gradient61. At last, it is worth mentioning that we do not completely rule out other possible mechanisms such as the presence of hidden structural asymmetry that is not apparent in the as-deposit layer structure. In addition, the joule heating effect has also been reported recently to play a crucial role in the switching behavior of Mn3Sn62,63. We hope all these combined may stimulate more investigations in the current-induced switching of non-collinear antiferromagnets.
Methods
Sample preparation
The stacks, except the Ti layer, were deposited on Si/SiO2 (300 nm) substrates using magnetron sputtering with a base and working pressure of <1 × 10−8 and 3 × 10−3 Torr, respectively. The Ti layer was deposited by e-beam evaporation in the same system without breaking the vacuum. Standard photolithography and lift-off techniques were used to fabricate the Hall bars. The Hall bar length, width, spacing between voltage electrodes, and width of voltage electrode are 120 μm, 15 μm, 30 μm, and 5 μm, respectively. The Mircotech laserwriter system with a 405 nm laser was used to directly expose the photoresist (Mircoposit S1805), after which it was developed in MF319 to form the Hall bar pattern. After film deposition, the photoresist was removed by a mixture of Remover PG and acetone to complete the Hall bar fabrication. The processes of photolithography and lift-off were repeated to form electrodes and contact pads with the layers of Ta(5)/Cu(150)/Pt(10) for Hall bars. After the device fabrication and deposition, the devices were annealed at 450 °C for an hour in vacuum.
Structural and magnetic characterizations
XRD measurements were performed in a Rigaku X-ray diffractometer. A Cu-Kα X-ray was used in the diffractometer with a wavelength of 1.541 Å. The cross-sectional transmission electron microscopy imaging was performed using a JEOL JEM 2100F. TEM specimen was prepared using focused ion beam milling. The magnetic properties were characterized using Quantum Design MPMS3, with the resolution of <1 × 10−8 emu.
Electrical measurements
The electrical measurements were performed in the Quantum Design VersaLab PPMS with a sample rotator. The ac/dc current is applied by the Keithley 6221 current source. The longitudinal or Hall voltage is measured by the Keithley 2182 nanovoltmeter.
MOKE imaging
The MOKE imaging of out-of-plane magnetic domain was performed in polar geometry in a wide-field Kerr microscopy from Evico Magnetics at room temperature. The in-plane magnetic field was generated by a pair of electromagnets. To enhance the contrast, the non-magnetic background was firstly subtracted. Afterwards, 10 repeated current pulses with amplitude larger than threshold current were injected to the long axis of Hall bar device. For the current-sweeping measurement, a large negative current pulse was applied first to initialize the magnetic state. Then, positive current pulses with increasing amplitude from zero were injected. Same current range was used as the electrical measurement. Images were taken after each pulsed current injection.
Supplementary information
Acknowledgements
Y.W. acknowledges the funding support by the Ministry of Education, Singapore under its Tier 2 Grants (Grant No. MOE2017-T2-2-011 and MOE2018-T2-1-076). B.Y. acknowledges financial support by the European Research Council (ERC Consolidator Grant, No. 815869) and the Israel Science Foundation (ISF No. 1251/19, No. 3520/20, and No. 2932/21). We thank professor Shufeng Zhang, Jianpeng Liu, and Guoping Zhao for helpful discussions.
Author contributions
Y.W. designed and supervised the project. H.X. and Y.W. designed the experiments. H.X. conducted most of the experiments. X.C. helped with sample fabrication and XRD measurement. Q.Z. helped with MOKE imaging. Z.M. performed TEM imaging. H.X., B.Y., and Y.W. analyzed the data. All authors discussed the results. H.X., B.Y., and Y.W. wrote the manuscript and all the authors contributed to the final version of the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Data availability
All the data related to this work are present in the main text and Supplementary Information. The data sets that support the findings of this work are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Binghai Yan, Email: binghai.yan@weizmann.ac.il.
Yihong Wu, Email: elewuyh@nus.edu.sg.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-33345-2.
References
- 1.Chen H, Niu Q, MacDonald AH. Anomalous hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 2014;112:017205. doi: 10.1103/PhysRevLett.112.017205. [DOI] [PubMed] [Google Scholar]
- 2.Kübler J, Felser C. Non-collinear antiferromagnets and the anomalous Hall effect. EPL. 2014;108:67001. doi: 10.1209/0295-5075/108/67001. [DOI] [Google Scholar]
- 3.Zhang Y, et al. Strong anisotropic anomalous Hall effect and spin Hall effect in the chiral antiferromagnetic compounds Mn3X (X = Ge, Sn, Ga, Ir, Rh, and Pt) Phys. Rev. B. 2017;95:075128. doi: 10.1103/PhysRevB.95.075128. [DOI] [Google Scholar]
- 4.Nakatsuji S, Kiyohara N, Higo T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature. 2015;527:212–215. doi: 10.1038/nature15723. [DOI] [PubMed] [Google Scholar]
- 5.Nayak AK, et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2016;2:e1501870. doi: 10.1126/sciadv.1501870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ikhlas M, et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 2017;13:1085–1090. doi: 10.1038/nphys4181. [DOI] [Google Scholar]
- 7.Šmejkal L, Mokrousov Y, Yan B, MacDonald AH. Topological antiferromagnetic spintronics. Nat. Phys. 2018;14:242–251. doi: 10.1038/s41567-018-0064-5. [DOI] [Google Scholar]
- 8.Higo T, et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics. 2018;12:73–78. doi: 10.1038/s41566-017-0086-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kuroda K, et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 2017;16:1090–1095. doi: 10.1038/nmat4987. [DOI] [PubMed] [Google Scholar]
- 10.Yang H, et al. Topological Weyl semimetals in the chiral antiferromagnetic materials Mn3Ge and Mn3Sn. N. J. Phys. 2017;19:015008. doi: 10.1088/1367-2630/aa5487. [DOI] [Google Scholar]
- 11.Suzuki MT, Koretsune T, Ochi M, Arita R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B. 2017;95:094406. doi: 10.1103/PhysRevB.95.094406. [DOI] [Google Scholar]
- 12.Železný J, Zhang Y, Felser C, Yan B. Spin-polarized current in noncollinear antiferromagnets. Phys. Rev. Lett. 2017;119:187204. doi: 10.1103/PhysRevLett.119.187204. [DOI] [PubMed] [Google Scholar]
- 13.Ghosh S, Manchon A, Železný J. Unconventional robust spin-transfer torque in noncollinear antiferromagnetic junctions. Phys. Rev. Lett. 2022;128:097702. doi: 10.1103/PhysRevLett.128.097702. [DOI] [PubMed] [Google Scholar]
- 14.Kimata M, et al. Magnetic and magnetic inverse spin Hall effects in a non-collinear antiferromagnet. Nature. 2019;565:627–630. doi: 10.1038/s41586-018-0853-0. [DOI] [PubMed] [Google Scholar]
- 15.Manna K, Sun Y, Muechler L, Kübler J, Felser C. Heusler, Weyl and Berry. Nat. Rev. Mater. 2018;3:244–256. doi: 10.1038/s41578-018-0036-5. [DOI] [Google Scholar]
- 16.Zang, J., Cros, V. & Hoffmann, A. Topology in Magnetism. Vol. 192 (Springer International Publishing, 2018).
- 17.Wadley P, et al. Electrical switching of an antiferromagnet. Science. 2016;351:587–590. doi: 10.1126/science.aab1031. [DOI] [PubMed] [Google Scholar]
- 18.Jungwirth T, Marti X, Wadley P, Wunderlich J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016;11:231–241. doi: 10.1038/nnano.2016.18. [DOI] [PubMed] [Google Scholar]
- 19.Bodnar SY, et al. Writing and reading antiferromagnetic Mn2Au by Néel spin-orbit torques and large anisotropic magnetoresistance. Nat. Commun. 2018;9:348. doi: 10.1038/s41467-017-02780-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Moriyama T, Oda K, Ohkochi T, Kimata M, Ono T. Spin torque control of antiferromagnetic moments in NiO. Sci. Rep. 2018;8:14167. doi: 10.1038/s41598-018-32508-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen XZ, et al. Antidamping-torque-induced switching in biaxial antiferromagnetic insulators. Phys. Rev. Lett. 2018;120:207204. doi: 10.1103/PhysRevLett.120.207204. [DOI] [PubMed] [Google Scholar]
- 22.Baltz V, et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018;90:015005. doi: 10.1103/RevModPhys.90.015005. [DOI] [Google Scholar]
- 23.Siddiqui SA, et al. Metallic antiferromagnets. J. Appl. Phys. 2020;128:040904. doi: 10.1063/5.0009445. [DOI] [Google Scholar]
- 24.Higo T, et al. Anomalous Hall effect in thin films of the Weyl antiferromagnet Mn3Sn. Appl. Phys. Lett. 2018;113:202402. doi: 10.1063/1.5064697. [DOI] [Google Scholar]
- 25.Ikeda T, et al. Anomalous Hall effect in polycrystalline Mn3Sn thin films. Appl. Phys. Lett. 2018;113:222405. doi: 10.1063/1.5051495. [DOI] [Google Scholar]
- 26.Ikeda T, et al. Fabrication and evaluation of highly c-plane oriented Mn3Sn thin films. AIP Adv. 2020;10:015310. doi: 10.1063/1.5130459. [DOI] [Google Scholar]
- 27.You Y, et al. Anomalous hall effect–like behavior with in-plane magnetic field in noncollinear antiferromagnetic Mn3Sn films. Adv. Electron. Mater. 2019;5:1800818. doi: 10.1002/aelm.201800818. [DOI] [Google Scholar]
- 28.Markou A, et al. Noncollinear antiferromagnetic Mn3Sn. Phys. Rev. Mater. 2018;2:051001. doi: 10.1103/PhysRevMaterials.2.051001. [DOI] [Google Scholar]
- 29.Yoon J, et al. Crystal orientation and anomalous Hall effect of sputter-deposited non-collinear antiferromagnetic Mn3Sn thin films. Appl. Phys. Express. 2019;13:013001. doi: 10.7567/1882-0786/ab5874. [DOI] [Google Scholar]
- 30.Liu ZQ, et al. Electrical switching of the topological anomalous Hall effect in a non-collinear antiferromagnet above room temperature. Nat. Electron. 2018;1:172–177. doi: 10.1038/s41928-018-0040-1. [DOI] [Google Scholar]
- 31.Tsai H, et al. Electrical manipulation of a topological antiferromagnetic state. Nature. 2020;580:608–613. doi: 10.1038/s41586-020-2211-2. [DOI] [PubMed] [Google Scholar]
- 32.Takeuchi Y, et al. Chiral-spin rotation of non-collinear antiferromagnet by spin–orbit torque. Nat. Mater. 2021;20:1364–1370. doi: 10.1038/s41563-021-01005-3. [DOI] [PubMed] [Google Scholar]
- 33.Wang X, et al. Integration of the noncollinear antiferromagnetic metal Mn3Sn onto ferroelectric oxides for electric-field control. Acta Mater. 2019;181:537–543. doi: 10.1016/j.actamat.2019.10.020. [DOI] [Google Scholar]
- 34.Zhao Z, Guo Q, Chen F, Zhang K, Jiang Y. Magnetic properties and anomalous Hall effect in antiferromagnetic Mn3Sn films. Phys. B: Condens. Matter. 2021;604:412692. doi: 10.1016/j.physb.2020.412692. [DOI] [Google Scholar]
- 35.Nagamiya T, Tomiyoshi S, Yamaguchi Y. Triangular spin configuration and weak ferromagnetism of Mn3Sn and Mn3Ge. Solid State Commun. 1982;42:385–388. doi: 10.1016/0038-1098(82)90159-4. [DOI] [Google Scholar]
- 36.Liu L, Lee OJ, Gudmundsen TJ, Ralph DC, Buhrman RA. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin hall effect. Phys. Rev. Lett. 2012;109:096602. doi: 10.1103/PhysRevLett.109.096602. [DOI] [PubMed] [Google Scholar]
- 37.Lee K-S, Lee S-W, Min B-C, Lee K-J. Threshold current for switching of a perpendicular magnetic layer induced by spin Hall effect. Appl. Phys. Lett. 2013;102:112410. doi: 10.1063/1.4798288. [DOI] [Google Scholar]
- 38.Lee OJ, et al. Central role of domain wall depinning for perpendicular magnetization switching driven by spin torque from the spin Hall effect. Phys. Rev. B. 2014;89:024418. doi: 10.1103/PhysRevB.89.024418. [DOI] [Google Scholar]
- 39.Pizzini S, et al. Chirality-induced asymmetric magnetic nucleation in Pt/AlOx ultrathin microstructures. Phys. Rev. Lett. 2014;113:047203. doi: 10.1103/PhysRevLett.113.047203. [DOI] [PubMed] [Google Scholar]
- 40.Zhang C, Fukami S, Sato H, Matsukura F, Ohno H. Spin-orbit torque induced magnetization switching in nano-scale Ta/CoFeB/MgO. Appl. Phys. Lett. 2015;107:012401. doi: 10.1063/1.4926371. [DOI] [Google Scholar]
- 41.Xie H, Luo Z, Yang Y, Wu Y. In situ study of oxygen and Mg effects on current-induced magnetization switching in Pt/Co bilayers in ultrahigh vacuum. Appl. Phys. Lett. 2020;116:122404. doi: 10.1063/1.5138242. [DOI] [Google Scholar]
- 42.Liu J, Balents L. Anomalous hall effect and topological defects in antiferromagnetic weyl semimetals: Mn3Sn/Ge. Phys. Rev. Lett. 2017;119:087202. doi: 10.1103/PhysRevLett.119.087202. [DOI] [PubMed] [Google Scholar]
- 43.Yamane Y, Gomonay O, Sinova J. Dynamics of noncollinear antiferromagnetic textures driven by spin current injection. Phys. Rev. B. 2019;100:054415. doi: 10.1103/PhysRevB.100.054415. [DOI] [Google Scholar]
- 44.Fujita H. Field-free, spin-current control of magnetization in non-collinear chiral antiferromagnets. Phys. Status Solidi RRL. 2017;11:1600360. doi: 10.1002/pssr.201600360. [DOI] [Google Scholar]
- 45.Timopheev AA, Sousa R, Chshiev M, Buda-Prejbeanu LD, Dieny B. Respective influence of in-plane and out-of-plane spin-transfer torques in magnetization switching of perpendicular magnetic tunnel junctions. Phys. Rev. B. 2015;92:104430. doi: 10.1103/PhysRevB.92.104430. [DOI] [Google Scholar]
- 46.Gomonay O, Loktev V. Using generalized Landau-Lifshitz equations to describe the dynamics of multi-sublattice antiferromagnets induced by spin-polarized current. Low. Temp. Phys. 2015;41:698–704. doi: 10.1063/1.4931648. [DOI] [Google Scholar]
- 47.Davidson A, Amin VP, Aljuaid WS, Haney PM, Fan X. Perspectives of electrically generated spin currents in ferromagnetic materials. Phys. Lett. A. 2020;384:126228. doi: 10.1016/j.physleta.2019.126228. [DOI] [Google Scholar]
- 48.Sukedai E, Yokoyama T. Investigation of tensile–compressive yield asymmetry and the role of deformation twin in extruded pure magnesium. Int. J. Mater. Res. 2010;101:736–740. doi: 10.3139/146.110332. [DOI] [Google Scholar]
- 49.Martinez M, et al. TEM analysis of the deformation microstructure of polycrystalline cobalt plastically strained in tension. Mater. Charact. 2017;134:76–83. doi: 10.1016/j.matchar.2017.09.038. [DOI] [Google Scholar]
- 50.Uttam P, Kumar V, Kim K-H, Deep A. Nanotwinning: generation, properties, and application. Mater. Des. 2020;192:108752. doi: 10.1016/j.matdes.2020.108752. [DOI] [Google Scholar]
- 51.Yan, G. Q. et al. Quantum sensing and imaging of spin-orbit-torque-driven spin dynamics in noncollinear antiferromagnet Mn3Sn. Adv. Mater., https://arxiv.org/abs/2203.11465 (2022). [DOI] [PubMed]
- 52.Wang W, et al. Anomalous spin–orbit torques in magnetic single-layer films. Nat. Nanotechnol. 2019;14:819–824. doi: 10.1038/s41565-019-0504-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhu L, Zhang XS, Muller DA, Ralph DC, Buhrman RA. Observation of strong bulk damping-like spin-orbit torque in chemically disordered ferromagnetic single layers. Adv. Funct. Mater. 2020;30:2005201. doi: 10.1002/adfm.202005201. [DOI] [Google Scholar]
- 54.Luo Z, et al. Spin-orbit torque in a single ferromagnetic layer induced by surface spin rotation. Phys. Rev. Appl. 2019;11:064021. doi: 10.1103/PhysRevApplied.11.064021. [DOI] [Google Scholar]
- 55.Zhang RQ, et al. Current-induced magnetization switching in a CoTb amorphous single layer. Phys. Rev. B. 2020;101:214418. doi: 10.1103/PhysRevB.101.214418. [DOI] [Google Scholar]
- 56.Chen X, et al. Electric field control of Néel spin–orbit torque in an antiferromagnet. Nat. Mater. 2019;18:931–935. doi: 10.1038/s41563-019-0424-2. [DOI] [PubMed] [Google Scholar]
- 57.Tsai H, et al. Spin–orbit torque switching of the antiferromagnetic state in polycrystalline Mn3Sn/Cu/heavy metal heterostructures. AIP Adv. 2021;11:045110. doi: 10.1063/9.0000229. [DOI] [Google Scholar]
- 58.Zhu L, Buhrman RA. Absence of significant spin-current generation in Ti/FeCoB bilayers with strong interfacial spin-orbit coupling. Phys. Rev. Lett. 2021;15:L031001. [Google Scholar]
- 59.Yang Y, Xie H, Xu Y, Luo Z, Wu Y. Multistate magnetization switching driven by spin current from a ferromagnetic layer. Phys. Rev. Appl. 2020;13:034072. doi: 10.1103/PhysRevApplied.13.034072. [DOI] [Google Scholar]
- 60.Go, D. et al. Non-collinear spin current for switching of chiral magnetic textures. arXivhttps://arxiv.org/abs/2201.11476 (2022). [DOI] [PubMed]
- 61.Dieny B, et al. Impact of intergrain spin-transfer torques due to huge thermal gradients in heat-assisted magnetic recording. IEEE Trans. Magn. 2018;54:0800111. doi: 10.1109/TMAG.2018.2863225. [DOI] [Google Scholar]
- 62.Pal B, et al. Setting of the magnetic structure of chiral kagome antiferromagnets by a seeded spin-orbit torque. Sci. Adv. 2022;8:eabo5930. doi: 10.1126/sciadv.abo5930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Krishnaswamy GK, et al. Time-dependent multistate switching of topological antiferromagnetic order in Mn3Sn. arXiv. 2022;2205:05309. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All the data related to this work are present in the main text and Supplementary Information. The data sets that support the findings of this work are available from the corresponding author upon reasonable request.