Abstract
Postpartum depression (PPD) is a serious condition associated with potentially tragic outcomes, and in an ideal world PPDs should be prevented. Risk prediction models have been developed in psychiatry estimating an individual’s probability of developing a specific condition, and recently a few models have also emerged within the field of PPD research, although none are implemented in clinical care. For the present study we aimed to develop and validate a prediction model to assess individualized risk of PPD and provide a tentative template for individualized risk calculation offering opportunities for additional external validation of this tool. Danish population registers served as our data sources and PPD was defined as recorded contact to a psychiatric treatment facility (ICD-10 code DF32-33) or redeemed antidepressant prescriptions (ATC code N06A), resulting in a sample of 6,402 PPD cases (development sample) and 2,379 (validation sample). Candidate predictors covered background information including cohabitating status, age, education, and previous psychiatric episodes in index mother (Core model), additional variables related to pregnancy and childbirth (Extended model), and further health information about the mother and her family (Extended+ model). Results indicated our recalibrated Extended model with 14 variables achieved highest performance with satisfying calibration and discrimination. Previous psychiatric history, maternal age, low education, and hyperemesis gravidarum were the most important predictors. Moving forward, external validation of the model represents the next step, while considering who will benefit from preventive PPD interventions, as well as considering potential consequences from false positive and negative test results, defined through different threshold values.
Subject terms: Depression, Scientific community
Introduction
Postpartum depression (PPD) is a serious condition with documented negative and potentially tragic consequences, including recurrence, self-harm, and suicide [1–3]. Prevalence of PPD is around 13%, but ranges substantially depending on case definition criteria and study population [4–7], and risk factors, among others, including past history of depression and pregnancy/obstetric complications [4, 8–10].
In an ideal world, PPD should be prevented, and interventions to do this have been developed and tested [11]. For targeted interventions, any effort to successfully identify individual women at particularly high risk of PPD is consequently preferable and also cost-effective [12]. Unfortunately, no such tools exist that are sufficiently validated [12], which directly impedes and averts the initiation of early treatment and individualized risk management in clinical care. So far, clinical practice can only apply a pragmatic approach based on a Grade B recommendation: Provide counseling interventions to women with one or more established risk factors, including a history of depressive episodes, current depressive symptoms, low socioeconomic status, recent intimate partner violence, or a history of significant negative life events [12]. However, such an approach will (A) provide counseling to women who despite having identified risk factors do not develop PPD and (B) miss the opportunity to help a group of women who will develop PPD without having any of the outlined risk factors. Consequently, this pragmatic approach will capture some high-risk PPD individuals but is at its best imprecise.
Risk prediction models have been developed in psychiatry in recent years, aiming to estimate an individual’s probability of a selected condition, including diagnostic, prognostic, or predictive models in response to interventions [13]. Examples of these tools include models to predict readmission [14], and disease-specific risks for, e.g., psychotic or affective disorders, and posttraumatic stress [13, 15], and mainly recently, models aimed at predicting PPD [16–21]. In comparison, there are several examples of risk prediction models outside the field of psychiatry, which are implemented in daily clinical practice. These include, for example, the identification of persons at high risk of breast cancer and cardiovascular disease [22–24]. A common denominator for these models is that the tools are dynamic and have been developed, fine-tuned, and trained across a longer period and have taken advantage of input from validation in external datasets and expansion of the predictor variables [25–28].
For the present study, we aimed to develop and validate a prediction model to assess an individualized risk of PPD, and furthermore provide a tentative template for individualized risk calculation, offering opportunities for additional external validation of this tool.
Methods
Data sources
Danish population registers served as our data sources, and linkage was possible as all individuals alive and living in Denmark from 1968 and onwards are assigned a unique identification number registered in the Danish Civil Registration System (CRS) [29]. This identification number enables linkage within and between registers and provides information on vital status and family relations. The Danish National Patient Registry contains information on all admitted patients with somatic diseases from 1977, and the Danish Psychiatric Central Research Registry (PCR) holds data on all patients admitted to psychiatric hospitals from 1969 [30]. Both registries also contain data on outpatient and emergency visits from January 1, 1995. The Danish National Prescription Registry (NPR) provides data on all redeemed prescriptions from 1995 [31], and contains the anatomical therapeutic chemical (ATC) classification codes and the dispensing date. The Danish Medical Birth Registry (MFR) includes data on all live births and stillbirths and contains information on gestational age and birth complications from 1973 [32]. Furthermore, data on socioeconomic status (education and cohabiting information) was obtained from the Population Statistics Register and the Danish Student Register and Qualification Register [33].
Study design and population
Through CRS, we identified Danish women who gave birth to their first live-born singleton.
To ensure sufficient registry information prior to and after childbirth, we only included Danish-born women aged 15 years or older and who resided in Denmark at delivery between January 1, 1997, and June 30, 2018 (N = 485,845). To ensure PPD was an incident psychiatric episode, we excluded 20,300 women with a psychiatric history within 6 months prior to conception until date of childbirth (International Classification of Diseases, 10th Revision (ICD-10) codes: F00-99 and ATC-codes: N03-N07). Furthermore, 4,088 had missing information on at least one predictor variable, leaving 461,457 women for the analysis: 352,608 (development sample) and 108,849 (validation sample) (Fig. 1).
Fig. 1.
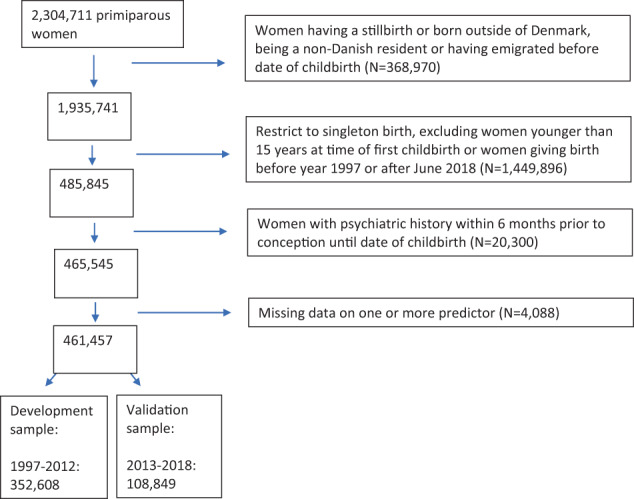
Study population details.
Definition of PPD
PPD was our outcome of interest and was defined as either a recorded contact to a specialized psychiatric treatment facility as in- or outpatient visit (ICD-10: codes: DF32-33) or as a redeemed antidepressant prescription in primary care (ATC code N06A) within 6 months after childbirth.
Identification and definition of candidate predictors
To develop our prediction model to assess the risk of PPD, we selected a set of predictors previously shown to be associated with PPD, which are easy to identify and readily available in clinical screening and care. We defined three prediction models with varying numbers of included candidate predictors: (1) Core model, (2) Extended model, and (3) Extended+ model. See details regarding identification and definition of all predictor variables in Supplementary, Table 1.
Core model—predictor variables including background information
In the Core model, we included predictor variables covering identified PPD risk factors related to background information, including cohabitation status (married or cohabiting/single, divorced, widowed), age, education, and previous psychiatric episodes of the index mother.
Extended model—adding PPD risk factors before and during pregnancy and around childbirth
In the Extended model, we included the predictors from the Core model and added identified risk factors from previous work from our group, including the following dichotomous (yes/no) variables registered during pregnancy: Hyperemesis gravidarum, eclampsia, preeclampsia, gestational hypertension, and gestational diabetes. Predictor variables around childbirth included postpartum hemorrhage, preterm birth, and acute cesarean section (C-section), while predictor variables before pregnancy included history of previous stillbirths and spontaneous or induced abortions [8].
Extended+ model—adding detailed information on health of the index mother and her family
For the Extended+ model, we added additional PPD risk factor variables to the Extended model. The added information constituted data that not all women will know and be able to disclose, including psychiatric history in at least one parent before date of childbirth and somatic comorbidities defined by Charlson Comorbidity index [34].
Statistical analyses
Model development
Complete case analysis was done as only a few women (N = 4088, 0.9%) had missing values on either education and/or cohabitation (Fig. 1) [35]. Applying a non-random split [36], the remaining 461,457 mothers were divided into a development and a validation sample based on the calendar year of childbirth: women with a first-time birth in 1997–2012 (development sample, N = 352,608), and women with a first-time birth in 2013–2018 (validation sample, N = 108,849). Note, the non-random split was chosen, instead of a random split, because it has superior properties for evaluating model performance allowing for non-random variation between the two datasets. The incidence of PPD within each of the two samples was 0.02 and the EPV (events per variable) was above 100.
We estimated the probability of PPD (yes/no) within 6 months after birth, using a logistic regression model. Within our follow-up period, 139 women either died or emigrated without a PPD diagnosis and were defined as non-PPD cases. Within the development sample, we considered the association between each predictor and the probability of PPD measured by odds ratios (ORs). The functional form used for age was assessed, examining piecewise linear functions, spline-, logarithmic- and power transformations. We used a full model approach [26], combining all the above-mentioned predictors in a multivariate logistic regression model for the three outlined models: Basic, Extended, and Extended+. We determined the best fit for each variable and found the optimal model by evaluating R2 and the Akaike information criterion (AIC), ending up with an optimally defined model for each of our three prediction models (Core, Extended, and Extended+).
Prediction model validation
To examine the extent to which our models can be generalized and used outside the development sample, reproducibility and transportability were assessed [26, 37]. Reproducibility measures the model performance within a similar dataset from the same population, whereas transportability measures the performance in samples that are different from the development sample but still from the same population and context. Overall, a good model performance captures both reproducibility and transportability.
Internal validation
Reproducibility was examined within each of the three models, considering the performance of the fitted model evaluated on the same data as it was developed (internal validation). A fitted model typically over-performs because it is evaluated within the same data, and this ‘optimism’ in performance is a measure of reproducibility. Constructing 200 bootstrapped samples at random with replacement using the function “validate” in R package rms, we estimated a logistic regression model in each sample and evaluated each of these with the original sample. The differences in the regression slope in all 200 samples were subsequently combined and pooled, as a measure of average optimism and used to shrink the original model to the mean, improving stability to enhance reproducibility in new datasets [38].
Internal-external validation
Transportability was assessed using temporal validation to evaluate model performance while considering the two different time periods for development and validation [39]. The three models were developed within women with a first-time birth in 1997–2012 (development sample), and each of the developed models was evaluated within more recent mothers (validation sample), predicting the risk of PPD in women with a first-time birth in 2013–2018 (internal-external validation [39]). If the predicted risk of PPD was far from the actual risk, we adjusted the models accordingly using recalibration techniques [40], as explained below.
Model performance assessment
The performance of the models was assessed by discrimination and calibration. Discrimination describes the models’ ability to distinguish between women with and without the event. It is measured by the c-statistic corresponding to the area under the ROC curve, representing the probability that within a randomly selected pair of women (one with and one without PPD), the woman with PPD was assigned a higher predicted probability than the woman without PPD.
Calibration measures if the model is precise in predicting the observed probability [41]. We considered this by plotting the predicted probabilities versus observed probabilities, where the identity line represents a perfect calibration. The predicted probabilities were explained by the logit model with the linear predictor LPi = αdev + βdev*Xi, where (αdev, βdev) is the coefficients estimated within the development sample and i indicates which dataset the predictors belong to. As we consider logistic regression with a dichotomous outcome, the observed probabilities were smoothed by the loess algorithm. The calibration slope, boverall, was estimated from the recalibration model, logit(Yval = 1) = a + boverall * LPval, and indicates whether the model is over- or underfitting depending on whether boverall is below or above 1, respectively. When the slope equals 1, calibration-in-the-large is the calibration intercept, a, which describes whether the model overestimates or underestimates the probability of PPD depending on whether it is below or above 0, respectively. The calibration slope and intercept were used to recalibrate the model to gain better calibration [40]. Additionally, we considered the le Cessie-van Houwelingen-Copas-Hosmer (CHCH) unweighted sum of squares test for global goodness of fit [42].
The final model is presented in a nomogram, illustrating how much each predictor affects the probability of PPD. Furthermore, a risk calculator is available online to calculate the probability of PPD based on the combination of an individual woman’s covariates (https://ncrr-au.shinyapps.io/PPDRiskCalc/). Note, the provided risk calculator is at present not ready for implementation into clinical care and is provided solely for validation purposes. TRIPOD guidelines were followed for the development and validation of our prediction model [36]. All analyses were performed using the R software [43] version 4.1.1, using the following packages: rms [44], DescTools [45], pROC [46], Hmisc [47], and caret [48], and shiny [49].
Ethics
Using population register data for the present study was approved by the Danish Data Protection Agency. No informed consent is required for these types of studies in accordance with Danish legislation.
Results
Data description
Characteristics of our cohort within the development and validation datasets are presented in Table 1.
Table 1.
Baseline characteristics of 352,608 mothers (development dataset) and 108,849 women (validation dataset).
| Development dataset (1997–2012) | Validation dataset (2013–2015) | |||
|---|---|---|---|---|
| Overall | PPD | Overall | PPD | |
| N (%) | 352,608 (100) | 6402 (1.8) | 108,849 (100) | 2379 (2.2) |
| CORE MODEL | ||||
| Mothers’ age at birth, median (IQR) | 28 (25, 31) | 28 (25, 32) | 28 (25, 31) | 29 (26, 33) |
| Cohabitation (%) | 395,051 (83.7) | 5064 (79.1) | 89,089 (81.8) | 1886 (77.3) |
| Education (%) | ||||
| Mandatory | 68,451 (19.4) | 1723 (26.9) | 16,460 (15.1) | 532 (22.4) |
| Short | 165,907 (47.1) | 2855 (44.6) | 41,383 (38.0) | 912 (38.3) |
| Medium | 16,340 (4.6) | 221 (3.5) | 5342 (4.9) | 106 (4.5) |
| High | 101,910 (28.9) | 1603 (25.0) | 45,664 (42.0) | 829 (34.8) |
| Previous psychiatric history (%) | ||||
| None | 282,076 (80.0) | 1648 (25.7) | 73,467 (67.5) | 315 (13.2) |
| 0-3 years before birth | 19,848 (5.6) | 1585 (24.8) | 6519 (6.0) | 576 (24.2) |
| 3-10 years before birth | 41,075 (11.6) | 2788 (43.5) | 20,446 (18.8) | 1130 (47.5) |
| 10+ years before birth | 9609 (2.7) | 381 (6.0) | 8417 (7.7) | 358 (15.0) |
| ADDED PREDICTOR VARIABLES IN THE EXTENDED MODEL | ||||
| Postpartum hemorrhage (%) | 21,429 (6.1) | 527 (8.2) | 2,485 (2.3) | 59 (2.5) |
| Gestational diabetes (%) | 6531 (1.9) | 219 (3.4) | 3870 (3.6) | 141 (5.9) |
| Gestational hypertension (%) | 6835 (2.0) | 171 (2.7) | 3153 (2.9) | 84 (3.5) |
| Preeclampsia (%) | 15,055 (4.3) | 363 (5.7) | 5083 (4.7) | 149 (6.3) |
| Eclampsia (%) | 241 (0.1) | 9 (0.1) | 89 (0.1) | 0 (0.0) |
| Previous stillbirths (%) | 1881 (0.5) | 37 (0.6) | 474 (0.4) | 14 (0.6) |
| Previous abortion (%) | 82,709 (23.5) | 1792 (28.0) | 23,764 (21.8) | 625 (26.3) |
| Acute C-section (%) | 52,896 (15.0) | 1262 (19.7) | 16,934 (15.6) | 457 (19.2) |
| Preterm birth (%) | 22,226 (6.3) | 609 (9.5) | 5265 (4.8) | 204 (8.6) |
| Hyperemesis gravidarum (%) | 4899 (1.4) | 200 (3.1) | 2562 (2.4) | 131 (5.5) |
| ADDED PREDICTOR VARIABLES IN THE EXTENDED+ MODEL | ||||
| Parents’ previous psychiatric history (%) | 219,854 (62.4) | 4967 (77.6) | 82,260 (75.6) | 2071 (87.1) |
| Charlson comorbidity index, within 10 years before birth (%) | ||||
| 0 | 337,084 (95.6) | 5944 (92.8) | 102,589 (94.2) | 2206 (92.7) |
| 1 | 12,092 (3.4) | 370 (5.8) | 4779 (4.4) | 130 (5.5) |
| 2+ | 3432 (1.0) | 88 (1.4) | 1481 (1.4) | 43 (1.8) |
PPD is defined within 6 months after birth.
Model development
In the univariate logistic regression models, all predictors were significantly associated with PPD except previous stillbirths, see Table 2. In particular, hyperemesis gravidarum (OR [95% CI] = 2.3 [2.0–2.7]) and gestational diabetes (OR [95% CI] = 1.9 [1.7–2.2] were associated with PPD, as well as previous psychiatric history among the mother and the mothers’ parents (OR [95% CI] = 2.1 [2.0–2.2]). Previous maternal psychiatric episodes increased PPD risk depending on how recent it was; with the ORs [95% CI] ranging from 7.0 [6.3–7.9] with psychiatric history more than 10 years to 14.8 [13.8-15.8] within 3 years prior to birth. A Wald test considering maternal age showed significant non-linearity in the log odds of PPD (χ2 = 98.4, df = 3, p < 0.0001). A transformation of maternal age using a third-degree polynomial provided the best fit, with a high value of R2 and a low AIC value in the univariate model and the lowest possible AIC when considering each of the three multivariate models. Mutual adjustment within the three multivariate models showed the same pattern as the univariate analyses, except for eclampsia and previous abortion, which now was not significant in any of the Extended models.
Table 2.
Odds ratios (crude and mutually adjusted) between predictor variables and PPD within 6 months after birth.
| Odd Ratio, OR [95% CI] | ||||
|---|---|---|---|---|
| Univariate | Multivariate (Core) | Multivariate (Extended) | Multivariate (Extended + ) | |
| Mothers age at birth | ||||
| Age (first order age) | 0.54 (0.42-0.70) | 0.74 (0.55-0.98) | 0.72 (0.54-0.96) | 0.74 (0.55-0.98) |
| Age2 | 1.02 (1.01-1.03) | 1.01 (1.00-1.02) | 1.01 (1.00-1.02) | 1.01 (1.00-1.02) |
| Age3 | 1.00 (1.00-1.00) | 1.00 (1.00-1.00) | 1.00 (1.00-1.00) | 1.00 (1.00-1.00) |
| Cohabitation | 0.73 (0.69-0.78) | 0.97 (0.91-1.04) | 0.97 (0.91-1.03) | 0.98 (0.92-1.04) |
| Education | ||||
| Mandatory | 1.62 (1.51-1.73) | 1.42 (1.30-1.54) | 1.39 (1.28-1.51) | 1.36 (1.25-1.48) |
| Short | 1.10 (1.03-1.17) | 1.17 (1.09-1.25) | 1.16 (1.08-1.23) | 1.15 (1.08-1.23) |
| Medium | 0.86 (0.75-0.99) | 0.89 (0.77-1.02) | 0.88 (0.76-1.02) | 0.88 (0.77-1.02) |
| High | 1.00 (ref) | 1.00 (ref) | 1.00 (ref) | 1.00 (ref) |
| Previous psychiatric history | ||||
| None | 1.00 (ref) | 1.00 (ref) | 1.00 (ref) | 1.00 (ref) |
| 0-3 years before birth | 14.77 (13.76-15.85) | 14.28 (13.29-15.34) | 14.09 (13.11-15.13) | 13.49 (12.55-14.49) |
| 3-10 years before birth | 12.39 (11.65-13.18) | 11.97 (11.25-12.74) | 11.75 (11.04-12.51) | 11.17 (10.48-11.89) |
| 10+ years before birth | 7.03 (6.27-7.87) | 6.69 (5.97-7.50) | 6.60 (5.88-7.40) | 6.27 (5.59-7.03) |
| Postpartum hemorrhage (%) | 1.40 (1.28-1.53) | ― | 1.39 (1.27-1.52) | 1.38 (1.26-1.51) |
| Gestational diabetes (%) | 1.91 (1.66-2.19) | ― | 1.32 (1.15-1.52) | 1.32 (1.14-1.51) |
| Gestational hypertension (%) | 1.40 (1.20-1.63) | ― | 1.21 (1.03-1.42) | 1.20 (1.02-1.40) |
| Preeclampsia (%) | 1.36 (1.22-1.51) | ― | 1.15 (1.03-1.29) | 1.15 (1.03-1.29) |
| Eclampsia (%) | 2.10 (1.08-4.09) | ― | 1.40 (0.70-2.81) | 1.43 (0.71-2.87) |
| Previous stillbirths (%) | 1.09 (0.78-1.51) | ― | 0.74 (0.53-1.03) | 0.74 (0.53-1.03) |
| Previous abortion (%) | 1.27 (1.21-1.35) | ― | 0.99 (0.93-1.05) | 0.98 (0.93-1.04) |
| Acute C-section (%) | 1.40 (1.32-1.49) | ― | 1.21 (1.13-1.29) | 1.20 (1.13-1.29) |
| Preterm birth (%) | 1.58 (1.45-1.72) | ― | 1.35 (1.23-1.47) | 1.35 (1.23-1.47) |
| Hyperemesis gravidarum (%) | 2.34 (2.03-2.71) | ― | 1.69 (1.46-1.96) | 1.67 (1.44-1.93) |
| Charlson comorbidity score, within 10 years before birth | ― | ― | ||
| 0 | 1.00 (ref) | ― | ― | 1.00 (ref) |
| 1 | 1.76 (1.58-1.96) | ― | ― | 1.11 (1.00-1.24) |
| 2+ | 1.47 (1.19-1.81) | ― | ― | 0.86 (0.69-1.07) |
| Parents previous psychiatric history (%) | 2.12 (1.99-2.24) | ― | ― | 1.44 (1.36-1.53) |
Data from development dataset, 1997–2012, N = 352,608.
Internal validation (reproducibility)
Performance of our three models was evaluated by calculating the predicted probability of PPD for each woman based on the estimated coefficients from the three developed models: Core, Extended, and Extended+. Within the development sample, the performance measured by the c-index ranged between 0.795-0.809, depending on how detailed the model was, Table 3. The average optimism of the performance within each model was small, resulting in an optimism-corrected c-index reducing the three c-estimates by a maximum of 0.001 (results not shown). This also implied that uniform shrinkage, using the optimism-corrected slope (Table 3), had limited influence on the models.
Table 3.
Performance within internal and internal-external validation, including recalibrated intercept and slope of the three models.
| AUC (95%CI) | Calibration intercept | Calibration slope | CHCH test, p | |
|---|---|---|---|---|
| Internal, 1997–2012 | ||||
| Core | 0.795 (0.790-0.802) | 0.001a | 1.000a | 0.082 |
| Ext | 0.801 (0.796-0.807) | −0.007a | 0.998a | 0.060 |
| Ext+ | 0.809 (0.804-0.815) | −0.005a | 0.999a | 0.003 |
| Internal-external, 2013–2015 | ||||
| Core | 0.804 (0.796-0.812) | 0.140 | 1.079 | 0.165b |
| Ext | 0.808 (0.800-0.816) | 0.107 | 1.068 | 0.144b |
| Ext+ | 0.812 (0.804-0.820) | 0.091 | 1.074 | 0.126b |
aThe optimism-corrected calibration intercept and –slope, estimated using 200 bootstrapped samples. The slope is equivalent to the uniform shrinkage factor mentioned in the section Internal validation.
bThe CHCH goodness of fit test is specified for the recalibrated models. The tests were rejected when considering the fit of the three developed models within the validation sample (p < 0.001, results not shown).
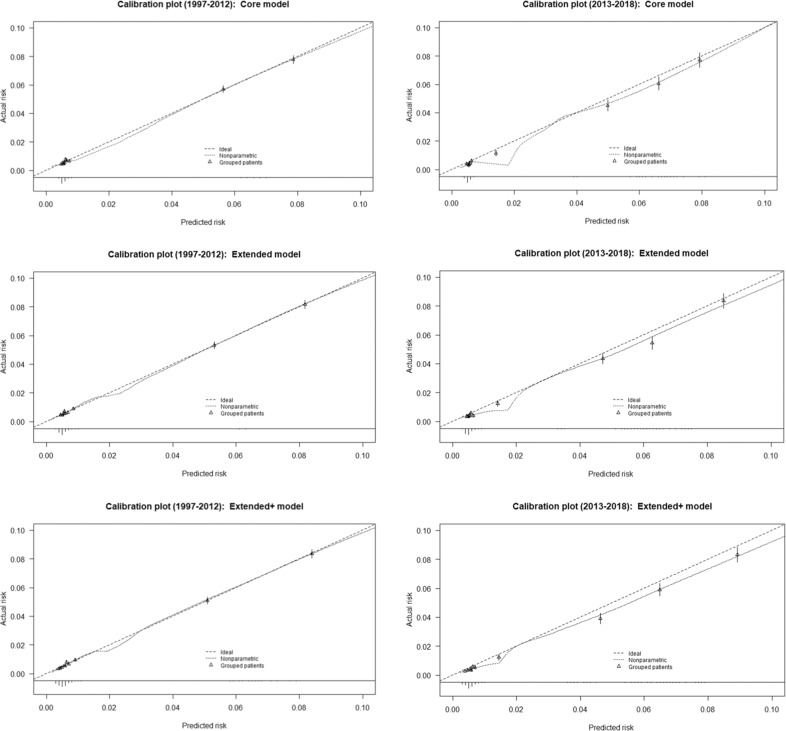
The calibration plots showed low predicted probabilities primarily distributed between 0 and 0.01, Fig. 2. Within predicted probabilities of around 0.02, each of the three models overestimated the risk of PPD. However, the CHCH goodness of fit test was not rejected for the Core and Extended model [42], see Table 3.
Fig. 2. Calibration plots.
Core, Extended and the Extended+ model for the development (years 1997–2012) and validation dataset (years 2013–2018).
Internal-external validation (transportability)
The performance of the models within another dataset (the validation dataset), containing women with a first-time birth in 2013–2018 showed slightly higher discrimination for all three models. The c-index ranged from 0.804-0.812 depending on how detailed the model was (Table 3) but was not significantly different from the c-index within each model from the development sample (DeLong test, p = 0.07–0.53 respectively).
The calibration plots (Fig. 2) showed the three models overestimated the risk of PPD within the validation sample. This was confirmed by the-calibration-in-the-large intercept within all three models being below zero (−0.13 to −0.10, results not shown). The calibration slope was between 1.07–1.08 (Table 3), suggesting the model was slightly underfitting. The CHCH goodness of fit test was rejected for all three models.
Because all three models on average overestimated risk of PPD within the validation sample, we updated our models using recalibrating methods [50]. We adjusted the logistic regression coefficients corresponding to the recalibration model, logit(Yval = 1) = a + boverall * LPval. These methods enhanced the calibration within all three models (Table 3) without changing the discrimination and the CHCH goodness of fit test was not rejected for any of the recalibrated models.
Recommended final model
Discrimination increased depending on the number of variables included in the models, but was good for all three models, and remained good and not significantly different from the validation sample. In contrast, calibration was not optimal, as plots indicated all models overpredicted the probability of PPD, which worsened within the validation sample. To improve calibration, we adjusted our models using recalibration techniques, and all three recalibrated models could not be rejected according to the CHCH goodness of fit test. The calibration slope closest to 1 was seen in the Extended model, where the calibration-in-the-large also was the smallest (−0.101). We did not see substantial differences in performance between the three models, but based on our joint results recommend the recalibrated Extended model for future methods development due to its test performance. Coefficients in the Extended model can be found in Table 4. Moving forward, we expect this particular model will be relatively easy to use in a clinical setting.
Table 4.
Coefficients in the Extended model.
| Development (1997–2012), αdev and βdev | Validation (2013–2018), αval and βval | Recalibrated model* | |
|---|---|---|---|
| Intercept | −2.74 | −4.22 | −2.82 |
| Mothers age at birth | −0.33 | −0.30 | −0.35 |
| Age2 | 0.01 | 0.01 | 0.01 |
| Age3 | −0.00 | −0.00 | −0.00 |
| Cohabitation | −0.03 | 0.12 | −0.04 |
| Education | |||
| Mandatory | 0.33 | 0.38 | 0.35 |
| Short | 0.14 | 0.16 | 0.15 |
| Medium | −0.13 | 0.00 | −0.13 |
| High | Ref | Ref | Ref |
| Previous psychiatric history | |||
| None | Ref | Ref | Ref |
| Within 3 years before birth | 2.65 | 3.12 | 2.83 |
| 3–10 years before birth | 2.46 | 2.55 | 2.63 |
| 10+ years before birth | 1.89 | 2.14 | 2.02 |
| Postpartum hemorrhage (%) | 0.33 | 0.02 | 0.35 |
| Gestational diabetes (%) | 0.28 | 0.23 | 0.30 |
| Gestational hypertension (%) | 0.19 | 0.05 | 0.20 |
| Preeclampsia (%) | 0.14 | 0.16 | 0.15 |
| Eclampsia (%) | 0.34 | −7.33 | 0.36 |
| Previous stillbirths (%) | −0.30 | −0.06 | −0.32 |
| Previous abortion (%) | −0.01 | −0.12 | −0.01 |
| Acute c-section (%) | 0.19 | 0.03 | 0.20 |
| Preterm birth (%) | 0.30 | 0.49 | 0.32 |
| Hyperemesis gravidarum (%) | 0.53 | 0.63 | 0.56 |
*To calculate the coefficients in the recalibrated model, the estimates αnew and βoverall has to be added and multiplied, respectively, to the original model (here the Extended model).
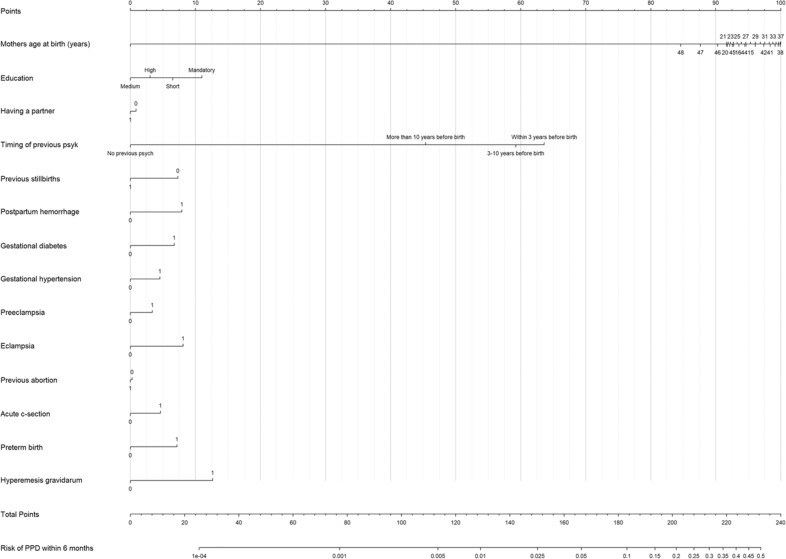
The final model (recalibrated version of the Extended model) is presented in a nomogram (Fig. 3), illustrating each predictor assigned certain points (first line in the figure), and can be used the following way: A woman’s probability of PPD can be calculated by summing up all individual points assigned to the woman’s covariates, and the total number of points is then translated into the probability of PPD, illustrated by the lowest two lines in the figure. As demonstrated in Fig. 3, predictors affecting the probability of PPD the most were previous psychiatric history closest to childbirth, maternal age around mid/late thirties, a low education, and hyperemesis gravidarum, corresponding to points around 100, 64, 11, and 13, respectively.
Fig. 3.
Nomogram.
Finally, a sensitivity of 0.87, a specificity of 0.69, and a positive predictive value (PPV) of 0.06 were observed within the validation sample. This was calculated with the predicted probabilities from the recalibrated Extended model, applying a threshold of 0.025 defined by maximizing the sum of sensitivity and specificity (Table 5a). Within the combined dataset, consisting of 461,457 women, the sensitivity decreased, and the specificity increased to 0.78 with the same optimal threshold and a slightly higher PPV (Table 5b). Considering increasing threshold values applied in Table 5b, we as expected observed the sensitivity decreased while the specificity and PPV increased.
Table 5.
Sensitivity and specificity in the recalibrated Extended model.
| (a) Confusion matrix, threshold = 0.025 | ||
|---|---|---|
| Threshold = 0.025 | PPD | No PPD |
| Predicted PPD: yes | 6813 | 98,754 |
| Predicted PPD: no | 1968 | 353,922 |
| (b) Sensitivity and specificity for different threshold values, within the combined dataset consisting of 461,457 women | |||
|---|---|---|---|
| Threshold | Sens | Spec | PPV |
| 0.005 | 0.844 | 0.597 | 0.039 |
| 0.025a | 0.776 | 0.782 | 0.065 |
| 0.05 | 0.657 | 0.837 | 0.072 |
| 0.1 | 0.059 | 0.991 | 0.114 |
| 0.15 | 0.005 | 0.999 | 0.144 |
aMaximizes the sum of sensitivity and specificity.
Discussion
For the present study, we developed three PPD prediction models (Core, Extended, and Extended+) in a large population-based cohort. Discrimination and calibration were best within the Extended and Extended+ models. As we found a negligible difference in performance between the Extended and Extended+ model, we recommend the recalibrated Extended model for further development in future work. Moving forward, we also speculate that this model can be implemented in the clinical setting whenever feasible.
Our models have been developed, acknowledging how this work could in the future guide clinicians in their decision making about additional testing, informing patients about their individualized risk with the use of a risk-calculator (https://ncrr-au.shinyapps.io/PPDRiskCalc/), but also support considerations about time-sensitive and cost-effective treatment/intervention [51]. In the future, prediction models hopefully will augment clinical decisions as suggested by Steyerberg et al. [52], raise clinician awareness of PPD, guide interventions, increase screening and referral rates [18], and through this, prevent serious psychiatric episodes. However, we strongly emphasize multiple steps are needed before our model or similar work can be implemented in real-world clinical routines. We note that this is a challenge not only related to PPD prediction, as Meehan et al. recently found only one out of 308 published prediction models within psychiatry was formally evaluated and assessed for usefulness in clinical care [53]. We propose that moving forward any efforts toward clinical implementation could include engagement with stakeholders, including patients, clinicians, and politicians, to evaluate how to maximize the translational potential of our model as well as models from other groups.
Prediction of PPD risk
Of the existing published papers on PPD risk prediction, several have applied machine learning approaches [17–20]. Among others, these studies considered predictor variables related to previous mental health, socioeconomic status, as well as obstetric and childbirth-related variables, and found past history of depression and anxiety as some of the most important predictor variables, as well as stress in pregnancy. Aggregate measures of model performance varied from 81 to 93 (AUCs) compared to AUCs of about 80 in the present study (Table 3), but direct comparisons are challenging as studies used different statistical methods, defined PPD at different time points and through different PPD measures, including self-reported symptoms not included in population registers, psychiatric admissions, and prescription drug use (antidepressants).
Methodological considerations, limitations, and next steps
To our knowledge, our study included the largest sample to date with 6402 PPD cases (development sample) and 2379 PPD cases (validation sample), and our cohort represents a national population of primiparous women diminishing potential bias due to attrition and low response rates. We suggest our Extended model will be preferable moving forward, among others, based on an acceptable AUC, discrimination, and calibration. However, our model is yet to be validated in an external dataset and this would be the next development step in our work. We also consider adding additional predictor variables to the model and test how this affects model performance, while at the same time remembering predicting rare outcomes and new PPD episodes is challenging [20, 54]. PPD prevalence in our current sample is only around 2%, reflecting the diagnosis/treatment prevalence but not the illness prevalence. Hence, another next step, after further validation, would be to evaluate whether the model can be used for a different outcome, e.g., PPD defined by symptoms assessed using the Edinburg Postnatal Depression Scale (EPDS) [55]. Limitations of the study must be considered, including the generalizability of our findings including considering to which extent our models reflect the Danish health care system and treatment standards for more severe PPD episodes, as well as acknowledging our list of PPD predictors is far from exhaustive. We additionally speculate that for subgroups of particularly vulnerable mothers, aspects related to socioeconomic conditions may trump our included variables, and issues related to e.g. history of trauma or immigration status will be highly relevant to consider moving forward. However, this type of information was unfortunately not available in our dataset and hence could not be included.
As pointed out by Fusar-Poli et al., more models are developed than are used in clinical settings, likely because many are too complex [51]. We prioritized including predictor variables in our work that are clinically applicable, easy to identify, and rely on information that should be readily available at time of delivery. We also prioritized presenting results for both discrimination, calibration, and validation, all aspects being equally important when developing prediction models. However, we acknowledge that prognostic models with increasing complexity could be relevant and preferable in cases where prediction ability also is improved. Such an expansion of the model could include self-reported measures (e.g., maternal resilience), as well as genetic vulnerability measured as polygenic scores or biomarkers measuring hormonal sensitivity, which all have been linked to PPD risk [18, 20, 56–58]. Moreover, we acknowledge that our final recommended model will have a substantial proportion of false positive tests, but importantly also capture 76% of the women who will end up developing PPD. In summary, we here argue that the field of perinatal psychiatry may not need more PPD prediction models, but progress can be ensured through existing models being further validated, expanded, and strengthened in relation to performance and reproducibility, calling for standardized data collection and extended collaborations.
In conclusion, we developed three prediction models for PPD (Core, Extended, and Extended+), and validated and recalibrated them accordingly. Our recalibrated Extended model with 14 variables achieved the highest performance, with satisfying calibration and discrimination. Previous psychiatric history, maternal age, low education, and hyperemesis gravidarum were the most important identified predictors in our final PPD prediction model in primiparous women.
The developed risk calculator is available online but is not at present ready for direct implementation in clinical care before additional validation has been performed. A future developed and validated PPD prediction model could ideally assist and add to prevention efforts, as recently recommended by the US Preventive Services Task Force [12]. A more specific focus on who will benefit from preventive PPD interventions is, however, to our knowledge, not included in any of the existing published PPD prediction models but will be an evident next step for the research field. This will be particularly relevant as part of a discussion on possible adjustments for how and when systematic screening can supplement the prediction of PPD, while also considering both potential consequences from false positive and false negative test results applied using different threshold values and which protective effects can reduce PPD risk.
Supplementary information
Author contributions
MLM had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis. Concept and design: TMO and MLM Drafting the manuscript: TMO Statistical analysis: MLM Interpretation of data and critical revision of the manuscript for important intellectual content: All authors. Obtained funding: TMO Administrative, technical, or material support: TMO.
Funding
T.M.O., V.B., and K.B.M. are supported by the National Institute of Mental Health (NIMH) (R01MH122869). T.M.O., M.Z.K., and M.L.M. are supported by Lundbeck foundation (R313-2019-569). X.L. is supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie (grant agreement No 891079). V.G.F. is supported by Independent Research Fund Denmark | Medical Sciences, Grant IDs: 7016-00265B & 7025-00111B. A.S. is supported by Swedish Research Council, Grant ID: 2020-01965
Competing interests
A.S. has earlier served as a consultant for Biogen and Ferring Pharmaceuticals. S.V. receives royalties from UpToDate Inc for authorship of materials related to depression and pregnancy. V.G.F. has served as a consultant for Sage Therapeutics and H. Lundbeck. The rest of the author group declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41398-022-02190-8.
References
- 1.Johannsen BM, Larsen JT, Laursen TM, Bergink V, Meltzer-Brody S, Munk-Olsen T. All-cause mortality in women with severe postpartum psychiatric disorders. Am J Psychiatry. 2016:173:638–42. [DOI] [PMC free article] [PubMed]
- 2.Johannsen BM, Larsen JT, Laursen TM, Ayre K, Howard LM, Meltzer-Brody S, et al. Self-harm in women with postpartum mental disorders. Psychol Med. 2019:50:1563–9. [DOI] [PubMed]
- 3.Meltzer-Brody S, Howard LM, Bergink V, Vigod S, Jones I, Munk-Olsen T, et al. Postpartum psychiatric disorders. Nat Rev Dis Prim. 2018;4:18022. doi: 10.1038/nrdp.2018.22. [DOI] [PubMed] [Google Scholar]
- 4.Howard LM, Molyneaux E, Dennis CL, Rochat T, Stein A, Milgrom J. Non-psychotic mental disorders in the perinatal period. Lancet. 2014;384:1775–88. doi: 10.1016/S0140-6736(14)61276-9. [DOI] [PubMed] [Google Scholar]
- 5.Stewart DE, Vigod S. Postpartum depression. N. Engl J Med. 2016;375:2177–86. doi: 10.1056/NEJMcp1607649. [DOI] [PubMed] [Google Scholar]
- 6.Liu X, Agerbo E, Li J, Meltzer-Brody S, Bergink V, Munk-Olsen T. Depression and anxiety in the postpartum period and risk of bipolar disorder: a Danish nationwide register-based cohort study. J Clin Psychiatry. 2017;78:e469–e476. doi: 10.4088/JCP.16m10970. [DOI] [PubMed] [Google Scholar]
- 7.Halbreich U, Karkun S. Cross-cultural and social diversity of prevalence of postpartum depression and depressive symptoms. J Affect Disord. 2006;91:97–111. doi: 10.1016/j.jad.2005.12.051. [DOI] [PubMed] [Google Scholar]
- 8.Meltzer-Brody S, Maegbaek ML, Medland SE, Miller WC, Sullivan P, Munk-Olsen T. Obstetrical, pregnancy and socio-economic predictors for new-onset severe postpartum psychiatric disorders in primiparous women. Psychol Med. 2017;47:1427–41. doi: 10.1017/S0033291716003020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meltzer-Brody SL, JT Pedersen, L. Munk-Olsen, T Early life adversity and risk of postpartum psychiatric episodes. Depress Anxiety. 2017; In press. [DOI] [PMC free article] [PubMed]
- 10.Wisner KL, Sit DK, McShea MC, Rizzo DM, Zoretich RA, Hughes CL, et al. Onset timing, thoughts of self-harm, and diagnoses in postpartum women with screen-positive depression findings. JAMA Psychiatry. 2013:70:490–8. [DOI] [PMC free article] [PubMed]
- 11.O’Connor E, Senger CA, Henninger ML, Coppola E, Gaynes BN. Interventions to prevent perinatal depression: evidence report and systematic review for the US Preventive Services Task Force. JAMA. 2019;321:588–601. doi: 10.1001/jama.2018.20865. [DOI] [PubMed] [Google Scholar]
- 12.Force USPST. Curry SJ, Krist AH, Owens DK, Barry MJ, Caughey AB, et al. Interventions to prevent perinatal depression: US Preventive Services Task Force Recommendation Statement. JAMA. 2019;321:580–7. doi: 10.1001/jama.2019.0007. [DOI] [PubMed] [Google Scholar]
- 13.Salazar de Pablo G, Studerus E, Vaquerizo-Serrano J, Irving J, Catalan A, Oliver D, et al. Implementing precision psychiatry: a systematic review of individualized prediction models for clinical practice. Schizophr Bull. 2021;47:284–97. doi: 10.1093/schbul/sbaa120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vigod SN, Kurdyak PA, Seitz D, Herrmann N, Fung K, Lin E, et al. READMIT: a clinical risk index to predict 30-day readmission after discharge from acute psychiatric units. J Psychiatr Res. 2015;61:205–13. doi: 10.1016/j.jpsychires.2014.12.003. [DOI] [PubMed] [Google Scholar]
- 15.Bernardini F, Attademo L, Cleary SD, Luther C, Shim RS, Quartesan R, et al. Risk prediction models in psychiatry: toward a new frontier for the prevention of mental illnesses. J Clin Psychiatry. 2017;78:572–83. doi: 10.4088/JCP.15r10003. [DOI] [PubMed] [Google Scholar]
- 16.Maracy MR, Kheirabadi GR. Development and validation of a postpartum depression risk score in delivered women, Iran. J Res Med Sci. 2012;17:1067–71. [PMC free article] [PubMed] [Google Scholar]
- 17.Shin D, Lee KJ, Adeluwa T, Hur J. Machine learning-based predictive modeling of postpartum depression. J Clin Med. 2020;9:2899. [DOI] [PMC free article] [PubMed]
- 18.Zhang Y, Wang S, Hermann A, Joly R, Pathak J. Development and validation of a machine learning algorithm for predicting the risk of postpartum depression among pregnant women. J Affect Disord. 2021;279:1–8. doi: 10.1016/j.jad.2020.09.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hochman E, Feldman B, Weizman A, Krivoy A, Gur S, Barzilay E, et al. Development and validation of a machine learning-based postpartum depression prediction model: a nationwide cohort study. Depress Anxiety. 2021;38:400–11. doi: 10.1002/da.23123. [DOI] [PubMed] [Google Scholar]
- 20.Andersson S, Bathula DR, Iliadis SI, Walter M, Skalkidou A. Predicting women with depressive symptoms postpartum with machine learning methods. Sci Rep. 2021;11:7877. doi: 10.1038/s41598-021-86368-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Beck CT. Revision of the postpartum depression predictors inventory. J Obstet Gynecol Neonatal Nurs. 2002;31:394–402. doi: 10.1111/j.1552-6909.2002.tb00061.x. [DOI] [PubMed] [Google Scholar]
- 22.Meads C, Ahmed I, Riley RD. A systematic review of breast cancer incidence risk prediction models with meta-analysis of their performance. Breast Cancer Res Treat. 2012;132:365–77. doi: 10.1007/s10549-011-1818-2. [DOI] [PubMed] [Google Scholar]
- 23.Al-Ajmi K, Lophatananon A, Yuille M, Ollier W, Muir KR. Review of non-clinical risk models to aid prevention of breast cancer. Cancer Causes Control. 2018;29:967–86. doi: 10.1007/s10552-018-1072-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Damen JA, Hooft L, Schuit E, Debray TP, Collins GS, Tzoulaki I, et al. Prediction models for cardiovascular disease risk in the general population: systematic review. BMJ. 2016;353:i2416. doi: 10.1136/bmj.i2416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Moons KG, Kengne AP, Grobbee DE, Royston P, Vergouwe Y, Altman DG, et al. Risk prediction models: II. External validation, model updating, and impact assessment. Heart. 2012;98:691–8. doi: 10.1136/heartjnl-2011-301247. [DOI] [PubMed] [Google Scholar]
- 26.Moons KG, Kengne AP, Woodward M, Royston P, Vergouwe Y, Altman DG, et al. Risk prediction models: I. Development, internal validation, and assessing the incremental value of a new (bio)marker. Heart. 2012;98:683–90. doi: 10.1136/heartjnl-2011-301246. [DOI] [PubMed] [Google Scholar]
- 27.Tzoulaki I, Liberopoulos G, Ioannidis JP. Assessment of claims of improved prediction beyond the Framingham risk score. JAMA. 2009;302:2345–52. doi: 10.1001/jama.2009.1757. [DOI] [PubMed] [Google Scholar]
- 28.Mahmood SS, Levy D, Vasan RS, Wang TJ. The Framingham Heart Study and the epidemiology of cardiovascular disease: a historical perspective. Lancet. 2014;383:999–1008. doi: 10.1016/S0140-6736(13)61752-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pedersen CB. The Danish Civil Registration System. Scand J Public Health. 2011;39:22–5. doi: 10.1177/1403494810387965. [DOI] [PubMed] [Google Scholar]
- 30.Mors O, Perto GP, Mortensen PB. The Danish Psychiatric Central Research Register. Scand J Public Health. 2011;39:54–7. doi: 10.1177/1403494810395825. [DOI] [PubMed] [Google Scholar]
- 31.Kildemoes HW, Sorensen HT, Hallas J. The Danish National Prescription Registry. Scand J Public Health. 2011;39:38–41. doi: 10.1177/1403494810394717. [DOI] [PubMed] [Google Scholar]
- 32.Bliddal M, Broe A, Pottegård A, Olsen J, Langhoff-Roos J. The Danish Medical Birth Register. Eur J Epidemiol. 2018;33:27–36. doi: 10.1007/s10654-018-0356-1. [DOI] [PubMed] [Google Scholar]
- 33.Petersson F, Baadsgaard M, Thygesen LC. Danish registers on personal labour market affiliation. Scand J Public Health. 2011;39:95–8. doi: 10.1177/1403494811408483. [DOI] [PubMed] [Google Scholar]
- 34.Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. J Chronic Dis. 1987;40:373–83. doi: 10.1016/0021-9681(87)90171-8. [DOI] [PubMed] [Google Scholar]
- 35.Royston P, Moons KG, Altman DG, Vergouwe Y. Prognosis and prognostic research: developing a prognostic model. BMJ. 2009;338:b604. doi: 10.1136/bmj.b604. [DOI] [PubMed] [Google Scholar]
- 36.Collins GS, Reitsma JB, Altman DG, Moons KG. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMJ. 2015;350:g7594. doi: 10.1136/bmj.g7594. [DOI] [PubMed] [Google Scholar]
- 37.Debray TP, Vergouwe Y, Koffijberg H, Nieboer D, Steyerberg EW, Moons KG. A new framework to enhance the interpretation of external validation studies of clinical prediction models. J Clin Epidemiol. 2015;68:279–89. doi: 10.1016/j.jclinepi.2014.06.018. [DOI] [PubMed] [Google Scholar]
- 38.Steyerberg EW. Clinical prediction models: a practical approach to development, validation, and updating. place of publication not identified. Springer; 2019.
- 39.Austin PC, van Klaveren D, Vergouwe Y, Nieboer D, Lee DS, Steyerberg EW. Geographic and temporal validity of prediction models: different approaches were useful to examine model performance. J Clin Epidemiol. 2016;79:76–85. doi: 10.1016/j.jclinepi.2016.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Steyerberg EW, Borsboom GJ, van Houwelingen HC, Eijkemans MJ, Habbema JD. Validation and updating of predictive logistic regression models: a study on sample size and shrinkage. Stat Med. 2004;23:2567–86. doi: 10.1002/sim.1844. [DOI] [PubMed] [Google Scholar]
- 41.Hosmer DW, Hosmer T, Le Cessie S, Lemeshow S. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med. 1997;16:965–80. doi: 10.1002/(SICI)1097-0258(19970515)16:9<965::AID-SIM509>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 42.Nattino G, Pennell ML, Lemeshow S. Assessing the goodness of fit of logistic regression models in large samples: a modification of the Hosmer-Lemeshow test. Biometrics. 2020;76:549–60. doi: 10.1111/biom.13249. [DOI] [PubMed] [Google Scholar]
- 43.R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria, www.R/project.org/.
- 44.Frank E. Harrell Jr. rms: Regression Modeling Strategies. R package version 6.2-0. cran.r-project.org/web/packages/rms. 2021.
- 45.hltest: Modified Hosmer-Lemeshow Test for Large Samples. https://rdrr.io/github/gnattino/largesamplehl/man/hltest.html.
- 46.Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez JC, et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Frank E. Harrell Jr, with contributions from Charles Dupont and many others (2020). Hmisc: Harrell Miscellaneous. R package version 4.4-2. CRAN.R-project.org/package=Hmisc.
- 48.Max Kuhn. caret: Classification and Regression Training. R package version 6.0-86. CRAN.R-project.org/package=caret. 2020.
- 49.Chang W, Cheng J, Allaire JJ, Sievert C, Schloerke B, Xie Y, et al. shiny: Web Application Framework for R. R package version 1.7.1. 2021. https://CRAN.R-project.org/package=shiny.
- 50.Steyerberg EW. Clinical prediction models. a practical approach to development, validation, and updating. Springer. 2009.
- 51.Fusar-Poli P, Hijazi Z, Stahl D, Steyerberg EW. The science of prognosis in psychiatry: a review. JAMA Psychiatry. 2018;75:1289–97. doi: 10.1001/jamapsychiatry.2018.2530. [DOI] [PubMed] [Google Scholar]
- 52.Steyerberg EW, Mushkudiani N, Perel P, Butcher I, Lu J, McHugh GS, et al. Predicting outcome after traumatic brain injury: development and international validation of prognostic scores based on admission characteristics. PLoS Med. 2008;5:e165. doi: 10.1371/journal.pmed.0050165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Meehan AJ, Lewis SJ, Fazel S, Fusar-Poli P, Steyerberg EW, Stahl D, et al. Clinical prediction models in psychiatry: a systematic review of two decades of progress and challenges. Mol Psychiatry. 2022;27:2700–8. doi: 10.1038/s41380-022-01528-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Poldrack RA, Huckins G, Varoquaux G. Establishment of best practices for evidence for prediction: a review. JAMA Psychiatry. 2020;77:534–40. doi: 10.1001/jamapsychiatry.2019.3671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cox JL, Holden JM, Sagovsky R. Detection of postnatal depression. Development of the 10-item Edinburgh Postnatal Depression Scale. Br J Psychiatry. 1987;150:782–6. doi: 10.1192/bjp.150.6.782. [DOI] [PubMed] [Google Scholar]
- 56.Byrne EM, Carrillo-Roa T, Penninx BW, Sallis HM, Viktorin A, Chapman B, et al. Applying polygenic risk scores to postpartum depression. Arch Womens Ment Health. 2014;17:519–28. [DOI] [PMC free article] [PubMed]
- 57.Bauer AE, Liu X, Byrne EM, Sullivan PF, Wray NR, Agerbo E, et al. Genetic risk scores for major psychiatric disorders and the risk of postpartum psychiatric disorders. Transl Psychiatry. 2019;9:288. doi: 10.1038/s41398-019-0629-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mehta D, Rex-Haffner M, Sondergaard HB, Pinborg A, Binder EB, Frokjaer VG. Evidence for oestrogen sensitivity in perinatal depression: pharmacological sex hormone manipulation study. Br J Psychiatry. 2019;215:519–27. doi: 10.1192/bjp.2018.234. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.