Combining egoformative and alloformative cues in a novel tabletop navigation task

Abstract

Previous work has shown how different interfaces (i.e., route navigation, maps, or a combination of the two) influence spatial knowledge and recollection. To test for the existence of intermediate representations along an egocentric-to-allocentric continuum, we developed a novel task, tabletop navigation, to provide a mixture of cues that inform the emergence of egocentric and allocentric representations or strategies. In this novel tabletop task, participants navigated a remote-controlled avatar through a tabletop scale model of the virtual city. Participants learned virtual cities from either navigating routes, studying maps, or our new tabletop navigation task. We interleaved these learning tasks with either an in situ pointing task (the scene- and orientation-dependent pointing [SOP] task) or imagined judgements of relative direction (JRD) pointing. In Experiment 1, performance on each memory task was similar across learning tasks and performance on the route and map learning tasks correlated with more precise spatial recall on both the JRD and SOP tasks. Tabletop learning performance correlated with SOP performance only, suggesting a reliance on egocentric strategies, although increased utilization of the affordances of the tabletop task were related to JRD performance. In Experiment 2, using a modified criterion map learning task, participants who learned using maps provided more precise responses on the JRD compared to route or tabletop learning. Together, these findings provide mixed evidence for both optimization and egocentric predominance after learning from the novel tabletop navigation task.

Supplementary Information

The online version contains supplementary material available at 10.1007/s00426-022-01739-y.

Encoding spatial information and retrieving spatial representations

Navigating the spaces that comprise our daily experiences requires the integration of many different forms of input. This includes cues like landmarks, which we can use (in part) to reorient and compute the locations of our goals, and orientation cues derived from movement, which we use to update our position within the environment continuously as we move (Ekstrom et al., 2014). Broadly speaking, these inputs can be classified into the categories of “alloformative” and “egoformative” cues or information,1 although note that these labels likely exist as a continuum rather than as distinct categories (Starrett & Ekstrom, 2018). Alloformative cues are primarily related to the layout of an environment (e.g., relative positions of landmarks) and lend themselves to the formation of allocentric knowledge. In contrast, egoformative cues are primarily related to one’s position within an environment and lend themselves to the formation of egocentric knowledge. As we navigate, it is necessary to update the relationship between egocentric and allocentric knowledge, for example, updating our position based on the surrounding landmarks.

To test egocentric and allocentric forms of knowledge, one needs assays that can provide partial insight into one form of knowledge compared to another. For example, success in the judgements of relative direction (JRD) pointing task (Waller & Hodgson, 2006) depends on knowing the positions of the three landmarks that make up a given trial (“Imagine standing at Landmark 1, facing Landmark 2; point to Landmark 3.”). The first two landmarks are used to establish the imagined location and heading, and the third establishes the angular relationship to be recalled. Because the JRD task puts high demands on remembering the configurations of landmarks in the environment, it is generally taken as a measure of allocentric knowledge (although note that the task also involves some aspects that can be considered egocentric, i.e., the heading implies a viewpoint; Huffman & Ekstrom, 2019). In contrast, egocentric knowledge is often tested using the scene- and orientation-dependent pointing (SOP) task. In the SOP task, participants point to hidden landmarks in the learned space while oriented within the learned space2; thus, only one landmark composes the prompt for an SOP trial (“Point to Landmark 4.”). As with the JRD, although SOP favors egocentric representations of space, knowing the configurations of Landmarks within the environment still provides some benefit to success on the SOP task (Ekstrom et al., 2014; Starrett & Ekstrom, 2018).

Two types of interfaces that appear to favor egoformative and alloformative cues are route and map learning, respectively (Meilinger et al., 2013; Richardson et al., 1999; Zhang et al., 2012, 2014). In such experiments, route learning typically occurs from a first-person perspective, such that participants must traverse the routes—multiple routes and vantage points are necessary to see relevant landmarks. In contrast, learning from a map typically occurs from an aerial (overhead) viewpoint of a flattened environment, providing information about landmarks and paths of travel within the environment.

Optimizing spatial memory with pre-integrated reference frame information

Previous work from our group has shown that participants can use either route learning or map learning, over time, to extract both alloformative information and/or egoformative information (Zhang et al., 2014). Thus, allocentric and egocentric representations, as measured by the JRD and SOP, respectively, can be established from a range of encoding conditions with varying ratios of alloformative and egoformative cues. In their study, participants completed interleaved blocks of learning from a map or navigation and a spatial memory task. Critically, in their first experiment, Zhang and colleagues demonstrated a selective benefit on the more allocentric JRD task after map learning compared to route learning, which emerged on the second learn-test cycle and diminished below significance by the fifth. In a second group of participants, they showed a selective benefit on the more egocentric SOP task. Thus Zhang et al. provided evidence that allocentric representations are optimized through alloformative learning and egocentric representations are optimized through egoformative learning (Zhang et al., 2014; see also Taylor & Tversky, 1992; Waller & Hodgson, 2006).

The primary motivation for the present study work was to determine whether it was possible to universally optimize participants spatial representations across egocentric and allocentric frames of reference. If so, participants should be able to deploy these representations flexibly and efficiently regardless of whether a spatial memory task is presumably more allocentric or egocentric. In light of findings that map and route learning provide selective benefits for allocentric and egocentric memory tasks, respectively, compared to one another, we sought to use the ‘sub-optimal’ learning modality (route learning for the JRD and map learning for the SOP) as a benchmark against which to contrast performance. A universally optimized learning task should then result in significantly enhanced performance on the JRD compared to route learning as well as significantly enhanced performance on the SOP compared to map learning. To this end, we designed a tabletop navigation task that combines route-based navigation learning with aerial viewpoints in a naturalistic desktop virtual reality (VR) learning task.

Hypothesized cognitive mechanisms for spatial cue-combination and integration

We expected that the tabletop navigation task would afford participants both turn-based information from their remote-controlled avatars paths through the tabletop environment to target stores and aerial views of the environment akin to a map (i.e., able to see all of it at once). The tabletop experience did not involve a fixed, “overhead” view but rather participants were free to dynamically change their preferred perspective by moving around the table. In Experiments 1a and 1b, we compared subsequent performance after route, map, or tabletop learning on judgements of relative direction (JRD) and scene- and orientation-dependent pointing (SOP) tasks. This allowed us to test the extent to which map learning contributes more to putative allocentric forms of knowledge, which should preferentially benefit the JRD task and allow determination of the extent to which route learning contributes more to egocentric forms of knowledge, which should preferentially benefit the SOP task. In Experiments 2a and 2b, we compared route and tabletop data from Experiment 1 with JRD and SOP performance after what we hypothesized to be a more ecologically variant of the map task—having participants reach a performance criterion rather than studying for a seemingly arbitrary period.3 In all experiments, we expected to observe a pattern of results across route and map learning on the JRD and SOP tasks consistent with the pattern described by Zhang et al.

Regarding tabletop navigation, our first prediction was that tabletop learning would yield a benefit for both JRD and SOP tasks such that the pattern of performance across blocks would resemble that of the optimal learning modality—map learning for the JRD and route learning for the SOP. Under this prediction, which we will refer to as the optimization hypothesis, we expected that performance on the JRD task would be superior after tabletop learning compared to route learning, while performance on the SOP task would be better after tabletop learning compared to map learning. The absence of any difference between tabletop navigation and an optimal encoding condition (JRD after map learning or SOP after route learning) would not, however, rule out the Optimization Hypothesis as it only makes predictions about differences between tabletop and a non-optimal encoding modality (SOP after map learning or JRD after route learning). An alternative, which we will refer to as the predomination hypothesis, would be consistent with previous work suggesting that allocentric reference frames may be established rapidly and are generally preferred or of greater utility, although egocentric reference frames may be favored when viewpoint information is present, especially if the allocentric knowledge is of low fidelity or contradicts available viewpoint information (Mou et al., 2006; Newman et al., 2007).

General method

Participants

Participants were Amazon Mechanical Turk (MTurk; Amazon.com Inc., Seattle, WA) workers, age 18–35, residing in the United States with an approval rate of at least 95% and at least 1000 approved MTurk submissions. The advertisement and instructions for the ‘human intelligence task’ on MTurk is shown in Supplemental Fig. S1. Participants were compensated $7.50 per block of the experiment that was completed, up to $45 for completing the entire experiment. Participants were not allowed to complete the study more than once. All participants provided informed consent prior to any study procedures, all of which were approved by the Institutional Review Board at the University of Arizona.

We estimated the sample size necessary based on the three-way interaction between encoding method (route, map), pointing task (JRD, SOP), and block (1–5)—reported by Zhang et al. (2014) using the Hotteling Lawyly Trace test in the online version of the General Linear Mixed Model Power and Sample Size (GLIMMPSE; Kreidler et al., 2013) calculator. A target power of 0.85 was selected instead of the traditional value of 0.80; this decision was informed by prior work showing a slight reduction in statistical power when recruiting from MTurk as compared to in-person laboratory studies (Sprouse, 2011). The power analysis resulted in an estimate of 32 participants per condition (256 total across the eight conditions in all experiments). Detailed information about the sample size estimation procedures can be found in the online supplemental materials.

In total, 448 MTurk workers participated in the experiments. Data from 256 participants were included in the final analyses across all conditions and experiments (see the section on data processing). Participants ranged from 18 to 35 years old (M = 30.54, SD = 3.73) and comprised 82 females and 173 males; one participant was missing demographic information due to a technical error. Demographics are reported for each experiment in-text and for each individual experimental condition in Supplemental Table S1.

Materials

Virtual environments

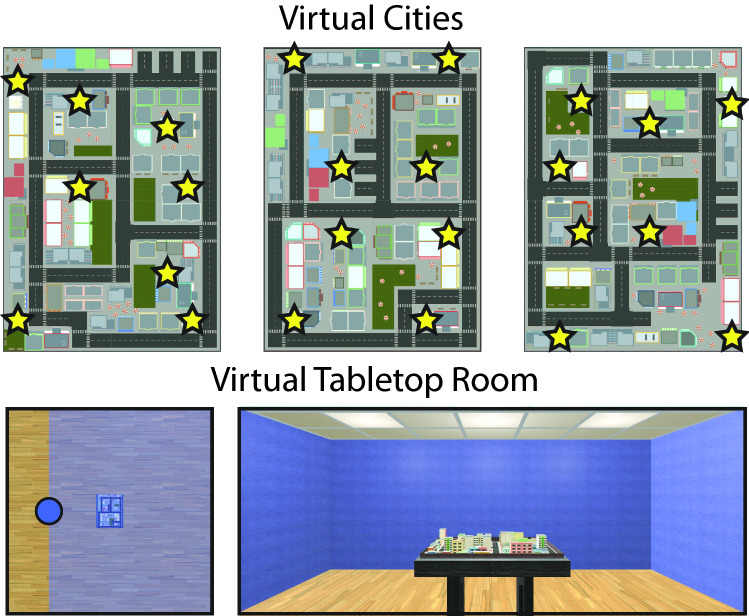
Three virtual cities, approximately 102 m × 142 m, were used in the study. Each contained the same collection of 3D models (grass, streets, sidewalks, arbitrary buildings) arranged in a different city configuration. Additionally, each city contained eight target locations, which were populated with target stores randomly sampled from a collection of 24 possible stores. Target stores were identifiable by a signboard on the front of the store with the name printed on it, icons in the windows and on the roof corresponding to that store (e.g., a bike for the Bike Shop), and exterior walls rendered in one unique, randomly selected color from the color alphabet (Green-Armytage, 2010). Each virtual city contained eight possible spawn points (i.e., starting locations) for navigation blocks, chosen to minimize visibility of any target location from a given spawn point. A list of possible store names and color information can be found in Supplemental Table S2. The three virtual cities are shown in the upper portion of Fig. 1.

Fig. 1.

Virtual Environments. Yellow (light gray) stars in the upper panels indicate the locations of target stores in the virtual cities. The blue (dark gray) circle and blue (gray) shading in the lower left panel frame the avatar position and field of view, respectively, shown in the lower right panel (color figure online)

An additional virtual environment was used for the tabletop navigation task, hereinafter referred to as the virtual tabletop room (Fig. 1, lower). We placed the scale model of the virtual environment on a table in a 6 m × 6 m virtual room. The virtual room was empty except for a table at its center—which was large enough accommodate a virtual city placed atop it without hanging over the edges—and was positioned such that, with a virtual city on the table, the virtual room was perceived as 6 m × 6 m with a 1:150 scale model of a virtual city on the table. The virtual room was only visible during the tabletop navigation task.

Encoding tasks

Route

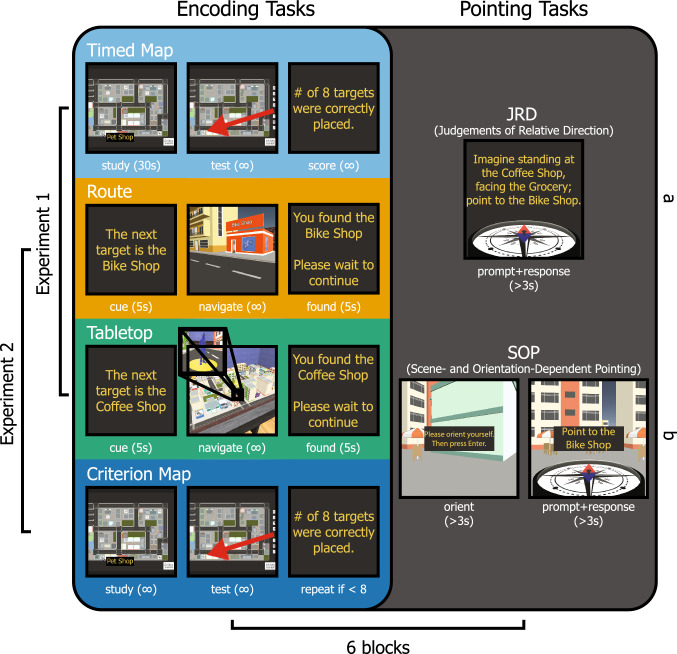
Participants’ virtual avatars began the task from one of eight pre-determined starting locations (randomized without replacement for subsequent blocks) around the virtual city. None of the target stores were visible from any of the starting locations. Participants viewed a black screen with a cue (5 s) indicating the current target store destination. Participants then freely navigated until they arrived at the target store, which was defined as moving the virtual avatar into the area in front of stores entryway; 1.5 m wide and extending 1 m out from the storefront. The “w”, “a”, “s”, and “d” keys on the keyboard were used for forward, left, back, and right translations, respectively, and the mouse was used to change the pitch and yaw of the viewpoint. Upon arrival the screen was blacked out and a confirmation message was displayed (5 s). The cue-navigate-arrival trial procedure was repeated for each target store in a randomized order, with participants beginning subsequent trials from the previous trial’s destination. An example trial sequence is shown in Fig. 2.

Fig. 2.

Spatial Encoding and Pointing Tasks. Left brackets and labels indicate the combination of encoding tasks (light blue: timed map, orange: route, green: tabletop, dark blue: criterion map; shades of gray in print) used in Experiment 1 and Experiment 2. Right labels and panel indicate the pointing tasks used in sub-experiments a (JRD) and sub-experiments b (SOP). Lower bracket and label indicate the number of encoding-pointing task cycles, or blocks. The combination of left and right labels indicates the encoding and pointing conditions for a given experiment (e.g., Experiment 2a: route, tabletop, or criterion map encoding task followed by the JRD pointing task; repeated for six blocks). JRD judgements of relative direction, SOP scene- and orientation-dependent pointing; $\mathit{\infty }$ = unlimited time (color figure online)

The primary dependent measure was navigational excess path, in meters, defined as the difference between the path length traveled by the participants virtual avatar from the starting location to the target location and the optimal Euclidean4 path from the starting location to the target location (Newman et al., 2007; Zhang & Ekstrom, 2013; Zhang et al., 2014).

Tabletop navigation

Participants’ virtual avatars began the task from one of eight possible starting locations in the virtual tabletop room (randomized without replacement for subsequent blocks) located around a 2 m radius of the tabletop in 45° increments. Participants viewed a black screen with a cue (5 s) indicating the current target store destination. Using the “w”, “a”, “s”, and “d” for translations and mouse for viewpoint pitch and yaw, participants then approached the tabletop and located a blue human figure within the scaled model of the virtual city (shown in an exploded view in Fig. 2; see online supplemental materials for more information). This human figure would serve as the participants’ remote-controlled avatar for navigating the virtual city.

Participants moved the remote-controlled avatar through the virtual city using the “o”, “k”, “l”, and “;” keyboard buttons for translations away from, to the left, toward, and to the right of the current viewpoint, respectively. Participants navigated the remote-controlled avatar until it arrived at the target store (defined as moving the remote-controlled avatar into the area in front of the store’s entryway; 1.5 m wide and extending 1 m out from the storefront). Upon arrival the screen was blacked out and a confirmation message was displayed (5 s). The cue-navigate-arrival trial procedure was repeated for each target store in a randomized order, with the participant’s remote-controlled avatar beginning subsequent trials from the previous trial’s destination. A sample tabletop navigation trial sequence is shown in Fig. 2.

The primary dependent measure was navigational excess path, in meters, defined as the difference between the path length traveled by the remote-controlled avatar from the starting location to the target location and the optimal Euclidean path from the starting location to the target location. This measure was similar and comparable to the primary dependent measure of avatar excess path for route encoding in this study and previous work (Newman et al., 2007; Zhang & Ekstrom, 2013; Zhang et al., 2014). In addition to moving the remote-controlled avatar, participants were able to move their own viewpoint by changing their position in the room relative to the tabletop scale model. Therefore, to test the extent to which participants used their ability to manipulate their perspective of the virtual city, we also measured the path length (in meters) of participants’ movement within the virtual tabletop room.

Timed map

Participants were given 30 s to study one of the virtual cities from an aerial view to learn the locations of the eight target stores, which was based on the timing used in Zhang et al., (2014), although note that the Zhang et al. study was performed in-person and the current study was performed online via MTurk, an issue we return to in the discussion. Participants could reveal store names by moving the cursor over a given store. When the study phase ended, participants’ knowledge for the store locations was tested. In the test phase, all target stores were removed from their locations in the city and placed outside the city wall in a column. Participants used the cursor to click and drag stores to the desired location, and a store would snap to a target location and orientation if it was dropped within 10 m of any target location. As indicated in Fig. 2, there was no time limit for the test phase, so participants clicked a button on the screen when they thought they had placed all target stores correctly. There was no score criterion.

The primary dependent measure was proportion misplaced, defined as the total number of stores that were not placed within 10 m of the correct location during the test phase divided by eight, the total number of stores in the virtual city.

Criterion map

This task was identical to the timed map encoding task, with a few important exceptions. First, there was no time limit on the study phase, so participants clicked a button on the screen to advance to the test phase. Second target stores did not snap to locations in the test phase, so participants were required to use the “d” or “a” key on their keyboard to rotate the stores clockwise or counterclockwise, respectively, and target stores remained wherever the participant released the mouse button. Lastly, participants were required to meet the score criterion of 100% correct placement on an attempt. This meant that instead of receiving a single score on a one-shot test of spatial knowledge, participants who did not achieve 100% correct placement were required to repeat the study and test procedure. Each round of study-test represents an attempt, and a correct placement was defined as being within 6 m of the correct target location and rotated to the correct orientation. The phases of the criterion map task are shown in Fig. 2.

The primary dependent measure was the average proportion misplaced, defined as the mean of the proportion misplaced stores across all attempts on a given block, excluding the last attempt. For example, if a participant placed five of the eight stores correctly, 0.375 of stores would be misplaced. If a participant reached criterion on the first attempt, the average proportion misplaced was zero. We chose this measure to be maximally comparable to the dependent measure for the timed map task, proportion misplaced on a one-shot map test.

Pointing tasks

Judgements of relative direction (JRD) pointing

On each trial of the JRD task, shown in Fig. 2, participants viewed a black screen with a prompt in the upper portion of the screen and a compass in the lower portion. The prompt indicated the imagined heading and the pointing target (e.g., “Imagine standing at the center of the Bike Shop, facing the Book Store; Point to the Pet Shop.”). Participants rotated the needle of the compass clockwise or counterclockwise (using the right and left arrow keys, respectively) to estimate the angle to the target from the imagined heading and then submitted their response (using the enter key). Participants had unlimited time to respond, but a response was required to advance to the next trial. To encourage task engagement, responses could not be submitted until a minimum of 3 s had passed. At the start of each new trial the compass arrow was reset to face directly forward (i.e., 0°).

The primary dependent measure was absolute pointing error, in degrees, defined as the absolute value of the difference between the correct pointing direction from the imagined heading and the participants recorded response. We did not consider pointing response latency as a measure in our analyses.

Scene- and orientation-dependent pointing (SOP)

On each trial of the SOP task, as shown in Fig. 2, participants initially viewed a perspective from one target location in the virtual city (e.g., the Bike Shop), facing another target location (e.g., the Book Store) with a prompt in the upper portion of the screen that read, “Orient yourself to the best of your ability. Press Enter when you are ready.” Participants then used the mouse or trackpad to adjust their viewpoint (pitch and yaw) and pressed the enter key to continue after at least 3 s had passed. Once oriented to the current facing direction to be maintained (yaw), the viewpoint was leveled (pitch set to zero), a compass was displayed in the lower portion of the screen, and the prompt was updated to indicate the pointing target (e.g., “Point to the Pet Shop.”). The target was never either of the two stores that was used to create the initial perspective (i.e., in this example neither the Bike Shop nor the Book store could be the target). Participants rotated the needle of the compass clockwise or counterclockwise (using the right and left arrow keys, respectively) to estimate the angle to the target from the current heading and then submitted their response (using the enter key). Participants had unlimited time to respond, but a response was required to advance to the next trial. To encourage task engagement, responses could not be submitted until a minimum of 3 s had passed. At the start of each new trial the compass arrow was reset to face directly forward (i.e., 0°). Note that this differed from Zhang et al., (2014) because participants did not navigate to a position in which they felt oriented before the stores were removed. We did this to better equate with the JRD task, which involves picturing an imagined heading without any movement, with the SOP task.

The primary dependent measure was absolute pointing error, in degrees, defined as the absolute value of the difference between the correct pointing direction from the oriented heading and the participants recorded response. As in our approach to analyzing the JRD task, no analyses were conducted on pointing response latency for the SOP task.

Procedure

After completing a questionnaire and several eligibility checks, MTurk workers downloaded a standalone application built using the Landmarks Unity package (Starrett et al., 2021) for either Windows (Microsoft Corp., Redmond, WA) or macOS (Apple Inc., Cupertino, CA). Data were automatically transferred using the WindowAzure.Storage5 Unity package (Version 9.3.3; Microsoft Corp., Redmond, WA) for communicating remotely with Microsoft Azure (Microsoft Corp., Redmond, WA). Workers were automatically, pseudo-randomly assigned to one of the learn-test conditions.

All participants began by familiarizing themselves with the eight target stores in the virtual city (for details on the target familiarization task, see the online supplemental materials). Afterward participants completed six blocks of alternating encoding and pointing tasks. In each encoding block, participants completed either the route, timed map, tabletop navigation, or criterion map (depending on the experiment or condition) task. In each pointing block, participants completed 56 trials of either the JRD or SOP task. For both pointing tasks, any given trial was created from a unique triad of target stores. The 336 possible permutations of triads from the eight target stores were randomized across the six blocks for the assigned pointing task. Between each block, participants received an attention check code to enter on the survey (in a separate window).

Data analysis

Data processing

In total, 448 MTurk workers provided informed consent and submitted work for these experiments. The total datasets removed for each experimental condition can be found in Supplemental Table S3. The datasets analyzed include newly collected data for the experiments presented and pre-existing data from Zhang et al. (2014) obtained upon request to the authors, which were used to estimate effects sizes.

Software and tools

Data wrangling and analyses were conducted in R (R Core Team, 2021) using RStudio (RStudio Team, 2020). In addition to R base functions, the following packages for R were used: afex (Singmann et al., 2021), ARTool (Kay et al., 2021), effectsize (Ben-Shachar et al., 2020), emmeans (Lenth, 2021), ggpattern (FC, 2020), ggpubr (Kassambara, 2020), lme4 (Bates et al., 2015), ppcor (Kim, 2015), QuantPsyc (Fletcher, 2012), remotes (Hester et al., 2021), rstatix (Kassambara, 2021), and tidyverse (Wickham et al., 2019; includes ggplot2, dplyr, tidyr, readr, purrr, tibble, stringr, and forcats packages). Sample size estimation additionally utilized the GLIMMPSE online power analysis tool (Kreidler et al., 2013).

Data transformations

When calculating the estimated sample size, it was determined that a log transformation of absolute pointing error would reduce the likelihood of violating the assumptions of General Linear Models. For each block, the distributions of the primary dependent measure of the pointing tasks (absolute angular pointing error) before and after the log transformation are shown in the top row of Supplemental Fig. S2. For distributions classified as log-normal, analyses were conducted on log-transformed values to better meet the assumptions of parametric statistical tests. When appropriate, model estimates were back-transformed (exponentiated) for presentation in figures, which provides a clearer interpretation in the original units of absolute angular pointing error.

For performance on the encoding tasks, separate transforms were applied depending on the primary dependent measure of the task. Route and tabletop navigation performance, measured by navigational excess path, were log transformed. As both the timed map task and criterion map task had a dependent measure derived from the proportion incorrect, a logit transformation was applied to convert the data from discrete values bounded by zero and one to a continuous measure (Dixon, 2008). Distributions from before and after transformations are shown in the lower four rows of Supplemental Fig. S2.

Incomplete or “inattentive” datasets

Previous work has suggested that additional efforts are required to ensure study compliance and data validity when recruiting MTurk workers (Aguinis et al., 2020; Aruguete, 2019). Datasets from 105 participants who did not complete the study for any reason (technical issues, fatigue, no longer wished to participate, etc.) or were classified as inattentive participants (e.g., no data received, missed attention/validity checks, straightlined6 the pointing task, reported drawing a map or receiving help from another individual, or provided an invalid or no survey code) were excluded.

Chance performance datasets

Data from 84 participants determined to be performing at chance on the pointing task were excluded from analysis (for a breakdown of chance performers across condition, Supplemental Table S3). To determine chance performance for each participant, the vector of raw responses was shuffled and median error was calculated based on the unshuffled vector of the correct angles. This process was repeated 10,000 times to generate a participant-specific null distribution against which the median error of the participant’s unshuffled raw data could be compared using a two-tailed t test (as in Starrett et al., 2019; for more details see Huffman & Ekstrom, 2019). Given large number of participants performing at chance, it seems possible that some fraction of these were in fact “inattentive” datasets that bypassed preliminary inspection (see previous paragraph on Incomplete or ‘Inattentive’ Datasets”).

Non-response and outlier trials

Trials in which participants did not attempt a response on the pointing task (i.e., did not rotate the compass), defined as any trial where the raw response angle was exactly 0°, were excluded from analyses. We used an outlier removal procedure identical to that of Zhang et al. (2014), whereby the mean of the log-transformed absolute pointing error on the pointing task (JRD or SOP) was calculated for each subject, collapsed across all trials and blocks, and any trials where absolute pointing error was beyond two standard deviations from this geometric mean (i.e., mean of log-transformed values) were considered outliers and removed from subsequent analyses. An average of 5.72% (Range = 2.08–16.07%) of trials were removed for each participant.

Measures

The primary dependent variable for all experiments was pointing task performance, measured by absolute angular pointing error in degrees. The signed, closed interval (− 180°, 180°) angle between the participants response angle and the correct response angle was calculated, and absolute angular pointing error was defined by the half-closed interval [0°, 180°) of its absolute value. The secondary dependent variable for all experiments was encoding performance, measured by navigational excess path in meters for the route and tabletop navigation tasks or by proportion misplaced in the timed map and criterion map tasks.

Confirmatory analyses

Analysis of variance (ANOVA)

For each experiment (1a, 1b, 2a, 2b), a 3 (Encoding Task: route, tabletop, timed map) × 6 (Block: 1–6) mixed ANOVA was conducted. For each pair of experiments (1a–1b, 2a–2b), a 3 (Encoding Task: route, tabletop, timed map) × 2 (Pointing Task: JRD, SOP) × 6 (Block: 1–6) mixed ANOVA was conducted. Violations of the assumptions for ANOVA were evaluated prior to observing the results of any given test to determine if an alternative test was more appropriate (see Supplemental Fig. S3). In cases where the aforementioned transformations did not mitigate violations, an aligned rank transform was applied to the data to conduct nonparametric factorial ANOVA (Wobbrock et al., 2011).

Planned contrasts

To test the predictions of the Optimization Hypothesis, planned t tests were conducted to compare pointing performance after tabletop navigation and the expected non-preferred encoding task (route encoding for the JRD pointing task in experiments 1a and 2a; map encoding for the SOP task in experiments 1b and 2b). Estimated marginal means of the log-transformed values, or estimated geometric marginal means, were calculated for each factorial condition using the emmeans package in R. For each contrast, an independent-sample t test was conducted to determine if the difference between two estimated geometric marginal means (i.e., the estimated marginal mean of the log-transformed values) was significantly different from zero. For interpretability, pursuant to the logarithm quotient rule7, this difference was then back-transformed (exponentiated), yielding a ratio of values in the original units of absolute angular error.

Secondary and exploratory analyses

Post hoc contrasts

To gain a more complete understanding of the relationship between tabletop navigation and the other encoding tasks as well as to test potential alternative hypotheses should the pattern of results not support the Optimization Hypothesis, t tests were also conducted to compare pointing performance after tabletop navigation and the expected preferred encoding task (map encoding for the JRD pointing task in experiments 1a and 2a; route encoding for the SOP task in experiments 1b and 2b). These exploratory post hoc tests were Bonferroni corrected to a threshold of p < 0.003 to adjust the familywise error rate to account for these tests as well as the 12 planned comparisons for each experiment. As with planned contrasts, these analyses were only conducted if the ANOVA for an experiment revealed a significant main effect of Encoding Task or an interaction effect.

Correlation analysis

To better understand how spatial knowledge is differentially acquired and deployed across more-or-less egocentric and allocentric encoding and pointing tasks, the Kendall rank correlation coefficient ($\tau$) was calculated for the raw, untransformed scores of encoding performance (navigational excess path for the route and tabletop tasks; proportion misplaced for the timed map and criterion map tasks) and pointing performance (absolute angular pointing error on the SOP and JRD tasks). For each participant, encoding and pointing performance were averaged across all trials and blocks, resulting in a single datapoint for each subject. The Kendall rank correlation test was then performed on all participant scores within a given encoding-pointing condition (e.g., JRD after tabletop learning). We also explored the effect of participants’ utilization of the multiple aerial viewpoints afforded by movement within the virtual tabletop room on the correlation between encoding and pointing error. If the total distance traveled in the virtual tabletop room by a participant across the entire experiment was correlated with encoding error, pointing error, or both then the semi-partial correlation (partial if correlated with both) was computed using the ppcor R package (Kim, 2015) to account for this effect in the relationship between encoding and pointing errors. Given the novelty of the tabletop task allowing participants to dynamically change viewpoints during navigation, we believed this variable, which was not present in other conditions, would be of interest for an unbiased comparison with the other tasks as well as for insight into our novel paradigm’s effect on spatial knowledge.

Experiment 1a

In Experiment 1a, we tested how encoding spatial information via tabletop navigation impacts performance on the JRD task and compares to route and map encoding. Specifically, we test the optimization hypothesis: that tabletop navigation will result in “optimal” improvements in JRD performance compared to map and route encoding.

Method

Participants

Data from 96 participants (35 female, 61 male) who had not participated in any of the other experiments were analyzed in Experiment 1a. Participants ranged from 19 to 35 (M = 30.59, SD = 3.77) years of age.

Experimental design and procedure

A 3 (Encoding Task: route, tabletop, timed map) × 6 (Block: 1–6) mixed factorial design was employed with Encoding Task as a between-subject manipulation, Block as a repeated measure (within-subject manipulation), and absolute angular pointing error (degrees) on the JRD task as the primary dependent measure. Additionally, performance on each Encoding task was measured and analyzed. Participants followed the procedures outlined in General Method, completing six blocks of either the route, timed map, or tabletop task interleaved with 56 trials of the JRD Pointing task.

Results and discussion

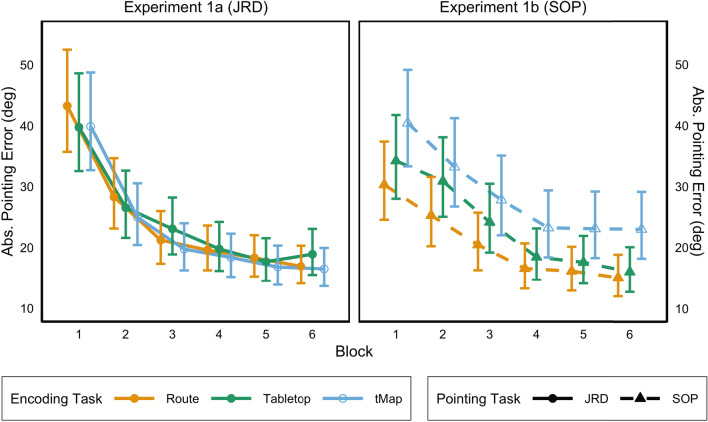
The 3 (Encoding Task: route, tabletop, timed map) × 6 (Block: 1–6) ANOVA on JRD absolute pointing error revealed a main effect of Block, F(2.80, 260.64) = 127.63, p < 0.001, ${\eta }_G^2$ = 0.19. Neither a main effect of Encoding Task, F(2, 93) = 0.23, p = 0.795, ${\eta }_G^2$ = 0, nor an interaction between Encoding Task and Block, F(5.61, 260.64) = 0.70, p = 0.644, ${\eta }_G^2$ = 0 reached significance. Degrees of freedom for all within-subjects factors were Greenhouse–Geisser corrected to account for violations of sphericity. JRD performance across Encoding Task groups and Block are shown in the left panel of Fig. 3. Given that we did not observe a significant main effect of Encoding Task or a significant the Encoding Task $\times$ Block interaction, we did not conduct any planned or exploratory t tests.

Fig. 3.

Pointing Task Performance in Experiment 1. Sample means and variability presented were back-transformed from log values (i.e., exponentiated) for qualitative interpretation. Error bars represent the standard error of the mean. Values for route encoding task are shown in solid orange (solid light gray), values for tabletop navigation encoding task are shown in solid green (solid dark gray), and values for the timed map encoding task are shown in outlined light blue (outlined light gray). tMap timed map, JRD judgments of relative direction, SOP scene- and orientation (color figure online)

The results of Experiment 1a indicate no distinct advantage or disadvantage for encoding spatial information during tabletop navigation as compared to timed map or route navigation tasks. In addition, surprisingly, we did not find evidence of significant differences in JRD error for map and route encoding conditions, in contrast to Zhang et al., (2014). It is likely that the 30 s of map encoding, particularly in an unsupervised situation such as that afforded by MTurk, was insufficient to result in comparable map knowledge to the timed map task used in Zhang et al., (2014). These and other possible explanations are addressed further in the General Discussion section.

Experiment 1b

Experiment 1b sought to again test how tabletop navigation impacts spatial memory by comparing against route and map encoding but this time including SOP task performance as the dependent measure.

Method

Participants

Data from 96 participants who had not participated in any of the other experiments were analyzed in Experiment 1b. Participants ranged from 20 to 35 (M = 31.12) years old and included 30 females, 65 males, and one unidentified participant.

Experimental design and procedure

A 3 (Encoding Task: route, tabletop, timed map) × 6 (Block: 1–6) mixed factorial design was employed with Encoding Task as a between-subject manipulation, Block as a repeated measure (within-subject manipulation), and absolute angular pointing error (degrees) on the SOP task as the primary dependent measure. Additionally, performance on each encoding task was measured and analyzed. Participants followed the procedures outlined in General Method, completing six blocks of either the route, timed map, or tabletop encoding task interleaved with 56 trials of the SOP memory task.

Results and discussion

The results of the 3 (Encoding Task: route, tabletop, timed map) × 6 (Block: 1–6) ANOVA on SOP absolute pointing error were similar to those of Experiment 1a (see Fig. 3, right panel). The analysis indicated a main effect of Block, F(2.20, 204.90) = 71.05, p < 0.001, ${\eta }_G^2$ = 0.10, no main effect of Encoding Task, F(2, 93) = 1.76, p = 0.178, ${\eta }_G^2$ = 0.03, and no interaction between Encoding Task and Block, F(4.41, 204.90) = 0.84, p = 0.512, ${\eta }_G^2$ = 0. A Greenhouse–Geisser correction was applied to degrees of freedom for each within-subjects factor to account for violations of sphericity. Given that we did not observe a significant main effect of Encoding Task or a significant the Encoding Task $\times$ Block interaction, we did not conduct any follow-up contrasts.

As in Experiment 1a, Experiment 1b lacked significant differences across encoding conditions for SOP error, although qualitatively, tabletop navigation performed numerically intermediate to route and map encoding. While the lack of a statistical difference does not provide support to any of our hypotheses, numerically, the trend is consistent with the optimization hypothesis.

Comparison with Experiment 1a

We next compared performance across Experiments 1a and 1b by including an additional factor, Pointing Task, in our model. The resulting 3 (Encoding Task: route, tabletop, timed map) × 2 (Pointing Task: JRD, SOP) × 6 (Block: 1–6) mixed ANOVA revealed a main effect of Block, consistent with the pattern of results for each experiment individually, and a significant interaction between Pointing Task and Block. ANOVA results can be found in Table 1 (tests of ANOVA assumptions are shown in Supplemental Fig. S3). Performance on both the JRD and SOP tasks, averaged across encoding tasks, improved over the course of both experiments, but the rate of improvement was greater for the JRD than the SOP. We did not observe a main effect of Pointing Task and none of the other interactions reached significance.

Table 1.

Comparing JRD and SOP performance in Experiment 1

Effect	F ratio	df	p value	${\eta }_G^2$
Encoding task	0.61	2, 186	0.547	0.01
Pointing task	0.05	1, 186	0.829	0
Encoding task × Pointing task	1.72	2, 186	0.182	0.02
Block	185.64***	2.56, 476.77	< 0.001	0.12
Encoding task × Block	0.71	5.13, 476.77	0.616	0
Pointing task × Block	5.76**	2.56, 476.77	0.001	0.01
Encoding task × Pointing task × Block	0.84	5.13, 476.77	0.527	0

N = 192. df = degrees of freedom; ${\eta }_G^2$ = generalized eta squared

**p < 0.01. ***p < 0.001

Performance on the encoding tasks was measured in terms of error. For both the route and tabletop encoding tasks, error was navigational excess path. For the timed map task, a one-shot test for each participant on each block, error was measured as the proportion of target stores placed incorrectly during the test phase; the proportion error was logit transformed to mitigate the effect of the upper and lower bounds of proportion values on the statistical analyses conducted (see Data Transformations under Data Analysis in the General Method).

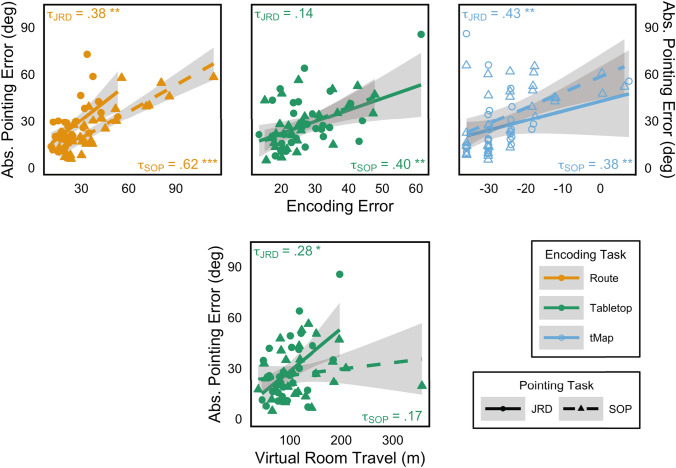
Participants were able to perform the JRD or SOP task effectively after any of the encoding conditions (i.e., above chance), suggesting that all encoding tasks facilitated both allocentric and egocentric strategy use (for additional analysis of encoding task performance, see Supplemental Results Including Supplemental Fig. S4 and Table S4). One possible index of egoformative or alloformative information is the relationship between participants’ performance on their respective encoding and pointing tasks. If encoding error is significantly correlated with error on only one of the pointing tasks, either the JRD or SOP, or the correlation with performance on one of the pointing tasks is significantly greater than the other, this could be interpreted as evidence for the presence of more ego- or alloformative information during encoding. Scatterplots of each participant’s raw absolute pointing compared with continuous8 scores on the respective encoding tasks are shown in Fig. 4. Scores were averaged across all blocks such that each datapoint, in Fig. 4, represents one participant.

Fig. 4.

Relationship between Encoding Task Performance and Pointing Task Performance in Experiment 1. The upper panel shows encoding error, on the x-axis, in units of meters for navigational excess path for the route and tabletop navigation encoding tasks—solid orange (solid light gray) and solid green (solid dark gray), respectively—and in units of log odds converted from proportion incorrect for misplacement error the timed map encoding task—outlined light blue (outlined light gray). Annotations in each plot indicate Kendall’s Tau ($\mathit{\tau }$) correlation coefficient for the JRD (upper left of each plot) and SOP (lower right of each plot). Shaded regions indicate standard error. The lower-middle panel shows the relationship between distance travelled in the virtual room during tabletop navigation and performance on the pointing tasks (same conventions as upper panels). tMap timed map, JRD judgements of relative direction, SOP scene- and orientation-dependent pointing. ^aPart (semi-partial) correlation accounting for the effect of movement through the virtual tabletop environment on pointing error. *p < 0.05. **p < 0.01. ***p < 0.001 (color figure online)

Kendall rank correlation coefficients ($\tau$) revealed that absolute pointing error on the JRD was significantly correlated with performance on the route encoding, $\tau$(32) = 0.38, p < 0.01, 95% CI [0.15, 0.57], and timed map encoding, $\tau$(32) = 0.43, p < 0.001, 95% CI [0.21, 0.61], tasks. Absolute pointing error on the SOP was significantly correlated with route, $\tau$(32) = 0.62, p < 0.001, 95% CI [0.45, 0.75], tabletop, $\tau$(32) = 0.40, p < 0.001, 95% CI [0.18, 0.58], and timed map, $\tau$(32) = 0.38, p < 0.01, 95% CI [0.15, 0.57], tasks. All Kendall correlation coefficients are displayed in the individual panels of Fig. 4 and labelled for statistical significance. These results suggests that both egoformative and alloformative information were readily available on both the route and map tasks. Interestingly, lower encoding error on the tabletop task reliably coincided with lower absolute pointing error on the SOP; the same relationship was not found for encoding performance and the JRD task. There were no significant differences between the JRD and SOP task performance correlations within a single encoding task (Supplemental Fig. S5). Figure 4 shows each encoding-pointing correlation across encoding and pointing task.

We sought to further explore the mechanisms by which tabletop navigation may be distinct from either navigation and route learning or traditional map learning. Because the task affords participants the ability to dynamically change their viewpoint, we were specifically interested in the extent to which moving around the table in the virtual room impacted learning and memory. Were the distance travelled in the virtual room to impact performance on the JRD or SOP task, it would suggest an implication of this novel format for how spatial information is represented or retrieved. Accordingly, the total distance traveled within the virtual tabletop room was calculated for each participant to measure the extent to which a participant utilized the affordance of being able to move to different vantage points around the scale model of the virtual city. To account for any effects of this on the relationship between performance on the tabletop navigation task and performance on either one of or both the pointing tasks, Kendall rank correlation coefficients ($\tau$) were first calculated to assess the relationship between total distance traveled in the virtual tabletop room and standardized encoding error for the tabletop navigation task as well as pointing error. Only pointing error on the JRD task was significantly correlated with distance traveled in the virtual tabletop room, $\tau$(32) = 0.28, p = 0.025, such that increased movement through the virtual room coincided with worse performance on the JRD pointing task (Fig. 4); all correlations are shown in Supplemental Table S5. As virtual tabletop room travel distance was only related to pointing error on the JRD task, a semi-partial correlation coefficient was computed for the relationship between encoding error and pointing error while controlling for this effect on pointing error, $s\tau$ = 0.14, p = 0.256. This semi-partial correlation was considered in place of the standard correlation coefficient (Fig. 4).

While the extent of participants’ movement around the tabletop environment was related to JRD performance, accounting for this relationship had little impact on the presence of a relationship, or lack thereof, between tabletop navigation performance and JRD pointing performance. This does not rule out the possibility of the optimization hypothesis, as features of the tabletop navigation task were associated with facilitating the formation of allocentric spatial representations, which are thought to bolster JRD pointing performance. Participants who did not utilize the multiple aerial viewpoints of the virtual city afforded by the tabletop task may not have optimized allocentric representations, instead only optimizing route-based, egocentric representations through navigation of the remote-control avatar from a more-or-less static position. This could explain the relationship between tabletop navigation performance and the SOP task but not the JRD pointing task. While our results are similarly unable to rule out the predomination hypothesis, the relationship between tabletop room movement and allocentric JRD pointing suggests that egocentric dominance is at least not absolute.

One factor that may have impacted our ability to interpret these results was the timed nature of the map learning task. Particularly when unsupervised on MTurk, there may have been insufficient exposure to or engagement with the map, which could have obscured differences in the JRD task. We address this issue in Experiment 2.

Experiment 2a

The timed map task used by Zhang et al. and in Experiment 1 differed notably from the route and tabletop encoding tasks in that there was no overt behavior on the part of the participant required to advance the experiment. In the route and tabletop tasks, participants must arrive at the current target location to continue. Conversely, a participant could, in theory, not have studied one or more of the target store identities or locations and still progress through the store placement test during timed map learning. To address this issue, we employed a criterion map task in Experiment 2. This version differed critically from the map task used in Experiment 1 (and by Zhang et al.) as participants were required to repeat the study-test cycle until they placed every store correctly. This also helped deal with the issue that in an unsupervised situation like MTurk, there was no way to ensure that participants used the 30 s to learn the map, unlike in supervised situations, in which compliance could be monitored. We collected an additional JRD and SOP sample for the criterion map encoding conditions and compared those to the route and tabletop encoding groups from Experiment 1.

Method

Participants

Data from an additional 32 participants who had not participated in any of the other experiments were combined with data for the route and tabletop conditions from Experiment 1a. This resulted in a final sample of 96 participants (32 female, 64 male), age 20 to 35 (M = 30.33, SD = 3.68) whose data were analyzed in Experiment 2a.

Experimental design and procedure

A 3 (Encoding Task: route, tabletop, criterion map) × 6 (Block: 1–6) mixed factorial design was employed with Encoding Task as a between-subject manipulation, Block as a repeated measure (within-subject manipulation), and absolute angular pointing error (degrees) on the JRD task as the primary dependent measure. Additionally, performance on each encoding task was measured and analyzed. Participants followed the procedures outlined in General Method, completing six blocks of the criterion map task—repeating study and test phases, if necessary, until all targets were correctly placed—interleaved with 56 trials of the JRD pointing task. These data were then combined with the data from the route and tabletop conditions of Experiment 1a.

Results and discussion

Absolute pointing error performance on the JRD was entered into a 3 (Encoding Task: route, tabletop, criterion map) × 6 (Block: 1–6) ANOVA. Significant main effects were found for both Encoding Task, F(2, 93) = 5.24, p = 0.007, ${\eta }_G^2$ = 0.09, and Block, F(3.23, 300.38) = 89.52, p < 0.001, ${\eta }_G^2$ = 0.13. The Encoding Task by Block interaction was also significant, F(6.46, 300.38) = 8.69, p < 0.001, ${\eta }_G^2$ = 0.03.

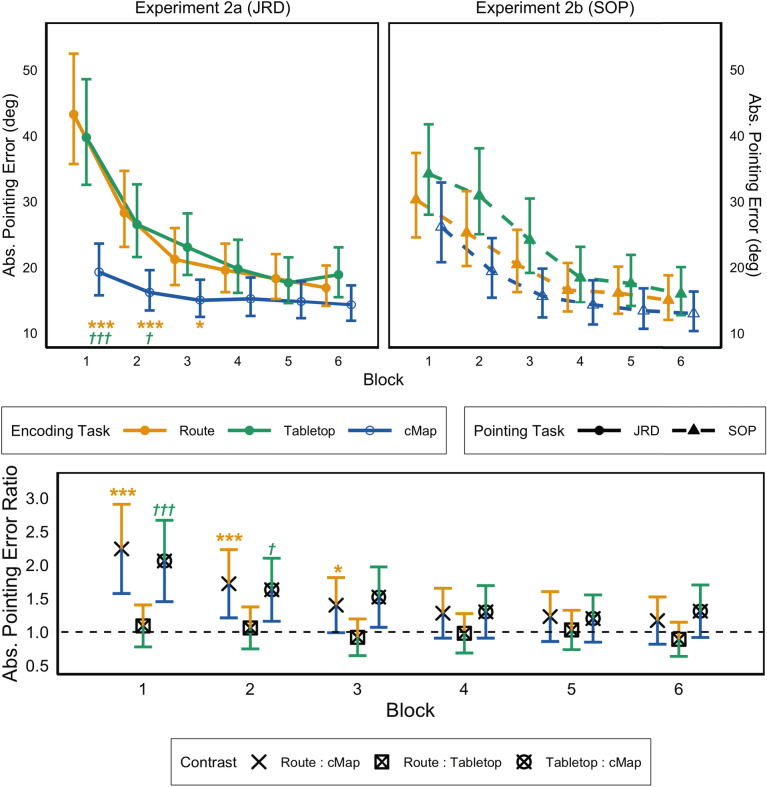
Planned independent samples t tests revealed significant differences in the ratios of pointing error after route and criterion map encoding across each of the first three blocks (Table 2 and the lower panel of Fig. 5). Error for route encoding was more than double that of criterion map encoding on the first block and this ratio decreased monotonically across blocks. Performance on the JRD was not statistically different across route and tabletop navigation for any of block of the experiment. We performed exploratory contrasts comparing tabletop and criterion map encoding. These contrasts revealed a significant difference between log-transformed performance on the JRD after tabletop navigation compared to after criterion map encoding across each of the first three blocks. Here, error on the JRD after tabletop navigation was more than twice that of JRD error after criterion map encoding. The significant difference between tabletop and criterion map encoding on the third block, however, did not survive Bonferroni correction for multiple comparisons, which accounted for all 18 contrasts that were conducted across confirmatory and exploratory analyses. Contrasts were back-transformed to ratios (see General Method) and these are reported in Table 2 along with associated statistics. The estimated marginal means for all conditions across blocks for Experiment 2a are shown in the left panel of 5.

Table 2.

Planned and exploratory pairwise comparisons for Experiment 2a

Contrast	Ratio	SE	t(128.17)	p	d	95% CI
Block 1
Route:cMap	2.24	0.34	5.37	< 0.001	0.95	[0.58, 1.31]
Route:Tabletop	1.09	0.16	0.56	0.577	0.10	[− 0.25, 0.45]
Tabletop:cMap	2.06	0.31	4.82	< 0.001	0.85	[0.49, 1.21]
Block 2
Route:cMap	1.72	0.26	3.62	< 0.001	0.64	[0.28, 0.99]
Route:Tabletop	1.06	0.16	0.37	0.713	0.07	[− 0.28, 0.41]
Tabletop:cMap	1.63	0.24	3.25	0.001	0.57	[0.22, 0.93]
Block 3
Route:cMap	1.40	0.21	2.25	0.026	0.40	[0.05, 0.75]
Route:Tabletop	0.92	0.14	− 0.56	0.580	− 0.10	[− 0.44, 0.25]
Tabletop:cMap	1.52	0.23	2.80	0.006a	0.50	[0.14, 0.85]
Block 4
Route:cMap	1.28	0.19	1.64	0.102	0.29	[− 0.06, 0.64]
Route:Tabletop	0.98	0.15	− 0.10	0.918	− 0.02	[− 0.36, 0.33]
Tabletop:cMap	1.30	0.20	1.75	0.083	0.31	[− 0.04, 0.66]
Block 5
Route:cMap	1.23	0.19	1.40	0.164	0.25	[− 0.1, 0.59]
Route:Tabletop	1.03	0.15	0.20	0.843	0.04	[− 0.31, 0.38]
Tabletop:cMap	1.20	0.18	1.20	0.232	0.21	[− 0.14, 0.56]
Block 6
Route:cMap	1.17	0.18	1.06	0.290	0.19	[− 0.16, 0.53]
Route:Tabletop	0.89	0.13	− 0.13	0.453	− 0.13	[− 0.48, 0.21]
Tabletop:cMap	1.31	0.20	1.81	0.072	0.32	[− 0.03, 0.67]

N = 96. Ratios are the back-transformed difference of estimated marginal means of log values. All p values uncorrected

SE standard error, d Cohen’s d, CI confidence interval, cMap criterion map

^aDid not survive Bonferroni correction for 18 comparisons ($\alpha$ = 0.003)

Fig. 5.

Pointing Task Performance in Experiment 2. The upper panel shows absolute pointing error sample means and variability back-transformed from log values (i.e., exponentiated) for qualitative interpretation. Performance after route encoding is shown in solid orange (solid light gray), after tabletop navigation is shown in solid green (solid dark gray), and performance after criterion map encoding is shown in outlined dark blue (outlined dark gray). Error bars represent the standard error of the mean. The lower panel depicts the pairwise contrasts for the JRD task from Experiment 2a as ratios (i.e., the difference in log means represented as the ratio of back-transformed means). Unbounded “$\times$” symobls represent the route:cMap contrast ratio, “$\times$” symbols bounded by a square represent the route:tabletop contrast ratio, and “$\times$” symbols bounded by a circle represent the tabletop:cMap contrast ratio. Error bars represent 95% confidence intervals for the contrast ratio; colors represent the exact contrast tested (e.g., orange on top with blue on bottom shows route:cMap contrast). cMap criterion map, JRD judgments of relative direction, SOP scene- and orientation-dependent pointing. *p < 0.05, uncorrected. ***p < 0.001, uncorrected. ^†p < 0.05, corrected. ^†††p < 0.001, corrected (color figure online)

Experiment 2a only differed from Experiment 1a in that the map task had a self-paced study portion and required participants to reach a score criterion on the test portion before they could continue. Notably, performance on the JRD task was significantly better after map encoding than after route and tabletop conditions early on, and performance on all three conditions converged later in the experiment. Also, a major difference from Experiment 1 is that the benefit of map encoding was evident on the first block of the JRD task. Note that, across subjects, there were no performance differences between the three virtual cities on either the JRD, F(2, 125) = 0.81, p = 0.445, ${\eta }_G^2$ = 0.01, or SOP, F(2, 125) = 0.84, p = 0.436, ${\eta }_G^2$ = 0.01. Our findings, overall, provide mixed support for the optimization hypothesis: while JRD performance following tabletop navigation was worse than following criterion map encoding, it did not differ from route encoding. In addition, our findings, particularly those showing (1) better map encoding initially and (2) an interaction effect such that map encoding resulted in different slopes from route encoding, are a conceptual replication of Zhang et al.

Experiment 2b

Method

Participants

As in Experiment 2a, data from an additional 32 participants who had not participated in any of the other experiments were combined with data for the route and tabletop conditions from Experiment 1b. This resulted in a final sample of 96 participants whose data were analyzed in Experiment 2b. Participants were 20 to 35 (M = 31.12) years old and made up of 32 females, 63 males, and the same unidentified participant reported in Experiment 1b.

Experimental design and procedure

A 3 (Encoding Task: route, tabletop, criterion map) × 6 (Block: 1–6) mixed factorial design was employed with Encoding Task as a between-subject manipulation, Block as a repeated measure (within-subject manipulation), and absolute angular pointing error (degrees) on the SOP task as the primary dependent measure. Additionally, performance on each encoding task was measured and analyzed. Participants followed the procedures outlined in General Method, completing six blocks of the criterion map task interleaved with 56 trials of the SOP task. These data were then combined with the data from the route and tabletop conditions of Experiment 1b.

Results and discussion

The pattern of results from the 3 (Encoding Task: route, tabletop, criterion map) × 6 (Block: 1–6) ANOVA on SOP absolute pointing error resembled those of Experiment 1b. The analysis indicated a main effect of Block, F(2.34, 217.76) = 95.33, p < 0.001, ${\eta }_G^2$ = 0.11, no main effect of Encoding Task, F(2, 93) = 1.63, p = 0.202, ${\eta }_G^2$ = 0.03, and no interaction between Encoding Task and Block, F(4.68, 217.76) = 1.13, p = 0.346, ${\eta }_G^2$ = 0. A Greenhouse–Geisser correction was applied to degrees of freedom for each within-subjects factor to account for violations of sphericity. SOP performance across block and encoding condition in Experiment 2b is shown in the right panel of Fig. 5. Given that we did not observe a significant main effect of Encoding Task or a significant the Encoding Task $\times$ Block interaction, we did not conduct any follow-up contrasts.

Comparison with Experiment 2a

As in Experiment 1, performance was compared across Experiments 2a and 2b by including Pointing Task factor in the ANOVA. The 3 (Encoding Task: route, tabletop, criterion map) × 2 (Pointing Task: JRD, SOP) × 6 (Block: 1–6) mixed ANOVA revealed main effects of Encoding Task and Block. Additionally, significant two-way interactions were found between Encoding Task and Block as well as Pointing Task and Block. Lastly, the three-way interaction between Encoding Task, Pointing Task, and Block was significant. Table 3 shows a summary of all effects tested.

Table 3.

Comparing JRD and SOP performance in Experiment 2

Effect	F ratio	df	p value	${\eta }_G^2$
Encoding task	5.61**	2, 186	0.004	0.05
Pointing task	0.31	1, 186	0.576	0
Encoding task × Pointing task	0.36	2, 186	0.697	0
Block	181.14***	2.75, 511.43	< 0.001	0.11
Encoding task × Block	5.14***	5.50, 511.43	< 0.001	0.01
Pointing task × Block	4.28**	2.75, 511.43	0.007	0
Encoding task × Pointing task × Block	3.93**	5.50, 511.43	0.005	0.01

N = 192. df = degrees of freedom; ${\eta }_G^2$ = generalized eta squared

**p < 0.01. ***p < 0.001

The three-way interaction effect here is consistent with previous findings on the difference between route and map encoding across spatial pointing tasks (Zhang et al., 2014). We found that the most alloformative mode of encoding spatial information, maps, resulted in a significant benefit on the more allocentric spatial memory task, the JRD, compared to the more egoformative route and tabletop encoding modalities. Given that only JRD performance did not correlate significantly with tabletop encoding error, it seems likely that the tabletop task may have either biased our participants to rely on egoformative cues or interfered with the use of alloformative ones. Possibly, this results from the lack of embodiment afforded by a desktop interface. Future work investigating the effect of tabletop encoding that utilizes immersive VR to allow participants to more naturalistically travel in the virtual tabletop room while actively moving their remote-control avatar would shed light on this.

The relationship between performance on the criterion map encoding task and performance on both the JRD and SOP tasks was evaluated using Kendall’s tau, as in Experiment 1. Criterion map encoding performance was not indicative of better or worse performance on either the JRD, $\tau$(32) = 0.07, p = 0.602, 95% CI [− 0.18, 0.30], or SOP, $\tau$(32) = 0.16, p = 0.201, 95% CI [− 0.08, 0.39], pointing tasks. The diminished relationship between encoding and testing performance, despite criterion map encoding resulting in significantly lower JRD error compared to route or tabletop (see Fig. 5), might speak to the efficacy of the criterion map encoding task. Additional analysis of encoding task performance for experiment 2 can be found in the Supplemental Results including Supplemental Fig. S6, Table S6, and Fig. S7). Several participants performed near ceiling on the pointing tasks even when encoding error was high (Supplemental Fig. S7).

General discussion

The existence of, and distinction between, egocentric and allocentric spatial reference frames and analogous representations has been a topic of considerable study (Burgess, 2006; Filimon, 2015; Marchette et al., 2014; Mou et al., 2004, 2006), with some arguing that spatial representations are better considered along an egocentric-to-allocentric continuum (Chrastil, 2018; Ekstrom et al., 2017; Starrett & Ekstrom, 2018; Wang, 2017). The degree to which encoded spatial information lends itself to the formation of a more egocentric or allocentric spatial representation, which we refer to as being more egoformative or alloformative, is largely influenced by the modality used to encode it (e.g., navigating versus studying a map). To better understand the implications of forming representations situated toward the center of this continuum (i.e., equally egocentric and allocentric), we developed a novel tabletop navigation learning paradigm in which participants interact with a scale model of a to-be-learned virtual city by navigating a remote-control avatar to various destinations within the tabletop model. We anticipated that representations derived from this new task would be better optimized across common egocentric and allocentric spatial memory pointing tasks. Across four experiments, participants completed six blocks of an encoding task and performance on interleaved blocks of a spatial memory pointing task were compared.

In Experiment 1, participants learned by either first-person navigation (route), tabletop navigation (tabletop), or studying a map for 30 s (timed map). In Experiment 1a, spatial memory was assessed using the more allocentric JRD pointing task; in experiment 1b, participants completed the more egocentric SOP task. Although participants performed above chance and showed monotonic decreases in absolute pointing error across all encoding-pointing condition combinations, there were no differences between any of the conditions across encoding task on the JRD or SOP. Performance on encoding tasks was reliably correlated across encoding tasks and pointing performance, except for JRD performance after tabletop navigation, and these correlations did not differ across JRD and SOP tasks for any of the encoding tasks. We also found a relationship between travel around the virtual room in the tabletop navigation task and JRD absolute pointing error. The use of a novel encoding paradigm, tabletop navigation, represents an innovative approach to studying the formation of egocentric and allocentric representations that may facilitate a clearer comparison with traditional navigation paradigms, especially with the adoption of immersive VR technology in spatial cognition research.

In Experiment 2, the route and tabletop groups were compared with another sample of map learners who were required to correctly locate all the target landmarks on the map before beginning each block of pointing (criterion map). While there were no differences in absolute pointing error across encoding tasks for the SOP task, we found evidence for an interaction wherein criterion map learning resulted in significantly lower absolute pointing error on the JRD when compared to both the route and tabletop encoding tasks, consistent with previous work (Zhang et al., 2014); no differences were observed on the SOP task. These differences were most prominent during the first two blocks of the experiment and became undetectable by the fourth block, as JRD performance approached asymptote for all encoding modalities. This was evidenced by a statistically significant three-way interaction between encoding task, pointing task, and block.

Overall, these findings provide mixed support for the optimization hypothesis and the predomination hypothesis. On one hand, the dominantly allocentric criterion map task was the only task that showed significantly lower JRD absolute pointing error suggesting that tabletop and route-derived representations may be more similar than different. An egocentric representational predominance from tabletop navigation was furthered evidenced by correlational analyses, which showed reliable performance relationships between encoding and pointing tasks except for the tabletop task, performance on which was correlated with SOP performance but not with JRD performance. Also, travel distance in the virtual tabletop room was only correlated with performance on the JRD task. We anticipated that this movement would have provided additional alloformative aerial viewpoints of the virtual city, from different perspectives around the tabletop, which could facilitate the establishment of the requisite imagined headings required by the JRD task. Instead, we found that increased travel in the vista space during tabletop navigation was positively correlated with error on the JRD task, suggesting that additional movement around the tabletop virtual environment may have either disoriented participants or prevented them from anchoring allocentric representations to a single, reliable axis (Fig. 4). Unfortunately, this is difficult to compare with the other encoding tasks as neither route nor map learning tasks provide both measures. Further study using this novel tabletop navigation paradigm may provide insight into a broader range of spatial variables contributing to successful egocentric or allocentric strategies.

Our approach to testing spatial memory after learning from tabletop navigation was largely influenced by the approach taken by Zhang et al. (2014), with several important commonalities and differences. The most salient difference is that Zhang and colleagues’ data were collected in the laboratory, while the present data were collected online via MTurk, which was necessary to mitigate risks related to the concurrent SARS-CoV-2 pandemic. While we employed a variety of attention and validity checks along with stringent data quality assessments, there is no substitute for laboratory oversight in terms of enforcing compliance with experimental procedures such as prohibiting the use of external aids. Zhang et al.’s study also employed a design where encoding task was manipulated within subject. The rationale for our fully between-subject design was increasing the trial count to 56 pointing trials per block, compared to 10 per block as in the Zhang paper. While increased trials may have provided more reliable point estimates especially in terms of accounting for the distribution of data and its impact on analyses (Supplemental Fig. S8), it also resulted in an experiment duration that dissuaded us from using within-subject manipulations. Ultimately, we interpret our findings as being generally consistent with those of Zhang and colleagues. In Experiment 2, we observed a similar interaction effect and similar effect sizes as well as a replication of the map benefit for the JRD pointing task, albeit only for criterion map learning and absent of any route learning benefit for the SOP.

Another limitation related to the SARS-CoV-2 pandemic relates to how the tabletop navigation task was implemented. The task, which affords simultaneous translations and rotations by both the participant and the remote-control player was designed for immersive VR using a head-mounted stereoscopic display. We suspect that, in immersive VR, vestibular and proprioceptive input would allow a more intuitive interface in which attention could be focused on control of the remote-control avatar. In the desktop VR version used in the present studies, simultaneous movement was likely restricted to translations of the participants in the virtual tabletop room (i.e., using one hand for controlling tabletop room translation and the other for controlling remote-control translations/rotations would make it difficult to adjust tabletop views using the mouse). This is particularly relevant given the relationship between movement in the virtual tabletop room and JRD performance that was observed in our data.

Previous work using a real-world tabletop apparatus examined participants’ ability to learn and recall spatial layouts from various viewpoints (Holmes et al., 2018). This study used an array of dollhouse furniture on a circular tabletop for their scale-model stimuli and participants studied four viewpoints of the environment. Crucially, transitions between viewpoints were manipulated such that one group of participants saw only static views, another group viewed rotations of the table, and a third physically moved around the table. Their results showed that participants performed significantly better, on a modified JRD task, when they moved around the table compared to the static or rotation group. While these results may provide some insights into the results from our tabletop task, there are several important differences between the experimental and task design used by Holmes et al. (2018) and the present work. First, Holmes and colleagues utilized a multiple-choice variant of the JRD task, which may have differed in terms of the relative demands on familiarity versus recollection when performing the recognition task. As such, the accuracy measure derived from their multiple-choice task may be difficult to compare with precision data from an angular pointing version of the JRD. Second, although our tabletop navigation task allowed participants to move their virtual avatar around the table, it more closely resembled the rotational task used by Holmes and colleagues in that participants did not utilize vestibular or proprioceptive cues as in their perspective taking condition. Lastly, while participants in Holmes et al.’s perspective taking condition performed best, participants in the static and rotation conditions did not reliably perform above chance in every experiment. This is consistent with results emphasizing the impact of proprioceptive and, more importantly, vestibular information during spatial learning (Chrastil & Warren, 2012, 2013, 2015; Ruddle & Lessels, 2006, 2009). Taken together, existing literature further suggests the value of reexamining our tabletop navigation task in an immersive VR paradigm.

Future research using desktop interfaces with the tabletop navigation task should consider how a fixed viewpoint might impact encoding and subsequent retrieval of spatial representations. Alternatively, it might be interesting to use more traditional desktop-based map and viewpoint combinations such as the ‘mini-maps’ used in videogames—although these may also impact spatial representations (Gardony et al., 2013; Khan & Rahman, 2018). Therefore, future experiments could use the tabletop encoding task in immersive VR and task instructions that either encourage or discourage/prevent participants to change their vantage points to further test the Optimization Hypothesis (e.g., to determine whether such conditions produce similar improvement on the JRD task as the criterion map condition).

While there were clear task demands for our participants to encode the locations of the targets in the tabletop encoding task and the navigation task, the navigation and tabletop learning tasks required participants to locate only a single target store on a given trial (more-or-less independent of the other stores), whereas the criterion map task evaluated accuracy for the global configuration (all stores were placed before determining if the participant could progress such that stores had to be placed correctly relative to one another). In this way, the criterion map task put a strong emphasis on learning the configuration of stores while the navigation and tabletop tasks put a stronger emphasis on specific routes. Perhaps it is not surprising then that map learning put a greater emphasis on configural knowledge important to the JRD task while route and tabletop learning put a stronger emphasis on orientation and scene dependent memory important to the SOP task. There are other “hybrid” ways we could have emphasized criterial learning of routes (for example, completing all exploration and then placing stores in the tabletop task) which could potentially have put more emphasis on learning the configurations. Nonetheless, it is notable that even with the overhead view emphasized by tabletop task, configuration knowledge was not as readily available as in the criterion map task.

In summary, here we introduce a novel tool for studying egocentric and allocentric human spatial representations along a continuum. Our results provide preliminarily insight into how manipulating the ratio of available egoformative and alloformative spatial cues can influence spatial memory and strategy use. Further study will be required to better understand the cognitive mechanisms engaged during tabletop navigation and contrast them with more traditional forms of spatial learning, especially in immersive laboratory settings.

Supplementary Information

Below is the link to the electronic supplementary material.

Author contributions

Conceptualization: MJS, DJH, and ADE; Data curation: MJS; Formal analysis: MJS, Funding acquisition: ADE; Investigation: MJS; Methodology: MJS, DJH, and ADE; Project administration: ADE; Resources: ADE; Software: MJS; Supervision: DJH and ADE; Validation: MJS, DJH, and ADE; Visualization: MJS; Writing—original draft: MJS; Writing—review and editing: MJS, DJH, and ADE.

Funding

This research was supported by the National Science Foundation (NSF) BCS-1630296 awarded to Arne D. Ekstrom.

Data and code availability

Upon publication, task materials, data, and analysis code will be made available on the Open Science Framework, https://osf.io. Portions of the design and analysis plan were registered at the Open Science Framework on December 14, 2020; these are publicly available at https://osf.io/c3y9a. Data and narrative interpretations from this research have been discussed at the Society for Neuroscience Global Connectome virtual conference (Jan 2021) and various internal academic presentations at the University of Arizona and the University of California, Irvine. A previous version of this manuscript was published as a chapter of Michael J. Starrett’s doctoral dissertation, to which he holds the copyright and has provided permission for reuse.

Declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose. The authors have full control of all primary data and have agreed to allow the journal to review this data if requested. The authors have no known conflicts of interest to disclose.

Ethics approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards. The study was approved by the Institutional Review Board at the University of Arizona.

Consent to participate

All participants gave their written, informed consent prior to their inclusion in the study.