LIMO: Latent Inceptionism for Targeted Molecule Generation

Abstract

Generation of drug-like molecules with high binding affinity to target proteins remains a difficult and resource-intensive task in drug discovery. Existing approaches primarily employ reinforcement learning, Markov sampling, or deep generative models guided by Gaussian processes, which can be prohibitively slow when generating molecules with high binding affinity calculated by computationally-expensive physics-based methods. We present Latent Inceptionism on Molecules (LIMO), which significantly accelerates molecule generation with an inceptionism-like technique. LIMO employs a variational autoencoder-generated latent space and property prediction by two neural networks in sequence to enable faster gradient-based reverse-optimization of molecular properties. Comprehensive experiments show that LIMO performs competitively on benchmark tasks and markedly outperforms state-of-the-art techniques on the novel task of generating drug-like compounds with high binding affinity, reaching nanomolar range against two protein targets. We corroborate these docking-based results with more accurate molecular dynamics-based calculations of absolute binding free energy and show that one of our generated drug-like compounds has a predicted K_D (a measure of binding affinity) of 6 · 10⁻¹⁴ M against the human estrogen receptor, well beyond the affinities of typical early-stage drug candidates and most FDA-approved drugs to their respective targets. Code is available at https://github.com/Rose-STL-Lab/LIMO.

1. Introduction

Modern drug discovery is a long and expensive process, often requiring billions of dollars and years of effort (Hughes et al., 2011). Accelerating the process and reducing its cost would have clear economic and human benefits. A central goal of the first stages of drug discovery, which comprise a significant fraction and cost of the entire drug discovery pipeline (Paul et al., 2010), is to find a compound that has high binding affinity to a designated protein target, while retaining favorable pharmacologic and chemical properties (Hughes et al., 2011). This task is difficult because there are on the order of 10³³ chemically feasible molecules in the drug-like size range (Polishchuk et al., 2013), and only a tiny fraction of these bind to any given target with an affinity high enough to make them candidate drugs. Currently, this is done with large experimental compound screens and iterative synthesis and testing by medicinal chemists.

Recently, deep generative models have been proposed to identify promising drug candidates (Guimaraes et al., 2017; Goḿez-Bombarelli et al., 2018; Jin et al., 2018; Ma et al., 2018; You et al., 2018; Popova et al., 2019; Zhou et al., 2019; Jin et al., 2020b; Xie et al., 2021; Luo et al., 2021b), potentially circumventing much of the customary experimental work. However, even the best generative methods are prohibitively slow when optimizing for molecular properties that are computationally expensive to evaluate, such as binding affinity.

Here, we present a novel approach called Latent Inceptionism on Molecules (LIMO), a generative modeling framework for fast de novo molecule design that

• builds on the variational autoencoder (VAE) framework, combined with a novel property predictor network architecture;

• employs an inceptionism-like reverse optimization technique on a latent space to generate drug-like molecules with desirable properties;

• is much faster than existing reinforcement learning-based methods (6 – 8× faster) and sampling-based approaches (12× faster), while maintaining or exceeding baseline performances on the generation of molecules with desired properties;

• allows for the generation of molecules with desired properties while keeping a molecular substructure fixed, an important task in lead optimization;

• markedly outperforms state-of-the-art methods in the novel task of generating drug-like molecules with high binding affinities to target proteins.

2. Related Work

Domain state of the art.

After a protein is identified as a potential drug target, a common drug discovery paradigm today involves performing an initial high-throughput experimental screening of available compounds to identify hit compounds, i.e., molecules that have some affinity to the target. Computational methods, such as docking (e.g. Santos-Martins et al. (2021); Friesner et al. (2004)) or more rigorous molecular dynamics-guided binding free energy calculations (Cournia et al., 2020) of compounds to a known 3D structure of the target protein can also play a role by prioritizing compounds for testing. Once hit compounds have been experimentally confirmed, they become starting points for the synthesis of chemically similar lead compounds that have improved activity but require further optimization (lead optimization) to become a drug candidate that is deemed promising enough to advance further through the drug discovery pipeline (Hughes et al., 2011). To accelerate this often years-long drug discovery stage, there is great interest in novel computational technologies.

An alternative to experimentally screening existing compounds is to design entirely novel compounds for synthesis and testing. This approach, termed de novo design, takes advantage of the target protein’s 3D structure. Genetic algorithms (e.g. Spiegel & Durrant (2020)) and rule-based approaches (e.g. Allen et al. (2017)) have been developed for this task. However, these techniques are often slow and tend to be too rigid to be fully integrated into the drug discovery process, where many molecular properties and synthesizability must be considered simultaneously. For example, AutoGrow4 (Spiegel & Durrant, 2020), a state-of-the-art genetic algorithm, produces molecules with high binding affinities, but can also lead to toxic moieties and excessive molecular weights, while also being limited in the molecular space available for exploration. In contrast, recent machine learning methods offer greater flexibility and hence new promise for de novo drug design (Carracedo-Reboredo et al., 2021), as summarized below.

Generative models for molecule design.

Deep generative models use a learned latent space to represent the distribution of drug-like molecules. Early work (Goḿez-Bombarelli et al., 2018) applies a variational autoencoder (VAE, Kingma & Welling (2013)) to map SMILES strings (Weininger, 1988) to a continuous latent space. But SMILES-based representations struggle with generating both syntactically and semantically valid strings. Other works address this limitation by incorporating rules into the VAE decoder to only generate valid molecules (Kusner et al., 2017; Dai et al., 2018). Junction tree VAEs (Jin et al., 2018; 2019) use a scaffold junction tree to assemble building blocks into an always-valid molecular graph, and have been improved with RL-like sampling and optimization techniques (Tripp et al., 2020; Notin et al., 2021). DruGAN (Kadurin et al., 2017) further extends VAEs to an implicit GAN-based generative model. OptiMol uses a VAE to output molecular strings, but takes molecular graphs as input (Boitreaud et al., 2020). Shen et al. (2021) forego a latent space altogether and assemble symbols directly.

Apart from sequence generation, graph generative models have also been proposed (Ma et al., 2018; Simonovsky & Komodakis, 2018; De Cao & Kipf, 2018; Li et al., 2018; Fu et al., 2022; Zang & Wang, 2020; Luo et al., 2021b; Jin et al., 2020a; Luo et al., 2021a). As generative models do not directly control molecular properties, existing methods often use a surrogate model (Gaussian process or neural network) to predict molecular properties from the latent space, and guide optimization on the latent space toward molecules with desired properties (e.g. logP, QED, binding affinity). For example, MoFlow (Zang & Wang, 2020) predicts molecular properties from a latent space using a neural network, but has difficulty generating molecules with high property scores. Instead, we propose the prediction of properties from the decoded molecular space, which appears to greatly increase the property scores of generated molecules. Xie et al. (2021) propose Monte Carlo sampling to explore molecular space and Nigam et al. (2020) propose a genetic algorithm with a neural network-based discriminator, both of which require an extremely large number of calls to property functions and therefore are less useful when optimizing complex, expensive-to-evaluate property functions.

In general, generative models are very fast in generating molecules. However, as current generative models cannot effectively find molecules in their latent spaces that have desired properties, they have so far been outperformed by reinforcement learning-based methods that directly optimize molecules for desired properties.

Reinforcement learning-based molecule generation.

Reinforcement learning (RL) methods directly optimize molecular properties by systematically constructing or altering a molecular graph (You et al., 2018; Zhou et al., 2019; Jin et al., 2020b; Guimaraes et al., 2017; Popova et al., 2019; De Cao & Kipf, 2018; Zhavoronkov et al., 2019; Olivecrona et al., 2017; Shi et al., 2020; Luo et al., 2021b; Jeon & Kim, 2020). These methods appear to be the most powerful at generating molecules with desired properties, but are slow and require many calls to the property estimation function. This is problematic when applying RL to computationally expensive but highly useful property functions like physics-based (e.g. docking) computed binding affinity, rather than simple, easily computed measures such as logP. RationaleRL (Jin et al., 2020b) theoretically avoids the need to sample a large number of molecules by collecting “rationales” from existing molecules with desired properties, and combining them into molecules with multiple desired properties, but by design this method is not applicable to de novo drug discovery.

3. Methodology

We present Latent Inceptionism on Molecules (LIMO), a molecular generation framework. We use a VAE to learn a real-valued latent space representation of the drug-like chemical space. However, contrary to previous work, we use two neural networks (a decoder and predictor) in sequence to perform inceptionism-like reverse optimization of molecular properties on the latent space. Figure 1 gives an overview of the framework.

Figure 1.

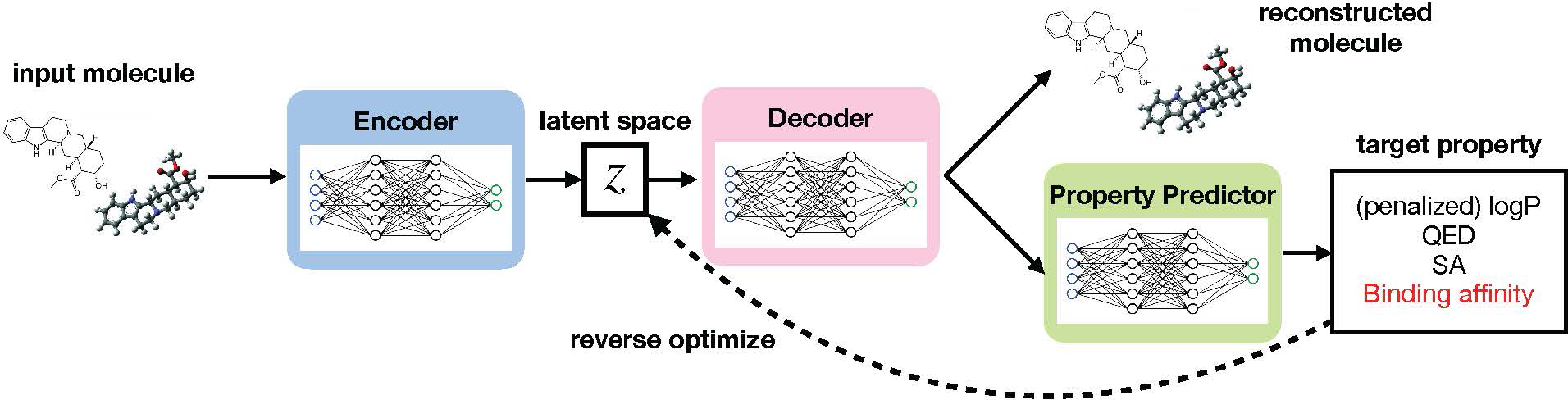
Overview of the LIMO framework. We train a variational autoencoder (“Encoder” and “Decoder”) to reconstruct input drug-like molecules. Then, a property predictor is trained to predict molecular properties (“target property”) using the output of the decoder. Using the property predictor, we generate molecules with desired properties by performing gradient descent on the output of the property predictor with respect to the latent space z, an inceptionism-like approach.

We use a decoder network to generate an intermediate real-valued molecular representation to improve the prediction, and therefore optimization, of molecular properties while keeping the prediction differentiable, allowing the use of efficient gradient-based optimizers. We use self-referencing embedded strings (SELFIES, Krenn et al. (2020)) to ensure chemical validity during optimization. With these novelties, LIMO is able to achieve performance on par with reinforcement learning methods while being orders of magnitude faster. On the highly useful task of structure-based computed binding affinity optimization, LIMO markedly outperforms state-of-the-art (including RL) methods, while also being much faster.

3.1. Variational Autoencoder

Define a string representation of a molecule x = (x₁,··· ,x_n). Each x_i takes its value from a set of d possible symbols $𝒮=\left\{s_1,\cdots ,s_d\right\}$, where each symbol is one component of a self-referencing embedded string (SELFIES) defining a molecule (Krenn et al., 2020). We aim to produce n independent distributions y = (y₁,··· ,y_n), where each y_i ∈ [0, 1]^d is the parameter for a multinomial distribution over the d symbols in $𝒮$. The output string $\widehat{\mathbf{x}}=\left({\widehat{x}}_1,\cdots ,{\widehat{x}}_n\right)$ is obtained from y by selecting the symbol with the highest probability:

$${\widehat{x}}_i=s_{d_i^{*}},d_i^{*}={\mathrm{argmax}}_d\left\{y_{i,1},\cdots ,y_{i,d}\right\}$$ (1)

All SELFIES strings correspond to valid molecules, allowing us to transform the continuous-value probabilities y into an always-valid discrete molecule.

We train a VAE (Kingma & Welling, 2013) to encode x to a latent space $\mathbf{z}\in {ℝ}^m$ of dimensionality m and decode to y. We optimize the VAE using the evidence lower bound (ELBO) loss function. Each input symbol in the representation string passes through an embedding layer, and then two fully-connected networks (the encoder and decoder). Reconstruction loss is calculated using the negative log-likelihood over a one-hot encoded representation of the input molecule. Once trained, the VAE can generate novel and drug-like molecules, with similar molecules lying next to each other in the latent space. To generate random molecules, we sample from the latent space z using $𝒩\left(0_m,I_m\right)$, and decode it into a string representation.

3.2. Property Predictor

We employ a separate network to predict molecular properties. While earlier works train the VAE and property predictor jointly (Jin et al., 2018; Gomez-Boḿbarelli et al., 2018), we train the property predictor after the VAE has been fully trained (i.e. we freeze the VAE weights) for three reasons: firstly, generative modeling requires significantly more molecular data than the regression task of predicting molecular properties. There is no need to acquire property data for all the molecules used by the generative model. This is especially relevant when such data is expensive to obtain, e.g. docking-based binding affinity that takes seconds to calculate per molecule. Secondly, the trained generative model allows us to query the ground-truth molecular property function with its generated molecules, giving an informative and diverse training set for property prediction. Thirdly, adding new properties under this training scheme does not require retraining of the VAE, only of the property predictor, which is much more efficient.

Crucially, we introduce a novel architecture consisting of stacking the VAE decoder and the property predictor. The property predictor uses the output of the VAE decoder as its input, as opposed to predicting properties directly from the latent space like previous works (e.g. Jin et al. (2018); Goḿez-Bombarelli et al. (2018); Zang & Wang (2020)). The intuition is that the map from molecular space to property is easier to learn than that from the latent space to property. We later present results confirming this intuition, both in terms of prediction accuracy and overall optimization ability, suggesting that the proposed stacking improves optimization by allowing more accurate prediction of molecular properties through a more direct molecular representation. Using such an intermediate molecular representation from the VAE decoder also allows us to fix a substructure of the generated molecule, giving LIMO the ability to perform the unique, compared to many other VAE-based architectures, ability to perform substructure-constrained optimization.

Define the VAE encoder f_enc : x ↦ z and decoder $f_{\text{dec}}:\mathbf{z}\mapsto \widehat{\mathbf{x}}$, a property prediction network $g_{\theta }:\widehat{\mathbf{x}}\mapsto ℝ$ with parameters θ, and a ground-truth property estimation function $\pi :\widehat{\mathbf{x}}\mapsto ℝ$ that computes a molecular property such as logP or binding affinity. We first generate examples to train g_θ by sampling random molecules from the latent space z using a normal distribution $𝒩\left(0_m,I_m\right)$. Then, we optimize the parameters θ of the property predictor by minimizing the mean square error (MSE) of predicted properties over the set of generated molecules:

$${\ell }_0(\theta )={\Vert g_{\theta }\left(f_{\text{dec}}(\mathbf{z})\right)-\pi \left(f_{\text{dec}}(\mathbf{z})\right)\Vert }^2$$ (2)

3.3. Reverse Optimization

After training, we freeze the weights of f_dec and g_θ, and make z trainable to optimize the latent space toward locations that decode to molecules with desirable properties. This is a similar technique to inceptionism, which involves backpropagating from the output of a network to its input so that the input is altered to affect the output in a desired way (Mordvintsev et al., 2015).

To maximize properties, given a set of k property predictors (g¹,··· ,g^k) and weights (w₁,··· ,w_k), we minimize the following function using the Adam optimizer, initialized from $\mathbf{z}~𝒩\left(0_m,I_m\right)$:

$${\ell }_1(\mathbf{z})=-\sum _{i=1}^k{w}_i\cdot g^i\left(f_{\text{dec}}(\mathbf{z})\right)$$ (3)

Crucially, since both f_dec and g are neural networks, gradient-based techniques can be used for efficient optimization of z. The weights (w₁,··· ,w_k) are hyperparameters determined by a random grid search.

In lead optimization, a common task is to generate molecules with desired properties while keeping a given substructure of the molecules fixed. To apply reverse optimization to this task, we define a mask M ∈ {0, 1}^n×d, where M_i,j corresponds to the SELFIES symbol of index j at position i in a molecular string. We assign M_i,j = 1 where the desired substructure is present and the corresponding symbol cannot be changed, 0 otherwise. For an optimization starting point, we then reconstruct a molecule x_start that has the desired substructure:${\widehat{\mathbf{x}}}_{\text{start}}=f_{\text{dec}}\left(f_{\text{enc}}\left({\mathbf{x}}_{\text{start}}\right)\right)$. To optimize z while also keeping a substructure constant, we add an additional loss ℓ₂ to the ℓ₁ used in Equation 3:

$${\ell }_2(\mathbf{z})=\lambda \sum _{i=1}^n\sum _{j=1}^d{(M_{i,j}\cdot (f_{\mathrm{dec}}{(\mathbf{z})}_{i,j}-{({\widehat{\mathbf{x}}}_{\text{start}})}_{i,j}))}^2$$ (4)

where λ is a weighting term we set to 1,000.

3.4. Refinement

Filtering.

Following multi-objective optimization, we perform a filtering step to exclude non drug-like molecules. Using the distributions of quantitative estimate of drug-likeness (QED) and synthetic accessibility (SA) scores on drug-like datasets (Bickerton et al., 2012; Ertl & Schuffenhauer, 2009), we define cutoff values reasonably within the range of currently marketed drugs. Molecules not reaching these cutoffs are excluded from consideration. We also exclude molecules with either too small or too large chemical cycles (rings), as these are usually difficult to synthesize but are not excluded effectively by the SA metric. Specifically, we exclude molecules not satisfying (QED > 0.4)∧(SA < 5.5) ∧ (no rings with < 5 or > 6 atoms).

Fine-tuning.

For some tasks, we observe that LIMO is effective in generating molecules with reasonably high property scores that could nonetheless be improved slightly by small, atom-level changes. To do this, we performed a greedy local search around the chemical space of a generated molecule by systematically replacing carbons with heteroatoms and retaining changes that lead to the most improvement. The algorithm is detailed in Appendix A.3.

4. Experiments

We apply LIMO to QED and penalized logP (p-logP) maximization, logP targeting (You et al., 2018), similarity-constrained p-logP maximization (Jin et al., 2018), substructure-constrained logP extremization, and single and multi-objective binding affinity maximization. All of these tasks are typical challenges in drug discovery, especially optimization around a substructure and maximization of binding affinity. See Appendix A.1 for description of each task, and Appendix B.1 for results from the random generation of molecules.

4.1. Experimental Setup

Dataset.

For all optimization tasks, we use the benchmark ZINC250k dataset, which contains ≈250,000 purchasable, drug-like molecules (Irwin et al., 2012). We use AutoDock-GPU (Santos-Martins et al., 2021) to compute binding affinity, as described in Appendix A.6, and RDKit to compute other molecular properties. For the random generation task, we train on the ZINC-based ≈2 million molecule MOSES dataset (Polykovskiy et al., 2020).

Model training.

All experiments use identical autoencoder weights and a latent space dimension of 1024. We select hyperparameters using a random grid search. The property predictor is trained independently for each of the following properties: logP (octanol-water partition coefficient), p-logP (Jin et al., 2018), SA (Ertl & Schuffenhauer, 2009), QED (Bickerton et al., 2012), and binding affinity to two targets (calculated by AutoDock-GPU, Santos-Martins et al. (2021)). 100k training examples were used for all properties except binding affinity, where 10k were used due to speed concerns. See Appendix A.5 for model training details.

Baselines.

We compare with the following state-of-the-art molecular design baselines: JT-VAE (Jin et al., 2018), GCPN (You et al., 2018), MolDQN (Zhou et al., 2019), MARS (Xie et al., 2021), and GraphDF (Luo et al., 2021b). Each technique is described in Appendix A.4.

Protein targets.

For tasks involving binding affinity optimization, we target the binding sites of two human proteins:

• Human estrogen receptor (ESR1): This well-characterized protein is a target of drugs used to treat breast cancer. It was chosen for its disease relevance and its many known binders, which are good points of comparison with generated molecules. Although known binders exist, LIMO was not fed any information beyond a crystal structure of the protein (PDB 1ERR) used for docking calculations and the location of the binding site.

• Human peroxisomal acetyl-CoA acyl transferase 1 (ACAA1): This enzyme has no known binders but does have a crystal structure (PDB 2IIK) with a potential drug-binding pocket, which we target to show the ability of LIMO for de novo drug design. We found this protein with the help of the Structural Genomics Consortium, which highlighted this protein as a potentially disease-relevant target with a known crystal structure, but no known binders.

4.2. QED and Penalized logP Maximization

Table 1 shows results of LIMO and baselines on the generation of molecules with high penalized logP and QED scores. For both properties, we report the top 3 scores of 100k generated molecules, as well as the total time (generation + testing) taken by each method. As an ablative study, we apply LIMO with property prediction directly on the latent space (“LIMO on z”) as opposed to regular LIMO, which performs property prediction on the decoded molecule $\widehat{\mathbf{x}}$ (see Section 3.2). Both methods underwent the same hyperparameter tuning as described in Appendix A.5. We see that the extra novel step of decoding the latent space and then performing property prediction offers a significant advantage for the optimization of molecules. To elucidate this improvement, an unseen test set of 1,000 molecules was generated using the VAE and used to test the prediction performance of the property predictor. We observe an r² = 0.04 between real and predicted properties for “LIMO on z”, and r² = 0.38 for LIMO. This large predictive performance boost explains the observed improvements in the optimization of molecules, as the model is better able to generalize what makes a molecule bind well. We also replaced LIMO’s fully-connected VAE encoder and decoder each with an 8-layer, 512 hidden dimension LSTM and found significantly worse performance, e.g. a maximum QED score of 0.3. The addition of a self-attention layer after the LSTM encoder did not significantly improve performance.

Table 1.

Comparison of QED and p-logP maximization methods. “LL” (length limit) denotes whether a model has a limited output length (about the maximum molecule size of ZINC250k), as p-logP score can increase linearly with molecule length. Baseline results taken from (You et al., 2018; Luo et al., 2021b; Xie et al., 2021).

Method	LL	penalized logP			QED			Time (hrs)
		1st	2nd	3rd	1st	2nd	3rd
JT-VAE	✘	5.30	4.93	4.49	0.925	0.911	0.910	24
GCPN	✔	7.98	7.85	7.80	0.948	0.947	0.946	8
MolDQN	✔	11.8	11.8	11.8	0.948	0.943	0.943	24
MARS	✘	45.0	44.3	43.8	0.948	0.948	0.948	12
GraphDF	✘	13.7	13.2	13.2	0.948	0.948	0.948	8
LIMO on z	✔	6.52	6.38	5.59	0.910	0.909	0.892	1
LIMO	✔	10.5	9.69	9.60	0.947	0.946	0.945	1

We observe that LIMO achieves competitive results among deep generative and RL-based models (i.e. all methods except MARS) while taking significantly less time. Note that p-logP is a “broken” metric that is almost entirely dependent on molecule length (Zhou et al., 2019). Without a length limit, MARS can easily generate long carbon chains with high p-logP. Among models with a molecule length limit (GCPN, MolDQN, and LIMO), LIMO generates molecules with p-logP similar to MolDQN, the strongest baseline. Similarly, QED suffers from boundary effects around its maximum score of 0.948 (Zhou et al., 2019), which LIMO gets very close to. Drugs with a QED score above 0.9 are very rare (Bickerton et al., 2012), so achieving close to this maximum score is sufficient for drug discovery purposes.

4.3. logP Targeting

Table 2 reports on the ability of LIMO to generate molecules with logP targeted to the range −2.5 < logP < −2.0. LIMO achieves the highest diversity among generated molecules within the targeted logP range, and, although it has a lower success rate than other methods, it generates 33 molecules per second within the target range. This is similar to the overall generation speed of other models, but due to a lack of available code for this task, we were not able to compare exact speeds.

Table 2.

Property targeting to −2.5 < logP < −2.0. Success (%): percent of generated molecules within the target range. Diversity: One minus the average pairwise Tanimoto similarity between Morgan fingerprints. Results for JT-VAE and GCPN taken from (You et al., 2018).

Method	Success (%)	Diversity
JT-VAE	11.3	0.846
GCPN	85.5	0.392
MolDQN	9.66	0.854
GraphDF	0	-
LIMO	10.4	0.914

4.4. Similarity-constrained Penalized logP Maximization

Following the procedures described for JT-VAE (Jin et al., 2018), we select the 800 molecules with the lowest p-logP scores in the ZINC250k dataset and aim to generate new molecules with a higher p-logP yet similarity to the original molecule. Similarity is measured by Tanimoto similarity between Morgan fingerprints with a cutoff value δ. Each of the 800 starting molecules are encoded into the latent space using the VAE encoder, 1,000 gradient ascent steps (Section 3.3) are completed for each, then the generated molecules out of all gradient ascent steps with the highest p-logP that satisfy the similarity constraint are chosen.

Results for the similarity-constrained p-logP maximization task are summarized in Table 3. For the two lowest similarity constraints (δ = 0.0, 0.2), LIMO achieves the highest penalized logP improvement, while its improvement is statistically indistinguishable from other methods at higher values of δ. This shows the power of LIMO for unconstrained optimization, and the ability to reach competitive performance in more constrained settings.

Table 3.

Similarity-constrained p-logP maximization. For each method and minimum similarity constraint δ, the mean ± standard deviation of improvement (among molecules that satisfy the similarity constraint) from the starting molecule is shown, as well as the percent of optimized molecules that satisfy the similarity constraint (% succ.). Baseline results taken from (Luo et al., 2021b; Zhou et al., 2019).

δ	JT-VAE		GCPN		GraphDF		MolDQN		LIMO
	Improv.	% Succ.	Improv.	% Succ.	Improv.	% Succ.	Improv.	% Succ.	Improv.	% Succ.
0.0	1.9 ± 2.0	97.5	4.2 ± 1.3	100	5.9 ± 2.0	100	7.0 ± 1.4	100	10.1 ± 2.3	100
0.2	1.7 ± 1.9	97.1	4.1 ± 1.2	100	5.6 ± 1.7	100	5.1 ± 1.8	100	5.8 ± 2.6	99.0
0.4	0.8 ± 1.5	83.6	2.5 ± 1.3	100	4.1 ± 1.4	100	3.4 ± 1.6	100	3.6 ± 2.3	93.7
0.6	0.2 ± 0.7	46.4	0.8 ± 0.6	100	1.7 ± 1.2	93.0	1.9 ± 1.2	100	1.8 ± 2.0	85.5

4.5. Substructure-constrained logP Extremization

Results for the substructure-constrained logP extremization task are shown in Figure 2. We chose two molecules from ZINC250k to act as starting molecules and defined the substructures of these starting molecules to be fixed, then performed both maximization and minimization of logP using LIMO, as described in Equation 4. As illustrated, we can successfully increase or decrease logP as desired while keeping the substructure constant in both cases.

Figure 2.

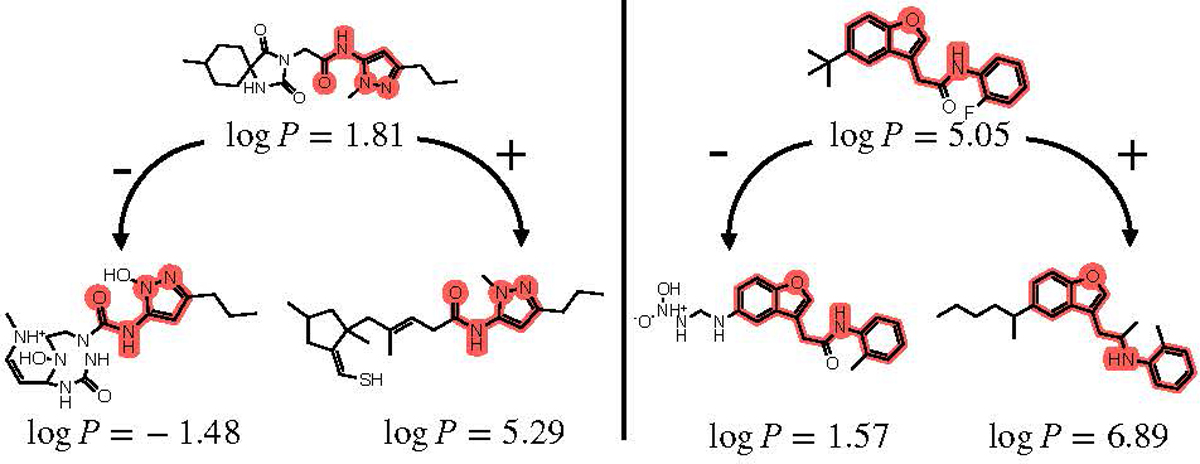
Examples of LIMO’s extremization of logP while keeping a substructure (denoted in red) constant.

This task is common during the lead optimization stage of drug development, where a synthetic pathway to reach an exact substructure with proven activity is established, but molecular groups around this substructure are more malleable and have not yet been determined. This is not captured in the similarity-constrained optimization task above, which uses more general whole-molecule similarity metrics.

While previous works address the challenge of property optimization around a fixed substructure (Hataya et al., 2021; Lim et al., 2020; Maziarz et al., 2021), LIMO is one of the few VAE-based methods that can easily perform such optimization. Thanks to its unique decoding step of generating an intermediate molecular string prior to property prediction, LIMO brings the speed benefits of VAE techniques to the substructure optimization task.

4.6. Single-objective Binding Affinity Maximization

Producing molecules with high binding affinity to the target protein is the primary goal of early drug discovery (Hughes et al., 2011), and its optimization using a docking-based binding affinity estimator, which is especially powerful in the de novo setting, is relatively novel to the ML-based molecule generation literature. Many previous approaches have attempted to optimize affinity by leveraging knowledge of existing binders (e.g. Zhavoronkov et al. (2019); Jeon & Kim (2020); Luo et al. (2021a)), but they often lack generalizability to targets without such binders. Therefore, we focus on molecule optimization in the de novo setting through the use of a docking-based affinity estimator.

We target the binding sites of two human proteins: estrogen receptor (PDB ESR1, UniProt P03372) and peroxisomal acetyl-CoA acyl transferase 1 (PDB ACAA1, UniProt P09110) (see Section 4.1 for details). For both of our protein targets we report the top 3 highest affinities (i.e., lowest dissociation constants, K_D, as estimated with AutoDockGPU) of 10k total generated molecules from each method. As shown in Table 4, LIMO generates compounds with higher computed binding affinities in far less time than prior state-of-the-art methods. We chose GCPN, MolDQN, GraphDF, and MARS as baseline comparisons because of their strong performance on other single-objective optimization tasks.

Table 4.

Generation of molecules with high computed binding affinities (shown as dissociation constants, K_D, in nanomoles/liter) for two protein targets, ESR1 and ACAA1.

Method	ESR1			ACAA1			Time (hrs)
	1st	2nd	3rd	1st	2nd	3rd
GCPN	6.4	6.6	8.5	75	83	84	6
MolDQN	373	588	1062	240	337	608	6
GraphDF	25	47	51	370	520	590	12
MARS	17	64	69	163	203	236	6
LIMO	0.72	0.89	L4	37	37	41	1

The chemical structures of two molecules generated by LIMO when only optimizing for binding affinity are shown in the bottom row of Figure 3 for both protein targets. While these molecules have relatively high affinities, they would have little utility in drug discovery because they are pharmacologically and synthetically problematic. For example, we highlight two major moieties, polyenes and large (≥8 atoms) cycles, that are regarded by domain experts as highly problematic due to reactivity/toxicity and synthesizability concerns, respectively (see Birch & Sibley (2017); Hussain et al. (2014); Abdelraheem et al. (2016)). Molecules generated from GCPN, MolDQN, GraphDF, and MARS had similar issues. These moieties are large structural issues that cannot be fixed with small tweaks following optimization, so we added measures of ligand quality into our optimization process as detailed in the following subsection.

Figure 3.

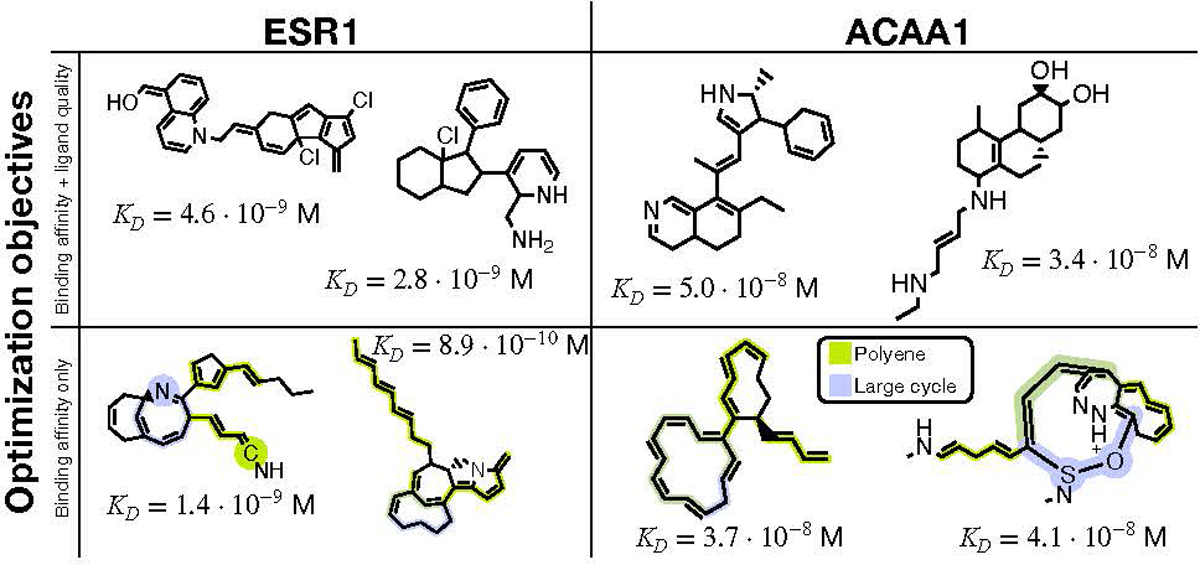
Generated molecules from the multi-objective (top row) and single-objective (bottom row) binding affinity maximization. The estimated dissociation constants, K_D, were obtained by docking each compound to the targeted protein using AutoDock-GPU. The dissociation constant is a measure of binding affinity, where lower is better. In the bottom row, we highlight two major problematic patterns that appeared when only considering computed binding affinity, motivating multi-objective optimization.

4.7. Multi-objective Binding Affinity Maximization

To generate molecules with high computed binding affinity and pharmacologic and synthetic desirability, we simultaneously optimize molecules for computed binding affinity, drug-likeness (QED), and synthesizability (SA) scores. Distributions of properties before and after multi-objective optimization are shown in Appendix B.2. For each protein target, we generate 100k molecules, then apply the two refinement steps described in Section 3.4. We selected the two compounds with the highest affinity from this process for each protein target, which are shown in the top row of Figure 3. These compounds are more drug-like and synthetically accessible than those generated by single-objective optimization (Figure 3, bottom row), but still have high predicted binding affinities (i.e., low K_D values), making them promising drug candidates. We analyze and compare these compounds in the subsequent section.

Compound analysis.

Table 5 shows the binding and drug-likeness metrics of two generated compounds for both ESR1 and ACAA1 (the same as those shown in the top row of Figure 3). For ESR1, we compare our compounds to tamoxifen and raloxifene, two modern breast cancer drugs on the market that target this protein. We also compare with compounds generated by GCPN, the second strongest method behind LIMO for single-objective binding affinity maximization, with identical multi-objective weights and the same filtering step as LIMO. For each compound, we report the metrics described in the Appendix A.2. The first three metrics given are “Optimized properties” that are explicitly optimized for, while the others are not used in optimization but are still useful for compound evaluation.

Table 5.

Comparison of generated ligands for ESR1 and ACAA1 following multi-objective optimization and refinement.

Ligand	Optimized prop.			Non-optimized prop.
	KD (AD) (↓)	QED (↑)	SA (↓)	KD (ABFE) (↓)	Lipinski	PAINS (↓)	Fsp3 (↑)	MCE-18 (↑)
ESR1
LIMO mol. #1	4.6	0.43	4.8	6 · 10−5	✔	0	0.16	90
LIMO mol. #2	2.8	0.64	4.9	1000	✔	0	0.52	76
GCPN mol. #1	810	0.43	4.2	-	✔	0	0.29	22
GCPN mol. #2	2.7 · 104	0.80	3.7	-	✔	0	0.56	47
Tamoxifen	87	0.45	2.0	1.5*	✔	0	0.23	16
Raloxifene	7.9 · 106	0.32	2.4	0.030*	✔	0	0.25	59
ACAA1
LIMO mol. #1	28	0.57	5.5	4 · 104	✔	0	0.52	52
LIMO mol. #2	31	0.44	4.9	No binding	✔	0	0.81	45
GCPN mol. #1	8500	0.69	4.2	-	✔	0	0.52	61
GCPN mol. #2	8500	0.54	4.3	-	✔	0	0.52	30

Arrows indicate whether a high score (↑) or low score (↓) is desired. High QED, Fsp³, and satisfying Lipinski’s Rule of 5 suggest drug-likeness. A low number of PAINS alerts indicates a low likelihood of false positive results in binding assays. MCE-18 is a measure of molecular novelty based on complexity, and SA is a measure of synthesizability. K_D values in nM are computed binding affinities from AutoDock-GPU (AD) and from more rigorous absolute binding free energy calculations (ABFE). See Appendix A.2 for a full description of each metric.

^*indicates an experimentally determined value obtained from BindingDB (Liu et al., 2007).

LIMO significantly outperforms GCPN, which generates molecules with such low computed affinity (high K_D) as to be of relatively low utility in drug discovery, regardless of drug-likeness or synthesizability metrics, because they are unlikely to bind their targets at all.

Visualization and corroboration of binding affinities.

To confirm that the ligands generated by LIMO are likely to bind their target proteins with high affinity and do not score well due to inaccuracies or shortcuts used in the AutoDock-GPU scoring function, we visualized their docked poses in 3D to look for physically reasonable bound conformations and energetically favorable ligand-protein interactions. The 3D binding poses produced by the docking software for one of the two generated ligands for each protein (Figure 4) show that they fit well into the protein binding pocket and promote favorable ligand-protein interactions.

Figure 4.

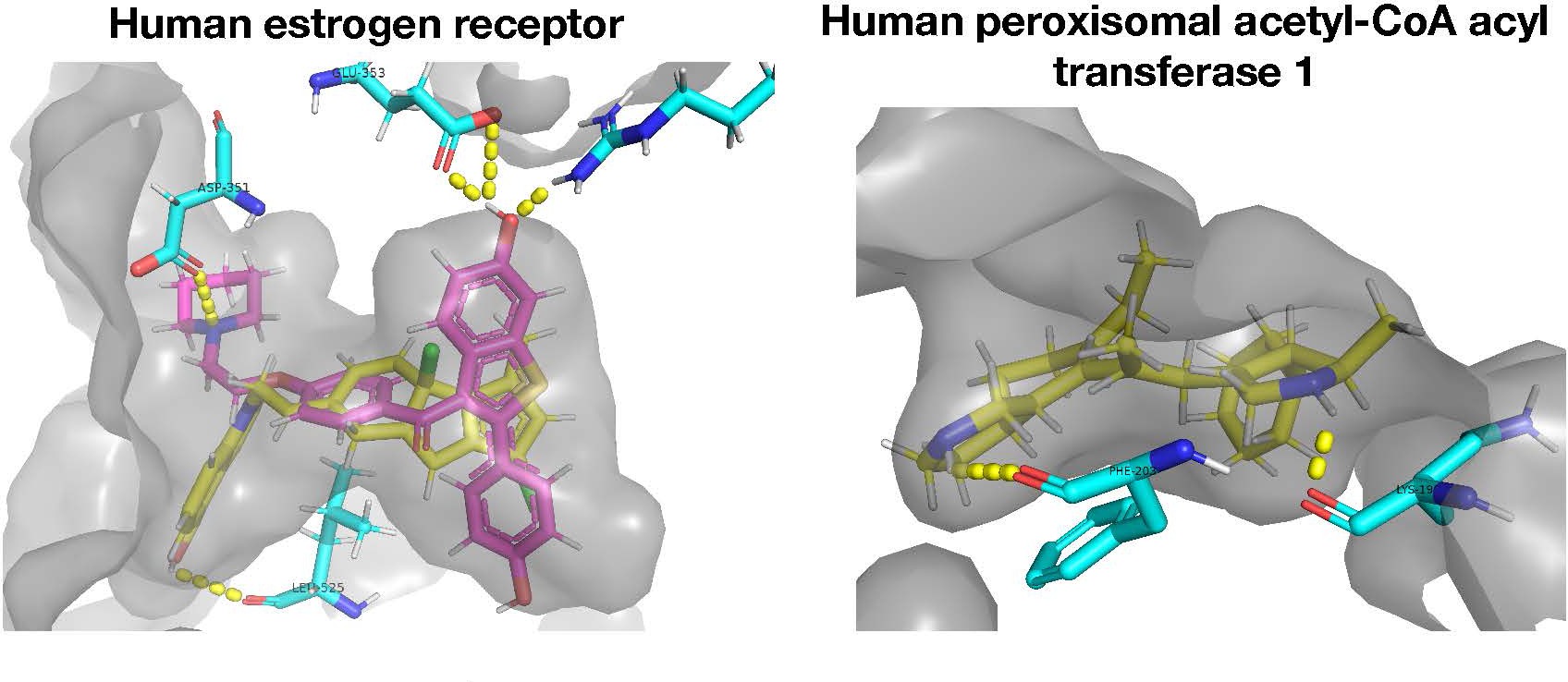
3D visualization of ligands docked against ESR1 and ACAA1. LIMO-generated ligands (one for each protein) are shown in yellow, and raloxifene, a cancer drug that targets ESR1, is shown in pink. The protein pocket is displayed as semi-opaque, and nearby structures of the protein are shown in blue. Docked poses were generated by GLIDE (Friesner et al., 2004) for ESR1 and AutoDock-GPU (Santos-Martins et al., 2021) for ACAA1. Favorable atom-atom interactions between ligand and protein are shown with a dashed yellow line.

We furthermore ran detailed, molecular dynamics-based, absolute binding free energy calculations (ABFE, Appendix A.7) (Gilson et al., 1997; Cournia et al., 2020) to obtain more reliable estimates of the affinities of LIMO-generated compounds for their targeted proteins than the predictions from docking. As shown in Table 5, LIMO generated an ESR1 ligand with an ABFE-predicted dissociation constant (K_D) of 6 · 10⁻⁵nM, much better than typical K_D values of e.g. 1000 nM obtained from experimental compound screening and better even than the K_D values of tamoxifen and raloxifene, two drugs that bind ESR1 with high affinity. The LIMO compounds even exceed these drugs on many drug-likeness metrics. Without experimental confirmation, we cannot be sure these molecules bind so well, but the results from these state-of-the-art calculations are encouraging.

5. Discussion and Conclusions

We present LIMO, a generative modeling framework for de novo molecule design. LIMO utilizes a VAE latent space and two neural networks in sequence to reverse-optimize molecular properties, allowing the use of efficient gradient-based optimizers to achieve competitive results on benchmark tasks in significantly less time. The ability to generate six times as many molecules per unit of time relative to competing methods (Table 4) increases the odds of producing high-quality drug candidates that survive successive rounds of refinement, thereby accelerating drug development as a whole, especially given LIMO’s high diversity of compounds (Table 2, 6). On the task of generating molecules with high binding affinity, LIMO outperforms all state-of-the-art baselines.

LIMO promises multiple applications in drug discovery. The ability to quickly generate high-affinity compounds can accelerate target validation with biological probes that can be used to confirm the proposed biological effect of a target. LIMO also has the potential to accelerate lead generation and optimization by jumping directly to drug-like, synthesizable, high affinity compounds, thus bypassing the traditional hit identification, hit-to-lead, and lead optimization steps. While “unconstrained” LIMO can quickly generate high-affinity compounds, it has the additional ability to perform substructure-constrained property optimization, which is especially useful during the lead optimization stage where one has an established substructure with a synthetic pathway and wishes to “decorate” around it for improved activity or pharmacologic properties.

While LIMO can generate very high affinity compounds as computed by docking software, as is its goal, the utility of compounds only vetted by docking software may be questioned. As shown in Table 5, AutoDock-GPU computed binding affinities do not correlate very well with more accurate ABFE results. This is a well-known result (Cournia et al., 2020), but we believe having docking-predicted high affinity compounds is still of relatively high utility in drug discovery, even if some (or most) generated compounds are “false positives.” As LIMO can generate hundreds of diverse docking-computed nanomolar range compounds against a target in hours, it is likely that some of those compounds will actually bind a target well. This is a unique advantage of LIMO, as it is able to generate many candidate compounds very quickly, allowing for aggressive filtering downstream. Indeed, we have generated a highly favorable compound (K_D = 6 · 10⁻¹⁴ M) as calculated by ABFE, even more favorable than AutoDock-GPU predictions, out of only two generated candidates. The addition of further automated binding affinity confirmation into the LIMO pipeline, e.g. with additional docking software or automated ABFE calculation, is a promising direction for future work. Other future directions include exploring the use of different molecular representation and model architectures in LIMO, the use of better optimizers beyond simple gradient-based methods, and the application of LIMO to more or multiple simultaneous protein targets.

A. Experiment description and baselines

A.1. Tasks

Random generation of molecules:

Generate random molecules by sampling from the latent space of the generative model. As later optimization relies on these generated molecules as starting points, it is important that they be novel, diverse, and unique.

QED and penalized logP maximization:

Generate molecules with high penalized logP (p-logP, estimated octanol-water partition coefficient penalized by synthetic accessibility (SA) score and number of cycles with more than six atoms (Jin et al., 2018)) and quantitative estimate of drug-likeness (QED, (Bickerton et al., 2012)) scores. These properties are important considerations in drug discovery, and this task shows the ability of a model to optimize salient aspects of a molecule, even if maximization of these properties by themselves is of low utility (Zhou et al., 2019).

logP targeting:

Generate molecules with logP within a specified range. In drug discovery, a logP within a given range is often taken as an approximate indicator that a molecule will have favorable pharmacokinetic properties.

Similarity-constrained penalized logP maximization:

For each molecule in a set of starting molecules, generate a novel molecule with a high penalized logP (p-logP) score while retaining similarity (as defined by Tanimoto similarity between Morgan fingerprints, Rogers & Hahn (2010)) to the original molecule. This mimics the drug discovery task of adjustment of an active starting molecule’s logP while keeping similarity to the starting molecule to retain biological activity.

Substructure-constrained logP extremization:

Generate molecules with either high or low logP scores while keeping a subgraph of a starting molecule fixed. This task mimics the drug discovery goal of optimizing around (“decorating”) an existing substructure to fine-tune activity or adjust pharmacologic properties. This is common in the lead optimization stage of drug development, where a synthetic pathway to reach an exact substructure with proven activity is established, but molecular groups around this substructure are more malleable and not yet established. This task is not captured in the similarity-constrained optimization task above, which uses more general whole-molecule similarity metrics.

Single-objective binding affinity maximization:

Generate molecules with high computed binding affinity for two protein targets as determined by docking software. Reaching high binding affinities is the primary goal of early drug discovery, and its optimization using a physics-based affinity estimator is a relatively novel task in the ML-based molecule generation literature. Previous attempts to optimize affinity have relied on knowledge of existing binders (Zhavoronkov et al., 2019; Jeon & Kim, 2020; Luo et al., 2021a), which lacks the generalizability of physics-based estimators to targets without known binders.

Multi-objective binding affinity maximization:

Generate molecules with favorable computed binding affinity, QED, and SA scores. This task has high utility in drug discovery, as it addresses targeting, pharmacokinetic properties, and ease of synthesis. Development of molecules satisfying all these considerations is challenging, and to the best of our knowledge, is a novel task in the ML-based molecule generation literature.

A.2. Molecule metrics

We report the following metrics for our multi-objective optimized molecules, all of which are given by ADMETLab 2.0 (Xiong et al., 2021) except binding affinities:

• K_D (AutoDock-GPU): Dissociation constant K_D in nanomolar, as calculated by AutoDock-GPU. Lower K_D is associated with better binding (i.e. higher affinity) (Santos-Martins et al., 2021)

• K_D (ABFE): Dissociation constant K_D in nanomolar, as calculated by absolute binding free energy (ABFE) calculations, which are generally more accurate than AutoDock-GPU scores (Cournia et al., 2020)

• QED: Quantitative estimate of drug-likeness score, higher is better (Bickerton et al., 2012)

• SA: Synthetic accessibility score, lower is better (Ertl & Schuffenhauer, 2009)

• Lipinksi: Lipinski’s rule of 5 is a commonly used rule of thumb for drug-likeness (Lipinski et al., 2001). Compounds that pass all or all but one of four components are considered more likely to be suitable as drugs.

• PAINS: Number of PAINS alerts. These alerts detect compounds likely to have non-specific activity against a wide array of biological targets, making them undesirable as drugs. Lower is better (Baell & Holloway, 2010)

• Fsp³: The fraction of sp3 hybridized carbons, which is thought to correlate with favorable drug properties. Higher is better (Wei et al., 2020)

• MCE-18: A measure of molecular novelty based on complexity measures. Higher is better (Ivanenkov et al., 2019)

A.3. Fine-tuning algorithm

Algorithm 1.

Molecule fine-tuning algorithm.

Require: The starting molecule $ℳ$ to be optimized and a function π(m) that calculates a property for molecule m

$ℛ\leftarrow \{\text{N},\text{O},\text{Cl},\text{F}\}$

$\text{bestProperty}\leftarrow \pi (ℳ)$

while bestProperty is improving do

$\text{bestMolecule}=ℳ$

for all carbon atoms in $ℳ$ not adjacent to any atoms ∈ $ℛ$ do

for all potential replacement atoms ∈ $ℛ$ do

$m\leftarrow ℳ$ with the carbon atom replaced

if m is valid and π(m) is better than π(bestMolecule) then

bestMolecule ← m

end if

end for

end for

$ℳ\leftarrow \text{bestMolecule}$

end while

A.4. Baselines

We compare with the following baselines:

• JT-VAE (Jin et al., 2018): a VAE-based generative model that first generates a scaffold junction tree and then assembles nodes in the tree into a molecular graph.

• GCPN (You et al., 2018): an RL agent that successively constructs a molecule by optimizing a reward composed of molecular property objectives and adversarial loss. For running baselines, we use code from https://github.com/bowenliu16/rl_graph_generation.

• MolDQN (Zhou et al., 2019): an RL framework that uses chemical domain knowledge and double Q-learning. For running baselines, we use code from https://github.com/aksub99/MolDQN-pytorch.

• MARS (Xie et al., 2021): a sampling method based on Markov chain Monte Carlo that uses an adaptive fragment-editing proposal distribution based on GNN.

• GraphDF (Luo et al., 2021b): a normalizing flow model for graph generation that uses a discrete latent variable model, fine-tuned with RL. For running baselines, we use code from https://github.com/divelab/DIG.

To generate results from baselines, we ran each method until little improvement was observed. For methods without an explicit generation process (i.e. GCPN, MolDQN, and MARS), we took the highest property scores from all molecules generated. For methods with an explicit generation process (GraphDF), we trained until little improvement was observed and then sampled the same number of molecules as was sampled from LIMO. All times reported include the total time from each method, including training, property calculation times, and generation times if applicable.

To run MolDQN for the property targeting task, which requires obtaining an optimized set of molecules, we used the last molecule of the most recent 1,000 training episodes to build a set on which success and diversity were calculated.

A.5. Experimental details

For the VAE, we use a 64-dimensional embedding layer that feeds into four batch-normalized 1,000-dimensional (2,000 for first layer) linear layers with ReLU activation. This generates a Gaussian output for the 1024-dimensional latent space that can be sampled from. For the decoder, we also use four batch-normalized linear layers with ReLU activation, with the same dimensions. Softmax is used over all possible symbols at each symbol location in the output layer, and the VAE is trained with evidence lower bound (ELBO), with the negative log-likelihood reconstruction term multiplied by 0.9 and the KL-divergence term multiplied by 0.1. The VAE is trained over 18 epochs with a learning rate of 0.0001 using the Adam optimizer.

For the property predictor, we use three 1,000-dimensional linear layers with ReLU activation. Layer width, number of layers, and activation function were determined after hyperparameter optimization for predicting penalized logP, and these hyperparameters were then used for all other property prediction tasks. Similarly, we did not tune baseline methods for specific tasks, and used only the default hyperparameters tuned on a single task. For each property to predict, we use PyTorch Lightning to choose the optimal learning rate with the Adam optimizer to train the predictor over 5 epochs, then perform backward optimization with a learning rate of 0.1 for 10 epochs.

All experiments, including baselines, were run on two GTX 1080 Ti GPUs, one for running PyTorch code and the other for running AutoDock-GPU, and 4 CPU cores with 32 GB memory.

A.6. Autodock-GPU

We use AutoDock-GPU, a GPU accelerated version of AutoDock4 with an additional AdaDelta local search method, to calculate binding affinities for LIMO. It is fast enough for our purposes while still generating reasonably accurate results (Santos-Martins et al., 2021).

To generate docking scores from a SMILES string produced by LIMO, we perform the following steps:

1. Generate grid files for docking using AutoGrid4. For human estrogen receptor, we set the bounding box for docking to include the well-known ligand binding site. For human peroxisomal acetyl-CoA acyl transferase 1, a novel target, we use fpocket (Guilloux et al., 2009) to predict the binding pocket and set the docking bounding box around it.

2. For each SMILES to evaluate, we convert it to a 3D .pdbqt file using obabel 2.4.0 (O’Boyle et al., 2011). We set pH=7.4 to assign hydrogens and set Gasteiger partial charges.

3. We run AutoDock-GPU (Santos-Martins et al., 2021) with default parameters on the .pdbqt files, in batch mode if applicable.

4. With the generated .dig files from AutoDock-GPU, we extract the top binding energy number in the results table.

A.7. Absolute binding free energy

To corroborate our AutoDock-GPU predicted binding affinities, we conducted absolute binding free energy (ABFE) calculations on our most promising ligands. ABFE calculations estimate the binding free energy ΔG_bind, i.e., the difference between the free energy of a molecule’s bound and unbound states, by computing the reversible work of moving a molecule from water into the binding site of the targeted protein. The dissociation constant is then obtained as $K_D(ABFE)=e^{-\mathrm{\Delta }{G}_{bind}/RT}$, where R is the gas constant and T is absolute temperature (Gilson & Zhou, 2007). The free energy calculation is done with detailed molecular dynamics simulations of the protein and the molecule dissolved in thousands of water molecules. This method is more detailed and computationally expensive, and typically more accurate, than docking (Cournia et al., 2020). Here, the 5 best-scoring poses from AutoDock-GPU were sent to the software BAT.py (Heinzelmann & Gilson, 2021) to compute the binding free energy, ΔG_i, for each pose i. The overall binding free energy accounting for all 5 poses was then obtained as $\mathrm{\Delta }{G}_{bind}=-RT\ln {\sum }_i{e}^{-\mathrm{\Delta }{G}_i/RT}$ (Gilson & Zhou, 2007). Note that the pose with the most favorable (negative) ΔG_i contributes the most to the overall binding free energy, and this is also the most stable and hence most probable binding pose of the ligand. We thus analyzed the protein-ligand interactions for this most stable pose. For each ligand, we use the mean free energy of two independent ABFE runs from calculations initiated with different random seeds.

B. Additional experiments

B.1. Random generation of molecules

Table 6.

Random generation of molecules trained on the MOSES dataset and calculated with the MOSES platform (Polykovskiy et al., 2020). % valid: percent of molecules that are chemically valid. U@1K: percent of 1,000 generated molecules that are unique. U@10K: percent of 10,000 generated molecules that are unique. Diversity: one minus average pairwise similarity between molecules. % novel: percent of valid generated molecules not present in training set. JT-VAE results taken from (Polykovskiy et al., 2020).

Method	% valid	% U@1k	% U@10k	Div.	% Nov.
JT-VAE	100	100	99.96	0.855	91.43
GraphDF	100	100	99.72	0.887	100
LIMO	100	99.8	97.56	0.907	100

Results from the random generation of 30,000 molecules are summarized in Table 6. LIMO achieves the highest diversity score among compared methods, an important metric when using the latent space as a basis for the optimization of molecules on a wide range of properties. This diversity provides the foundation for LIMO’s ability to generate a diverse set of molecules with desirable properties.

B.2. Justification of multi-objective optimization

Figure 5.

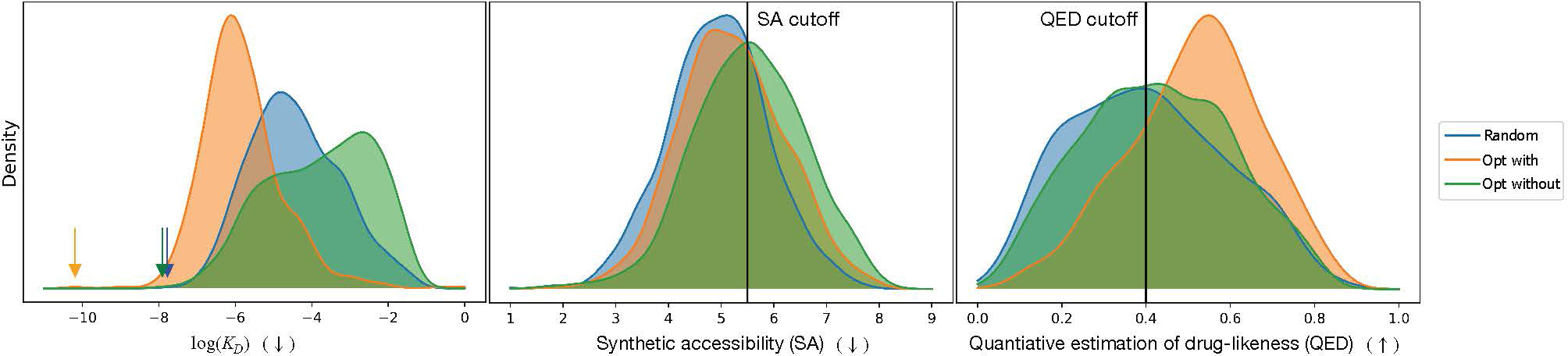
Distribution of molecular properties of randomly generated molecules (Random), after performing optimization on all three properties (Opt with), and after performing optimization on the two other properties, leaving out the one on the x-axis (Opt without). For QED and SA, cutoff values are shown for the minimum and maximum (respectively) scores that we consider sufficient for further optimization. For the K_D distributions, arrows mark the minimum value of each. On the x-axis, (↓) indicates that a low value is desired, and (↑) indicates that a high value is desired.

Figure 5 shows distributions of properties from randomly sampled molecules, molecules optimized on all three objectives (computed binding affinity against ESR1, QED, and SA), and optimized molecules leaving out one objective. We also show our QED and SA cutoff values used in the filtering step defined in Section 3.4. As shown, inclusion in the objective function pushes each property in the direction of improvement, or, in the case of SA, prevents it from decreasing more than it would have if it had not been included. Therefore, multi-objective optimization is successful in generating more molecules with potentially high binding affinity within the defined cutoff ranges, so is advantageous over single-objective optimization.