Utilizing patient information to identify subtype heterogeneity of cancer driver genes

Abstract

Identifying cancer driver genes is essential for understanding the mechanisms of carcinogenesis and designing therapeutic strategies. Although driver genes have been identified for many cancer types, it is still not clear whether the selection pressure of driver genes is homogeneous across cancer subtypes. We propose a statistical framework MutScot to improve the identification of driver genes and to investigate the heterogeneity of driver genes across cancer subtypes. Through simulation studies, we show that MutScot properly controls the type I error in detecting driver genes. In addition, we demonstrate that MutScot can identify subtype heterogeneity of driver genes. Applications to three studies in The Cancer Genome Atlas (TCGA) project showcase that MutScot has a desirable sensitivity for detecting driver genes and that MutScot identifies subtype heterogeneity of driver genes in breast cancer and lung cancer with regards to the status of hormone receptor and to the smoking status, respectively.

1. Introduction

With The rapid advance of next-generation sequencing technology, large-scale sequencing projects, such as The Cancer Genome Atlas (TCGA), have characterized the landscape of genetic alterations in cancers, suggesting that only a small number of driver genes are related to cancer initiation and progression.¹ In contrast, most genes are passengers that are irrelevant to carcinogenesis. Distinguishing driver genes from passenger genes is a crucial step to understand tumorigenesis and disease progression.

Typically, driver genes are nominated based on the following steps in a tumor sequencing study. First, somatic mutations are identified as ones present in the tumor tissue but not in the paired normal tissue or blood sample. Somatic mutations are then classified as either non-silent mutations if they change the corresponding amino acid sequence, or silent mutations otherwise. Finally, driver genes are nominated if the observed non-silent mutation rate is significantly higher than the background mutation rate estimated by silent mutations across all patients.

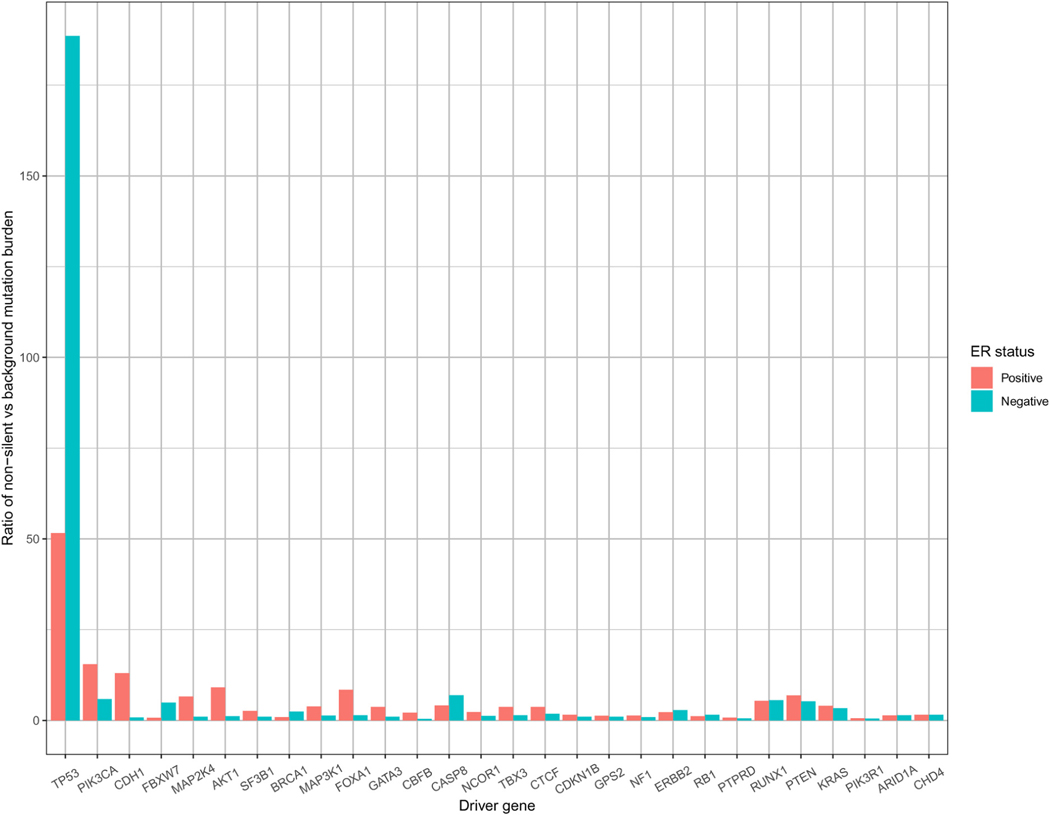
Based on this framework, a number of methods have been proposed to identify driver genes.^2–7 These methods work well under the assumption of homogeneous selection pressure. However, when selection pressure differs across cancer subtypes, ignoring the heterogenicity may mislead the interpretation of results. For example, breast cancer subtypes are commonly defined by the hormone receptor status, e.g., estrogen receptor positive (ER+) or negative (ER-). Exploratory data analysis of the TCGA breast cancer samples reveals that a few driver genes, including TP53, PIK3CA, CDH1 and FBXW7, show a significant difference (false discovery rate adjusted p-value < 0.05, by Mann–Whitney U test) in the ratio of non-silent mutation burden relative to the background mutation burden between ER positive and negative breast tumors (Figure 1). Modeling such heterogeneity across cancer subtypes will bring new biological insight to the subtype-specific breast cancer progression.

Figure 1.

Mutation burden ratio for known driver genes of breast cancer study (BRCA) in The cancer genome atlas (TCGA). Y-axis represents the ratio of non-silent mutation burden relative to the background mutation burden; specifically, the non-silent mutation burden is calculated by the total number of non-silent mutations out of the total number of mutable bases, while the background mutation burden is estimated by MutSigCV.

In this paper, we propose a statistical framework, the mutation score test (MutScot), to approach the two problems. First, we propose a Poisson regression model for non-silent mutations, allowing patients’ characteristics to define cancer subtypes. Next, we formulate two statistical hypothesis tests: one for testing whether the selection pressure parameter equals one (i.e. detecting driver genes) and the other for testing whether the selection pressure parameter of a driver gene does not differ between cancer subtypes.⁸ proposed a similar method using an unsupervised learning method to identify clusters among identified driver genes but did not compare the disparity of selection pressure between cancer subtypes.

We compare MutScot with MutSigCV⁵ and dNdScv,⁷ the two most widely used software for nominating driver genes. We do not consider DriverSub⁸ since it focuses on clustering instead of testing statistical hypothesis. MutSigCV considers the background mutation rate varying across the genome. dNdScv is proposed to further refine the background mutation model by considering a more comprehensive mutation context and adjusting chromatin states. Both methods ignore subtype heterogeneity and implicitly assume selection pressures are the same across cancer subtypes.

The remaining sections are organized as follows. In section 2, we propose the model framework and the hypothesis test statistics. In section 3, we perform simulations to compare the performance of MutScot over MutSigCV and dNdScv. In section 4, MutScot is applied to three TCGA studies. Finally, we summarize our results and provide some discussions in section 5. Computation details are included in the Supplemental Materials.

2. Method

2.1. Modeling non-silent mutations

Let y_gpm denote the number of non-silent mutations for gene g, patient (or tumor) p and mutation context m, $g=1,\dots ,\text{G}$, $p=1,\dots ,\text{P}$ and $m=1,\dots ,\text{M}$. Following the previous methods,^4,7,9 we specify a Poisson model:

$$y_{gpm}\sim \text{Poisson}\left({\theta }_{gp}{\text{N}}_{gm}{\lambda }_g{\tau }_m{\delta }_p\right).$$

Here, N_gm is the number of non-silent mutable bases; λ_g is the gene-specific average background mutation rate across mutation contexts and subjects; τ_m models the heterogeneity of background mutational rate due to mutational context; and δ_p models the heterogeneity of background mutational rate across subjects. In addition, θ_gp, the selection pressure parameter, is the parameter of interest Under the null hypothesis $H_0:{\theta }_{gp}=1$, the non-silent mutation rate is equivalent to the background mutation rate. A positive selection (and thus a driver gene) is detected if θ_gp > 1.

Note that τ_m and δ_p are crucial for modeling the heterogeneity of background mutation rate. The somatic mutation rate depends not only on the mutation itself but also on its neighboring bases. Typically, a somatic mutation is labeled with one base upstream and one base downstream,¹⁰ e.g. the T(A->C)G mutation for which adenine A mutates to cytosine C with thymine T and guanine G as neighboring bases. In addition, mutation rates vary substantially across subjects. More details about defining the mutation context and estimating τ_m and δ_p are provided in Section S.3 of Supplemental Materials.

Different from the previous methods, the parameter of interest θ_gp is patient-specific and depends on patient characteristics through a log link function

$$\log \left({\mathit{\theta }}_g\right)=W{\alpha }_g,$$

where ${\mathit{\theta }}_g={\left[{\theta }_{g1},{\theta }_{g2},\dots ,{\theta }_{g\text{P}}\right]}^{\text{T}}\otimes 1_{\text{M}}^{\text{T}}$ is a (PM) x 1 vector of selection parameters with $1_{\text{M}}^{\text{T}}$ a M x 1 vector of ones and $\otimes$ an operation of the Kronecker product; W is a (PM) x 1 vector of pre-specified weights; α_g represents the log-scaled selection pressure parameter adjusted by the weights.

We introduce weights W to address the variation of selection pressure across subjects due to subject-specific background mutation rates. Based on empirical investigation on breast carcinoma (BRCA), lung adenocarcinoma (LUAD), and lung squamous cell carcinoma (LUSC) studies from TCGA, we frequently notice that for many known driver genes, selection pressure is higher in patients with lower background mutation rates. To address this, classical statistical approaches can be adopted, such as quasi-likelihood that considers over-dispersion, or mixed effect model that considers random selection parameter across; however, we found them to be computationally infeasible for the application of a large number of genes (around 20,000). In exchange for affordable computation, we introduce the weight parameter W, inversely proportional to the average ${\widehat{\delta }}_p$ in a stratum, to stratify patients. Specifically, we specify the W in the following way.

First, without loss of generality, we assume the sequence of ${\widehat{\delta }}_p$ is sorted such that ${\widehat{\delta }}_1\le {\widehat{\delta }}_2\le \dots \le {\widehat{\delta }}_P$. We then divide the sequence of ${\widehat{\delta }}_p$ into 10 groups with equal size, denoted by G_i, $i=1,\dots ,10$. Note that G_i is ascending in that, for example, every ${\widehat{\delta }}_p$ of G₁ is no greater than ${\widehat{\delta }}_p$ of G_i, i > 1. Next, we identify q such that the group G_q contains min $\left\{{\widehat{\delta }}_p:{\widehat{\delta }}_p\ge 1\right\}$. Finally, given the fixed q, we combine all the G_i with i ≤ q into a new group $G_1^{*}$, which includes all patients with ${\widehat{\delta }}_p<1$; for G_i with i > q, we keep their original grouping of ${\widehat{\delta }}_p$, but denote them by ${\text{G}}_2^{*},{\text{G}}_3^{*},\dots ,{\text{G}}_{\text{J}}^{*}$, with J being subject to q + J = 11. Hence, patients with ${\widehat{\delta }}_p\ge 1$ are grouped into J − 1 groups.

Finally, for patient $p\in G_1^{*}$, we assign the weight w_p1 = 1 and for patient $p\in G_j^{*}$, we assign the weight

$$w_p={\left\{\frac{1}{{\overline{\delta }}_{\left\{p\in G_j^{*}\right\}}}\right\}}^k,$$

where ${\overline{\delta }}_{\left\{p\in G_j^{*}\right\}}$ denotes the mean of collection $\left\{{\widehat{\delta }}_p\mid p\in G_j^{*}\right\}$. In this way, smaller weight is assigned to patients with higher background mutation rates. The power k in the weight w_p allows additional flexibility. For example, k = 0 implies w_p = 1; and the larger value of k would further downweigh the group with higher background mutation rates. In the analysis of TCGA dataset, we chose k = 3 based on simulation studies which evaluate the impact of the choice of k on the performance of MutScot.

2.2. Estimating background mutation rate

The background mutation rate is estimated based on silent mutations that are assumed to be functionally irrelevant to tumor initiation and progression. The gene-specific maximum likelihood estimation (MLE) estimator for λ_g is simply the ratio between the number of silent mutations and silent mutable bases for the targeted gene g across patients. However, mutations are extremely rare, usually a few mutations per million bases, while the coding region size of human genes ranges 6 bp (gene RP11–146D12.2) to 108 kilobases (gene TTN) with a median length of 1.7 kilobases; mutations would be absent in most genes for the study with a moderate number of samples. Consequently, the gene-specific MLE estimator would be zero due to insufficient sample size. The possible remedy is to borrow strength across a set of “bagel” genes that are assumed to share similar background mutation rates with the target gene. For example, MutSigCV⁶ notices that background mutation rates depend on gene expression level, replication time and Hi-C chromatin state; thus, MutSigCV specifies “bagel” genes using these factors. Another method dNdScv⁷ utilizes a number of epigenomic biomarkers of local chromatin state to estimate background mutation rates of all genes simultaneously. Gene-specific estimate of background mutation is unbiased but provides a very limited statistical power for driver gene detection. On the other hand, “bagel” type analyses increase power but may cause seriously inflated type-I error rate if the assumption of a similar background mutation rate is violated.

Thus, we propose to estimate the background mutation rate using weighted average of three methods to balance the bias and variance of various background mutation rate estimators. Let ${\widehat{\lambda }}_g^G$, ${\widehat{\lambda }}_g^B$, and ${\widehat{\lambda }}_g^D$ denote background mutation rate estimators by the gene specific MLE, MutSigCV and dNdScv for gene g, respectively. Similarly, let ${\widehat{\sigma }}_{gG}^2$, ${\widehat{\sigma }}_{gB}^2$ and ${\widehat{\sigma }}_{gD}^2$ be the variance of the estimators. Weighting by the variance of the estimators, the background mutation rate is estimated as

$${\widehat{\lambda }}_g^W=\frac{{\sum }_{i\in \{G,B,D\}}{\widehat{\lambda }}_g^i/{\widehat{\sigma }}_{gi}^2}{{\sum }_{i\in \{G,B,D\}}1/{\widehat{\sigma }}_{gi}^2}.$$

Details about computing ${\widehat{\lambda }}_g^G$, ${\widehat{\lambda }}_g^B$, and ${\widehat{\lambda }}_g^D$ and their variances are provided in Section S.1 and S.3 of the Supplemental Materials.

2.3. Hypothesis tests

In what follows, we specify the hypotheses to be tested, propose score test statistics, and provide details about computing p-values. Since hypotheses are tested for one gene at a time, we drop the subscript of gene g to avoid notational complexity.

2.3.1. Test for driver genes

Detecting driver genes can be formulated as the following hypothesis testing problem for

$${\text{H}}_0:\alpha =0{\text{vs H}}_1:\alpha >0.$$

Equivalently, the null hypothesis suggests θ_p = 1 while the alternative hypothesis suggests θ_p > 1, positive selection pressure for all patients.

To test for driver genes, we consider a one-sided score test statistic,

$${\mathcal{T}}_{\alpha }={\mathcal{U}}^2/\mathcal{I}-\inf \left\{{(\mathcal{U}-\xi )}^2/\mathcal{I}:\xi \ge 0\right\},$$

where $\mathcal{U}=W^T(Y-N\lambda )$ is the score evaluated at $H_0;Y={\left[y_{11},y_{12},\dots ,y_{\text{PM}}\right]}^{\text{T}}$ denotes the vector of non-silent mutation counts; $N=1_{\text{P}}^{\text{T}}\otimes {\left[{\text{N}}_1,{\text{N}}_2,\dots ,{\text{N}}_{\text{M}}\right]}^{\text{T}}$ denotes the vector of non-silent mutable bases; and $\lambda =\lambda \times {\left[{\delta }_1,{\delta }_2,\dots ,{\delta }_{\text{P}}\right]}^{\text{T}}\otimes {\left[{\tau }_1,{\tau }_2,\dots ,{\tau }_M\right]}^{\text{T}}$ denotes the vector of background mutation rates. The Fisher information $\mathcal{I}=W^{T}D(N\lambda )W$, where D(Nλ) denotes a diagonal matrix with diagonal entries equal to elements of Nλ. Both $\mathcal{U}$ and $\mathcal{I}$ are derived with respect to α. Furthermore, the infimum term inf $\left\{{(\mathcal{U}-\xi )}^2/\mathcal{I}:\xi \ge 0\right\}$ is the minimization of ${(\mathcal{U}-\xi )}^2/\mathcal{I}$ under the constraint of $\xi \ge 0$. This form of score test statistic is derived in a fashion that mimics the likelihood ratio test of two normal distributions under the one-sided alternative hypothesis: ${\mathcal{U}}^2/\mathcal{I}$ and the infimum term correspond to the kernel of log likelihood under the null and under the alternative space, respectively. For more details, we refer readers to the paper.¹¹

2.3.2. Test for subtype heterogeneity of driver genes

For the identified driver genes, we further test if heterogeneity exists across cancer subtypes defined by patients’ characteristics. To proceed, we assume

$$\alpha ={\beta }_0+Z_p^{\text{T}}\mathit{\gamma },$$

where Z_p is the vector of p th patient’s characteristics (e.g. cancer subtype and/or smoking status), and γ represents the selection heterogeneity associated with the patient characteristics. Note that if the variable $Z={\left[Z_1^{\text{T}},Z_2^{\text{T}},\mathrm{..},Z_P^{\text{T}}\right]}^{\text{T}}$ is continuous, it is standardized with mean zero and variance one.

Next, we specify the null and alternative hypotheses as

$${\text{H}}_0:\mathit{\gamma }=0\mid \alpha >0{\text{vs H}}_1:\mathit{\gamma }\ne 0\mid \alpha >0.$$

Finally, we test for subtype heterogeneity of driver genes as a two-sided test with the following test statistic,

$${\mathcal{T}}_{\gamma \mid {\widehat{\beta }}_0}={\mathcal{R}}^{\text{T}}{\mathcal{V}}^{-1}\mathcal{R},$$

where $\mathcal{R}=X^T(Y-N\lambda )$ is the score vector with $X={\left[X_1^{\text{T}},X_2^{\text{T}},\dots ,X_P^{\text{T}}\right]}^{\text{T}}$ and $X_p={\left[w_p,w_p{Z}_p^{\text{T}}\right]}^T\otimes 1_M$, and $\mathcal{V}=X^{T}D(N\lambda )X$ is the Fisher information matrix, both derived with respect to the parameter vector [β₀, γ] with β₀ evaluated at ${\widehat{\beta }}_0$, the MLE of β₀ under $\mathit{\gamma }=0$.

2.3.3. Computing p-values

P-values of the test for driver genes are obtained as follows:

$$P\left({\mathcal{T}}_{\alpha }\ge t\right)=P\left(W^{\text{T}}Y\ge W^{\text{T}}{Y}_{\mathit{o}\mathit{b}\mathit{s}}\right),$$

where t is the realization of ${\mathcal{T}}_{\alpha }$ given Y_obs the vector of observed non-silent mutation counts. W^TY follows a Poisson distribution for which p-values could be quickly calculated. This computational efficiency is appealing when analyzing a large number of genes.

Computing the p-value of the test for subtype heterogeneity of driver genes is more challenging since its exact null distribution does not exist Moreover, the asymptotic distribution does not approximate the null distribution well because the non-silence mutations are extremely rare for most genes. Consequently, we resort to a parametric bootstrap to approximate the null distribution of the test statistic ${\mathcal{T}}_{\gamma \mid {\beta }_0}$. The steps are summarized as follows.

First, compute the test statistic ${\mathcal{T}}_{\gamma \mid {\widehat{\beta }}_0}$ given Y_obs. Second, generate Y from the null model with β₀ fixed at the MLE ${\widehat{\beta }}_0$ and γ = 0, and compute the test statistic ${\mathcal{T}}_{0\mid {\widehat{\beta }}_0}$ given Y. This step is repeated until a set of ${\mathcal{T}}_{0\mid {\beta }_0}$ for the null model is obtained. Finally, an empirical p-value is computed as the proportion of ${\mathcal{T}}_{0\mid {\widehat{\beta }}_0}\ge {\mathcal{T}}_{\gamma \mid {\widehat{\beta }}_0}$.

3. Simulation studies

We conduct two simulation studies. One is designed to compare MutScot with competing methods in testing for driver genes under a variety of simulation settings. The other is to investigate key factors that affect the performance of MutScot in detecting subtype heterogeneity of driver genes.

3.1. Test for driver genes

We compare MutScot with MutSigCV and dNdScv for the driver gene test of one gene. To make a fair comparison, we focus on the case when selection pressure is homogeneous across patients, which is assumed by MutSigCV and dNdScv. Non-silent mutations are generated by

$$y_p~\mathrm{Poisson}(\theta \text{N}\lambda ).$$

We specify the number of mutable bases N = 4500 for P = 500 patients and consider a set of scenarios with various combination of selection pressure θ and background mutation rate λ. We choose six values for θ (1, 5, 10, 15, 20, and 25), and four values for λ (1 × 10⁻⁷, 2.5 × 10⁻⁷, 5 × 10⁻⁷, and 10 × 10⁻⁷), which mimic the values observed in real data studies. For other parameters required by MutSigCV or dNdScv, we substitute with estimates from the breast cancer study of TCGA. The hypothesis of interest states: H₀: θ = 1 versus H₁: θ > 1.

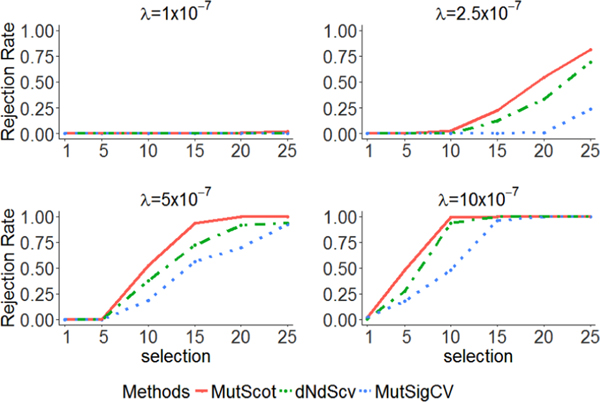
For each scenario, we repeat the assessment 10⁵ times and report rejection rates of the null hypothesis. The nominal alpha value is set at 0.01. Note that when the selection pressure parameter θ = 1, the rejection rate estimates the type I error rate; when θ > 1, the rejection rate estimates the power. The results are illustrated in Figure 2, with each subplot corresponding to one λ value. Given any λ, we find that all three methods control the type I error rate well. The power to identify a driver gene increases with the values of θ for all three methods as expected. It’s of interest to observe that the power also increases with the values of λ, since a larger λ value would lead to a smaller variance of test statistic. Among three methods, MutScot always has the highest power. While the simulation results are favorable to MutScot given the same values of λ and θ, we are aware that in practice, each method will estimate its own λ, which contributes to the inconsistency between the identified driver genes by different methods. In this simulation study, we specify w_p = 1 (equivalently, k = 0) for both simulation model and fitted model of MutScot. In Supplementary Materials, we conduct additional simulation studies to show that the powers are insensitive to the choice of k when k does not equal to zero.

Figure 2.

Performance of testing subtype heterogeneity of driver genes. Each panel corresponds to a distinct background mutation rate and shows the rejection rates of different methods by different line types: MutScot (solid), dNdScv(dotdash), and MutSigcv (dotted).

3.2. Test for subtype heterogeneity of driver genes

We now assess the performance of MutScot for testing subtype heterogeneity of driver genes, which is infeasible for MutSigCV or dNdScv. We assume the non-silent mutations are generated from a Poisson model with mean θ_pNλ, using the same values for N, P, and λ in the first simulation study, and specify

$$\log (\mathit{\theta })=W\left({\beta }_0+Z\gamma \right),$$

where θ denotes a vector of θ_p. The hypothesis of interest states: ${\text{H}}_0:\gamma =0$ versus ${\text{H}}_1:\gamma \ne 0$.

We consider 5 values for β₀ (log(5), log(10), log(15), log(20), and log(25)) and 6 values for γ (log(2), log(4), log(6), log(8), and log(10)). Without loss of generality, we assume W = 1. We consider $Z={\left[-1_{\text{Pa}}^{\text{T}},1_{\text{P}(1-\text{a})}^{\text{T}}\right]}^{\text{T}}$, where $a\in \{0.1,0.3,0.5\}$ is the proportion of patients who carry negative effect on selection pressure. The nominal alpha value is set at 0.01.

Rejection rates of the null hypothesis are reported in Table 1, excluding the scenario with λ = 1 × 10⁻⁷. For such a low background mutation rate, there is no statistical power of identifying driver genes (top left panel of Figure 2). We find that MutScot could control the type I error well under the nominal alpha value. In addition, MutScot shows increasing power with β₀, a, and λ. Note that when β₀ is small, the power of testing subtype heterogeneity on selection is low except γ being very large. This suggests that one should consider genes with large β₀, such as driver genes, for this test

Table 1.

The rejection rates of testing for subtype heterogeneity of driver genes under a variety of parameter settings. The rows are organized by the background mutation rates (λ), the proportion of subgroups (a), and the effect size of log-scaled selection pressure parameter (β₀). The columns are organized by the effect size of subtype heterogeneity (γ). The rejection rates higher than 0.8 are highlighted.

	0	γ
		log2	log4	log6	log8	log10
λ	10 × 10−7	0.00	0.41	0.85	0.93	0.95	0.99
	5 × 10−7	0.00	0.17	0.60	0.79	0.88	0.92
	2.5 × 10−7	0.01	0.04	0.35	0.51	0.64	0.73
a	0.1	0.01	0.01	0.26	0.44	0.58	0.71
	0.3	0.00	0.23	0.71	0.86	0.93	0.95
	0.5	0.00	0.38	0.84	0.94	0.97	0.99
β 0	log5	0.02	0.02	0.25	0.40	0.54	0.66
	log10	0.00	0.11	0.49	0.71	0.80	0.87
	log15	0.00	0.21	0.67	0.83	0.89	0.91
	log20	0.00	0.31	0.76	0.88	0.92	0.98
	log25	0.00	0.39	0.84	0.90	0.98	0.99

Overall, the results indicate that MutScot performs well in testing subtype heterogeneity of driver genes under a wide range of settings. In particular, we identify four factors that determine the performance of testing for subtype heterogeneity of driver genes: the background mutation rate λ, the proportion of subgroups a, the effect size of log-scaled selection pressure parameter β₀, and finally the effect size of subtype heterogeneity γ.

4. Real data applications

We analyze three tumor sequencing studies in TCGA, including breast carcinoma (BRCA), lung adenocarcinoma (LUAD), and lung squamous cell carcinoma (LUSC). Somatic mutation calling files are downloaded from the TCGA data portal (https://portal.gdc.cancer.gov/) for 1016 BRCA patients, 567 LUAD patients, and 484 LUSC patients, respectively. MutScot, dNdScv and MutSigCV are used to identify driver genes with hyper-mutated tumors (>10 Mut/Mb) excluded. We choose k = 3 for MutScot, since simulation analysis results in the Supplementary Materials show that the results are insensitive to the choice of k when k ≠ 0. For examining subtype heterogeneity of identified driver genes, only MutScot is feasible and performed. The Benjamini-Hochberg procedure is used to control false discovery rate (FDR).

4.1. Test for driver genes

To compare three methods, we adopt the driver gene list by Bailey et al.¹² as the benchmark. They conducted a comprehensive analysis that merged eight different methods utilizing different types of prior biological information to increase statistical power, such as the pattern of mutation locations and functional impact of mutation, which is not utilized by MutScot, dNdScv and MutSigCV. Given the benchmark, each method identifies a list of candidate driver genes that are labeled as true positives (TP), false positives (FP), true negatives (TN), or false negatives (FN) with respect to Bailey’s driver gene list We use the F1 score (F1) for the comparison, defined as the weighted harmonic mean of precision and recall, $\frac{2}{\frac{1}{\text{TP}/(\text{TP}+\text{FP})}+\frac{1}{\text{TP}/(\text{TP}+\text{FN})}}$. The higher the F1 score represents better accuracy of testing for driver gene.

Table 2 summarizes the results of testing for driver genes. Among three methods across three cancer sequencing studies, MutSigCV always has the lowest TP, which is consistent with simulation studies. In terms of F1 score, MutScot (with the weight BMR and patient rate adjusted) has the best performance in BRCA study, and the second-best performance in LUAD and LUSC study. For MutScot, we find that the false positive would significantly increase when patient rates are not adjusted (i.e. W = 1, Table 2). Hence, we recommend incorporating weights in the analysis. Finally, we evaluate the performance of MutScot with different background mutation models. Specifically, we consider MutScot with the background mutation rates (BMR) calculated by individual gene, MutSigCV or dNdScv and compare them against MutScot with the inverse variance weighted background mutation rate estimator (Table 2). The results show that using weight BMR achieves higher F1 score than using individual gene BMR and dNdScv’s BMR, and achieves similar F1 score to using MutSigCV’s BMR

Table 2.

Results of testing driver genes. TP denotes true positive; FP denotes false positive; and F1 is defined as the weighted harmonic mean of the precision and recall.

		MutScot					dNdScv	MutSigCV
		Patient rate not adjusted	Patient rate adjusted
		${\widehat{\lambda }}_{\text{g}}^{\text{W}}$ (Weighted BMR)	${\widehat{\lambda }}_{\text{g}}^G$ (Individual Gene BMR)	${\widehat{\lambda }}_{\text{g}}^B$ (MutSigCV’s Bagel BMR)	${\widehat{\lambda }}_{\text{g}}^{\text{D}}$ (dNdScv’s Model Based BMR)	${\widehat{\lambda }}_{\text{g}}^{\text{W}}$ (Weighted BMR)
BRCA	TP	25	20	22	24	24	24	20
	FP	37	11	4	13	7	11	2
	F1	0.55	0.67	0.80	0.73	0.80	0.75	0.78
LUAD	TP	17	7	12	17	13	15	9
	FP	22	3	2	18	3	3	2
	F1	0.58	0.47	0.71	0.62	0.72	0.79	0.58
LUSC	TP	13	6	8	13	10	12	6
	FP	14	4	0	21	3	2	2
	F1	0.53	0.37	0.53	0.46	0.57	0.67	0.40

4.2. Test for subtype heterogeneity of driver genes

Breast cancer is a heterogeneous disease with subtypes commonly defined by hormone receptor status. For the BRCA study, we define subtypes by the status of estrogen receptor (ER) and tested for subtype heterogeneity of driver genes. ER positive patients are coded as 1, ER negative as −1, and undetermined ER as 0. MutScot can easily model other hormone receptor status (e.g. progesterone receptor and human epidermal growth factor receptor 2) and clinical information (e.g. age at diagnosis and stage), simultaneously.

We test for selection heterogenicity for 20 driver genes which are identified by MutScot and also included in the driver gene list by Bailey et al..¹² For each gene, we perform 10⁵ times parametric bootstrap to evaluate the p-value and then perform FDR control at 0.1. We identify 2 genes PIK3CA and TP53 that show significant subtype heterogeneity. Table S1 shows the p-values and q-values of MutScot and the estiamtes of selection pressure for ER positive and negative subtypes, respectively. Consistent with the exploratory analysis, the selection pressure of PIK3CA is higher in ER positive breast cancer, while the selection pressure of TP53 is higher in ER negative breast cancer. The gene FBXW7 found in the exploratory analysis does not pass the driver gene test by MutScot and hence is not included in testing subtype heterogeneity of driver genes; CDH1 passed the driver gene test and its q-value for testing subtype heterogeneity of driver genes (0.105) is slightly below the significant cutoff 0.1. The discrepancy between the results of exploratory data analysis and MutScot is likely due to the oversimplified assumptions of exploratory data analysis; in particular, exploratory data analysis does not consider the heterogeneity of background mutational rate due to mutational context, and the heterogeneity of background mutational rate across subjects.

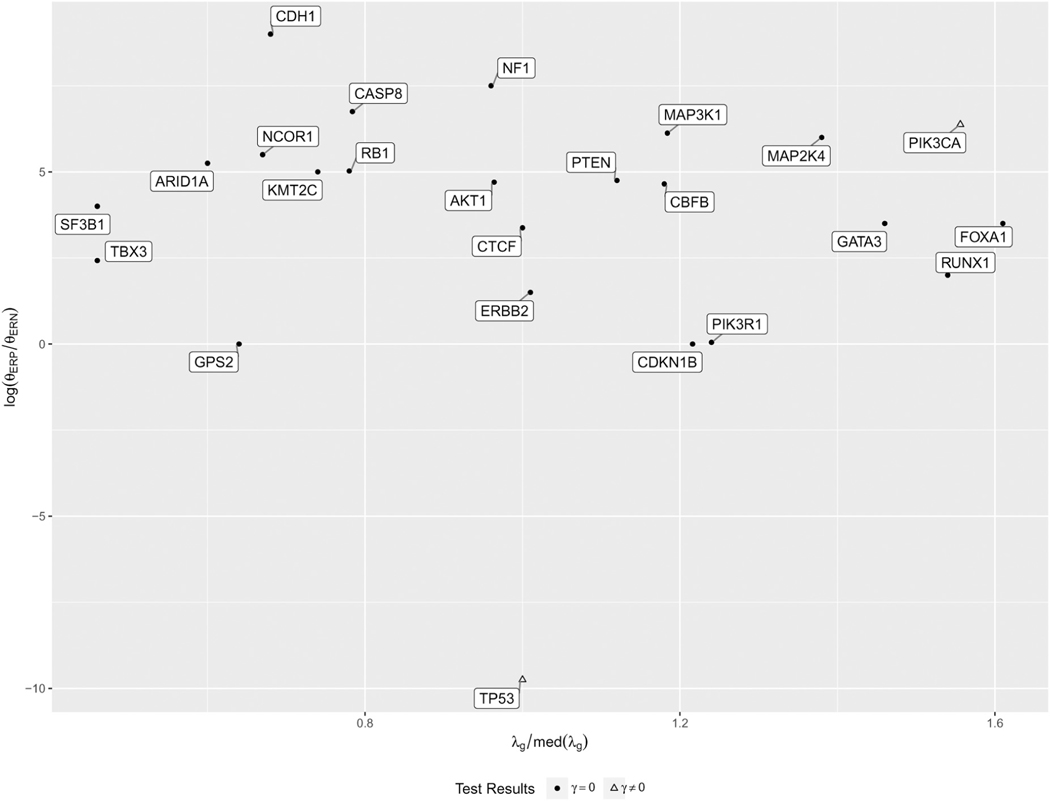
We further investigate why these two genes show subtype heterogeneity. Recall that the simulation study identifies 4 factors that impact the power of testing subtype heterogeneity, including the background mutation rate, the proportion of subgroup, the effect size of selection, and the effect size of subtype heterogeneity. In terms of these factors, 23% of patients are ER negative; all 20 genes are driver genes with large effect size of selection pressure; Figure 3 illustrates the patient effects and the background mutation rates. TP53 is detected because of very large size of heterogenicity; PIK3CA is detected because the gene has high background mutation rate. These are consistent with our simulation studies.

Figure 3.

Scatterplot of driver genes in BRCA. The X-axis is the ratio of background mutation rate of a given gene versus the median of background mutation rates across genes. The Y-axis is the log scale difference of selection between ER positive (ERP) and negative (ERN), indicating the size of selection heterogeneity between two subtypes of breast cancer.

Next, we investigate the impact of smoking status (current-smoker, past-smoker and non-smoker), a major risk factor for lung cancer, on selection heterogenicity for LUAD and LUSC patients. LUAD and LUSC are analyzed separately since they arise from different tissue types (bronchial glands vs. squamous cells) with distinct driver genes. For example, EGFR and KRAS are driver genes for LUAD but not for LUSC.^12,13 The smoking statuses are missing in 10 and 4 subjects of LUAD and LUSC respectively and are predicted based on RNA expression of 168 smoking-related genes.¹⁴ Specially, we fit LASSO regression models¹⁵; among 168 genes, the models selected 47 and 9 genes which are associated with the observed smoking status of LUAD and LUSC, respectively. Next, we use the LASSO regression models with the selected smoking-related genes to predict the missing smoking status. Among LUAD, 25% of subjects are non-smoker, 61% past-smoker and 14% current-smoker; the smoking percentages are 5%, 65% and 30% for non-smoker, past-smoker, and current-smoker in LUSC.

Similar to BRCA, we apply MutScot to test the selection heterogenicity of 13 and 10 driver genes in LUAD and LUSC, respectively. Six genes of LUAD (TP53, STK11, KRAS, KEAP1, ATM and BRAF; Table S2) and two genes of LUSC (TP53 and NFE2L2; Table S3) are identified with significant selection heterogenicity. For example, the selection pressure of nonsense mutations at LUAD tumor suppressor genes TP53 and STK11 is higher in current smokers than in past or non-smokers.

5. Discussion

In This paper, we propose MutScot to identify driver genes and to investigate subtype heterogeneity of driver genes, the latter of which has not been approached previously. MutScot employs a Poisson model with score-type test statistics to leverage patient level information for examining subtype heterogeneity of driver genes. It would help advance the understanding of mechanisms of subtype-specific cancer progression and is of both biological and clinical/translational importance. In addition, MutScot employs an inverse variance weighting procedure to integrate several estimators of background mutation rate, incorporating various types of biological prior knowledge. Finally, MutScot considers a weighting scheme to address the population heterogeneity and at the same time enjoys fast computation of P-values.

The simulation studies show that MutScot controls type I error well and has desirable power in finding driver genes than MutSigCV and dNdScv. We demonstrate that MutScot is able to identify subtype heterogeneity of driver gene under a wide range of settings. We also identify, in addition to the sample size, four factors that determine the performance of identifying subtype heterogeneity of driver genes: the background mutation rate, the proportion of samples from subtype, the effect size of selection, and finally the effect size of subtype heterogeneity. For the real data applications, we apply MutScot to one breast cancer study and two lung cancer studies in TCGA. The results show that MutScot maintains a good balance between precision and recall rates. Furthermore, we showcase that MutScot is able to identify subtype heterogeneity of driver genes using ER status in breast cancer study, and using smoking status for lunc cancer studies.

There are a few possible directions for future research. First, MutScot can be extended to borrow information across cancer types. One can treat cancer type as a kind of patient information, and then run MutScot to generate a list of driver genes and to identify between-type heterogeneity of driver genes. Second, besides testing for the selection pressure at the gene level, we may investigate the selection pressure at the pathway level. Finally, another interesting but challenging direction will be the identification of driver events in non-coding regions. In the past decade, advances in finding the driver event have been mostly focused on coding regions. To detect driver events in non-coding regions, one may need to incorporate the information of functional impact of non-coding mutations. The regression framework of MutScot provides flexibility to consider such additional information.

Overall, we expect that our proposed MutScot will be useful in cataloguing driver genes and investigating subtype heterogeneity of driver genes, as well as in planning future cancer genome sequencing projects.