Accurate pK_a Calculations in Proteins with Reactive Molecular Dynamics Provide Physical Insight Into the Electrostatic Origins of Their Values

Abstract

Classical molecular dynamics simulations are a versatile tool in the study of biomolecular systems, but they usually rely on a fixed bonding topology, precluding the explicit simulation of chemical reactivity. Certain modifications can permit the modeling of reactions. One such method, multiscale reactive molecular dynamics, makes use of a linear combination approach to describe condensed-phase free energy surfaces of reactive processes of biological interest. Before these simulations can be performed, models of the reactive moieties must first be parametrized using electronic structure data. A recent study demonstrated that gas-phase electronic structure data can be used to derive parameters for glutamate and lysine which reproduce experimental pK_a values in both bulk water and the staphylococcal nuclease protein with remarkable accuracy and transferability between the water and protein environments. In this work, we first present a new model for aspartate derived in similar fashion and demonstrate that it too produces accurate pK_a values in both bulk and protein contexts. We also describe a modification to the prior methodology, involving refitting some of the classical force field parameters to density functional theory calculations, which improves the transferability of the existing glutamate model. Finally and most importantly, this reactive molecular dynamics approach, based on rigorous statistical mechanics, allows one to specifically analyze the fundamental physical causes for the marked pK_a shift of both aspartate and glutamate between bulk water and protein and also to demonstrate that local steric and electrostatic effects largely explain the observed differences.

Introduction

Molecular dynamics (MD) simulations have typically been used to investigate systems and phenomena, such as protein folding or ligand docking, involving force fields with a constant bonding topology. These classical MD methods, so-called because they do not involve a quantum mechanical treatment of the bonds or atoms involved, have been successfully applied to a wide range of biomolecular systems.¹ Despite the versatility of classical MD, alternative methods are required for any process where chemical reactivity plays a central role, such as protonation/deprotonation events by amino acids. Such alternative methods are valuable, indeed essential, for accurately calculating fundamental chemical properties accessible to experiment like the free energy of a reaction or the pK_a of an amino acid in a biological context. To that end, a number of modifications of classical MD to permit reactivity have been developed. Ab initio molecular dynamics² (AIMD) and hybrid quantum mechanics/molecular mechanics³ (QM/MM) methods permit reactivity by incorporating on-the-fly electronic structure calculations. Naturally, these approaches are much more computationally intensive than classical MD given the need to carry out an electronic structure calculation, and typically they are only feasible for short (<1 ns) time scales. Another approach is to incorporate information from electronic structure calculations into a reactive MD force field (FF) called “fitRMD”. In such a simulation, electronic structure is treated implicitly, resulting in much greater efficiency than QM methods. Such reactive molecular dynamics (RMD) methods include bond-order formalisms, like ReaxFF,⁴ in which the bond order between pairs of atoms is computed as a function of atomic positions and reactivity is the result of changes in bond order over time.⁵ RMD also encompasses multistate methods as described below, which compute interatomic potentials and forces from a linear combination of possible bonding topologies, or diabatic states.

The multiscale reactive molecular dynamics (MS-RMD) method combined with a fitRMD reactive FF follows the latter approach.⁶⁻⁸ (It should be noted that in this paper we associate the acronym MS-RMD with the reactive MD algorithm and fitRMD with the reactive MD FF, which has not always been done in past papers.) Because it does not require on-the-fly solutions to the electronic Schrödinger equation, MS-RMD is several orders of magnitude faster than AIMD and QM/MM. This lower cost renders microsecond-scale reactive MD simulations tractable, meaning that MS-RMD can be applied to study complex biomolecular phenomena where fast electronic degrees of freedom are coupled to slower, larger-scale processes like protein conformational changes. At the same time, a recent fitRMD advance⁹ has demonstrated that MS-RMD parameters can be trained by diabatic matching (DM) on gas-phase constrained density functional theory (CDFT) data and then used, rather remarkably, without modification in condensed phase simulations in both liquid water and in the staphylococcal nuclease (SNase) protein to produce pK_a predictions in quantitative agreement with experiment. This represents an advantage over other RMD methods, which generally require more extensive or more system-specific FF parametrization to achieve the same level of accuracy.

The ultimate end of any reactive MD simulation is to produce insights into the system in question which are difficult or impossible to probe experimentally or (often) by other computational means. By correctly describing the fundamental, microscopic physics of a reactive process, MS-RMD simulations using DM-derived parameters do not just reproduce macroscopically observable “single value” quantities like pK_a (although in many instances, even determining the pK_a of an amino acid (AA) in a protein can be experimentally challenging¹⁰). Rather, such MS-RMD simulations can produce an entire multidimensional free energy surface for the reactive process at hand, which can then be used to not only compute quantities of interest but also to understand the physics behind them.¹¹ This degree of insight into the microscopic physics of the system permits elucidation of the mechanism of the process and identification of the features which have the largest effects on its energetics. Put another way, while other methods might possibly correctly predict the value of the pK_a of an amino acid, the MS-RMD approach produces not just what the pK_a value is but why it is what it is, by describing all of the interactions which collectively determine the physical equilibrium characterized by the pK_a value.

The current fitRMD approach⁹ represents a form of physics-constrained supervised machine learning (ML). The training set in our recent study and in this work contains gas-phase diabatic state energies of reactive complex configurations computed by CDFT, but it should be noted that the procedure is agnostic to the QM method chosen; in principle, any diabatic method could be used. The key physical insight is that the information necessary to accurately reproduce a reaction event in a diabatic model must be primarily encoded in the electronic structure of the few diabatic states which dominate the linear combination of diabatic states that describes the entire reactive complex. Although the relationship between these electronic structure calculations and the proper fitRMD parameters is not intuitively obvious, by minimizing the residual of the diabatic state vector (rather than, as in past iterations of fitRMD model development, minimizing the residual of the atomistic forces^8,12−14), the fitRMD model learns how to properly reproduce the diagonal elements of the quantum mechanical Hamiltonian (corresponding to the contributions of the diabatic states to the ground state energy) as well as the off-diagonal elements (corresponding to the transition probabilities between states). Once trained, these parameters can be used in environments like bulk water and proteins, which differ greatly from the gas-phase training set conditions, and still achieve quantitatively accurate pK_a predictions evidently without further modification.⁹

In this work, we expand on recent developments of our MS-RMD models in two ways: first, we present newly computed fitRMD parameters for aspartate (Asp; D) from CDFT data, analogous to those previously presented⁹ for glutamate (Glu; E) and lysine (Lys; K) and demonstrate quantitative accuracy and transferability similar to our earlier results. Second, we report even better transferability of the fitRMD model to a protein environment by first fitting the side chain carboxyl group O–H bond force field potential parameters to DFT data. Afterward, we discuss the notable experimental pK_a shift of both the aspartate and glutamate side chains between bulk water and SNase in light of the computed potentials of mean force (PMF) of deprotonation. We conclude that a large part of this difference is due to side chain flexibility with regard to rotation and extension, and show how these considerations constrain the minimum free energy path (MFEP) of proton transport from the protonated residue to the bulk water, thus helping to define the physical origins of the pK_a value.

Methods

MS-RMD

In a classical MD simulation, unlike MS-RMD, there is a single, fixed bonding topology throughout the simulation, and the dynamical evolution of the system is governed by a force field (FF) which describes the forces between the atoms as a function of their positions. The heart of the MS-RMD approach is to treat a reactive system as a linear combination of different bonding topologies, each with its own potential energy described by a classical FF. These possible bonding topologies, or diabatic states, are evaluated on-the-fly, and allowed to change as the system evolves, so that all those topologies and only those topologies (lest the computation become intractably complex) that significantly contribute to the linear combination are considered. Consider the deprotonation of the generic acid HA in water into its conjugate base and a hydrated proton:

1

In this representation, the reactant state and product state of the hydrated excess proton shown are two of the diabatic states whose bonding topologies’ potential energies enter into the linear combination from which the total system potential energy and interatomic forces are derived. In practice, however, many other diabatic states make contributions to the energy which cannot be neglected. These are taken into account by algorithmically identifying all the reasonable possible bonding topologies out to the third solvation shell of the hydrated excess proton,¹⁵ including topologies representing binding of the proton to nearby titratable amino acids (AAs). That set of states |i⟩ forms the basis for the MS-RMD Hamiltonian as

2

where when i = j, h_ii represents the energy of state |i⟩, typically defined as the classical FF potential energy of the corresponding bonding topology, and when i ≠ j, h_ij represents a coupling term corresponding to the transition probability between the two states. Each of these terms is dependent on the coordinates of the system nuclei. The eigenvalue problem

3

then produces eigenvectors c whose components c_i correspond to the contributions of the various diabatic state energies to the eigenvalues of the Hamiltonian. The ground state energy of the system is the lowest eigenvalue of the Hamiltonian (and also a function of the instantaneous set of positions of the nuclei). The system is evolved in time by computing forces using the Hellman-Feynman theorem:

4

The diabatic state vector c is also useful for defining the position of the net positive charge defect associated with the excess proton. This “center of excess charge” (CEC) is defined as¹⁶

5

where r_i^COC is the center of charge of the hydronium or other protonated species in state |i⟩. For a more complete treatment of aspects of the MS-RMD method, please see refs (7 and 8).

fitRMD Parameterization

The electronic structure approach taken in this work to develop fitRMD parameters follows the CDFT-based protocol of ref (9). We restate the essential relationships here but refer the reader to ref (9) for more thorough derivations and to ref (17) for in-depth discussion of CDFT generally. We also emphasize that this particular choice of electronic structure method is not essential to the broader ML paradigm being described. There is no theoretical obstacle to choosing a different diabatic electronic structure method.

In order to perform an electronic structure calculation on a diabatic basis state of an adiabatic ground state system for a given configuration of nuclear coordinates, constraints must be placed on the electron density. Considering again the dissociation of a generic acid HA, the diabatic states of greatest importance are those corresponding to the reactant (HA + H₂O) and the product (A^– + H₃O⁺). For a single nuclear configuration, these states differ only in the charges of the two molecules, and thus the electron density. So, we can find the energy of a fragment of the system subject to some constraint on the electron density by the minimization

6

where E[ρ(r)] is the density functional and λ(∫_Ω ρ(r) d³r – N) is a Lagrange multiplier term which enforces a constraint N on the number of electrons in the volume Ω.¹⁷ The Becke partition scheme¹⁸ was used to assign volumes of space to each of the fragments in each diabatic state. Having computed E^CDFT for both diabatic states, the ground state energy, analogous to the MS-RMD ground state energy, can be expressed as the lowest eigenvalue of

7

where S is the overlap matrix between the diabatic states.

With electronic structure data for the diabatic states in hand, parametrization of the MS-RMD model is achieved by minimizing the residual of the diabatic state vectors c, given by⁹

8

Density Functional Theory

DFT simulations were performed on protonated Asp and Glu residues in CP2K¹⁹ using the ωB97X functional²⁰ and TZV2P basis set. Eleven single-point energy calculations were performed for each residue, varying the length of the side chain carboxyl O–H bond from 0.9 to1.9 Å in 0.1 Å increments. The resulting bond dissociation energy curves were used to optimize Morse potential parameters for the side chain carboxyl O–H bond for both residues prior to the more extensive optimization of MS-RMD parameters described below.

For Asp only, DFT simulations at the same level of theory were performed on 63 configurations of a protonated Asp/water molecule complex, where the distance between the water oxygen and the nearest side chain carboxyl oxygen varied between 2.2 and 2.8 Å in increments of 0.1 Å and the position of the proton shared by the side chain carboxyl group and the water molecule varied from 1.0 Å from the nearest carboxyl oxygen to 1.0 Å from the water oxygen in nine equally spaced increments. The entire Asp residue was modeled, rather than just its side chain. This was found to affect the values of c computed, unlike earlier work on Glu, due to the smaller size of the Asp side chain and proximity of the carboxyl group to the backbone. The analogous simulations for Glu were already performed in ref (9) and no further electronic structure data was required.

CDFT

The CDFT calculations were performed on the same Asp configurations as above in CP2K at the same level of theory. The fragments were defined as the molecules of the diabatic states discussed in the Methodology; namely, for the reactant state the fragments were AspH and H₂O and for the product state the fragments were Asp^– and H₃O⁺, where the constraint on the number of electrons per fragment was set to achieve the correct overall charge per fragment and the volumes of space corresponding to each fragment were defined by the Becke partition scheme.

Parameter Optimization

Several sets of parameters were optimized simultaneously for each residue:

9

10

Equations 9 and 10 represent repulsive corrections to the classical FF between the hydronium oxygen and Asp/Glu side chain carboxyl oxygen (U_OX^rep) and hydronium hydrogen and Asp/Glu side chain carboxyl oxygen (U_HX). Parameters B, b, b^′, C, and c were optimized algorithmically; d_OX⁰ and d_HX were 2.4 and 1.0 Å, respectively. (A and a correspond, respectively, to parameters C and c of refs (9 and 14)) The sum in eq 9 runs over the hydronium hydrogens and the exponential term becomes unity if a proton is equidistant between the two oxygens involved in the interaction. Nonbonded interaction parameters between (1) Glu/Asp carboxyl oxygen (OP) and water oxygen (Ow), (2) Glu/Asp carboxyl proton (HP) and Ow, (3) Glu^–/Asp^– carboxylate oxygen (O) and hydronium oxygen (OH), and (4) O and hydronium proton (HH) were fit to a 12–6 Lennard-Jones (LJ) potential (see Supporting Information, SI). The off-diagonal coupling term between diabatic states in the MS-RMD Hamiltonian, h_ij, was defined as¹⁴

11

where r_HX is the distance between the nearest Asp/Glu carboxyl oxygen and the proton shared with a water molecule, while parameters g₁, g₂, and g₃ were tunable and correspond, respectively, to c₁, c₂, and c₃ of refs (9 and 14). (Note that in this section all parameters “c” are not the same as the diabatic coefficients in eqs 7 and 8.) A final tunable term, V_ii, which is a constant energy correction for the difference in energy between the protonated and deprotonated forms of Glu/Asp in the classical FF, was also included. In total, 17 parameters were fit for each AA. Optimization was accomplished by a Nelder–Mead^21,22 minimization followed by Broyden-Fletcher-Golfdfarb-Shanno (BFGS) minimization of the residual in eq 8. The initial guess parameter set for Glu was the model of ref (9) while for Asp it was the model in ref (14).

MS-RMD Simulations

All MS-RMD simulations were performed in LAMMPS MD software²³ using the RAPTOR⁸ extension. Enhanced free energy sampling used the PLUMED2 plugin^24,25 to LAMMPS. Classical FF parameters were from CHARMM36.²⁶ The SPC/Fw water model²⁷ was used for classical waters throughout. Except where noted for the AAs, the MS-RMD parameters used for when the dissociated hydrated excess proton was in water molecules were those of MS-EVB 3.2.²⁸ Prior to any reactive MD simulations, all systems were equilibrated classically with the GROMACS MD package.²⁹

The MS-RMD simulations employed a Nose-Hoover chain³⁰ thermostat using a damping parameter of 100 fs and were performed at 300 K with a time step of 1 fs. The particle–particle, particle–mesh method was used to compute long-range electrostatic interactions in reciprocal space with a cutoff of 10 Å and a precision of 10^–4.³¹ Well-tempered metadynamics³² (WT-MTD) was performed to improve the free energy sampling of the proton dissociation event. The reaction coordinate (RC) of proton dissociation, denoted by ξ_CEC, was defined as the distance between the nearest side chain carboxyl oxygen and the excess proton CEC (eq 5), as done previously.⁹ The WT-MTD Gaussian height and bias factor were 0.8 kcal/mol and 12, respectively, and Gaussians of width 0.1 Å were deposited every 1 ps. A harmonic potential of 25 kcal/mol * Ų was applied beyond a ξ_CEC value of 8 Å to avoid needless sampling of bulk-like excess proton configurations far from the protonatable residue.

Bulk Water and Protein pK_a Calculations

Two different types of MS-RMD simulations were performed for each Asp and Glu model. First, each system was simulated as a protonated single residue in a box of bulk water consisting of 238 water molecules for Asp and 241 water molecules for Glu. The pK_a in bulk water was calculated from statistical mechanics via the formula⁹

12

where ξ_CEC is the distance between the excess proton CEC and the AA side chain carboxyl group, F(ξ_CEC) is the conditional free energy (PMF) as a function of that distance, and 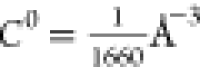is the standard state concentration expressed as a number density. F(+ ∞) is the value of the free energy at infinite distance between the proton and the AA, taken to be the value of the free energy curve when ξ_CEC is sufficiently large that F(ξ_CEC) has plateaued. The symbol † denotes the position of the transition state.^9,14

Second, SNase (PDB: 1U9R(33)) structures were prepared by computationally mutating E66 to D66, if necessary, protonating E/D66, solvating in a cubic box of water 70 Å to a side containing ∼10 000 water molecules (9973 for Glu, 9911 for Asp), adding NaCl to a concentration of 0.15 M, and equilibrating under constant NPT conditions at 298 K and 1 atm for 200 ns. A Nose-Hoover chain thermostat with a damping parameter of 100 fs and Parrinello–Rahman barostat³⁴ with a damping parameter of 1 ps were used. A time step of 2 fs was used and the LINCS algorithm³⁵ constrained bonds involving hydrogen atoms. Subsequent biased MS-RMD simulations used a time step of 1 fs at a temperature of 298 K in the constant NVT ensemble. For the protein systems, two-dimensional umbrella sampling (US) simulations were carried out with respect to two collective variables (CVs): ξ_CEC and d_SC.⁹ ξ_CEC is defined identically to the bulk water case, while d_SC is a relative measure of the orientation of the Asp/Glu side chain with respect to rest of the protein; negative values correspond to buried conformations of the side chain, interacting with various internal water molecules,^33,36,37 while positive values are exposed to bulk (see SI). For V66E, a total of 900 US windows were used spanning ξ_CEC = 0.4–11.25 Å and d_SC= −1.5–4.2 Å, with starting configurations taken from the US windows of ref (9). For V66D, 580 windows were used spanning ξ_CEC = 0.25–8.75 Å and d_SC= −1.5–3.0 Å. Each window was simulated for a minimum of 1 ns, with individual simulations extended as necessary to achieve convergence. A radially symmetric constraint u_res (r_⊥) of 10 kcal/mol*Ų was placed on the CEC beyond a radius of 7 Å from the mouth of the cavity containing E/D66 to prevent lateral diffusion (see SI). The weighted histogram analysis method (WHAM)³⁸ was used to obtain the PMF from the US data per the following.

First, the d_SC degree of freedom was integrated out in order to express the free energy only as a function of ξ_CEC according to

13

The pK_a can then be calculated from the resulting PMF by

14

S_u = ∫_o^∞ 2πr_⊥ exp[−βu_res (r_⊥)]dr_⊥ is a correction factor to account for the presence of the radial restraint u_res (r_⊥) on the excess proton position.

Results and Discussion

DM-Derived Asp Model

The DM-optimized Asp MS-RMD parameters are reported in Table 1. The pK_a was computed by eq 12 as 3.8 ± 0.2. These parameters produce quantitative agreement with the experimental pK_a of Asp in bulk water of 3.71,³⁹ in line with our previous results for Glu and Lys. This validation against experimental data is persuasive evidence for the model’s accuracy, but it must also be noted that it is encouraging that the parameter sets for Glu and Asp are quite similar to each other. As these AAs differ in their structure only by a methyl group and their side chain pK_a by less than one unit, they ought to have substantial similarities in a model which, as our does, aims to encode the proper fundamental physics of the systems. Especially with regard to the LJ parameters, which intuition suggests ought to be almost identical for an Asp side chain interacting with water compared to a Glu side chain interacting with water, the two sets of parameters differ very little. This was not a constraint placed on the optimization, nor were the optimizations even conducted from the same initial guess, indicating that the DM paradigm is properly motivated, and that appropriate choice of training set allows the model to learn the physics essential to the reaction being described.

Table 1. MS-RMD Parameters for Asp and Glu Obtained by DM to CDFT Data^a.

	Asp	Glu		Asp	Glu
B	0.000928477	3.94487	Vii	–139.912	–153.282
b	1.41581	1.41583	ϵOE-HHLJ	0.231526	0.227986
b′	1.08883	1.09180	σOE-HHLJ	1.36801	1.37334
A	2.72026	3.85746	ϵOw-HEPLJ	0.717000	0.730093
a	1.15572	1.15358	σOw-HEPLJ	1.22018	1.24711
g1	–20.2207	–25.0434	ϵOE-HHLJ	0.141951	0.112701
g2	3.03394	2.99967	σOE–OHLJ	3.00880	3.00179
g3	1.43771	1.40739	ϵOEP-OwLJ	0.150728	0.195512
			σOEP-OwLJ	3.08218	3.11138

^aDefinitions of these parameters are provided in Simulation Details. Units of energy are kcal/mol and units of distance are Å.

Improved Glu Model

In our previous study, to accurately model the bond dissociation energy for the deprotonation of lysine, it was necessary to replace the side chain NH₂–H⁺ harmonic bond potential with a Morse potential, as has been done for all reactive species in previous fitRMD models.¹⁴ To determine the appropriate Morse potential parameters, a DFT single point energy scan along different lengths of the NH₂–H⁺ bond was performed, and the Morse parameters optimized by the BFGS method. It was suggested at the time that a similar procedure might be used to improve the existing models which make use of the Morse potential described in ref (14). The greater accuracy of the Lys model in SNase compared to Glu lent credence to this proposal.

In that vein, we report here new Morse potential parameters for the side chain carboxyl OH bond in both Glu and Asp in Table 2. Note that these parameters were computed before optimization of the MS-RMD parameters. Two facts are immediately apparent: (1) Both new sets of Morse parameters differ significantly from the old set, especially in the depth of the well D, but also in a somewhat shorter equilibrium bond length r_e. The older parameters were fit to condensed-phase QM/MM forces computed using the B3LYP functional⁴⁰ and a double-ζ basis set, while these here were computed using gas-phase ωB97X/TZV2P diabatic state energies. At least one study,⁴¹ published after ref (14), concluded that while B3LYP is certainly not a bad choice of functional, others offer better performance across several criteria when dealing with water systems specifically. Another recent publication²⁰ showed that ωB97X often produced more accurate results than B3LYP for a variety of test sets, and specifically for reaction barrier heights, which is of particular importance to this work. Taken together these indicate that our new Morse parameters rest on more reliable electronic structure data. They also produce better results across the board in terms of convergence of the DM fitting procedure, agreement with experiment, and transferability. A direct comparison can also be made between the parameters of the recently published Glu model⁹ and the new model by evaluating eq 8 for each. For the older model this is 0.014 while the current model produces a value of 0.0042. Figure 1 represents this same data visually by plotting the values of c^CDFT against c^RMD. It is clear from this data that the current model, in which only the Glu carboxyl OH Morse potential was changed before reoptimization, produces fitRMD parameters which better replicate the training data. (2) The two sets of Morse parameters are much alike, especially in comparison with the prior set. This is not unexpected. Asp and Glu, as already noted, have similar structures. Additionally, their experimental pK_a’s in bulk water, which are largely determined by the OH bond dissociation energy, differ by only about half a unit. In fact, the earlier force-matched Glu and Asp models used Morse parameters that were actually identical, because they had been fit to a harmonic CHARMM bond potential that was the same for the carboxyl OH of both molecules.¹⁴ Once again, these values were not constrained to be identical in the present work. The underlying DFT energy data, though computed analogously, were different. That they nevertheless produced such similar results reflects well on the choice of electronic structure and optimization methods.

Table 2. Morse Potential Parameters Where U(r) = D (1 – e^{–α(r–r_e)}))²; D, α, and r_e Were Fit to a DFT Scan along the Asp/Glu Side Chain Carboxyl OH Bond^a.

	D	α	re
Nelson14	143.003	1.80	0.975
Asp	164.564	1.74	0.960
Glu	163.527	1.73	0.962

^aThe first row shows the parameters derived and used in earlier MS-RMD models for comparison.

Figure 1.

Plots of c^CDFT versus c^RMD for the training set after optimization for Left: the Glu model of ref (9); Right: this work. Points farther from the red line indicate training configurations where the optimized MS-RMD model less accurately reproduced the relative contributions of the diabatic states to the ground state energy of the Glu-water complex. The new model generally reproduces the CDFT training data better.

Model Performance in SNase and pK_a Analysis

The goal of this model parametrization effort is to perform simulations in biomolecular contexts that have predictive value with quantitative accuracy. To assess the models’ ability to perform well in systems different from the training environment, deprotonation simulations in the SNase protein were performed. SNase is ideal for our purposes not just because it allows for direct comparison with our earlier results but also because it is a well-studied system for which the pK_a values of several mutated internal residues have been experimentally determined.⁴² Notably, the experimental pK_as of E66 in the V66E mutant and D66 in the V66D mutant are both ∼9 (see Table 3), some 5 units more basic than in bulk. Two-dimensional umbrella sampling calculations were performed with respect to the CVs defined in Simulation Details; the resulting 2D PMFs are presented in Figure 2 and the pK_a values of the mutant residues calculated by eq 14 are shown in Table 3 below.

Table 3. pK_a Values for Deprotonation of Asp and Glu in Bulk and SNase Derived from PMFs Computed According to Eq 14 by Biased MS-RMD Simulations.

		SNase	Water
Asp	computed	8.5 ± 0.2	3.8 ± 0.2
	experimental	8.45–9.03b	3.71a
Glu	computed	9.3 ± 0.2	4.1 ± 0.2
	experimental	8.73–9.28b	4.15a

^aValues from ref (39).

^bValues from ref (42) from chemical denaturation.

Figure 2.

2D PMFs in units of kcal/mol of E/D66 deprotonation in SNase with respect to a distance CV ξ_CEC and a side chain orientation CV d_SC. In A/B the black lines represent the MFEP of proton dissociation from the side chain, corresponding to the likeliest reaction pathway. The dashed boxes indicate the location of the detail shown in C/D. Negative values of d_SC indicate a buried E/D66 side chain, while positive values indicate a solvent-exposed side chain (see SI). (A) D66. (B) E66. (C) Detail of the well of (A). (D) Detail of the well of (B).

In line with prior results, and buttressing the evidence for the transferability of DM-derived MS-RMD parameters, the pK_a computed for D66 is within the range of values determined by experiment. Note also that the E66 pK_a with the inclusion of the new Morse parameters and subsequent reoptimization has been reduced compared to our earlier study (which found a value of 9.8 ± 0.2)⁹ and is now in better agreement with experiment. This transferability of gas-phase-matched models to the biomolecular systems is remarkable and gives us confidence that not just the overall energetics of the reaction but also the mechanism suggested by the MFEP across the PMF is correct and has explanatory power for the large pK_a shift for Glu and Asp in the V66E/D SNase mutants. Several features of these PMFs thus merit further discussion as follows.

The most obvious feature of each of the 2D PMFs is the narrow (in the ξ_CBC dimension) and deep free energy well. Each is centered around ξ_CEC ≈ 0.5 Å with a depth of ∼15 kcal/mol relative to the bulk, but perhaps more conspicuously a depth of ∼14 kcal/mol relative to the position of the contact ion pair (CIP) local minimum. The prominence of the CIP well in both plots comports with the suggestion of a prior study that ns-scale persistent CIP interactions modulate the local electrostatic environment.⁴³ Compare this with a well depth in bulk of 9–11 kcal/mol for both Glu and Asp.⁹ This difference accounts almost entirely for the large pK_a shift–even if the integral in eq 14 is only performed out to ξ_CBC = 3 Å for V66E (approximately the position of the CIP), the resulting pK_a is 8.2. This indicates that the most important factor in the pK_a shift compared to bulk is the difference in the initial bond dissociation event energetics, modulated by the local protein environment, with only a small contribution to the overall change in free energy from the remainder of the proton translocation process out to the bulk. It should be noted that, while such an approximate viewpoint is useful for understanding the origins of the differing behavior of Glu/Asp in SNase compared to bulk, quantitatively accurate, physics-motivated pK_a predictions must include the entire free energy curve of the dissociation event. Because pK_a is a logarithmic scale, an approximation which only includes the first few Å of the curve and neglects the remainder of the process, while appearing to result in a fairly accurate pK_a (differing from experiment by “just” one unit), overestimates the degree of dissociation by a factor of 10. For example, a popular pK_a prediction tool, PROPKA 3,^44,45 yields a pK_a value of 8.02 for E66, similar to the value approximately obtained here by considering only the first few Å of the dissociation curve. While this is useful for quickly gauging the direction of a pK_a shift in a given environment, it indicates that for reliably accurate predictions, the full proton dissociation curve based on a statistical mechanics formulation and an explicitly reactive MD model is essential.

Several differences between the E66 and D66 dissociation curves are also worth discussing. Note the difference in shape of the MFEP between the two plots (Figure 2 A,B). Where the MFEP is vertical or horizontal, the reaction is proceeding along only one of the CVs, while the other remains constant. Where the MFEP is sloped, the two CVs are said to be coupled, or change concurrently as the reaction proceeds. The D66 MFEP suggests an almost purely stepwise mechanism; that is, the MFEP is either vertical or horizontal for most of the dissociation event, demonstrating significant coupling between the CVs only beyond ξ_CEC > 4 Å, where the free energy surface is basically bulk-like and the relevance of the MFEP diminishes. The dissociation takes place in three distinct steps: first, a partial exposure of the Asp side chain; next, movement of the proton away from the Asp side chain to a distance of ξ_CEC ≈ 2.5 Å; and finally, another reorientation of the Asp carboxylate group to establish the CIP local minimum. The E66 MFEP, by comparison, is not so starkly stepwise, but shows greater coupling between the two CVs. The likeliest explanation for this seems the greater length, and therefore flexibility, of the Glu side chain compared to Asp. In a study of ligand binding in proteins, binding pocket Glu residues were found to be flexible about twice as often as Asp residues, owing to one more rotatable bond (3 compared to 2) in the side chain.⁴⁶ An analogous effect is at work here. This difference in side chain flexibility manifests itself in another way: compare the values of d_SC at the end of the MFEP for E66 and D66. The minimum for E66 at high values of ξ_CEC is broad but generally between d_SC values of 2 and 3 Å. For D66, the equivalent minimum is closer to 1 to 2 Å. This is a subtle difference but corresponds to greater exposure of deprotonated Glu to the bulk compared to deprotonated Asp. Figure 3 sheds some light on the causes. In the first panel, corresponding to the global minimum, the Asp side chain is buried, far from bulk water molecules and participating in a hydrogen bond with an internal water molecule. In the second panel, corresponding to the saddle point in the PMF, the side chain has both rotated to interact strongly with the bulk and translocated, while the relative position of the excess proton CEC to the carboxyl group remains largely constant (notice the large relative distance between the side chain and the internal water molecules.) In the third panel, corresponding to the hill above the saddle point, the Asp side chain is still interacting strongly with bulk water molecules, but the alpha helical structure of the nearby backbone has been significantly disrupted to achieve the desired orientation. The energetic penalty associated with that disruption appears to explain the different behavior of E/D66 with respect to their side chain orientations during deprotonation. This D66 behavior, threading a needle between significant protein secondary structure disruption on the one side and the need to establish contact with the solvent on the other, sheds light on prior studies which describe greater local protein disorganization in V66D.^36,37,42,47 We also note that our simulations support the hypothesis of α-helix unfolding,^37,42,47 rather than that of ref (36) of β-sheet melting. The more flexible Glu side chain can rotate toward the bulk more easily, without destabilizing the protein secondary structure, and so the minimum of the PMF is at higher values of d_SC, despite otherwise very similar deprotonation curves and pK_a values for the two residues. We also note that the consistently high value of d_SC at large values of ξ_CEC in the MFEP of both structures indicates that the reorientation necessary for deprotonation is persistent, allowing the negatively charged carboxylate side chain to be well-hydrated, in agreement with a number of prior works suggesting that deprotonation of E/D66 is coupled to conformational reorganization.^37,42,43,47

Figure 3.

Representative structures of SNase D66 taken from three different umbrella sampling windows. The CEC is shown in green. (A) ξ_CEC = 0.5, d_SC = −0.75, the global minimum of the PMF. The distance between the D66 proton and a nearby internal water molecule oxygen is shown in Å. (B) ξ_CEC = 1.5, d_SC = 0.5, the saddle point between the global minimum and the CIP well. The same distance as in (A) is shown for comparison. (c) ξ_CEC = 1.5, d_SC = 2.00, atop the energetic barrier associated with entering the CIP local minimum along a constant value of d_SC = 2.00 (see Figure 2B).

Conclusions

We have presented a new DM-based fitRMD model for Asp and an updated model for Glu which both produce quantitative agreement with experimental values of pK_a in bulk water and in the SNase protein. Comparison of the MFEPs of 2D PMFs of deprotonation of E/D66 in SNase reveals subtle differences in mechanism not apparent from the pK_a values alone, and supported by prior experimental and computational studies. Specifically, the deprotonation event for Asp appears to take place in a nearly perfectly stepwise fashion, with little coupling between the chosen CVs, while more significant coupling is apparent in the PMF of Glu deprotonation; additionally, the Asp side chain rotates to a lesser degree into the bulk. The transferability of the Asp model to a protein context is further evidence that the DM approach to fitRMD model parametrization correctly captures the fundamental physics of AA deprotonation reactions. The updated DM paradigm proposed here, of first refitting classical potentials for reactive bonds to electronic structure data and then optimizing the MS-RMD parameters by minimizing the residual of the diabatic state vector, yields powerful tools for investigating the mechanistic features of reactive events. We anticipate that we will be able to extend this paradigm to other titratable AAs and to other types of reactions to broaden the set of systems that can currently be investigated by our combined fitRMD/MS-RMD methodology. We also expect that these mechanistic insights into protonation equilibria and other reactions in biomolecular contexts will advance our understanding of proton coupling in proteins in general and will aid in the design of new experiments to study such systems.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c04899.

• Form of the 12–6 Lenard-Jones potential, table of all fitRMD parameters used in the simulations in this work, graphical description of d_SC and its mathematical form, and the form of u_res (r_⊥) (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Biomolecular Electrostatic Phenomena”.