Practical notes on popular statistical tests in renal physiology

Abstract

Competent statistical analysis is essential to maintain rigor and reproducibility in physiological research. Unfortunately, the benefits offered by statistics are often negated by misuse or inadequate reporting of statistical methods. To address the need for improved quality of statistical analysis in papers, the American Physiological Society released guidelines for reporting statistics in journals published by the society. The guidelines reinforce high standards for the presentation of statistical data in physiology but focus on the conceptual challenges and, thus, may be of limited use to an unprepared reader. Experimental scientists working in the renal field may benefit from putting the existing guidelines in a practical context. This paper discusses the application of widespread hypothesis tests in a confirmatory study. We simulated pharmacological experiments assessing intracellular calcium in cultured renal cells and kidney function at the systemic level to review best practices for data analysis, graphical presentation, and reporting. Such experiments are ubiquitously used in renal physiology and could be easily translated to other practical applications to fit the reader’s specific needs. We provide step-by-step guidelines for using the most common types of t tests and ANOVA and discuss typical mistakes associated with them. We also briefly consider normality tests, exclusion criteria, and identification of technical and experimental replicates. This review is supposed to help the reader analyze, illustrate, and report the findings correctly and will hopefully serve as a gauge for a level of design complexity when it might be time to consult a biostatistician.

INTRODUCTION

Statistical analysis of acquired data is the cornerstone of physiological research. Statistics provides a universal toolkit for a rational study design based on reasonable predictions as well as for rigorous collection and correct interpretation of data. Meaningful deployment of statistical tools critically relies on a comprehensive understanding of fundamental statistical principles behind the used techniques. Flawed statistical reasoning translates into erroneous conclusions and incorrect data interpretation. It is not an exaggeration to say that science based on misleading deductions is both inferior and unethical. Adequate presentation of statistics is equally important to the goal of upholding the high standards of the scientific method. Consistent reporting of statistics facilitates independent data verification and improves the reproducibility of research findings. Not surprisingly, the American Physiological Society (APS) and APS journal Editorial Boards have made the detailed reporting on statistical tests in physiological studies a well-promoted necessity (APS Rigor and Reproducibility Checklist with a list of relevant publications, https://journals.physiology.org/author-info.rigor-and-reproducibility-checklist).

Regrettably, the growing legacy of physiological research is tainted by statistical errors and inefficiencies. Even one statistical error can negate the results of an otherwise elegantly conceived and executed study. The extraordinary power of statistical tools becomes dangerous in incompetent hands, jeopardizing data reproducibility and hampering generation of new knowledge. Recent studies surveying the quality of scientific literature have revealed an unsettling reality: more than 50% of the published research is not reproducible (1–3) and often contains statistical errors (2, 4–8). These worrisome observations are not materially different from the assessment made 55 years ago (9). At least in part, the abundance of statistical shortcomings in physiological reports can be explained by the lack of negative reinforcement (10). Generally, journal reviewers have no special statistical expertise. With rare exceptions, without a designated statistical reviewer it is unreasonable to expect an in-depth assessment or elaborate recommendations on statistical approaches when a manuscript is under review (10–12). Major deficiencies are more likely to be caught and censored. However, the statistical inconsistencies that require a more insightful consideration or those based on persistent misconceptions often slip through the cracks of the peer review process. As a result, substandard statistical practices are not being entirely forestalled.

In line with the rest of the biomedical community, APS has taken a proactive stance to mitigate inconsistencies in statistical data reporting. Statistical guidelines were issued, and a series of articles on how to analyze and present data was published to positively reinforce high standards. It is impossible to give proper credit to all people who tirelessly contributed to this educational mission. Nevertheless, we would like to draw attention to the guidelines for reporting statistics in journals published by APS (2, 3, 13). These guidelines were developed and subsequently updated by Douglas Curran-Everett and Dale Benos to summarize the best statistical practices in the biomedical field. Advances in Physiology Education also has an outstanding collection of papers exploring various aspects of statistical analysis and the best practices for reporting statistical outcomes (https://journals.physiology.org/advances/collections).

In this review, we used a simulated study to discuss the application of the most common statistical hypothesis tests in the experimental setting familiar to any renal physiologist. Using artificially generated “mock” data sets, we put forward a set of relevant experimental scenarios demonstrating when and how to use paired and unpaired t tests and one-way, two-way, and mixed-effects ANOVA models. Each contrived scenario provides a checklist of practical considerations pertaining to the use of a given statistical test. Figures illustrate how statistical results can be appropriately presented. The review was intentionally written without any formulas using plain English and a “learn by example” intuitive approach. Multiple comparison tests, critical to control for false discovery rates, are only briefly mentioned here. Instead, we refer readers to a number of comprehensive reviews on the topic. This review is narrowly focused on parametric hypothesis testing; where possible, we refer the reader to comprehensive publications on related subjects, such as multiple comparison tests. We also hope that our review will inspire further publications pertaining to other aspects of statistical analysis in renal physiology.

METHODS: EXPERIMENTAL DESIGN (A SIMULATED/“MOCK” STUDY)

Clopodavin (CLPD), a new blocker of calcium channel ABCD that is expressed in glomerular fakeocytes, is suggested to rescue calcium balance in these cells. Dr. Misc hypothesizes that CLPD can increase the viability of these cells by inhibiting the calcium-mediated apoptotic cascades downstream of calcium entry via calcium channel ABCD. Encouraged by a strong antiapoptotic effect of CLPD in fakeocytes, Dr. Misc would like to evaluate the drug as a new medication for diabetic nephropathy. In their first experiments, Dr. Misc uses a culture of primary fakeocytes to test the hypothesis, where they measure calcium signaling in response to CLPD and other known blockers of channel ABCD. Dr. Misc discovers that CLPD downregulates calcium signaling in these cells, in a more specific and powerful manner than other known drugs. Next, they perform power analysis and administer CLPD chronically via infusion to a rat model of diabetic nephropathy. These experiments reveal that there is an attenuation of glomerular injury and albuminuria following the administration of CLPD. Finally, Dr. Misc shows that although in a wild-type (WT) rat CLPD administration reduces protein cast formation, the drug does not have this effect in a knockout (KO) rat lacking ABCD in fakeocytes. They conclude that CLPD might be a new promising way to alleviate renal damage in diabetic nephropathy.

NOTES REGARDING THE RESULTS

Before we dive into the discussion of the data, design, and statistical tests to be used, it is essential to discuss some definitions and explain some of the presets for this mock study. Hypothesis testing requires a clear definition of a study outcome (e.g., a response to treatment), a null hypothesis (e.g., the mean response is equal to zero), a type 1 error (α) to be controlled (e.g., α = 5%), and an appropriate statistical test to address the problem (e.g., a one-sided one-sample t test). The null hypothesis typically suggests no difference between the analyzed groups (i.e., no effect of treatment or no difference between the treated and placebo groups). If the analyzed data contain sufficient evidence against the null hypothesis, it can be rejected in favor of the alternative or research hypothesis (i.e., the mean response to treatment is greater than zero). Type 1 error is the probability of erroneously rejecting the null hypothesis. Type 2 error (β) is the probability of erroneously rejecting an alternative hypothesis. Statistical power is defined as 1 − β. When a sample size calculation is needed, type 2 error is typically associated with a simple alternative hypothesis (e.g., the mean response is equal to 2.5). The sample size can then be calculated to secure 80% power (β = 20%) at α = 5%. A standard deviation (SD, reflecting the variability of data) is the last ingredient needed for sample size calculations.

The most popular tests used in renal physiology are t tests and ANOVA tests. These tests are applied for independent (unpaired t tests and one- and two-way ANOVA) and dependent observations (paired t tests and mixed-effects ANOVA). Below we consider a few artificial but practically relevant examples where these five tests are applied, discuss underlying assumptions, and show how the data and findings can be visualized and tested.

Note 1: Normality

All data discussed in this study intentionally approximate normality; data that violate normality merit an additional extensive discussion that is beyond the scope of this review. In short, typical normality tests are Kolmogorov-Smirnov, Shapiro-Wilk, or similar tests (14). It is important to not expect the statistical software to check data normality for you; this is rarely built in. If your data are skewed, check for nonstatistical errors (experimental errors). Some statistical tests may not be applicable if data violate normality, and you may consider the use of a normalization transformation (e.g., log₁₀ or square root). These transformations may convert data to an approximately normal form as determined by various normality assessment tools shown in Table 1. It is important to know that even if the data violate normality, it is still possible to apply many parametric statistical methods [such as t tests, ANOVA, multivariate ANOVA (MANOVA), analysis of covariance (ANCOVA), and many regression models] and get a valid inference about means if the sample size is large enough and certain other conditions are met. Specifically, if the data have a bounded variance, then sample means, as well as regression coefficients, are asymptotically normal in distribution as asserted by the central limit theorem (CLT). Thus, even if there are some moderate outliers and the Shapiro-Wilks test tells us that the data are not normal, but the sample size is large, then the effect of moderate outliers will be suppressed when the distribution of regression coefficients will continue to be approximately normal. Reliance on the CLT has to be taken with caution due to underlying distributions, such as Cauchy or Levy. These and other heavy-tailed distributions are situations where the sample mean never suppresses outliers even at large samples, which makes the CLT not applicable. Moreover, there are some distributions (like the lognormal distribution) for which the CLT holds, but it takes a really large sample size to suppress the effect of outlying observations to rely on the normality of the sample mean. This is the case where the normalizing transformation (the natural logarithm) solves the nonnormality issue even for small samples.

Table 1.

A few tools that are used to evaluate normality and detect outliers

Tools	Comments
Visual tools
QQ plots	Quantile-quantile (empirical vs. theoretical normal quantiles)
PP plots	Probability-probability (relative frequency against the probability of a normal distribution)
Histograms	Visual assessment of normality
Statistical tests
Shapiro-Wilks	A very powerful statistical test to detect nonnormality, relies of simulated P values, which makes it difficult to apply at large samples due to high computational burden
Anderson-Darling	Slightly less powerful alternative to the Shapiro-Wilks test
Kolmogorov-Smirnov	Relatively low power but detects departures from normality from virtually any distributions
Outlier detection
Grubbs test	Used to detect a single outlier in a univariate data set that follows an approximately normal distribution

Please note that normalization and variance stabilization are related but not the same. The goal of normalization is to make the data look approximately normally distributed. The goal of variance stabilization is to transform data so that the residual variance is approximately the same for different levels of predictor variables, which is one of the main underlying assumptions for many linear mixed models.

Note 2: Confirmatory Versus Exploratory Studies

For the mock data set, we assume that all experiments were preplanned, a power analysis was done, and the hypotheses had been predefined before the experiment began. This is an example of the confirmatory analysis, where everything is prescribed at the study’s design stage. The hypotheses were written down in advance, the sample size was predetermined, and the P value is used as a tool to measure the validity of the null hypothesis. In this study, we are not discussing the exploratory analysis. Confirmatory studies are often hypothesis-driven studies carefully planned so that there is minimal chance to deviate from the preplanned data collection and analyses. Confirmatory studies control operational characteristics such as type 1 and 2 errors and familywise error rates (probability to make at least one type 1 error) if multiple hypotheses are involved. Exploratory studies are not as strict, and researchers typically explore multiple interesting research ideas on previously collected data without formal type 1 control and power considerations. Exploratory studies provide important insights into a data set, but the findings are preliminary until separately validated using an external data set. Exploratory studies can be viewed as a hypothesis-generating activity for future confirmatory research. We refer interested readers to a short article by Tukey (15) for more details on confirmatory and exploratory studies.

Note 3: P Values

A P value quantifies the probability that the null hypothesis is actually true. For instance, if the null hypothesis suggests no effect or difference between the groups, a P value of 0.03 says that there is a 3% probability of a random nonzero effect (i.e., a difference between the groups). To claim that the observed effect or difference is significant, we compare the obtained P value with a certain significance level, α. If P ≤ α, we consider the difference statistically significant or worth reporting. α = 0.05 is a widely accepted significance level in academic publications, meaning that a given finding has less than a 5% chance of not detecting a nonzero effect. It is important to understand that the 0.05 cutoff is arbitrary. In a clinical setting, a 5% type 1 error rate might make a difference between life and death and thus would be unacceptably high. On the other hand, some researchers think that a finding with P = 0.06 might still be worth reporting or even acting as if it were true rather than false. Overall, in confirmatory studies, the determination of a significance level is driven by the study objectives and should be preplanned during the design stage before any experiments are conducted. P values and their interpretation are a heated debate in the statistical literature. We refer interested readers to the American Statistical Association’s statement on P values and their interpretation (https://www.tandfonline.com/doi/full/10.1080/00031305.2016.1154108). This statement includes many important references regarding P values and related statistical inference, including a popular report by Greenland et al. (16).

Note 4: Population and Outliers

Exclusion criteria are defined as factors that would allow the experimenter to exclude data from the final data set, such as sickness of the animal that is not related to the experiment, cells that got contaminated, accidental use of an expired reagent in cell culture studies, etc. These criteria must be predefined and disclosed before any study begins. If data were excluded, this should be reported. Most importantly, no data can be excluded just as a result of a statistical test for outliers (such as a Grubb’s test).

Note 5: Unit of Analysis

It is important to recognize your technical versus experimental replicates, your unit of analysis, and how to factor possible dependencies into your analysis. For instance, when working with cells, should an average value per dish be used for the statistical analysis or a value from each cell? Another example is when damage scoring is done in histology and several data points are collected from each animal (for instance, 100 glomerular damage scores obtained from 1 rat). It is critical to correctly identify a unit of analysis, which is directly linked to analytic methods and the sample size (see Note 6: Sample Size). For example, if the intervention is applied to tissue samples taken from a rat, then the tissue sample can be viewed as the unit of analysis, which typically substantially increases the sample size. Alternatively, if the unit of analysis is one rat, the sample size is determined by the number of rats. Observations within a rat can then be averaged for analytic purposes.

Note 6: Sample Size

Many statistical methods rely on independent data (t tests and ANOVA models), whereas some others account for dependence (repeated-measures ANOVA, mixed-effects ANOVA, and random effect models). In these models, the sample size is an entry value for calculating standard errors (SEs) and P values. In most cases, the sample size denotes the number of independent units. In a paired t test, the sample size is the number of pairs; in a two-sample t test, the sample size is the total number units in both samples. When rats are observed over time and mixed-effect ANOVA is used to compare profiles over time between groups of rats, the sample size is typically defined by the total number of rats. On the other hand, in an extreme situation, when 100 random samples are taken from a single rat, the response measured for each tissue sample may seriously depend on this rat. Admitting the limitation of a single rat experiment, researchers may still declare that their sample size is equal to 100 if valid in the interpretation of their experiment design (e.g., evaluating differences in the tissue response to two different reagents applied to the individual tissue samples). The recommendation is for researchers to determine (experimental/observation/analysis) units and the total sample size on the basis of common sense, study/experimental limitations, and, importantly, how software used for data analysis defines the sample size. One can find different definitions and descriptions of what experimental, observational, and units of analyses are, which are often linked to sample size. To avoid confusion with varying definitions of units and their relationships with sample sizes, we suggest the following: 1) rely on a definition of a “unit” that is used by the analytic methods applied to a problem at hand (statistical data analysis methods and sample size calculation methods) and 2) clearly state underlying limitations associated with the use of these analytic methods (see the example of 100 samples obtained from a single rat).

Note 7: Randomization and Permutation Tests

In addition to the typical choices of nonparametric alternatives to t tests and ANOVA tests, such as Mann-Whitney and Kruskal-Wallis tests, there exists a large body of randomization and permutation tests. These tests rely on resampling approaches. For example, a permutation version of the MANOVA model is called PERMANOVA (17, 18); this model suggested to extend PERMANOVA to a more general class of distances, and some of these distances are shown to be robust to heteroscedasticity, a typical violation of linear model assumptions. Melas and Salnikov (19) considered pairwise distance permutation tests for two group comparisons and found their large sample properties. For randomized studies, we refer readers to an applied but comprehensive book on randomization tests (20).

USEFUL PRACTICES FOR DATA PRESENTATION

The following are useful practices for data presentation:

• Report raw data points using scatterplots, histograms, boxplots, and other graphs to visually assess distributions and overall trends.

• Clearly identify the measure(s) of variability (also known as the “error bars'') used in the study. Numerous articles and guidelines have discussed whether SD or SE should be used to describe the variations in the observed data, often arriving at controversial conclusions (2, 3, 21, 22). SD shows the dispersion of individual observations around the sample means. It reflects the variability of observations (i.e., the spread of data) in the analyzed sample and represents an inherent feature of the cohort being studied. A box plot with an interquartile range can also be shown to demonstrate the dispersion of individuals in the sample. In contrast, SE reflects how precisely the true value of the population mean can be estimated from the studied sample mean. The precision of such estimation increases as the sample size grows. Thus, SE is influenced by the sample size (n). SE essentially describes the same variability as confidence intervals, and the researcher has the option of using confidence intervals instead. The existing guidelines recommend using SD as a descriptive parameter to quantify the variability of observations in the sample. The use of SE, as an inferential parameter, should be limited to cases when the estimation of the true population mean is necessary. SD is a constant that is independent of the sampling process, and SE is random and influenced by sampling, especially by the sample size (n). Finally, both SD and SE are positive numbers. It is therefore recommended to report them as mean (SD) or mean (SE) and refrain from using the redundant mean ± SD or mean ± SE format (3).

• Report the number of experimental replicates, technical replicates, and statistical tests used in the figure legend.

• Clearly separate hypothesis-driven confirmatory analyses from exploratory analyses.

• We encourage researchers to report exact P values up to a sensible number of decimal points rather than P value thresholds (e.g., P < 0.01) so that potential readers can evaluate the amount of evidence in favor of the null hypothesis. At the same time, we encourage careful experiment planning and reporting P values only for the planned hypothesis tests. Excessive reporting of (unplanned) P values often leads to readers’ overinterpretation of significant and nonsignificant findings and notoriously increases the familywise error rate. A good confirmatory study starts with a clear set of hypotheses and a strategy to control (at least partially) familywise error rate. Unplanned analyses can be used for hypothesis-generating purposes but cannot substitute for a well-planned confirmatory study.

• In confirmatory analyses, avoid statements such as “almost reached statistical significance” or “trended toward significance.” Your experiment, including the appropriate sample size, should be preplanned and the cutoff on P values for declaring statistical significance should be predetermined at the design stage. If, at the analysis stage, the P value is slightly above this predetermined cutoff, say, 0.051, it is frustrating, but the proper way is not to declare statistical significance. Some researchers may be tempted to round this P value to 0.05, which will not be correct and is an example of scientific misconduct. P values provide valuable information beyond confirmatory hypothesis testing, but researchers have to be cautious in their interpretation of P values (see our comment on P values as well as the American Statistical Association’s statement on P values).

• Exact P values cannot be used to compare the significance of different studies or findings. It is not appropriate to state that one comparison is more significant than the other based on a lower P value. It is not acceptable to change the significance level (i.e., from 0.001 to 0.01 or 0.05) after the experiments have been performed, so that a new comparison with the P value reveals statistical significance (2).

• If several preplanned hypothesis tests are performed, it is important to plan to control for multiple comparisons.

RESULTS

Now that the notes and presets are out of the way, we can discuss the study. The data are divided into two data sets: one is cell culture based (data set A) and the other is based on animal studies (data set B).

A. Cell Culture-Based Studies

Experiment 1.

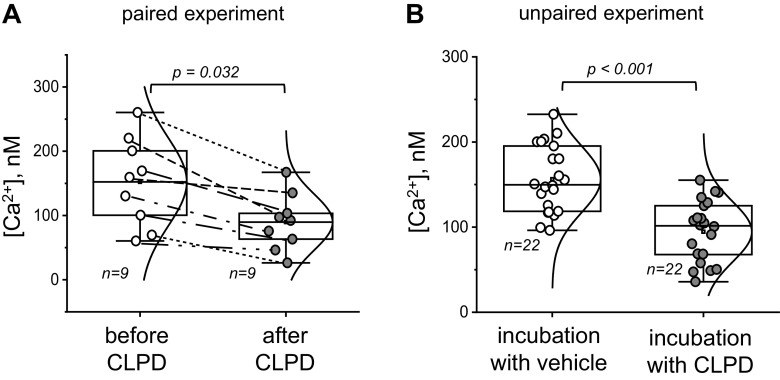
In this paired experiment, an acute effect of a new drug, CLPD, is tested on basal calcium levels in primary fakeocytes (Fig. 1A). Basal calcium (in nM) was recorded in the same cells before and after CLPD treatment.

Figure 1.

Effect of clopodavin (CLPD) on basal calcium levels in primary fakeocytes. A: basal calcium level recorded in the cells before and after CLPD treatment. Statistical analysis was performed with a Student’s paired t test (normal distribution of the data was tested with the Kolmogorov-Smirnov test). Please note that paired data points are connected by lines to illustrate the consistency of the fall in calcium concentration ([Ca²⁺]) in response to the drug. B: basal calcium level in the cells following a 1-h incubation with vehicle or CLPD. Statistical analysis was performed using a Student’s two-sample t test (normal distribution of the data was tested with the Kolmogorov-Smirnov test). There were three experimental replicates (independent dishes with cells) in A and B; no effect of the dish is assumed, and data points from individual regions of interest are reported (n is shown on the graph). No data were excluded from the analysis; exact P values (if the data are significantly different) are shown on the graphs unless the P value is <0.001. The boxes on the graphs represent the 25th and 75th percentile boundaries, and the error bars mark the minimum and maximum values of the data set.

Null hypothesis.

Acute application of CLPD does not change calcium concentration in cells.

Research hypothesis.

Acute application of CLPD decreases calcium concentration in cells.

Experiment.

Primary fakeocytes were loaded with a fluorescent dye, and baseline calcium concentration was recorded. Cells were then acutely treated with CLPD, and basal calcium levels were recorded once again in the same cells. The calcium level was calculated in individual regions of interest (ROIs; technical replicates, three per dish) in three independent dishes.

Experimental readout.

Intracellular calcium concentration.

How to run statistical analysis:

1. Determine units of analysis (ROIs within the field of view of a separate dish). Please note that we assume here that there is no “dish” effect to justify that ROI is a “unit of analysis.”

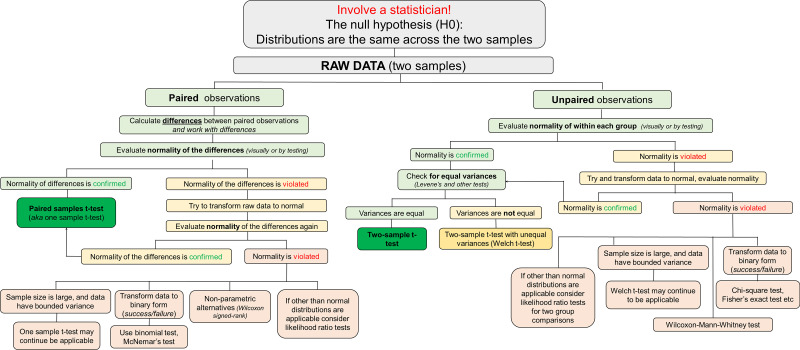
2. See Fig. 5 for a diagram illustrating a potential algorithm for the analysis. Check normality first; a t test will not be applicable if data are not approximately normally distributed. Note that for a paired t test, you check the normality of the differences between paired observations.

3. If the data are approximately normal, use a paired t test.

4. If the data violate normality, proceed with the alternative preplanned methods such as normalization transformation. If the transformed data are approximately normal, use the paired t test. If the transformation is unsuccessful, use nonparametric alternatives to the paired t test (Wilcoxon signed-rank test or dichotomize the data and apply McNemar’s test). Data dichotomization is a standard statistical approach for converting a continuous variable (say, “age”) to a binary form (“old” vs. “young”). Typically, a value above a particular threshold (say, 6 mo) is denoted by one value (say, “old”) and by another (“young”) otherwise. The reasons for dichotomization can be because “everyone does it” or statistical (such as bimodal distribution or a nonlinear bivariate association that can be conveniently simplified when one or both of the variables are dichotomized). Statistically, the cutoff (threshold) for dichotomization is often selected to improve the fit of a statistical model, which is often simplified to selecting a cutoff with the smallest P value.

Figure 5.

Graphical algorithm illustrating which direction to take at each stage of the statistical analysis: comparison of two samples (paired and unpaired observations).

Note 1.

Here, we assumed that a dish effect is negligible and can be ignored for practical reasons. After stating this assumption, the sample size can be determined at the level of technical replicates (ROIs). Certainly, it is possible that the observed calcium responses to CLPD (difference between baseline calcium level and calcium level after CLPD application) were high in one dish and low in another dish. If the mean calcium responses to CLPD differ from dish to dish, then there is likely a correlation between the observed calcium response to CLPD (i.e., observation) and a dish (i.e., cluster). A dish effect can be quantified by the intraclass correlation coefficient and should be accounted for by the mixed model analysis. The intraclass correlation coefficient is a ratio of within-cluster variance (variation among dish means) to the total variance. The total variance is a sum of between-cluster variance and within-cluster variance (reflecting how far individual observation within a cluster is from a cluster mean). Finally, it is important to reiterate that the sample size, the definition of an analytic unit, and an analytic method are tightly linked with each other.

Note 2.

A paired t test only compares means without comparing changes in variances. For instance, a treatment could change the variance but not the mean, rendering it undetectable by the applied paired t test. A distance-based permutation test is a viable solution for detecting such effects (see Melas and Salnikov’s work).

Experiment 2.

In this unpaired experiment, the authors tested the effect of a 1-h incubation with a new drug, CLPD, on basal calcium levels in primary fakeocytes (Fig. 1B). Basal calcium (in nM) was recorded in cells treated with either vehicle (control group) or CLPD.

Null hypothesis.

One-hour-long incubation with CLPD does not change basal calcium levels compared to incubation with the vehicle.

Research hypothesis.

One-hour-long incubation with CLPD decreases basal calcium level compared with incubation with the vehicle.

Experiment.

Primary fakeocytes were loaded with a fluorescent dye to label intracellular calcium and incubated with CLPD or vehicle for 1 h. Basal calcium levels were recorded in both groups postincubation. Calcium levels were calculated in ROIs containing several cells (units of analyses) in at least three independent dishes. Data are not paired (not a “before − after” setting), and the samples are independent.

Experimental readout.

Intracellular calcium levels.

How to run statistical analysis:

1. Determine units of analysis.

2. See Fig. 5 for a diagram illustrating a potential algorithm for the analysis. Check normality in each group first; a t test will not be applicable if data violate normality.

3. If data are approximately normal, use a two-sample t test.

4. If normality is violated, apply alternative preplanned methods, such as normalization transformations; if the transformed data are approximately normal, use a two-sample t test. If the transformation is unsuccessful, use nonparametric alternatives to paired t tests (Wilcoxon-Mann-Whitney test or dichotomize the data and apply either a χ²-test or Fisher’s exact test for low counts).

5. Check equality of variances between the two groups using Levene’s test or another test for homogeneity of variances.

6. If variances are equal between the two groups you are comparing, proceed with an independent samples t test. If variances are not equal between the two groups, use a t test with unequal variances (Welch t test).

Experiment 3.

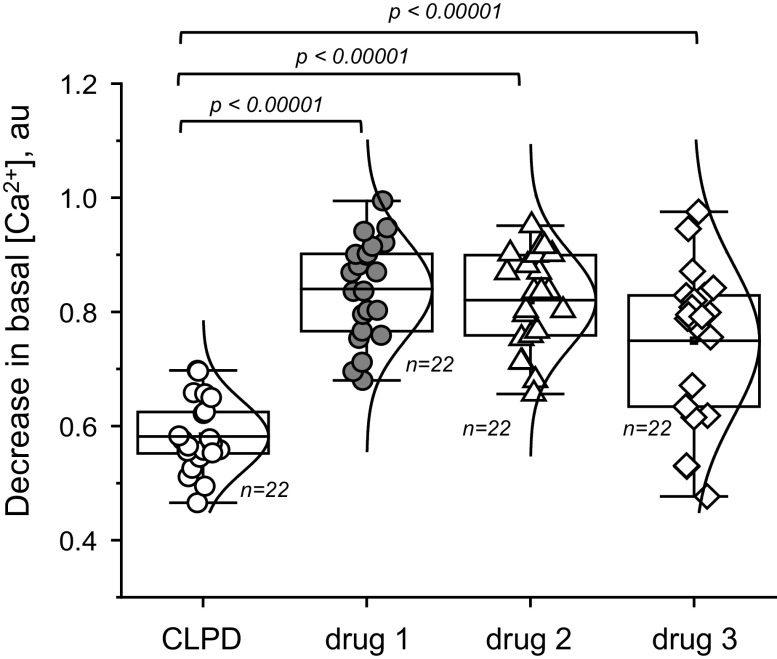
In this experiment, the authors wanted to assess how effective the new drug CLPD versus other drugs (drugs 1-3) would be at decreasing basal calcium levels in primary fakeocytes (Fig. 2).

Figure 2.

Effects of clopodavin (CLPD) and other known blockers of channel ABCD (drugs 1−3) on the basal Ca²⁺ level in primary fakeocytes. Normal distribution of the data was confirmed with the Kolmogorov-Smirnov test and Levene’s test showed that population variances were significantly different at the 0.05 level; therefore, one-way ANOVA was not applicable, and the Kruskal-Wallis test was used. Each data point on the graphs depicts a measurement of the calcium level in a ×20 field of view. There were five experimental replicates (independent dishes with cells). No effect of the dish was assumed; therefore, data points from individual regions of interest were reported (n is shown on the graph). No data were excluded from the analysis. The boxes on the graphs represent the 25th and 75th percentile boundaries, and the error bars mark the minimum and maximum values of the data set. au, arbitrary units; [Ca²⁺], calcium concentration.

Null hypothesis.

The effect of CLPD on intracellular calcium is equivalent to that of drugs 1−3.

Research hypothesis.

Application of CLPD versus incubation with drugs 1−3 elicits a more profound decrease in intracellular calcium levels than drugs 1−3. Importantly, there is no comparison between drugs 1−3 planned in this hypothesis, and this research hypothesis determines three comparisons of hypotheses comparing CLPD with each of the three drugs separately.

Experiment.

Primary fakeocytes were loaded with a fluorescent dye to label intracellular calcium. Basal calcium levels in response to CLPD or the other drugs were then recorded. Calcium levels were calculated in individual cells (technical replicates) in at least three independent dishes (experimental replicates). The data shown in Fig. 2 demonstrate the decrease in intracellular calcium in response to CLPD and the other drugs.

Experimental readout.

Intracellular calcium levels.

How to run statistical analysis:

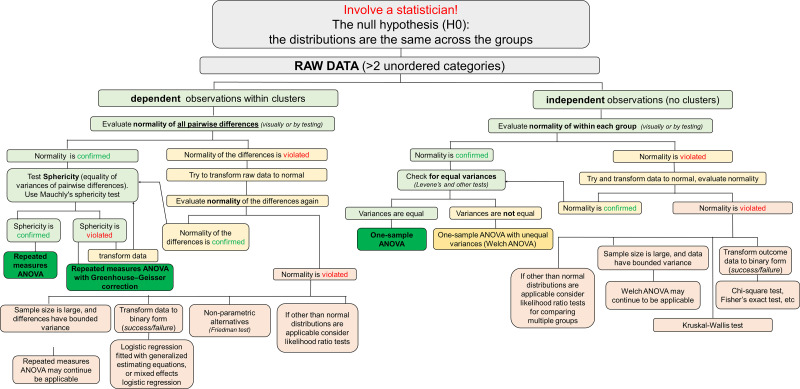
Use one-way ANOVA or another global test if variances are equal. If variances are not equal but data continue to be approximately normal within each group, apply ANOVA with unequal variances (Welch ANOVA). Distributions of nonnormal data can be compared between the groups with the Kruskal-Wallace test. See Fig. 6 for a diagram illustrating a potential algorithm for the analysis.

Figure 6.

Graphical algorithm illustrating which direction to take at each stage of the statistical analysis: comparison of two or more unordered categories (dependent and independent).

Note 1.

In the presence of multiple comparisons, for example, comparing each treatment among themselves (on a pair-wise basis) or versus control group, proper adjustment is needed to control family-wise type I error (probability to make at least one type I error is controlled at a predetermined level, for instance, 5%). Dunnett’s multiple comparisons adjustment typically works well when one group is compared against other groups, as in this experiment (Fig. 2). Tukey’s test ensures a predetermined family-wise error rate across all pairwise comparisons. Bonferroni-type adjustments guarantee control of family-wise error rates across a set of predetermined hypotheses, but they are known to be overly conservative. We refer readers interested in multiple comparison adjustments to a few comprehensive reviews (23–26).

B. Animal Studies

Power analysis.

Power analysis allows you to estimate the required number of animals (replicates, etc.) for the study given that you know the minimally relevant effect that you need to detect, and you have a general idea about the SD. Minimally relevant effects should be determined upfront, when possible. If the researcher cannot determine a minimally relevant effect size (the ratio of the effect to the SD), pilot studies will be needed to estimate the SD. A minimally relevant effect is typically determined by an expert in the applied area. A new study can then be designed with new power assumptions. As a rule of thumb, always do your power analysis and estimate your numbers before you start doing the experiment.

Low sample sizes typically lead to low statistical power. The usual requirement for statistical power is 80%, meaning that if there exists a treatment effect, then the probability to identify it with a statistically significant P value should be 80%. Power analysis is a pivotal component of the experimental design process and therefore is beyond the scope of this review. An interested reader could benefit from comprehensive publications discussing the subject in greater detail and providing links to online resources for power analysis (2, 27, 28).

A related issue is that most parametric statistical tests require normal distribution of the data. Small sample size does not allow for a reliable assessment of the normality of the distribution, with only very large departures from normality being detected.

Experiment 4.

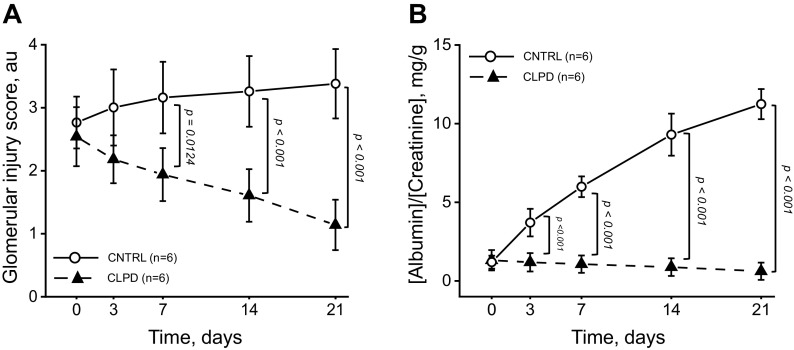
In this experiment (Fig. 3A), the authors administered CLPD or vehicle systemically to rats treated with streptozotocin (STZ; to induce diabetic nephropathy). At the end of the experiments, they assessed if CLPD alleviates renal damage.

Figure 3.

Systemic administration of clopodavin (CLPD) alleviated renal damage in a streptozotocin-induced diabetic nephropathy rat model. A: glomerular damage 3, 7, 14, and 21 days post-CLPD administration. Each point on the graph denotes an average damage score value obtained from 100 random glomeruli from kidneys of 3 individual animals. Animals were euthanized to collect the data; time points were independent of each other. Two-way ANOVA showed a significant group by time interaction (P < 0.01); therefore, the group effect at each time point was assessed using a t test on a post hoc basis. The number of animals per group (n) is shown for each group. B: proteinuria at 3, 7, 14, and 21 days of CLPD administration. Each point on the graph denotes the average albumin-to-creatinine ratio from six individual animals. Animals were not euthanized to collect the data; data are paired. Groups were compared at each time point on a post hoc basis using a Student’s t test. The number of animals per group (n) is shown for each group. Exact P values (if the data are significantly different) are shown on the graphs unless P < 0.001. Error bars on the graphs represent SEs. au, arbitrary units; CNTRL, control.

Experiment.

CLPD or vehicle was administered systemically to rats treated with STZ. Animals were euthanized 3, 7, 14, and 21 days post-CLPD or vehicle administration. Tissues were collected and fixed, histological staining was performed, and the glomerular damage score was quantified (100 random glomeruli were scored for each animal). Power analysis estimated that six animals per group should be sufficient. Animals were euthanized to collect the data; therefore, tissue samples collected over time belong to different rats and consequently were independent of each other.

How to report the data.

First, the average value of glomerular damage for each animal was calculated from 100 randomly collected damage scores. The averaged value from n = 6 rats is shown for each time point. Error bars are SD. The unit of analysis is one rat; a single rat generates one observation.

Experimental readout.

Glomerular injury score.

Null hypothesis.

Systemic administration of CLPD does not change the glomerular injury score in a STZ-induced rat model of diabetic nephropathy.

Research hypothesis.

Systemic administration of CLPD decreases the glomerular injury score in a STZ-induced rat model of diabetic nephropathy.

How to run statistical analysis:

1. Run two-way ANOVA includes a group effect, time effect, and group by time interaction.

2. Check ANOVA model assumptions. The distributions of model residuals (difference between predicted and observed values) should be approximately normally distributed. Strictly speaking, even if model assumptions hold, the distribution of model residuals is not exactly normal, but gross departures from the model assumptions can be visually detected. Distributions of residuals should be approximately symmetric, bell shaped, single mode at zero, and without heavy tails (no outlying observations).

3. Check the P value for group and group/time effect. If both are not significant, then there is no group effect, and we stop the analysis.

4. If the effect of the drug over time is different in between two groups (significant group by time interaction), then we can look separately at each time point and test the group effect at each time point using a t test on a post hoc basis or contrasts within the ANOVA model.

5. There are pros and cons for adding to and removing interactions from an ANOVA model. Interaction testing adds an extra step in data analysis and, as with every testing, is associated with type 1 and 2 errors. The danger of dropping an interaction due to its statistical insignificance is that the interaction term may still have a nonzero effect (type 2 error). Consequently, researchers will make a statistical inference using a misspecified model, leading to bias and potentially erroneous findings. On the other hand, the exclusion of a nonsignificant interaction term from ANOVA model reduces the number of parameters to be estimated in the model, which allows for a more accurate estimate of model parameters and more powerful statistical inferences. For example, in an experiment where a total of 60 rats are allocated to four treatment groups and euthanized at five time points, there are three rats per group per time point. If a researcher proceeds with an ANOVA model with interaction, there are 20 parameters to estimate in the model. Without an interaction term, the number of parameters is reduced to eight and the error term can be more accurately estimated. Noninclusion of interaction assumes that the over time pattern between the treatment groups does not change. In linear models, type 2 error of including a nonexistent interaction does not produce bias in the estimation of treatment effect; it only reduces statistical power. This phenomenon of unbiasedness after the inclusion of a nonexistent interaction allows researchers to worry less about testing for interaction and always include it despite its significance status.

Note 1.

Similar to experiment 1 (see Note 1), we assumed that there is no significant difference between the data collected from different rats. The “rat effect” was ignored, and the sample size was determined at the level of technical replicates (randomly selected glomeruli). If such assumption cannot be justified by nonstatistical arguments, researcher should investigate the magnitude of the intraclass correlation coefficient and account for the cluster effect if needed (a mixed model analysis).

Note 2.

The main difference between the mixed-model ANOVA and two-way ANOVA is the presence of repeated observations in mixed-effects ANOVA. In mixed-effects ANOVA, rats are not euthanized and observed over time (for example, six rats with four observations per rat), whereas two-way ANOVA deals with independent observations (24 rats with groups of six euthanized at four time points). The main difference between the mixed-model ANOVA and two-way ANOVA is the presence of repeated observations in mixed-effects ANOVA.

Experiment 5.

In this experiment (Fig. 3B), the authors administered CLPD or vehicle systemically to rats treated with streptozotocin (STZ; to induce diabetic nephropathy). At the end of the experiments, they assessed if CLPD alleviates renal damage

Design.

CLPD or vehicle was administered systemically to rats treated with STZ. Urine was collected from the same animals in metabolic cages 3, 7, 14, and 21 days post-CLPD or vehicle administration, and creatinine and albumin levels in the urine were assessed in each sample. Animals were not euthanized to collect the data, and time points are related. Power analysis predicted seven animals per group.

Experimental readout.

Albumin-to-creatinine ratio.

Null hypothesis.

Systemic administration of CLPD does not change proteinuria (albumin-to-creatinine ratio) in an STZ-induced rat model of diabetic nephropathy.

Research hypothesis.

Systemic administration of CLPD decreases proteinuria in an STZ-induced rat model of diabetic nephropathy.

How to report the data.

Averaged across seven rats, the outcome value is shown for each time point. Error bars are equal to SD. The unit of analysis is a single rat at a specific time point.

How to run statistical analysis:

1. A mixed-effects model is usually used with this type of data. Specifically, the outcome values depend on two factors: group (CLPD or control) and time (0, 3, 7, etc. days). Each group uses its own set of rats, and animals are randomized between the groups. The albumin-to-creatinine ratio is repeatedly measured at different time points in the same rats, making time a “repeated” factor.

2. Mixed-effects ANOVA allows the comparison of group means affected by a “within-rat” variable (time) and a “between-rat” variable (treatment).

3. By analogy with two-way ANOVA, there may exist a significant interaction between group and time variables. A significant interaction indicates that the “time” dynamics of the averaged outcome values differ between the groups. If the group by time interaction is not significant, the interaction term can be assumed to be equal to zero. In this case, a mixed-effect ANOVA model without interaction can be fitted, which forces “time” profiles to differ only by a shift of the y-axis.

4. If the interaction is significant, the groups can be compared at each time point on a post hoc basis using either t tests or contrasted based on a mixed-effect ANOVA model. To reduce type 1 error, post hoc tests can be adjusted for multiple comparisons.

5. It is important to note that the variance-covariance structure should be correctly specified for repeated data. In its simplest form, mixed-effects ANOVA assumes compound symmetry of the variance-covariance matrix. In our experiment, this means that the variability of observations does not change with time (same variances) and every pair of observations within the same rat has exactly the same correlation (same correlation). A less strict sphericity assumption assumes that over time changes have the same variance. If the sphericity is not assumed, researchers often use Greenhouse and Geisser correction to make P values more conservative to compensate for possible violation of sphericity. For more details on this topic, we refer interested readers to Armstrong (29).

Note 1.

Repeated-measures ANOVA compares means across one or more variables that are based on repeated observations and represents a generalization of the paired t test for comparing more than two groups. One-way ANOVA generalizes an independent sample t test for comparing more than two groups. Mixed-effect ANOVA is a two-way ANOVA where one factor splits the sample into independent groups (rats with different genotypes) and another (repeated) factor defines repeated observations (e.g., over time assessments done for the same rat). Any of the above methods can be used in the presence of missing data if a proper missing data approach is used. Multiple imputations with variance adjustment, as previously described by Little and Rubin (30), allow applying each of the above methods to imputed data sets.

Experiment 6.

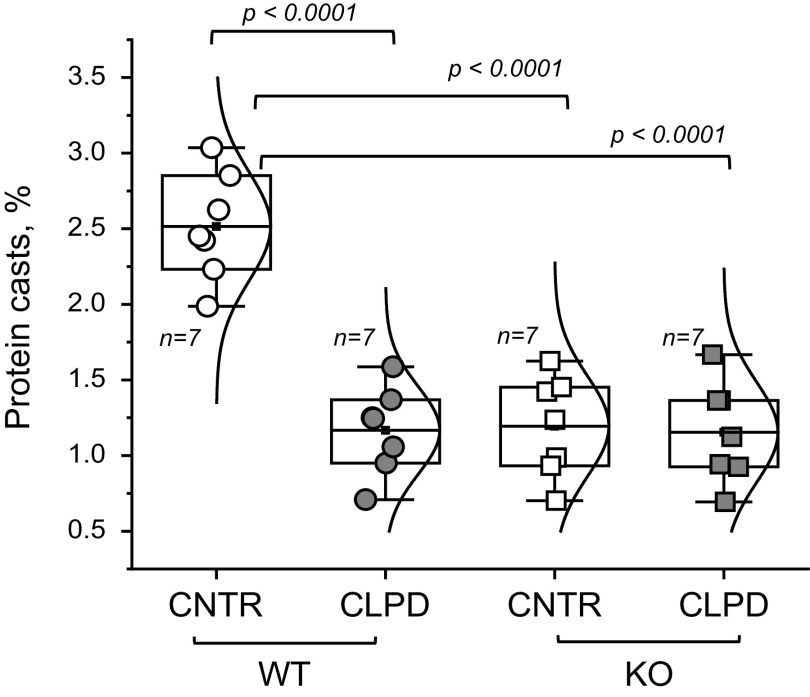
In this experiment, protein cast formation was assessed in WT and ABCD KO STZ-induced diabetic rats (Fig. 4).

Figure 4.

Assessment of protein cast formation in wild-type (WT) and ABCD knockout (KO) streptozotocin-induced diabetic nephropathy rats. Shown is a summary graph of protein cast area (percentage of the total kidney area) for each studied group. Animals were euthanized to collect the data. Data were analyzed using two-way ANOVA for the main effects of genotype and treatment and their interaction. The P value for interaction is P = 0.00021. Therefore, the magnitude of the treatment effect was assessed separately for each group (WT and KO) using a t test with a multiple comparison correction (Bonferroni). The boxes on the graphs represent the 25th and 75th percentile boundaries, and the error bars mark the minimum and maximum values of the data set. The number of animals per group (n) is shown for each group. CNTR, control.

Design.

Here, the authors used four groups of animals: WT and ABCD KO rats treated with vehicle or CLPD for 4 wk following the induction of diabetic nephropathy. At the end of the study, protein cast area (percentage of total kidney area) was assessed in every animal for each studied group. Animals were euthanized to collect the data; power analysis predicted n = 7 animals will be needed per group.

Experimental readout.

Relative protein cast area.

Null hypothesis.

The effect of treatment (CLPD) is the same in WT animals compared with KO animals.

Research hypothesis.

The effect of treatment (CLPD) is stronger in the WT group than in the KO group.

How to run statistical analysis:

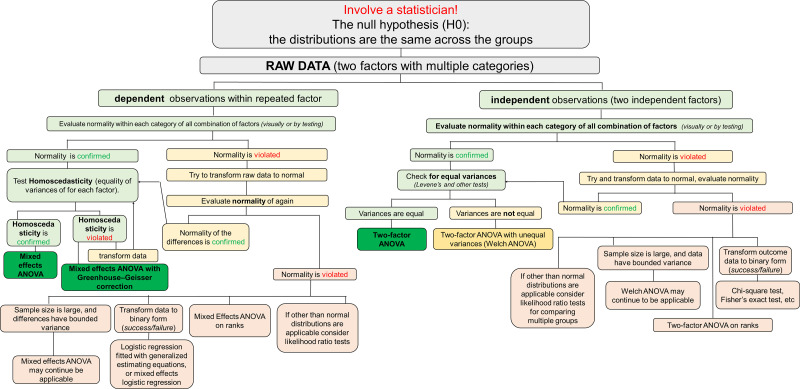
1. Apply two-way ANOVA with the main effects of genotype and treatment and their interaction. See Fig. 7 for a diagram illustrating a potential algorithm for the analysis.

2. To test if the treatment effect differs between KO and WT animals, we check if the interaction P value is <5%.

   • If the interaction is not significant, we assume that the effect of treatment is the same between groups, so we eliminate interaction from the model and evaluate the treatment (main) effect by controlling for the group effect.

   • If the interaction P value is significant, we explain the result by evaluating the magnitude of the treatment effect separately for each group. On a post hoc basis, we can also test the effect of treatment within the WT and KO groups, separately.

Figure 7.

Graphical algorithm illustrating which direction to take at each stage of the statistical analysis: comparison of multiple categories with two factors (dependent and independent).

Note 1.

The main differences between the mixed-model ANOVA and two-way ANOVA are outlined in Experiment 4, Note 2.

To facilitate researchers’ decisions for handling a few seemingly simple experimental settings, we prepared several decision trees (see Figs. 5, 6, and 7) covering possible approaches for analyzing such experiments.

CONCLUDING REMARKS

Experimental approaches and study design in physiology continue to increase in their complexity. The acquired data become progressively more elaborate, requiring meticulous and sophisticated analysis. Statistics provides powerful tools necessary for high-quality study planning, data collection, interpretation, and reproducibility. Good command of statistical methods carries greater weight in modern physiological research. Unfortunately, statistical errors remain relatively common, and misconceptions persist among authors and reviewers alike. In our view, the most effective roadblocks preventing erroneous results from being published are negative selection through peer review and positive reinforcement via improved quality of the submitted studies. Both mechanisms can be enhanced by sustained efforts promoting statistical consciousness in physiology. Our review is a part of the larger endeavor to bring statistics to the stage and help physiologists identify and manage common statistical issues. Hypothesis testing is one of the most routine applications of statistical analysis in physiological studies. Thus, this article was designed to serve as an easy to navigate hands-on practical guide on a few popular statistical hypothesis tests in the field of renal physiology. We hope that the scenarios considered here will help the reader to tackle the practical aspects of parametric data analysis and clarify how to select a test appropriate to the proposed experiment. For the questions and statistical procedures that fall beyond the scope of this article, we encourage the reader to explore the comprehensive collection of papers available from the Advances in Physiology Education (https://journals.physiology.org/advances/collections). Finally, cooperation with a professional statistician is always a prudent strategy to confront sophisticated questions. The modern scientific process is synergized by collaborations and concerted teamwork. This review, written by physiologists and a statistician, is a fruitful embodiment of such an approach.

GRANTS

This work was supported by National Institutes of Health (NIH) Grant R01HL148114 and Augusta University Department of Physiology startup funds (to D.V.I.), NIH Grant R01DK125464 and Augusta University Department of Physiology startup funds (to M.M.), and a Diversity Supplement to an NIH R01 (R01HL148114-02S1) and American Heart Association Postdoctoral Fellowship 903584 (to D.R.S.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.M., S.S.T., and D.V.I. conceived and designed research; M.M., D.V.L., D.R.S., and D.V.I. analyzed data; M.M., D.V.L., D.R.S., S.S.T., and D.V.I. interpreted results of experiments; M.M., D.V.L., D.R.S., S.S.T., and D.V.I. prepared figures; M.M., S.S.T., and D.V.I. drafted manuscript; M.M., D.V.L., D.R.S., S.S.T., and D.V.I. edited and revised manuscript; M.M., D.V.L., D.R.S., S.S.T., and D.V.I. approved final version of manuscript.