Humans adaptively resolve the explore-exploit dilemma under cognitive constraints: Evidence from a multi-armed bandit task

Abstract

When navigating uncertain worlds, humans must balance exploring new options versus exploiting known rewards. Longer horizons and spatially structured option values encourage humans to explore, but the impact of real-world cognitive constraints such as environment size and memory demands on explore-exploit decisions is unclear. In the present study, humans chose between options varying in uncertainty during a multi-armed bandit task with varying environment size and memory demands. Regression and cognitive computational models of choice behavior showed that with a lower cognitive load, humans are more exploratory than a simulated value-maximizing learner, but under cognitive constraints, they adaptively scale down exploration to maintain exploitation. Thus, while humans are curious, cognitive constraints force people to decrease their strategic exploration in a resource-rational-like manner to focus on harvesting known rewards.

Effective learning and decision-making requires balancing two strategies: exploiting known good options versus exploring uncertain, potentially better ones (Sutton & Barto, 1998). Exploration involves forgoing short-term rewards to reduce uncertainty and discover better long-term values, while exploitation maximizes short-term rewards at the expense of learning about other options. The inherent tradeoff between exploration and exploitation requires learners to shift adaptively between these behavioral strategies to maximize long-term rewards. Factors that affect explore-exploit decisions are essential to our understanding of how learners navigate uncertain environments. Reducing uncertainty through exploration is potentially advantageous but features of the environment can limit the utility of exploration. For example, in environments with a short horizon, when learners anticipate few future encounters with a choice, the benefit of exploring to reduce uncertainty for future choices is low. Accordingly, humans reduce their exploration in such environments (Rich & Gureckis, 2018; Wilson et al., 2014). Environment size is another, less studied feature affecting exploration; humans can use spatially structured values to explore (Schulz, Bhui, et al., 2019; Wu et al., 2018), but effects of systematic manipulations of environment size on exploration have not been investigated. As the number of options available to choose from relative to the horizon increases, exploration should become less advantageous; however, whether humans can adaptively adjust exploratory strategies as they do with horizon changes is unknown.

In addition to normative reductions in exploration with increasing environment size, cognitive constraints may cause humans to adjust their exploration rate. Tracking and updating many potential options to enable effective exploration places demands on cognitive resources, as does maintaining accurate value estimates for exploitation. Cognitive constraints interfere with learning and valuation processes, but humans can anticipate and adjust for this interference: people proactively employ strategies for efficient learning under cognitive constraints, such as adjusting effort based on the expected value of control (Shenhav et al., 2013, 2017), exploiting hidden structure (Collins & Frank, 2013; Wu et al., 2018), and balancing resource-intensive but fast and flexible working memory with reinforcement learning (Collins et al., 2017). These adjustments allow performance to be maintained even with cognitive challenges, but how cognitive constraints affect how humans adjust the tradeoff between exploration and exploitation is less clear.

Work manipulating cognitive load during exploratory choices has used techniques such as concurrent working memory tasks or time pressure; these manipulations have been found to variously change exploratory strategies or reduce exploration in favor of exploitation (Cogliati Dezza et al., 2019; Otto et al., 2014; Wu et al., 2022). Exploration strategies in more complex environments also likely involve a shift from simpler subcortical explore-exploit processes to more sophisticated cortical strategies (Badre et al., 2012; Costa et al., 2019; Daw et al., 2006; Ebitz et al., 2018). Much of this work to date, however, has examined cognitive demands and exploration in stylized bandit tasks, whereas most real-world explore-exploit decisions are made in large option spaces where option values are spatially structured, forming advantageous or disadvantageous subspaces (Schulz, Wu, et al., 2019; Wu et al., 2018). The strategies people use to adaptively resolve the explore-exploit dilemma when navigating large action spaces are debated: it is unclear what factors promote uncertainty-seeking vs. uncertainty-averse behaviors, for example (Frank et al., 2009; Hallquist & Dombrovski, 2019). In particular, we lack empirical knowledge of how human exploration is affected by naturalistic cognitive demands, such as environment size or the need to maintain multiple latent option values. Another question is to what extent behavioral responses to increased cognitive demands reflect proactive strategies like those in resource-rational models (Lieder & Griffiths, 2020; Wu et al., 2022) versus cognitive failures such as inability to maintain precise value representations.

Specifically, shifts in exploratory behavior under cognitive demands could result from several factors (Dubois et al., 2021; Frank et al., 2009; Gershman, 2018; Sutton & Barto, 1998; Wilson et al., 2014; Wu et al., 2018). At the simplest level, less precise value representations would manifest in increased choice stochasticity or random exploration. Another, strategic process potentially sensitive to cognitive constraints is the directed exploration of more uncertain options guided by exploration bonuses (Auer, 2002; Sutton, 1990). Here, choices are based on both the expected value and the uncertainty (exploration bonus) of each option. In their full form, exploration bonuses require tracking both value and uncertainty of all options; a simpler form that may be adopted in cognitively challenging environments is switching (inverse of perseveration) or novelty bonuses. In this form, uncertainty is reduced to choice history and uncertainty seeking behavior simply favors options less recently chosen. Random and directed exploration differ in their purpose and interpretation: increases in random exploration reduce the influence of value on choice and so make choices more noisy, while increases in directed exploration specifically prioritize more uncertain options. For example, imagine ordering a dish at an Italian restaurant, where one has enjoyed some previously ordered dishes (e.g., cacio e pepe) and not others (e.g., lasagna), while other dishes (e.g., gnocchi) are novel. Increased random exploration would make one less value-sensitive and decrease how often one chooses higher-valued relative to lower-valued dishes (e.g., more likely to order lasagna relative to cacio e pepe), while increased directed exploration would increase the probability of a novel choice (e.g., ordering gnocchi).

Competing explanations for exploratory choices can be hard to differentiate on standard learning tasks for two reasons. The first is the natural anticorrelation between value and uncertainty that emerges during value-based decision-making, as options with higher values will be selected more often, reducing their uncertainty. Paradigms with initial forced choice trials can decorrelate value and uncertainty to enable assessment of different exploratory strategies (random versus directed) on the first free choice (Dubois et al., 2021; Wilson et al., 2014). This manipulation also experimentally controls the local uncertainty of each choice to assess effects of environment size and memory demands. Second, the pattern of choices only provides a rough picture of different strategies, such as exploitation or directed exploration. Computational models instantiate these strategies explicitly. Thus, by inferring model parameters corresponding to each strategy from human behavior, we can test hypotheses about alternative underlying strategies more precisely. Computational models of choice behavior during exploration represent choice stochasticity, exploration bonuses, and perseveration as specific parameters (Dubois et al., 2021; Frank et al., 2009; Gershman, 2018; Wu et al., 2018).

In the present study, participants made decisions to maximize rewards with long choice horizons (30 free choices per block) to encourage initial exploration. We then assessed how manipulations changed this exploratory behavior. First, we used initial forced choice sampling to manipulate value and uncertainty independently under varying cognitive demands. Then, we assessed exploratory and exploitative strategies to understand how different cognitive demands – environment size and memory demands – affected exploratory and exploitative behavior. We focused on the first free choice in each block to assess independent effects of value and uncertainty, a strategy enabled by the initial forced choice sampling. We then compared participants’ choices to chance and value-maximizing behavior to determine if changes in exploratory and exploitative behavior were proactive adjustments or cognitive failures. We hypothesized that increased environment size would decrease exploration in empirical data, and that this decrease in exploration was adaptive based on normative models. We further examined whether this decreased exploration was due to increased memory load by comparing effects of environment size (where decreases in exploration may or may not be memory-dependent) and memory demands (which explicitly measures memory-dependent changes in exploration) and whether exploration was affected by spatial generalization. We then sought to characterize, using regression and formal computational models, what choice strategies drove changes in exploration with these manipulations.

Methods

Participants

Participants were 95 undergraduate students enrolled in psychology courses who completed the experiment in exchange for course credit. Seventy-two (76%) identified as female (22 [23%] male, 1 [1%] declined to answer), median age was 19 years (range: 16-22), 73 (77%) identified as White (9 [9%] as Asian, 7 [7%] as Black, 3 [3%] as multiracial, and 2 [2%] as American Indian/Alaskan Native), and 92 (97%) identified as non-Hispanic (3 [3%] Hispanic). All participants gave informed consent and the study was approved by the Pennsylvania State University IRB.

Task

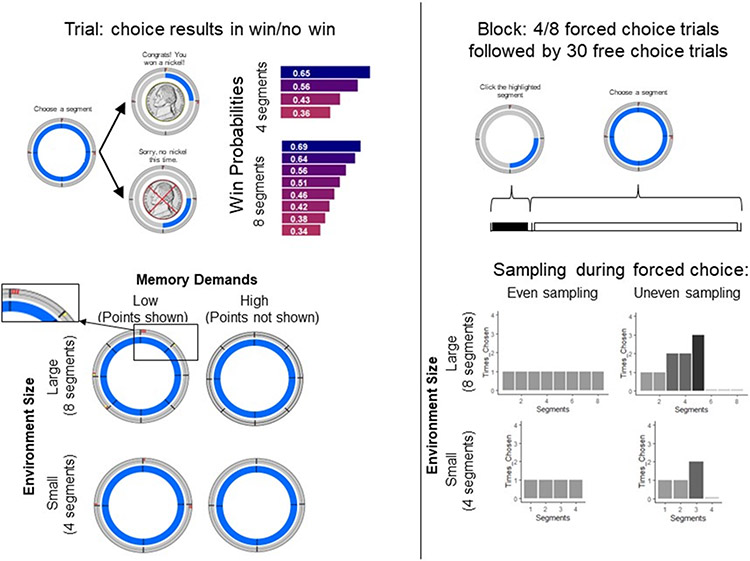
Participants completed eight blocks of the PiE (Probabilistic Exploration) task (Figure 1). This task was based on a task previously used to study exploration (the ‘clock’ task; (Moustafa et al., 2008)) but with explicitly spatially arranged segments requiring fewer assumptions about how learners binned state spaces, and with varied cognitive demands based on environment size and memory demands. Participants were instructed that the goal of the task was to maximize winnings by learning which segments in the pie were the most likely to provide a reward (nickel shown) versus no reward (nickel crossed out). The probabilities of reward for each segment ranged from 0.35 to 0.65 and were stable within a block of trials. Participants were not instructed on the reward distributions. Each block consisted of 4 or 8 initial forced choice trials, followed by 30 free choice trials. The task had a 2 (environment size: 4 or 8 segments) x 2 (memory demands: outcomes for each action in the block shown or hidden) x 2 (initial forced choice trials: even or uneven sampling) design, such that each combination of conditions was consistent throughout each block and was experienced in one block only.

Figure 1.

Task schematic. On each trial, participants choose a segment and receive feedback of reward (nickel shown) or no reward (nickel crossed out). Each segment has a stable, randomly assigned probability of reward per block. In each block, participants choose from either 4 or 8 segments (manipulating environment size) and are shown points representing past outcomes or not (manipulating memory demands). At the beginning of each block, participants have 4 or 8 forced choice trials (equivalent to the number of segments in that block), during which only one segment is highlighted and available to choose. The remaining 30 trials are free choice and participants can choose any segment. The initial forced choice sampling is either even (each segment chosen once) or uneven (some segments chosen multiple times while some segments are unchosen). Participants completed eight blocks and each block was a unique combination of environment size, memory demands, and initial sampling (even or uneven).

During the initial forced choice trials at the beginning of each block, all but one segment was grayed out on each trial and participants were instructed to select the highlighted segment. As reward probabilities were consistent throughout free and forced choice sampling, observed outcomes during forced choice sampling were informative about the reward probability for those segments. During the remaining free choice trials, participants freely selected from all segments. The number of forced choice trials was equal to the number of segments in each block (4 or 8). During blocks with even sampling during forced choice trials, each segment was highlighted and chosen once. During blocks with uneven sampling, segments were highlighted 3, 2, 2, 1, 1, 0, and 0 times (for 8 segments) or 2, 1, 1, and 0 times (for 4 segments). How often segments were highlighted and in what order was randomly chosen each block. This design, modeled after (Wilson et al., 2014), allowed for value and uncertainty to be independently manipulated for each segment for the trial of interest, the first free trial, in each block.

Statistical Regression Analyses

All analyses used R (version 4.1.1) and focused on choices during the first free trial in each block. Multilevel logistic regressions assessed differences between participants’ probability of choosing segment types versus chance performance. Segment types were defined as previously sampled, always rewarded (segment chosen during forced choice sampling and all selections during forced choice sampling resulting in a reward), previously unsampled (segment not chosen during forced choice sampling), and previously sampled, not always rewarded (segment chosen during forced choice sampling but not always rewarded). These segment types are a model-free approximation of exploitative, directed exploratory, and random exploratory choices. Since we focused on factors affecting uncertainty and exploration, present analyses focused on blocks with unsampled segments and full manipulation of uncertainty (i.e., those with uneven initial sampling). Chance performance was estimated as the proportion of segments in each segment type for each combination of conditions, averaged across all participants. Separate regressions were run for each segment type, predicting the probability of choosing it as a function of condition and participant’s random intercept. As standard logistic regression assumes a chance level of 0.5 rather than the true chance probabilities, log odds were adjusted based on the calculated chance proportions of each segment type for each combination of conditions. Identical analyses were run on simulated choices compared to chance behavior (see below for simulation details); additional analyses compared simulated choices and participants’ empirical choices, with log odds adjusted to account for the empirical probability of each type of choice in the same way as adjustments for chance performance.

Beyond changes in how sampled versus unsampled segments are chosen, another form of reduced exploration that may be adaptive in large environments is spatial generalization (Wu et al., 2018). To assess the extent of spatial generalization based on participants’ choices, multilevel linear regressions assessed the distance between segments chosen on consecutive trials (only on trials in which the participant switched segments), measured as number of segments traveled versus chance as a function of previous reward receipt, points shown vs. hidden, initial even vs. uneven sampling, and the interactions of these effects. Segment distance ranged from 1 if a neighboring segment was chosen to 2 (for 4 segment blocks) or 4 (for 8 segment blocks) if a segment across the circle from the previous choice was chosen. Chance performance was calculated from the average distance of all segments (4 segments: 2*1 + 2, divided by 3; 8 segments: 2*1 + 2*2 + 3, divided by 7).

Regression models were estimated in a Bayesian framework using the ‘brms’ package in R (Bürkner, 2017; Carpenter et al., 2017)(brms version 2.16.1; rstan version 2.21.1). Three Monte Carlo chains were run with 3000 samples each (500 of which were warmup samples), for a total of 7500 samples used for inference. Significance was defined as 97.5% of samples falling above or below 0; however, as any binary significance threshold is arbitrary (McElreath, 2020), results where 85-97.4% of samples fell above or below 0 are noted but qualified as weaker evidence for an effect.

Generative Computational Model

Categorizing choices by reward and sampling history gives a rough approximation of influences on choice. For a more accurate measurement of the influences of exploitation and directed and random exploration, we constructed a process-based computational model including these influences. The computational model used an ideal Bayesian learner to learn the value distribution of each segment and a choice rule incorporating choice stochasticity, exploration bonuses, and perseveration. The Bayesian learner was chosen as a parsimonious learning rule to focus on influences on choice behavior.

The ideal Bayesian learner represented the value of each segment as a beta distribution that was updated with the outcome of each trial. At the beginning of each block, the α and β parameters of each segments’ beta distribution were reset to 1, yielding an expectation of 0.5. After the outcome was revealed for a chosen segment, the α (if a reward was received) or β (if a reward was not received) parameter for that segment was increased by 1:

$${\alpha }_{\mathrm{t}+1}=\mathrm{W}+{\alpha }_{\mathrm{t}};{\beta }_{\mathrm{t}+1}=(1\text{−}\mathrm{W})+{\beta }_{\mathrm{t}};\mathrm{W}=1\text{if reward}∕0\text{if no reward}$$ (1)

The choice rule was based on a softmax function transforming the mean value of each segment into a probability of being chosen relative to other segments (equation 2). Free parameters affecting choice were inverse temperature (β), which controlled the level of choice stochasticity versus sensitivity to mean values (S_mean), an exploration bonus (ω), which changed the probability of a segment being chosen based on its uncertainty (S_var; positive values increased probability whereas negative values decreased probability), and perseveration (τ), which increased the probability of choosing the segment chosen on the last forced choice trial. For the exploration bonus, uncertainty was defined as the variance of the mean value of each option, reflecting the uncertainty about the true value of each option. This variance was calculated from the beta distribution of each segment’s value (Bach & Dolan, 2012; E. Payzan-LeNestour & Bossaerts, 2011).

$$\mathrm{P}(\mathrm{S}{)}_{\mathrm{t}}=1∕(1+\text{exp}(\text{−}({\beta }^{\ast }{\mathrm{S}}_{\text{mean}}(\mathrm{S}{)}_{\mathrm{t}}+{\omega }^{\ast }{\mathrm{S}}_{\text{yar}}(\mathrm{S}{)}_{\mathrm{t}}+{\tau }^{\ast }{\mathrm{C}}_{\mathrm{t}\text{−}1})));{\mathrm{C}}_{\mathrm{t}\text{−}1}=1\text{if S chosen on trial}\text{t-1}\text{and}\text{−}1\text{otherwise}$$ (2)

Generative Model Fitting

Models were fit using the ‘rstan’ package in R, which uses a Hamiltonian Monte Carlo sampler for Bayesian estimation (rstan version 2.21.1; (Carpenter et al., 2017). For each model, three chains were run with 3000 samples per chain (1000 of which were used for warmup), for 6000 total samples used for inference. Hamiltonian Monte Carlo diagnostics did not indicate a lack of convergence. Data were estimated hierarchically, with parameter values estimated for each participant and for the distribution over the sample.

All free parameters (β, ω, and τ) were estimated using a non-centered parameterization with a mean, standard deviation, and participant-specific variation. Priors for mean parameter values were normally distributed, with means of 0 and standard deviations of 5 (β and ω) or 1 (τ). Priors for standard deviation parameter values used Student’s t distributions with 10 (β), 5 (ω), or 3 (τ) degrees of freedom, means of 0, and standard deviations of 3 (β and ω) or 2 (τ). All participant-specific variation parameter values used priors of a normal distribution with mean of 0 and standard deviation of 1. Values of prior distributions were based on prior predictive checks simulating behavior on the task.

To assess the effects of environment size and memory demands, a regression estimated changes in the mean of each parameter value with greater number of segments (8 vs. 4) and with points hidden (hidden versus shown). Multiple univariate regressions were run simultaneously with model estimation as recommended by (Brown et al., 2020). Therefore, the reference parameter values were fit to behavior from the blocks with four segments and points shown (minimal cognitive load condition), with additional dummy-coded estimated effects of 8 segments, points hidden, and the interaction of these effects on each parameter. These estimated effects were all given priors that were normally distributed with means of 0 and standard deviations of 1. Effects of environment size and memory demands were assessed based on the posterior distribution of each condition and their interaction. Similar to the regression analyses above, effects were deemed significant if 97.5% of the posterior was above or below 0, with effects with 85-97.4% of the posterior above or below 0 interpreted as providing more limited evidence for an effect. Identical analyses were run on simulated behavior, with the exception of eliminating the effects of memory demands. Additionally, to test possible changes in behavior once people learned the overall structure of the task, changes in each parameter in the minimal cognitive load condition were tested with the linear effect of block number and by comparing parameter values in the first versus second half of the task.

Parameter Recovery

To check whether generative model parameters could be independently estimated and related to changes in performance with changes in cognitive demands, parameters were simulated and recovered. This approach assessed the proportion of times that the median of the parameter recovered from simulated data fell within the 95% credible interval for the distribution of the empirically estimated parameter used to simulate the data. Specifically, we simulated behavior for 95 participants (the empirical sample size) using the median parameter values estimated for each condition from the empirical data. We then refit these simulated data with the same computational models to determine whether the recovered parameter values (during the minimal cognitive load condition and with changes in cognitive demands) match those that were originally estimated. This simulation was carried out 100 times and the median recovered parameter values for each simulation were plotted against the posterior distribution of the parameter values fit to empirical data. Successful recovery was further quantified as the proportion of recovered posterior median parameter values falling within the 95% credible interval for the posterior distribution of the parameter values fit to empirical data.

Simulations

To assess whether changes in exploration with increased environment size represented value-maximizing behavior, task behavior was simulated for different environment size. Simulated behavioral performance was measured by the proportion of free choice trials resulting in reward, averaged over 100 simulated participants. For the primary simulations, as a parameter reflecting noise in participants’ value estimates, β was fixed at the median empirical reference condition value of the human sample, 7.9. Ranges of parameter values for ω (−10 to 10) and τ (−1 to 1) parameters were based on ranges of values estimated from participants’ behavior. In follow-up simulations with a smaller environment size and when allowing inverse temperature to vary, β was allowed to vary from 0 to 10. Additionally, behavior was simulated for a smaller environment size of 2 segments. In this condition, initial uneven sampling meant that one segment was sampled twice and the other not at all; probabilities of reward for each segment were set to 0.4 and 0.6.

Results

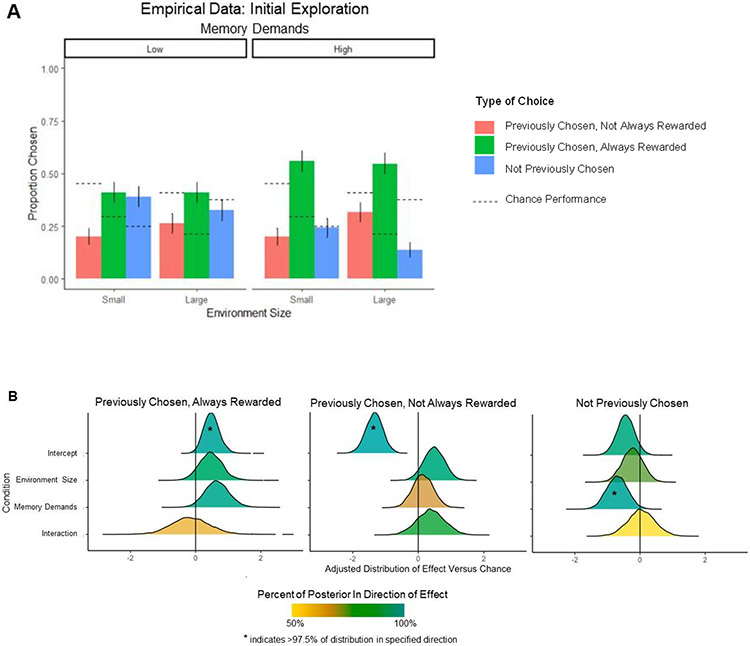
In all conditions, participants made a mix of exploitative and exploratory choices (Figure 2A). The proportion of choices attributable to different choice policies (previously sampled, always rewarded, reflecting primarily exploitative choices; previously sampled, not always rewarded, reflecting possible random exploration; and previously unsampled, reflecting directed exploration) differed by both memory demands and environment size. Notably, none of the condition effects were in the direction of chance performance (chance performance illustrated by dotted lines in Figure 2A). To confirm that behavior in the minimal cognitive load condition was adaptive and differed from chance and to quantify differences with increased cognitive demands, a multilevel Bayesian logistic regression was run. In this regression, log odds were adjusted for proportion of choices under chance performance. Distributions of coefficients are displayed in Figure 2B. Relative to chance performance, participants in the minimal cognitive load condition were more likely to choose options that were previously sampled and always rewarded (median log odds = 0.481; 98.6% of samples from the posterior distribution of log odds greater than 0) and less likely to choose options previously sampled and not always rewarded (median log odds = −1.34; 100% less than 0), with somewhat reduced tendency to choose the previously unsampled options as well (median log odds = −0.439; 94.8% less than 0). With greater memory demands, participants chose the previously unsampled options less (median log odds = −0.700; 98.4% less than 0) and the previously sampled, always rewarded options somewhat more (median log odds = 0.649; 96.6% greater than 0), with little change in frequency of choosing previously sampled, not always rewarded options (median log odds = 0.140; 67.3% greater than 0). Further, in a larger environment, participants chose the previously sampled, always rewarded (median log odds = 0.464; 90.8% greater than 0) and previously sampled, not always rewarded (median log odds = 0.484; 93.6% greater than 0) options somewhat more, with no change in choosing previously unsampled options (median log odds = −0.228; 76.4% less than 0). Taken together, both forms of cognitive load manipulation increased exploitation, as shown by choosing previously sampled, always rewarded options more, but had dissociable effects on directed exploration of unsampled options (decreased with greater memory demands) and random exploration of previously sampled, not always rewarded options (increased with larger environment size). Regarding spatial generalization, participants chose marginally closer segments than chance in larger, but not smaller environments. For 8 segment blocks, the average distance traveled between choices was 2.04 segments (91.3% of samples less than the chance distance of 2.29) and for 4 segments the average distance was 1.37 (31.5% of samples less than chance distance). In both environment sizes, spatial generalization did not significantly differ by memory demands, initial sampling, or reward receipt on the previous trial.

Figure 2.

Initial free choices compared to chance performance. A: Types of choices on the first free trial in each block versus chance performance, blocks with uneven sampling only. Choices likely due to exploitation (green) occurred when participants chose a segment that had been consistently rewarded during forced choice sampling. Choices resembling directed exploration (blue) occurred when participants chose a segment that was unchosen during forced choice sampling, and choices resembling random exploration (salmon) occurred when participants chose a segment that had been chosen but not always rewarded during forced choice sampling. Chance performance is indicated by dotted lines for each type of choice. B: Statistical comparison of the likelihood of each first free choice type, with log odds (x axis) adjusted for chance performance. Y axis shows differences from chance in the minimal cognitive load condition (intercept) and with change in each type of cognitive demand and their combination. Posterior distributions from Bayesian hierarchical regressions are shown, with shading and asterisks indicating the percentage of samples from the posterior greater than or less than 0.

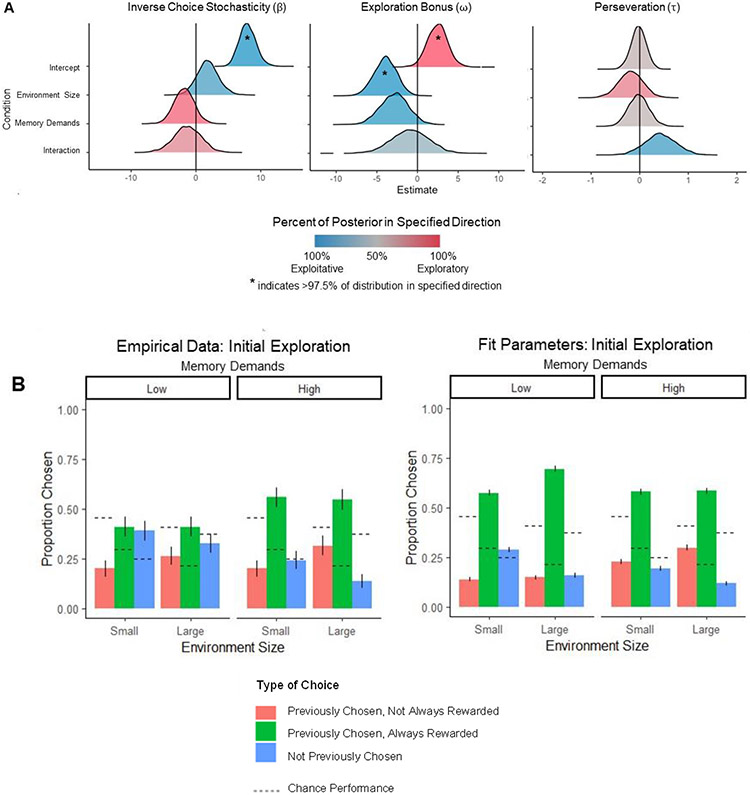
These behavioral results broadly support the notion that directed exploration decreases under memory demands and, possibly, in larger environments (a point we examine in-depth in normative simulations below). To more precisely measure how participants’ choice policies shifted under cognitive demands, a learning model was fit to participants’ first free choices on each block. Choice models (based on an ideal Bayesian learner; Figure 3A) included parameters representing inverse choice stochasticity (β), exploration bonus (ω), and perseveration (τ). Model checks showed that parameters from the model could measure changes in choice policies accurately: reference (minimal cognitive load) condition parameters and their shifts with cognitive demands (memory demands and environment size) were uncorrelated (Supplementary Figure 2A) and were well recovered from simulated behavior (Supplementary Figure 2B). Specifically, for parameter recovery, the percentage of median recovered parameter values that fell within the 95% credible interval of posterior distribution fit to empirical behavior ranged from 90-100%, with a median of 98%. Initial choices simulated from median fit parameters per condition also recapitulated patterns seen in participants’ empirical choices (Figure 3B), indicating that the model captured participants’ choice behavior well.

Figure 3.

Model parameters fit to initial free choices. A. Distributions of model parameters fit to empirical data. X axis indicates model parameters under the minimal cognitive load condition (intercept) and effects of changes in each type of cognitive demand. Y axis indicates parameter values, with shading and asterisks indicating the percentage of samples from the posterior supporting exploitative or exploratory behavior. Positive inverse choice stochasticity, negative exploration bonus, and positive perseveration parameter values indicate more exploitative vs. exploratory behavior. B. Distribution of initial free choices on each block for empirical data (left; identical to Figure 2A) versus simulated performance from median fitted parameters (right).

Compared to chance, parameters of the model under the minimal cognitive load condition showed less choice stochasticity (reflecting value-sensitive choices, β: median=7.94, 100% greater than 1 [chance]), greater exploration bonus (ω: median=2.48, 97.7% greater than 0), and negligible change in perseveration (τ: median=−0.02, 55.5% less than 0). This basic result confirms that participants made value-sensitive choices and favored options with higher uncertainty (greater variance), and did not rely on simpler, choice history-driven exploration as would be measured by changes in perseveration. Participants’ choice strategies did not meaningfully change across blocks (relationship between block number and parameter: beta median = 0.425, 80.9% greater than 0; tau median = −0.083, 83.1% less than 0; omega median = 0.012, 50.5% greater than 0; results were similar when comparing parameters estimated from trials in the first versus second half of the task instead of assuming a linear change in parameters across blocks), ruling out participants’ initial unfamiliarity with the task as an explanation for their high exploration rate. Under greater memory demands, participants became moderately less sensitive to values and decreased the exploration bonus, with little effect on perseveration, indicating that choices became slightly noisier and less uncertainty-seeking (median β change=−1.81, 88.4% less than 0; median ω change=−2.80, 95.5% less than 0; median τ change=−0.02, 54.6% less than 0). With larger environment size, participants showed a reduced exploration bonus and a slightly decreased choice stochasticity parameter (median ω change=−3.92, 99.8% less than 0; median β change=1.79, 86.9% greater than 0) and little change in perseveration (median τ change=−0.18, 76.7% less than 0), suggesting their choices were less uncertainty-seeking and more value-driven. The interaction of memory demands and environment size was modest, with participants becoming slightly more perseverative (median β change=−1.31, 73.0% less than 0; median ω change=−0.88, 64.7% less than 0; median τ change=0.42, 90.5% greater than 0). Therefore, both conditions independently reduced the uncertainty seeking seen in the minimal cognitive load condition, with greater memory demands leading to increased noise and larger environment size causing increased value sensitivity.

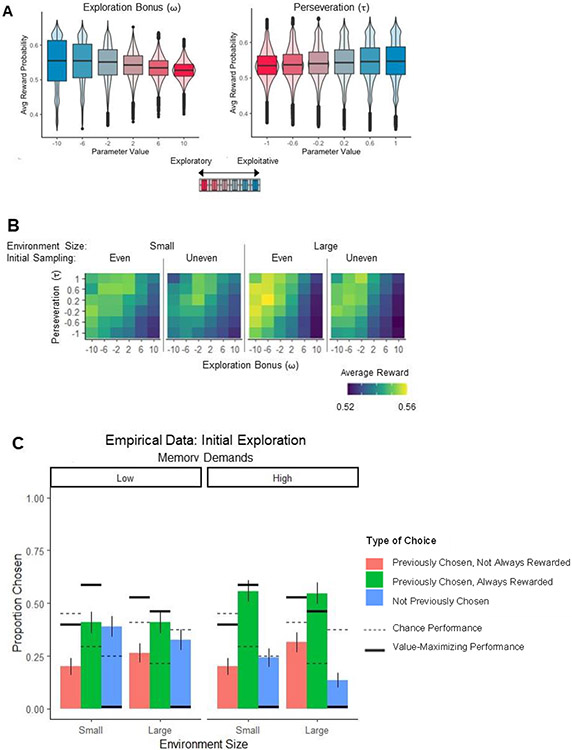
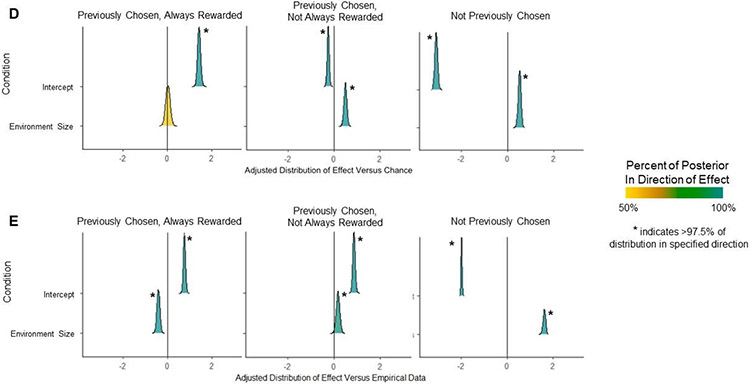
Decreased exploration may be adaptive as environment size increases relative to the choice horizon and exploring all options becomes infeasible. To test this idea, behavior was simulated at different levels of exploration bonus and perseveration. Parameter values were then related to average probability of reward for chosen options for all free trials in a block. For both exploration bonus and perseveration, parameter values representing more exploitative behavior (higher, more negative values of ω and higher, more positive values of τ) resulted in choices with a greater average probability of reward (effect of parameter value on average reward probability of chosen option, ω: t = −24.29, p < .001; τ: t = 14.12, p < .001; Figures 4A and 4B). This effect was present regardless of initial sampling type (even vs. uneven) and number of segments. Interestingly, parameter values resulting in greater average probability of reward also had more variance in performance across participants. This pattern suggests that more exploitative agents perform better on average even though they can become stuck in local maxima (good but not great segments), since the performance overall is improved more than the occasionally poor performance is harmful. Simulated initial free choices from the combination of parameters leading to the highest average reward probability (β=7.9, ω=−10, τ=1) are shown with thick solid lines in Figure 4C. A Bayesian multilevel logistic regression (Figure 4D) compared value-maximizing simulated initial choices to chance to relate value-maximizing simulated behavior to regression-based analyses of empirical behavior. This analysis showed that simulated value-maximizing choices, relative to random choices, were much less likely to be previously unsampled options (median log odds = −3.09, 100% below 0) or previously sampled, not always rewarded options (median log odds = 0.26, 100% below 0) and more likely to be previously sampled, always rewarded options (median log odds = 1.42; 100% greater than 0). Next, these simulated value-maximizing choices were compared to the frequency of choosing each option in participants’ empirical data (Figure 4E). When compared to empirical choice frequencies, simulated value-maximizing choices were more likely to be either previously sampled, always rewarded (median log odds = 0.75, 100% greater than 0) or previously sampled, not always rewarded options (median log odds = 0.85, 100% greater than 0), and less likely to be previously unsampled options (median log odds = −2.00, 100% less than 0). Therefore, although participants chose previously unsampled options less than chance (as shown above), they still chose these options more than a value-maximizing agent.

Figure 4.

Value-maximizing simulated behavior. A. Reward probability of behavior simulated at each parameter value, averaged within each simulated participant. Violin plots and boxplots indicate variability in average reward probability across simulated participants. Shading indicates exploitative vs. exploratory parameter values. X axis on each plot indicates the simulated parameter value and Y axis indicates the average reward probability per simulated participant. B. Simulated performance (average reward across participants) for all combinations of exploration bonus (X axis) and perseveration (Y axis) parameter values. Each panel indicates performance by the environment size and type of initial sampling. C. Distribution of initial free choices on each block for empirical data with simulated performance from parameters from model with value-maximizing performance (solid thick lines) and chance performance (dotted lines). D. Statistical comparison of the likelihood of each first free choice type of behavior from simulated value-maximizing model, with log odds (x axis) adjusted for chance performance. Y axis shows differences from chance during the minimal cognitive load condition (intercept) and with change in each type of cognitive demand and their combination. Posterior distributions from Bayesian hierarchical regressions are shown, with shading and asterisks indicating the percentage of samples from the posterior greater than or less than 0. E. Statistical comparison of the likelihood of each first free choice type of behavior from simulated value-maximizing model, with log odds (x axis) adjusted for comparison to empirical performance. Y axis shows differences from empirical performance during the minimal cognitive load condition (intercept) and with change in each type of cognitive demand and their combination. Posterior distributions from Bayesian hierarchical regressions are shown, with shading and asterisks indicating the percentage of samples from the posterior greater than or less than 0.

Overall, these results suggest that the shift from chance to value-maximizing behavior involves increased exploitation and decreased directed exploration. Relative to participants’ actual choices, value-maximizing choices were more likely to be known options, regardless of whether they had been consistently rewarded, and less likely to be unsampled options. Therefore, participants explored novel, uncertain options more than was needed to maximize value. The reduction in both directed and random exploration suggests that humans deliberately explore more than is needed in this task; in contrast, if only random exploration was reduced in simulated compared to empirical data, this pattern would suggest that behavior may be more exploratory due to noise only.

This uniformly high cost of directed exploration could be due to two factors: the large environment size in the task and the degree of random exploration shown by participants. To understand if directed exploration improves performance in smaller environments or with higher random exploration, ω, τ, and β parameters were allowed to vary simultaneously for environments with 2 segments as well as 4 and 8. With inverse temperature fixed at a relatively high value (10), a gradient emerged as the number of segments decreased (Supplementary Figure 1A). Specifically, in the smallest environment (2 segments), a combination of greater directed exploration and increased perseveration led to the best performance. Conversely, with a relatively low inverse temperature (3), more exploitative behavior led to better performance, particularly in 4 and 8 segment conditions (Supplementary Figure 1B). This finding suggests that under certain conditions – small environment size and less random exploration, and when accompanied with perseveration – greater directed exploration can be beneficial, but is not helpful with greater environment size and with relatively low random exploration.

Changes in participants’ behavior with increasing cognitive demands could reflect cognitive failures or a shift towards value-maximizing behavior given the cognitive constraints in the task. To determine what drove behavior changes, changes in value-maximizing behavior with greater environment size were simulated. With greater environment size relative to the reference condition, simulated value-maximizing choices were more likely to be both previously sampled, not always rewarded (median log odds = 0.485, 100% greater than 0) and previously unsampled options (median log odds = 0.51, 100% greater than 0), with little change in previously sampled, always rewarded options (median log odds = 0.01; 55.6% greater than 0; Figure 4D). Memory demands reflect cognitive constraints and do not affect value-maximizing behavior and so were not simulated. Compared to the frequency of choosing each option in participants’ empirical data (Figure 4E), increases in environment size caused simulated value-maximizing behavior to increase the frequency of previously sampled, not always rewarded (median log odds = 0.16, 97.8% greater than 0) and previously unsampled options (median log odds = 1.61, 100% greater than 0) and did not increase the frequency of choosing previously sampled, always rewarded options with greater environment size as much as in empirical choices (median log odds = −0.42, 100% less than 0). As the frequency of choosing unsampled options with simulated value-maximizing choices was still very low with greater environment size, the increases relative to chance and empirical choices represent a significant but very small increase from negligible directed exploration with minimal cognitive load, while the increase in previously sampled, not always rewarded options relative to both chance and empirical data suggests that increased environment size causes value-maximizing behavior to encompass less-frequently rewarded options.

Discussion

We investigated how human exploration responds to cognitive challenges often encountered in the real world – large environment sizes and memory demands. We found that in the baseline low-demand condition participants made exploitative choices but also engaged in both random and directed exploration (Wilson et al., 2014). Under cognitive demands, people adjusted their behavior to maintain exploitation. These adjustments did not reflect a shift towards chance characteristic of cognitive failures; instead, they were consistent with anticipating and proactively maintaining exploitation with increases in cognitive load.

Under cognitive load, participants became even more exploitative and shifted their exploratory choices. The adjustment depended on the type of cognitive demand: in a larger environment participants chose previously sampled but infrequently rewarded choices, reflecting greater random exploration, while under memory demands, participants reduced directed exploration by choosing fewer options that were unsampled to that point. Fitting participants’ behavior with a generative model allowing choice stochasticity (representing ability to maintain accurate values), an exploration bonus, and perseveration to affect value-based choices showed that, in a smaller environment and with low memory demands, behavior was driven by exploiting intact value representations and an exploration bonus, with little effect of perseveration. Increased environment size decreased the exploration bonus and further decreased choice stochasticity, while increased memory demands decreased the exploration bonus and increased choice stochasticity.

These changes with increased cognitive load could be due to two effects: first, participants may change their behavior in response to increasingly noisy value representations once their cognitive resources are overwhelmed. Conversely, they may proactively adjust behavior when they anticipate that the demands of the environment will exceed their capacity to maintain and update the reinforcement history for each of the many options. Our data suggest that participants engage in the latter strategy by increasing exploitative choices and decreasing directed exploration. If participants instead became overwhelmed by noisy value representations, behavior would have shifted closer to chance, resulting in decreased exploitative choices and increased random exploration, or have showed a shift from a more complex form of exploration driven by exploration bonuses to a simpler form driven by reduced perseveration. This proactive adjustment was mirrored in the parameters governing the computational model that best captured participants’ choices: chance performance would have resulted from large increases in choice stochasticity, but instead the clearest shift was a decrease in the exploration bonus. This shift in behavior was present even under memory demands, which should not shift optimal behavior away from exploration (unlike increased environment size). Taken together, these results suggest that when entering a cognitively demanding environment, participants proactively shift choices to maintain exploitative, value-driven behavior at the expense of exploration. Therefore, the uncertainty aversion participants show with increased cognitive demands suggests that participants engage in meta-reasoning about their cognitive capacity. This shift is similar to a resource-rational strategy (Lieder & Griffiths, 2020; Shenhav et al., 2017); to further test resource rationality, future work should explicitly derive a resource-rational model to measure against behavior in this paradigm.

Choices simulated from a computational model, composed of an ideal Bayesian learner with a choice rule incorporating choice stochasticity, exploration bonuses, and perseveration, revealed that this shift away from exploration was in line with value-maximizing behavior. The best performance resulted from parameter values that severely curtailed exploration. With an even smaller environment size than used here (two segments only), some exploratory behavior was adaptive, but in the environment sizes in the present task (four and eight segments), returns increased monotonically with reductions in exploration. These results indicate that, given the reward structure of the task, exploration can be helpful in small but detrimental in large environments. Therefore, the decreased exploration seen in larger environments adaptively reflects both a value-maximizing strategy and, by reducing the cognitive load associated with maintaining the uncertainty of each choice’s outcome, a further adjustment to cognitive demands. Interestingly, although participants decreased exploration under cognitive demands, their exploration in the minimal cognitive load condition, as measured by the exploration bonus parameter, was higher than needed to maximize value. Positive exploration bonuses, indicated by good fits of models incorporating upper confidence bound (UCB) choice rules, have been found in a variety of tasks (Frank et al., 2009; Gershman, 2018; Schulz, Bhui, et al., 2019); however, participants show ambiguity aversion with greater environment size (É. Payzan-LeNestour & Bossaerts, 2012) or when learning from continuous action spaces is approximated by many discrete values (Hallquist & Dombrovski, 2019). The presence of directed exploration under lower cognitive load in this task and others indicates that while people may explore more than indicated by value-maximizing behavior, when faced with increasing cognitive demands, they are able to decrease exploration and adjust in the direction of maximizing value. Why, despite the ability to adjust exploration with increasing cognitive load, do people explore more than a value-maximizing agent overall? We have found that exploration can be beneficial when rewards in an environment are very sparse (Hallquist & Dombrovski, 2019), or when the reward functions are monotonic across the task, and the agent can therefore assume a coarse segmentation across the environment (Frank et al., 2009). When navigating a rewarding environment, greater exploratory behavior may reflect an optimistic prior on the utility of exploring that enables rewarding options to be discovered even in discontinuous or non-stationary environments. This belief in the utility of exploration may persist even in stable environments and with reward functions that are monotonic across choices that do not encourage exploration, as participants’ exploratory behavior did not decrease as they gained more experience with the task. Further work should seek to understand the causes of this above-optimal exploration.

The two cognitive load manipulations– increased environment size and increased memory demands – had partially dissociable effects on exploratory and exploitative behavior. In a larger environment, participants became more value-sensitive at the expense of both random and uncertainty-directed exploration. They also showed some evidence for spatial generalization of values. This pattern of behavior suggests that as environment size increases beyond participants’ capacity to track value and uncertainty simultaneously, they forgo tracking uncertainty and engage in spatial generalization to maintain value estimates. Meanwhile, memory demands degrade representations of both value and uncertainty. Although participants’ behavior did not shift toward chance performance overall, the increased choice stochasticity with increased memory demands reflected noisier value representations. Therefore, participants may be able to adjust their exploration/exploitation tradeoff in a more resource-rational way with increasing environment size, whereas with increased memory demands people may show a mix of proactive adjustment (decreased uncertainty seeking) and reactive inability to maintain value estimates leading to noisier choices. Increased working memory demands with greater memory demands and not increased environment size may explain this difference in behavioral adjustments between conditions.

Neurally, reductions in exploration are accompanied by increased value-related signals in ventromedial prefrontal cortex and decreases in associative neocortical areas, including frontopolar cortex, insula, dorsal anterior cingulate cortex, and inferior parietal cortex (Blanchard & Gershman, 2018; Daw et al., 2006; McGuire et al., 2014); future work should investigate the role of these neural systems in cognitive load-based adjustments in directed exploration and exploitation. Additionally, noradrenergic activity (balanced by acetylcholine signals (Yu & Dayan, 2005) or tonic versus phasic activity (Aston-Jones & Cohen, 2005)) may regulate exploring novel options versus optimizing performance on the task at hand. Our finding that increased cognitive load decreases uncertainty seeking may indicate that anticipated increases in cognitive demands shift noradrenergic activity away from an exploratory state to maximize focus on value-driven behavior.

The present findings add to the existing literature on exploration, complex environments, and cognitive load. In large environments where outcomes are correlated, participants use the underlying structure of the environment to guide exploration (Schulz, Bhui, et al., 2019; Wu et al., 2018). In the present task, where outcomes of different options were unrelated, we found minimal spatial generalization with greater environment size. Previous work attempting to study effects of cognitive load on exploration has used simultaneous working memory tasks alongside learning tasks (Cogliati Dezza et al., 2019; Otto et al., 2014). These concurrent working memory tasks decreased exploration or, alternatively, reduced model-based choices with no effect on exploration. In the current task, we found decreased exploratory behavior across cognitive demand types (environment size, memory demands). Completing two concurrent tasks may not represent real-world cognitive demands well, since performance on the working memory task is not needed (and is, in fact, detrimental) to perform well on the learning task. By incorporating cognitive demands into the task, we show that the reduction in directed exploration is adaptive rather than reflecting increased noise in value representations. Another type of cognitive demand, adding time pressure to a learning task (Wu et al., 2022) simultaneously reduces exploitation and directed exploration while increasing perseveration. Time pressure may make maintaining values more difficult, leading to increased perseveration and decreased exploitation, whereas increased environment size led to greater exploitation and no cognitive demands affected perseveration.

In summary, we found that increased cognitive demands, in the form of a larger environment and increased memory demands, shifted participants’ exploratory and exploitative strategies. These behavioral adjustments were consistent with a shift towards value-maximizing, rather than chance, behavior, and indicated that participants responded to cognitive demands in a proactive, resource-rational-like way.