Mitigating Bias in Radiology Machine Learning: 2. Model Development

Abstract

There are increasing concerns about the bias and fairness of artificial intelligence (AI) models as they are put into clinical practice. Among the steps for implementing machine learning tools into clinical workflow, model development is an important stage where different types of biases can occur. This report focuses on four aspects of model development where such bias may arise: data augmentation, model and loss function, optimizers, and transfer learning. This report emphasizes appropriate considerations and practices that can mitigate biases in radiology AI studies.

Keywords: Model, Bias, Machine Learning, Deep Learning, Radiology

© RSNA, 2022

Summary

This report reviews potential biases during machine learning model development and proposes possible mitigation strategies for radiology artificial intelligence studies.

Key Points

• ■ Machine learning studies are susceptible to bias in their model development phase.

• ■ Different types of bias include selection bias, social bias, and fairness bias.

• ■ Possible approaches to mitigate different types of bias during model development include data augmentation, model and loss function, optimizers, and transfer learning.

Introduction

Machine learning (ML)–based systems can be affected by systematic errors across various stages of their development and implementation, such as data collection, model development, model evaluation, and deployment (1). Given the increasing challenges in health care delivery due to algorithmic bias, the U.S. Food and Drug Administration released an action plan in 2021 emphasizing the importance of identifying and mitigating bias in clinical artificial intelligence (AI) and ML-based systems (2). Model development is a part of the ML process that uses mathematical algorithms to process, predict, and classify medical data. Recognizing how model development impacts bias offers new mitigation techniques beyond data handling. Sources of systematic error can be classified as error = bias2 1 variance 1 noise (3). Among the three components, bias is defined as the difference between the model’s output and the correct solution, variance is defined as the oscillations from the expected estimator value that any particular sampling of the data is likely to cause, and noise is the random error that is irreducible.

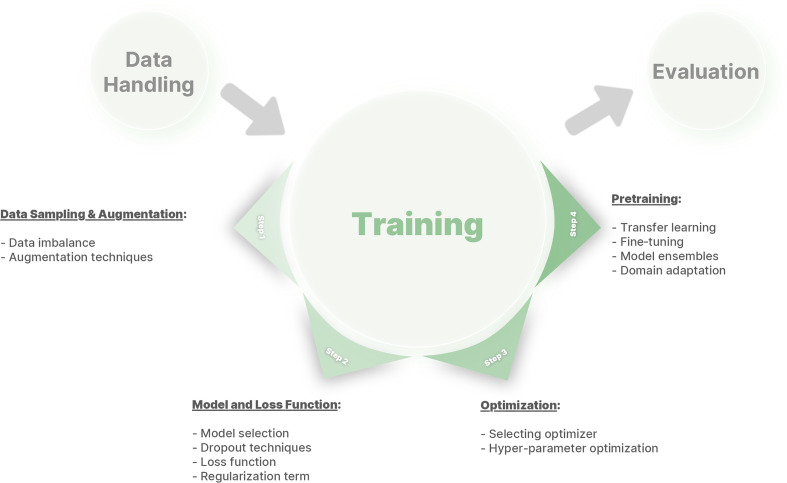
In the following sections, we first explain a more fundamental overview of bias in the ML model, as bias may have different meanings depending on the context. Then, we present technical practices that can be employed to mitigate bias through different aspects of model development, such as selection of the network and loss function, data augmentation, optimizers, and transfer learning (Fig 1). By discussing challenges in model training and the appropriate solutions, this report recommends appropriate practices and considerations to mitigate algorithm bias in radiology AI studies.

Figure 1:

A framework of different phases in deep learning model development to mitigate bias.

Bias, Variance, and Fairness in ML Algorithms

Overview of Sources of Bias in ML

Error is the difference between the model’s predictions and the ground truth labels for a dataset. Bias refers to showing preference for one group over another. When applied in AI, the presence of bias typically means that the predictions consistently err in one direction. Model predictions can also be biased for subpopulations of patients, leading to health care unfairness. Recognizing that bias can come in these two forms, we will first cover the “offset” form of bias in these first three sections and then the “fairness” form of bias.

The more subtle form of ML bias, which is of concern for clinical practice, is when a certain input feature is over- or underweighted because the data are not sufficiently broad. In other words, a model with a bias will have many wrong predictions on the “true” population that favor a certain direction (eg, overcalling or undercalling disease). To calculate bias and variance, one can retrain their model several times and measure these variables. Suppose that we have a training set consisting of n pairs of inputs _xi and ground truth values _yi for i = 1,…,n. Ground truth y is the measured or labeled data of the true quantity Y with a function Y = y + ε, where ε is the coherent noise with zero mean and variance σ². The noise ε is randomly distributed and irreducible due to measurement precision. However, researchers can introduce label or measurement bias if they fail to recognize a pattern in how they mislabel examples. For instance, if melanomas are harder to detect in people with dark skin, there will be a bias in the training data. If the researchers do not recognize this increased difficulty, the bias will result in a poorer and unfair model (4).

Suppose an ML model is trying to approximate the true value Y by its prediction f(x). The mean square error (MSE) can be formulated as:

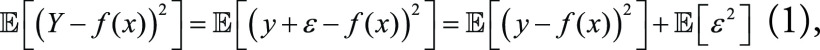because 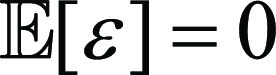, and ε is independent from the predicting deviation y – f(x). The first term on the right-hand side of Equation (1) can be rewritten as:

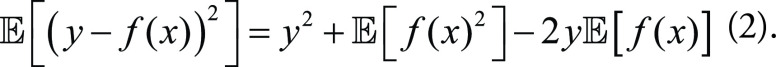Meanwhile, model bias and variance can be expressed respectively as:

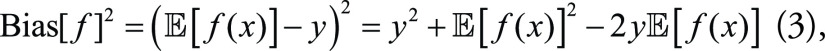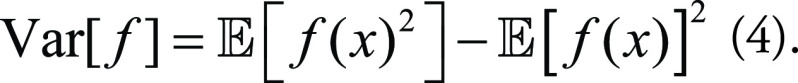Combining Equations (2), (3), and (4), the MSE of the ML model from Equation (1) can be decomposed as:

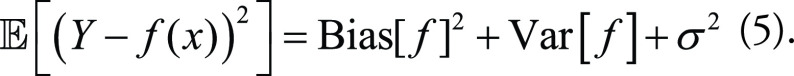A good model is one with low bias (being valid) and low variance (being reliable). Unfortunately, there is empirical evidence that bias and variance have an inverse relationship in ML models, which is called the bias-variance trade-off (5). This means that lowering the model’s bias leads to increasing its variance and vice versa.

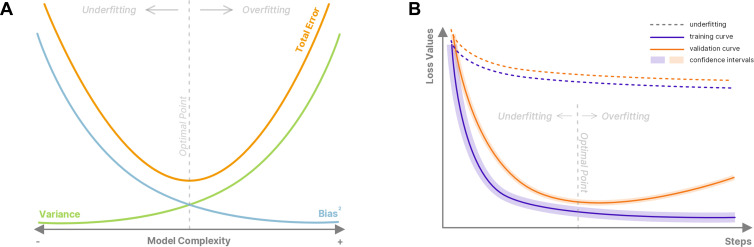
For example, an untrained model intended to detect a fracture in wrist radiographs will randomly classify images without considering representative features of a fracture. This untrained model has a high bias. During training, this model tries to reduce its loss value and learn representations that can help it solve the task at hand, hence minimizing its bias. However, as the training progresses, the model may start to learn, or memorize, the random noise in the training data and rely on those unique noise patterns rather than representative features to detect fractures. When training a new model, the noise potentially used for predictions could be very different from that of the previous model, resulting in different predictions for real-world examples. At this stage, the model has high variance. To detect wrist bone fractures on unseen radiographs, the model should learn visual representations of how a fracture appears on radiographs and ignore irrelevant information specific to each patient (eg, osteoarthritis in patients). Figure 2A shows the bias-variance trade-off when training a deep learning (DL) model.

Figure 2:

(A) Bias-variance trade-off and the total error in terms of model complexity. Underfitting can occur due to use of an overly simplistic model that does not have the capacity to capture the complex relationships in the data, resulting in relatively high bias and low variance (indicated by the leftward arrow). On the other hand, a very complex model can lead to overfitting with relatively low bias and high variance (indicated by the rightward arrow). (B) Observation of underfitting and overfitting in typical training curves with representative underfitting learning curves shown as the dashed lines and overfitting as the solid lines. Of note, underfitting may occur due to premature stopping, and overfitting may arise due to late stopping.

Identification of Underfitting and Overfitting

This trade-off between bias and variance causes DL models to underfit or overfit the training data. Underfitting is the stage in which the model is not or only partially learning helpful information to solve the problem. It usually happens during the initial stage of training in which the training metrics of the model are relatively high. At this stage, the model has high bias and low variance. On the other hand, overfitting happens later in training, when the model learns the noise in the data and uses it to solve the problem and minimize its loss value. At this stage, the model has low bias on the training set but will pay attention to different signals, causing high variance in predictions.

Differentiating underfitting and overfitting is a critical task. Underfitting can be detected when the results on the training set have high bias and are not improving, which means that the model cannot learn from the signal (either useful or noise) present in the data (Fig 2B). This occurs mainly because the model is not suitable for the task; either the model capacity is too low, or there is a misconfiguration in the pipeline. To recognize an overfitted model, performance on the validation and training sets should be evaluated. Overfitting is present if the performance on training data improves while the performance on the validation data deteriorates. Approaches to avoid overfitting will be briefly discussed in the following section (6).

Overview of Reducing Bias and Overfitting

One option to reduce overfitting is to use early stopping, which monitors the model’s performance on the validation set and stops the training when the validation metric decreases or its validation loss increases over a few steps (an increase in a single epoch can be due to noise). Early stopping is a common and simple-to-deploy approach, but it might cause bias in the model. When training is stopped based on the validation set, information is leaked from the validation set to the training set. This highlights the value of cross-validation and nested cross-validation in evaluating ML models. Nested cross-validation can minimize data leakage but might not always be feasible. Thus, many studies fall back to cross-validation to decrease leakage, though this is not optimal (7). To train a model with cross-validation, one fold is put aside as the validation set, and the other folds are used for training. This process is performed “n” times (for n-fold cross-validation), with each fold treated as a validation set once. If there is a relatively high variance in performance, cross-validation offers an opportunity to perform model ensembling among folds, which can efficiently reduce overfitting.

A separate (third) test set can also be used to evaluate model performance on unseen data after model training is completed. This set should not be used for fine-tuning or early stopping to prevent data leakage. Testing on a separate dataset, ideally one that is external, potentially ensures a more robust trained model than using an internal dataset. However, a review reported that only 6% of AI studies for medical imaging diagnosis included an external dataset for testing (8).

Another approach to reducing overfitting is to make the model capacity smaller (ie, fewer layers). By having fewer parameters, there is less capacity to learn spurious features, forcing the network to learn only those features that are important. This has the side benefit of being less computationally intense; however, a model that is too simple may not perform as well.

Overfitting can also be addressed by having more examples, which does not necessarily entail collecting additional training data. A more intense augmentation strategy, such as adding noise (9) or synthetic data with the same distribution, such as from a generative adversarial network (GAN), can be used for model training (10).

Curse of dimensionality describes the explosive nature of increasing data dimensions and its resulting decrease in the density of data. Adding features without also increasing data size causes the feature space dimensionality to expand and become sparser and sparser, which may result in overfitting. Dimensionality reduction algorithms, such as principal component analysis, can make the data befitting. For clinical imaging tasks, features are imaging pixels. For instance, a 512 × 512 MR image has 262 144 features. Thus, one way to reduce the number of features is through image compression.

Regularization is another way to minimize overfitting. Regularization techniques include adding dropout layers and L1 and L2 regularizations. Weight decay, which can be thought of as a form of L2 regularization, prevents network weights from growing too large (11). One last approach to minimize overfitting is ensemble modeling. It is assumed that if a model focuses on random noise, then different models should learn different noise patterns; therefore, using the consensus of these models will provide superior results to each of them individually (12). Further details for these techniques will be discussed in the following sections.

Bias and Fairness in ML Algorithms

Up to this point, we have largely described bias from a mathematical perspective that describes it as an offset in output accuracy, but bias can also refer to the fairness of the developed ML algorithms (13). Algorithmic fairness, an emerging field of ML, aims to mitigate the differences in modeling outcomes between social groups.

One might argue that the best AI tool is one that is “blind” to patient demographics: An ideal model should not depend on any protected features of a patient, such as sex, race, or geodiversity. However, such an approach may have undesirable consequences due to the value of demographic information in making correct diagnoses. Age, sex, and race are all known to have an impact on the probabilities of disease development, and they may also impact disease appearance (13). Therefore, blinding an AI system to such information could lead to poorer patient care, just as it would for a human diagnostician. Given the high dimensionality of clinical AI tasks with image-based or large-sized datasets, algorithms can still leverage proxy features to reconstruct the protected features even if sensitive attributes are excluded (14).

Instead, we must recognize and respect the differences within a population. As noted in the first report of this series, it is critical to sample the entire population as much as is feasible. Algorithmic bias can be addressed by adding regularization constraints to penalize the relative “cost” between groups, or through adversarial learning (15), in which the adversarial model is trained to minimize its ability to identify the protected attributes from hidden features. In practice, the proper methods to assess and report clinical variations while ensuring some form of parity for different protected groups are still challenging and may need to be addressed on a task-by-task basis to create a bias-free system.

Technical Practice in Mitigating Algorithmic Bias

Data Sampling and Augmentation

ML algorithms have optimal performance when the number of samples of different classes is approximately equal in the training set. However, we mentioned earlier that real-world applications in medicine often have imbalanced datasets. A screening test aimed at detecting cancer within a normal population may result in many more negative diagnoses than positive. Training on such an imbalanced dataset may cause the model to learn to predict all cases as the dominant class and achieve very high accuracy; however, false-negative cases will introduce substantial bias into the model. Moreover, depending on the specific application (eg, for the purpose of screening or diagnosis), researchers may intentionally tune the model toward false-positive cases (unnecessary further evaluation) or false-negative cases (missed diagnoses). Imbalanced datasets can be rebalanced by undersampling or oversampling to enhance the model’s focus on rare cases. In DL frameworks, this can be achieved by defining sampler algorithms such as WeightedRandomSampler in PyTorch (https://pytorch.org) (16), in which the sampling weight for each class is calculated by taking the reciprocal of the class counts. A more convenient approach to enable sampling from each class with equal probability is possible by using third-party packages called StratifiedSampler. Oversampling and undersampling will prevent the model from seeing substantially more instances of one class over others during training, therefore reducing the risk of overfitting (17).

Data augmentation can mitigate both issues of data scarcity and data imbalance. For the purpose of oversampling, data augmentation seems to be a more advanced technique than simply replicating data, as fake data can be generated by transforming the existing data or can be synthesized using DL approaches (eg, GANs) (18). By creating a more versatile dataset, data augmentation helps the model understand the data, rather than memorize it.

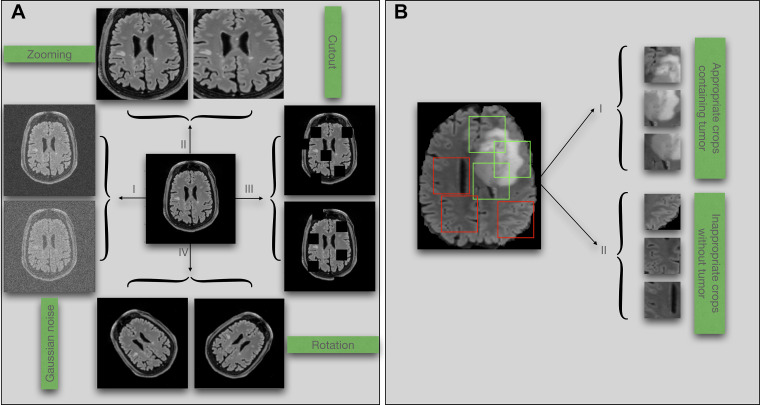
Geometric and resolution transformations, also known as data warping, are often applied to augment existing data and include techniques like zooming, flipping, rotation, cropping, scaling, affine transformations, and cutout (19) (Fig 3A). These popular transformations are usually embedded in software libraries for ML such as PyTorch (16), Keras and TensorFlow (20), and Medical Open Network for AI (ie, MONAI) (21). When training on a specific dataset, there may be considerations for using different data augmentation techniques. For example, flipping chest radiographs or CT scans may generate imaging data with the heart located on the right (but incorrect) side. A model trained on flipped imaging data may mispredict dextrocardia, a rare anatomic variation (22). On the contrary, flipping is often considered a safe augmentation technique when training models that do not have an apparent side, such as the brain. However, the subtle differences between the two sides may cause problems during the completion of certain tasks, and any differences in race, sex, or age across patients will likely result in bias.

Figure 3:

(A) Examples of data augmentation techniques: (I) adding noise, (II) zooming, (III) cutout, and (IV) rotation. (B) Illustration of potential bias associated with random cropping in classification tasks. Green boxes denote accurate crops, and red boxes denote inaccurate crops.

Knowledge of medicine is critical to selecting augmentations that will not degrade diagnostic performance. For instance, when detecting COVID-19 on chest radiographs, zoom or crop augmentations may remove the pathologic area, which is typically found in the periphery of the lungs (23). Random cropping when training models for a tumor classification task will randomly break each section into multiple patches. The model is then trained on a collection of patches generated from different sections. Because the tumor usually occupies only a small region of the positive sections, there may be many patches that come from a positive section and are hence labeled as tumor positive while they actually contain no tumor (Fig 3B). In contrast, random cropping is often helpful to train tumor segmentation models because model labels are patch-specific segmentation masks. Adding more patches and labels can help the model learn more efficiently. Indeed, the type of ML task, clinical domain expertise, and even the dataset characteristics all affect the choices when using data augmentation techniques.

Model and Loss Function

To cure the bias-variance dilemma in supervised learning, we start by choosing the model capacity. We can build our model efficiently from existing feature-extractor network backbones such as VGG (24), ResNet (25), EfficientNet (26) and DenseNet (27). Depending on the size and complexity of the dataset, overfitting may occur. Accordingly, we can reduce model capacity by using models with fewer parameters or simpler architecture (eg, ResNet18 or Vgg16 over ResNet50), which have a smaller chance to adapt and learn the noise of the data. Furthermore, models with smaller capacities can both train and run faster, an important consideration for outcome inference. Self-configuring methods are proposed in the literature to automatically set the model capacity on the basis of dataset properties (28).

Another approach is to use dropout techniques, which are able to retain the complexity of the model. During the training process, nodes are randomly dropped (meaning their output is set to 0) (29), helping the model avoid dependency on any specific neuron. The dropout intensity is controlled by an additional hyperparameter p valued between 0 and 1, which describes the probability of removing a node. Because the number of active nodes after applying a p-valued dropout on an n-sized model is equal to n(1−p), a higher value of p removes more nodes. Dropout prevents coadaptation of nodes and therefore can make the trained model more general and robust to data distribution shift. However, too much dropout may cause excess reduction of model capacity, introducing underfitting. Because dropout is active during training but not inference, the outputs need to be scaled by a factor of 1/(1−p) during training to keep consistent outputs for inference, which is usually a built-in feature of dropout layers in DL frameworks. In practice, we can either assign different p values for each layer or use stochastic dropout, in which the dropout ratio itself is randomly determined by a probability distribution, making it tunable among different iterations (30).

The loss function is by convention an objective function that we wish to minimize during model training. While metrics such as accuracy are functions used to judge model performance, they are not always suitable to be used as loss functions, as ML algorithms require the loss function to be smooth and convex. Loss functions may result in algorithmic bias if not properly designed to meet data or task requirements. For example, while MSE is a well-known loss function for regression, it usually generates blurry images for image-generative tasks such as super-resolution and in-painting. Therefore, training models for such tasks is usually done with other loss functions, including perceptual loss (31,32). Medical imaging segmentation is another example in which region-based loss functions, such as Dice loss, or boundary-based loss functions, such as Hausdorff distance loss, can be selected for certain segmentation tasks or used at different training stages (33). Compound loss functions can be designed by summing different types of loss functions, such as Dice + cross entropy and Dice + focal Tversky loss, and each can be given unique weights reflecting their importance. While Dice and focal loss are helpful for imbalanced datasets that we often face in medicine, Tversky loss is found to detect small-region signals (eg, liver tumors) more accurately (34). By better capturing minority signals or subgroups of data, those loss functions can be used to potentially improve the fairness form of bias.

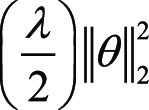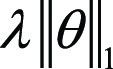Adding a regularization term to the loss function can also help address overfitting. L1 and L2 are the most popular regularizations ( and , respectively), where λ is the regularization rate, an additional hyperparameter introduced to penalize the amplitude of weights θ in the model. As overfitting models usually have large weights, λ tunes the penalty of the regularization to the complexity of the model. However, if λ is too high, the model may become too simple, increasing the risk of underfitting. Thus, the goal is to strike the right balance between low model complexity and prevention of bias. By simple derivations, we can observe that L2 regularization is equivalent to weight decay, which is a hyperparameter often included in the training optimizer (discussed later). Domain knowledge is crucial in selecting the correct form and amount of regularization into the loss function. For instance, in tasks of MRI reconstruction, compressed sensing uses a regularization term subject to prior sparsity constraints to penalize the optimization problem (35,36). In summary, different types of regularization techniques, including dropout, can improve the generalizability and accuracy of ML algorithms when applied to unseen data.

Optimizer and Hyperparameters

During the training process of ML models, the loss function is minimized by a specific algorithm called an optimizer. With each iteration, the optimizer is searching for optimal values of the model’s learnable parameters, such as weights and biases (which are clearly not either of the two forms of bias, offset or fairness, discussed in the paper). Because various optimizers are available in ML frameworks, there is often no need to build a new optimizer from scratch. However, it is useful to learn about different types of optimizers available to developers and know how they work to minimize the loss function, avoiding possible training bias. Stochastic gradient descent (a variant of gradient descent) is a very basic but heavily used optimizer for ML. The parameter updates depend on the loss function J(θ) from iteration t to t + 1 as

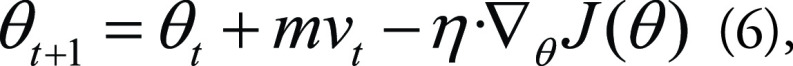in which θ are the learnable parameters, η is the learning rate, m is the momentum, and v_t is the velocity. Choosing a proper learning rate can be difficult because the optimizer will converge slowly if the learning rate is too small and may oscillate or diverge if the learning rate is too large. Momentum provides inertia to the moving curve of θ in terms of t in the parametric space, thus increasing the stability of the optimizer. On the other hand, adaptive moment estimation (Adam) develops an adaptive learning rate for each parameter and also combines advantages of the RMS-Prop and Adadelta methods (37), making Adam one of the most popular optimizers to train ML models efficiently. As using a fixed learning rate is cumbersome in practice, a learning rate scheduler can be used to update the learning rate value dynamically during training. For example, for the cyclic learning rate, the criterion is to use learning rate annealing (a higher learning rate) at the early stage of the cycle to quickly approach the regions of minima and then set a decaying learning rate to gradually find the minimum (38).

ML algorithms have several configurable options to better fit to the data at hand, which are called hyperparameters, including but not limited to learning rate, the amount of dropout, data augmentation, number of layers, and number of nodes in each layer. Finding the best combination of these options is called hyperparameter optimization (39), which can be the most time-consuming part of the training, as the number of combinations to explore can grow exponentially. A model without optimized hyperparameters is essentially underfitting the data and is considered more biased than ideal.

There are several techniques for finding the best set of hyperparameters. A simple approach is performing a grid search, which defines a list of hyperparameters and then tries all their combinations with respect to each other to select the best combination on the basis of the model’s performance on a holdout set. Although this approach seems to be very applicable, it can be computationally expensive. For instance, suppose there are four hyperparameters with only three different choices for each. A grid search to tune these hyperparameters requires 81 (or, 3⁴) training experiments, which is not always feasible.

Another approach is to randomly select different combinations of hyperparameters for training and to compare the combined effects of those hyperparameter choices on the model’s performance. For hyperparameters that have no effect on the training performance, tuning is therefore redundant. Randomly searching for hyperparameters has shown to be more effective than the grid search to identify such redundant hyperparameters (40).

The last approach for finding the best set of hyperparameters is to use Bayesian optimization. This method uses uncertainty estimates for finding the best set of hyperparameters. This approach will fit a surrogate model to the results of an already available hyperparameter search and then use an uncertainty estimate to choose what other points need to be explored. After several iterations, the overall trend will be evident, and the best hyperparameters will be selected (41). Overall, researchers should use at least one of these approaches to ensure a suitable combination of hyperparameters.

Transfer Learning and Ensemble Modeling

Clinical ML models may underperform because of lack of sufficient labeled clinical data to train them. Manual labeling of medical images is time-consuming, costly, and prone to error. Researchers may attempt to battle data scarcity by integrating data from different cohorts; however, representation bias can arise when there is a distribution shift between the adopted populations. Additionally, disease patterns may evolve (eg, diagnosis of COVID-19 prior to 2019), leading to a mismatch between the data initially collected for training and the target data observed during the inference. Such situations can predispose ML models to prediction bias and reinforce that bias over time.

Using transfer learning, ML models with knowledge of a previous task can be borrowed and fine-tuned on the current task, mitigating overfitting on small datasets. Depending on the size of the dataset, certain hidden layers of a previously trained model can remain frozen (the associated weights are not changed) during the fine-tuning, while the weights of a few fully connected top layers are allowed to be changed.

ImageNet is the most well-known dataset used for transfer learning to improve the performance of computer vision tasks such as segmentation, detection, and classification (42). Although routinely used, this dataset contains photographic images, which differ substantially from medical images. Therefore, using weights from models trained on ImageNet may not always be the ideal transfer learning solution for ML models trained on medical data. On the contrary, transfer learning from in-domain datasets such as ChestX-ray8 (43) and CheXpert (44) has been shown to improve performance compared with ImageNet pretrained models (45). Additionally, more and more clinical AI tasks entail three-dimensional models, while ImageNet and other public datasets can only assist in pretraining two-dimensional models, favoring the use of in-domain transfer learning. For example, a three-dimensional U-Net tumor-segmentation model pretrained on the preoperative Multimodal Brain Tumor Segmentation, or BraTS, dataset can be used for fine-tuning on postoperative brain MRI (46).

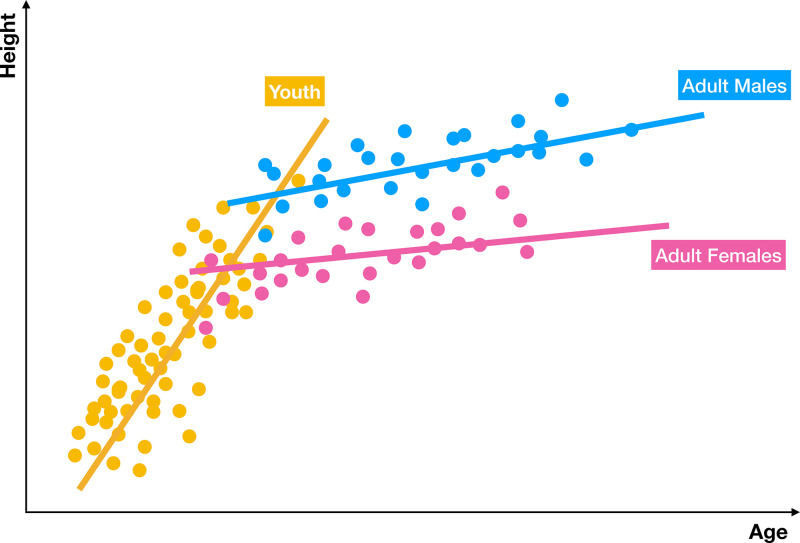
Ensemble models can mitigate prediction bias by training several models and producing a hybrid prediction based on them, as the ensemble is usually more generalized than each base model. There are many different approaches for training base models. For instance, in bootstrap aggregating, also known as bagging, base models are trained in parallel on randomly sampled datasets; whereas, in the boosting approach, base models are trained sequentially to focus on the errors from previous models. Predictions of base models can be combined by different strategies such as unweighted or weighted model averaging and majority voting. While the former method takes the average of the probability outcomes of the base learners, the latter one counts the votes of the base learners to determine the final decision, making it less biased toward a particular base learner outlier (Fig 4) (47). As a result, majority voting seems to be an appropriate strategy when the base models are homogeneous in terms of performance (48). For cases with heterogeneous base models, weighted model averaging is preferred (eg, in a study on COVID-19 detection) (49).

Figure 4:

Graphic display of ensemble modeling. An ensemble model takes predictions from several specialized models and then combines them into a more accurate, hybrid prediction. Often, the prediction of the ensemble is better than the prediction of a single monolithic model. In this example, three separate models are trained for predicting height in terms of age for three different populations—youth, men, and women. The combined model produces better results than each model individually.

Semisupervised learning is another approach to alleviate algorithmic bias originating from insufficient data annotations (50). Pretext or auxiliary tasks are designed to help models learn visual features of the data in an unsupervised manner (51). Examples of such tasks are enforced predictions, data generation, or contrastive learning, by which vanishing gradient and overfitting issues may be mitigated. For example, a classifier that aims to detect COVID-19 on chest radiographs may benefit from a previously trained model that has learned to do unsupervised in-painting on chest radiographs, either by regarding that in-painting model as a source for transfer learning or by using it for adding an auxiliary loss (52) to the main training. Recent works on medical images using semi- or self-supervised learning achieve good results on small datasets, with applications such as tumor segmentation, chest radiograph classification, and body decomposition (53).

Conclusion

This report discussed how ML studies are susceptible to bias in their model development phase. We reviewed possible approaches and recent advances to mitigate different types of bias during the development of ML models (eg, selection bias, social bias, and fairness bias). Specifically, we explored four basic aspects of clinical AI model development: data augmentation, model and loss function, optimizers, and transfer learning. Given the wide spectrum of biases in ML, it was not possible to cover all suboptimal practices in model development. This report may provide guidance for developers to identify erroneous practices and biases in their clinical ML systems.