Abstract
Dye aggregates and their excitonic properties are of interest for their applications to organic photovoltaics, non-linear optics, and quantum information systems. DNA scaffolding has been shown to be effective at promoting the aggregation of dyes in a controllable manner. Specifically, isolated DNA Holliday junctions have been used to achieve strongly coupled cyanine dye dimers. However, the structural properties of the dimers and the DNA, as well as the role of Holliday junction isomerization are not fully understood. To study the dynamics of cyanine dimers in DNA, molecular dynamics simulations were carried out for adjacent and transverse dimers attached to Holliday junctions in two different isomers. It was found that dyes attached to adjacent strands in the junction exhibit stronger dye-DNA interactions and larger inter-dye separations compared to transversely attached dimers, as well as end-to-end arrangements. Transverse dimers exhibit lower inter-dye separations and more stacked configurations. Furthermore, differences in Holliday junction isomer are analyzed and compared to dye orientations. For transverse dyes exhibiting the smaller inter-dye separations, excitonic couplings were calculated and shown to be in agreement with experiment. Our results suggested that dye attachment locations on DNA Holliday junctions affect dye-DNA interactions, dye dynamics, and resultant dye orientations which can guide the design of DNA-templated cyanine dimers with desired properties.
Molecular dynamics simulations reveal dye attachment and DNA Holliday junction isomer effects on dye dimer orientations and excitonic couplings. These simulations can guide synthesis and experiments of dye-DNA structures for excitonic applications.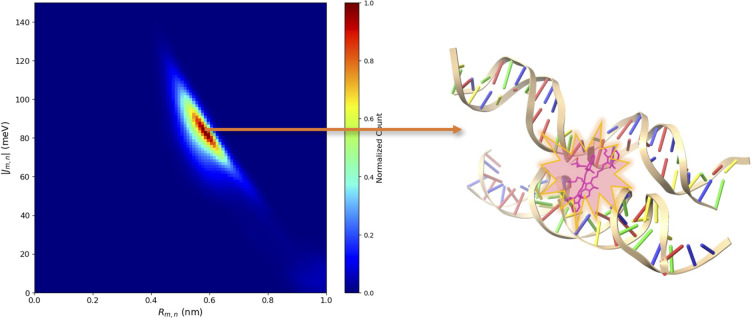
1. Introduction
Aggregates of dye molecules play a critical role in numerous applications, including organic photovoltaics,1,2 non-linear optics,3 and quantum information systems.4–8 Central to such applications are delocalized excitations, or excitons, which reside on the dye aggregates to facilitate highly efficient energy transfer. This energy transfer allows for the movement of excitons across excitonic wires,5,9 from antennae to reaction centers,10,11 or to charge separation interfaces between electron donor and acceptor materials.12,13 The functionality of molecular materials employing excitons relies on the properties of the dyes and their aggregates. In the case of quantum information and computing systems, the precise control and knowledge of dye orientations are necessary.
Dyes are known to aggregate in natural systems via proteins,1,10 as well as artificial systems due to the spontaneous aggregation of dyes in concentrated solutions.14,15 However, the spontaneous aggregation of free dyes in solution does not allow for the control of the number of dyes in an aggregate or dye orientations, which are vital to the excitonic properties of aggregates. The dynamics of excitons on dye aggregates depend on both the electronic properties of individual dyes and the orientations of the dyes in the aggregate.16–19 Following the work of Scheibe and Jelley,14,15,20 considerable effort has been made to study the properties of dye aggregates. Building upon Davydov's initial work on molecular excitons,21,22 Kasha described how the orientation of the transition dipole moments of dyes in an aggregate can explain the aggregate's optical properties.16,17 In the case of a simple dimer, two energy states are allowed. The stacked configuration of two dyes (called an H-dimer aggregate), yields a blue-shifted absorption spectrum where excitations to the higher energy state, compared to the monomers, are allowed and excitations to the lower energy state are forbidden. An end-to-end orientation (J-dimer aggregate) yields a red-shifted spectrum, where the higher energy transition is forbidden and the lower energy transition is allowed. A third orientation in which the transition dipoles are at 90° to one another (termed oblique) leads to a splitting of the absorption peak (both higher and lower energy transitions are allowed), known as Davydov splitting.22 In Kasha's model,16,17 the strength of the coupling of the transition dipole moments is quantified by the exciton exchange energy (Jm,n). This term, also known as excitonic hopping parameter,23 enables exciton delocalization and depends upon the strength of the constituent monomer transition dipole moment magnitudes, relative transition dipole moment orientations, and inter-dye distances.16–19 Thus, the control of dye orientations is crucial to construct excitonic devices.
An emerging method to control the number and orientation of dyes in an aggregate is through the use of DNA scaffolding. The Watson–Crick DNA base pairing allows for the programmable assembly of DNA into complex structures.24–26 It has been shown that DNA scaffolds can be effectively used to form dye aggregates by either non-covalent27–30 or covalent binding of the dyes to the DNA via tethers.31–39 In the case of non-covalent binding, there is a lack of precise control of the dye orientations. Conversely, by attaching dyes to DNA using linkers, a variety of aggregates can be formed. For example, dyes attached to DNA duplexes have been shown to exhibit red-shifted absorption spectra33,38,40,41 and blue-shifted absorption spectra.35,39,42 Recently, multiple dyes (i.e., trimers and tetramers) attached sequentially on a single strand of a duplex have been shown to form H-aggregates.42 More complex DNA scaffolds have also been used, such as DNA origami structures4,8,43–45 and isolated Holliday junctions.23,41,46–49 The latter consists of two bridged DNA duplexes to form a four-arm junction. Cannon et al.46 and Huff et al.41 have shown that two dyes attached to DNA Holliday junctions via dual tethers can from both J- and H-aggregates, depending on if the dyes are attached to adjacent or transverse strands, respectively. Furthermore, Huff et al. have demonstrated that Cy5 dimers attached adjacently to DNA Holliday junctions exhibit heterogeneity in their configurations, indicating that the precise control of the orientations can be improved.41 Chowdhury et al. have recently shown that, compared to homodimers, heterodimers consisting of a Cy5 and a Cy5.5 dye can change the optical properties of the aggregate by affecting the dye orientations and couplings.47
Efforts have been made to study the electronic and structural properties of dyes and dye-DNA constructs using computational modeling. Density functional theory (DFT) and time-dependent (TD-) DFT have been employed to determine the effects of substituents on the ground and excited state properties of dye monomers.50–52 However, DFT and TD-DFT are limited to only a few hundred atoms, and so are not suited for the modeling of dyes attached to DNA scaffolds. Molecular dynamics (MD) simulations have been employed to study the orientations of dyes attached to DNA structures.33,44,45,53–56 MD simulations of dye dimers33,53 and trimers53 attached to DNA duplexes have been shown to yield dye orientations in agreement with experimental observations. MD simulations of dyes attached to larger DNA complexes, such as bundles and origami,44,45 have also been shown to yield dye orientations and dynamics in agreement with experiment. Furthermore, MD simulations of Holliday junctions have also been performed.44,57–59 Mathur et al. has showed that MD simulations of dyes attached to the Holliday junctions of large DNA bundles can yield dye orientations in agreement with experimental fluorescence data.44 Wheatley et al. found that isolated, four-arm Holliday junctions initialized in an open conformation stabilize in a stacked configuration at both high and low salt concentrations, indicating that MD is able to capture the conformational transitions of the Holliday junction.57 Simmons et al. successfully used MD simulations to explore ion binding sites in isolated Holliday junctions.58 Adendorff et al. utilized MD to study the structure and dynamics of four-arm isolated Holliday junctions to understand the impact of base sequences on the junction structure.59 However, the role of the DNA Holliday junction conformations and the interactions between the DNA and dyes that affect dye orientations and resultant excitonic properties are not fully understood.
In this work, MD simulations of Cy5 and Cy5.5 dyes attached to Holliday junctions were performed to understand dye orientations, dye interactions with DNA, and how they influence the homodimers and heterodimers, consisting of Cy5 and Cy5.5 dyes, in comparison with experimental measurements in support of previous studies.41,46,47 To obtain dye orientations from experimental measurements, an in-house program developed based on the theoretical model of Kühn, Renger, and May (KRM) was used. A full description of the model is given in ref. 23, 40 and 46, but in short, the model accounts for the dominant vibrational mode of each molecule in the aggregate non-perturbatively, producing theoretical absorbance and circular dichroism (CD) spectra of various dye configurations. The produced theoretical spectra are then compared to the experimental spectra until a best fit is found. An extended dipole approximation is used to determine Jm,n between the two dyes in the resultant orientation.19 In the past few years, our group has successfully used the KRM model to study the aggregates of dyes covalently bound to DNA scaffolds.23,38,40,42,46–49,60 Specifically, the four-arm isolated Holliday junction has been shown to be useful to produce strongly coupled dimers.23,41,46,47,49 MD is an alternative option to study the dye–dye and dye–DNA interactions to provide further insight into the systems of interest.
To study the intermolecular interactions of dyes attached to isolated DNA Holliday junctions, we first performed μs long simulations of Cy5 homodimers, Cy5.5 homodimers, and Cy5–Cy5.5 heterodimers attached to DNA Holliday junctions in either adjacent or transverse configurations. The MD trajectories were then used to compute the dye orientation factors (κm,n), dye center-to-center distances (Rm,n), Jm,n, and contact maps with the surrounding DNA. The dye orientation results were also compared to the results obtained from the modeling of experimental excited state measurements of dimers on DNA Holliday junctions.41,47
2. Methods
2.1. Molecular dynamics simulations
MD simulations were performed to determine the orientations of the dye dimers and interactions of the dyes with the DNA. The OL15 forcefield,58,61,62 which had been tested for base flipping in DNA and TNA duplexes,63,64 was used with non-bonded modifications for the DNA phosphate-ion interactions.65 Similar to previous studies,45,53 the general Amber forcefield (also known as GAFF) was used for dye bonded and van der Waals parameters66 that were generated using the ANTECHAMBER software.67 The dye atomic point charges were derived using the restrained electrostatic potential fit method68 to reproduce the electrostatic potential calculated at the HF/6-31G* theory level. The dye-DNA structures were solvated in TIP3P water and neutralized with Mg2+ (ref. 69 and 70) and Cl− (ref. 71) ions, with 15 mM MgCl2 excess salt concentration added to match experimental conditions.41,47 A truncated octahedron box was used, ensuring 1.2 nm separation between dye-DNA and box edges. Neighbor-searching was utilized with a cutoff of 1.2 nm and van der Waals interactions were limited to 1.2 nm with the forces smoothly switched to zero starting at 1.0 nm, like similar studies.72,73 Long range dispersion corrections were applied for energy and pressure. The particle-mesh Ewald method74,75 was utilized with a real-space coulomb cutoff of 1.2 nm. Bonds to hydrogen atoms were constrained via the LINCS algorithm76 and a timestep of 2 fs was used. All simulations were performed using the GROMACS 2020.3 software package.77
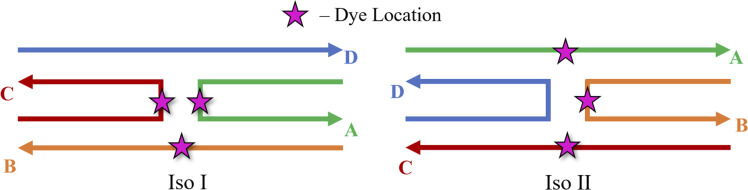
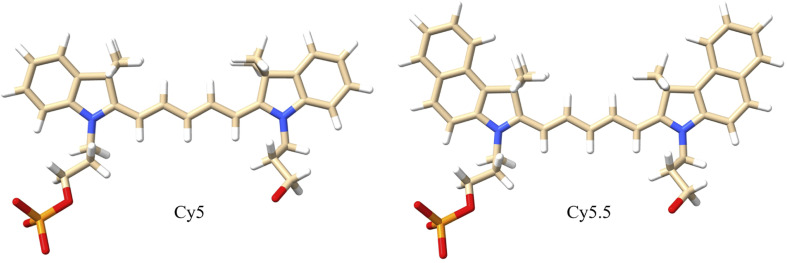
It is theorized that isolated Holliday junctions exist predominantly in stacked configurations in 15 mM MgCl2 solution,41 labeled as Iso I and Iso II in Fig. 1. Because of this, the Holliday junctions for the MD simulations were built in both the Iso I and Iso II configurations. Using the Nanoengineer-1 software,78 the DNA Holliday junctions were first constructed in both configurations and energy-minimized. Then, the dyes were added to construct the initial DNA–dye structures using the UCSF ChimeraX software.79 Following the work done by Huff et al.41 and Chowdhury et al.,47 two types of dimers were considered – adjacent and transverse. Adjacent dimers refer to dyes residing on adjacent DNA strands (i.e., strands A and B in Fig. 1), whereas transverse dimers refer to dyes residing on transverse DNA strands (strands A and C). Furthermore, homodimers and heterodimers consisting of Cy5 and Cy5.5 dyes were used. The dyes were placed at positions shown in Fig. 1, and attached to the DNA backbone via dual phosphoramidite linkers, as shown in Fig. 2. In total, twelve systems were simulated to encompass all combinations of dye types, isomers, and dimer types. DNA Holliday junction sequences and dye attachment schemes used in the present study are the same as the ones used by Huff et al.41 and Chowdhury et al.47
Fig. 1. Schematics of the Holliday junction isomers considered for MD simulations from Huff et al.41 and Chowdhury et al.47 The stars represent possible dye locations depending on the system – for transverse dimers, dyes are attached on the A and C strands and for adjacent dimers, dyes are attached to the A and B strands.
Fig. 2. Molecular structures of Cy5 and Cy5.5 dyes with dual phosphoramidite linkers that attach to the 5′ and 3′ ends of the DNA backbone. The dyes consist of pentamethine bridges flanked by two dimethyl indolenine rings. The Cy5.5 dye contains two extra aryl rings that extend the π-conjugation. White atoms are hydrogen, tan atoms are carbon, blue atoms are nitrogen, red atoms are oxygen, and orange atoms are phosphorus.
To prepare the dye–DNA systems for production MD simulations, the total energy of the systems was first minimized using the steepest descent method for 5000 steps. Following energy minimization, in order to equilibrate the water and ions, two 1 ns equilibration steps were performed with restraints of 1000 kJ mol−1 nm−2 and 500 kJ mol−1 nm−2 on the heavy dye-DNA atoms, respectively, keeping the number of atoms, volume, and temperature constant (i.e., the NVT ensemble). After that, a third equilibration step of 1 ns was performed without restraints. Production MD simulations were run for 1 μs, keeping the number of atoms, pressure, and temperature constant (i.e., the NPT ensemble), and it was ensured that the pressure and temperature were well converged prior to data collection. All simulations were run at 300 K and 1 atm. The velocity-rescale thermostat80 was used with a coupling time of 0.1 ps. The Parrinello–Rahman81 barostat was used with a coupling time of 1.0 ps. Coordinates were written every 10 ps, and the first 100 ns of the final production simulations was not used for data analysis. For each system, three 1 μs simulation trials were run with different initial velocities for enhanced numerical sampling.
2.2. Analysis of dye orientation and dye–DNA interaction
To quantify the orientations of the dye dimers, κm,n of the two dyes was calculated using the equation33
| κm,n = m· n − 3(R̂m,n· m)(R̂m,n· n) | 1 |
where i is the unit transition dipole moment vector pointing along the long axis of dye m or n and R̂m,n is the unit vector between the centers of the transition dipole moment vectors of dyes m and n. A value of |κm,n| between 0 and 1 indicates two dyes are predominantly stacked and a |κm,n| of greater than 1 means the dyes are predominantly end-to-end.
For comparison, with experimental studies of the excited state properties of dimers attached to DNA Holliday junctions, Jm,n values were calculated using the extended dipole approximation:19
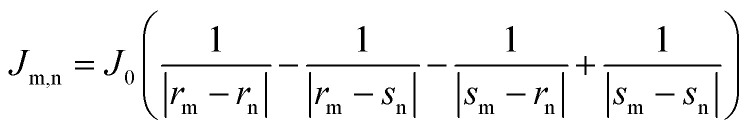 |
2 |
where ri and si correspond to the two ends of dye m or n along the long axis. The prefactor term J0 was calculated as19
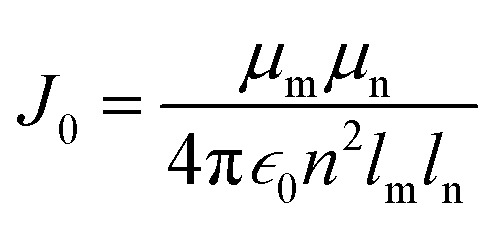 |
3 |
where μi is the transition dipole moment magnitude of dye m or n, ∈0 is vacuum permittivity constant, n is the refractive index of water, and li is the length of dye m or n such that li = |ri − si|. For the calculations of Jm,n, our previous TD-DFT results for μCy5 = 15.35 D and μCy5.5 = 15.57 D (ref. 56) were used.
The dye orientations, quantified using κm,n and Rm,n, were calculated every 100 ps for each MD simulation. The results for each MD trial were combined into one plot for comparison. To clarity, the adjacent and transverse Cy5 homodimers are denoted as ACy5BCy5 and ACy5CCy5, respectively. The Cy5.5 homodimers and Cy5–Cy5.5 heterodimers are denoted similarly. Dye orientations and resultant Jm,n from the MD simulations were compared to experimental data from Chowdhury et al.47 in which dye orientations and Jm,n were extracted from steady-state absorption and CD spectra using the KRM model.
Contact maps of the dyes and DNA bases were generated to quantify how the dyes would interact with the surrounding DNA environment. Each dye and the six center bases of each DNA strand were considered for contact calculations, resulting in 26 groups (or residues). For each DNA residue pair, the distance between the centers of mass of the two constituent residues was calculated. For residue pairs involving dyes, the whole dye center of mass and the ends of the dye (ri and si locations) were used for contact calculations to account for the anisotropic structure of the dye. Two residues were considered to be in contact if the shortest distance between their centers of mass (or ends if the residues were dyes) was within 1.2 nm (the same as the simulation short range interaction cut-off). Contacts were calculated every 500 ps for the three simulation trials.
3. Results
3.1. Adjacent dimers
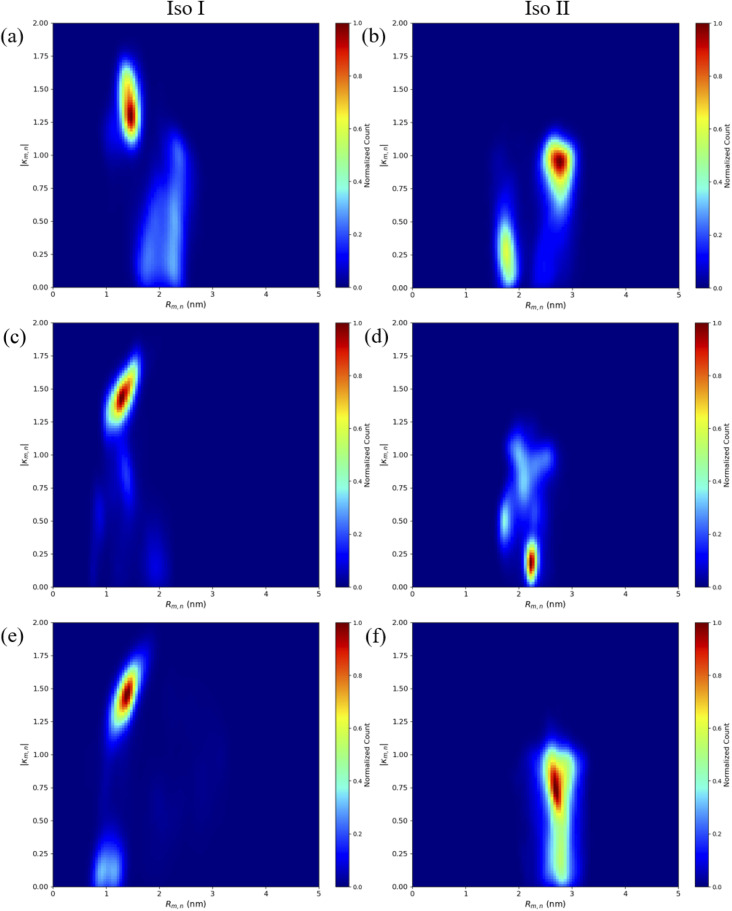
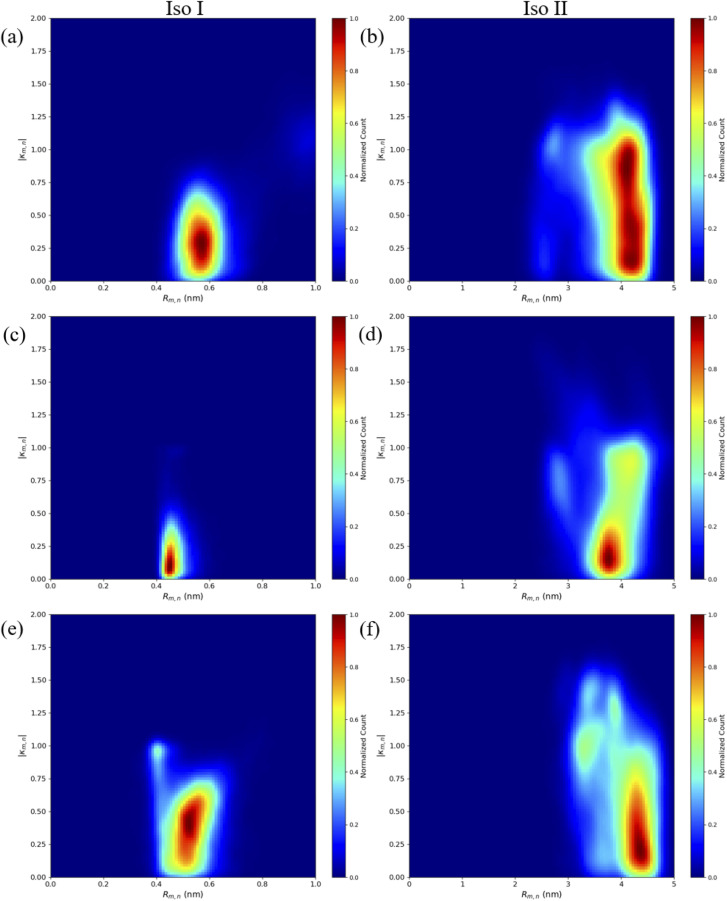
The MD results for the adjacent dimers in both Iso I and Iso II Holliday junction conformations are presented in Fig. 3 and 4. Fig. 3 shows heatmap plots of |κm,n|, calculated using eqn (1), versus Rm,n. The heatmaps represent 2-dimensional histograms consisting of “binned” data (e.g., |κm,n| and Rm,n), where the color scale represents the normalized count in each bin. Data from the three separate, 1 μs MD simulations (i.e., trial 1, trial 2, and trial 3) are combined in each heatmap. Plots of the adjacent dimer orientations as a function of time for the three 1 μs MD simulation trials are given in Fig. S2.† As shown in Fig. S2,† the calculated Rm,n and κm,n of the three MD simulation trials are comparable over the 900 ns trajectories, indicating that the sampled dye configurations are consistent with each other. One exception is the adjacent Cy5 homodimer – for both Iso I and Iso II, the trajectories shown in Fig. S2a and b† indicate that the dyes may be exploring different local minima. One reason for this, compared to the Cy5.5 homodimer and the Cy5/Cy5.5 heterodimer, may be due to the smaller size of the Cy5 dyes in the Cy5 homodimer. The smaller size of the Cy5 dyes may allow for additional configurations when interacting with the DNA. This may be addressed by performing more simulations, longer simulations, or different sampling techniques, which are outside the scope of this paper. Furthermore, Rm,n for all simulations converge to stable values after approximately 100 ns, indicating that the MD simulations have achieved stable dye distances. For additional comparison between the three trials, the average values of Rm,n and κm,n (as well as Jm,n for ACy5CCy5, ACy5.5CCy5.5, and ACy5CCy5.5 Iso I) are provided in Table S2.† Overall, the average values are largely consistent across the three trials for each systems.
Fig. 3. Heatmap plots of |κm,n| calculated using eqn (1)versus Rm,n for (a) ACy5BCy5 Iso I, (b) ACy5BCy5 Iso II, (c) ACy5.5BCy5.5 Iso I, (d) ACy5.5BCy5.5 Iso II, (e) ACy5BCy5.5 Iso I, and (f) ACy5BCy5.5 Iso II.
Fig. 4. Representative snapshots of ACy5BCy5 Iso I showing the dye orientations when the dyes are (a) in a closely spaced J-like dimer (κm,n ≈ 1.6) and (b) a separated, H-like arrangement (κm,n ≈ 0.2).
As can be seen in Fig. 3a and b, the ACy5BCy5 system adopts four dominant configurations. A |κm,n| between 0 and 1 indicates that the dyes are stacked and correspond to a H-like orientations while a |κm,n| greater than 1 indicates that the dyes are end-to-end and thus correspond to a J-like orientation. For Iso I Holliday junction configurations, there are two peaks in the heatmap plot (Fig. 3a). The less populated peak at around Rm,n = 2.2 nm and |κm,n| ≈ 0.3–0.75 corresponds to the dyes being in an H-like orientation (based on the value of |κm,n|) but not considered to be in a dimer due to the large inter-dye distance. Conversely, the dominant peak in Fig. 3a corresponds to a smaller Rm,n ≈ 1.4 nm and |κm,n| ≈ 1.25–1.7, which correlates to a slightly oblique J-like dimer. Examining Fig. 3b, it can be seen that the change in Holliday junction isomer results in different dye orientations and distances. The two main peaks correspond to H-like dye arrangements with some obliqueness at roughly Rm,n ≈ 1.8 nm and R ≈ 2.9 nm, respectively, indicating the dyes do not form closely spaced dimers. From Fig. 3c–f, it can be seen that the ACy5.5BCy5.5 and ACy5BCy5.5 dimers follow similar trends with the Iso I Holliday junction configurations having large peaks that correspond to J-like dimers at Rm,n and |κm,n| values comparable to that of the ACy5BCy5 Iso I dimers. Furthermore, the ACy5.5BCy5.5 and ACy5BCy5.5 dimers on the Iso II Holliday junctions adopt H-like stacking arrangements at around Rm,n ≈ 2.2 nm and Rm,n ≈ 2.7 nm, respectively, slightly larger than that of the ACy5BCy5 Iso II system. Snapshots of ACy5BCy5 are shown in Fig. 4 to highlight the two dye orientations (J-like and H-like) observed in the MD simulations. Additional snapshots corresponding to the heatmaps in Fig. 3 are shown in Fig. S5 and S6.† As can be seen in Fig. S5,† the Iso I configurations yield the end-to-end dye dimer (i.e., J-like).
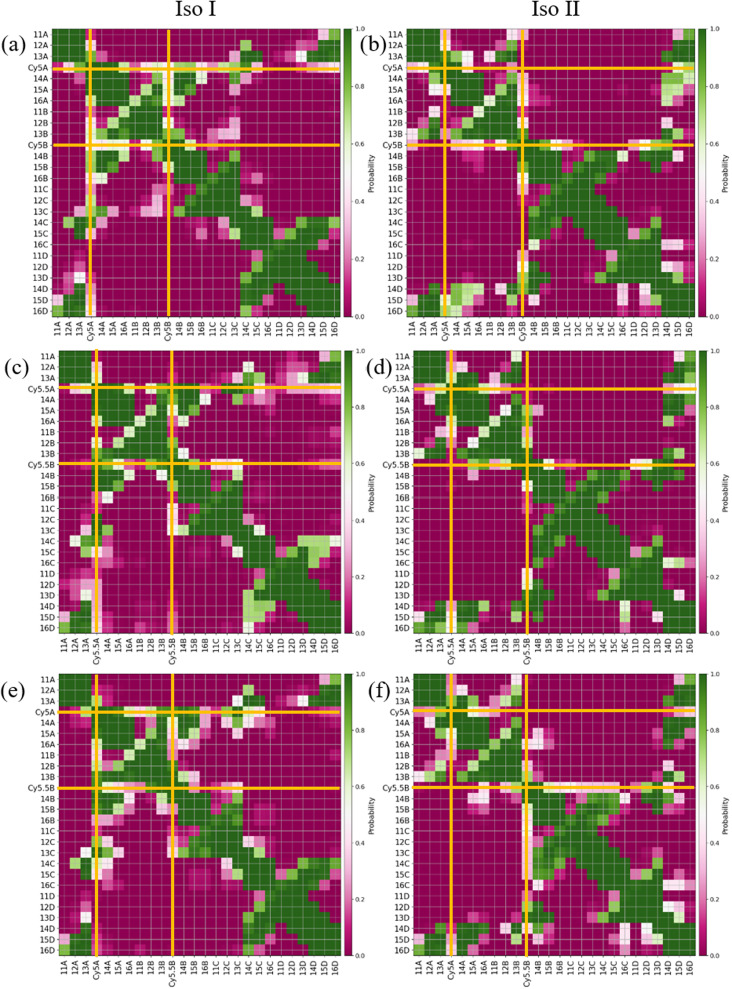
Contact maps between the dyes and DNA bases were calculated from all three simulation trials to elucidate how the dyes interact with the nearby DNA environment. Fig. 5 shows contact maps for the adjacent dimers in both Iso I (Fig. 5a, c and e) and Iso II (Fig. 5b, d and f) Holliday junction configurations. Contact maps were generated for simulation trials 1, 2, and 3, and the bases and/or dyes (collectively termed residues) are said to be in contact if their centers of mass (or ends if the residues are dyes) are within 1.2 nm (the short-range interaction cut-off set for the MD simulation). The diagonal of the contact maps correspond to residues in contact with themselves (i.e., a probability of 1). The axes on Fig. 5 show the residue names of either the DNA bases or dyes. For DNA bases, the residue name consists of the residue number and strand the base belongs to (A, B, C, or D). Each DNA strand consists of 26 bases, so base numbers 11–16 correspond to the bases near the center of the Holliday junction. The dye residue names consist of the dye type (Cy5 or Cy5.5) and the DNA strand the dye is attached to, in regard to Fig. 1. The bins in the contact maps, centered at the intersections of each residue, are color-coded to show the probability of those two residues to be within 1.2 nm of each other (i.e., in contact).
Fig. 5. Contact maps for (a) ACy5BCy5 Iso I, (b) ACy5BCy5 Iso II, (c) ACy5.5BCy5.5 Iso I, (d) ACy5.5BCy5.5 Iso II, (e) ACy5BCy5.5 Iso I, and (f) ACy5BCy5.5 Iso II. The x- and y-axes correspond to the dye or base residue names. Two residues are considered to be in contact if they are within 1.2 nm. Dye contacts with all other residues are indicated in the plots with bold orange lines.
Fig. 5a and b show the contact maps for ACy5BCy5 Iso I and Iso II, respectively. It can be seen that the two dyes are in contact with a probability of around 0.2, which coincides with the two peaks shown in Fig. 3a since the cut-off radius for the contact maps is 1.2 nm. For both Iso I and Iso II, there are peaks present corresponding to the dyes in contact with DNA bases near the center of the Holliday junction. For Iso I (Fig. 5a, c and e), the dye attached to the A strand is in contact with high probability with DNA bases on the C strand. Similarly, for Iso II (Fig. 5b, d and f), the dye on the B strand is in contact with high probability with DNA on the D strand. Comparing Fig. 5a and b, one notable difference is that for Iso I, the dye on the B strand has a non-zero probability of being in contact with the dye on the A strand, as well as the A bases in the center of the junction. Similarly, the dye on the A strand has non-zero probabilities of being in contact with the B strand dye and bases. Conversely, there are little-to-no contacts between the A strand dye and B bases as well as between the B strand dye and A bases for Iso II. As can be seen in the snapshots in Fig. S5 and S6,† in some cases, the dyes appear to intercalate into the base regions or major grooves of the duplexes constituting the Holliday junction, indicating that some steric effects may play a role in the dye–dye interactions. The lack of short Rm,n (less than 1.5 nm) in Fig. 5 and contacts between dyes and surrounding DNA bases for Iso II in Fig. 5 may indicate a stronger propensity of dyes in the Iso I configuration to overcome the steric effects of the DNA to form J-dimers. Furthermore, contacts between the DNA bases on the 3′ end of the dyes (i.e., bases 14 and 15) for the Iso I configurations are consistent with dimer formation and low Rm,n. In other words, contacts are observed between bases 14 and 15 on the A and B strands for Iso I, which are missing in Iso II. Overall, the evidence for DNA base hindrance on dye aggregation may explain the lack of smaller Rm,n, despite the dyes being attached near the center of the Holliday junction.
3.2. Transverse dimers
Similar to the adjacent dimer systems, heatmap plots of |κm,n| versus Rm,n for the transverse dimers are presented in Fig. 6 for both simulation trials 1, 2, and 3. Transverse dimer orientations plotted as a function of simulation time for trials 1, 2, and 3 are given in Fig. S7.† Like the adjacent dimers, the Iso I and Iso II transverse dimers show distinct differences compared to one another. For the ACy5Ccy5 Iso I system shown in Fig. 6a, there is a single, prominent peak at around Rm,n ≈ 0.57 nm and |κm,n| ≈ 0.4, indicating a closely spaced, H-like dimer configuration. Conversely, the ACy5Ccy5 Iso II dimer exhibits minimal evidence of dye–dye interactions with the prominent peak in Fig. 6b at around Rm,n ≈ 4.2 nm and |κm,n| ≈ 0.2–1.1. As shown in Fig. 1, this is expected since the A and C strands are closely spaced for Iso I Holliday junctions and the furthest away for Iso II. The same trend is observed for ACy5.5CCy5.5 and ACy5CCy5.5 Iso I and Iso II dimers. The major peaks in the Iso I configuration occur at Rm,n ≈ 0.43 nm and |κm,n| ≈ 0.2 for ACy5.5CCy5.5 and Rm,n ≈ 0.55 nm and |κm,n| ≈ 0.50 for ACy5CCy5.5. Notably, the spread of Rm,n and |κm,n| values is the tightest for ACy5.5CCy5.5. Like the ACy5CCy5 Iso II case, the major peaks in the Iso II configuration occur at Rm,n ≈ 3.8 nm and |κm,n| ≈ 0.2–1 for ACy5.5CCy5.5 and Rm,n ≈ 4.4 nm and |κm,n| ≈ 0.2–1 for ACy5CCy5.5. Snapshots corresponding to the heatmaps in Fig. 6 are shown in Fig. S10 and S11.† As seen in Fig. S10,† the transverse dimers are predominantly outside of the DNA base region in the center of the Holliday junction. This behavior is different from the adjacent dimers that show an evidence of intercalation and DNA base hindrance on dye aggregation. Conversely, as seen in Fig. S11,† the dyes are located on the opposite sides of the DNA Holliday junction without any apparent dye–dye interactions.
Fig. 6. Heatmap plots of the |κm,n| calculated using eqn (1)versus Rm,n for (a) ACy5CCy5 Iso I, (b) ACy5CCy5 Iso II, (c) ACy5.5CCy5.5 Iso I, (d) ACy5.5CCy5.5 Iso II, (e) ACy5CCy5.5 Iso I, and (f) ACy5CCy5.5 Iso II.
Similar to what was done for the adjacent dimers, contact maps were generated for the transverse dimers in the Iso I Holliday junction configuration, shown in Fig. 7. The Iso I configuration is presented since the Iso II does not show any evidence of dye–dye interactions (i.e., Iso II exhibits large Rm,n). The contact maps for the Iso II configurations are shown in Fig. S12.† The most notable difference compared to the adjacent dimers are the much higher probabilities for the dyes to be in contact for the transverse, Iso I dimer systems (as seen from the intersections of the A and C dyes in Fig. 7). Another notable difference is the lack of dye contacts with DNA strands that a dye is not attached to. For transverse Iso I systems, the dyes are predominantly in contact with DNA bases on the same strand the dyes are attached to, as well as with the dye and DNA bases on the transverse strand.
Fig. 7. Contact maps for (a) ACy5CCy5 Iso I, (b) ACy5.5CCy5.5 Iso I, and (c) ACy5CCy5.5 Iso I. Two residues are considered to be in contact if they are within 1.2 nm. The x- and y-axes correspond to the dye or base residue names. Dye contacts with all other residues are indicated in the plots with bold orange lines.
3.3. Comparison with experiment
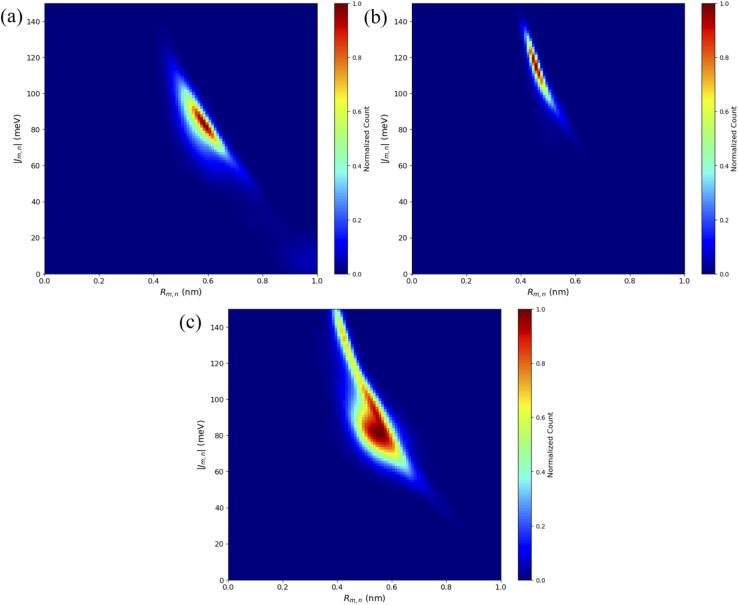
To compare computational results with available experimental data, Jm,n values were calculated for the transverse, Iso I dimers, since those dimers showed the smallest Rm,n and largest amounts of dye–dye interactions (i.e., strong excitonic coupling). Currently, dimer experimental data for |Jm,n| and Rm,n only exists for transversely attached dyes. The |Jm,n| values were calculated using eqn (2) and the transition dipole moments (μi) for Cy5 and Cy5.5 were calculated using TD-DFT, with values of μCy5 = 15.35 D and μCy5.5 = 15.57 D.51,56 The values of r and s in eqn (2) were chosen to be the ends of the dye along the long axis, resulting in dye lengths of about 1.4 nm and 1.5 nm for Cy5 and Cy5.5, respectively.
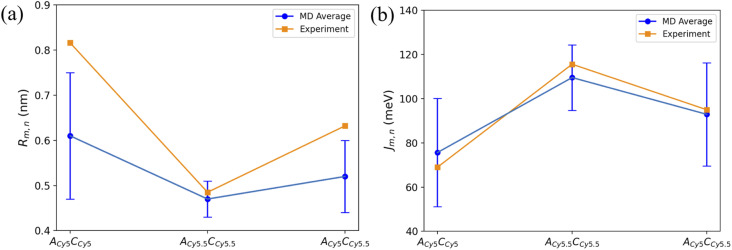
As expected, based on the Rm,n values in Fig. 6, the |Jm,n| values increase in the order of ACy5CCy5, ACy5CCy5.5, and ACy5.5CCy5.5. The relative magnitudes and orientations of the transition dipole moments also play a role in the trend of |Jm,n| values since μCy5.5 is slightly larger than μCy5, however, that is somewhat mitigated by the longer dye length for Cy5.5. Furthermore, as seen in Fig. 8, the ACy5.5CCy5.5 system has the smallest spread of Rm,n and |Jm,n| values compared to ACy5CCy5 and ACy5CCy5.5. That being said, ACy5CCy5.5 exhibits |Jm,n| comparable to ACy5.5CCy5.5, indicating instances of more closely spaced and stronger coupled dimer configurations. Fig. 9 shows the average Rm,n and |Jm,n| obtained from the three trials of the ACy5CCy5, ACy5.5CCy5.5, and ACy5CCy5.5 in the Iso I configurations compared to the experimentally available values obtained using the KRM model.47 The average MD results, standard deviations, and experimental values are given in Table 1. Overall, the average values obtained from the MD simulations follow the experimental trends, with ACy5CCy5 having the largest Rm,n and smallest |Jm,n|, and ACy5.5CCy5.5 having the smallest Rm,n and largest Jm,n. Additionally, all of the experimental |Jm,n| values fall within the MD average standard deviations. The MD simulations underestimate Rm,n values for the transverse, Iso I systems, however the simulations could reproduce the experimental trends. This may be due to differences in how the KRM model treats the transition dipole moment vectors compared to how we defined them based on the molecular structure of the dye – slight bending or stretching of the dyes during the MD simulations may cause small fluctuations in the transition dipole moments and the resultant Rm,n. Furthermore, Fig. 9 shows that the standard deviations for ACy5.5CCy5.5 are smaller than ACy5CCy5 and ACy5CCy5.5. It suggests that the transverse Cy5.5 dimer are stabilized to be a more closely pack and strongly coupled dimer, which may be due to the stronger dye–dye interactions for the Cy5.5 homodimer.
Fig. 8. Heatmap plots of the |Jm,n| calculated using eqn (2)versus Rm,n for (a) ACy5CCy5 Iso I, (b) ACy5.5CCy5.5 Iso I, and (c) ACy5CCy5.5 Iso I.
Fig. 9. Plots of (a) Rm,n and (b) |Jm,n| obtained from MD simulations and experiment. MD simulation results were obtained by averaging the data over the 900 ns simulations. Error bars denote the standard deviation of the average MD values. Experimental data acquired from Chowdhury et al.47 Lines connecting the points are to denote trends in the data, not fits.
Average MD results for the three simulation trials over the entire 900 ns trajectories along with their standard deviations. Experimental results are given in brackets and were obtained from Chowdhury et al. who used the KRM model to extract Rm,n and |Jm,n| from experimental data.47.
| System | R m,n (nm) | |Jm,n| (meV) |
|---|---|---|
| ACy5CCy5 Iso I | 0.61 ± 0.14 [0.816] | 75.64 ± 24.50 [69.0] |
| ACy5.5CCy5.5 Iso I | 0.47 ± 0.04 [0.485] | 109.56 ± 14.81 [115.6] |
| ACy5CCy5.5 Iso I | 0.52 ± 0.08 [0.632] | 92.92 ± 23.35 [95.0] |
4. Discussion
MD simulations of the Cy5 and Cy5.5 homodimers and heterodimers attached to adjacent Holliday junction DNA strands show that the Holliday junction isomer plays a major role in the resultant dye orientations. For all systems in this study, there are a variety of dye orientations that occur, indicating some structural heterogeneity that differs between Iso I and Iso II configurations. Furthermore, as seen in Fig. S3, S4, S8, and S9,† the Holliday junction inter-duplex angles (IDAs) and twist angles (angles between the constituent duplexes), calculated according to Fig. S1,† show a wide range of values. Typical Holliday junction IDAs and twist angles fall in the range of ∼60° and ∼40–60°, respectively.57–59,82 It should be noted that these values are for Holliday junctions without dyes attached to the DNA backbone – the dyes in our study act as an additional base or spacer in the DNA sequence, which may affect the DNA dynamics and conformations. This could lead to discrepancies observed between pure DNA Holliday junctions and Holliday junctions with dyes. The IDA and twist angle values still indicate the Holliday junctions for most systems predominantly remain in the stacked Iso I or Iso II configurations.
Based on the diagram in Fig. 1, the initial inter-dye separations and conditions of the adjacent dimers should be approximately the same for both Iso I and Iso II configurations. However, as shown in Fig. 3, the Iso I Holliday junction configurations preferentially form J-like dimers while the Iso II configurations do not. For adjacent dimers on the Iso II Holliday junction, the values of Rm,n are in the range of 1.5–2.8 nm. Furthermore, they are oriented predominantly in an H-like fashion with some obliqueness, as indicated by the |κm,n| values ranging from 0–1, but do not form closely spaced dimers. Conversely, the adjacent dimers attached to the Iso I Holliday junctions achieve a smaller Rm,n of approximately 1.4 nm. The main peak in the heatmaps of Fig. 3b, d and e correspond to J-like stacking of the dyes as indicated by the range of |κm,n| from 1.25–1.75. Compared to the adjacent dimer systems, the transverse dimer systems either form closely spaced H-like aggregates (Iso I) or don't form dimers at all (Iso II), which is intuitive based on Fig. 1. However, as can be seen in Fig. 8 and 9, ACy5.5CCy5.5 has the smallest spread of Rm,n and |Jm,n|, which may be due to the stronger dye–dye interactions between the Cy5.5 dyes that “lock” them into the closely spaced, H-like configuration. This is also highlighted by the smaller standard deviations for the average Rm,n and |Jm,n| values of ACy5.5CCy5.5 compared to ACy5CCy5 and ACy5CCy5.5. This may possibly be explained by the larger conjugated Cy5.5 structure compared to Cy5, enhancing the dye–dye interactions. Furthermore, we have shown via DFT calculations of the partition coefficient in water and n-octanol that Cy5.5 is slightly more hydrophobic than Cy5, which may also lead to the smaller Rm,n and the larger |Jm,n|.56 The differences between the adjacent dimers and transverse dimers in the Iso I configurations may also be explained in part by the contact maps shown in Fig. 5 and 9. For adjacent dimers in the Iso I configuration, there exist numerous contacts between the dyes and the DNA bases in the center of the Holliday junction, as well as the bases flanking the dyes. This indicates that to form a dimer (in this case, J-like dimers), the dyes need to overcome the barriers set by the surrounding DNA. Conversely, the transverse dimers exist in the center of the Holliday junction and do not show many contacts with the surrounding DNA, which may otherwise limit closely spaced dimer formation.
Our adjacent dimer MD data agrees qualitatively with experimental results from Cannon et al.46 that showed red-shifted absorption peaks for adjacent Cy5 homodimers in Holliday junctions and small amounts of Davydov splitting, indicating J-like dye orientations with some obliqueness. Similar results were obtained by Huff et al.41 However, the presence of dye orientations at large inter-dye distances (>2.5 nm) suggests that the dyes may not always form closely coupled dimers when they are bound to adjacent DNA strands. Experimentally, it was found that Holliday junctions with two Cy5 dyes attached to adjacent DNA arms exhibit lower denaturing temperature compared to that of unlabeled junctions, indicating weaker dye–dye interactions and larger Rm,n.41 Furthermore, it has been shown that there exists red-shifted and blue-shifted absorption features for the adjacent dimers, suggesting that there are subpopulations of J- and H-like dimers in the solution.41 Similar results were found for heterodimers consisting of Cy5 and Cy5.5 dyes.47 Absorption results of the Cy5–Cy5.5 heterodimer suggest structural heterogeneity in the dye–DNA solutions with subpopulations of excitonically and non-excitonically interacting dyes.47 Our MD results suggest that, depending on if the Holliday junction is in the Iso I or Iso II configuration, adjacent dimers can adopt both H-like and J-like arrangements with Rm,n larger than 1.4 nm. The DNA surrounding the dyes near the center of the junction may inhibit the dyes achieving smaller Rm,n values, as shown in the contact map plots. These results coincide with experimental findings of structural heterogeneity and larger inter-dye separations.41,46,47
Compared to the adjacent dimers, the transverse dimers exhibit two vastly different dye orientations depending on the Holliday junction configuration. Transverse dimers attached to the Iso II Holliday junctions exhibit Rm,n predominantly over 4.0 nm, suggesting weak dye–dye interactions. Experimental measurements of transverse Cy5–Cy5.5 heterodimers suggest that there may exist subpopulations of monomers in the solution. However, experimental evidence suggests that Iso I dominates.41,47 Since the experimental measurements include the ensemble average of the system, the subpopulation of weakly interacting dyes may still be present in the experimental spectra and resultant KRM data. This could explain the larger Rm,n values observed experimentally compared to the MD results since only Iso I conformers were considered for the results presented in Fig. 8 and 9. If a small percentage of Iso II data was included in the Rm,n and Jm,n calculations, better agreement with experiment might be obtained. Based on our MD results, these subpopulations may be occurring due to the Holliday junctions organizing into the Iso II configuration, which results in essentially two isolated monomers. The Iso I Holliday junctions, however, yield dye orientations that are predominantly H-like with much smaller Rm,n compared to both the adjacent dimers and Iso II transverse dimers. Furthermore, there is a lack of interactions of the dyes with the opposing DNA strands for the transverse, Iso I configurations, allowing for closer inter-dye distances. The H-like stacking and Rm,n of 0.4–0.7 nm lead to |Jm,n| values of 60–150 meV. These results agree well with the experimental evidence for H-like transverse Cy5 and Cy5.5 dye dimers, showing small Rm,n values and thus large |Jm,n|, consistent with our MD results as shown in Fig. 9 and Table 1.41,46,47 Additionally, it was found experimentally that DNA Holliday junctions with transversely attached Cy5 dyes have higher denaturing temperatures compared to adjacently attached dyes, indicating stronger dye–dye interactions.41 In the future, we will explore the role of DNA Holliday junction dynamics and isomerization in-depth with more advanced sampling methods.
5. Conclusions
MD simulations were carried out to examine the role of dye attachment locations and DNA Holliday junction isomerization on dimer orientations. Dimers consisting of either two Cy5 dyes, two Cy5.5 dyes, or one each of Cy5 and Cy5.5 dyes, were attached to either adjacent or transverse strands of DNA Holliday junctions in the stacked, Iso I or Iso II configurations. Overall, Iso I configurations agree well with experimental measurements. Adjacent dimers in the Iso I configuration exhibits predominantly J-like dye orientations while the Iso II configuration exhibits H-like dimers with large Rm,n. For the dye–DNA interactions, we found that dyes intercalate and stack with surrounding DNA bases, which might hinder dimer formation. Transverse dimers in the Iso II configuration exhibit little evidence of dye–dye interactions and essentially behave like independent monomers. Conversely, transverse dimers in the Iso I configuration have the smallest Rm,n and exhibit H-like stacking with negligibly few dye–DNA interactions. Furthermore, the calculated |Jm,n| for transverse, Iso I systems agree well with experiments. Our MD results reveal dye attachment schemes and DNA Holliday junction isomers on dye–DNA interactions, dye dynamics, and resultant dimer orientations, which can guide the synthesis and experimental studies for tailoring the dye–DNA structures towards applications that exploit dye aggregates and exciton dynamics.
Funding
Molecular dynamics research was supported by the Department of the Navy, Office of Naval Research (ONR), via ONR award no. N00014-19-1-2615. Modeling was performed at the High Performance Computing Center at Idaho National Laboratory, which is supported by the Office of Nuclear Energy of the U.S. Department of Energy and the Nuclear Science User Facilities, under Contract No. DE-AC07-05ID14517. Further computational modeling and data analysis were performed on the computing servers sponsored by the U.S. Department of Energy (DoE), Office of Basic Energy Sciences, Division of Materials Science and Engineering through the Established Program to Stimulate Competitive Research (EPSCoR), via award no. DE-SC0020089. Y.-C. K and J. S. M. of the U.S. Naval Research Laboratory (NRL) were supported by NRL base funding, the NRL Institute for Nanoscience, and ONR award no. 770 N0001419WX01811.
Conflicts of interest
There are no conflicts of interest to declare.
Supplementary Material
Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra05045e
References
- Scholes G. D. Fleming G. R. Olaya-Castro A. Van Grondelle R. Lessons from nature about solar light harvesting. Nat. Chem. 2011;3:763–774. doi: 10.1038/nchem.1145. [DOI] [PubMed] [Google Scholar]
- Collado-Fregoso E. Boufflet P. Fei Z. Gann E. Ashraf S. Li Z. Mcneill C. R. Durrant J. R. Heeney M. Increased Exciton Dipole Moment Translates into Charge-Transfer Excitons in Thiophene-Fluorinated Low-Bandgap Polymers for Organic Photovoltaic Applications. Chem. Mater. 2015;27(3):7934–7944. doi: 10.1021/acs.chemmater.5b02948. [DOI] [Google Scholar]
- Markov R. V. Plekhanov A. I. Shelkovnikov V. V. Knoester J. Giant Nonlinear Optical Response of Interacting One-Dimensional Frenkel Excitons in Molecular Aggregates. Phys. Status Solidi B. 2000;221:529–533. doi: 10.1002/1521-3951(200009)221:1<529::AID-PSSB529>3.0.CO;2-A. [DOI] [Google Scholar]
- Graugnard E. Kellis D. L. Bui H. Barnes S. Kuang W. Lee J. Hughes W. L. Knowlton W. B. Yurke B. DNA-controlled excitonic switches. Nano Lett. 2012;12:2117–2122. doi: 10.1021/nl3004336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon B. L. Kellis D. L. Davis P. H. Lee J. Kuang W. Hughes W. L. Graugnard E. Yurke B. Knowlton W. B. Excitonic AND Logic Gates on DNA Brick Nanobreadboards. ACS Photonics. 2015;2:398–404. doi: 10.1021/ph500444d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurke B. Kuang W. Passive linear nanoscale optical and molecular electronics device synthesis from nanoparticles. Phys. Rev. A: At., Mol., Opt. Phys. 2010;81:033814. doi: 10.1103/PhysRevA.81.033814. [DOI] [Google Scholar]
- Sawaya N. P. D. Rappoport D. Tabor D. P. Aspuru-Guzik A. Excitonics: A Set of Gates for Molecular Exciton Processing and Signaling. ACS Nano. 2018;12:6410–6420. doi: 10.1021/ACSNANO.8B00584/SUPPL_FILE/NN8B00584_SI_001.PDF. [DOI] [PubMed] [Google Scholar]
- Kellis D. L. Sarter C. Cannon B. L. Davis P. H. Graugnard E. Lee J. Pensack R. D. Kolmar T. Jäschke A. Yurke B. et al., An All-Optical Excitonic Switch Operated in the Liquid and Solid Phases. ACS Nano. 2019;13:2986–2994. doi: 10.1021/acsnano.8b07504. [DOI] [PubMed] [Google Scholar]
- Zang L. Che Y. Moore J. S. One-dimensional self-assembly of planar π-conjugated molecules: Adaptable building blocks for organic nanodevices. Acc. Chem. Res. 2008;41:1596–1608. doi: 10.1021/AR800030W/ASSET/IMAGES/MEDIUM/AR-2008-00030W_0002.GIF. [DOI] [PubMed] [Google Scholar]
- Mirkovic T. Ostroumov E. E. Anna J. M. Van Grondelle R. Govindjee R. Scholes G. D. Light absorption and energy transfer in the antenna complexes of photosynthetic organisms. Chem. Rev. 2017;117:249–293. doi: 10.1021/acs.chemrev.6b00002. [DOI] [PubMed] [Google Scholar]
- Brixner T. Hildner R. Köhler J. Lambert C. Würthner F. Exciton Transport in Molecular Aggregates - From Natural Antennas to Synthetic Chromophore Systems. Adv. Energy Mater. 2017;7:1700236. doi: 10.1002/aenm.201700236. [DOI] [Google Scholar]
- Jailaubekov A. E. Willard A. P. Tritsch J. R. Chan W. L. Sai N. Gearba R. Kaake L. G. Williams K. J. Leung K. Rossky P. J. et al., Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfaces in organic photovoltaics. Nat. Mater. 2013;12:66–73. doi: 10.1038/nmat3500. [DOI] [PubMed] [Google Scholar]
- Rita Narayan M. Singh J. Study of the mechanism and rate of exciton dissociation at the donor-acceptor interface in bulk-heterojunction organic solar cells. J. Appl. Phys. 2013;114:073510. doi: 10.1063/1.4818813. [DOI] [Google Scholar]
- Scheibe G. Über die Veränderlichkeit der Absorptionsspektren in Lösungen und die Nebenvalenzen als ihre Ursache. Angew. Chemie. 1937;50:212–219. doi: 10.1002/ANGE.19370501103. [DOI] [Google Scholar]
- Jelley E. E. Spectral Absorption and Fluorescence of Dyes in the Molecular State. Nature. 1936;138(3502):1009–1010. doi: 10.1038/1381009a0. [DOI] [Google Scholar]
- Kasha M. Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates. Radiat. Res. 1963;20:55–70. doi: 10.2307/3571331. [DOI] [PubMed] [Google Scholar]
- Kasha M. Rawls H. R. Ashraf El-Bayoumi M. The Exciton Model In Molecular Spectroscopy. Pure Appl. Chem. 1965;11:371–392. doi: 10.1351/pac196511030371. [DOI] [Google Scholar]
- Abramavicius D. Palmieri B. Mukamel S. Extracting single and two-exciton couplings in photosynthetic complexes by coherent two-dimensional electronic spectra. Chem. Phys. 2009;357:79–84. doi: 10.1016/j.chemphys.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czikklely V. Forsterling H. D. Kuhn H. Extended dipole model for aggregates of dye molecules. Chem. Phys. Lett. 1970;6:207–210. doi: 10.1016/0009-2614(70)80220-2. [DOI] [Google Scholar]
- Scheibe K. Ecker N. Jelley E. E. Molecular, Nematic and Crystal States of I: I-Diethyl-Cyanine Chloride. Nat. 1937;139(3519):631. doi: 10.1038/139631b0. [DOI] [Google Scholar]
- Davydov A. S., Theory of Absorption Spectra of Molecular Crystals, Institute of Physics, Academy of Sciences of Ukrainian SSr, Kiyiv, Ukraine, 1948, 18 [Google Scholar]
- Davydov A. S. The Theory of Molecular Excitons. Sov. Phys. Usp. 1964;7:393–448. [Google Scholar]
- Mass O. A. Wilson C. K. Roy S. K. Barclay M. S. Patten L. K. Terpetschnig E. A. Lee J. Pensack R. D. Yurke B. Knowlton W. B. Exciton Delocalization in Indolenine Squaraine Aggregates Templated by DNA Holliday Junction Scaffolds. J. Phys. Chem. B. 2020;124:9636–9647. doi: 10.1021/acs.jpcb.0c06480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeman N. C. Kallenbach N. R. Design of immobile nucleic acid junctions. Biophys. J. 1983;44:201. doi: 10.1016/S0006-3495(83)84292-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winfree E. Liu F. Wenzler L. A. Seeman N. C. Design and self-assembly of two-dimensional DNA crystals. Nature. 1998;394:539–544. doi: 10.1038/28998. [DOI] [PubMed] [Google Scholar]
- Rothemund P. W. K. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440:297–302. doi: 10.1038/NATURE04586. [DOI] [PubMed] [Google Scholar]
- Seifert J. L. Connor R. E. Kushon S. A. Wang M. Armitage B. A. Spontaneous Assembly of Helical Cyanine Dye Aggregates on DNA Nanotemplates. J. Am. Chem. Soc. 1999;121:2987–2995. doi: 10.1021/ja984279j. [DOI] [Google Scholar]
- Garoff R. A. Litzinger E. A. Connor R. E. Fishman I. Armitage B. A. Helical aggregation of cyanine dyes on DNA templates: Effect of dye structure on formation of homo- and heteroaggregates. Langmuir. 2002;18:6330–6337. doi: 10.1021/la025742f. [DOI] [Google Scholar]
- Wang M. Silva G. L. Armitage B. A. DNA-Templated Formation of a Helical Cyanine Dye J-Aggregate. J. Am. Chem. Soc. 2000;122(41):9977–9986. doi: 10.1021/ja002184n. [DOI] [Google Scholar]
- Banal J. L. Kondo T. Veneziano R. Bathe M. Schlau-Cohen G. S. Photophysics of J-Aggregate-Mediated Energy Transfer on DNA. J. Phys. Chem. Lett. 2017;8:5827–5833. doi: 10.1021/acs.jpclett.7b01898. [DOI] [PubMed] [Google Scholar]
- Asanuma H. Fujii T. Kato T. Kashida H. Coherent interactions of dyes assembled on DNA. J. Photochem. Photobiol., C. 2012;13:124–135. doi: 10.1016/J.JPHOTOCHEMREV.2012.04.002. [DOI] [Google Scholar]
- Sohail S. H. Otto J. P. Cunningham P. D. Kim Y. C. Wood R. E. Allodi M. A. Higgins J. S. Melinger J. S. Engel G. S. DNA scaffold supports long-lived vibronic coherence in an indodicarbocyanine (Cy5) dimer. Chem. Sci. 2020;11:8546–8557. doi: 10.1039/d0sc01127d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham P. D. Kim Y. C. Díaz S. A. Buckhout-White S. Mathur D. Medintz I. L. Melinger J. S. Optical Properties of Vibronically Coupled Cy3 Dimers on DNA Scaffolds. J. Phys. Chem. B. 2018;122:5020–5029. doi: 10.1021/acs.jpcb.8b02134. [DOI] [PubMed] [Google Scholar]
- Cunningham P. D. Khachatrian A. Buckhout-White S. Deschamps J. R. Goldman E. R. Medintz I. L. Melinger J. S. Resonance energy transfer in DNA duplexes labeled with localized dyes. J. Phys. Chem. B. 2014;118:14555–14565. doi: 10.1021/JP5065006/SUPPL_FILE/JP5065006_SI_001.PDF. [DOI] [PubMed] [Google Scholar]
- Hart S. M. Wang X. Guo J. Bathe M. Schlau-Cohen G. S. Tuning Optical Absorption and Emission Using Strongly Coupled Dimers in Programmable DNA Scaffolds. J. Phys. Chem. Lett. 2022;13:1863–1871. doi: 10.1021/ACS.JPCLETT.1C03848/SUPPL_FILE/JZ1C03848_SI_001.PDF. [DOI] [PubMed] [Google Scholar]
- Melinger J. S. Khachatrian A. Ancona M. G. Buckhout-White S. Goldman E. R. Spillmann C. M. Medintz I. L. Cunningham P. D. FRET from Multiple Pathways in Fluorophore-Labeled DNA. ACS Photonics. 2016;3:659–669. doi: 10.1021/ACSPHOTONICS.6B00006/SUPPL_FILE/PH6B00006_SI_001.PDF. [DOI] [Google Scholar]
- Markova L. I. Malinovskii V. L. Patsenker L. D. Häner R. J- vs. H-type assembly: Pentamethine cyanine (Cy5) as a near-IR chiroptical reporter. Chem. Commun. 2013;49:5298–5300. doi: 10.1039/c3cc42103a. [DOI] [PubMed] [Google Scholar]
- Huff J. S. Davis P. H. Christy A. Kellis D. L. Kandadai N. Toa Z. S. D. Scholes G. D. Yurke B. Knowlton W. B. Pensack R. D. DNA-Templated Aggregates of Strongly Coupled Cyanine Dyes: Nonradiative Decay Governs Exciton Lifetimes. J. Phys. Chem. Lett. 2019;10:2386–2392. doi: 10.1021/acs.jpclett.9b00404. [DOI] [PubMed] [Google Scholar]
- Nicoli F. Roos M. K. Hemmig E. A. Di Antonio M. de Vivie-Riedle R. Liedl T. Proximity-Induced H-Aggregation of Cyanine Dyes on DNA-Duplexes. J. Phys. Chem. A. 2016;120:9941–9947. doi: 10.1021/acs.jpca.6b10939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon B. L. Kellis D. L. Patten L. K. Davis P. H. Lee J. Graugnard E. Yurke B. Knowlton W. B. Coherent Exciton Delocalization in a Two-State DNA-Templated Dye Aggregate System. J. Phys. Chem. A. 2017;121(37):6905–6916. doi: 10.1021/acs.jpca.7b04344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huff J. S. Turner D. B. Mass O. A. Patten L. K. Wilson C. K. Roy S. K. Barclay M. S. Yurke B. Knowlton W. B. Davis P. H. et al., Excited-State Lifetimes of DNA-Templated Cyanine Dimer, Trimer, and Tetramer Aggregates: The Role of Exciton Delocalization, Dye Separation, and DNA Heterogeneity. J. Phys. Chem. B. 2021;125(36):10240–10259. doi: 10.1021/acs.jpcb.1c04517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S. K. Mass O. A. Kellis D. L. Wilson C. K. Hall J. A. Yurke B. Knowlton W. B. Exciton Delocalization and Scaffold Stability in Bridged Nucleotide-Substituted, DNA Duplex-Templated Cyanine Aggregates. J. Phys. Chem. B. 2021;125:13670–13684. doi: 10.1021/acs.jpcb.1c07602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubner K. Joshi H. Aksimentiev A. Stefani F. D. Tinnefeld P. Acuna G. P. Determining the In-Plane Orientation and Binding Mode of Single Fluorescent Dyes in DNA Origami Structures. ACS Nano. 2021;15(3):5109–5117. doi: 10.1021/acsnano.0c10259. [DOI] [PubMed] [Google Scholar]
- Mathur D. Kim Y. C. Diaz S. A. Ellis G. A. Cunningham P. D. Brian Rolczynski S. Ancona M. G. Medintz I. L. Melinger J. S. Exploring the Holliday Junction in a DNA nanostructure for creating excitonic dimers. Proc. IEEE Conf. Nanotechnol. 2021:360–363. doi: 10.1109/NANO51122.2021.9514330. [DOI] [Google Scholar]
- Mathur D. Kim Y. C. Díaz S. A. Cunningham P. D. Rolczynski B. S. Ancona M. G. Medintz I. L. Melinger J. S. Can a DNA Origami Structure Constrain the Position and Orientation of an Attached Dye Molecule? J. Phys. Chem. C. 2021;125:1509–1522. doi: 10.1021/acs.jpcc.0c09258. [DOI] [Google Scholar]
- Cannon B. L. Patten L. K. Kellis D. L. Davis P. H. Lee J. Graugnard E. Yurke B. Knowlton W. B. Large Davydov Splitting and Strong Fluorescence Suppression: An Investigation of Exciton Delocalization in DNA-Templated Holliday Junction Dye Aggregates. J. Phys. Chem. A. 2018;122:2086–2095. doi: 10.1021/acs.jpca.7b12668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowdhury A. U. Díaz S. A. Huff J. S. Barclay M. S. Chiriboga M. Ellis G. A. Mathur D. Patten L. K. Sup A. Hallstrom N. et al., Tuning between Quenching and Energy Transfer in DNA-Templated Heterodimer Aggregates. J. Phys. Chem. Lett. 2022;13:2782–2791. doi: 10.1021/acs.jpclett.2c00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay M. S. Roy S. K. Huff J. S. Mass O. A. Turner D. B. Wilson C. K. Kellis D. L. Terpetschnig E. A. Lee J. Davis P. H. et al., Rotaxane rings promote oblique packing and extended lifetimes in DNA-templated molecular dye aggregates. Commun. Chem. 2021;4:19. doi: 10.1038/s42004-021-00456-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mass O. A. Wilson C. K. Barcenas G. Terpetschnig E. A. Obukhova O. M. Kolosova O. S. Tatarets A. L. Li L. Yurke B. Knowlton W. B. et al., Influence of Hydrophobicity on Excitonic Coupling in DNA-Templated Indolenine Squaraine Dye Aggregates. J. Phys. Chem. C. 2022;126(7):3475–3488. doi: 10.1021/acs.jpcc.1c08981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barcenas G. Biaggne A. Mass O. A. Wilson C. K. Obukhova O. M. Kolosova O. S. Tatarets A. L. Terpetschnig E. Pensack R. D. Lee J. et al., First-principles studies of substituent effects on squaraine dyes. RSC Adv. 2021;11:19029–19040. doi: 10.1039/d1ra01377g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biaggne A. Knowlton W. B. Yurke B. Lee J. Li L. Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations. Molecules. 2021;26:524. doi: 10.3390/molecules26030524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abou-Hatab S. Spata V. A. Matsika S. Substituent Effects on the Absorption and Fluorescence Properties of Anthracene. J. Phys. Chem. A. 2017;121:1213–1222. doi: 10.1021/acs.jpca.6b12031. [DOI] [PubMed] [Google Scholar]
- Hart S. M. Chen W. J. Banal J. L. Bricker W. P. Dodin A. Markova L. Vyborna Y. Willard A. P. Häner R. Bathe M. et al., Engineering couplings for exciton transport using synthetic DNA scaffolds. Chem. 2021;7:752–773. doi: 10.1016/j.chempr.2020.12.020. [DOI] [Google Scholar]
- Stennett E. M. S. Ma N. van der Vaart A. Levitus M. Photophysical and Dynamical Properties of Doubly Linked Cy3–DNA Constructs. J. Phys. Chem. B. 2014;118:152–163. doi: 10.1021/jp410976p. [DOI] [PubMed] [Google Scholar]
- Nicoli F. Roos M. K. Hemmig E. A. Di Antonio M. De Vivie-Riedle R. Liedl T. Proximity-Induced h-Aggregation of cyanine dyes on DNA-Duplexes. J. Phys. Chem. A. 2016;120:9941–9947. doi: 10.1021/acs.jpca.6b10939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biaggne A. Spear L. Ketteridge M. Kim Y. C. Melinger J. S. Knowlton W. B. Yurke B. Li L. Data-Driven and Multiscale Modeling of DNA-Templated Dye Aggregates. Molecules. 2022;27(11):3456. doi: 10.3390/molecules27113456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheatley E. G. Pieniazek S. N. Mukerji I. Beveridge D. L. Molecular dynamics of a DNA Holliday junction: The inverted repeat sequence d(CCGGTACCGG) 4. Biophys. J. 2012;102:552–560. doi: 10.1016/j.bpj.2011.11.4023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons C. R. MacCulloch T. Krepl M. Matthies M. Buchberger A. Crawford I. Šponer J. Šulc P. Stephanopoulos N. Yan H. The influence of Holliday junction sequence and dynamics on DNA crystal self-assembly. Nat. Commun. 2022;13:3112. doi: 10.1038/s41467-022-30779-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adendorff M. R. Tang G. Q. Millar D. P. Bathe M. Bricker W. P. Computational investigation of the impact of core sequence on immobile DNA four-way junction structure and dynamics. Nucleic Acids Res. 2021;50(2):717–730. doi: 10.1093/nar/gkab1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu S. Cervantes-Salguero K. Yurke B. Knowlton W. B. Lee J. Mass O. A. Photocrosslinking Probes Proximity of Thymine Modifiers Tethering Excitonically Coupled Dye Aggregates to DNA Holliday Junction. Molecules. 2022;27:4006. doi: 10.3390/molecules27134006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galindo-Murillo R. Robertson J. C. Zgarbová M. Šponer J. Otyepka M. Jurečka P. Cheatham T. E. Assessing the Current State of Amber Force Field Modifications for DNA. J. Chem. Theory Comput. 2016;12:4114–4127. doi: 10.1021/acs.jctc.6b00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zgarbová M. Šponer J. Otyepka M. Cheatham T. E. Galindo-Murillo R. Jurečka P. Refinement of the Sugar-Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA. J. Chem. Theory Comput. 2015;11:5723–5736. doi: 10.1021/ACS.JCTC.5B00716/SUPPL_FILE/CT5B00716_SI_001.PDF. [DOI] [PubMed] [Google Scholar]
- Sun Z. Wang X. Zhang J. Z. H. He Q. Sulfur-substitution-induced base flipping in the DNA duplex. Phys. Chem. Chem. Phys. 2019;21:14923–14940. doi: 10.1039/C9CP01989H. [DOI] [PubMed] [Google Scholar]
- Sun Z. Zhang J. Z. H. Thermodynamic insights of base flipping in TNA duplex: Force fields, salt concentrations, and free-energy simulation methods. CCS Chem. 2021;3:1026–1039. doi: 10.31635/ccschem.020.202000202. [DOI] [Google Scholar]
- Yoo J. Aksimentiev A. Improved parametrization of Li +, Na +, K +, and Mg 2+ ions for all-atom molecular dynamics simulations of nucleic acid systems. J. Phys. Chem. Lett. 2012;3:45–50. doi: 10.1021/jz201501a. [DOI] [Google Scholar]
- Wang J. Wolf R. M. Caldwell J. W. Kollman P. A. Case D. A. Development and testing of a general Amber force field. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J. Wang W. Kollman P. A. Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006;25:247–260. doi: 10.1016/J.JMGM.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Bayly C. I. Cieplak P. Cornell W. D. Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993;97:10269–10280. doi: 10.1021/j100142a004. [DOI] [Google Scholar]
- MacKerell A. D. Banavali N. K. All-Atom Empirical Force Field for Nucleic Acids: II. Application to Molecular Dynamics Simulations of DNA and RNA in Solution. J. Comput. Chem. 2000;21:105–120. doi: 10.1002/(SICI)1096-987X(20000130)21:2<105::AID-JCC3>3.0.CO;2-P. [DOI] [Google Scholar]
- Beglov D. Roux B. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J. Chem. Phys. 1994;100:9050–9063. doi: 10.1063/1.466711. [DOI] [Google Scholar]
- Joung I. S. Cheatham T. E. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray A. Di Felice R. Protein-Mutation-Induced Conformational Changes of the DNA and Nuclease Domain in CRISPR/Cas9 Systems by Molecular Dynamics Simulations. J. Phys. Chem. B. 2020;124:2168–2179. doi: 10.1021/acs.jpcb.9b07722. [DOI] [PubMed] [Google Scholar]
- Hozhabr Araghi S. John A. Sadeghi Googheri M. S. A molecular dynamics simulations study of the ionic liquid effect on the β-glucosidase active site interactions with a flavonoid glycoside. J. Mol. Liq. 2021;340:117115. doi: 10.1016/j.molliq.2021.117115. [DOI] [Google Scholar]
- Darden T. York D. Pedersen L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1998;98:10089. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- Essmann U. Perera L. Berkowitz M. L. Darden T. Lee H. Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1998;103:8577. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- Hess B. Bekker H. Berendsen H. J. C. Fraaije J. G. E. M. L. I. N. C. S. A linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
- Van Der Spoel D. Lindahl E. Hess B. Groenhof G. Mark A. E. Berendsen H. J. C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Sims M., Smith B., Helfrich B., Sathaye N., Messick E., Moore T., Fish R.; Rajagopalan M., Rotkiewicz P. and Drexler E., et al., Nanoengineer-1 – A CAD-based molecular modeling program for structural DNA nanotechnology, 2008, 175–178.
- Pettersen E. F. Goddard T. D. Huang C. C. Meng E. C. Couch G. S. Croll T. I. Morris J. H. Ferrin T. E. UCSF ChimeraX: Structure visualization for researchers, educators, and developers. Protein Sci. 2021;30:70–82. doi: 10.1002/pro.3943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bussi G. Donadio D. Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126(1):014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M. Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
- Watson J. Hays F. A. Ho P. S. Definitions and analysis of DNA Holliday junction geometry. Nucleic Acids Res. 2004;32:3017. doi: 10.1093/NAR/GKH631. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.