Cyclosporin A: Conformational Complexity and Chameleonicity

Abstract

The chameleonic behavior of cyclosporin A (CsA) was investigated through conformational ensembles employing multicanonical molecular dynamics simulations that could sample the cis and trans isomers of N-methylated amino acids; these assessments were conducted in explicit water, dimethyl sulfoxide, acetonitrile, methanol, chloroform, cyclohexane (CHX), and n-hexane (HEX) using AMBER ff03, AMBER10:EHT, AMBER12:EHT, and AMBER14:EHT force fields. The conformational details were discussed employing the free-energy landscapes (FELs) at T = 300 K; it was observed that the experimentally determined structures of CsA were only a part of the conformational space. Comparing the ROESY measurements in CHX-d12 and HEX-d14, the major conformations in those apolar solvents were essentially the same as that in CDCl₃ except for the observation of some sidechain rotamers. The effects of the metal ions on the conformations, including the cis/trans isomerization, were also investigated. Based on the analysis of FELs, it was concluded that the AMBER ff03 force field best described the experimentally derived conformations, indicating that CsA intrinsically formed membrane-permeable conformations and that the metal ions might be key to the cis/trans isomerization of N-methylated amino acid before binding a partner protein.

Graphical Abstract

Introduction

Cyclosporin A (CsA, Figure 1) is a cyclic undecapeptide, which was discovered in the 1970s as a potent immunosuppressive agent.¹ Because CsA is a good model compound for the “beyond the rule-of-five” (bRo5) chemical space owing to its good permeability and chameleonic behavior, there are numerous experimental and theoretical studies into its conformation in various media.^2–11 The experimental results, as obtained by crystallography and NMR, reveal that CsA exhibits chameleonic behaviors, i.e., “closed,” “open,” “very open” conformations, etc., depending on the environment (solvent polarity, presence of metal ions or micelles, and complex formation with proteins).^2,3,12–18

Figure 1.

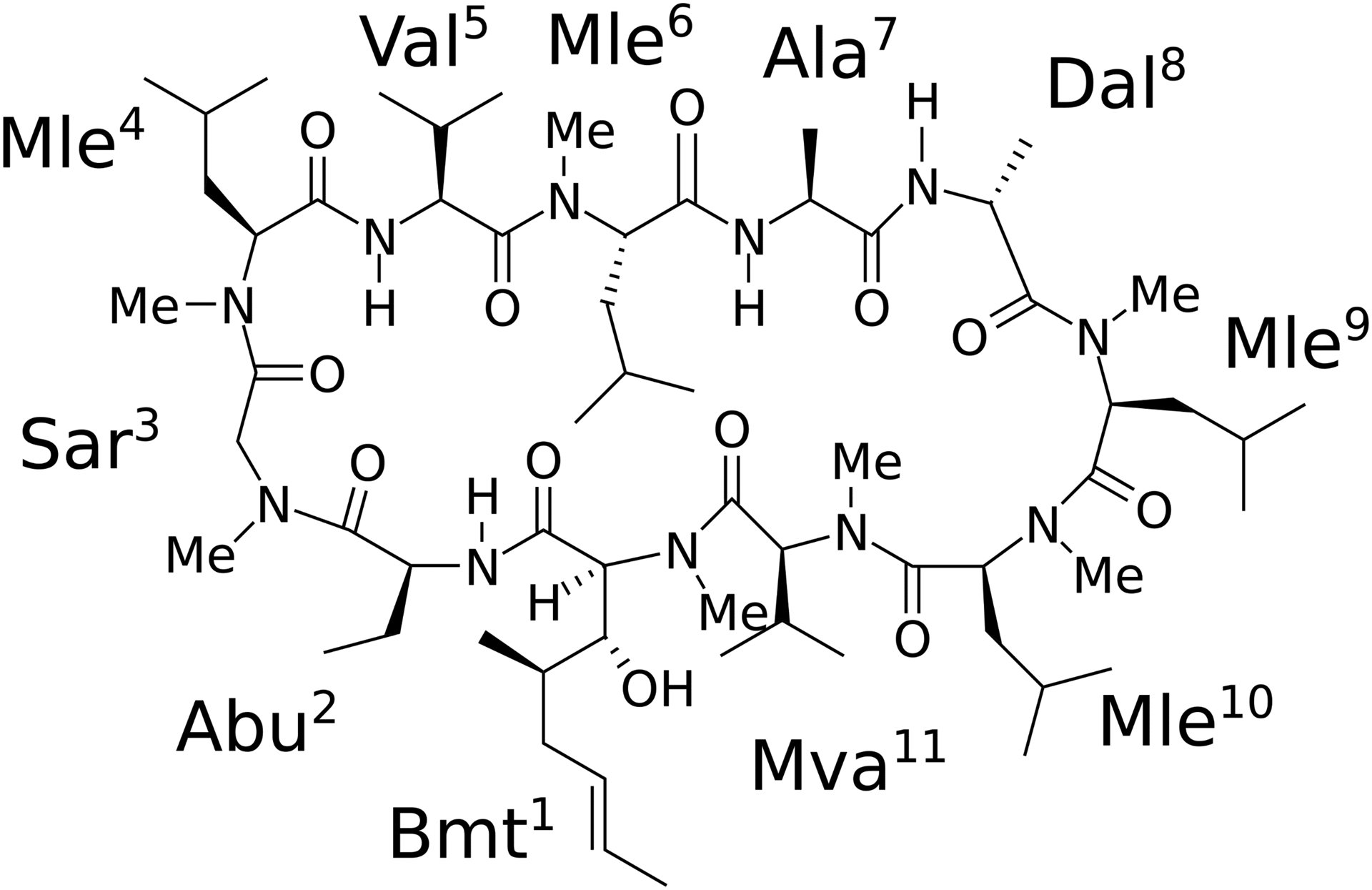
Chemical structure of CsA.

A crystal structure in the closed conformation with four intramolecular hydrogen bonds (IMHBs; i.e., Abu²-H–Val⁵-O, Val⁵-H–Abu²-O, Ala⁷-H–Mva¹¹-O, and Dal⁸-H–Mle⁶-O) has been reported (ID: DEKSAN,² source: CSD). A similarly closed conformation has also been reported in CDCl₃.^2,3 Crystal structures in open conformations with no IMHB have been observed in the complex with cyclophilin (e.g., IDs: 1CSA¹² and 2Z6W,¹³ source: PDB). A crystal structure in a “very open” conformation has been observed in the complex with FAB (ID: 1IKF,¹⁴ source: PDB). Notably, the open and “very open” conformations exhibit all-trans isomers, whereas the closed conformation exhibits a cis-amide structure between Mle⁹ and Mle¹⁰ (denoted as 9–10 cis).

The structures for CsA, complexed with Pb²⁺ and Sr²⁺, as solved by combining experimental and density functional theory, have been reported; the results revealed that many carbonyl groups were bonded to those metal ions (Pb²⁺ and Sr²⁺).^16,17 The conformation of CsA complexed with sodium dodecyl sulfate (SDS) micelles, as determined by nuclear Overhauser effect (NOE) measurements, was reported;¹⁸ the major conformation exhibited a twisted backbone with no IMHB and with the 9–10 amide structure in the cis conformation.

Furthermore, many minor conformations, including the cis and trans isomers, might exist in certain environments.^3,15,19–21 For example, it is known that minor conformation(s), which have not be characterized experimentally, constitute 6% of the ensemble in chloroform (CHCl₃).³ A cis-amide conformation might exist between Mle⁶ and Ala⁷ in dimethyl sulfoxide (DMSO).²¹ A minimum of six sets of signals have been observed in methanol (MeOH).²² Recently, Gray et al.¹¹ proposed a bent conformation, which forms a more compact conformation than the canonical closed one via combined ion-mobility spectrometry–mass spectrometry (IMS–MS), and proposed that it might exhibit multiple cis peptide bonds.

It is also believed that the binding mechanism of CsA to its partner protein(s) induces or requires a conformational change in CsA. The proposed mechanisms include (i) induced-fit during binding, (ii) conformational selection during binding, or (iii) simultaneous occurrence of both.²³ A fourth postulated binding mechanism of CsA to its partner protein(s) is a conformational change induced by metal ion binding.^11,24

Very recently, an excellent review of cyclosporin’s structure and its permeability was published.²⁵ These authors summarized chemical structure, dynamics, and permeability data for cyclosporin A and its analogues from the literatures and proposed two permeation models; (i) simplified induced-fit-like (IFL) model and (ii) conformational-selection-like (CSL) model which is a modified version of the congruent model proposed by Witek et al.⁸; membrane permeation is assisted by congruent conformations, which are significantly populated in water and the membrane.

The early computational simulations of CsA were performed in vacuo.^3,4,26 Molecular dynamics (MD) simulations in explicit solvents have been adopted recently to simulate the conformational features and dynamics of CsA.^8–10 However, due to a large energy barrier for the cis/trans isomerization of N-methylated amino acids, exhaustive conformational sampling of macrocycles containing multiple N-methyl residues remains challenging. Indeed, there are few if any in silico studies providing a detailed free-energy analysis of CsA or similarly complex systems in multiple explicit solvents.

Multicanonical MD (McMD)²⁷ simulation is a powerful, enhanced sampling method in which the potential energy is equally sampled between low and high-temperature regions. Noteworthily, those regions can be arbitrarily determined by the systems of interest. By reweighting a set of sampled structures, the canonical ensemble can be obtained at any temperature between the low and high regions. Another advantage of McMD is that it does not depend on the initial structure. McMD simulations and their derivatives have been successfully applied to small peptides,^28–30 intrinsically disordered proteins (IDPs) and disordered regions (IDRs),^31–33 antibody CDR-H3 loop,³⁴ and protein–ligand docking simulations,^35–37 in explicit water.

Recently, we reported that McMD simulations in explicit cyclohexane (CHX), rather than in CHCl₃, revealed an excellent correlation between the solvent-accessible surface area (SASA) and the experimental cell permeability, indicating that the choice of solvent was key to predicting the permeability.³⁸ Furthermore, we explored the conformational space via the free-energy landscapes (FELs) and proposed permeation models for small cyclic peptides.³⁸ We also predicted the difference between the rigidity and chameleonicity of peptide–peptoid scaffolds via McMD; Peptoids are located at β-turn region of scaffold A whereas peptoids are in the middle of β-sheet of scaffold B. We observed that scaffold A remains rigid in apolar to polar solvents, whereas scaffold B is rigid in apolar solvents only, although it becomes chameleonic in polar solvents.³⁹

Here, we report the assessment of CsA in different solvents (polar and apolar) to elucidate the changes in its conformational changes in those environments. The following solvents were selected: water (WAT), DMSO, acetonitrile (ACN), and MeOH with dielectric constants of 78.0, 46.8, 35.7, and 32.6, respectively, employed as polar solvents, and CHCl₃, CHX, and n-hexane (HEX) with dielectric constants of 4.8, 2.0, and 1.9, respectively, utilized as apolar solvents. The experimental solubilities of CsA were 5.5 and 17 mg/g in HEX and CHX, respectively.⁴⁰ However, the conformation of CsA in those solvents is expected to best mimic the conformation in the membrane interior. We also investigated the effect of metal ions on the conformational space. Although we successfully predicted the conformations of cyclic hexapeptides using the AMBER ff03 force field,³⁸ we also performed McMD to assess the other AMBER force fields.

Methods

NMR experiments.

The samples in CDCl₃, CHX-d12, and HEX-d14 were prepared by saturating ~1 mg CsA sample in 0.5 mL of the solvent, thereby obtaining 300 μL of a soluble supernatant, which were diluted in another 300 μL of the solvent, through glass fibers. The data acquisition and processing are described in the Supporting Information (SI). Further, the interatomic distances were directly calculated via ROESY cross-peak integrations and normalized to the integration for the alpha protons of Sar³; the measured distances, which were >4.5 Å, were not considered in this study.

Force field setups.

Regarding the AMBER ff03 force field,⁴¹ default parameters were used for the amino acids (Val, Ala, and Dal). ForceField_NCAA⁴² was used for the Abu and N-methylated amino acids (Sar, Mle, and Mva). The General AMBER Force Field (GAFF)⁴³ was applied to obtain the missing parameters (CT for the carbon atom of N-methyl amino acids and c2 for the double bonded carbons) for building a residue, Bmt. The RESP ESP charges from R.E.D. version III.52⁴⁴ were employed, following the procedure in the reference.⁴² The topology file was created by the LEaP program. Regarding the AMBER10:EHT (based on the ff99SB for amino acids),⁴⁵ AMBER12:EHT (based on ff12SB),⁴⁶ and AMBER14:EHT (based on ff14SB)⁴⁶ force fields, the missing atom types (c3 and c2) were set up by the default values of Molecular Operating Environment (MOE)⁴⁷, missing charges were assigned by AM1-BCC⁴⁸ through the rotamer library module implemented in MOE, and a topology file was exported as a parmtop file. Note that in this case, the Extended Hückel Theory (EHT) is not relevant to the charge assignment of amino acids. The ω dihedral angle parameters were modified according to the report by Doshi and Hamelberg⁴⁹ to accurately calculate the cis/trans isomerization. The TIP3P water model⁵⁰ was adopted, and the parameters for CHCl₃ and MeOH were obtained from AmberTools18.⁵¹ The parameters of ACN⁵² and DMSO⁵³ were adopted, as shown in the references. For CHX and HEX, the atom types, cD and hL, from the Lipid14 force field⁵⁴ were adopted to mimic the membrane internal environment. The parameters of the metal ions, Pb²⁺ and Sr²⁺, as well as the counter ion, Cl⁻, were acquired from AmberTools18. The AMBER topology file was converted into the GROMACS format by the ParmEd program in AmberTools18. The topology files of CsA in this study, as well as those of some metastable coordinates found in the FELs, are available in the Supporting Information.

Simulation details.

The initial conformer was built by the MOE protein builder, and LowModeMD,⁵⁵ implemented in MOE, was employed to explore the most stable conformer in vacuo. PACKMOL⁵⁶ was used to solvate the molecules (the numbers of the WAT, DMSO, ACN, MeOH, CHCl₃, CHX, and HEX molecules were 2350, 460, 800, 1326, 467, 300, and 209, respectively). The solvated system was initially minimized by the steepest descent, followed by 50,000 steps of NVT calculation. Thereafter, the system was equilibrated via NPT calculation at atmospheric pressure by applying the Berendsen barostat⁵⁷ for 500,000 steps. A positional restraint was imposed on the C_α atoms during the equilibration, and the resultant system was used as an initial structure for the following simulations.

Further, the virtual-system-coupled trivial-trajectory parallelization of multicanonical MD (TTP-V-McMD)^58–60 was adopted to effectively simulate the conformations of the cyclic peptides. In this report, the term “McMD simulations” denotes “TTP-V-McMD simulations” since TTP-V-McMD is a derivative of McMD. Further, 288 pre-McMD runs were initiated for each atom with random velocities at T = 300 K. Afterward, the systems were heated to 1503 K with 5,000 steps, followed by 495,000 steps at 1503 K to randomize the initial structures. Higher temperature 1503 K was adopted to effectively samples cis and trans isomers for the N-methylated amino acids.⁶¹ Flat potential-energy distributions were obtained between 280 K and 1503 K by repeating McMD simulations 10 times in the following eight virtual states: v₀ = [0.0, 0.2], v₁ = [0.1, 0.3], v₂ = [0.2, 0.4], v₃ = [0.3, 0.5], v₄ = [0.4, 0.6], v₅ = [0.5, 0.7], v₆ = [0.6, 0.8], and v₇ = [0.7, 1.0]. The cut-off distance for the Coulombic and van der Waals interactions was 1.0 nm, and PME was employed to calculate the long-range electrostatic interaction. The NVT ensemble was employed for the McMD simulations via the velocity rescaling method (Bussi thermostat).⁶² The LINCS algorithm⁶³ was employed to constrain the bonds with a hydrogen atom, thus enabling a time step of 2.0 fs. For each solvent, 1 × 10⁷ steps × 288 production runs (aggregating 5.76 μs) were performed. The structure and potential energy were stored every 2 ps, and only the coordinates of non-solvent (CsA and metal cation) were saved in the trajectories. The virtual states were exchanged after every 5,000 steps. A resampling method was employed to extract the canonical ensemble at T = 300 K, where the structures were drawn from the simulated ensemble with relative probabilities, following their Boltzmann weights. Typically, ~20,000 conformers were obtained from the resampling method, after which 10,000 conformers were randomly selected to analyze the population of the isomers, as well as their surface areas and NOE violations. The 2.88 million conformers were considered to determine FEL by calculating the potential of mean force (PMF): W = −k_BT ln ρ (k_B is the Boltzmann constant and ρ is the density of states).⁶⁴ An in-house implemented TTP-V-McMD using GROMACS⁶⁵ (version 5.1.4) was employed for the simulations. The densities of bulk solvents were obtained by NPT ensemble at T = 300 K and are confirmed to be close to the experimental values.

Analysis.

Detailed sampling efficiency and convergence analysis of McMD is described in the Figure S1 (See Supporting Information). FELs were analyzed via Principal Component Analysis (PCA; along axes PC-1 and PC-2 at T = 300 K) in each solvent and force field. The distance matrix was calculated from the distances between the C_α atoms of each conformer by aggregating 1,000 conformers at T = 300K in seven solvents using four force fields (28,000 conformers in total). The proportions of variances were 65.1%, 14.6%, and 6.8% for the first, second, and third principal axes, respectively. The free energy value of each representative metastable conformation at (PC-1, PC-2) was calculated from the PMF(PC-1, PC-2) = − k_BT ln P′(PC-1, PC-2), where P′(PC-1, PC-2) is a summation of the density of states near the metastable states with a cut off value of 2k_BT. The NOE violations were calculated, as follows: 20% tolerance was added to the distance of the upper of NOE. The average violation was calculated from the selected ensemble by the program, cpptraj,⁶⁶ in AmberTools18. The number of violations (denoted as cNviol) was also calculated from the summation of Nviolaions, which was obtained from cpptraj for each conformation.

Results and Discussion

FEL using ff03 and representative conformations.

Figure 2a shows the FELs of each solvent using ff03 (For comparison with the other force fields, see Figures S3 and S4 in the Supporting Information). At first glance, a wider conformational space was observed in the polar solvents than in the apolar ones. Figure 2b show the positions of the conformers in PC plane of the experimentally (or a combination of the experimentally and computationally) derived 3D conformations under different conditions, 1–7, and the other representative metastable conformations, A–F found in the FELs. Aligning the closed conformation 1 of the antiparallel beta-strand structure as the horizontal direction and superimposing other conformations on 1, the PC-1 feature can be described as follows: oblong in the vertical direction (PC-1 ≈ −1.2; E), circular shape (PC-1 ≈ 0.0; 4 and D), and oblong in the horizontal direction (PC-1 ≈ 1.5; 1). PC-2 can roughly be considered as the degree of twistedness of the backbone. Notably, except for 7, the experimentally derived conformations were located in the PC-1 > 0 and PC-2 ≤ 0 quadrant, whereas they were scattered from rod- to disk-like phases in the molecular shape space (See the molecular shape discussion in the Supporting Information and Figures S4a–e). The root-mean-square deviations (RMSDs) between the C_α atoms of these conformations are listed in Table S2. The largest RMSD (between the experimentally and computationally derived conformations) was between 3 and C since they were almost orthogonal. Moreover, the smallest RMSDs for the closed and open conformations were observed between 1 and A, and 3 and B, respectively.

Figure 2.

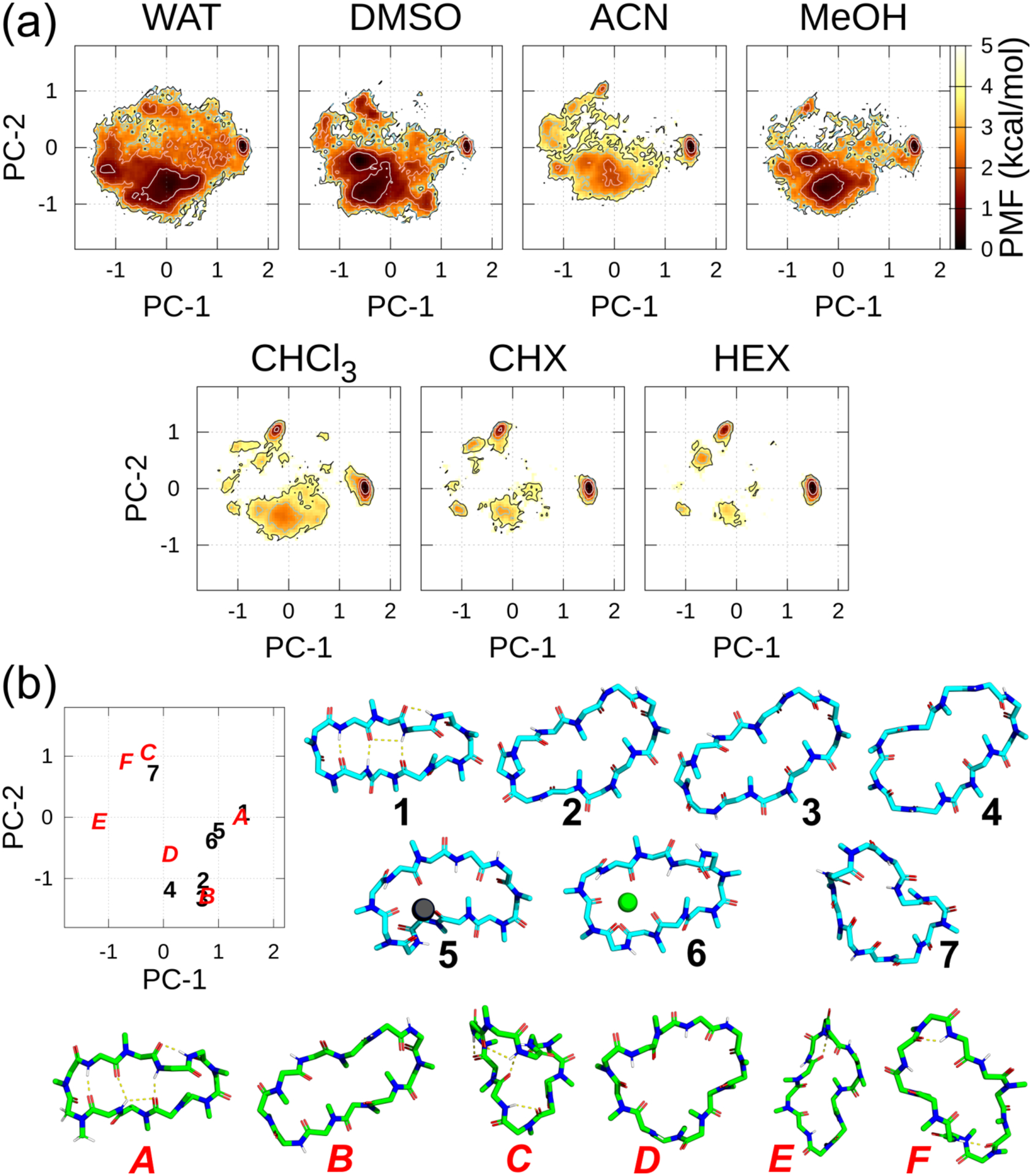
(a) FELs along the PC-1 and PC-2 axes in each solvent at 300 K using ff03. The contour lines of the PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are represented by the white, pink, sky-blue, and black lines, respectively. (b) Relations between the position on the graph and the 3D conformation along the PC plane. In the PC plane, experimentally derived conformations are denoted as black Arabic numbers and actual conformations are shown in sky-blue carbons. The other selected metastable conformations along the PC plane in the T = 300 K ensembles are denoted by red italicized capital letters and conformations are shown in green carbons. Notably, 1 and A almost overlapped completely along the PC plane. Experimentally derived main chain and N-methyl conformations: 1, closed (DEKSAN, source: CSD); 2, open (2Z6W, source: PDB); 3, open (1CSA, source: PDB); and 4, “very open” (1IKF, source: PDB). The following conformations were derived by combining the experimental and computational methods: 5, complexed with Pb²⁺ (the atomic coordinates of the complex listed in SI of Ref. 16); 6, complexed with Sr²⁺ (the atomic coordinates of the complex listed in SI of Ref. 17); and 7, complexed with SDS micelles (the atomic coordinates in SI of Ref. 18). Some selected metastable conformations that were detected in FELs: A–F. The antiparallel beta-strand structure 1 was set as the horizontal orientation, and conformations 2–7, as well as A–F, were superimposed to 1.

With AMBER ff03 (Figure 2a and Table 1), a (meta)stable region in the FELs common to all solvents was found in a small region near (PC-1, PC-2) = (1.4, 0.0). This corresponds to the closed conformation, 1, in Figure 2b, indicating that it can be formed in any of the solvent^22,67 adopted for the calculation. Although its population was relatively low (PMF = 1.2 ~ 2.0 kcal/mol), only the FEL in DMSO exhibited a metastable region for the open conformations (2 and 3) around (PC-1, PC-2) = (0.65, −1.2). The observation of the circular conformation (D) being the most stable conformer and 1 showing relatively low stability in DMSO is consistent with the powerful hydrogen bond accepting capability of DMSO compared to the other polar solvents. In WAT, there was no evident metastable region for 2, although it was on the contour line at PMF = 4.0 kcal/mol. In ACN, although FEL exhibited many metastable conformations, convergence was experimentally observed at one major conformation (population > 90%).¹⁵ However, the distribution in ACN was significantly narrow compared with those in the other polar solvents. It has been reported that 1 was dominant in MeOH and coexisted with a minimum of five minor conformations.²² The FEL of MeOH (Figure 2a) elucidated these phenomena. Notably, the stable region in polar solvents mainly exists around PC-1 ≈ −0.05, indicating that a circular C_α shape (conformation D) was favored in those environments.

Table.1.

Positions of the representative conformation and its free energy value obtained from the FEL in Figure 2a.

ID	(PC1, PC2)	WAT	DMSO	ACN	MeOH	CHCl3	CHX	HEX
1	(1.40, 0.00)	1.00	0.71	0.00	0.75	0.00	0.00	0.00
2	(0.65, −1.05)	2.41	1.35	3.91	3.25	5.41	np	5.79
3	(0.65, −1.35)	3.87	1.98	Np	np	np	np	np
4	(0.15, −1.15)	np	np	Np	np	np	np	np
5	(0.95, −0.20)	2.22	2.92	3.62	2.61	4.36	5.50	5.63
6	(0.95, −0.35)	1.92	2.41	2.87	2.82	4.28	5.43	5.72
7	(−0.20, 0.65)	2.64	4.09	4.34	6.02	3.98	3.67	4.53
A	(1.40, 0.00)	1.00	0.71	0.00	0.75	0.00	0.00	0.00
B	(0.75, −1.30)	2.37	1.21	3.91	3.25	5.41	np	5.79
C	(−0.35, 1.00)	2.90	4.47	1.73	np	0.81	0.91	1.14
D	(0.05, −0.60)	0.00	0.00	0.84	0.00	1.49	2.64	3.03
E	(−1.15, −0.05)	1.92	2.13	2.52	2.83	3.47	3.51	3.85
F	(−0.65, 0.85)	3.89	1.90	2.88	3.47	3.14	2.93	3.42

Unit in kcal/mol. np: no population or higher than 10.0 kcal/mol. For the detailed positions and their values, see Table S3 in the Supporting Information.

Interestingly, the metastable region in the apolar solvents around (PC-1, PC-2) ≈ (−0.2, 0.8) exhibited the same PC-1 and PC-2 values, although two types of conformations were observed. Conformation 7 in Figure 2b, which was observed in the SDS micelles, was located at (PC-1, PC-2, PC-3) = (−0.2, 0.65, 0.3); the number of IMHB (#IMHB) was equal to 0 and 9–10 cis; whereas, conformation C in FELs (Figure 2a) was observed at (PC-1, PC-2, PC-3) ≈ (−0.3, 1.0, −0.1) where it formed twisted saddle-shaped “baseball-stitch” with a 9–10 cis conformation and #IMHB = 3, i.e., Abu²-H–Mva¹¹-O, Val⁵-H–Sar³-O, and Dal⁸-H–Abu²-O. Furthermore, Ala⁷-H was partially H-bonded to Abu²-O or Val⁵-O, which shielded almost all the amide NHs. The average RMSDs of the C_α atoms between 7 and those conformations in CHX and HEX were 2.43 and 2.45 Å, respectively. These correspond to the metastable region around (PC-1, PC-2, PC-3) ≈ (−0.35, 1.0, −0.2) in the polar solvents, indicating that it could act as a “congruent conformation,” as proposed by Witek, et al.⁸

There was no evident metastable region in the metal ion-binding conformations, 5 and 6, in Figure 2a and Table 1, indicating that these conformations required the formation of complex between the metal ion and many carbonyl groups inside the CsA ring. Notably, these conformations could not be simulated in bulk solvents without the ions (conformational changes with a metal ion are discussed below).

FEL using AMBER1x:EHTs.

With AMBER10:EHT, the (meta)stable region in 1 was observed in all the solvents (Figure 3 and Table S4), however, the population in WAT and MeOH was considerably small (PMF = 1.5 ~ 2.2 kcal/mol). There were no metastable regions in the open or “very open” conformations in the polar solvents. Interestingly, AMBER10:EHT with AM1-BCC atomic charges only predicted closed conformation 1 in CHX and HEX.

Figure 3.

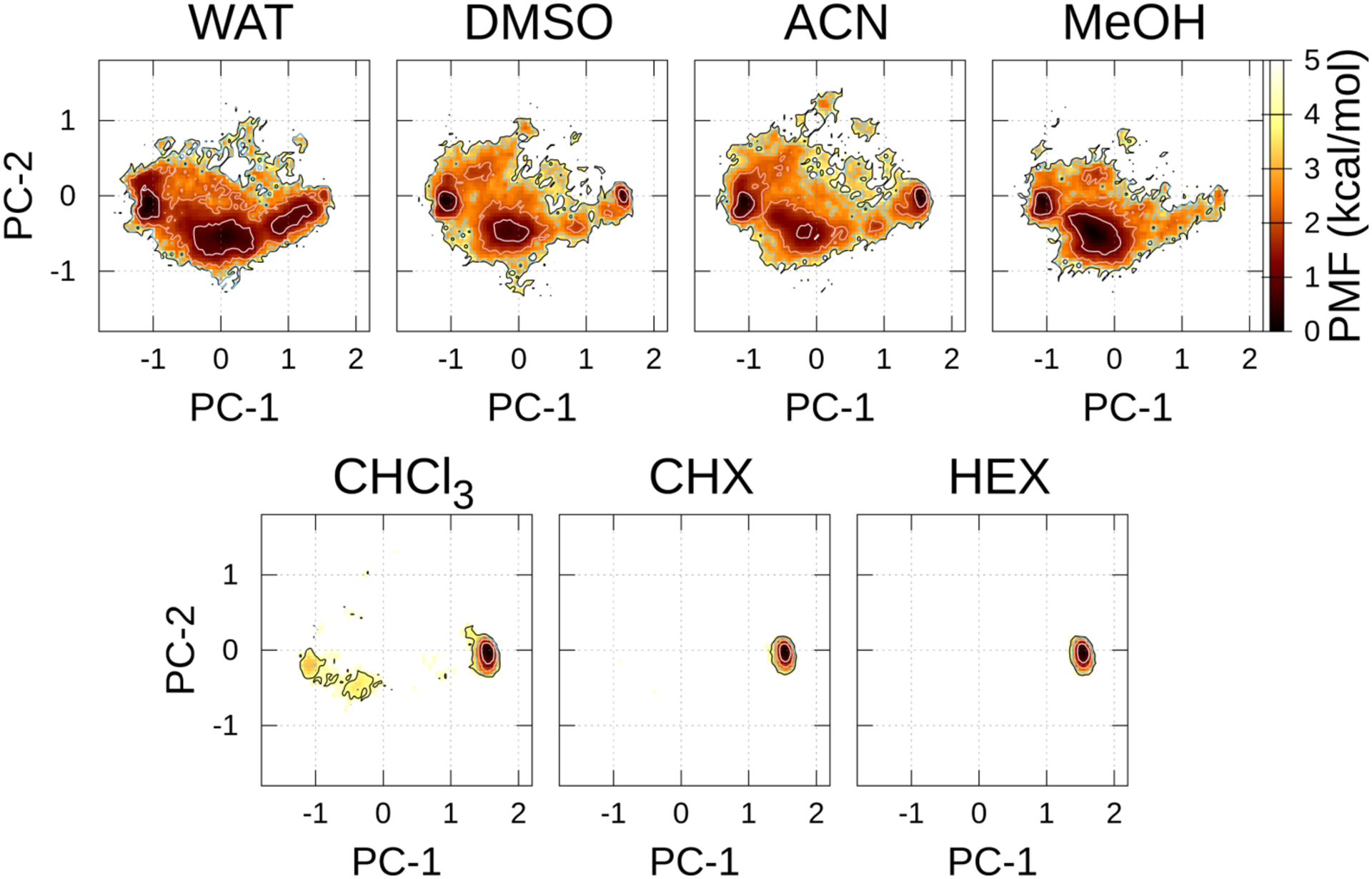
FELs along the PC-1 and PC-2 axes in each solvent at 300 K using AMBER10:EHT. The contour lines of the PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are represented by the white, pink, sky-blue, and black lines, respectively.

With AMBER12:EHT (See Figure S3c and Table S5), metastable region in 1 was observed in apolar solvents, however, no stable region was observed in polar solvents. Additionally, no metastable region was observed for the open or “very open” conformations in the polar solvents, indicating that conformation PC-1 < 0 was favored in the polar and apolar solvents. These results indicated that this force field shows that the vertical conformations (D and E) are dominant. Further, conformation F was mainly observed in the apolar solvents, which formed two IMHB, i.e., Abu²-H–Mle¹⁰-O and Val⁵-H–Sar³-O; Dal⁸-H was exposed to the solvents, and this was not appropriate for membrane-permeable conformation.

With the AMBER14:EHT force field (Figure S3d and Table S6), 1 was observed in the apolar solvents even though many metastable regions existed therein. Further, there was no metastable region for open or “very open” conformations in the polar solvents. Thus, the conformation, PC-1 ≈ −1.0 is favored in the polar solvents, indicating that this force filed shows that the vertical conformations (E and F) are dominant.

Conformational varieties of ω.

The rotational barriers for the cis/trans isomerization of proline or N-methylated amino acid had been experimentally determined (ca. 20 kcal/mol)⁶⁸ and estimated as 14–20 kcal/mol via several enhanced sampling in MD simulations.^9,49,61 Since the McMD protocol in this study can sample the cis/trans isomers of amide and N-methylated amide, the populations of the isomers in each residue, as well as their free-energy profiles along ω, were plotted (Figures 4 and S6–S9). Here an 11-letter code was assigned to each conformation to represent an omega space (cis or trans was denoted as “c” or “t,” respectively) for each of the 11 amino acids. For example, ttttttttttt and tttttttttct (Figure 4) represent all trans and 9–10 cis conformations, respectively. Expectedly, the canonical amino acids (Abu², Val⁵, Ala⁷, and Dal⁸) formed only trans isomers. Regarding the N-methyl amino acids, Mva¹¹ formed only a trans isomer, whereas the other N-methylated amino acids formed the cis and trans isomers.

Figure 4.

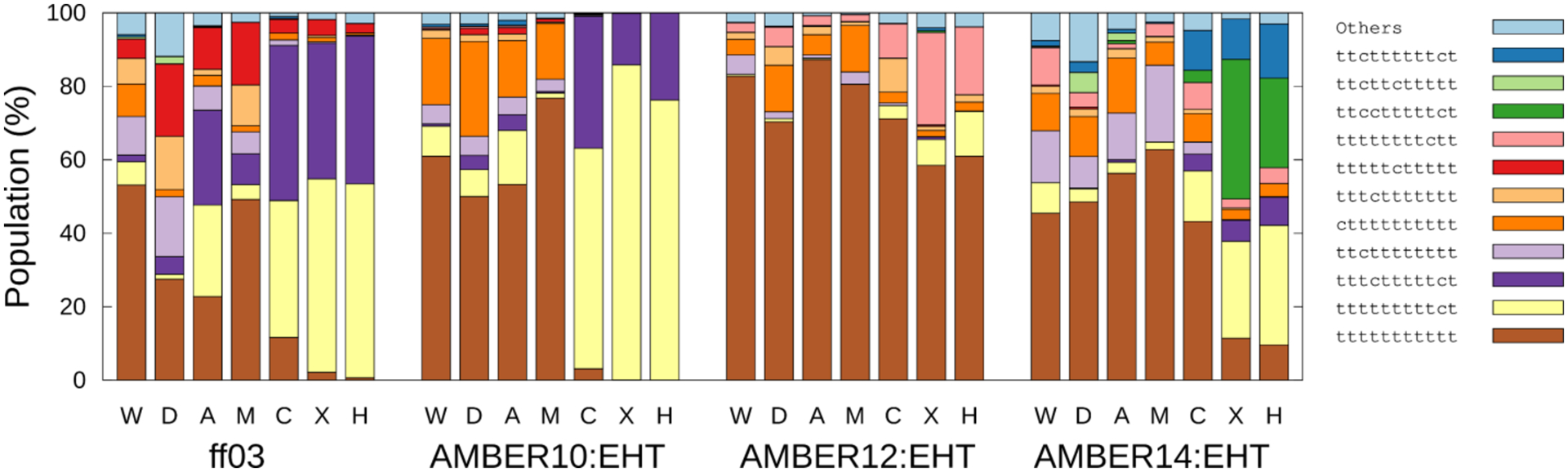
Populations of the cis (c) and trans (t) isomers in the residual position of each solvent and force field. W, D, A, M, C, X, and H denote WAT, DMSO, ACN, methanol, chloroform, CHX, and HEX, respectively.

Unexpectedly, the major conformations using ff03 and AMBER10:EHT in apolar solvents showed the 3–4 cis (cis amide between Sar³ and Mle⁴) and 9–10 cis (tttctttttct) conformations, while the other major conformation showed only one 9–10 cis (tttttttttct) conformation. (See the ω profiles of Mle⁴ and Mle¹⁰ (Figures S6–S9)). Although two cis amide bonds at 3–4 and 9–10 can be a candidate for the minor conformation,^69,70 the population was quite large. Most of both conformations were attributed to the closed conformation 1 which is locate at (PC-1, PC-2) ≈ (1.40, 0.00). These conformations could not be separated along the PC plane, as well as along the molecular shape space (See Figures S4a–d), because only the local structures were different (see below). Although AMBER12:EHT and AMBER14:EHT showed 9−10 cis (tttttttttct) in apolar solvents, it was a minor conformation. AMBER12:EHT exhibited a certain population (up to 75%) of all-trans amide in apolar solvents.

Polar solvents using ff03 showed a wide variety of cis and trans isomers of N-methylated amino acids, indicating that the solvent affects the ratio of cis/trans isomerization. For example, tttttcttttt (the cis isomer between Mle⁶ and Ala⁷) was proposed in DMSO.²¹ However, the effects of the solvents on cis/trans isomerization in the polar solvents were lesser in AMBER1x:EHTs than in ff03 because they were mainly (50%–90%) trans isomers. However, a few conformers with multiple cis amides were mainly observed in DMSO in the ff03 force field, thus contradicting the major trends.

Recently, Gray et al. proposed the compact bent-twisted conformation of CsA via the results of the collision cross-section (CCS) employing the distance geometry conformational sampling.¹¹ They confirmed that a minimum of two cis isomers (3–4 cis and 9–10 cis) existed in the conformation. This conformation is corresponding to the position at (PC-1, PC-2) = (0.5, 0.45), where only AMBER12:EHT exhibited PMF ~ 1.7 kcal/mol and the other force fields has PMF >2.5 kcal/mol using our bulk solvent simulations (Figures 2a and S3), which is completely different from the one we found at (PC-1, PC-2) = (1.4, 0.0) which contains same two cis isomers. Here, the CCSs were also calculated by the CoSIMS program⁷¹ for the ensembles at T = 300 K, although we could not obtain CCS = 271 Ų that correspond to the bent conformation reported by Gray et al. Rather, a bent-twisted conformer comprising only 9–10 cis (C in Figure 2b) might be a candidate for a minor conformation employing the McMD simulations, as discussed above. Another CCS study by Hyung et al.⁵ revealed the bimodal distributions at 272 and 278 Ų via solvent-free replica exchange MD, whereas the three modal distributions at 283, 295, and 315 Ų were determined by our simulation in CHCl₃ using ff03 (See Figure S10a). These differences may be due to the conditions of the simulation, i.e., the selection of an implicit or explicit solvent and the choice of the force field.

The classification, which was adopted by Coco-MD,¹⁰ was also obtained by aggregating the trajectory and in the T = 300 K ensemble, i.e., a 33-letter code was assigned to each conformer in the regions of the ϕ and ψ spaces (gauche-plus, trans, and gauche-minus denoted as “p,” “t,” and “m,” respectively), as well as ω space (c or t) for each of the 11 amino acids. For example, 5847 unique conformations were obtained out of 10,000 in WAT at T = 300 K, and this is larger than the conformations obtained by Coco-MD (9822 out of 20,000), whereas 2594 unique conformations were obtained in CHCl₃ with ff03 at T = 300 K. The unique conformation occupied about 60% of the aggregating trajectory in all the solvents and force fields. However, the populations of the unique conformation depended on the solvent at T = 300 K (Figure S11). These results revealed the effectiveness of sampling conformations via McMD simulation.

NOE violations in the apolar solvents.

We obtained 57, 61, and 79 NOE distances in CDCl₃, CHX-d12, and HEX-d14, respectively (Tables S7–S10). cNviol was obtained by counting the number of NOE violations for each conformer with each force field in the apolar solvents at T = 300 K and projecting them toward the (PC-1, PC-2) plane with a color classified by cNviol (Figure 5). Note that since unrestrained MD trajectories were used to calculate the NOE violations, these are larger than the violation of the structure optimized based on the NOE. Only a few cNviol (0–4; red filled circle) were observed using ff03 and AMBER10:EHT at (PC-1, PC-2) ≈ (1.4, 0.0) in CHCl₃, and this corresponds to 1. However, many cNviol (5−8; dark blue open circle) were observed in this area using ff03 and AMBER10:EHT, indicating the conformation is close to 1, however, some common violations exist in CHCl₃. In contrast, many populations of cNviol (0–4) were observed in CHX and HEX at this area. AMBER12:EHT showed low populations in this area and cNviols were relatively large. AMBER14:EHT showed a certain number of populations in this area with a 9–10 cis (tttttttttct) conformation (Figure 4), however cNviols were large. Although the backbone conformation in this area was predicted in AMBER12:EHT and AMBER14:EHT, neither of them could predict the entire conformation in apolar environments. Therefore, we focused on the ff03 and AMBER10:EHT force fields at (PC-1, PC-2) ≈ (1.4, 0.0) to further investigate the NOE violations.

Figure 5.

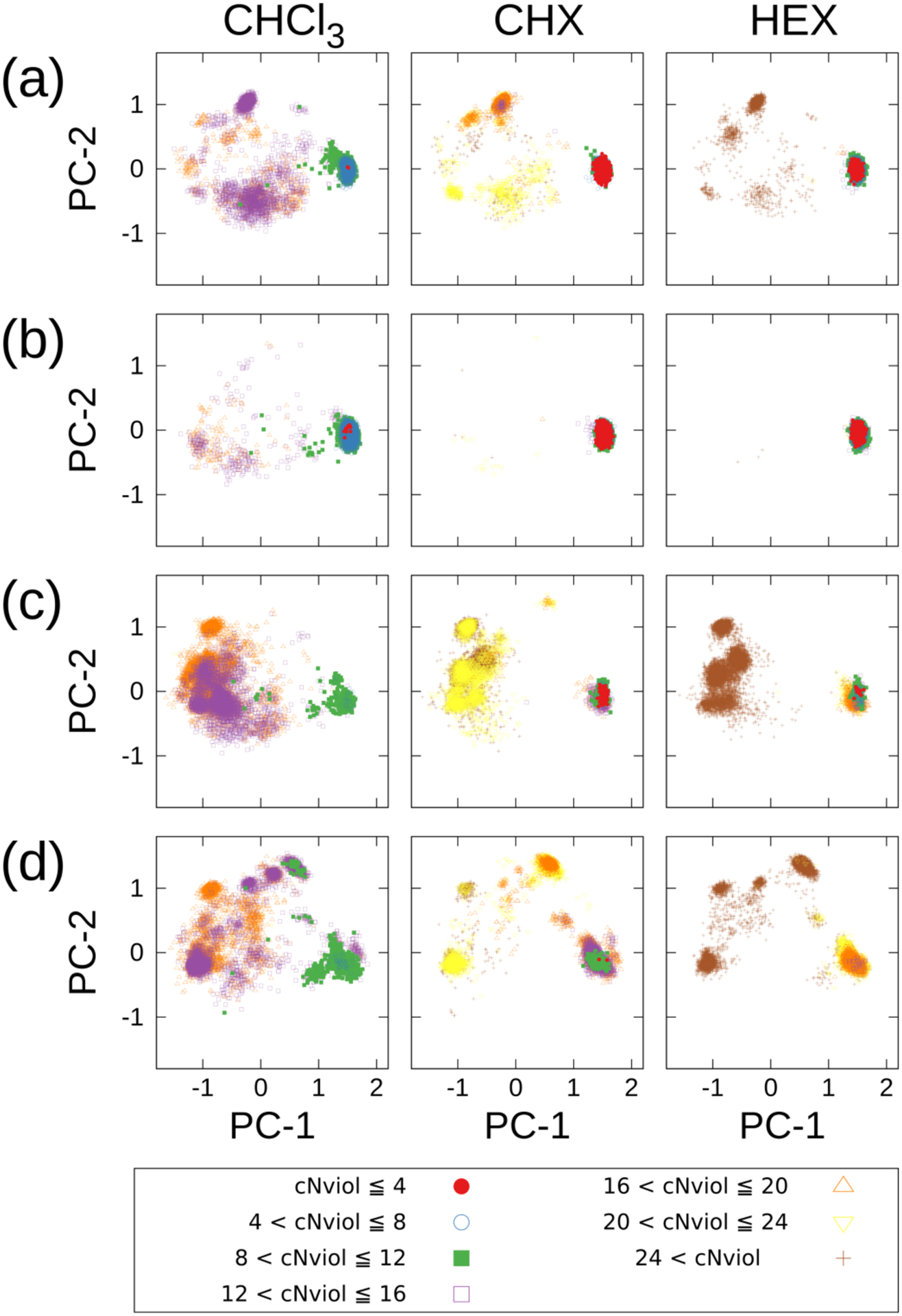
Each conformer in CHCl₃, CHX, and HEX at T = 300K (10,000 conformers) is projected along the (PC-1, PC-2) plane with the color of cNviol’s classes. The color coding was categorized by cNviol = 4. The cNviol was obtained by counting the number of NOE violations for each conformer with each force field. (a) AMBER ff03, (b) AMBER10:EHT, (c) AMBER12:EHT, and (d) AMBER14:EHT.

Types of β-turns between Sar³ and Mle⁴.

Three types of β-turn conformations namely type II′, type II, and 3–4 cis, were obtained between Sar³ and Mle⁴. Although it has been reported that 3–4 cis exists in some CsA analogs,^69,72 direct evidence has not yet been reported regarding CsA in apolar solvents. Figures 6a–f show the violations of type II′, type II, and 3–4 cis β-turns in CHCl₃, CHX, and HEX in the ff03 and AMBER10:EHT force fields. The term, “intercycle,” corresponded to when the atoms of at least two residues were separated, while “sequential” referred to one residue apart. The comprehensive lists of the NOE distances in CDCl₃, CHX-d12, and HEX-d14 are presented in Tables S7–S9. Furthermore, the β-turn conformations are shown in Figures 7a–c. Overall, the positions of the C_α atoms were similar (Figure 7d and Table 2), and the positions of FELs were identical (the stable positions of CHCl₃, CHX, and HEX (Figure 1a)). Notably, neither FELs, which were obtained by the main chains nor heavy atoms, could separate the three types of β-turns (data not shown). However, via the analysis of the NOE violations (Figures 6a–f), type II′ β-turn was favored for the conformations in CHCl₃, CHX, and HEX. First, the overall violations in residues Abu² to Val⁵ are small for type II′ β-turn. Second, the large violations, which were generally observed in type II and 3–4 cis conformations, were between the sequential residual atoms, Sar³-HA12 and Mle⁴-HN? (NOE sequence Nos. 16, 24, and 38 in CHCl₃, CHX, and HEX, respectively. “?” is an atom mask selection syntax that represents one character), in ff03 and AMBER10:EHT. Another large violation, which was observed for type II and 3–4 cis was the intraresidue atoms between Mle⁴-HN? and Mle⁴-HG (No. 65 HEX) using ff03. The average potential energies of the systems were almost the same for the three types of turns within standard deviations (Table 3). Therefore, based on the analysis of ω (discussed above), the excess appearance of the major conformation of 3–4 cis could be ascribed to the accuracy of the force fields.

Figure 6.

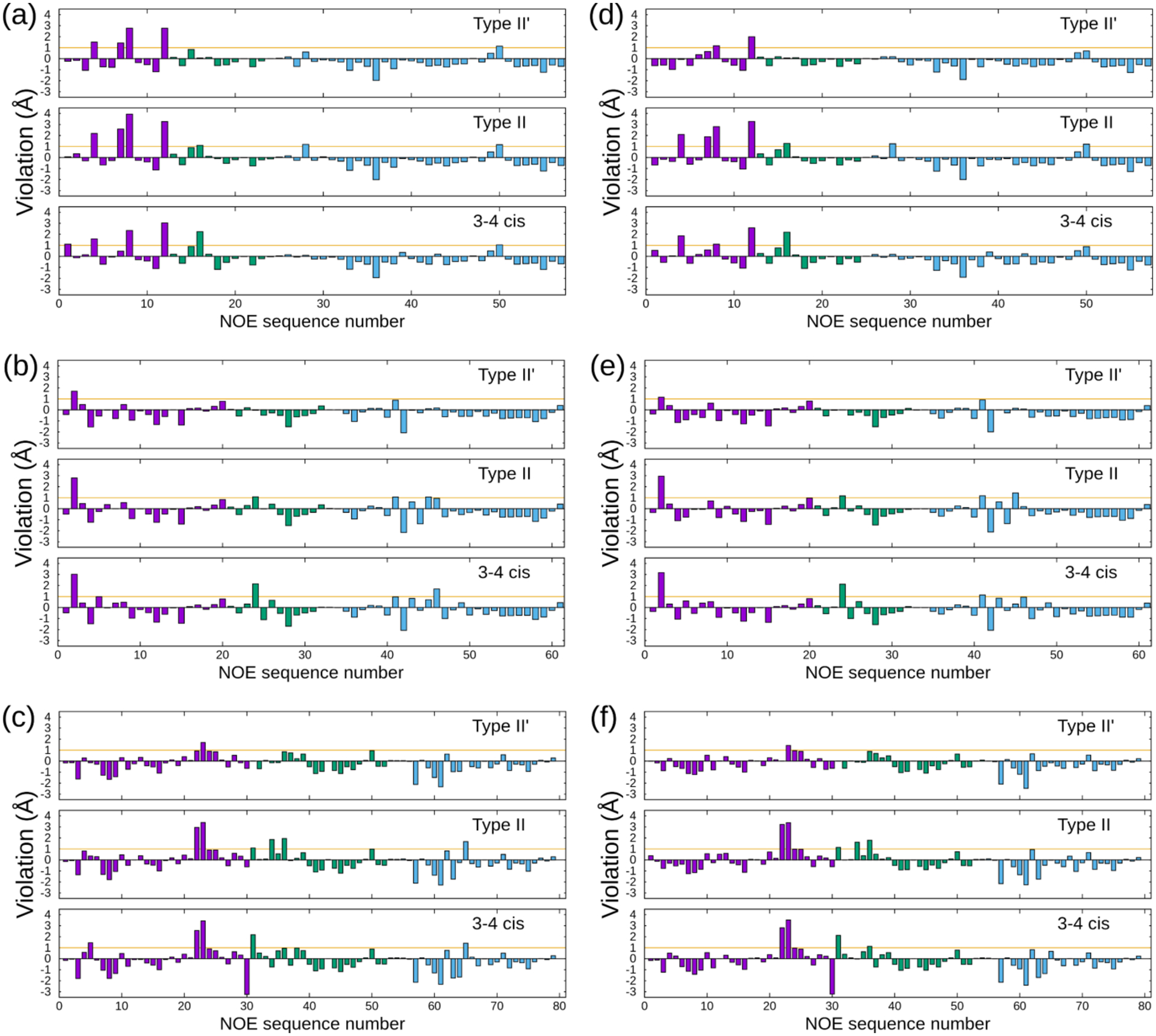
NOE violations of each β-turn conformation using ff03 in (a) CDCl₃, (b) CHX-d12, and (c) HEX-d14. Violations using AMBER10:EHT in (d) CDCl₃, (e) CHX-d12, and (f) HEX-d14. The magenta, green, and cyan bars represent the NOE violations between the intercycle, sequential, and intraresidue, respectively. The numbers of conformations (N_conf), which were employed to calculate the violations, are listed in Table 3.

Figure 7.

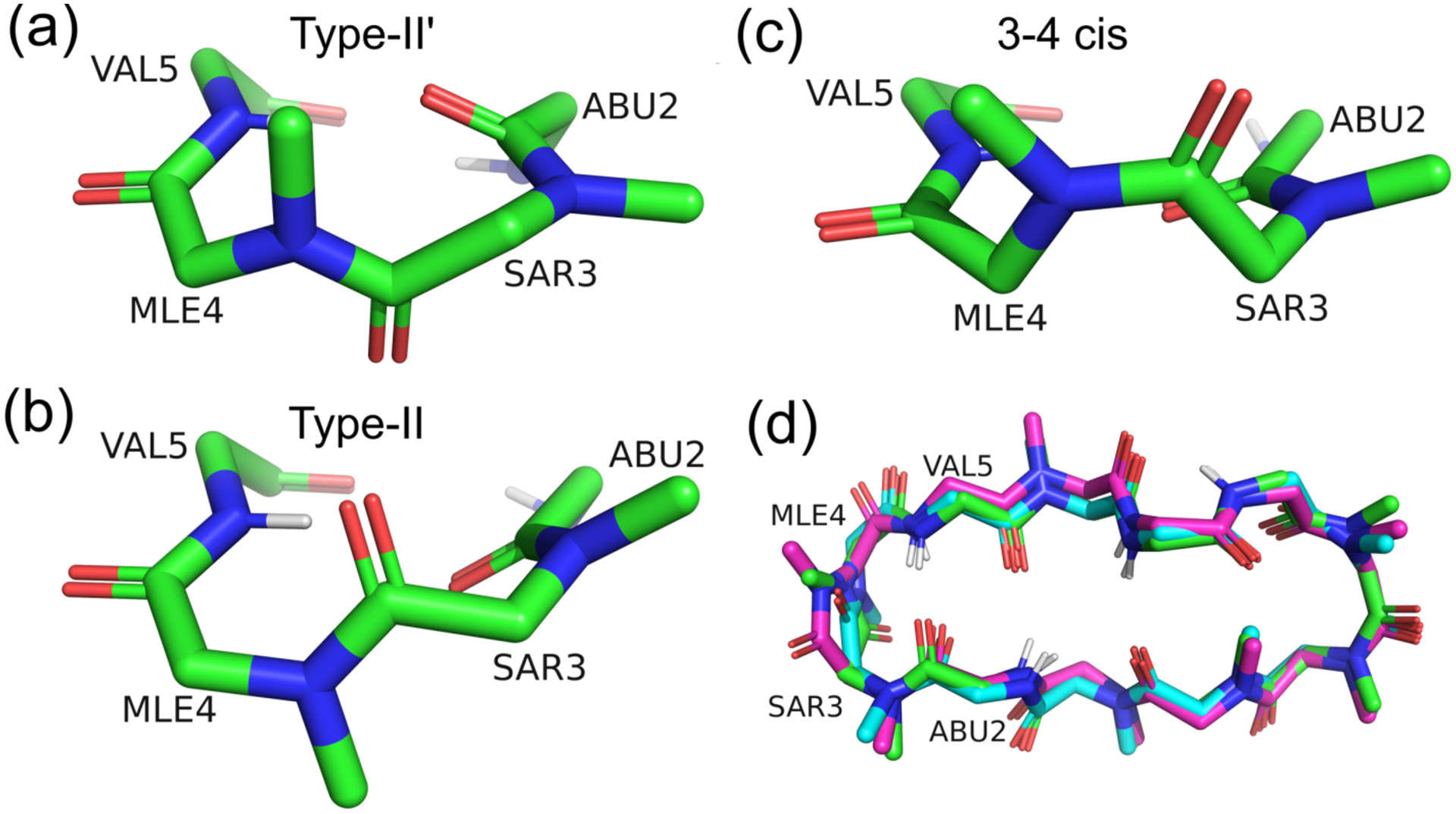
Representative structures of the (a) type II′ β-turn, (b) type II β-turn, and (c) 3–4 cis conformations. (d) Superimpositions of the three types of β-turns. The carbon atoms represented by green, cyan, and magenta correspond to the type II′, type II, and 3–4 cis conformations, respectively. The RMSDs among these conformations are listed in Table 2.

Table 2.

RMSDs Between the C_α Atoms of the β-Turn Conformations in Figure 7d

β-turns	type II′	type II	3–4 cis
type II′	0.00
type II	0.27	0.00
3–4 cis	0.47	0.46	0.00

Unit in angstrom.

Table 3.

Average Potential Energy of Each β-Turn

Solvent	Type	AMBER ff03		AMBER10:EHT
		Potential energiesa	Nconf/Nallb	Potential energiesa	Nconf/Nallb
CHCl3	type II′	−2068.16 ± 31.10	100/1343	−1967.47 ± 30.42	100/5821
	type II	−2062.39 ± 31.51	100/547	−1966.19 ± 31.65	100/357
	3–4 cis	−2063.76 ± 34.82	100/4224	−1966.41 ± 33.07	100/3595
CHX	type II′	2504.51 ± 47.28	100/3046	2652.29 ± 52.29	100/8401
	type II	2516.80 ± 47.43	100/422	2644.81 ± 44.47	100/158
	3–4 cis	2514.66 ± 39.71	100/3741	2654.49 ± 51.12	100/1405
HEX	type II′	2764.98 ± 46.33	100/3835	2884.28 ± 45.13	100/7539
	type II	2765.23 ± 58.91	100/220	2895.75 ± 46.66	49/49
	3–4 cis	2755.76 ± 41.99	100/4027	2890.36 ± 52.69	100/3150

^aUnit in kcal/mol.

^bN_conf was employed to calculate the average potential energy and NOE violations. N_all is the total number of corresponding β-turn conformations out of 10,000 at T = 300 K.

It is critical to know the degrees of fluctuations of the conformers that were attributed to the same conformations. The RMSD of C_α between the top 10 lowest cNviol conformers (type II′ conformation A with tttttttttct) that were obtained using ff03 and AMBER10:EHT in CHCl₃, CHX, and HEX are listed in Tables S11–S13. In CHCl₃, the RMSDs between ff03 and AMBER10:EHT were relatively large; the largest was 1.17 Å (between conformer S4 and S8 with AMBER10:EHT in Table S11). Although the orientations between the sidechains of BMT¹ were different, they formed the antiparallel beta-strand structure. Therefore, they are within the range of thermal fluctuations. Interestingly, much smaller fluctuations were observed in CHX and HEX, indicating the rigidness of 1 in those apolar solvents (Tables S12 and S13).

Sidechain rotamers in apolar solvents.

The relatively large violations, which were observed in the intercycle residues (No. 8) in CHCl₃ using ff03, were investigated by inspecting the conformers of the top 20 lowest cNviols. We observed that the flexibility of the sidechain of Bmt¹ caused this situation. Similarly, a large violation was observed in CHCl₃ between Mle⁶-HB3 and Mle¹⁰-HA (No.12) with ff03 and AMBER10:EHT; it was attributed to the flipping of the sidechain of Mle⁶, which could be due to the accuracy of the force field. The discrepancy between the distance of NOE (2.304 and 3.957 Å in CHX and HEX, respectively) in Mle⁴-HN? and Mle⁴-HB2 (No. 45 and No. 64 in CHX and HEX, respectively) could be attributed to the rotations of their sidechains (the sidechain of Mle⁴ rotated easily in CHX, although it did not in HEX) probably owing to the solvent effects. HEX closely interacted with the Mle sidechain, while CHX loosely interacted with it, implying that there were spaces around the Mle sidechain, which allowed rotation.

Selection of the force field for CsA.

One of the main differences between the ff03 and AMBER1x:EHT force fields is their charge-derivation methods. The atomic charges of ff03 were derived from an implicit solvent model with a low dielectric constant (ε = 4.24), whereas those of AMBER1x:EHTs with AM1-BCC were derived in vacuo. Notably, the atomic charges of all AMBER1x:EHTs were identical; thus, the atomic charge is not the main factor that accounted for the differences in the conformational distributions of AMBER1x:EHTs. Another difference among the force fields is that they have their own main-chain dihedral angle parameters. The force fields of the amino acids were mainly parameterized for the linear peptides and proteins, or recently for IDP/IDR with experimental values and high-level quantum mechanical calculation for the amino acid residues to reproduce their experimental structures.^41,45,46 These parametrizations are generally evaluated by certain amounts of helices, beta structures, loops, and disordered structures. However, those results might be violated for the cyclic peptides. For example, some force fields have been assessed by cyclic peptides.^73,74 Furthermore, our previous study revealed that ff03 adequately supported the experimental structures of some cyclic peptides without requiring the modification of the force field.³⁸

The FELs of the backbone in each solvent and force field (ϕ, ψ) at T = 300 K were plotted (Figures S12–S15). Using ff03, the alpha and beta regions appeared to be well-balanced, whereas with AMBER1x:EHTs, the beta regions were favored and an unusual alpha region (ϕ, ψ) = (−135, 0) was stable. An interesting characteristic of N-methylated amino acids was mainly observed in Mle at (ϕ,ψ) ≈ (‒120, 70), which was proposed to denote the conformation as δ_L⁷⁵ or ζ⁷⁶. Although it was rarely observed in natural amino acids, this region was assigned to a cis isomer of N-methylated amino acids.

Based on the appearances of many 3–4 cis conformers with ff03 and AMBER10:EHT, the accuracy of the ω dihedral angle between the Sar³ and Mle⁴ residues (the simplest peptoid that is connected to an N-methylated amino acid, or two consecutive N-methylated amino acid) was verified. Following two evaluations of the other cyclic compounds were conducted. A peptoid–peptide hybrid (L2N); cyclic-(Leu¹-Pep²-MeLeu³-Leu⁴-D-Pro⁵-MeTyr⁶),^77,78 which exhibited a peptoid at position 2; and NMR experiment in CDCl₃ revealed that L2N showed a major trans isomer (67%) and a minor cis isomer (33%) at position 3. The β-turn structure at Pep²-MeLeu³ is similar to that (i.e., closed conformation (1)) at Sar³-Mle⁴ of CsA. Thus, the McMD simulations of L2N in CHCl₃ and CHX revealed that the cis-MeLeu³ isomer was 0.5–0.9 and 0.0–0.5 kcal/mol more stable than the trans amide isomer with ff03 and AMBER10:EHT, respectively. Therefore, it was evident that those force fields overestimated the cis isomer in this kind of β-turn structure. Another test was conducted for a model system of cyclic peptoid (cyclic-(Sar)₈) in CHCl₃. The ff03 force field correctly estimated that the major conformation exhibited an ω pattern with ccttcctt (80.7%) in the T = 300 K ensemble, and this agrees with the experimental result.^79–81 Conversely, AMBER10:EHT predicted only 25.2% for the ccttcctt pattern.

Based on these results, we concluded that the ff03 force field best described the CsA conformations in different solvents via the analyses of FELs, NOE violations in the apolar solvents, surface areas, populations of the cis/trans isomers, the reproducibility of the closed conformations in all the solvents, and correctly samples open conformation in polar solvent. Although the refinement of the force-field parameters was out of the scope of this study, it is necessary for N-methylated and noncanonical amino acids that are commonly found in cyclic peptides. Consequently, the remaining discussion will only focus on the ff03 force field to evaluate the thermodynamic properties via FEL analyses.

The driving force from a closed conformation to an open one.

To assess this phenomenon via FELs is rather challenging. A direct pathway was not acquired via FELs, e.g., WAT or DMSO (Figure 2a). Previous studies^8,9have conducted at high temperatures (T = 400 K–490 K) to force the transition from a closed to an open conformation. Since the McMD simulations could obtain the FELs at any temperature between 280 K and 1503 K via the reweighting method, we first investigated the FELs at T = 400 K and 500 K with ff03 in Figures S16a and b, respectively. The closed conformation (1) was observed in all the solvents at T = 400 K and 500 K, indicating the stability of this conformation. Moreover, the distributions of FELs were broadened at high temperatures. However, the open conformation (2), which was found on the edges (Figure 2a) of WAT and DMSO disappeared at increased temperatures. Interestingly, a metastable region (PC-1, PC-2) = (0.05, −0.6), i.e., conformation D, in the apolar solvents became more stable at an increased temperature, indicating that the high-temperature canonical MD simulations could not explain the transitions between the open and closed conformations. Thus, there might be another factor that accounted for the conformational change.

Next, we investigate the effects of the metal ions. The addition of a metal ion (Ca²⁺) induced a 9–10 cis to trans isomeric change.^6,11 To explore the effects of metal ions on the conformation, McMD was performed with Pb²⁺ or Sr²⁺ in ACN using ff03 (Figure 8), because the coordinates for those complexes have been proposed using a combination of experimental and computational methods. The overall distributions of the metastable conformations were significantly different from that in pure ACN (without the metal ions). There was no obvious stable region in pure ACN for conformations 5 and 6. Although many metastable conformations, including 5 and 6, appeared in ACN containing metal ions, thereby decreasing the population of 1; the PMF value of 5 in pure ACN was 3.62 kcal/mol, however it decreased to 1.62 kcal/mol when complexed with Pb²⁺. Similarly, the PMF value of 6 in pure ACN was 2.87 kcal/mol, it decreased to 1.08 kcal/mol when complexed with Sr²⁺. In contrast, 1 was the most stable in pure ACN (i.e., 0.0 kcal/mol), but it became less stable 1.28 and 2,26 kcal/mol when complexed with Pb²⁺ and Sr²⁺, respectively. The metal ions break the IMHBs by forming complex with carbonyl groups.^16,17 The radial distribution functions between metal ion and carbonyl oxygens revealed that many carbonyl groups were strongly binding to the metal ions (See Figures S17a and b) except Mle⁴-O, Val⁵-O, and Ala⁷-O. Thus, their effects comprise changing the population of cis/trans isomers of the N-methylated amide; all the trans isomers in pure ACN (22.8%) were increased to 40.0% and 44.7% in the presence of Pb²⁺ and Sr²⁺, respectively. Moreover, the 9–10 cis isomers, including 3–4 cis (50.8%), were decreased to 4.6% and 0.6% in the presence of Pb²⁺ and Sr²⁺, respectively. Therefore, the presence of the metal ions might account for one of the driving forces that determined the population of the 9–10 trans isomers, i.e., the trans isomer between Mle⁹ and Mle¹⁰.

Figure 8.

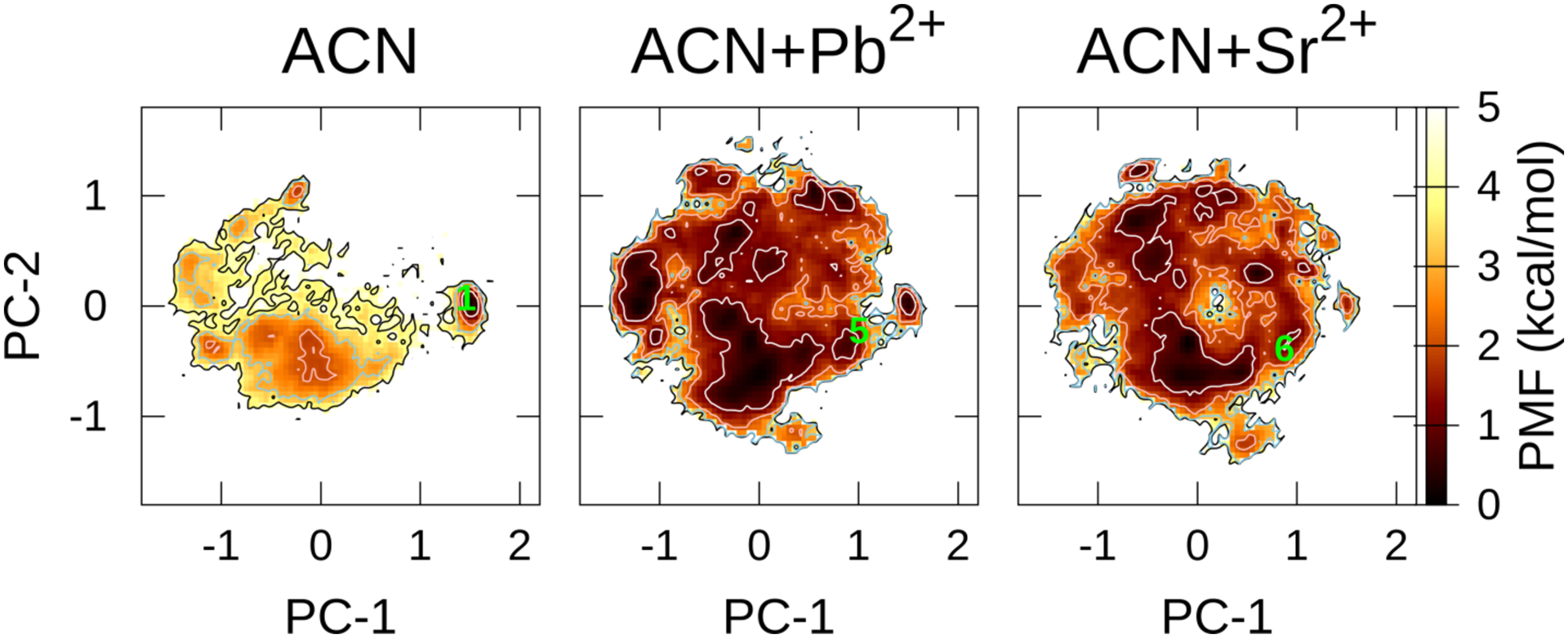
PCA of FELs along the PC-1 and PC-2 axes at T = 300 K in ACN without or with metal ions using ff03. The contour lines of PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are represented by the white, pink, sky-blue, and black, respectively. The Number 1 projected toward FEL is the crystal structures DEKSAN (source: CSD); The Numbers 5 and 6 are derived by combining the experimental and computational methods: 5, complexed with Pb²⁺ (the atomic coordinates of the complex listed in SI of Ref. 16); 6, complexed with Sr²⁺ (the atomic coordinates of the complex listed in SI of Ref. 17). The leftmost panel in ACN using ff03 is identical with one in Figure 2a and is shown here again for comparison with other FELs.

Minor structural changes in CsA.

To evaluate how a minor change in the chemical structure of CsA could affect the FEL, the McMD simulations of cyclosporin E (CsE; Mva¹¹ → Val¹¹) and cyclosporin H (CsH; l-Mva¹¹ → d-Mva¹¹) were performed in CHCl₃ with ff03. These structural changes dramatically affected the FELs (Figure 9). For CsE, similar closed conformation as for CsA was maintained in the metastable conformation near 8 (ID: SUQNUN,⁸² source: CSD). Additional hydrogen-bond donor in CsE was generated a new hydrogen bond (Val¹¹-H–Dal⁸-O), which was not observed in CsA. For CsH, due to the chiral inversion of Mva¹¹, the distribution of the metastable region in the FEL was different from that of the parent molecule. Notably, the crystal conformation (9; ID: AMIFAE,⁸³ source: CSD), which formed the saddle-shaped “baseball-stitch,” was located in a less-stable region (PMF = 3.0 kcal/mol along the PC plane), whereas the crystal structure (10; ID: DUDQAU,⁸⁴ source: CSD) was found in the metastable region of FEL. These structural differences could be attributable to the difference between the crystal and solution environments, as well as the crystal forms.⁸³

Figure 9.

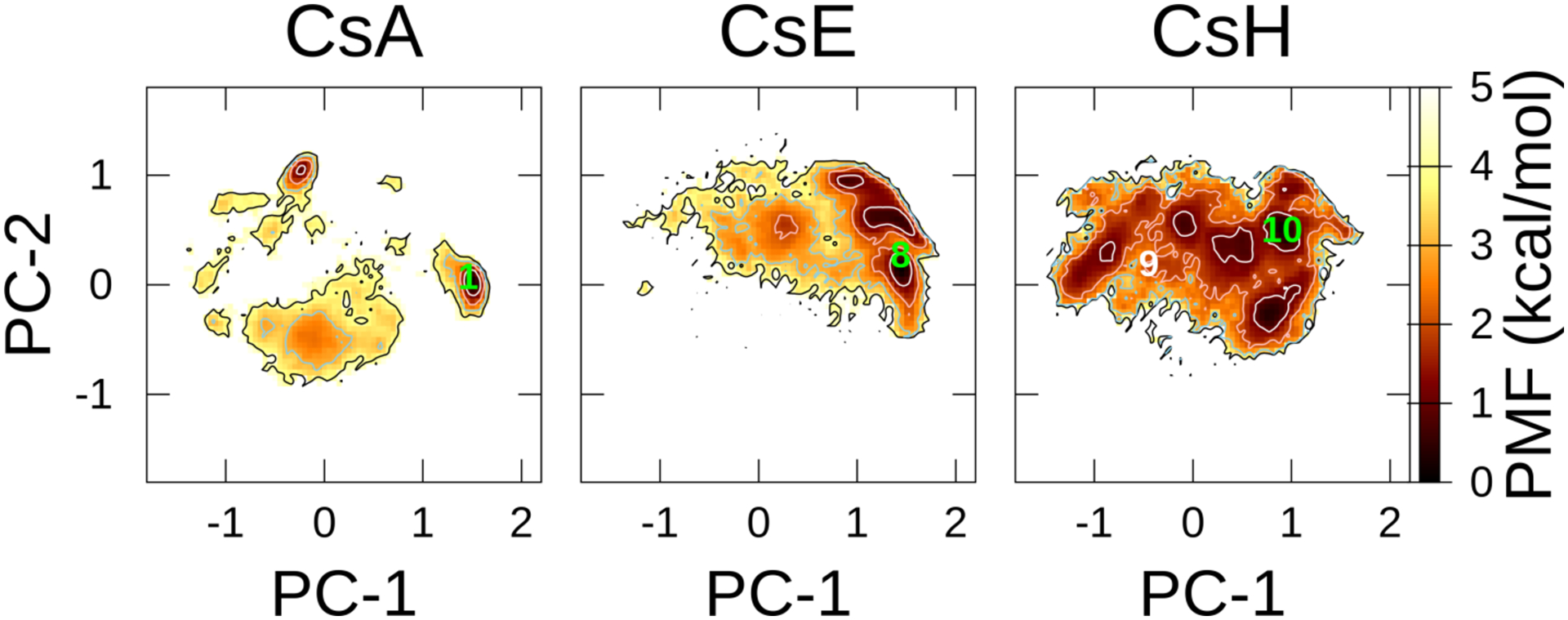
FELs of CsA, CsE, and CsH in CHCl₃ at T = 300 K using ff03. The contour lines of PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are represented by the white, pink, sky-blue, and black colors, respectively. Numbers 1, 8, 9, and 10 that are projected toward FELs are the crystal structures, DEKSAN, SUQNUN, AMIFAE, and DUDQAU (source: CSD), respectively. The leftmost panel of CsA is identical with the one in Figure 2a and is shown here again for comparison with the other FELs.

These results demonstrate that only a minor chemical structural change (N-methylation or chiral inversion) could exert a major impact on the distribution of FEL. Therefore, what we would like to emphasize here is, detailed conformational space analysis of each cyclic peptide is required, even for a minor structural change.

Conclusions

We conducted McMD to assess CsA in different solvents using different AMBER force fields and concluded that the AMBER ff03 force field best described the chameleonic behaviors of CsA. The cis and trans isomers between Mle⁹ and Mle¹⁰ (9–10 cis and 9–10 trans) were correctly predicted in polar and apolar solvents. NOEs valuably revealed that largely the same conformations (closed conformation in CHCl₃) existed in CHX and HEX.

The chameleonic behaviors, which were inferred by ff03, were summarized, as follows: CsA intrinsically exhibited stable closed forms with 9–10 cis in polar and apolar solvents. When permeating a membrane, the closed-form (1) or minor conformations in CHCl₃, CHX, and HEX (twisted saddle-shaped “baseball-stitch” conformation, C) were formed in the polar and apolar solvents, thus supporting the “congruent conformational states” model.⁸ The conformational selection like (CSL) model²⁵ is considered to be an oversimplified model for CsA, as it was shown from our results that there might be exist some common minor conformations in polar and apolar solvents. When binding to the partner protein(s), it was speculated that a metal ion near the protein would interact with CsA to facilitate cis/trans isomerization and form 9–10 trans, thus generating the binding conformations (2–4). Many minor conformations present in all solvents could be studied from the ensemble; each of them could be a candidate for the experimentally undetermined minor conformations (e.g., in DMSO, MeOH, and CHCl₃).

Although further studies are required to modify the force fields regarding the ϕ, ψ, ω, and χ dihedral angles to accurately predict the populations of the cis and trans amide isomers, this McMD simulation protocol employing different solvents ensures the conformational sampling, permeation modeling, and the prediction of the binding conformation of cyclic peptides.

ABBREVIATIONS

ACN

acetonitrile

CCS

collision cross-section

CHX

cyclohexane

CsA

cyclosporin A

CsE

cyclosporin E

CsH

cyclosporin H

DMSO

dimethyl sulfoxide

EHT

extended Hückel theory

FEL

free energy landscape

HEX

n-hexane

IDP

intrinsically disordered protein

IDR

intrinsically disordered region

IMHB

intramolecular hydrogen bond

McMD

multicanonical molecular dynamics

MeOH

methanol

PCA

principal component analysis

SASA

solvent-accessible surface area

WAT

water

Data and Software Availability

The topology files of CsA using each force field, as well as the sample coordinate files, are provided in section SI2 in SI.

Further information and requests for custom scripts and an McMD patch of GROMACS should be directed to the corresponding author (S.O.). All the production trajectories generated in this study are available from the corresponding author (S.O.) upon request. The free software can be obtained via the following links: GROMACS (https://manual.gromacs.org/documentation/), AmberTools (tleap, parmed, cpptraj) (https://ambermd.org/AmberTools.php), R.E.D. version III (https://upjv.q4md-forcefieldtools.org/RED/), PyMol (https://github.com/schrodinger/pymol-open-source), gnuplot (http://www.gnuplot.info/), CoSIMS (https://github.com/ChristopherAMyers/CoSIMS), and PACKMOL (https://github.com/m3g/packmol). The commercial software, MOE, was purchased from Molsis (https://www.molsis.co.jp/lifescience/moe/). The NMR spectra were processed by the software, MNova, from Mestrelab Research (https://mestrelab.com/download/mnova/).