Analysis of serological surveys of antibodies to SARS-CoV-2 in the United States to estimate parameters needed for transmission modeling and to evaluate and improve the accuracy of predictions

Abstract

Seroprevalence studies can estimate proportions of the population that have been infected or vaccinated, including infections that were not reported because of the lack of symptoms or testing. Based on information from studies in the United States from mid-summer 2020 through the end of 2021, we describe proportions of the population with antibodies to SARS-CoV-2 as functions of age and time. Slices through these surfaces at arbitrary times provide initial and target conditions for simulation modeling. They also provide the information needed to calculate age-specific forces of infection, attack rates, and – together with contact rates – age-specific probabilities of infection on contact between susceptible and infectious people.

We modified the familiar Susceptible-Exposed-Infectious-Removed (SEIR) model to include features of the biology of COVID-19 that might affect transmission of SARS-CoV-2 and stratified by age and location. We consulted the primary literature or subject matter experts for contact rates and other parameter values. Using time-varying Oxford COVID-19 Government Response Tracker assessments of US state and DC efforts to mitigate the pandemic and compliance with non-pharmaceutical interventions (NPIs) from a YouGov survey fielded in the US during 2020, we estimate that the efficacy of social-distancing when possible and mask-wearing otherwise at reducing susceptibility or infectiousness was 31% during the fall of 2020. Initialized from seroprevalence among people having commercial laboratory tests for purposes other than SARS-CoV-2 infection assessments on 7 September 2020, our age- and location-stratified SEIR population model reproduces seroprevalence among members of the same population on 25 December 2020 quite well.

Introducing vaccination mid-December 2020, first of healthcare and other essential workers, followed by older adults, people who were otherwise immunocompromised, and then progressively younger people, our metapopulation model reproduces seroprevalence among blood donors on 4 April 2021 less well, but we believe that the discrepancy is due to vaccinations being under-reported or blood donors being disproportionately vaccinated, if not both. As experimenting with reliable transmission models is the best way to assess the indirect effects of mitigation measures, we determined the impact of vaccination, conditional on NPIs. Results indicate that, during this period, vaccination substantially reduced infections, hospitalizations and deaths.

This manuscript was submitted as part of a theme issue on “Modelling COVID-19 and Preparedness for Future Pandemics.”

1. Introduction

Mitigating outbreaks with pandemic potential has been compared to building ships while sailing or planes while flying, metaphors that emphasize the uncertainties associated with newly emerging human pathogens. While each pathogen is unique, historical pandemics share many characteristics. Most have resulted from respiratory diseases caused by airborne pathogens (Wang et al., 2021), the substance of much mathematical epidemiology. Model evaluations of possible strategies can inform public policymaking, but unless predictions are accurate, the utility of forecasts or simulated scenarios is questionable (Ioannidis et al., 2022).

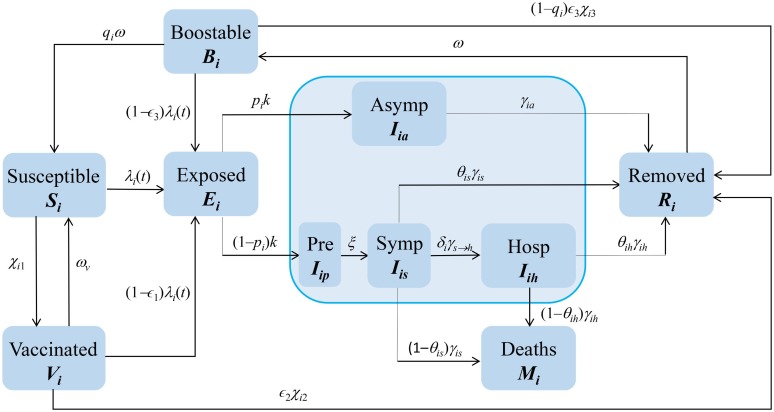
Early in the COVID-19 pandemic, we built a framework (superstructure in the airplane or shipbuilding analogy) that we could use, together with local information, to answer urgent public health questions. We chose the Susceptible-Exposed-Infectious-Removed (SEIR) epidemiological structure, but included biological features of COVID-19 that might affect the transmission and control of SARS-CoV-2, including asymptomatic, pre-symptomatic and hospitalized states, disease-induced mortality, and vaccination (Fig. 1 ).

Fig. 1.

Diagram of a modified SEIR Model. This metapopulation model includes asymptomatic and pre-symptomatic stages, disease-induced mortality, vaccination, and the waning and boosting of immunity, features of COVID-19 that affect SARS-CoV-2 transmission. It is cross-classified by age and location.

In earlier work, we modeled SARS-CoV-2 transmission in host populations stratified by age or location to assess the impact of various non-pharmaceutical interventions (NPIs). Here we model transmission in the United States’ population stratified by both age and location (the 50 states plus Washington, DC, but neither Puerto Rico nor other territories) considering infection- and vaccination-acquired immunity equivalent. As susceptibility to SARS-CoV-2 reinfection may depend on the variant with which previously infected (Rössler et al., 2022) and waning of immunity from that infection or vaccination, elsewhere we have stratified hosts by exposure to more or less related variants and by infection, vaccination, and both (in preparation).

Here we determine the simpler model’s ability to reproduce transmission in the United States during the last quarter of 2020, when the ancestral strain was circulating and NPIs were in effect, and first of 2021, when vaccination began and the alpha variant became dominant (Lambrou et al., 2022). After demonstrating the accuracy of this particular metapopulation (a term coined by Levins in 1969 for a population composed of sub-populations) framework, we evaluate the impact of vaccinating healthcare and other essential workers, then elderly, otherwise immunocompromised, and finally, healthy younger people, conditional on NPIs. And we discuss an alternative strategy, results of whose evaluation we report elsewhere (Vo et al., submitted).

2. Methods

2.1. Model Equations

The model diagrammed in Fig. 1 can be represented as a system of ordinary differential equations, where S_i is the number who are susceptible in group i (here i indexes ages, locations, or combinations; there are n such groups), E_i is the number who have been infected, but are not yet infectious, V_i is the number who have received one dose of vaccine (≥14 days ago), I_iw (w = a, p, s, h) are the numbers infectious in group i who are asymptomatic, pre-symptomatic, symptomatic, or hospitalized, R_i is the number who have recovered or been vaccinated a second time (≥14 days ago), and are temporarily immune, B_i is the number whose immunity has waned, but can be boosted by revaccination, and M_i is the number in group i who have died:

$$\begin{array}{l}\begin{array}{l}{S}_i^{\text{'}}=q_i\omega B_i+{\omega }_v{V}_i-\left[{\lambda }_i\left(t\right)+{\chi }_{1i}\right]S_i,\\ B_i^{\text{'}}=\omega R_i-\left[q_i\omega +(1-q_i){∊}_3{\chi }_{3i}+(1-{∊}_3){\lambda }_i\left(t\right)\right]B_i,\end{array}\\ \begin{array}{l}{E}_i^{\text{'}}={\lambda }_i\left(t\right)S_i+(1-{∊}_1){\lambda }_{\mathrm{i}}\left(t\right)V_i+(1-{∊}_3){\lambda }_i\left(t\right)B_i-k{E}_i,\\ V_i^{\text{'}}={\chi }_{1i}{S}_i-\left[(1-{∊}_1){\lambda }_i\left(t\right)+{\omega }_v+{∊}_2{\chi }_{2i}\right]V_i,\end{array}\\ I_{\mathit{ia}}^{\text{'}}=k{p}_i{E}_i-{\gamma }_{\mathit{ia}}{I}_{\mathit{ia}},\\ I_{\mathit{ip}}^{\text{'}}=k(1-p_i)E_i-\xi I_{\mathit{ip}},\\ I_{\mathit{is}}^{\text{'}}=\xi I_{\mathit{ip}}-[{\gamma }_{\mathit{is}}+{\delta }_i{\gamma }_{\mathit{is}\to h}]I_{\mathit{is}},\\ I_{\mathit{ih}}^{\text{'}}={\delta }_i{\gamma }_{\mathit{is}\to h}{I}_{\mathit{is}}-{\gamma }_{\mathit{ih}}{I}_{\mathit{ih}},\\ R_i^{\text{'}}={\gamma }_{\mathit{ia}}{I}_{\mathit{ia}}+{\theta }_{\mathit{is}}{\gamma }_{\mathit{is}}{I}_{\mathit{is}}+{\theta }_{\mathit{ih}}{\gamma }_{\mathit{ih}}{I}_{\mathit{ih}}+{∊}_2{\chi }_{2i}{V}_i+(1-q_i){∊}_3{\chi }_{3i}{B}_i-\omega R_i,\\ M_i^{\text{'}}=(1-{\theta }_{\mathit{is}}){\gamma }_{\mathit{is}}{I}_{\mathit{is}}+(1-{\theta }_{\mathit{ih}}){\gamma }_{\mathit{ih}}{I}_{\mathit{ih}},i=1,2,...,n,\end{array}$$

where the force or hazard rate of infection among susceptible people in group i (and those receiving one vaccine dose, whose susceptibility to infection is 1 – ∊ ₁, where ∊ ₁ is the efficacy of a single dose) is

$$\begin{array}{c}{\lambda }_i(t)={\psi }_{\mathit{iS}}{a}_i{\beta }_i\sum _{j=1}^n{c}_{\mathit{ij}}{\psi }_{\mathit{jI}}\frac{{\eta }_{\mathit{ja}}{I}_{\mathit{ja}}(t)+{\eta }_{\mathit{jp}}{I}_{\mathit{jp}}(t)+I_{\mathit{js}}(t)+{\eta }_{\mathit{jh}}{I}_{\mathit{jh}}(t)}{N_j},\text{where}\\ N_j=S_j+B_j+E_j+V_j+I_{\mathit{ja}}+I_{\mathit{jp}}+I_{\mathit{js}}+I_{\mathit{jh}}+R_j+M_j\text{and}N=\sum _{j=1}^n{N}_j.\end{array}$$

In this expression, ${\psi }_{\mathit{iS}}=1-c_i{b}_{\mathit{iS}}$ and ${\psi }_{\mathit{iI}}=1-c_i{b}_{\mathit{iI}}$ represent reductions in susceptibility and infectiousness, respectively, due to physical-distancing if possible and mask-wearing otherwise, c_i is the proportion of group i that comply with such recommendations and b_iS and b_iI are their respective efficacies. Here the parameter a_i is the per capita contact rate, β_i is the probability of transmission per contact between susceptible and infectious people (a_i × β_i is the effective contact rate), and c_ij is the proportion of their contacts that members of group i have with those of group j. As we are interested in relatively short periods during which M_j is small relative to N_j, we maintain N constant by including M_j in the equation for N_j.

Values for most transmission model parameters can be found by carefully reviewing the primary literature or consulting subject-matter experts (Table 1, Table 2 ). But the probabilities of infection upon contact must be obtained from populations of interest. In the following sections, we describe seroprevalence – the humoral (versus cell-mediated) component of the adaptive immune response – as a function of age and time from a study involving assays of residual sera from commercial laboratory tests for purposes other than SARS-CoV-2 infection assessments, and then estimate forces of infection and attack rates for n discrete age groups. Finally, given age-specific contact rates and proportions with each of those groups from the literature, we calculate the requisite probabilities by solving n equations, each with one unknown.

Table 1.

Symbol definitions, approximate values, and sources.

Symbol	Meaning	Values	Source
pi	Proportions of Infectious people who are Asymptomatic (or Symptomatic, 1 – pi)	Tbl 2	Clark, et al. 2020
qi	Proportions not receiving booster doses when eligible	‡
k	Per capita rate of progression from Exposed, E to Asymptomatic, Ia or Pre-symptomatic, Ip (1/3 to 1/5 days depending on variant)	1/4 dys	He, et al. 2020
ξ,γs→h	Per capita rates of progression from Pre-symptomatic, Ip to Symptomatic, Is and Symptomatic to Hospitalized, Ih	1/2 dys	He, et al. 2020
γa	Per capita rate at which people with Asymptomatic infections recover (become no longer infectious)	1/7
γs	Per capita rate at which people with Symptomatic infections who are not hospitalized recover (again, become no longer infectious)	1/5 dys	He, et al. 2020
γh	Per capita rate at which Hospitalized people recover (NB: may well differ from the discharge rate)	1/10 dys
θw	Proportions of Symptomatic people who Recover (or Die, 1 – θw), which may differ among those Hospitalized (w = s, h)	Tbl 2	Levin, et al. 2020
δi	Proportions of Symptomatic people who are Hospitalized (proportions with 2+ co-morbidities)	Tbl 2	Clark, et al. 2020
χ1i, χ2i, χ3i,	Per capita immunization rates, ${\chi }_i=-\ln [1-{\nu }_i]/\delta t,$where vi is the coverage attained during period δt	‡
∊1, ∊2, ∊3	Probabilities of protection upon contact with infectious people 14 or more days after first, second, and booster doses	0.93	El Sahly, et al. 2021
ω, ωv	Per capita rates at which infection- and vaccine-induced immunity is lost	1/365 dys
ci	Proportion of people complying with social distancing or mask wearing recommendations (compliance)	Tbl 2	Jones et al., 2021
bS, bI	Reduced susceptibility or infectivity (efficacy) by virtue of complying with physical-distancing where possible and mask-wearing otherwise	0.31	Estimated
ηw	Scaling constants (w = a, p, h) representing the infectivity of Iia, Iip, Iih relative to Iis	0.5, 1.25, 0.1

Notes: We assume that people with asymptomatic infections are less infectious than those with symptomatic ones, but that their sojourns are the same. ‡Calculated from reports summarized on https://data.cdc.gov/.

Table 2.

Parameter values for age-stratified transmission modeling in the United States

Age	Population numbers	Population proportions	Pr(asymp|inf)	Pr(hosp|inf)	IFR (percentages)	Compliance
0-4	19,676,332	0.059444636	0.981400373	1.0435E-05	0.0008	0.706360069
5-9	20,045,152	0.060558887	0.972064267	0.000143099	0.001312163	0.715211185
10-14	21,089,487	0.063713953	0.969763501	0.00027027	0.002400084	0.71952257
15-19	21,242,908	0.064177457	0.960291933	0.003637205	0.004390005	0.720175768
20-24	22,258,745	0.067246426	0.941577238	0.006854725	0.00802978	0.71795013
25-29	23,835,330	0.072009485	0.913456364	0.017709616	0.014687309	0.713574937
30-34	23,052,479	0.069644395	0.880594618	0.025217824	0.026864628	0.707771036
35-39	21,615,791	0.065303982	0.839642887	0.035166793	0.049138219	0.701279533
40-44	20,294,599	0.061312498	0.775783537	0.037368978	0.08987895	0.694876881
45-49	20,053,798	0.060585008	0.708076043	0.051520404	0.164398026	0.689376822
50-54	20,577,807	0.062168104	0.623043155	0.062486388	0.300701205	0.685620487
55-59	21,542,270	0.065081866	0.521907521	0.083247801	0.550014019	0.684456022
60-64	20,669,143	0.062444041	0.421531351	0.090697794	1.006033295	0.686708224
65-69	17,819,027	0.053833488	0.328351424	0.110144916	1.840140307	0.693136453
70-74	14,354,863	0.043367819	0.2503706	0.118491978	3.365809369	0.704376296
75+	22,874,916	0.069107955	0.163464241	0.139755917	14.30030403	0.744380002
Wtd Avg			0.715196	0.047154	1.373312	0.705841

Notes: Populations, proportions without co-morbidities (assumed asymptomatic) and requiring hospitalization if infected are from Clark et al. (2020), the infection-fatality ratios (IFRs) are from Levin et al. (2020), and the compliances are our estimates, obtained from Jones (2020) as described in the text.

2.2. Forces of Infection

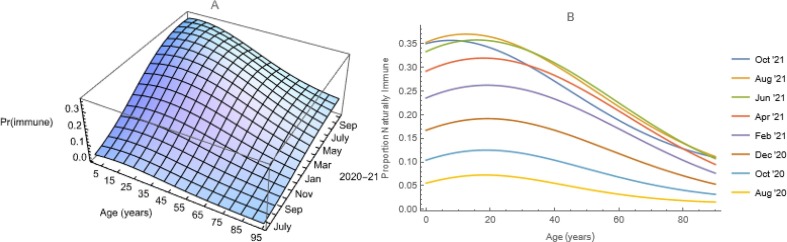
First, we model national and location-specific proportions seropositive from studies of commercial laboratory tests, described by Bajema et al. (2021), or blood donors, described by Jones et al. (2021), as functions of both age and time via bivariate logistic regressions in which the independent variables are represented via third-order polynomials and, because subjects aged a at time t are aged a+1 at time t+1, all interactions (Fig. 2 a). Where observations were lacking, we used adjacent ones (e.g., DC is a composite of MD and VA). While we used line-listings, public-use summaries of these and other CDC data are available at: https://covid.cdc.gov/covid-data-tracker/#datatracker-home.

Fig. 2.

Seroprevalence in the United States. a) Bivariate logistic regression of observations from analyses of surplus sera from commercial laboratory testing for purposes other than evaluation of possible exposures to SARS-CoV-2. b) Slices through the surface at arbitrary times.

Then we discretize these proportions (i.e., assume that they are constant within intervals, Feng and Glasser 2019a). Ages and times were recorded in conventional units, but such surfaces are continuous, so we can choose any intervals. Information needed for transmission modeling typically is available in 5-year age groups, so we chose age unit years. Time is continuous in most of our models, so we chose time unit days. We number these discrete periods a ₀ = 0, a ₁ = 1, a ₂ = 2, ...; t ₀ = 0, t ₁ = 1, t ₂ = 2, and so on. Here we use the indices a and t to denote continuous age and time and i and j to denote their discrete analogs.

Because all SARS-CoV-2 vaccines used in the United States target the spike protein, most vaccinated people have anti-spike (anti-S) antibodies. Most infected people also have antibodies to a nucleocapsid protein (anti-N antibodies). The national commercial laboratory seroprevalence study includes all ages, but measures only anti-N. The blood-donor study measures antigens to both spike and nucleocapsid proteins, but does not include children. While neither study population is a random sample, their anti-N seroprevalences are comparable (results not shown). We use results from both studies in this work.

Post-vaccination onset, we let S(i, j) = 1 – I_B(i, j) denote the proportion susceptible among those aged a_{i -1} ≤ a < a_i at time t_{j -1} ≤ t < t_j, where the proportion immune, I_B = I_I + I_V, with I_I by virtue of infection and I_V vaccination (i.e., 1 – I_B is the probability of having escaped both). Further, we let λ(i, j) and χ(i, j) denote the specific rates of infection and immunization in the appropriate intervals of age and time.

Because neither I_I(i, j) nor I_V(i,j) increases monotonically with age, but both increase monotonically with time (Fig. 2b), and forces of infection and vaccination can be calculated using either (Hens et al., 2010), we write $S(i,j)=S(i,j-1)exp\left\{-\left[\lambda (i,j)+\chi (i,j)\right]\right\},$ which leads, first by rearrangement and then by substitution, to $\lambda \left(i,j\right)+\chi \left(i,j\right)=-ln\left[S\left(i,j\right)/S\left(i,j-1\right)\right]=-ln\left\{\left[1-I_B\left(i,j\right)\right]/\left[1-I_B\left(i,j-1\right)\right]\right\}.$ Similarly, writing $\chi \left(i,j\right)=-ln\left\{\left[1-I_V\left(i,j\right)\right]/\left[1-I_V\left(i,j-1\right)\right]\right\},$ we obtain the forces or hazard rates of infection, λ(i, j) as the difference. Pre-vaccination, S(i, j) = 1 – I_I(i, j), whereupon $\lambda \left(i,j\right)=-ln\left\{\left[1-I_I\left(i,j\right)\right]/\left[1-I_I\left(i,j-1\right)\right]\right\}$.

2.3. Attack rates

We calculate age-specific attack rates as products of probabilities of remaining susceptible at time t and the corresponding forces of infection. Because for any age, $P_S\left(t\right)=exp\left[-{\int }_{\tau =0}^t\lambda \left(\tau \right)+\chi \left(\tau \right)d\tau \right],$ where P_S(t) denotes the probability of remaining susceptible at time t (i.e., neither infected nor immunized), and 1 – P_S(t) the cumulative probability of being immune (i.e., either or both), – dP_S(t)/dt = – P_S’(t) = [λ(t) + χ(t)] × P_S(t). Further, λ(t) × P_S(t) are rates of new infections at time t, commonly called attack rates, and χ(t) × P_S(t) are rates of new immunizations.

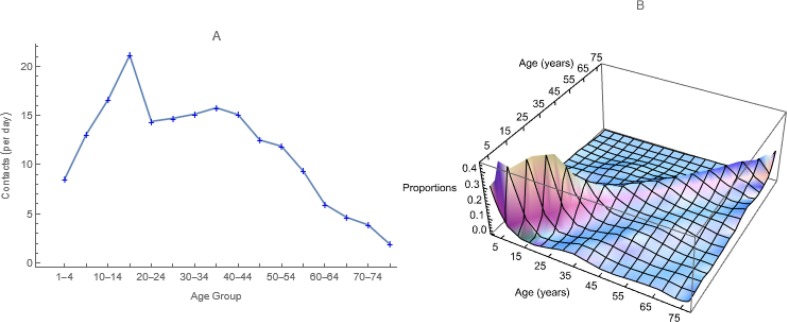
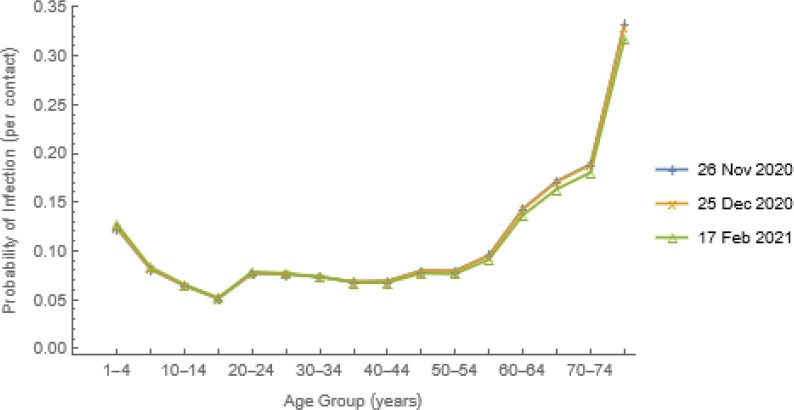
As explained earlier, given contact rates, a_i and proportions with each age group, c_ik from a contact study (those illustrated in Fig. 3 are from Prem et al., 2017), we calculate the age-specific probabilities of infection on contact, β_i by solving n equations, ${\lambda }_i=a_i{\beta }_i{\sum }_{k=1}^n{c}_{\mathit{ik}}\left(I_k/N_k\right),$ each with one unknown (Fig. 4 ). The quantity I_k/N_k represents the probability that an individual aged k is infectious and – P_S’(t) is the rate at which individuals are removed (from the susceptible state) at exactly time t. Thus, integrating the derivative over time intervals yields probability density functions. Because vaccination moves individuals from the S to V, not I state, however, equating those probabilities and I _k/N_k, as we do here, is safest pre-vaccination.

Fig. 3.

Parameters Derived from Synthetic US Contacts. We use these a) average marginal contact rates by age group, a_i, to which authors commonly refer as activities, and b) proportions of the contacts that members of each age group have with members of all age groups, including their own, c_ij.

Fig. 4.

Probabilities of Infection upon Contact. We estimated other parameters of the n equations, ${\lambda }_i=a_i{\beta }_i{\sum }_{k=1}^n{c}_{\mathit{ik}}\left(I_k/N_k\right),$ from the information illustrated in Fig. 2a and synthetic US contact matrix (Fig. 3) and then solved them simultaneously for these unknown probabilities, β_i.

As vaccination began on 14 December 2020 and the β_i had declined slightly among older people having commercial laboratory testing by 17 February 2021 (Fig. 4), the probabilities of infection on contact used in our transmission modeling were derived from the forces of infection and attack rates on 26 November 2020.

2.4. Mixing

In the simplest models, host populations are constant in size and homogeneous. In more complex models, they may be stratified, generally by age, a proxy for conditions (e.g., co-morbidities) that may increase the risk of serious disease. Age stratification also permits demographic dynamics (e.g., ageing, births by age of mother, deaths by age) that may be needed for long-term simulations. Model populations also may be spatially stratified, permitting locations to differ in population density (e.g., urban and rural) and other characteristics affecting transmission. Stratification also permits non-random mixing.

Age-specific observations usually are contacts per participant aged x with people aged y together with the numbers of participants aged x. One calculates average numbers of contacts per participant aged x with people aged y, $C_{\mathit{ij}}$ if x and y are grouped. Contacts should balance (i.e., N_i × C_ij = N_j × C_ji), but rarely do, so we calculate means of corresponding elements (e.g., square roots of products of empirical matrices and their transposes). Then $c_{\mathit{ij}}=C_{\mathit{ij}}/a_i,\mathrm{where}{a}_i={\sum }_k{C}_{\mathit{ik}}.$ Matrices of the proportions, c_ij, are referred to as mixing matrices and marginal sums of the contact matrix, a_i as activities. In our age-structured models, we create mixing matrices from local contact studies where possible or use synthetic ones (Fig. 3).

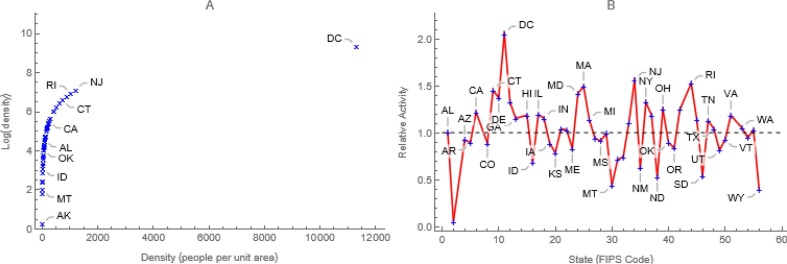
In the spirit of Hethcote and van Ark (1987), we model contacts within locations as a saturating function of population density (e.g., natural logarithms increase with density at decreasing rates, Fig. 5a). Consequently, the average per capita contact rate, $a_i=\ln \left({\rho }_i\right),$ where ρ_i is the quotient of the population size and land area of location i, and decay exponentially with distance between locations, d_ip at rates, b. Thus,

$$\begin{array}{c}{C}_{ip}=a_i\exp (-b\times d_{\mathit{ip}})/\sum _k\exp (-b\times d_{\mathit{ik}}),\\ c_{ip}=C_{ip}/\sum _k{C}_{ik},\end{array}$$

where C_ip is the contact matrix (e.g., contacts per person per day) and c_ip is the mixing matrix (i.e., proportions of contacts between members of group i and all groups k, including i).

Fig. 5.

Contacts are a Function of Population Density. Multiplying contacts within locations (Fig. 3a) by ratios of natural logs of population density, a) saturating functions of density, and that of the entire country, b) reduces to twofold the difference in activities between the most and least densely populated locations.

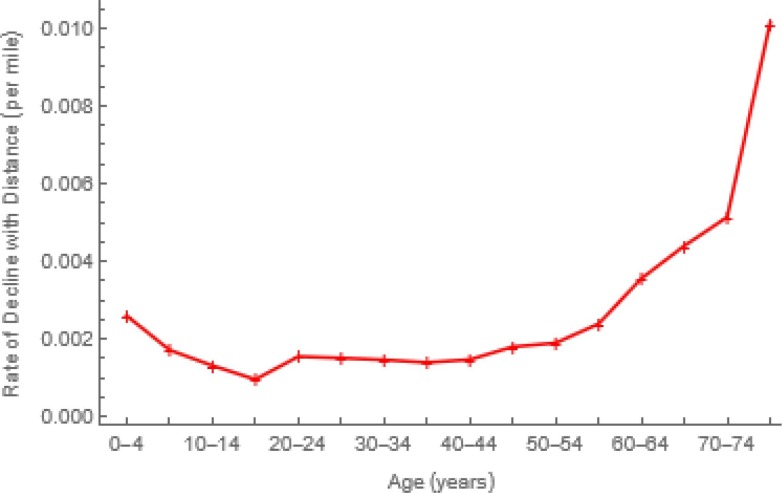
In our age- and location-stratified models, we combine these approaches, multiplying age-specific contacts within locations by ratios of the natural logs of location-specific and overall population densities (Fig. 5 b). Consequently, marginal contacts within more (less) densely populated locations are greater (less) than the average (Fig. 3a). The District of Columbia, for example, is almost 12K times as densely populated as Alaska (Fig. 5a), but their respective log ratios differ from average only by a factor of 2 (Fig. 5b). Between locations, contacts decline exponentially with distance at age-specific rates (Fig. 6 ) whose calculation Feng et al. (2017) describe. Here distances are “as the crow flies” between population centers, but other measures may be indicated (e.g., in a mountainous Argentine province, distances were shortest routes by car).

Fig. 6.

Rates at which Contacts Decline with Distance. Proximity to others affects the probability of contacting them. Feng et al. (2017) assumed an exponential function. Distances are between population centers (https://www.census.gov/geographies/reference-files/2010/geo/2010-centers-population.html).

Thus, in our age- and location-stratified models, mixing matrix elements are

$$c_{l_i{a}_j{l}_p{a}_q}=\frac{c_{a_j{a}_q}^{(p)}{e}^{-b_{a_q}{d}_{l_i{l}_p}}}{{\sum }_{r=1}^n{\sum }_{s=1}^m{c}_{a_j{a}_r}^{(s)}{e}^{-b_{a_r}{d}_{l_i{l}_s}}},$$

where

$$c_{a_j{a}_q}^{(p)}=c_{a_j{a}_q}\times \frac{\ln ({\rho }^{(p)})}{\ln (\rho )},1⩽i,p⩽m;1⩽j,q⩽n.$$

In these expressions, ρ is population density, with the indices i and p denoting locations, of which in the model described here there are m = 51 (50 states plus Washington, DC), and j and q denoting age groups, of which there are n = 16 (ages 0-4, 5-9, ..., 75+ years). Thus, the m matrices $c_{a_j{a}_q}^{(p)}$ and one matrix $c_{l_i{a}_j{l}_p{a}_q}$ have n ² = 256 and (m×n)² = 665,856 elements, respectively. We drop the compound notation in future equations. For more about our mixing models, please see Feng and Glasser (2019b).

3. Other Parameter Values and Initial Conditions

Other parameter values were gleaned from the primary literature or subject-matter experts (Table 1, Table 2). Our proportions asymptomatic are US proportions without co-morbidities from Clark et al. (2020), which vary inversely with age (Table 2). Dichotomizing what likely is a spectrum of illness is bound to lead to a range, but our weighted average exceeds most estimates of the proportion asymptomatic.

Clark et al. (2020) also provide proportions requiring hospitalization if infected, but – as people with asymptomatic infections don’t require hospitalization – we applied their proportions (Table 2) to symptomatic infections. We assumed that hospitalized people sought care within two days of symptom onset, but – as only about 70% of deaths were among inpatients (https://www.cdc.gov/nchs/nvss/vsrr/covid_weekly/index.htm#PlaceDeath) – evidently some people who needed hospital-based care did not receive it. Similarly, we converted the infection fatality ratios (IFRs) of Levin et al. (2020) into symptomatic infection fatality ratios (i.e., so-called case fatality rates). Sojourns (residence times) in our various states are largely from He et al. (2020).

We initialized our age- and location-stratified model of the transmission of SARS-CoV-2 in the United States from location-specific surfaces like that illustrated for the entire United States in Fig. 2a on 7 September 2020 (t = 251 days from 31 December 2019) and incidence on the preceding x days:

$$\begin{array}{l}{S}_{ij}\left(t\right)=1-R_{ij}\left(t\right),\\ E_{ij}\left(t\right)=\sum _{x=0}^{-12}{\lambda }_{ij}(t-x)\times S_{ij}(t-x)\times e^{-x/k},\\ I_{ij}\left(t\right)=\sum _{x=0}^{-12}{\lambda }_{ij}(t-x)\times S_{ij}(t-x)\times (1-e^{-x/k}),\\ I_{a\left(ij\right)}\left(t\right)={\gamma }_a^{-1}\times I_{ij}\left(t\right)\times {(1-Pr[CM+])}_j,\\ I_{p\left(ij\right)}\left(t\right)={\xi }^{-1}\times I_{ij}\left(t\right)\times Pr{[CM+]}_j,\\ I_{s\left(ij\right)}\left(t\right)={\gamma }_s^{-1}\times I_{ij}\left(t\right)\times Pr{[CM+]}_j,\\ R_{ij}\left(t\right)=Pr{[S+]}_{ij}\left(t\right).\end{array}$$

In these approximations, i and j denote location and age, t denotes time, $e^{-x/k}$ the exponential survival probability for an epidemiological state with a mean sojourn of k^-1 days, Pr[CM+] proportions with any co-morbidity that increases the risk of severe disease or hospitalization (Table 2), which vary only with age in our US model, Pr[S+] proportions with antibodies to nucleocapsid (with or without antibodies to spike), and the respective mean sojourns in E, I_p and I_s are 1/k, 1/ξ, and 1/γ_s days (Table 1).

4. Interventions

In prior work with populations subject to national regulations, officials in ministries of health and education helped us to model imposing and relaxing NPIs (e.g., closing schools and non-essential businesses, restricting meeting sizes, imposing curfews, requiring physical-distancing or mask-wearing in public places, and recommending outdoor or adequately-ventilated indoor activities) mechanistically for impact assessments, but – because their nature and timing was spatially heterogeneous in the United States – that was impractical.

4.1. Non-Pharmaceutical

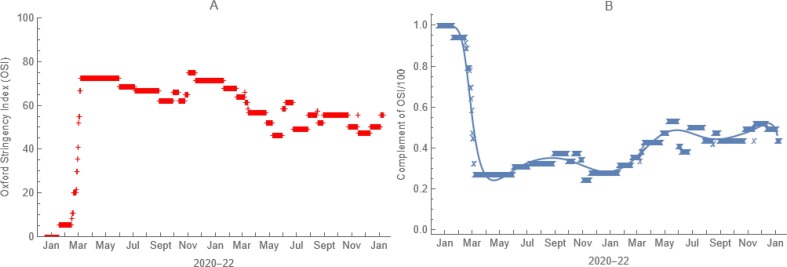
In our model of the transmission of SARS-CoV-2 in the United States, consequently, we multiplied contact rates within locations by time-varying complements of Oxford Stringency Indices (Hale et al., 2021) expressed as proportions (Fig. 7 ). For compliance, we scored responses (always = 1, frequently = 0.75, sometimes = 0.5, rarely = 0.25, never = 0) to “How often have you worn a face mask outside your home (e.g., when on public transport, going to a supermarket, going to a main road)?” by n = 33,940 US YouGov survey participants aged 18 to 99 years surveyed from March to December of 2020 (Jones, 2020). Our parameter values are age-group averages from logistic regressions of scored responses as a cubic function of age (Table 2).

Fig. 7.

Effect of Non-pharmaceutical Interventions. From a) time-varying Oxford Stringency Indices for each location, illustrated here for the entire United States, we derive b) functions by which we multiply age-specific contact rates to account for local governmental efforts to mitigate the pandemic.

4.2. Vaccination

In the United States, vaccination began on 14 December 2020 with healthcare and other essential workers, followed by those at risk of serious illness, hospitalization, or death (i.e., older adults and people who were immunocompromised), and then progressively younger people. Booster doses were not reported before 4 April 2021. Federal eligibility recommendations were generally followed, but jurisdictions differed in the levels of vaccine coverage or disease incidence at which NPIs were imposed and relaxed.

We have modeled vaccination using either 1) age-, time-, and location-specific immunization rates from the serological survey of blood donors (calculated as described in section 2.3) or 2) age-, time-, location-, and dose-specific reports to the CDC of vaccines administered.

In the first, susceptible people move directly to the removed class at weekly immunization rates. In the second, employed in the work described here, we determined age- and location-specific numbers of people eligible for vaccination (i.e., susceptible and vaccinated with one dose) at the beginning of each week by simulation, calculated the proportions vaccinated from the reported first and second doses administered that week, simulated with the corresponding rates, χ _1(ij) and χ _2(ij), and repeated the next week. We would have calculated χ _3(ij) similarly, but no booster doses were reported during the periods studied.

5. Simulation results

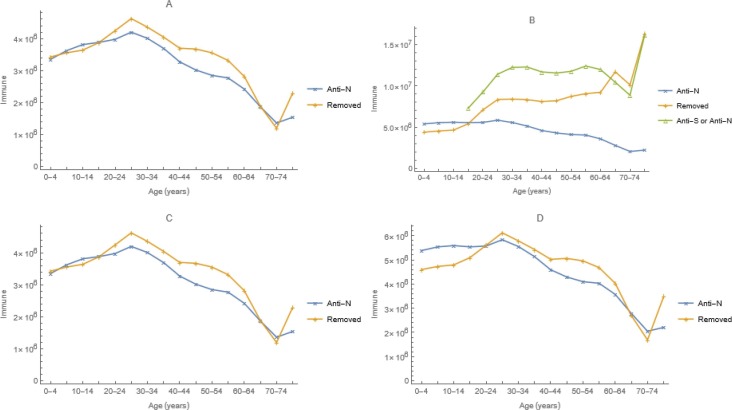
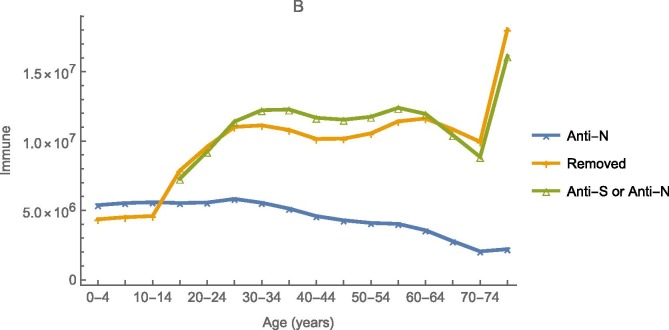
Adjusting only the efficacy of physical-distancing when possible and mask-wearing otherwise at reducing susceptibility or infectiousness, b_I = b_S,= 0.31, our model fits the prevalence of anti-N among those having commercial laboratory testing on 25 December 2020 quite well (Fig. 8 a). Using the second method described above, doses administered reports to the CDC and efficacies of vaccination at preventing infections, ∊ ₁ = ∊ ₂ = 0.93 from El Sahly et al. (2021), the lower of the two mRNA vaccines authorized for use at the time (Polack et al., 2020), it fits the prevalence of anti-N or anti-S among blood donors on 4 April 2021 less well (Fig. 8b).

Fig. 8.

Observed numbers with antibodies to SARS-CoV-2, from the national commercial laboratory (Anti-N) or blood donor (Anti-S or Anti-N) seroprevalence study, and predicted numbers temporarily immune (Removed) from simulations with (A and B) and without (C and D) vaccination on 25 December 2020 (A and C) and 4 April 2021 (B and D). Vaccination had no discernible impact on 25 December 2020 serology.

We compare reported and simulated symptomatic infections and deaths during the last quarter of 2020 and first of 2021 (Table 3 ). Case and death reports are from information summarized on the CDC’s COVID Data Tracker, cited above. Our model predicts more infections, but fewer symptomatic ones than reported, and more deaths than reported between 7 September and 25 December 2020 and fewer between 25 December 2020 and 4 April 2021. The age-specific hospitalization rates of Clark et al. (2020) are comparable to those from COVID-NET (https://www.cdc.gov/coronavirus/2019-ncov/covid-data/covid-net), which are based on surveillance of about 10% of the US population.

Table 3.

Reported infections and deaths (https://covid.cdc.gov/covid-data-tracker/#datatracker-home) and simulated infections, hospitalizations, and deaths during the periods from 7 September to 25 December 2020 and from 25 December 2020 to 4 April 2021.

	7 Sep to 25 Dec 2020		25 Dec to 4 Apr 2021
Outcomes	Reported	Simulated	Reported	Simulated
Cases or Infections	12,545,671	45,075,200	11,603,565	23,635,060
Hospitalizations		1,766,850		974,486
Deaths	147,776	176,342	214,902	120,978

Notes: Cases are reported, infections are simulated, of which roughly 75% are asymptomatic. Consequently, fewer symptomatic infections are predicted than cases reported. More deaths were simulated than reported during the first period, but fewer during the second. Hospitalizations are not compiled, but rates from surveillance of about 10% of the US population are available (https://gis.cdc.gov/grasp/COVIDNet/COVID19_3.html).

Predicted 4 April infections without vaccination resemble serology among commercial laboratory clients (Fig. 8d), suggesting that the discrepancy with vaccination (Fig. 8b) may be attributable to blood donors being disproportionately vaccinated (Busch et al., 2022), including those previously infected. The discrepancy also may be explicable by vaccine doses administered being under-reported. Similarly, the above-mentioned comparison of reported and simulated cases and deaths suggests that infections were under-reported too.

5.1. Impact of vaccination

Rather than comparing disparate simulations and reports, we compare simulated infections, hospitalizations, and deaths with and without vaccination (Table 4 ). As one would expect, given that vaccination began mid-December in the United States, impact was modest during the last quarter of 2020 (7 September to 25 December). In contrast, impact during the period from 25 December 2020 to 4 April 2021 was substantial, particularly on symptomatic infections and hospitalizations.

Table 4.

Results of simulations with and without vaccination to deduce by difference its impact during the periods from 7 September to 25 December 2020 and from 25 December 2020 to 4 April 2021.

	7 Sep to 25 Dec 2020			25 Dec 2020 to 4 Apr 2021
Outcomes	Without	With	Averted	Without	With	Averted
Asymptomatic Infections	34,739,600	33,911,200	828,400 (2.38%)	26,721,000	17,958,500	8,762,500 (32.79%)
Symptomatic Infections	11,447,400	11,164,000	283,400 (2.48%)	9,389,030	5,676,560	3,712,470 (39.54%)
Hospitalizations	1,813,190	1,766,850	46,340 (2.56%)	1,608,080	974,486	633,594 (39.4%)
Deaths	176,349	176,342	7 (<0.01%)	172,549	120,978	51,571 (29.89%)

Notes: As vaccination began mid-December 2020 in the United States, one would not expect much impact during the first period.

We could also compare actual and hypothetical vaccination strategies the same way. The purpose of the initial strategy was to protect healthcare and other essential workers, then elderly people and others at risk of serious disease, hospitalization, and death. Younger and healthier people were vaccinated subsequently.

Unquestionably, the optimal strategy for protecting healthcare and other essential workers is to vaccinate them. This direct approach also might be best for people at risk of serious disease, hospitalization, and death for reasons other than age, but the immune responses of older adults may be less effective than those of younger people. Accordingly, for example, higher dose influenza vaccines are recommended (https://www.cdc.gov/flu/highrisk/65over.htm).

6. Discussion

Early in the COVID-19 pandemic, we developed an SEIR-based framework for modeling the transmission of SARS-CoV-2 that we could use, together with locally-available information, to answer policy questions. In one instance, we used information from cell phone transmissions to determine which restrictions affected movements and then a location-stratified version of this model to determine the impact of movement restriction on transmission. In another, we used an age-stratified version to determine the impact of closing schools and otherwise limiting inter-personal contacts.

For this more recent US work, we estimated some parameters of an age- and location-stratified version of our model from nationwide seroprevalence studies and used others from the literature. Initialized via seroprevalence on and incidence shortly before 7 September 2020, this model predicts seroprevalence well on 25 December 2020 and less well on 4 April 2021. The first evaluation compared seroprevalence from the same survey, among people having commercial laboratory tests, from which it was initialized and the probabilities of infection on contact were estimated. The second compared seroprevalence among blood donors, who may be unusually wellness-oriented and hence disproportionately vaccinated. Also, results using immunization rates estimated from the survey of blood-donations (via the first approach described in section 4.2) are more concordant with observations from that survey (appendix), suggesting that vaccine doses administered may have been under-reported to the CDC.

Our model predicts more than twice as many infections as reported, most presumably asymptomatic or mildly symptomatic infections among people who were not tested, but the factor by which simulated infections exceed reported ones declines over time (cf. Jones et al., 2021). It also predicts more deaths than attributed to COVID-19 during the last quarter of 2020, most among older adults (because of the IFRs in Table 2), and fewer afterwards.

Ability to experiment (i.e., to deduce the effects of phenomena by altering them individually) underlies the scientific method. While withholding measures of proven efficacy is unethical, we can experiment with models of pathogen transmission among the members of host populations. Because such models account for infections not caused by ones that are averted (i.e., indirect as well as direct effects of mitigation measures), these experiments assess the total impact of public health interventions, be they actual or hypothetical.

All models are imperfect, but alternative approaches also have shortcomings. Because it is impossible to control statistically for the extent to which the vaccination of others reduces the forces of infection to which unvaccinated people are subjected, natural experiments (e.g., Loeb et al., 2010) under-estimate indirect effects. Similarly, all else never is equal, even in the best matched community intervention trials. In models, however, the impact of vaccination is the difference between infections, hospitalizations, and deaths with and without vaccination, but all other conditions identical (e.g., the same NPIs).

6.1. An alternative strategy

Vaccination policymakers generally envision protecting vulnerable people for whom vaccination is contra-indicated by attaining a population immunity above which infectious people contact, on average, fewer than one susceptible person intimately enough to infect them. However, as Morens et al. (2022) explain, waning immunity and pathogen evolution make attaining an effective reproduction number of one difficult for COVID-19. Moreover, in heterogeneous population models (e.g., with age or spatial structure), if not the real world, that condition could be attained via an infinite number of combinations of sub-population immunity (Feng et al., 2015). The gradient (multivariate partial derivative) answers the question, “Which is optimal?”

Besides simulating our model with and without the actual vaccination strategy, we could also compare the actual strategy with a hypothetical alternative derived via the gradient of the effective reproduction number with respect to possible immunization rates. Fewer elderly people might be infected if those who otherwise might infect them were vaccinated instead. Feng et al. (2015) advocated, and have since used (Feng et al., 2017, Hao et al., 2019, Feng et al., 2020, Su et al., 2021), the gradient of the effective reproduction number with respect to possible vaccination rates to identify strategies that would reduce the average number of secondary infections per primary most expeditiously. This is tantamount to determining which groups contribute most.

6.2. Limitations

We began modeling the transmission of SARS-CoV-2 long before effective vaccines were developed, much less approved for use, but – to keep pace with vaccination policy – added one, then two doses, and finally boosting of infection- or vaccine-induced immunity. However, we have since learned that the duration and possibly other characteristics of immunity may depend on whether an individual was infected, vaccinated or both, and possibly even the sequence of those events (Goldberg et al., 2022). These developments and the evolution of variants, several successively dominant, motivated us to develop different models for later pandemic periods.

We have derived the reproduction numbers from our models and quantities, such as the gradient and population-immunity threshold, that can be derived from the effective number. We have written about this analytical work, including simulations comparing the actual and this alternative strategy (i.e., direct with indirect protection), elsewhere (Vo et al., submitted).

7. Summary

All models are imperfect, but – because measures to mitigate infectious diseases have indirect effects that are difficult to estimate via field studies – reliable transmission modeling arguably is the best way to assess their impact. Observations from cross-sectional serological surveys conducted in the United States from mid-summer 2020 through the end of 2021 using stable assays (Peluso et al., 2021) provided the wherewithal for us to demonstrate that accurate transmission modeling is possible during pandemics. We modified the familiar SEIR model to include features of the biology of COVID-19 that might affect transmission of SARS-CoV-2 and consulted the primary literature or subject matter experts for contact rates and most other parameter values. We assessed the impact of vaccination, conditional on NPIs, in an age- and location-stratified model US population during the first quarter of 2021. Vaccination substantially reduced symptomatic infections, hospitalizations, and deaths.

8. Disclaimer

The findings and conclusions in this report are those of the authors and do not necessarily represent the official positions of the Centers for Disease Control and Prevention, National Science Foundation, or Purdue University.

CRediT authorship contribution statement

John W. Glasser: Conceptualization, Methodology, Visualization, Writing – original draft, Writing – review & editing. Zhilan Feng: Conceptualization, Formal analysis, Funding acquisition, Methodology, Visualization, Writing – review & editing. MyVan Vo: Formal analysis, Methodology, Visualization, Writing – review & editing. Jefferson N. Jones: Data curation, Funding acquisition, Supervision, Writing – review & editing. Kristie E.N. Clarke: Data curation, Funding acquisition, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix

As described in the main text, we calculated vaccination rates from reports to the CDC of weekly doses administered by age and dose number, which – together with efficacy from El Sahly et al. (2021) – determined the numbers immunized. We believe that the discrepancy between the observed prevalence of antibodies to spike and nucleocapsid proteins among blood donors (anti-S or anti-N on Fig. 8b) and modeled numbers temporarily immune by virtue of infection or vaccination (removed on Fig. 8b) is due to the disproportionate vaccination of health-conscious blood donors, under-reporting of doses administered, or both.

This figure differs from 8b in the main text in that vaccination occurred at immunization rates estimated from seroprevalence among blood donors instead of rates calculated from reported doses administered together with vaccine efficacy, corroborating our explanation for the discrepancy between predictions and observations.

Data availability

We have cited published data and included links to public-use datasets.