Toward a unified framework for interpreting machine-learning models in neuroimaging

Lada Kohoutová; Juyeon Heo; Sungmin Cha; Sungwoo Lee; Taesup Moon; Tor D Wager; Choong-Wan Woo

doi:10.1038/s41596-019-0289-5

. Author manuscript; available in PMC: 2022 Oct 5.

Published in final edited form as: Nat Protoc. 2020 Mar 18;15(4):1399–1435. doi: 10.1038/s41596-019-0289-5

Toward a unified framework for interpreting machine-learning models in neuroimaging

Lada Kohoutová ^1,², Juyeon Heo ³, Sungmin Cha ³, Sungwoo Lee ^1,², Taesup Moon ³, Tor D Wager ^4,^5,^6,^✉, Choong-Wan Woo ^1,^2,^✉

PMCID: PMC9533325 NIHMSID: NIHMS1835286 PMID: 32203486

Abstract

Machine learning is a powerful tool for creating computational models relating brain function to behavior, and its use is becoming widespread in neuroscience. However, these models are complex and often hard to interpret, making it difficult to evaluate their neuroscientific validity and contribution to understanding the brain. For neuroimaging-based machine-learning models to be interpretable, they should (i) be comprehensible to humans, (ii) provide useful information about what mental or behavioral constructs are represented in particular brain pathways or regions, and (iii) demonstrate that they are based on relevant neurobiological signal, not artifacts or confounds. In this protocol, we introduce a unified framework that consists of model-, feature- and biology-level assessments to provide complementary results that support the understanding of how and why a model works. Although the framework can be applied to different types of models and data, this protocol provides practical tools and examples of selected analysis methods for a functional MRI dataset and multivariate pattern-based predictive models. A user of the protocol should be familiar with basic programming in MATLAB or Python. This protocol will help build more interpretable neuroimaging-based machine-learning models, contributing to the cumulative understanding of brain mechanisms and brain health. Although the analyses provided here constitute a limited set of tests and take a few hours to days to complete, depending on the size of data and available computational resources, we envision the process of annotating and interpreting models as an open-ended process, involving collaborative efforts across multiple studies and laboratories.

Introduction

Machine learning (ML) and predictive modeling^1,2—which encompasses many use cases of ML to predict individual observations—have provided the ability to develop models of the brain systems underlying clinical, performance and other outcomes, and to quantitatively evaluate the performance of those models to validate or falsify them as biomarkers. Because of these characteristics, ML has rapidly increased in popularity in both basic and translational research^2–5 and forms the core of several now-common approaches, including brain decoding^6–10, multivariate pattern analysis¹¹, information-based mapping¹² and pattern-based biomarker development^2,13–16. By enabling the investigation of brain information that is simultaneously (i) finer-grained and more precise than traditional brain mapping and (ii) distributed across multiple brain regions and voxels, the use of ML in neuroimaging experiments has provided new answers to many enduring research questions^11,17–19.

However, this rise in popularity is accompanied by concerns about the ‘blackbox-ness’ of ML models^20,21. For basic neuroscientists, it is unclear how ML models will advance our neuroscientific knowledge if the models rely on hidden or complex patterns that are uninterpretable to researchers. For users in applied settings, it is unclear whether, and under what conditions, complex ML models will be trustworthy enough to contribute to the life-altering decisions made every day in medical and legal settings²⁰. Without knowing why and how a model works, it is difficult to know when the model will fail, to which individuals or subgroups it applies and how it can advance our understanding of the neurobiological mechanisms underlying clinical and behavioral performance. In addition, some models are neurobiologically plausible and capture important aspects of brain function, whereas others capitalize on confounds such as head movement²². These models do not contribute equally to our understanding of the brain. Therefore, there is a pressing need for methods to help interpret and explain the model decisions^23–26 and provide neuroscientific validation for neuroimaging ML models².

Methods for interpreting predictive models in neuroimaging studies must address several key issues. First, neuroscience has a long-standing interest in understanding localized functions of individual brain areas or connections, whereas ML often focuses on developing integrative brain models (e.g., using patterns of whole-brain activity) that are highly complex and difficult to understand. Second, there is a tension between the goals of achieving high predictive accuracy versus providing mechanistic insights into underlying neural or disease processes^27–30. Ideally models would achieve both goals, but these often do not go hand in hand. Biologically plausible models, such as biophysical generative models^31–33 or biologically plausible neural network models³⁴, use biological constraints (e.g., imaging data or findings in literature) and are built upon neurobiological principles. Predictive performance is usually less of a concern; rather, the goal is to capture and manifest human-like behaviors³⁵. On the other hand, models that focus solely on predictive performance may achieve high accuracy but are often not human readable and reveal little about the underlying neural mechanisms involved³⁶. Although neuroscientific explanation and predictive accuracy are distinct goals, they are not in opposition, and models developed for prediction can provide biological insights at several levels of abstraction. For example, deep neural networks trained for accurate image classification share common properties with the human visual system³⁷ and are being used to understand the types of information represented in discrete brain regions³⁸. Predictive models can also be inspired by neuroscientific findings, as deep neural networks for image recognition have been^39,40. Third, ML, as well as traditional statistical methods, can be sensitive to variables that are correlated with, but not causally related to, outcomes of interest, and thus can be sensitive to systematic noise and confounds in data (e.g., head motion, eye movement, physiological noise). Models that use confounding variables to predict are not only uninterpretable but also behave unpredictably in new samples.

Therefore, for neuroimaging-based ML models to be interpretable to neuroscientists and users in applied settings, the models should (i) be readable and understandable to humans, (ii) provide useful information about what mental or behavioral constructs are represented in particular brain pathways or regions, and (iii) demonstrate that they are based on relevant neurobiological signals, not confounds. These goals require prioritizing model simplicity and sparsity over a complete description of brain function. The most interpretable models are not necessarily the most ‘correct’ ones—the brain and human behaviors are intrinsically complex and high dimensional, creating an unavoidable trade-off between biological precision and interpretability. However, as George Box famously wrote⁴¹, ‘All models are wrong, but some are useful’. On the other hand, this trade-off must be managed carefully. More complex models may better reflect the structure of the underlying biological mechanisms; therefore, prioritizing interpretability may come at a cost in biological realism, undercutting our understanding of how the brain works. As Albert Einstein said, ‘Everything should be made as simple as possible, but no simpler’.

Whatever the chosen level of complexity of a model, tools for interpreting it can increase its usefulness by showing that the model can provide a useful approximation to more complex biological mechanisms. However, the nature of neuroimaging data makes interpretation of the models challenging (Fig. 1a). Neuroimaging produces high-dimensional data with a low signal-to-noise ratio and strong correlations between features. Moreover, the number of observations in neuroimaging studies (the sample size n, often in the tens or hundreds) is small in general compared to the number of features (p = ~10⁵ in the case of whole-brain functional magnetic resonance imaging (fMRI) activation pattern-based models). Models built with p ≫ n data are susceptible to overfitting and often do not generalize well. Numerous studies have been focused on decreasing dimensionality or solving the p ≫ n problem as a way of enhancing interpretability. For example, regularizing model parameters by imposing sparsity has often been considered as one of the key strategies for enhancing model interpretability, and thus many different regularization methods have been developed^42–46. However, these statistical methods do not provide a unified framework that can be used with a heterogeneous set of methods and algorithms to evaluate and improve interpretability of neuroimaging-based ML models. In addition, the ML algorithms do not, in themselves, provide any constraints related to neuroscientific interpretation and validity. Therefore, interpreting a neuroimaging ML model is a complex problem that is not solvable at the algorithmic level; it requires a multi-level framework and a multi-study approach.

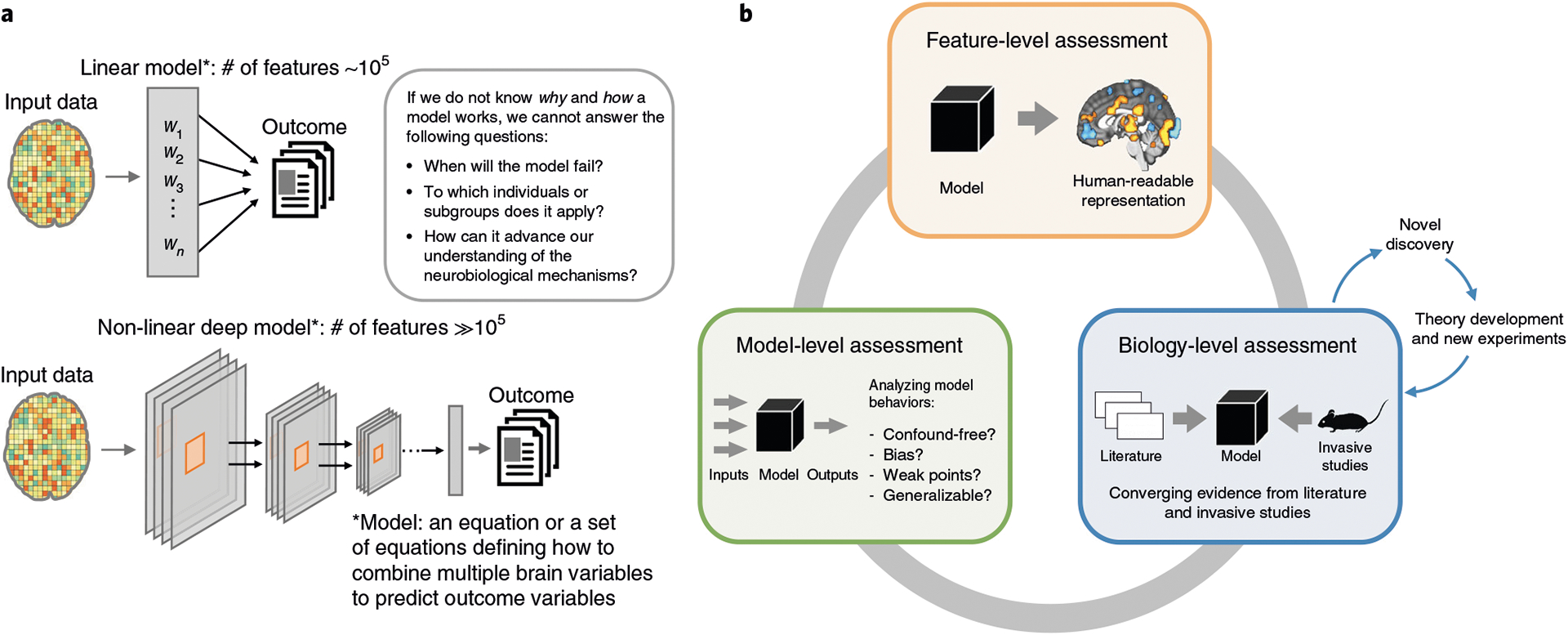
Fig. 1 | — a, Neuroimaging-based ML models are usually built upon a large number of features (e.g., ~10⁵ in the case of whole-brain fMRI), which, along with considering potential confounds and correlations between features, makes even linear models complex. In the case of nonlinear models, the situation is more complicated, as it is not clear what a model uses as features. To trust models and find them useful in basic neuroscience and clinical settings, researchers need to know why and how a model works. b, The model interpretation framework consists of three levels of assessment. In the model-level assessment, the model is evaluated as a whole, and the characteristics of the model are derived mainly from observations of the input–output relationship. The assessment includes tests of specificity, sensitivity and generalizability, analyses of model’s representations and decisions and analyses of noise contribution. The feature-level assessment aims to identify features significant for a prediction within a model. The feature significance can be evaluated based on the feature’s impact on predictions or the feature’s stability across multiple samples of the training data. The explanation obtained by this level of assessment should enhance human readability of the model. The biology-level assessment aims to prove the neuroscientific plausibility of the model with evidence from previous literature and other studies using different methodology (e.g., invasive studies). In case a model suggests a novel finding that cannot be verified by the current state of the art, the model can serve as a basis for theory development, which should subsequently be corroborated by studies employing other (e.g., invasive) experimental methods.

In this protocol, we first propose a unified framework for interpreting ML models in neuroimaging based on model-level, feature-level and neurobiology-level assessments. Then, we provide a workflow that illustrates how this framework can be employed to predictive models, along with practical examples of analyses for each level of assessment with a sample fMRI dataset (available for download at https://github.com/cocoanlab/interpret_ml_neuroimaging). Although these methods can in principle be used for any type of model and data (e.g., predicting individual differences in personality or clinical symptoms based on structural neuroimaging data or functional connectivity patterns; predicting trial-by-trial responses within individuals), our example code focuses on classification models based on whole-brain, task-related fMRI activity patterns combining multiple participants’ data. Nevertheless, the analyses can be easily adapted to regression-based problems (e.g., predicting ratings of task stimuli) and can be extended to models built on other feature types, such as structural data or functional connectivity data.

Overview of the framework

In this section, we first establish a broader context for our proposed framework. Based on this framework, we provide a protocol that includes some selected analysis methods from each assessment level. As shown in Fig. 1b, the proposed framework consists of three levels of assessment: model-, feature- and biology-level assessments. Table 1 provides descriptions and example methods for subcategories of each level of assessment.

Table 1 |.

Descriptions and example methods for different levels of assessments

Category	Description	Example methods
Model-level assessment	Models are characterized by…
Sensitivity and specificity	Examining the response patterns of predictive models to different inputs and experimental conditions	Positive and negative controls^13,47,118; testing models across a range of different conditions¹⁸; construct validity⁸⁴; tuning curves of brain patterns⁸⁶
Generalizability	Testing models on multiple datasets from different samples, contexts and populations	Research consortia and multisite collaborations¹¹⁹
Behavioral analysis	Analyzing the patterns of model decisions and behaviors over many instances and examples (or over time for adaptive models)	Methods analogous to psychological tests⁵⁰; analyses at given time points⁵²; error analysis¹²⁰
Representational analysis	Analyzing model representations using examples or representational distance	Deep dream⁷¹; deep k-nearest neighbors¹²¹; representational similarity analysis⁵⁶
Analysis of confounds	Examining whether any confounding factors contribute to the model (e.g., head movement, physiological confounds or other nuisance variables)	Comparison of the model of the signal of interest with a model of the nuisance variables¹²²
Feature-level assessment	Significant features are identified by…
Stability	Measuring the stability of the selected features and predictive weights over multiple tests (e.g., cross-validation or resampling)	Stability analysis^61,123; bootstrap test^13,124; surviving count on random subspaces¹²⁵; pattern reproducibility¹²⁶
Importance	Measuring the impact of features on a prediction	rFe^63,127,128; variable importance in projection⁶¹; sensitivity analysis⁶⁶; feature importance ranking measure¹²⁹; measure of feature importance¹³⁰; leave-one-covariate-out¹³¹; LRP^64,69; local model-agnostic explanations (LIME)⁶⁷; deep learning feature importance¹³²; Shapley additive explanations (SHAP)¹³³; regularization^42–44; virtual lesion analysis⁴⁷; in silico node deletion¹³⁴; weight-activation product¹³⁵
Visualization	Visualizing feature-level properties	Class model visualization¹³⁶; saliency map⁷⁰; weight visualization¹⁸
Biology-level assessment	Neurobiological basis is established by…
Literature	Relating predictive models to previous findings from literature across different tasks, modalities and species (e.g., meta-analysis)	Meta-analysis^18,77; large-scale resting-state brain networks^83,84
Invasive studies	Using more invasive methods, such as molecular, physiological and intervention-based approaches	Gene overexpression and drug injection⁸⁸; transcranial magnetic stimulation⁹⁰; postmortem assay⁹¹; optogenetic fMRI⁸⁹

Open in a new tab

Model-level assessment

Model-level assessment treats and evaluates a model as a whole and characterizes the model based on its response patterns in different testing contexts and conditions. This includes, for example, various measures of model performance. Sensitivity and specificity concern whether a model shows a positive response when there is true signal (e.g., an outcome of interest has occurred) and negative response when there is no true signal. Generalizability concerns whether a model performs accurately on data collected in different contexts or with different procedures—e.g., data from out-of-sample individuals not used in model training or data from different laboratories, scanners, populations and experimental paradigms² (for more detailed definitions of these terms, please see ref. ¹). These types of measurement properties should be rigorously evaluated to understand what the model really measures and how it performs in different test contexts^2,13,47,48. More broadly, these analyses can be seen as behavioral analyses of a model—investigating patterns of model behaviors (e.g., model decisions and responses) over multiple instances and examples⁴⁹. This is similar to the study of human behavior using psychological tests. For example, a previous study examined a model’s ‘implicit biases’ using behavioral experiments and measures designed for ML models⁵⁰. In another study, researchers developed a new ML model that can learn other ML models’ internal states (e.g., machine theory of mind⁵¹). For adaptive models, one can examine changes in model behaviors and learning over time, similar to the study of human developmental psychology⁵².

In addition, representational similarity analyses can be used to examine models’ internal representations and their relationships with different models and different brain regions^53–55. Representational similarity analyses examine the similarity among a set of experimental conditions or stimuli on two multivariate measures—for example, vector representations across units in an artificial neural network or multi-voxel patterns of fMRI activity. As an example, a previous study examined representational similarities and differences between multiple computational models, including a deep neural network, and activity patterns in the inferior temporal cortex⁵⁶.

Finally, one of the most important assessments at the model level is to examine potential contributions of noise and nuisance variables to a model and its predictions. Many different confounding factors such as physiological and motion-related noise are pervasive in neuroimaging data and present challenging issues that need careful attention^57–60. These confounds can creep into training data and be utilized by predictive models to enhance their performance. The problem is that, if a model relies on information from the confounding variables, the model cannot be robust across contexts, because it will fail in samples without the same confounds or when methodological improvements (e.g., better noise-removal techniques) mitigate them. More importantly, those models that rely on nuisance variables will teach us nothing about the neurobiology of target outcomes. Therefore, researchers should provide evidence that their models are not influenced by confounds and nuisance variables to the degree possible. One way to do this is to test and show whether model predictions, features or outcomes are independent from nuisance variables. For example, one can test whether an ML model based on nuisance variables, such as in-scanner motion parameters, can predict either (i) responses/predictions made by a model of interest or (ii) the outcomes of interest^13,18. If the nuisance model cannot predict these, model performance is unlikely to be driven by those nuisance variables.

This protocol includes multiple model-level assessment steps, including evaluation of model performance and generalizability (Steps 2 and 3 and Steps 8–10), potential influences of confounds (Steps 4–6) and a representational similarity analysis on multiple predictive models based on their performance (Steps 12–15).

Feature-level assessment

Feature-level assessment includes methods that evaluate the significance of individual features, such as voxels, regions or connections, that are used in prediction. The methods can be broadly categorized as (i) methods for evaluating feature stability, (ii) methods for evaluating feature importance, and (iii) methods for visualization.

Methods for assessing stability of features measure how stable each feature’s contribution (or predictive weight) is over multiple models trained on held-out datasets using resampling methods or cross-validation^13,61. For example, in bootstrap tests, data are randomly resampled with replacement, and a model is trained on the resampled data⁶². This procedure is repeated multiple times (e.g., 10,000 iterations), and the stability of predictive weights can then be evaluated using the z and P values based on the mean and standard deviation of the sampling distribution of predictive weights. After correction for multiple comparisons, the features with predictive weights significantly different from zero based on the P values can be selected and visualized in standard brain space.

Methods for assessing feature importance focus on the impact of a feature on a prediction. These include methods that directly use the magnitude of predictive coefficients (e.g., recursive feature elimination (RFE)⁶³), methods using feature-wise decomposition of the prediction (e.g., layer-wise relevance propagation (LRP)⁶⁴ and Shapley values⁶⁵) and methods using perturbation or ‘lesions’ (omission) of features^47,66–68, among many others (see Table 1). For example, in RFE, the importance of a feature is estimated by the absolute value of its corresponding predictive weight, and less important features (i.e., with low predictive weights) are eliminated recursively. The ‘virtual lesion’ analysis⁴⁷ has also been used to assess the feature importance. In the ‘virtual lesion’ analysis, a researcher first defines meaningful groups of features (e.g., brain parcellations or functional networks), removes each group of features from a model at each iteration and tests the predictive performance of the reduced model. A large decrease in the model performance indicates that the virtually lesioned features are necessary for the model to perform well. In LRP, the prediction score of a nonlinear classifier (e.g., neural network) is decomposed and recursively propagated back to the input feature level so that the contribution of each feature to the final prediction can be quantitatively identified and visualized^64,69. These methods cannot fully explain complex models, because isolated features are often insufficient to predict either outcomes or full model performance, but they can help explain what is driving a model’s predictions.

Visualization methods provide ways to make a model human readable and thus enhance its interpretability. In case of linear models, visualizing important features is straightforward because significant predictive weights can be directly displayed on a feature space (e.g., a brain map). For nonlinear models, visualizing feature-level interpretation is not simple, but it is possible to visualize importance or stability scores calculated at the feature level on a feature space (using, e.g., a heat map⁶⁴ or saliency map⁷⁰). Another visualization technique for artificial neural networks is to examine what individual units or layers in a network represent by adjusting input patterns to maximize the activation of a target unit or layer (e.g., DeepDream⁷¹). Table 2 provides more details on a few selected feature-level assessment methods.

Table 2 |.

Selected methods of feature-level assessment

Method	Applicability	Purpose of the method	Description	References
Stability analysis	Linear models	Feature selection based on feature stability	A model is repeatedly trained on resampled data using a sparse method. In each iteration, only a subset of features is selected by the algorithm. Features selected with a frequency above a threshold are considered stable.	Refs. 61, 123,125
Bootstrap tests	Linear models	Identification of significant features within the training dataset based on feature stability	Training data are repeatedly resampled with replacement. Each sample serves as training data for a new model. Features with stable weights across the models are identified as stable and significant.	Refs. 13,124
RFE	Linear models	Feature selection based on feature importance	A model is iteratively trained, and features corresponding to its lowest weights are eliminated from the training dataset. The process is repeated until the desired number of features is reached.	Ref. 128
Sensitivity analysis	Model agnostic	Identification of significant features within a given data point based on feature importance	The input features are disrupted (e.g., by additive noise). The resulting error in the output is measured. Features that caused the largest error after being disrupted are considered important for the prediction.	Ref. 66
LRP	Neural networks	Same as above	A prediction score is decomposed backward through the layers of the model until it reaches the input when a relevance score is assigned to each input feature.	Ref. 64
LIME	Model agnostic	Same as above	A prediction is explained by an interpretable model fitted to sampled instances around the instance being explained.	Ref. 67
SHAP	Model agnostic	Unified measure of feature importance	SHAP is a framework that provides the incremental impact of each feature on model decisions using Shapley values. This framework unifies some other model explanation methods (e.g., LIME and LRP).	Ref. 133

Open in a new tab

In this protocol, we propose four options for feature-level assessment (Step 7 of the protocol): bootstrap tests, RFE and ‘virtual lesion’ analysis for linear models and LRP for explaining nonlinear models. We visualize the significant features (or feature relevance scores in the case of LRP) on a standardized brain space.

Biology-level assessment

Biology-level assessment aims to provide additional validation for a model based on its neurobiological plausibility. Plausibility is based on converging evidence from other types of neuroscientific data, including previous studies, additional datasets or other techniques, particularly those that provide more direct measures of brain function or direct manipulation of brain circuits (e.g., intracranial recordings, optogenetics). Such validation is important for at least two reasons. First, it helps to elucidate what types of mental and behavioral representations are being captured in a predictive model. Second, it provides a bridge between ML models and neuroscience, helping neuroimaging-based ML models contribute to understanding mental processes and behaviors.

However, there are inherent challenges in identifying the neurobiological mechanisms underlying neuroimaging-based ML models and validating them against other techniques and datasets. Most ML algorithms have no intrinsic constraints related to neuroscientific plausibility. In addition, ML models are usually developed to maximize the model’s performance while being agnostic about its neurobiological meaning and validity. It may not be possible to provide definitive answers for biology-level assessment in many cases. Rather, the assessment should be regarded as an open-ended investigation that requires long-term sharing and testing the properties of established models. This is a multi-study, multi-technique and multidisciplinary process.

One way to examine neurobiological plausibility and validity of an ML model is to evaluate results from feature- and model-level assessments in the light of neuroscience literature across various modalities and species. For example, Woo et al.¹⁸ developed an fMRI-based ML model for predicting pain and examined the local pattern topography of predictive weights for some key brain regions in the model, including basal ganglia and amygdala, and found that their local patterns of predictive weights were largely consistent with previous findings in rodents^72–74 and non-human primates^75,] as well as in human literature^76–78. In addition, one can examine what an ML model may represent (‘decode’ a model) using a meta-analytic approach^77,79—for example, term-based decoding with automated meta-analysis tools (e.g., neurosynth.org⁸⁰) and map-based decoding using an open neuroimaging database (e.g., openneuro.org⁸¹ or neurovault.org⁸²). Another possibility is to examine the current ML model in relation to previously established large-scale resting-state brain networks^48,83–85 or existing multivariate pattern-based neuroimaging markers⁸⁶. The protocol below specifies two options for biology-level assessment: the analysis of the model in terms of its overlap with large-scale resting-state networks defined by Yeo et al.⁸⁷ and meta-analysis–based decoding using Neurosynth⁸⁰ (Step 11).

Other types of biological validation are beyond the scope of the current protocol but are important, particularly, searching for converging evidence from invasive studies that employ molecular, physiological and intervention-based approaches in animal^88,89 or human studies^90,91. Some methodologies may not be practical for widespread use as predictive models because they are more invasive, are testable only in special populations or cannot be tested in humans at all; however, they can provide valuable converging evidence, increasing our understanding of what a model measures. For example, Hultman et al.⁸⁸ recently developed electrical neuroimaging biomarkers of vulnerability to depression using local field potentials in mice. They then assessed their models using multiple biological methods, including gene overexpression (molecular) and drug injection (physiological and intervention-based methods), and showed that their models responded to multiple ways of inducing vulnerability to depression. For humans, researchers cannot easily use invasive methods, but non-invasive interventions, such as transcranial magnetic stimulation⁹⁰, and some more invasive methods, such as electrocorticography or post-mortem evaluation⁹¹, can also be used in some cases.

Although converging evidence from existing studies and theories can help validate a model, even the models that are not corroborated by existing neurobiological knowledge can also play an important role by promoting new discovery and theory building in neuroscience. For example, neuroimaging-based ML models for pain could reveal new substrates for pain perception in regions not previously understood as ‘pain-processing’ regions, leading to new discoveries of potential brain targets for further research and intervention⁹². Thus, the biology-level assessment does not need to be limited to currently available theories. Rather, researchers should be open to building new hypotheses and theories inspired by ML models, which can be subsequently tested with invasive methods or other modalities.

Development of the protocol

The proposed framework and analyses have been developed and discussed in multiple previous publications from our research group^{2,13,18,19,47,48,93}, in which we have developed fMRI-based ML models for several different target outcomes. These previous studies used different methods and approaches to validate and interpret the models. Here, we aim to unify these various approaches into one framework and implement a workflow that can guide model validation and interpretation (Fig. 2). To practically demonstrate the use of the workflow, we apply its methods to a published fMRI dataset⁹³. In the fMRI experiment, participants (N = 59) completed a somatic pain task and a social rejection task. In the somatic pain task, participants experienced painful heat or non-painful warmth, whereas in the social rejection task, participants viewed photographs of their ex-partners or friends. We used these data to build and interpret classification models. Although this protocol provides examples of only a few selected analyses and covers only non-invasive methods, other validation methods and steps should be employed as available. In addition, although the previous studies from our research group have generally used linear models, this framework can be applied to any type of ML model, including deep learning models.

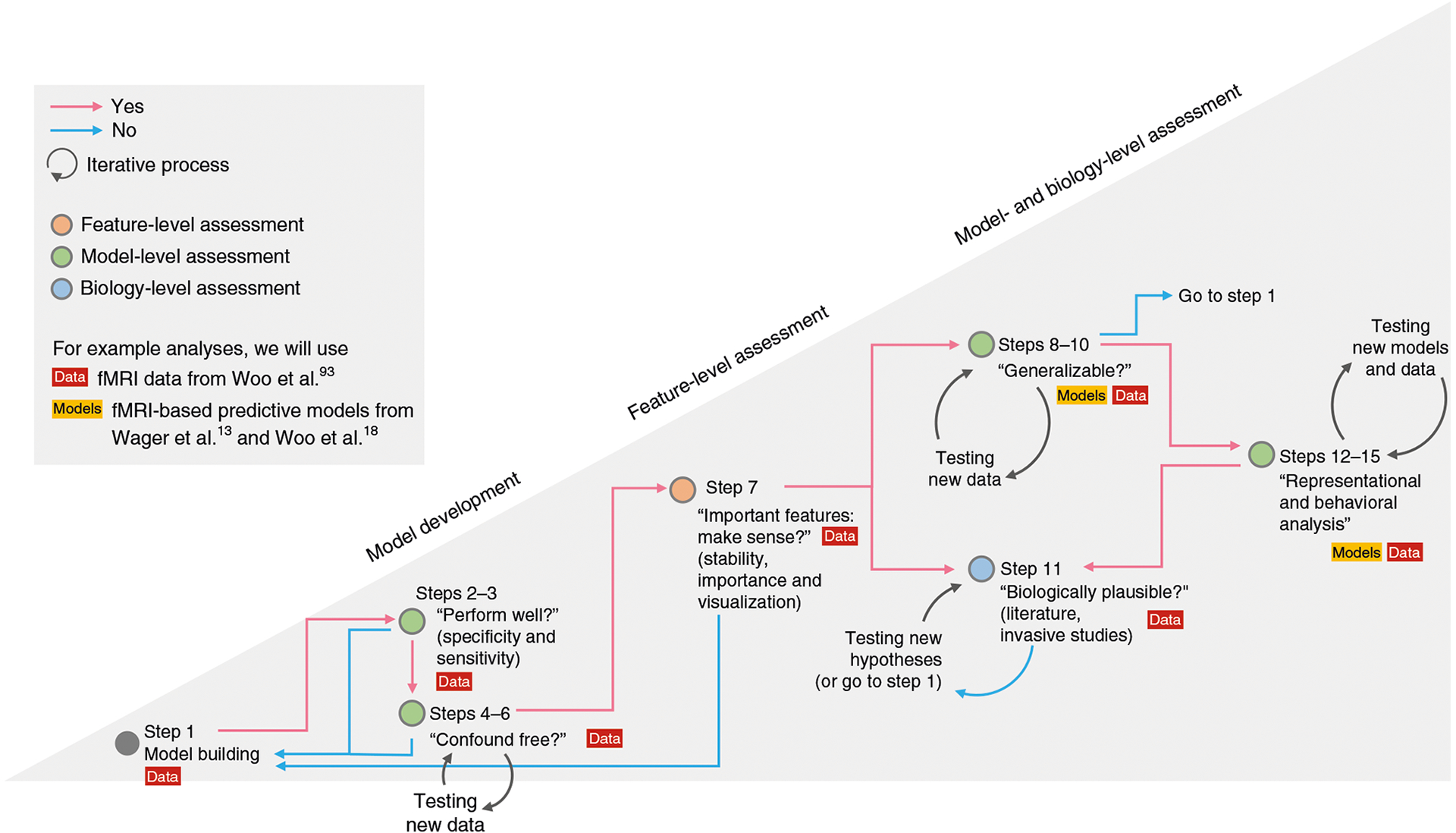
Fig. 2 | — In this protocol, we present an example workflow that implements the unified model interpretation framework. The first step is the model building (Step 1). This is a prerequisite step that stands outside the interpretation framework. However, we include a brief description of this step to emphasize its importance. This protocol includes examples of building linear support vector machines (option A) and a convolutional neural network model (option B) using an example dataset from our previous publication⁹³. Next, we evaluate the basic properties of a model, such as its predictive power (Steps 2 and 3) and contributions of confounds (Steps 4–6). In case either of the two steps shows insufficient quality of the model, one should return to Step 1 to review the data quality and to revise the model. Note that obtaining a definitive answer to the question of Steps 4–6 (i.e., whether the model is confound free) is challenging, and therefore Steps 4–6 should be an open-ended investigation. If the results from Steps 2 and 3 and Steps 4–6 are good enough to move forward, the next step (Step 7) is the feature-level assessment. This protocol provides analysis examples of four options of identifying significant features: bootstrap tests, RFE, ‘virtual lesion’ analysis and LRP. If the identified significant features provide sensible results, one can continue to Steps 8–10 and Step 11. Otherwise (e.g., all the significant features are located within the ventricles), one should revisit the model building. Generalizability testing (Steps 8–10) and biology-level assessment (Step 11) can be performed in an arbitrary order. In Steps 8–10, a model is tested for its generalizability to unseen data from new individuals, different laboratories, scanners and contexts. Testing generalizability requires new test data, which can take a long time to collect. Therefore, one can first examine the model’s biological validity (Step 11) and then test its generalizability, or vice versa. Both generalizability testing and biology-level assessment require open-ended test processes and should support each other; more generalizable models are likely to be more biologically plausible. For Step 11, we provide examples of two options: examining the relationship of the model with the large-scale resting-state functional networks (option A) and term-based meta-analytic decoding using Neurosynth⁸⁰ (option B). In practice, this step should also include exhaustive literature reviews and support of invasive studies. The step can also be performed multiple times in case the model suggests novel theories that should be evaluated. The final step of this workflow is the representational analysis (Steps 12–15), which can provide a better understanding of the model’s decision principles by examining the patterns of model behaviors over multiple instances and examples. This step often requires other models with which to be compared, and for this reason, we include this as the last step of the workflow. However, if other models are already available, this step can be done earlier. The results from Steps 12–15 could provide converging evidence for Step 11. Since interpreting an ML neuroimaging model is, in fact, an open-ended process, this workflow should be regarded as the bare minimum, and more analyses other than the ones proposed here can help the model interpretation.

Comparison with other methods

Many previous approaches to improving interpretability have focused on model sparsity or constraining models to include a small number of variables. Various regularization techniques have been used for this purpose. Least-absolute-shrinkage-and-selection-operator (LASSO)⁴² and ElasticNet⁴³ regression, for example, impose non-structured sparsity, without constraints on how variables are grouped when considering their inclusion. GraphNet⁴⁴ and hierarchical region-network sparsity⁴⁵ are examples of methods that impose structured sparsity, incorporating prior knowledge of brain anatomical specialization into the model-selection process. These structured methods result in grouped voxels in few clusters and promise easier interpretation than non-structured sparse models. However, imposing sparsity may not always be relevant to establishing neurobiologically valid brain models: sparse solutions may not provide the whole picture of complex interactions among many different players involved in a complex biological system.

Other studies have considered additional objective functions beyond predictive accuracy. Model stability, or reproducibility of model parameters across samples, is important for interpretability: models with unstable parameters have no consistent biological features to interpret. For example, Rasmussen et al.⁹⁴ showed that there is a trade-off between prediction accuracy and the spatial reproducibility of a model, and concluded that regularization parameters should be selected considering both model reproducibility and interpretability. Baldassarre et al.⁹⁵ also investigated the effects of several regularization methods on model stability and suggested that model stability can be enhanced by adding reproducibility as a model selection criterion.

Another important approach for enhancing model interpretability is dimensionality reduction. Principal component analysis or independent component analysis has often been used, and they can be combined with methods imposing sparsity^96,97. However, at present, principal component analysis and independent component analysis are also used to extract characteristic features from single-modality or multimodal neuroimaging data^98–100.

Most of these studies, however, focused only on one or a small number of aspects of model interpretation that can partially improve the interpretability. We aim to provide a unified framework for assessing model interpretability in multiple ways, along with concrete example analyses.

Limitations

This protocol aims to provide concrete analysis examples of the minimum set of components for the different levels of model interpretation. However, interpreting ML models in neuroimaging is intrinsically an open-ended process, and therefore the protocol provided here cannot cover all possible methods. In addition to the presented methods, users of the protocol may want to, for example, support the biological interpretation of their models by thorough literature review or conducting additional experiments focusing on the underlying neurobiological mechanisms of the models using invasive animal and human studies.

In this protocol, we sometimes make choices on algorithms and parameters based on previous research, though some of the decisions could have a direct impact on the model performance and interpretation. We recommend that researchers do not blindly use our choices as defaults. The algorithms we use (e.g., support vector machines (SVMs)) are not the only or even the best for many applications. The validation and process we implement could be used with many choices of algorithms (including both regression and classification algorithms), many outcomes (e.g., decoding stimulus conditions, predicting within-person behavior or predicting between-person clinical characteristics) and multiple types of data (e.g., structural images, functional task-related images, functional connectivity or arterial spin labeling/positron emission tomography/magnetic resonance spectroscopy images). However, for all of these choices, additional data- and outcome-type specific validation procedures are likely to be useful. Therefore, this protocol is a useful starting point but should not be taken as a complete description of the validation steps for all algorithms, data types and outcome types. Researchers should make deliberate choices on algorithms and parameters to answer their research questions. In addition, although our model interpretation framework can be applied to many types of models and data (e.g., fMRI connectivity, structural MRI and other imaging modalities), we do not provide example code for all possible applications.

This protocol provides analysis examples for feature-level assessment for a nonlinear model as well as a linear model. For a nonlinear model, we used LRP⁶⁴, but only one previous neuroimaging study has used this method⁶⁹. Although the method for the nonlinear model yielded similar results to the methods for the linear model in our analyses, the method for the nonlinear model presented here should be considered as an example and investigated further in future studies. In addition, other components of the model-level assessment (e.g., noise analysis and representational analysis) have not been tested with nonlinear models.

Finally, this protocol includes only two simple methods for biology-level assessment. However, in practice, biology-level validation should involve experiments using multiple modalities and approaches and collaborative efforts among multiple laboratories to search for converging evidence. We emphasized the importance of these approaches above, but such methods cannot be fully summarized in one protocol.

Overall, this protocol should serve as a sample practical implementation of the framework. There can be multiple equally valid analysis options that can achieve the same level of model interpretation. We encourage investigators to use the analysis methods and workflow proposed here but also to use different methods and a workflow that suits their research goals and experimental contexts.

Overview of the procedure

In this protocol, we provide a workflow that can guide a practical implementation of the framework (Fig. 2). To achieve most of the components of the workflow, we use the CANlab interactive fMRI analysis tools (Box 1), which are publicly available MATLAB-based analysis tools (see Materials for details on availability). The list of functions from the CANlab tools used in the protocol can be found in Table 3.

Box 1 |. CANlab interactive fMRI analysis tools.

Neuroimaging analyses are widely performed in well-established pipelines with optimized procedures. However, to discover new and better ways of neuroimaging data analysis, and to avoid spurious results, there is also a need for flexibility to allow users to be creative and explore the data and analysis methods. The CANlab neuroimaging analysis tools were designed with this goal in mind. The tools provide a high-level language for interacting with fMRI data. Users can apply simple commands to perform various analyses and to explore the distribution of data and consequences of different analysis choices. As a result, analysis scripts can be short, transparent and easy to read, write and interpret.

The CANlab imaging analysis tools enable interactive neuroimaging data analysis using objects with simple methods operating in MATLAB. There are eight main object classes suitable for different types of analyses. To perform analyses in this protocol, we use fmri_data and statistic_image objects, which both represent subclasses of the image_vector data class. A representative object of the image_vector data class contains basic information about loaded images, such as the data values in the .dat field, indicators of removed data in .removed_voxels and .removed_images fields, details about the volume information of the image in the .volInfo field or a record of past manipulations with the object in the .history field. Its subclasses, such as fmri_data and statistic_image, then inherit these basic properties. There are also various methods that can be performed on image_vector objects or other objects from its all subclasses. For example, one can save memory using the remove_empty method, which removes all empty voxels and images from the object but keeps track of the removal in .removed_voxels and .removed_images fields of the object. There is also a reverse method, replace_empty, which replaces the missing data values with zeros. One can also resample the image to match the space of another image using the resample_space method or mask the data with a mask image using the apply_mask method.

The fmri_data subclass is one of the main objects for the fMRI data analysis. It stores neuroimaging data in 2D space, enabling simple manipulations with the data. Properties of the fmri_data object include the properties inherited from the image_vector data class and additional information about the data, such as outcomes in the .Y field and covariates in the .covariates field. There are various useful methods that can be operated on the fmri_data objects, some of which are used in this protocol. For example, one can easily visualize raw data and examine data quality using the plot method, run one-sample t-test using ttest, conduct a regression analysis using regress, threshold the images using threshold, write image data as NIfTI or Analyze files using the write method and build a predictive model using the predict method. To see the full list of available methods, one can type methods(fmri_data) in the MATLAB Command Window.

The statistic_image subclass is another important object for the fMRI data analysis. It stores statistical test outputs, such as beta or t-values, P values, standard error, degree of freedom, sample size and significance. In the current protocol, the statistic_image object stores the output of the bootstrap tests performed with the predict function. It can be easily thresholded with desired thresholding methods, such as FDR, using the threshold method, and significant voxels can be visualized using the orthviews method. More detailed tutorials for the CANlab fMRI analysis tools are available at https://canlab.github.io/.

Table 3 |.

Key functions in the CanlabCore MATLAB toolbox used in the protocol

Function	Description	Used in…
`filenames`	Lists file names that match a specific pattern in a directory	Step 1A; Step 8
`fmri_data`	Loads images into the object or creates an empty `fmri_data` object	Step 1A; Step 5; Step 7C; Step 8; Step 11A
`apply_mask`	Masks an image with a defined mask or calculates pattern expression values	Step 1A; Step 9
`predict`	Trains and evaluates predictive models and performs cross-validation and bootstrap tests	Step 1A; Step 2; Step 6; Step 7A
`roc_plot`	Calculates accuracy, sensitivity and specificity and visualizes the ROC curve	Step 3; Step 7C; Step 10; Step 12
`threshold`	Applies a statistically valid threshold to the images with statistical test results	Step 7A
`orthviews`	Displays the image data stored in CANlab tools	Step 7A; Step 7B
`write`	Writes data stored in the `fmri_data` or `statistic_image` objects into a NIfTI (.nii) or Analyze (.img) file	Step 7A; Step 7B
`svm_rfe`	Performs recursive feature elimination with support vector machines	Step 7B
`canlab_pattern_similarity`	Calculates similarity between each column in a data matrix and a vector of pattern weights	Step 11A

Open in a new tab

Step 1 of the workflow is model building. It is a prerequisite step, which is not included in the model interpretation framework, but successful and correct implementation of this step defines the success of the following methods of model interpretation. A crucial point in Step 1 is to divide data into a training set and a test set for cross-validation performed in Steps 2 and 3 (for more detailed information, see Step 1A). Steps 2–15 can then be divided into three parts: model development (Steps 2–6), feature-level assessment (Step 7) and model- and biology-level assessment (Steps 8–15).

In the model development stage, Steps 2 and 3 and Steps 4–6 evaluate the intrinsic quality of the new model in terms of its predictive power and a potential contribution of confounds. More specifically, Steps 2 and 3 evaluate the model’s accuracy, sensitivity and specificity. In these steps, it is critical to obtain unbiased estimates of model performance using cross-validation (though cross-validation is prone to bias in some cases¹⁰¹) and, ideally, held-out test data tested on only a single, final model. In this protocol, we provide examples of leave-one-subject-out (LOSO) and 8-fold cross-validation. If the model shows good performance, one can go to the next step. Steps 4–6 aim to ensure that a model is independent of potential confounds. However, obtaining a definitive answer to this question is challenging (e.g., potential confounds may be unmeasured), and therefore this should be an open-ended investigation. Although the order of these analysis steps is flexible, Steps 2–6 should logically precede other analyses as they validate the quality of the model.

Step 7 includes methods for the feature-level assessment of the model. We propose several options to identify important features, and these options can be selected depending on the types of models (e.g., linear or nonlinear) or desired properties (e.g., stability or importance). In this protocol, we describe (i) bootstrap tests as an example of feature stability evaluation in linear models, which were used in previous studies^13,93; (ii) RFE as an example of evaluation of feature importance in linear models commonly used in neuroimaging⁶³; and (iii) a ‘virtual lesion’ analysis in which features are groups of voxels defining regions or networks of interest⁴⁷. We also describe (iv) LRP⁶⁴ as an example of feature importance evaluation in nonlinear models. There are numerous other ways to identify significant features in models, and thus we encourage investigators to use other methods that suit their goals. For a list of possible options, see Table 1. When visualizing important features, researchers need to examine whether the identified important features make sense based on a priori domain knowledge. For example, important features should not be located outside of the brain, and if a condition involves a visual process, some of the important features should be located in the visual cortex.

Following the feature-level assessment of the model, investigators should examine whether the new model can generalize across individuals and populations, different scanners and test contexts (Steps 8–10) and whether the model is biologically plausible (Step 11). The order of these two analyses is not important, but both analyses are critical in evaluating how robust and useful the model is for both an applied use and neuroscience. These steps should also be an open-ended process; for Steps 8–10, the generalizability tests can start with testing the model on a few independent datasets locally collected, but the tests should be scaled up to new data from broader contexts, such as data from different laboratories, populations, scanners and task conditions, with increasing levels of evidence. For Step 11, investigators need to keep seeking converging evidence from related literature and invasive studies with different experimental modalities and multiple species to understand the model’s neurobiological meaning. In the current protocol, for Steps 8–10, we provide an example of testing generalizability of two previously developed predictive models for pain, the Neurologic Pain Signature (NPS)¹³ and Stimulus Intensity Independent Pain Signature-1 (SIIPS1)¹⁸, on example fMRI data from a previous publication⁹³ (for more details of the models and dataset, see Materials). For Step 11, we provide two basic analyses: first, term-based decoding based on a large-scale meta-analysis database, Neurosynth⁸⁰, and second, comparisons of the model to large-scale networks identified by Yeo et al.⁸⁷.

Representational and behavioral analyses can further our understanding of the model (Steps 12–15). For example, one can better understand the model’s decision making by examining the patterns of model behaviors (e.g., decisions and responses) over multiple instances and examples. Investigators can also analyze model representations by directly comparing weight vectors or measuring representational distances among different models. In this protocol, we provide an example of the representational analysis using two a priori predictive models applied to the sample dataset (see Materials for details about the predictive models and sample dataset).

Level of expertise needed to implement the protocol

Creating one’s own codes to perform the analyses described below is a demanding task in terms of programming abilities and knowledge of statistics and ML. However, we provide CanlabCore tools (https://github.com/canlab/CanlabCore), a MATLAB-based interactive analysis tool for fMRI data. With the CanlabCore tools, one can readily run most of the analyses described. To successfully use the CanlabCore tools, users should be familiar with the MATLAB programming environment, and they should be able to implement simple codes using predefined functions and different variable types (e.g., objects, structures and cell arrays). To implement the nonlinear model and LRP analysis, users should be familiar with Python and some deep learning libraries in Python, such as Tensorflow and Keras.

Materials

Equipment

Software

A computer with MATLAB and a web browser to access Neurosynth at http://neurosynth.org (or one can also use the Neurosynth Python toolbox available at https://github.com/neurosynth)
For linear models: The CanlabCore toolbox is available at https://github.com/canlab/CanlabCore ▲CRITICAL For full functionality, it is necessary to install the following dependencies: (i) MATLAB Statistics and Machine Learning toolbox, (ii) MATLAB Signal Processing toolbox, (iii) Statistical Parametric Mapping (SPM) toolbox available at https://www.fil.ion.ucl.ac.uk/spm/, and (iv) some external toolboxes (in the directory named ‘/External’), including the Spider toolbox (for SVMs), contained in the CanlabCore ▲CRITICAL Ensure that all the toolboxes are added with subfolders to the MATLAB path.

Note that our protocol could be readily adapted to other software platforms, particularly open-source alternative programming languages such as Python. Although we do not provide sample code in this protocol, the COSAN Lab (led by Luke Chang) has developed a Python package based on the CANlab tools, called NLTools, available at https://github.com/cosanlab/nltools. This package relies on Nilearn (http://nilearn.github.io) and scikit-learn (https://scikit-learn.org), providing an alternative, open-source format for implementing this protocol
For deep learning models: Python 3.6.5 or higher available at https://www.python.org/downloads/; NumPy 1.14.5 (Python library for scientific computing) available at https://github.com/numpy/numpy; Keras 2.2.4 (Python library for Deep Learning) available at https://keras.io/ and TensorFlow 1.8.0 available at http://www.tensorflow.org/install/; Matplotlib 3.0.2 (Python library for plotting) available at https://matplotlib.org/users/installing.html; scikit-learn 0.20.3 (Python library for ML) available at https://scikit-learn.org/stable/install.html; pandas 0.25.1 (Python library for data analysis) available at https://pandas.pydata.org/pandas-docs/stable/install.html; Scipy 1.3.0 (Python library for mathematics, science and engineering); Nilearn 0.5.2 (Python library for ML on neuroimaging data) available at http://nilearn.github.io/introduction.html#installation; Nipype 1.2.0 (Python library for an interface to neuroimaging analysis pipelines) available at https://pypi.org/project/nipype/; iNNvestigate¹⁰² 1.0.8.3 (Keras explanation toolbox) available at https://github.com/albermax/innvestigate; other dependencies: Compute Unified Device Architecture (CUDA) and CUDA Deep Neural Network (CuDNN) library with an appropriate graphical processing unit (GPU)

Input data

Statistical parametric maps (used in all steps): The level of input data can be varied. For example, one can use first-level contrast or beta maps for event regressors, single-trial beta series, or repetition time (TR)-level images. The amount of data needed for model training depends on whether a researcher aims to build a model to predict between-person individual differences or within-person behaviors or stimulus conditions. In the case of between-individual prediction, N > 100 participants is usually required, but N > 300 is recommended¹. For the prediction of within-person effects using group-level data, data from >20 participants are usually used, but >50 participants and 1–2 h of scanning for each person are recommended¹⁰³. The recommended amount of data can also be varied depending on the types of data or algorithms (e.g., refs. ^104,105). Note that these recommendations are heuristic only, as a full discussion of power and model reproducibility is beyond the scope of this review. In addition, it is extremely beneficial to have an independent hold-out dataset for prospective model validation and generalizability testing ▲CRITICAL The CanlabCore tools can read images in NIfTI format (.nii) or Analyze format (.img and .hdr). For deep learning models, we used data with 4D matrices (x, y, z, t) for each subject, created by the Nibabel library. The CanlabCore toolbox provides an easy way to create 4D matrices (see reconstruct_image.m) ▲CRITICAL If you are using single-trial level data, some trial estimates could be strongly affected by acquisition artifacts or sudden motion. For this reason, we recommend excluding images from trials with high variance inflation factors (VIFs). In previous studies, we usually removed trials with VIFs that exceeded 2.5^18,106. VIFs can be calculated with getvif.m in the CanlabCore toolbox ▲CRITICAL If you are using TR-level data, ensure that the data are properly filtered (e.g., high-pass filtering) and denoised (e.g., confound regression or signal decomposition methods)⁶⁰. For in-depth quality checks for image data, please refer to ref. ⁶⁰ or use the MRI Quality Control (MRIQC) tool¹⁰⁷ to perform an automated data quality check. In the case of individual- or group-level preprocessed data (e.g., contrast maps), one can use the qc_metrics_second_level.m function from the CanlabCore toolbox. The function assesses, for example, signals from white matter and ventricles and their effect sizes or scale inhomogeneities across subjects in gray matter and ventricles. To use this tool, data should be spatially normalized to the Montreal Neurological Institute (MNI) template ! CAUTION A study collecting neuroimaging and behavioral data must be approved by an appropriate institutional ethical review committee, and all subjects must provide informed consent to the acquisition and use of the data in the case of a local study. In the case of certain public datasets, a data-sharing agreement must be approved. In the example dataset used in this protocol, all participants provided written informed consent in accordance with a protocol approved by Columbia University’s Institutional Review Board.
Nuisance data (used in Steps 4–6): Here, we used time series data for six head-motion parameters (x, y, z, roll, pitch and yaw)
A priori pattern-based predictive models (used in Steps 8–10 and 12–15): To run the example analyses provided here, one also needs two a priori pattern-based predictive models, the NPS and the SIIPS1. The NPS is available upon request with a data use agreement. The SIIPS1 can be downloaded from the CANlab Neuroimaging_Pattern_Masks repository (https://github.com/canlab/Neuroimaging_Pattern_Masks)
Functional Atlas data (used in Steps 7 and 11): We used seven functional networks from Yeo et al.⁸⁷ (available at https://github.com/ThomasYeoLab/CBIG/tree/master/stable_projects/brain_parcellation)

Example dataset

We used an fMRI dataset (N = 59) from a previous publication⁹³ as an example dataset for demonstration
In an fMRI experiment, all participants completed two tasks: a somatic pain task, in which participants experienced painful heat or non-painful warmth, and a social rejection task, in which participants viewed pictures of their ex-partners or friends
In this protocol, trial-level data are used for Steps 1–7 and Step 11, and participant-level contrast images are used for Steps 8–10 and 12–15. For the trial-level data, we use data from the painful heat trials (heat condition, eight trials per participant) and the ex-partner trials (rejection condition, eight trials per participant). For the contrast images, we use data from all four conditions (59 images per condition)

The example data and codes can be downloaded from https://github.com/cocoanlab/interpret_ml_neuroimaging. Its directory structure can be found below, and our example codes use this data structure

/data
   /derivatives
      /trial_images/
       /sub_01
          heat_trial01.nii
          heat_trial02.nii
          …
          rejection_trial08.nii
       /sub_02
       …
       /sub_59
   /contrast_images
      heat_sub_01.nii
      heat_sub_02.nii
      …
      friend_sub_59.nii
/masks
/scripts

Procedure

Build a model ● Timing 20 min to a few hours

1
This step builds fMRI-based ML models that are predictive of a target outcome. This is a prerequisite step to the workflow of the model interpretation framework. Although details of this step are not the main focus of the current protocol, we briefly describe the procedure for the model building to provide information about the two types of models used in this protocol. Option A describes the training of a widely used linear algorithm, SVMs. We chose SVMs because it is one of the most popular ML algorithms in current neuroimaging literature—for example, from the survey we conducted in ref. ², 46.4% of the 481 ML models in neuroimaging studies used SVMs, which were followed by discriminant analysis and logistic regression with 12.7% and 7.5% prevalence, respectively. The steps in option A describe how to build an SVM model using the CanlabCore tools (Box 1). Option B is a procedure to build a nonlinear model. As an example of nonlinear models, we chose a Convolutional Neural Network (CNN), a successful deep learning model for a variety of applications on prediction. The steps in option B describe how to build a CNN model using Keras¹⁰⁸.

Option Module

1A Linear model (SVMs)

1B Nonlinear model (CNN)

Open in a new tab
1. Training SVMS
  1. Prepare a data matrix. You can use the following lines to import the fMRI data from image data with a gray matter mask.
    basedir = ‘/The/base/directory’; % base directory gray_matter_mask = which(‘gray_matter_mask.img’); heat_imgs = filenames(fullfile(basedir, ‘data’, ‘derivatives’, … ‘trial_images’, ‘sub*’, ‘heat_*.nii’)); % read image file names for the heat condition rejection_imgs = filenames(fullfile(basedir, ‘data’, … ‘derivatives’, ‘trial_images’, ‘sub*’, ‘rejection_*.nii’)); % file names for the rejection condition data = fmri_data([heat_imgs; rejection_imgs], gray_matter_mask);
    
    The variable data.dat contains the activation data in a flat (2-D) and space-efficient # voxels × # observations matrix.
    
    ? TROUBLESHOOTING
  2. (Optional) Apply a mask. One can apply a mask to include only selected brain features before training a model. For example, the following lines of code apply the mask that was used in Woo et al.⁹³:
    mask = fullfile(basedir, ‘masks’, ‘neurosynth_mask_Woo2014.nii’); data = apply_mask(data, mask);
  3. Prepare an outcome variable and add it into dat.Y. For classification tasks, the outcome vector is defined using a categorical variable (e.g., binary values for different conditions), and for regression, the outcome vector is a continuous variable (e.g., trial-by-trial ratings). The following code defines the outcome vector for the SVM binary classifier in our example analysis. Coding observations with [1, −1] values is compatible with the Spider package and should be used:
    data.Y = [ones(numel(heat_imgs),1); … −ones(numel(rejection_imgs),1)]; % heat:1, rejection:−1
  4. Define training and test sets for cross-validation. To obtain an unbiased estimate of model performance, one should internally validate the model using cross-validation. A crucial step in cross-validation is to choose a suitable strategy of splitting the data into training and test sets. One can define a certain percentage of data as the test set (k-fold cross-validation) (e.g., 10% for 10-fold cross-validation) or use one subject’s data as test data in each fold (LOSO cross-validation). Because with increasing k, bias of the predictive accuracy decreases and variance increases, one needs to find a suitable solution for the trade-off, taking into account the size of the available dataset. LOSO cross-validation can be used in small datasets, whereas in large datasets, 5-fold or 10-fold cross-validation can be more efficient¹. Care should be taken that no dependencies between training and test data have been introduced (see below).
    
    The optional input argument, ‘nfolds’, of the predict function can specify which types of cross-validation will be used. With a scalar value input k, it will run k-fold cross-validation. The optional input can also be a vector for using customized cross-validation folds (e.g., LOSO, leave-two-trials-out). If the optional input equals one, the function will not run cross-validation. If no optional input is given, it will run fivefold cross-validation stratified on the outcome variable as a default. For example, we can use LOSO cross-validation in our example dataset. That is, we reserve one subject’s data as test data and use the remaining 58 subjects’ data as the training set. The input argument ‘nfolds’ can then be defined as follows.
    n_folds = [repmat(1:59, 8,1) repmat(1:59, 8,1)]; % Each subject % has 8 trial image data for each condition n_folds = n_folds(:); % flatten the matrix
    
    ▲CRITICAL STEP It is crucial to keep the training and test sets truly independent. Performing some analyses, such as denoising, feature selection or scaling, across training and test sets can create dependence between the training and test datasets, resulting in a bias in the estimate of the prediction performance^1,2. Dependence between the training and test datasets can also occur if participants are related, as is typical in twin studies and occurs in some other studies, such as the Human Connectome Project¹⁰⁹, ABCD¹¹⁰ and UK Biobank¹¹¹ studies. In addition, other common situations can introduce some dependence, such as nesting participants within a scanning day, variation in scan timing relative to academic deadlines and other seasonal variables, or subsets tested by the same experimenter in a multi-experimenter study. These issues do not categorically invalidate cross-validation, but they make it more important to test generalizability in independent test cohorts—and ultimately in cohorts that are explicitly dissimilar in population and procedures to the training sample.
    
    ▲CRITICAL STEP If k-fold cross-validation is used with the regression approach, we recommend using stratified cross-validation—stratifying holdout test sets for each fold based on the level of the outcome. To see how the CanlabCore tools implement stratified cross-validation, see stratified_holdout_set.m.
  5. Fit an SVM model to the training data. We use the predict function, which is a method of the fmri_data object in the CanlabCore tools (see Box 2). This function allows us to easily run many different ML algorithms on fMRI data with cross-validation. The following lines of code will fit an SVM classifier to the data and test the cross-validated error rate of the classifier. We explain the details of cross-validation in Step 2.
    [cverr, stats_loso] = predict(data, ‘algorithm_name’, …’cv_svm’, ‘nfolds’, n_folds, ‘error_type’, ‘mcr’);
    
    The output variable stats provides many kinds of information, including model weights, predicted y values $(\hat{y})$ based on cross-validation, and performance values (for more details, see Box 2).
    
    Note that one can use nested cross-validation to find the optimal hyper-parameters of the model. In nested cross-validation, an additional, nested cross-validation loop is performed on the training set to tune the hyper-parameters, while the outer cross-validation loop is used to estimate the model performance^1,101. In our example, for simplicity, we use the default setting of the function for the SVM algorithm, where C = 1.
    
    If multiple models with a number of different parameters are tested on a single training set, a correction for multiple comparisons (e.g. False Discovery Rate (FDR) correction) must be conducted. Note that the corrections for multiple comparisons are designed to protect against false-positive feature identification but not against the inflated accuracy that comes from testing multiple models outside of cross-validation loops. Therefore, a more important step is to test the final model on additional validation or independent test datasets.
    
    In the following steps, we apply the analysis methods to the linear SVM model, a classifier model. Nonetheless, the predict function can also build regression-based models for predicting continuous outcomes. For example, the code below runs principal component regression (PCR):
    [cverr, stats_loso] = predict(data, ‘algorithm_name’, …’cv_pcr’, ‘nfolds’, n_folds, ‘error_type’, ‘mse’);
    
    ? TROUBLESHOOTING
2. Training a CNN
  1. Prepare the data matrix. We used the pandas DataFrame (to create a data template) and Nilearn (to load data from NIfTI files). These are implemented in ‘Part 1: Initializing Data Matrix’ and ‘Part 2: Loading Data Function’ of our example Jupyter Notebook file, cnn_lrp.ipynb, which is available at https://github.com/cocoanlab/interpret_ml_neuroimaging/blob/master/scripts/cnn_lrp.ipynb.
  2. Define a CNN model. With Keras, one can define a CNN model using the following code, which defines four convolution layers and two fully connected layers, followed by a softmax output layer. One can also define the loss function with the Adam optimizer¹¹² for the model training (‘Part 3: CNN Model’ of cnn_lrp.ipynb).
    def make_custom_model_cnn_2D(): model = Sequential() model.add(Conv2D(8, (3,3), kernel_initializer=‘he_normal’, padding=‘same’, input_shape=fmri_shape)) model.add(Activation(‘relu’)) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Conv2D(16, (3,3), kernel_initializer=‘he_normal’, padding=‘same’)) model.add(Activation(‘relu’)) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Conv2D(32, (3,3), kernel_initializer=‘he_normal’, padding=‘same’)) model.add(Activation(‘relu’)) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Conv2D(64, (3,3), kernel_initializer=‘he_normal’, padding=‘same’)) model.add(Activation(‘relu’)) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Flatten()) model.add(Dense(128, kernel_initializer=‘he_normal’)) model.add(Activation(‘relu’)) model.add(Dense(2, kernel_initializer=‘he_normal’)) model.add(Activation(‘linear’)) model.add(Activation(‘softmax’)) adam = Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) model.compile(loss=‘categorical_crossentropy’, optimizer=adam, metrics=[‘accuracy’]) return model
  3. Split the data into training and test sets. As described above in the case of the linear SVM model, define the amount of data used as training and testing data for cross-validation. We used scikit-learn to create the cross-validation testing framework, which is implemented in ‘Part 4: Model Training example’ and ‘Part 5: Leave-One-Subject-Out Cross-validation’ of cnn_lrp.ipynb.
  4. Fit a CNN model on the training data. A CNN model can be trained with a variant of a mini-batch stochastic gradient descent method, such as Adam¹¹², which is realized by the fit function in the Keras package. In the example code, we trained the model with 32 mini-batch size for every iteration. When running the train_model function we defined here, we evaluate the training loss (error) every epoch with the evaluate function in Keras. The following code also defines the number of epochs for training the CNN model (the second section of ‘Part 3. CNN Model’ of cnn_lrp.ipynb).
    import tensorflow as tf config = tf.ConfigProto() config.gpu_options.allow_growth = True session = tf.Session(config=config) def train_model(train_X, train_y, test_X, test_y): # Optional: when you do not have enough GPUs, add the following line: # with tf.device(‘/cpu:0’): tr_data = {} tr_data[‘X_data’] = train_X tr_data[‘y_data’] = train_y te_data = {} te_data[‘X_data’] = test_X te_data[‘y_data’] = test_y tr_data[‘y_data’] = keras.utils.to_categorical(tr_data[‘y_data’], 2) te_data[‘y_data’] = keras.utils.to_categorical(te_data[‘y_data’], 2) # Initialize and compile the model model = make_custom_model_cnn_2D() model.compile(loss=“categorical_crossentropy”, optimizer=Adam(), metrics=[“accuracy”]) history = model.fit(tr_data[‘X_data’], tr_data[‘y_data’], batch_size=mini_batch_size, epochs=20, verbose=1) score = model.evaluate(te_data[‘X_data’], te_data[‘y_data’], verbose=0) return model,score
  5. Test the model on test data. Once the training of CNN is done, we can test the model on a separate test dataset as in the following code, which returns the prediction accuracy on the test set.
    score = model.evaluate(te_data[‘X_data’], te_data[‘y_data’], verbose=0)

Box 2 |. The `predict` function in the CanlabCore toolbox.

The predict function is a versatile tool for running many different ML algorithms with cross-validation. It operates on the fmri_data object, which stores the data matrix used for prediction in .dat (features×observations) and the corresponding outcome vector in .Y (observations×1). Users can specify the prediction algorithm, including multiple regression, LASSO regression, PCR, LASSO-PCR, SVMs and support vector regression.

In addition, the function includes an option to perform cross-validation. Users can define the number of cross-validation folds (i.e., k-fold cross-validation; the predict function stratifies cross-validation folds based on the outcome) or custom cross-validation fold, such as leave-one-out cross-validation. The function also evaluates performance with either misclassification rate or mean square error. There is also an option to automatically perform the bootstrap tests. Users can enter a desired number of bootstrap samples to use, and they can also save the bootstrapped weights if needed.

The output of the function provides many kinds of information, including predictive model weights, predicted outcomes $(\hat{y})$ based on cross-validation and performance values, such as prediction error or correlation between actual and predicted outcomes. For example, the .weight_object field in the output contains an fmri_data object (or a statistic_image object if the bootstrap tests are performed) that contains the weights of the trained model in the .dat field. Another important field of the output is the .other_output_cv field. It stores the weights of all models trained during the cross-validation in the first column, the corresponding predicted values in the second column, the intercept in the third column and additional information about the algorithm in the fourth column. If the bootstrap tests are performed, the results of the analysis are stored in the .WTS field, which contains the mean, P and z values and standard errors, as well as the bootstrapped weights if the ‘savebootweights’ option was used. You can find more information and some use cases in the help document of the predict function by typing help fmri_data.predict in the command window.

Assess the cross-validated performance ● Timing 5–20 min

▲CRITICAL This step evaluates the new model’s predictive performance in terms of accuracy, sensitivity and specificity. It is critical to obtain unbiased estimates of model performance using cross-validation or held-out test data. Below, we provide an analysis example of LOSO and eightfold cross-validation. Note that we made an arbitrary choice of k = 8 cross-validation folds for convenience, as cross-validation is typically largely insensitive to the choice of k, but researchers should consider other choices and/or cross-validation strategies. For further discussion on this topic, please see Step 1A(iv) and refs. ^1,101.

2
Iteratively fit models using a training set, test the models on each fold’s holdout set and aggregate predicted outcome values across folds. In Step 1, we divided the data into the training and test sets. As an example, we split the data to perform LOSO cross-validation. Therefore, we reserve one participant’s data as a test set and fit a model (an SVM in our example) to the remaining 58 participants’ data. Subsequently, we use the model to classify the left-out data and save the distance from the hyperplane for each data point. We repeat this process 59 times. This process is automated in the predict function.
In addition, the following code shows how to run eightfold stratified cross-validation.
```
[~, stats_8fold] = predict(data, ‘algorithm_name’, ‘cv_svm’, … ‘nfolds’, 8, ‘error_type’, ‘mcr’);
```
▲CRITICAL STEP Hyper-parameters of the models should be kept the same for all iterations of cross-validation, but a nested cross-validation, a common method to choose an optimal hyper-parameter, can use different hyper-parameters for each fold.

Calculate the predictive accuracy, sensitivity and specificity by comparing the model prediction and the actual outcome. In the context of classification, the accuracy can be defined as 1 minus the misclassification rate, which is the ratio of the number of incorrectly classified data points and total number of data points. Classification decision can be made with a single threshold value θ (in SVMs, typically θ = 0 if the bias term is included in the model). One can also use a two-alternative forced-choice (2AFC) test if each data point has its counterpart (e.g., which of two conditions was the heat condition?). Sensitivity is defined as the ratio of correctly classified positives to the number of positive data points, and specificity as the ratio of correctly classified negatives to the number of negative data points. Figure 3a illustrates results of the accuracy estimation of the cross-validated classification. The roc_plot function from the CanlabCore tools provides all these performance metrics:

% LOSO cross-validation
ROC_loso = roc_plot(stats_loso.dist_from_hyperplane_xval, … data.Y == 1, ‘threshold’, 0);
% 8-fold cross-validation
ROC_8fold = roc_plot(stats_8fold.dist_from_hyperplane_xval, … data.Y == 1, ‘threshold’, 0);

Example output:

LOSO cross-validation
`ROC_PLOT Output: Single-interval, A priori threshold`
`Threshold: 0.00`	`Sens: 94% CI(92%–96%)`	`Spec: 91% CI(88%–93%)`
`PPV: 91% CI(88%-93%)`	`Nonparametric AUC: 0.97`	`Parametric d_a: 2.53`
`Accuracy: 92% +− 0.9% (SE),`	`P = 0.000000`
Eightfold cross-validation
`ROC_PLOT Output: Single-interval, A priori threshold`
`Threshold: 0.00`	`Sens: 96% CI(94%–97%)`	`Spec: 95% CI(93%–97%)`
`PPV: 95% CI(93%–97%)`	`Nonparametric AUC: 0.98`	`Parametric d_a: 2.83`
`Accuracy: 96% +− 0.7% (SE),`	`P = 0.000000`

Open in a new tab

! CAUTION Examining the reliability of the outcome measures and model responses can be helpful to make sure that the model performance is not biased^113,114. In general, the model performance cannot exceed the reliability of the outcome measures. However, this is not strictly true, as reliability measures are themselves estimated with error, and the estimated reliability can be affected by variables other than the brain-outcome relationship¹¹⁴. Nonetheless, the reliability of the outcome generally provides an upper bound for any predictive model and therefore can be considered as a sanity check.

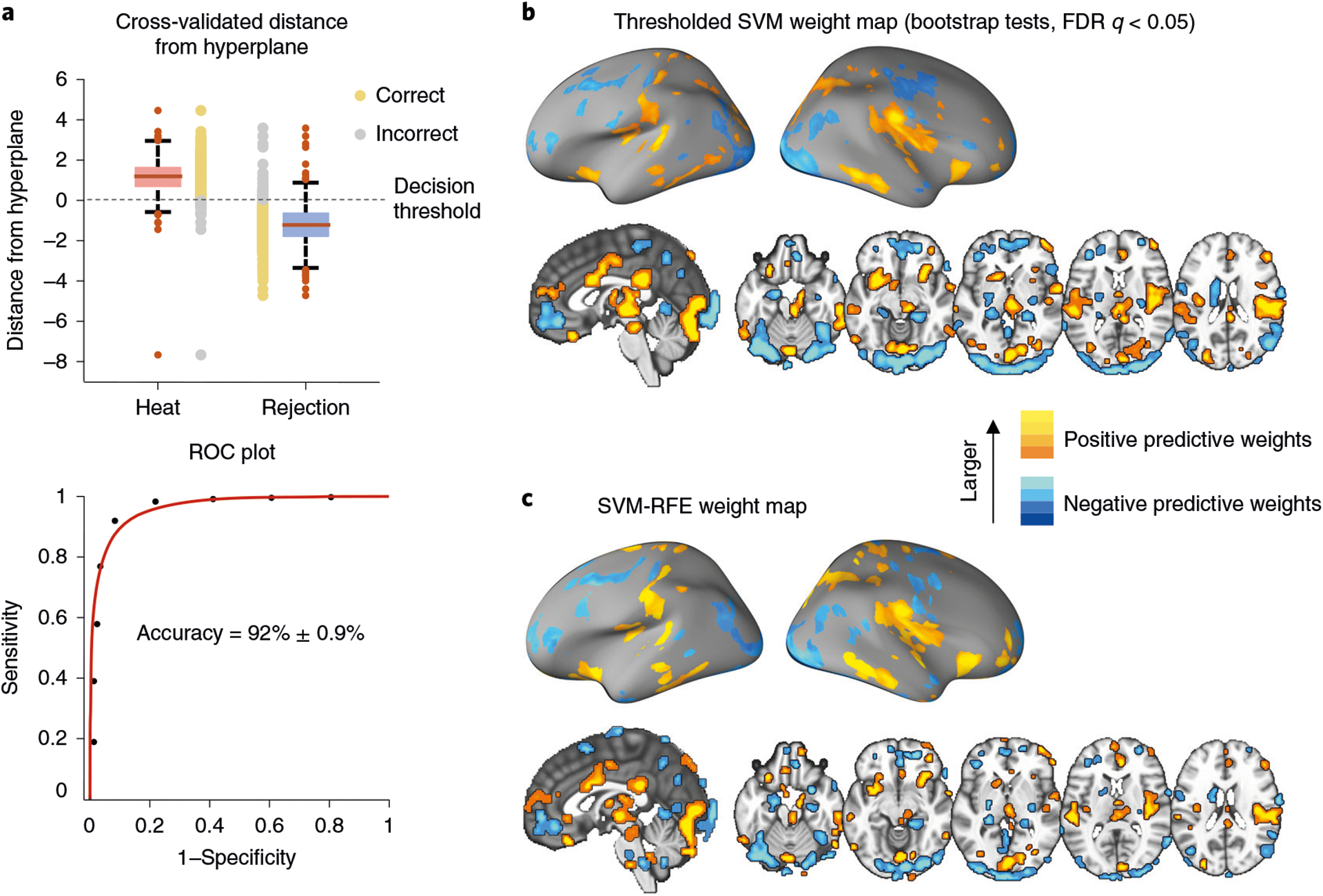
Fig. 3 | — a, The plots illustrate the classification performance of the SVM model tested by LOSO cross-validation with the threshold for misclassification set to 0 (Steps 2 and 3 of the procedure). The top panel shows the cross-validated distance from hyperplane and the decision threshold, and the bottom panel shows the receiver operating characteristic (ROC) plot. The yellow dots indicate correct classification, and the gray dots indicate misclassification. The accuracy of the SVM model reached 92% ± 0.9%. b, The weight map shows significant feature weights of the SVM model identified by the bootstrap tests and thresholded at an FDR of q < 0.05 (Step 7 of the procedure, option A). c, The weight map shows the final predictive SVM features after the RFE procedure, with the final number of features = 20,000 and the number of removed features at each step = 5,000 (Step 7 of the procedure, option B).

Analyze the model for the presence of confounds and artifacts ● Timing 5–20 min

▲CRITICAL To ensure that the model responses cannot be explained by confounds or artifacts, investigators can use the relevant confounding and nuisance variables (e.g., in-scanner head motion) to predict the responses of the model. If the confounds and nuisance variables can predict the model response, the model is likely to be influenced by them. Similarly, one can also examine whether the outcomes of interest are related to potential confounds and other nuisance variables (see refs. ^1,60 for more detailed discussion about other considerations related to confounds and nuisance variables).

The following steps describe an example of how to perform this type of analysis.

4
Create a set of nuisance variables (e.g., trial-level mean framewise displacement for six movement parameters (roll, pitch, yaw, x, y and z)). One can also use different types of confounding variables (e.g., physiology confounds, noise components from independent component analysis) or TR- or subject-level data. In this example analysis, we used trial-level movement parameters.
5
Prepare an fmri_data object variable. The nuisance variable should be assigned to the obj.dat field, and the model response (in the example analysis, we used distance from hyperplane) into the obj.Y (outcome) field.

Predict the model response using the nuisance data. For an example analysis, we used multiple regression because there are only a few features in this example. We did not use cross-validation in this example, but one can also use cross-validation (e.g., 5- or 10-fold cross-validation; see Step 1A(iv)). The model’s predictive performance can be examined with the correlation between the predicted

(\hat{y})

and actual values (y).

% Load nuisance data that are previously saved
nuisance_file = fullfile(basedir, ‘data’, ‘derivatives’, ‘nuisance.mat’);
    % Example nuisance data: Mean framewise displacement (z-scored;
    % roll, pitch, yaw, x, y, z; 6 columns)
load(nuisance_file);
% prepare fmri_data object variable
dat_nuistest = fmri_data;
dat_nuistest.dat = R’;
dat_nuistest.Y = stats_loso.dist_from_hyperplane_xval;
% train a regression model (without cross-validation)
[~, stats_nuistest] = predict(dat_nuistest, ‘algorithm_name’, … ‘cv_multregress’,’nfolds’, 1, ‘error_type’, ‘mse’);

? TROUBLESHOOTING

Identify significant features ● Timing 20 min to a few days

7
Identify significant features. Here, we propose four methods of evaluation of feature significance: bootstrap tests as an example of a method evaluating feature stability in linear models, RFE and ‘virtual lesion’ analysis as examples of methods evaluating feature importance in linear models and LRP as an example of a method evaluating feature importance in nonlinear models.

Bootstrap tests identify features that make reproducible (stable) contributions to prediction across units (e.g., participants in this example). Bootstrap tests have been successfully used in previous publications^13,19,47,93. The steps in option A describe the bootstrap test in more detail.

Unlike bootstrap tests, RFE is primarily a wrapper feature selection method. The model is repeatedly trained while a certain number of features, defined by an elimination step, are removed in each iteration until a stopping criterion is satisfied (e.g., when it reaches a specified number of features). The investigator can also select the final model according to the highest cross-validated predictive accuracy. The steps in option B describe how to perform RFE generally in linear models.

In a ‘virtual lesion’ analysis⁴⁷, the importance of features can be evaluated by examining (i) how much predictive performance decreases when a set of features (regions or networks) is removed from a model or (ii) how well a model performs if only a set of features is used. The analysis is illustrated in Fig. 4, and its example results are shown in Table 4. The analysis can be performed according to the steps in option C.
The goal of the LRP (described in option D) is to decompose the final prediction score and highlight the contribution of each input feature of the model to the prediction. LRP is particularly useful for hierarchical nonlinear models like CNN (see Step 1B), since it can efficiently propagate the decomposed contributions from the upper layers of the model down to the input feature level. A unique property of LRP that differentiates it from other assessment methods is that it can separately obtain the importance assessment of each feature for each prediction class of the model. Moreover, the assessments computed by LRP can have either positive or negative values, which concretely show whether each feature is for or against increasing the prediction score of the prediction class for which the assessments are computed, respectively. Although this method originally serves to explain predictions for individual instances, in the current protocol, we focus on the group-level explanations and present the final explanation as an average over the individual explanations (Fig. 5).

Option Module

7A Bootstrap tests

7B RFE

7C ‘Virtual lesion’ analysis

7D LRP

Open in a new tab
1. Bootstrap tests
  1. Resample the data. The essential step in the bootstrap tests is to create a sufficient number of new data samples (i.e., bootstrap samples). Create m bootstrap samples by sampling n data points with replacement from the dataset of size n. For example, our dataset contains 944 trials (i.e., n = 944), and we randomly draw 10,000 bootstrap samples (m = 10,000), each consisting of 944 data points.
  2. Train a model with each bootstrap sample. Each bootstrap sample serves as training data for a new model. The hyper-parameters of the model should be the same as the original model. This step is computationally expensive as it requires a large number of iterations depending on the number of bootstrap samples. With 1,000 samples, the minimum P value is 1/1,000 or 0.001. Thus, ≥10,000 samples is desirable when one wishes to have reasonable numerical precision in the tails of the distribution, which is often the case in neuroimaging.
  3. Calculate P values for the predictive weights. Calculate two-tailed uncorrected P values as the proportion of weights above and below zero across the models. An alternative option is to calculate z and P values with the mean and standard deviation of the sampling distribution.
  4. Perform a correction for multiple comparisons. For example, a popular choice of correction for multiple comparisons is the FDR correction, which we used to achieve the results visualized in Fig. 3b. The corrected threshold determines which features consistently contribute to the prediction over bootstrap samples.
    
    All these analysis steps can be performed using the ‘bootweights’ optional input argument of the predict function. The optional input, ‘bootsamples’ can be used to set the number of bootstrap samples. The default is 100, but 5,000 or 10,000 was used in our previous publications^13,19,47,93.
    [~, stats_boot] = predict(data, ‘algorithm_name’, ‘cv_svm’, … ‘nfolds’, 1, ‘error_type’, ‘mcr’, ‘bootweights’, … ‘bootsamples’, 10000);
    
    The results of bootstrap tests are stored in stats_boot.WTS. In addition, stats_boot.weight_obj also contains the bootstrap test results in a statistic_image object, including model weights and P values. The threshold method of the statistic_image object can be used to perform a correction for multiple comparisons (e.g., q < 0.05, FDR corrected).
    data_threshold = threshold(stats_boot.weight_obj, .05, ‘fdr’);
    
    ▲CRITICAL STEP If the size of data is large, the bootstrap tests can take several days. To shorten the duration, investigators can use the ‘useparallel’ option for parallel processing, or if multiple computers or nodes are available, one can use the optional input, ‘savebootweights’, to save the bootstrapped weights from multiple bootstrap samples, and combine the results afterward.
2. RFE
  1. Set the parameters of RFE. The basic parameters of RFE include a stopping criterion and elimination step. The stopping criterion determines when the process of repeated elimination and training should terminate. It depends on the desired characteristics of the final model. The elimination step is the number of features eliminated at each iteration. The size of the elimination step, often defined as a percentage of the remaining features, has varied in previous studies^63,115. To achieve our results shown in Fig. 3c, we used a fixed size (5,000 features) of the elimination step.
  2. Iteratively train a model on the gradually reduced number of features using predefined model parameters. In every iteration, fit a new model to the surviving feature set and evaluate its performance with cross-validation. The cross-validated results should be saved for later assessment. Sort the weights of the model by their absolute values and eliminate a certain number of features corresponding to the weights with the smallest absolute values. The number of eliminated features is defined by the elimination step. In the next iteration, fit a new model to the dataset with the reduced feature set. Repeat this procedure until the stopping criterion is satisfied.
    
    All these analysis steps can be performed with the svm_rfe function, which performs the RFE with SVMs. In the example below, the input data is an fmri_data object containing the training data, the ‘n_removal’ option specifies the number of features eliminated in each iteration and the ‘n_finalfeat’ option defines the stopping criterion. The remaining options are the same as for the predict function.
    out = svm_rfe(data, ‘n_removal’, 5000, ‘n_finalfeat’, 20000, … ‘algorithm_name’, ‘cv_svm’, ‘nfolds’, n_folds, … ‘error_type’, ‘mcr’);
3. ‘Virtual lesion’ analysis
  1. Prepare a parcellation mask. Choose the parcellation of interest (e.g., large-scale networks or contiguous supra-threshold regions) and prepare a mask for the parcellation. For the protocol, we prepared a mask for the large-scale networks defined by refs. ^87,116,117.
    %% Load mask: BucknerLab_wholebrain img = fullfile(basedir, ‘masks’, … ‘Bucknerlab_7clusters_all_combined.nii’); mask = fmri_data(img, gray_matter_mask); network_names = {‘Visual’, ‘Somatomotor’, ‘dAttention’, … ‘vAttention’, ‘Limbic’, ‘Frontoparietal’, ‘Default’};
  2. Iteratively remove a set of features and test the reduced models. In each iteration, a network or a region is removed from the full model, and the predictive performance is recorded while the reduced model is tested.
    %% One network removed for prediction in each iteration for network_i = 1:7 for subj_i = 1:59 masked_weights = … stats_loso.other_output_cv{subj_i,1}.* … double(mask.dat ~= network_i); dat_subj = data.dat(:, n_folds==subj_i); pexp(:,subj_i) = masked_weights’ * dat_subj; end pexp_sorted = [reshape(pexp(1:8,:), … numel(heat_imgs), 1); reshape(pexp(9:16,:), … numel(rejection_imgs), 1)]; roc = roc_plot(pexp_sorted, data.Y==1); out.num_vox(network_i,1) = sum(mask.dat ~= network_i); out.acc(network_i,1) = roc.accuracy; out.se(network_i,1) = roc.accuracy_se; out.p(network_i,1) = roc.accuracy_p; end
    
    ▲CRITICAL STEP If the training dataset is used for the ‘virtual lesion’ analysis, the analysis should also be conducted with cross-validation. In each iteration, one should apply the mask to the full model from the cross-validation folds and test the reduced model on the left-out data. One can calculate the predictive performance of the reduced models after collecting all the cross-validated predictions.
    
    ▲CRITICAL STEP To obtain the predictions of the reduced model, we calculated pattern expression values using the dot product, but other similarity metrics (e.g., Pearson’s correlation, Spearman correlation, cosine similarity) can also be used:
    $Pattern expression = \overset{⇀}{w} \cdot \overset{⇀}{x} = \sum_{i = 1}^{n} w_{i} x_{i}$
    where n is the number of voxels of the model, w is the voxel-level predictive weights and x is the test data. A predictive model is composed of predictive weights $(\overset{⇀}{w})$ across voxels, specifying locations and patterns of activation. The weights tell us how to integrate fMRI data into a single prediction, which then can be used for classification tests or regression analyses.
    
    ▲CRITICAL STEP As the model is not optimized for a zero threshold after removing a part of the model, one can use the balanced accuracy threshold option of the roc_plot function, which finds and uses an optimal threshold that maximizes the balanced classification accuracy (the average accuracy across classes). Enter the input keyword ‘Optimal balanced error rate’ to threshold based on balanced accuracy.
  3. Iteratively keep a set of features for prediction, and test the reduced models. The second option for the ‘virtual lesion’ analysis is removing all features except for a target set of features (e.g., those belonging to a particular resting-state network) and testing the predictive performance of the retained set of features jointly.
    %% Only one network used for prediction in each iteration for network_i = 1:7 for subj_i = 1:59 masked_weights = … stats_loso.other_output_cv{subj_i,1} .* … double(mask.dat == network_i); dat_subj = data.dat(:, n_folds==subj_i); pexp(:,subj_i) = masked_weights’ * dat_subj; end pexp_sorted = [reshape(pexp(1:8,:), … numel(heat_imgs), 1); reshape(pexp(9:16,:), … numel(rejection_imgs), 1)]; roc = roc_plot(pexp_sorted, data.Y==1); out.num_vox(network_i,1) = sum(mask.dat == network_i); out.acc(network_i,1) = roc.accuracy; out.se(network_i,1) = roc.accuracy_se; out.p(network_i,1) = roc.accuracy_p; end
4. LRP
  1. For a given set of data, run the classifier (e.g., CNN) to obtain the prediction score for each output class. Choose a prediction class c for which the importance assessment of each feature will be computed. The chosen prediction score is set as the initial relevance score and denoted as $R_{c}^{(L)}$ where L denotes the final output layer.
  2. Propagate the relevance score to the lower layer. By assuming there are total d nodes in the layer right before the final prediction layer, we compute
    $R_{i}^{(L - 1)} = \frac{z_{i c}}{z_{c}} R_{c}^{(L)}$
    for each i = 1, …, d, in which z_ic is the contribution of the activation value for node i to the classification score for class c, and $z_{c} = \sum_{i = 1}^{d} z_{i c}$ .
  3. Recursively propagate the relevance score to the input layer. For any intermediate layer l + 1 of the neural network, given that the relevance scores of all j nodes of the layer, $R_{j}^{(l + 1)}$ , are given, compute the decomposition of the scores to the i-th node of the lower layer as follows:
    $R_{i \leftarrow j}^{(l, l + 1)} = \frac{z_{i j}}{z_{j}} R_{j}^{(l + 1)},$
    in which z_ij is again the contribution of the activation of the i-th node of layer l to the activation of the j-th node of layer l + 1, and $z_{j} = \sum_{i} z_{i j}$ . Then, the relevance score for the i-th node of layer l is obtained by
    $R_{i}^{(l)} = \sum_{j} R_{i \leftarrow j}^{(l, l + 1)}$
    Moreover, when the widely used Rectified Linear Unit (ReLU) is used as an activation function for the i-th node, the relevance score becomes
    $R_{i}^{(l)} = {\begin{matrix} R_{i}^{(l)}, & a_{i}^{(l)} > 0 \\ 0, & otherwise \end{matrix}$
    in which $a_{i}^{(l)}$ is the activation value of the i-th node.
    
    This process is continued all the way down to the input layer, and the relevance scores for each input feature are computed.
    
    By iterating the process above for all available input data, one can obtain a group-level explanation for the feature-level relevance by averaging the individual explanations. In addition, a one-sample t-test can be used to examine which features consistently have relevance scores above or below zero. After obtaining P values from the t-test, one needs to perform a correction for multiple comparisons using FDR or family-wise error rate.
    
    To realize LRP, one can use the iNNvestigate package that is compatible with Keras (‘Part 7. Layer-wise Relevance Propagation’ of cnn_lrp.ipynb).
    import innvestigate import innvestigate.utils as iutils import innvestigate.utils.visualizations as ivis # Create model without softmax model_wo_softmax = iutils.keras.graph.model_wo_softmax(model) # Create analyser method = (“lrp.epsilon”, {“epsilon”:1, “neuron_selection_mode”: “max_activation”}, ivis.heatmap, “LRP-Epsilon”) analyzer = innvestigate.create_analyzer(method[0], model_wo_softmax, **method[1]) R = [] for i in range(len(test_X)): a = analyzer.analyze(test_X[i]) R.append(a)
    
    Once the important features are identified, investigators need to visualize them to see if they make sense. There are numerous ways and tools for model visualization, and one can choose any visualization tools that are suitable for their purposes. Generally, for the linear model, the significant features can be visualized on a standardized brain space, such as the MNI space. In our examples, we visualize significant weights identified by the bootstrap tests (Fig. 3b) and by the RFE method (Fig. 3c) using the following MATLAB code:
    % visualizing bootstrap test results orthviews(data_threshold); montage(data_threshold); % writing thresholded bootstrap test results as a Nifti file data_threshold.fullpath = fullfile(basedir, ‘results’, … ‘svm_bootstrap_results_fdr05.nii’); write(data_threshold, ‘thresh’); % visualizing RFE results orthviews(out.smallestnfeat_stats.weight_obj); montage(out.smallestnfeat_stats.weight_obj); % writing RFE analysis results as a Nifti file out.smallestnfeat_stats.weight_obj.fullpath = … fullfile(basedir, ‘results’, ‘svm_RFE_results.nii’); write(out.smallestnfeat_stats.weight_obj, ‘thresh’);
    
    With the orthviews function, you can display images on the canonical MNI brain image. In addition, using the write function with an optional input, ‘thresh’, you can save the result images as NIfTI image files, which then can be used with other visualization tools. For the LRP results with a CNN model, we show the thresholded mean relevance scores in Fig. 5a, which visualizes relevance scores that explain prediction of the heat condition when the input was an image acquired during the heat condition. Figure 5b shows the visualization of the relevance scores that explain the prediction of the rejection condition when the input was an image acquired during the rejection condition.
    
    For the purpose of creating publication-quality brain figures, the CanlabCore toolbox provides the fmridisplay object. For example, canlab_results_fmridisplay.m with the fmridisplay object is very useful. In addition, the CanlabCore toolbox also provides for creating surface images, cluster_surf.m and surface() methods for the fmri_data and region object classes. In Python, one can use many different visualization options, including plotting.plot_stat_map, plotting.plot_glass_brain and plotting.plot_surf_stat_map. We included some examples in our Jupyter notebook, cnn_lrp.ipynb, available at https://github.com/cocoanlab/interpret_ml_neuroimaging.

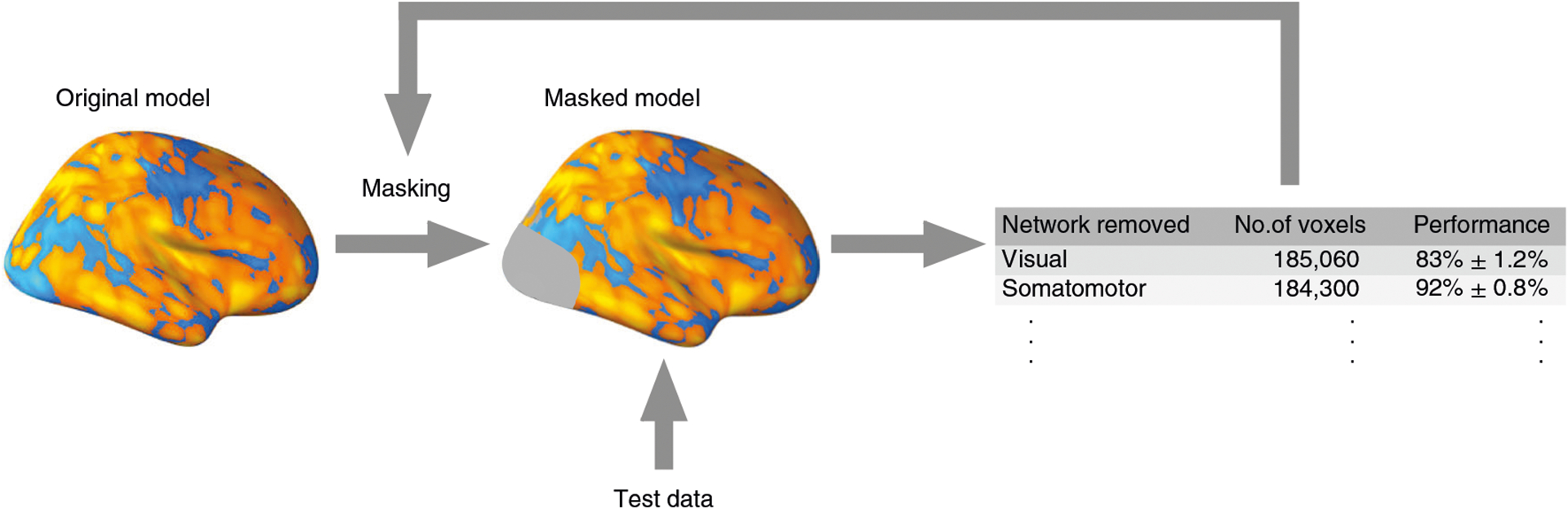
Fig. 4 | — The ‘virtual lesion’ analysis investigates how individual regions or networks contribute to final predictions of a model by removing or using one region or network at a time from the model. Based on a selected parcellation, regions in the original model are masked (either one region is removed, or only one region is used for prediction), and the performance of the masked model is evaluated.

Table 4 |.

Example results of the ‘virtual lesion’ analysis

Networks	One network removed for prediction		One network used for prediction
Networks	No. of voxels used	Performance (%)	No. of voxels used	Performance (%)
Visual	185,060	84 ± 1.2	21,740	82 ± 1.2
Somatomotor	184,300	93 ± 0.8	22,503	68 ± 1.5
dAttention	190,610	93 ± 0.8	16,192	65 ± 1.6
vAttention	188,610	93 ± 0.8	18,194	75 ± 1.4
Limbic	191,840	93 ± 0.8	14,959	56 ± 1.6
Frontoparietal	180,900	92 ± 0.9	25,902	77 ± 1.4
Default	169,970	92 ± 0.9	36,828	70 ± 1.5

Open in a new tab

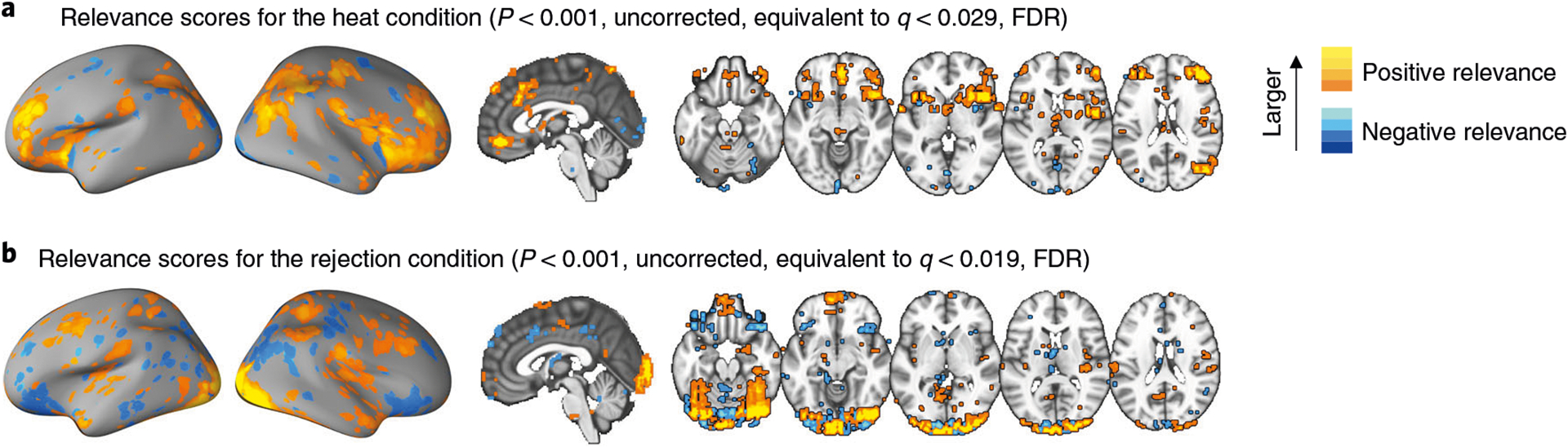
Fig. 5 | — a and b, We ran the LRP to explain predictions of each trial in each subject and condition (Step 7 of the procedure, option D). We then calculated the average relevance scores across subjects for both conditions. In a, we show the average relevance score map for the heat condition, thresholded at uncorrected P < 0.001, which is equivalent to an FDR at q < 0.029. Similarly, in b, we show the average relevance score map for the rejection condition, thresholded at uncorrected P < 0.001 (equivalent to an FDR at q < 0.019).

Test generalizability with independent datasets ● Timing 1 – 2 h

▲CRITICAL This stage tests the new model’s ability to generalize over new individuals, multiple datasets from different laboratories and scanners and variants in experimental and testing conditions. The test for generalizability is an open-ended process of evaluating a model’s robustness across variations, and thus this stage should be repeatedly performed with many different datasets from different contexts and test conditions. For demonstration, here we provide example analyses of testing the generalizability of two a priori predictive models developed to predict pain intensity in previous studies: the NPS¹³ and the SIIPS1¹⁸ (Fig. 6a,c). The example dataset⁹³ is used as an independent test dataset.

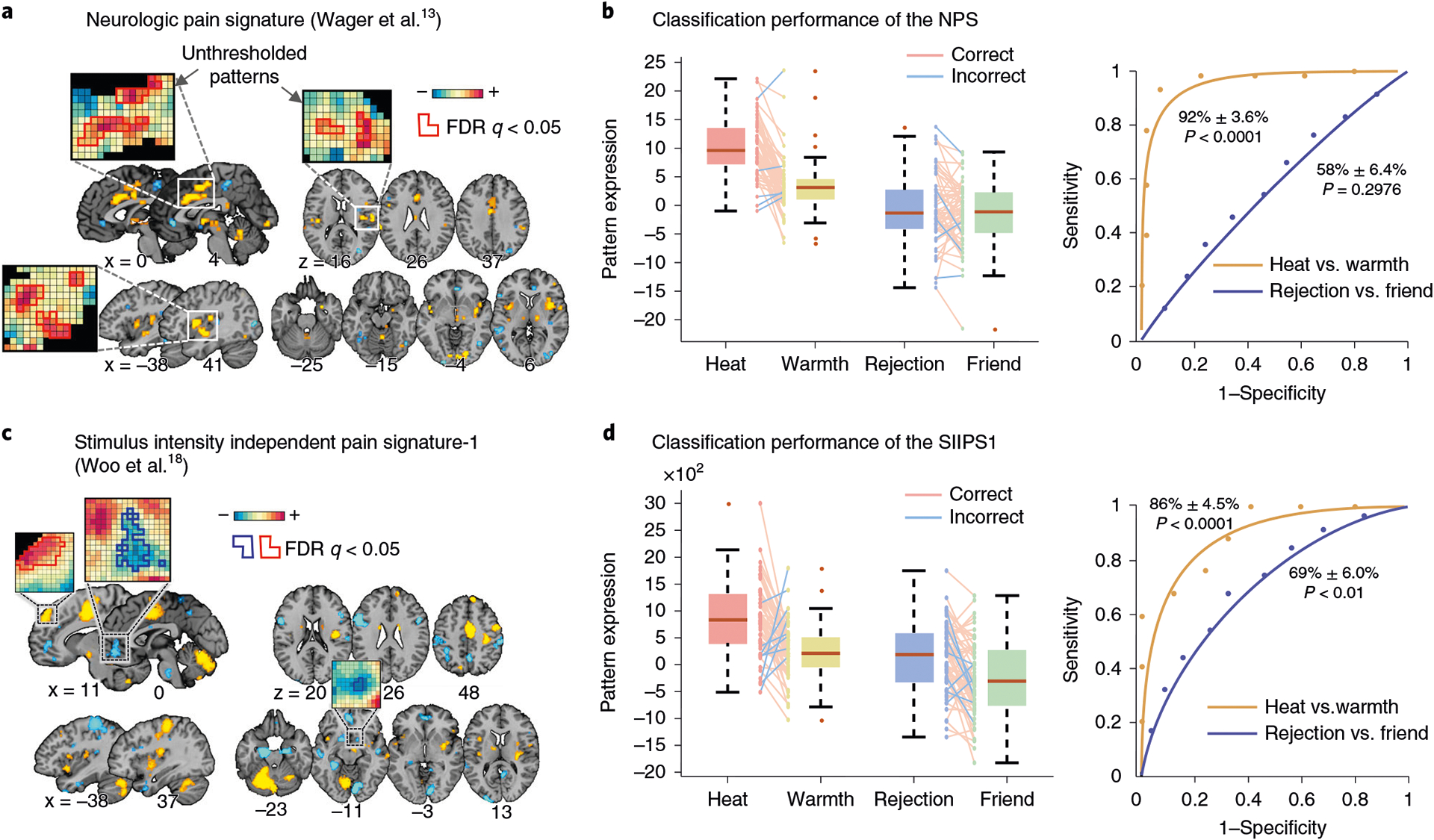
Fig. 6 | — a, The predictive weight map of the NPS¹³ that exceeds an FDR threshold of q < 0.05. b, To assess the generalizability of the NPS (Steps 8–10 of the procedure), we calculated the pattern expression values using the dot product between the signature pattern weights and activation maps for different conditions. Then, we performed the 2AFC test for heat versus warmth and rejection versus friend conditions. The box plot shows the NPS response to the four conditions. The lines between the boxes depict the correct (pink lines) and incorrect (blue lines) classifications. The ROC plot shows the sensitivity and specificity for discriminating between heat and warmth conditions (yellow) and between rejection and friend conditions (blue). c, The predictive weight map of the SIIPS1¹⁸ that exceed an FDR threshold of q < 0.05. d, The box plot shows the SIIPS1 response to the four conditions. The lines between the boxes depict the correct (pink lines) and incorrect (blue lines) classifications. The ROC plot shows the sensitivity and specificity for discriminating between heat and warmth conditions (yellow) and between rejection and friend conditions (blue).

Prepare the predictive models to be tested and test data. Make sure that the masks are included in the MATLAB path. We read the contrast image data using the fmri_data object.

% Prepare a priori models: NPS and SIIPS1
nps = which(‘weights_NSF_grouppred_cvpcr.img’);
siips = which(‘nonnoc_v11_4_137subjmap_weighted_mean.nii’);
% load contrast image data
cont_imgs{1} = filenames(fullfile(basedir, ‘data’, ‘derivatives’, … ‘contrast_images’, ‘heat*nii’), ‘char’);
cont_imgs{2} = filenames(fullfile(basedir, ‘data’, ‘derivatives’, … ‘contrast_images’, ‘warmth*nii’), ‘char’);
cont_imgs{3} = filenames(fullfile(basedir, ‘data’, ‘derivatives’, … ‘contrast_images’, ‘rejection*nii’), ‘char’);
cont_imgs{4} = filenames(fullfile(basedir, ‘data’, ‘derivatives’, … ‘contrast_images’, ‘friend*nii’), ‘char’);
data_test = fmri_data(cont_imgs, gray_matter_mask);

? TROUBLESHOOTING

Calculate the pattern expression values. We used the apply_mask function with the ‘pattern_expression’ option to calculate a dot product between the model weights and brain data. We obtained one pattern expression value per participant and condition, resulting in 59 values per condition.

% calculate pattern expression values
pexp_nps = apply_mask(data_test, nps, ‘pattern_expression’, … ‘ignore_missing’);
pexp_siips = apply_mask(data_test, siips, ‘pattern_expression’, … ‘ignore_missing’);
% reshape pexp values to have different conditions in different
columns pexp_nps = reshape(pexp_nps, 59, 4);
pexp_siips = reshape(pexp_siips, 59, 4);

10
Evaluate the models’ predictive performance, including specificity and sensitivity. In this example analysis, we tried to discriminate between the heat and warmth conditions and between the rejection and friend conditions using the NPS and SIIPS1. Given that we have one value per person, we used the 2AFC test, which compares the pattern expression values for the two contrasting conditions within the same participant without using a threshold. The higher value within a participant is classified as a positive condition. The 2AFC test can be performed using the roc_plot function with the ‘twochoice’ option. The inputs to the function are a vector of pattern expression and a corresponding binary outcome. The results are illustrated in Fig. 6b,d.
```
% NPS for pain vs. warmth
roc_nps_pain_warmth = roc_plot([pexp_nps(:,1);pexp_nps(:,2)], … [true(59,1);false(59,1)], ‘twochoice’);
% NPS for rejection vs. friend
roc_nps_rejection_friend = roc_plot([pexp_nps(:,3); … pexp_nps(:,4)], [true(59,1);false(59,1)], ‘twochoice’);
% SIIPS1 for pain vs. warmth
roc_siips_pain_warmth = roc_plot([pexp_siips(:,1); … pexp_siips(:,2)], [true(59,1);false(59,1)], ‘twochoice’);
% SIIPS1 for rejection vs. friend
roc_siips_rejection_friend = roc_plot([pexp_siips(:,3); … pexp_siips(:,4)], [true(59,1);false(59,1)], ‘twochoice’);
```

Evaluate the neurobiological validity of the model ● Timing 1–2 h

11
Evaluate the neurobiological validity of the model. This step aims to evaluate the neurobiological plausibility and validity of a model by examining converging evidence from previous literature and more invasive studies. As discussed above, it may not be possible to provide definitive answers to this biology-level assessment, but rather it should be regarded as an open-ended investigation that requires long-term and collaborative efforts from diverse disciplines and multi-modal and multi-level approaches. One way to examine the neurobiological plausibility of the model is to evaluate results from feature- and model-level assessments in the light of neuroscience literature. Therefore, in the current protocol, we provide two examples of biology-level assessment: evaluating overlaps of the model with large-scale resting-state functional networks and term-based decoding based on a large-scale meta-analysis database, Neurosynth⁸⁰.

The analysis in Option A examines which resting-state functional networks play important roles in a predictive model by calculating the overlaps (or pattern similarity) between a thresholded or unthresholded map (predictive weights or feature importance) and the functional networks. For the analysis results shown in Fig. 7a, we used the thresholded predictive weight map from Step 7A (bootstrap tests) and examined its overlaps with seven large-scale functional brain networks^87,116,117.
Follow the steps in option B to perform decoding analysis based on a meta-analytic database.

Option Module

11A Overlap with resting-state functional networks

11B Decoding analysis based on a meta-analytic database

Open in a new tab
1. Overlap with large-scale resting-state functional networks
  1. Prepare a parcellation of interest. Here we loaded the mask image file that had unique values for seven resting-state functional networks using the fmri_data object. For the next step of the analysis, we created an indicator matrix, of which the dimension is the number of voxels × the number of networks.
    img = fullfile(basedir, ‘masks’, … ‘Bucknerlab_7clusters_all_combined.nii’); mask = fmri_data(img, gray_matter_mask); dat = [mask.dat==1 mask.dat==2 mask.dat==3 mask.dat==4 … mask.dat==5 mask.dat==6 mask.dat==7];
  2. Prepare a thresholded image vector based on the feature significance. For this example, we prepared the thresholded map based on bootstrap test results from Step 7A.
    pattern_thresh = stats_boot.weight_obj.dat .* … double(stats_boot.weight_obj.sig);
  3. Calculate the proportions of overlap between the thresholded pattern map and each of the networks. For this analysis, one can use the canlab_pattern_similarity.m function with the ‘posterior_overlap’ option, which provides the posterior probability of observing the thresholded map given each network. We calculated the overlap-based similarity separately for positive and negative predictive weights.
    % calculate posterior probability of observing thresholded % regions given each network overlap_pos = canlab_pattern_similarity(dat, … pattern_thresh>0, ‘posterior_overlap’, ‘ignore_missing’); overlap_neg = canlab_pattern_similarity(dat, … pattern_thresh<0, ‘posterior_overlap’, ‘ignore_missing’);
2. Decoding analysis based on a meta-analytic database
  1. Using a large-scale meta-analytic decoding framework provided by Neurosynth⁸⁰, one can identify the psychological terms associated with a thresholded or unthresholded map of predictive weights or feature importance values. The Neurosynth decoder uses meta-analytic maps generated for various psychological terms and assesses their similarity to the input brain maps. It returns a list of the terms with correlation coefficients between the input and the meta-analytic maps. Investigators can use either the decoder in the Neurosynth Python package (https://github.com/neurosynth/neurosynth/blob/master/neurosynth/analysis/decode.py) or the Neurosynth decoder web application (http://neurosynth.org/decode/). Here, we provide a Python code for the decoding analysis, and Fig. 7b shows an example result of the decoding analysis for the unthresholded SVM model.
    import neurosynth as ns ns.dataset.download(path=‘.’, unpack=True) from neurosynth import decode from neurosynth.base.dataset import Dataset dataset = Dataset(‘data/database.txt’) dataset.add_features(‘data/features.txt’) decoder = decode.Decoder(dataset) data = decoder.decode([‘svm_heat_rejection_pattern.nii’], save=‘decoding_ svm_heat_rejection_pattern.txt’)

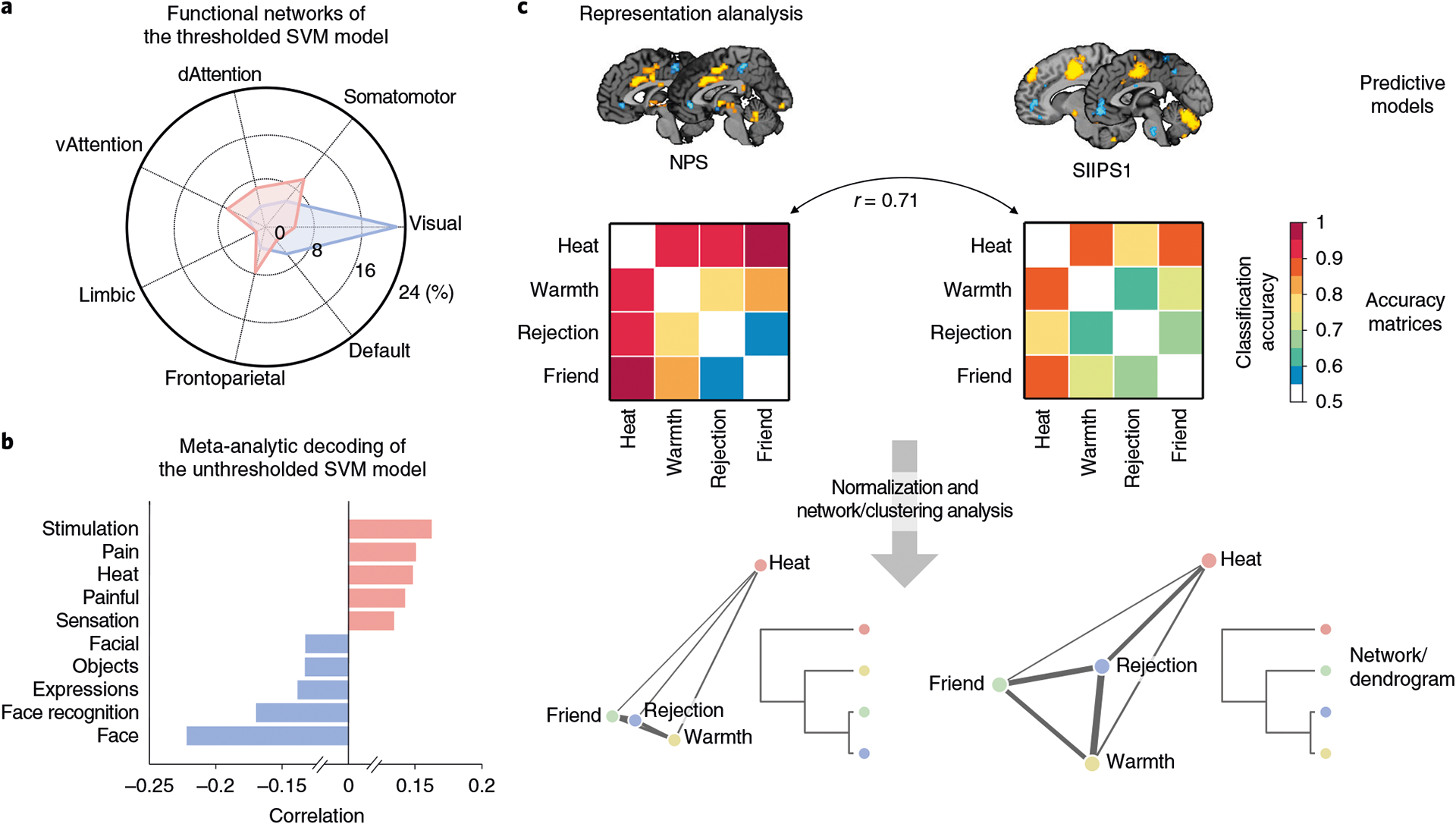
Fig. 7 | — a, The radar chart depicts the posterior probability of observing overlaps between the thresholded SVM model and the resting-state functional networks⁸⁷ (Step 11, option A). The pink chart represents the overlaps with the positive predictive weights of the model, and the blue chart represents the overlaps with the negative predictive weights of the model. b, The bar plot shows the functional terms obtained from the Neurosynth decoder applied to the unthresholded SVM model (Step 11, option B). The pink bars represent the decoding results for positive weights, and the blue bars represent the decoding results for negative weights. c, In the representational analysis (Steps 12–15), we compared the NPS¹³ and SIIPS1¹⁸ responses to four stimulus conditions. We first compared two accuracy matrices using correlation coefficients and then visualized the relationship between conditions using network and hierarchical clustering methods.

Perform representational similarity analysis ● Timing 1–2 h

▲CRITICAL This step aims to clarify the model’s representations and decision principles by examining and comparing model decisions over multiple instances and conditions. There can be many different ways to achieve this step, but here we provide an example of representational similarity analysis on two a priori predictive models for pain, the NPS¹³ and the SIIPS1¹⁸. We tested these predictive models on the example dataset⁹³, which has data from four conditions: pain, warmth, rejection and friend. Then, we conducted forced-choice tests for each pair of conditions to obtain the classification accuracy matrix, which was then used as a distance metric (i.e., a higher classification accuracy for [A vs. B] means that A and B conditions are far from each other for the predictive model). The example analysis results are shown in Fig. 7c.

Obtain classification accuracy matrices for different models. Using the pattern expression values obtained from Step 9, run the forced-choice classification tests for different pairs of conditions.

nps_acc = zeros(4,4);
siips_acc = zeros(4,4);
for i = 1:4
    for j = 1:4
        if i < j
           roc_nps = roc_plot([pexp_nps(:,i); pexp_nps(:,j)], … [true(59,1); false(59,1)], ‘twochoice’, ‘noplot’);
           nps_acc(i,j) = roc_nps.accuracy;
           nps_acc(j,i) = roc_nps.accuracy; % make it symmetric
           roc_siips = roc_plot([pexp_siips(:,i); … pexp_siips(:,j)], [true(59,1);false(59,1)], … ‘twochoice’, ‘noplot’);
           siips_acc(i,j) = roc_siips.accuracy;
           siips_acc(j,i) = roc_siips.accuracy; % make it symmetric
        end
    end
end

13
Compare the patterns of classification accuracy between two models (Steps 13–15). Many different methods can be used for examining and comparing the model representations over multiple conditions. In this protocol, we first use Pearson’s correlation between two vectorized accuracy matrices. To do this, run the following code:
```
r = corr(nps_acc(tril(true(4,4),−1)), siips_acc(tril(true(4,4),−1)));
```
In the example data, the correlation between the accuracy matrices was 0.71, indicating that the models are fairly closely related (Fig. 7c).

Visualize the relationship between conditions using MATLAB’s graph analysis tools. Turn the accuracy matrices into weights by subtracting the accuracy from one and divide it by the vector sum. With the weighted adjacency matrix, plot undirected, weighted networks. The network plots reveal some differences between the two predictive models—for the NPS, the heat condition is far from all other conditions, but for the SIIPS1, the heat and rejection conditions are more closely located than for the NPS (Fig. 7c). To perform this step, use the following code:

% vectorize the accuracy matrices
nps_acc = nps_acc(tril(true(4,4),−1));
siips_acc = siips_acc(tril(true(4,4),−1));
% make the accuracy values into weights
w_nps = (1-nps_acc)./sum(1-nps_acc);
w_siips = (1-siips_acc)./sum(1-siips_acc);
% draw network plots
[i, j] = find(tril(true(4,4),−1));
subplot(1,2,1);
G_nps = graph(i,j,w_nps);
plot(G_nps,’Layout’,’force’, ‘WeightEffect’, ‘inverse’, … ‘LineWidth’,w_nps*10);
subplot(1,2,2);
G_siips = graph(i,j,w_siips);
plot(G_siips,’Layout’,’force’, ‘WeightEffect’, ‘inverse’, … ‘LineWidth’,w_siips*10);

? TROUBLESHOOTING

15
Plot a dendrogram with the single linkage method to examine how the conditions were hierarchically clustered (Fig. 7c). Given the small number of the conditions in the example dataset, the clustering analysis might not be very useful here. However, the clustering analysis will become much more useful if there are a larger number of conditions. To plot the dendrograms for the two models examined here, run this code:
```
subplot(1,2,1);
Z_nps = linkage(nps_acc(tril(true(4,4),−1))’);
h_nps = dendrogram(Z_nps);
subplot(1,2,2);
Z_siips = linkage(siips_acc(tril(true(4,4),−1))’);
h_siips = dendrogram(Z_siips);
```

Troubleshooting

Possible problems in running the protocol and how to troubleshoot the issues can be found in Table 5.

Table 5 |.

Troubleshooting table

Step	Problem	Possible reason	Solution
1A	Errors when calling `gray_matter_mask.img` or when using `filenames.m`	The CanlabCore is not in the MATLAB path	In MATLAB, go to the CanlabCore directory and run the following: `addpath (genpath(pwd))`
	Error message when calling `fmri_data` says “`Undefined function` ‘`spm_vol`’ `for input arguments of type` ‘`char`’“	SPM12 is not in the MATLAB path	In MATLAB, go to the SPM12 directory and run the following: addpath (genpath(pwd))
	Cannot find the help text of the `predict.m` function by help predict	If there are functions with the same name in other toolboxes in the path, MATLAB can show the help text of other functions	Use the following: `help fmri_data.predict`
6	An error message says ‘`obj.dat must be` [`predictors × observations`] `and obj.Y must be` [`observations × 1`]’	The nuisance matrix is [observations × predictors]	Transpose the nuisance matrix when adding it into the .dat field
8	An error message says ‘`weights_NSF_grouppred_cvpcr.img`’ not found	The NPS model is not in your path	If you do not have the NPS model, please email the corresponding authors (T.D.W. or C.-W.W). The NPS will be shared upon request with a data use agreement. If you already have the NPS model, make sure the NPS file is in your path
14	An error message says ‘`Edge properties must be a table`’	Malfunctioning `istable.m` function (which is used in `graph.m`) is being used	Remove `spm12/external/fieldtrip/compat/matlablt2013b` from your MATLAB path

Open in a new tab

Timing

Step 1, model building: 20 min to a few hours. A, SVMs: 20 min to a few hours; B, CNN: a few hours
Steps 2–3, cross-validated performance assessment: 5–20 min
Steps 4–6, analysis of confounds: 5–20 min
Step 7, identify important features: 20 min to a few days. A, bootstrap tests: 1 h to a few days; B, RFE: 1–6 h; C, ‘virtual lesion’ analysis: 20 min to 1 h; D, LRP: 20 min to 1 h
Steps 8–10, testing generalizability with independent datasets: 1–2 h
Step 11, evaluate the neurobiological validity of the model: 1–2 h
Steps 12–15, representational analysis: 1–2 h

Anticipated results

The current protocol proposes a workflow that is expected to yield complementary results that support validation and interpretation of neuroimaging ML models. The workflow is based on the unified model interpretation framework introduced here.

Along with the methods explained here in the Procedure, we included examples of graphs and visualizations of the expected results based on our demonstration dataset. Figure 3a shows an example result of assessing the model’s performance using LOSO cross-validation, which we describe in Steps 2 and 3. In Figs. 3b,c and 5, the significant features identified by the bootstrap test, RFE and LRP (Step 7, options A, B and D), respectively, are visualized on the brain underlay. Table 4 illustrates example results of the ‘virtual lesion’ analysis described in Step 7, option C. Example results of generalizability testing performed in Steps 8–10 are illustrated in Fig. 6b,d. Results of the biology-level assessment (Step 11) are depicted in Fig. 7a,b. Finally, Fig. 7c shows visualizations of the representational similarity analysis described in Steps 12–15.

Although interpreting neuroimaging-based ML models is an open-ended process, the current protocol will serve as an important step toward developing interpretable and neuroscientifically plausible neuroimaging ML models and biomarkers and eventually a cumulative science of neuroimaging. The use of the proposed model interpretation framework and the carefully designed tests for different levels of assessment will produce a number of pieces of converging evidence, which could then constitute an overall interpretation and understanding of neuroimaging ML models.

Supplementary Material

Supplementary

NIHMS1835286-supplement-Supplementary.pdf^{(73.5KB, pdf)}

Acknowledgements

We would like to thank CANlab members who have contributed to the CANlab tool development, including Yoni Ashar, Luke Chang, Stephan Geuter, Phil Kragel, Bogdan Petre and Dan Weflen (who made >10 GitHub commits) among others. This work was supported by IBS-R015-D1 (Institute for Basic Science, Korea), 2019R1C1C1004512 (National Research Foundation of Korea) and 18-BR-03, 2019-0-01367-BabyMind (Ministry of Science and ICT, Korea) (to C.-W.W.); AI Graduate School Support Program [2019-0-00421] and ITRC Support Program [2019-2018-0-01798] of MSIT/IITP of the Korean government (to J.H., S.C. and T.M.); and NIH R01DA035484 and R01MH076136 (to T.D.W.). The authors have no conflicts of interest to declare.

Footnotes

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Code availability

Codes used in this protocol are publicly available at https://github.com/cocoanlab/interpret_ml_neuroimaging.

Competing interests

The authors declare no competing interests.

Supplementary information is available for this paper at https://doi.org/10.1038/s41596-019-0289-5.

Data availability

Sample data used in this protocol are publicly available at https://github.com/cocoanlab/interpret_ml_neuroimaging.

References

1.Scheinost D et al. Ten simple rules for predictive modeling of individual differences in neuroimaging. Neuroimage 193, 35–45 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Woo C-W, Chang LJ, Lindquist MA & Wager TD Building better biomarkers: brain models in translational neuroimaging. Nat. Neurosci 20, 365–377 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Haxby JV Multivariate pattern analysis of fMRI: the early beginnings. Neuroimage 62, 852–855 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Haynes JD A primer on pattern-based approaches to fMRI: principles, pitfalls, and perspectives. Neuron 87, 257–270 (2015). [DOI] [PubMed] [Google Scholar]
5.Norman KA, Polyn SM, Detre GJ & Haxby JV Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends Cogn. Sci 10, 424–430 (2006). [DOI] [PubMed] [Google Scholar]
6.Horikawa T, Tamaki M, Miyawaki Y & Kamitani Y Neural decoding of visual imagery during sleep. Science 340, 639–642 (2013). [DOI] [PubMed] [Google Scholar]
7.Kragel PA, Knodt AR, Hariri AR & LaBar KS Decoding spontaneous emotional states in the human brain. PLoS Biol. 14, e2000106, 10.1371/journal.pbio.2000106 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Mitchell TM et al. Predicting human brain activity associated with the meanings of nouns. Science 320, 1191–1195 (2008). [DOI] [PubMed] [Google Scholar]
9.Brodersen KH et al. Decoding the perception of pain from fMRI using multivariate pattern analysis. Neuroimage 63, 1162–1170 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Schulz E, Zherdin A, Tiemann L, Plant C & Ploner M Decoding an individual’s sensitivity to pain from the multivariate analysis of EEG data. Cereb. Cortex 22, 1118–1123 (2012). [DOI] [PubMed] [Google Scholar]
11.Haxby JV et al. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science 293, 2425–2430 (2001). [DOI] [PubMed] [Google Scholar]
12.Kriegeskorte N, Goebel R & Bandettini P Information-based functional brain mapping. Proc. Natl Acad. Sci. USA 103, 3863–3868 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Wager TD et al. An fMRI-based neurologic signature of physical pain. N. Engl. J. Med 368, 1388–1397 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Rosenberg MD et al. A neuromarker of sustained attention from whole-brain functional connectivity. Nat. Neurosci 19, 165–171 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Mano H et al. Classification and characterisation of brain network changes in chronic back pain: a multicenter study. Wellcome Open Res. 3, 19 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Shen X et al. Using connectome-based predictive modeling to predict individual behavior from brain connectivity. Nat. Protoc 12, 506–518 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Peelen MV, Wiggett AJ & Downing PE Patterns of fMRI activity dissociate overlapping functional brain areas that respond to biological motion. Neuron 49, 815–822 (2006). [DOI] [PubMed] [Google Scholar]
18.Woo C-W et al. Quantifying cerebral contributions to pain beyond nociception. Nat. Commun 8, 14211 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Krishnan A et al. Somatic and vicarious pain are represented by dissociable multivariate brain patterns. Elife 5, e15166, 10.7554/eLife.15166 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Castelvecchi D Can we open the black box of AI? Nat. N 538, 20 (2016). [DOI] [PubMed] [Google Scholar]
21.Rudin C Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell 1, 206–215 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Eloyan A et al. Automated diagnoses of attention deficit hyperactive disorder using magnetic resonance imaging. Front. Syst. Neurosci 6, 61 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Vellido A, Martín-Guerrero JD & Lisboa PJ Making machine learning models interpretable. In Proceedings of European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning 163–172 (ESANN, 2012). [Google Scholar]
24.Lipton ZC The mythos of model interpretability. Preprint at https://arxiv.org/abs/1606.03490 (2016).
25.Cabitza F, Rasoini R & Gensini GF Unintended consequences of machine learning in medicine. JAMA 318, 517–518 (2017). [DOI] [PubMed] [Google Scholar]
26.Doshi-Velez F & Kim B Towards a rigorous science of interpretable machine learning. Preprint at https://arxiv.org/abs/1702.08608 (2017).
27.Paulus MP Pragmatism instead of mechanism: a call for impactful biological psychiatry. JAMA Psychiatry 72, 631–632 (2015). [DOI] [PubMed] [Google Scholar]
28.Pine DS & Leibenluft E Biomarkers with a mechanistic focus. JAMA Psychiatry 72, 633–634 (2015). [DOI] [PubMed] [Google Scholar]
29.Bzdok D & Ioannidis JPA Exploration, inference, and prediction in neuroscience and biomedicine. Trends Neurosci. 42, 251–262 (2019). [DOI] [PubMed] [Google Scholar]
30.Bennett D, Silverstein SM & Niv Y The two cultures of computational psychiatry. JAMA Psychiatry 76, 563–564 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Breakspear M Dynamic models of large-scale brain activity. Nat. Neurosci 20, 340–352 (2017). [DOI] [PubMed] [Google Scholar]
32.Ritter P, Schirner M, McIntosh AR & Jirsa VK The virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connect. 3, 121–145 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Deco G, Jirsa VK, Robinson PA, Breakspear M & Friston K The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput. Biol 4, e1000092 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
34.O’Reilly RC Biologically based computational models of high-level cognition. Science 314, 91–94 (2006). [DOI] [PubMed] [Google Scholar]
35.Frank MJ, Seeberger LC & O’Reilly RC By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science 306, 1940–1943 (2004). [DOI] [PubMed] [Google Scholar]
36.Cole JH et al. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage 163, 115–124 (2017). [DOI] [PubMed] [Google Scholar]
37.Horikawa T & Kamitani Y Generic decoding of seen and imagined objects using hierarchical visual features. Nat. Commun 8, 15037, 10.1038/ncomms15037 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Kragel PA, Reddan MC, LaBar KS & Wager TD Emotion schemas are embedded in the human visual system. Sci. Adv 5, eaaw4358 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Hassabis D, Kumaran D, Summerfield C & Botvinick M Neuroscience-inspired artificial intelligence. Neuron 95, 245–258 (2017). [DOI] [PubMed] [Google Scholar]
40.Banino A et al. Vector-based navigation using grid-like representations in artificial agents. Nature 557, 429–433 (2018). [DOI] [PubMed] [Google Scholar]
41.Box GEP Science and statistics. J. Am. Stat. Assoc 71, 791–799 (1976). [Google Scholar]
42.Tibshirani R Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol 58, 267–288 (1996). [Google Scholar]
43.Zou H & Hastie T Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol 67, 301–320 (2005). [Google Scholar]
44.Grosenick L, Klingenberg B, Katovich K, Knutson B & Taylor JE Interpretable whole-brain prediction analysis with GraphNet. Neuroimage 72, 304–321 (2013). [DOI] [PubMed] [Google Scholar]
45.Bzdok D, Eickenberg M, Varoquaux G & Thirion B Hierarchical region-network sparsity for high-dimensional inference in brain imaging. In International Conference on Information Processing in Medical Imaging. (eds. Niethammer M, Styner M, Aylward S, Zhu H, Oguz I et al. ) 323–335 (Springer, 2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Yamashita O, Sato M, Yoshioka T, Tong F & Kamitani Y Sparse estimation automatically selects voxels relevant for the decoding of fMRI activity patterns. Neuroimage 42, 1414–1429 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Chang LJ, Gianaros PJ, Manuck SB, Krishnan A & Wager TD A sensitive and specific neural signature for picture-induced negative affect. PLoS Biol. 13, e1002180 10.1371/journal.pbio.1002180 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Kragel PA, Koban L, Barrett LF & Wager TD Representation, pattern information, and brain signatures: from neurons to neuroimaging. Neuron 99, 257–273 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Rahwan I et al. Machine behaviour. Nature 568, 477–486 (2019). [DOI] [PubMed] [Google Scholar]
50.Caliskan A, Bryson JJ & Narayanan A Semantics derived automatically from language corpora contain human-like biases. Science 356, 183–186 (2017). [DOI] [PubMed] [Google Scholar]
51.Rabinowitz NC et al. Machine theory of mind. Preprint at https://arxiv.org/abs/1802.07740 (2018).
52.Silver D et al. Mastering the game of Go without human knowledge. Nature 550, 354–359 (2017). [DOI] [PubMed] [Google Scholar]
53.Haxby JV, Connolly AC & Guntupalli JS Decoding neural representational spaces using multivariate pattern analysis. Ann. Rev. Neurosci 37, 435–456 (2014). [DOI] [PubMed] [Google Scholar]
54.Kriegeskorte N & Kievit RA Representational geometry: integrating cognition, computation, and the brain. Trends Cogn. Sci 17, 401–412 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Yamins DL & DiCarlo JJ Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci 19, 356–365 (2016). [DOI] [PubMed] [Google Scholar]
56.Khaligh-Razavi SM & Kriegeskorte N Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Comput. Biol 10, e1003915 10.1371/journal.pcbi.1003915 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Raj D, Anderson AW & Gore JC Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Phys. Med. Biol 46, 3331 (2001). [DOI] [PubMed] [Google Scholar]
58.Caballero-Gaudes C & Reynolds RC Methods for cleaning the BOLD fMRI signal. NeuroImage 154, 128–149 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Power JD, Schlaggar BL & Petersen SE Recent progress and outstanding issues in motion correction in resting state fMRI. NeuroImage 105, 536–551 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Ciric R et al. Mitigating head motion artifact in functional connectivity MRI. Nat. Protoc 13, 2801–2826 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Labus JS et al. Multivariate morphological brain signatures predict patients with chronic abdominal pain from healthy control subjects. Pain 156, 1545–1554 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Efron B Bootstrap methods: another look at the jackknife. Ann. Stat 7, 1–26 (1979). [Google Scholar]
63.Craddock RC, Holtzheimer PE, Hu XPP & Mayberg HS Disease state prediction from resting state functional connectivity. Magn. Reson. Med 62, 1619–1628 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Bach S et al. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One 10, e0130140 10.1371/journal.pone.0130140 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Lundberg SM et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng 2, 749–760 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
66.Hanson SJ, Matsuka T & Haxby JV Combinatorial codes in ventral temporal lobe for object recognition: Haxby (2001) revisited: is there a “face” area? NeuroImage 23, 156–166 (2004). [DOI] [PubMed] [Google Scholar]
67.Ribeiro MT, Singh S & Guestrin C “Why should I trust you?”: explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1135–1144 (ACM, 2016). [Google Scholar]
68.Kermany DS et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell 172, 1122–1131 (2018). [DOI] [PubMed] [Google Scholar]
69.Gotsopoulos A et al. Reproducibility of importance extraction methods in neural network based fMRI classification. NeuroImage 181, 44–54 (2018). [DOI] [PubMed] [Google Scholar]
70.Simonyan K, Vedaldi A & Zisserman A Deep inside convolutional networks: visualising image classification models and saliency maps. Preprint at https://arxiv.org/abs/1312.6034 (2013).
71.Mordvintsev A, Olah C & Tyka M Inceptionism: Going Deeper into Neural Networks. https://ai.googleblog.com/2015/06/inceptionism-going-deeper-into-neural.html (2015).
72.Lee M et al. Activation of corticostriatal circuitry relieves chronic neuropathic pain. J. Neurosci 35, 5247–5259 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
73.Ren W et al. The indirect pathway of the nucleus accumbens shell amplifies neuropathic pain. Nat. Neurosci 19, 220–222 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
74.Carrasquillo Y & Gereau RW IV Hemispheric lateralization of a molecular signal for pain modulation in the amygdala. Mol. Pain 4, 24 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
75.Kim HF & Hikosaka O Distinct basal ganglia circuits controlling behaviors guided by flexible and stable values. Neuron 79, 1001–1010 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
76.Baliki MN et al. Parceling human accumbens into putative core and shell dissociates encoding of values for reward and pain. J. Neurosci 33, 16383–16393 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
77.Pauli WM, O’Reilly RC, Yarkoni T & Wager TD Regional specialization within the human striatum for diverse psychological functions. Proc. Natl Acad. Sci. USA 113, 1907–1912 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
78.Simons LE et al. The human amygdala and pain: evidence from neuroimaging. Hum. Brain Mapp 35, 527–538 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
79.Ashar YK, Andrews-Hanna JR, Dimidjian S & Wager TD Empathic care and distress: predictive brain markers and dissociable brain systems. Neuron 94, 1263–1273.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
80.Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC & Wager TD Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 8, 665–670 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
81.Gorgolewski K, Esteban O, Schaefer G, Wandell B & Poldrack R OpenNeuro—a free online platform for sharing and analysis of neuroimaging data. 1677 (Organization for Human Brain Mapping, Vancouver, Canada, 2017). [Google Scholar]
82.Gorgolewski KJ et al. NeuroVault.org: a web-based repository for collecting and sharing unthresholded statistical maps of the human brain. Front. Neuroinform 9, 8 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
83.Wager TD et al. A Bayesian model of category-specific emotional brain responses. PLoS Comput. Biol 11, e1004066, 10.1371/journal.pcbi.1004066 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
84.Kragel PA et al. Generalizable representations of pain, cognitive control, and negative emotion in medial frontal cortex. Nat. Neurosci 21, 283–289 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
85.Eisenbarth H, Chang LJ & Wager TD Multivariate brain prediction of heart rate and skin conductance responses to social threat. J. Neurosci 36, 11987–11998 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
86.Zaki J, Wager TD, Singer T, Keysers C & Gazzola V The anatomy of suffering: understanding the relationship between nociceptive and empathic pain. Trends Cogn. Sci 20, 249–259 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
87.Yeo BTT et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol 106, 1125–1165 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
88.Hultman R et al. Brain-wide electrical spatiotemporal dynamics encode depression vulnerability. Cell 173, 166–180.e14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
89.Grosenick L et al. Functional and optogenetic approaches to discovering stable subtype-specific circuit mechanisms in depression. Biol. Psychiatry: Cogn. Neurosci. Neuroimaging 4, 554–566 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
90.Drysdale AT et al. Resting-state connectivity biomarkers define neurophysiological subtypes of depression. Nat. Med 23, 28–38 (2017). Erratum in: Nat. Med. 23, 264 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
91.Vemuri P et al. Antemortem MRI based STructural Abnormality iNDex (STAND)-scores correlate with postmortem Braak neurofibrillary tangle stage. NeuroImage 42, 559–567 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
92.Apkarian AV A brain signature for acute pain. Trends Cogn. Sci 17, 309–310 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
93.Woo C-W et al. Separate neural representations for physical pain and social rejection. Nat. Commun 5, 5380, 10.1038/ncomms6380 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
94.Rasmussen PM, Hansen LK, Madsen KH, Churchill NW & Strother SC Model sparsity and brain pattern interpretation of classification models in neuroimaging. Pattern Recognit. 45, 2085–2100 (2012). [Google Scholar]
95.Baldassarre L, Pontil M & Mourao-Miranda J Sparsity is better with stability: combining accuracy and stability for model selection in brain decoding. Front. Neurosci 11, 62, 10.3389/fnins.2017.00062 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
96.de Pierrefeu A et al. Structured sparse principal components analysis with the TV-elastic net penalty. IEEE Trans. Med. Imaging 37, 396–407 (2018). [DOI] [PubMed] [Google Scholar]
97.Zou H, Hastie T & Tibshirani R Sparse principal component analysis. Hui. J. Comput. Graph. Stat 15, 265–286 (2006). [Google Scholar]
98.Leonardi N et al. Principal components of functional connectivity: a new approach to study dynamic brain connectivity during rest. NeuroImage 83, 937–950 (2013). [DOI] [PubMed] [Google Scholar]
99.Calhoun VD, Maciejewski PK, Pearlson GD & Kiehl KA Temporal lobe and “default” hemodynamic brain modes discriminate between schizophrenia and bipolar disorder. Hum. Brain Mapp 29, 1265–1275 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
100.Baker BT et al. Decentralized temporal independent component analysis: leveraging fMRI data in collaborative settings. NeuroImage 186, 557–569 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
101.Varoquaux G et al. Assessing and tuning brain decoders: cross-validation, caveats, and guidelines. NeuroImage 145, 166–179 (2017). [DOI] [PubMed] [Google Scholar]
102.Alber M et al. iNNvestigate neural networks. J. Mach. Learn. Res 20, 1–8 (2019). [Google Scholar]
103.Lindquist MA et al. Group-regularized individual prediction: theory and application to pain. NeuroImage 145, 274–287 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
104.Riley RD et al. Minimum sample size for developing a multivariable prediction model: PART II—binary and time-to-event outcomes. Stat. Med 38, 1276–1296 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
105.Riley RD et al. Minimum sample size for developing a multivariable prediction model: Part I—continuous outcomes. Stat. Med 38, 1262–1275 (2019). [DOI] [PubMed] [Google Scholar]
106.Woo CW, Roy M, Buhle JT & Wager TD Distinct brain systems mediate the effects of nociceptive input and self-regulation on pain. PLoS Biol. 13, e1002036, 10.1371/journal.pbio.1002036 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
107.Esteban O et al. MRIQC: advancing the automatic prediction of image quality in MRI from unseen sites. PLoS One 12, e0184661 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
108.Chollet F Keras. Deep learning for humans. Github repository. https://github.com/keras-team/keras (2015). [Google Scholar]
109.Van Essen DC et al. The WU-Minn Human Connectome Project: an overview. NeuroImage 80, 62–79 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
110.Casey BJ et al. The Adolescent Brain Cognitive Development (ABCD) study: imaging acquisition across 21 sites. Dev. Cogn. Neurosci 32, 43–54 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
111.Sudlow C et al. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med 12, e1001779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
112.Kingma DP & Ba J Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
113.Vul E, Harris C, Winkielman P & Pashler H Puzzlingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspect. Psychol. Sci 4, 274–290 (2009). [DOI] [PubMed] [Google Scholar]
114.Woo C-W & Wager TD What reliability can and cannot tell us about pain report and pain neuroimaging. Pain 157, 511–513 (2016). [DOI] [PubMed] [Google Scholar]
115.De Martino F et al. Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage 43, 44–58 (2008). [DOI] [PubMed] [Google Scholar]
116.Buckner RL, Krienen FM, Castellanos A, Diaz JC & Yeo BT The organization of the human cerebellum estimated by intrinsic functional connectivity. J. Neurophysiol 106, 2322–2345 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
117.Choi EY, Yeo BT & Buckner RL The organization of the human striatum estimated by intrinsic functional connectivity. J. Neurophysiol 108, 2242–2263 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
118.Yahata N et al. A small number of abnormal brain connections predicts adult autism spectrum disorder. Nat. Commun 7, 11254 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
119.Poldrack RA & Gorgolewski KJ Making big data open: data sharing in neuroimaging. Nat. Neurosci 17, 1510–1517 (2014). [DOI] [PubMed] [Google Scholar]
120.Karpathy A, Johnson J & Fei-Fei L Visualizing and understanding recurrent networks. Preprint at https://arxiv.org/abs/1506.02078 (2015).
121.Papernot N & McDaniel P Deep k-nearest neighbors: towards confident, interpretable and robust deep learning. Preprint at https://arxiv.org/abs/1803.04765 (2018).
122.Wisniewski D, Reverberi C, Tusche A & Haynes JD The neural representation of voluntary task-set selection in dynamic environments. Cereb. Cortex 25, 4715–4726 (2015). [DOI] [PubMed] [Google Scholar]
123.Ye JP et al. Sparse learning and stability selection for predicting MCI to AD conversion using baseline ADNI data. BMC Neurol. 12, 46, 10.1186/1471-2377-12-46 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
124.Erlikhman G & Caplovitz GP Decoding information about dynamically occluded objects in visual cortex. NeuroImage 146, 778–788 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
125.Rondina JM, Shawe-Taylor J & Mourão-Miranda J Stability-based multivariate mapping using ScoRS. In PRNI ‘13: Proceedings of the 2013 International Workshop on Pattern Recognition in Neuroimaging 198–202 (IEEE Computer Society, 2013). [Google Scholar]
126.Strother SC et al. Activation pattern reproducibility: measuring the effects of group size and data analysis models. Hum. Brain Mapp 5, 312–316 (1997). [DOI] [PubMed] [Google Scholar]
127.Habes I et al. Pattern classification of valence in depression. Neuroimage Clin. 2, 675–683 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
128.Zhang FQ, Wang JP, Kim J, Parrish T & Wong PCM Decoding multiple sound categories in the human temporal cortex using high resolution fMRI. PLoS One 10, e0117303, 10.1371/journal.pone.0117303 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
129.Zien A, Krämer N, Sonnenburg S & Rätsch G The feature importance ranking measure. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases 694–709 (Springer, 2009). [Google Scholar]
130.Vidovic MM-C, Görnitz N, Müller K-R & Kloft M Feature importance measure for non-linear learning algorithms. Preprint at https://arxiv.org/abs/1611.07567 (2016).
131.Lei J, G’Sell M, Rinaldo A, Tibshirani RJ & Wasserman L Distribution-free predictive inference for regression. J. Am. Stat. Assoc 113, 1094–1111 (2017). [Google Scholar]
132.Shrikumar A, Greenside P & Kundaje A Learning important features through propagating activation differences. Preprint at https://arxiv.org/abs/1704.02685 (2017).
133.Lundberg S & Lee S-I A unified approach to interpreting model predictions. Preprint at https://arxiv.org/abs/1705.07874 (2017).
134.Vetere G et al. Chemogenetic interrogation of a brain-wide fear memory network in mice. Neuron 94, 363–374.e364 (2017). [DOI] [PubMed] [Google Scholar]
135.Polyn SM, Natu VS, Cohen JD & Norman KA Category-specific cortical activity precedes retrieval during memory search. Science 310, 1963–1966 (2005). [DOI] [PubMed] [Google Scholar]
136.Erhan D, Bengio Y, Courville A & Vincent P Visualizing Higher-Layer Features of a Deep Network http://www.iro.umontreal.ca/~lisa/publications2/index.php/publications/show/247 (2009).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary

NIHMS1835286-supplement-Supplementary.pdf^{(73.5KB, pdf)}

Data Availability Statement

Sample data used in this protocol are publicly available at https://github.com/cocoanlab/interpret_ml_neuroimaging.

[R1] 1.Scheinost D et al. Ten simple rules for predictive modeling of individual differences in neuroimaging. Neuroimage 193, 35–45 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] 2.Woo C-W, Chang LJ, Lindquist MA & Wager TD Building better biomarkers: brain models in translational neuroimaging. Nat. Neurosci 20, 365–377 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] 3.Haxby JV Multivariate pattern analysis of fMRI: the early beginnings. Neuroimage 62, 852–855 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.Haynes JD A primer on pattern-based approaches to fMRI: principles, pitfalls, and perspectives. Neuron 87, 257–270 (2015). [DOI] [PubMed] [Google Scholar]

[R5] 5.Norman KA, Polyn SM, Detre GJ & Haxby JV Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends Cogn. Sci 10, 424–430 (2006). [DOI] [PubMed] [Google Scholar]

[R6] 6.Horikawa T, Tamaki M, Miyawaki Y & Kamitani Y Neural decoding of visual imagery during sleep. Science 340, 639–642 (2013). [DOI] [PubMed] [Google Scholar]

[R7] 7.Kragel PA, Knodt AR, Hariri AR & LaBar KS Decoding spontaneous emotional states in the human brain. PLoS Biol. 14, e2000106, 10.1371/journal.pbio.2000106 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] 8.Mitchell TM et al. Predicting human brain activity associated with the meanings of nouns. Science 320, 1191–1195 (2008). [DOI] [PubMed] [Google Scholar]

[R9] 9.Brodersen KH et al. Decoding the perception of pain from fMRI using multivariate pattern analysis. Neuroimage 63, 1162–1170 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Schulz E, Zherdin A, Tiemann L, Plant C & Ploner M Decoding an individual’s sensitivity to pain from the multivariate analysis of EEG data. Cereb. Cortex 22, 1118–1123 (2012). [DOI] [PubMed] [Google Scholar]

[R11] 11.Haxby JV et al. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science 293, 2425–2430 (2001). [DOI] [PubMed] [Google Scholar]

[R12] 12.Kriegeskorte N, Goebel R & Bandettini P Information-based functional brain mapping. Proc. Natl Acad. Sci. USA 103, 3863–3868 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.Wager TD et al. An fMRI-based neurologic signature of physical pain. N. Engl. J. Med 368, 1388–1397 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.Rosenberg MD et al. A neuromarker of sustained attention from whole-brain functional connectivity. Nat. Neurosci 19, 165–171 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] 15.Mano H et al. Classification and characterisation of brain network changes in chronic back pain: a multicenter study. Wellcome Open Res. 3, 19 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] 16.Shen X et al. Using connectome-based predictive modeling to predict individual behavior from brain connectivity. Nat. Protoc 12, 506–518 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] 17.Peelen MV, Wiggett AJ & Downing PE Patterns of fMRI activity dissociate overlapping functional brain areas that respond to biological motion. Neuron 49, 815–822 (2006). [DOI] [PubMed] [Google Scholar]

[R18] 18.Woo C-W et al. Quantifying cerebral contributions to pain beyond nociception. Nat. Commun 8, 14211 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] 19.Krishnan A et al. Somatic and vicarious pain are represented by dissociable multivariate brain patterns. Elife 5, e15166, 10.7554/eLife.15166 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Castelvecchi D Can we open the black box of AI? Nat. N 538, 20 (2016). [DOI] [PubMed] [Google Scholar]

[R21] 21.Rudin C Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell 1, 206–215 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] 22.Eloyan A et al. Automated diagnoses of attention deficit hyperactive disorder using magnetic resonance imaging. Front. Syst. Neurosci 6, 61 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] 23.Vellido A, Martín-Guerrero JD & Lisboa PJ Making machine learning models interpretable. In Proceedings of European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning 163–172 (ESANN, 2012). [Google Scholar]

[R24] 24.Lipton ZC The mythos of model interpretability. Preprint at https://arxiv.org/abs/1606.03490 (2016).

[R25] 25.Cabitza F, Rasoini R & Gensini GF Unintended consequences of machine learning in medicine. JAMA 318, 517–518 (2017). [DOI] [PubMed] [Google Scholar]

[R26] 26.Doshi-Velez F & Kim B Towards a rigorous science of interpretable machine learning. Preprint at https://arxiv.org/abs/1702.08608 (2017).

[R27] 27.Paulus MP Pragmatism instead of mechanism: a call for impactful biological psychiatry. JAMA Psychiatry 72, 631–632 (2015). [DOI] [PubMed] [Google Scholar]

[R28] 28.Pine DS & Leibenluft E Biomarkers with a mechanistic focus. JAMA Psychiatry 72, 633–634 (2015). [DOI] [PubMed] [Google Scholar]

[R29] 29.Bzdok D & Ioannidis JPA Exploration, inference, and prediction in neuroscience and biomedicine. Trends Neurosci. 42, 251–262 (2019). [DOI] [PubMed] [Google Scholar]

[R30] 30.Bennett D, Silverstein SM & Niv Y The two cultures of computational psychiatry. JAMA Psychiatry 76, 563–564 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] 31.Breakspear M Dynamic models of large-scale brain activity. Nat. Neurosci 20, 340–352 (2017). [DOI] [PubMed] [Google Scholar]

[R32] 32.Ritter P, Schirner M, McIntosh AR & Jirsa VK The virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connect. 3, 121–145 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.Deco G, Jirsa VK, Robinson PA, Breakspear M & Friston K The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput. Biol 4, e1000092 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] 34.O’Reilly RC Biologically based computational models of high-level cognition. Science 314, 91–94 (2006). [DOI] [PubMed] [Google Scholar]

[R35] 35.Frank MJ, Seeberger LC & O’Reilly RC By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science 306, 1940–1943 (2004). [DOI] [PubMed] [Google Scholar]

[R36] 36.Cole JH et al. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage 163, 115–124 (2017). [DOI] [PubMed] [Google Scholar]

[R37] 37.Horikawa T & Kamitani Y Generic decoding of seen and imagined objects using hierarchical visual features. Nat. Commun 8, 15037, 10.1038/ncomms15037 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] 38.Kragel PA, Reddan MC, LaBar KS & Wager TD Emotion schemas are embedded in the human visual system. Sci. Adv 5, eaaw4358 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] 39.Hassabis D, Kumaran D, Summerfield C & Botvinick M Neuroscience-inspired artificial intelligence. Neuron 95, 245–258 (2017). [DOI] [PubMed] [Google Scholar]

[R40] 40.Banino A et al. Vector-based navigation using grid-like representations in artificial agents. Nature 557, 429–433 (2018). [DOI] [PubMed] [Google Scholar]

[R41] 41.Box GEP Science and statistics. J. Am. Stat. Assoc 71, 791–799 (1976). [Google Scholar]

[R42] 42.Tibshirani R Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol 58, 267–288 (1996). [Google Scholar]

[R43] 43.Zou H & Hastie T Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol 67, 301–320 (2005). [Google Scholar]

[R44] 44.Grosenick L, Klingenberg B, Katovich K, Knutson B & Taylor JE Interpretable whole-brain prediction analysis with GraphNet. Neuroimage 72, 304–321 (2013). [DOI] [PubMed] [Google Scholar]

[R45] 45.Bzdok D, Eickenberg M, Varoquaux G & Thirion B Hierarchical region-network sparsity for high-dimensional inference in brain imaging. In International Conference on Information Processing in Medical Imaging. (eds. Niethammer M, Styner M, Aylward S, Zhu H, Oguz I et al. ) 323–335 (Springer, 2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] 46.Yamashita O, Sato M, Yoshioka T, Tong F & Kamitani Y Sparse estimation automatically selects voxels relevant for the decoding of fMRI activity patterns. Neuroimage 42, 1414–1429 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] 47.Chang LJ, Gianaros PJ, Manuck SB, Krishnan A & Wager TD A sensitive and specific neural signature for picture-induced negative affect. PLoS Biol. 13, e1002180 10.1371/journal.pbio.1002180 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] 48.Kragel PA, Koban L, Barrett LF & Wager TD Representation, pattern information, and brain signatures: from neurons to neuroimaging. Neuron 99, 257–273 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.Rahwan I et al. Machine behaviour. Nature 568, 477–486 (2019). [DOI] [PubMed] [Google Scholar]

[R50] 50.Caliskan A, Bryson JJ & Narayanan A Semantics derived automatically from language corpora contain human-like biases. Science 356, 183–186 (2017). [DOI] [PubMed] [Google Scholar]

[R51] 51.Rabinowitz NC et al. Machine theory of mind. Preprint at https://arxiv.org/abs/1802.07740 (2018).

[R52] 52.Silver D et al. Mastering the game of Go without human knowledge. Nature 550, 354–359 (2017). [DOI] [PubMed] [Google Scholar]

[R53] 53.Haxby JV, Connolly AC & Guntupalli JS Decoding neural representational spaces using multivariate pattern analysis. Ann. Rev. Neurosci 37, 435–456 (2014). [DOI] [PubMed] [Google Scholar]

[R54] 54.Kriegeskorte N & Kievit RA Representational geometry: integrating cognition, computation, and the brain. Trends Cogn. Sci 17, 401–412 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] 55.Yamins DL & DiCarlo JJ Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci 19, 356–365 (2016). [DOI] [PubMed] [Google Scholar]

[R56] 56.Khaligh-Razavi SM & Kriegeskorte N Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Comput. Biol 10, e1003915 10.1371/journal.pcbi.1003915 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] 57.Raj D, Anderson AW & Gore JC Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Phys. Med. Biol 46, 3331 (2001). [DOI] [PubMed] [Google Scholar]

[R58] 58.Caballero-Gaudes C & Reynolds RC Methods for cleaning the BOLD fMRI signal. NeuroImage 154, 128–149 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] 59.Power JD, Schlaggar BL & Petersen SE Recent progress and outstanding issues in motion correction in resting state fMRI. NeuroImage 105, 536–551 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] 60.Ciric R et al. Mitigating head motion artifact in functional connectivity MRI. Nat. Protoc 13, 2801–2826 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] 61.Labus JS et al. Multivariate morphological brain signatures predict patients with chronic abdominal pain from healthy control subjects. Pain 156, 1545–1554 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] 62.Efron B Bootstrap methods: another look at the jackknife. Ann. Stat 7, 1–26 (1979). [Google Scholar]

[R63] 63.Craddock RC, Holtzheimer PE, Hu XPP & Mayberg HS Disease state prediction from resting state functional connectivity. Magn. Reson. Med 62, 1619–1628 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] 64.Bach S et al. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One 10, e0130140 10.1371/journal.pone.0130140 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] 65.Lundberg SM et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng 2, 749–760 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] 66.Hanson SJ, Matsuka T & Haxby JV Combinatorial codes in ventral temporal lobe for object recognition: Haxby (2001) revisited: is there a “face” area? NeuroImage 23, 156–166 (2004). [DOI] [PubMed] [Google Scholar]

[R67] 67.Ribeiro MT, Singh S & Guestrin C “Why should I trust you?”: explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1135–1144 (ACM, 2016). [Google Scholar]

[R68] 68.Kermany DS et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell 172, 1122–1131 (2018). [DOI] [PubMed] [Google Scholar]

[R69] 69.Gotsopoulos A et al. Reproducibility of importance extraction methods in neural network based fMRI classification. NeuroImage 181, 44–54 (2018). [DOI] [PubMed] [Google Scholar]

[R70] 70.Simonyan K, Vedaldi A & Zisserman A Deep inside convolutional networks: visualising image classification models and saliency maps. Preprint at https://arxiv.org/abs/1312.6034 (2013).

[R71] 71.Mordvintsev A, Olah C & Tyka M Inceptionism: Going Deeper into Neural Networks. https://ai.googleblog.com/2015/06/inceptionism-going-deeper-into-neural.html (2015).

[R72] 72.Lee M et al. Activation of corticostriatal circuitry relieves chronic neuropathic pain. J. Neurosci 35, 5247–5259 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] 73.Ren W et al. The indirect pathway of the nucleus accumbens shell amplifies neuropathic pain. Nat. Neurosci 19, 220–222 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] 74.Carrasquillo Y & Gereau RW IV Hemispheric lateralization of a molecular signal for pain modulation in the amygdala. Mol. Pain 4, 24 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R75] 75.Kim HF & Hikosaka O Distinct basal ganglia circuits controlling behaviors guided by flexible and stable values. Neuron 79, 1001–1010 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] 76.Baliki MN et al. Parceling human accumbens into putative core and shell dissociates encoding of values for reward and pain. J. Neurosci 33, 16383–16393 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] 77.Pauli WM, O’Reilly RC, Yarkoni T & Wager TD Regional specialization within the human striatum for diverse psychological functions. Proc. Natl Acad. Sci. USA 113, 1907–1912 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R78] 78.Simons LE et al. The human amygdala and pain: evidence from neuroimaging. Hum. Brain Mapp 35, 527–538 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R79] 79.Ashar YK, Andrews-Hanna JR, Dimidjian S & Wager TD Empathic care and distress: predictive brain markers and dissociable brain systems. Neuron 94, 1263–1273.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] 80.Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC & Wager TD Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 8, 665–670 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] 81.Gorgolewski K, Esteban O, Schaefer G, Wandell B & Poldrack R OpenNeuro—a free online platform for sharing and analysis of neuroimaging data. 1677 (Organization for Human Brain Mapping, Vancouver, Canada, 2017). [Google Scholar]

[R82] 82.Gorgolewski KJ et al. NeuroVault.org: a web-based repository for collecting and sharing unthresholded statistical maps of the human brain. Front. Neuroinform 9, 8 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] 83.Wager TD et al. A Bayesian model of category-specific emotional brain responses. PLoS Comput. Biol 11, e1004066, 10.1371/journal.pcbi.1004066 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R84] 84.Kragel PA et al. Generalizable representations of pain, cognitive control, and negative emotion in medial frontal cortex. Nat. Neurosci 21, 283–289 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] 85.Eisenbarth H, Chang LJ & Wager TD Multivariate brain prediction of heart rate and skin conductance responses to social threat. J. Neurosci 36, 11987–11998 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] 86.Zaki J, Wager TD, Singer T, Keysers C & Gazzola V The anatomy of suffering: understanding the relationship between nociceptive and empathic pain. Trends Cogn. Sci 20, 249–259 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R87] 87.Yeo BTT et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol 106, 1125–1165 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R88] 88.Hultman R et al. Brain-wide electrical spatiotemporal dynamics encode depression vulnerability. Cell 173, 166–180.e14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] 89.Grosenick L et al. Functional and optogenetic approaches to discovering stable subtype-specific circuit mechanisms in depression. Biol. Psychiatry: Cogn. Neurosci. Neuroimaging 4, 554–566 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R90] 90.Drysdale AT et al. Resting-state connectivity biomarkers define neurophysiological subtypes of depression. Nat. Med 23, 28–38 (2017). Erratum in: Nat. Med. 23, 264 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R91] 91.Vemuri P et al. Antemortem MRI based STructural Abnormality iNDex (STAND)-scores correlate with postmortem Braak neurofibrillary tangle stage. NeuroImage 42, 559–567 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R92] 92.Apkarian AV A brain signature for acute pain. Trends Cogn. Sci 17, 309–310 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R93] 93.Woo C-W et al. Separate neural representations for physical pain and social rejection. Nat. Commun 5, 5380, 10.1038/ncomms6380 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R94] 94.Rasmussen PM, Hansen LK, Madsen KH, Churchill NW & Strother SC Model sparsity and brain pattern interpretation of classification models in neuroimaging. Pattern Recognit. 45, 2085–2100 (2012). [Google Scholar]

[R95] 95.Baldassarre L, Pontil M & Mourao-Miranda J Sparsity is better with stability: combining accuracy and stability for model selection in brain decoding. Front. Neurosci 11, 62, 10.3389/fnins.2017.00062 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R96] 96.de Pierrefeu A et al. Structured sparse principal components analysis with the TV-elastic net penalty. IEEE Trans. Med. Imaging 37, 396–407 (2018). [DOI] [PubMed] [Google Scholar]

[R97] 97.Zou H, Hastie T & Tibshirani R Sparse principal component analysis. Hui. J. Comput. Graph. Stat 15, 265–286 (2006). [Google Scholar]

[R98] 98.Leonardi N et al. Principal components of functional connectivity: a new approach to study dynamic brain connectivity during rest. NeuroImage 83, 937–950 (2013). [DOI] [PubMed] [Google Scholar]

[R99] 99.Calhoun VD, Maciejewski PK, Pearlson GD & Kiehl KA Temporal lobe and “default” hemodynamic brain modes discriminate between schizophrenia and bipolar disorder. Hum. Brain Mapp 29, 1265–1275 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R100] 100.Baker BT et al. Decentralized temporal independent component analysis: leveraging fMRI data in collaborative settings. NeuroImage 186, 557–569 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R101] 101.Varoquaux G et al. Assessing and tuning brain decoders: cross-validation, caveats, and guidelines. NeuroImage 145, 166–179 (2017). [DOI] [PubMed] [Google Scholar]

[R102] 102.Alber M et al. iNNvestigate neural networks. J. Mach. Learn. Res 20, 1–8 (2019). [Google Scholar]

[R103] 103.Lindquist MA et al. Group-regularized individual prediction: theory and application to pain. NeuroImage 145, 274–287 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R104] 104.Riley RD et al. Minimum sample size for developing a multivariable prediction model: PART II—binary and time-to-event outcomes. Stat. Med 38, 1276–1296 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R105] 105.Riley RD et al. Minimum sample size for developing a multivariable prediction model: Part I—continuous outcomes. Stat. Med 38, 1262–1275 (2019). [DOI] [PubMed] [Google Scholar]

[R106] 106.Woo CW, Roy M, Buhle JT & Wager TD Distinct brain systems mediate the effects of nociceptive input and self-regulation on pain. PLoS Biol. 13, e1002036, 10.1371/journal.pbio.1002036 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R107] 107.Esteban O et al. MRIQC: advancing the automatic prediction of image quality in MRI from unseen sites. PLoS One 12, e0184661 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R108] 108.Chollet F Keras. Deep learning for humans. Github repository. https://github.com/keras-team/keras (2015). [Google Scholar]

[R109] 109.Van Essen DC et al. The WU-Minn Human Connectome Project: an overview. NeuroImage 80, 62–79 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R110] 110.Casey BJ et al. The Adolescent Brain Cognitive Development (ABCD) study: imaging acquisition across 21 sites. Dev. Cogn. Neurosci 32, 43–54 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R111] 111.Sudlow C et al. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med 12, e1001779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R112] 112.Kingma DP & Ba J Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).

[R113] 113.Vul E, Harris C, Winkielman P & Pashler H Puzzlingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspect. Psychol. Sci 4, 274–290 (2009). [DOI] [PubMed] [Google Scholar]

[R114] 114.Woo C-W & Wager TD What reliability can and cannot tell us about pain report and pain neuroimaging. Pain 157, 511–513 (2016). [DOI] [PubMed] [Google Scholar]

[R115] 115.De Martino F et al. Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage 43, 44–58 (2008). [DOI] [PubMed] [Google Scholar]

[R116] 116.Buckner RL, Krienen FM, Castellanos A, Diaz JC & Yeo BT The organization of the human cerebellum estimated by intrinsic functional connectivity. J. Neurophysiol 106, 2322–2345 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R117] 117.Choi EY, Yeo BT & Buckner RL The organization of the human striatum estimated by intrinsic functional connectivity. J. Neurophysiol 108, 2242–2263 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R118] 118.Yahata N et al. A small number of abnormal brain connections predicts adult autism spectrum disorder. Nat. Commun 7, 11254 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R119] 119.Poldrack RA & Gorgolewski KJ Making big data open: data sharing in neuroimaging. Nat. Neurosci 17, 1510–1517 (2014). [DOI] [PubMed] [Google Scholar]

[R120] 120.Karpathy A, Johnson J & Fei-Fei L Visualizing and understanding recurrent networks. Preprint at https://arxiv.org/abs/1506.02078 (2015).

[R121] 121.Papernot N & McDaniel P Deep k-nearest neighbors: towards confident, interpretable and robust deep learning. Preprint at https://arxiv.org/abs/1803.04765 (2018).

[R122] 122.Wisniewski D, Reverberi C, Tusche A & Haynes JD The neural representation of voluntary task-set selection in dynamic environments. Cereb. Cortex 25, 4715–4726 (2015). [DOI] [PubMed] [Google Scholar]

[R123] 123.Ye JP et al. Sparse learning and stability selection for predicting MCI to AD conversion using baseline ADNI data. BMC Neurol. 12, 46, 10.1186/1471-2377-12-46 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R124] 124.Erlikhman G & Caplovitz GP Decoding information about dynamically occluded objects in visual cortex. NeuroImage 146, 778–788 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R125] 125.Rondina JM, Shawe-Taylor J & Mourão-Miranda J Stability-based multivariate mapping using ScoRS. In PRNI ‘13: Proceedings of the 2013 International Workshop on Pattern Recognition in Neuroimaging 198–202 (IEEE Computer Society, 2013). [Google Scholar]

[R126] 126.Strother SC et al. Activation pattern reproducibility: measuring the effects of group size and data analysis models. Hum. Brain Mapp 5, 312–316 (1997). [DOI] [PubMed] [Google Scholar]

[R127] 127.Habes I et al. Pattern classification of valence in depression. Neuroimage Clin. 2, 675–683 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R128] 128.Zhang FQ, Wang JP, Kim J, Parrish T & Wong PCM Decoding multiple sound categories in the human temporal cortex using high resolution fMRI. PLoS One 10, e0117303, 10.1371/journal.pone.0117303 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R129] 129.Zien A, Krämer N, Sonnenburg S & Rätsch G The feature importance ranking measure. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases 694–709 (Springer, 2009). [Google Scholar]

[R130] 130.Vidovic MM-C, Görnitz N, Müller K-R & Kloft M Feature importance measure for non-linear learning algorithms. Preprint at https://arxiv.org/abs/1611.07567 (2016).

[R131] 131.Lei J, G’Sell M, Rinaldo A, Tibshirani RJ & Wasserman L Distribution-free predictive inference for regression. J. Am. Stat. Assoc 113, 1094–1111 (2017). [Google Scholar]

[R132] 132.Shrikumar A, Greenside P & Kundaje A Learning important features through propagating activation differences. Preprint at https://arxiv.org/abs/1704.02685 (2017).

[R133] 133.Lundberg S & Lee S-I A unified approach to interpreting model predictions. Preprint at https://arxiv.org/abs/1705.07874 (2017).

[R134] 134.Vetere G et al. Chemogenetic interrogation of a brain-wide fear memory network in mice. Neuron 94, 363–374.e364 (2017). [DOI] [PubMed] [Google Scholar]

[R135] 135.Polyn SM, Natu VS, Cohen JD & Norman KA Category-specific cortical activity precedes retrieval during memory search. Science 310, 1963–1966 (2005). [DOI] [PubMed] [Google Scholar]

[R136] 136.Erhan D, Bengio Y, Courville A & Vincent P Visualizing Higher-Layer Features of a Deep Network http://www.iro.umontreal.ca/~lisa/publications2/index.php/publications/show/247 (2009).

Option	Module
11A	Overlap with resting-state functional networks
11B	Decoding analysis based on a meta-analytic database

PERMALINK

Toward a unified framework for interpreting machine-learning models in neuroimaging

Lada Kohoutová

Juyeon Heo

Sungmin Cha

Sungwoo Lee

Taesup Moon

Tor D Wager

Choong-Wan Woo

Abstract

Introduction

Fig. 1 |. Model complexity in neuroimaging and the model interpretation framework.

Overview of the framework

Table 1 |.

Model-level assessment

Feature-level assessment

Table 2 |.

Biology-level assessment

Development of the protocol

Fig. 2 |. A proposed workflow for the procedure.

Comparison with other methods

Limitations

Overview of the procedure

Box 1 |. CANlab interactive fMRI analysis tools.

Table 3 |.

Level of expertise needed to implement the protocol

Materials

Equipment

Software

Input data

Example dataset

Procedure

Build a model ● Timing 20 min to a few hours

Box 2 |. The predict function in the CanlabCore toolbox.

Assess the cross-validated performance ● Timing 5–20 min

Fig. 3 |. Predictive performance of the SVM model (Steps 2 and 3) and the results of feature-level assessment of the linear models (Step 7, options A and B).

Analyze the model for the presence of confounds and artifacts ● Timing 5–20 min

Identify significant features ● Timing 20 min to a few days

Fig. 4 |. A schematic of the ‘virtual lesion’ analysis (Step 7, option C).

Table 4 |.

Fig. 5 |. Layer-wise relevance propagation results (Step 7, option D).

Test generalizability with independent datasets ● Timing 1 – 2 h

Fig. 6 |. Generalizability tests (Steps 8–10).

Evaluate the neurobiological validity of the model ● Timing 1–2 h

Fig. 7 |. Examples of biology-level assessment (Step 11) and the representational analysis (Steps 12–15).

Perform representational similarity analysis ● Timing 1–2 h

Troubleshooting

Table 5 |.

Timing

Anticipated results

Supplementary Material

Acknowledgements

Related links

Key reference(s) using this protocol

Footnotes

Data availability

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Box 2 |. The `predict` function in the CanlabCore toolbox.