Abstract
The dependence of downstream waters on upstream ecosystems necessitates an improved understanding of watershed-scale hydrological interactions including connections between wetlands and streams. An evaluation of such connections is challenging when, (1) accurate and complete datasets of wetland and stream locations are often not available and (2) natural variability in surface-water extent influences the frequency and duration of wetland/stream connectivity. The Upper Choptank River watershed on the Delmarva Peninsula in eastern Maryland and Delaware is dominated by a high density of small, forested wetlands. In this analysis, wetland/stream surface water connections were quantified using multiple wetland and stream datasets, including headwater streams and depressions mapped from a lidar-derived digital elevation model. Surface-water extent was mapped across the watershed for spring 2015 using Landsat-8, Radarsat-2 and Worldview-3 imagery. The frequency of wetland/stream connections increased as a more complete and accurate stream dataset was used and surface-water extent was included, in particular when the spatial resolution of the imagery was finer (i.e., <10 m). Depending on the datasets used, 12% to 60% of wetlands by count (21% to 93% of wetlands by area) experienced surface-water interactions with streams during spring 2015. This translated into a range of 50% to 94% of the watershed contributing direct surface water runoff to streamflow. This finding suggests that our interpretation of the frequency and duration of wetland/stream connections will be influenced not only by the spatial and temporal characteristics of wetlands, streams and potential flowpaths, but also by the completeness, accuracy and resolution of input datasets.
Keywords: Accuracy, connectivity, depressions, forested wetlands, headwater streams, inundation, Landsat, lidar, Radarsat-2, resolution, SAR, stream network, Worldview-3
1. Introduction
The dependence of large rivers, lakes, and coastal waters on upstream ecosystems highlights the importance of an improved understanding of watershed-scale hydrological interactions, such as variable surface water flows between wetlands and streams (Lowe and Likens 2005; USEPA 2015; Cohen et al. 2016). In the U.S., for example, regulation of some streams and wetlands under the U.S. Clean Water Act depends on understanding the impacts of these streams and wetlands on the integrity of downstream “navigable” waters (Downing et al. 2007). Evaluating complex hydrological interactions at watershed scales can be difficult even in a highly instrumented research watershed (e.g., Spence and Phillips 2015). This is because non-permanent hydrological connections between wetlands and downstream waters occur along a continuum or gradient defined by the frequency, duration, magnitude, timing and rate of change of such connections (Rains et al. 2008; Sass and Creed 2008; Wilcox et al. 2011; Mushet et al. 2015; USEPA 2015). The detection and quantification of these connections have taken several different strategies including using hydrological models to predict the impact of wetlands on streamflow (McLaughlin et al. 2014; Evenson et al. 2015, 2016; Golden et al. 2016), collecting field-based measurements of flow or water quality, such as dissolved ion concentrations (Shaw et al. 2012; Nachshon et al. 2014; McDonough et al. 2015; Leibowitz et al. 2016), predicting connectivity from topographic analysis, modeling and unit hydrograph theory (Spence 2007; Huang et al. 2011; Shaw et al. 2013; Chu 2015), and using remotely sensed imagery to detect surface water connections (Kahara et al. 2009; Niemuth et al. 2010; Vanderhoof and Alexander 2015; Vanderhoof et al. 2016a). In this study, we remotely detected surface water connections between depressional wetlands and streams in the Upper Choptank River watershed on the Delmarva Peninsula in eastern Maryland, an area where the majority of wetlands are forested. We explored how the accuracy and completeness of existing and newly developed stream and wetland datasets as well as the spatial resolution of surface-water maps influenced our interpretation of within-watershed connectivity during the seasonal peak of surface water wetness (i.e., following snowmelt and prior to leaf-out).
Remotely sensed imagery can be an effective means to monitor surface water extent (SWE) and distribution over time at a landscape scale (Alsdorf et al. 2007). Landsat, at 30 m resolution, can be used to map and monitor changes in SWE (Sethre et al. 2005; Rover et al. 2011; Frohn et al. 2012; Jin et al. 2017) as well as document the occurrence of surface water connections, for example, as lakes expand or wetlands merge (Vanderhoof and Alexander 2015). Because of the moderate spatial resolution of Landsat, however, it is unlikely to detect narrow fill-and-spill connections (Huang et al. 2011; Leibowitz et al. 2016) and is challenging to use in landscapes dominated by small wetlands (Huang et al. 2014; Halabisky et al. 2016; Vanderhoof et al. 2016a). Fine spatial resolution imagery (2 m resolution or finer) can improve efforts to map SWE for small wetlands (<1 ha in size) (White and Lewis 2011; Whiteside and Bartolo 2015), while synthetic aperture radar (SAR) imagery can be helpful to map surface water in forested environments (Lang and Kasichke 2008; Clewley et al. 2015; Hess et al. 2015; Schlaffer et al. 2016). These sources of imagery could potentially improve our ability to detect narrower connections, at least relative to Landsat. For example, Simon et al. (2015) paired synthetic aperture radar (SAR) imagery with fine-resolution optical imagery to improve detection of changes in water level for smaller water features. We note that identifying SWE cannot be considered equivalent to mapping wetlands, but areas that are inundated just prior to or at the beginning of the growing season (i.e., mid-March to mid-April at the study site) are very likely to meet the U.S. federal regulatory, hydrologic definition of a wetland (i.e., inundated or saturated in the root zone for two weeks within the growing season) (USACE 1987). Areas that are not inundated, but instead have near-surface saturated soils may also meet wetland definitions.
A landscape or watershed-scale assessment of surface-water connectivity between streams and wetlands requires accurate input maps regarding stream and wetland locations (Baker et al. 2007; Habtezion et al. 2016). However, due in part to the limited spatial resolution of most existing topographic data sources, the majority of headwater streams have not yet been mapped (Hansen 2001; Heine et al. 2004). Lidar-derived digital elevation models (DEMs) have been used to predict and map tributaries that are not consistently documented by current hydrographic maps, including ephemeral streams and constructed channels or ditches that function as tributaries within a drainage network (James et al. 2006; Murphy et al. 2008; White et al. 2012). The U.S. Geological Survey (USGS), which produces a national stream dataset (i.e., the National Hydrography Dataset (NHD)), is presently experimenting with automated and semi-automated methods to delineate hydrographic features from lidar DEMs to enhance NHD. However, NHD has not yet been updated to include these approaches (Steve Aichele, oral communication, 2016). For wetlands, the National Wetland Inventory (NWI) maps, produced by the U.S. Fish and Wildlife Service, are the most spatially and categorically detailed and accurate wetland maps in the United States. However, NWI funding has not been sufficient to maintain a consistently up-to-date dataset. This is particularly an issue in regions that have experienced extensive land-use change in the past few decades (Tiner 2009). Additionally, as NWI wetlands were visually interpreted from aerial photography, errors of omission and commission are highest for wetland types that are difficult to detect with photointerpretation, including small, forested wetlands, farmed wetlands, and partly drained wetlands (Stolt and Baker 1995; Tiner 1999). To help refine existing estimates of wetland location and extent, lidar-derived DEMs have been used to map depressional wetlands (during both leaf-on and leaf-off periods), most often to estimate wetland surface-water storage capacity (Gleason et al. 2007; Lane and D’Amico 2010; Huang et al. 2011) or to map wetlands that are difficult to detect, such as vernal pools (Wu et al. 2014), sinkholes (Wu et al. 2016) or forested wetlands (Creed et al. 2003; Lang et al. 2013).
The northern Delmarva Peninsula in eastern Maryland and Delaware is characterized by a high density of forested, depressional wetlands, commonly referred to as Delmarva bays (Tiner 2003). Delmarva bays are shallow, closed depressions, normally elliptical or ovate in shape, with 80% ranging in size from 0.5 to 5.7 ha and show a high degree of similarity to Carolina bays (Sharitz and Gibbons 1982; Fenstermacher et al. 2014). SWE in forested portions of the region has been mapped using C-band SAR (2003 and 2004) (Lang et al. 2008; Lang and Kasischke 2008), and lidar (Lang et al. 2012), while efforts using Landsat imagery have targeted leaf-off periods and paired Landsat with lidar backscatter intensity (Huang et al. 2014; Jin et al. 2017). Surface-water extent has been shown to vary interannually and be positively correlated with stream flow (Huang et al. 2014). Most efforts to date have focused on characterizing total SWE, while efforts to map SWE at the scale of individual wetlands has been limited to efforts using lidar backscatter intensity and lidar-derived topographic metrics (Lang and McCarty 2009; Lang et al. 2013). Efforts to predict wetland connectivity have examined stream dataset accuracy (Lang et al. 2012), but have not incorporated SWE. Documentation of actual wetland/stream connectivity has been limited to field observations of a few select sites (McDonough et al. 2015; Epting 2017). In this study, we examined how the completeness, accuracy and spatial resolution of stream, wetland and SWE datasets influenced our interpretation of wetland/stream surface-water connectivity in the Upper Choptank River watershed. Our research questions were:
How does the completeness and accuracy of wetland and stream datasets influence our interpretation of wetland/stream connections?
How does the spatial resolution of imagery influence estimates of total surface water extent and the detection of wetland/stream connections (Landsat [30 m], Radarsat-2 [5.6 m], Worldview-3 [2 m])?
2. Methods
To explore how the completeness, accuracy and spatial resolution of input datasets influenced our interpretation of the abundance of wetland/stream connections, we used two datasets to define wetlands, (1) NWI wetlands (USFWS 2010) and (2) wet topographic depressions derived from a lidar DEM; three datasets to define streams, (1) the high-resolution National Hydrography Dataset (NHD) (USGS 2013), (2) a previously published semi-automated stream dataset (Lang et al. 2012), and (3) a stream dataset that estimated headwater stream extent; and three sources of imagery to define SWE, (1) Landsat, (2) Radarsat-2 and (3) Worldview-3. A complete list of products used in our analysis is shown in Table 1.
Table 1.
Products used to identify wetland-stream connections, data sources, spatial resolution of data and acquisition dates. DEM: Digital elevation model. NHD: National Hydrography Dataset. SWE: Surface-water extent.
| Product | Source | Resolution | Image Acquisition/Product Processing Date |
|---|---|---|---|
| Wetlands | National Wetland Inventory | 1:24,000 | 1981, 1982, 2007 |
| Wetland Depressions | Lidar DEM | 2 m | April–June 2003, March–April 2006, April 2007 |
| Streams - NHD | NHD (High resolution) | 1:24,000 | May 2001–June 2016 |
| Streams – Semi-automated | Lidar DEM | 2 m | April–June 2003, March–April 2006, April 2007 |
| Streams – Total network | Lidar DEM | 2 m | April–June 2003, March–April 2006, April 2007 |
| SWE - Landsat | Landsat-8, Landsat-7 | 30 m | April 4, 11, 12, 2015 |
| SWE - Radarsat-2 | Radarsat-2 | 5.6 m | March 16, 24, 26, 31, April 2, 9, 2015 |
| SWE - Worldview-3 | Worldview-3 | 2 m | April 6, 2015 |
2.1. Study Area
Our study area was defined as the Upper Choptank River watershed (123,730 ha), upstream from the intersection of Tuckahoe Creek and Choptank River, on the Delmarva Peninsula in eastern Maryland and Delaware (Figure 1). The Delmarva Peninsula is within the ecoregion, the Outer Coastal Plain, and is dominated by poorly drained soils on floodplains and well-drained soils in the uplands (Lowrance et al. 1997). The surficial aquifer is unconfined with sediments dominated by sand and gravel (Lowrance et al. 1997). During dry periods the wetlands serve to recharge groundwater, while during wet periods, these wetlands receive water from adjacent upland areas via surface and subsurface water, as well as groundwater. During such periods, groundwater can discharge into wetlands (i.e., high water table) resulting in wetlands filling and spilling into downstream wetlands or streams, or flooding adjacent upland areas (Snodgrass et al. 1996; Sun et al. 2006; Pyzoha et al. 2008).
Figure 1.
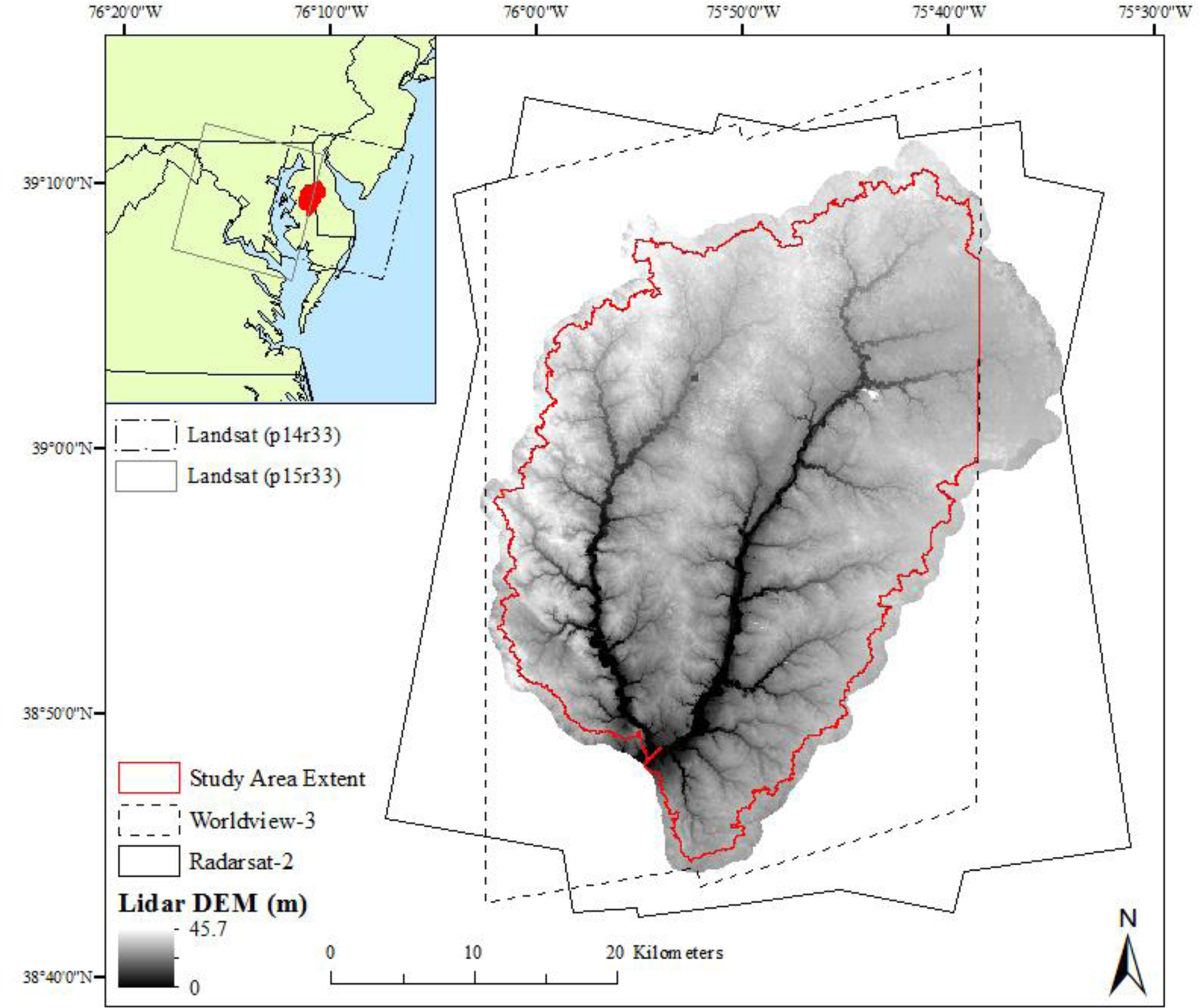
The study area consisted of the Upper Choptank River watershed. Study area extent was limited by extent of the Worldview-3 imagery.
Land cover within the study area is dominated by agricultural crops and grazed grass (59%), woody wetlands (20%), and deciduous forest (10%) (Homer et al. 2015). Much of the watershed has been hydrologically modified to accommodate agricultural activities. Maryland and Delaware have lost more than 73% and 54% of their wetlands, respectively (Dahl 1990). The primary types of wetlands remaining within the watershed are wetland depressions (e.g., Delmarva bays) and wetland flats, as well as riparian wetlands. Average weather conditions were derived from National Oceanic and Atmospheric Administration (NOAA) weather stations within and adjacent to the study area. Long-term (1950 – 2014) summer (June – August) temperatures averaged 23.6°C, while winter (December – February) temperatures averaged 2.2°C. Winter precipitation averaged 7.9 cm per month while summer precipitation averaged 11.2 cm per month. The 2014˗15 winter prior to the image collection was colder and wetter than average (temperature averaged 0.6°C and precipitation averaged 10.2 cm per month (29% wetter than normal)).
2.2. Lidar Processing
2.2.1. Lidar DEMs
The lidar DEM used in the analysis was created from three separate lidar data collection efforts (April–June 2003 (vertical accuracy root mean square error (RMSE) = 14.3 cm) and March–April 2006 (vertical accuracy RMSE = 18.5 cm) for Maryland (1 m resolution) and April 2007 (vertical accuracy RMSE = 18.5 cm) for Delaware (3 m resolution)) (Lang et al. 2012). The DEM was calculated from the adjusted bare-earth lidar point files using inverse distance-weighted interpolation. The 1 m and 3 m resolution DEMs were resampled to 2 m resolution using cubic convolution.
2.2.2. Mapping Wetland Depressions and Wetland Contributing Area
Depressions were identified using the Stochastic Depression Analysis Tool in Whitebox Geospatial Analysis Tools, an open source software (Lindsay 2014), largely following methods by Wu et al. (2014). The Depression Analysis Tool aims to separate out error artifacts in the DEM from “true” depressions. We used a Gaussian probability function (mean = 0, RMSE = 18.5 cm) to derive a normal distribution of potential error values. In each of the 20 iterations, a random sample from the potential error values was added to the original DEM prior to depressions being filled and identified using the depression filling technique of Wang and Liu (2006). Cells were considered part of a depression if identified as such in 80% of the 20 iterations (Wu et al. 2014). An edge-preserving smoothing filter with a 3-pixel by 3-pixel window was applied to reduce noise, or random error, within the final depression raster. Depressions smaller than 50 m2 were removed (17,217 of 52,560 depressions) (Wu et al. 2014). To improve our confidence that depressions represented water or wetland features, only depressions that overlapped with surface water extent, as identified by the Worldview-3 water classification were retained. This step was meant to reduce errors of commission, but could have resulted in an underestimation of wetland features, particularly for features that store water for only short periods of time.
We also utilized an existing wetland dataset, the NWI dataset (U.S. Fish and Wildlife Service 2010). Non-riverine, palustrine and lacustrine wetlands were analyzed separately from riverine wetlands to improve comparability between the depression and NWI datasets. Further, internal divisions indicating a change in wetland type within a spatially continuous wetland feature were dissolved to more accurately compare feature counts between the NWI and depression datasets. Contributing area was calculated for each depression and NWI wetland using the standard D8 flow direction algorithm from the hydrologically filled lidar DEM using ArcHydro in ArcGIS 10.3 (McCauley and Anteau 2014).
2.2.3. Mapping the Stream Network
Three versions of the stream network, representing a range of accuracy and completeness, were included in the analysis (Table 1). The stream network was first defined by the high resolution NHD (USGS 2013). A semi-automated stream network was also used (Lang et al. 2012). This version was meant to include the same stream types as NHD (i.e., perennial and intermittent), but because it was derived from a lidar DEM, it showed improved accuracy relative to NHD (Lang et al. 2012). Third, ephemeral headwater streams were mapped and added onto the existing semi-automated stream network (Lang et al. 2012) to create an estimate of the total stream network (i.e., perennial, intermittent, and ephemeral). The total stream network dataset was created to account for streams typically excluded from the NHD dataset such as ephemeral streams and stream lengths <1.6 km (USGS 2000).
To map the total stream network, flow accumulation was calculated on the filled lidar DEM using the FD8 flow accumulation algorithm (Freeman 1991) in Whitebox GAT. The selection of a flow-accumulation threshold was guided by field-based points (n=30) collected in 2014 and 2015 in ephemeral and intermittent streams (Epting 2017). The location of these points were often near but not at the start of the stream origin due to limited land access (Epting 2017). A flow accumulation threshold of 50,000 m2 captured 95% of the non-ditch ephemeral and intermittent streams and showed the most realistic headwater-stream extent based on our field experience regarding stream extent in the watershed. The headwater-stream extensions were added to the existing semi-automated stream network to create our estimate of the total stream network. Despite differences in the digital accuracy of the NHD (horizontal inaccuracy of 14 m) (USGS 2000) versus the semi-automated and total stream network versions (horizontal inaccuracy of 50 cm or less), for consistency purposes, all three datasets were buffered by 2 m to account for stream width and riparian habitat. To account for stream width in the main stem of the Choptank River and larger tributaries, the NHD area was added to each of the three buffered stream networks. NHD area was restricted to the Upper Choptank River.
2.3. SWE Mapping and Validation
SWE was mapped across the Upper Choptank River watershed using Landsat (30 m resolution), Radarsat-2 (5.6 m resolution) and Worldview-3 (2 m resolution). The SWE maps were validated using field-collected data as well as points visually identified from the raw Worldview-3 imagery.
2.3.1. Worldview-3 and Landsat Image Processing
A Worldview-3 image was collected across the watershed on April 6, 2015, and delivered as nine separate images. In addition, three Landsat images were processed: Landsat-8 images collected on April 4, 2015 (p14r33) and April 11, 2015 (p15r33) and a Landsat-7 ETM+ image collected on April 12, 2015 (p14r33) (Table 2). The Landsat images were atmospherically corrected and converted to surface reflectance using the Landsat Ecosystem Disturbance Adaptive Processing System (Masek et al. 2006). In ENVI, the Worldview-3 images were atmospherically corrected and converted to ground reflectance using Fast Line-of-sight Atmospheric Analysis of Hypercubes (FLAASH) (Adler-Golden et al. 1998, 1999). The Landsat and Worldview-3 imagery were then similarly processed in ENVI by first applying a minimum noise fraction transformation to reduce noise in the data (Green et al. 1988). Surface water was identified using the Matched Filtering algorithm, which is designed to detect the abundance of a known endmember (e.g., water) against a composite of unknown background endmembers (e.g., vegetation, soil) using a partial unmixing technique (Turin 1960; Vanderhoof et al. 2016a). The algorithm is similar to Spectral Mixture Analysis (SMA), but does not require knowledge of all of the endmembers within a scene. The output values were linearly stretched to maximize the spread of pixel values, enhancing our ability to distinguish inundated from non-inundated pixels. A Frost filter with a 3-pixel by 3-pixel window was applied to reduce noise in the data (Shi and Fung 1994). The imagery was co-registered to the lidar DEM using approximately 30 tie points. Worldview-3 pixels with a water per-pixel fraction of >0.25 were classified as inundated. Landsat pixels with a water per-pixel fraction of >0.4 were classified as inundated. Thresholds were specific to the source of imagery in order to balance errors of omission and commission for a given inundation map. The classified Worldview-3 images were mosaicked together. The Worldview-3 imagery did not extend to the farthest northeast corner of the watershed, necessitating our usage of a “clipped” watershed extent for the analysis (Figure 1). For the Landsat inundation map, the Landsat-8 image collected on April 11, 2015 (p15r33) was used as the primary image. The Landsat-8 image collected on April 4, 2015 (p14r33) and Landsat-7 ETM+ image collected on April 12, 2015 (p14r33) were mosaicked with the April 11, 2015 image to compensate for limited extent of the primary image, cloud-cover data gaps, and data gaps due to the Landsat-7 ETM+ scan-line error.
Table 2.
Characteristics and date of collection for the Radarsat-2 (Single Look Complex, 4.7–4.9 m resolution), Worldview-3 (2 m resolution) and Landsat (30 m resolution) imagery used to identify wetland-stream connections. Precipitation was averaged from four nearby weather stations.
| Satellite | Acquisition Date | Polarization (Beam Mode) | Incidence Angle (near to far) | Orbit (Look Direction) | Precip. 7 days prior (cm) | Precip. 2 days prior (cm) |
|---|---|---|---|---|---|---|
| Radarsat-2 | 24-Mar-15 | Polarimetric (FQ12) | 31.4–33.0 | Descending (Right) | 1.8 | 0.0 |
| Radarsat-2 | 26-Mar-15 | Polarimetric (FQ29) | 46.8–48.0 | Ascending (Right) | 1.9 | 0.0 |
| Radarsat-2 | 31-Mar-15 | Polarimetric (FQ18) | 37.4–38.9 | Descending (Right) | 1.6 | 0.1 |
| Radarsat-2 | 2-Apr-15 | Polarimetric (FQ23) | 41.9–43.3 | Ascending (Right) | 1.8 | 0.2 |
| Radarsat-2 | 9-Apr-15 | Polarimetric (FQ18) | 37.4–38.9 | Ascending (Right) | 0.8 | 0.6 |
|
| ||||||
| Satellite | Acquisition Date | Number of Bands | Incidence Angle (near to far) | Scan Direction | Precip. 7 days prior (cm) | Precip. 2 days prior (cm) |
|
| ||||||
| Landsat-8 | 4-Apr-15 | 7 | Nadir | ~ | 1.2 | 0.1 |
| Landsat-8 | 11-Apr-15 | 7 | Nadir | ~ | 0.7 | 0.1 |
| Landsat-7 | 12-Apr-15 | 7 | Nadir | ~ | 0.6 | 0.0 |
| Worldview-3 | 6-Apr-15 | 8 | 29.5 – 31.2 | Reverse | 0.6 | 0.2 |
2.3.2. Radarsat-2 Image Pre-processing
Fine-resolution, quad-polarization Radarsat-2 imagery was acquired on March 24, 26, and 31, as well as April 2 and 9, 2015, across the study area and provided in Single Look Complex (SLC) data format. Specific details regarding the Radarsat-2 image acquisitions are included in Table 2. The Radarsat-2 imagery was processed using PCI Geomatica’s SAR Polarimetric Workstation. Raw digital numbers were converted to Sigma Naught or the backscattering coefficient with units of decibels for analysis (Parmuchi et al. 2002). The SLC quad-polarization data, which represents complex data, were extracted to a 3×3 covariance matrix (Lee and Pottier 2009). Three decompositions were applied to the covariance matrix, including the Cloude-Pottier (Cloude and Pottier 1997), Touzi (Touzi et al. 2007) and Freeman-Durden (Freeman-Durden, 1998) decompositions. The SLC data were also extracted to the normalized Kennaugh scattering matrix, which has been found to optimize detection of surface water under vegetation (Schmitt and Brisco, 2013; Schmitt et al. 2015). The Polar Lee Adaptive Filter was applied to the covariance matrix and normalized Kennaugh scattering matrix outputs with a 5-pixel by 5-pixel window to reduce noise, but preserve edges. Output rasters were resampled to 5.6 m resolution using cubic convolution to ensure identical cell resolutions between image dates and coregistered to the lidar DEM using tie points. The mathematical details of these procedures are provided in Schmitt and Brisco (2013) and Touzi et al. (2007). Pre-processing steps are shown in Figure 2.
Figure 2.
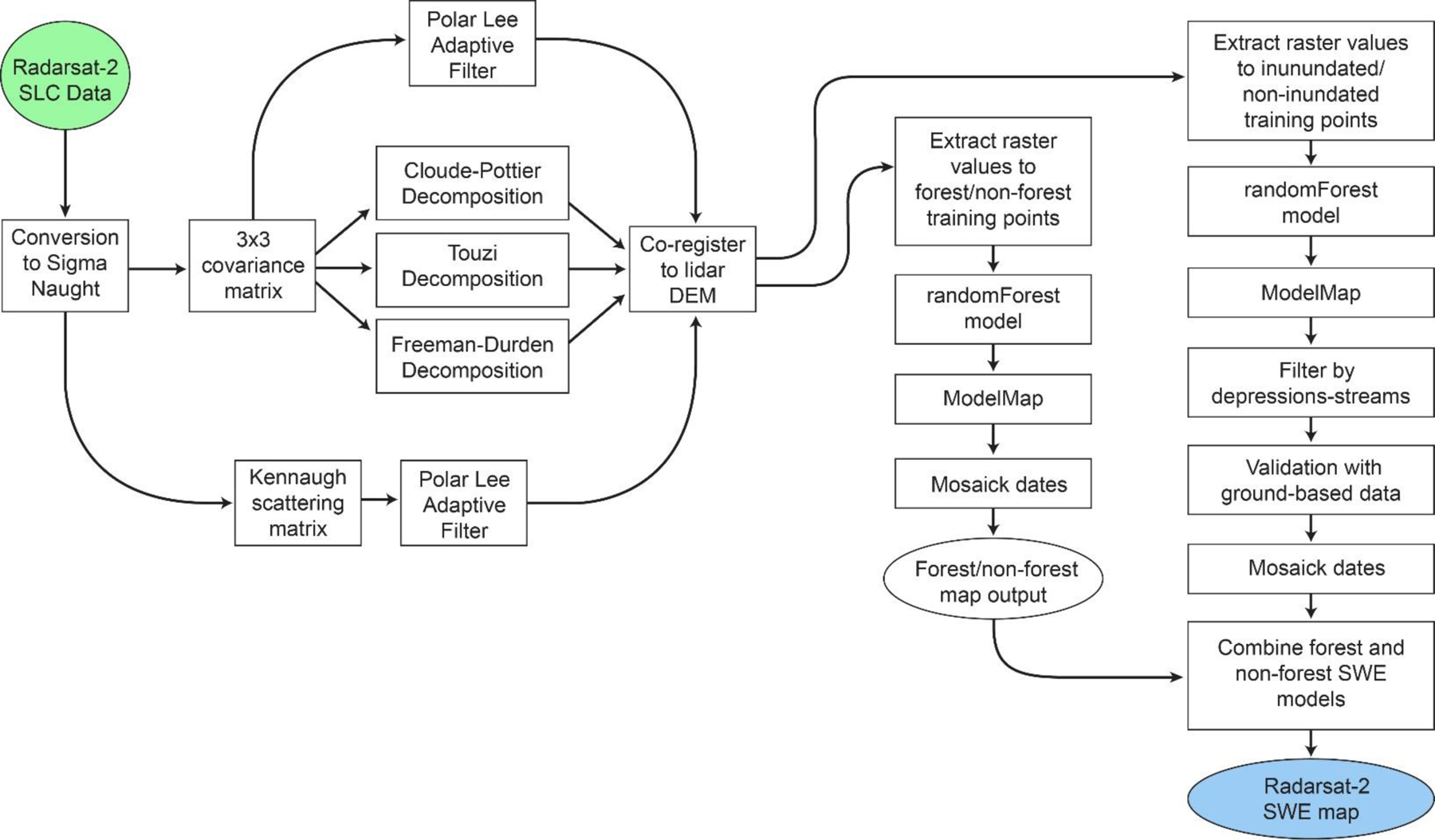
Flowchart of Radarsat-2 processing steps. ModelMap and randomForest refer to R packages. SLC: Single Look Complex. DEM: digital elevation model. SWE: surface water extent.
2.3.3. Mapping Forest Extent with Radarsat-2
Differences in vegetation structure between forest and non-forest land-cover types influence the SAR backscatter signal from water (Kandus et al. 2001; Yuan et al. 2015); therefore, separate SWE models were derived for forest and non-forest cover types for each of the Radarsat-2 dates. Forest extent was mapped from Radarsat-2. All Radarsat-2 imagery outputs were used in a random forest model and spatially implemented using ModelMap in R for each of the six Radardsat-2 dates. The random forest model was trained on four cover categories, non-inundated forest, inundated forest, open water and non-inundated non-forest. The training points (250 points for each of the four cover categories) were derived from the raw Worldview-3 imagery. The model used 500 binary trees or bootstrap iterations using out-of-bag (OOB) samples (70% of points used to train, 30% of points used to validate). The output maps were consolidated into forest (non-inundated forest + inundated forest) and non-forest (open water + non-inundated non-forest) cover types. The consolidated validation statistics reported by the random forest models indicated an overall accuracy of 99% to distinguish forest from non-forest cover types. The outputs from the six dates were mosaicked into a single forest/non-forest map for the watershed.
2.3.4. Mapping SWE with Radarsat-2
To map SWE from Radarsat-2, training points for forested models were identified primarily using the field data and supplemented using the raw Worldview-3 imagery (502 inundated points, 535 non-inundated points). For the non-forested models, training points were identified from the raw Worldview-3 imagery (923 inundated points, 904 non-inundated points). The images were classified into inundated/non-inundated using a random forest model (Liaw and Wiener 2015) with the spatial component implemented using ModelMap (Freeman et al. 2016) in R (R Development Core Team, 2015). Variables included per Radarsat-2 date were selected using variable selection (varSelRF package) which uses backwards variable elimination and selection based on the importance spectrum to select the smallest number of non-redundant metrics (Díaz-Uriarte and de Andrés 2005) (Table A1). A random forest model was derived for each date to take into account between-image differences in image extent and angle of inclination. Similar to mapping forest extent, we ran 500 binary trees or bootstrap iterations using OOB samples (70% of points used to train, 30% of points used to validate). The output SWE maps were filtered so that inundated polygons were only retained if they overlapped buffered streams, as defined by the total stream network or lidar-derived depressions. This step has been shown to reduce errors of commission, particularly within forested cover types (Vanderhoof et al. 2017). The Radarsat-2 SWE maps for each of the six dates were mosaicked together to produce a single forest-model SWE map and a single non-forest-model SWE map. Dates with higher accuracy within the forested cover type were prioritized (Vanderhoof et al. 2017). March 24 showed the highest accuracy, and was therefore used as the primary surface-water extent and covered 77.6% of the study area. The two models were then combined using the forest extent map to create a final Radarsat-2 surface-water extent map across the watershed.
2.3.5. Field Data Collection
Field data to validate the forest portions of the SWE maps were collected on March 16, 17, 24, 25, and 31, as well as April 1 and 6, 2015, on two properties, one located east of Tuckahoe Creek and the other west of the main stem of the Choptank River. The field effort coincided with the Radarsat-2 and Worldview-3 satellite flyover dates. Multiple two-person teams identified and walked areas of homogenous surface-water status using GPS units. Homogenous patches of non-inundated land cover were only recorded if they were at least 20 m from the nearest inundated area with standing water. A total of 12.8 ha (73 polygons) of forested, inundated area and a total of 4.4 ha (34 polygons) of forested non-inundated area were identified and co-registered to a lidar DEM (2 m resolution) using tie points.
2.3.6. SWE Validation
Accuracy statistics were derived using an independent set of data points, not used to train the random forest models. Each final SWE map was validated using 400 inundated points (200 within forest, 200 within non-forest cover types) and 400 non-inundated points (200 within forest, 200 within non-forest cover types). Validation points within forest were randomly selected from the polygons created during field sampling and supplemented using the raw Worldview-3 imagery to obtain enough validation points. Validation points within non-forest cover types were randomly selected from the raw Worldview-3 imagery. For Worldview-3 and Radarsat-2, points were a minimum distance of 6 m apart. For Landsat, points were a minimum distance of 30 m apart. Accuracy metrics presented included overall accuracy, omission error, commission error, Dice coefficient, and relative bias. Omission and commission errors were calculated for the category “inundated.” The Dice coefficient is the conditional probability that if one classifier (product or reference data) identifies a pixel as inundated, the other one will as well, and therefore integrates omission and commission errors (Fleiss 1981; Forbes 1995). The relative bias provides the proportion that inundated area is under- or overestimated relative to the inundated area of the reference product (Padilla et al. 2014). Accuracy statistics are provided in Table 3.
Table 3.
Accuracy of Landsat (April 11, 2015), Radarsat-2 (March 24, 2015), and Worldview-3 (April 6, 2015) surface-water extent (SWE) maps. Errors of omission and commission are presented for surface water. For image types in which multiple raw images were originally processed and mosaicked into a single SWE map, accuracy results are presented for the primary image used in the final SWE map.
| Forest | Non-Forest | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | Primary Date | Omission Error (%) | Commission Error (%) | Overall Accuracy (%) | Dice Coefficient | Relative Bias | Omission Error (%) | Commission Error (%) | Overall Accuracy (%) | Dice Coefficient | Relative Bias |
| Landsat-8 | 11-Apr-15 | 21.5 | 10.8 | 84.5 | 0.8 | −0.1 | 14.5 | 1.2 | 92.3 | 0.9 | −0.1 |
| Radarsat-2 | 24-Mar-15 | 20.5 | 11.7 | 84.5 | 0.8 | −0.1 | 3.7 | 3.4 | 98.0 | 1.0 | 0.0 |
| Worldview-3 | 6-Apr-15 | 18.0 | 4.1 | 89.3 | 0.9 | −0.1 | 2.5 | 0.0 | 98.8 | 1.0 | 0.0 |
2.4. Wetland/Stream Connection Analysis
Surface-water connection and wetland/stream connection were used as general terms indicating multiple mechanisms through which wetlands can contribute surface water to downstream waters, including wetland fill-and-spill, a stream flowing in or out of a wetland, stream overbank flow, and flood-and-merge. In using these terms, we made no assumption about the mechanism of connection or shifts or loss of wetland function that can co-occur with changes in surface-water extent. A wetland was assumed to demonstrate a stream connection if it (1) intersected the stream network (Figure 3A), or (2) intersected a stream-connected patch of surface water, as mapped by Landsat, Radarsat-2 or Worldview-3 (Figure 4). Wetlands that did not intersect the stream network, but became connected to the stream network once we mapped actual surface-water extent, were referred to as variably connected (VC) wetlands or depressions (Figure 4). Wetlands or depressions that neither intersected the total stream network nor intersected stream-connected SWE were referred to as no connection observed or NCO wetlands or depressions. It is important to note that inaccuracies in the stream networks, the spatial resolution of the imagery, and the limited temporal extent of the imagery all acted to limit the number of connections detectable using this approach. Cyclical or episodic linear connections (e.g., ephemeral and intermittent streams, swales, ditches) that connect some waters (e.g., Tromp-van Meerveld and McDonnell 2006) may not have been mapped by the stream networks and are often narrow (e.g., <1 m in width), and therefore will be difficult to detect, even with fine-resolution imagery. In addition, other connections are likely to occur only in very wet years (Vanderhoof et al. 2016a). For example, although the 2015 winter was 29% wetter than normal, snow melted and accumulated multiple times over the early spring period meaning that a different distribution of the winter precipitation could have elevated spring surface-water extents. However, this approach allowed us to quantify how data inputs may influence our interpretation of connection abundance. Additional details regarding data processing methods are supplied in the Appendix as Supplemental Online Material.
Figure 3.
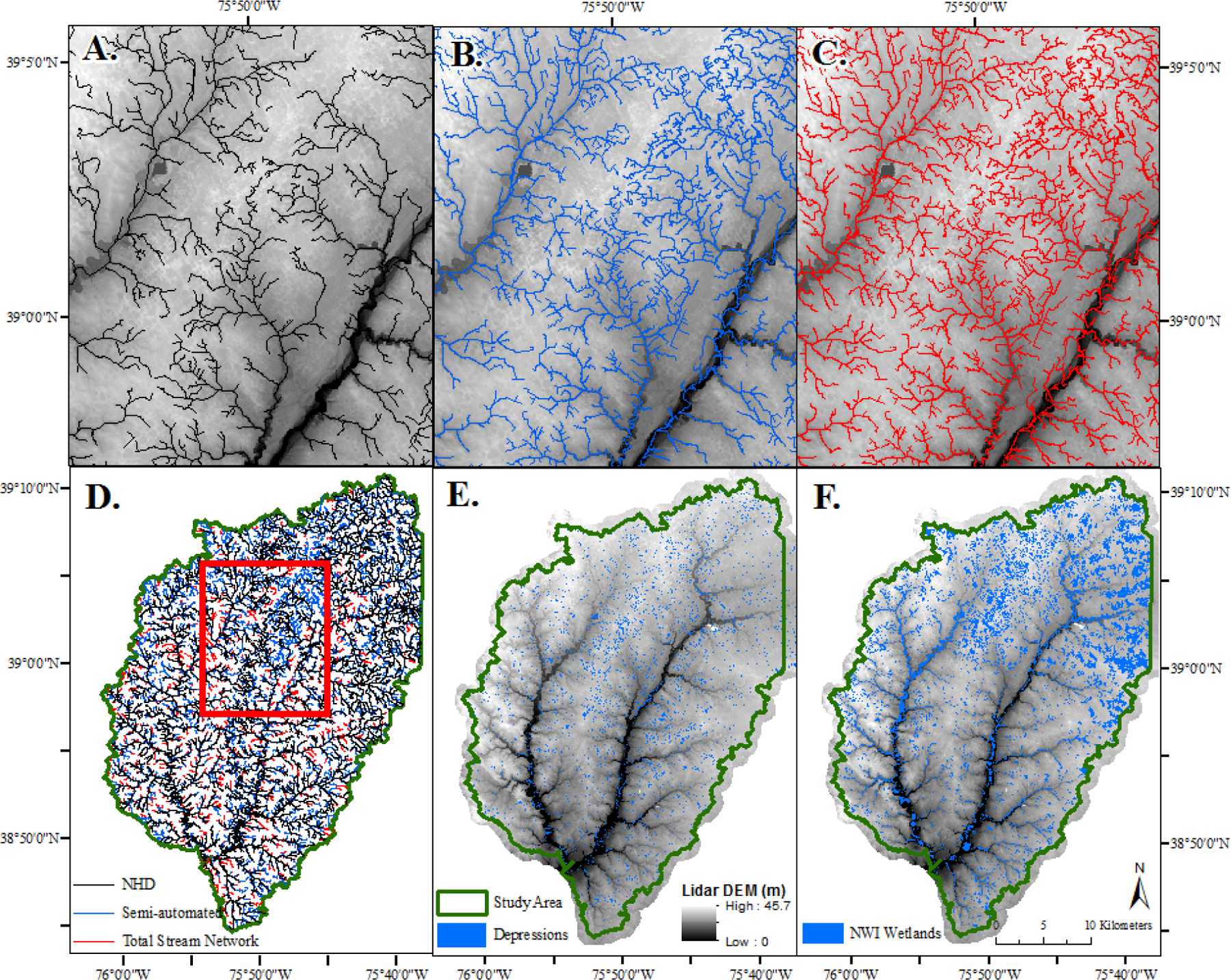
A comparison between the stream network by A) the National Hydrography Dataset (NHD), B) the semi-automated dataset, C) total stream network, D) three stream networks overlaid on one another, E) distribution of lidar-derived depressions and, F) distribution of National Wetland Inventory (NWI) wetlands (includes both riverine and non-riverine wetlands). The stream datasets in part D are layered to show the “novel” contributions of the semi-automated and total stream network so that the National Hydrography Dataset (NHD) is shown on top, followed by the semi-automated dataset, and the total stream network on the bottom.
Figure 4.
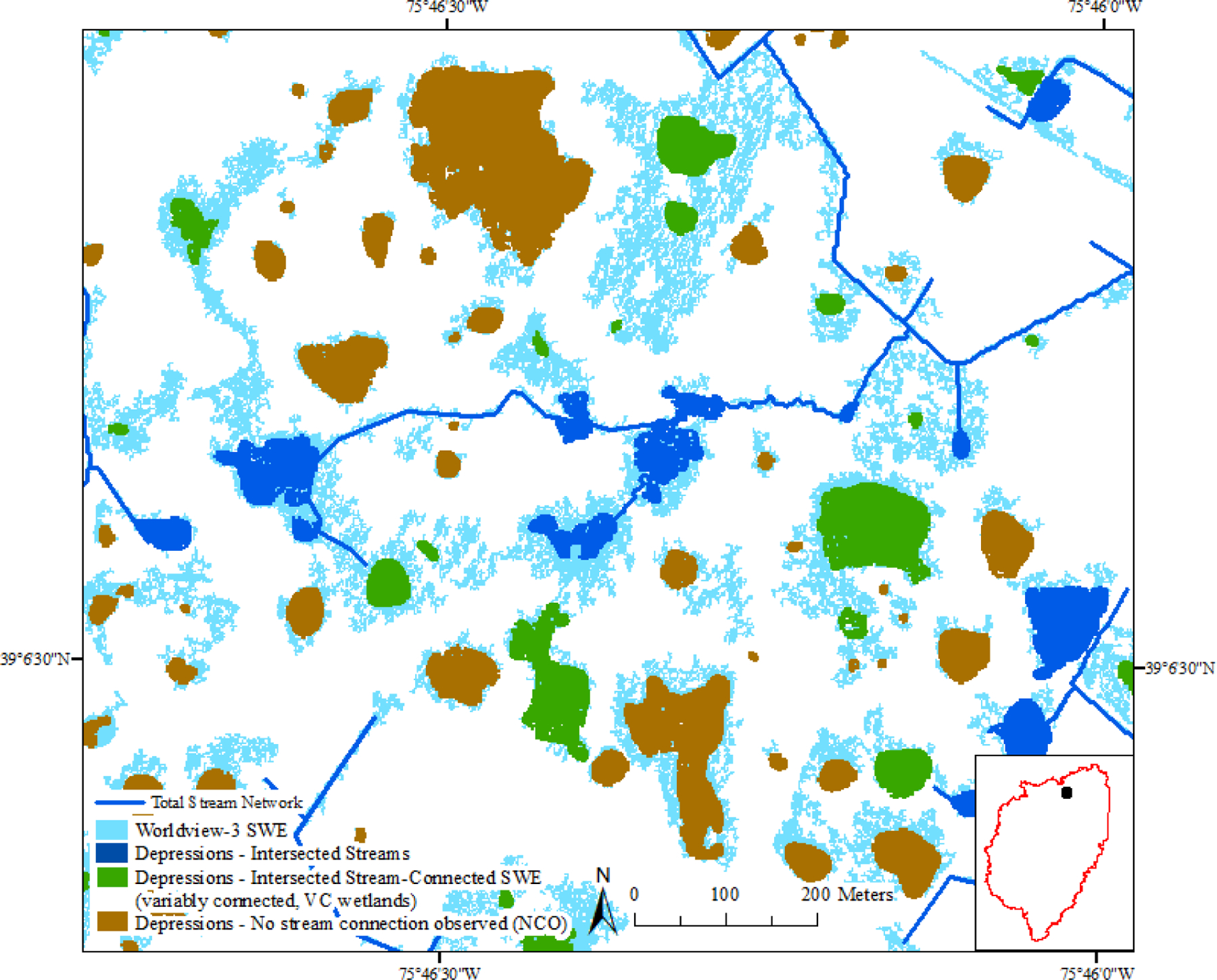
An example showing how wetland/stream surface water connections were classified using the stream network and surface water extent, as defined by Worldview-3 surface water extent (SWE). A wetland was assumed to demonstrate a stream-connection if it: (1) intersected a version of the stream network (dark blue) or (2) intersected a stream-connected patch of surface water (green). Depressions that neither intersected the total stream network nor intersected stream-connected SWE at the date the imagery was collected (in this example as defined by Worldview-3, April 6, 2015) were referred to as no connection observed or NCO depressions (brown).
3. Results
3.1. Wetlands and Stream Dataset Comparisons
The lidar-derived depressions showed high spatial overlap with the NWI wetlands. By area, 95% of the NWI wetlands co-occurred with a depressional feature, while 77% of the depressions, by area, co-occurred with NWI wetlands, after excluding agricultural areas, defined as the 2011 National Land Cover Dataset (NLCD) categories cultivated crops and hay/pasture (Table 4). The depressions, however, diverged substantially from NWI wetlands when comparing total count and area. We mapped 400% more depressions by count than NWI wetlands, while the NWI mapped almost 600% more area as wetland than the depression dataset (Figure 3B and 3C). Visually, both the depressions and NWI wetlands spatially aligned with patterns of SWE. However, in general, SWE seemed to correspond more closely with depression extent, while the NWI wetland extent tended to overestimate SWE (Figure 5). When comparing surface-water extent with the NWI wetland extent, its overestimation of wetland extent was particularly common in the northern portion of the watershed where it was common for wetland boundaries to closely follow forest boundaries (Figure 3C). Relative to the high-resolution flowline of the NHD, the semi-automated stream dataset of Lang et al. (2012) contributed 53% more stream length, while the total stream network that estimated headwater extent added an additional 17% stream length relative to the semi-automated stream dataset (Table 5, Figure 3A).
Table 4.
A comparison between National Wetland Inventory (NWI) wetlands and lidar-derived depressions across the Upper Choptank River watershed (123,825 ha total, 51,154 ha excluding agriculture). Agricultural cover types were excluded to reduce differences in whether drained wetlands were mapped. Agricultural cover types were defined using the 2011 National Land Cover Dataset cover types of cultivated crops and hay/pasture.
| Source | Count | Total Area (ha) | Cover (non-ag) (%) | NWI wetlands that co-occur with depressions (count, %) |
NWI wetlands that co-occur with depressions (area, %) |
Depressions that co-occur with NWI wetlands (count, %) |
Depressions that co-occur with NWI wetlands (area, %) |
|---|---|---|---|---|---|---|---|
| National Wetland Inventory | 5,410.0 | 17,519.8 | 34.2 | 71.8 | 95.1 | 60.8 | 77.3 |
| Lidar-derived depressions (avg precip conditions) | 21,532.0 | 3,009.1 | 5.9 | ~ | ~ | ~ | ~ |
Figure 5.
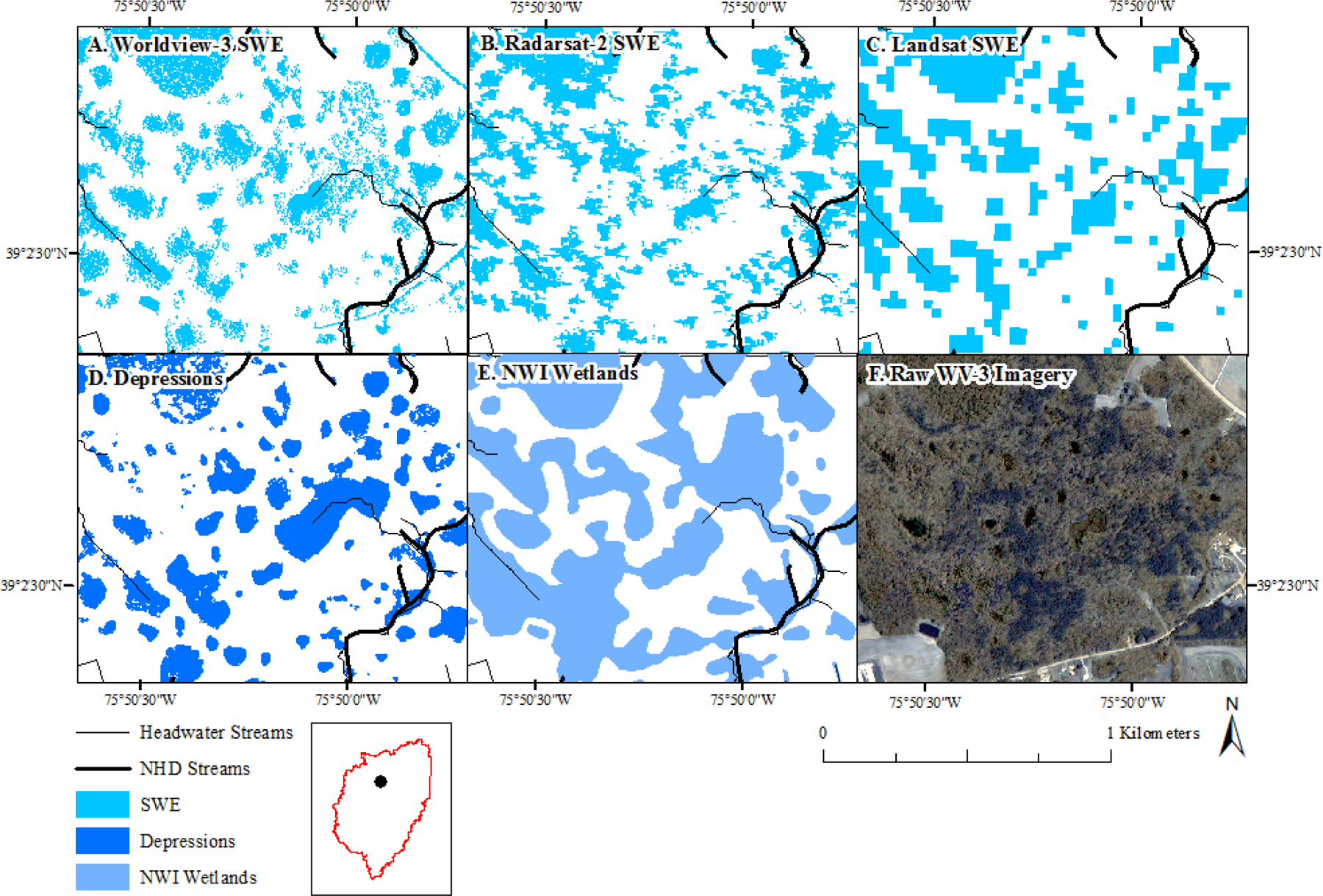
A comparison of surface water extent (SWE) as mapped in forested wetlands using: A) Worldview-3, B) Radarsat-2, C) Landsat, and compared with wetland datasets, including: D) lidar-derived depressions and E) National Wetland Inventory (NWI) wetlands, and F) raw Worldview-3 (WV-3) imagery. Copyright 2017 Digital Globe, Next View License.
Table 5.
Comparison of three stream datasets used to identify wetland-stream connections.
| Stream Dataset | Total Length (km) | Drainage Density (km km−2) | Stream length increase relative to NHD (%) | Stream length increase relative to semi-automated (%) |
|---|---|---|---|---|
| National Hydrograph Dataset (NHD) (USGS, 2013) | 1914.0 | 1.9 | ||
| Semi-automated streams (Lang et al. 2012) | 2926.7 | 2.8 | 52.9 | |
| Total stream network | 3411.7 | 3.3 | 78.3 | 16.6 |
3.2. Wetland/stream Connections
The percent of SWE connected to the stream network depended on (1) the stream dataset used and (2) on the source of imagery used to define SWE (Figure 6). The percent of total SWE that was stream connected varied from 56% to 71% for Landsat, 48% to 68% for Radarsat-2 and 62% to 75% for Worldview-3 depending on the stream network used (Table 6). As greater stream length was mapped, more of the SWE, by area, was shown to be connected to the stream network. In addition to the stream dataset and source of imagery, the percent of wetlands shown to be stream connected also depended on how wetlands were defined. For depressions, the percent shown to have a surface-water connection ranged from 12% by count (21% by area) using NHD to 49% by count (56% by area) using the total stream network and including SWE defined by all three sources of imagery (Table 7, Figure 7). Non-riverine NWI wetlands ranged from 23% stream-connected by count (60% by area) to 60% stream-connected by count (93% by area) (Table 7, Figure 7). Not considering SWE, increasing stream extent to include headwater streams increased depression/stream connections 9% by count and 13% by area and NWI wetland/stream connections 12% by count and 20% by area.
Figure 6.
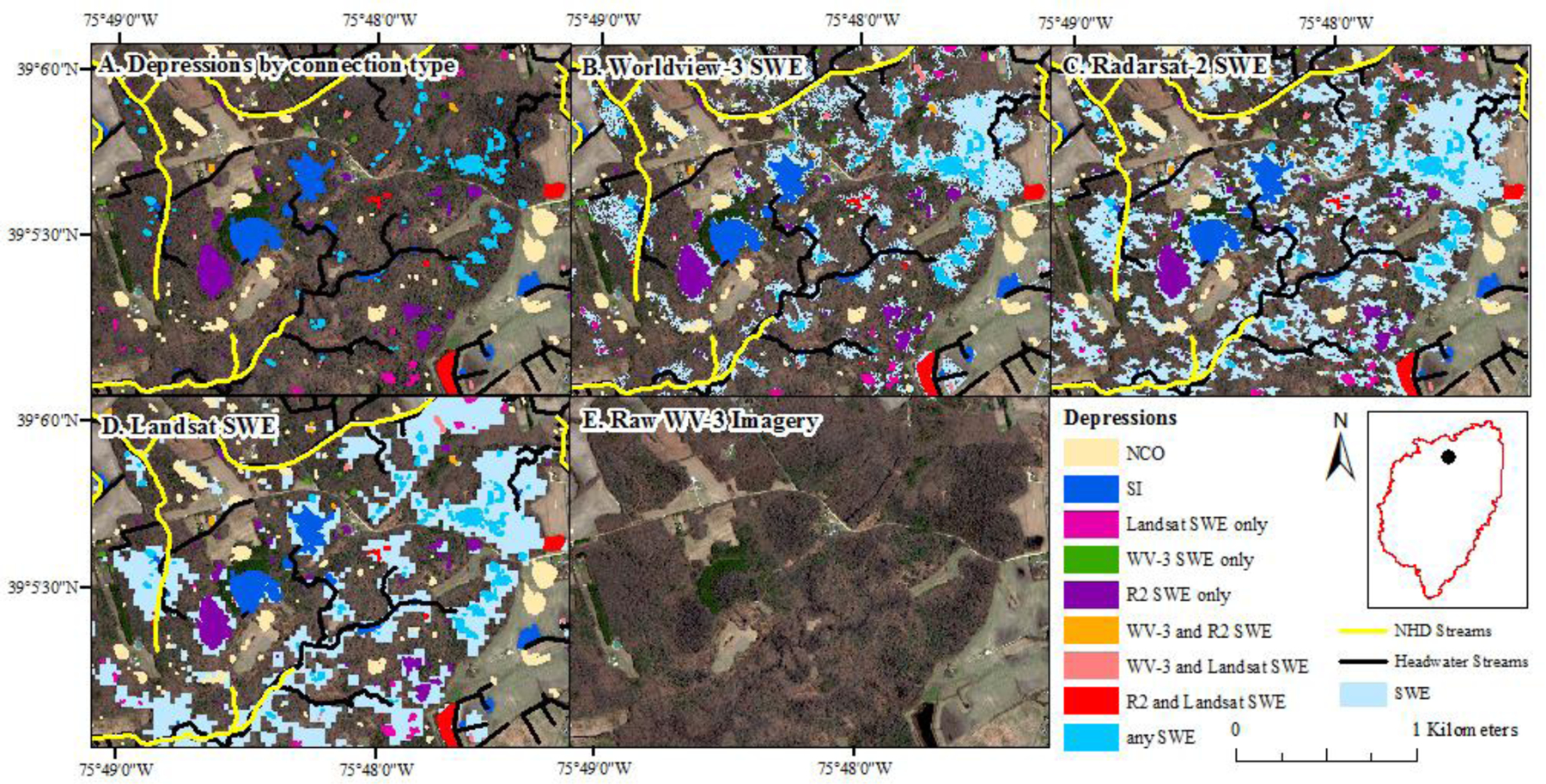
Forested depressions that showed a connection to a stream via surface water varied depending on the source of imagery used to define surface-water extent (SWE). Wetland/stream connections were defined as (1) wetlands directly intersected the stream network (SI) or (2) intersected a stream-connected surface water polygon (Landsat, WV-3 or R2 SWE). Wetlands for which no connection to a stream was observed for this point in time were labeled as NCO. NCO: no stream-connection observed. SI: depression intersected a stream. R2: Radarsat-2. WV-3: Worldview-3. NHD: National Hydrography Dataset. Copyright 2017 Digital Globe, Next View License.
Table 6.
Portion of surface-water extent that is stream-connected, as mapped with Landsat, Radarsat-2 and Worldview-3 and using three stream-dataset versions.
| Imagery Type | Total surface water (ha) | Stream-connected surface water (NHD, %) | Stream-connected surface water (Semi-automated, %) | Stream-connected surface water (Total network, %) |
|---|---|---|---|---|
| Landsat | 7,331.3 | 56.3 | 60.9 | 70.7 |
| Radarsat-2 | 10,986.7 | 47.6 | 58.3 | 68.0 |
| Worldview-3 | 9,120.8 | 61.9 | 69.7 | 75.4 |
Table 7.
Variability in depressions and National Wetland Inventory (NWI) wetlands that show a stream connection depending on the stream dataset used, integration of surface-water extent and source of imagery. Greyed rows indicate changes from baseline “alone” percentages. NHD: National Hydrography Dataset. WV-3: Worldview-3. R2: Radarsat-2.
| Intersection Type | Depressions (count, %) | NWI (non-riverine) (count, %) | NWI (riverine) (count, %) | Depressions (area, %) | NWI (non-riverine) (area, %) | NWI (riverine) (area, %) | Contributing Area (%) (Depressions) | Contributing Area (%) (NWI) |
|---|---|---|---|---|---|---|---|---|
| NHD (alone) | 11.9 | 22.9 | 99.6 | 21.1 | 60.0 | 100.0 | 50.1 | 75.3 |
| NHD + Landsat | 18.3 | 27.3 | 99.8 | 25.1 | 63.4 | 100.0 | 57.6 | 78.0 |
| NHD + R2 | 24.6 | 38.2 | 99.9 | 29.6 | 78.8 | 100.0 | 64.1 | 83.9 |
| NHD + WV-3 | 25.2 | 33.5 | 100.0 | 33.7 | 74.1 | 100.0 | 66.9 | 82.9 |
| Landsat inclusion (% change) | 6.4 | 4.4 | 0.2 | 4.0 | 3.4 | 0.0 | ||
| R2 inclusion (% change) | 12.7 | 15.3 | 0.3 | 8.5 | 18.8 | 0.0 | ||
| WV-3 inclusion (% change) | 13.4 | 10.6 | 0.3 | 12.6 | 14.1 | 0.0 | ||
|
| ||||||||
| Semi-automated (alone) | 16.4 | 30.0 | 57.4 | 23.5 | 71.7 | 96.0 | 65.1 | 82.3 |
| Semi-automated + Landsat | 23.0 | 35.4 | 65.3 | 28.1 | 75.4 | 96.7 | 68.9 | 84.4 |
| Semi-automated + R2 | 30.6 | 48.7 | 76.6 | 34.2 | 87.2 | 97.8 | 72.0 | 88.5 |
| Semi-automated + WV-3 | 29.6 | 42.4 | 78.5 | 37.0 | 81.8 | 98.0 | 72.6 | 87.8 |
| Landsat inclusion (% change) | 6.6 | 5.4 | 7.9 | 4.6 | 3.7 | 0.7 | ||
| R2 inclusion (% change) | 14.2 | 18.7 | 19.2 | 10.7 | 15.6 | 1.8 | ||
| WV-3 inclusion (% change) | 13.2 | 12.4 | 21.2 | 13.5 | 10.1 | 2.0 | ||
|
| ||||||||
| Total stream network (alone) | 20.7 | 34.9 | 60.5 | 34.5 | 80.1 | 96.6 | 71.4 | 87.2 |
| Total stream network + Landsat | 28.8 | 40.5 | 68.9 | 39.8 | 82.0 | 97.4 | 75.4 | 88.5 |
| Total stream network + R2 | 37.9 | 54.1 | 80.3 | 46.7 | 91.3 | 98.4 | 78.7 | 91.9 |
| Total stream network + WV-3 | 35.0 | 47.5 | 81.6 | 47.0 | 87.4 | 98.5 | 78.3 | 91.3 |
| Landsat inclusion (% change) | 8.1 | 5.6 | 8.4 | 5.3 | 1.9 | 0.8 | ||
| R2 inclusion (% change) | 17.2 | 19.3 | 19.8 | 12.2 | 11.2 | 1.8 | ||
| WV-3 inclusion (% change) | 14.3 | 12.6 | 21.1 | 12.5 | 7.3 | 1.8 | ||
| NHD to Total stream network (% change) | 8.8 | 11.9 | −39.1 | 13.4 | 20.1 | −3.4 | ||
|
| ||||||||
| Total stream network + Landsat or R2 or WV-3 | 49.3 | 60.0 | 88.3 | 55.7 | 92.8 | 99.1 | 81.8 | 93.5 |
|
| ||||||||
| Count or total hectares* | 26,329 | 6,477 | 2,296 | 5,090.6 | 15,583.6 | 2,155.6 | ||
Calculated within the Worldview-3 extent within the watershed.
Figure 7.
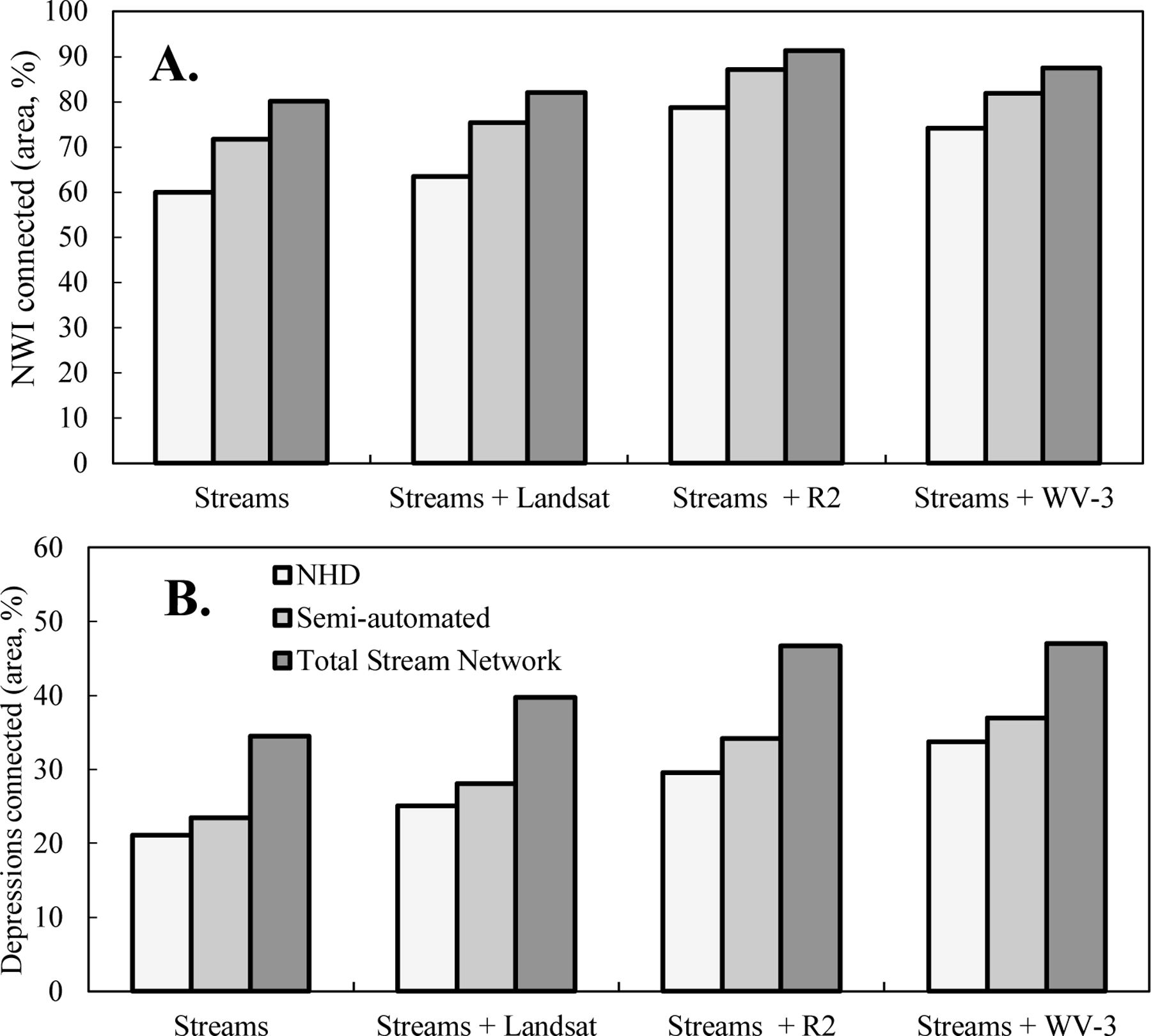
The percent of: A) National Wetland Inventory (NWI) non-riverine wetland area and B) depression area connected to streams by stream dataset and integrating surface water extent. R2: Radarsat-2. WV-3: Worldview-3. NHD: National Hydrography Dataset.
Including SWE from spring 2015 improved our ability to detect wetland/stream connections, but its contribution for this point in time was influenced by the spatial resolution of the imagery. Landsat showed a slightly higher rate of omission in non-forest cover, relative to Radarsat-2 and Worldview-3 (Table 3), likely because of the prevalence of small ponds in agricultural fields that were difficult to detect with Landsat. In forested cover, however, Landsat showed a similar ability to detect wetlands as Radarsat-2 and Worldview-3 (Table 3), the difference was most prominent at the edge of wetlands where the spatial resolution influenced the ability of Landsat to detect narrower connections between wetlands and between wetlands and streams. Consequently, Landsat SWE contributed less to identifying additional wetland/stream connections while Radarsat-2 and Worldview-3 SWE showed a similar ability to identify additional wetland/stream connections. Across the three stream datasets, adding Landsat SWE identified on average an additional 7% and 5% depressions and wetlands, respectively as stream-connected. These percentages increased to 15% and 18% for Radarsat-2 SWE, and 14% and 12% for Worldview-3 SWE (Table 7). By calculating the contributing area for each depression and wetland, we were also able to quantify the variability in our interpretation of the percent of the watershed contributing to streamflow in the Choptank River. Depending on the datasets used, the estimated contributing area varied from 50% to 94% (Table 7, Figure 8). These findings suggest that incorporating fine-resolution SWE imagery was most important for identifying wetland/stream connections remotely, while identifying streams not mapped by NHD was also important.
Figure 8.

Contributing area estimated from: A) depressions intersecting the National Hydrography Dataset (NHD) (50% contributing), B) depressions intersecting the total stream network and surface water extent (SWE) defined by Landsat, Radarsat-2 and Worldview-3 (82% contributing), C) National Wetland Inventory (NWI) wetlands intersecting the NHD (75% contributing), and D) NWI wetlands intersecting the total stream network and SWE defined by Landsat, Radarsat-2 and Worldview-3 (94% contributing). Minimum and maximum refer to the range of percent contributing area using different combinations of input datasets.
3.3. Non-permanent wetland/stream connections
A subset of the depressions during spring 2015 only became connected to the stream network as surface water expanded (VC depressions), in this case during spring high-water conditions when groundwater was discharging to wetlands and wetlands had filled-and-spilled. These depressions occurred in many different land-cover types including woody wetlands, forest, and cultivated crops, but relative to the distribution of all wetlands depressions by land cover type, VC depressions identified during spring 2015 occurred disproportionately in woody wetlands and less often in cultivated crops, likely due to agriculture-related modifications to water flow (Table 8). VC depressions occurred closer to each of the three stream datasets relative to all depressions, as well as depressions in which we did not observe a stream connection during the spring 2015 observations (Table 9). VC wetlands showed a mean Euclidean distance of 60 m to 94 m from a stream, depending on the source of imagery used to define SWE, and stream dataset used. However the maximum Euclidean distance from VC wetland to the total stream network was much larger than the mean value, approximately 466 m. We generally observed longer distances for VC wetlands using the less extensive stream datasets (e.g., NHD and semi-automated) relative to the total stream network (Table 9), which suggests that surface water extent may be contributing more towards creating VC wetlands than the extensiveness of the mapped stream network. The version of stream network showed a strong influence, however, on the mean distance for depressions to the streams. For all non-stream intersecting depressions, the mean distance to nearest stream ranged from an average of 199 m using the NHD dataset to 102 m using the total stream network (Table 9).
Table 8.
The distribution of depressions that showed a non-permanent surface-water connection to a stream within the total stream network (variably connected or VC depressions) versus those for which no connection was observed (NCO depressions) by land cover type using the 2011 National Land Cover Dataset (NLCD). Depressions that intersected the stream network directly were excluded from this analysis.
| NLCD Cover Class | VC depressions (%) | NCO depressions (%) | All depressions (%) |
|---|---|---|---|
| Open water | 0.7 | 0.0 | 1.6 |
| Developed/Barren | 15.9 | 8.8 | 11.1 |
| Forest | 18.4 | 26.1 | 21.4 |
| Shrub/scrub | 2.3 | 3.2 | 2.7 |
| Grassland | 0.4 | 0.6 | 0.5 |
| Pasture/Hay | 3.2 | 7.0 | 5.7 |
| Cultivated Crops | 17.1 | 27.9 | 23.4 |
| Woody wetlands | 40.2 | 26.3 | 31.5 |
| Emergent Herbaceous wetlands | 1.8 | 0.2 | 2.0 |
Table 9.
The mean Euclidean distance between categories of depressions to each of the three stream datasets. The depressions that showed a variable or non-permanent connection (VC depressions) were specific to each source of imagery and stream dataset combination. NCO (no connection observed) depressions showed no stream connection regardless of the source of imagery. Depressions have been separated out by imagery type including Radarsat-2 (R2) and Worldview-3 (WV-3). NHD: National Hydrograph Dataset, SE: standard error.
| Depression Category | Mean distance (SE) (NHD) | Mean distance (SE) (semi-automated) | Mean distance (SE) (total stream network) |
|---|---|---|---|
| All depressions | 176.0 (1.1) | 121.9 (0.8) | 81.8 (0.5) |
| all non-stream intersecting depressions | 198.8 (1.2) | 144.2 (0.9) | 102.0 (0.6) |
| VC depressions (Landsat) | 77.4 (2.6) | 88.4 (2.6) | 67.9 (1.4) |
| VC depressions (R2) | 72.3 (2.0) | 68.7 (1.5) | 59.7 (0.9) |
| VC depressions (WV-3) | 93.9 (2.1) | 89.5 (1.8) | 66.1 (1.1) |
| NCO depressions | 219.5 (1.5) | 155.0 (1.1) | 118.5 (0.7) |
4. Discussion
Characterizing the frequency, duration and magnitude of wetland/stream connections is relevant not only to the implementation of federal, state, and local wetland policies, but also to understanding how water, nutrients, and pollutants are retained or move within a watershed and contribute to or influence the amount and quality of downstream waters. Detecting and characterizing such connections, which can vary through time and occur via the exchange of surface water, shallow subsurface water or groundwater, is extremely challenging, in part, because of incomplete data about influencing factors such as surface storage, geology, and soil characteristics, as well as wetland and stream extent. Existing approaches to identify and monitor wetland/stream connections show distinct advantages and disadvantages. While field-based approaches can help detect connections, and may be necessary to detect narrow and temporary connections, it is typically cost prohibitive to attempt to detect all wetland/stream connections throughout a watershed or even sub-watershed in the field. Semi-distributed hydrological models are beginning to be applied to model wetland/stream connections by incorporating structural wetland-connectivity relationships (Evenson et al. 2015, 2016). The advantage of this approach is that the summed contribution of wetlands to streamflow can be modeled for a continuous temporal record. However, such models are typically calibrated and validated using stream gage data and often calculate SWE as a residual of the model, meaning that uncertainty associated with the SWE contributes to uncertainty associated with predictions of which wetlands are connected to streams.
Approaches that rely on remotely sensed imagery can provide estimates of wetland/stream connectivity at much greater spatial extents than field-based efforts, and may provide greater certainty by reducing errors of commission when identifying wetland/stream connections, relative to current hydrological models. However, as shown in this analysis, the detection of such connections depends on the quality of the wetland and stream input datasets, and the temporal and spatial resolution of the imagery used to map SWE. This means that errors of omission (i.e., missing existing wetland/stream connections) can be expected to be high due to the spatial and temporal limitations of the imagery, in particular when connections are temporary in response to precipitation events, or when subsurface connections play an important role. Regardless, remotely sensed imagery, particularly when analyses are targeted to wet periods or points in time and use fine-resolution imagery as in this analysis, can provide a baseline picture to improve our estimation in particular of the frequency of surface-water connections. It is possible that pairing fine spatial resolution imagery, which tends to have a longer temporal return interval, with moderate spatial resolution imagery, such as Landsat, which can provide a more continuous record (1984-present, every 8 to 16 days) could also help characterize the timing and duration of surface-water connections. Continued collection and processing of fine-resolution imagery can also be used to monitor the influence of landscape changes, including degradation (e.g., agricultural drainage) and restoration of depressional wetlands on wetland/stream connectivity, but this effort would be greatly helped by occasional lidar data collection which can allow for documentation of topographic changes influencing surface storage and flow.
In this analysis, we found that our interpretation of the total frequency of wetland/stream connections and the corresponding estimates of watershed contributing area ranged widely depending on (1) the accuracy and completeness of the wetland and stream maps, and (2) the spatial resolution of imagery used to define SWE for spring 2015. Including headwater streams increased the amount of wetland/stream interactions detected; however, we can’t assume that all streams in the stream network are active at a given point in time. Work by others in the watershed has shown that many of these streams are ephemeral or intermittent (McDonough et al. 2015; Epting, 2017), meaning that at times of year when the stream network is disconnected, remotely sensed surface-water connections may overestimate water contributing to stream-flow. In addition, our analysis suggests that including any SWE map improves our ability to detect wetland/stream connections, but both Radarsat-2 and Worldview-3 showed an improved ability, relative to Landsat to detect narrower connections, likely because of the finer spatial resolution of these data sources, relative to Landsat. It also became evident that minor differences in SWE can change which wetlands are identified as stream-connected (Figure 6). This suggests that uncertainty in SWE, particularly in forested environments, can introduce uncertainty in estimates of wetland/stream connectivity.
The abundance of wetland/stream connections was also found to depend on the wetland dataset used. A higher wetland count when using depressions instead of NWI was likely a consequence of deriving the depressions using a finer map scale. In addition, errors within the NWI dataset were likely due to the difficulty of mapping forested wetlands with aerial imagery (Tiner 2009). However, the Delmarva Peninsula is a low gradient landscape in which Delmarva bays co-occur with large, forested wetland flats that may not have been adequately captured by stochastic depression analysis, due to the shallower depth and less distinct shape of these wetlands. In addition, although filtering depressions using SWE helped increase confidence that depressions represented wetlands, it could have excluded wetland features that were saturated or dry at the time of imagery collection. To minimize this potential source of error, the imagery was collected at the seasonal peak in wetness during a wet year (29% more winter precipitation than normal). The differences between the two datasets had several implications for our study. First, because the depression dataset divided the landscape into many more potential wetland features, the percent of depressions that showed a connection to a stream tended to be lower than when the NWI dataset was used. Alternatively, fewer wetland/stream connections were detected by count using the NWI dataset, because several depressions were typically represented by a single wetland polygon in the NWI dataset.
This study builds upon a very limited number of studies using remotely sensed SWE to characterize wetland/stream connections. We can compare our findings in the Delmarva Peninsula to findings in other regions with a high density of depressional wetlands. In the Prairie Pothole Region (PPR), Vanderhoof et al. (2016b), using the NWI wetland dataset, NHD streams and Landsat imagery, found that the percent of wetlands that showed a wetland/stream connection varied between 7.5% and 35% across different ecoregions within the PPR. In comparison, using the identical datasets we found a similar proportion, 27% of the NWI wetlands showed a stream connection within the Upper Choptank River watershed. However, improving the stream network and adding fine-resolution sources of SWE increased this percent to 60% of the NWI wetlands showing a wetland/stream connection across the Upper Choptank River watershed. This finding suggests that improved datasets (e.g., Baker et al. 2007) could lead to more accurate estimates of wetland/stream surface water connectivity in other regions, such as the Prairie Pothole Region (Baker et al. 2007; Nadeau and Rains 2007).
Similar to the Prairie Pothole Region, the Upper Choptank River watershed also contains an abundance of agricultural activities, which have substantially modified the flow of water across the watershed (Lang et al. 2012; Homer et al. 2015; McDonough et al. 2015). Agricultural activities can both increase and decrease wetland/stream connections. Filling wetlands with soil and lowering the water table through increased water withdrawal can decrease expected surface-water connectivity, while ditches can extend the stream network, potentially increasing surface-water connectivity (De Laney 1995; Blann et al. 2009; McCauley and Anteau 2014). Lang et al. (2012) made specific efforts to manually digitize ditches across the Upper Choptank River watershed when they created their stream dataset. Ditch location is driven by human needs and often does not follow surrounding topography. This means that ditches are often not identified by topography-based efforts to map streams (Lang et al. 2012). However, the difference in wetland/stream connectivity between the NHD and semi-automated stream datasets suggest that ditch networks, which are typically connected to the stream network, contribute wetland/stream connections in agriculturally dominated landscapes.
In addition to the role of agriculture, the geology of the Delmarva is also critical to consider in our analysis. Our interpretation of the frequency of wetland/stream surface water connections within the Upper Choptank River watershed must also consider that groundwater exchanges in the Delmarva and Carolina bays ranges from episodic to nearly continuous (Schalles and Shure 1989; Lide et al. 1995; Sun et al. 2006) with many bays serving as both recharge and discharge sites at different points in time (De Laney 1995; Pyzoha et al. 2008). The prevalence of groundwater exchange in the region means that surface water represents only one mechanism for water exchange between wetlands and streams. This is dissimilar to other regions dominated by a high density of depressional wetlands, such as the Prairie Pothole Region, in which glacial deposits limit groundwater contributions to streams (Winter & Rosenberry 1995; van der Kamp & Hayashi 2009).
Advances in airborne and satellite technology continue to improve our ability to detect and monitor SWE and wetland/stream connections. The 3D Elevation Program of the USGS has recently begun systematically collecting lidar data over the conterminous U.S. and Hawaii that could be used to improve both wetland and stream maps. Unmanned aerial vehicles (UAVs, or “drones”) have been used to collect sub-decimeter multispectral imagery for surveying wetlands (Jensen et al. 2011; Chabot and Bird 2013), but have not yet been widely applied for monitoring SWE. Additionally, the recent and planned launches of the Sentinel satellite series, which includes radar, multispectral and hyperspectral sensors will support continuous data collection at short return intervals (2 to 6 days) and will greatly improve our ability to monitor temporal variation in SWE and wetland/stream connections.
5. Conclusion
Improved characterization of wetland/stream interactions is necessary to predict how water, nutrients and pollutants will move within a watershed, and to improve our understanding of watershed-scale hydrological interactions (Marton et al. 2015). Remotely sensed imagery can help characterize the spatial and temporal frequency of wetland/stream interactions at a landscape scale. Although obtaining and processing fine-resolution sources of imagery, such as lidar or Worldview-3, can be time intensive, this analysis suggests that improving the accuracy and completeness of the input datasets can substantially improve your ability to detect wetland/stream connections for a point in time. The identification of wetland/stream interactions is also more challenging in forested environments in which uncertainty in SWE is elevated relative to non-forest environments. Consideration of what datasets to use will depend not only on the land-cover type and wetland and stream size, but also on the dominant mechanisms through which water is exchanged between wetlands and streams. In the future, characterizing wetland/stream interactions, in particular to quantify not just surface, but also subsurface and ground-based interactions, will likely require a coupling of field-based, hydrological modeling and remote sensing approaches.
Supplementary Material
Acknowledgements
This work was funded by the U.S. EPA Office of Research and Development, National Center for Environmental Assessment (EPA-USGS IA- 92410201–1, Multi-scale analyses and hydrologic simulation models of wetland/stream hydrologic connectivity in the Prairie Pothole Region). We would like to thank everyone who assisted in collecting field data for validation purposes. This includes Greg McCarty, Vincent Kim, Jason Todd, Sergio Torres, and Derek Raisanen. Thank you to Di Ana Mendiola for her help with processing the Radarsat-2 imagery. Thank you also to Jay Christensen, Charles Lane and anonymous reviewers for their valuable comments. Findings and conclusions in this presentation are those of the authors and the U.S. Geological Survey. They do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency or the U.S. Fish and Wildlife Service. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
References
- Adler-Golden SM, Berk A, Bernstein LS, Richtsmeierl S, Acharyal PK, Matthew MW, Anderson GP, Allred CL, Jeong LS, Chetwynd JH (1998) FLAASH, A MODTRAN4 atmospheric correction package for hyperspectral data retrievals and simulations. In: AVIRIS 1998 Proceedings JPL Publication; 97–21:1–6 [Google Scholar]
- Adler-Golden SM, Matthew MW, Bernstein LS, Levine RY, Berk A, Richtsmeier SC, Acharya PK, Anderson GP, Felde G, Gardner J, Hike M, Jeong LS, Pukall B, Mello J, Ratkowski A, Burke HH (1999) Atmospheric correction for shortwave spectral imagery based on MODTRAN4. In: SPIE Proceedings Imaging Spectrometry V 3753:61–69 [Google Scholar]
- Ahrens BDC (2012) Identifying closed depressions in the hummocky topography of the Waterloo and Paris-Galt-Guelph Morraines of southwestern Ontario Thesis, University of Guelph [Google Scholar]
- Alsdorf DE, Rodríguez E, Lettenmaier DP (2007) Measuring surface water from space. Rev Geophys 45:RG2002,1–24 [Google Scholar]
- Baghdadi N, Bernier M, Gauthier R, Neeson I (2001) Evaluation of C-band SAR data for wetlands mapping. Int J Remote Sens 22(1):71–88 [Google Scholar]
- Baker ME, Weller DE, Jordan TE (2007) Effects of stream map resolution on measures of riparian buffer distribution and nutrient retention potential. Landscape Ecology 22(7):973–992. [Google Scholar]
- Blann KL, Anderson JL, Sands GR, Vondracek B (2009) Effects of agri-cultural drainage on aquatic ecosystems: A review. Critical Reviews in Environmental Science and Technology 39:909–1001. doi: 10.1080/10643380801977966 [DOI] [Google Scholar]
- Chabot D, Bird DM (2013) Small unmanned aircraft: precise and convenient new tools for surveying wetlands. Journal of Unmanned Vehicle Systems 1(1):15–24. [Google Scholar]
- Chu X (2015) Delineation of pothole-dominated wetlands and modeling of their threshold behaviors. J Hydrol Eng D5015003:1–11 doi: 10.1061/(ASCE)HE.1943-5584.0001224 [DOI] [Google Scholar]
- Clewley D, Whitcomb J, Moghaddam M, McDonald K, Chapman B, Bunting P (2015) Evaluation of ALOS PALSAR data for high-resolution mapping of vegetated wetlands in Alaska. Remote Sens 7(6):7272–7297 [Google Scholar]
- Cloude S, Pottier E (1997) An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans Geosci Remote Sens 35(1):68–78 [Google Scholar]
- Cohen MJ, Creed IF, Alexander L, Basu NB, Calhoun AJK, Craft C, D’Amico E, DeKeyser E, Fowler L, Golden HE, Jawitz JW, Kalla P, Kirkman LK, Lane CR, Lang M, Leibowitz SG, Lewis DB, Marton J, McLaughlin DL, Mushet DM, Raanan-Kiperwas H, Rains MC, Smith L, Walls SC (2016) Do geographically isolated wetlands influence landscape functions? In: Proceedings of the National Academy of Sciences 113:1978–1986. doi: 10.1073/pnas.1512650113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creed IF, Sanford SE, Beall FD, Molot LA, Dillon PJ (2003) Cryptic wetlands: Integrating hidden wetlands in regression models of the export of dissolved organic carbon from forested landscapes. Hydrol Processes 17:3629–3648 [Google Scholar]
- Dahl TE. (1990). Wetlands losses in the United States, 1780’s to 1980’s. Report to the Congress (No. PB-91–169284/XAB) National Wetlands Inventory, St. Petersburg, FL (USA). [Google Scholar]
- De Laney TA (1995) Benefits to downstream flood attenuation and water quality as a result of constructed wetlands in agricultural landscapes. J Soil Water Conserv 50:620–626 [Google Scholar]
- Díaz-Uriarte R, Alvarez de Andrés S (2006) Gene selection and classification of microarray data using random forest. BMC Bioinf 7(3):1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downing D, Nadeau TL, Kwok R (2007) Technical and scientific challenges in implementing Rapanos “Water of the United States”. Nat Resour Environ 22(1):45–63 [Google Scholar]
- Epting SM (2017) Using landscape metrics to predict hydrologic connectivity patterns between forested wetlands and streams in a coastal plain watershed Thesis, University of Maryland. doi: 10.13016/M2SB88 [Google Scholar]
- Evenson GR, Golden HE, Lane CR, D’Amico E (2015) Geographically isolated wetlands and watershed hydrology: A modified model analysis. J Hydrol 529:240–256 [Google Scholar]
- Evenson GR, Golden HE, Lane CR, D’Amico E (2016) An improved representation of geographically isolated wetlands in a watershed-scale hydrologic model. Hydrol Processes doi: 10.1002/hyp.10930 [DOI] [Google Scholar]
- Fenstermacher DE, Rabenhorst MC, Lang MW, McCarty GW, Needelman BA (2014) Distribution, morphometry, and land use of Delmarva Bays. Wetlands 34(6):1219–1228 [Google Scholar]
- Fleiss JL (1981) Statistical methods for rates and proportions, 2nd edn. Wiley, New York [Google Scholar]
- Forbes AD (1995) Classification-algorithm evaluation: Five performance measures based on confusion matrices. J Clin Monitor Comput 11(3):189–206 [DOI] [PubMed] [Google Scholar]
- Freeman A, Durden S (1998) A three-component scattering model for polarimetric SAR data. IEEE Trans Geosci Remote Sens 36(3):963–973 [Google Scholar]
- Freeman EA, Frescino TS, Moisen GG (2016) ModelMap: An R package for model creation and map production, R package version 4.6–12 R Foundation for Statistical Computing, Vienna [Google Scholar]
- Freeman TA (1991) Calculating catchment-area with divergent flow based on a regular grid. Comput Geosci 17:413–422 [Google Scholar]
- Frohn RC, D’Amico E, Lane C, Autry B, Rhodus J, Liu H (2012) Multi-temporal sub-pixel Landsat ETM+ classification of isolated wetlands in Cuyahoga County, Ohio, USA. Wetlands 32:289–299 [Google Scholar]
- Gleason RA, Tangen BA, Laubhan MK, Kermes KE, Euliss NH Jr (2007) Estimating water storage capacity of existing and potentially restorable wetland depressions in a subbasin of the Red River of the North. U.S. Geological Survey Open-File Report 2007–1159, 36p [Google Scholar]
- Golden HE, Sander HA, Lane CR, Zhao C, Price K, D’Amico E, Christensen JR (2016) Relative effects of geographically isolated wetlands on streamflow: A watershed-scale analysis. Ecohydrology 9(1):21–38 [Google Scholar]
- Green AA, Berman M, Switzer P, Craig MD (1988) A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans Geosci Remote Sens 26(1):65–74 [Google Scholar]
- Habtezion N, Nasab MT, Chu X (2016) How does DEM resolution affect microtopographic charteristics, hydrologic connectivity, and modelling of hydrologic processes? Hydrol Processes doi: 10.1002/hyp.10967 [DOI] [Google Scholar]
- Halabisky M, Moskal LM, Gillespie A, Hannam M (2016) Reconstructing semi-arid wetland surface water dynamics through spectral mixture analysis of a time series of Landsat satellite images (1984–2011). Remote Sens Environ 177:171–183 [Google Scholar]
- Hansen WF (2001) Identifying stream types and management implications. For Ecol Manage 143(1–3):39–46 [Google Scholar]
- Heine RA, Lant CL, Sengupta RR (2004) Development and comparison of approaches for automated mapping of stream channel networks. Ann Assoc Am Geogr 94(3):477–490 [Google Scholar]
- Henderson F, Lewis A (2008) Radar detection of wetland ecosystems: A review. Int J Remote Sens 29(20):5809–5835 [Google Scholar]
- Hess LL, Melack JM, Affonso AG, Barbosa C, Gastil-Buhl M, Novo EMLM (2015) Wetlands of the lowland Amazon basin: Extent, vegetative cover, and dual-season inundated area as mapped with JERS-1 synthetic aperture radar. Wetlands 35(4):745–756 [Google Scholar]
- Homer C, Dewitx J, Yang L, Jin S, Danielson P, Xian G, Coulston J, Herold N, Wickham J, Megown K (2015) Completion of the 2011 National Land Cover Database for the conterminous United States – representing a decade of land cover change information. Photogramm Eng Remote Sens 81:345–354 [Google Scholar]
- Huang C, Peng Y, Lang M, Yeo IY, McCarty G (2014) Wetland inundation mapping and change monitoring using Landsat and airborne LiDAR data. Remote Sens Environ 141:231–242 [Google Scholar]
- Huang S, Young C, Feng M, Heidemann K, Cushing M, Mushet DM, Liu S (2011) Demonstration of a conceptual model for using LiDAR to improve the estimation of floodwater mitigation potential of Prairie Pothole Region wetlands. J Hydrol 405(3–4):417–426 [Google Scholar]
- James LA, Watson DG, Hansen WF (2007) Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena 71(1):132–144 [Google Scholar]
- Jensen AM, Hardy T, McKee M, Chen YQ (2011) Using a multispectral autonomous unmanned aerial remote sensing platform (AggieAir) for riparian and wetlands applications In: Geoscience and Remote Sensing Symposium (IGARSS), 2011 IEEE International 3413–3416. [Google Scholar]
- Jin H, Huang C, Lang MW, Yeo IY, Stehman SV (2017) Monitoring of wetland inundation dynamics in the Delmarva Peninsula using Landsat time-series imagery from 1985 to 2011. Remote Sens Environ 190:26–41. [Google Scholar]
- Kahara SN, Mockler RM, Higgins KF, Chipps SR, Johnson RR (2009) Spatiotemporal patterns of wetland occurrence in the prairie pothole region of eastern South Dakota. Wetlands 29(2):678–689 [Google Scholar]
- Kandus P, Karszenbaum H, Pultz T, Parmuchi G, Bava J (2001) Influence of flood conditions and vegetation status on the radar backscatter of wetland ecosystems. Can J Remote Sens 6:651–662 [Google Scholar]
- Lane CR, D’Amico E (2010) Calculating the ecosystem service of water storage in isolated wetlands using LiDAR in North Central Florida, USA. Wetlands 30(5):967–977 [Google Scholar]
- Lang MW, Kasischke ES (2008) Using C-band synthetic aperture radar data to monitor forested wetland hydrology in Maryland’s Coastal Plain, USA. IEEE Trans Geosci Remote Sens 4:535–546 [Google Scholar]
- Lang MW, McCarty GW (2009) Lidar intensity for improved detection of inundation below the forest canopy. Wetlands 29(4):1166–1178 [Google Scholar]
- Lang M, McDonough O, McCarty G, Oesterling R, Wilen B (2012) Enhanced detection of wetland-stream connectivity using LiDAR. Wetlands 32:461–473 [Google Scholar]
- Lang M, McCarty G, Oesterling R (2013) Topographic metrics for improved mapping of forested wetlands. Wetlands 33(1):141–155 [Google Scholar]
- Lee JS, Pottier E (2009) Polarimetric radar imaging: From basics to applications CRC Press, Boca Raton, FL [Google Scholar]
- Leibowitz SG, Mushet DM, Newton WE (2016) Intermittent surface water connectivity: Fill and spill vs. fill and merge dynamics. Wetlands doi: 10.1007/s13157-016-0830-z [DOI] [Google Scholar]
- Liaw A, Wiener M (2015) Breiman and Cutler’s random forests for classification and regression, R package version 4.6–12 R Foundation for Statistical Computing, Vienna [Google Scholar]
- Lide RF, Meentemeyer VG, Pinder JE III, Beatty LM (1995) Hydrology of a Carolina bay located on the upper coastal plain of western South Carolina. Wetlands 15(1):47–57 [Google Scholar]
- Lindsay JB (2014) The Whitebox Geospatial Analysis Tools project and open-access GIS In: Proceedings of the GIS Research UK 22nd Annual Conference, Glasgow [Google Scholar]
- Lowe WH, Likens GE (2005) Moving headwater streams to the head of the class. BioScience 55(3):196–197 [Google Scholar]
- Lowrance R, Altier LS, Newbold D, Schnabel RR, Groffman PM, Denver JM, Correll DL, Gilliam JW, Robinson JL, Brinsfield RB, Staver KW, Lucas W, Todd AH (1997) Water quality functions of riparian forest buffers in Chesapeake Bay watersheds. Environ Manage 21(5):687–712 [DOI] [PubMed] [Google Scholar]
- Marton JM, Creed I, Lewis D, Lane CR, Basu N, Cohen MJ, Craft C (2015) Geographically isolated wetlands are important biogeochemical reactors on the landscape. Bioscience 65(4): 408–418. [Google Scholar]
- Masek JG, Vermote EF, Saleous N, Wolfe R, Hall EF, Huemmrich F, Gao F, Kutler J, Teng-Kui L (2006) A Landsat surface reflectance data set for North America, 1990–2000. IEEE Geoscience and Remote Sensing Letters 3:68–72 [Google Scholar]
- Matheron G (1973) The intrinsic random functions and their applications. Adv Appl Probab 5:439–468 [Google Scholar]
- McCauley LA, Anteau MJ (2014) Generating nested wetland catchments with readily-available digital elevation data may improve evaluations of land-use change on wetlands. Wetlands 34(6):1123–1132 [Google Scholar]
- McCauley LA, Anteau MJ, Van Der Burg MP, Wiltermuth MT (2015) Land use and wetland drainage affect water levels and dynamics of remaining wetlands. Ecosphere 6(6):1–20 [Google Scholar]
- McDonough OT, Lang MW, Hosen JD, Palmer MA (2015) Surface hydrologic connectivity between Delmarva Bay wetlands and nearby streams along a gradient of agricultural alteration. Wetlands 35(1):41–53 [Google Scholar]
- McLaughlin DL, Kaplan DA, Cohen MJ (2014) A significant nexus: Geographically isolated wetlands influence landscape hydrology. Water Resour Res 50(9):7153–7166 [Google Scholar]
- Murphy MA, Evans JS, Storfer A (2010) Quantifying Bufo boreas connectivity in Yellowstone National Park with landscape genetics. Ecology 91(1):252–261 [DOI] [PubMed] [Google Scholar]
- Murphy PNC, Oglivie J, Meng FR, Arp P (2008) Stream network modelling using lidar and photogrammetric digital elevation models: a comparison and field verification. Hydrol Processes 22(12):1747–1754 [Google Scholar]
- Mushet DM, Calhoun AJK, Alexander LC, Cohen MJ, DeKeyser ES, Fowler L, Lane CR, Lang MW, Rains MC, Walls SC (2015) Geographically Isolated Wetlands: Rethinking a Misnomer. Wetlands 35:423–431 [Google Scholar]
- Nachshon U, Ireson A, van der Kamp G, Davies SR, Wheater HS (2014) Impacts of climate variability on wetland salinization in the North American prairies. Hydrol Earth Syst Sci 18:1251–1263. doi: 10.5194/hess-18-1251-2014 [DOI] [Google Scholar]
- Nadeau TL, Rains MC (2007) Hydrological Connectivity Between Headwater Streams and Downstream Waters: How Science Can Inform Policy. Journal of the American Water Resources Association 43(1):118–133. [Google Scholar]
- Niemuth ND, Wangler B, Reynolds RE (2010) Spatial and temporal variation in wet area of wetlands in the prairie pothole region of North Dakota and South Dakota. Wetlands 30:1053–1064 [Google Scholar]
- NOAA National Climatic Data Center (2014) Data Tools: 1981–2010 Normals http://www.ncdc.noaa.gov/cdo-web/datatools/normals. Accessed 28 October 2014 [Google Scholar]
- Padilla M, Stehman SV, Chuvieco E (2014) Validation of the 2008 MODIS-MCD45 global burned area product using stratified random sampling. Remote Sens Environ 144:187–196 [Google Scholar]
- Parmuchi M, Karszenbaum H, Kandus P (2002) Mapping wetlands using multi-temporal RADARSAT-1 data and a decision-based classifier. Can J Remote Sens 28(2):175–186 [Google Scholar]
- Pyzoha JE, Callahan TJ, Sun G, Trettin CC, Miwa M (2008) A conceptual hydrologic model for a forested Carolina bay depressional wetland on the Coastal Plain of South Carolina, USA. Hydrol Processes 22:2689–2698 [Google Scholar]
- Rains MC, Dahlgren RA, Fogg GE, Harter T, Williamson RJ (2008) Geological control of physical and chemical hydrology in California vernal pools. Wetlands 28:347–362 [Google Scholar]
- Rover J, Wright CK, Euliss NH Jr, Mushet DM, Wylie BK (2011) Classifying the hydrologic function of Prairie Potholes with remote sensing and GIS. Wetlands 31:319–327 [Google Scholar]
- Sass GZ, Creed IF (2008) Characterizing hydrodynamics on boreal landscapes using archived synthetic aperture radar imagery. Hydrol Processes 22:1687–1699 [Google Scholar]
- Schalles JF, Shure DJ (1989) Hydrology, community structure and productivity patterns of a dystrophic Carolina bay wetland. Ecol Monogr 59(4):365–385 [Google Scholar]
- Schlaffer S, Chini M, Dettmering D, Wagner W (2016) Mapping wetlands in Zambia using seasonal backscatter signatures derived from ENVISaT ASaR time series. Remote Sens 8(5):1–24 [Google Scholar]
- Schmitt A, Brisco B (2013) Wetland monitoring using the curvelet-based change detection method on polarimetric SAR imagery. Water 5:1036–1051 [Google Scholar]
- Schmitt A, Wendleder A, Hinz S (2015) The Kennaugh element framework for multi-scale, multi-polarized, multi-temporal and multi-frequency SAR image preparation. ISPRS J Photogramm Remote Sens 102:122–139 [Google Scholar]
- Sethre PR, Rundquist BC, Todhunter PE (2005) Remote detection of Prairie Pothole ponds in the Devils Lake basin, North Dakota. GISci Remote Sens 42:277–296 [Google Scholar]
- Sharit RR, Gibbons JW (1982) The ecology of evergreen shrub bogs, pocosins and Carolina bays of the Southeast: A community profile. FWS/OBS-82/04. U.S. Fish and Wildlife Service, Office of Biological Services, Washington DC, 93p [Google Scholar]
- Shaw DA, Pietroniro A, Martz LW (2013) Topographic analysis for the prairie pothole region of Western Canada. Hydrolo Processes 27:3105–3114 [Google Scholar]
- Shaw DA, Vanderkamp G, Conly FM, Pietroniro A, Martz L (2012) The fill-spill hydrology of prairie wetland complexes during drought and deluge. Hydrol Processes 26:3147–3156 [Google Scholar]
- Shi Z, Fung KB (1994) A comparison of digital speckle filters. Proceedings of IGARSS 94, August 8–12, 1994, 2129–2133. [Google Scholar]
- Simon RN, Tormos T, Danis PA (2015) Very high spatial resolution optical and radar imagery in tracking water level fluctuations of a small inland reservoir. Int J Appl Earth Obs Geoinf 38:36–39 [Google Scholar]
- Snodgrass JW, Bryan, Jr. AL, Lide RF, Smith GM (1996) Factors affecting the occurrence and structure of fish assemblages in isolated wetlands of the upper coastal plain, U.S.A. Canadian Journal of Fish Aquatic Science 53:443–454. [Google Scholar]
- Spence C (2007) On the relation between dynamic storage and runoff: A discussion on thresholds, efficiency, and function. Water Resour Res 43:W12416,1–11. doi: 10.1029/2006WR005645 [DOI] [Google Scholar]
- Spence C, Phillps RW (2015) Refining understanding of hydrological connectivity in a boreal catchment. Hydrolo Processes 29(16):3491–3503 [Google Scholar]
- Stolt MH, Baker JC (1995) Evaluation of National Wetland Inventory maps to inventory wetlands in the southern blue ridge of Virginia. Wetlands 15:346–353 [Google Scholar]
- Sun G, Callahan TJ, Pyzoha JE, Trettin CC (2006) Modeling the climatic and subsurface stratigraphy controls on the hydrology of a Carolina bay wetland in South Carolina, USA. Wetlands 26(2):567–580 [Google Scholar]
- Tiner RW (1999) Wetland indicators: a guide to wetland identification, delineation, classification, and mapping CRC Press, Boca Raton, FL [Google Scholar]
- Tiner RW (2003) Geographically isolated wetlands of the United States. Wetlands 23(3):494–516 [Google Scholar]
- Tiner RW(ed) (2009) Status report for the National Wetlands Inventory Program: 2009. U.S. Fish and Wildlife Service, Division of Habitat and Resource Conservation, Branch of Resource and Mapping Support, Arlington, VA [Google Scholar]
- Touzi R, Deschamps A, Rother G (2007) Wetland characterization using polarimetric RADARSAT-2 capability. Can J Remote Sens 33(1):S56–S67 [Google Scholar]
- Tromp-van Meerveld HJ, McDonnell JJ (2006) Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis. Water Resour Res 42:W02411,1–11 [Google Scholar]
- Turin G (1960) An introduction to matched filters. IRE Trans Inf Theory 6:311–329 [Google Scholar]
- U.S. Army Corps of Engineers (1987) Corps of Engineers wetlands delineation manual. Wetlands Research Program Technical Report Y-87–1, Environmental Laboratory, Waterways Experiment Station [Google Scholar]
- U.S. EPA (2015) Connectivity of streams and wetlands to downstream waters: A review and synthesis of the scientific evidence (Final Report). EPA/600/R-14/475F U.S. Environmental Protection Agency, Washington DC [Google Scholar]
- U.S. Fish and Wildlife Service (2010) National Wetlands Inventory website U.S. Department of the Interior, Fish and Wildlife Service, Washington DC. http://www.fws.gov/wetlands/. [Google Scholar]
- U.S. Geological Survey (2000) The national hydrography dataset concepts and content http://nhd.usgs.gov/chapter1/chp1_data_users_guide.pdf [Google Scholar]
- U.S. Geological Survey (2013). The National Hydrography Dataset (NHD) U.S. Geological Survey, Reston, Virginia. ftp://nhdftp.usgs.gov/DataSets/Staged/States/FileGDB/ HighResolution/ [Google Scholar]
- Van der Kamp G, Hayashi M (2009) Groundwater-wetland ecosystem interaction in the semiarid glaciated plains of North America. Hydrogeol J 17(1):203–214 [Google Scholar]
- Vanderhoof MK, Alexander LC (2015) The role of lake expansion in altering the wetland landscape of the Prairie Pothole Region. Wetlands doi 10.1007/s13157-015-0728-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanderhoof MK, Alexander LC, Todd MJ (2016a) Temporal and spatial patterns of wetland extent influence variability of surface water connectivity in the Prairie Pothole Region, United States. Landscape Ecology 31(4):805–824 [Google Scholar]
- Vanderhoof MK, Christensen JR, Alexander LC (2016b) Patterns and drivers for wetland connections in the Prairie Pothole Region, United States. Wetlands Ecology and Management DOI: 10.1007/s11273-016-9516-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanderhoof MK, Distler HE, Mendiola DA, Lang M (2017) Integrating Radarsat-2, lidar and Worldview-3 imagery to maximize detection of forested inundation extent in the Delmarva Peninsula, USA. Remote Sens 9(105), doi: 10.3390/rs9020105 [DOI] [Google Scholar]
- Wang L, Liu H (2006) An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int J Geogr Inf Sci 20(2):193–213 [Google Scholar]
- White B, Ogilvie J, Campbell DMH, Hiltz D, Gauthier B, Chisholm KH, Wen HK, Murphy PNC, Arp PA (2012) Using the cartographic depth-to-water index to locate small streams and associated wet areas across landscapes. Can Water Resour J 37(4):333–347 [Google Scholar]
- White DC, Lewis MM (2011) A new approach to monitoring spatial distribution and dynamics of wetlands and associated flows of Australian Great Artesian Basin springs using QuickBird satellite imagery. J Hydrol 408(1–2):140–152 [Google Scholar]
- Whiteside TG, Bartolo RE (2015) Use of WorldView-2 time series to establish a wetland monitoring program for potential offsite impacts of mine site rehabilitation. Int J Appl Earth Obs Geoinf 42:24–37 [Google Scholar]
- Wilcox BP, Dean DD, Jacob JS, Sipocz A (2011) Evidence of surface connectivity for Texas Gulf Coast depressional wetlands. Wetlands 31:451–458 [Google Scholar]
- Wu Q, Deng C, Chen Z (2016) Automated delineation of karst sinkholes from LiDAR-derived digital elevation models. Geomorphology 266:1–10 [Google Scholar]
- Wu Q, Lane C, Liu H (2014) An effective method for detecting potential woodland vernal pools using high-resolution LiDAR data and aerial imagery. Remote Sens 6:11444–11467 [Google Scholar]
- Yuan T, Lee H, Jung HC (2015) Toward estimating wetland water level changes based on hydrological sensitivity analysis of PALSAR backscattering coefficients over different vegetation fields. Remote Sens 7:3153–3183 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


