Modelling bistable tumour population dynamics to design effective treatment strategies

Abstract

Despite recent advances in targeted drugs and immunotherapy, cancer remains “the emperor of all maladies” due to almost inevitable emergence of resistance. Drug resistance is thought to be driven by genetic alterations and/or dynamic plasticity that deregulate pathway activities and regulatory programs of a highly heterogeneous tumour. In this study, we propose a modelling framework to simulate population dynamics of heterogeneous tumour cells with reversible drug resistance. Drug sensitivity of a tumour cell is determined by its internal states, which are demarcated by coordinated activities of multiple interconnected oncogenic pathways. Transitions between cellular states depend on the effects of targeted drugs and regulatory relations between the pathways. Under this framework, we build a simple model to capture drug resistance characteristics of BRAF-mutant melanoma, where two cell states are determined by two mutually inhibitory – main and alternative – pathways. We assume that cells with an activated main pathway are proliferative yet sensitive to the BRAF inhibitor, and cells with an activated alternative pathway are quiescent but resistant to the drug. We describe a dynamical process of tumour growth under various drug regimens using the explicit solutions of mean-field equations. Based on these solutions, we compare efficacy of three treatment strategies from simulated data: static treatments with continuous and constant dosages, periodic treatments with regular intermittent active phases and drug holidays, and treatments derived from optimal control theory (OCT). Periodic treatments outperform static treatments with a considerable margin, while treatments based on OCT outperform the best periodic treatment. Our results provide insights regarding optimal cancer treatment modalities for heterogeneous tumours, and may guide the development of optimal therapeutic strategies to circumvent plastic drug resistance. They can also be used to evaluate the efficacy of suboptimal treatments that may account for side effects of the treatment and the cost of its application.

Graphical Abstract

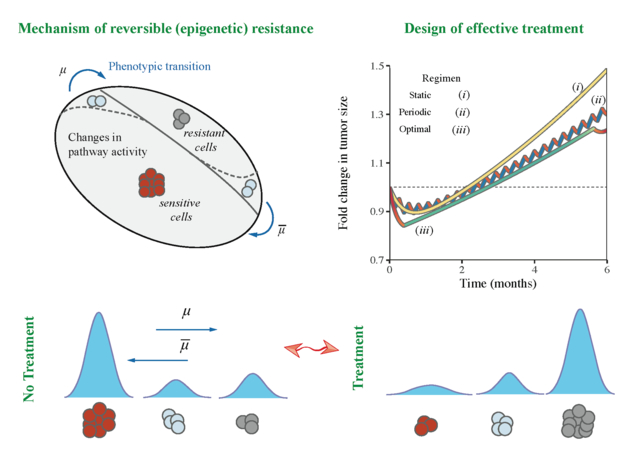
Introduction

Despite the recent advances of targeted treatments and immunotherapy, complete nonsurgical cure of cancer is still rare due to the almost inevitable emergence of resistance (Bozic and Nowak, 2017; Garraway and Jänne, 2012; Iwasa et al., 2006; Komarova and Wodarz, 2005). Drug resistance arises from a wide range of complex processes at multiple levels (Dagogo-Jack and Shaw, 2017; Hu and Zhang, 2016; Sharma et al., 2017). At the tumour level, drug response emerges primarily from population dynamics of cancer cells. The most well-known mechanism is clonal evolution (Greaves and Maley, 2012; Williams et al., 2018). A bulk tumour is often populated by a heterogeneous group of cancer cells with diverse mutational landscapes, epigenomic states, pathway activities and gene regulatory programs. Treatments induce differential fitness of subclones and consequently select for the most resistant ones. Beside clonal evolution, treatments may also induce differential plasticity of tumour cells by shifting their pathway activities (Shaffer et al., 2017) and regulatory programs (Stites, 2012), or by copy number changes (Das Thakur et al., 2013). The major difference between these two processes pertains to reversibility of drug resistance. For clonal evolution, drug sensitivity of an individual cell is determined solely by its genetic landscape and thus remains invariant during its life span. Drug resistance of a subclone is thus an irreversible phenotype as a resistant subclone will rarely revert. For differential plasticity, drug sensitivity of an individual cell is in a reversible dynamic state rather than a fixed phenotype. Both mechanisms are supported by numerous experimental evidence (e.g., for clonal evolution, (Gerlinger et al., 2012); for differential plasticity of tumour cells (Hangauer et al., 2017; Shaffer et al., 2017; Sharma et al., 2010; Sun et al., 2014; Tirosh et al., 2016)). However, the latter process may account for drug resistance that can be reverted when the therapy is lifted (Fischer et al., 2015; Kuczynski et al., 2013).

There is a rich literature of mathematical models for tumour clonal evolution that undergoes treatments (e.g., (Ashcroft et al., 2015; Beerenwinkel et al., 2015; Dingli et al., 2009; Klement, 2016; Michor and Beal, 2015; Sprouffske et al., 2011; You et al., 2017)). In contrast, models of cellular plastic responses to treatments are relatively limited and recent (e.g., (Bacevic et al., 2017; Chen et al., 2014; Kim et al., 2018; Paudel et al., 2018; Taylor–King et al., 2018), see also reviews (Jolly et al., 2018; Kolch et al., 2015; Marusyk et al., 2012)). The ultimate purpose of those models is to quantitatively predict tumour’s drug responses and employ this information to design effective treatments. Previously, we proposed a unified framework encompassing both mathematical models of tumour population dynamics and treatment design (Beckman et al., 2012). We considered a simple evolution model involved in subclones with differential resistance of two drugs, and tested efficacy of six heuristic treatment strategies by simulating population dynamics with a large number of parameter combinations informed by literature and clinical experience. We further extended the work to a three-drug system and generalized treatment strategies that incorporated long-term prediction of tumour population composition (Yeang and Beckman, 2016).

An important missing piece in this framework is a mathematical model that tackles reversible drug responses of cancer cells and also offers an explicit design of optimal treatments serving as a golden standard to all other, eventually suboptimal, regimens. To fill this gap, we propose a model to explore the population dynamics of cancer cells during or after treatment with targeted agents that produce reversible effects. The state of each cell is determined by the activities of multiple inter-dependent pathways, whereas the fitness of each cell depends on its internal state and the external environment (i.e. drug dosage). Treatments alter the cellular state composition of the population by both facilitating the single-cell state transitions in certain directions and inhibiting proliferation of subpopulations with differential efficiencies. To capture the essence of reversible cellular state transitions, we consider a simple scenario in which cell proliferation is driven by two mutually antagonistic signalling pathways. The main pathway promotes cell proliferation more efficiently but is also sensitive to a therapeutic agent. The alternative pathway induces slow proliferation but is also resistant to the agent. Due to reversibility of the states, the treatment strategy aims to balance between controlling the tumour load and reducing the influence of resistant cells. Similar models were previously proposed (see, e.g., (Cunningham et al., 2018)), yet they lacked the exact construction of globally optimal treatment regimens and considered only numerical schemes for their design.

Despite its simplicity, our model captures reasonably well the switching behaviour of BRAF^V600E mutant melanomas treated with BRAF inhibitor (vemurafenib) (Das Thakur et al., 2013; Sosman et al., 2012). Melanoma is a frequently lethal form of skin cancer with incidence rates continuing to rise in many countries (Siegel et al., 2018). Approximately half of cases harbour a BRAF^V600 mutation (Davies et al., 2002). The resulting mutation leads to constitutive activation of a down-stream cascade of the mitogen activated protein (MAPK) pathway including MEK and ERK that promote proliferation of cancer cells. Treatment with a single-agent BRAF inhibitor disrupts MAPK signalling and achieves remission but leads to relapse in 6.7 months on average (Sosman et al., 2012). As of 2014, the standard of care for BRAF^V600 mutant melanoma is the combination of inhibitors of BRAF and MEK (Dummer et al., 2018; Larkin et al., 2014). Still, resistance emerges through numerous genetic mechanisms (Johannessen et al., 2010; Montagut et al., 2008; Nazarian et al., 2010; Poulikakos et al., 2011) or phenotypic changes, such as switching from the suppressed MAPK pathway to an alternative pathway involving activation of NFκB (Konieczkowski et al., 2014; Lehraiki et al., 2015; Müller et al., 2014; Sun et al., 2014; Tirosh et al., 2016). The latter process of switching between two major oncogenic programs is accompanied by physiological changes in cancer cells (Kemper et al., 2014).

These characteristics allow us to abstract the problem and formulate a minimal dynamic model. To describe the dynamics of tumour growth and state composition, we derive master equations and find their analytic solutions under arbitrary drug regimens. Based on these solutions, we compare the performance of three treatment strategies on simulated data: i) static treatments with continuous and constant dosages, ii) periodic treatments with regular intermittent treatment days and drug holidays, and iii) the treatments that minimize the tumour size at a fixed time horizon. Alternative targets for optimization may include minimization of the time integral for the tumour size, so that the probability of a genetically resistant subclone would be minimized, maximization of the time at which the tumour cell count remains below a threshold number (Beckman, Schemmann, and Yeang, 2012) or minimization of the total drug application or time to recovery as in (Gluzman et al., 2018). We note that our choice to minimize the tumour size at a fixed time provides the lowest estimate of tumour size under any possible (suboptimal) treatment. We finalize our work with discussion of obtained results and conclusions envisioning possible recommendations for treatment of cancer patients whose tumours exhibit reversible mechanism of resistance.

Model and methods

1. Assumptions and concepts

We consider a general and abstract model where each cancer cell is a self-replicating entity possessing one of multiple possible internal states. Each internal state has a distinct proliferative capacity, sensitivity to treatments, and can transition to other internal states. From this more general case, we study a particular instance in detail as outlined below:

1. The mutational landscape of tumour cells does not acquire major driver events (“hallmarks of cancer” (Hanahan and Weinberg, 2000)) or new resistance mutations during the course of therapy. This assumption alleviates the burden of simultaneously modelling both clonal evolution and cellular plasticity, but may not be realistic in a longer time scale (e.g. with an order of one year or more).

2. The dominant subclone of tumour cells, which is the focus here, by default possesses elevated activities of the “main” pathway that render it highly proliferative.

3. Proliferation can also be sustained by an “alternative” pathway with lower efficiency. The two pathways are mutually inhibitory, thus without external intervention the tumour population is dominated by cells with an active main pathway over those with an active alternative pathway.

4. A targeted agent or targeted combination inhibits proliferation of cells with an active main pathway and concomitantly facilitates activity transitions from the main to the alternative pathway.

Fig 1A illustrates the conceptual framework of the model. This may be seen as an archetypical bistable state model that covers a particular class of internal “wirings” of a cell.

Fig 1: Mathematical modelling framework.

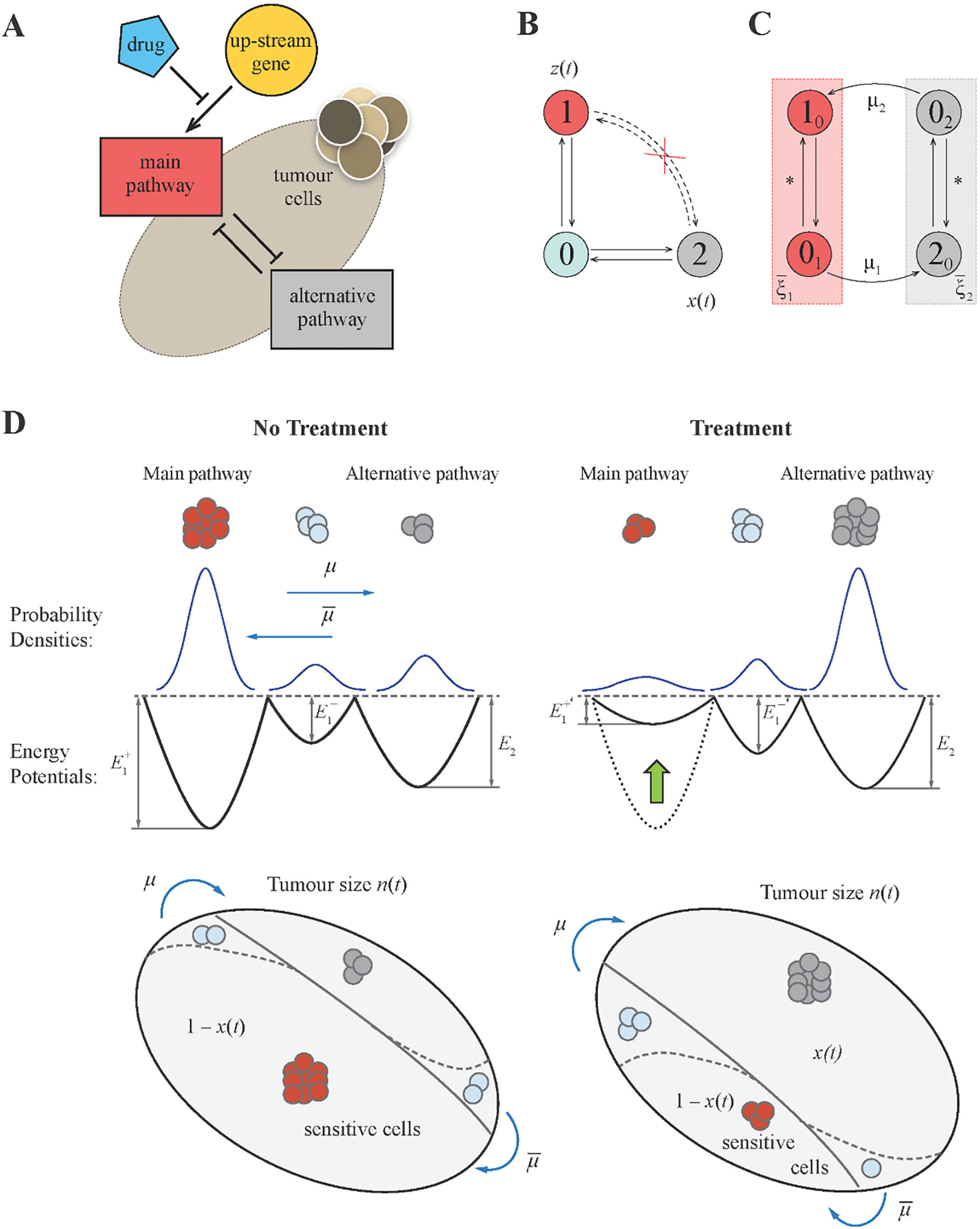
(A) Schematic diagram of the pathway interaction within tumour cells. Activity of the main pathway is induced by an upstream gene, e.g. a driver oncogene, that can be blocked by the drug action. The regulation of the alternative resistant pathway remains unaffected. Both pathways are antagonistic to each other. (B) Original framework to model the switch between activated pathways “1” and “2” occurring through a transient state “0” where both pathways are shut down. (C) Flow diagram for a modified model with two states used to derive main equations. (D) Characteristics of a system without and with treatment. Each pathway activity is modelled by a stochastically moving particle in a potential well. The treatment changes the potential for the main pathway but does not affect that for the alternative pathway.

Activities of the two pathways demarcate three cellular states (Fig 1BC): active main / inactive alternative pathway (state “1”), inactive main / active alternative pathway (state “2”), and inactive main / inactive alternative pathway (state “0”). Simultaneous activation of both pathways is not allowed since they are mutually inhibitory. 0 is a transient state between 1 and 2.

Cells expressing the main or alternative pathway may encounter three stochastic events: proliferation, death, and state transition (1 → 0 → 2 or 2 → 0 → 1). The population dynamics of the birth-death process can be well approximated by ordinary differential equations. To determine the population dynamics of cellular states, we adopt a well-known approach from statistical physics by treating cells as particles undergoing Brownian motions inside a double-well potential (Krapivsky et al., 2010). In this model, each pathway possesses a double-well potential. The two equilibria of the system (the two local minima of the potential) represent up and down regulation of the pathway activities (Fig 1D). Probabilities of staying in each state (and thereby the fraction of cells in each state) are determined by the “energy gap” between two local minima. Without external intervention, lower wells (more likely states) of the main pathway correspond to up-regulation of the main pathway and down-regulation of the alternative pathway.

The drug has a cytostatic effect on a cell. It inhibits both the main pathway activity and proliferation of main pathway-active cells, but has no effect on the alternative pathway. The former effect also facilitates the state transition 1 → 0 → 2 and thus induces drug resistance. Mathematically the drug action lifts the well of the up-regulation state and lowers the well of the down-regulation state of the main pathway potential function. However, it does not change the shape of the alternative pathway potential function. The extent of potential function change depends on administered dosage that we decode by a variable σ, the treatment intensity with values constrained between zero and one. Two extremes are σ = 0 for no treatment, and σ = 1 for a maximally tolerated dosage (MTD) administered. The latter shuts down the main pathway and turns on the alternative pathway driving emergence of drug resistance. Although drug toxicity is an important concern in any cancer treatment, it is generally difficult to model toxicity due to the diversity of proper dosage quantities related to drug toxicity. Toxicity can be related to the maximum dose, the average dose intensity, or the duration of therapy without interruption and recovery periods, depending on the types of administered drugs. In the current study, toxicity was taken into account by requiring that the dosage at any time could not exceed an upper bound, and hence considered the normalized dosage level in the interval [0,1] throughout the entire treatment schedule. However, the upper bound can be restricted to a value lower than one due to existent toxicity of the applied drug. We do not consider this aspect fully in the paper but assume that it can be incorporated once the drug efficacy – profile and maximum tolerated dosage are known from Phase 1 clinical studies. We note that many patients will prioritize maximizing survival at the maximum tolerated dose, as long as toxicity has a low risk of inducing permanent morbidity or mortality. Others will prioritize and value lower toxicity and improved quality of life. Individualized optimal therapies may in principle be calculated if the efficacy-toxicity tradeoff for any given individual can be determined.

The setting described above makes the disease incurable by continuous administration of a single therapeutic agent since the tumour inevitably relapses (Chmielecki et al., 2011). However, the patient’s life span can be significantly improved with proper arrangements of treatment dosage and schedule even of this single agent. A possible aim is to minimize the tumour size at a fixed time horizon. To fulfil this goal, one obliges to maintain a subtle balance of proliferative but sensitive cells vs. quiescent but resistant cells, such that the tumour remains responsive to the drug but has a limited growth rate.

2. Modelling framework

We start with formulation of a model of two antagonistic pathways for individual tumour cells. We consider a stochastic birth-death process and apply the mean-field approximation to describe the evolution of tumour size and resistance level at any particular time of the treatment.

(a). Modelling pathway activity

A system of two interconnected pathways and an up-stream gene is shown in Fig 1A. For simplicity, we denote the main pathway by the index “1” and the alternative pathway by the index “2”. We characterize each pathway with a normalized activity level y_i (0 ≤ y_i ≤ 1, i = 1,2), and construct the protein expression model with two consistent reactions (Assaf et al., 2013; Roberts et al., 2015). First, the production function f_i(y_i) identifies the rate of protein production. Second, the degradation of proteins occurs at rate 1. The dynamics hold the form:

$${\delta }^{-1}\frac{\text{d}{y}_i(t)}{\text{d}t}=f_i\left(y_i(t)\right)-y_i(t)+{\eta }_i,$$

where η_1,2 are random noise terms, the constant δ is a relative adjustment rate between updates in the pathway activity and the birth-death process of tumour cells. Following the experimental evidence that cell fate is guided by Boolean logic (Bernardo-Faura et al., 2014; Olsson et al., 2016), we assign the production function f_i(y_i) to a step-wise function: it equals to one for any y_i above threshold θ_i, and to α_i for any y_i below it:

$$\begin{gathered} f_i\left(y_i\right)=A_i(\sigma )\cdot \left[{\alpha }_i+\left(1-{\alpha }_i\right)\cdot H\left(y_i-{\theta }_i\right)\right], \\ 0\le {\alpha }_i<{\theta }_i\le 1,(i=1,2) \end{gathered}$$

where H(∘) is the Heaviside function, the function A_i(σ) describes the reduction in expression level of the pathway due to the effect of the drug (Fig S1A). As noted above, A₁(σ) decreases with the treatment intensity σ, while A₂(σ) ≡ 1. Overall, we impose the restriction: α_i < A_i(σ) < θ_iα_i to preserve a bimodality of the potential.

The activation dynamics are described by the Brownian motion in a double-well potential: $U_i\left(y_i\right)=-\int f_i\left(y_i\right)\text{d}{y}_i+\left(y_i^2-{\theta }_i^2\right)/2$ or equivalently:

$$U_i\left(y_i\right)=-f_i\left(y_i\right)\cdot \left(y_i-{\theta }_i\right)+\frac{y_i^2-{\theta }_i^2}{2}.$$

We impose that the potential 𝑈₁(y₁), which is a double well for any treatment intensity σ < 1 and is unimodal only for σ = 1 (Fig S1B). The potential has two stable equilibria: up and down regulation states, that correspond to two minima of the potential (Fig 1D). The state y_i fluctuating near the attractor y^± may eventually jump from one potential well to another. The transition rate follows the Van’t Hoff-Arrhenius law (Hänggi et al., 1990) and defines the escape rate from one of the equilibria $y_i^{\pm }$ in the form: ${\lambda }_i\exp \left(-{\kappa }_i{E}_i^{\pm }\right)$, where $E_i^{\pm }$ are the heights of potential barriers: $E_i^{+}(\sigma )=U_i\left({\theta }_i(\sigma )\right)-U_i\left(A_i(\sigma )\right)$ and $E_i^{-}(\sigma )=U_i\left({\theta }_i(\sigma )\right)-U_i\left({\alpha }_i{A}_i(\sigma )\right)$. The robustness parameter κ_i indicates how likely pathway i switches between active and inactive states due to internal stochastic effects, and the constant 𝜆_i depends on the curvature of the potential in the proximity of the equilibrium and also at the boundary of the region of attraction θ_i ± ε (ε → 0).

Since the two pathways are mutually inhibitory, the two double potential well systems are coupled and hence give rise to dynamics of stochastic state transitions illustrated in Fig 1B. Transitions between the two steady states 1 (active main pathway) and 2 (active alternative pathway) are mediated by the transient state 0 (both pathways off). We assume that up/down regulation of protein expressions and activities in each pathway occurs arbitrarily fast, yet transformations of cellular phenotypes (such as proliferation rates and drug sensitivities) occur at a much slower rate. To account for these two-tier processes, we encode each cellular state by two values k_a, where k is the current pathway state and a is the previous pathway state (k ≠ a; k, a = {0,1,2}; Fig 1C). The current pathway state index k determines the activities of the two pathways according to the previous definition, whereas the prior pathway state index a alludes the cellular phenotype. Steady states 1₀ and 2₀ denote cells with consistent pathway activities and phenotypes (up-regulated main pathway and proliferative phenotype for 1₀ and up-regulated alternative pathway and quiescent phenotype for 2₀). Transient states 0₁ and 0₂ denote cells with both pathways down-regulated and phenotypes carried from the prior steady states (proliferative for 0₁ and quiescent for 0₂). The transition k₀ ↔ 0_k alters pathway expressions and activities relatively rapidly (rate $\tilde{\mu }\gg 1$), so that the equilibrium in corresponding subsystems (red and grey compartments in Fig 1C) is achieved instantaneously. In contrast, the transition 0_i, → i₀ (i′ = 3 − i, i = {1,2}) transforms cellular phenotypes and occurs at a slow scale with rates μ_i ~ 1.

(b). Tumour growth

We further derive the dynamics of tumour growth at population level from the process of aforementioned individual pathway activities. In this sense, the number of cells n_ka in each dynamic compartment k_a follows the change according to continuous-time equations (Paudel et al., 2018):

$$\frac{\text{d}{n}_{i0}(t)}{\text{d}t}={\omega }_i{n}_{i0}(t)+{\tilde{\mu }}_i(n_{0i}(t)e^{-{\kappa }_i{E}_i^{-}(\sigma )}-n_{i0}(t)e^{-{\kappa }_i{E}^{+}(\sigma )})+{\mu }_{i^{\prime }}{e}^{-{\kappa }_i{E}_i^{-}(\sigma )}{n}_{0i^{\prime }}(t),$$

$$\frac{\text{d}{n}_{0i}(t)}{\text{d}t}={\omega }_0{\xi }_{0i}(t)-{\tilde{\mu }}_i(n_{0i}(t)e^{-{\kappa }_i{E}_i^{-}(\sigma )}-n_{i0}(t)e^{-{\kappa }_i{E}^{+}(\sigma )})-{\mu }_i{e}^{-{\kappa }_{i^{\prime }}{E}_{i^{\prime }}^{-}(\sigma )}{n}_{0i}(t),$$

where the variable ω_k is the net proliferation rate of a cell with state k (i.e. the difference between birth and death rates). The last terms in each equation are factored by the exponent due to explicit transition from inactivated to activated state for a new phenotypic state.

The fast-time dynamics requires the term of ${\tilde{\mu }}_i$ to be zero:

$$n_{0i}(t)=n_{i0}(t)e^{-{\kappa }_i\mathrm{\Delta }{E}_i(\sigma )},$$ (1)

so that we have:

$$\begin{gathered} \frac{d{n}_{i0}(t)}{dt}={\omega }_i{n}_{i0}(t)+{\mu }_{i^{\prime }}{e}^{-{\kappa }_i{E}_i^{-}(\sigma )}{n}_{0i^{\prime }}(t), \\ \frac{\text{d}{n}_{0i}(t)}{\text{d}t}={\omega }_0{n}_{0i}(t)-{\mu }_i{e}^{-{\kappa }_{i^{\prime }}{E}_{i^{\prime }}^{-}(\sigma )}{n}_{0i}(t). \end{gathered}$$ (2)

Since both state variables n_i0 and n_0i describe the same phenotype (proliferative when i = 1 and quiescent when i = 2), we introduce a new variable n_i(t) = n_i0(t) + n_0i(t) to specify the dynamics of phenotype i. We use (1) and (2) to express the dynamics in terms of these new variables:

$$\begin{gathered} \frac{\text{d}{n}_i(t)}{\text{d}t}=\frac{{\omega }_i{e}^{{\kappa }_i\mathrm{\Delta }{E}_i(\sigma )}+{\omega }_0}{e^{{\kappa }_i\mathrm{\Delta }{E}_i(\sigma )}+1}{n}_i(t)-\frac{{\mu }_i{e}^{-{\kappa }_{i^{\prime }}{E}_{i^{\prime }}^{-}(\sigma )}}{e^{{\kappa }_i\mathrm{\Delta }{E}_i(\sigma )}+1}{n}_i(t) \\ +\frac{{\mu }_{i^{\prime }}{e}^{-{\kappa }_i{E}_i^{-}(\sigma )}}{e^{{\kappa }_{i^{\prime }}\mathrm{\Delta }{E}_{i^{\prime }}(\sigma )}+1}{n}_{i^{\prime }}(t). \end{gathered}$$ (3)

We impose no effect of the treatment on the cells with active alternative pathway that allows to write (3) in the form:

$$\begin{gathered} \frac{\text{d}{n}_1(t)}{\text{d}t}=\frac{{\omega }_1{e}^{{\kappa }_1\mathrm{\Delta }{E}_1(\sigma )}+{\omega }_0}{e^{{\kappa }_1\mathrm{\Delta }{E}_1(\sigma )}+1}{n}_1(t)-\frac{{\mu }_1{e}^{-{\kappa }_2{E}_2^{-}}}{e^{{\kappa }_1\mathrm{\Delta }{E}_1(\sigma )}+1}{n}_1(t)+\frac{{\mu }_2{e}^{-{\kappa }_1{E}_1^{-}(\sigma )}}{e^{{\kappa }_2\mathrm{\Delta }{E}_2}+1}{n}_2(t), \\ \frac{\text{d}{n}_2(t)}{\text{d}t}=\frac{{\omega }_2{e}^{{\kappa }_2\mathrm{\Delta }{E}_2}+{\omega }_0}{e^{{\kappa }_2\mathrm{\Delta }{E}_2}+1}{n}_2(t)-\frac{{\mu }_2{e}^{-{\kappa }_1{E}_1^{-}(\sigma )}}{e^{{\kappa }_2\mathrm{\Delta }{E}_2}+1}{n}_2(t)+\frac{{\mu }_1{e}^{-{\kappa }_2{E}_2^{-}}}{e^{{\kappa }_1\mathrm{\Delta }{E}_2}+1}{n}_1(t), \end{gathered}$$ (4)

Additionally, we stipulate that state 2 cells are less proliferative than state 1 cells with a fitness cost c₂: ω₂ = ω₁ − c₂. Thus, the following relation holds: ω₀ < 0 < ω₂ < ω₁. The first inequality in the chain reflects the fact that the cell becomes nonviable when both pathways are shut down. The ω_k parameters can be re-parametrized in terms of the birth and death rates and fitness cost: ω₀ = b(1 − χ) − d, ω₁ = b − d, ω₂ = b − c₂ − d, where b and d are default birth and death rates, and χ is the penalty to the birth rate when both main and alternative pathways are disabled. This expresses the fitness of the sensitive cells in the form:

$$\frac{{\omega }_1{e}^{{\kappa }_1\mathrm{\Delta }{E}_1(\sigma )}+{\omega }_0}{e^{{\kappa }_1\mathrm{\Delta }{E}_1(\sigma )}+1}=b\left(1-\frac{\chi }{e^{K_1\mathrm{\Delta }{E}_1(\sigma )}+1}\right)-d,$$

of the resistant cells:

$$\frac{{\omega }_2{e}^{{\kappa }_2\mathrm{\Delta }{E}_2}+{\omega }_0}{e^{{\kappa }_2\mathrm{\Delta }{E}_2}+1}=b\left(1-\frac{c_2{e}^{{\kappa }_2\mathrm{\Delta }{E}_2}+\chi }{e^{{\kappa }_2\mathrm{\Delta }{E}_2}+1}\right)-d.$$

(c). Dynamic equations

The system of differential equations (4) gives rise to our main intermediate result: the dynamic equations describing the change in tumour load n(t) = n₁(t) + n₂(t), and fraction of resistant cells x(t) = n₂(t)/n(t) over time:

$$\frac{\text{d}n(t)}{\text{d}t}=\left(b\left(1-\frac{\chi (1-x(t))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-cx(t)\right)-d\right)n(t),$$ (5)

$$\begin{gathered} \frac{\text{d}x(t)}{\text{d}t}=b\left(\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-c\right)x(t)(1-x(t))+\frac{\mu (1-x(t))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1} \\ -\overline{\mu }{e}^{-\kappa E^{-}(\sigma )}x(t), \end{gathered}$$ (6)

where the subindices were introduced for short hand: κ ≡ κ₁, $E^{-}(\sigma )\equiv E_1^{-}(\sigma )$, ΔE(σ) ≡ ΔE₁(σ), as well as few transformations of parameters: $c=\frac{c_2{e}^{{\kappa }_2\mathrm{\Delta }{E}_2+\chi }}{e^{{\kappa }_2\mathrm{\Delta }{E}_{2+1}}}$, $\mu =\frac{{\mu }_1{e}^{-{\kappa }_2{E}_2^{-}}}{e^{{\kappa }_1\mathrm{\Delta }{E}_{2+1}}}$, and $\overline{\mu }=\frac{{\mu }_2}{e^{{\kappa }_2\mathrm{\Delta }{E}_2+1}}$.

Fig 1D shows the resulting flow diagram of the dynamics. The main terms of (5)–(6): (e^κΔE(σ) + 1) and e^{−κE−(σ)}, are monotonic decreasing functions of the treatment intensity σ (Fig S2). Hence, the resistant cells overgrow sensitive cells for any value μ and $\overline{\mu }$ only if χ/(e^κΔE(σ) + 1) > c, which is expected for large values of drug dosages σ.

Despite the complex structure of the derived equations (5)–(6), they represent a rather conventional form. The equation (5) rewritten with respect to log n(t) gives a simple first order dependence on x(t). The first term of (6) resembles the replicator dynamics (Nowak, 2006), where the growth rate is equal to the difference between two fitness costs – it describes cell competition between different types. The two following terms in (6) indicate the transition flows between the sensitive state 1 and the resistant state 2. In population genetics, those are known under the names of selection and mutation terms, respectively.

(d). Model simulation and determination of the model parameter values

We simulated tumour growth with or without drug administration by solving the aforementioned dynamical equations. To make the simulation outcomes comparable to the real data, we estimated and extracted model parameters from experimental literature. Below we list the source and criteria for determining model parameters.

Bozic et al. (Bozic et al., 2013) reported the average daily net growth rate of a melanoma cell line with BRAF mutation at 0.01. They set the death rate to 0.13 per day, while the birth rate was set to 0.14 per day to ensure the cells to divide every 7 days on average. The treatment with BRAF inhibitor vemurafenib led to the observed tumour shrinkage at average rate of 0.03 per day.

If the drug has a weak cytotoxic effect, there is no change in the death rate, while there is an apparent disruption of the internal cellular machinery that makes a cell unable to divide. If we assume that Bozic et al. used the drug intensity close to maximally tolerated dosage (MTD), the following conditions for particular cases of the dynamics (1) are implemented:

$$b\left(1-\frac{\chi }{e^{K\mathrm{\Delta }E(\sigma =0)}+1}\right)-d=0.01{\text{day}}^{-1},b\left(1-\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma =1)}+1}\right)-d=-0.03{\text{day}}^{-1},$$

where d = 0.13 day⁻¹. This leads to the following:

$$b=\frac{0.1(e^{\kappa \mathrm{\Delta }E(\sigma =1)}+1)-0.14(e^{\kappa \mathrm{\Delta }E(\sigma =0)}+1)}{e^{\kappa \mathrm{\Delta }E(\sigma =1)}-e^{\kappa \mathrm{\Delta }E(\sigma =0)}},$$

$$\chi =1-\frac{0.14\left(e^{\kappa \mathrm{\Delta }E(\sigma =0)}+1\right)-b{e}^{\kappa \mathrm{\Delta }E(\sigma =0)}}{b}.$$

From the fixed parameters characterizing the dynamics of the main pathway activity, we set the low level and the threshold of the production function to α = 0.3 and θ = 0.45 respectively, and robustness parameter κ = 40.0. Substituting these values into the aforementioned formulas we obtain b = 0.14 day⁻¹ and χ = 0.326.

The characteristic time of switching from the main to the alternative pathway μ⁻¹ is set to be 10.5 days, and of the reversed switch ${\overline{\mu }}^{-1}$ to be 14 days. The former number is chosen by assuming that the direct switch is faster than the reversed (Konieczkowski et al., 2014) and that rewiring of cellular machinery requires at least one or two cell divisions. The latter number is based on the data in the experimental study of melanoma growth with a resistance mechanism identical to our model (Lehraiki et al., 2015). Lehraiki et al. indicated that the acquired resistance can be reversed in two weeks.

We set the cost of resistance relative to the fitness of sensitive cells under no treatment to be c_relative = 10% (Akhmetzhanov and Hochberg, 2015). This imposed the following condition to the cost c used in our model:

$$b(1-c)-d=\left(b\left(1-\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma =0)}+1}\right)-d\right)\left(1-c_{\text{relative}}\right)=0.009{\text{day}}^{-1},$$

that led to:

$$c=\frac{b-d}{b}{c}_{\text{relative}}+\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma =0)}+1}\left(1-c_{\text{relative}}\right)=\mathrm{0.008.}$$

Table 1 summarizes our choice of model parameters values. Since the proposed model parameter values are often obtained from either educated guesses or similar theoretical studies (Bozic and Nowak, 2017; Garraway and Jänne, 2012; Tirosh et al., 2016), especially regarding the choice of values for μ and $\overline{\mu }$, we have conducted sensitivity analysis on simulation outcomes.

Table 1.

Baseline parameter values used in this study.

Parameter	Variable	Value	Ref.
Birth rate	b	0.14 day−1	fitted, (Bozic et al., 2010)
Death rate	d	0.13 day−1	(Bozic et al., 2010)
Relative cost of resistance	c relative	10%	(Akhmetzhanov and Hochberg, 2015)
Cost of inactivation of both pathways	χ	32.6%	fitted
Switching rate from the main to the alternative pathway	μ	0.095 day−1	-
Switching rate from the alternative to the main pathway	$\overline{\mu }$	0.071 day−1	(Lehraiki et al., 2015)
Expression of the main pathway at down state	α	0.3	(Miyamoto et al., 2015)
Threshold level for the production function of the main pathway	θ	0.45	(Miyamoto et al., 2015)
Robustness parameter for the main pathway	κ	40.0	-
Initial level of resistance	ε	1%	(Iwasa et al., 2006)

3. Design of the optimal treatment

We examine the efficacy of three treatment strategies in the aforementioned tumour population dynamics model: static treatments by administering a constant dosage through the entire episode, periodic treatments with regular active phases interleaved with drug holidays, and treatments derived from the optimal control theory. The first two strategies are self-explanatory and will be described in the presentation of simulation results. The last strategy is much more mathematically involved and is thus separately elaborated in this section. At a conceptual level, an optimal regimen proposes the drug intensity as a time-varying function σ(t) that also depends on the current tumour size and composition to optimize a pre-defined payoff function under the constraint of the tumour population dynamics (5)–(6). In optimal control theory, this problem is translated into solving an associated Hamilton-Jacobi-Bellman (HJB) equation (Bellman, 1957; Melikyan, 1998).

Here we provide a closed-form (exact) solution of the optimal control problem respectively to our modelling framework of two competing pathways. According to the optimal control theory, the designed optimal treatment guarantees that there is no other strategy of the treatment regimen that would possess a better outcome than this optimal solution. In this perspective, the optimal regimen does not only provide the best-possible strategy, but can be also used to evaluate performance of any other suboptimal strategy, such as periodic or any other state-dependent adaptive treatments (Fischer et al., 2015; Yoon et al., 2018).

(a). Formulation of the optimal control problem

The design of the optimal regimen is aimed to minimize the tumour size after a fixed time length T. As guided by the optimal control theory, we first introduce the target function as the logarithm of the tumour fold change by the time T relative to the initial tumour size:

$$\ln \left(\frac{n(T)}{n(0)}\right)={\int }_0^T\left[b\left(1-\frac{\chi (1-x(t))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-cx(t)\right)-d\right]\text{d}t\to \underset{\sigma \in [0,1]}{\min }.$$

Equivalently, after omitting the constants from the integral and changing the sign in front of the integral, it writes as follows:

$${\int }_0^T\left(\frac{\chi (1-x(t))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}+cx(t)\right)dt\to \underset{\sigma \in [0,1]}{\max }.$$

We notice that the optimal regimen can be completely identified only by two variables t and x, whereas the tumour size n has already been accounted in the formula for the payoff function by itself. Hence, we restrict the resulting time-state space only to two dimensions (t, x).

The HJB equation: $\underset{\sigma \in [0,1]}{\max }\mathscr{H}\left(x,\sigma ,{\varphi }_0,\varphi \right)=0$, is defined with the Hamiltonian $\mathscr{H}$ of the form:

$$\begin{gathered} \mathscr{H}\left(x,\sigma ,{\varphi }_0,\varphi \right)\doteq -{\varphi }_0 \\ +\varphi \left(b\left(\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-c\right)x(1-x)+\frac{\mu (1-x)}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-\overline{\mu }{e}^{-\kappa E^{-}}x\right) \\ +\frac{\chi (1-x)}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}+cx, \end{gathered}$$

where two co-state variables ϕ₀ and ϕ are the components of the gradient of a so-called value function V(t, x) (ϕ₀ = −∂V/∂t and ϕ = ∂V/∂x). Following the optimal control theory, the function V(t, x) by itself is an expected outcome of the tumour management from given intermediate state at (t, x):

$$V(t,x)={\int }_t^T\left(\frac{\chi (1-x(t))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}+cx(t)\right)\text{d}t.$$

As we can directly see from the form of the integral: ϕ(T) = 0. Because of this terminal condition, we will construct the solution of the optimal control problem in backward time with new time variable: τ = T − t.

The field of optimal trajectories can be obtained by applying the method of characteristics for HJB equation (Melikyan, 1998). In this case, each characteristic represents a solution of a system of two ordinary differential equations:

$$\frac{\text{d}x(\tau )}{\text{d}\tau }=-\frac{\partial \mathscr{H}}{\partial \varphi }=-b\left(\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-c\right)x(\tau )(1-x(\tau ))+\frac{\mu (1-x(\tau ))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-\overline{\mu }{e}^{-\kappa E^{-}(\sigma )}x(\tau ),$$

$$\begin{gathered} \frac{\text{d}\varphi (\tau )}{\text{d}\tau }=\frac{\partial \mathscr{H}}{\partial x}=\varphi (\tau )\left(b\left(\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-c\right)(1-2x(\tau ))-\frac{\mu }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}-\overline{\mu }{e}^{-\kappa E^{-}(\sigma )}\right) \\ -\frac{\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}+c. \end{gathered}$$

Each characteristic stipulates the optimal backward time trajectory of (x(τ), ϕ(τ)) with a specific initial condition at τ = 0 (t = T, the terminal time point). The optimal dosage sequence σ*(t) drives the system to follow the characteristic trajectory with a specific initial condition. Precisely, the optimal control of a tumour is expressed by using the first order optimality condition:

$$\begin{gathered} {\sigma }^{*}(t)=\arg \underset{\sigma \in [0,1]}{\max }\mathscr{H}\left(x,\sigma ,{\varphi }_0,\varphi \right) \\ =\arg \underset{\sigma \in [0,1]}{\max }\left(\frac{\varphi (b\chi x+\mu )+\chi }{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}(1-x)-\overline{\mu }\varphi e^{-\kappa E^{-}(\sigma )}x\right). \end{gathered}$$ (7)

σ* equals to zero or one if the maximum of the Hamiltonian is reached at one of the boundaries of the segment [0,1]. Otherwise, it has an intermediate value between zero and one, such that $\partial \mathscr{H}/\partial \sigma =0$ at that point.

We obtain that the optimal drug dosage is MTD at the terminal time moment T:

$${\sigma }^{*}(T)=\arg \underset{\sigma \in [0,1]}{\max }\left(\frac{\chi (1-x(T))}{e^{\kappa \mathrm{\Delta }E(\sigma )}+1}\right)=1,$$

At all other t < T, to define the value of σ*(t) one needs to know the exact values of both state and costate variables (x(t), ϕ(t)). Consequently, finding the optimal dosage sequences σ*(t) for all possible combinations of time lengths and initial conditions amounts to finding the characteristic trajectories to cover the entire state space (x(t), ϕ(t)). We name the collection of these trajectories the field of optimal trajectories.

(b). Primary field of optimal trajectories

To proceed further, we study the function in the brackets of (7) that is key to define the optimal regimen σ*(t). Specifically, the evolution of that function is considered along particular characteristics (τ, x(τ), ϕ(τ)), each emitted from a given terminal point x(T). If we denote the function in the brackets as ρ(σ; τ, x, ϕ), so that ${\sigma }^{*}(\tau )=\arg \underset{\sigma \in [0,1]}{\max }\rho (\sigma ;\tau ,x,\varphi )$, we first represent it by the sum of two other functions:

$$\rho (\sigma ;\tau ,x,\varphi )={\rho }_1(\sigma ;\tau ,x,\varphi )+{\rho }_2(\sigma ;\tau ,x,\varphi ),$$

where the first function:

$${\rho }_1(\sigma ;\tau ,x,\varphi )=(\varphi (b\chi x+\mu )+\chi )(1-x)/\left(e^{\kappa \mathrm{\Delta }E(\sigma )}+1\right)$$

is monotonically increasing with σ for any τ ≥ 0; and the second function:

$${\rho }_2(\sigma ;\tau ,x,\varphi )=-\overline{\mu }\varphi e^{-\kappa E^{-}(\sigma )}x$$

is monotonically decreasing with σ for any τ > 0, and exact zero at τ = 0.

As we could expect, the terminal time yields the global maximum of ρ(σ; τ = 0, x(T),0) at σ* = 1 (Fig 2A). However, at τ > 0, the function ρ₂(σ; τ, x(τ), ϕ(τ)) starts to elevate above zero, and the global maximum σ* drifts away from the extreme value σ = 1. At first, the elevation resolves in appearance of the intermediate global maximum 0 < σ* < 1 (Fig 2B), but then some trajectories ρ₂(σ; τ, x(τ), ϕ(τ)) continues going even higher, so that an abrupt switch to σ* = 0 occurs (Fig 2C). These trajectories are emitted with x(T) above some threshold $\overline{x}(x(T)>\overline{x})$. Whereas all other trajectories with $x(T)<\overline{x}$ do not exhibit such continued elevation of the function ρ₂(σ; τ, x(τ), ϕ(τ)) and the situation remains as shown in Fig 2B, so that ρ₂(σ = 0; τ, x(τ), ϕ(τ)) stays always lower than the intermediate maximum at 0 < σ* < 1. The switching points form the switching curve ${𝒮}_1$ in the space (τ, x) shown as a dashed line in Fig 3. Whereas the primary field of trajectories is shown in blue.

Fig 2: Behaviour of the function (σ; τ, x, ϕ) depending on the point within the extended phase space (τ, x, ϕ).

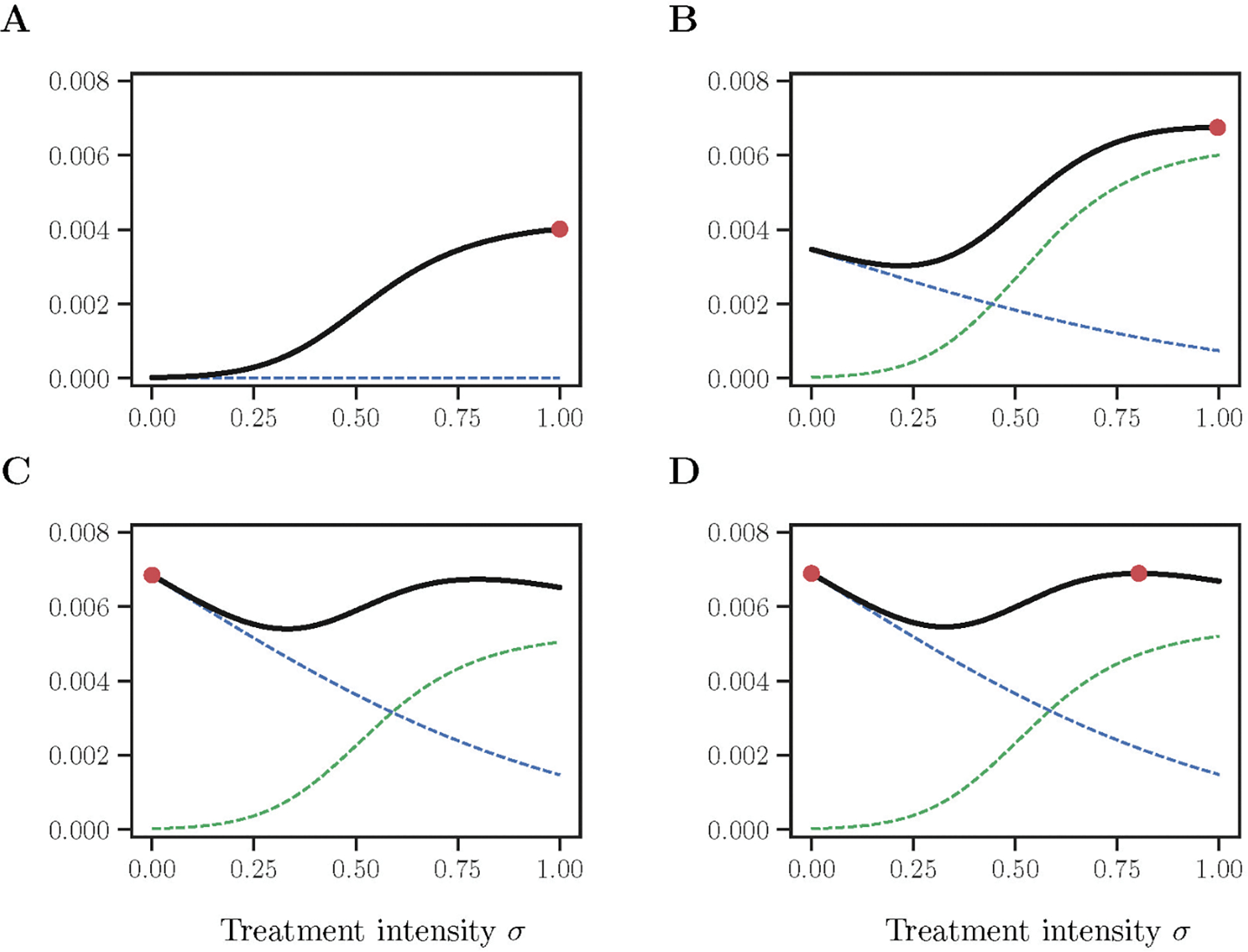
Each caption shows different states: (A) on the terminal surface with x(T) = 0.9; (B) within the primary field of optimal trajectories before the switch with τ = 3.06, x = 0.78, ϕ = −0.10; (C) within the primary field of optimal trajectories after the switch with τ = 12.6, x = 0.70, ϕ = −0.20; (D) along the singular trajectory with τ = 81.15, x = 0.62, ϕ = −0.23. The sub-functions ρ₁(σ; τ, x, ϕ) and ρ₂(σ; τ, x, ϕ) are shown in dashed green and dashed blue respectively. Red dots indicate the location of the global maxima and correspond to the optimal control σ*. Baseline parameter values are as Table 1.

Fig 3: Pattern of optimal trajectories characterized by a switching curve ${𝒮}_1$ (black dashed) and a singular trajectory ${𝒮}_2$ (black solid).

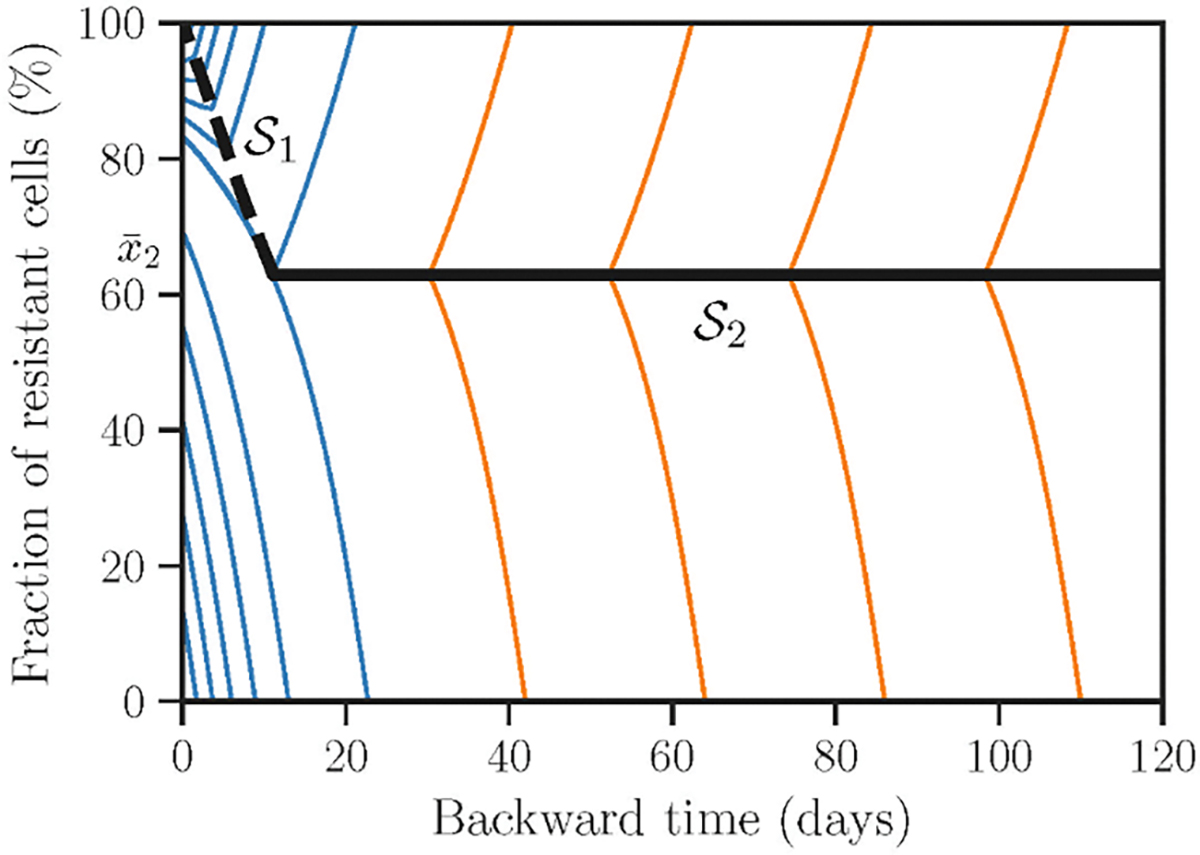
Primary field of optimal trajectories is shown in blue. Whereas, the rest of the field of optimal trajectories is shown in orange and was constructed by using the conditions on ${𝒮}_2$. The threshold $\overline{x}$ distinguishes optimal trajectories with and without a switch on ${𝒮}_1$. Baseline model parameters are as in Table 1.

(c). Construction of the singular trajectory

A part of the state space still remains uncovered by the optimal trajectories. Indeed, monotonic behaviour of x (τ), that is emitted from a terminal point slightly above the threshold $\overline{x}(x(T)=\overline{x}+\epsilon$, where ε → +0) changes from decreasing to increasing at the moment of switch on ${𝒮}_1$. In contrast, the trajectory emitted from a terminal point slightly below $\overline{x}(x(T)=\overline{x}-\epsilon )$ does not exhibit such change. As it is shown in Fig 3, the final solution consists of trajectories in orange. Their construction finalizes the solution of the optimal control problem, allowing all state space (τ, x) to be covered by optimal trajectories. Hence, our next aim is to identify the method on how to construct the trajectories in orange and a special curve ${𝒮}_2$.

To cover the whole state space with optimal trajectories, we emit a special (singular) trajectory ${𝒮}_2$ from the ending point of the switching curve ${𝒮}_1$. This represents a usual resolution admitted in optimal control theory. Such a curve is called a singular arc in the theory of linear control (Melikyan, 1998), or a universal singular characteristic in the theory of non-linear control (Melikyan and Ovseevich, 1984, 2011).

The trajectory ${𝒮}_2$ is characterized by non-smoothness of the value function, and the control σ* used along it is of the chattering type, consisting of on’n’off phases with vanishingly short time lengths. Intuitively, such curve corresponds to a situation when two local maxima of the function ρ(σ; τ, x(τ), ϕ(τ)) remain on the same level that provide two different values for σ (Fig 2D). This gives an ambiguity in the argmax.

To construct the trajectory ${𝒮}_2$, we use the method of singular characteristics (Melikyan, 1998). Specifically, we consider a so-called singular Hamiltonian that is written as follows:

$$v{\mathscr{H}}^{\text{sing}}\doteq \left\{{\mathscr{H}}_1,{\mathscr{H}}_0\right\}{\mathscr{H}}_{-1}+\left\{{\mathscr{H}}_0,{\mathscr{H}}_{-1}\right\}{\mathscr{H}}_1+\left\{{\mathscr{H}}_{-1},{\mathscr{H}}_1\right\}{\mathscr{H}}_0,$$

where three necessary conditions are held on the curve yield ${\mathscr{H}}_1=0$, ${\mathscr{H}}_0=0$, and ${\mathscr{H}}_{-1}=0$, and ν represents a scaling parameter. The curly brackets denote the Poisson brackets, e.g., for two particular Hamiltonians $ℱ\left(x,{\varphi }_0,\varphi \right)$ and $𝒢\left(x,{\varphi }_0,\varphi \right)$:

$$\{ℱ,𝒢\}\doteq \frac{\partial ℱ}{\partial x}\cdot \frac{\partial 𝒢}{\partial \varphi }-\frac{\partial ℱ}{\partial \varphi }\cdot \frac{\partial 𝒢}{\partial x}.$$

Then the singular trajectory is given by the solution of the characteristic system similar to the system of characteristics for regular trajectories but with only one difference: instead of ordinary Hamiltonian $\mathscr{H}$, we have a singular Hamiltonian ${\mathscr{H}}^{\text{sing}}$, i.e.:

$$\frac{dx(\tau )}{d\tau }=-v\frac{\partial {\mathscr{H}}^{\text{sing}}}{\partial \varphi },\frac{d\varphi (\tau )}{d\tau }=v\frac{\partial {\mathscr{H}}^{\text{sing}}}{\partial x}.$$

In our case: ${\mathscr{H}}_1\left(x,{\varphi }_0,\varphi \right)=\mathscr{H}\left(x,{\sigma }^{+},{\varphi }_0,\varphi \right)$, where σ⁺ possesses an intermediate local maximum in $\mathscr{H}\left(0<{\sigma }^{+}\le 1\right)$, ${\mathscr{H}}_0\left(x,{\varphi }_0,\varphi \right)=\mathscr{H}\left(x,0,{\varphi }_0,\varphi \right)$, and ${\mathscr{H}}_{-1}\left(x,{\varphi }_0,\varphi \right)=\left\{{\mathscr{H}}_1,{\mathscr{H}}_0\right\}$. These three conditions guarantee that there are two local maxima to determine σ* from (7): at σ = 0 and also at some 0 < σ⁺ ≤ 1, both are located at the same level of the Hamiltonian $\mathscr{H}$ (i.e. $\mathscr{H}\left(x,0,{\varphi }_0,\varphi \right)=\mathscr{H}\left(x,{\sigma }^{+},{\varphi }_0,\varphi \right)$, or equivalently with respect to function ρ as in Fig 2D).

(Melikyan and Ovseevich, 1984) sets the scaling parameter ν to the form of two: ν = γ₀ + γ₁, where ${\gamma }_0=\left\{\left\{\mathscr{H},{\mathscr{H}}_0\right\},\mathscr{H}\right\}$ and ${\gamma }_1=\left\{\left\{{\mathscr{H}}_0,\mathscr{H}\right\},{\mathscr{H}}_0\right\}$. Then the singular trajectory is given by solving the following system of two ordinary differential equations:

$$\frac{dx(\tau )}{d\tau }=-\frac{1}{{\gamma }_0+{\gamma }_1}\left({\gamma }_0\frac{\partial {\mathscr{H}}_0}{\partial x}+{\gamma }_1\frac{\partial \mathscr{H}}{\partial x}\right),\frac{d\varphi (\tau )}{d\tau }=\frac{1}{{\gamma }_0+{\gamma }_1}\left({\gamma }_0\frac{\partial {\mathscr{H}}_0}{\partial x}+{\gamma }_1\frac{\partial \mathscr{H}}{\partial x}\right),$$

complemented with boundary conditions at the end of the switching curve ${𝒮}_1$. We solved the obtained system numerically to construct the trajectory ${𝒮}_2$ shown as a solid black line in Fig 3.

At our finalizing step, we emit two other fields of trajectories: one goes above the singular curve characterized by the control σ*(τ) > 0, another one goes below the singular curve characterized by zero control σ*(τ) = 0. Fig 3 shows the resulting field of optimal trajectories covering the whole state space (τ, x). This constitutes a closed-form solution of the optimal control problem.

Last, we validate that the constructed field of optimal trajectories satisfies two conditions: (i) the consistency condition that any initial condition determines a unique optimal trajectory; (ii) the viscosity condition that applied to a solution of the HJB equation (Crandall et al., 1992). Both statements can be routinely verified. The condition (i) is obviously satisfied for our solution. The viscosity property (ii) is easily checked for any point of a regular field of characteristics and for the switching curve ${𝒮}_1$, but it requires an additional analysis for the trajectory ${𝒮}_2$. As Theorem 1 in (Melikyan and Ovseevich, 2011) states, the sufficiency conditions are consolidated in the form:

$$\begin{gathered} \left\{\left\{{\mathscr{H}}_0,\mathscr{H}\right\},{\mathscr{H}}_0\right\}<0,\left\{\left\{\mathscr{H},{\mathscr{H}}_0\right\},\mathscr{H}\right\}<0, \\ \frac{\partial \mathscr{H}}{\partial \varphi }\ne 0,\frac{\partial {\mathscr{H}}_0}{\partial \varphi }\left\{\mathscr{H},\left\{{\mathscr{H}}_0,\mathscr{H}\right\}\right\}+\frac{\partial \mathscr{H}}{\partial \varphi }\left\{\left\{{\mathscr{H}}_0,\mathscr{H}\right\},{\mathscr{H}}_0\right\}\ne 0. \end{gathered}$$

We explicitly checked their correctness for any point of the trajectory ${𝒮}_2$.

Results

We compare the outcomes of three treatment strategies in simulated data: (1) static treatments with a constant dosage over the entire episode, (2) periodic treatments with regular active phases interleaved with drug holidays, (3) treatments derived from the optimal control theory with time-varying dosage sequences. The outcome is measured by the tumour size in six months. This short time horizon is chosen because we focus on the reversible drug resistance mechanism due to cellular plasticity. At a longer time scale other irreversible mechanisms such as somatic mutations will play more important roles and are beyond the scope of our study.

1. Static treatment.

First, we report in Fig 4A the dynamics of tumour size of static treatments where the drug is administered at a constant dosage. Treatments with low intensities (e.g. σ = 0.2, green curve) yield exponential tumour growth. Treatments with intermediate or high intensities (e.g. σ ≥ 0.4, pink and brown curves) cause initial shrinkage of a tumour due to elimination of the proliferative cells but later relapse due to survival and continued growth of the remaining resistant cells.

Fig 4: Comparison of static and periodic treatments.

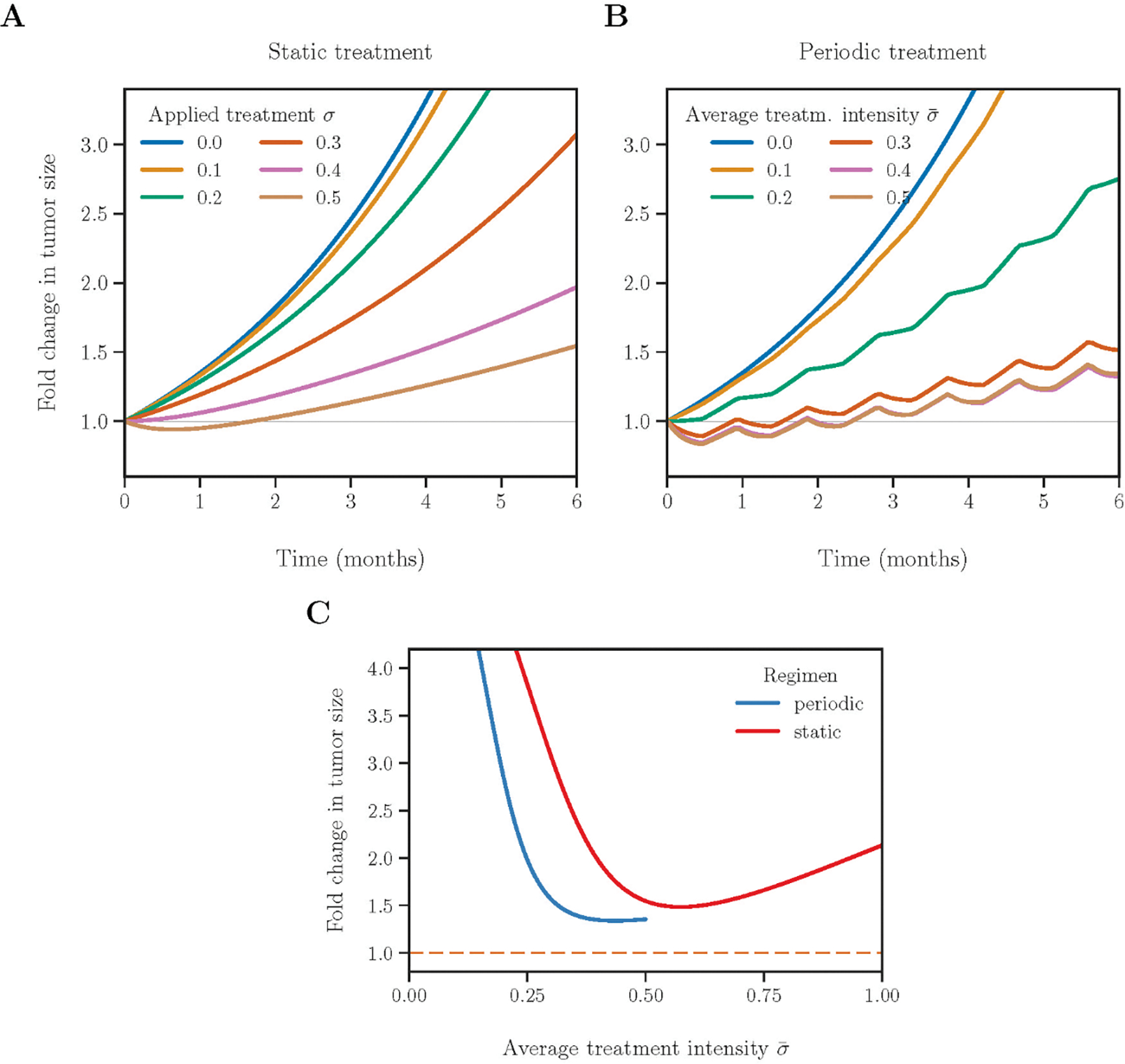
(A) Change in tumour size in two years of static treatments. Responses of treatments with six drug intensities are shown in different colours. (B) Tumour dynamics in six months of periodic treatments. Each period consists of 14 days of active phases interleaved with 14 days of drug holidays. To equalize the cumulative drug effect of the two strategies over the entire treatment duration, two treatments are comparable when the drug intensity of the periodic treatment is two-fold as that of the corresponding static treatment. Static treatments with intensities >0.5 (not shown in A) may perform better than periodic regimens due to higher cumulative drug dosage. (C) Change in tumour size after two years of treatment for static (red) and periodic (blue) regimens. The dashed orange line indicates the best outcome for the tumour management obtained by solving an optimal control problem.

To compare the outcomes of different treatment regimens, we report in Fig 4C the fold change in tumour size after six months. For static treatments with varying intensities (red curve), the best outcome is reached at an intermediate level of applied treatment intensity (1.48-fold increase at σ = 0.57). Treatment intensities higher or lower than the minimizer will lead to larger tumour sizes, yet the level of increase is highly skewed towards the left. For example, the treatment of σ = 0.1 gives a rather large 5.60-fold final increase in tumour size, while the treatment of a MTD (σ = 1.0) leads to a 2.13-fold final increase in tumour size.

Treatment outcomes can also be quantified by the time until the tumour regains its initial size. We confirm again that the optimal setting for static treatments is to apply an intermediate treatment intensity. The maximal relapse time of 2.3 months is achieved at σ = 0.64 (Fig S3A). The MTD yields a relapse time of 1.8 months, despite the fact that it reduces the tumour size by the maximal amount of 22% during the initial remission period compared to all other regimens (Fig S3B). The MTD is thus beneficial only in a short-term. The static treatment of low intensity (e.g. σ = 0.1) only slows down tumour growth and does not lead to a remission. This confirms that therapy of adequate intensity is required and beneficial. Tumour shrinkage may not predict subsequent outcomes when dynamics of heterogeneous populations are considered.

2. Periodic treatment.

Tumour relapse is driven by emergence of resistant cells. This process is reversible in our model (Fig S3C), so we may expect improvement in the therapeutic outcomes by leveraging treatment and non-treatment to create a subtle balance of proliferative and resistant cells. The simplest strategy of this kind is a periodic treatment with an equal length of active phases and drug holidays. Preliminary analysis reveals a better outcome of periodic treatments over constant treatment regimens (cf Fig 4AB).

For a fixed time horizon T, we characterize each periodic treatment by three parameters: the applied treatment intensity σ, the number of periods of active treatments K (K = 1,2, …), and the length of each period Δ. There are two scenarios in terms of the phases of the period (Fig 5A). First, the time horizon T ends with a drug holiday (T − (2K − 1)Δ > 0, terminal phase angle π ≤ θ_T < 2π), then there are K full active phases, and the average treatment intensity is given by $\overline{\sigma }=\sigma (K\mathrm{\Delta })/T$. Second, the time horizon T ends with an active phase (T − (2K − 1) Δ < 0, terminal phase angle 0 ≤ θ_T < π), then there are (K − 1) full drug holidays. The total time of drug administration is T − (K − 1) Δ, and the average treatment intensity is given by $\overline{\sigma }=\sigma (T-(K-1)\mathrm{\Delta })/T$. Consequently, the range of all possible average treatment intensities for a given K is: ${\overline{\sigma }}_K\in \left[{\overline{\sigma }}_{\min },{\overline{\sigma }}_{K,\max }\right]$, where ${\overline{\sigma }}_{\min }=\sigma /2$ (total period T consists of K full active phases and drug holidays, θ_T = 0), and ${\overline{\sigma }}_{K,\max }=\sigma K/(2K-1)$ (total period T consists of K full active phases and (K − 1) full drug holidays, θ_T = π), see Fig 5B.

Fig 5: Analysis of periodic treatments.

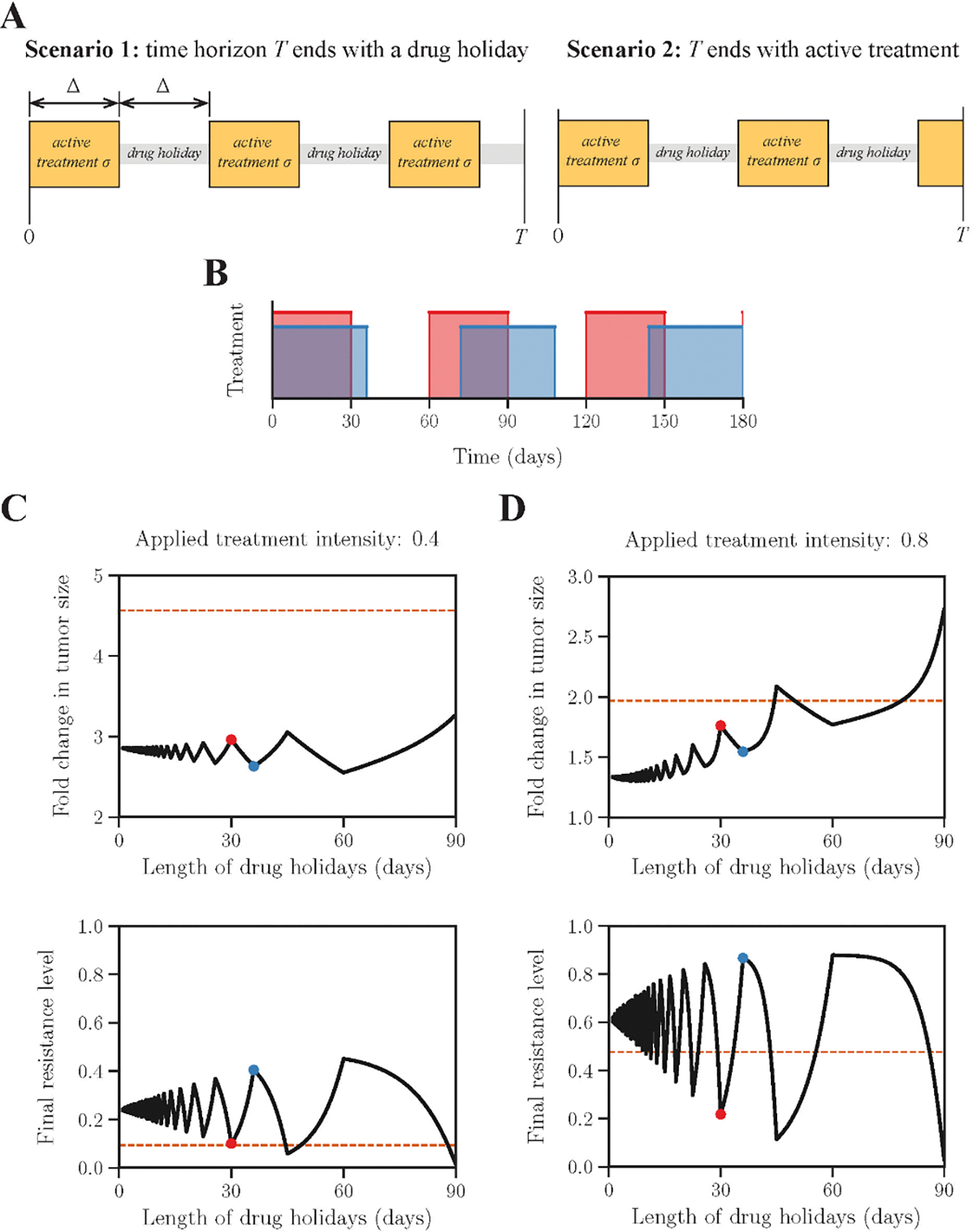
(A) Two scenarios of periodic treatment phases. Average treatment intensity equals $\overline{\sigma }=\sigma K\mathrm{\Delta }/T$ (Scenario 1), and $\overline{\sigma }=\sigma (T-(K-1)\mathrm{\Delta })/T$ (Scenario 2). K = 3 for both scenarios shown in A. (B) Two possible periodic regimens with maximal (red) and minimal (blue) numbers of drug holidays respectively. (C) and (D) shows the outcome of periodic treatments for intermediate and high treatment intensities respectively. Horizontal axes indicate the length of drug holidays per period. Vertical axes indicate the fold change of tumour size after six months. The outcomes of the equivalent static treatments (applied treatment $\overline{\sigma }/2$) are shown as dashed orange lines. Blue and red dots in panels C and D correspond to two periodic schedules shown in panel B.

To assess the influence of treatment schedules on final outcomes, we fix the average dosage intensity and compare tumour size changes in six months with varying period lengths Δ. Dosages of all periodic treatments are adjusted to equalize their cumulative dosages. We first consider treatments of a relatively low intensity σ = 0.4 (Fig 5C). The local maxima of the tumour size are achieved with the terminal phase angle θ_T = 0 (e.g., the red dot in Fig 5CD and the red waveform in Fig 5B). In contrast, the schedules with the terminal phase angle θ_T = π (e.g., the blue dot in Fig 5CD and the blue waveform in Fig 5B) yield the local minima in tumour size. All treatment schedules under σ = 0.4 lead to a low terminal level of resistance (Fig 5C bottom panel), indicating they are incapable of eliminating the proliferative (sensitive) part of the tumour.

We further find the values of σ and Δ that jointly optimize the treatment outcome (Fig S4A). Low treatment intensities with σ < 0.4 are incapable of controlling tumour growth regardless of treatment schedules. The gradient along Δ is drastically heightened around σ = 0.6. The global minimum of the tumour size change 1.30 is reached at σ = 0.88 and Δ = 4 days (the red star in Fig S4A and S4B).

Another free parameter of periodic treatments is the duty cycle a (length of the active phase of one cycle / length of one cycle). We fix the length of each treatment period to Δ_c = 2 ⋅ Δ = 8 days and vary a and σ (Fig S5C). Fig S5 indicates the best outcome is achieved at approximately the same treatment as before: a = 0.57, σ = 0.82, and the fold increase is 1.30 compared to 1.48 for static treatment.

3. Optimal treatment.

Both static and periodic treatments are straightforward to implement but often not optimal in terms of the outcome. Here we define optimality as minimizing the tumour size at a fixed terminal time (or time horizon) T. To solve this problem, we apply optimal control theory to update treatment intensities at each moment depending on the tumour state (tumour size and level of resistance). This requires a constant monitoring of the patient, see (Fischer et al., 2015) for discussion. In brief, treatment design is translated into the problem of controlling the temporal function of treatment intensity σ(t) to minimize the log ratio of final to initial tumour sizes ln(n(T)/n(0)), subjected to the tumour population dynamics (equations 5–6). Solution of the optimal control problem is obtained in a closed form based on the method of generalized characteristics (Melikyan, 1998; Melikyan and Ovseevich, 1984, 2011), see Methods section.

The optimal σ(t) is determined by both the initial proportion of resistant cells and the length of the time horizon. Fig 6 illustrates optimal trajectories of three initial conditions. (i) The time horizon T is shorter than a threshold: T = T₋ < T₀, and initially the proportion of resistant cells is zero. The optimal treatment applies a dosage close to MTD for the whole period. Proportion of resistance cells increases over time and reaches a level of about 70% for given baseline parameters at the terminal point. (ii) T is longer than the same threshold: T = T₊ > T₀, and initially the proportion of resistant cells is zero. The optimal treatment comprises three stages. It starts with a high intensity close MTD for about one month, then sharply lowers the dose to a moderate level till about one month before the terminal point, and finally resumes the high dosage till the end. Proportion of resistance cells climbs up and reaches about 70% in the first stage, maintains at this level in the second stage, and further increases again in the third stage. (iii) T is the same as (ii) and initially the proportion of resistant cells is one. The optimal treatment also consists of three stages. In the first stage the drug is not administered. Proportion of resistant cells thus decreases to 70%. Treatment intensities and resistance trajectories in the second and third stages coincide with (ii). Importantly, a dose-sparing regimen in the middle of (ii) and (iii) concurs with the periodic treatment in its efficiency by keeping the balance between sensitive and resistant parts of the tumour. This prepares the patient for the final stage of the treatment when the sensitive part of the tumour is eradicated with greater efficiency. Overall, optimal treatments aim for establishing and maintaining a fixed balance between proliferative and resistant cells as long as possible until near the terminal point, and then switch to the maximal dosage throughout the remaining time to eradicate as many proliferative cells as possible (curves (ii) and (iii) in Fig 6; Fig 7B). Yet when the time horizon is short, the long-term benefit of a balanced population is no longer relevant, and the optimal treatment is to reduce the current tumour size by administering the maximal dosage (curve (i) in Fig 6; Fig 7B). The clinically relevant time horizon may depend on other factors such as the emergence of genetically distinct subclones with different properties. However, the adoption of longer time horizons based on already calculated shorter periods would require only partial recalculation of the treatment schedule (Fig S6). We varied time horizons from one to forty months and demonstrated that the final tumour size under the OCT treatment could reach 20-fold enlargement in 40 months (Fig S6B). In a more realistic range, the final tumour size reached 1.5-fold enlargement for the time horizon of 8 months (Fig S6A). Equivalently, the OCT treatment strategy can control the tumour size within 1.5-fold of the initial size in 8 months.

Fig 6: Optimal treatment intensity is determined by the current level of resistance and the total time span of treatment.

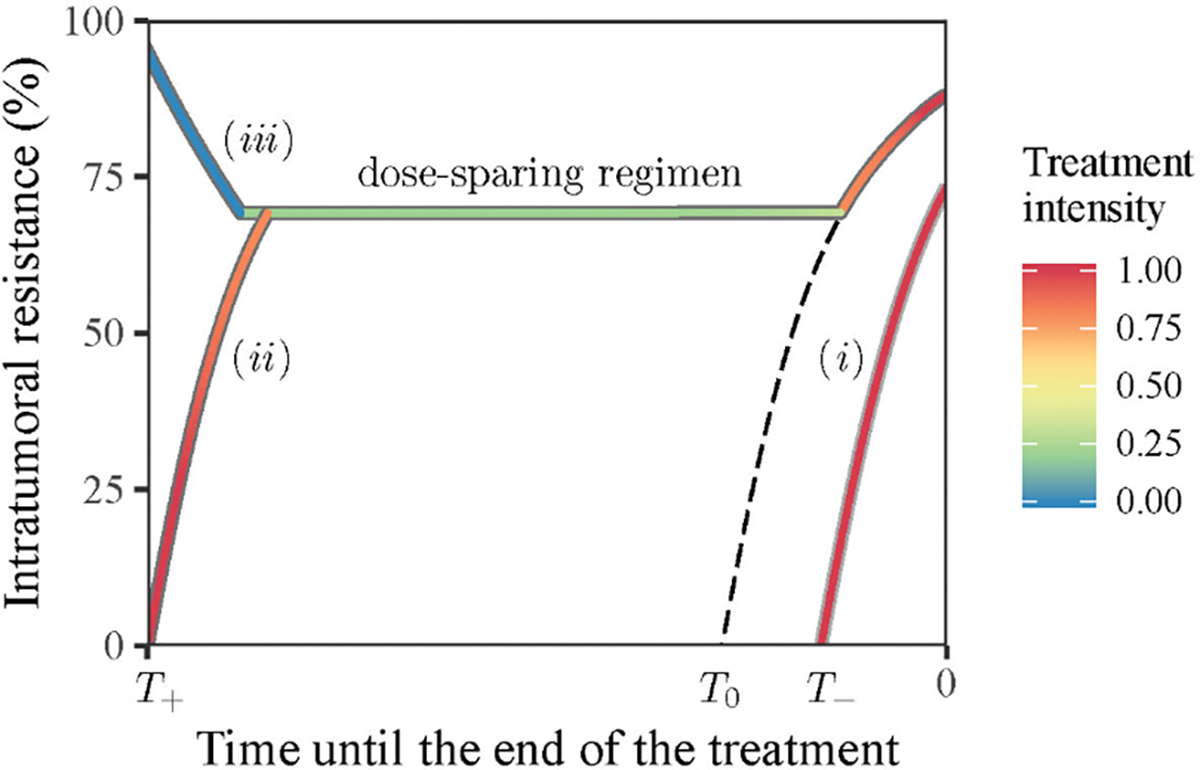
The temporal axis marks the direction from the start of a treatment (a positive number) to the terminal point of treatment. The threshold value 𝑇₀ separates the trajectories with and without a dose-sparing regimen whose trajectory is marked by the dashed line. Trajectories of three regimens are illustrated (see description in the text). Trajectory colours indicate the applied treatment intensity (legend).

Fig 7: Comparison of three different treatment schedules in terms of fold-change in tumour size (A) and dynamics of intratumoral resistance (B).

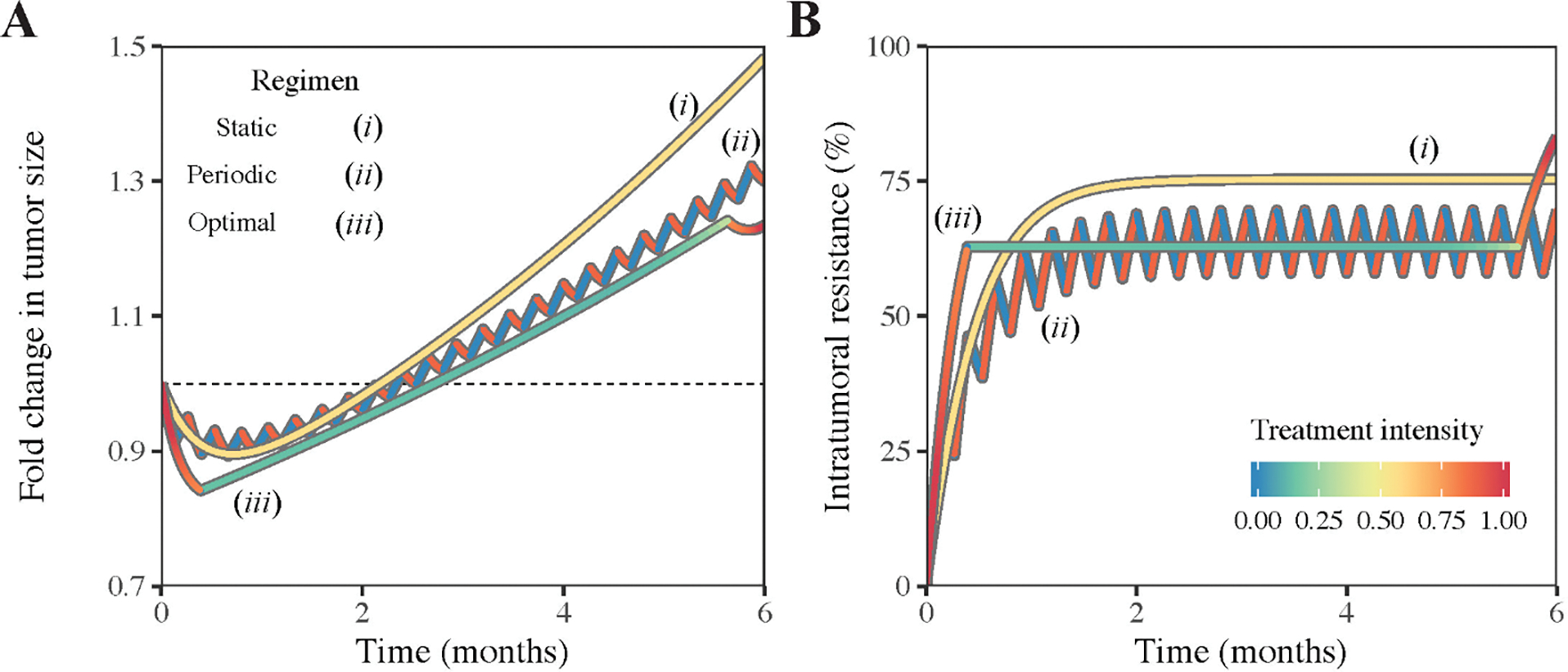
The dashed horizon indicates the fold-change equal to one. Line colours indicate the applied treatment intensity.

4. Comparison of different treatments.

The performances of the three aforementioned treatment strategies conform with the following order: the best static treatment ≤ the best periodic treatment ≤ the optimal treatment. Superiority of periodic over static treatments is illustrated in Fig 4. The treatment derived from the optimal control theory is superior to all dynamic treatments including periodic treatments. To quantitatively compare their performances, we fix the time horizon to six months, set the best static treatment intensity to σ = 0.57, the best periodic treatment intensity to σ = 0.88 and period to 4 days according to Fig S4A, and find the optimal dynamic treatment by solving the optimal control problem. Fig 7 shows the comparison outcomes of those three treatments. The terminal tumour sizes (relative the initial tumour size) are consistent with the aforementioned order. The static treatment yields a relatively poor outcome (1.48-fold increase of tumour size after six months). The periodic treatment gives a better result (1.30-fold increase after six months), which is just marginally inferior to the minimally achievable estimate obtained from the optimal treatment (1.24-fold change after six months). The optimal treatment provides a balance between the sensitive and resistant cells and allows more efficient reduction of the tumour size at the final stage. The population composition trajectories of the three treatments are shown in Fig 7B. Proportion of resistant cells steadily increases to a fixed value and maintains onward in the static treatment due to the constant administration of the drug. Proportion of resistant cells in the periodic treatment rises rapidly at an initial transient stage and oscillates around a fixed value, synchronous with the period of the treatment. Proportion of resistant cells in the optimal treatment sharply reaches a fixed level, remains invariant most of the time, and suddenly increases in the last stage.

5. Sensitivity analysis.

The baseline parameter values in the model (Table 1) are not guaranteed to be accurate and unique. To investigate the influence of parameter values in optimal treatment outcomes, we assess the fold change in tumour size after six months by varying parameter values. Fig 8A shows the effect of variation in characteristic switching times between the main and alternative pathways with the relative cost of resistance c_relative = 10%. The tumour does not shrink if the inverse switch from the alternative to the main pathway is slower than the direct switch from the main to the alternative pathway (the red-yellow region above the solid black line), while remission can be achieved if the reciprocal relation between the two switching times holds (the blue region below the solid black line). However, the result depends on the cost of resistance: a higher cost induces slower proliferation of resistant cells and thus accommodates a wider range of switching times leading to tumour reduction (Fig 8C), while a lower cost has the opposite effect (Fig 8B). We further investigate how the optimal proportion of resistant and sensitive cells depends on aforementioned parameters (Fig S7). The optimal proportion of resistant cells is positively correlated with $1/\overline{\mu }$ (Fig S7B) and negatively correlated with 1/μ (Fig S7A). We also notice that the optimal proportion is below 50% only when μ is approximately four times slower than $\overline{\mu }$ (area below dashed line in Fig S7C). Fig S8 shows the variation of tumour size with respect to other model parameters.

Fig 8: Sensitivity of tumour size after six months of optimally designed treatment.

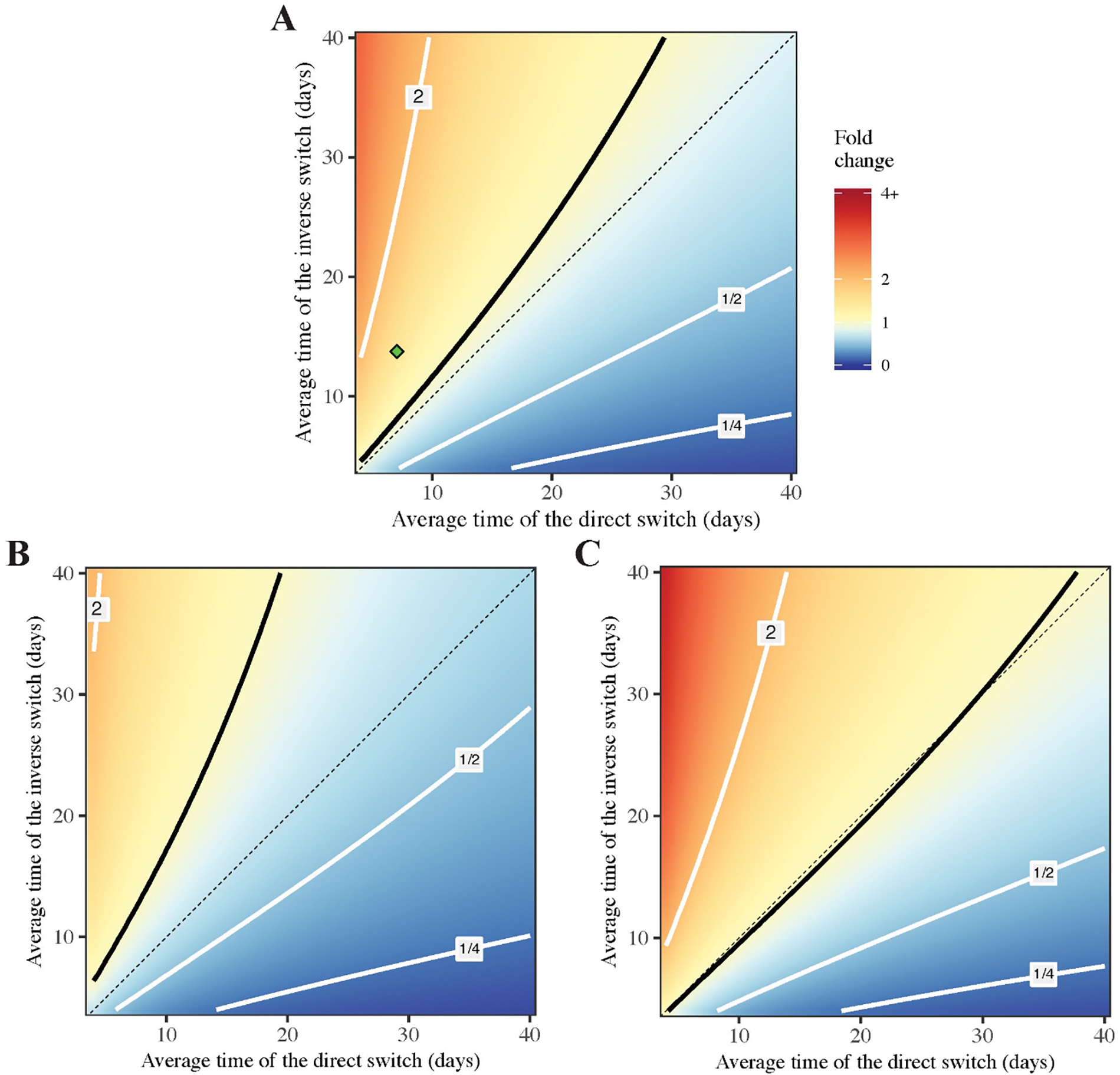
The varied parameters are characteristic switching times 1/μ and $1/\overline{\mu }$ (horizontal and vertical axis respectively). Three panels refer to different values of relative resistance cost: 10% (baseline, A), 5% (B), 40% (C). Other parameters are fixed according to Table 1. The contour line for the fold change equal to one is indicated by solid black, three other contours are shown in grey and correspond to the fold change in the panel to each line. Diagonal for $\mu =\overline{\mu }$ is shown in dashed black. The location of the baseline parameters is indicated by the green point in A.

Discussion

Treatments determined from optimal control theory are superior to static and periodic treatments. The increase in tumour size after six months of optimal, periodic, and static treatment is 1.24, 1.30, and 1.48, respectively. While the relative improvement with periodic treatment is small in this instance, the principle is clear. Further, this approach for reversible resistance may be synergistic when combined with consideration of irreversible genetic resistance in a multi-level model. Efficacy of periodic treatments was discussed in prior studies (Fischer et al., 2015; Foo and Michor, 2009). Drug addiction is one possible cause (Das Thakur et al., 2013): resistant subclones not only tolerate the administered drug but also depend on it. Drug holidays in these cases deplete the “nutrient” supply and reduce the resistant subclone population. Gatenby et al. (Gatenby et al., 2009) considered a more general “adaptive therapy” as a means to maintain proper balance of genetically distinct sensitive and resistant subclone populations undergoing competition. Our simulation outcomes corroborate the superiority of periodic treatments and concur with the prior discussions about their benefits, albeit the proposed mechanisms causing the benefits are different. Those mechanisms may co-exist and can be all tackled by periodic treatments, at least in the setting of a single therapy as modelled here. In spite of a good approximation to the global optimum and simplicity of implementation, the best periodic treatment is still marginally inferior to the optimal treatment strategy. In principle, one should always adopt the treatment strategy that yields the best outcome. In practice, physicians have to consider multiple factors when deciding the treatment, including cost-effectiveness, the higher risk of medical errors when implementing complex recommendations, and the feasibility of repeated tumour sampling or liquid biopsy to provide accurate input data to correctly design and execute an optimal control algorithm. Both periodic and optimal treatments likely require substantial modifications of current clinical practice. In clinical studies the treatment aborts when there is a 20% increase in the sum of the longest linear dimension of large measurable lesions, corresponding to a 73% increase in volume (Eisenhauer et al., 2009). Such a practice does not allow for periodic treatments. Also, the optimal treatment in our model requires continuous monitoring of the tumour population composition. If such monitoring is either costly or infeasible, then a properly designed periodic treatment is a reasonable surrogate for the optimal treatment. Dynamic treatments of cancer require biomarkers for functional states that can be continuously and non-invasively monitored. This may be a greater challenge for complex gene expression changes and their associated physiological changes than it is for mutations for which highly sensitive polymerase chain reaction techniques are available.

Intriguingly, the best treatment plans of all three strategies attempt to establish and maintain an optimal proportion of sensitive and resistant cells (fraction of sensitive cells is about 70% in our simulations) throughout the entire period (Fig 7B). The best static treatment drives the population toward a value above such optimal composition. The best periodic treatment quickly leads the population to the optimal composition and then makes it oscillate around this value. The global optimal treatment quickly forces the population toward the optimal composition, alters the dosage to maintain it, and finally maximizes the dosage for final most efficient curbing of the tumour at the very end. The outcome of a treatment strategy seems to depend critically on its controllability to reach this composition as quickly as possible and stay there as long as possible. In this sense, the static treatment is a poor controller, because it cannot reach that target. Both periodic and optimal treatments are good controllers as they quickly reach the target value and maintain it onward. Curiously, while the total population under the best periodic treatment increases with small ripples, the total population under the optimal treatment steadily grows and finally plunges to a much lower value (Fig 7A). This is because the higher growth rate allowed by the optimal treatment leads to a more optimal balance of sensitive and resistant cells for efficient final curbing of the tumour. This also identifies a possible hurdle in implementing an optimal treatment regimen into clinical practice because its performance at the initial state is even worse than that of a static treatment, and this is likely to result in earlier termination of the therapy per current paradigms (Fig 7A). Nevertheless, despite its implementation difficulty the optimal treatment may serve as a high-end benchmark and a yardstick to assess the performance of other suboptimal treatments such as periodic or adaptive regimens. Since the optimal treatment gives a theoretical upper bound for all possible treatment outcomes, by comparing the performance of a realistic (yet suboptimal) treatment strategy with this benchmark we can assess its efficacy and margin for improvement.

Estimation of most parameters in the model such as the characteristic time of switching between two genetic programs is still subjected to uncertainty. Despite the impressive progress, recent studies (Shaffer et al., 2017; Tirosh et al., 2016) indicated that the technology of single-cell transcriptomics still does not allow rigorous measurements of the kinetic shifts of sensitive and resistant cells due to epigenetic reprogramming. Laboratory studies in cell lines may not reflect net growth rates of tumours in vivo (cf reported proliferation rates in (Sun et al., 2014) and (Bozic et al., 2013)). Therefore, any model-based approach for cancer treatments has to take parameter uncertainty and imprecision into account. Sensitivity analysis – such as Fig 8 and Figs S7, S8 in our study – can help assessing the robustness of treatment outcomes with respect to fluctuations of parameter values.

We assume that cancer cells reprogram themselves to resist treatments by both altering their pathway activities at a shorter time scale and shifting their physiology at a longer time scale (Taylor–King et al., 2018). This model is consistent with a recent study (Shaffer et al., 2017) about a special “meta-resistant state” that becomes reversible upon changes of the tumour environment. By integrating with our prior work concerning irreversible genetic processes of drug resistance (Beckman et al., 2012; Yeang and Beckman, 2016), we plan to build a relatively complete model capturing both reversible and irreversible processes and design the treatment strategies accordingly. Outgrowth of rare subclonal resistance mutations or acquisition of new resistance mutation may occur at a longer time scale than the phenomena discussed herein. Further extensions of the model would be desirable in principle, such as incorporating the activities of the major cancer pathways in the cellular internal states, expanding the drugs and treatment options, and including molecular-level resistance mechanisms. However, such extensions will also substantially increase the model complexity and data requirements, a particular problem for clinical translation. A principled method to balance the required features of the model and their associated data requirements, as well as specific methods for dealing with uncertainty and incomplete information, remain critical tasks.

Highlights.

• Tumour growth model with reversible (non-genetic) mechanism of resistance is developed

• Melanoma response to the treatment of a single (BRAF) inhibitor is chosen for a basal model system

• Optimal control theory is applied to construct treatment regimen minimizing a tumour size at given time horizon

• Other treatment regimens such as with constant drug dosage, periodic with intermittent drug holidays are optimized and compared with the optimal treatment