Abstract
Amphibian populations are undergoing a global decline worldwide. Such decline has been attributed to their unique physiology, ecology, and exposure to multiple stressors including chemicals, temperature, and biological hazards such as fungi of the Batrachochytrium genus, viruses such as Ranavirus, and habitat reduction. There are limited toxicity data for chemicals available for amphibians and few quantitative structure-activity relationships (QSAR) have been developed and presently available. Such QSARs provide important tools to assess the toxicity of chemicals particularly in a data poor context. QSARs provide important tools to assess the toxicity of chemicals particularly when no toxicological data are available. This manuscript provides a description and validation of a regression-based QSAR model to predict, in a quantitative manner, acute lethal toxicity of aromatic chemicals in tadpoles of the Japanese brown frog (Rana Japonica). QSAR models for acute median lethal concentrations (LC50–12 hours) using the Monte Carlo method were developed. The statistical characteristics of the QSARs were described as average values obtained from five random distributions into training and validation sets. Predictions from the model gave satisfactory results for both the training set (R2 = 0.661 and RMSE = 0.368) and were even more robust for the validation set (R2 = 0.965 and RMSE = 0.110). Further development of QSAR models in amphibians, particularly for other life stages and species, are discussed.
Keywords: acute toxicity, Rana Japonica tadpole, QSAR, Monte Carlo method, Index of ideality of correlation
1. Introduction
I’m not a diva. I’m a tadpole trying to be a frog. Toni Braxton
The vertebrate class Amphibia, with over 8,420 species, constitutes an important taxonomical group for which all modern amphibians belong to the subclass Lissamphibia. They are divided into three orders: Anura (frogs, toads, and relatives) with over 7,440 species from 58 families, Caudata (salamanders, newts, and relatives) with over 770 species from 9 families and Gymnophiona (caecilians and relatives) with over 210 species from 10 families (Frost, 2021). Currently, Amphibian populations are undergoing a global decline in numbers and, over the last five decades, hundreds of species have gone extinct. Such decline has been attributed to their unique physiology, ecology, and exposure to multiple stressors including chemicals, temperature, biological hazards such as fungi of the Batrachochytrium genus, viruses such as Ranavirus, and habitat reduction (e.g. Wilson and Famini, 1991; Wang et al., 2001; Huang et al., 2003a,b; Roy and Ghosh, 2006; Wang et al., 2019a; Wang et al., 2019b).
Ecotoxicological studies in amphibian species investigating chemical toxicity for substances such as plant protection products and environmental contaminants are still limited since historically more focus has been given to aquatic vertebrates such as fish test species (e.g., rainbow trout, zebrafish) (EFSA PPR, 2018). Data gaps include to the lack of experimental data for different life stages of amphibians as well as lack of regulatory legislation requiring environmental risk assessment (ERA) of chemicals in amphibians. European directives for industrial chemicals and plant protection products require data on aquatic organisms such as insects, fish, daphnia and algae, but not amphibians. However, the European Food Safety Authority (EFSA) has recently published a scientific opinion on the state of the science on pesticide ERA for amphibians and reptiles to provide a scientific rationale addressing their sensitivity to pesticides, data gaps and to formulate recommendations to further support the inclusion of these taxa in ERA (EFSA PPR, 2018).
In addition, since amphibians have different life stages (i.e., egg, embryo, tadpole, juvenile, and adult), an aquatic phase, and a terrestrial phase; understanding chemical toxicity requires testing such different life stages and consequently considerable economic and experimental efforts. Due to the limited availability of experimental toxicity data in amphibians and the currently limited requirements to address such taxa as ecotoxicological targets, an initial option is to move towards the use of New Approach Methodologies (NAMs) as it has been applied recently to non-target species such as honey bees and collembola (Carnesecchi et al., 2020; Lavado et al., 2021). NAMs include in silico models such as quantitative structure-activity relationship (QSAR) models and provide an effective way to predict chemical and toxicological properties based on structural properties of the chemical (ECHA, 2016). The development of QSAR models for tadpoles may be particularly relevant since they are fully aquatic and may be exposed to a range of chemicals throughout their developmental stages making them potentially sensitive as they undergo metamorphosis. However, fewQSARs have been published for frog tadpoles, since experimental values are still rather limited, and have been mostly focused on the prediction of acute toxicity for benzene derivatives in Rana Japonica, a limited number of alcohol compounds in Rana temporaria, R. chensinensis, and for undescribed species (Agrawal et al., 2003; Huang et al., 2004; Jaiswal and Khadikar, 2004; Sahoo et al., 2016; Adhikari and Mishra, 2018; Wang et al., 2019a; Wang et al., 2019b; Wang et al., 2020).
The aim of the present study is to develop a regression-based QSAR model to predict acute toxicity of aromatic chemicals in tadpoles of the Japanese brown frog (Rana japonica) using available acute toxicity data and the CORAL software (http://www.insilico.eu/coral). It represents the largest database on available experimental values available in this species. The relevance of this tool for hazard and risk assessment of chemicals and recommendations for future work in this area are discussed to further address chemical toxicity in amphibians.
2. Method
2.1. Database on the acute toxicity of chemicals in Rana Japonica tadpoles
Available databases reporting ecotoxicological data on acute median lethal molar concentration in tadpoles of Rana japonica were searched for including the Ortiz-Santaliestra et al. (2017) toxicological database on amphibians and reptiles and the US-EPA ECOTOX knowledgebase database, as well as the peer-reviewed literature (Huang et al., 2003a; Wang et al., 2001).
Available compounds in the curated database were distributed into five random splits for four specific subsets from which the last set is used for validation. In contrast, the remaining three sets are used to build the model and optimise parameters. The full procedure which has been shown to provide robust results has been described in detail elsewhere (Toropov et al., 2019, 2020a):
Active training set (≈25%) applied for the development of the model and thegeneration of so-called correlation weights. Correlation weights are then used to calculate 2D optimal descriptors for all compounds involved in the modelling process.
Passive training set (≈25%) applied to assess the model robustness for compounds that are independent from those used to build the model. This set is used to assess the improvement of the modelling process in the learning phase.
Calibration set (≈25%) applied to identify when the process of learning reaches it maximum value allowing to extract the general model components providing robust results and identify suitable associated correlation coefficients while reducing the risk of of overfitting.
Validation set (≈25%) providing an independent assessment of the statistical quality of the model using data for substances which were not included in model development and optimisation (Toropov et al., 2017, 2020b; Toropova and Toropov, 2019).
Distributions from the active, passive and calibration sets and the validation set support the assessment of the prediction capacity of a QSAR model (Puzyn et al., 2011). In addition, the Kennard-Stone algorithm (Kennard and Stone, 1969; Morais et al., 2019), duplex algorithm (Snee, 1977), and the response-based division algorithm (Puzyn et al., 2011) provide practical tools to split available data into training and validation sets. In our case, a random distribution was used to split substances, and the non-identity of the splits was assessed.
2.2. Optimal SMILES-based descriptor
The structures associated with the chemicals being modelled in this work using the CORAL models are represented by the simplified molecular input line entry system (SMILES) (Weininger, 1988). The CORAL model is the one-variable correlation between the SMILES-based 2D descriptor and the acute toxicity endpoint (pLC50), according to Equation 1:
| (1) |
DCW (Descriptor of Correlation Weights) is a function of the molecular architecture expressed via SMILES, as in Equation 2:
| (2) |
Sk is a SMILES atom, i.e. one symbol (e.g. ‘C’, ‘c’, ‘N’, ‘O’, etc.) or a group of symbols which cannot be examined separately (e.g. ‘Cl’, ‘Br’, etc.). CW(Sk) is the correlation weight of the Sk, i.e. a coefficient which is combined to the value of the descriptor if the corresponding SMILES contains the Sk. The numerical data on the correlation weights are obtained from the Monte Carlo optimisation carried out with the so-called Index of Ideality of Correlation (IIC), i.e. a special component of the target function described in the literature (Toropov and Toropova, 2017; Toropova and Toropov, 2017). The SMILES represent a harmonised format to describe substances for a wide range of in silico models, and the structure itself provides a means to calculate molecular descriptors. However, in the case of the CORAL models, SMILES are used directly to extract the information related to the presence of certain encoded molecular features. Such features are represented by atoms, molecular groups, branched structure, presence of rings, and other classical chemical characteristics and have been successfully applied to predict a range of physicochemical and toxicological properties (Toropov and Toropova, 2017; Toropova and Toropov, 2017).
3. Results and Discussion
3.1. Database on acute toxicity of chemicals in Rana japonica tadpoles
Available experimental data were reported and extracted as acute lethal concentrations for 50% of Rana japonica tadpoles in [mol/L], i.e., negative logarithm of the acute median lethal molar concentrations after 12 h, expressed as 12 h log1/LC50, (pLC50) (Huang et al., 2003a; Wang et al., 2001). The analysis of duplicates confirmed that the same endpoint has been analysed in all available papers and duplicates were excluded from the final database (Supplementary Materials) on acute lethal toxicity data for 58 organic compounds (Table S1). Confirmation of the non-identity of the splits generated is listed in Table S2. Finally, Tables S3-S7 highlights the five splits, with SMILES, experimental and predicted values as well as information regarding the applicability domain of the model and its relevance for each substance.
3.2. QSAR model for predicting acute toxicity of chemicals in Rana japonica tadpoles
The Monte Carlo optimisation with and without IIC resulted in different models. Table 1 provides the statistical characteristics of the above-mentioned models and the comparison of the data shows that the IIC-based optimisation resulted in models with improved statistical quality R2 (correlation coefficient) and RMSE (root mean squared error expressed by R2 ) and particularly while considering the results from the validation set.
Table 1.
Statistical characteristics of the QSAR model using five random splits
| Split | Set | n | R2 | CCC | IIC | Q2 | Q2F1 | Q2F2 | Q2F3 | <Rm2> | RMSE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimisation without IIC | |||||||||||
| 1 | A* | 14 | 0.807 | 0.893 | 0.499 | 0.721 | 0.284 | ||||
| P | 15 | 0.810 | 0.891 | 0.594 | 0.748 | 0.335 | |||||
| C | 15 | 0.171 | 0.318 | 0.225 | 0.0 | 0.0 | 0.0 | 0.224 | 0.071 | 0.612 | |
| V | 14 | 0.822 | 0.495 | ||||||||
| 2 | A | 14 | 0.753 | 0.859 | 0.651 | 0.673 | 0.349 | ||||
| P | 15 | 0.902 | 0.722 | 0.397 | 0.876 | 0.577 | |||||
| C | 15 | 0.754 | 0.574 | 0.160 | 0.641 | 0.108 | 0.0 | 0.756 | 0.569 | 0.384 | |
| V | 14 | 0.558 | 0.308 | ||||||||
| 3 | A | 15 | 0.699 | 0.823 | 0.558 | 0.595 | 0.443 | ||||
| P | 14 | 0.736 | 0.844 | 0.748 | 0.662 | 0.325 | |||||
| C | 15 | 0.816 | 0.874 | 0.4688 | 0.759 | 0.759 | 0.7491 | 0.880 | 0.738 | 0.250 | |
| V | 14 | 0.583 | 0.366 | ||||||||
| 4 | A | 15 | 0.928 | 0.9629 | 0.843 | 0.902 | 0.166 | ||||
| P | 15 | 0.708 | 0.838 | 0.688 | 0.609 | 0.432 | |||||
| C | 14 | 0.833 | 0.899 | 0.568 | 0.770 | 0.773 | 0.7733 | 0.871 | 0.736 | 0.247 | |
| V | 14 | 0.709 | 0.356 | ||||||||
| 5 | A | 14 | 0.8544 | 0.922 | 0.693 | 0.822 | 0.246 | ||||
| P | 14 | 0.8145 | 0.867 | 0.5477 | 0.741 | 0.358 | |||||
| C | 15 | 0.5607 | 0.732 | 0.3723 | 0.368 | 0.381 | 0.365 | 0.688 | 0.417 | 0.401 | |
| V | 15 | 0.5971 | 0.346 | ||||||||
| Optimisation with IIC (Eq. 3 – Eq.7). | |||||||||||
| 1 | A* | 14 | 0.603 | 0.753 | 0.777 | 0.476 | 0.407 | ||||
| P | 15 | 0.458 | 0.671 | 0.578 | 0.278 | 0.566 | |||||
| C | 15 | 0.942 | 0.967 | 0.967 | 0.923 | 0.933 | 0.928 | 0.961 | 0.860 | 0.136 | |
| V | 14 | 0.876 | 0.215 | ||||||||
| 2 | A | 14 | 0.586 | 0.739 | 0.765 | 0.462 | 0.453 | ||||
| P | 15 | 0.839 | 0.893 | 0.474 | 0.805 | 0.379 | |||||
| C | 15 | 0.789 | 0.840 | 0.888 | 0.744 | 0.772 | 0.545 | 0.938 | 0.567 | 0.194 | |
| V | 14 | 0.869 | 0.177 | ||||||||
| 3 | A | 15 | 0.667 | 0.800 | 0.715 | 0.564 | 0.466 | ||||
| P | 14 | 0.709 | 0.840 | 0.557 | 0.636 | 0.327 | |||||
| C | 15 | 0.925 | 0.932 | 0.902 | 0.900 | 0.826 | 0.819 | 0.913 | 0.693 | 0.212 | |
| V | 14 | 0.962 | 0.140 | ||||||||
| 4 | A | 15 | 0.623 | 0.767 | 0.690 | 0.528 | 0.381 | ||||
| P | 15 | 0.573 | 0.749 | 0.572 | 0.456 | 0.511 | |||||
| C | 14 | 0.969 | 0.981 | 0.981 | 0.9554 | 0.965 | 0.965 | 0.980 | 0.900 | 0.097 | |
| V | 14 | 0.965 | 0.110 | ||||||||
| 5 | A | 14 | 0.656 | 0.792 | 0.607 | 0.559 | 0.378 | ||||
| P | 14 | 0.624 | 0.699 | 0.337 | 0.426 | 0.502 | |||||
| C | 15 | 0.885 | 0.900 | 0.938 | 0.827 | 0.832 | 0.828 | 0.915 | 0.734 | 0.209 | |
| V | 15 | 0.918 | 0.178 | ||||||||
A = active training set; P = passive training set; C = calibration set; V = validation set; n = number of compounds in each set; R2 = correlation coefficient; RMSE = root mean squared error; Q2 = cross validated R2; CCC = concordance correlation coefficient (Lin, 1992); IIC = index of ideality of correlation (Toropov and Toropova, 2017); Q2F1; Q2F2; Q2F3 (Chirico and Gramatica, 2011); <Rm2> (Roy and Kar, 2014) are criteria of the predictive potential suggested in the literature.
The QSAR models for the prediction of acute toxicity in tadpoles of the Japanese brown frog (Rana Japonica) (pLC50, mol/L) obtained for the five random splits via the IIC-optimisation are the following:
Split 1
| (3) |
Split 2
| (4) |
Split 3
| (5) |
Split 4
| (6) |
Split 5
| (7) |
Table 1 provides a comparison of the prediction results from the QSAR models using optimisation without the IIC and models using optimisation with the IIC.
The resulting QSAR model using optimisation with the IIC provided satisfactory predictions for the validation and training sets compared to the model using optimisation without the IIC considering the R2 on all 58 compounds. However, predictions obtained from the active and passive training sets were slightly less satisfactory (Toropov and Toropova, 2017; Toropova and Toropov, 2017; Toropov et al., 2020; Toropova et al., 2020). The use of optimisation with the IIC is judicious particularly to develop a QSAR model which is not affected by overtraining and is able to predict acute toxicity for substances with no available data. In this way, the model extracts the general components of the algorithm, disregarding those which are closely linked to the training set. The use of multiple sets (active training, passive training, calibration) within the IIC strategy is functional here and establishes a dialogue and feed-back loops between the results from the different sets. Finally, the system filters the SMILES attributes with a higher probability to generate a generic model with a broader applicability domain.
Considering the average values for the determination coefficient on the validation sets together with corresponding dispersion provides a measure of uncertainty that supports an assessment of predictions’ robustness. In the case of the Monte Carlo optimisation without IIC, the average value of the determination coefficient is 0.65 with dispersion 0.10 in contrast to the IIC-optimisation with respective values of 0.92 and 0.04. Hence the IIC reduces the uncertainty of the prediction for the five computational experiments with splits 1–5.
The average R2 for the five splits is 0.77 using IIC, while without ICC the R2 is 0.72. The QSAR model generated with the third split provided better prediction results while considering the overall statistics (R2 = 0.82) and is concluded to represent the most robust model to be applied for the prediction of acute toixicty in tadpole of Rana japonica for data porr compounds.
3.3. Mechanistic interpretation
Table 2 provides the correlation weights (CW(Sk)) of the third QSAR model (Eq. 5) including in relation to SMILES attributes (Sk). These values are associated with quantitative coefficients, thus, providing a score on the relative influence of each parameter. The size of the coefficient is highly informative since it indicates the parameters playing a major role in the determination of acute toxic potency and the sign of the coefficient indicates an increase or decrease of such toxic potency. Table 2 shows that bromine and chlorine atoms increase acute toxicity. Indeed, none of the 10 substances with the lowest acute toxicity potency have chlorine or bromine, while 8 out of 10 of the most toxic substances contain these two atoms. Furthermore, it can also be observed that there are four substances containing three of these atoms, and these four substances are among the five most toxic substances in our dataset. Generally speaking, if the substance contains a single atom of chlorine or bromine, it may have a moderate level of toxicity, unless a nitro group is also present, as discussed below. Overall, the role of chlorine in the determination of toxic potency is in agreement with the conclusions of Huang et al. highlighting that toxicity is associated with chlorine’s presence (Huang et al., 2003a). In contrast, fluorine atoms did not impact potency, since this is a relatively small atom with very stable carbon bonds.
Table 2.
Correlation weights (CW(Sk)) obtained by Monte Carlo optimisation for the third split (Eq. 5).
| Sk | CW(Sk) |
|---|---|
| (........... | −0.0813 |
| 1........... | 0.8421 |
| 2........... | 1.0824 |
| =........... | −0.2139 |
| C........... | 0.4530 |
| F........... | −0.2871 |
| Br.......... | 1.1052 |
| Cl.......... | 1.0972 |
| N........... | 0.0 |
| O........... | 0.1401 |
| S........... | 0.0 |
| [N+]........ | 1.1961 |
| [O−]........ | 0.1351 |
| c........... | −0.1438 |
The presence of a nitro group was associated with an increase in toxic potency accounted for by the [N+] and [O−] SMILES attributes in Table 2. Indeed, none of the 10 substances with the lowest toxic potency contain chlorine or bromine, while 6 out of 10 of the most toxic substances contain the nitro group. Furthermore, we can also observe that all substances containing two nitro groups have a pLC50 superior to 4. Overall, it can also be noted that the co-presence of halogens (bromine and chlorine) and nitro group increases toxic potency.
Conversely, structural features associated with a reduction in toxic potency (negative correlation coefficients) included atoms increasing polarity, such as oxygen and nitrogen in Table 2. Indeed, 9 out of the 10 substances with the lowest toxic potency from the database contain a hydroxy group, while the hydroxy group is present only once in the 10 most toxic substances. This conclusion is also in agreement Huang et al. (Huang et al., 2003a).
The calculation was performed using Eq. 5. Figure 1 contains the graphical representation of the model observed for split #3.
Figure 1.
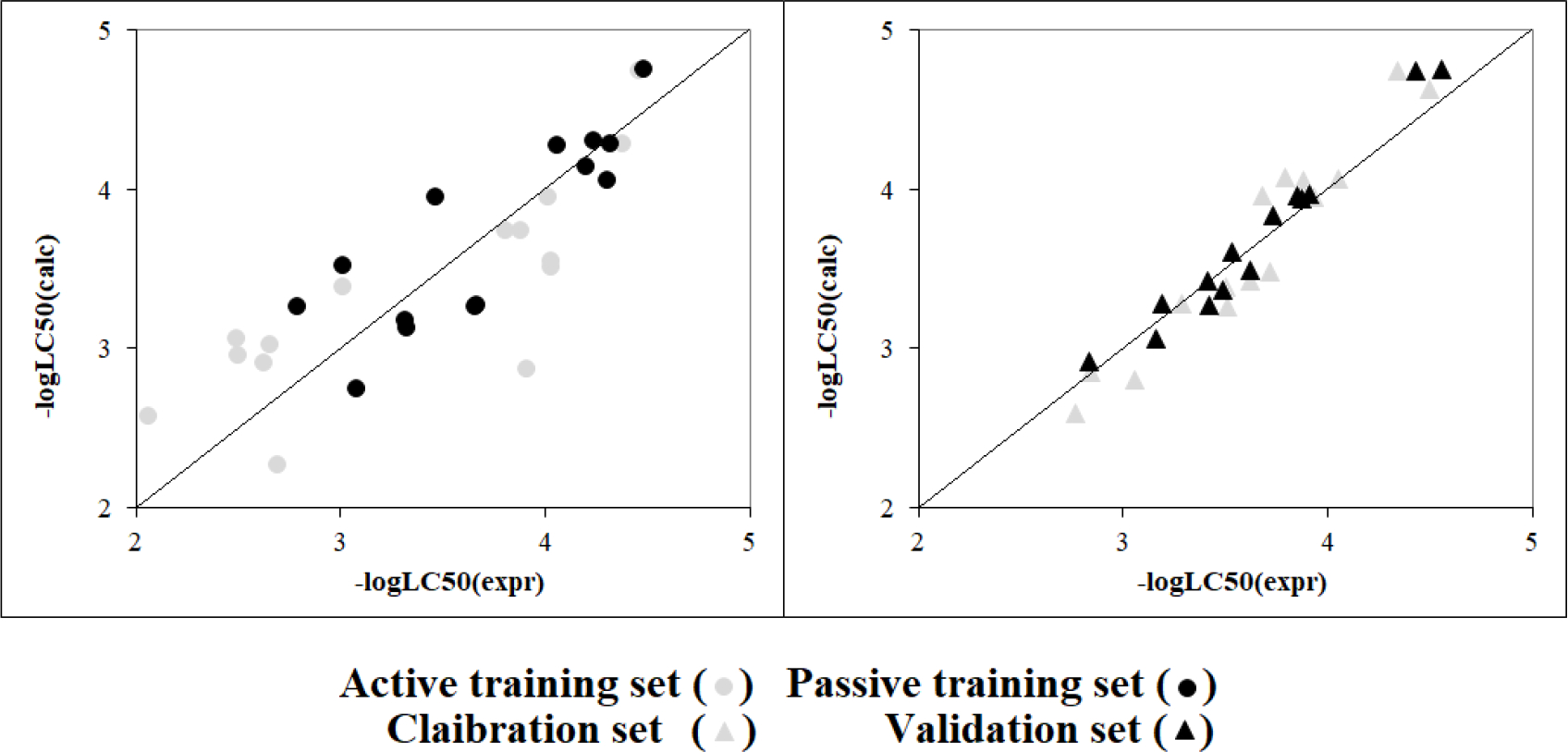
Models observed for split #3 from Monte Carlo optimisation using IIC.
X axis: -LogLC50 (calc): calculated negative logarithm of the acute median lethal molar concentrations after 12 h, in Rana Japonica tadpoles; Y axis: -LogLC50 (expr): experimental negative logarithm of the acute median lethal molar concentrations after 12 h, in Rana Japonica tadpoles.
3.4. Comparison with previous QSAR models on Rana japonica
Table 4 provides a comparison of the statistical quality of QSAR models from the literature and the model built developed here (Eq.5). The models from the literature applied the quantum mechanics descriptors (Wang et al., 2019a); different physicochemical descriptors, i.e. hydrophobicity, electric property, and molecular size (Huang et al., 2003a) as well, the multiple linear regression based on the extended topochemical atom indices (Roy and Ghosh, 2006). It is to be noted that the models developed here are based on the representation of the molecular structure by SMILES without additional data on physicochemical and quantum mechanics descriptors.
Table 4.
Comparison of the statistical performance of the QSAR models for acute toxicity in tadpoles of the brown Japanese frog (Rana japonica)
| N | R2(training) | RMSE(training) | N | R2(validation) | RMSE(validation) | Reference |
|---|---|---|---|---|---|---|
| 9 | 0.930 | 0.220 | - | - | - | Wang et al., 2019a |
| 51 | 0.834–0.914 | 0.243– 0.175 | - | - | - | Huang et al., 2003a |
| 51 | 0.915 | 0.183 | - | - | - | Roy and Ghosh, 2006 |
| 44 | 0.722 | 0.330 | 14 | 0.965 | 0.110 | Eq.5 |
Our QSAR CORAL model is based on 58 substances based on a homogeneous toxicological protocol and dataset. Prediction results and the associated statistics are satisfactory and the tool issimple to used requiring only SMILES without the need for the calculation of chemical descriptors.
4. Discussion and future perspectives
This manuscript describes the development of a regression-based QSAR model predicting acute toxicity in tadpoles of Rana Japonica for a range of aromatic compounds with satisfactory results based on the IIC metric, particularly for the validation set. There are several interesting points related to the present study. (1) There are only few QSAR models are available for amphibians; (2) this study is based on a relatively large data set of substances tested for the same species; (3) it is based on a quite simple approach which only requires SMILES format, without the need for calculating chemical descriptors; (4) it identifies a number of chemical features which can be used to characterise acute toxicity in tadpoles; (5) such chemical features can be used pro-actively prioritise substances with high toxic potency and compared to substances associated with low toxic potency.
In terms of ERA, the future development of QSAR models also requires consideration of the taxonomic framework of “true frogs” and is important to pinpoint which species can be considered as representative of the whole genus and sub-genus for different geographical locations. In this context, the genus and sub-genus Rana is considered the lineage of “true frogs” (family Ranidae) and associated with 106 associated species that are present in Europe, Asia and the Americas (Najibzadeh et al., 2017). So far, 106 and 54 species have been described depending on the different taxonomic considerations of the subspecific levels amongst the different (AmphibiaWeb, 2021; Frost, 2021; Najibzadeh et al., 2017). Yuan et al., (2016) carried out a comprehensive phylogenetic assessment of the taxon, considering 101 species distributed in Eurasia and the Americas and divided the subgenus Rana into a number of clades and subclades: two in East Asia, one in Europe and Central Asia (see Figure 2 in Yuan et al., 2016). The Eurasian species of the subgenus Rana “brown frogs” are phylogenetically related, morphologically conserved and characterised by a dorsal colour with different shades of brown, the presence of evident dorsolateral folds and a dark temporal mask (Boulenger, 1920; Liu and Hu, 1961; Yuan et al., 2016). This implies that the identification on a morphological basis is often difficult and the description of new species nowadays is based on molecular features using nuclear and mitochondrial DNA (Yuan et al., 2016; Zhao et al., 2017). In this context, the Japanese brown frog Rana japonica (Boulenger, 1920) was originally described as Rana temporaria var. japonica (Gunther, 1859) and is distributed in Japan (Honshu, Kyushu and Shikoku islands and Tanegashima Group) (Amphibian species of the world 6.1, 2021). The taxon belongs to the aforementioned Eurasian clade which also includes the European common frog Rana temporaria and is widespread from northern to southern Europe (Yuan et al., 2016). A focus on the phylogenetic relationship between the two species is shown in Figure 2.
Figure 2.
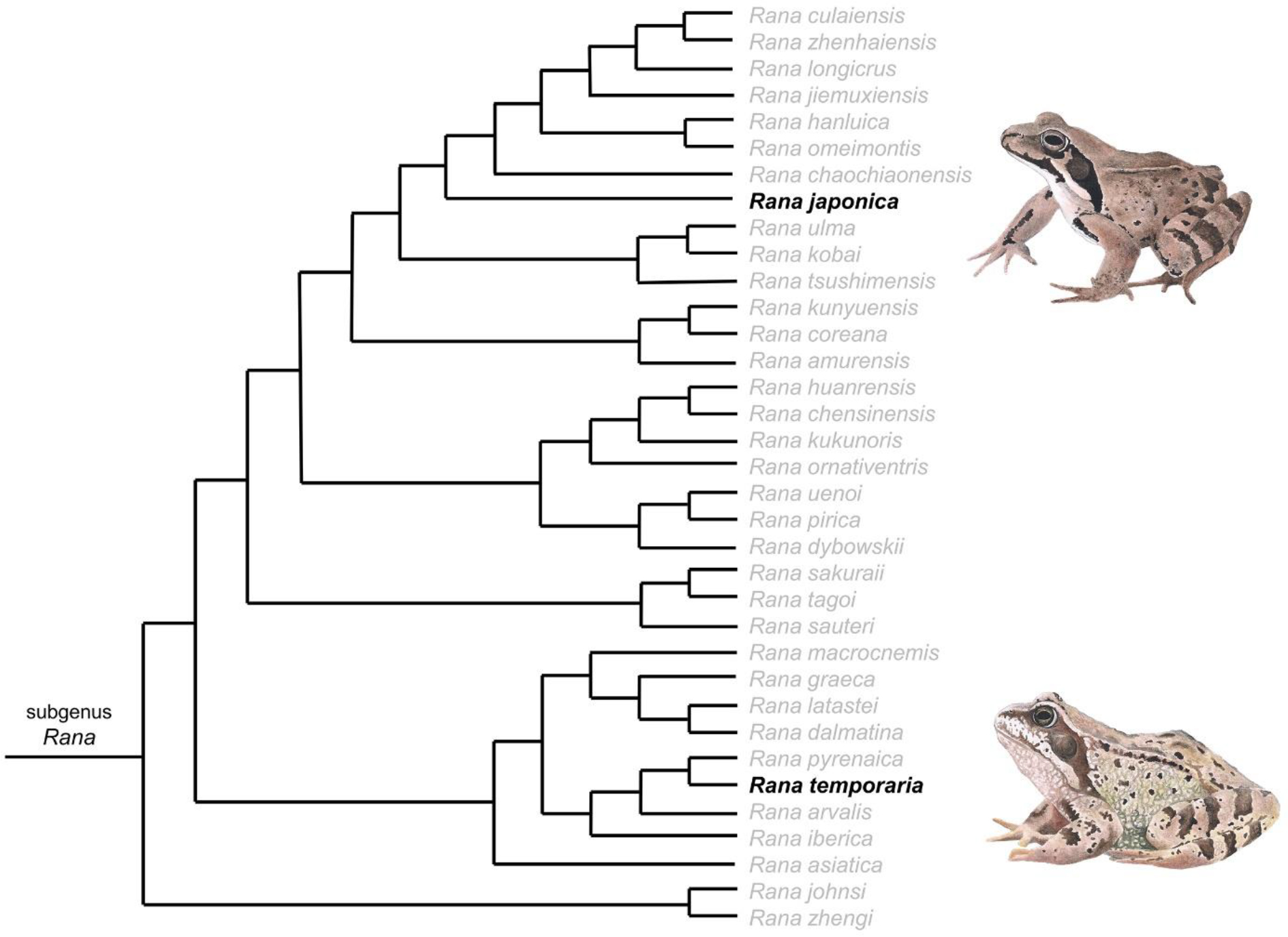
Simplified tree that shows phylogenetic relationship between Rana japonica and Rana temporaria. Modified from Yuan et al. (2016).
In addition to the similar morphology common to all “brown frogs”, Rana japonica and Rana temporaria are both taxa that live in the temperate belt of the northern hemisphere occupying assimilable environmental typologies characterised by the presence of four distinct seasons and also share an explosive breeding modality, which takes place in late winter / early spring (Di Nicola et al., 2021; Lanza et al., 2007; Matsushima and Kawata, 2005). Hence, available chemical toxicity data for Rana japonica is well suited for the development of regression-based QSAR models to address chemical toxicity in anuran amphibians including the European brown frog (Rana temporaria). However, developments of regression-based QSAR models for anuran amphibian species is warranted to predict acute toxicity in different life stages of Rana japonica and Rana temporaria as well as North American species such as the Northern leopard frog (Rana pipiens) and the American bullfrog (Lithobates catesbeianus) within their aquatic and terrestrial phase (egg, embryo, tadpole, juvenile and adult). In addition, the development of similar QSAR models for the African clawed frog (Xenopus laevis), as an OECD amphibian test species with a strictly speaking aquatic lifestyle, can provide another important tool for risk assessors for predicting chemical toxicity in amphibians particularly for plant protection products and environmental contaminants.
Two major data gaps for hazard and risk assessment in amphibians include the lack of chronic toxicity in anuran amphibians and the lack of toxicity data and QSAR models in Caudata (salamanders and newts) as well as Gymnophiona (caecilians and relatives). Moreover, since very limited kinetic information is available for anuran amphibians, options to further investigate fate and bioaccumulation in anuran amphibians is compromised. Since chemical toxicity data in fish are more readily available, an option is to use such data for cross-species read-across as well as data collection and generation of kinetic data, as well as quantitative physiological data and life cycle data for amphibians, would allow for the development of physiologically-based kinetic models and the derivation of bioactive concentrations on an internal basis for acute and chronic endpoints. It would also allow for the calibration and validation of dynamic energy budget models to investigate the impact of chemicals at the individual and population level (Grech et al., 2016; Baas et al., 2018).
Supplementary Material
Table 3.
Experimental and predicted acute toxicity in tadpoles of the brown Japanese frog (Rana japonica) for the third split.
| Set | CAS | SMILES | DCW (1,15) | pLC50 Expr | pLC50 Calc | Expr-Calc |
|---|---|---|---|---|---|---|
| C | 6627-55-0 | Cc1cc(Br)c(O)cc1 | 2.1944 | 3.7200 | 3.4823 | 0.2377 |
| A | 831-82-3 | Oc2ccc(Oc1ccccc1)cc2 | 2.2405 | 4.0300 | 3.5155 | 0.5145 |
| V | 87-61-6 | Clc1cccc(Cl)c1Cl | 3.9502 | 4.4310 | 4.7462 | −0.3152 |
| C | 120-82-1 | Clc1cc(Cl)c(Cl)cc1 | 3.7876 | 4.5000 | 4.6292 | −0.1292 |
| V | 56961-77-4 | Clc1cccc(Br)c1Cl | 3.9582 | 4.5600 | 4.7520 | −0.1920 |
| P | 19393-92-1 | Clc1cccc(Cl)c1Br | 3.9582 | 4.4810 | 4.7520 | −0.2710 |
| C | 541-73-1 | Clc1cccc(Cl)c1 | 2.8530 | 3.6790 | 3.9564 | −0.2774 |
| V | 106-46-7 | Clc1ccc(Cl)cc1 | 2.8530 | 3.8500 | 3.9564 | −0.1064 |
| C | 95-50-1 | Clc1ccccc1Cl | 3.0155 | 3.7900 | 4.0734 | −0.2834 |
| V | 108-90-7 | Clc1ccccc1 | 1.9183 | 3.1950 | 3.2836 | −0.0886 |
| C | 108-95-2 | Oc1ccccc1 | 0.9612 | 2.7690 | 2.5947 | 0.1743 |
| A | 95-57-8 | Oc1ccccc1Cl | 2.0584 | 3.0110 | 3.3845 | −0.3735 |
| P | 106-41-2 | Oc1ccc(Br)cc1 | 1.9039 | 3.6640 | 3.2732 | 0.3908 |
| V | 106-48-9 | Oc1ccc(Cl)cc1 | 1.8959 | 3.4210 | 3.2675 | 0.1535 |
| A | 371-41-5 | Fc1ccc(O)cc1 | 0.5116 | 2.6930 | 2.2710 | 0.4220 |
| A | 90-05-1 | Oc1ccccc1OC | 1.5543 | 2.6540 | 3.0216 | −0.3676 |
| V | 95-48-7 | Cc1ccccc1O | 1.4142 | 2.8370 | 2.9207 | −0.0837 |
| A | 150-76-5 | Oc1ccc(OC)cc1 | 1.3918 | 2.6240 | 2.9046 | −0.2806 |
| C | 106-44-5 | Cc1ccc(O)cc1 | 1.2517 | 3.0570 | 2.8037 | 0.2533 |
| A | 98-54-4 | CC(C)(C)c1ccc(O)cc1 | 2.2856 | 4.0330 | 3.5480 | 0.4850 |
| P | 576-26-1 | Cc1cccc(C)c1O | 1.7047 | 3.3240 | 3.1298 | 0.1942 |
| A | 90-15-3 | Oc2cccc1ccccc12 | 2.5506 | 3.8070 | 3.7388 | 0.0682 |
| A | 135-19-3 | Oc1ccc2ccccc2c1 | 2.5506 | 3.8860 | 3.7388 | 0.1472 |
| V | 120-83-2 | Clc1cc(Cl)c(O)cc1 | 2.8305 | 3.8730 | 3.9403 | −0.0673 |
| A | 108-46-3 | Oc1cccc(O)c1 | 0.9388 | 2.0660 | 2.5785 | −0.5125 |
| P | 80-5-7 | CC(C)(c1ccc(O)cc1)c2ccc(O)cc2 | 3.1118 | 4.2010 | 4.1427 | 0.0583 |
| V | 612-00-0 | CC(c1ccccc1)c2ccccc2 | 2.8663 | 3.9140 | 3.9660 | −0.0520 |
| V | 554-00-7 | Clc1cc(Cl)c(N)cc1 | 2.6904 | 3.7320 | 3.8394 | −0.1074 |
| V | 74-11-3 | OC(=O)c1ccc(Cl)cc1 | 2.1125 | 3.4170 | 3.4234 | −0.0064 |
| C | 586-76-5 | OC(=O)c1ccc(Br)cc1 | 2.1206 | 3.6250 | 3.4292 | 0.1958 |
| C | 69-72-7 | OC(=O)c1ccccc1O | 1.3180 | 2.8400 | 2.8515 | −0.0115 |
| P | 321-14-2 | Oc1ccc(Cl)cc1C(=O)O | 2.2526 | 3.0110 | 3.5243 | −0.5133 |
| P | 123-08-0 | O=Cc1ccc(O)cc1 | 1.1779 | 3.0800 | 2.7506 | 0.3294 |
| C | 98-95-3 | [O−][N+](=O)c1ccccc1 | 1.9159 | 3.2860 | 3.2819 | 0.0041 |
| V | 88-72-2 | Cc1ccccc1[N+](=O)[O−] | 2.3689 | 3.5300 | 3.6080 | −0.0780 |
| V | 99-99-0 | Cc1ccc(cc1)[N+](=O)[O−] | 2.2063 | 3.6240 | 3.4910 | 0.1330 |
| C | 88-75-5 | O=[N+]([O−])c1ccccc1O | 2.0560 | 3.5020 | 3.3827 | 0.1193 |
| C | 554-84-7 | O=[N+]([O−])c1cccc(O)c1 | 1.8934 | 3.5100 | 3.2657 | 0.2443 |
| P | 100-02-7 | O=[N+]([O−])c1ccc(O)cc1 | 1.8934 | 3.6570 | 3.2657 | 0.3913 |
| C | 100-00-5 | O=[N+]([O−])c1ccc(Cl)cc1 | 2.8505 | 3.9340 | 3.9547 | −0.0207 |
| A | 100-11-8 | O=[N+]([O−])c1ccc(CBr)cc1 | 3.3116 | 4.3830 | 4.2866 | 0.0964 |
| P | 100-14-1 | O=[N+]([O−])c1ccc(CCl)cc1 | 3.3035 | 4.3210 | 4.2808 | 0.0402 |
| C | 89-64-5 | Oc1ccc(Cl)cc1[N+]([O−])=O | 2.9906 | 3.8820 | 4.0555 | −0.1735 |
| V | 601-89-8 | O=[N+]([O−])c1c(O)cccc1O | 2.0335 | 3.4920 | 3.3666 | 0.1254 |
| P | 6283-25-6 | Nc1cc(ccc1Cl)[N+]([O−])=O | 2.8505 | 3.4660 | 3.9547 | −0.4887 |
| P | 776-34-1 | [O−][N+](=O)c1ccc(N)c2ccccc12 | 3.3427 | 4.2360 | 4.3090 | −0.0730 |
| C | 528-29-0 | O=[N+]([O−])c1ccccc1[N+]([O−])=O | 3.0107 | 4.0500 | 4.0700 | −0.0200 |
| A | 99-65-0 | O=[N+]([O−])c1cccc(c1)[N+]([O−])=O | 2.8481 | 4.0150 | 3.9529 | 0.0621 |
| P | 121-14-2 | Cc1ccc(cc1[N+](=O)[O−])[N+]([O−])=O | 3.3011 | 4.0610 | 4.2790 | −0.2180 |
| P | 51-28-5 | O=[N+]([O−])c1cc(ccc1O)[N+]([O−])=O | 2.9882 | 4.3060 | 4.0538 | 0.2522 |
| A | 584-48-5 | O=[N+]([O−])c1cc(ccc1Br)[N+]([O−])=O | 3.9534 | 4.4610 | 4.7485 | −0.2875 |
| C | 97-00-7 | O=[N+]([O−])c1cc(ccc1Cl)[N+]([O−])=O | 3.9453 | 4.3420 | 4.7428 | −0.4008 |
| A | 90-02-8 | O=Cc1ccccc1O | 1.3404 | 3.9140 | 2.8676 | 1.0464 |
| P | 119-36-8 | Oc1ccccc1C(=O)OC | 1.7710 | 3.3150 | 3.1776 | 0.1374 |
| V | 99-76-3 | Oc1ccc(cc1)C(=O)OC | 1.6084 | 3.1600 | 3.0605 | 0.0995 |
| P | 945-51-7 | O=S(c1ccccc1)c2ccccc2 | 1.8865 | 2.7900 | 3.2607 | −0.4707 |
| A | 99-93-4 | O=C(C)c1ccc(O)cc1 | 1.4683 | 2.5030 | 2.9597 | −0.4567 |
| A | 156-38-7 | Oc1ccc(CC(=O)O)cc1 | 1.6084 | 2.4970 | 3.0605 | −0.5635 |
A = active training set; P = passive training set; C = calibration set; V = validation set
Highlights.
Few QSAR models are available for the prediction of chemical toxicity in amphibians
QSAR models have been developed here to predict acute lethal toxicity of aromatic chemicals in Rana japonica
Satisfactory prediction results for the training set and robust results for validation set
QSAR model development for other life stages and amphibian species are proposed
Acknowledgments
The authors are grateful for the contribution of the project LIFE-VERMEER (contract LIFE16 ENV/IT/000167) and the EFSA project OptiTox (contract OC/EFSA/SCER/2018/01) for financial support. E. Carnesecchi, N. Kramer and M. R. Di Nicola are thankful to the Lush prize. The authors are thankful to Chiara Papa for the realization of the drawings for Figure 2.
The views expressed in this article are the authors only and do not reflect the views of the European Food Safety Authority or the US-Environmental Protection Agency.
Funding:
This work was supported by Efsa contract: OC/EFSA/SCER/2018/01, and by the LUSH prize 2021 in the area of alternative methods to animal testing.
Footnotes
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Adhikari C, Mishra BK, 2018. Quantitative structure-activity relationships of aquatic narcosis: A review. Curr. Comput. Aided Drug Des. 14 (1), 7–28 DOI: 10.2174/1573409913666170711130304 [DOI] [PubMed] [Google Scholar]
- Agrawal VK, Chaturvedi S, Abraham MH, Khadikar PV, 2003. QSAR study on tadpole narcosis. Bioorg. Med. Chem. 11 (20), 4523–4533. DOI: 10.1016/S0968-0896(03)00446-2 [DOI] [PubMed] [Google Scholar]
- AmphibiaWeb (Accessed on January, 20, 2021). https://amphibiaweb.org. University of California, Berkeley, CA, USA [Google Scholar]
- Baas J, Augustine S, Marques GM, Dorne JL, 2018. Dynamic energy budget models in ecological risk assessment: from principles to applications. Sci. Total Environ. 628, 249–260. DOI: 10.1016/j.scitotenv.2018.02.058 [DOI] [PubMed] [Google Scholar]
- Boulenger GA, 1920. A monograph of the American frogs of the genus Rana. Proc. Am. Acad. Arts Sci. 55, 413–480. DOI: 10.2307/20025810 [DOI] [Google Scholar]
- Chirico N, Gramatica P, 2011. Real external predictivity of QSAR models: How to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient. J. Chem. Inf. Model. 51(9), 2320–2335. DOI: 10.1021/ci200211n [DOI] [PubMed] [Google Scholar]
- Di Nicola MR, Cavigioli L, Luiselli L, Andreone F, 2021. Anfibi & Rettili d’Italia. Edizione aggiornata. Edizioni Belvedere, Latina, “historia naturae” (8), pp. 576. [Google Scholar]
- EFSA PPR, 2018. EFSA PPR Panel (EFSA Panel on Plant Protection Products and their Residues), Ockleford C, Adriaanse P, Berny P, Brock T, Duquesne S, Grilli S, Hernandez-Jerez AF, Bennekou SH, Klein M, Kuhl T, Laskowski R, Machera K, Pelkonen O, Pieper S, Stemmer M, Sundh I, Teodorovic I, Tiktak A, Topping CJ, Wolterink G, Aldrich A, Berg C, Ortiz-Santaliestra M, Weir S, Streissl F, Smith RH, Scientific Opinion on the state of the science on pesticide risk assessment for amphibians and reptiles. EFSA J. 16(2)(5125), 301. 10.2903/j.efsa.2018.5125ISSN [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frost DR, 2021. Amphibian Species of the World: an Online Reference. Version 6.1 (Accessed on January, 27, 2021). Electronic Database accessible at https://amphibiansoftheworld.amnh.org/index.php. American Museum of Natural History, New York, USA. 10.5531/db.vz.0001 [DOI] [Google Scholar]
- Grech A, Brochot C, Dorne JL, Quignot N, Bois FY, Beaudouin R, 2017. Toxicokinetic models and related tools in environmental risk assessment of chemicals. Sci. Total Environ. 578, 1–15. DOI: 10.1016/j.scitotenv.2016.10.146 [DOI] [PubMed] [Google Scholar]
- Huang H, Wang X, Ou W, Zhao J, Shao Y, Wang L, 2003a. Acute toxicity of benzene derivatives to the tadpoles (Rana japonica) and QSAR analyses. Chemosphere 53 (8), 963–970. DOI: 10.1016/S0045-6535(03)00715-X [DOI] [PubMed] [Google Scholar]
- Huang H, Wang X, Shao Y, Chen D, Dai X, Wang L, 2003b. QSAR for Prediction of Joint Toxicity of Substituted Phenols to Tadpoles (Rana japonica). Bull. Environ. Contam. Toxicol. 71 (6), 1124–1130. DOI: 10.1007/s00128-003-8790-4 [DOI] [PubMed] [Google Scholar]
- Jaiswal M, Khadikar P, 2004. QSAR study on tadpole narcosis using PI index: A case of heterogenous set of compounds. Bioorg. Med. Chem. 12 (7), 1731–1736. DOI: 10.1016/j.bmc.2004.01.009 [DOI] [PubMed] [Google Scholar]
- Kennard RW, Stone LA, 1969. Computer Aided Design of Experiments. Technometrics, 11 (1), 137–148. DOI: 10.1080/00401706.1969.10490666 [DOI] [Google Scholar]
- Lanza B, Andreone F, Bologna MA, Corti C, Razzetti E (Eds.), 2007. Fauna d’Italia, Vol. XLII, Amphibia. Calderini, Bologna, pp. 537. [Google Scholar]
- Lin LI-K, 1992. Assay validation using the concordance correlation coefficient. Biometrics 48(2), 599–604. DOI: 10.2307/2532314 [DOI] [Google Scholar]
- Liu CC, Hu SQ, 1961. Chinese Tailless Amphibians. Science Press, Peking (Beijing), China, pp. 364. [Google Scholar]
- Mekenyan OG, Schultz TW, Veith GD, Kamenska V, 1996. ‘Dynamic’ QSAR for semicarbazide-induced mortality in frog embryos. J. Appl. Toxicol. 16 (4), 355–363. DOI: [DOI] [PubMed] [Google Scholar]
- Matsushima N, Kawata M, 2005. The choice of oviposition site and the effects of density and oviposition timing on survivorship in Rana japonica. Ecol. Res. 20 (1), 81–86. DOI: 10.1007/s11284-004-0010-0 [DOI] [Google Scholar]
- Morais CLM, Santos MCD, Lima KMG, Martin FL,2019. Improving data splitting for classification applications in spectrochemical analyses employing a random-mutation Kennard-Stone algorithm approach. Bioinformatics, 35 (24), 5257–5263. DOI: 10.1093/bioinformatics/btz421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najibzadeh M, Veith M, Gharzi A, Rastegar-Pouyani N, Rastegar-Pouyani E, Kieren S, Pesarakloo A, 2017. Molecular phylogenetic relationships among Anatolian-Hyrcanian brown frog taxa (Ranidae: Rana). Amphib.-reptil. 38 (3), 339–350. DOI: 10.1163/15685381-00003114 [DOI] [Google Scholar]
- Puzyn T, Mostrag-Szlichtyng A, Gajewicz A, Skrzyński M, Worth AP, 2011. Investigating the influence of data splitting on the predictive ability of QSAR/QSPR models. Struct. Chem. 22 (4), 795–804. DOI: 10.1007/s11224-011-9757-4 [DOI] [Google Scholar]
- Roy K, Ghosh G, 2006. QSTR with extended topochemical atom (ETA) indices. VI. Acute toxicity of benzene derivatives to tadpoles (Rana japonica). J. Mol. Model. 12 (3), 306–316. DOI: 10.1007/s00894-005-0033-7 [DOI] [PubMed] [Google Scholar]
- Roy K, Kar S, 2014. The rm2 metrics and regression through origin approach: Reliable and useful validation tools for predictive QSAR models (Commentary on ‘Is regression through origin useful in external validation of QSAR models?’). Eur. J. Pharm. Sci. 62, 111–114. DOI: 10.1016/j.ejps.2014.05.019 [DOI] [PubMed] [Google Scholar]
- Sahoo S, Adhikari C, Kuanar M, Mishra BK, 2016. A short review of the generation of molecular descriptors and their applications in quantitative structure property/activity relationships. Curr. Comput. Aided Drug Des. 12 (3), 181–250. DOI: 10.2174/1573409912666160525112114 [DOI] [PubMed] [Google Scholar]
- Snee RD, 1977. Validation of Regression Models: Methods and Examples. Technometrics, 19 (4), 415–428. DOI: 10.1080/00401706.1977.10489581 [DOI] [Google Scholar]
- Toropov AA, Toropova AP, 2017. The index of ideality of correlation: A criterion of predictive potential of QSPR/QSAR models? Mutat. Res. Genet. Toxicol. Environ. Mutagen. 819, 31–37. DOI: 10.1016/j.mrgentox.2017.05.008 [DOI] [PubMed] [Google Scholar]
- Toropov AA, Toropova AP, Como F, Benfenati E, 2017. Quantitative structure–activity relationship models for bee toxicity. Toxicol. Environ. Chem. 99(7–8), 1117–1128. DOI: 10.1080/02772248.2016.1242006 [DOI] [Google Scholar]
- Toropov AA, Toropova AP, Raitano G, Benfenati E, 2019. CORAL: Building up QSAR models for the chromosome aberration test. Saudi J. Biol. Sci. 26(6), 1101–1106. DOI: 10.1016/j.sjbs.2018.05.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toropov AA, Toropova AP, Marzo M, Benfenati E, 2020a. Use of the index of ideality of correlation to improve aquatic solubility model. J. Mol. Graph. Model. 96, 107525. 10.1016/j.jmgm.2019.107525 [DOI] [PubMed] [Google Scholar]
- Toropov AA, Toropova AP, Benfenati E, 2020b. QSAR model for pesticides toxicity to Rainbow Trout based on “ideal correlations”. Aquat. Toxicol. 227, 105589. DOI: 10.1016/j.aquatox.2020.105589 [DOI] [PubMed] [Google Scholar]
- Toropova AP, Toropov AA, 2017. The index of ideality of correlation: A criterion of predictability of QSAR models for skin permeability? Sci. Total Environ. 586, 466–472. DOI: 10.1016/j.scitotenv.2017.01.198 [DOI] [PubMed] [Google Scholar]
- Toropova AP, Toropov AA, 2019. Whether the Validation of the Predictive Potential of Toxicity Models is Solved Task? Curr. Top. Med. Chem. 19(29), 2643 – 2657. DOI: 10.2174/1568026619666191105111817 [DOI] [PubMed] [Google Scholar]
- Toropova AP, Toropov AA, Carnesecchi E, Benfenati E, Dorne JL, 2020. The using of the Index of Ideality of Correlation (IIC) to improve predictive potential of models of water solubility for pesticides. Environ. Sci. Pollut. Res. 27 (12), 13339–13347. DOI: 10.1007/s11356-020-07820-6 [DOI] [PubMed] [Google Scholar]
- Wang X, Dong Y, Wang L, Han S, 2001. Acute toxicity of substituted phenols to Rana japonica tadpoles and mechanism-based quantitative structure-activity relationship (QSAR) study. Chemosphere 44 (3), 447–455. DOI: 10.1016/S0045-6535(00)00198-3 [DOI] [PubMed] [Google Scholar]
- Wang S, Yan LC, Zheng SS, Li TT, Fan LY, Huang T, Li C, Zhao YH, 2019a. Toxicity of some prevalent aromatic chemicals to tadpoles and comparison with toxicity to fish based on mode of toxic action. Ecotox. Environ. Safe. 167, 138–145. DOI: 10.1016/j.ecoenv.2018.09.105 [DOI] [PubMed] [Google Scholar]
- Wang L, Xing P, Wang C, Zhou X, Dai Z, Bai L, 2019b. Maximal information coefficient and support vector regression based nonlinear feature selection and QSAR modeling on toxicity of alcohol compounds to tadpoles of Rana temporaria. J. Braz. Chem. Soc. 30 (2), 279–285. DOI: 10.21577/0103-5053.20180176 [DOI] [Google Scholar]
- Weininger D, 1988. SMILES, a Chemical Language and Information System: 1: Introduction to Methodology and Encoding Rules. J. Chem. Inform. Comput. Sci. 28 (1), 31–36. DOI: 10.1021/ci00057a005 [DOI] [Google Scholar]
- Wilson LY, Famini GR, 1991.Using Theoretical Descriptors in Quantitative Structure-Activity Relationships: Some Toxicological Indices. J. Med. Chem. 34 (5), 1668–1674. DOI: 10.1021/jm00109a021 [DOI] [PubMed] [Google Scholar]
- Yuan ZY, Zhou WW, Chen X, Poyarkov NA Jr, Chen HM, Jang-Liaw NH, Chou WH, Matzke JN, Izuka K, Min MS, Kuzmin SL, Zhang YP, Cannatella DC, Hillis DM, Che J, 2016. Spatiotemporal diversification of the true frogs (genus Rana): a historical framework for a widely studied group of model organisms. Syst. Biol, 65 (5), 824–842. DOI: 10.1093/sysbio/syw055 [DOI] [PubMed] [Google Scholar]
- Zhao H, Yang J, Wang C, Li P, Murphy RW, Che J, Yuan Z, 2017. A new species of the genus Rana from Henan, central China (Anura, Ranidae). ZooKeys, 694, 95–108. DOI: 10.3897/zookeys.694.12513 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


