Enhancing estimation methods for integrating probability and nonprobability survey samples with machine‐learning techniques. An application to a Survey on the impact of the COVID‐19 pandemic in Spain

Abstract

Web surveys have replaced Face‐to‐Face and computer assisted telephone interviewing (CATI) as the main mode of data collection in most countries. This trend was reinforced as a consequence of COVID‐19 pandemic‐related restrictions. However, this mode still faces significant limitations in obtaining probability‐based samples of the general population. For this reason, most web surveys rely on nonprobability survey designs. Whereas probability‐based designs continue to be the gold standard in survey sampling, nonprobability web surveys may still prove useful in some situations. For instance, when small subpopulations are the group under study and probability sampling is unlikely to meet sample size requirements, complementing a small probability sample with a larger nonprobability one may improve the efficiency of the estimates. Nonprobability samples may also be designed as a mean for compensating for known biases in probability‐based web survey samples by purposely targeting respondent profiles that tend to be underrepresented in these surveys. This is the case in the Survey on the impact of the COVID‐19 pandemic in Spain (ESPACOV) that motivates this paper. In this paper, we propose a methodology for combining probability and nonprobability web‐based survey samples with the help of machine‐learning techniques. We then assess the efficiency of the resulting estimates by comparing them with other strategies that have been used before. Our simulation study and the application of the proposed estimation method to the second wave of the ESPACOV Survey allow us to conclude that this is the best option for reducing the biases observed in our data.

1. INTRODUCTION

Ten years have passed since the American Association for Public Opinion Research (AAPOR) appointed a task force to evaluate nonprobability survey sampling methods that were more and more frequently used in applied research contexts at the time (Couper et al., 2013). During the last decade, nonprobability sampling designs have continued to grow as the use of Big Data and web surveys spread (Lenau et al., 2021). The lockdowns that followed the onset of the COVID‐19, together with the need of quick data to grasp the impacts of the pandemic and to inform policymakers' decisions, further bolstered nonprobability sampling designs (Kohler, 2020). Web surveys mushroomed during COVID‐19‐related confinements and have further displaced traditional survey modes, such as Face to Face and CATI, that still face important restrictions due to social distancing rules and population fear to COVID‐19 infection.

Most web surveys conducted during this time have relied on online convenience samples using social media and/or river sampling to recruit participants or on quota samples selected from online opt‐in panels (Schaurer & Weib, 2020). Nonprobability sampling designs account for 38% of the 63 COVID‐19‐related surveys included in the Oxford Supertracker, a global directory that compiles the most significant efforts to collect information on the social and policy‐related impacts of the pandemic (Daly et al., 2020). Two other, less restrictive, trackers of COVID‐19‐related surveys conducted in 2020 put this figure up to 73% (of 78 surveys) in Cabrera‐León and Sánchez‐Cantalejo (2020) and 78% (of 177 surveys) in Matias and Levitt (2020).1 In the case of COVID‐19 social science project tracker (Matias & Levitt, 2020), we have retrieved the documentation of 177 cases of research using surveys that were already initiated at the time of being included in the data set. Of these, 138 (73%) used web survey as the main mode of data collection. A total of 90% of these web surveys used nonprobability‐based sample designs such as quota sampling from opt‐in commercial panels (48%) and crowdsourcing marketplaces such as Amazon MTurk (14%), Social Media ads and snowball sampling (34%) or a combination of them.

The lack of an adequate sampling frame that enables probability‐based sample selection of the general population initially hindered the usage of web surveys in official statistics and government and academic research, where high‐quality samples of the general population are required (Callegaro et al., 2015). In those settings, web surveys have been used mainly as an auxiliary mode to interview sample units prerecruited with other modes (i.e., follow‐up waves in longitudinal surveys or cross‐sectional survey samples selected from probability‐based online panels) or as the main survey mode exclusively in those cases where there was a comprehensive list of email contacts available for the population of interest. However, the steep decline in response rates together with the high data collection costs in probability surveys increased the interest in alternative data sources and sampling designs (Beaumont, 2020). With the pandemic, the trend toward the use of nonprobability web survey designs have definitely reached academic research and several initiatives experimenting with the integration of data obtained from probability and nonprobability web surveys have been conducted in official statistics and government research projects (Beaumont & Rao, 2021; Wiśniowski et al., 2020). Some people have even come to believe that probability surveys could be phased out for the production of official statistics. However, for other authors such as Beaumont (2020), the time has not yet come because the alternatives are not reliable and general enough to eliminate the use of probability surveys without severely sacrificing the quality of the estimates. Indeed, although nonprobability surveys usually have large sample sizes, they present important selection and coverage problems since the sample generation process is unknown in most cases, so they can compromise the generalization of the results to the population under study (Bethlehem, 2010; Elliott & Haviland, 2007; Vehovar et al., 2016).

Despite these limitations, nonprobability survey designs may prove useful in some cases. They can provide relevant information that would not be available otherwise (Lenau et al., 2021). In other cases, where small subpopulations are the group under study and probability sampling is unlikely to meet sample size requirements (Disogra et al., 2011; Robbins et al., 2021), complementing a small probability sample with a larger nonprobability one may improve the efficiency of the estimates (Wiśniowski et al., 2020). Nonprobability samples may also be designed as a mean for compensating for known biases in probability‐based web survey samples by purposely targeting respondent profiles that tend to be underrepresented in these surveys as it is the case in the Survey on the impact of the COVID‐19 pandemic in Spain (ESPACOV) that motivates this paper (Rinken et al., 2020). The most rigorous uses of these designs entail the integration of data from both probability and nonprobability samples to produce a single inference that compensates for biases observed in both kind of samples.

Survey statisticians have provided different methods for combining information from multiple data sources. Current reviews of statistical methods of data integration for finite population inference can be seen in Valliant (2020), Buelens et al. (2018), and Rao (2020). Among the most important methods, we could mention inverse probability weighting (Kim & Wang, 2019; Lee, 2006; Lee & Valliant, 2009), inverse sampling (Kim & Wang, 2019), mass imputation (Rivers, 2007), doubly robust methods (Chen et al., 2019), kernel smoothing methods (Wang & Katki, 2020), or statistical matching combined with propensity score adjustment (PSA; Castro‐Martín et al., 2021a). Yang and Kim (2020) provide a good review of some of these techniques. Most of these works assume that the variable of interest is only available in the nonprobability sample, whereas other auxiliary variables are present in both data sources. However, as described above, there are other scenarios where both the probability and nonprobability‐based samples share the same questionnaire and measures, meaning that it is possible to combine both of them in order to maximize the efficiency of the estimates.

Most surveys that integrate probability and nonprobability samples simply pool the samples and make inference using the Horvitz–Thompson or Hàjek estimator assuming the entire sample is probabilistic (Rinken et al., 2020). This method is rarely appropriate because usually nonprobability samples are not distributed proportionally with respect to demographic or other relevant subgroups in the population. Some efforts have been undertaken to combine both probability and nonprobability samples to make inference while dealing with the different sources of bias. Elliott and Haviland (2007) studies a composite estimator that is a linear combination of an unbiased sample mean estimate from a probability sample and a biased sample mean estimate from a convenience sample. The weight of the mean estimator based on the probability sample is determined by the ratio of its mean squared error (MSE) to the sum of that term and the MSE of the convenience sample mean. Disogra et al. (2011) propose an alternative procedure using calibration. These authors combine the previously calibrated probability sample with the nonprobability sample and then recalibrate overall to the probability sample's benchmarks from the previous step. Their simulation study shows that calibrating nonprobability samples with probability samples using early adopter questions minimizes bias in the resulting estimates in the larger combined sample. Recently, Robbins et al. (2021) proposed weighting techniques that enable the two data sets to be analyzed as a single one (i.e., a blended sample) by assuming four conditions for the probability and nonprobability samples. Authors consider four separate methods for blending based on propensity score methods or on calibration weighting and warn on the challenges of integrating both kind of samples. Finally, Sakshaug et al. (2019) propose a Bayesian approach to combine information from probability and nonprobability samples. Data from the nonprobability sample are used to build an informative prior distribution that is subsequently used to inform the estimates from the probability sample. The simulation study and the application with real data suggest that resulting Bayesian estimates are more efficient than estimates exclusively based in probability samples, even when their sample sizes are quite small.

In this paper, we explore other alternatives that combine some of these ideas with the help of machine‐learning methods. Our main contributions to this area of research are the development of a new estimation method for integrating data from probability and nonprobability samples in those situations where the variables of interest are observed in both samples. We then assess the efficiency of the resulting estimates by comparing them with other strategies that have been used before. The application of this method to the second wave of the ESPACOV allows us to conclude that the estimation method that we propose is the best option for reducing observed biases in our data.

This paper is structured as follows. Section 2 introduces the ESPACOV II survey that is our motivating case study. Section 3 establishes notation and describes the proposed methods for integrating probability and nonprobability samples. Section 4 reports the results of an extensive simulation study run on a set of synthetic populations in which the performance of the proposed estimators is analyzed for finite size samples. The proposed methods are applied in a real‐world scenario in Section 5. Finally, the implications of our findings are discussed in Section 6.

2. MOTIVATING CASE STUDY

This new estimation technique was designed to analyze the data obtained in a web survey on the effects of the COVID‐19 pandemic in Spain (ESPACOV Survey) that used a mixed multiphase sampling design inspired by the responsive approach (Groves & Heeringa, 2006). This survey was designed, implemented, and funded by the Institute for Advanced Social Studies at the Spanish National Research Council (IESA‐CSIC) (Rinken et al., 2020). There were two editions of the survey: the first one was fielded from April 4 through April 11, 2020 in the fourth week of the lockdown, that in Spain began on March 14. The second edition was conducted from January 18 to 25, 2021, almost 1 year into the pandemic. This paper focuses on the measurement of the direct impact of the COVID‐19 pandemic in terms of infection and severity of the disease and the consequences of the pandemic on the overall physical and mental health self‐perception as well as the economic situation in the respondents households. For that reason, we use data from the second edition of the survey that allows to assess the situation almost 1 year after the beginning of this major health crisis.

Questionnaires addressed the opinions and attitudes of the Spanish population regarding the COVID‐19 crisis, as well as the assessments of its management and its consequences, either anticipated (ESPACOV I) or endured (ESPACOV II).2

Both editions of the ESPACOV Survey were web based and followed a sampling design that combined the use of SMS invitations to take part in the survey—sent to a list of randomly generated mobile phone numbers—(probability‐based sample) with the publication of Facebook, Instagram, and Google Ads segmented to purposely oversample the sociodemographic profiles that were underrepresented in the probability‐based sample (nonprobability sample). In the first edition of the ESPACOV Survey, both sampling procedures were applied sequentially so that the outcomes of the probability‐based sample informed the design of the purposive sample. In the second edition, both samples were fielded simultaneously taking advantage of the knowledge acquired in the previous edition. An in‐depth explanation and justification of this methodology is provided in Rinken et al. (2020). The combined use of SMS invitations and an RDD (random digit dialing) sampling frame minimizes sampling and coverage problems for collecting web survey data in countries where unsolicited text messages are allowed and there is a high coverage of smartphones (Kim & Couper, 2021) as it is the case in Spain.3

A total of 66,439 SMS invitations with links to the questionnaire were sent in January 2021 for the probability‐based sample in the second edition of ESPACOV Survey, of which 51.3% were delivered. The effective sample size after 8 days in fieldwork was $n=973$ (2.97% of delivered SMS). Invitations to complete the survey were advertised via Facebook, Instagram, and Google ads from January 18 to 22. The invitation reached 1,054,301 impressions and 7647 clicks for a total number of 671 completed interviews. A question was included in order to ascribe to each respondent the sampling procedure by which they had reached the online questionnaire. Respondents' answers to this question were confirmed with the web survey paradata (i.e., user agent strings) and duplicates were managed selecting those that were the most complete (for incomplete questionnaires) or the most recent (for complete questionnaires). As expected, given the low response rates that RDD smartphones surveys typically get, data from the probability‐based sample presented significant nonresponse bias in relevant variables such as age, sex, region, municipal size, educational level, professional activity, and ideology. Once the biases were detected and analyzed, raw data were weighted by iterative (raking) adjustments regarding municipality size, region (aggregated as NUTS‐1), age group, sex, and education level. This weight adjustment procedure has proved useful for correcting biases in both editions of ESPACOV as well as in previous surveys conducted by IESA‐CSIC.

As shown in Table 1, the integration of data from both sampling schemes partially accomplished its aim of maximizing representativeness of the Spanish resident population aged 18 and more. The distribution of the unweighted blended survey is more similar to the population than those of the individual samples (with the exception of gender). Moreover, the profiling of ads worked as intended oversampling respondents aged 65 and more and reducing, although less than needed, the proportion of employed respondents and those with higher education. Contrary to expectations, the profiling resulted in a significant overrepresentation of women in the blended sample.

TABLE 1.

Population data sources

		Probability	Nonprobability	Blended sample (Unweighted)	Population
Gender a	Male	48.4%	40.7%	45.3%	48.5%
	Female	51.6%	59.3%	54.7%	51.5%
Age a	18–29	18.2%	3.3%	12.1%	15.0%
	30–44	33.0%	15.8%	26.0%	25.4%
	45–64	41.3%	37.4%	39.7%	35.9%
	65 or more	7.5%	43.5%	22.2%	23.7%
Age (mean)		44.2	58.3	50	51
Education level b	First degree	21.0%	20.7%	20.9%	17.1%
	Second degree	18.7%	26.1%	21.7%	49.1%
	Higher ED	60.3%	53.2%	57.4%	33.8%
Labor status b	Employed	69.2%	41.3%	57.8%	48.5%
	Unemployed	9.1%	6.4%	8.0%	9.2%
	Inactive	21.7%	52.3%	34.2%	42.3%

^aContinuous population register, official population data as of January 1, 2021

^bEconomically active population survey (EAPS), first quarter 2021.

National Statistics Institute of Spain (INE).

The next section develops the methods followed for correcting biases in both probability and nonprobability samples and blending the data so that they can be analyzed as a single data set.

3. METHODS

3.1. Context and survey design

Let U denote a finite population of size N, $U=\{1,\text{…},i,\text{…},N\}$. Let $s_r$ be a probability sample of size $n_r$ selected from U under a probability sampling design $(s_r,p_r)$ with ${\pi }_i={\sum }_{s_r\ni i}{p}_r(s_r)$ the first‐order inclusion probability for individual i. Let $s_v$ be a nonprobability (volunteer) sample of size $n_v$, self‐selected from U. Let y be the variable of interest in the survey estimation and let ${\mathbf{x}}_i$ be the values presented by individual i for a vector of covariates $\mathbf{x}$. The variable of interest and the covariates have been measured in both samples.

The population total, Y, can be estimated via the Horvitz–Thompson estimator:

$${\widehat{Y}}_R=\sum _{i\in s_r}{d}_i{y}_i$$ (1)

being $d_i=1/{\pi }_i$. This estimator is design‐unbiased of the population total if there is not lack of response. The design‐based variance of this estimator is given by

$$V_p({\widehat{Y}}_R)=\sum _{i,j\in U}\frac{y_i}{{\pi }_i}\frac{y_j}{{\pi }_j}\left({\pi }_{ij}-{\pi }_i{\pi }_j\right),$$ (2)

where ${\pi }_{ij}$ are the second‐order probabilities of the sampling design $p_r$. If ${\pi }_{ij}>0$ $\forall (i,j)$, an unbiased estimator is given by

$${\widehat{V}}_p({\widehat{Y}}_R)=\sum _{i,j\in s_r}\frac{{\pi }_{ij}-{\pi }_i{\pi }_j}{{\pi }_{ij}}\frac{y_i}{{\pi }_i}\frac{y_j}{{\pi }_j}.$$ (3)

Large‐scale surveys generally have sample units that do not provide the desired data. In order to mitigate the effects of nonresponse on survey estimates, adjustments are made to the estimator after the data have been collected. Various nonresponse adjustments can be made to the survey data ranging from simple nonresponse adjustment cell methods to more advanced nonresponse propensity adjustments, being calibration weighting (Särndal & Lundström, 2005) the most popular. In the reweighting process, the design weights $d_i$ are replaced by new weights ${\stackrel{\sim }{d}}_i$ that are used for the construction of the estimator given by (1).

Y can be also estimated with the naive estimator based on the sample mean of y in $s_v$:

$${\widehat{Y}}_v=N\sum _{i\in s_v}\frac{y_i}{n_v}.$$ (4)

If the convenience sample $s_V$ suffers from selection bias, this estimator will provide biased results. This can happen if there is an important fraction of the population with zero chance of being included in the sample (coverage bias) and if there are significant differences in the inclusion probabilities among the different members of the population (selection) (Couper, 2011; Elliott & Valliant, 2017).

3.2. Estimating propensities in the nonprobability sample

In this context, PSA can be used to reduce the selection bias that would affect the unweighted estimates. This approach aims to estimate the propensity of an individual to be included in the nonprobability sample by combining the data from both samples, $s_r$ and $s_v$.

Propensity scores, ${\pi }_{vi}$, can be defined as the propensity of the ith individual of participating in the survey, this is, the probability that $I_{vi}=1$, being $I_{vi}$ the indicator variable for unit i being included in the sample $s_v$

$$I_{vi}=\left\{\begin{array}{cc}1\hfill & i\in s_v\hfill \\ 0\hfill & i\in U-s_v\hfill \end{array}\right.,i=1,\text{…},N.$$ (5)

PSA assumes that the selection mechanism of $s_V$ is ignorable and follows a parametric model:

$${\pi }_{vi}=P(I_{vi}=1|{\mathbf{x}}_i)=p_i(\mathbf{x})=m(\gamma ,{\mathbf{x}}_i)i=1,\text{…},N$$ (6)

for some known function $m(·)$ with second continuous derivatives with respect to an unknown parameter γ.

The procedure is to estimate the propensity scores by using data of both, the volunteer and the probability sample. The maximum likelihood estimator (MLE) of ${\pi }_{vi}$ is $m(\widehat{\gamma },{\mathbf{x}}_i)$ where $\widehat{\gamma }$ maximizes the log‐likelihood function:

$$\begin{array}{ccc}\hfill l(\gamma )& =& \sum _U(I_{vi}\log (m(\gamma ,{\mathbf{x}}_i))+(1-I_{vi})\log (1-m(\gamma ,{\mathbf{x}}_i))\hfill \\ & =& \sum _{s_v}\log \frac{m(\gamma ,{\mathbf{x}}_i)}{1-m(\gamma ,{\mathbf{x}}_i)}+\sum _U\log (1-m(\gamma ,{\mathbf{x}}_i)).\hfill \end{array}$$ (7)

As is usual in survey sampling, we consider the pseudo‐likelihood since we do not observe all units in the finite population:

$$\stackrel{\sim }{l}(\gamma )=\sum _{s_v}\log \frac{m(\gamma ,{\mathbf{x}}_i)}{1-m(\gamma ,{\mathbf{x}}_i)}+\sum _{s_p}\frac{1}{{\pi }_i}log(1-m(\gamma ,{\mathbf{x}}_i)).$$ (8)

Once the MLE of ${\pi }_{vi}$ has been obtained, we transform the estimated propensities ${\widehat{\pi }}_{vi}=m(\widehat{\gamma },{\mathbf{x}}_i)$ to weights by inverting them (Valliant, 2020) and obtain the inverse probability weighted (IPW) estimator:

$${\widehat{Y}}_{IPW}=\sum _{i\in s_V}{y}_i/{\widehat{\pi }}_{vi}=\sum _{i\in s_V}{y}_i{d}_{vi.}$$ (9)

The properties of the IPW estimators (under both the model for the propensity scores and the survey design for the probability sample) are developed in Chen et al. (2019). These authors prove that under certain regularity conditions and assuming the logistic regression model for the propensity scores, the IPW estimator ${\widehat{Y}}_{IPW}$ is asymptotically unbiased for the population total (${\widehat{Y}}_{IPW}-Y=O_p(n_v^{-1/2}$)) and they obtain an asymptotic expression for its variance:

$$V({\widehat{Y}}_{IPW})=\sum _U{(y_i/{\widehat{\pi }}_{vi}-{\mathbf{b}}_1^T{\mathbf{x}}_i)}^2(1-{\widehat{\pi }}_{vi}){\widehat{\pi }}_{vi}+{\mathbf{b}}_1^{T}D{\mathbf{b}}_1,$$ (10)

where ${\mathbf{b}}_1^T={\sum }_U(1-{\widehat{\pi }}_{vi})y_i{\mathbf{x}}_i^T/{\sum }_U{\widehat{\pi }}_{vi}(1-{\widehat{\pi }}_{vi}){\mathbf{x}}_i{\mathbf{x}}_i^T$, and $D=V_p({\sum }_{i\in s_r}{d}_i{\widehat{\pi }}_{vi}{\mathbf{x}}_i)$ where $V_p$ denotes the design‐based variance under the sampling design p.

The above asymptotic variance provides a plug‐in method for variance estimation. Thus, we propose the variance estimator given by

$$\widehat{V}({\widehat{Y}}_{IPW})=\sum _{s_v}{(y_i/{\widehat{\pi }}_{vi}-{\stackrel{\sim }{\mathbf{b}}}_1^T{\mathbf{x}}_i)}^2(1-{\widehat{\pi }}_{vi})+{\stackrel{\sim }{\mathbf{b}}}_1^T\stackrel{\sim }{D}{\stackrel{\sim }{\mathbf{b}}}_1,$$ (11)

where

$${\stackrel{\sim }{\mathbf{b}}}_1^T=\sum _{s_v}\frac{(1-{\widehat{\pi }}_{vi})}{{\widehat{\pi }}_{vi}}{y}_i{\mathbf{x}}_i^T/\sum _{s_v}(1-{\widehat{\pi }}_{vi}){\mathbf{x}}_i{\mathbf{x}}_i^T$$ (12)

and

$$\stackrel{\sim }{D}=\sum _{i,j\in s_r}\frac{{\pi }_{ij}-{\pi }_i{\pi }_j}{{\pi }_{ij}}\frac{{\widehat{\pi }}_{vi}{\widehat{\pi }}_{vj}}{{\pi }_i{\pi }_j}{\mathbf{x}}_i{\mathbf{x}}_i^T.$$ (13)

This estimator require knowledge of second‐order inclusion probabilities, which are often impossible to compute or unavailable to data analysts for complex sampling designs. There are some alternative estimators of the design variance $V_p({\sum }_{i\in s_r}{d}_i{\widehat{\pi }}_{vi}{\mathbf{x}}_i)$ without involving ${\pi }_{ij}$ (Haziza et al., 2008; Särndal, 1996). From a practical viewpoint is better the use of jackknife and bootstrap techniques (Wolter, 2007) by their applicability in many cases and under different conditions and because they are implemented in general purpose software packages.

3.3. Combining the probability and the nonprobability samples

We are going to consider the situation in which there are no coverage biases in either the probability or the nonprobability sample. Let $U_r$ and $U_v$ be two sampling frames, in this situation $U_r$ and $U_v$ coincide with the population under study U.

A simple estimator is calculated by weighting the estimators obtained from each sample:

$${\widehat{Y}}_{com}=\alpha {\widehat{Y}}_R+(1-\alpha ){\widehat{Y}}_{IPW},$$ (14)

where α is a nonnegative constant such that $0\le \alpha \le 1$.

We denote the values of the variance of ${\widehat{Y}}_R$ and the MSE of the estimator of ${\widehat{Y}}_{IPW}$ by V ₁, V ₂, respectively. Since frames $U_r$ and $U_v$ are sampled independently, the MSE of ${\widehat{Y}}_{com}$ is given by

$$MSE({\widehat{Y}}_{com})={\alpha }^2{V}_1+{(1-\alpha )}^2{V}_2,$$ (15)

where the first component of the right‐hand side is computed under the sampling design $p_R$ and the second one under the selection mechanism model.

Next, we consider the problem of selection of the best coefficients. The value of α that minimizes the variance in (15) is given by

$${\alpha }_{opt}=\frac{V_2}{V_1+V_2}$$ (16)

and the minimum MSE is

$$MSE({\widehat{Y}}_{opt})=\frac{V_1{V}_2}{V_1+V_2},$$ (17)

but the values V ₁ and V ₂ are unknown. One possibility is to estimate them from the sample and substitute them in the previous expression. In this way, we can calculate the coefficients ${\alpha }_o=\frac{{\widehat{V}}_2}{{\widehat{V}}_1+{\widehat{V}}_2}$, where ${\widehat{V}}_1$ and ${\widehat{V}}_2$ are estimators of the variance of ${\widehat{Y}}_R$ and the MSE of ${\widehat{Y}}_{IPW}$ (e.g., the estimators obtained in Equations 3 and 11 ). Other solutions are to weight each estimator by the weight that sample has in the total sample ${\alpha }_n=n_r/(n_r+n_v)$ or ${\alpha }_e=0.5$.

The resulting estimator (14) can be rewritten as

$${\widehat{Y}}_{com}=\sum _{i\in s}{y}_i{d}_i^{★}$$ (18)

being $s=s_r\bigcup s_v$ and

$$d_i^{★}=\left\{\begin{array}{cc}\alpha d_i\hfill & \text{if}i\in s_r,\hfill \\ (1-\alpha )d_{vi}\hfill & \text{if}i\in s_v.\hfill \end{array}\right.$$ (19)

Besides the modification of weights for handling selection bias, other adjustments may also be carried out to take into account auxiliary information. Calibration (Deville & Särndal, 1992) is the most used technique for weights adjustment, aiming at ensuring consistency among estimates of different sample surveys and some improving the precision of estimators (Devaud & Tillé, 2019; Rueda et al., 2006). Calibration weighting was previously used in this context by Disogra et al. (2011) who proposes calibrating auxiliary information in the nonprobability sample with that in the probability sample, so that after calibration the weighted distribution of the nonprobability sample is similar to that of the target population.

Using the calibration paradigm, we wish to modify, as little as possible, basic weights $d_i^{★}$ to obtain new weights $w_i^{★}$, for $i\in s$ to account for auxiliary information and derive a more accurate estimation of the total Y. Let ${\underset{\_}{\mathrm{z}}}_i=(z_{1i},\text{…},z_{pi})$ be the value taken on unit i by a vector of auxiliary variables $\underset{\_}{\mathrm{z}}$ of which we assume to know the population total ${\underset{\_}{\mathrm{t}}}_z={\sum }_{k=1}^N{\underset{\_}{\mathrm{z}}}_k$ and that is available for the units of each sample. The vector of calibration variables ${\underset{\_}{\mathrm{z}}}_i$ does not have to match the vector $\mathbf{x}$ used in the propensity model.

A general calibration estimator can be defined as

$${\widehat{Y}}_{CAL}=\sum _{i\in s}{w}_i^{★}{y}_i,$$ (20)

where $w_i^{★}$ is such that

$$\min \sum _{i\in s}G(w_i^{★},d_i^{★})\text{s.t.}\sum _{i\in s}{w}_i^{★}{\underset{\_}{\mathrm{z}}}_i={\underset{\_}{\mathrm{t}}}_z,$$ (21)

where $G(w,d)$ is a distance measure satisfying the usual conditions required in the calibration paradigm. Given the set of constraints, different calibration estimators are obtained by using alternative distance measures. If we take the Euclidean type of distance function $G(w_i^{★},d_i^{★})={(w_i^{★}-d_i^{★})}^2/2d_i^{★}$, we can obtain an analytic solution that produces the linear calibration estimator:

$${\widehat{Y}}_{\mathrm{CAL}}=\sum _{i\in s}{w}_i^{★}{y}_i.$$ (22)

The asymptotic properties of this calibration estimator can be obtain by adapting the asymptotic framework of Isaki and Fuller (1982), to the case of the dual‐frame finite population as in Ranalli et al. (2016).

3.4. Using machine‐learning techniques

Logistic models are often used to estimate the propensity to participate in the survey of each individual. In recent decades, numerous machine‐learning (ML) methods have been considered in the literature for the treatment of nonprobability samples and have proved to be more suitable for regression and classification than linear regression methods (Castro‐Martín et al., 2020; Chu & Beaumont, 2019; Ferri‐García & Rueda, 2020; Kern et al., 2020).

Among the most important ML methods are boosting algorithms. Boosting algorithms have been applied in propensity score weighting (Lee et al., 2010, 2011) showing on average better results than conventional parametric regression models. A common machine‐learning algorithm under the Gradient Boosting framework is XGBoost (Chen & Guestrin, 2016). Given its theoretical advantage over Gradient Boosting, which could lead to even better results in a broader range of situations (Castro‐Martín et al., 2021b), we propose the use of this method for estimating propensities that will be used to define the estimators previously proposed.

XGBoost works as a decision tree ensemble. Decision trees are basic machine‐learning models which define split points for the auxiliary variables until reaching a final node containing the corresponding prediction. Once K decision trees are trained, the final propensity given by XGBoost is given by the following formula:

$$\begin{array}{c}\hfill {\widehat{\pi }}_{xgi}=\varphi ({\mathbf{x}}_i)=\sum _{k=1}^K{f}_k({\mathbf{x}}_i),f_k\in \mathcal{F},\end{array}$$ (23)

where $\mathcal{F}=\{f(\mathbf{x})={\omega }_{q(\mathbf{x})}\}$; with $q:{\mathbb{R}}^m\to T$ being the structure of a tree that calculates the final node j, with a value of ${\omega }_j$, associated with ${\mathbf{x}}_i$.

Similarly to logistic regression, the pseudo log‐likelihood function (8) is maximized. However, a regularizing function is also considered in order to penalize complex decision trees:

$$\mathrm{\Omega }(f)=\gamma T+\frac{1}{2}\lambda {\parallel \omega \parallel }^2,$$ (24)

where T is the number of final nodes and γ and λ are hyperparameters. Therefore, the final objective function is defined as

$$\begin{array}{c}\hfill \mathcal{L}(\varphi )=\sum _{i\in s}{l}_{loss}({\widehat{\pi }}_{xgi},I_{vi})+\sum _k\mathrm{\Omega }(f_k),\end{array}$$ (25)

where $l_{loss}$ is the logistic loss.

In order to minimize this objective function, each tree is trained iteratively. In this manner, the following function is minimized when training the tth decision tree:

$$\begin{array}{c}\hfill {\mathcal{L}}^{(t)}=\sum _{i\in s}{l}_{loss}(I_{vi},{\widehat{\pi }}_{xgi}^{(t-1)}+f_t(x_i))+\mathrm{\Omega }(f_t),\end{array}$$ (26)

where ${\widehat{\pi }}_{xgi}^{(t-1)}$ is the propensity given by the previous iteration. The process is optimized via the Gradient Tree Boosting method (Friedman, 2001).

However, the importance of choosing the right hyperparameters has also been underlined for the proper functioning of the algorithm. Therefore, a grid search of the optimal parameters is also performed before training. Each considered set is validated with cross‐validation (Refaeilzadeh et al., 2009). The grid includes the following hyperparameters:

• (i)Maximum depth: The depth limit which is applied to each tree forming the ensemble. The considered values are 1, 2, and 3.
• (ii)Number of rounds: The number of boosting iterations which are computed. The considered values are 50, 100, and 150.
• (iii)Learning rate: A step size shrinkage rate used in order to avoid overfitting. The considered values are 0.3 and 0.4.
• (iv)Colsample by tree: The ratio of variables considered when training the trees. The variables are chosen by simple random sampling independently for each tree. The considered values are 0.6 and 0.8.
• (v)Subsample: The ratio of training data considered by simple random sampling at each boosting iteration. The considered values are 0.5, 0.75, and 1.

XGBoost, including the hyperparameter optimization process, can be easily applied with Caret (Kuhn, 2018), an R package. The proposed estimators may then be reformulated in the following manner:

$${\widehat{Y}}_{XIPW}=\sum _{i\in s_v}{y}_i/{\widehat{\pi }}_{xgi}=\sum _{i\in s_v}{y}_i{d}_{xgi},$$ (27)

$${\widehat{Y}}_{xgcom}=\sum _{i\in s_v}{y}_i{d}_{xgi}^{★}$$ (28)

being

$$d_{xgi}^{★}=\left\{\begin{array}{cc}\alpha d_i\hfill & \text{if}i\in s_r,\hfill \\ (1-\alpha )d_{xgi}\hfill & \text{if}i\in s_v,\hfill \end{array}\right.$$ (29)

and

$${\widehat{Y}}_{\mathrm{XCAL}}=\sum _{i\in s}{w}_{xgi}^{★}{y}_i,$$ (30)

where $w_{xgi}^{★}$ are the weights obtained after applying calibration to $d_{xgi}^{★}$.

It is not easy to obtain an explicit expression for the MSE of this estimator from which to obtain error estimators since the asymptotic behavior of the XGBoost method is not studied in the survey sampling context. In the simulation section and in the application, we will use resampling methods for the construction of confidence intervals.

4. SIMULATION STUDY

We carry out a simulation study to see which of the proposed estimators works best.

We simulate a population of size 500,000 in which we have three target variables y ₁ y ₂, and y ₃, and eight auxiliary variables to perform the PSA algorithms and the calibration, $x_1,\text{…},x_8$. Four variables ($x_1,x_3,x_5,x_7$) follow a Bernoulli distribution with $p=0.5$ and four others ($x_2,x_4,x_6,x_8$) follow Normal distributions with a standard deviation of one and a mean parameter dependent on the value of the previous Bernoulli variable for each individual

$$\begin{array}{c}\hfill x_{1i},x_{3i},x_{5i},x_{7i}\sim B(0.5),i\in U\\ \hfill x_{ji}\sim N({\mu }_{ji},1),i\in U,j=2,4,6,8,\\ \hfill {\mu }_{ji}=\left\{\begin{array}{cc}2,\hfill & \hfill \text{if}{x}_{(j-1)i}=1,\\ 0,\hfill & \hfill \text{if}{x}_{(j-1)i}=0,\end{array}\right.i\in U,j=2,4,6,8.\end{array}$$ (31)

The target variables were simulated as follows:

$$\begin{array}{c}\hfill y_{1i}=N(10,4)+5{\pi }_i,i\in U,\\ \hfill y_{2i}=N(10,4)+2(x_{7i}=1)-2(x_{7i}=0)+x_{8i}+5{\pi }_i,i\in U,\\ \hfill y_{3i}=\left\{\begin{array}{cc}1\hfill & \text{if}{y}_1>12.87,\hfill \\ 0\hfill & \text{if}{y}_1\le 12.87,\hfill \end{array}\right.i\in U.\end{array}$$ (32)

Variables y ₁ and y ₂ are treated as numeric variables in the estimation procedure, while variable y ₃ is treated as binary, where the class 1 represents a feature of interest. The different types of target variables allow the results to reproduce the behavior of different kinds of population parameter estimation that are often done in official statistics.

Five hundred iterations are carried out and in each one of them we draw a probability sample of size $n_P=250$ and a nonprobability sample of sizes $n_{NP}=500;1000;2000$. The probability sample is drawn by simple random sampling without replacement (SRSWOR) from the full population, but we include a mechanism to reproduce nonresponse bias in our simulation, which is a prevalent bias in real probability surveys. This mechanism works by defining the probability of response, $p_R$, for each individual of the pseudopopulation:

$$p_{Ri}=\frac{\text{exp}(-2-(x_{1i}=1)+0.15·x_{2i}+(x_{5i}=1)-0.06·x_{6i})}{1+\text{exp}(-2-(x_{1i}=1)+0.15·x_{2i}+(x_{5i}=1)-0.06·x_{6i})},i=1,2,\text{…},N.$$ (33)

If the individual i is selected for sample $s_P$, a Bernoulli trial with probability $p=p_{Ri}$ is performed, and if the result is 1, the individual is finally included in $s_P$. If the result is 0, the individual is not selected. Therefore, the final probability sample has a random size $n_P\le 250$ (specifically the average sample size over the 500 iterations is 215). The nonprobability sample is drawn with a Poisson sampling design where π is proportional to the vector of inclusion probabilities. This probability was made dependent on $x_5,x_6,x_7$, and x ₈ (which allowed the experiment to cover Missing At Random situations) as:

$$\ln \left(\frac{{\pi }_i}{1-{\pi }_i}\right)=-0.5+2.5(x_{5i}=1)+\sqrt{2\pi }{x}_{6i}{x}_{8i}-2.5(x_{7i}=1),i\in U.$$ (34)

The first four explanatory variables ($x_1,x_2,x_3,x_4$) do not have any relationship with any target variable or any other explanatory variable. The propensity models are fitted using all of the eight variables, but the first four variables only add noise to the final propensity model. This is done in order to simulate a common situation in real‐world studies, where irrelevant variables are included in propensity models, and therefore constituting a misspecification of the model.

The evaluated estimators are the following:

• (i)Reference estimator (${\widehat{Y}}_{REF}$): the two samples are joined and calibration is performed to obtain the final estimator.
• (ii)Elliott and Haviland estimator (${\widehat{Y}}_{EH}$): we join the probabilistic and nonprobabilistic sample and obtain the final estimator using the formulas proposed in the paper by Elliott and Haviland (2007).
• (iii)Based on the article by Robbins et al. (2021), we calculate four estimators:
  • (i)the disjoint propensity score (DPS) weights estimator (section 2.1.1. of Robbins et al., 2021): ${\widehat{Y}}_{RDR1}$
  • (ii)the simultaneous weights estimator (section 2.1.2. of Robbins et al., 2021): ${\widehat{Y}}_{RDR2}$
  • (iii)the disjoint calibration (DC) weights estimators (section 2.2 of Robbins et al., 2021):${\widehat{Y}}_{RDR3}$
  • (iv)the combined calibration estimator (section 2.2 of Robbins et al., 2021): ${\widehat{Y}}_{RDR4}$
• (iv)Propensities estimator (${\widehat{Y}}_{PPSA}$): the probability and nonprobability sample propensities are obtained, both samples are merged and calibration is performed to obtain the final estimator using the inverse of propensities as initial weights.
• (v)Calibration—PSA estimator (${\widehat{Y}}_{CPSA}$): calibration is performed in the probability sample (${\widehat{Y}}_{calR}$) using the variables $x_1,x_3,x_5$, and x ₆, and in the nonprobability sample we calculate the propensities by XGBoost using all variables that are common to both the probability and the nonprobability sample ($x_1,\text{…},x_8$). To obtain the final estimator, we combine ${\widehat{Y}}_{calR}$ and ${\widehat{Y}}_{XIPW}$ in several ways, considering α_0.5, ${\alpha }_n$, and ${\alpha }_0=\frac{\widehat{ECM}({\widehat{Y}}_{XIPW})}{\widehat{V}({\widehat{Y}}_{calR})+\widehat{ECM}({\widehat{Y}}_{XIPW})}$. We will denote these estimators ${\widehat{Y}}_{CPSA-0.5-x}$, ${\widehat{Y}}_{CPSA-n-x}$, and ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$.
  $\widehat{V}({\widehat{Y}}_{calR})$ is calculated with the residuals' method using the $calibev$ function of sampling package (Tillé & Matei, 2021) and $\widehat{ECM}({\widehat{Y}}_{XIPW})$ is calculated as a sum of two terms:

  $$\widehat{ECM}({\widehat{Y}}_{XIPW})=\sum _{i,j\in s_v}\frac{{\widehat{\pi }}_{xgi}{\widehat{\pi }}_{xgj}-{\widehat{\pi }}_{xgi}{\widehat{\pi }}_{xgj}}{{\widehat{\pi }}_{xgi}{\widehat{\pi }}_{xgj}}\frac{y_i}{{\widehat{\pi }}_{xgi}}\frac{y_j}{{\widehat{\pi }}_{xgj}}+\widehat{B^2},$$ (35)

  the first that estimates the variance of ${\widehat{Y}}_{XIPW}$ and $\widehat{B}={\widehat{Y}}_{XIPW}-{\widehat{Y}}_{calR}$ that estimates the bias as is considered in Elliott and Haviland (2007).

  ${\widehat{Y}}_{CPSA-0.5-l}$, ${\widehat{Y}}_{CPSA-n-l}$, and ${\widehat{Y}}_{CPSA-{\alpha }_0-l}$ are calculated in a similar way but changing XGBoost by logistic regression in the estimation of the propensities.

In all the estimators in which the propensities are calculated, we use both XGBoost and logistic regression methods to see if there are differences in the results derived from the classification method used. We use x for XGBoost and l for logistic regression in the subscripts to distinguish among methods.

The procedure is repeated across 500 iterations, and finally the Absolute Relative Bias (|RB|) and the root mean square relative error (RMSRE) is obtained for each method

$$\begin{array}{c}\hfill |RB|=\frac{1}{B}\sum _{i=1}^B\frac{|\widehat{Y_i}-Y|}{Y}\ast 100\\ \hfill RMSRE=\sqrt{\frac{1}{B}{\sum }_{i=1}^B{\left(\frac{\widehat{Y_i}-Y}{Y}\right)}^2}\ast 100,\end{array}$$ (36)

where B is the number of iterations, $\widehat{Y_i}$ is the estimator based on the iteration i, and Y is the true value.

In Tables 2, 3, and 4, values of |RB| and RMSRE can be seen for each of the proposed estimators.

TABLE 2.

Values of |RB| and RMSRE, for each estimator and combination of sample sizes, in the estimation of target variable y ₁

	$n_P\le$ 250 , $n_{NP}$=500		$n_P\le$ 250, $n_{NP}$=1000		$n_P\le$ 250, $n_{NP}$=2000
	|RB|	RMSRE	|RB|	RMSRE	|RB|	RMSRE
${\widehat{Y}}_{REF}$	4.031	4.282	3.935	4.179	3.990	4.188
${\widehat{Y}}_{EH}$	1.954	2.415	2.085	2.584	2.004	2.488
${\widehat{Y}}_{PPSA-x}$	2.025	2.537	2.909	3.574	3.661	4.506
${\widehat{Y}}_{PPSA-l}$	3.641	3.926	3.574	3.856	3.644	3.856
${\widehat{Y}}_{RDR1-x}$	5.489	5.663	8.141	8.211	9.673	9.698
${\widehat{Y}}_{RDR1-l}$	5.489	5.663	8.141	8.211	9.673	9.698
${\widehat{Y}}_{RDR2-x}$	2.562	2.990	2.641	3.125	3.359	3.701
${\widehat{Y}}_{RDR2-l}$	5.865	6.028	7.462	7.546	8.621	8.652
${\widehat{Y}}_{RDR3-x}$	3.057	3.425	2.544	2.966	2.005	2.391
${\widehat{Y}}_{RDR3-l}$	4.379	4.603	4.269	4.488	4.329	4.498
${\widehat{Y}}_{RDR4-x}$	3.496	3.851	3.081	3.493	2.320	2.722
${\widehat{Y}}_{RDR4-l}$	5.648	5.816	6.744	6.837	7.636	7.678
${\widehat{Y}}_{CPSA-0.5-x}$	3.270	3.621	2.702	3.120	2.084	2.465
${\widehat{Y}}_{CPSA-0.5-l}$	4.425	4.646	4.302	4.516	4.359	4.521
${\widehat{Y}}_{CPSA-n-x}$	4.495	4.792	4.327	4.707	3.470	3.937
${\widehat{Y}}_{CPSA-n-l}$	6.131	6.283	7.109	7.195	7.847	7.887
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	1.869	2.305	1.920	2.360	1.757	2.185
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	1.912	2.360	1.980	2.445	1.897	2.369

TABLE 3.

Values of |RB| and RMSRE, for each estimator and combination of sample sizes, in the estimation of target variable y ₂

	$n_P\le$ 250, $n_{NP}$=500		$n_P\le$ 250, $n_{NP}$=1000		$n_P\le$ 250, $n_{NP}$=2000
	|RB|	RMSRE	|RB|	RMSRE	|RB|	RMSRE
${\widehat{Y}}_{REF}$	4.453	4.749	4.449	4.701	4.501	4.696
${\widehat{Y}}_{EH}$	2.423	3.045	2.274	2.904	2.268	2.850
${\widehat{Y}}_{PPSA-x}$	2.032	2.512	2.702	3.387	3.607	4.466
${\widehat{Y}}_{PPSA-l}$	3.112	3.546	3.053	3.491	3.183	3.600
${\widehat{Y}}_{RDR1-x}$	7.106	7.296	9.933	10.011	11.459	11.492
${\widehat{Y}}_{RDR1-l}$	7.106	7.296	9.933	10.011	11.459	11.492
${\widehat{Y}}_{RDR2-x}$	2.496	2.985	2.547	3.065	3.143	3.653
${\widehat{Y}}_{RDR2-l}$	6.090	6.393	8.011	8.160	9.414	9.493
${\widehat{Y}}_{RDR3-x}$	3.376	3.765	2.740	3.181	2.298	2.796
${\widehat{Y}}_{RDR3-l}$	4.153	4.463	4.105	4.405	4.190	4.424
${\widehat{Y}}_{RDR4-x}$	3.745	4.096	3.243	3.653	2.522	3.004
${\widehat{Y}}_{RDR4-l}$	5.371	5.582	6.400	6.523	7.262	7.336
${\widehat{Y}}_{CPSA-0.5-x}$	3.505	3.854	2.871	3.275	2.311	2.762
${\widehat{Y}}_{CPSA-0.5-l}$	4.207	4.478	4.119	4.360	4.201	4.401
${\widehat{Y}}_{CPSA-n-x}$	4.825	5.109	4.610	4.970	3.779	4.321
${\widehat{Y}}_{CPSA-n-l}$	5.832	6.016	6.741	6.852	7.459	7.528
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	1.932	2.394	1.821	2.287	1.740	2.166
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	1.961	2.434	1.879	2.369	1.855	2.311

TABLE 4.

Values of |RB| and RMSRE, for each estimator and combination of sample sizes, in the estimation of target variable y ₃

	$n_P\le$ 250, $n_{NP}$=500		$n_P\le$ 250, $n_{NP}$=1000		$n_P\le$ 250 $n_{NP}$=2000
	|RB|	RMSRE	|RB|	RMSRE	|RB|	RMSRE
${\widehat{Y}}_{REF}$	9.652	10.500	9.677	10.392	9.510	10.125
${\widehat{Y}}_{EH}$	5.657	6.991	5.506	6.897	5.680	7.101
${\widehat{Y}}_{PPSA-x}$	5.446	6.785	7.462	9.034	9.951	11.792
${\widehat{Y}}_{PPSA-l}$	8.748	9.676	8.752	9.515	8.690	9.379
${\widehat{Y}}_{RDR1-x}$	13.114	13.715	19.896	20.108	23.223	23.307
${\widehat{Y}}_{RDR1-l}$	13.114	13.715	19.896	20.108	23.223	23.307
${\widehat{Y}}_{RDR2-x}$	6.198	7.467	6.274	7.530	8.006	8.910
${\widehat{Y}}_{RDR2-l}$	14.009	14.588	18.213	18.473	20.660	20.767
${\widehat{Y}}_{RDR3-x}$	7.377	8.550	6.437	7.581	5.031	6.133
${\widehat{Y}}_{RDR3-l}$	10.489	11.302	10.436	11.102	10.333	10.901
${\widehat{Y}}_{RDR4-x}$	8.403	9.512	7.505	8.658	5.720	6.839
${\widehat{Y}}_{RDR4-l}$	13.498	14.127	16.461	16.795	18.259	18.403
${\widehat{Y}}_{CPSA-0.5-x}$	7.854	8.995	6.822	7.952	5.221	6.312
${\widehat{Y}}_{CPSA-0.5-l}$	10.590	11.385	10.494	11.151	10.394	10.944
${\widehat{Y}}_{CPSA-n-x}$	10.641	11.695	10.851	11.985	8.403	9.855
${\widehat{Y}}_{CPSA-n-l}$	14.644	15.224	17.307	17.623	18.765	18.904
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	5.255	6.453	5.300	6.512	5.155	6.435
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	5.272	6.474	5.849	7.303	5.214	6.509

It can be observed that calibration in both samples is not enough to completely remove selection bias, although this approach provides smaller |RB| and RMSRE than other methods. The method proposed by Elliott and Haviland (2007) is vastly efficient at removing part of the selection bias that exists in the simulation data, where the selection mechanism of the nonprobability sample could be considered Missing At Random.

The combination of calibration and PSA (propensity weights are used as base weights in calibration) reduces |RB| and RMSRE, particularly when the algorithm used in PSA is XGBoost, although the advantage of this algorithm vanishes as the nonprobability sample size increases.

The behavior of the estimators considered in Robbins et al. (2021) is very diverse. In some cases, particularly ${\widehat{Y}}_{RDR1}$, the relative bias is even larger than the case where only calibration is used. This could happen because some of the assumptions made for these estimators do not apply in our simulation study. On the other hand, ${\widehat{Y}}_{RDR2}$ and ${\widehat{Y}}_{RDR3}$ are able to reduce |RB| and RMSRE in comparison to ${\widehat{Y}}_{REF}$, as long as XGBoost is used; in fact, they seem to be particularly sensitive to the algorithm used for propensity estimation.

${\widehat{Y}}_{PPSA-x}$ works better when the sample sizes $n_P$ and $n_{NP}$ are similar, but the behavior gets worse as the sample size $n_{NP}$ increases. The behavior of ${\widehat{Y}}_{RDR3-x}$ is the opposite: as the sample size $n_{NP}$ increases, the estimator gets better. This is something that can be observed for ${\widehat{Y}}_{EH}$ as well.

Finally, the behavior of the proposed estimators ${\widehat{Y}}_{CPSA}$ depends on the factor used in weighting. The best estimator in our simulator has been, by a huge margin, ${\widehat{Y}}_{CPSA-{\alpha }_0}$, which is the estimator that weights the samples by the MSE.

It is worth mentioning that the results on |RB| and RMSRE are very similar between methods and sample sizes. This can be explained by the fact that the target variables y ₁ and y ₂ have a very similar behavior, only varying because of the relationship between y ₂ and the variables x ₇ and x ₈. The Missing At Random nature of both variables, which means that the ignorability assumption of PSA applies in this study, explains why the application of adjustment methods can lead to substantial reductions in |RB| and RMSRE.

Regarding the difference between the continuous variables, y ₁ and y ₂, and the binary variable y ₃, it is noticeable that the results of every single method are worse in the estimation of y ₃. More precisely, the values of |RB| and RMSRE in the estimation of y ₃ using any method are more than the double of their counterpart in the estimation of y ₁ and y ₂, and the differences tend to increase as $n_{NP}$ increases. The smallest difference can be observed for ${\widehat{Y}}_{RDR1}$ (between 2.08 and 2.20 times larger |RB| and between 2.12 and 2.21 times larger RMSRE for y ₃ in comparison to the average of y ₁ and y ₂, regardless the algorithm used), while the largest difference can be observed for ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$ (between 2.77 and 2.95 times larger |RB|, and between 2.75 and 2.96 times larger RMSRE for y ₃ in comparison to the average of y ₁ and y ₂).

For the estimators that work best in the first part of the simulation, we perform a comparison between the estimations of jackknife variance, also calculating the length of the intervals obtained at 95% confidence level and their real coverage, considering the three initial sample sizes. The results obtained considered 500 iterations can be seen in the Tables 5, 6, and 7. The results show that ${\widehat{Y}}_{REF}$, ${\widehat{Y}}_{RDR3-x}$, and ${\widehat{Y}}_{PPSA-x}$ present larger estimated variances and length of the confidence intervals in comparison to the rest of the estimators, and the difference increases as the sample size $n_{NP}$ gets larger. The coverage rates of the intervals are close to 0.95 for the proposed estimators ${\widehat{Y}}_{CPSA-{\alpha }_{0-x}},{\widehat{Y}}_{CPSA-{\alpha }_{0-l}}$ in different setups, especially when the sample sizes are large while the interval based on ${\widehat{Y}}_{REF}$ performs significantly poorer than the rest in terms of coverage. Thus, the intervals based on the proposed estimators ${\widehat{Y}}_{CPSA-{\alpha }_0}$ seem to perform well in terms of length and coverage, even when the size of the nonprobabilistic sample increases. It is also noticeable that the estimation of binary variable y ₃ yields confidence intervals with larger confidence intervals' mean coverage in comparison to continuous variables y ₁ and y ₂, which points out that variance estimation may be slightly more reliable in the binary case than in the continuous case, according to our simulation.

TABLE 5.

Mean jackknife estimate of the variance and confidence intervals' mean coverage and length from the simulation runs in the estimation of target variable y ₁

	$n_P\le$ 250, $n_{NP}$=500			$n_P\le$ 250, $n_{NP}$=1000			$n_P\le$ 250, $n_{NP}$=2000
	J. variance	Coverage	Length	J. variance	Coverage	Length	J. variance	Coverage	Length
${\widehat{Y}}_{REF}$	1.801	0.610	3.867	3.083	0.628	4.956	4.718	0.558	5.819
${\widehat{Y}}_{EH}$	0.099	0.948	1.230	0.099	0.936	1.231	0.100	0.952	1.238
${\widehat{Y}}_{PPSA-x}$	0.441	0.938	1.888 x	2.890	0.940	4.480	7.217	0.968	8.536
${\widehat{Y}}_{RDR3-x}$	1.102	0.820	3.254	1.720	0.884	4.148	3.475	0.972	6.075
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	0.086	0.942	1.149	0.084	0.932	1.135	0.088	0.948	1.152
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	0.089	0.940	1.169	0.090	0.940	1.173	0.104	0.952	1.259

TABLE 6.

Mean jackknife estimate of the variance and confidence intervals' mean coverage and length from the simulation runs in the estimation of target variable y ₂

	$n_P\le$ 250, $n_{NP}$=500			$n_P\le$ 250, $n_{NP}$=1000			$n_P\le$ 250, $n_{NP}$=2000
	J. variance	Coverage	Length	J. variance	Coverage	Length	J. variance	Coverage	Length
${\widehat{Y}}_{REF}$	19.259	0.582	12.054	36.202	0.568	16.214	54.922	0.542	19.548
${\widehat{Y}}_{EH}$	0.114	0.896	1.321	0.113	0.908	1.314	0.114	0.914	1.320
${\widehat{Y}}_{PPSA-x}$	3.104	0.932	3.765	9.887	0.960	8.360	26.854	0.976	15.752
${\widehat{Y}}_{RDR3-x}$	14.488	0.830	10.963	23.012	0.888	14.303	43.755	0.974	20.984
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	0.102	0.932	1.248	0.099	0.934	1.229	0.108	0.954	1.273
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	0.105	0.932	1.265	0.104	0.942	1.262	0.121	0.972	1.359

TABLE 7.

Mean jackknife estimate of the variance and confidence intervals' mean coverage and length from the simulation runs in the estimation of target variable y ₃

	$n_P\le$ 250, $n_{NP}$=500			$n_P\le$ 250, $n_{NP}$=1000			$n_P\le$ 250, $n_{NP}$=2000
	J. variance	Coverage	Length	J. variance	Coverage	Length	J. variance	Coverage	Length
${\widehat{Y}}_{REF}$	0.017	0.708	0.377	0.028	0.648	0.466	0.045	0.636	0.570
${\widehat{Y}}_{EH}$	0.001	0.952	0.140	0.001	0.960	0.141	0.001	0.960	0.141
${\widehat{Y}}_{PPSA-x}$	0.005	0.944	0.196	0.021	0.946	0.431	0.071	0.974	0.856
${\widehat{Y}}_{RDR3-x}$	0.011	0.882	0.323	0.023	0.944	0.455	0.034	0.976	0.602
${\widehat{Y}}_{CPSA-{\alpha }_0-x}$	0.001	0.962	0.133	0.001	0.930	0.132	0.001	0.934	0.127
${\widehat{Y}}_{CPSA-{\alpha }_0-l}$	0.001	0.964	0.134	0.001	0.934	0.142	0.001	0.972	0.142

5. APPLICATION TO A SURVEY ON THE SOCIAL EFFECTS OF COVID‐19 IN SPAIN

In this section, we apply the calibration and XGBoots PSA estimation method proposed in Section 3, to several variables that assess the impact of the COVID‐19 in Spain and compare the results with the measurements obtained when both probability and nonprobability‐based samples are merged and calibrated to correct observed deviations from population benchmarks in relevant sociodemographic variables, ${\widehat{Y}}_{REF}$.

IESA carried out a previous study comparing the probabilistic sample with the target population to study the possible difference between different population groups. The data set has 1644 observations and 101 variables. The variables of age, sex, autonomous community, municipal size, educational level, professional activity, and ideology were used. Once the biases were analyzed, raw data were weighted by iterative (raking) adjustments regarding municipality size, region (aggregated as NUTS‐1), age group, sex, and education level. We used these calibrated adjusted weights that were included in the data file provided by IESA, to calculate the estimator ${\widehat{Y}}_R$. This weight adjustment procedure has been used for several years in IESA surveys and has shown that it is good for correcting biases in the various waves of ESPACOV.

The propensity models are fitted using all variables available in the data set, previously eliminating those that are recodings of main variables.

In this studio, we calculate the estimation based on calibration and XGBoots PSA and their confidence interval to 95% of confidence level calculating the variance estimate using resampling techniques.

The variables analyzed are the following:

• (i)COVID‐19 infection (respondent) (V₁ )
• (ii)COVID‐19 infection (close relatives) (V₂ )
• (iii)Severity of infection – No symptoms (V₃ )
• (iv)Severity of infection – Mild symptoms (V₄ )
• (v)Severity of infection – Serious symptoms (V₅ )
• (vi)Severity of infection – Hospital admission (V₆ )
• (vii)Self‐assessed health status (V₇ )
• (viii)Mood self‐assessment (V₈ )
• (ix)Household income decreased as a result of COVID‐19 pandemic (V₉ )

Tables 8 and 9 and Figure 1 show the outcomes of these variables measuring these direct and indirect effects of the pandemic in Spain considering probability and nonprobability‐based samples separately as well as the integrated file using the estimation methods described above.

TABLE 8.

Estimates of selected variables on the direct impact of COVID‐19 in Spain from integrated data using a new estimation method based on calibration and XGBoost PSA (${\widehat{Y}}_{CPSA-{\alpha }_0-x}$) and direct calibration of the integrated sample (${\widehat{Y}}_{REF}$).

	Individual samples				Integrated sample
	Probability		Nonprobability		${\widehat{Y}}_{CPSA-{\alpha }_0-x}$		${\widehat{Y}}_{REF}$
Variable	Estimation	CI	Estimation	CI	Estimation	CI	Estimation	CI
V1	0.127	0.106–0.148	0.095	0.073–0.117	0.112	0.090–0.134	0.122	0.102–0.142
V2	0.306	0.277–0.336	0.291	0.256–0.325	0.299	0.265–0.333	0.285	0.258–0.313
V3	0.147	0.076–0.219	0.146	0.045–0.247	0.188	0.123–0.253	0.186	0.113–0.259
V4	0.716	0.625–0.807	0.688	0.555–0.820	0.650	0.567–0.734	0.660	0.484–0.837
V5	0.116	0.051–0.180	0.104	0.017–0.191	0.111	0.063–0.159	0.104	0.019–0.189
V6	0.021	0.000–0.050	0.042	0.000–0.099	0.012	0.000–0.031	0.037	0.000–0.088

TABLE 9.

Estimates of selected variables on indirect effects of COVID‐19 in Spain from integrated data using a new estimation method based on calibration and XGBoost PSA (${\widehat{Y}}_{CPSA-{\alpha }_0-x}$) and direct calibration of the integrated sample (${\widehat{Y}}_{REF}$).

	Individual samples				Integrated sample
	Probability		Nonprobability		${\widehat{Y}}_{CPSA-{\alpha }_0-x}$		${\widehat{Y}}_{REF}$
Variable	Estimation	CI	Estimation	CI	Estimation	CI	Estimation	CI
V7	0.067	0.051–0.083	0.076	0.056–0.096	0.064	0.046–0.082	0.075	0.058–0.092
V8	0.277	0.248–0.305	0.235	0.203–0.267	0.265	0.228–0.303	0.261	0.234–0.288
V9	0.425	0.393–0.456	0.305	0.269–0.340	0.398	0.365–0.431	0.403	0.374–0.431

FIGURE 1.

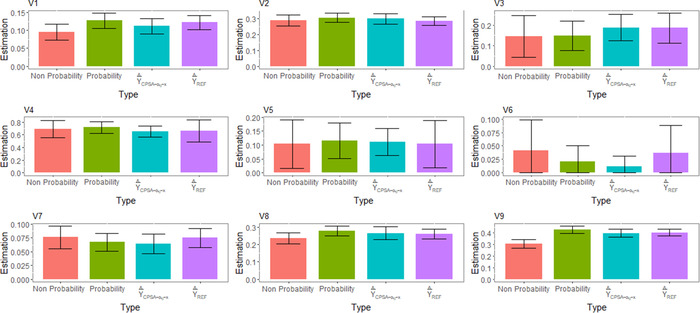
Estimation of the selected variables including confidence intervals

The main differences between both samples in the survey are the infection rate and the severity of the disease. The proportion of respondents that have suffered the infection is more than three points higher in the probability‐based sample. Also, hospitalization seems to be less likely for COVID‐19 patients in this sample, although the difference is not statistically significant. Both trends may be explained by the differences in the age structure of both samples, with the nonprobability sample being considerably older than the probability‐based (58.3 vs. 44.2). Those differences are consistent with what we already know regarding disease severity, with elders more at risk of developing serious illness, and compliance with COVID‐19 preventative measures (Wright & Fancourt, 2021).

Similarly, the age distribution of samples would explain the difference, statistically significant, on the assessment of the impact of the pandemic on household income. This evaluation is considerably worse in the probability‐based sample where the weight of employment incomes is most important. In all these cases, the estimator that seems to correct best the impact of the differences in age structure between both samples is the estimator that we develop in Section 3.

If we compare the estimates provided by only calibration, ${\widehat{Y}}_{REF}$ and PSA and calibration, ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$, we observe differences in different directions for each variable: in some variables the estimator ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$ provides lower estimates compared to ${\widehat{Y}}_{REF}$ and in other variables the opposite occurs. Regarding the width of the intervals, a uniform pattern is not observed either. However, in the simulation study it is observed that estimator ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$ does not have coverage problems, while estimator ${\widehat{Y}}_{REF}$ in many cases is not capable of eliminating the bias. For this reason, we consider prevalence estimates based on method ${\widehat{Y}}_{CPSA-{\alpha }_0-x}$ to be more reliable.

6. CONCLUSIONS

With more than 8 million official cases and almost 91,000 casualties as of mid‐January 2022, Spain is one of the EU countries that has been worst affected by COVID‐19. Spanish GDP declined by 10.8% in 2020 and working hours for the equivalent of 2 million of jobs were lost according to the International Labour Organization (ILO) data. Using a design that combines probability and nonprobability‐based sampling methods and proper estimation techniques, the second edition of the ESPACOV Survey fully reflects the relevance of this impact. According to main survey estimators, 11.2% of the Spanish population had COVID‐19 and 29.9% had witnessed the infection of close relatives until January 2021, 10 months after the World Health Organization (WHO) declared the novel coronavirus (COVID‐19) outbreak a global pandemic. Although the majority of those infections were asymptomatic or endured with mild symptoms (65%), the pandemic was taking a huge toll on the economy of families (39.8% declared that household income had decreased) and on mental well‐being, with more than one in four (26.5%) assessing their mood as very bad or bad.

The estimates suggested in literature that could be applied to the data from this survey were based on the simple integration of both samples. In this paper, we address the problem of how to improve these estimates. We introduce four methods for calculating weights that blend probability and convenience samples; these methods combine calibration and PSA using machine‐learning techniques for those situations where the variables of interest are observed in both samples.

Before their application to the survey, we evaluate the behavior of the proposed estimators against other techniques for integrating probability and nonprobability samples used in the literature. As in many simulation studies, the number of simulation conditions we have generated is limited. However, we considered a simulation study with several sample sizes to cover different Missing At Random situations and we compared the performance of standard logistic regression model with a machine‐learning algorithm (XGBoost) when estimating the propensity score. Our simulation study shows that the proposed estimator based on calibration and PSA techniques is very efficient at reducing self‐selection bias and RMSRE with this kind of data. The intervals based on these proposed estimators seem to perform well in terms of length and coverage, for different model setups, especially for large sizes of the nonprobabilistic sample.

In our simulations, the best performing techniques for the estimation of the propensity scores were those based on boosting, which guaranteed considerably lower bias and RMSRE in comparison to a similar estimator based on logistic regression and other techniques considered in the study.

Before applying ML techniques, we have considered hyperparameter tuning. The simulation proved that, in the context of integrating probability and nonprobability data, tuning is data‐dependent and therefore we strongly suggest that researchers consider tuning parameters before using ML techniques in this context.

Based on the simulation results, we consider the use of the proposed estimator ${\widehat{Y}}_{CAL-PSA-{\alpha }_0}$ (which is the estimator that weights the samples by the MSE) as an alternative to the usual estimators for the estimation of the effects of the COVID‐19 pandemic in Spain. The application of this method to ESPACOV II Survey proves successful incorporating response patterns observed in the nonprobability sample into the final integrated data set.

This study has some limitations. In our opinion, the main limitation to consider lies in the lack of response of the probabilistic sample. This nonresponse may affect the representativity of the sample. The possible bias implied should be evaluated and corrected in a more advanced way, previously to the application of the proposed methods in order to ensure their validity.

For the future, we want to compare the proposed methodology with other techniques that are appearing to combine probability and nonprobability samples as Kim and Tam (2021) or Nandram et al. (2020). Extensions to small domain estimation (Rao & Molina, 2015) and variance estimation under nonparametric PSA will also be future research topics.

Finally, we would like also to investigate the impact of weight trimming. In general, methods that lead to greater bias reductions also tend to produce larger weight variations. Kernel weighting (Wang et al, 2020) distribute survey weights fractionally to nonprobability sample units and can be an alternative to PSA to control variances.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest that could be perceived as prejudicing the impartiality of the research reported.

OPEN RESEARCH BADGES

This article has earned an Open Data badge for making publicly available the digitally‐shareable data necessary to reproduce the reported results. The data is available in the Supporting Information section.

This article has earned an open data badge “Reproducible Research” for making publicly available the code necessary to reproduce the reported results. The results reported in this article could fully be reproduced.

Supporting information

Supporting Information

Rueda, M. M. , Pasadas‐del‐Amo, S. , Rodríguez, B. C. , Castro‐Martín, L. , & Ferri‐García, R. (2022). Enhancing estimation methods for integrating probability and nonprobability survey samples with machine‐learning techniques. An application to a Survey on the impact of the COVID‐19 pandemic in Spain. Biometrical Journal, 00, 1–19. 10.1002/bimj.202200035

DATA AVAILABILITY STATEMENT

The dataset was made available online (Serrano‐del‐Rosal et al., 2020). https://digital.csic.es/handle/10261/211271.